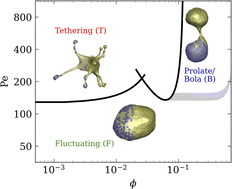
Active vesicles, constructed through the confinement of self-propelled particles (SPPs) inside a lipid membrane shell, exhibit a large variety of non-equilibrium shapes, ranging from the formation of local tethers and dendritic conformations, to prolate and bola-like structures. To better understand the behavior of active vesicles, we perform simulations of membranes modelled as dynamically triangulated surfaces enclosing active Brownian particles. A systematic analysis of membrane deformations and SPP clustering, as a function of SPP activity and volume fraction inside the vesicle is carried out. Distributions of membrane local curvature, and the clustering and mobility of SPPs obtained from simulations of active vesicles are analysed. There exists a feedback mechanism between the enhancement of membrane curvature, the formation of clusters of active particles, and local or global changes in vesicle shape. The emergence of active tension due to the activity of SPPs can well be captured by the Young–Laplace equation. Furthermore, a simple numerical method for tether detection is presented and used to determine correlations between the number of tethers, their length, and local curvature. We also provide several geometrical arguments to explain different tether characteristics for various conditions. These results contribute to the future development of steerable active vesicles or soft micro-robots whose behaviour can be controlled and used for potential applications.