Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Methylene glycol-sulfite pH-clocks for the time-programming of soft materials: advantages, limitations, and yet unexplored opportunities
Guido
Panzarasa

Institute for Building Materials, Department of Civil, Environmental and Geomatic Engineering, ETH Zürich, Laura-Hezner-Weg 7, 8093 Zürich, Switzerland. E-mail: guidop@ethz.ch
First published on 12th July 2024
Abstract
Coupling nonlinear reaction networks with soft matter building blocks holds great potential for the design of life-mimicking, time-programmable dissipative self-assembly systems. In this regard, clock reactions are especially useful triggers since they allow to autonomously generate in situ chemical stimuli such as pH changes. The methylene glycol-sulfite (MGS) is a well-known acid-to-base pH-clock reaction which is able to produce sharp and intense pH jumps (up to 5 pH units) after a reliable, yet relatively short (tens of seconds rather than minutes), induction time. Here, after an introductory discussion on the main chemical aspects of MGS and MGS-based systems, their applications for the time-programming of soft matter will be showcased – from micelles, vesicles, and droplets to supramolecular aggregates, polymers and gels. Hopefully, this will help attracting more attention and foster research on the broader field of materials programming with chemical reaction networks.
Introduction
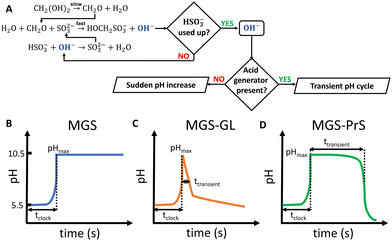
Living organisms depend for their growth, functioning and overall existence on finely-tuned dissipative self-assembly processes which are time-controlled by networks of enzymes.1 Mimicking such design for the fabrication of artificial active materials is a challenging task, and the research on this subject can greatly benefit from systems that allow to program chemical changes without relying on external control.2–7 Despite decades of research, which can be traced back to the discovery of the Belousov–Zhabotinsky oscillating reaction (BZ) and its successive applications to materials science, the development of such chemical control systems is still in its infancy. Although enzymatic systems still have the spotlight,8 small-molecule networks such as clock reactions show great untapped potential.A characteristic feature of clock reactions is the abrupt accumulation of product(s) after an induction time following the mixing of reactants (tclock).9 As such, they are useful for programming the autonomous in situ generation of chemical stimuli, such as pH and/or redox changes, which in turn can trigger the self-(dis)assembly of the building blocks of choice.
Recently, the applications of iodine-based clock reactions (“iodine clocks”) to materials science have been reviewed.10 Here, the focus will be on the time-programming of soft materials using the methylene glycol-sulfite (MGS, “formaldehyde clock”)† pH-clock, as well as systems derived by the addition of slow acid generators (such as δ-gluconolactone GL, 1,3-propanesultone PrS). One of the most distinctive traits of the MGS system is its unicity, as so far it is the only veritable example of a non-enzymatic acid-to-base pH-clock.
The methylene glycol-sulfite (MGS) pH-clock reaction and derived systems
Methylene glycol-sulfite (MGS)
The reaction between formaldehyde CH2O and sulfite SO32− is fast and produces the formaldehyde-sulfite adduct hydroxymethanesulfonate (HMS) CH3CH2SO3− together with base OH− (eqn (1)):| CH2O + SO32− → CH3CH2SO3− + OH− | (1) |
The mechanism of the MGS reaction is represented in Fig. 1(A), and its characteristic pH–time profile in Fig. 1(B). The induction period tclock is relatively short, up to tens of seconds, and can be tuned by changing the initial bisulfite/sulfite concentration as well as that of MG. In general tclock increases with decreasing initial concentration of sulfite and of MG, but the longer the induction time the less sharp is the pH jump. The pH increase produced is between 4 and 5 units, and remains relatively stable except for a small gradual decrease in the long term.19 The amount of base OH− generated is roughly equal to the initial concentration of sulfite. From a practical standpoint, the MGS is a relatively robust system. Commercial methanol-stabilized formaldehyde aqueous solutions (“formalin”) can be routinely used, and results are highly reproducible provided that the actual concentration of formaldehyde is known (as it can be altered e.g. by spontaneous polymerization, especially in concentrated solutions) and that the aerial oxidation of bisulfite stock solutions is prevented. The latter can be achieved by bubbling an inert gas, by the addition of metal-chelating agents such as EDTA,15 or by producing bisulfite in situ by neutralizing sulfite with sulphuric acid.23,24 The toxicity of formaldehyde may be of concern, and a variation that uses glyoxal instead has been proposed.25 However, so far this latter system has not been investigated further.
The MGS reaction behaves as a one-way acid-to-base kinetic switch. A pH-clock that would allow the system to spend a certain amount of time (ttransient) in the basic state before going back to acidic would be of great practical utility, especially if such behavior could be “coded” into the initial systems conditions so that no external intervention would be needed for it to happen. Such systems have indeed be realized (Fig. 1(C) and (D)), and are discussed in the following.
Methylene glycol-sulfite–gluconolactone (MGS–GL)
Introducing a suitable acid-generating feedback mechanism into the MGS reaction should allow to generate an acid–base–acid cycle, and even oscillations. This concept was explored by Kovacs et al., first theoretically20 in 2006 and then concretely one year later21,22 by coupling the MGS reaction with the hydrolysis of δ-gluconolactone (GL) (eqn (2)).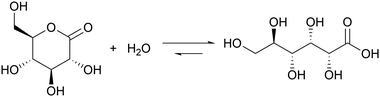 | (2) |
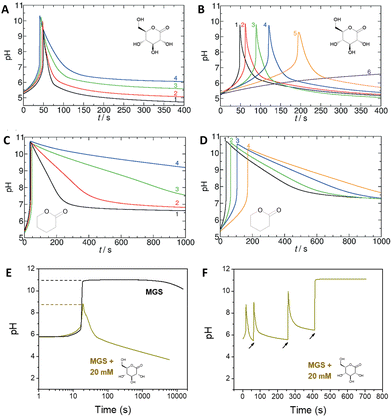 | ||
| Fig. 2 (A) and (B) Effect of the initial concentration of (A) GL, (B) MG on the pH–time evolution profile, as well as on tclock and ttransient, for the MGS–GL system. The initial concentration of sulfite and bisulfite is respectively 5 mM and 50 mM. In (A) the initial concentration of MG is 200 mM, while the initial concentration of GL varies in the order 20/10/5/4 mM (curves 1–4). In (B) the initial concentration of GL is 10 mM, while the initial concentration of MG varies in the order 200/175/150/125/112.5/100 mM (curves 1–6). (C) and (D) Same as (A) and (B) but for the MGS–VL system. In (D) the initial MG concentrations are 200/150/125/112.5 mM (curves 1–4). The molecular structures of GL and VL are shown as insets. (E) Comparison of the pH–time profile for the MGS clock (initial concentrations: sulfite 5 mM, bisulfite 50 mM, MG 200 mM) without and with the addition of 20 mM GL. In (F), in the attempt to make semi-batch pH cycles, the pH is brought back to alkaline by the external addition (black arrows) of a 2 M sodium hydroxide solution. The first two additions are of 30 μL and the third one of 40 μL, corresponding to a total of 20 mM NaOH. Already after the first cycle the time required to reach the same final pH increases dramatically, while after the third cycle the GL is completely hydrolyzed (pH plateau) preventing the generation of further cycles. The images in (A)–(D) are reproduced from ref. 31, those in (E) and (F) are reproduced from ref. 32. | ||
GL could be substituted with other lactones, for example δ-valerolactone (VL),31 depending on the desired outcome. Indeed, not only the kinetic behavior but also the final pH achievable depends on the strength of the acid produced by hydrolysis: for example, gluconic acid from GL is a stronger acid (pKa = 3.86) than 5-hydroxypentanoic acid (pKa = 4.59) from VL, which also affects the pH–time profile evolution (Fig. 2(C) and (D)).
One of the limitations of the MGS–GL system is the very short, almost negligible lifetime of the transient alkaline state (ttransient) (Fig. 2(E)). Moreover, GL is a solid that needs to be dissolved beforehand (solubility in water 0.59 g mL−1) and the age of the stock solution can affect the behavior of the system, especially the tclock. This also results in a limited capability to generate semi-autonomous pH cycles in batch conditions e.g. by repeated external additions of base (Fig. 2(F)). As will be shown later, this issue can be solved by using 1,3-propanesultone (PrS) instead.
Methylene glycol-sulfite–propanesultone (MGS–PrS)
Sultones are the cyclic esters of sulfonic acids. Compared to lactones, they tend to have slower hydrolysis rates and generate acids of higher strength. 1,3-Propanesultone (PrS) has good solubility in water (0.1 g mL−1) and hydrolyzes into the strong (pKa = 1.53) 3-hydroxypropanesulfonic acid (eqn (3)):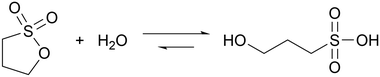 | (3) |
The coupling of MGS with PrS, first reported32 in 2020 by Panzarasa et al., allows to generate autonomous acid–base–acid cycles with controllable transient state lifetimes (ttransient) (Fig. 1(D) and 3(A), (B)). The increased hydrolytic stability of PrS has several important consequences: first, it allows the introduction of significantly higher initial PrS amounts (up to 200 mM) in the MGS system without affecting its tclock. Moreover, it allows to generate several semi-autonomous base–acid cycles, with ttransient values of tens of minutes, by “resetting” the pH through the external addition of base (Fig. 3(C)–(F)). Last but not least, with PrS it is possible to reach much lower final pH values (pHfinal ∼ 3–2.5) compared to GL (pHfinal ∼ 5–4.5). It goes without saying that, by performing the MGS–PrS reaction in a CSTR, it could be possible to obtain a new type of pH-oscillator.
 | ||
| Fig. 3 (A) and (B) Effect of the initial concentration of (A) PrS, (B) MG on the pH–time evolution profile, as well as on tclock and ttransient, for the MGS–PrS system. The initial concentration of sulfite and bisulfite is respectively 5 mM and 50 mM. In (A) the initial concentration of MG is 200 mM, while the initial concentration of PrS varies from 10 mM to 100 mM. In (B) the initial concentration of PrS is 100 mM while that of MG varies from 75 mM to 500 mM. (C)–(F) Repeated semi-batch pH cycles obtained with the MGS–PrS system through the successive addition of few microliters of NaOH 2 M (black arrows). Cycles with periods of 7.5 ± 0.5 min, 21 ± 3 min, 49 ± 1 min and 165 ± 42 min could be obtained respectively with 200, 100, 50 and 20 mM initial concentrations of PrS. For initial PrS concentrations ≤20 mM, the onset of PrS hydrolysis becomes visible as a kink in correspondence of pH = 7. The images are reproduced from ref. 32. | ||
However, the non-negligible toxicity and alkylating properties (especially in alkaline conditions, as will be mentioned later) of PrS can limit its use. 1,4-Butanesultone (BuS) could be used instead, but its hydrolysis is significantly slower (kH2O = 6 × 10−7 s−1).33 The possibility of using substituted sultones has also not been explored yet.
Supramolecular and colloidal self-assembly
Vesicle-to-micelle conversion and nanoparticle (dis)assembly
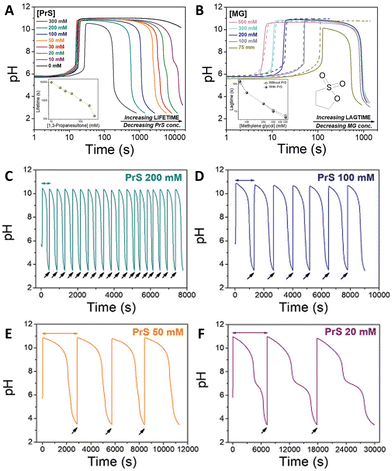
The MGS–GL system has been used for the time-programming of vesicle–micelle transformation by controlling the self-assembly and disassembly of oleic acid molecules. In 2010, Grzybowski et al.34 obtained an oscillating vesicle-to-micelle conversion with a period of ∼2 min by reacting the MGS–GL–oleic acid system in CSTR conditions. The apparent pKa ∼ 8.3 of oleic acid (OA) lies well within the range of pH oscillations (from ∼7.0 to ∼10) of the MGS–GL system. When the oscillator was in the low-pH state (pH ∼ 7.0–8.3), the reaction mixture contains significant fractions of both protonated and deprotonated oleic acid molecules. Under such conditions, the OA form unilamellar vesicles (spherical bilayers), burying the hydrophobic chains and presenting inner and outer hydrophilic surfaces with interspersed protonated and deprotonated carboxylic groups. For pH ∼ 7 these vesicles had hydrodynamic radii of 100 ± 25 nm, enough to make the reaction mixture hazy due to the Tyndall effect, and a zeta potential of ∼−66 mV. However, in correspondence of the jump of the oscillator to the high-pH state, the mixture turns transparent. At high pHs, the OA molecules become deprotonated and form spherical unilamellar micelles with an average diameter of ∼5 nm (6.4 ± 0.4 nm in correspondence of the peak pH value) and exposed –COO− headgroups, as showed by a lower zeta potential of ∼−73 mV. When the oscillator returns back to the low-pH state thanks to gluconolactone hydrolysis, the micelles revert back to vesicles (the mixture becomes again opaque), and the cycle continues as long as the pH oscillations are sustained (Fig. 4(A) and (B)). The main driving force for the vesicle–micelle transformation is the changing of the packing parameter influenced by the electrostatic interaction (repulsion) between the carboxylate head groups. The vesicles can be considered as a mixture of ionic and non-ionic surfactant molecules, and in this state the head groups can be densely packed allowing the formation of a supramolecular structure with less curvature – the spherical bilayers. When the pH changes to alkaline, more and more carboxylic groups become deprotonated (charged), thus the effective surface area of the head groups increases because of the electrostatic repulsion. The bilayer structure cannot be maintained, and the deprotonated fatty acid molecules develop a thermodynamically more stable, high-curvature supramolecular assembly – the spherical micelles.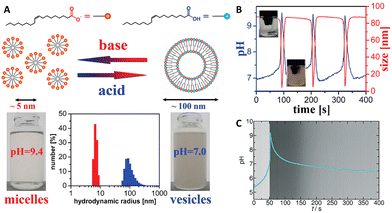 | ||
| Fig. 4 (A) Schematic representation of deprotonated (orange) and protonated (blue) oleic acid molecules, along with their self-assembly structures, respectively micelles (transparent solution, basic pH) and vesicles (turbid suspension, acidic pH). The difference in size is confirmed by hydrodynamic radius measurements. (B) Cyclic, oscillatory vesicle-to-micelle transition obtained using a MGS–GL–oleic acid system in a CSTR, visualized through pH and hydrodynamic size measurements. The reactor was continuously fed by a constant (1.52 mL min−1 in each channel) flow of two solutions, one containing 10 mM sulfite, 100 mM bisulfite and 1% m/m oleic acid, the other containing 200 mM formaldehyde and 13.4 mM GL. The reaction volume was kept fixed (10 mL) by removing reaction products at a constant rate (3.04 mL min−1). Adapted with permission from ref. 34. Copyright 2010 American Chemical Society. (C) Evolution over time of pH (blue line) and solution turbidity (background) in a batch MGS–GL system containing 1.25 mM oleic acid (initial concentrations: 5 mM sulfite, 50 mM bisulfite, 200 mM MG, 10 mM GL). Image reproduced from ref. 31. | ||
Noteworthy, the same type of MGS–GL pH oscillator was applied also to control the aggregation state in time of pH-responsive plasmonic metal nanoparticles.35
In 2017, Lagzi et al.31 re-investigated the self-(dis)assembly of oleic acid (and of pH-responsive gold nanoparticles) with the MGS–GL/VL system in batch conditions (Fig. 4(C)). They measured the evolution of turbidity and absorbance as a function of time in parallel with that of pH, to correlate their variations with the different OA self-assembly processes. Their results showed that if the pH jump to alkaline is fast, the vesicle-to-micelle transformation happens simultaneously with the pH change. However, they noticed that when the pH returned back to the neutral/slightly acidic range, the reconfiguration of the building blocks was somewhat delayed. While the transformation of a large supramolecular structure (a vesicle) to a smaller one (a micelle) is a fast process, the rearrangement of a compound structure involving a bigger number of building blocks takes more time. This was further confirmed by the observation of bistability and hysteresis during the process of redispersion and reaggregation of carboxylate-modified gold nanoparticles (5.6 nm average diameter) in the batch MGS–GL system.
These kinds of experiments help to point out two crucial parameters for clock reaction-controlled processes, namely: (i) the response time of the clock-controlled subsystem, and (ii) the chemical compatibility between the clock system and the clock-controlled subsystem. Point (i) means that the building blocks should be able to perform the desired rearrangement within the time domain of the clock system, and the more asymmetric the stimulus profile (e.g. the pH change) is, or simply if ttransient is too short, the more care must be taken to choose the order of the (dis)assembly processes for ensuring a more efficient operation. Point (ii) highlights that, to avoid interferences, the subsystem is supposed to interact only with the product(s) of the clock system, e.g. H+ or OH− in the case of a pH-clock. However, especially in the case of a cycle (e.g. acid–base–acid), this could become a problem if the consumption of the clock product(s) by the subsystem would affect the negative feedback mechanism. For example, in the work of Lagzi et al.31 the addition of increasing amounts of carboxylic acid, irrespectively as oleic acid or carboxylate-functionalized gold nanoparticles, to the MGS–GL/VL system was found to result in a systematic decrease of the pH maxima and also in a decreased sharpness of the peak profile.
Reversible supramolecular (dis)assembly of pH-responsive perylene diimides
As discussed before, the successful coupling of a pH-clock control system with a self-assembly subsystem requires their mutual optimization to ensure chemical and kinetic compatibility. The use of the MGS–PrS system to control the self-(dis)assembly of a pH-responsive perylene diimide offers a comprehensive example of such factors. | (4) |
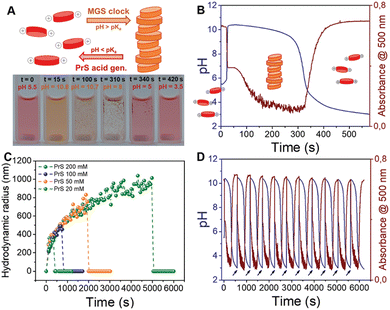 | ||
| Fig. 5 Autonomous self-assembly/disassembly cycle of a pH-responsive perylene diimide controlled by the MGS–PrS system (initial concentrations: sulfite 5 mM, bisulfite 50 mM, MG 200 mM, PrS 100 mM). (A) Schematic representation and experimental photographic sequence. (B) and (C) The transient formation of aggregates in correspondence of the pH increase to basic (MGS clock) and their subsequent dissolution when the pH becomes acidic (PrS hydrolysis) can be visualized (B) by measuring pH while acquiring absorption spectra over time, or (C) by measuring the evolution of hydrodynamic radius by dynamic light scattering (DLS) over time. As shown in (D), cycles of self-(dis)assembly can be repeated with remarkable stability in semi-batch conditions by the external addition of a base (NaOH aqueous solution, black arrows). The images are reproduced from ref. 32. | ||
These features make pH-responsive symmetric perylene diimides highly efficient supramolecular building blocks,27 allowing to reduce their concentration down to 25 μM without losing in self-assembly efficiency, as testified also by the repeated cycles of assembly and disassembly that can be obtained by successive additions of base (Fig. 5(D)).
This latter point makes it noteworthy to highlight the reasons that informed the choice of the pH-responsive moiety. During initial experiments, it was observed (unpublished results) that a perylene diimide featuring N,N′-dimethylamine groups would not re-assemble after the first acid–base–acid cycle. This behavior was most probably due to the alkylation of the tertiary amine by the PrS, facilitated by the basic environment, resulting the formation of a pH-insensitive sulfobetaine. Substituting this group with the more bulky N,N′-diisopropylamino one eliminated this inconvenient. Nevertheless, it is possible to envisage that the same principle could be used e.g. to achieve an autonomous dynamic self-sorting of different building blocks.
Polymerization and polymer self-assembly
Time-lapse thiol-acrylate polymerization
Time-lapse polymerization exhibits a programmable induction time between the mixing of the reagents and the onset of polymerization, a behavior often manifested by free-radical polymerization systems in presence of a limited amount of inhibitor. In 2010, Pojman et al. showed that the MGS clock can be used to program the onset time of a base-catalyzed thiol-acrylate polymerization. The monomers, trimethylolpropane tris(3-mercaptopropionate) and trimethylolpropane triacrylate in equimolar amounts, are dispersed in the aqueous MGS clock. The resulting two-phase system is initially transparent and it becomes opaque owing to polymer formation, allowing to monitor the progress of the reaction by measuring turbidity over time, in addition to terminating it at the desired times by quenching with acid and collecting the polymer formed. The polymerization was found to proceed quickly, the mass conversion reaching 83% already 3 min after the increase in pH. The authors also suggested that the polymerization rate could be a function of the monomer droplet size. Observed with a scanning electron microscope, the polymer product was found to be in the form of highly polydisperse hollow spheres (with an average diameter of 360 μm), possibly because the polymerization could happen only at the interface of the droplets.The clock time tclock was changed (from 52 s to 470 s) by keeping constant the initial bisulfite/sulfite ratio (as 50/5 mM) while increasing the initial concentration of formaldehyde (from 50 mM to 100 mM). The observation that the time-lapse period for the polymerization (indicated by turbidity) was always longer than tclock (measured with a pH-meter), supported the hypothesis that the polymerization was in fact triggered by the pH change produced by the MGS clock.
According to the authors, these findings could be of inspiration for the design of time-lapse curable adhesives and coatings.
Autonomous viscosity changes in poly(acrylic acid) solutions
In 2017, Escala et al. reported that coupling MGS and MGS–GL clocks in batch conditions with poly(acrylic acid) (PAA) results in large temporally-controlled viscosity changes.36 Poly(acrylic acid) is a pH-responsive polyelectrolyte: in its deprotonated state, the intra- and intermolecular electrostatic repulsion keeps the polymer chains in an extended, separated state (low viscosity), while when protonated hydrogen bond-mediated interactions prevail leading to a more collapsed, entangled structure (high viscosity). Different chain lengths (4000 kDa and 450 kDa) did not result in a remarkably different behavior. Because of the intrinsic pH-buffering effect of PAA, bisulfite was omitted from the reaction. In the MGS–PAA system, increasing the polymer concentration led to a decreased final pH and longer tclock values, especially for PAA concentrations exceeding 0.35 wt%. The best balance, ensuring a satisfactory increase of both pH and viscosity, was obtained using an initial PAA concentration of 0.4386 wt (Fig. 6(A) and (B)). The addition of GL to the system (MGS–GL–PAA) resulted in a simultaneous transient pH and viscosity peak rather than a stable increase. The authors suggested that, by operating the MGS–GL–PAA in a CSTR, it should be possible to observe temporal oscillations in viscosity.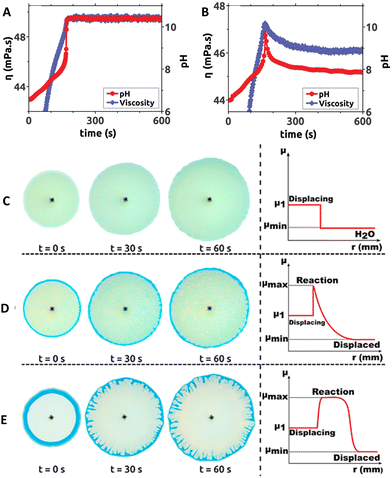 | ||
| Fig. 6 Temporal evolution of pH and viscosity in (A) MGS and (B) MGS–GL systems containing poly(acrylic acid) PAA. Initial concentrations: sulfite 68.4 mM, formaldehyde 65.3 mM, PAA 0.4386 wt%. In (B) the initial concentration of GL is 7 mM. For the viscosity measurement, the shear rate and temperature were fixed respectively at 500 s−1 and 23 °C, respectively. Image reproduced with permission from ref. 36 (C)–(E) Solution displacement experiments performed in a Hele–Shaw cell. The initial formaldehyde concentration in the displaced solution is (C) 0 mM, (D) 49.6 mM, (E) 750 mM. In (E) the appearance of viscous fingering instability is clearly visible. The other initial concentrations are, in all cases, sulfite 68.4 mM, PAA 0.4386 wt%, bromothymol blue (yellow for pH < 6, green for pH ∼ 6–7, blue for pH > 7) 0.021 wt%. The injection speed of the displacing solution was 7 mL min−1. In the schematic profiles on the right, μmin, μmax and μ1 indicate respectively the minimum, maximum, and displacing solution viscosity values. Adapted with permission from ref. 37. Copyright 2019 American Chemical Society. | ||
In 2019, a follow-up work from Escala et al.37 reported on the possibility to use the MGS clock to trigger and control viscous fingering by modifying the hydrodynamics of a reacting system. A Hele-Shaw cell, made with two glass plates separated by a thin gap, was filled with a formaldehyde solution. Then, a fixed volume of a more viscous sulfite and PAA solution was injected in the cell, which did not result in hydrodynamical perturbations. However, as soon as the MGS clock became activated, the local pH change generated a non-monotonic viscosity profile with a maximum. As a result, subsequent injections of the sulfite–PAA solution could result in the generation of a viscous fingering instability, depending on the initial concentrations of the reactants (Fig. 6(C)–(E)).
Controlled self-assembly of chitosan particles
Chitosan is a glucosamine biopolymer and a cationic polyelectrolyte (pKa ∼ 6.5) whose solubility in water is highly pH-dependent (Fig. 7(A)). In 2018, Panzarasa et al.38 explored the use of the MGS clock to control the formation of chitosan particles. Chitosan is soluble in the initial conditions of the MGS clock, but precipitates due to the formation of base in correspondence of tclock (Fig. 7(B) and (C)). The direct addition of base to a chitosan solution usually results in the uncontrolled formation of large heterogeneous aggregates. By contrast, with the MGS clock the result is a stable suspension of chitosan particles, thanks to the homogeneous in situ generation of base. It was found that, by adjusting the tclock through the initial formaldehyde concentration, particles with a tunable average diameter (ca. 200–600 nm) could be obtained (Fig. 7(D)). Zeta potential measurements showed that the particles were positively charged, with values (+14 ± 0.6 mV) consistent for chitosan particles prepared by more conventional routes and essentially independent from tclock (Fig. 7(E)).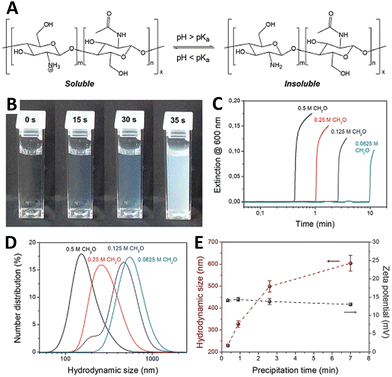 | ||
| Fig. 7 (A) Molecular structure and pH-responsive behavior of chitosan. (B) Sequence of pictures and (C) turbidity evolution over time showing the sudden formation of a stable suspension in a MGS system (initial conditions: 4.5 mM sulfite, 45 mM bisulfite, 500 mM formaldehyde) containing 0.1% m/v of chitosan (degree of deacetylation 85%, nominal viscosity 200 mPa s). The formation of chitosan particles, weakly stabilized by positive charges, is confirmed by (D) DLS and (E) zeta potential measurements. Images reproduced with permission from ref. 38. | ||
As judged from infrared spectroscopy, the chemical structure of chitosan was not significantly changed during the process. Most importantly, despite formaldehyde being a well-known crosslinking agent for chitosan, solubility tests showed that no or negligible chain crosslinking took place. This suggests a sufficient compatibility of the MGS clock with other (bio)polymers, which could further widen the potential fields of application.
Time-programmable polyelectrolyte assembly
The interaction of polyelectrolytes with different charge signs (polycations and polyanions) can result in a variety of complexes with different degrees of order, from random aggregates to coacervates to core–shell structures. In this framework, the introduction of a pH-clock can result in unforeseen remarkable consequences for the self-assembly system.Inspired by the compatibility observed between the MGS clock and polyelectrolytes such as poly(acrylic acid) and chitosan, in 2020 Voets et al.39 introduced poly(allylamine hydrochloride) (PAH, pKa ∼ 8.8) in a MGS system as a first step towards time-programmable polyelectrolyte coassembly. Unexpectedly, PAH was found to interact with the negatively charged sulfite ions, forming micron-sized coacervate-like complexes. This led to two remarkable effects: first, the complex formation did not have a dramatic influence of tclock but rather on the final pH state, and second, the aggregates were found to dissolve upon the completion of the clock reaction itself. However, under specific conditions, after tclock a subsequent reaction between the polymer's deprotonated amine groups and formaldehyde could take place, locking-in the preformed supramolecular structure and giving rise to covalently crosslinked colloidal particles (Fig. 8).
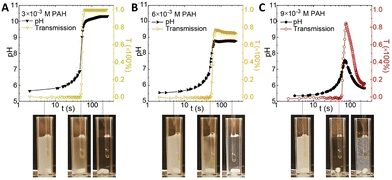 | ||
| Fig. 8 Evolution of pH and transmission over time in a batch MGS clock (initial concentrations: 5 mM sulfite, 50 mM bisulfite, 100 mM formaldehyde) in presence of different initial concentrations (respectively (A) 3 mM, (B) 6 mM and (C) 9 mM) of poly(allylamine hydrochloride) PAH. As shown by the associated experimental pictures, for all initial PAH concentrations the reaction mixture is initially turbid (due to PAH–sulfite complex formation), then becomes clear in correspondence of tclock (sulfite depletion), and eventually, for sufficiently high PAH concentrations, becomes turbid again due to the formation of crosslinked particles. Image reproduced with permission from ref. 39. | ||
The possibilities offered by such behavior were further explored in a successive work,40 in which PAH and poly(sodium methacrylate) were first mixed with the sulfite–bisulfite buffer, forming nanoscopic complex coacervates, then formaldehyde was added to trigger the pH-clock reaction. This latter was found to affect the polyelectrolyte assembly in two subsequent ways: first the sudden pH increase affected the charge density of the polyelectrolytes, changing the ratio of anionic and cationic species, then the crosslinking reaction between the polyamine and formaldehyde took place. As a result, core–shell polymeric nanoparticles were formed. By contrast, without the pH-clock reaction aggregation and phase separation occurred in a timeframe variable from minutes to days.
Chemomechanical effects
Self-division and movement of pH-responsive oil droplets
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (v/v) mixture of 2-hexyldecanoic acid (pKa ∼ 8.3) and paraffin, or of sunflower oil) was deposited on the surface of a water layer contained in a Petri dish. Then, an aqueous solution containing the premixed MGS pH-clock (ca. 8 μL) was injected into the oil droplet, where it formed a stable compartment covered with a thin organic layer from below and above, lasting for about 20 s (tclock). The autonomous pH change generated by the MGS clock inside the compartment caused the deprotonation of the fatty acid molecules leading to a negative interfacial tension at the water–oil interface inside the droplet. This, in turn, induced the expansion of the droplet into a torus, followed by its division into daughter droplets governed by the Plateau–Rayleigh instability (Fig. 9(A)). That this process of self-division was actually driven by a pH-induced surface tension change was demonstrated by injecting a drop of basic (pH = 10) solution into the organic droplet, which caused division to happen immediately afterwards.
2 (v/v) mixture of 2-hexyldecanoic acid (pKa ∼ 8.3) and paraffin, or of sunflower oil) was deposited on the surface of a water layer contained in a Petri dish. Then, an aqueous solution containing the premixed MGS pH-clock (ca. 8 μL) was injected into the oil droplet, where it formed a stable compartment covered with a thin organic layer from below and above, lasting for about 20 s (tclock). The autonomous pH change generated by the MGS clock inside the compartment caused the deprotonation of the fatty acid molecules leading to a negative interfacial tension at the water–oil interface inside the droplet. This, in turn, induced the expansion of the droplet into a torus, followed by its division into daughter droplets governed by the Plateau–Rayleigh instability (Fig. 9(A)). That this process of self-division was actually driven by a pH-induced surface tension change was demonstrated by injecting a drop of basic (pH = 10) solution into the organic droplet, which caused division to happen immediately afterwards.
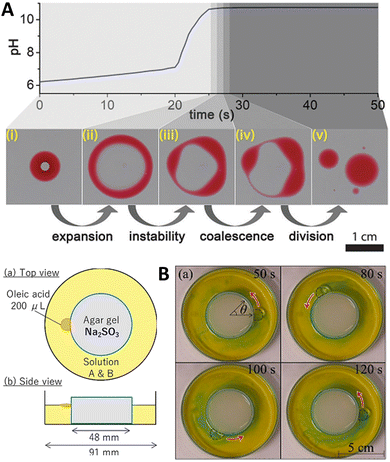 | ||
| Fig. 9 (A) Self-division of a compartmentalized oil droplet (2-hexyldecanoic acid in paraffin, red) containing a MGS clock mixture (colorless; initial concentrations: 10 mM sulfite, 100 mM bisulfite, 200 mM formaldehyde), floating on a water surface. When the pH inside the compartment becomes basic, the deprotonation of the fatty acid molecules results in a surface tension change leading to the destabilization and expansion of the droplet into a ring-like structure. The latter undergoes Plateau–Rayleigh instability and divides into smaller droplets. Image reproduced from ref. 41. (B) Schematic representation and experimental pictures of the setup used by Shioi and coworkers to obtain the autonomous movement of an oleic acid droplet around a sulfite-containing agarose gel, sustained by the MGS–GL system (“solution A & B”) with initial concentrations of 1.25 mM sulfite, 208 mM bisulfite, 500 mM formaldehyde, 3.40 mM GL, and a small amount of bromothymol blue for visualizing local pH changes (blue pH > 7.6, yellow pH < 6.0). Images reproduced from ref. 42. | ||
A statistical analysis of repeated experiments (n = 120) revealed that, under the investigated experimental conditions and associated geometrical constrains, the most probable (P = 50%) outcome was the generation of two equally-sized daughter droplets (due to geometrical considerations). Only in a minority (ca. 10%) of cases no droplet division into at least two parts could be observed.
Enabling small artificial compartments (such as droplets) with the ability to self-divide is a challenging task of great relevance for the engineering of minimal cell prototypes, and even though this specific oil droplet self-division process cannot repeat itself autonomously, it demonstrates the feasibility of using an autonomous feedback system (such as a pH-clock) for such purpose.
If the MGS–GL solution in the Petri dish was replaced with pure water, the droplet would still move (thanks to the alkalinity of sulfite leaching from the gel) but with a noticeably different behavior, especially in terms of motion duration. Without formaldehyde, caeteris paribus, the droplets could not maintain contact with the gel, suggesting that the pH increase produced by the MGS system is a necessary condition for the droplet's active motion. However, if GL was added to the system in absence of formaldehyde, the droplet remained motionless because GL suppressed the increase in pH from the sulfite leaching from the gel.
Coupling a pH pulse with the droplet self-motion enables a pH difference between the front and rear of the droplet to be maintained to a larger extent. Upon the appearance of such twin-roll convection, the droplet actively keeps contact with the gel, ensuring a longer sustained motion.
Chemomechanical actuation of pH-responsive gels
Chemomechanical conversion processes are commonplace in living systems, from amoeboidal motion to muscle contraction. Achieving chemomechanical feedback in synthetic systems is challenging, but highly relevant for fields such as soft robotics and microfluidics.In 2017, Lagzi and coworkers31 coupled the MGS–GL/VL system with pH-responsive poly(N-isopropylamide) (PNIPAM)-based macroporous hydrogel fibers (ca. 0.75–1 mm in diameter and 14 mm in length), resulting in single-cycle chemomechanical actuation due to the reversible collapse and rehydration of the polymer network (Fig. 10(A)). The pH-responsiveness was provided by tertiary amine groups (pKa ∼ 8.7) covalently bound to the polymer chains. When the amine groups are charged (initial acidic conditions) the gel is swollen because of the water uptake. By reverse, during the basic pH spike, the amine groups are deprotonated i.e. uncharged the chains aggregate and gradually coil up because the solvation of the polymer chains is no more thermodynamically favourable. This collective rearrangement is accompanied by the expulsion of water and contraction of the whole gel fiber, leading to the collapse of the entire network. As the pH turns back to acidic thanks to lactone hydrolysis, rehydration occurs again upon protonation of the amine groups, followed by the expansion of the polymer chains and consequently the macroscopic reswelling of the gel. This behavior can be used to perform mechanical work such as lifting and lowering a load: by attaching a glass bead (about 10–14 times heavier than the swollen gel itself) on one end of the gel fiber, this load is lifted upon contraction during the basic pH pulse. Using lactones with different hydrolysis behavior (faster in the case of GL, slower for VL) it was also possible to control, on a scale of minutes, the temporal dynamics of the chemomechanical actuation.
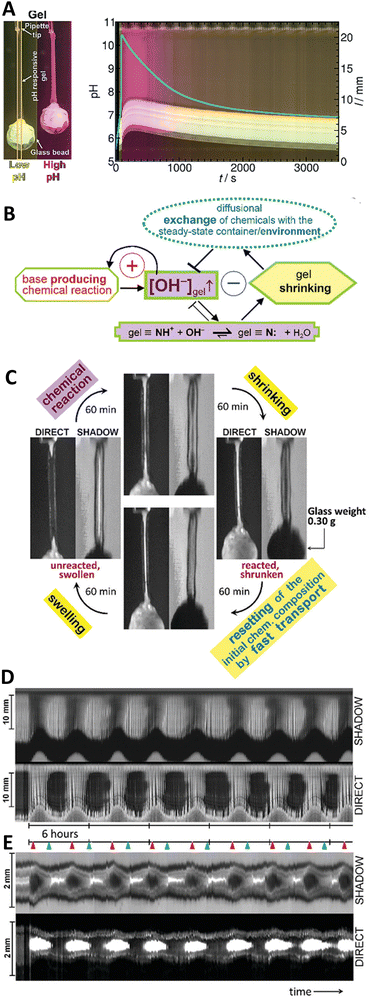 | ||
Fig. 10 (A) Space-time plot of gel length and the synchronous pH-change (blue line) in a batch MGS–VL system (initial concentrations: sulfite 5 mM, bisulfite 50 mM, MG 112.5 mM, 10 mM VL). The background color is from phenol red (0.0145 mM). The yellow frames indicate the vertical cut taken to make the space-time plots. Image reproduced from ref. 31. (B) Schematic representation of positive and negative feedback loops occurring in a pH-controlled synergistic chemomechanical oscillator. The symbol 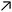 stands for activation while stands for activation while 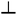 for inhibition. The green frames indicate processes taking place within the pH-responsive gel. (C)–(E) Synergistic chemomechanical oscillations of a suspended cylindrical (initial radius 0.500 mm) gel filament, at constant temperature (29.1 °C) and pH = 6.40, in a CSTR (feed conditions: 25 mM MG, 25 mM bisulfite, 2.31 mM NaOH, residence time 8.44 min). (C) Snapshots of the four characteristic chemomechanical phases within one oscillation period. (D) Variations in length between 16.0 to 12.00 mm. (E) Variations in diameter between 1.15 to 1.50 mm. Red arrows indicate the maximum diameter while blue arrows the minimum diameter. Images reproduced with permission from ref. 24. for inhibition. The green frames indicate processes taking place within the pH-responsive gel. (C)–(E) Synergistic chemomechanical oscillations of a suspended cylindrical (initial radius 0.500 mm) gel filament, at constant temperature (29.1 °C) and pH = 6.40, in a CSTR (feed conditions: 25 mM MG, 25 mM bisulfite, 2.31 mM NaOH, residence time 8.44 min). (C) Snapshots of the four characteristic chemomechanical phases within one oscillation period. (D) Variations in length between 16.0 to 12.00 mm. (E) Variations in diameter between 1.15 to 1.50 mm. Red arrows indicate the maximum diameter while blue arrows the minimum diameter. Images reproduced with permission from ref. 24. | ||
However, this kind of approach would not allow the system to go beyond single cycles, as the spiky pH-waveform of the MGS–GL oscillator does not make it appropriate to drive large size changes. The ability of the pH-responsive gel to follow the superimposed pH changes is directly linked to the diffusivity of H+ and OH− inside its network, which in turn depends on a complex interplay between chemical and geometrical factors. To facilitate diffusion, Lagzi et al. used relatively small fibers with a high aspect ratio and a macroporous structure, but this comes at the expense of the scale of the size changes.
In this regard, a major breakthrough was reported (also in 2017) by Judit Horváth who described24 the first synergistic actuator operating with a base-producing non-redox clock reaction. Periodic large size-changes (over 20% in length), which could be sustained for days in a CSTR, were obtained thanks to the coupling of the MGS clock with variations of the exchange time induced between the core of a pH-responsive gel (swollen-to-shrunken transition between pH 8–9) and a steady chemical environment (Fig. 10(B)). This impressive achievement was the result of a painstakingly careful and accurate experimental planning, from finding the right comonomer gel composition (89% N-isopropylacrylamide, 9% N-tert-butylacrylamide, 1.52% N-[3-(dimethylamino)propyl]methacrylamide as pH-responsive unit, and 0.41% N,N′-methylenebis(acrylamide) as crosslinker) and polymerization technique (sulfite/persulfate system instead of TEMED/persulfate because of the buffering effect of TEMED residues, choice of polymerization medium choice to obtain sufficiently porous networks) to the engineering of reaction–diffusion flow systems able to run stably for several days.
Eventually, chemomechanical oscillations in-phase along a cylindrical gel filament with a load of 0.30 g (ten times the mass of the swollen gel) and length changes between 16 to 12 mm were sustained over 33 hours with periods of ca. 4 h and without any sign of gel degradation (Fig. 10(C)–(E)).
Given the practical limitations imposed by the MGS–GL system, it would be of great interest to try the MGS–PrS one in CSTR conditions for the purpose of obtaining chemomechanical oscillations.
Such chemomechanical actuators could be very useful for soft robotics applications and, if the toxicity of the chemical system could be further reduced, for cell and tissue culture – not only to facilitate harvest, also to apply periodic mechanical stimulation in situ during growth. One even wonders whether by weaving together two or more different kinds of pH-responsive fibers it would not be possible even to obtain a novel kind of smart textiles.
Conclusions
The methylene glycol-sulfite (MGS) reaction is a versatile pH-clock thanks to its simplicity of operation, robustness and reliability. Its non-redox nature makes it less aggressive towards delicate building blocks compared to more classical inorganic-based clock reactions. The MGS system allows to generate sudden, intense pH increase events which, in presence of slow acid generators such as lactones and sultones, can transform into transient acid–base–acid cycles.On the other hand, the toxicity of formaldehyde, the relatively short induction times tclock and the need for an acidic onset somewhat limit the range of possible applications for the MGS clock. Toxicity problems also plague the MGS–PrS system, for which the search of alternatives as well as a dedicated (re)investigation of the hydrolysis kinetics of PrS and similar compounds could be helpful to promote its further use and development. Nevertheless, while gazing at the examples that have been discussed in this review, the huge untapped potential – not only of the MGS and derived systems, but of pH-clocks in general – for the time-programming of materials becomes evident. Much has been done, and even more remains to be explored by cultivating the fertile ground of nonlinear chemical reaction networks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. P. is grateful to all his collaborators, and especially to Prof. Dr Eric Dufresne and Prof. Dr Ingo Burgert for their support. The help from anonymous reviewers is kindly acknowledged.Notes and references
- O. R. Maguire and W. T. S. Huck, Emerging Top. Life Sci., 2019, 3, 517–527 CrossRef PubMed
.
- X. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Nature, 2012, 487, 7406 CrossRef
.
- K. Das, L. Gabrielli and L. J. Prins, Angew. Chem., Int. Ed., 2021, 60, 20120–20143 CrossRef CAS PubMed
.
- T. Heuser, A. K. Steppert, C. Molano Lopez, B. Zhu and A. Walther, Nano Lett., 2015, 15, 2213–2219 CrossRef CAS PubMed
.
- R. Yoshida, Adv. Mater., 2010, 22, 3463–3483 CrossRef CAS PubMed
.
- A. Osypova, M. Duebner and G. Panzarasa, Materials, 2020, 13, 2957 CrossRef CAS PubMed
.
- G. Panzarasa and E. R. Dufresne, Chimia, 2020, 74, 612 CrossRef CAS
.
- S. Ghosh, M. G. Baltussen, N. M. Ivanov, R. Haije, M. Jakštaitė, T. Zhou and W. T. S. Huck, Chem. Rev., 2024, 124, 2553–2582 CrossRef CAS PubMed
.
- A. K. Horvath and I. Nagypal, ChemPhysChem, 2015, 16, 588–594 CrossRef CAS PubMed
.
- G. Panzarasa, React. Kinet., Mech. Catal., 2022, 135, 1349–1364 CrossRef CAS
.
- C. Wagner, Ber. Dtsch. Chem. Ges., 1929, 62, 2873–2877 CrossRef
.
- R. P. Bell and P. G. Evans, Proc. R. Soc. London, Ser. A, 1966, 291, 297–323 CAS
.
- R. L. Barrett, J. Chem. Educ., 1955, 32, 78 CrossRef
.
- T. Cassen, J. Chem. Educ., 1976, 53, 197 CrossRef CAS
.
- M. G. Burnett, J. Chem. Educ., 1982, 59, 160–162 CrossRef CAS
.
- P. Wameck, J. Chem. Educ., 1989, 66, 334–335 CrossRef
.
- F. T. Chau and K. W. Mok, J. Autom. Chem., 1992, 14, 79–83 CAS
.
- Y. G. Adewuyi, S.-Y. Cho, R.-P. Tsay and G. R. Carmichael, Atmos. Environ., 1984, 18, 2413–2420 CrossRef CAS
.
- K. Kovacs, R. McIlwaine, K. Gannon, A. F. Taylor and S. K. Scott, J. Phys. Chem. A, 2005, 109, 283–288 CrossRef CAS
.
- R. McIlwaine, K. Kovacs, S. K. Scott and A. F. Taylor, Chem. Phys. Lett., 2006, 417, 39–42 CrossRef CAS
.
- K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, Phys. Chem. Chem. Phys., 2007, 9, 3711–3716 RSC
.
- K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, J. Phys. Chem. A, 2007, 111, 549–551 CrossRef CAS PubMed
.
- J. Horváth, J. Phys. Chem. B, 2014, 118, 8891–8900 CrossRef
.
- J. Horváth, Chem. Commun., 2017, 53, 4973–4976 RSC
.
- J. B. Ealy, A. R. Negron, J. Stephens, R. Stauffer and S. D. Furrow, J. Chem. Educ., 2007, 84, 1965–1967 CrossRef CAS
.
- Y. Pocker and E. Green, J. Am. Chem. Soc., 1973, 95, 113–119 CrossRef CAS
.
- G. Panzarasa, T. Sai, A. L. Torzynski, K. Smith-Mannschott and E. R. Dufresne, Mol. Syst. Des. Eng., 2020, 5, 445–448 RSC
.
- R. Wilson and A. P. F. Turner, Biosens. Bioelectron., 1992, 7, 165–185 CrossRef CAS
.
- G. P. Misra and R. A. Siegel, J. Controlled Release, 2002, 81, 1–6 CrossRef CAS
.
- A. S. Bhalla and R. A. Siegel, J. Controlled Release, 2014, 196, 261–271 CrossRef CAS PubMed
.
- E. Tóth-Szeles, J. Horváth, G. Holló, R. Szcs, H. Nakanishi and I. Lagzi, Mol. Syst. Des. Eng., 2017, 2, 274–282 RSC
.
- G. Panzarasa, A. L. Torzynski, T. Sai, K. Smith-Mannschott and E. R. Dufresne, Soft Matter, 2020, 16, 591–594 RSC
.
- S. Osterman-Golkar and C. A. Wachtmeister, Chem. – Biol. Interact., 1976, 14, 195–202 CrossRef CAS
.
- I. Lagzi, D. Wang, B. Kowalczyk and B. A. Grzybowski, Langmuir, 2010, 26, 13770–13772 CrossRef CAS
.
- I. Lagzi, B. Kowalczyk, D. Wang and B. A. Grzybowski, Angew. Chem., Int. Ed., 2010, 49, 8616–8619 CrossRef CAS PubMed
.
- D. M. Escala, A. P. Muñuzuri, A. De Wit and J. Carballido-Landeira, Phys. Chem. Chem. Phys., 2017, 19, 11914–11919 RSC
.
- D. M. Escala, A. De Wit, J. Carballido-Landeira and A. P. Muñuzuri, Langmuir, 2019, 35, 4182–4188 CrossRef CAS
.
- G. Panzarasa, A. Osypova, A. Sicher, A. Bruinink and E. R. Dufresne, Soft Matter, 2018, 14, 6415–6418 RSC
.
- C. C. M. Sproncken, B. Gumi-Audenis, G. Panzarasa and I. K. Voets, ChemSystemsChem, 2020, 2, e2000005 CrossRef CAS
.
- C. C. M. Sproncken, B. Gumí-Audenis, S. Foroutanparsa, J. R. Magana and I. K. Voets, Macromolecules, 2023, 56, 226–233 CrossRef CAS
.
- I. Derényi and I. Lagzi, Phys. Chem. Chem. Phys., 2014, 16, 4639–4641 RSC
.
- Y. Okamoto, Y. Sasaki, E. Nawa-Okita, D. Yamamoto and A. Shioi, Langmuir, 2019, 35, 14266–14271 CrossRef CAS
.
Footnote |
| † For consistency, throughout the text the terms “methylene glycol (MG)” and “formaldehyde” will be used as reported in the original publications. |
| This journal is © The Royal Society of Chemistry 2024 |