Open Access Article
Open Access ArticlePredicting polymer solubility from phase diagrams to compatibility: a perspective on challenges and opportunities
Jeffrey
Ethier
 a,
Evan R.
Antoniuk
a,
Evan R.
Antoniuk
 b and
Blair
Brettmann
b and
Blair
Brettmann
 *cd
*cd
aMaterials and Manufacturing Directorate, Air Force Research Laboratory, Wright-Patterson AFB, Ohio 45433, USA
bMaterials Science Division, Physical and Life Sciences Directorate, Lawrence Livermore National Laboratory, Livermore, California 94550, USA
cChemical and Biomolecular Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332, USA. E-mail: blair.brettmann@chbe.gatech.edu
dMaterials Science and Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332, USA
First published on 8th July 2024
Abstract
Polymer processing, purification, and self-assembly have significant roles in the design of polymeric materials. Understanding how polymers behave in solution (e.g., their solubility, chemical properties, etc.) can improve our control over material properties via their processing-structure–property relationships. For many decades the polymer science community has relied on thermodynamic and physics-based models to aid in this endeavor, but all rely on disparate data sets and use-case scenarios. Hence, there are still significant challenges to predict a priori the solubility of a polymer, whether it is for selecting sustainable solvents, obtaining thermodynamic parameters for phase separation, or navigating the coexistence curve. This perspective aims to discuss the different approaches of applying computational tools to predict polymer solubility, with a significant focus on machine learning techniques to capture the rapid progress in that space. We examine challenges and opportunities that remain for creating a comprehensive solubility toolset that can accelerate the design of a broad range of applications including films, membranes, and pharmaceuticals.
1. Introduction
For decades, the solubility of polymers in solvents has been of interest to polymer and materials scientists. Polymer solutions are prevalent in areas where purification, self-assembly, and compatibility of polymers in solution have critical roles in formulating a material with desired optical, electrical, and mechanical properties, as well as in material conversion processes including coatings and fiber spinning. Determining the role of solvent during polymer design has led to many questions: What is a good solvent? Which solvents will completely dissolve a specific polymer? How does the role of solvent affect the macroscopic behavior of the solidified polymer during a liquid–liquid phase transition? In the past, semi-empirical techniques using well-known thermodynamic equations and parameters have helped answer these questions (e.g., Flory–Huggins χ parameter).1,2 While we have learned much about the physical phenomena of polymer phase separation, an accurate, quantitative prediction of polymer solubility from first principles has remained undiscovered for many different polymer chemistries. Additionally, the role of solubility differs from one subject, experiment, or application to another. For instance, is determining whether a polymer–solvent pair is compatible sufficient in the design process, or does the entire phase diagram need to be known? Thus, prediction tools that can address each of these questions while generalizing to various approaches and applications can help accelerate, and precisely control, the synthesis and design of novel polymer chemistries.One of the most important impacts of polymer solubility is in polymer processing: in processes such as solution coating, fiber spinning, and 3D printing, polymers are first dissolved in a solvent and that solvent is evaporated or extracted to solidify the polymer. Specifically, film processing techniques such as spin-coating, blade coating, and slot-die coating are often applied with mixtures of polymer and solvent followed by temperature-induced or non-solvent induced phase separation, each of which can control the resulting morphology or film structure.3 These methods have been found in technologies such as adhesives, hydrophobic coatings, and flexible electronics.4–6 However, the complexity of polymer behavior in solution gives rise to challenges of predicting a priori the resulting material performance from the processing conditions (e.g., solvent evaporation rate, concentrations, temperature, pressure, etc.). For instance, studies have shown that solvent quality and incomplete dissolution of the polymer before casting can affect the aggregation behavior7 and electronic properties,8 respectively, in semiconducting polymer films. Additionally, solvent evaporation rate can affect film properties such as the surface roughness.9 Therefore, tools that can predict solubility behavior (interaction parameters, phase diagrams, solvent selection, etc.) can benefit materials science, drug delivery, and other areas.
The types of predictions that are most valuable will depend on the specific question being asked. For designing formulations for polymer processing, predictions of specific solubility values (mg mL−1) are impactful during solvent selection and process design. Such specific, experiment-relevant information can affect industrial processes, such as when supply chain challenges or regulations produce a shortage of a solvent and a new solvent must be quickly selected. However, quantitative solubility values may not be necessary in all applications. In cases where general compatibility is more important, such as when selecting tubing material for a solvent-containing process or when selecting membranes, a classification of solvent/non-solvent or estimating relative empirical interaction parameters may be sufficient for materials design. However, for chemical process design and development of process models, thermodynamic parameters such as activity coefficients and solid/liquid equilibrium diagrams are necessary and an important target of prediction tools. Throughout all of the aforementioned applications, the common practice for R&D is to experimentally assess different solvent/polymer combinations, leading to long development times and high costs. Hence, prediction tools that provide a targeted output required for a specific application can speed up R&D for polymer materials.
Predicting a priori the solubility of a polymer in solution has in the past relied on quantum-chemical or group contribution estimates for thermodynamic interaction or solubility parameters,10 or estimating the miscible-immiscible phase boundary from thermodynamic lattice models and field theory at equilibrium.11 For instance, Flory–Huggins theory is arguably the most common choice to estimate the phase boundary in binary and ternary mixtures of polymer solutions and blends due to its simplicity.11 These calculations provide semi-quantitative phase boundary predictions, due to its underlying assumptions, and typically rely on empirical expressions with fit coefficients to achieve better agreement with experimental data (see Section 2.2 phase diagram prediction and applications). Alternatively, simulation methods (e.g., Gibbs-ensemble, molecular dynamics, field-theoretic, etc.) can provide insight into phase separation behavior as well as provide estimates of the phase diagram for solutions and blends.12–17 While these methods can explain phase separation mechanisms at a molecular level, simulations can be computationally expensive and/or chemistry agnostic, making these models inefficient to simulate a vast number of polymer/solvent chemistries as a predictive tool. Related to soluble/insoluble classification, estimating solubility parameters such as Hansen solubility parameters (HSPs) for polymers from first principles is typically done via group contribution methods. We discuss the impact and challenges of these models in more detail throughout the perspective.
Aside from first principles calculations and modeling, data-driven methods are a viable way to accelerate predictions of polymer solubility. With the rise of artificial intelligence and machine learning as tools for materials design, there is increasing interest in predicting properties of complex materials that are not well described by simple models.18 Given their large size, dispersity, and time- and history- dependent response to stimuli, polymers typically fall into this category. However, one significant tradeoff of data-driven models is that, compared to physics-based approaches, they provide minimal insight into understanding the input-output mapping. For instance, these models typically only give insight into which of the model inputs impact the prediction the most, and they do not give any physical relation between the two. Nonetheless, machine learning is extremely efficient, can be generalizable, and provides tools that accelerate our understanding of complex data. Recently, research to predict polymer properties using data science approaches has rapidly increased and spanned a huge range of properties including crystallization tendency,19 dielectric properties,20–22 optical properties,23,24 glass transition temperature,25 solubility26,27 and more. Many of these approaches are regression tasks that output a continuous value for the property, such as glass transition temperature, dielectric constant, density, etc. For solubility, however, prior work has explored various types of solubility model outputs, ranging from classifying solvents as “solvent” or “non-solvent”27,28 to phase diagrams29 to interaction parameters.30 Although it appears inconsistent, the variety of model outputs reflects the varied needs for understanding and using information on polymer solubility.
In this perspective, we aim to assess the current state of physics-based and data-driven prediction methods for polymer solubility such as solvent/non-solvent classification, thermodynamically- and empirically-derived interaction parameters, and coexistence curves (binodals), and discuss how these approaches can be integrated in design approaches to accelerate polymer materials development. We place a heavier emphasis on the data-driven and machine learning approaches, due to the rapid progress in that space. We categorize the approaches into three groups: prediction of coexistence curves, prediction of thermodynamic parameters, and point predictions of solubility (Fig. 1). Although these are inherently linked through the thermodynamics of phase separation, they provide different levels of granularity, use different types of data in their predictions, and would be applied differently by practitioners. Thus, there is value in critically analyzing the different categories. Throughout, we discuss tradeoffs in amount and quality of data needed, computational time, and overall accuracy of predictions. The overall discussion will enable a clearer understanding of the tools available, as well as the challenges and opportunities present, for predictions of polymer–solvent solubility.
2. Polymer solution phase diagrams
2.1. Thermodynamics of polymer solutions
To understand how polymer–solvent phase diagrams are predicted, a brief review of the thermodynamics of polymer solution mixing is necessary. We begin with Flory and Huggins theory. Our goal is not to go in depth into the theory but to provide context to existing methods for predicting polymer phase diagrams. A more detailed discussion can be found in a recent perspective on phase behavior of polymer solutions and blends.11 Here, we start with the simplest expressions for a binary polymer solution and briefly review several more complex thermodynamic models for predicting the phase diagrams for multicomponent polymer solutions. We then summarize the current state of phase diagram predictions and their use-case scenarios.The classical Flory and Huggins (FH) solution theory, originating in 1942, uses a lattice-fluid model where fluid particles occupy lattice sites and polymer segments are connected along neighboring sites.31,32 The Gibbs free energy of mixing for an ideal polymer solution (where the polymer takes a random walk configuration) is derived from the mean field as,
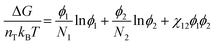 | (1) |
The liquid–liquid coexistence curve, or binodal, can be determined by solving for the exchange chemical potential relative to the pure components for the coexisting phases, Δµi = (∂ΔG/∂ni)p,T where ni is the moles of species i. The chemical potential in the coexisting phases are equal, ΔµIi = ΔµIIi, which leads to solving for the concentrations of species i in each phase ϕIi and ϕIIi given a known χ12. The spinodal, where spinodal decomposition occurs, can also be determined from the second derivative of the Gibbs free energy and resides within the binodal. The region in between the binodal and spinodal is a metastable zone, where there is thermodynamic instability of the two phases but the mixture is robust to small fluctuations in concentration and temperature. In other words, there is a local free energy minimum and a thermodynamic barrier to complete macrophase separation. It is in this region where the nucleation and growth phenomenon is known to occur, whereas spinodal decomposition is a spontaneous phase separation and has no such barrier.
While this fundamental theory provides crucial insights into liquid–liquid equilibrium behavior of polymer solutions and blends, the primary shortcoming of FH theory is that quantitative agreement between the binodal and experimental coexistence curves is poor due to the highly idealized assumptions, which were acknowledged by Flory. First, the theory assumed the interaction parameter χ (we henceforth drop the subscript for simplicity) was a function of temperature only, and was later shown to be an oversimplification.33 Secondly, eqn (1) assumes incompressibility and that there are no changes in volume upon mixing. This prompted additional derivations by Flory and co-workers,34–36 including an equation of state (EoS) approach that accounted for the thermodynamic parameters of the pure components. Similar in nature to the Flory derivations, a generalized statistical mechanical model for liquid and gas mixtures was later developed by Sanchez and Lacombe, namely the Lacombe–Sanchez lattice fluid model (LS–LF),37 which qualitatively predicted liquid–liquid and liquid-vapor phase transitions. These EoS theories reduced to the classical FH theory expressions at low temperatures. However, compared to experiments, phase diagram predictions were mostly qualitative.38
We note that the above theories established a foundation for explaining the physical phenomena behind polymer solution coexistence behavior. Additional thermodynamic models continued being developed thereafter to better capture the quantitative agreement with experimental phase diagrams, with many focusing on the classical Flory–Huggins expression and its modifications. In doing so, these models were developed to improve upon the oversimplified thermodynamics in the original expressions. For instance, the lattice cluster theory of Freed and co-workers was developed as a mathematical solution to Flory–Huggins theory.39,40 Furthermore, the double lattice and modified versions thereof were subsequently introduced based on Freed's lattice-field theory.41–43 These theories, unlike the original FH theory, introduced a concentration dependence to χ and did not use the mean-field approximations for the Helmholtz free energy of mixing. Alternatively, several extended Flory–Huggins equations were introduced to obtain better quantitative agreement with experiments.44–47 In the extended FH theory, χ was generalized to a temperature and concentration-dependent interaction parameter g(T,ϕ2) that was related to χ as χ = g − ϕ1g′, where g′ = (∂g/∂ϕ2)T. The parameter χ12 was written to include separate functions for the effect of T and ϕ, χ = D(T)B(ϕ2). In that expression, D(T) is commonly written as d0 + d1/T + d2/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T and B(ϕ2) can either take the form b0 + b1ϕ2 + b2ϕ22 as in ref. 44–46 or 1/1(1 − bϕ2) as found in ref. 47.
T and B(ϕ2) can either take the form b0 + b1ϕ2 + b2ϕ22 as in ref. 44–46 or 1/1(1 − bϕ2) as found in ref. 47.
We note here that these extended expressions for the interaction parameter were not derived from a theoretical basis, rather, an empirical approach was used to fit experimental data. The expressions for D(T) and B(ϕ2) were simply algebraic and included parameters that were fit to each polymer–solvent chemistry and polymer molecular weight to obtain the correct phase behavior. In many cases, accurate predictions of the phase diagram were observed, but required extensive fitting procedures (see Section 2.2 phase diagram prediction and applications). Additionally, the equations above only apply to binary polymer–solvent mixtures, whereas multicomponent mixtures require additional terms, which create additional complexities for predicting phase diagrams for ternary mixtures. Lastly, without experimental data, the Flory–Huggins χ parameter is challenging to estimate and known values in the literature often fail to report the monomer or solvent reference volume. For polymer-polymer mixtures, it is important to fix the reference volume to compare interactions between two chemically distinct chains, however for polymer–solvent mixtures the choice is often the volume of a solvent molecule11 (additional discussion can be found in Section 3.0 thermodynamic parameter predictions).
2.2. Phase diagram prediction & applications
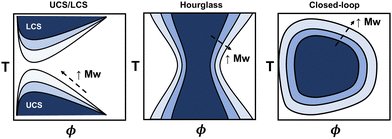
The phase diagram represents the complete thermodynamic space at which polymer mixtures are miscible, or where multiple different phases can coexist (i.e., phase separation). It is typically measured via turbidity (cloud point) experiments using the transmittance from ultraviolet visible spectroscopy (UV-vis) or higher fidelity thermo-optical measurements.48 Alternatively, coexistence curves may be reported in which the concentrations of two coexisting phases are measured. From these experiments, various phase behaviors have been observed, including upper critical solubility (UCS), lower critical solubility (LCS), hourglass, and closed-loop curves (see Fig. 2), and depend on the specific polymer and solvent chemistries. The latter two, hourglass and closed-loop, are often observed for polymers in poor solvent, or for polymers with orientation-dependent interactions (e.g. hydrogen bonds), respectively.48–50 For instance, poly(ethylene glycol) in water exhibits closed-loop behavior, polystyrene in acetone exhibits an hourglass-like phase diagram, and polystyrene in cyclohexane exhibits both upper critical and lower critical solubility curves.48 For some polymers, the lower critical solubility curve is not feasible to measure due to polymer degradation or solvent boiling points when approaching the higher temperatures. Generally, the phase diagram for a particular polymer will highly depend on its chemistry, architecture, molecular weight, and other thermodynamic properties, making quantitative predictions a challenge.Many existing phase diagram predictions are semi-quantitative, but there are several examples of when the theory, via fitting empirical expressions for χ, has shown good quantitative agreement when compared to cloud point curves. For instance, several authors have extensively demonstrated that all types of phase diagrams are obtainable with fitting parameters associated with the extended FH equations. They were able to obtain good agreement among various polymer–solvent chemistries and phase diagrams.44–47 More recently, statistical associating fluid theory (SAFT) and coarse-grained molecular simulations have, in some instances, quantitatively captured the phase behavior using intermolecular interaction fitting parameters for the EoS.13 The main drawback of using these models is that fitting procedures are required to capture the phase diagram quantitatively for each phase boundary. However, the theory improves on our understanding of these systems from the empirical expressions and free energy equations derived.
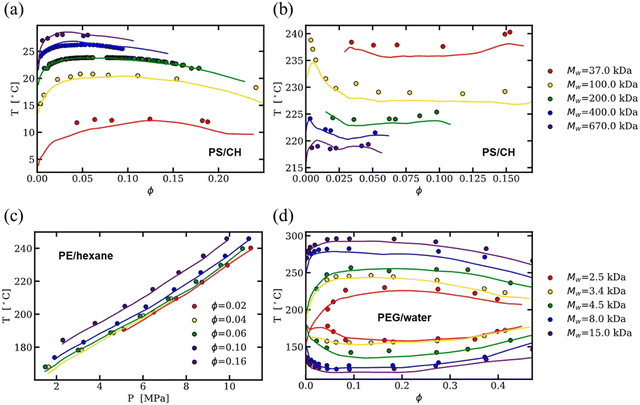
As an alternative to physics-based models, much of the published binary solution data in the literature has been used to train data-driven regression models, such as neural networks and theory-informed neural networks, to predict the cloud point curve of various polymer–solvent systems.29,51,52 For instance, one of us showed that a single ML model can predict the cloud point curves of various chemistries and phase behaviors such as UCS, LCS and closed-loop diagrams (see Fig. 3). Compared to theory, ML models learn a mapping from inputs to outputs, improving accuracy and efficiency but often with limited physical insight. Nonetheless, contrary to fitting each polymer–solvent mixture individually as in previous theories, ML has the ability to learn the various phase behaviors observed experimentally, and with sufficient data can interpolate to similar polymer–solvent chemistries. While extrapolation to new polymer–solvent systems is poor due to the lack of polymer chemistries represented in the data set, adding a small amount of experimental data to the training set can allow the model to predict the phase diagrams for these unseen polymers with reasonable uncertainty. Incorporating existing theory (such as the extended FH equations) with ML can help improve predictions in the small data limit and provide physics insight to the phase diagram predictions.29 Thus, while theory provides a fundamental understanding of the phase behavior, data-driven models are a powerful way for predicting phase diagrams of polymer solutions.
We note here that all calculated or estimated binodal curves (e.g., from theory) are most commonly compared to cloud point data as these can be, experimentally, simple to measure. This was first shown in work comparing the precipitation temperature of polyisobutylene in diisobutyl ketone and polystyrene in cyclohexane.53 The cloud point represents the temperature (or composition) at which a mixture is observed to macrophase separate. However, it is important to note that the cloud point curve (CPC) does not always represent the binodal curve. In real systems, the CPC lies on the binodal only for monodisperse molecular weight distributions, but the CPC deviates from the binodal when the distribution broadens. This was extensively demonstrated by comparing quasi-binary cloud point curves to theory.46,54,55 Furthermore, the cloud point is often measured via a fixed turbidity level, but a recent discussion has pointed out that this can lead to biased results of the phase boundary.56 Lastly, slow kinetics also play a large role in phase separation behavior and can depend on whether the solution is being cooled or heated. For instance, the onset of turbidity depends on time, and if the temperature ramp is too steep compared to the slow kinetics, the measured cloud point temperature can include these artifacts.57 Hence, it is clear then that the experimental technique for measuring the phase diagram, as well as the molecular weight distribution of the polymer sample, can introduce noise and lead to deviations between experimental observations and predicted binodals from existing theoretical and data-driven methods, and must be considered when developing future models.
The models discussed above have many potential use cases in processing polymer materials. For example, it is well-known that the phase diagram is closely tied to the formation of films and porous membranes, which are typically processed via solvent casting where the solvent is allowed to evaporate from an initial concentration of the polymer solution.58 Then, the resulting morphology depends on the processing conditions and path in the phase diagram. Both nonsolvent- and evaporation-induced phase separation are common in film formation, where both lead to driving the mixture through the phase boundary. Ternary phase diagrams are also strongly correlated to film processing via nonsolvent-induced phase separation. For instance, pore size distribution is significantly impacted by the starting concentrations and path in the phase diagram.59,60 In other multicomponent mixtures, such as polymer nanocomposites, evaporation-induced phase separation can impact the microstructure during the direct ink writing process.61 These examples demonstrate that a more precise control of the microstructure would be feasible if the phase diagram of these more complex polymer materials were known prior to processing. Thus, there are opportunities to combine processing methods with phase diagram models to tailor material properties for specific applications.
Overall, the thermodynamics and solubility of polymer solutions is a direct result of the phase diagram. Generally, our understanding of the phase behavior directly impacts the ability to classify a polymer solvent or nonsolvent, estimate their thermodynamic interaction or solubility parameters, or process materials via navigation through the coexistence curve. In Fig. 1, we show these three example categories with a schematic of the phase diagram in the center, emphasizing that all of these are tied to the phase diagram. However, as previously mentioned, predicting the entire phase behavior from first-principles theory and modeling has remained a challenge. Therefore, we emphasize that it is not always efficient to predict the entire phase diagram where less detailed predictions would suffice, such as for solvent selection and solubilizing a particular polymer. In the future, a combination of tools to predict the solubility of polymers would accelerate and improve the processing, sustainability, and design of new materials.
3. Thermodynamic parameter predictions
A number of models use data from and aim to predict thermodynamic parameters rather than coexistence curves and full phase diagrams. This comes in part from the challenge in obtaining sufficient data for full phase diagrams and in part from the successful use of thermodynamic parameters in industrial process design.62–64 In examining the industrial use of thermodynamics as part of studies by the Working Party of Thermodynamics and Transport Properties of the European Federation of Chemical Engineering, Kontogeorgis et al. noted that industrial survey respondents were enthusiastic for predictive thermodynamic models, especially those that were accurate and validated for complex materials and mixtures. However, there was a significant concern across the industry about the lack of available high-quality data to fit and validate the models. The lack of data was more significant for systems that are not “trendy” but are industrially relevant, and they specifically mention the lack of “high-quality data in the literature for the solubility of larger molecules in solvents”.62 Due to this weakness, thermodynamic parameters are often estimated through group contribution methods, molecular simulations, or quantum chemical calculations, which can lead to inaccuracies for complex systems. In this section, we discuss progress in predicting thermodynamic parameters including the Flory–Huggins χ parameter, Hansen solubility parameters, and activity coefficients, focusing on advances made possible through computational tools and data science but highlighting the tradeoff between accuracy and effort for the different cases.For polymer solubility analysis and prediction, three sets of thermodynamic parameters are widely used (Fig. 4). The first is the Flory–Huggins χ parameter, which represents the degree of interaction between two materials, such as a polymer and a solvent and is tied to the free energy of mixing as discussed previously. The second set of parameters includes solubility parameters, most commonly the Hansen solubility parameters, but also the Hildebrand solubility parameters. These characterize the chemical similarity between polymer and solvent and prediction of solubility is based on a “like dissolves like” principle. Finally, the activity coefficients for a polymer in a solvent are used to capture the thermodynamic solubility, in particular capturing non-idealities. We will discuss each of these parameter sets, examining prediction methodologies based on both physics-based and data-driven prediction, with discussion of machine learning techniques that can incorporate both types of input data. Overall we see that these thermodynamic parameters are helpful for industrial product and process design, but are very sensitive to the data quality and become more problematic as the complexity of the materials increases.
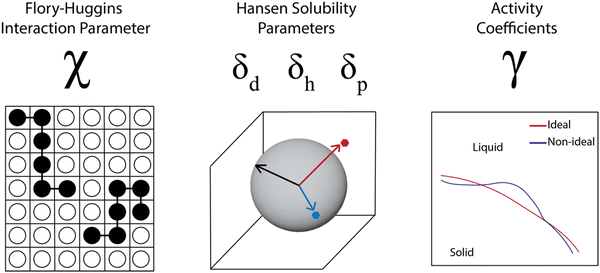 | ||
| Fig. 4 Three common types of thermodynamic parameters calculated and used to predict polymer solubility. | ||
3.1. The Flory–Huggins interaction parameter
The Flory–Huggins theory for polymer solutions ties phase equilibrium to a parameter that represents the interactions between the polymer and solvent, the χ parameter. Knowledge of the χ parameter at the temperature and molecular weight of interest combined with the volume fraction of the polymer in the solvent enable calculation of the free energy of mixing through eqn (1). Flory–Huggins theory assumes that the volume does not change on mixing and uses a mean-field approximation, leading to some limitations (see Section 2.1 thermodynamics of polymer solutions), but it's success in predictions relies most heavily on how well the χ parameter represents the system.65,66 Hence significant effort has been expended to measure the χ-parameter for existing systems and predict the temperature and molecular weight-dependent χ parameter for new polymer–solvent mixtures.Experimental measurement of the χ parameter can be performed through osmotic pressure measurements,67 vapor pressure measurement,68 scattering,69,70 and inverse gas chromatography (IGC).71 These techniques are time and money intensive and thus are not well-suited to collecting a large amount of data.72 Additionally, their utility is limited in the polymer/solvent property space. For example, for IGC the polymer must be able to form a film on the test substrate, which is not possible for all polymer/solvent combinations.71 In many cases, information is left out when reporting experimental results for χ, such as the molar reference volume, which makes it challenging to directly compare to computational predictions. These weaknesses lead to insufficient data for direct look-up, and results in biased data for more recent modeling techniques such as machine learning. It is particularly concerning for applications where the solubility behavior of a wide variety of polymer–solvent pairs must be predicted.
Complementing direct measurement of the χ parameter is computational prediction, the most common of which is the Hansen solubility parameter (HSP) approach. HSP uses an empirical model with three components: the dispersion (van der Waals forces), polarity, and hydrogen-bonding forces between the polymer and solvent. We will discuss the HSP model, its relation to χ, and solubility parameter predictions in more detail later. Other computational predictions of the χ parameter include the use of corresponding states theory,73,74 or the use of quantum chemical calculations such as the conductor-like screening model for realistic solvation (COSMO-RS)75 and molecular simulations.76–78 These methods can be highly accurate; however, for polymers they are computationally expensive, making it challenging to screen a large chemical space. Thus, there is increasing interest in using machine learning to improve predictions over a large parameter space with limited experimental or computational data.
Recent efforts have focused on using machine learning models to rapidly estimate polymer–solvent interaction parameters directly from the chemical structures of polymer–solvent pairs. For instance, Nistane et al. used a Gaussian process regression–based machine learning model to predict temperature-dependent χ parameters for pairs of polymers and solvents using experimental data from literature and online databases. Both the polymers and solvents were represented with a hierarchical fingerprint method that captures essential chemical features spanning from the atomistic level descriptors (such as the presence of atomic fragments), up to high-level morphological descriptors that describe the overall chemical species (such as the side chain length or van der Waals volume).79 The temperature at which χ was measured was also included as a feature, allowing the model to capture the temperature dependence. The model performed well, especially when trained on a data set containing a random sampling of all polymers and solvents, as seen by high test R2 values (0.83 for random split training) and low root mean square error (RMSE) values (0.27 for random split training). However, they did show that if a particular polymer group was held-out for testing, the model performed significantly worse (R2 = 0.36 and RMSE = 0.44) because there are only 58 polymers in the data set and thus there is insufficient polymer diversity to extrapolate well to unseen polymers. They also tested the predictive performance of the model on two new polymers with properties that did not occur in the data set, spirobiflourene aryl diamine (SBAD-1) and PIM-1, a polymer of intrinsic microporosity. The model significantly underpredicted the χ parameter for these polymers, likely due to their significantly different structure (ladder and semi-ladder polymers) compared to the polymers in the database (linear and branched).79 This highlights the challenge in data-driven predictions of the χ parameter for novel polymers and for a broad parameter space, especially with limited experimental data.
The work by Nistane et al. used a training data set of 1586 data points with 58 polymers and 140 solvents, which is a relatively small data set for ML models. Aiming to provide better predictions with an improved data set, Aoki et al. used a combination of an experimental data set containing 766 pairs from 46 polymers/140 solvents with a polymer property database PoLyInfo80 containing 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 polymer–solvent pairs and a new χ parameter data set predicted by COSMO-RS with 9575 polymer–solvent pairs.26 The goals of using the three data sets were to increase the amount of training data and to decrease the bias that occurs when only the experimental data is used due to the limitations of the experimental techniques discussed earlier. This work by Aoki et al. represents the polymer and solvent with 397-dimensional chemical descriptor vectors that are formed from concatenating chemical features from the RDKit Cheminformatics package, force-field descriptors, and the measurement temperature. This input is then fed into a neural-network architecture that simultaneously outputs predictions of the experimental χ parameter, the COSMO-RS computational χ parameter, and a binary soluble/insoluble label. Using this multi-task approach, the predictions for the experimental χ-parameter (R2 = 0.834) were significantly better than when using COSMO-RS (R2 = 0.620) and HSP (R2 = 0.629) methods alone.26 Furthermore, the authors demonstrate that training on all three datasets results in improved performance over single-dataset learning- thereby highlighting the performance improvement that is possible through generating larger solubility datasets from multiple data sources.26 Interestingly, this strong performance was achieved even though there was insufficient data to capture the trends in the temperature and molecular weight dependence of the χ parameter.
777 polymer–solvent pairs and a new χ parameter data set predicted by COSMO-RS with 9575 polymer–solvent pairs.26 The goals of using the three data sets were to increase the amount of training data and to decrease the bias that occurs when only the experimental data is used due to the limitations of the experimental techniques discussed earlier. This work by Aoki et al. represents the polymer and solvent with 397-dimensional chemical descriptor vectors that are formed from concatenating chemical features from the RDKit Cheminformatics package, force-field descriptors, and the measurement temperature. This input is then fed into a neural-network architecture that simultaneously outputs predictions of the experimental χ parameter, the COSMO-RS computational χ parameter, and a binary soluble/insoluble label. Using this multi-task approach, the predictions for the experimental χ-parameter (R2 = 0.834) were significantly better than when using COSMO-RS (R2 = 0.620) and HSP (R2 = 0.629) methods alone.26 Furthermore, the authors demonstrate that training on all three datasets results in improved performance over single-dataset learning- thereby highlighting the performance improvement that is possible through generating larger solubility datasets from multiple data sources.26 Interestingly, this strong performance was achieved even though there was insufficient data to capture the trends in the temperature and molecular weight dependence of the χ parameter.
3.2. The Hansen solubility parameters
Although the χ parameter is an important tool for assessing polymer/solvent compatibility and the phase diagram, Hansen solubility parameters (HSP) are the most widely used predictors of solubility. They are an empirical and quantitative representation of the concept that molecules that are more similar are more likely to dissolve one another. HSP can be broken into three components, the dispersion (van der Waals forces), δd, polarity, δp, and hydrogen-bonding tendency, δh of the molecule.81 The distance of the solubility parameters, Ra, for a polymer, p, and solvent, s, can be determined from:| Ra2 = 4(δdp − δds)2 + (δpp − δps)2 + (δhp − δhs)2 | (2) |
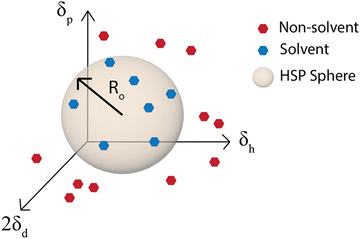 | ||
| Fig. 5 Hansen solubility parameter sphere. Ro is the radius of the sphere in δd, δp, and δh space that contains all the good solvents. | ||
The ability to use the HSP approach to predict polymer solubility requires knowledge of the solubility parameters for the polymer and solvent and the interaction radius, Ro. The determination of the HSP values is labor intensive and cannot be directly measured for large molecules such as polymers. Generally, the solubility parameter, δ, as defined first by Hildebrand, is the square root of the cohesive energy density:
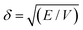 | (3) |
We briefly note here that HSPs have a direct relation to the Flory–Huggins χ parameter through both the Hildebrand and Hansen solubility parameters, allowing one to estimate χ based on these parameters (note that the reverse is not possible for HSPs). For a nonpolar solvent and nonpolar polymer, one can use the relation,
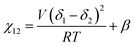 | (4) |
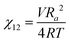 | (5) |
The simplest way to determine the HSP experimentally is to test the solubility of a polymer in a wide variety of solvents that have known solubility parameters. With the solvents plotted on a 3D graph with axes for δd, δp, and δh, a sphere of radius Ro can then be drawn around the good solvents and the center of the sphere is the set of HSP for the polymer (Fig. 5).81 This method is used by the HSPiP software85 and requires experimental testing of the solubility in a large number of solvents, with the HSPiP recommending 20–30 solvents across the δd, δp, and δh space. There are different optimization methods used for correlating the solubility in the large set of solvents with a predicted set of solubility parameters, with HSPiP providing a number of options including optimal binary, dividing the data into sets of 0 (bad solvent) and 1 (good solvent) and finding the best fit to HSPs with an exponential penalty function and a genetic algorithm from YAMAMOTO.86 Others have developed their own optimization schemes, for example Vebber et al. also used a genetic algorithm, but with a stochastic evolutionary strategy that improves coverage of the Hansen parameter space. This led to significantly improved HSP fits, for instance the improved HSP found for polyether sulfone.87
Given the experimental challenges with determining HSP, but its wide use for industrial applications, there has been significant interest in computational predictions beyond fitting of experimental data for each new polymer. One approach to accomplish this is to use the existing data on HSP of polymers and solvents and apply machine learning algorithms to predict the solubility parameters for unknown polymers. Early work on this used a large data set for the overall solubility parameter, δ2 = δd2 + δp2 + δh2 to develop a quantitative structure–property relationship (QSPR). They correlated a training set of 51 polymers to a set of 13 descriptors and found that 6 descriptors were significant and the solubility parameter could be predicted by the following optimal equation with an R2 of 0.973,88
| δ = 18.078 − 163.375hb − 0.039Eint + 2.222nN − 2.249alk + 15.263QH − 0.071Qii | (6) |
Newer machine learning modeling approaches are also being explored to use existing HSP data sets to predict solvent/non-solvent behavior. Venkatram et al. aimed to provide a baseline for performance of data-driven ML models that use HSP data sets to predict HSP for unknown polymers.30 They assessed prediction accuracy separately for solvent (defined as pairs with δ within 8 MPa1/2) and non-solvent (defined as pairs with a δ difference >8 MPa1/2) and found that the ML model for HSP had an accuracy of 69% with solvents and 76% with non-solvents.30 Surprisingly, this was a similar accuracy to predictions for solvent/non-solvent for a ML model with the Hildebrand solubility parameters, despite the supposed improved accuracy of HSP. They suggest that this is due to the bias of the HSP towards its dispersion component (multiplier of 2), leading to problems predicting polar solvent behavior as well as to the complexity of polymer solubility and its dependence on other factors such as temperature, concentration, polymer molecular weight and more that are not accounted for in the data that comprises the HSP database.30 Furthermore, the baseline assumption that R0 = 8 is poor for polymers. Nonetheless, this work provides a baseline for predicting a polymer's HSP and could be improved through more comprehensive and curated data sets and advanced ML models.
Rather than treating experimental, computational, and machine-learned solubility methods separately, combining all of these methods into a unified framework can be a powerful approach for predicting solubility. Sanchez-Lengeling et al. developed gpHSP, a Gaussian process machine learning model that combines molecular information from COSMOtherm simulations and quantum chemistry simulations to predict experimentally measured HSP values.89 Specifically, this approach represents each molecule with Morgan fingerprints, the σ-profile (charge density from the COSMO solvation model), electrostatic descriptors obtained from electronic structure calculations, and the molecular shape, which is given by the COSMO solvation surface. These molecular descriptors were chosen due to their known relevance for predicting HSPs. All of these molecular descriptors are then fed into the Gaussian process model and trained to predict experimental HSP values.89 The authors found that this approach consistently outperformed comparable baseline models at predicting the HSP values for both polymers and their solvents, predicting experimental polymer HSP coefficients with R2 values of 0.56, 0.58, and 0.62 for δd,δp, and δh, respectively. The development of such prediction tools that combine multiple information sources is an exciting direction since the strengths of different sources can compensate for the drawbacks of others.
Another approach to overcoming limited datasets for polymers in solvents is to use representative small molecule data sets, which tend to be available in larger numbers and with greater chemical variety. Ethier et al. showed that ML predictions of small molecule HSPs can be used to estimate polymer repeat unit HSPs for predicting coexistence curves. The method was very accurate when training on ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 small molecules from the HSPiP dataset (best R2 of 0.95, 0.88, and 0.92 for δd, δp, and δh, respectively).52 This is much improved over the gpHSP model discussed above, with reductions in the mean absolute error of approximately 60% and reductions in the root mean square error of 50–60%, an improvement that is in part due to the larger amount of small molecule data available to train the model and its applicability to linear polymer repeat unit structure (which are small compared to the polymerized structure).
000 small molecules from the HSPiP dataset (best R2 of 0.95, 0.88, and 0.92 for δd, δp, and δh, respectively).52 This is much improved over the gpHSP model discussed above, with reductions in the mean absolute error of approximately 60% and reductions in the root mean square error of 50–60%, an improvement that is in part due to the larger amount of small molecule data available to train the model and its applicability to linear polymer repeat unit structure (which are small compared to the polymerized structure).
In addition to improved predictions of HSP, there is interest in identifying features beyond the three contributions from HSP (i.e., hydrogen-bonding, dipole interaction, and dispersion forces). Aoki et al. created a machine-learned parameter system that is analogous to the HSP.26 Within their neural network architecture, a 397-dimensional descriptor vector that describes the polymer (subscript p) and solvent (subscript s) is encoded into 34-dimensional machine-learned latent vectors, (up, rp) and (us, rs). In a manner analogous to HSP distance, they propose that these latent vectors can be interpreted similarly as:
| distance = (up,i − us,i)2 − rp,i2 − rs,i2 (i = 1,…, k) | (7) |
Specifically, the first term captures the similarity of the latent vectors up and us, and the second and third terms are analogous to the HSP sphere interaction radius. They examined how correlated the 34-dimensional latent vectors were with the three HSP factors (hydrogen-bonding, dipole interaction, dispersion force) and found that a number of them correlated well with each HSP term. Among the 34 latent dimensions, they showed that 5 of the latent variables were correlated with both the hydrogen-bonding and polarity HSP term.26 A completely separate set of 5 latent variables were shown to be highly correlated with the three HSP energy terms. This is important in that it shows that the machine-learned latent variables have a grounding in chemical interactions represented by the commonly-used HSP. Interestingly, there were a number of these variables that did not correlate with any HSP, indicating that they capture forces or other chemical behavior that are not represented well by the HSP and are excellent candidates for future research into the physical phenomena driving solubility.
While data-driven approaches are promising because they can exploit existing experimental data sets, the χ parameter and HSP data sets still do not cover a sufficient chemical space, leading to sparse data sets that independently lead to low accuracy predictions. In addition, pure data-driven models (aside from QSPR models) are unable to provide meaningful insight into the mapping between the models inputs to its predictive target. Thus, combining physics-based models such as quantum chemical calculations with data-driven models currently show the most promise in predictive performance while also providing model interpretability, especially for novel polymers that have not been seen before.
When considering what types of solubility predictions would be most valuable to an end user, we notice that the χ parameter and HSP have two major areas of impact. The first is for predicting solubility for a newly synthesized polymer, which could be needed for purification or for developing processing techniques. In this case, the more extensive predictions that combine experimental data and quantum chemical calculations, which were shown to be most accurate for novel polymers, would be the most appropriate. The other common use case for χ parameters and HSP is in formulation and process development, where solvents or non-solvents need to be selected for existing compounds, often as part of a balance of multiple properties (vapor pressure, surface tension, etc.) or for mixtures. In this case, the prediction tools need to cover a broad chemical space, but do not need to be able to handle novel materials, so the existing data-driven approaches, either through machine learning or fits to experimental data, are a strong choice.
Another important consideration when using prediction tools for HSP (e.g., RED) is the acceptable amount of uncertainty in the prediction. For example, when predicting solvents for selective dissolution of components from mixed plastic waste, Soyemi and Szilvási suggested that a spread of at least 0.2 in the RED is needed to be conclusive about whether a solvent would dissolve one polymer and not the other, although in their final recommendations they suggest a RED < 0.6 for a good solvent and RED > 0.9 for non-solvent. This means that the error in predictions must be significantly lower than 0.2 so that one can be confident in the predictions and ability to apply them.90 Sanchez-Lengeling et al. considered the error in the Ra and Ro values as well as the uncertainty in the experimental data, analyzing the accuracy of the model at different extremes of Ro values. They found that the average model accuracy at low values of Ro was low when RED < 1 and high when RED > 1 and vice versa when Ro was high. Although they did not set a specific target error in RED to consider the model acceptable, they highlight the complexity in drawing conclusions from the results and the importance of assessing how each contribution impacts the mean error.89 This is a particularly important point when considering the end user of the prediction tools, as the acceptable error and relevant differences between parameter values will vary based on the precision needed for the application. As discussed here, HSP and χ parameter are most frequently used industrially for solvent selection and, while some precision is needed to differentiate a solvent vs. non-solvent, the values are not often used for phase equilibrium calculations (although both could be) and thus categorical and ranking accuracy (e.g., ranking solvents by their RED value) is more important than their numerical accuracy.
3.3. Activity coefficients
The third important thermodynamic parameter, the activity coefficient, accounts for how phase equilibrium deviates from ideality and is a function of the temperature, pressure, composition, and chemical species. The calculated activity coefficients can be used to perform thermodynamic calculations for process design and to predict the phase diagrams, though prior work has shown that this is complex due to the high molecular weight asymmetry between polymer and solvent91 and insufficiently detailed experimental data.92 The activity of component i in a polymer solution mixture is related to the activity coefficient as, ai = γixi where xi is the mole fraction of species i. From Flory–Huggins theory, the activity coefficient can be determined from the activity of the solvent a2,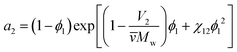 | (8) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is the particle specific volume of the polymer. We note here that the activity can also be written in relation to the osmotic pressure as −ln
is the particle specific volume of the polymer. We note here that the activity can also be written in relation to the osmotic pressure as −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a2 = RTΠV2 and can be combined with eqn (8) and expanded in powers of concentration to obtain the Flory–Huggins expression for the osmotic virial expansion,
a2 = RTΠV2 and can be combined with eqn (8) and expanded in powers of concentration to obtain the Flory–Huggins expression for the osmotic virial expansion,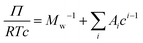 | (9) |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) . The second virial coefficient A2 can further be shown to be related to χ as,
. The second virial coefficient A2 can further be shown to be related to χ as,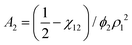 | (10) |
Activity coefficients have frequently been predicted based on theoretical models fit to experimental data. These methods are limited in that they require experimental values and often the molecules must be able to be split into representative functional groups since, for polymers, the models are built on group contribution theory. This makes these methods appropriate for common polymer/solvent pairs that are well-characterized, but have limited utility for new materials. In addition to the existing theoretical models, molecular dynamics-based calculations have been used for thermodynamic property prediction, including activity coefficients.10,92 Most promising of these is use of the COSMO-RS model, which uses quantum chemical calculations to predict the chemical potential in the liquid state, and thus many thermodynamic properties.75 COSMO-RS does not need experimental data on the polymer molecule and only relies on element-specific parameters, but it does require expensive calculations to arrive at the predictions. Thus, COSMO-RS and similar approaches are promising in that they do not require extensive experimental data, but they are still limited for screening a large polymer–solvent chemical space.
To overcome the weaknesses of classic theoretical models and simulation-based prediction tools like COSMO-RS, machine learning tools trained on experimental measurements are being explored. Sanchez Medina et al. developed a novel Gibbs–Helmholtz graph neural network (GH-GNN) approach to predict infinite dilution activity coefficients of polymer solutions.10 The GH-GNN architecture first represents the polymer and solvent with separate graphs. These graphs are passed through a GNN to create vector embeddings of the chemical species, which are then used to build a mixture graph that represents the solute/solvent interactions. They curated a data set of weight fraction-based activity coefficients, which was drawn from volume XIV of the DECHEMA Chemistry Data series.93 They showed that for interpolation, where the model predicted systems within the polymer and solvent space of the training data, their GNN-based methods significantly outperformed a random forest model for predicting activity coefficients (Fig. 6). Interestingly, the authors show that pretraining their GH-GNN on a dataset of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 small molecule activity coefficients reduced the error for predicting polymer activity coefficients by up to 23.5% (GH-GNN (PSS) in Fig. 6).10 This result highlights the effectiveness of transfer learning in overcoming persistent challenges of data scarcity for polymer informatics. The performance of the models when extrapolated to new solvents that had not previously been seen was poorer, though it still had a lower mean absolute error than when the UNIFAC-ZM and Entropic-FV phenomenological models were used.10
219 small molecule activity coefficients reduced the error for predicting polymer activity coefficients by up to 23.5% (GH-GNN (PSS) in Fig. 6).10 This result highlights the effectiveness of transfer learning in overcoming persistent challenges of data scarcity for polymer informatics. The performance of the models when extrapolated to new solvents that had not previously been seen was poorer, though it still had a lower mean absolute error than when the UNIFAC-ZM and Entropic-FV phenomenological models were used.10
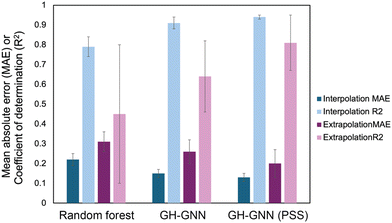 | ||
| Fig. 6 Mean absolute error (MAE, darker colors) and coefficient of determination (R2, lighter colors) for both interpolation (blue colors) and extrapolation (purple colors) predictions of activity coefficient for three models used in Sanchez Medina et al., the random forest model, the GH-GNN (Gibbs–Helmholtz graph neural network) and the GH-GNN (PSS), which is the GH-GNN with transfer learning through pre-training. Data was extracted from Table 2 in ref. 10 using the data set for the system trained on the weight average molar mass. | ||
Interestingly, Sanchez Medina et al. created three data sets, one with the number-average molar mass, Mn, one with the weight-average molar mass, Mw, and one with Mn/Mw, which accounts for the distribution of molecular weights. This polymer molar mass information is added directly into the polymer graph global features, allowing the model to input the polymer mass distribution.10 This helps overcome one of the challenges in making material property predictions for polymers: the molar mass of a polymer is not a single, well-defined value. In splitting this data set, however, they decreased the number of data points for each category, with the number of Mn/Mw data points being approximately 60–70% of the number of data points for Mn and Mw since not all data sources reported both Mn and Mw. Nevertheless, for the systems tested in Sanchez Medina et al. the mean absolute error for the activity coefficients was not significantly different with each data set.10 This could be due to the use of the infinite dilution activity coefficient, where variations in polymer molar mass are less important, or due to the particular polymers chosen. It highlights the unique challenges in creating data sets for polymer property predictions and the need to examine how important it is to include complex behavior in the model development for a given property.
We discussed three important thermodynamic parameters: the Flory–Huggins interaction parameter, the Hansen solubility parameters, and the activity coefficient. In all cases, there are challenges in obtaining sufficient data for accurate predictions using purely data-driven approaches, especially for extrapolation to unseen polymer–solvent pairs. This can limit the use of these approaches for novel polymers or uncommon solvents. However, improvements can be made through additional experimental data collection and integration of computationally predicted data. When considering use of these predictions for process design, greater quantitative accuracy is needed than for uses such as assessing solvent compatibility or some formulation applications. Strong consideration of both the type of desired output (i.e. whether HSP values alone are sufficient or whether a specific difference in RED between two polymer/solvent pairs is needed) and the level of accuracy needed can help research and development scientists and engineers assess the value of a given solubility prediction tool. Similarly, tool developers can consider how the target customer would use the predictions and optimize the experimental data collection and computational time to provide the right level of output. Taken together, the significant number of approaches used in prior studies for these three parameters for polymer solubility show the diversity of approaches and needs for considering the thermodynamic compatibility of polymers and solvents.
4. Point predictions of polymer solubility
Although thermodynamic parameters have great value in designing chemical processes and understanding solubility behavior, they require significant data from each polymer/solvent pair to predict accurately and thus are labor intensive to determine for new materials. There are also many instances when that level of detail is unnecessary and classifications, such as labeling a chemical a “solvent” or “nonsolvent” for a polymer can still greatly aid experimentalists in designing systems, in particular for preparing formulations with polymer solutions or selecting nonsolvents to drive precipitation. Additionally, given the complex parameter space in most multi-component formulations, reporting solubilities in experimentally useful units such as mg mL−1 or weight percent is desirable to speed up formulation development. Thus, many researchers have been developing methods to classify solvent/nonsolvent and make quantitative solubility predictions, outcomes we refer to as “point predictions of polymer solubility.”These point predictions can be developed with different levels of granularity. For example, one could classify the mixture based on a “solvent” or nonsolvent” description, or use multiple descriptions of solubility as is done in the pharmaceutical industry using the USP29-NF24 solubility criteria shown in Table 1.94 In addition to these classifications, one may group solvents into “good solvent,” “poor solvent,” and “theta solvent,” which have a specific meaning in polymer science based on the second virial coefficient (note that the second virial coefficient can be mathematically shown to be related to χ). The second virial coefficient for the chemical potential of the polymer and solvent mixture is positive for a good solvent, zero for a theta solvent, and negative for a poor solvent.95 We will not discuss this case specifically here, as it is related to thermodynamic parameters discussed previously, but it is important to be cautious with nomenclature for solvent classifications due to these precise definitions.
| Descriptive term | Parts of solvent required for 1 part of solute |
|---|---|
| Very soluble | Less than 1 |
| Freely soluble | From 1–10 |
| Soluble | From 10–30 |
| Sparingly soluble | From 30–100 |
| Slightly soluble | From 100–1000 |
| Very slightly soluble | From 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Practically insoluble or insoluble | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and greater 000 and greater |
Simple classification of solvent/nonsolvent is particularly valuable for covering a wide chemical space where selection of a solvent or nonsolvent is the desired outcome. Chandrasekaran et al. used a fully data-driven approach with a large database of 4500 polymers and provided information on whether 24 solvents were solvents or nonsolvents for a given polymer.27 They trained a neural network model on the dataset, with the neural network functioning as a binary classifier. They found the model accuracy to be 93.8% accurate for the test set containing polymers/solvents that the model was not trained on. To assess how this compares to existing methods, they predicted the Hildebrand parameter for all polymers in the data set and classified the solvents into solvent or nonsolvent for the polymers based on the predicted Hildebrand parameter. The accuracy of the classification of “solvent” was only 50% and 70% for nonsolvent using this method, significantly worse than the neural network classification model.27 The predictions from this classification model have been implemented in the Polymer Genome informatics platform.96
Although the polymer space in Chandrasekaran et al. was large, only 24 solvents were used and therefore predictions were unable to be made outside of the 24 solvents. This was in part due to the use of one-hot encoding, which gives each solvent a specific numerical value but does not account for the solvent properties, thus limiting its generalization ability. Further work by Kern et al. aimed to overcome this through use of a hierarchical fingerprinting method with 690 features at 3 different length scales.28 Using an expanded data set with 3373 polymers and 51 solvents, they found that when encoding solvent structure, the model performed better and had less uncertainty than when using a one-hot encoding for the solvent structure. The performance of a random forest classifier model on unseen solvents, which was only possible with the solvent structural encoding fingerprinting, was only modest, which was attributed to the model not seeing many solvents that were similar to the test solvent given a total of 51 solvents in the data set.28 This highlights that, although classification models are promising for experimental guidance with less data than thermodynamic solubility predictions, a diverse chemical space for training data is still necessary to enable good predictions of unseen polymers and solvents.
Another type of point prediction for solubility is prediction of a specific amount of polymer that can dissolve in a given amount of solvent at a specified temperature. Although this has similarities to the phase diagram predictions, and finally connects all aspects discussed in this perspective, it can also be done with simulation and data-driven approaches. Furthermore, the specific output of these models is more convenient for experimentalists to use. In one example, Zhou et al. predicted the solubility for polymers typically encountered in plastic waste using MD simulations and COSMO-RS.97 Specifically, MD simulations were used to predict conformations of oligomers and DFT calculations were performed on selected conformations to generate screening charge densities. COSMO-RS was then used to predict thermodynamic properties including the chemical potential of the polymer in the solvent from which the solubility was quantitatively predicted through the following equation,
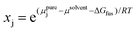 | (11) |
The results from this method reported in Zhou et al. were found to match reasonably well to experimental solubility measurements, though the solubilities were overestimated for nonsolvents. The accuracy was found to be very sensitive to both the length of the oligomer chosen and the number of conformations taken from the MD simulations through the DFT and COSMO-RS calculations, with a clear tradeoff between accuracy and computational cost.97 Although this initial study (2021) focused on two polymers, polyethylene and ethylene vinyl alcohol (EVOH), further work in 202398 extended this to 8 waste polymers and 1007 solvents. Interestingly, in the 2021 study, the authors took the specific solubility predictions and set classification standards, defining solvents to selectively dissolve a polymer in a 2-polymer mixture as solvents having solubility greater than 10 wt% for one polymer and lower than 1 wt% for the other. From the predictions of solubility and subsequent classification, a few solvents were determined to be selective for EVOH over polyethylene, providing value to the solvent-targeted recovery and precipitation (STRAP) process.98 This highlights the value of classification results for industrial problems, but in this case using thermodynamic predictions rather than the machine learning models discussed above.27,28 The 2023 Zhou et al. work used a similar method to determine selective polymers as the 2021 work, but instead of a single classification (selective or not), they ranked the solvents through a selectivity value based on the solubility difference between the target polymer and the other polymers at the operating temperature, with the best solvents having the maximum separation (highest selectivity), providing greater granularity to classifying the solvents and more valuable predictions.98
To our knowledge, there are no current studies that use a purely data-driven approach to predict quantitative values of polymer solubility. This is likely due to the low availability and low quality of polymer solubility data (e.g., important information is often missing from reported values, including polymer molecular weight, degree of crystallinity, temperature, etc.). However, existing data sets for organic small molecule compounds, in particular active pharmaceutical ingredients (API), are more controlled, diverse, and well-reported. Thus, we will briefly discuss a purely data-driven approach from the pharmaceutical industry that focused on predicting API solubility values at a single temperature.99 The model performance for the scenario where the API/solvent pair were previously seen was relatively good with an R2 of 0.68 and an MAE of 0.43, but when applying the model to previously unseen solutes, the performance dropped significantly, with an R2 of 0.39 and MAE of 0.69.99 In practical terms, the first scenario applies when some API solubility points are known, but more are desired, while the second applies when a new API molecule is being investigated, a more common industrial need. Interestingly, the study compared these purely data driven predictions to COSMO-RS predictions and to a hybrid method of the data driven and COSMO-RS approaches. The purely data driven approach significantly outperformed the purely COSMO-RS approach, but was not as accurate as the hybrid method.99 This highlights that, at least for the data set size used (75 API and 49 solvents), supplementing data-driven models with thermodynamic calculations and vice versa can significantly improve predictive performance, especially for components unseen in the training data, a scenario of significant value in new materials development.
Predicting polymer solubility at points or through generalized compatibility has value in leading experimental planning and decreasing trial-and-error approaches used to find suitable solvents for polymers. These point predictions of solubility range in granularity from the most specific solubility values (e.g., in parts polymer/parts solvent at a given temperature and molecular weight) to binary classification (e.g. solvent/nonsolvent). Moreover, there is a positive correlation between the levels of granularity (e.g., solvent/nonsolvent classification can be estimated from thermodynamic interaction parameters, which can in turn be determined from the phase diagram) and the number of data points (experimental or computational) needed to obtain accurate predictions. Often the tradeoff is made between data fidelity and chemical composition space. For instance, models developed to cover a broad parameter space are restricted to binary classification or other simple point predictions, while models providing entire phase diagrams (broader applicability) are developed for only select polymers. Combining experimental and computational data for model training can improve accuracy in the small data limit, but they still require significant investment in time and money to improve accuracy. Considering these types of predictions as a spectrum, rather than each application separately, can help in developing models for specific R&D needs and enables assessment and management of the tradeoffs in level of detail vs. effort required. Although the discussion of granularity here focused on classification schemes and specific quantitative values, it can also be considered for granularity in temperature, molecular weight, crystallinity and other polymer solution properties that are known to affect the observed solubility, but add significant experimental needs if they were to be fully included in predictions.
5. Future outlook
We have shown throughout this perspective that there are many approaches to predicting the ability of a solvent to dissolve a polymer. The output of these models ranges from phase diagrams to classifications of solvent/nonsolvent to thermodynamic parameters, with each providing their own value for research and product/process development. This analysis of the field also highlights the need to combine disparate data sets for one purpose. The rising capabilities in ML provide an opportunity to take a new approach to solve a decades-old challenge, providing prediction capabilities beyond what is covered in an experimental dataset and incorporating experimental and simulation data to improve prediction accuracy. However, there are still a number of persistent challenges in developing accurate predictions for a broad polymer chemistry and structure space. A large hurdle is the small amount of high-quality data available, a common problem throughout materials informatics, but particularly significant in the polymer field. As we showed here, computational predictions merged with experimental data and integration of small molecule datasets can help for some simple cases, but due to the complexity of polymers, these models are limited. A second crucial challenge is the availability of next-level polymer features. The commonly used databases have a strong set of representative solubility, thermodynamic parameter, or classification data that is tied to the polymer name, but further details such as molecular weight, dispersity, temperature, monomeric composition and ratios, degree of crystallinity, and process history are lacking and, if available, do not cover a broad space. Given the known sensitivity of solubility to these factors, the prediction capability is limited without more available information on these features.In addition to the broader array of polymer chemical and structural features that would improve generalizability of the predictions, applications in polymer processing and assembly would benefit from additional data and prediction of the kinetics during dissolution and precipitation. For instance, Amrihesari et al. developed an experimental method for data collection of two kinetic parameters, the induction time and delta-t, which tie to the time to first measurable precipitates and plateau extent of precipitation, respectively, with a moderately high throughput method.57 As large molecules, polymer dissolution and precipitation can be prohibitively slow, preventing some formulations from being used beyond the lab. However, to our knowledge, predictive capabilities for polymer dissolution and precipitation kinetics have not yet been investigated, especially by data-driven methods, which would be particularly valuable given the scarcity of computational predictions for these long timescale kinetics.
Moving beyond the property prediction capabilities that are the primary focus in this perspective, there is potential in using explainable artificial intelligence (AI), or combining the datasets with AI tools to develop new theories. In the simplest view, this could include identification of new patterns that might indicate new directions for research, as was done in Aoki et al. with the identification of latent variables beyond those that correlated with the three HSP forces and that could be potential significant contributors to solubility.26 However, in the long term, explainable AI could be used to find corrections to current theory, derive new functional forms, or seed development of new theoretical models, pushing forward fundamental science on the backbone of data science.
Throughout this perspective, we have highlighted the potential use cases for the different approaches to predicting polymer solubility. What we have not thoroughly considered here is how accurate the predictions need to be in practice. As we have noted, to improve accuracy, the most important developments require increasing the amount of available data. Running computational models, especially when they require simulation-provided data, is energy intensive and can have a large carbon footprint. Additionally, experimentation, even when high throughput methods can be used, is resource intensive. Two of the studies discussed in the HSP section analyzed the allowable error that would enable these predictions.89,90 However, most research is focused on maximizing the accuracy without assessing what an acceptable error tolerance should be for the application of interest. Further collaboration between end users and scientists and engineers developing the models could provide interesting insights that save significant time and money as these tools mature.
Overall, exciting developments in predicting solubility, polymer/solvent phase behavior, and compatibility have been made in recent years and, importantly, these innovations are coming from many directions. The breadth of approaches provides usable predictions for many industries and research applications, while also helping overcome weaknesses in some methods to still inform material and process design. For example, classification methods can more easily cover a broad chemical space and improve screening, while predictions of phase diagrams can inform processing pathways for precise control. Despite the progress, challenges exist in obtaining sufficient high quality datasets and covering a broad enough feature space for complex polymer material needs. Collaborative efforts between end users and model developers as well as between scientific domains of chemistry, physics, computer science, chemical engineering and materials science provide exciting opportunities for further advancing these predictions and pushing forward the science and engineering of polymer solutions.
Author contributions
Jeffrey Ethier: conceptualization, formal analysis, investigation, visualization, writing – original draft, writing – review and editing. Evan Antoniuk: conceptualization, writing – review and editing. Blair Brettmann: conceptualization, formal analysis, investigation, visualization, writing – original draft, writing – review and editing.Data availability
Article does not contain original data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was produced under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. JE would like to acknowledge the support of the Materials and Manufacturing Directorate of the Air Force Research Laboratory. BB would like to acknowledge the support of the Office of Naval Research through a Multidisciplinary University Research Initiative (MURI) Grant N00014-20-1-2586.References
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- M. A. Butt, Thin-Film Coating Methods: A Successful Marriage of High-Quality and Cost-Effectiveness—A Brief Exploration, Coatings, 2022, 12(8), 1115, DOI:10.3390/coatings12081115.
- A. Pierre, M. Sadeghi, M. M. Payne, A. Facchetti, J. E. Anthony and A. C. Arias, All-Printed Flexible Organic Transistors Enabled by Surface Tension-Guided Blade Coating, Adv. Mater., 2014, 26(32), 5722–5727, DOI:10.1002/adma.201401520.
- P. Cognard, Chapter 2 – Equipment for the Application of Adhesives and Sealants: Mixing, Metering, Coating or Applying the Adhesives, in Handbook of Adhesives and Sealants, ed. P. Cognard, Adhesives and Sealants, Elsevier Science Ltd, 2006, vol. 2, pp. 51–xxxvii DOI:10.1016/S1874-5695(06)80013-8.
- X. Wang and R. A. Weiss, A Facile Method for Preparing Sticky, Hydrophobic Polymer Surfaces, Langmuir, 2012, 28(6), 3298–3305, DOI:10.1021/la204564b.
- Y. M. Gross and S. Ludwigs, P(NDI2OD-T2) Revisited – Aggregation Control as Key for High Performance n-Type Applications, Synth. Met., 2019, 253, 73–87, DOI:10.1016/j.synthmet.2019.04.017.
- T.-Q. Nguyen, R. Y. Yee and B. J. Schwartz, Solution Processing of Conjugated Polymers: The Effects of Polymer Solubility on the Morphology and Electronic Properties of Semiconducting Polymer Films, J. Photochem. Photobiol., A, 2001, 144(1), 21–30, DOI:10.1016/S1010-6030(01)00377-X.
- K. E. Strawhecker, S. K. Kumar, J. F. Douglas and A. Karim, The Critical Role of Solvent Evaporation on the Roughness of Spin-Cast Polymer Films, Macromolecules, 2001, 34(14), 4669–4672, DOI:10.1021/ma001440d.
- E. I. Sanchez Medina, S. Kunchapu and K. Sundmacher, Gibbs–Helmholtz Graph Neural Network for the Prediction of Activity Coefficients of Polymer Solutions at Infinite Dilution, J. Phys. Chem. A, 2023, 127(46), 9863–9873, DOI:10.1021/acs.jpca.3c05892.
- P. Knychała, K. Timachova, M. Banaszak and N. P. Balsara, 50th Anniversary Perspective: Phase Behavior of Polymer Solutions and Blends, Macromolecules, 2017, 50(8), 3051–3065, DOI:10.1021/acs.macromol.6b02619.
- J. K. Brennan and W. G. Madden, Phase Coexistence Curves for Off-Lattice Polymer−Solvent Mixtures:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gibbs-Ensemble Simulations, Macromolecules, 2002, 35(7), 2827–2834, DOI:10.1021/ma0112321.
Gibbs-Ensemble Simulations, Macromolecules, 2002, 35(7), 2827–2834, DOI:10.1021/ma0112321. - M. Fayaz-Torshizi and E. A. Müller, Coarse-Grained Molecular Simulation of Polymers Supported by the Use of the SAFT-Γ\gamma\ Mie Equation of State, Macromol. Theory Simul., 2022, 31(1), 2100031, DOI:10.1002/mats.202100031.
- Q. P. Chen, S. Xie, R. Foudazi, T. P. Lodge and J. I. Siepmann, Understanding the Molecular Weight Dependence of χ and the Effect of Dispersity on Polymer Blend Phase Diagrams, Macromolecules, 2018, 51(10), 3774–3787, DOI:10.1021/acs.macromol.8b00604.
- N. Blagojevic and M. Müller, Simulation of Membrane Fabrication via Solvent Evaporation and Nonsolvent-Induced Phase Separation, ACS Appl. Mater. Interfaces, 2023, 15(50), 57913–57927, DOI:10.1021/acsami.3c03126.
- S. Najafi, J. McCarty, K. T. Delaney, G. H. Fredrickson and J.-E. Shea, Field-Theoretic Simulation Method to Study the Liquid–Liquid Phase Separation of Polymers, in Phase-Separated Biomolecular Condensates: Methods and Protocols, ed. H.-X. Zhou, J.-H. Spille and P. R. Banerjee, Springer US, New York, NY, 2023, pp. 37–49 DOI:10.1007/978-1-0716-2663-4_2.
- G. H. Fredrickson, V. Ganesan and F. Drolet, Field-Theoretic Computer Simulation Methods for Polymers and Complex Fluids, Macromolecules, 2002, 35(1), 16–39, DOI:10.1021/ma011515t.
- T. B. Martin and D. J. Audus, Emerging trends in machine learning: a polymer perspective, ACS Polym. Au, 2023, 3(3), 239–258, DOI:10.1021/acspolymersau.2c00053.
- S. Venkatram, R. Batra, L. Chen, C. Kim, M. Shelton and R. Ramprasad, Predicting Crystallization Tendency of Polymers Using Multifidelity Information Fusion and Machine Learning, J. Phys. Chem. B, 2020, 124(28), 6046–6054, DOI:10.1021/acs.jpcb.0c01865.
- L. Chen, C. Kim, R. Batra, J. P. Lightstone, C. Wu, Z. Li, A. A. Deshmukh, Y. Wang, H. D. Tran, P. Vashishta, G. A. Sotzing, Y. Cao and R. Ramprasad, Frequency-Dependent Dielectric Constant Prediction of Polymers Using Machine Learning, npj Comput. Mater., 2020, 6(1), 1–9, DOI:10.1038/s41524-020-0333-6.
- E. R. Antoniuk, P. Li, B. Kailkhura and A. M. Hiszpanski, Representing Polymers as Periodic Graphs with Learned Descriptors for Accurate Polymer Property Predictions, J. Chem. Inf. Model., 2022, 62(22), 5435–5445, DOI:10.1021/acs.jcim.2c00875.
- A. L. Nazarova, L. Yang, K. Liu, A. Mishra, R. K. Kalia, K. Nomura, A. Nakano, P. Vashishta and P. Rajak, Dielectric Polymer Property Prediction Using Recurrent Neural Networks with Optimizations, J. Chem. Inf. Model., 2021, 61(5), 2175–2186, DOI:10.1021/acs.jcim.0c01366.
- A. Patra, R. Batra, A. Chandrasekaran, C. Kim, T. D. Huan and R. Ramprasad, A Multi-Fidelity Information-Fusion Approach to Machine Learn and Predict Polymer Bandgap, Comput. Mater. Sci., 2020, 172, 109286, DOI:10.1016/j.commatsci.2019.109286.
- H. Doan Tran, C. Kim, L. Chen, A. Chandrasekaran, R. Batra, S. Venkatram, D. Kamal, J. P. Lightstone, R. Gurnani, P. Shetty, M. Ramprasad, J. Laws, M. Shelton and R. Ramprasad, Machine-Learning Predictions of Polymer Properties with Polymer Genome, J. Appl. Phys., 2020, 128(17), 171104, DOI:10.1063/5.0023759.
- L. Tao, V. Varshney and Y. Li, Benchmarking Machine Learning Models for Polymer Informatics: An Example of Glass Transition Temperature, J. Chem. Inf. Model., 2021, 61(11), 5395–5413, DOI:10.1021/acs.jcim.1c01031.
- Y. Aoki, S. Wu, T. Tsurimoto, Y. Hayashi, S. Minami, O. Tadamichi, K. Shiratori and R. Yoshida, Multitask Machine Learning to Predict Polymer–Solvent Miscibility Using Flory–Huggins Interaction Parameters, Macromolecules, 2023, 56(14), 5446–5456, DOI:10.1021/acs.macromol.2c02600.
- A. Chandrasekaran, C. Kim, S. Venkatram and R. Ramprasad, A Deep Learning Solvent-Selection Paradigm Powered by a Massive Solvent/Nonsolvent Database for Polymers, Macromolecules, 2020, 53(12), 4764–4769, DOI:10.1021/acs.macromol.0c00251.
- J. Kern, S. Venkatram, M. Banerjee, B. Brettmann and R. Ramprasad, Solvent Selection for Polymers Enabled by Generalized Chemical Fingerprinting and Machine Learning, Phys. Chem. Chem. Phys., 2022, 24(43), 26547–26555, 10.1039/D2CP03735A.
- J. G. Ethier, D. J. Audus, D. C. Ryan and R. A. Vaia, Integrating Theory with Machine Learning for Predicting Polymer Solution Phase Behavior, Giant, 2023, 15, 100171, DOI:10.1016/j.giant.2023.100171.
- S. Venkatram, C. Kim, A. Chandrasekaran and R. Ramprasad, Critical Assessment of the Hildebrand and Hansen Solubility Parameters for Polymers, J. Chem. Inf. Model., 2019, 59(10), 4188–4194, DOI:10.1021/acs.jcim.9b00656.
- P. J. Flory, Thermodynamics of High Polymer Solutions, J. Chem. Phys., 1942, 10(1), 51–61, DOI:10.1063/1.1723621.
- M. L. Huggins, Theory of Solutions of High Polymers1, J. Am. Chem. Soc., 1942, 64(7), 1712–1719, DOI:10.1021/ja01259a068.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- P. J. Flory, Statistical Thermodynamics of Liquid Mixtures, J. Am. Chem. Soc., 1965, 87(9), 1833–1838, DOI:10.1021/ja01087a002.
- P. J. Flory, R. A. Orwoll and A. Vrij, Statistical Thermodynamics of Chain Molecule Liquids. I. An Equation of State for Normal Paraffin Hydrocarbons, J. Am. Chem. Soc., 1964, 86(17), 3507–3514, DOI:10.1021/ja01071a023.
- P. J. Flory, R. A. Orwoll and A. Vrij, Statistical Thermodynamics of Chain Molecule Liquids. II. Liquid Mixtures of Normal Paraffin Hydrocarbons, J. Am. Chem. Soc., 1964, 86(17), 3515–3520, DOI:10.1021/ja01071a024.
- I. C. Sanchez and R. H. Lacombe, Statistical Thermodynamics of Polymer Solutions, Macromolecules, 1978, 11(6), 1145–1156, DOI:10.1021/ma60066a017.
- R. H. Lacombe and I. C. Sanchez, Statistical Thermodynamics of Fluid Mixtures, J. Phys. Chem., 1976, 80(23), 2568–2580, DOI:10.1021/j100564a009.
- K. F. Freed, New Lattice Model for Interacting, Avoiding Polymers with Controlled Length Distribution, J. Phys. A: Math. Gen., 1985, 18(5), 871, DOI:10.1088/0305-4470/18/5/019.
- J. Dudowicz and K. F. Freed, Effect of Monomer Structure and Compressibility on the Properties of Multicomponent Polymer Blends and Solutions: 1. Lattice Cluster Theory of Compressible Systems, Macromolecules, 1991, 24(18), 5076–5095, DOI:10.1021/ma00018a014.
- Y. Hu, S. M. Lambert, D. S. Soane and J. M. Prausnitz, Double-Lattice Model for Binary Polymer Solutions, Macromolecules, 1991, 24(15), 4356–4363, DOI:10.1021/ma00015a017.
- Y. Hu, H. Liu, D. S. Soane and J. M. Prausnitz, Binary Liquid-Liquid Equilibria from a Double-Lattice Model, Fluid Phase Equilib., 1991, 67, 65–86, DOI:10.1016/0378-3812(91)90048-C.
- J. S. Oh and Y. C. Bae, Liquid-Liquid Equilibria for Binary Polymer Solutions from Modified Double-Lattice Model, Polymer, 1998, 39(5), 1149–1154, DOI:10.1016/S0032-3861(97)00305-4.
- C. Qian, S. J. Mumby and B. E. Eichinger, Phase Diagrams of Binary Polymer Solutions and Blends, Macromolecules, 1991, 24(7), 1655–1661, DOI:10.1021/ma00007a031.
- C. Qian, S. J. Mumby and B. E. Eichinger, Existence of Two Critical Concentrations in Binary Phase Diagrams, J. Polym. Sci., Part B: Polym. Phys., 1991, 29(5), 635–637, DOI:10.1002/polb.1991.090290514.
- R. Koningsveld, L. A. Kleintjens and A. R. Shultz, Liquid–Liquid Phase Separation in Multicomponent Polymer Solutions. IX. Concentration-Dependent Pair Interaction Parameter from Critical Miscibility Data on the System Polystyrene–Cyclohexane, J. Polym. Sci., Part A-2, 1970, 8(8), 1261–1278, DOI:10.1002/pol.1970.160080802.
- Y. C. Bae, J. J. Shim, D. S. Soane and J. M. Prausnitz, Representation of Vapor–Liquid and Liquid–Liquid Equilibria for Binary Systems Containing Polymers: Applicability of an Extended Flory–Huggins Equation, J. Appl. Polym. Sci., 1993, 47(7), 1193–1206, DOI:10.1002/app.1993.070470707.
- Y. C. Bae, S. M. Lambert, D. S. Soane and J. M. Prausnitz, Cloud-Point Curves of Polymer Solutions from Thermooptical Measurements, Macromolecules, 1991, 24(15), 4403–4407, DOI:10.1021/ma00015a024.
- S. Saeki, N. Kuwahara, M. Nakata and M. Kaneko, Upper and Lower Critical Solution Temperatures in Poly (Ethylene Glycol) Solutions, Polymer, 1976, 17(8), 685–689, DOI:10.1016/0032-3861(76)90208-1.
- K. S. Siow, G. Delmas and D. Patterson, Cloud-Point Curves in Polymer Solutions with Adjacent Upper and Lower Critical Solution Temperatures, Macromolecules, 1972, 5(1), 29–34, DOI:10.1021/ma60025a008.
- J. G. Ethier, R. K. Casukhela, J. J. Latimer, M. D. Jacobsen, A. B. Shantz and R. A. Vaia, Deep Learning of Binary Solution Phase Behavior of Polystyrene, ACS Macro Lett., 2021, 10(6), 749–754, DOI:10.1021/acsmacrolett.1c00117.
- J. G. Ethier, R. K. Casukhela, J. J. Latimer, M. D. Jacobsen, B. Rasin, M. K. Gupta, L. A. Baldwin and R. A. Vaia, Predicting Phase Behavior of Linear Polymers in Solution Using Machine Learning, Macromolecules, 2022, 55(7), 2691–2702, DOI:10.1021/acs.macromol.2c00245.
- A. R. Shultz and P. J. Flory, Phase Equilibria in Polymer—Solvent Systems1,2, J. Am. Chem. Soc., 1952, 74(19), 4760–4767, DOI:10.1021/ja01139a010.
- R. Koningsveld and A. J. Staverman, Determination of Critical Points in Multicomponent Polymer Solutions, J. Polym. Sci., Part C: Polym. Symp., 1967, 16(3), 1775–1786, DOI:10.1002/polc.5070160352.
- S. J. Mumby, P. Sher and B. E. Eichinger, Phase Diagrams of Quasi-Binary Polymer Solutions and Blends, Polymer, 1993, 34(12), 2540–2545, DOI:10.1016/0032-3861(93)90586-Y.
- V. J. Klenin and S. L. Shmakov, Features of Phase Separation in Polymeric Systems: Cloud-Point Curves (Discussion), Univers. J. Mater. Sci., 2013, 1(2), 39–45, DOI:10.13189/ujms.2013.010205.
- M. Amrihesari, A. Murry and B. Brettmann, Towards Standardized Polymer Solubility Measurements Using a Parallel Crystallizer, Polymer, 2023, 278, 125983, DOI:10.1016/j.polymer.2023.125983.
- S. Matsuda, Thermodynamics of Formation of Porous Polymeric Membrane from Solutions, Polym. J., 1991, 23(5), 435–444, DOI:10.1295/polymj.23.435.
- R. Pervin, P. Ghosh and M. G. Basavaraj, Tailoring Pore Distribution in Polymer Films via Evaporation Induced Phase Separation, RSC Adv., 2019, 9(27), 15593–15605, 10.1039/C9RA01331H.
- J. Zhao, G. Luo, J. Wu and H. Xia, Preparation of Microporous Silicone Rubber Membrane with Tunable Pore Size via Solvent Evaporation-Induced Phase Separation, ACS Appl. Mater. Interfaces, 2013, 5(6), 2040–2046, DOI:10.1021/am302929c.
- A. L. Fassler, G. A. Horrocks, R. R. Kohlmeyer and M. F. Durstock, Microstructure Control in Printable Porous Polymer Composites, Composites, Part B, 2023, 264, 110926, DOI:10.1016/j.compositesb.2023.110926.
- G. M. Kontogeorgis, R. Dohrn, I. G. Economou, J.-C. de Hemptinne, A. ten Kate, S. Kuitunen, M. Mooijer, L. F. Žilnik and V. Vesovic, Industrial Requirements for Thermodynamic and Transport Properties: 2020, Ind. Eng. Chem. Res., 2021, 60(13), 4987–5013, DOI:10.1021/acs.iecr.0c05356.
- J.-C. de Hemptinne, G. M. Kontogeorgis, R. Dohrn, I. G. Economou, A. ten Kate, S. Kuitunen, L. Fele Žilnik, M. G. De Angelis and V. Vesovic, A View on the Future of Applied Thermodynamics, Ind. Eng. Chem. Res., 2022, 61(39), 14664–14680, DOI:10.1021/acs.iecr.2c01906.
- O. Pfohl and R. Dohrn, Provision of Thermodynamic Properties of Polymer Systems for Industrial Applications, Fluid Phase Equilib., 2004, 217(2), 189–199, DOI:10.1016/j.fluid.2003.06.001.
- C. E. Sing and M. Olvera de la Cruz, Polyelectrolyte Blends and Nontrivial Behavior in Effective Flory–Huggins Parameters, ACS Macro Lett., 2014, 3(8), 698–702, DOI:10.1021/mz500202n.
- B. C. Bussamra, D. Sietaram, P. Verheijen, S. I. Mussatto, A. C. da Costa, L. van der Wielen and M. Ottens, A Critical Assessment of the Flory–Huggins (FH) Theory to Predict Aqueous Two-Phase Behaviour, Sep. Purif. Technol., 2021, 255, 117636, DOI:10.1016/j.seppur.2020.117636.
- K. Kamide, K. Sugamiya, T. Kawai and Y. Miyazaki, The Concentration Dependence of the Polymer–Solvent Interaction Parameter for Polystyrene–Methylcyclohexane System, Polym. J., 1980, 12(1), 67–69, DOI:10.1295/polymj.12.67.
- M. Karimi, W. Albrecht, M. Heuchel, T. Weigel and A. Lendlein, Determination of Solvent/Polymer Interaction Parameters of Moderately Concentrated Polymer Solutions by Vapor Pressure Osmometry, Polymer, 2008, 49(10), 2587–2594, DOI:10.1016/j.polymer.2008.03.036.
- J. S. Pedersen and C. Sommer, Temperature Dependence of the Virial Coefficients and the Chi Parameter in Semi-Dilute Solutions of PEG, in Scattering Methods and the Properties of Polymer Materials, ed. N. Stribeck and B. Smarsly, Springer, Berlin, Heidelberg, 2005, pp. 70–78 DOI:10.1007/b107350.
- C. Fürst, P. Zhang, S. V. Roth, M. Drechsler and S. Förster, Self-Assembly of Block Copolymers via Micellar Intermediate States into Vesicles on Time Scales from Milliseconds to Days, Polymer, 2016, 107, 434–444, DOI:10.1016/j.polymer.2016.09.087.
- E. Díez, G. Ovejero, M. D. Romero and I. Díaz, Polymer–Solvent Interaction Parameters of SBS Rubbers by Inverse Gas Chromatography Measurements, Fluid Phase Equilib., 2011, 308(1), 107–113, DOI:10.1016/j.fluid.2011.06.018.
- J. K. Lee, S. X. Yao, G. Li, M. B. G. Jun and P. C. Lee, Measurement Methods for Solubility and Diffusivity of Gases and Supercritical Fluids in Polymers and Its Applications, Polym. Rev., 2017, 57(4), 695–747, DOI:10.1080/15583724.2017.1329209.
- D. Patterson, Role of Free Volume Changes in Polymer Solution Thermodynamics, J. Polym. Sci., Part C: Polym. Symp., 1967, 16(6), 3379–3389, DOI:10.1002/polc.5070160632.
- J. Biroa, L. Zeman and D. Patterson, Prediction of the x Parameter by the Solubility Parameter and Corresponding States Theories, Macromolecules, 1971, 4(1), 30–35, DOI:10.1021/ma60019a008.
- COSMO-RS. https://www.scm.com/product/cosmo-rs/, (accessed 2024-04-10).
- X.-Z. Zhang, Z.-Y. Lu and H.-J. Qian, Temperature Transferable and Thermodynamically Consistent Coarse-Grained Model for Binary Polymer Systems, Macromolecules, 2023, 56(10), 3739–3753, DOI:10.1021/acs.macromol.3c00315.
- D. J. Kozuch, W. Zhang and S. T. Milner, Predicting the Flory–Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations, Polymers, 2016, 8(6), 241, DOI:10.3390/polym8060241.
- D. Ghonasgi and W. G. Chapman, Prediction of the Properties of Model Polymer Solutions and Blends, AIChE J., 1994, 40(5), 878–887, DOI:10.1002/aic.690400514.
- J. Nistane, L. Chen, Y. Lee, R. Lively and R. Ramprasad, Estimation of the Flory–Huggins Interaction Parameter of Polymer-Solvent Mixtures Using Machine Learning, MRS Commun., 2022, 12(6), 1096–1102, DOI:10.1557/s43579-022-00237-x.
- Polymer Database (PoLyInfo). https://polymer.nims.go.jp/.
- C. M. Hansen, The Universality of the Solubility Parameter, I&EC Prod. Res. Dev., 1969, 8(1), 2–11 Search PubMed.
- A. F. Barton, Solubility Parameters, Chem. Rev., 1975, 75(6), 731–751 CrossRef CAS.
- H. Ahmad and M. Yaseen, Application of a Chemical Group Contribution Technique for Calculating Solubility Parameters of Polymers, Polym. Eng. Sci., 1979, 19(12), 858–863, DOI:10.1002/pen.760191208.
- C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, Second Edition, 2nd edn, CRC Press, Boca Raton, 2007 DOI:10.1201/9781420006834.
- S. Abbott, Hansen Solubility Parameters in Practice. https://www.hansen-solubility.com/HSPiP/.
- S. Abbott, HSPiP Optimal Fitting. HSPiP. https://www.hansen-solubility.com/HSPiP/Optimal-Fitting.php (accessed 2024-04-07).
- G. C. Vebber, P. Pranke and C. N. Pereira, Calculating Hansen Solubility Parameters of Polymers with Genetic Algorithms, J. Appl. Polym. Sci., 2014, 131(1), 39696, DOI:10.1002/app.39696.
- X. Yu, X. Wang, H. Wang, X. Li and J. Gao, Prediction of Solubility Parameters for Polymers by a QSPR Model, QSAR Comb. Sci., 2006, 25(2), 156–161, DOI:10.1002/qsar.200530138.
- B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, A Bayesian Approach to Predict Solubility Parameters, Adv. Theory Simul., 2019, 2(1), 1800069, DOI:10.1002/adts.201800069.
- A. Soyemi and T. Szilvási, Calculated Physicochemical Properties of Glycerol-Derived Solvents to Drive Plastic Waste Recycling, Ind. Eng. Chem. Res., 2023, 62(15), 6322–6337, DOI:10.1021/acs.iecr.2c04567.
- G. M. C. Silva, D. A. Pantano, S. Loehlé and J. A. P. Coutinho, The Challenges of Using COSMO-RS To Describe Polymer Solution Behavior, Ind. Eng. Chem. Res., 2023, 62(48), 20936–20944, DOI:10.1021/acs.iecr.3c03310.
- C. Loschen and A. Klamt, Prediction of Solubilities and Partition Coefficients in Polymers Using COSMO-RS, Ind. Eng. Chem. Res., 2014, 53(28), 11478–11487, DOI:10.1021/ie501669z.
- W. Hao, H. Elbro and P. Alessi, DECHEMA Chemistry Data Series Vol XIV. Polymer Solution Data Collection. Part 2,3, 1993. https://dechema.de/en/Analysis+_+Consulting/Publications/Chemistry+Data+Series/Volume+XIV.html.
- USP29-NF24, 2006. https://ftp.uspbpep.com/v29240/usp29nf24s0_desc-sol-2-5.html, (accessed 2024-04-07).
- J. F. Douglas, J. Dudowicz and K. F. Freed, Lattice Model of Equilibrium Polymerization. VI. Measures of Fluid “Complexity” and Search for Generalized Corresponding States, J. Chem. Phys., 2007, 127(22), 224901, DOI:10.1063/1.2785187.
- Polymer Genome. https://www.polymergenome.org/, (accessed 2024-04-07).
- P. Zhou, K. L. Sánchez-Rivera, G. W. Huber and R. C. Van Lehn, Computational Approach for Rapidly Predicting Temperature-Dependent Polymer Solubilities Using Molecular-Scale Models, ChemSusChem, 2021, 14(19), 4307–4316, DOI:10.1002/cssc.202101137.
- P. Zhou, J. Yu, K. L. Sánchez-Rivera, G. W. Huber and R. C. V. Lehn, Large-Scale Computational Polymer Solubility Predictions and Applications to Dissolution-Based Plastic Recycling, Green Chem., 2023, 25(11), 4402–4414, 10.1039/D3GC00404J.
- A. D. Vassileiou, M. N. Robertson, B. G. Wareham, M. Soundaranathan, S. Ottoboni, A. J. Florence, T. Hartwig and B. F. Johnston, A Unified ML Framework for Solubility Prediction across Organic Solvents, Digital Discovery, 2023, 2(2), 356–367, 10.1039/D2DD00024E.
| This journal is © The Royal Society of Chemistry 2024 |