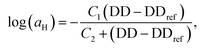Open Access Article
Open Access ArticleHydrophobically modified complex coacervates for designing aqueous pressure-sensitive adhesives†
Larissa
van Westerveld
a,
Julien
Es Sayed
a,
Marijn
de Graaf
a,
Anton H.
Hofman
 *a,
Marleen
Kamperman
*a,
Marleen
Kamperman
 a and
Daniele
Parisi
a and
Daniele
Parisi
 *b
*b
aZernike Institute for Advanced Materials (ZIAM), University of Groningen, Nijenborgh 4, 9747 AG Groningen, the Netherlands. E-mail: a.h.hofman@rug.nl
bEngineering and Technology Institute Groningen (ENTEG), University of Groningen, Nijenborgh 4, 9747 AG Groningen, the Netherlands. E-mail: d.parisi@rug.nl
First published on 7th November 2023
Abstract
The rheology of complex coacervates can be elegantly tuned via the design and control of specific non-covalent hydrophobic interactions between the complexed polymer chains. The well-controlled balance between elasticity and energy dissipation makes complex coacervates perfect candidates for pressure-sensitive adhesives (PSAs). In this work, the polyanion poly(3-sulfopropyl methacrylate) (PSPMA) and the polycation quaternized poly(4-vinylpyridine) (QP4VP) were used to prepare complex coacervates in water. Progressive increase of hydrophobicity is introduced to the polyanion via partial deprotection of the protected precursor. Hence, the polymer chains in the complex coacervates can interact via both electrostatic (controlled by the amount of salt) and hydrophobic (controlled by the deprotection degree) interactions. It was observed that: (i) a rheological time-salt-hydrophobicity superposition principle is applicable, and can be used as a predictive tool for rheology, (ii) the slowdown of the stress relaxation dynamics, due to the increase of hydrophobic stickers (lower deprotection degree), can be captured by the sticky-Rouse model, and (iii) the systematic variation of hydrophobic stickers, amount of salt, and molecular weight of the polymers, enables the identification of optimizing parameters to design aqueous PSA systems. The presented results offer new pathways to control the rheology of complex coacervates and their applicability as PSAs.
1. Introduction
Coacervation is an associative liquid–liquid phase separation into two immiscible liquid phases, often driven by electrostatic and/or hydrophobic interactions, resulting in a polymer-dense phase (the coacervate) and a dilute phase. When coacervation is caused by the interaction of two (oppositely charged) components it is referred to as complex coacervation. Such coacervates are water-based viscoelastic materials and contain typically between 60% and 90% of water.1,2 The great tunability of coacervate flow behaviour spanning from quasi-Newtonian liquid to strong elastic solids has been exploited for a wide range of applications, such as food and cosmetics,3 membranes,4 tissue scaffolds,5 drug carriers,6 and to study the origin of life.7,8 Moreover, it has been discovered that aquatic animals like sandcastle worms are able to use complex coacervates made of oppositely charged proteins as adhesives in underwater conditions.9,10 This finding opened new research directions for soft matter science, where inspiration was obtained from nature and used for the development of synthetic complex coacervate-based adhesives.10–14Water-containing adhesives such as hydrogels, are highly desirable for certain applications, e.g., biomedicine, because of the inherent biocompatibility of water-based systems.15 In the world of adhesion science, the presence of water is detrimental to reach high adhesion performances.16 Water leads to a set of undesired phenomena such as poor contact between adhesive and substrate, and swelling and erosion of the adhesive. Typical hydrogels, in which hydrophilic polymers are covalently crosslinked,17 display a rheological response that is often dominated by the elastic contribution, regardless of the parameters used to tune their mechanical response (crosslink density, pH, temperature, light source, etc.).18,19 Due to the combination of topological, electrostatic and hydrophobic interactions, complex coacervates obtained in a water medium offer a broad range of rheological properties, including highly dissipative contributions to the overall response, making them perfect candidates as adhesives.12,20,21 Previous studies reported the use of complex coacervates as pressure sensitive adhesives (PSAs).11–13 The latter refers to a special class of adhesives, designed to adhere on a wide plethora of surfaces, by simple contact under light pressure. That is, the bonding process occurs without any physical change or chemical reaction.22 The PSA performance mainly depends on bulk energy dissipation during separation of the surfaces, while maintaining a certain degree of elasticity.22 Furthermore, PSAs must be able to quickly make contact via rapid spreading or deformation at the interfaces.22 Extensive work has been performed by the group of Creton on the debonding mechanism, work of adhesion and confinement of PSAs.14,23–26 Usually, the viscoelasticity of PSAs can only be controlled at the molecular level through the density of crosslinks, entanglements and addition of a tackifier.14,22,26,27 The interest for complex coacervates lies in the possibility of tuning, to a great extent, the viscoelasticity, by the formation and control of non-covalent interactions, such as electrostatic, hydrophobic, metal–ligand or cation–π interactions.9,11,16,28,29 Among the various tunable parameters, salt concentration,30 temperature,31 polyelectolyte stoichiometry,32 alcohol,32 water,33 and pH34 were found suitable for generating rheological master curves via superposition principles. That is, frequency-extended viscoelastic spectra can be obtained by systematically changing the above-mentioned parameters, without affecting the nature of the relaxation modes of the systems. Temperature, salt and pH are certainly the most investigated parameters. Very recently, Schröder et al.35 thoroughly discussed the time-temperature, -salt and -pH superposition principles in complex coacervates. Their analysis revealed that for the time-temperature superposition principle, both Arrhenius36–38 and William–Landell–Ferry31–33,35 trend for the horizontal shift factors were found.35 This typically depends on whether the probing temperature is well above the glass transition temperature (Tg) (Arrhenius), or comprised between Tg and +100 K (WLF). Activation energies between 38 and 57 kJ mol−1 were reported by the authors on various complex coacervates systems, and attributed to thermal energy needed to dissociate chain associating sites (stickers), enabling molecular motion.35 The horizontal shift factors in the time-salt superposition principle of complex coacervates follow an Arrhenius trend,13,35,39–41 where typically between 100–500 mM of salt (NaCl) is needed to speed up the dynamics (via the screening of the electrostatic interactions) by one order of magnitude.35 The time-pH superposition principle in complex coacervates, based on weak polyelectrolytes, yields horizontal shift factors that can be captured by a cubic function with varying pH,35 attaining a plateau for pH > 7. To this end, Tekaat et al.34 have shown that the dynamics of complex coacervates are particularly sensitive in the pH range 5–7, as further increase in pH saturates the degree of dissociation (or the charge density) of poly(acrylic acid) (the polyanion), and the shear moduli become pH-insensitive. The effect of controlled hydrophobicity in the complex coacervates on the viscoelasticity has also been the subject of several investigations.40,42,43 However, a systematic study to test whether or not a time-hydrophobicity superposition principle holds for complex coacervates is less known, and therefore addressed in the present work.
Hence, the use of molecularly controlled hydrophobic interactions is here adopted to tune the viscoelasticity and thereby the adhesive properties of complex coacervates. Whereas a few studies successfully introduced a controlled amount of hydrophobic moieties in the sequence of polymer chains,40,44–46 the effect of well-controlled hydrophobic moieties on the rheology of complex coacervate-based adhesives has been marginally investigated.
Mende et al.44 pioneered the studies on the effect of hydrophobicity on the colloidal stability of polyelectrolyte complexes. The polyelectrolytes consisted of maleic anhydride copolymers that were modified to be cationic or anionic and hydrophobic groups were varied to be ethylene, isobutylene or styrene. The authors concluded that the complexes containing more hydrophobic polyelectrolytes were less swollen and more compact. No rheological data were presented in that research. Sadman et al.40 showed that the increase from methyl to ethyl to propyl on quaternized poly(4-vinylpyridine) (QP4VP) complexed with poly(styrene sulfonate) (PSS) had a significant effect on the mechanical behaviour of the formed complex coacervate. More salt was needed to obtain similar viscoelastic behaviour when longer quaternizing alkyl chains were used. It was suggested that hydrophobicity slowed down the viscoelastic response and that swelling with water ultimately determined the viscoelastic properties and stability. The group of Laaser investigated the effect of hydrophobic alkyl groups with variable chain length and charge density on the phase behaviour.45,46 When longer alkyl chains were incorporated into both polyelectrolytes, an increase of salt-resistance similar to Sadman et al. was observed.40,46 Besides the influence of the chemistry on macroscopic properties, several efforts have also been paid on the microstructural understanding of complex coacervates and largely reported in the literature.41,47,48
In this work, we report on the use of complex coacervates as PSAs, consisting of statistical and partially hydrophobic copolymers based on the strong anion poly(3-sulfopropyl methacrylate) (PSPMA) and quaternized poly(4-vinylpyridine) (QP4VP) as polycation. As it is not possible to prepare these statistical copolymers via conventional methods, we propose the partial deprotection of a fully hydrophobic precursor.49,50 The hydrophobicity can be tuned by the degree of deprotection (DD), which allows for a direct correlation between rheological response and amount of hydrophobic groups per chain. The hydrophobic/anionic polymers were complexed with a polycation; two different chain lengths were studied for each polymer. Water content and salt resistance were measured to assess the influence of hydrophobicity on the complex coacervates. Linear shear rheology, the sticky-Rouse molecular model and probe-tack experiments were adopted for an in-depth analysis of the designed complex coacervates as PSAs.
2. Materials and methods section
2.1 Materials
Anhydrous N,N-dimethylformamide (DMF; 99.8%), 3-sulfopropyl methacrylate potassium salt (K·SPMA) (98%), triethylamine (TEA) (99.5%), iodomethane (MeI), deuterated solvents, and the RAFT agent 4-cyano-4-(thiobenzoylthio)pentanoic acid (CTP) were acquired from Sigma-Aldrich. Oxalyl chloride (98.0%) was purchased from TCI Europe N.V. Sodium iodide (NaI) (99.5%, anhydrous) was obtained from Acros Organics. Azobisisobutyronitrile (AIBN) was obtained from Sigma-Aldrich and recrystallized twice from methanol. All other analytical grade chemicals were obtained from Boom B.V. Water was of R.O. quality (10 μS cm−1, equivalent to 10−4 M NaCl). Two lengths of poly(4-vinylpyridine) (P4VP) were synthesized via RAFT polymerization, as described previously.51,52 The degree of polymerization of the low molecular weight P4VP (L-P4VP) was 119 (Mn = 12.5 kg mol−1, Đ = 1.21) and 467 for the high molecular weight P4VP (H-P4VP) (Mn = 49.3 kg mol−1, Đ = 1.26). 3-(Isobutoxysulfonyl)propyl methacrylate (BSPMA) was synthesized and subsequently polymerized according to a previously reported procedure (Table S1, ESI†).49 Further details can be found in the ESI.†2.2 Polymer synthesis and characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol/pentane, filtered over a glass filter (pore size 4) and subsequently thoroughly washed with 1
1 ethanol/pentane, filtered over a glass filter (pore size 4) and subsequently thoroughly washed with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol/pentane mixture and finally with pentane, until the filtrate did not appear yellow anymore. This procedure was followed for all polymers, except for the lowest DD, which was precipitated into a 1
1 ethanol/pentane mixture and finally with pentane, until the filtrate did not appear yellow anymore. This procedure was followed for all polymers, except for the lowest DD, which was precipitated into a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ethanol/pentane mixture and washed with pentane. The DD of the P(BSPMA-co-SPMA) statistical copolymer was determined by 1H NMR (Fig. S2–S5, ESI†) through comparison of methylene groups 5a and 5b. The code names of the obtained polymers were adapted to their DD (i.e., percentage of charged monomers) as follows: L/100, L/87, L/74, L/61, H/100, H/86, H/73 and H/60, with L and H denoting the low and high molecular weight, respectively.
2 ethanol/pentane mixture and washed with pentane. The DD of the P(BSPMA-co-SPMA) statistical copolymer was determined by 1H NMR (Fig. S2–S5, ESI†) through comparison of methylene groups 5a and 5b. The code names of the obtained polymers were adapted to their DD (i.e., percentage of charged monomers) as follows: L/100, L/87, L/74, L/61, H/100, H/86, H/73 and H/60, with L and H denoting the low and high molecular weight, respectively.
A Viscotek GPCmax system equipped with a TDA 302 triple detector array (refractive index, viscosity, and light scattering) and two analytical columns (Agilent Technologies PolarGel-M and PolarGel-L, 30 cm/8 μm) was used to perform Gel Permeation Chromatography (GPC). N,N-Dimethylformamide (DMF) containing 0.01 M LiBr was used as eluent at a flow rate of 1.0 ml min−1 and both columns as well as detectors were held at 50 °C. Calibration was performed with narrow PMMA standards and samples were filtered over a 0.2 μm PTFE filter prior to injection. Molecular weights of the homopolymers were calculated by applying conventional calibration (Table S1, ESI†) using Viscotek OmniSEC software. Mn,NMR is the calculated molecular weight based on the monomer conversion (1H-NMR) and the theoretical maximum molecular weight (monomer/CTA ratio).
2.3 Complex coacervate formation
Polymer stock solutions were prepared by dissolving the (partially) deprotected PBSPMA/x polyanion and QP4VP polycation in water at 0.20 M charged monomer concentration. For NaCl, a stock solution of 5.00 M was used. The salt concentrations were varied from 0.00 M to 1.50 M by increments of 0.25 M. For the preparation of a complex coacervate, first water and the NaCl solution were added and mixed together, then the QP4VP stock and the P(BSPMA-co-SPMA) stock were successively added. Finally, the mixture was vortexed for 30 seconds and the samples were left to equilibrate overnight. For complexation, the total charged monomer concentration was set to 0.10 M with a positive to negative charge ratio of 1 to 1. The next morning, the mixtures were centrifuged for 15 minutes at 4500 g in order to collect the complex coacervate phase at the bottom of the tube. Complex coacervates prepared with the two anionic polymers of different molecular weight were named cc-L/x and cc-H/x, where cc stands for the complex coacervate that is formed with the matching QP4PV chain length (i.e., L or H) and x corresponds to the DD. A schematic of this procedure is illustrated in Fig. 1.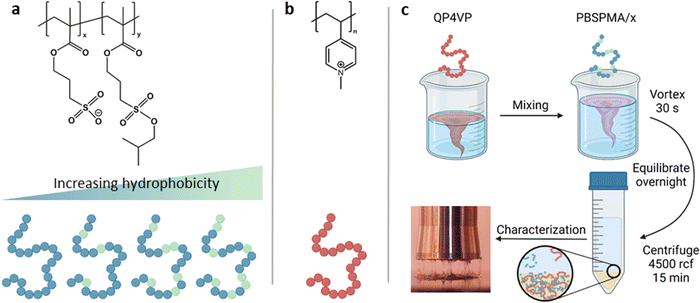 | ||
| Fig. 1 Molecular structures and schematic representation of (a) P(BSPMA-co-SPMA) and (b) QP4VP. (c) Representation of the preparation procedure of complex coacervates. | ||
2.4 Water content
For the determination of the water content of the complex coacervates, the samples were dried in an oven. The complex coacervates were made at a total volume of 2 ml and the dense phase was dried in an oven for four hours at 120 °C – the weights were monitored and became constant within one hour. Before drying, most of the supernatant was removed by decanting, and the remaining part was carefully removed. The relative weight loss before and after drying was attributed to the full evaporation of water and therefore considered as the water content. All measurements were done in triplicate. This method was found to give more consistent and reliable results compared to thermogravimetric analysis (TGA) due the larger sample size.2.5 Rheology
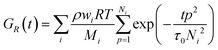 | (1) |
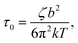 with ζ being the Kuhn monomer friction, b its length and kT the thermal energy.56 When the index p is equal to one, the whole ith chain is considered, whereas when p = Ni, the elementary Rouse segment is intended. Eqn (1) indicates that the Rouse modulus is the sum of Rouse contributions from fraction of chains with different Mi, with each fraction containing Ni segments.
with ζ being the Kuhn monomer friction, b its length and kT the thermal energy.56 When the index p is equal to one, the whole ith chain is considered, whereas when p = Ni, the elementary Rouse segment is intended. Eqn (1) indicates that the Rouse modulus is the sum of Rouse contributions from fraction of chains with different Mi, with each fraction containing Ni segments.
For associating polymers, the Rouse modes persist until the chains feel the presence of the associating sites (stickers). For length scales larger than the distance between two consecutive stickers, the motion of the chain is controlled by the sticker association lifetime τs. The breaking and reformation of such reversible stickers are still Rouse-like, and the modes from p = 1 and p = Ns are delayed by the presence of the stickers. Ns,i= Mi/Ms is the number of Rouse strands between stickers in the ith chain, with Ms being the number-average molecular weight between two consecutive stickers. That is, the relaxation of the whole chain can be expressed as a combination of high order Rouse modes with Ns,i +1 < p < Ni, controlled by the monomer time τ0, and low order sticky-Rouse modes with 1 < p < Ns,i, delayed by the association time τs. The stress relaxation modulus of a Rouse chain with stickers then writes as:
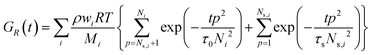 | (2) |
As it will be shown later in the text, the sticky-Rouse model is here adopted to capture the slowdown of the relaxation dynamics of the complex coacervates, with decreasing DD.
To validate the time-salt-hydrophobicity superposition principle (TSHS), van Gurp–Palmen plots were used as well. The horizontal shift factors (ah) were determined by shifting the loss factor onto the reference data, cc-X/100.
2.6 Probe tack experiments
The probe tack measurements were performed on an Anton Paar MCR302e rheometer in ‘tack penetration’ mode, inspired by the procedure reported by Vahdati et al.13 The probe consisted of a flat stainless steel sand-blasted plate with a diameter d = 10 mm (PP10/S) connected to transducer of the rheometer. All the samples were placed on the flat and smooth stainless steel bottom-plate of the rheometer that was maintained at 20 °C. The samples were placed on the bottom plate either with a pipette or with a spatula, depending on the viscosity of the system. For all the measurements, the probe was lowered to an initial gap of 150 μm (h0) at a speed of 100 μm s−1. After a contact time of one minute the probe was retracted at a speed of v = 100 μm s−1 (nominal strain rate is 0.67 s−1) and the normal force (FN) was recorded as a function of the displacement (h). Multiple measurements were performed on different aliquots of the same coacervate sample.Stress–strain curves were obtained by converting the displacement into strain (ε) using eqn (3) and converting the normal force into stress (σ) using eqn (4).
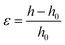 | (3) |
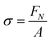 | (4) |
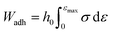 | (5) |
3. Results and discussion
3.1 Polyelectrolyte synthesis
Both strong polyelectrolytes used in this work were obtained via Reversible Addition–Fragmentation chain Transfer (RAFT) polymerization of uncharged monomers in organic solvent. Next, charges to ensure full water solubility were introduced through either deprotection or post-modification (Materials and Methods section, Fig. 1a, b and Fig. S1–S5, ESI†).49 More precisely, the strong polycation QP4VP was obtained by first polymerizing 4-vinylpyridine to obtain poly(4-vinylpyridine) (P4VP) chains with a DP of 119 and 469 monomers, named L-P4VP and H-P4VP, respectively, with a narrow molecular weight distribution. Further details are listed in Table 1. Then, both molecular weight P4VP chains were quaternized through complete methylation of the tertiary amine moieties using methyl iodide (MeI) (Fig. S6, ESI†) to obtain L-QP4VP and H-QP4VP.40| Polymer | M n,NMR/(kg mol−1) | M n,GPC/(kg mol−1) | DP | Đ |
|---|---|---|---|---|
| L-PBSPMA | 29.1 | 36.4 | 110 | 1.11 |
| H-PBSPMA | 135.8 | 121.8 | 514 | 1.36 |
| L-QP4VP | 12.5 | 13.5 | 119 | 1.21 |
| H-QP4VP | 49.3 | 52.7 | 467 | 1.26 |
For the anionic polymer, first the protected monomer 3-(isobutoxysulfonyl)propyl methacrylate (BSPMA) was synthesized, which was subsequently polymerized to give two poly(3-(isobutoxysulfonyl)propyl methacrylate) (PBSPMA) homopolymers of varying molecular weight (Table 1). The obtained chains had a degree of polymerization (DP) of 110 and 514 and are further named as L/x and H/x, respectively (x being the DD). To (partially) deprotect PBSPMA, the only parameter that was varied was the amount of NaI. The temperature, reaction time and polymer concentration were all kept constant. The deprotection is a facile method for obtaining strong anionic copolyelectrolytes (P(BSPMA-co-SPMA)) with varying numbers of hydrophobic groups. The removal of the protecting groups is expected to occur randomly, since both the protected and deprotected forms of PBSPMA are soluble in the reaction medium (DMSO). This approach thus resulted in polyanions where the charged and hydrophobic groups are homogeneously distributed along the chain, which is supported by the full solubility of even the least deprotected polymer in (deuterated) water (40% hydrophobic groups). Furthermore, correct integration of the hydrophobic groups in 1H NMR (D2O) further confirmed that the polymers were dissolved as unimers in water. The deprotection degrees that were obtained were 100%, 87%, 74% and 61% for L/x and 100%, 86%, 73% and 60% for H/x. The control over the deprotection is reproducible, as both L/x and H/x yielded nearly similar DD for the same NaI equivalents (Table S2, ESI†). Table 1 reports the molecular characteristics of all polymers utilized in this work.
3.2 Complex coacervate formation
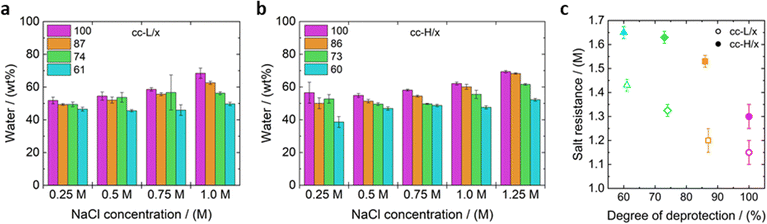
Complex coacervates were prepared in water with a 1 to 1 positive to negative charge ratio of the charged monomeric units of the strong polyelectrolytes, which remain fully charged irrespective of the pH. The polyelectrolyte stocks were mixed with aqueous solutions containing different concentrations of salt (NaCl) (Fig. 2). It should be noted that the counterions were not included in the total salt concentration; properties are investigated and reported as a function of added salt (NaCl). The short L-QP4VP was combined with L/100, L/87, L/74 and L61 resulting in the following complex coacervate samples: cc-L/100, cc-L/87, cc-L/74 and cc-L/61. Similarly, the long H-QP4VP was combined with H/100, H/86, H/73 and H/60 resulting in the following complex coacervate samples, respectively: cc-H/100, cc-H/86, cc-H/73 and cc-H/60.One of the most important parameters that determines the adhesive performance of a water-based material is the water content.59 For this reason, we first measured the water content of the different formulations by drying the samples in an oven at 120 °C for 1 hour. As a general trend, when the salt concentration was increased, the water content increased as well regardless of the DD. For example, for cc-L/100 the water content increased from 52 to 68 wt% by increasing the salt concentration from 0.25 M to 1.25 M NaCl (Fig. 2). This effect of salt is commonly reported for complex coacervates: the increased salt concentration decreases the driving force for polyelectrolyte association – a combination of Coulombic attraction and entropic gain through counterion release – which results in a higher water content.14,42,60 In parallel, decreasing the DD (i.e. more hydrophobic groups) leads to a decrease in the water content regardless of the salt concentration. At higher salt concentrations (NaCl ≥ 1 M), this effect is more pronounced, where the difference in water content for both molecular weights is 18 wt% between the highest and lowest DD (Fig. 2). The electrostatic interactions are more screened at high salt concentrations, which renders the effect of hydrophobic interactions more prominent concerning the water content. The presence of the hydrophobic isobutyl groups seems to inhibit the water uptake at higher salt concentrations, resulting in a more constant (and lower) water content.12,14 For example, the water content only increased from 47 wt% to 56 wt% for cc-L/61 between 0.25 M and 1.0 M NaCl. Similar results, with reduced swelling in complex coacervates that contained a more hydrophobic propyl-functionalized QP4PV, have been reported before.40
The salt resistance is directly related to the water content. When the salt concentration is increased, the water content in the complex coacervates increases until phase separation is no longer observed. The salt resistance of the formulated coacervates was visually assessed, and a series of photographs of cc-L/74 prepared at different NaCl concentrations is provided in Fig. S7 (ESI†). The salt resistance gradually increased for both cc-L/x and cc-H/x with decreasing DD, where cc-H/x consistently had a higher salt resistance for a given hydrophobicity degree compared to the cc-L/x samples. It has been widely reported for complex coacervates that when the chain length increases, the salt resistance increases as well.1,42,61–63 This is related to the smaller entropy loss when long chains are incorporated in the complex coacervate phase.64 Usually, replacing charges with neutral water-soluble (inert) moieties reduces the salt resistance due to a lower charge density on the polyelectrolytes.45,65 However, here, the opposite trend was observed. This indicates that hydrophobicity can be regarded as an additional driving force for complex coacervation.42,66
Several research groups have investigated the influence of hydrophobicity on salt resistance, although not all of them came to the same conclusion.40,42,43,46 Sadman et al.40 and Huang et al.46 found, similar to our work, that the salt resistance increased with increasing hydrophobicity. Huang et al. showed an increase in salt resistance for the longest alkyl chains (6 to 12 carbons).46 However, shorter alkyl chains (1 to 4 carbons) first had a decreasing salt resistance at high charge densities and a turnover point where the salt resistance would increase again when the charge density was further decreased. Similarly, Liu et al. found that changing the backbone from an acrylate to a methacrylate increased the salt resistance and broadened the phase diagram.42 On the other end, the group of Schlenoff reported that QP4VP-PAA coacervates became more salt unstable when QP4VP's alkyl chain length was increased from one to four.43 Notably, while in Schlenoff's QP4VPs, all units remain fully charged, our PSPMA copolymers contain true hydrophobic monomer units. When considering two weak natural polyelectrolytes, Es Sayed et al.48 shown that a decrease in ionization of chitosan resulted in completely different behaviour due to the formation of hydrogen bonds. Since complex coacervate systems can be made with an infinite number of combinations of polyelectrolytes and hydrophobic groups, comparing specific systems is difficult. However, the general trend that an increase in hydrophobicity causes a decrease in water content and a higher salt resistance is evident in most studies.
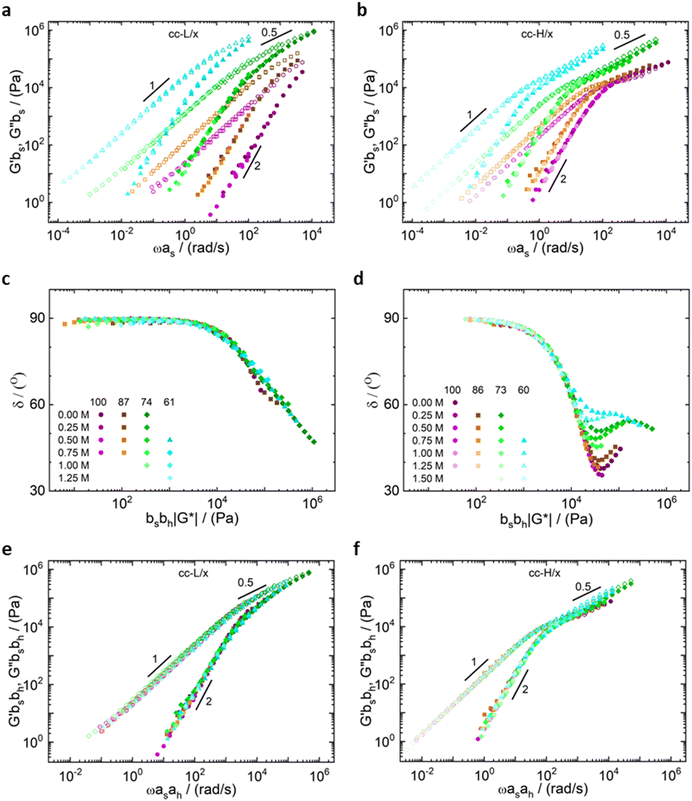
3.3 Rheology
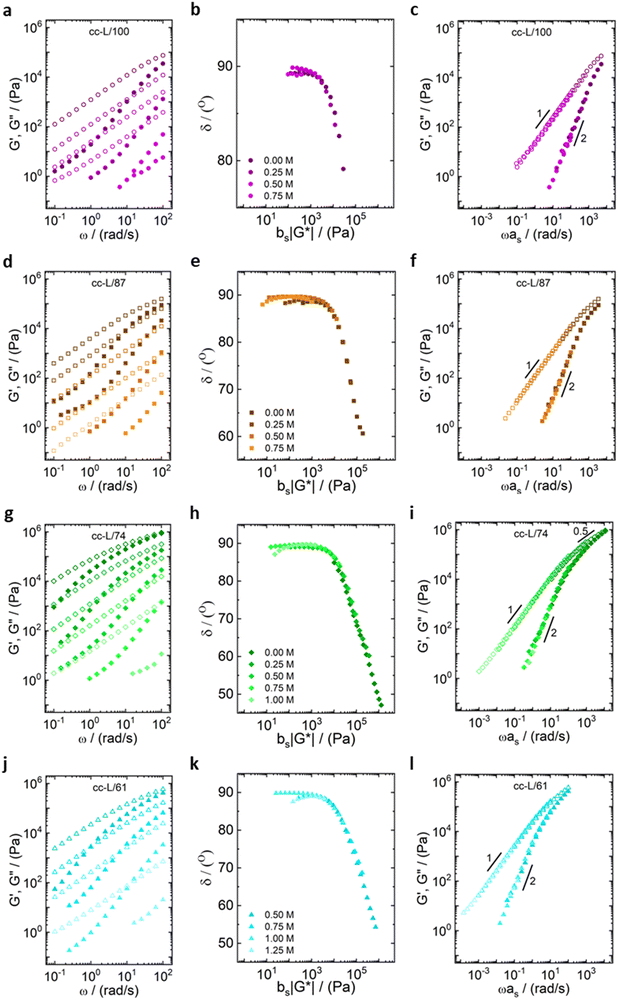
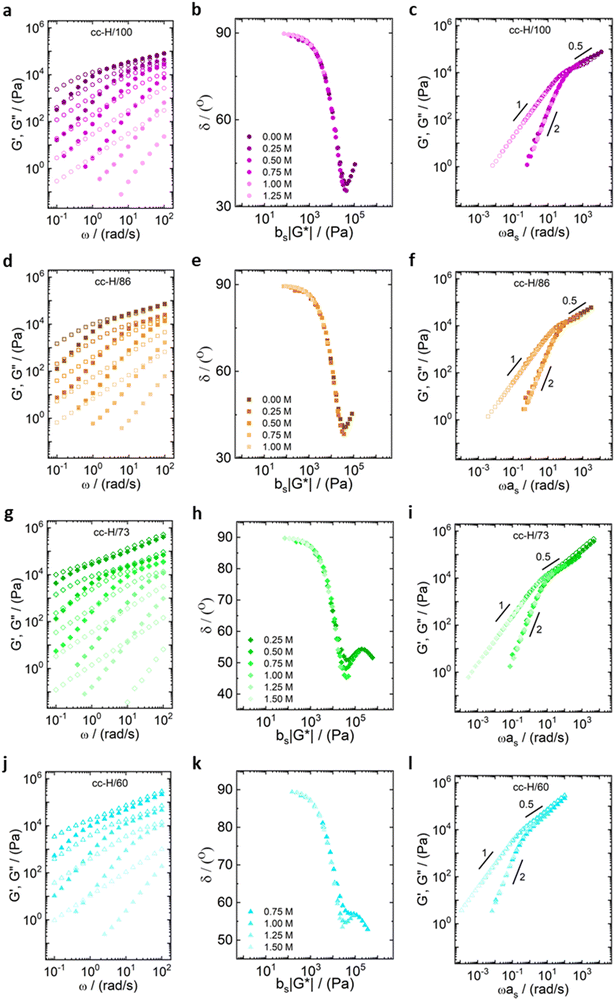
All the samples show a viscoelastic liquid-like behaviour, with the loss modulus (G′′) being larger than the storage modulus (G′), or overlapping at most, over the full frequency range probed by the experiments (panels a, d, g, j of Fig. 3 and 4).38,68 The absence of a rubbery plateau excludes the presence of entanglements in the systems, suggesting a Rouse-like stress relaxation dynamics, as was reported in a previous work on complex coacervates,67 and clarified later in the text.
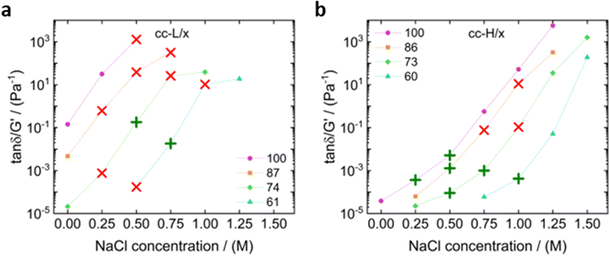
The effect of salt on the dynamics of the complex coacervates called for the applicability of the time-salt superposition principle, for each degree of hydrophobicity. The loss factor, tan(δ) = G′′/G′, curves were shifted with respect to the 0.75 M NaCl samples, regardless the molecular weight, to form a master curve (see Fig. 3 and 4, panels c, f, i, l, and Fig. S8 in the ESI,† in terms of loss factor).
The validity of the superposition principle was verified through the van Gurp–Palmen representation which shows that, for each hydrophobicity degree, a reasonably good overlap of the data is attained (panels b, e, h, k of Fig. 3 and 4). This suggests that the nature of the internal relaxation modes remains unaffected by the addition of salt, as shown by other investigators on complex coacervates.39,69
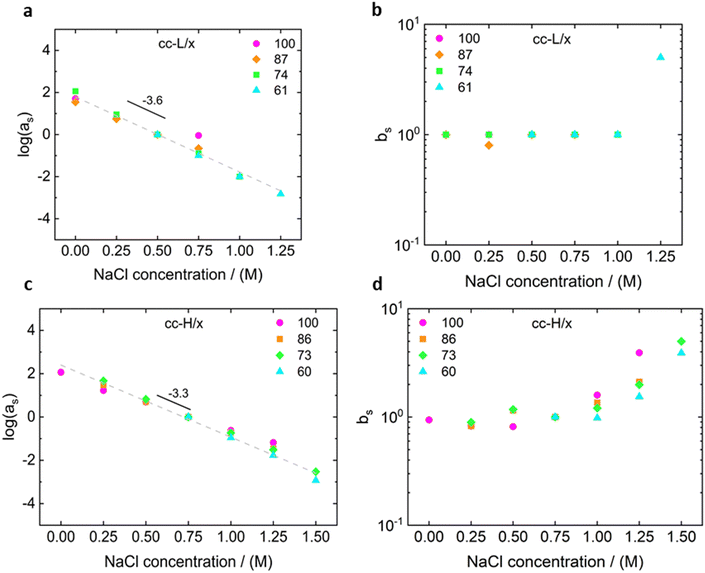
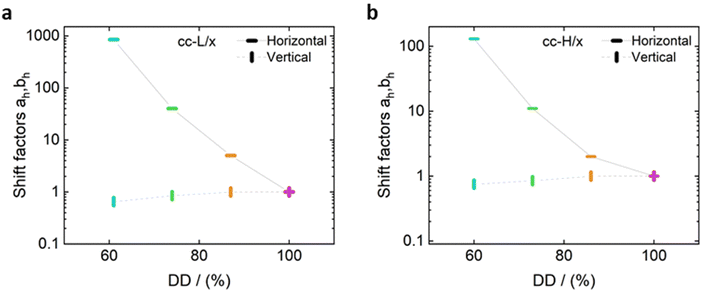
For both cc-L/x and cc-H/x samples, the terminal regime, indicating full relaxation of the system, is attained, as indicated by a slope of 1 and 2 for G′′ and G′, respectively (see Fig. 3 and 4).13,68,70 A slope of 0.5 at higher frequencies for both G′ and G′′ suggests that the stress relaxation of these complex systems occurs via Rouse dynamics.56 Specifically, a slope of 0.5 refers to ideal chains and 0.46 to real chains in good solvent.56 However, as suggested by Spruijt et al.1,67 the polymer content in complex coacervates is rather high, and the hydrodynamic interactions are screened by segments of other polymer chains. Nevertheless, at length scales smaller than the hydrodynamic screening length, approximately equal to the static correlation length, Zimm modes govern the polymer dynamics. This is reflected by the high-frequency regions of the viscoelastic spectra, showing power-law behavior with exponent equal to 0.57 (in good solvent). While the limited high-frequency data reported in Fig. 4i and l suggest a slope larger than 0.5, indication of Zimm dynamics, we refrain from drawing conclusions on the nature of the relaxation modes. However, it can be noted that the increase in hydrophobicity tends to reduce the water content in the complex coacervates, therefore further diminishing the effect of the hydrodynamic interactions (Zimm modes). The horizontal, as, and vertical, bs, shift factors are reported in Fig. 5 as a function of salt concentration, for both cc-L/x and cc-H/x. The sensitivity of as, or in other words the variation of the relaxation dynamics to salt concentration, is in agreement with other works on complex coacervates.13,35,39–41 The amount of salt needed to vary log(as) by one unit is around 300 mM (see Fig. 5a and c). Several investigators reported similar values on diverse complex coacervates: Schröder et al.35 100 mM for chitosan/gum arabic, Sadman and co-workers40 150 mM for quaternized poly(4-vinylpyridine)/polystyrene sulfonate, Sun et al.39 200 mM for chitosan/hyaluronic acid, Vahdati et al.13 300 mM for poly(2-acrylamido-2-methylpropanesulfonic acid)/poly(N,N-[(dimethylamino) propyl]methacrylamide), and Marciel et al.41 500 mM for poly(L-lysine)/poly(glutamic acid). Note that the sensitivity of the relaxation dynamics to salt concentration significantly depends on the nature of the salt, and the strength of the electrostatic interactions between the oppositely charged polyelectrolytes. On the other hand, the vertical shift factors are close to the unit value for most of the salt concentration range (≤1.0 M), as also observed in other works on complex coacervates.35,40,41 Deviations from one are observed for high salt content, where clear rheological complexities were observed in the van Gurp–Palmen plots. This is tentatively attributed to the fact that at this high salt content, the polymer density in the complex coacervates may be significantly affected.
Unlike the time-salt superposition principle, the horizontal shift factors aH as a function of the degree of the deprotection were found to follow a William–Landel–Ferry (WLF)71 trend (see Fig. 7), similar to what other investigators have found in complex coacervates with temperature variations.35 The determined WLF constants,71C1 and C2, are respectively 1.5 and 66% (degree of deprotection), regardless of the chain length.
Note that the observed trend for the horizontal shift factors could have been captured by other mathematical functions, but the WLF choice was supported by the widespread knowledge of this function in the soft matter community, rendering the comparison of results straightforward. It is also important here to note that both cc-L/x and cc-H/x do not exhibit a rubbery plateau, a signature of chain–chain entanglements. Therefore, the WLF constants can have predictability utilization only in the unentangled regime.
As expected, the molecular weight of the chains dictates the relaxation dynamics and the elastic character of the resulting complex coacervates (see Fig. 6, panels e and f). Indeed, chains with higher degree of polymerization give birth to slower dynamics and higher elasticity. Remarkably, the time-salt-hydrophobicity superposition principle enables the prediction of the dynamics of P(SPMA-co-BSPMA)/QP4VP complex coacervates with varying salt concentration and/or hydrophobicity of the polyanion. The obtained frequency-extended viscoelastic spectra can then be used to assess the adhesion properties of viscoelastic materials.25
It is important to highlight two competing effects of the deprotection strategy to modify the rheology of such complex coacervates. First, by only partially deprotecting the polyanion, the charge density decreases, resulting into a speed up of the dynamics in the system, without influencing the underlying relaxation mechanisms.34,45 Secondly, these protected monomers are not just inert spacers, but hydrophobic isobutyl moieties. As a consequence, they can be considered as additional stickers that slow down the overall dynamics of the chains. As we discussed before, we expected an extra sticker interaction from the hydrophobic groups, which was observed in the slowed down dynamics with increasing hydrophobicity (Fig. 6, panels a and b). This effect on the dynamics is also favoured by a slight decrease in water content with decreasing DD (see Fig. 2), as also observed in the literature.34,59,72,73 Hence, by repelling water, the interactions between hydrophobic groups on different chains might even be stronger. An explanation of the preserved nature of the relaxation mechanisms, and therefore validity of the time-salt-hydrophobicity superposition principle, might be found in the homogenous distribution of charges and hydrophobic groups in the anionic polymer. Indeed, the presence of a homogeneous distribution of hydrophobic groups prevents the formation of hydrophobic clusters, rendering the dynamics of the system controlled by the same relaxation modes at different length scales. In that sense, only a more organized charged-hydrophobic block copolymer could be able to form hydrophobic clusters inside the complex coacervate and have a more pronounced influence on the viscoelastic behaviour.
Similar to our results, it has been observed that strongly hydrophobic complex coacervates need more salt to obtain a fluid coacervate.40 Huang and coworkers published two papers on their method of functionalizing poly(N-acryloxy succinimide).45,46 Using this method, the charge density with hydrophilic or hydrophobic groups and the length of the hydrophobic chain was changed. However, rheology was not performed to characterize the influence of the chain length on the coacervate.
The effect of hydrophobicity also manifests in the polymer–solvent interactions. The latter tend to decrease when more hydrophobic side groups or a hydrophobic backbone are present, even though the polymer is still water-soluble.63 Li et al.63 looked at this effect by using polymers with either a hydrophilic peptide backbone or an aliphatic all-carbon hydrophobic backbone. A higher water content and lower salt resistance were observed for the hydrophilic peptide polyelectrolytes compared to the aliphatic hydrophobic polyelectrolytes. The polymer–solvent interactions can also be changed by introducing a cosolvent, as shown by Sun et al. in a recent publication.39 In their work, alcohols (methanol or ethanol) were used as a cosolvent, resulting in higher salt resistance and higher rheological moduli. These cosolvents have a lower dielectric constant and therefore reduce the solvency conditions, especially compared to water. The effect of cosolvents was also studied for a polyelectrolyte pair where both polymers were synthesized from permanently charged styrenic monomers.74 Because these polymers were more hydrophobic due to the aromatic moieties, the opposite was observed when introducing cosolvents: both ethylene glycol and ethanol lowered the salt resistance of the complexes. In this particular situation the cosolvents were actually a better solvent than water. Overall, the effect of hydrophobicity on the relaxation times is dependent on the polymer–solvent interactions in terms of enhancing or reducing phase separation and dynamics.
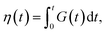 finding that the model yielded a viscosity value at most twice as high as the experimental one. For instance, for the cc-H/60 sample, the experimental value of the viscosity is 29.9 kPa s against 49.4 kPa s yielded by the model. This result indicates that the sticky-Rouse model can be adopted, to a large extent, to predict the linear shear rheology of complex coacervate systems with varying DD, in addition to the already explored effect of salt concentration and molecular weight (Spruijt et al.30,67). While our approach demonstrated the potential of the sticky-Rouse model to predict the dynamics of hydrophobically modified complex coacervates, some assumptions were made and a few remarks follow in order. We considered a monodisperse system, although the stress relaxation moduli reported in Fig. 8 show broader relaxation dynamics, compared to the monodisperse model. By implementing the molecular weight distribution of the polymers, a much more accurate fit is expected.75 We are also assuming that all the stickers can be described by an average sticker lifetime, but it could also be that a distribution is present instead. As shown in Fig. 2, the increase in hydrophobicity reduces the amount of water in the complex coacervate. By looking at the cc-H/x sample at 0.75 M (Fig. 2 – panel b), a decrease in water content of about 10% occurs when the DD decreases from 100% to 60%. This would naturally suggest that an effect of concentration is also contributing to the slowdown of the stress relaxation dynamics. However, the water content between 73% and 60% is nearly the same, though, the stress relaxation modulus of the cc-H/60 decays significantly slower (see Fig. 8). This result suggests that the relaxation dynamics are indeed controlled by the hydrophobicity degree imparted to the system. Rigorously, glassy and fast Rouse modes should have been included in the model. However, their contribution to the long-time dynamics would have been negligible, and in the absence of experimental data to compare with, less useful. The sticky-Rouse model also assumes dimeric associations, and this may not always be the case in the presence of many hydrophobic groups, that could drive local phase separation and thereby affect material functions, such as the relaxation time and modulus.76–78Table 2 reports the molecular parameters used in the model. For instance, the mol% of charged groups based on NMR was used to calculate the average monomer molar mass M0. The molecular weight of the protected and deprotected monomer was then used to calculate the average monomer molar mass for the different DD. For example H/86 is calculated as follows: (230.2 × 0.86 + 264.3 × 0.14) g mol−1 = 235.0 g mol−1.
finding that the model yielded a viscosity value at most twice as high as the experimental one. For instance, for the cc-H/60 sample, the experimental value of the viscosity is 29.9 kPa s against 49.4 kPa s yielded by the model. This result indicates that the sticky-Rouse model can be adopted, to a large extent, to predict the linear shear rheology of complex coacervate systems with varying DD, in addition to the already explored effect of salt concentration and molecular weight (Spruijt et al.30,67). While our approach demonstrated the potential of the sticky-Rouse model to predict the dynamics of hydrophobically modified complex coacervates, some assumptions were made and a few remarks follow in order. We considered a monodisperse system, although the stress relaxation moduli reported in Fig. 8 show broader relaxation dynamics, compared to the monodisperse model. By implementing the molecular weight distribution of the polymers, a much more accurate fit is expected.75 We are also assuming that all the stickers can be described by an average sticker lifetime, but it could also be that a distribution is present instead. As shown in Fig. 2, the increase in hydrophobicity reduces the amount of water in the complex coacervate. By looking at the cc-H/x sample at 0.75 M (Fig. 2 – panel b), a decrease in water content of about 10% occurs when the DD decreases from 100% to 60%. This would naturally suggest that an effect of concentration is also contributing to the slowdown of the stress relaxation dynamics. However, the water content between 73% and 60% is nearly the same, though, the stress relaxation modulus of the cc-H/60 decays significantly slower (see Fig. 8). This result suggests that the relaxation dynamics are indeed controlled by the hydrophobicity degree imparted to the system. Rigorously, glassy and fast Rouse modes should have been included in the model. However, their contribution to the long-time dynamics would have been negligible, and in the absence of experimental data to compare with, less useful. The sticky-Rouse model also assumes dimeric associations, and this may not always be the case in the presence of many hydrophobic groups, that could drive local phase separation and thereby affect material functions, such as the relaxation time and modulus.76–78Table 2 reports the molecular parameters used in the model. For instance, the mol% of charged groups based on NMR was used to calculate the average monomer molar mass M0. The molecular weight of the protected and deprotected monomer was then used to calculate the average monomer molar mass for the different DD. For example H/86 is calculated as follows: (230.2 × 0.86 + 264.3 × 0.14) g mol−1 = 235.0 g mol−1.
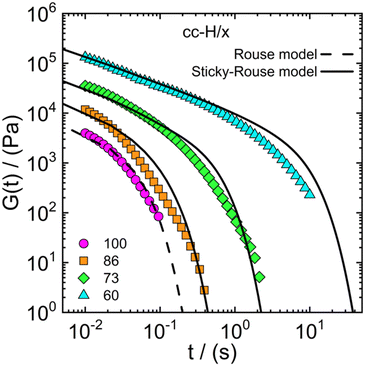 | ||
| Fig. 8 Stress relaxation modulus as a function of time for the cc-H/x samples with varying DD (see legend). Symbols represent observed data, the dashed line the Rouse model (eqn (1)) and the solid line the sticky-Rouse model (eqn (2)). The stress relaxation moduli were obtained by converting the dynamic moduli reported in Fig. 4 at 0.75 M. | ||
| Polymer | N s | M 0/(g mol−1) |
|---|---|---|
| H100 | 0 | 230.2 |
| H86 | 72 | 235.0 |
| H73 | 139 | 239.4 |
| H60 | 206 | 243.9 |
3.4 Adhesion performance
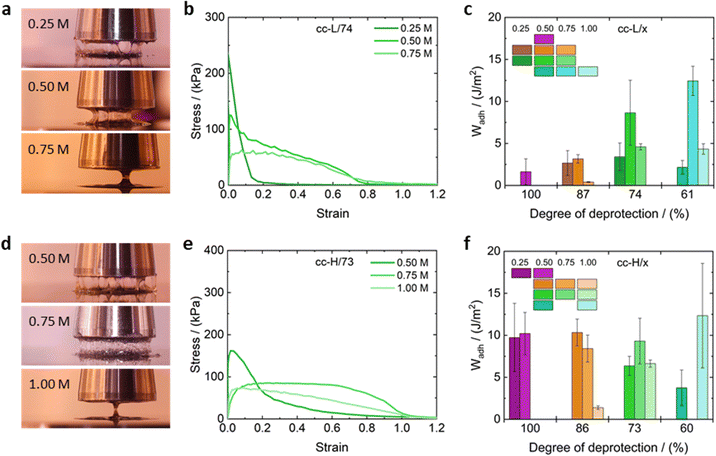
Assessing the adhesion properties of soft materials requires various experimental tests, and a rigorous protocol has not been defined yet,25 due to the complexity of the adhesion phenomenon. It is known that PSAs should be characterized by significant energy dissipation during the peeling process (typical property of viscous liquids), and being resistant to shear creep (typical for elastic solids).25 The balance between those two contributions is key to design high-performance PSAs. The combination of small amplitude oscillatory shear and probe tack tests are acknowledged as powerful techniques to infer about the adhesive properties of soft materials.25 We adopted such methodology to test the adhesive properties of the complex coacervates reported in this work.Fig. 9 shows the nominal stress–strain curves obtained for cc-L/74 (panel b) and cc-H/73 (panel e) at various salt concentrations, along with some exemplary pictures taken during the experiments (panels a and d). The calculated work of adhesion (Wadh) is reported in panels c and f of the same fig., for cc-L/74 and cc-H/73, respectively. Stress–strain curves for the remaining samples can be found in the ESI† (Fig. S9). The probe-tack results display three regimes of debonding, as proposed by Verdier et al.79
At low salt concentrations (0.25 M), low molecular weight and any degree of deprotection, samples reached a high peak stress value (>200 kPa), but the strain dropped rapidly to low values (<0.2) before debonding occurred (e.g., cc-L/74 at 0.25 M NaCl in Fig. 9b). The shape of the curve indicates a mode of failure directed by interfacial crack propagation, where the high elasticity of the material prevents the dissipation of energy upon debonding.25 This typically results in low adhesion energies, Wadh < 4 J m−2. The brittle adhesive failure of the corresponding complex coacervates samples can be confirmed in most cases by direct observation (see Movies S1–S4, ESI†). Conversely, the high-Mw sample, at low salt concentrations, yielded an adhesion energy Wadh ∼ 10 J m−2, without introducing any hydrophobicity (see histogram in Fig. 9f). Higher salt concentrations (between 0.5 and 0.75 M), promote a stronger viscous contribution to the overall rheological response of the complex coacervates, and a cohesive failure via a single capillary bridge was observed (Fig. 9a, d and Movie S1–S4, ESI†). These samples show weaker peak stress, compared to the law-salt regime, but a much-extended shoulder towards larger deformations is present. A shoulder in nominal stress–strain curves implies fibril formation in the material, suggesting better adhesion properties.25 This was confirmed by visual inspection of the debonding of the complex coacervate adhesives (Movies S1–S4, ESI†), where multiple fibrils cover the probe area and are extended over a large distance before cohesive failure occurred. Note that for low-Mw samples, lower degrees of deprotection are needed to attain Wadh values in the range 5–10 J m−2.
On the contrary, high-Mw samples display Wadh around 10 J m−2 only at higher deprotection degrees. This reflects the fact that the elasticity imparted by the hydrophobic modification of the chains is pivotal only for short chains, to increase the elastic contribution to the overall material response. For high salt concentrations (1 M) the peak stress vanishes, stress levels are lower, although the extended shoulder towards larger strains is still present in most cases. The adhesion energy seems to drop for all the coacervate systems, except for the cc-H/60 samples, where the significant screening of the electrostatic interactions compensates for the elasticity imparted by the large number of hydrophobic interactions. However, due to the large standard deviation observed in such a system, we refrain from drawing a strong conclusion out of it.
The obtained adhesion energies resonate well with similar systems reported in the literature.
Vahdati et al.13 reported one complex coacervate adhesive system composed of electrostatically interacting weak polyelectrolytes with a Wadh of approximately 16 J m−2. Similar values were previously reported by Dompé et al.12 for their complex coacervate-based adhesive.
Probe-tack tests suggest that the introduction of hydrophobic groups to the polyanion is essential for the short chains to obtain good adhesive properties. This, in addition to partial screening of the electrostatic interactions (salt range 0.5–0.75 M). Note that in many cases, salt has a nonmonotonic effect on the adhesion energy, reflecting the fact that a balance between elasticity due to the hydrophobic interactions, and enhanced viscous dissipation due to salt addition, is necessary to obtain optimized adhesion performances.
To better link the linear viscoelastic data of our complex coacervates to their adhesion properties, the two-criterium method proposed by Deplace et al.25 was adopted. The first requirement, as the Dahlquist criterion,80 is that the storage modulus G′ should not exceed 105 Pa at the frequency at which the contact between surface and adhesive is established (inverse of the contact time). Otherwise, the adhesive might not have enough time to establish good contact with the surface. In this work, we apply a relatively long contact time of approximately 60 seconds (0.17 rad s−1), and at this condition the first requirement was always fulfilled. The second criterion involves two critical physical parameters for the bonding/debonding of a PSA. One is related to the resistance to crack propagation between the interface of the probe and the adhesive (viscous effect), and the other is related to the bulk (elastic) properties of the adhesive. Deplace et al.25 combined the effect of these independent components into the tan(δ)/G′ ratio, which can be easily determined from small amplitude oscillatory shear experiments. Note that, if the geometry and surface of the substrate are constant, as in the present case, the ratio tan(δ)/G′ is inversely proportional to the Young's modulus of the material.25
In Fig. 10 we plotted the value of tan(δ)/G′ as a function of the salt concentration for a frequency of 3.98 rad s−1.
The latter was close to the debonding frequency (4.19 rad s−1), calculated as per Deplace et al.:25
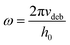 | (6) |
It appears that there is an upper and lower boundary for these systems to achieve the maximum amount of work of adhesion. At the lower boundary the material was too elastic and, in most cases, adhesive failure was observed, as also described in the probe tack results. At the upper boundary the coacervate started to become too liquid, which resulted in a capillary bridge that broke at small gap distances. The most evident difference between the two chain lengths was the number of suitable samples for high adhesion performance. For cc-L/x samples, only two combinations displayed fibrillation; those that relate to low degree of deprotection and medium salt content (0.5–0.75 M). On the other hand, six combinations of the cc-H/x samples displayed fibrillation, and therefore yielded good adhesion performances. Remarkably, the best adhesion properties for both cc-L/x and cc-H/x samples were found at different tan(δ)/G′ values (0.1 and 0.001 Pa−1 for cc-L/x and cc-H/x, respectively), rendering the method weakly rigorous. Two reasons were identified for such a discrepancy: (i) as nonlinear deformations occur in the bulk, this linear viscoelastic method may not be very accurate, (ii) limiting the study to a single frequency can be misleading. Indeed, Vahdati et al.13 observed that complex coacervates with nearly equal storage and loss moduli over a large range of frequencies (tan(δ) ∼ 1), showed the best adhesion performance, as a result of a balance between viscous dissipation and elastic response. Here, the cc-H/x samples cover a broader range where the two moduli are close (see Fig. 3 and 4), compared to the cc-L/x samples, which is certainly caused by the longer chain length, in addition to a strong effect of hydrophobic interactions as the degree of deprotection decreases. While the Deplace approach, combined with nonlinear viscoelastic tests, is very powerful in generating a map to identify the best adhesion properties, a universal value for tan(δ)/G′ cannot be identified. Nevertheless, by combining small amplitude oscillatory shear rheology and probe tack tests it is possible to infer that: (1) hydrophobic modification of the polyanion are pivotal to make adhesives out of cc-L/x samples, in addition to balancing the electrostatic interactions with salt, and (2) high molecular weight complex coacervates offer remarkable adhesive properties with no or low degree of hydrophobicity imparted to the system.
4. Conclusion
We have studied the influence of hydrophobicity on the properties of complex coacervates properties via an elegant protection/deprotection method of a strong anionic polymer, while keeping its chain length constant. The homogeneously deprotected polymers were used to make complex coacervates. The water content, rheological behaviour and adhesion performance were assessed, using the molecular weight, salt concentration and degree of deprotection as varying parameters. A time-salt-hydrophobicity superposition principle was found applicable, and this feature can be employed as a predictive means to design complex coacervates with desired rheological behavior. The slowdown of the dynamics due to the increased number of hydrophobic groups (i.e., lower degree of deprotection) at a given salt concentration, can be captured by the sticky-Rouse model, using the fully deprotected sample as a reference to estimate the monomer relaxation time τ0.The monomer friction was considered unvaried with degree of deprotection, and only one average sticker lifetime was assumed. Despite these assumptions, the sticky Rouse model appears to be a powerful tool to predict the relaxation dynamics of complex coacervates, treating the hydrophobic groups as stickers.
Finally, the combination of small amplitude oscillatory rheology and probe tack tests enabled the identification of the best design parameters for PSAs. For low molecular weight systems (cc-L/x), the hydrophobic modification of the polyanion is essential to provide an elastic character to the material, and confer good adhesive properties. For cc-H/x samples, a high degree or even full deprotection suffice to generate good adhesion properties. Salt enables tuning (screening) of the electrostatic interactions, thereby giving birth to a nonmonotonic behaviour of the adhesion properties of both cc-L/x and cc-H–x samples, suggesting that there is a balance between hydrophobic and electrostatic interactions that ensures optimized adhesive properties. The complexity of such systems certainly calls for more investigations on the effect of the intra and intermolecular associations on the chain conformation and macroscopic structure at various concentration regimes and length scales. Future studies will be conducted along this direction.
Nevertheless, the results presented in this work offer new pathways for tuning the rheological properties of complex coacervates via simple hydrophobic modification of the polyanion. The simultaneous presence of electrostatic and hydrophobic interactions provides a unique strategy to obtain complex coacervates with superior mechanical properties, making them ideally suitable for pressure-sensitive adhesives.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. H. acknowledges the University of Groningen for an FSE Postdoctoral Fellowship.References
- E. Spruijt, A. H. Westphal, J. W. Borst, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 6476–6484 CrossRef CAS.
- J. van der Gucht, E. Spruijt, M. Lemmers and M. A. Cohen Stuart, J. Colloid Interface Sci., 2011, 361, 407–422 CrossRef CAS PubMed.
- B. Muhoza, S. Xia, X. Wang, X. Zhang, Y. Li and S. Zhang, Crit. Rev. Food Sci. Nutr., 2022, 62, 1363–1382 CrossRef CAS PubMed.
- J. Kamp, S. Emonds, J. Borowec, M. A. Restrepo Toro and M. Wessling, J. Membr. Sci., 2021, 618, 118632 CrossRef CAS.
- Ö. Karabıyık Acar, S. Bedir, A. B. Kayitmazer and G. T. Kose, Int. J. Biol. Macromol., 2021, 188, 300–312 CrossRef PubMed.
- K. O. Margossian, M. U. Brown, T. Emrick and M. Muthukumar, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- B. Ghosh, R. Bose and T. Y. D. Tang, Curr. Opin. Colloid Interface Sci., 2021, 52, 101415 CrossRef CAS.
- N. A. Yewdall, A. A. André, T. Lu and E. Spruijt, Curr. Opin. Colloid Interface Sci., 2021, 52, 101416 CrossRef CAS.
- R. J. Stewart, J. Exp. Biol., 2004, 207, 4727–4734 CrossRef CAS PubMed.
- H. Shao, K. N. Bachus and R. J. Stewart, Macromol. Biosci., 2009, 9, 464–471 CrossRef CAS PubMed.
- R. J. Stewart, C. S. Wang and H. Shao, Adv. Colloid Interface Sci., 2011, 167, 85–93 CrossRef CAS PubMed.
- M. Dompè, F. J. Cedano-Serrano, O. Heckert, N. van den Heuvel, J. van der Gucht, Y. Tran, D. Hourdet, C. Creton and M. Kamperman, Adv. Mater., 2019, 31, 1808179 CrossRef PubMed.
- M. Vahdati, F. J. Cedano-Serrano, C. Creton and D. Hourdet, ACS Appl. Polym. Mater., 2020, 2, 3397–3410 CrossRef CAS.
- M. Vahdati, G. Ducouret, C. Creton and D. Hourdet, Macromol. Rapid Commun., 2020, 41, 1–7 CrossRef PubMed.
- M. Li, G. Pan, H. Zhang and B. J. Guo, Polym. Sci., 2022, 60, 1328–1359 CrossRef CAS.
- A. H. Hofman, I. A. van Hees, J. Yang and M. Kamperman, Adv. Mater., 2018, 30, 1704640 CrossRef PubMed.
- V. Nele, J. P. Wojciechowski, J. P. K. Armstrong and M. M. Stevens, Adv. Funct. Mater., 2020, 30, 2002759 CrossRef CAS.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC.
- G. M. Conley, C. Zhang, P. Aebischer, J. L. Harden and F. Scheffold, Nat. Commun., 2019, 10, 2436 CrossRef PubMed.
- J. van der Gucht, E. Spruijt, M. Lemmers and M. A. Cohen Stuart, J. Colloid Interface Sci., 2011, 361, 407–422 CrossRef CAS PubMed.
- M. Dompè, F. J. Cedano-Serrano, M. Vahdati, L. van Westerveld, D. Hourdet, C. Creton, J. van der Gucht, T. Kodger and M. Kamperman, Adv. Mater. Interfaces, 2020, 7, 1901785 CrossRef.
- C. Creton, MRS Bull., 2003, 28, 434–439 CrossRef CAS.
- C. Creton and H. Lakrout, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 965–979 CrossRef CAS.
- C. Creton, J. Hooker and K. R. Shull, Langmuir, 2001, 17, 4948–4954 CrossRef CAS.
- F. Deplace, C. Carelli, S. Mariot, H. Retsos, A. Chateauminois, K. Ouzineb and C. Creton, J. Adhes., 2009, 85, 18–54 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- K. Brown, J. C. Hooker and C. Creton, Macromol. Mater. Eng., 2002, 287, 163–179 CrossRef CAS.
- B. J. Endrizzi and R. J. Stewart, J. Adhes., 2009, 85, 546–559 CrossRef CAS.
- A. D. Filippov, J. Sprakel and M. Kamperman, Soft Matter, 2021, 17, 3294–3305 RSC.
- E. Spruijt, J. Sprakel, M. Lemmers, M. A. Cohen Stuart and J. van der Gucht, Phys. Rev. Lett., 2010, 105, 1–4 CrossRef PubMed.
- R. F. Shamoun, H. H. Hariri and R. A. Ghostine, Macromolecules, 2012, 45, 9759–9767 CrossRef CAS.
- Y. Chen, M. Yang, S. A. Shaheen and J. B. Schlenoff, Macromolecules, 2021, 54, 7890–7899 CrossRef CAS.
- P. C. Suarez-Martinez, P. Batys, M. Sammalkorpi and J. L. Lutkenhaus, Macromolecules, 2019, 52, 3066–3074 CrossRef CAS.
- M. Tekaat, D. Bütergerds, M. Schönhoff, A. Fery and C. Cramer, Phys. Chem. Chem. Phys., 2015, 17, 22552–22556 RSC.
- P. Schröder, M. Schönhoff and C. Cramer, Macromolecules, 2023, 56, 4966–4980 CrossRef.
- F. G. Hamad, Q. Chen and R. H. Colby, Macromolecules, 2018, 51, 5547–5555 CrossRef CAS.
- K. Akkaoui, M. Yang, Z. A. Digby and J. B. Schlenoff, Macromolecules, 2020, 53, 4234–4246 CrossRef CAS.
- M. Yang, J. Shi and J. B. Schlenoff, Macromolecules, 2019, 52, 1930–1941 CrossRef CAS.
- J. Sun, J. D. Schiffman and S. L. Perry, ACS Appl. Polym. Mater., 2022, 4, 1617–1625 CrossRef CAS.
- K. Sadman, Q. Wang, Y. Chen, B. Keshavarz, Z. Jiang and K. R. Shull, Macromolecules, 2017, 50, 9417–9426 CrossRef CAS.
- A. B. Marciel, S. Srivastava and M. V. Tirrell, Soft Matter, 2018, 14, 2454–2464 RSC.
- Y. Liu, C. F. Santa Chalarca, R. N. Carmean, R. A. Olson, J. Madinya, B. S. Sumerlin, C. E. Sing, T. Emrick and S. L. Perry, Macromolecules, 2020, 53, 7851–7864 CrossRef CAS.
- M. Yang, S. L. Sonawane, Z. A. Digby, J. G. Park and J. B. Schlenoff, Macromolecules, 2022, 55, 7594–7604 CrossRef CAS.
- M. Mende, S. Schwarz, S. Zschoche, G. Petzold and A. Janke, Polymers, 2011, 3, 1363–1376 CrossRef CAS.
- J. Huang, F. J. Morin and J. E. Laaser, Macromolecules, 2019, 52, 4957–4967 CrossRef CAS.
- J. Huang and J. E. Laaser, ACS Macro Lett., 2021, 10, 1029–1034 CrossRef CAS PubMed.
- S. Meng, J. M. Ting, H. Wu and M. V. Tirrell, Macromolecules, 2020, 53, 7944–7953 CrossRef CAS.
- J. Es Sayed, C. Caïto, A. Arunachalam, A. Amirsedeghi, L. van Westerveld, D. Maret, R. A. Mohamed Yunus, E. Calicchia, O. Dittberner, G. Portale, D. Parisi and M. Kamperman, Macromolecules, 2023, 56, 5891–5904 CrossRef CAS PubMed.
- A. H. Hofman, R. Fokkink and M. Kamperman, Polym. Chem., 2019, 10, 6109–6115 RSC.
- A. H. Hofman, M. Pedone and M. Kamperman, ACS Polym. Au, 2022, 2, 169–180 CrossRef CAS PubMed.
- A. H. Hofman, G. O. R. Alberda Van Ekenstein, A. J. J. Woortman, G. Ten Brinke and K. Loos, Polym. Chem., 2015, 6, 7015–7026 RSC.
- A. H. Hofman, M. Reza, J. Ruokolainen, G. ten Brinke and K. Loos, Angew. Chem., Int. Ed., 2016, 55, 13081–13085 CrossRef CAS PubMed.
- Q. Chen, G. J. Tudryn and R. H. Colby, J. Rheol., 2013, 57, 1441–1462 CrossRef CAS.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- L. G. Baxandall, Macromolecules, 1989, 22, 1982–1988 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- M. van Gurp and J. Palmen, J. Rheol. Bull., 1998, 65, 5–8 Search PubMed.
- J. M. Dealy, D. J. Read and R. G. Larson, Structure and Rheology of Molten Polymers, Carl Hanser Verlag GmbH Co KG, 2018 Search PubMed.
- M. Dompè, M. Vahdati, F. van Ligten, F. J. Cedano-Serrano, D. Hourdet, C. Creton, M. Zanetti, P. Bracco, J. van der Gucht, T. Kodger and M. Kamperman, ACS Appl. Polym. Mater., 2020, 2, 1722–1730 CrossRef.
- C. E. Sing and S. L. Perry, Soft Matter, 2020, 16, 2885–2914 RSC.
- R. Chollakup, J. B. Beck, K. Dirnberger, M. V. Tirrell and C. D. Eisenbach, Macromolecules, 2013, 46, 2376–2390 CrossRef CAS.
- S. Kim, M. Lee, W. B. Lee and S. H. Choi, Macromolecules, 2021, 54, 7572–7581 CrossRef CAS.
- L. Li, A. M. Rumyantsev, S. Srivastava, S. Meng, J. J. De Pablo and M. V. Tirrell, Macromolecules, 2021, 54, 105–114 CrossRef CAS.
- A. B. Kayitmazer, A. F. Koksal and E. Kilic Iyilik, Soft Matter, 2015, 11, 8605–8612 RSC.
- A. E. Neitzel, Y. N. Fang, B. Yu, A. M. Rumyantsev, J. J. De Pablo and M. V. Tirrell, Macromolecules, 2021, 54, 6878–6890 CrossRef CAS PubMed.
- A. B. Kayitmazer, Adv. Colloid Interface Sci., 2017, 239, 169–177 CrossRef CAS PubMed.
- E. Spruijt, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2013, 46, 1633–1641 CrossRef CAS.
- F. J. Morin, M. L. Puppo and J. E. Laaser, Soft Matter, 2021, 17, 1223–1231 RSC.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1942, 10, 98–105 CrossRef CAS.
- B. Yu, P. M. Rauscher, N. E. Jackson, A. M. Rumyantsev and J. J. De Pablo, ACS Macro Lett., 2020, 9, 1318–1324 CrossRef CAS PubMed.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707 CrossRef CAS.
- H. H. Hariri, A. M. Lehaf and J. B. Schlenoff, Macromolecules, 2012, 45, 9364–9372 CrossRef CAS.
- M. Yang, Z. A. Digby and J. B. Schlenoff, Macromolecules, 2020, 53, 5465–5474 CrossRef CAS.
- S. Meng, Y. Liu, J. Yeo, J. M. Ting and M. V. Tirrell, Colloid Polym. Sci., 2020, 298, 887–894 CrossRef CAS.
- Y. Shi, S. R. Chen, G. Fragkiadakis, D. Parisi, V. Percec, D. Vlassopoulos and M. J. Monteiro, Macromolecules, 2023, 56, 545–555 CrossRef CAS.
- I. M. Rasid, C. Do, N. Holten-Andersen and B. D. E. Olsen, Soft Matter, 2021, 17, 8960–8972 RSC.
- M. Nébouy, J. Morthomas, C. Fusco, L. Chazeau, S. Jabbari-farouji and G. P. Baeza, Macromolecules, 2022, 55, 9558–9570 CrossRef.
- M. Ahmadi, A. Jangizehi and S. Seiffert, Macromolecules, 2022, 55, 5514–5526 CrossRef CAS.
- C. Verdier and J. M. Piau, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 3139–3149 CrossRef CAS.
- C. A. Dahlquist, Pressure-Sensitive adhesives, in Treatise on adhesion and adhesives, ed. R. L. Patrick, Marcel Dekker, Inc, 1969, pp. 219–260 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01114c |
| This journal is © The Royal Society of Chemistry 2023 |