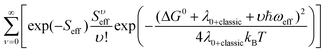Understanding the structural and charge transport property relationships for a variety of merocyanine single-crystals: a bottom up computational investigation†
Nora
Gildemeister
a,
Gaetano
Ricci‡
b,
Lukas
Böhner
a,
Jörg M.
Neudörfl
c,
Dirk
Hertel
a,
Frank
Würthner
 de,
Fabrizia
Negri
de,
Fabrizia
Negri
 *bf,
Klaus
Meerholz
*a and
Daniele
Fazzi
*bf,
Klaus
Meerholz
*a and
Daniele
Fazzi
 *a
*a
aInstitut für Physikalische Chemie, Department für Chemie, Universität zu Köln, Greinstr. 4-6, 50939 Köln, Germany. E-mail: klaus.meerholz@uni-koeln.de; dfazzi@uni-koeln.de
bUniversità di Bologna, Dipartimento di Chimica ‘Giacomo Ciamician’, Via F. Selmi, 2, 40126 Bologna, Italy. E-mail: fabrizia.negri@unibo.it
cInstitut für Organische Chemie, Department für Chemie, Universität zu Köln, Greinstr. 4-6, 50939 Köln, Germany
dInstitut für Organische Chemie, Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
eCenter for Nanosystems Chemistry, Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
fINSTM UdR Bologna, Via F. Selmi, 2, 40126 Bologna, Italy
First published on 16th June 2021
Abstract
Merocyanines consist of electronic donor (D) and acceptor (A) subunits connected via a methine bridge. They are highly polar organic π-conjugated molecules investigated for their self-assembly and optoelectronic properties. The accurate description of their structure–property relationships remains challenging. We report a comprehensive analysis modelling intra- and inter-molecular charge transport parameters for a library of merocyanines featuring different D/A combinations and lateral substituents. We found that constrained DFT correctly assesses the molecular and electronic structure in single crystals. The most effective charge transport pathways were identified and charge carrier mobilities were computed. We analyzed a large variety of single crystals highlighting the impact of alkyl substituents and casting conditions, drawing clear structure vs. charge transport relationships. Our modelling suggests that hole transport is maximized when dipolar molecules are packed in slipped not centrosymmetric pairs, arranged in 2D interconnected architectures. Computed and experimental charge mobilities for single crystals are in good agreement.
1. Introduction
A remarkable aspect of π-conjugated molecular materials is the possibility to tune their properties (e.g., electrical, optical, magnetic) by manipulating their structure, from the single molecule up to the supramolecular level. Prominent examples belong to the class of dipolar π-conjugated molecules, in which the absorption and emission spectra can be altered by changing the donor (D) and acceptor (A) groups, or by inducing structural reorganizations via thermal annealing or solvent casting procedures. Amongst D/A conjugated systems,1 merocyanines are one of the most studied compounds over the past four decades.2 Their ability to tune the optical gap via chemical and physical approaches made them good candidates for opto-electronic applications.Merocyanines were extensively investigated in various applications, from textile colorants towards more high-tech solutions.3 Pioneering works by Marder,4 Blanchard-Desce,5 Meerholz and Würthner6,7 paved the way towards their application in the area of nonlinear optics,1,8 photorefractivity,6,9,10 solar cells (OSC),11 and only recently organic field effect transistors (OFETs). Initially, it was believed that merocyanines would be poor p-type semiconductors due to their strong dipolar character.12,13 However, over the last two decades, researchers were able to increase the charge carrier mobility (μ) of merocyanines by orders of magnitude (10−5–2 cm2 V−1 s−1),14–16 approaching or even surpassing values as high as those of gold-standard organic semiconductors, like tetracene (2.4 cm2 V−1 s−1),17 TIPS-pentacene (5.0 cm2 V−1 s−1)18 and copper phthalocyanine (1.0 cm2 V−1 s−1).19 Even though merocyanines have not reached the performance of archetype p-type single crystalline molecular semiconductors (e.g., rubrene, μ ∼ 40 cm2 V−1 s−1)20 yet, their highly tunable structural and opto-electronic properties make them unique and versatile functional materials.
In this regard, merocyanines represent the prototypical system for understanding the role played by inter-molecular interactions in affecting the supramolecular architecture. By modulating the bulkiness of the side groups or the D/A units, crystals with different molecular packing motifs were obtained, allowing to correlate the structure with respect to, for instance, the exciton and the charge transport properties.21–25 In particular for the field of vacuum-processable organic solar cells, merocyanines are among the best donor materials because they inherit high absorptivity and in some cases (vide infra) good hole mobility at rather small molecular size, as required for sublimation.26,27
Liess et al. demonstrated that moving from rigid/small to flexible/large side groups for a given π-conjugated merocyanine, the molecular packing varies from card- to slipped-stack arrangements, strongly affecting the optical and charge transfer properties. Card- and slipped-stack aggregates lead to H- and J-exciton couplings, respectively, causing a blue- or red-shift of the absorption band with respect to that of the monomer. Such features were successfully exploited for ultranarrow bandwidth organic photodiodes.28
Similarly, a modulation of the hole mobility by orders of magnitude was achieved for poly-crystalline films28 by controlling the casting conditions, ranging from 2.4 × 10−3 cm2 V−1 s−1 for solution processed thin films up to 4.8–6.0 × 10−1 cm2 V−1 s−1 for vacuum-deposited layers.16
Supporting an earlier observation by Brückstürmer et al.,3 it was found that it is not the high permanent dipole moment of merocyanines limiting their charge-carrier (hole) mobility, but rather the way they self-assemble in crystalline domains.29 Notably, in crystals characterized by moderate hole mobility (μ > 0.05 cm2 V−1 s−1), individual merocyanines are organized in one-dimensional (1D) columns or 2D brickwork-type architectures. The latter allows the molecules to minimize their steric interactions, by adopting a shifted anti-parallel dipole–dipole configuration, and at the same time to maximize the electronic overlap between neighbouring units, leading to efficient charge percolation pathways.14 By optimizing the casting conditions to form extended single-crystalline domains, the highest hole mobility of a merocyanine was measured in a single-crystal Organic Field Effect Transistor (SC-OFET), resulting in about 1 cm2 V−1 s−1.15
Despite a massive number of experimental investigations, only limited computational studies aiming at understanding the charge transport properties of merocyanines can be found in literature. A prominent work was provided by Brückner et al.30,31 By combining a variety of methods, encompassing valence bond self-consistent field (VBSCF), density functional theory (DFT), coupled-cluster (CC) and time-dependent TD-DFT, they correlated the charge reorganization energies to the molecular structure of few merocyanines. Their molecular geometry can in fact be described as a linear combination of two resonant forms, the polyenic (neutral) and the zwitterionic (charge transfer) configurations.1 It was found that the intra-molecular charge reorganization energy is minimized at the cyanine limit, where both polyenic and zwitterionic configurations are equally weighted in the description of the ground state electronic structure, resulting in a geometry with a vanishing bond length alternation (BLA).8
Such pioneering work30 remains, to the authors’ knowledge, one of the few computational studies attempting to rationalize the charge transport properties of merocyanines, though on the basis of a single-molecule parameter. Despite its relevance, the study does not report any mechanistic insights attempting to describe the charge transport processes of merocyanines in general, namely by modelling intra- and inter-molecular mechanisms,32,33 and by comparing different crystal structures in order to draw general structure–property relationships for such class of highly dipolar organic materials.
Aiming at filling this gap in understanding, we performed a comprehensive computational analysis evaluating both intra- and inter-molecular charge transport parameters for an extended library of merocyanines, altogether six families of molecules were chosen to cover various combinations of D/A groups. The systems were selected amongst the latest experimental literature, reflecting merocyanines with optimized opto-electronic properties.15,22,25,28 Inspired by the experimental work by Liess et al.,28 within a given class of D/A units, different side groups were also investigated (e.g., alkyl chains vs. saturated ring), thus expanding the spectrum of the structures analysed.
We draw clear structure–property relationships, by connecting the solid-state packing motifs with respect to their charge diffusion pathways. Our findings support recent experimental data reporting the highest single crystal hole mobility measured so far (>1 cm2 V−1 s−1) for a certain class of merocyanines.15 Furthermore, from our computational analysis an alternative class of D/A merocyanine emerged as potential candidate for scoring high (single-crystal) hole mobilities exceeding 1 cm2 V−1 s−1.
2. Computational methods
DFT calculations were performed using the range separated hybrid functional ωB97X-D3 and the polarized Pople split-valence triple-zeta 6-311G** basis set with diffusion and polarisation functions. Both gas phase and solvent calculations were carried out, the latter within the polarizable continuum model approach (PCM) considering as solvents: THF, chloroform, acetone and DMSO. The constrained DFT (C-DFT) calculations were performed by using the CAM-B3LYP functional with D3 dispersion and the 6-311G** basis set. Details concerning the calculations and the codes used are reported in ESI.†Neutral ground state calculations were performed at the restricted DFT level, while calculations of the charged states were performed at the spin-polarized unrestricted (UDFT) level. Charged states were optimized both in gas and solvents environments.
Internal reorganization energies (λi) were computed both via the adiabatic potential approach (four points method) and by evaluating the vibrational normal mode contributions via the determination of the Huang–Rhys (HR) factors (for details see ref. 34 and ESI†).
Charge transfer integrals (Vij) were computed at the DFT level (ωB97X-D3/6-311G**) according to the dimer approach and one-electron approximation, as reported in ref. 34 and 35.
Charge transfer rates (keT) were evaluated using the semi-classical Marcus (1) and Marcus-Levich-Jortner (MLJ) (2) formulations.34,36–39
The Marcus formula (1) reads:
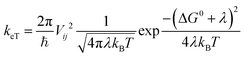 | (1) |
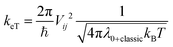 | (2) |
where the quantum description of the non-classical degrees of freedom is represented by a single effective mode of frequency (ωeff) and associated HR factor (Seff) determined from the all set of computed HR factors (see Table S16, ESI†). Following previous works34,39,40 the contributions below ca. 150–200 cm−1 were not included in the evaluation of ωeff, because at room temperature these frequency vibrations can be described to a good approximation in classical terms and due to their possible anharmonicity. The exceeding classical contributions were summed to λ0 and the total contribution reads λ0+classic in (2).
Charge carrier mobilities (μ) were computed via kinetic Monte-Carlo (kMC) simulations considering both the Brownian diffusion scheme (yielding the zero-field mobility(μ0)) as well as application of an external electric field E (yielding the field-dependent mobility (μ(E))), often in the theoretical context referred to as time-of-flight (TOF) simulations due to the fact that in TOF experiments the charge transport is measured in an essentially empty density-of-states (DOS).12μ0 was determined by computing the diffusion coefficient D with a set of kMC simulations.39,40 An approximately linear dependence of the mean square displacement (MSD) of the charge 〈[r(t) − r(0)]〉 2 as a function of time t was obtained by averaging over the subsets of 1000 kMC trajectories. The diffusion coefficient D was obtained from the fitted linear dependence of MSD employing the Einstein's eqn (3):
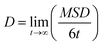 | (3) |
The charge mobility was obtained by the Einstein–Smoluchowski's eqn (4):
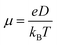 | (4) |
In the presence of an electric field, μ(E) was computed viaeqn (5) by applying an electric field E of magnitude 105 V cm−1 (voltage of 1 Volt applied on a film with a thickness of 100 nm, i.e. corresponding to typical experimental conditions):
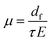 | (5) |
3. Results and discussion
3.1. Equilibrium structures and BLA
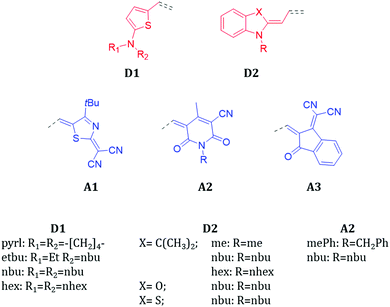
Fig. 1 shows the chemical structures of the donor (D) and acceptor (A) units investigated in this work. The molecular library is divided into classes, depending on the D/A combinations defining the π-conjugated backbone, namely D1A1, D1A2, D1A3, D2A1, D2A2 and D2A3. The donor and acceptor groups are the following: D1 – 2-amino-thiophene, D2 – 1-butyl-3,3-dimethylindolin-2-ylidene (‘Fischer base’), A1 – 2-(4-alkylthiazol-2(3H)-ylidene)malonitrile, A2 – 1,4-dialkyl-3-cyano-6-hydroxy-2pyridone and A3 – 2-(3-oxo-2,3-dihydro-1H-inden-1-ylidene)malonitrile.The electron donating strength of the donor groups follows the order D1 > D2, while for the withdrawing scale of the acceptors it is A1 > A2 > A3. As verified experimentally, the D1A1 combination features the strongest internal charge-transfer contribution (largest dipole moment) amongst all.3
The ground state electronic structure and equilibrium geometry of each merocyanine are determined by the weights of the polyenic (neutral) and zwitterionic (charge transfer) forms (see Scheme 1 for D1A1).30,41,42
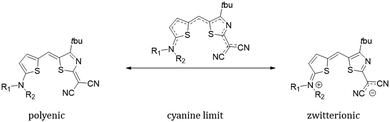 | ||
| Scheme 1 Polyenic and zwitterionic resonant forms for a representative merocyanine of our study, namely D1A1. | ||
The polyenic vs. zwitterionic equilibrium depends on the strength of the D/A groups, on the length of the π-conjugated bridge, and on the environment surrounding the molecule.1,2,8 Strong D/A units or polar solvents shift the equilibrium towards the zwitterionic form, leading to an intra-molecular charge transfer. Because of such interplay between the resonant forms, the correct description of both ground and excited state structures challenges the majority of standard quantum chemical approaches.43–45
It has been shown that for the excited states analysis, time-dependent DFT (TD-DFT) largely overestimates the transition energies, a feature that can be traced back to the lack in DFT of the differential correlation energy between the ground and the excited states.43,46–49 Double-hybrid functionals (e.g., B2PLYP) seem not to solve the problem, though improving the description of the excited states.50,51 Remarkable results have been obtained by treating the electron correlation effects via quantum Monte Carlo (QMC), Coupled Cluster (CC)46 or Bethe-Salpeter GW (GW/BSE) methods.52
Aiming at an efficient and accurate computational scheme to describe the ground state structure of merocyanines (generally, high dipolar molecules), and recalling the intuitive chemical notion of resonant forms, we used the constrained-DFT (C-DFT) method to optimize the geometry of each molecule, while certain electronic constraints (i.e., partial charges, δ) are applied. C-DFT can be seen as an effective approach to embed external electronic or magnetic perturbations into the electronic structure of a system.53
For each merocyanine we tuned the electronic partial charges, as localized on D (δD) and A (δA) groups, to mimic the polyenic vs. zwitterionic forms, and for each δD/A value we optimized the corresponding geometry. The polyenic form is thus characterized by δD = δA = 0q, while the zwitterionic by δD = +1.0q and δA = −1.0q (q is the electronic charge). In such partitioning scheme, the cyanine limit would be represented by δD = +0.5q and δA = −0.5q. Intermediate values for δD/δA lead to differently weighted polyenic vs. zwitterionic forms.
For each class of merocyanine we tuned the partial charges by ±0.1q ranging from 0.0q to ±1.0q, and we selected the optimized geometries that best reproduce the experimental BLAs, as derived from XRD single crystal diffraction measurements (XRD, see Table S1 and Fig. S2, ESI† for a comparison between C-DFT BLA patterns by changing δD/A). Low δD/A values (0.1 ≤ δD/A ≤ 0.4q) lead to polyenic-like BLA, while high δD/A values (0.7 ≤ δD/A ≤ 1.0q) lead to zwitterionic-like patterns.
In Fig. 2 are reported the comparisons between the C-DFT (δD/A = ±0.6q), DFT (gas phase) and XRD BLA patterns (see bond numbering) for two representative classes of our library, namely D1A1 and D2A1.
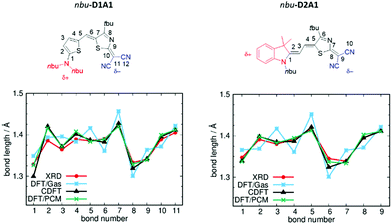 | ||
| Fig. 2 Chemical structures and BLA paths (as defined by bond numbering) for nbu-D1A1 (left) and nbu-D2A1 (right) merocyanine – upper panels (nbu-D1A1, known also as HB238).3 Bond lengths (Å) from XRD data (red lines), DFT (ωB97X-D3/6-311G**, gas phase, blue lines), C-DFT (CAM-B3LYP-D3/6-311G**, gas phase, black lines, δD/A = ±0.6q) and DFT (ωB97X-D3/6-311G**/PCM(DMSO), green lines) calculations – bottom panels. | ||
For both merocyanines, the C-DFT structures overlap the experimental ones for almost all bonds by using a δD/A = ±0.6q, thus reflecting a weak zwitterionic character. Slight deviations can be observed at the extremes (e.g., bonds R1 and R2 for D1A1, and bond R1 for D2A1), being those bonds close to the domains defining the constraints (see details Fig. S1 and S3, ESI†).
The standard DFT calculation (gas phase), in which both a range-separated functional (ωB97X-D3) and a double hybrid functional (B2PLYP) (see Table S3 and Fig. S3, ESI†) were considered to minimize the effects of electron delocalization and self interaction error, largely overestimate the BLA with a pronounced zigzag pattern over all the conjugated path. Notably, D1A1 and D2A1 experimental structures are characterized by an almost vanishing BLA in the central part of the molecule (bonds R5–R6–R7 for D1A1 and R2–R3–R4 for D2A1). This is a crucial structural feature, documenting the balanced polyenic vs. zwitterionic linear combination in determining a quasi-cyanine structure.
Focusing on the central bonds for each molecule (e.g., R5, R6 for D1A1 and R2, R3, R4 for D2A1), and defining a BLA parameter (dBLA) as the difference between single- and double-like bonds (e.g., dBLA = R5–R6 for D1A1 and R3 − (R2 + R4)/2 for D2A1),54 it can be seen that for dBLA > 0 a polyenic form would be the prevalent resonance structure, while for dBLA < 0 a zwitterionic one. Same considerations can be drawn by defining the dBLA as the difference between the average of single and double bonds 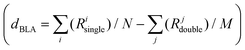 (see Table S1, ESI†).
(see Table S1, ESI†).
In Table 1 are reported the experimental and computed dBLA. In some cases, as for D1A1, D2A1 and D2A3 multiple side chains were considered, resulting in different single crystal structures. With exception of D2A3, all merocyanines present a dBLA close to zero or negative, showing a quasi-cyanine resonant structure slightly unbalanced towards the zwitterionic form.
| Class | Side chain | XRD | DFT (gas) | C-DFT (gas) | DFT/PCM (DMSO) |
|---|---|---|---|---|---|
| D1A1 | pyrl | −0.009 | 0.038 | −0.010 | −0.015 |
| et/bu | −0.012 | 0.039 | −0.010 | −0.013 | |
| nbu-P1 | −0.003 | 0.038 | −0.010 | −0.013 | |
| nbu-P2 | −0.010 | ||||
| nbu-P3 | −0.023 | ||||
| nbu-P4 | −0.013 | ||||
| nhex | −0.017 | 0.039 | −0.010 | −0.013 | |
| D1A2 | nhex/mePh | −0.016 | 0.016 | −0.025 | −0.018 |
| D1A3 | et | −0.017 | 0.017 | −0.028 | −0.011 |
| D2A1 | nhex | −0.002 | 0.054 | 0.003 | −0.007 |
| nbu | 0.001 | 0.047 | 0.002 | −0.008 | |
| D2A2 | me/nbu | −0.003 | 0.039 | 0.004 | 0.005 |
| D2A3 | nbu(C(CH3)2) | 0.014 | 0.030 | −0.008 | 0.006 |
| nbu(O) | 0.005 | 0.033 | −0.014 | 0.003 | |
| nbu(S) | 0.002 | 0.030 | −0.018 | 0.001 |
In the C-DFT scheme dBLA is affected by the choice of δD/A: for example, for pyrl-D1A1 (see Table S1, ESI†) dBLA varies from 0.064 Å with δD/A = ±0.1q, to −0.076 Å with δD/A = ±1.0q. On average, optimized C-DFT structures with δD/A = ±0.6q lead to dBLA in good agreement with the experimental data. Small deviations were observed for those cases where dBLA is almost zero. For such cases, best BLAs could be obtained by partial charges ranging from ±0.5q to ±0.7q (see Table S1 and Fig. S3, ESI†).
Notably, by analysing the experimental dBLA, we can observe that within a single class, such as D1A1, there is a variation of circa |0.020| Å just by changing the side groups. Rigid groups (e.g., pyrrolidine, pyrl-D1A1) or floppy lateral chains (e.g., n-hexyl, nhex-D1A1), affect in different ways the molecular packing (vide infra) causing changes in the mutual polarization amongst molecules. Such effect shifts the polyenic vs. zwitterionic equilibrium and consequently affects the molecular geometry.
Generally, the unit D1 induces negative dBLA, approaching the cyanine limit for D1A1.2 The D2 unit results in more positive dBLA than for D1 (see D2A3), showing a more pronounced neutral character,29 in line with the reduced strength of the donor unit.
Gas phase DFT calculations overestimate the BLA, leading to positive dBLA for all compounds (see Table 1).
As documented in literature,6,30,41 the polyenic vs. zwitterionic forms are affected by solvent/environment effects, and they can be described by a polarizable continuum method (PCM). For the sake of completeness we compared in Table 1 the computed dBLA as derived from DFT/PCM calculations with respect to C-DFT (δD/A = ±0.6q) and DFT(gas) data.
Within DFT/PCM we considered four solvents with increasing dielectric constants (see ESI,† Table S3), namely chloroform (ε = 4.71), tetrahydrofuran (THF, ε = 7.43), acetone (ε = 20.50) and dimethylsulfoxide (DMSO, ε = 46.83), as previously documented for some merocyanines (e.g., D2A2 and nbu-D2A3).30 DMSO is usually reported in literature as the solvent that best approximates the polar environment in the solid state.30,54
The computed DFT/PCM dBLA show a better match with the experimental values than the DFT(gas) calculations. The dBLA values (see Table 1 and Table S3, ESI†) show the following trend: dBLA becomes negative by increasing the solvent polarity, reflecting an internal charge transfer and favouring the zwitterionic form. For some cases (e.g., D1A1), dBLA switches from positive to negative values by increasing ε, showing a polyenic to zwitterionic variation of the structure. Focussing on pyrl-D1A1, dBLA is varying from 0.007 Å (THF) to −0.015 Å (DMSO). The experimental dBLA (−0.009 Å) would be better caught by acetone (−0.011 Å).
In general, we found that the best match with the experimental data can be achieved either with acetone or DMSO (high ε), for instance for the D1A1 class, or with chloroform (low ε) as for the case of D2A3 class (Table 1 and Table S3, ESI†). Unless the dielectric constants of the crystals are known, it appears to be difficult to suggest a unique value of ε to get a reliable and general description of dBLA in the solid state. Unambiguously, DFT/PCM improves the description of the BLA pattern with respect to DFT(gas) calculations, and the use of solvents with high ε leads towards cyanine- or zwitterionic-like structures.
Based on the above comparisons, we suggest C-DFT as an alternative embedding method to describe the structure and BLA of highly polar molecules in the solid state, providing results that are in good agreement with experimental XRD data.
The correct prediction of the ground state BLA plays a crucial role in the quantitative evaluation of the charge reorganization energy, as reported in the next session.
3.2. Internal hole reorganization energies: a single molecule approach
Merocyanines are p-type semiconductors, therefore the charge carriers to be considered are holes. Generally, a small (<150 meV) hole internal reorganization energy (λhi) is one of the prerequisites for good charge transport. The internal contribution to λhi was evaluated via the adiabatic potential method, by following three single-molecule based strategies to describe the structure of the neutral and charged states.For strategy (i) both neutral and charged states were described by gas phase DFT and (U)DFT calculations; for (ii) the neutral state was described by gas phase C-DFT and the charged by (U)DFT; for (iii) both neutral and charged states were modelled by DFT/ and (U)DFT/PCM.
As discussed previously, the BLA pattern is strongly affected by the choice of the environment or, in C-DFT, by the values of the constrained partial charges. Therefore, the effect of such approaches is, primarily, to displace the potential energy surface (PES) of the neutral ground state from a polyenic to a cyanine- or zwitterionic-like region. As a consequence, strategies (i–iii) should result in very different internal reorganization energies, given the different energy projections on the neutral and charged PESs.
Table 2 reports the computed λhi by comparing strategies (i–iii). Differences amongst λhi follow the differences in the neutral ground state BLAs (see Table 1).
| Class | Side chain | (i) DFT (gas) | (ii) C-DFT (gas) | (iii) DFT/PCM (DMSO) |
|---|---|---|---|---|
| D1A1 | pyrl | 358 | 127 | 185 |
| et/bu | 361 | 140 | 192 | |
| nbu | 355 | 126 | 188 | |
| nhex | 366 | 123 | 192 | |
| D1A2 | nhex/mePh | 269 | 221 | 213 |
| D1A3 | et | 256 | 278 | 221 |
| D2A1 | nhex | 405 | 177 | 157 |
| nbu | 439 | 177 | 157 | |
| D2A2 | me/nbu | 281 | 237 | 156 |
| D2A3 | nbu | 190 | 266 | 163 |
| nbu(O) | 241 | 252 | 173 | |
| nbu(S) | 221 | 262 | 183 |
DFT(gas) predicts higher (positive) dBLA than C-DFT or DFT/PCM (see Table 1), resulting in high reorganization energies. In fact, DFT(gas) structures are characterized by pronounced BLA in the neutral state (polyenic form) being far from the experimental solid state structures. Upon charging, BLA reverses (see dBLA for the charged state in Tables S2 and S5, ESI†), overall resulting in high λhi. Such observation is remarkable, pointing out the importance of predicting the correct neutral ground state geometry of merocyanines, due to its impact on the internal charge reorganization energy.
By exploring solvent effects we found that different dielectric constants ε (e.g., THF, chloroform, acetone, DMSO) lead to different dBLA (Table S3, ESI†), however reflecting similar reorganization energies. For pyrl-D1A1 the computed DFT/PCM λhi values are: 189 meV (THF), 202 meV (chloroform), 184 meV (acetone) and 185 meV (DMSO). A factor of six in ε (7.43 for THF vs. 46.83 for DMSO) leads to similar λhi, though representing different polarizable environments. Within DFT/PCM caution should be taken in the choice of the dielectric constant to be used in the calculation of the neutral ground state structure and reorganization energy.
The class D1A1 shows the lowest λhi (140–123 meV) followed by D2A1 (177 meV) at the C-DFT level, the latter being the merocyanine with the highest hole mobility (μ = 0.11–2.34 cm2 V−1 s−1) reported in literature.15 Within the validity of the Marcus theory (vide infra) our C-DFT calculations would suggest class D1A1 as a good candidate for OFET applications as well, showing hole reorganization energy as low as the state-of-the-art D2A1. At the DFT/PCM level the situation is slightly different: D2A1 shows the lowest λhi (157 meV), while D1A1 shows a λhi few meV higher (192–185 meV). However, such difference would not affect the charge transport properties in a relevant way.
Classes D1A3 and D2A3 show the highest λhi at the C-DFT level, suggesting A3 unit as an unfavourable choice for the minimization of the reorganization energy.
Gas phase DFT values would suggest an opposite trend than C-DFT or DFT/PCM, leading to very large λhi values for D1A1 and D2A1 (366–358 meV and 439–405 meV). For such reasons, obviously these data are largely overestimated and not representative of the real structural changes occurring upon charging the molecules.
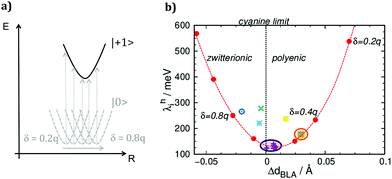
To show the impact of the structural relaxations in affecting the charge reorganization energy of merocyanines, we correlated λhi with the variation of dBLA upon charging (ΔdBLA = dNEUTRALBLA − dCHARGEDBLA). Furthermore, for a representative case study, such as pyrl-D1A1, we calculated λhi for different values of the constrained partial charges (δD/A). Results are collected in Fig. 3.
The parabolic relationship obtained for the C-DFT study by varying δD/A, see red dots in Fig. 3b, reflects the gradual shift of the neutral ground state geometry from the polyenic (δ = 0.2q) to the zwitterionic (δ = 0.8q) structure, crossing the cyanine region where ideally ΔdBLA would be close to zero (δ ∼ 0.6q) (Fig. 3a). The lowest reorganization energy was obtained for those molecules whose structure in the neutral state is close to the cyanine limit. Class D1A1 shows the lowest C-DFT reorganization energy (see purple dots and circle in Fig. 3b), minimizing amongst all other classes the ΔdBLA due to its cyanine-like neutral ground state structure (Table 1)
Our C-DFT approach well matches previous findings (VBSCF and DFT(B3LYP/cc-pVTZ)/PCM calculations),30 reporting the minimization of the reorganization energy at the cyanine limit.
3.3. Internal and external hole reorganization energy: a supramolecular approach
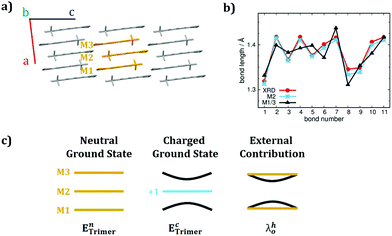
As described in Marcus theory, the total charge reorganization energy (λ) is the sum of the internal (λi) and external (λ0) contributions, the latter resulting from the dynamical response of the environment upon charge transfer.35 The correct evaluation of λ0 would encompass either quantum electrodynamic approaches or quantum mechanical molecular mechanics (QM/MM) methods. Most of the time, and for practical reasons, λ0 is computed via continuum approaches55 or it is considered as an empirical parameter ranging from 0.001 to 0.010 eV. Works by Norton et al.56 and McMahon et al.57 on oligoacenes, reported that the majority of the polarization effects induced by a localised charge, involve the first nearest neighbour molecules.58Inspired by such studies, though aiming at simpler and feasible schemes, we introduced a supramolecular approach combined with the C-DFT method to evaluate both the internal and the external contributions to the reorganization energy. We choose as a prototype case-study for the class of merocyanines pyrl-D1A1, given its low λhi (C-DFT, 127 meV) and its simple crystal structure (i.e., 1D columns of packed anti-parallel molecules, Fig. 4, vide infra). We extracted a minimal cluster (i.e., three molecules, M1M2M3) from the crystal structure and we optimized the neutral ground state at the DFT level (CAM-B3LYP-D3/6-311G**), by comparing the given BLA patterns for M1, M2 and M3 with the experimental single crystal data, as reported in Fig. 4. We found that the external molecules M1 and M3 are enough to polarize the electronic structure of the central one (M2), whose geometry – in turn – relaxes, matching the XRD data (see Fig. 4b). This aspect shows that a minimal cluster like M1M2M3 can reasonably catch the polarization and inter-molecular effects surrounding M2, as occurring in the crystal.
Further, we localized a positive charge (+1q) on M2 and re-optimized the geometry of the entire cluster at the C-DFT level. In such way, by comparing the charged cluster (M1M2+M3) with respect to the neutral one (M1M2M3, see Fig. 4c) we could estimate λhi and λh0via simple single point energy calculations. Precisely, λhi was computed by extracting the central molecule from the neutral (M1M2M3) and charged (M1M2+M3) clusters respectively, and by performing four-single-point calculations for the M2 and M2+ geometry projections. λh0 was approximated as the energy contribution coming from the structural deformations and polarizations occurring on M1 and M3 upon charge localization on M2 (see Fig. 4c).
With such simple C-DFT supramolecular approach the computed λhi and λh0 for pyrl-D1A1 resulted to be 90 and 25 meV, respectively. λhi found with the supramolecular approach is lower than that derived with the single molecule approach (Table 2), regardless C-DFT (127 meV) or DFT/PCM (185 meV) methods are considered. There are no experimental data to corroborate our findings, however the good match between the experimental BLAs and the C-DFT approaches (both single molecule and supramolecular) indirectly suggests that reasonable values for the hole internal reorganization energy of pyrl-D1A1 should lie between 90 and 130 meV.
The computed value for the λh0 contribution is in very good agreement with literature data as derived from crystalline oligoacenes (1–10 meV) or disorder organic semiconductors (e.g., Alq3, 24 meV).35,57
The C-DFT single molecule and supramolecular approaches here proposed are both valuable tools to derive the structure and the reorganization energy of push–pull dyes in the solid state.
3.4. Electronic couplings analysis for D1A1 and D2A1 single crystals
To understand the role played by different supramolecular architectures on the charge transport properties in merocyanine single crystals, we modelled the hole transfer processes via a combined use of electron transfer theories and kMC simulations (see Computational methods, eqn (1)–(5) and Tables S6–S12, ESI†).37,59–61Firstly, we focused the analysis on the class D1A1, because these merocyanines feature one of the lowest hole reorganization energy (see Table 2 and Fig. 3), potentially leading to high hole mobilities. Further, we considered D2A1 as it shows the highest hole mobility measured on a single crystal OFET (0.11 up to 2.34 cm2 V−1 s−1).15 Crystal structures are available in the literature,28 as well as additional ones were determined in the current work.
The crystal structures we considered involve D1A1 featuring different side groups, namely pyrrolidone ring (pyrl-), ethyl/butyl alkyl chains (et/bu-), and n-hexyl (nhex-).28 For the case of n-butyl chains (nbu-D1A1, reported also under the name HB238)3 three polymorphic crystals (Pn) were here studied and derived by changing the casting solvent (see Table S3, ESI†) or the XRD temperature.28 Such polymorphs were labeled as: (i) nbu-P1, obtained from chloroform and XRD at room temperature; (ii) nbu-P2, like nbu-P1 but XRD at low temperature (100 K); (iii) nbu-P3, from mesitylene and XRD at 100 K. A fourth polymorph of nbu-D1A1 was already reported by Liess et al.,28 here named nbu-P4-D1A1. We focused the analysis on the new found polymorphs (P1–P3), details concerning the coupling integrals, the computed charge trajectories and mobilities for P4 are included in the ESI† (see Table S17, ESI†). An overview of all nbu-Pn-D1A1 polymorphs is reported in Fig. 5.
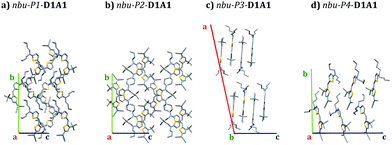 | ||
| Fig. 5 Crystal structures (supercell) of nbu-Pn-D1A1 polymorphs as obtained in the current work, namely (a) nbu-P1- (chloroform, XRD at room temperature), (b) nbu-P2- (chloroform, XRD at 100 K), (c) nbu-P3-D1A1 (mesitylene, XRD at 100K); (d) nbu-P4-D1A1 as reported in ref. 28. | ||
The impact different polymorphs might have in affecting the charge transport properties becomes clear from Fig. 5. We can speculate that, by considering a typical OFET architecture with the substrate set along the c-axis (Fig. 5, blue axis) and the molecules lying according to an edge-on configuration, the charge carrier mobility would differ depending on the polymorph constituting the thin film. Presumably, nbu-P3-D1A1 would be the case amongst all with the most favorable charge transport, featuring molecules with a nearly perfect edge-on orientation with respect to the substrate (see bc-plane Fig. 5).
Overall, we modelled the charge transport for seven crystals belonging to the D1A1 class, precisely: pyrl-, et/bu-, nbu-P1, nbu-P2, nbu-P3-, nbu-P4 and nhex-D1A1. Experimental data on the charge mobility of D1A1 are only available for amorphous and polycrystalline thin films, whereas investigations on single crystals do not yet exist. To check the quality of our computational approach and quantitatively compare the computed charge mobility with experimental data, we modelled the charge transport also for the D2A1 class, where SC-OFET measurements exist, yielding to the highest mobility for merocyanines (average value 0.87 cm2 V−1 s−1).15
Given such variability, the D1A1 class shows a wide spectrum of possible crystals, spanning from 1D columns (pyrl-D1A1) to 2D brickwork-type packing (nbu-P3-D1A1), representing an ideal case-study to correlate the structure to the charge transport properties for single crystals.
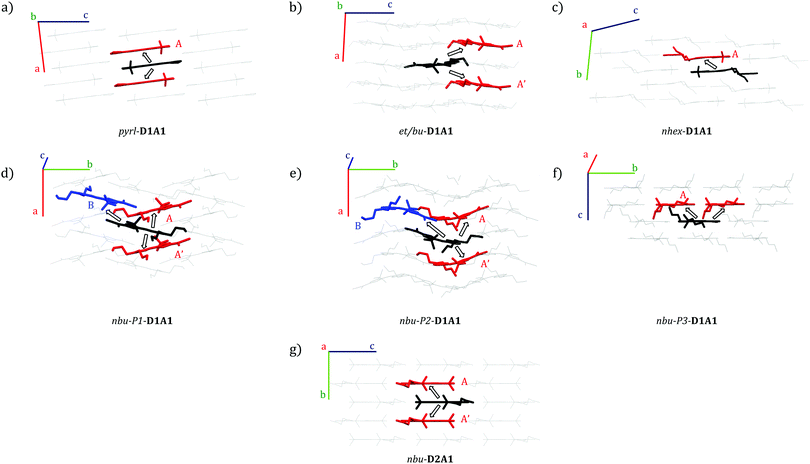
Different packing motifs and dimers featuring significant electronic coupling integrals (i.e., Vij > 10 meV) are shown in Fig. 6. Table 3 collects the computed coupling integrals, transfer rates keT and hole mobility μ (vide infra) for D1A1 and D2A1 classes.
pyrl-D1A1 crystal is characterised by 1D columns with high intra-column and weak inter-column interactions (see Fig. 6a and Fig. S4, ESI†). The intra-column coupling (dimer A, central molecule in black, nearest neighbor in red, Fig. 6) is 56 meV (see Table 3). The inter-column couplings are very low (<2 meV, see Table S6, ESI†). From here, we can already state the charge percolation pathway will mainly occur within single columns (Fig. 6a), rather than from one column to the other, therefore, it is expected to be highly anisotropic (1D).
| Dimer | |Vij| (meV) | CoM (Å) | k eT (s−1) | μ 0 (cm2 V−1 s−1) MLJ | μ(E)b (cm2 V−1 s−1) MLJ | |
|---|---|---|---|---|---|---|
| a Cut-off in Huang–Rhys analysis at 200 cm−1. b The largest computed μ(E) is reported. | ||||||
| D1A1 | ||||||
| pyrl | A | 56 | 3.64 | 2.2 × 1013 | 0.718 | 2.075 |
| et/bu | A | 14 | 8.43 | 1.3 × 1012 | 0.131a | 0.227a |
| A′ | 18 | 8.70 | 2.0 × 1012 | |||
| nbu-P1 | A | 14 | 5.09 | 1.5 × 1012 | 0.162 | 0.245 |
| B | 10 | 10.44 | 6.6 × 1011 | |||
| nbu-P2 | A | 20 | 4.95 | 3.0 × 1012 | 0.506 | 1.126 |
| A′ | 15 | 5.05 | 1.7 × 1012 | |||
| B | 50 | 10.27 | 1.9 × 1013 | |||
| nbu-P3 | A | 35 | 6.60 | 9.0 × 1012 | 0.623 | 1.936 |
| nhex | A | 23 | 6.34 | 3.9 × 1012 | 0.366 | 0.803 |
| D2A1 | ||||||
| nbu | A | 16 | 6.26 | 1.0 × 1012 | 0.091 | 0.151 |
| A′ | 11 | 6.26 | 4.9 × 1011 | |||
In the case of et/bu-D1A1, molecules organize in a brickwork type arrangement, along which the couplings are moderate (Vij = 18 and 14 meV, see the two dimers A and A′ Fig. 6b and Table 3). Vij of the remaining nearest neighbor pairs are below 6 meV (see Table S7, ESI†). The main percolation pathway will occur in a 2D zigzag pattern. Long alkyl chains as in nhex-D1A1 cause a sliding between π–π stacked molecules, leading to isolated dimers, with Vij of 23 meV (see dimer A in Fig. 6c and Table 3). All other couplings are below 8 meV (see Table S8, ESI†).
From such analysis we can infer that there is not a smooth and continuous pathway for the charge transport in nhex-D1A1 single crystal. The charge will reside on dimer A for several hops before it will advance further along other nearest neighbors. Such temporary trapping will globally decrease the charge mobility, as was previously shown for some perylene bis-imide derivatives.39,62
Quite different than et/bu- and nhex-is the symmetric nbu-D1A1 species (HB238). For both nbu-P1 and nbu-P2 crystals, the molecules are rotated by 90° forming a quasi 1D column to best accommodate the lateral chains (see Fig. 6d and e). The couplings within a column are rather similar for both crystals, being 15 and 20 meV for nbu-P2 (dimers A and A′, Fig. 6e and Table 3), and 14 meV for nbu-P1 (dimer A, Fig. 6d and Table 3). The two crystals however show a different distance between neighboring columns, resulting in different inter-columnar couplings. Such interaction is represented by dimer B (see black–blue molecular pair, Fig. 6d and e).
For nbu-P2, dimer B has a higher Vij (50 meV) than in nbu-P1 (10 meV). The reason for that is because the overlap between the two molecules (Fig. 6d and e) is higher in nbu-P2 than nbu-P1.
The charge transport in nbu-P2 single crystal should therefore occur via alternating jumps between and within the columns, forming an interconnected 2D network. In nbu-P1 instead the inter-column coupling (dimer B, Vij = 10 meV) is comparable to the intra-column one (dimer A, Vij = 14 meV), possibly leading to a charge transport that would be more isotropic than nbu-P2.
For the third crystal polymorph of nbu-species (i.e., nbu-P3-D1A1), molecules form layers of anti-parallel shifted dimers with molecular planes rotated by circa 45° (see Fig. 6f). The highest coupling (dimer A, Vij = 35 meV) is lower than that of nbu-P2 (Table 3). All remaining couplings are below 8 meV (see Table S11, ESI†). Based on such analysis, the most probable charge percolation pathway for nbu-P3 will be along shifted molecules, forming a 2D brickwork pattern. The fourth polymorph nbu-P4-D1A1 shows the highest coupling similar to P3 (Vij = 36 meV, see Table S17, ESI†).
3.5. Kinetic Monte Carlo simulations of charge-carrier mobility
The analysis of the electronic couplings for different merocyanine single crystals suggests peculiar charge transport directions depending on the supramolecular architecture. Therefore, we evaluated the hole transport by computing the transfer rates keT and the charge carrier mobilities (both μ0 and μ(E)) via kinetic Monte-Carlo (kMC) simulations (see Computational Methods).The transfer rates for nhex-D1A1 and et/bu-D1A1 crystals is an order of magnitude (∼1012 s−1) lower than pyrl-D1A1. Furthermore, in nhex-D1A1 during the kMC charge propagation, the charge resides on dimer A for several hops, as all other possible transfers show kinetic constants one order of magnitude lower (see Table S8, ESI†). This trapping effect reduces the final diffusion length of the charge, hence the mobility.39,62
The variations in the kinetic constants reflect the differences in the crystal structures: et/bu- and nhex-D1A1 show less packed structures than pyrl-D1A1, leading overall to lower μ0 for et/bu- (0.131 cm2 V−1 s−1) and nhex- (0.366 cm2 V−1 s−1) (Table 3).
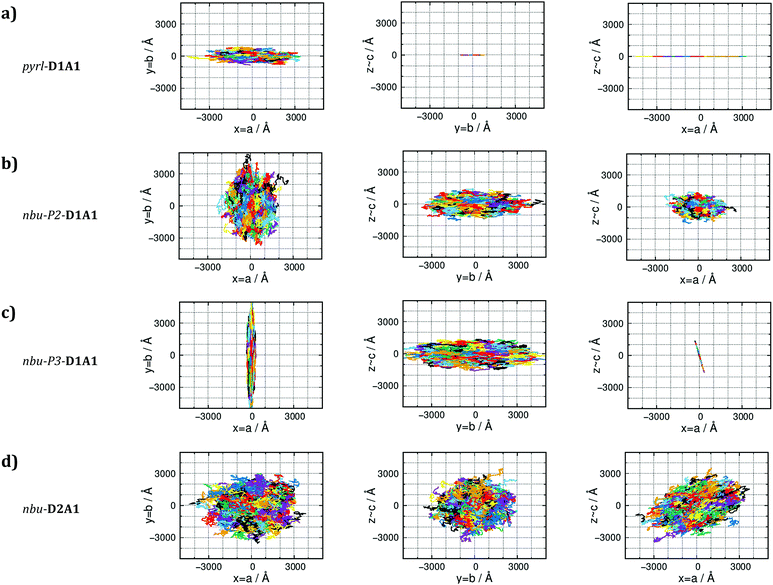
For the n-butyl species (nbu-Pn-D1A1, i.e., HB238), the room-temperature polymorph nbu-P1-shows transfer rates of ∼1012 s−1, resulting in μ0 of 0.162 cm2 V−1 s−1. This value is comparable to et/bu-D1A1. On the contrary, for the other polymorphs nbu-P2- and nbu-P3- the computed averaged μ0 raises, approaching the value of pyrl-D1A1 (0.718 cm2 V−1 s−1): μ0 = 0.506 cm2 V−1 s−1 for nbu-P2-, 0.623 cm2 V−1 s−1 for nbu-P3-. The charge mobility increases from nbu-P1- to nbu-P2/P3-D1A1. This increment is because the percolation pathway along the inter-column direction (dimer B, Fig. 6d and e) in nbu-P2/P3 is switched on due to a higher coupling than nbu-P1 (50 meV vs. 10 meV), leading to higher kinetic constants (∼1013 s−1vs. ∼1011 s−1). For nbu-P2-D1A1 the charge can hop both across columns (via dimer B) and within a column (via dimers A and A′) (Fig. 6e). Such hopping mechanism results in a 2D/3D-like diffusive charge transport (see kMC trajectories in Fig. 7b). For nbu-P3-D1A1 molecules form a brickwork-like pattern, favoring a continuous charge percolation pathway across neighboring layers (mainly the cb crystal plane, Fig. 7c). For nbu-P4-D1A1 (see Table S17, ESI†), molecules form a brickwork-like pattern similarly to P3, leading to charge percolation pathways in the cb plane.
Summarizing the charge transport modeling for D1A1 class, we found that pyrl-, nbu-P3/P4-D1A1 are the merocyanines featuring the highest zero-field hole mobility in single crystals, reaching values approaching 0.6–0.7 cm2 V−1 s−1 (or exceeding unity, as in the case of P4, see Table S17, ESI†). For a comparison between the Marcus and the MLJ values, see (Tables S6–S12 and S10, ESI†). μ0 overcomes unity if an electric field (μ(E)) was applied (see Table 3). Such values are in good agreement with recent findings by Lv et al., reporting hole mobilities of 0.48–0.60 cm2 V−1 s−1 in an OFET prepared by vacuum-deposition of diphenylaminothienyl-dicyanovinylthiazol (named Ph2ATTA), that is a merocyanine belonging to the D1A1 class, featuring di-phenyl as side group.16
pyrl- and nbu-P3/P4-D1A1, however show very different charge diffusion and percolation mechanisms resulting from their different single crystal structures. For pyrl-D1A1 charge transport is highly anisotropic (Fig. 7a), occurring prevalently in one dimension (intra-column, a-axis of the crystal). For nbu-P3-D1A1 (as well as for P4, see Table S17, ESI†) charge transport occurs mainly in two-dimensions (Fig. 7c), covering a zigzag trajectory between neighboring layers (Fig. 6f).
For polymorph nbu-P2-D1A1 holes hop in an alternating pattern across and within columns, the transport being less anisotropic than for nbu-P3-D1A1 (see Fig. 7b).
For asymmetric et/bu- or long symmetric nhex-D1A1 species, charge transport is rather disfavored as compared to pyrl- and nbu- species (though notable hole mobilities are computed, see Table 3). A similar situation occurs for nbu-P1-D1A1 crystal.
Such characteristics lead to a more isotropic charge diffusion pathways for nbu-D2A1 than for pyrl-D1A1 (Fig. 7d and a). We can speculate that due to the isotropic nature, charge transport in nbu-D2A1 might be less sensitive to structural disorder at the microscopic level (e.g., poly-crystalline domains, grain boundaries, amorphous regions, structural defects, impurities) than pyrl-D1A1.
The computed charge mobility for nbu-D2A1 spans from μ0 = 0.091 cm2 V−1 s−1 up to μ(E) = 0.151 cm2 V−1 s−1 (see Table 3), approaching the same order of magnitude of the bottom and averaged charge mobility values as measured on single crystal OFETs, namely 0.11 and 0.86 cm2 V−1 s−1.15
Given the computed charge mobilities, we believe that the D1A1 class might potentially show superior charge transport properties at the single crystal level than the D2A1.
To put our findings in perspective and highlight some trends within and between merocyanines, in Fig. 8 we correlated the computed field-dependent charge mobilities of D1A1 and D2A1 classes with respect to the experimental ones, the latter either taken from literature or measured in the current work.
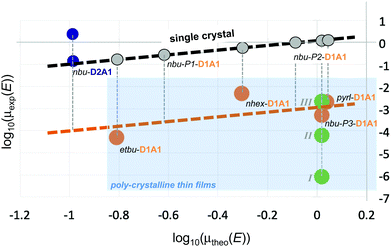 | ||
| Fig. 8 Correlation between the experimental and the theoretical single-crystal hole mobilities, μexp(E) and μtheo(E), for D2A1 and D1A1 classes. For nbu-D2A1 the lowest and the highest experimental values are reported (blue circles; ref. 15). In the case of D1A1 class (orange circles; ref. 28), it was assumed that the crystal structure determined by XRD is present in the OFET thin film as well. For nbu-P3-D1A1, the crystal structure was verified and in addition to published data,28 the charge mobility was measured on thin films thermally annealed, namely I (T = 50 °C), II (T = 110 °C) and III (T = 130 °C) – green circles. The dashed black line indicates the theoretical limit of the charge mobility by considering single crystal conditions, without the inclusion of thermal oscillations (grey circles). Vertical grey dashed lines represent the assumed variation of the charge mobility due to the polycrystalline morphology. The polycrystalline regime is highlighted in light blue. | ||
For a proper comparison between computed and experimental results, some cautionary notes should be added here. First of all, for the D1A1 class the experimental data taken from Liess et al.28 were obtained from polycrystalline thin films, while for the D2A1 experimental data were obtained from single-crystals.15 Our simulations refer to single crystal samples. Secondly, for both cases, OFET mobilities in the linear regime are reported. We should point out that our simulations assume a (field dependent) charge transport in an empty density of state (DOS), a condition which is however only valid in TOF experiments. In an OFET device, on the contrary, the DOS is not empty (due to trap filling induced by applying the gate electric field) and the charge mobility increases by increasing the carrier concentration.64 The latter effect is not taken into account in our computational treatment. Such differences justify eventual discrepancies between the computed and the experimental charge mobility, besides other factors (e.g., contact resistance, chemical impurities, structural defects) that can not be taken into account in our simulations.
Within the D1A1 class, both theoretical (μtheo(E)) and experimental (μexp(E)) mobilities (orange circles, Fig. 8) increase for crystals showing either 1D (pyrl-) or 2D (nbu-P3/P4-) brickwork-like packing. The experimental data are lower than the theoretical ones, lying below the ideal linear correlation (i.e., single crystal) highlighted by the black dashed line and grey circles in Fig. 8. This discrepancy, as previously mentioned, can be related to the fact that experiments were carried out on poly-crystalline thin films rather than a single crystal.
Further, it is uncertain, whether the crystal structure determined by XRD on a micron-sized crystal is identical to the one realized in an OFET thin film. As here documented, we discovered three new polymorphs (P1–P3) of nbu-D1A1 (HB238), in addition to the one already reported (P4) by Liess et al.28 (see Fig. 5). By combining optical and Atomic Force Microscopy (AFM) investigations, we were able to prove that after thermal annealing the nbu-D1A1 molecules assume an edge-on orientation in thin films (see Fig. 5), independently of the substrate [L. Böhner et al., unpublished data], and we could demonstrate that this corresponds to polymorph nbu-P3 (i.e. a crystalline structure which differs from the one reported in Liess et al.28).
To stress the impact of the thin-film morphology, the charge carrier mobility was measured in this work for nbu-P3-D1A1 over a series of thin films annealed at different temperatures (see green circles for nbu-D1A1, Fig. 8). By increasing the annealing temperature, the crystallinity (crystal size) increases, rising μexp(E) by four orders of magnitude (from 8.57 × 10−7 cm2 V−1 s−1 initial pristine state I, to 2.1 × 10−3 cm2 V−1 s−1 final annealed state III). We may speculate that, if (i) a single-crystal OFET were to be prepared similar to the one reported for D2A1,15 and if (ii) the orientation of the nbu-D1A1 single crystal were such, that the crystal axis featuring the largest hole mobility (b-axis, see Fig. 5c and 7c and Table S16, ESI†) would coincide with the electric field vector, the expected experimental charge mobility of nbu-D1A1 might reach the theoretical range of 0.2–2 cm2 V−1 s−1 (Table 3), as computed for a single crystal. An indirect evidence of such high mobility values for the D1A1 class (e.g., >0.1 cm2 V−1 s−1) can be already found in literature for the merocyanine Ph2ATTA. For such case, the experimental charge mobility increases by orders of magnitude, from 2.4 × 10−3 cm2 V−1 s−1 for solution processed thin films, up to 0.48–0.6 cm2 V−1 s−1 for vacuum-deposited layers.16
Notably, the computed μ(E) for the D2A1 class (0.151 cm2 V−1 s−1) is in good agreement with the one measured on single crystals,15 as evident from Fig. 8 (see blue circles representing the lowest and highest μexp(E) for nbu-D2A1, namely 0.11 and 2.34 cm2 V−1 s−1, respectively).
However, the maximum experimental mobility (2.34 cm2 V−1 s−1) exceeds the computed one by more than one order of magnitude.15 A possible reason for such underestimation could be the anisotropy of the charge transport, whereas we reported average values. However, this could account for a factor of 3 at best, and as can be seen in Fig. 7d charge transport within the D2A1 crystal is isotropic. Among other possible reasons, we attribute a relevant role to the fact that we have computed the charge mobility by considering static crystal structures, namely by neglecting the impact of thermal motions. As documented in literature,65–67 the electronic couplings are very sensitive to the inter-molecular oscillations as activated by the temperature, therefore small geometrical displacements can lead to huge variations of Vij. Usually, thermal effects introduce structural disorder, localizing the polaron over one or few sites and broadening the distribution of the couplings, thus leading to a decrease of the charge mobility.65 However, for some crystal structures, thermal motions can open new charge percolation channels at the molecular scale,39,68,69 increasing the coupling integrals and rising the charge mobility.70,71
To explore such possibility and the effect of small oscillations on the coupling integrals72 and site energies, we displaced one molecule belonging to the dimer showing the highest coupling for both nbu-D2A1 and pyrl-D1A1, along the longitudinal direction (see Fig. S11, ESI†). By considering oscillations within the thermal energy kBT (25 meV), Vij for pyrl-D1A1 vary from 25 meV to 129 meV (being 56 meV the value at the crystal equilibrium geometry). For nbu-D2A1Vij vary from few meV up to 79 meV (being 16 meV the value at equilibrium). This first preliminary evaluation shows that the couplings, as well as the charge mobility, might increase for both cases when thermal effects are taken into account. Such aspect can further justify, in first approximation, our underestimation of the single crystal charge mobility for D2A1 as compared to the maximum experimental value. Further investigations in this direction are currently ongoing.
4. Conclusions
We investigated a library of merocyanines by varying the donor (D) and acceptor (A) groups, aiming at modelling their structure and charge transport properties. Following a bottom-up approach, we found that C-DFT is an effective embedding method to quantitatively describe the BLA patterns of merocyanines in the solid state. All compounds show cyanine- or zwitterionic-like BLAs, in agreement with XRD data. Such feature is of paramount importance for the prediction of the reorganization energy.Hole reorganization energies were computed following both the adiabatic (single molecule) method and a supramolecular (cluster) approach. Both schemes provided similar internal contributions (∼90–130 meV), the latter allowing to derive also the external contribution (∼25 meV), otherwise assumed as an empirical parameter. By increasing the strength of the D/A units the reorganization energy decreases for molecules close to the cyanine limit. The lowest value was computed for the D1A1 class, as derived by coupling the 2-amino-thiophene donor group (D1) and the 2-(4-alkylthiazol-2(3H)-ylidene)malonitrile acceptor unit (A1).
We computed the charge transfer integrals and kMC charge carrier trajectories for a variety of D1A1 crystals, as obtained either by varying the side groups or by changing the casting conditions. We found that the charge mobility is tremendously affected by tiny variations of the packing structures.
We demonstrated that asymmetric (e.g., ethyl/butyl, et/bu-D1A1) or long symmetric (e.g., n-hexyl, nhex-D1A1) side groups are detrimental for charge transport, leading to isolated dimers where the charge resides during the dynamics, decreasing the mobility.
Small rigid side groups (e.g., pyrrolidine, pyrl-D1A1) lead to crystals characterised by one-dimensional columns with stacked anti-parallel molecules. The computed charge mobility for pyrl-D1A1 resulted to be high (>0.7 cm2 V−1 s−1) and anisotropic, being the hole diffusion within the columnar direction.
Symmetric alky chains (e.g., n-butyl, nbu-D1A1, i.e.HB238) show a balanced situation between rigid (pyrl-) and flexible (et/bu-, nhex-) groups. In addition to the crystal structure already reported in literature, three new crystal polymorphs for nbu-D1A1 were discovered by changing the temperature and casting solvents. Generally, the molecules pack in slipped and rotated configurations creating layers of two-dimensional networks. Such arrangement allows the charge transport to be less anisotropic than pyrl-D1A1, though showing similar high hole mobilities (<0.6 cm2 V−1 s−1). Amongst the four polymorphs of nbu-D1A1, the computed mobility varies by one order of magnitude, whereas the maximum value is received for a brickwork-like supramolecular architecture.
To strengthen our predictions, we modelled the charge transport for the D2A1 class, consisting of 1-butyl-3,3-dimethylindolin-2-ylidene as donor (D2) unit, coupled with the A1 group. Such class shows the highest measured charge mobility on a single crystal OFET so far (average value, 0.87 cm2 V−1 s−1). The computed value (0.151 cm2 V−1 s−1) matches well the experimental average mobility, validating our modelling scheme and its predictive power. Reasons for the underestimate of the computed mobility might be attributed to the role of electron–phonon couplings, here not taken into account. Indeed, within the hopping regime, molecular vibrations can play a role in enhancing charge transport, leading to a phonon-assisted process possibly raising the computed charge mobility.
Based on our computational investigation we suggest that the D1A1 class of merocyanines, in particular species having nbu- or pyrl- side groups, can overtake the state-of-the-art D2A1, leading to comparable hole mobilities at the single crystal level, a feature that will be of high relevance for OSCs as well as OFETs.
Author contributions
L. B., D. H. and J. N. performed the experimental analyses. N. G., F. N., and D. F. performed the computational analyses. N. G., F. N., K. M. and D. F. conceptualized the work. All authors contributed to rationalize the data and write the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
D. F. acknowledges the Deutsche Forschungsgemeinschaft (DFG) for the grant (FA 1502/1-1), the Regional Computing Centre (RRZK) of University of Cologne for providing computing time and resources on the HPC RRZK CHEOPS. K. M., D. F. and N. G. acknowledge the excellence initiative of the University of Cologne, “Quantum Matter and Materials” (QM2), and the DFG Research Training Group 2591 “Template-designed Organic Electronics (TIDE)” for supporting their research. F. N. acknowledges the RFO funds from the University of Bologna. The authors acknowledge Dr S. Canola for her help with the kMC simulations and for fruitful discussions.Notes and references
- S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J.-L. Brédas and B. M. Pierce, Science, 1994, 265, 632–635 CrossRef CAS PubMed.
- F. Würthner, G. Archetti, R. Schmidt and H.-G. Kuball, Angew. Chem., Int. Ed., 2008, 47, 4529–4532 CrossRef PubMed.
- H. Bürckstümmer, E. V. Tulyakova, M. Deppisch, M. R. Lenze, N. M. Kronenberg, M. Gsänger, M. Stolte, K. Meerholz and F. Würthner, Angew. Chem., Int. Ed., 2011, 50, 11628–11632 CrossRef PubMed.
- S. R. Marder, L.-T. Cheng, B. G. Tiemann, A. C. Friedli, M. Blanchard-Desce, J. W. Perry and J. Skindhøj, Science, 1994, 263, 511–514 CrossRef CAS PubMed.
- V. Parthasarathy, R. Pandey, M. Stolte, S. Ghosh, F. Castet, F. Würthner, P. K. Das and M. Blanchard-Desce, Chem. – Eur. J., 2015, 21, 14211–14217 CrossRef CAS PubMed.
- F. Würthner, R. Wortmann, R. Matschiner, K. Lukaszuk, K. Meerholz, Y. DeNardin, R. Bittner, C. Bräuchle and R. Sens, Angew. Chem., Int. Ed. Engl., 1997, 36, 2765–2768 CrossRef.
- H. Bürckstümmer, N. M. Kronenberg, M. Gsänger, M. Stolte, K. Meerholz and F. Würthner, J. Mater. Chem., 2010, 20, 240–243 RSC.
- C. B. Gorman and S. R. Marder, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11297–11301 CrossRef CAS PubMed.
- K. Meerholz, B. L. Volodin, Sandalphon, B. Kippelen and N. Peyghambarian, Nature, 1994, 371, 497–500 CrossRef CAS.
- F. Würthner, R. Wortmann and K. Meerholz, ChemPhysChem, 2002, 3, 17–31 CrossRef.
- F. Würthner and K. Meerholz, Chem. – Eur. J., 2010, 16, 9366–9373 CrossRef PubMed.
- H. Bässler and D. Hertel, ChemPhysChem, 2008, 9, 666–688 CrossRef PubMed.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef.
- A. Liess, L. Huang, A. Arjona-Esteban, A. Lv, M. Gsänger, V. Stepanenko, M. Stolte and F. Würthner, Adv. Funct. Mater., 2015, 25, 44–57 CrossRef CAS.
- A. Liess, M. Stolte, T. He and F. Würthner, Mater. Horiz., 2016, 3, 72–77 RSC.
- A. Lv, M. Stolte and F. Würthner, Angew. Chem., Int. Ed., 2015, 54, 10512–10515 CrossRef CAS PubMed.
- C. Reese, W.-J. Chung, M.-M. Ling, M. Roberts and Z. Bao, Appl. Phys. Lett., 2006, 89, 202108 CrossRef.
- G. Xue, C. Fan, J. Wu, S. Liu, Y. Liu, H. Chen, H. L. Xin and H. Li, Mater. Horiz., 2015, 2, 344–349 RSC.
- R. Zeis, T. Siegrist and C. Kloc, Appl. Phys. Lett., 2005, 86, 022103 CrossRef.
- J. Takeya, M. Yamagishi, Y. Tominari, R. Hirahara, Y. Nakazawa, T. Nishikawa, T. Kawase, T. Shimoda and S. Ogawa, Appl. Phys. Lett., 2007, 90, 102120 CrossRef.
- A. Liess, A. Lv, A. Arjona-Esteban, D. Bialas, A.-M. Krause, V. Stepanenko, M. Stolte and F. Würthner, Nano Lett., 2017, 17, 1719–1726 CrossRef CAS PubMed.
- L. Huang, M. Stolte, H. Bürckstümmer and F. Würthner, Adv. Mater., 2012, 24, 5750–5754 CrossRef CAS PubMed.
- E. Kirchner, D. Bialas, F. Fennel, M. Grüne and F. Würthner, J. Am. Chem. Soc., 2019, 141, 7428–7438 CrossRef CAS PubMed.
- D. Bialas, C. Zhong, F. Würthner and F. C. Spano, J. Phys. Chem. C, 2019, 123, 18654–18664 CrossRef CAS.
- D. Bialas, A. Zitzler-Kunkel, E. Kirchner, D. Schmidt and F. Würthner, Nat. Commun., 2016, 7, 12949 CrossRef CAS PubMed.
- Y. Li, H. K. M. Sheriff Jr., X. Liu, C.-K. Wang, K. Ding, H. Han, K.-T. Wong and S. R. Forrest, J. Am. Chem. Soc., 2019, 141, 18204–18210 CrossRef CAS PubMed.
- N. M. Kronenberg, V. Steinmann, H. Bürckstümmer, J. Hwang, D. Hertel, F. Würthner and K. Meerholz, Adv. Mater., 2010, 22, 4193–4197 CrossRef CAS PubMed.
- A. Liess, A. Arjona-Esteban, A. Kudzus, J. Albert, A.-M. Krause, A. Lv, M. Stolte, K. Meerholz and F. Würthner, Adv. Funct. Mater., 2018, 29, 1805058 CrossRef.
- A. Arjona-Esteban, J. Krumrian, A. Liess, M. Stolte, L. Huang, D. Schmidt, V. Stepanenko, M. Gsänger, D. Hertel, K. Meerholz and F. Würthner, J. Am. Chem. Soc., 2015, 137, 13524–13534 CrossRef CAS PubMed.
- C. Brückner, C. Walter, M. Stolte, B. Braïda, K. Meerholz, F. Würthner and B. Engels, J. Phys. Chem. C, 2015, 119, 17602–17611 CrossRef.
- C. Brückner and B. Engels, J. Phys. Chem. A, 2015, 119, 12876–12891 CrossRef PubMed.
- C. Brückner, F. Würthner, K. Meerholz and B. Engels, J. Phys. Chem. C, 2017, 121, 4–25 CrossRef.
- C. Brückner, F. Würthner, K. Meerholz and B. Engels, J. Phys. Chem. C, 2017, 121, 26–51 CrossRef.
- S. Di Motta, E. Di Donato, F. Negri, G. Orlandi, D. Fazzi and C. Castiglioni, J. Am. Chem. Soc., 2009, 131, 6591–6598 CrossRef CAS PubMed.
- V. Rühle, A. Lukyanov, F. May, M. Schrader, T. Vehoff, J. Kirkpatrick, B. Baumeier and D. Andrienko, J. Chem. Theory Comput., 2011, 7, 3335–3345 CrossRef PubMed.
- H. Oberhofer, K. Reuter and J. Blumberger, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- V. Stehr, R. F. Fink, M. Tafipolski, C. Deibel and B. Engels, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 694–720 CAS.
- V. Stehr, J. Pfister, R. F. Fink, B. Engels and C. Deibel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155208 CrossRef.
- E. Di Donato, R. P. Fornari, S. Di Motta, Y. Li, Z. Wang and F. Negri, J. Phys. Chem. B, 2010, 114, 5327–5334 CrossRef CAS PubMed.
- S. Canola and F. Negri, Phys. Chem. Chem. Phys., 2014, 16, 21550–21558 RSC.
- A. Capobianco, R. Borelli, A. Landi, A. Velardo and A. Peluso, J. Phys. Chem. A, 2016, 120, 5581–5589 CrossRef CAS PubMed.
- F. Würthner, C. Thalacker, R. Matschiner, K. Lukaszuk and R. Wortmann, Chem. Commun., 1998, 1739–1740 RSC.
- B. Le Guennic and D. Jacquemin, Acc. Chem. Res., 2015, 48, 530–537 CrossRef CAS PubMed.
- H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- C. Brückner and B. Engels, Chem. Phys., 2017, 482, 319–338 CrossRef.
- R. Send, O. Valsson and C. Filippi, J. Chem. Theory Comput., 2011, 7, 444–455 CrossRef CAS PubMed.
- H. Zhekova, M. Krykunov, J. Autschbach and T. Ziegler, J. Chem. Theory Comput., 2014, 10, 3299–3307 CrossRef CAS PubMed.
- B. Moore Li and J. Autschbach, J. Chem. Theory Comput., 2013, 9, 4991–5003 CrossRef PubMed.
- S. Knippenberg, R. L. Gieseking, D. R. Rehn, S. Mukhopadhyay, A. Dreuw and J.-L. Brédas, J. Chem. Theory Comput., 2016, 12, 5465–5476 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Grimme and F. Neese, J. Chem. Phys., 2007, 127, 154116 CrossRef PubMed.
- P. Boulanger, D. Jacquemin, I. Duchemin and X. Blase, J. Chem. Theory Comput., 2014, 10, 1212–1218 CrossRef CAS PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2011, 112, 321–370 CrossRef PubMed.
- J. Hoche, A. Schulz, L. M. Dietrich, A. Humeniuk, M. Stolte, D. Schmidt, T. Brixner, F. Würthner and R. Mitric, Chem. Sci., 2019, 10, 11013–11022 RSC.
- H.-S. Ren, M.-J. Ming, J.-Y. Ma and X.-Y. Li, J. Phys. Chem. A, 2013, 117, 8017–8025 CrossRef CAS PubMed.
- J. E. Norton and J.-L. Brédas, J. Am. Chem. Soc., 2008, 130, 12377–12384 CrossRef CAS PubMed.
- D. P. McMahon and A. Troisi, J. Phys. Chem. Lett., 2010, 1, 941–946 CrossRef CAS.
- T. Xu, W. Wang and S. Yin, J. Phys. Chem. A, 2018, 122, 8957–8964 CrossRef CAS PubMed.
- C. Poelking, E. Cho, A. Malafeev, V. Ivanov, K. Kremer, C. Risko, J.-L. Brédas and D. Andrienko, J. Phys. Chem. C, 2013, 117, 1633–1640 CrossRef CAS.
- K.-H. Lin, A. Prlj, L. Yao, N. Drigo, H.-H. Cho, M.-K. Nazeeruddin, K. Sivula and C. Corminboeuf, Chem. Mater., 2019, 31, 6605–6614 CrossRef CAS.
- S. Canola and F. Negri, J. Phys. Chem. C, 2015, 119, 11499–11505 CrossRef CAS.
- S. Di Motta, M. Siracusa and F. Negri, J. Phys. Chem. C, 2011, 115, 20754–20764 CrossRef CAS.
- S. M. Gali, M. Matta, B. H. Lessard, F. Castet and L. Muccioli, J. Phys. Chem. C, 2018, 122, 2554–2563 CrossRef CAS.
- W. F. Pasveer, J. Cottaar, C. Tanase, R. Coehoorn, P. A. Bobbert, P. W. M. Blom, D. M. de Leeuw and M. A. J. Michels, Phys. Rev. Lett., 2005, 94, 206601 CrossRef CAS PubMed.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843 CrossRef PubMed.
- T. Nematiaram and A. Troisi, Mater. Horiz., 2020, 7, 2922–2928 RSC.
- T. F. Harrelson, V. Dantanarayana, X. Xie, C. Koshnick, D. Nai, R. Fair, S. A. Nuñez, A. K. Thomas, T. L. Murrey, M. A. Hickner, J. K. Grey, J. E. Anthony, E. D. Gomez, A. Troisi, R. Faller and A. J. Moulé, Mater. Horiz., 2019, 6, 182–191 RSC.
- N. G. Martinelli, Y. Olivier, S. Athanasopoulos, M.-C. Ruiz Delgado, K. R. Pigg, D. A. da Silva Filho, R. S. Sánchez-Carrera, E. Venuti, R. G. Della Valle, J.-L. Brédas and D. Beljonne, ChemPhysChem, 2009, 10, 2265–2273 CrossRef CAS PubMed.
- T. He, Y. Wu, G. D’Avino, E. Schmidt, M. Stolte, J. Cornil, D. Beljonne, P. P. Ruden, F. Würthner and C. D. Frisbie, Nat. Commun., 2018, 9, 2141 CrossRef PubMed.
- V. Coropceanu, R. S. Sánchez-Carrera, P. Paramonov, G. M. Day and J.-L. Brédas, J. Phys. Chem. C, 2009, 113, 4679–4686 CrossRef CAS.
- P. Gosar and I. Vilfan, Mol. Phys., 1970, 18, 49–61 CrossRef CAS.
- X. Xie, A. Santana-Bonilla and A. Troisi, J. Chem. Theory Comput., 2018, 14, 3752–3762 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2073437, 2073438 and 2073461. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc01511g |
| ‡ Present address: Unité de Chimie Physique Théorique et Structurale and Laboratoire de Physique du Solide, Namur Institute of Structured Matter, Université de Namur, B-5000 Namur, Belgium. |
| This journal is © The Royal Society of Chemistry 2021 |