Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Binding affinities of cucurbit[n]urils with cations†
Shuai
Zhang‡
a,
Laura
Grimm‡
 b,
Zsombor
Miskolczy
b,
Zsombor
Miskolczy
 c,
László
Biczók
c,
László
Biczók
 c,
Frank
Biedermann
c,
Frank
Biedermann
 *b and
Werner M.
Nau
*b and
Werner M.
Nau
 *a
*a
aDepartment of Life Sciences and Chemistry, Jacobs University, Campus Ring 1, 28759, Bremen, Germany. E-mail: w.nau@jacobs-university.de
bInstitute of Nanotechnology, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: frank.biedermann@kit.edu
cInstitute of Materials and Environmental Chemistry, Research Centre for Natural Sciences, P. O. Box 286, 1519 Budapest, Hungary
First published on 23rd October 2019
Abstract
High binding constants of 19 inorganic cations with the cucurbit[n]uril homologues (CBn, n = 5, 6, 7, 8) in water were determined and the far-reaching consequences and interferences of the high affinities (millimolar to micromolar) are discussed.
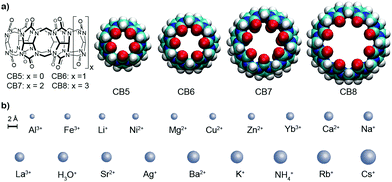
The design of artificial receptors for inorganic cations has underpinned the development of supramolecular chemistry.1,2 Through advances in the understanding of non-covalent interactions,3 carefully designed supramolecular receptors for (earth) alkaline cations emerged in the 1980's such as Cram's spherands4,5 displaying high selectivity for Li+. Conversely, Lehn's cryptands6,7 and the more recently introduced orthoester cryptands by von Delius8,9 can strongly and selectively bind (earth) alkali cations. In contrast to these designer hosts, other classes of macrocyclic receptors were originally tailored for organic guests but later also found to be interesting metal ion binders, for example, p-sulfonatocalix[4]arene (CX4). For supramolecular applications, this behavior is often undesirable because alkali ion binding competes for the binding of the target guests (e.g., choline) in biologically relevant, aqueous saline media.10,11 Likewise, cucurbit[n]uril (CBn, Fig. 1) macrocycles were long known to interact with (earth) alkaline cations, leading to an increase in their aqueous solubility but a decrease in their organic–guest binding affinities.12–17 CBn have found widespread use as solubility enhancers,18 for materials applications,19,20 and for assay development,17,21 which often take place in buffered aqueous media.12,16,22,23 The influence of metal cation binding to CBn macrocycles is therefore a critical factor. However, while the interaction of CB6 with Ca2+ was inferred already a century ago,24 and while absolute affinity values for some ions such as Na+ have been reported,23,25–29 (see also Table S1 in the ESI†) binding affinities for metal cations to CBn in water have not been systematically studied across the homologous series and associated structure-affinity relationships are unknown.
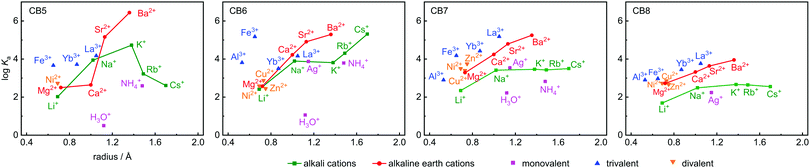
We now provide a comprehensive data set for the complexation of 19 inorganic cations with CB5, CB6, CB7, and CB8 in water. The determination of cation–CBn binding is challenging because their interaction does not provide a diagnostic signal change in conventional NMR or UV-vis absorption spectra and phase-extraction protocols30 are inapplicable for water-soluble hosts such as CX4 or CBn. As alternatives, fluorescence displacement titrations and isothermal titration calorimetry (ITC) experiments came to mind for the determination of macrocycle-cation binding constants (Ka).10,31,32 The experimental details are shown in the ESI† and the aggregated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka values are shown in Table 1, along with the ionic radii and their hydration free energies in order to correlate with size fitting and desolvation effects. Additional reference data for classical cation–receptor macrocycles such as 18-crown-6,2,33,34p-sulfonatocalix[4]arene (CX4),10,32,35,36 and Cryptand [2.2.2]6,31,37,38 are also shown. Monovalent alkali metal ions, Ag+, NH4+, and H3O+, divalent earth alkaline ions, transition metal ions, and trivalent cations were investigated. It transpires from Table 1 and from the comparison to the data for the established hosts that CBn are highly competitive inorganic cation receptors, although they are much better known for their tight binding of organic guests. Correlations of the log
Ka values are shown in Table 1, along with the ionic radii and their hydration free energies in order to correlate with size fitting and desolvation effects. Additional reference data for classical cation–receptor macrocycles such as 18-crown-6,2,33,34p-sulfonatocalix[4]arene (CX4),10,32,35,36 and Cryptand [2.2.2]6,31,37,38 are also shown. Monovalent alkali metal ions, Ag+, NH4+, and H3O+, divalent earth alkaline ions, transition metal ions, and trivalent cations were investigated. It transpires from Table 1 and from the comparison to the data for the established hosts that CBn are highly competitive inorganic cation receptors, although they are much better known for their tight binding of organic guests. Correlations of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka values with ionic cation radius are shown in Fig. 2; the interconnected lines for the alkali and alkaline earth ions reveal a general trend in favour of a stronger binding for the larger and less strongly hydrated metal ions; only for the smallest CB5 a bell-shaped curve for the alkaline metal ions is obtained, which points to an ideal size matching as an additional determinant (see Fig. 1 for size comparison). Within a homologous series, the most rigid macrocycle, CB5 in our series, is in general known to display a pronounced peak selectivity.6,31 Rb+ and Cs+ appear to be too large to penetrate into the carbonyl portal region of CB5, where the dipolar interaction with the oxygen lone pairs is most effective. Ag+ follows the trend for the alkaline metal ions, but NH4+ and H3O+ fall binding-wise below the correlation for (similarly sized) monovalent ions (Fig. 2), presumably because they engage as potent hydrogen bond donors in bulk water. This demonstrates that the formation of hydrogen bonds to the cucurbituril portals presents no significant driving force for organic guest complexation. Instead, the enhanced binding of organic guests upon introduction of cationic groups can be satisfactorily explained by ion–dipole interactions with the portals. Cationic centers that do not act as hydrogen-bond donors and that are less strongly hydrated, such as quaternary ammonium groups, present accordingly the better choice if optimized binding to CBn is desired.43 Hydrogen-bond proximity patterns, that are frequently observed in crystal structures of CBn,14,44,45 do not reflect on the driving force of host–guest binding in aqueous solution.
Ka values with ionic cation radius are shown in Fig. 2; the interconnected lines for the alkali and alkaline earth ions reveal a general trend in favour of a stronger binding for the larger and less strongly hydrated metal ions; only for the smallest CB5 a bell-shaped curve for the alkaline metal ions is obtained, which points to an ideal size matching as an additional determinant (see Fig. 1 for size comparison). Within a homologous series, the most rigid macrocycle, CB5 in our series, is in general known to display a pronounced peak selectivity.6,31 Rb+ and Cs+ appear to be too large to penetrate into the carbonyl portal region of CB5, where the dipolar interaction with the oxygen lone pairs is most effective. Ag+ follows the trend for the alkaline metal ions, but NH4+ and H3O+ fall binding-wise below the correlation for (similarly sized) monovalent ions (Fig. 2), presumably because they engage as potent hydrogen bond donors in bulk water. This demonstrates that the formation of hydrogen bonds to the cucurbituril portals presents no significant driving force for organic guest complexation. Instead, the enhanced binding of organic guests upon introduction of cationic groups can be satisfactorily explained by ion–dipole interactions with the portals. Cationic centers that do not act as hydrogen-bond donors and that are less strongly hydrated, such as quaternary ammonium groups, present accordingly the better choice if optimized binding to CBn is desired.43 Hydrogen-bond proximity patterns, that are frequently observed in crystal structures of CBn,14,44,45 do not reflect on the driving force of host–guest binding in aqueous solution.
| Cations |
r
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Å) (Å) |
−ΔGhydb (kJ mol−1) | CB5c | CB6d | CB7e | CB8f | 18-Crown-6g | CX4h | Cryptand [2.2.2]i |
|---|---|---|---|---|---|---|---|---|---|
a Ionic radius, from ref. 39.
b Hydration free energy, from ref. 39.
c By ITC experiments with desalinated CB5 and the respective nitrate salts at 283 K; error ± 0.10.
d By fluorescence displacement titrations with the reporter pair CB6·DSMI at 298 K; error ± 0.10.
e By fluorescence displacement titrations with the reporter pair CB7·BE at 298 K; error ± 0.10; values in parentheses determined by ITC experiments with CB7 at 298 K; error ± 0.10.
f By UV-vis displacement titrations with CB8·PDI at 298 K; error ± 0.10.
g From ref. 10, 34 and 40.
h From ref. 10, 32, 35 and 36.
i From ref. 6, 31, 37 and 38.
j Large heats of dilution compared to binding heats prevented determination of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka by ITC.
k Derived from ref. 41 by using the affinity for cyclohexylmethylamine from ref. 42 extrapolated for neat water.
l Cryptand [2.2.2] is being protonated.
m From fluorescence displacement titrations, error ± 0.3.
n Mean log Ka by ITC.
k Derived from ref. 41 by using the affinity for cyclohexylmethylamine from ref. 42 extrapolated for neat water.
l Cryptand [2.2.2] is being protonated.
m From fluorescence displacement titrations, error ± 0.3.
n Mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka values and standard deviations for each host type; values in parentheses are for subset of alkali and earth alkaline metal ions. Ka values and standard deviations for each host type; values in parentheses are for subset of alkali and earth alkaline metal ions.
|
|||||||||
| H3O+ | 1.12 | — | ≤0.5 | 1.06k | 2.22 | — | 1.46 | 1.6 | (9.66)l |
| NH4+ | 1.48 | 285 | 2.59 | 3.79 | 2.82 | — | 1.23 | 2.22 | |
| Li+ | 0.69 | 475 | 2.02 | 2.41 | 2.34 | 1.69 | ∼ 0 | 2.14 | 1.3 |
| Na+ | 1.02 | 365 | 3.94 | 3.89 | 3.41 | 2.49 | 0.8 | 2.26 | 3.9 |
| K+ | 1.38 | 295 | 4.73 | 3.81 | 3.46 (3.29) | 2.66 | 2.03 | 2.33 | 5.3 |
| Rb+ | 1.49 | 275 | 3.22 | 4.30 | 3.43 (3.42) | 2.64 | 1.56 | 2.40 | 4.2 |
| Cs+ | 1.70 | 250 | 2.61 | 5.31 | 3.50 (3.51) | 2.55 | 0.99 | 2.88 | 1.4 |
| Ag+ | 1.15 | 430 | —j | 3.87 | 3.54 | 2.32 | 1.50 | 2.43 | 9.6 |
| Mg2+ | 0.72 | 1830 | 2.50 | 2.57 | 3.24 | 2.72 | ∼0 | 3.58 | <0 |
| Ca2+ | 1.00 | 1505 | 2.64 | 4.22 | 4.25 (4.01) | 3.31 | 1.26 | 3.89 | 4.4 |
| Sr2+ | 1.13 | 1380 | 5.16 | 4.91 | 4.79 (4.31) | 3.63 | 2.72 | 3.66 | 8.0 |
| Ba2+ | 1.36 | 1250 | 6.44 | 5.29 | 5.28 (4.78) | 3.95 | 3.87 | 3.83 | 9.5 |
| Ni2+ | 0.69 | 1980 | 2.73 | 2.59 | 3.50 | 2.73 | — | 3.75 | <2.0 |
| Cu2+ | 0.73 | 2010 | — | 2.88 | 3.75 | 2.86 | — | 3.75 | 6.8 |
| Zn2+ | 0.75 | 1955 | — | 2.45 | 3.40 | 2.67 | — | 3.75 | <2.5 |
| Al3+ | 0.53 | 4525 | —j | 3.81 | 2.90 | 2.90 | — | — | — |
| Fe3+ | 0.65 | 4265 | 3.66 | 5.17 | 4.18 | 3.0m | — | — | — |
| Yb3+ | 0.87 | 3570 | 3.71 | 3.50 | 4.42 | 3.44 | — | 3.81 | — |
| La3+ | 1.05 | 3145 | 4.17 | 4.16 | 5.28 | 3.76 | 4.23 | 6.45 | |
Mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka valuen Ka valuen |
3.42 (3.74) | 3.68 (4.03) | 3.66 (3.93) | 2.90 (2.85) | 1.58 (1.65) | 3.09 (3.18) | 4.67 (4.22) | ||
StDev of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka valuen Ka valuen |
1.42 (1.27) | 1.10 (0.92) | 0.82 (0.87) | 0.55 (0.64) | 0.97 (1.13) | 0.80 (0.75) | 2.97 (2.94) | ||
Ion–dipole interactions are supported by the dependence on metal ion valency, with the general trend trivalent > divalent > monovalent at comparable ionic radius, see colour coding in Fig. 2. The three divalent transition metal ions Ni2+, Zn2+, and Cu2+ bind with similar affinity, as expected from their similar cation size and hydration free energy, but the trivalent Fe3+ binds more tightly, regardless of its higher hydration free energy. Within the series of trivalent ions, the hydration free energies (Al3+ > Fe3+ > Yb3+ > La3+) are a good indicator, but CB6 is an outlier here; it binds the lanthanide ions less tightly. CB6 is also the only CBn homologue that shows a markedly enhanced affinity to Rb+ and Cs+ compared to K+, which reveals the complex interplay in underlying factors.
To ease quantitative discussion, we define in Table 1 (bottom) also the average binding constants as an overall measure of the “strength” of the different cation receptors and the standard deviation as a measure of their “selectivity”. In terms of strength, the sequence Cryptand [2.2.2] > CB6 ≈ CB7 > CB5 > 18-crown-6 > CB8 > CX4 is obtained. In terms of selectivity, the order Cryptand [2.2.2] > CB5 > CB6 > 18-crown-6 > CB7 ≈ CX4 > CB8. As can be seen, within the CBn series, the selectivity decreases systematically as the portal size increases, but the intermediary sized CB6 is the strongest inorganic metal ion binder, presumably because its cavity provides the best size match for most of the investigated ions (see Fig. 1 for size comparison). All CBn homologues easily outperform the more flexible 18-crown-6, compete with CX4, but cannot reach the goodness of the diligently designed and three-dimensionally optimized receptor Cryptand [2.2.2]. In direct comparison, although CB6 and 18-crown-6 have comparable O⋯O cross-portal distances (r = 1.4 Å), the rigid portals of CB6 have clear advantages for metal ion binding in terms of preorganization. Similarly, CX4 is usually compared to CB7, because both macrocycles have a comparable preferred organic guest capacity (ca. 130 Å3), but CX4 is conformationally much more flexible, which renders it a less potent inorganic ion receptor, despite its penta- or tetraanionic charge status.10 As it comes to absolute binding potential, CB5 is the CBn homologue of choice for binding of Ba2+ and CB6 excels in binding Cs+ in aqueous solution, reaching micromolar affinity in these cases. The binding constant between CB6 and Cs+ is at least two orders of magnitude higher than that with other hosts (Fig. 2). For CB7 and CB8, La3+ and Ba2+ emerge as strongest binders.
Apart from potential application aspects related to the (metal) ion binding, e.g., for sensing, the measured affinities of CBn with common inorganic ions have important practical implications for the determination of binding constants with (organic) guest molecules. As quantitatively demonstrated earlier,17,46 the common (and for biological measurements necessary) practice to determine binding constants in buffered solution rather than in neat water16,22,23 leads to apparent binding constants (Kapp) of organic guest molecules with CBn, because the large concentrations of buffer cations compete effectively with CBn binding and, thereby, lower them.
The decrease of the binding constants can be estimated from eqn (1),10 which assumes a direct stoichiometric competition, similar to the competitive displacement principle used to determine the ion binding constants in this study. At high buffer cation concentrations (>10 mM) and with sizable affinities to CBn (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka > 2), significant reductions of the measured guest binding constants result, which are tabulated in Table 2 by using the average binding constants from Table 1 as example (the use of the affinity of Na+ as the most common buffer cation affords comparable values). As can be seen, the error introduced by measuring binding constants in buffer solution can easily reach factors of 100–1000, and it is only for the largest homologue, CB8, where the variation is much smaller but still significant.
Ka > 2), significant reductions of the measured guest binding constants result, which are tabulated in Table 2 by using the average binding constants from Table 1 as example (the use of the affinity of Na+ as the most common buffer cation affords comparable values). As can be seen, the error introduced by measuring binding constants in buffer solution can easily reach factors of 100–1000, and it is only for the largest homologue, CB8, where the variation is much smaller but still significant.
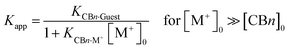 | (1) |
| [M+]/mM | Systematic “error”: KCBn·Guest/Kapp | |||
|---|---|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCB5·M+ = 3.4 KCB5·M+ = 3.4 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCB6·M+ = 3.7 KCB6·M+ = 3.7 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCB7·M+ = 3.7 KCB7·M+ = 3.7 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KCB8·M+ = 2.9 KCB8·M+ = 2.9 |
|
| 0 | 1 | 1 | 1 | 1 |
| 5 | 15 | 25 | 25 | 5 |
| 20 | 50 | 100 | 100 | 20 |
| 100 | 250 | 500 | 500 | 80 |
| 200 | 500 | 1000 | 1000 | 160 |
The underestimation of the magnitude of the salt effects may account in part for the large variations in affinities of the same guests reported in the literature. The best practice is the determination of CBn binding constants in neat water.17,18,42,47–49 The presence of cations present in the CBn samples themselves, e.g., ammonium ions in CB5, also needs to be kept in mind (see also Table S7, ESI†),50 similar to the omnipresence of Na+ cations in CX4 samples.10 For biological measurements, the choice of NH4+ instead of Na+,21 may reduce the variation, but does not eliminate it. We found that for CB6, where buffers are frequently used to increase its solubility, the smallest variation is obtained when using 1 mM HCl (H3O+) as additive,49 but the resulting pH of 3 must be tolerated. In contrast to the strong influence of buffers on the CBn–guest binding affinities (Table 2), the use of D2O as an NMR solvent is inoffensive because solvent isotope effects on the affinity are only ca. 20%.51
The situation with using buffers becomes even more intricate when measurements of thermochemical parameters other than the binding constants are concerned, e.g., complexation enthalpies and entropies obtained by ITC. The measured released or absorbed heat in ITC experiments may reflect the heat associated with the decomplexation/displacement of the inorganic cation present in the solution rather than for the host–guest binding process. In these cases, the complexation enthalpies or entropies are invariably incorrect, and in extreme cases host–guest binding events which are intrinsically exothermic may appear as being endothermic, and enthalpically driven reactions may come out as entropically driven ones. In ITC experiments with CX4, we have previously demonstrated such a worst-case scenario, where the binding enthalpies of two competitors canceled out, which gave rise to the impression that there is no binding.10 For CB5-cation binding, the complexation enthalpies and entropies were found to span a remarkable wide range from very favorable to unfavorable; ΔH varied from +24 kJ mol−1 to −35 kJ mol−1 and −TΔS ranged from +21 to −47 kJ mol−1, see Table S2 (ESI†). Consequently, thermochemical parameters measured for CBn in the presence of buffer cations, including our own measurements, contain a systematic error and are incorrect in absolute terms. Strictly speaking, they do not only report on the host–guest binding event, but on the differences in complexation enthalpies between guest and cation binding.
Another sequential but severe shortcoming is that the apparent binding constants in the presence of buffers have already been used in the literature as benchmark values not only to evaluate the performance of computational methods in so-called challenges,52–54 but in some cases also for the parameterization and calibration of computational methods.55 Assuming that the experimental values underestimate the binding by up to three orders of magnitude (Table 2), corresponding to 17 kJ mol−1 at 298 K, an incorrect calibration of computational methods, which aim in part for an accuracy better than 8 kJ mol−1, may have resulted. It appears essential that computational challenges that aim at host–guest binding of CBn or other ion receptors either explicitly consider the presence of buffer ions or address the true guest affinities, namely those in neat water.
This work was supported by the DFG (F. B. and W. M. N.), the China Scholarship Council (doctoral scholarship for S. Z.), and the NKFIH (L. B. and Z. M.). Mara Florea is acknowledged for preliminary CB6–cation binding studies.
Conflicts of interest
There are no conflicts of interest to declare.Notes and references
- C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 7017–7036 CrossRef CAS.
- G. W. Gokel, W. M. Leevy and M. E. Weber, Chem. Rev., 2004, 104, 2723–2750 CrossRef CAS PubMed.
- F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5300 CrossRef CAS PubMed.
- D. J. Cram, T. Kaneda, R. C. Helgeson, S. B. Brown, C. B. Knobler, E. Maverick and K. N. Trueblood, J. Am. Chem. Soc., 1985, 107, 3645–3657 CrossRef CAS.
- D. J. Cram and G. M. Lein, J. Am. Chem. Soc., 1985, 107, 3657–3668 CrossRef CAS.
- E. Kauffmann, J.-M. Lehn and J.-P. Sauvage, Helv. Chim. Acta, 1976, 59, 1099–1111 CrossRef CAS.
- J. M. Lehn, Acc. Chem. Res., 1978, 11, 49–57 CrossRef CAS.
- R.-C. Brachvogel, F. Hampel and M. von Delius, Nat. Commun., 2015, 6, 7129 CrossRef PubMed.
- H. Löw, E. Mena-Osteritz and M. von Delius, Chem. Sci., 2018, 9, 4785–4793 RSC.
- V. Francisco, A. Piñeiro, W. M. Nau and L. García-Río, Chem. – Eur. J., 2013, 19, 17809–17820 CrossRef CAS PubMed.
- J. Murray, K. Kim, T. Ogoshi, W. Yao and B. C. Gibb, Chem. Soc. Rev., 2017, 46, 2479–2496 RSC.
- J. Lagona, P. Mukhopadhyay, S. Chakrabarti and L. Isaacs, Angew. Chem., Int. Ed., 2005, 44, 4844–4870 CrossRef CAS PubMed.
- W. S. Jeon, K. Moon, S. H. Park, H. Chun, Y. H. Ko, J. Y. Lee, E. S. Lee, S. Samal, N. Selvapalam and M. V. Rekharsky, J. Am. Chem. Soc., 2005, 127, 12984–12989 CrossRef CAS PubMed.
- S. Liu, C. Ruspic, P. Mukhopadhyay, S. Chakrabarti, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2005, 127, 15959–15967 CrossRef CAS PubMed.
- S. Moghaddam, C. Yang, M. Rekharsky, Y. H. Ko, K. Kim, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2011, 133, 3570–3581 CrossRef CAS PubMed.
- K. I. Assaf and W. M. Nau, Chem. Soc. Rev., 2015, 44, 394–418 RSC.
- S. Sinn, E. Spuling, S. Bräse and F. Biedermann, Chem. Sci., 2019, 10, 6584–6593 RSC.
- A. I. Lazar, F. Biedermann, K. R. Mustafina, K. I. Assaf, A. Hennig and W. M. Nau, J. Am. Chem. Soc., 2016, 138, 13022–13029 CrossRef CAS PubMed.
- E. A. Appel, F. Biedermann, U. Rauwald, S. T. Jones, J. M. Zayed and O. A. Scherman, J. Am. Chem. Soc., 2010, 132, 14251–14260 CrossRef CAS PubMed.
- K. M. Park, J.-A. Yang, H. Jung, J. Yeom, J. S. Park, K.-H. Park, A. S. Hoffman, S. K. Hahn and K. Kim, ACS Nano, 2012, 6, 2960–2968 CrossRef CAS PubMed.
- A. Hennig, H. Bakirci and W. M. Nau, Nat. Methods, 2007, 4, 629 CrossRef CAS PubMed.
- S. J. Barrow, S. Kasera, M. J. Rowland, J. del Barrio and O. A. Scherman, Chem. Rev., 2015, 115, 12320–12406 CrossRef CAS PubMed.
- S. Sinn and F. Biedermann, Isr. J. Chem., 2018, 58, 357–412 CrossRef CAS.
- R. Behrend, E. Meyer and F. Rusche, Eur. J. Org. Chem., 1905, 1–37 Search PubMed.
- V. F. Pais, E. F. Carvalho, J. P. Tomé and U. Pischel, Supramol. Chem., 2014, 26, 642–647 CrossRef CAS.
- W. L. Mock and N. Y. Shih, J. Org. Chem., 1986, 51, 4440–4446 CrossRef CAS.
- I. Hwang, Woo S. Jeon, H.-J. Kim, D. Kim, H. Kim, N. Selvapalam, N. Fujita, S. Shinkai and K. Kim, Angew. Chem., Int. Ed., 2007, 46, 210–213 CrossRef CAS PubMed.
- H.-J. Buschmann, E. Cleve, L. Mutihac and E. Schollmeyer, J. Inclusion Phenom. Macrocyclic Chem., 2009, 65, 293 CrossRef CAS.
- M. Megyesi, L. Biczók and I. Jablonkai, J. Phys. Chem. C, 2008, 112, 3410–3416 CrossRef CAS.
- C. A. Schalley, Analytical methods in supramolecular chemistry, John Wiley & Sons, 2012 Search PubMed.
- R. M. Izatt, K. Pawlak, J. S. Bradshaw and R. L. Bruening, Chem. Rev., 1991, 91, 1721–2085 CrossRef CAS.
- H. Bakirci, A. L. Koner and W. M. Nau, Chem. Commun., 2005, 5411–5413 RSC.
- J. S. Bradshaw and R. M. Izatt, Acc. Chem. Res., 1997, 30, 338–345 CrossRef CAS.
- R. Izatt, R. Terry, B. Haymore, L. Hansen, N. Dalley, A. Avondet and J. Christensen, J. Am. Chem. Soc., 1976, 98, 7620–7626 CrossRef CAS.
- H. Bakirci, A. L. Koner, T. Schwarzlose and W. M. Nau, Chem. – Eur. J., 2006, 12, 4799–4807 CrossRef CAS PubMed.
- C. Bonal, Y. Israëli, J.-P. Morel and N. Morel-Desrosiers, J. Chem. Soc., Perkin Trans. 2, 2001, 1075–1078 RSC.
- M. H. Abraham, A. F. D. De Namor and R. A. Schulz, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 869–884 RSC.
- J. H. Burns and C. F. Baes, Inorg. Chem., 1981, 20, 616–619 CrossRef CAS.
- Y. Marcus, Biophys. Chem., 1994, 51, 111–127 CrossRef CAS.
- A. J. Smetana and A. I. Popov, J. Solution Chem., 1980, 9, 183–196 CrossRef CAS.
- C. Marquez and W. M. Nau, Angew. Chem., Int. Ed., 2001, 40, 3155–3160 CrossRef CAS.
- C. Marquez, R. R. Hudgins and W. M. Nau, J. Am. Chem. Soc., 2004, 126, 5806–5816 CrossRef CAS PubMed.
- M. A. Gamal-Eldin and D. H. Macartney, Org. Biomol. Chem., 2013, 11, 488–495 RSC.
- O. A. Gerasko, M. N. Sokolov and V. R. Fedin, Pure Appl. Chem., 2004, 76, 1633–1646 CAS.
- V. P. Fedin, V. Gramlich, M. Wörle and T. Weber, Inorg. Chem., 2001, 40, 1074–1077 CrossRef CAS.
- W. Ong and A. E. Kaifer, J. Org. Chem., 2004, 69, 1383–1385 CrossRef CAS.
- F. Biedermann, V. D. Uzunova, O. A. Scherman, W. M. Nau and A. De Simone, J. Am. Chem. Soc., 2012, 134, 15318–15323 CrossRef CAS PubMed.
- D. Sigwalt, M. Šekutor, L. Cao, P. Y. Zavalij, J. Hostaš, H. Ajani, P. Hobza, K. Mlinarić-Majerski, R. Glaser and L. Isaacs, J. Am. Chem. Soc., 2017, 139, 3249–3258 CrossRef CAS PubMed.
- M. Florea and W. M. Nau, Angew. Chem., Int. Ed., 2011, 50, 9338–9342 CrossRef CAS PubMed.
- S. He, F. Biedermann, N. Vankova, L. Zhechkov, T. Heine, R. E. Hoffman, A. De Simone, T. T. Duignan and W. M. Nau, Nat. Chem., 2018, 10, 1252–1257 CrossRef CAS PubMed.
- F. Biedermann, M. Vendruscolo, O. A. Scherman, A. De Simone and W. M. Nau, J. Am. Chem. Soc., 2013, 135, 14879–14888 CrossRef CAS PubMed.
- A. T. Fenley, N. M. Henriksen, H. S. Muddana and M. K. Gilson, J. Chem. Theory Comput., 2014, 10, 4069–4078 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Chem. Theory Comput., 2015, 11, 3785–3801 CrossRef CAS PubMed.
- H. S. Muddana, A. T. Fenley, D. L. Mobley and M. K. Gilson, J. Comput.-Aided Mol. Des., 2014, 28, 305–317 CrossRef CAS PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods, experimental details, as well as fitting equations. See DOI: 10.1039/c9cc07687e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |