Melting transition in lipid vesicles functionalised by mobile DNA linkers
Stephan Jan
Bachmann†
a,
Jurij
Kotar†
b,
Lucia
Parolini
b,
Anđela
Šarić
 cd,
Pietro
Cicuta
b,
Lorenzo
Di Michele
*b and
Bortolo Matteo
Mognetti
*a
cd,
Pietro
Cicuta
b,
Lorenzo
Di Michele
*b and
Bortolo Matteo
Mognetti
*a
aUniversité Libre de Bruxelles (ULB), Department of Physics, Interdisciplinary Center for Nonlinear Phenomena and Complex Systems & Service de Physique des Systèmes Complexes et Mécanique Statistique, Campus Plaine, CP 231, Blvd du Triomphe, B-1050 Brussels, Belgium. E-mail: bmognett@ulb.ac.be
bBiological and Soft Systems, Cavendish Laboratory, University of Cambridge, JJ Thomson Avenue, Cambridge CB3 0HE, UK. E-mail: ld389@cam.ac.uk
cDepartment of Chemistry, University of Cambridge, Cambridge CB2 1EW, UK
dDepartment of Physics and Astronomy, Institute for the Physics of Living Systems, University College London, WC1E 6BT, UK
First published on 19th August 2016
Abstract
We study phase behaviour of lipid-bilayer vesicles functionalised by ligand–receptor complexes made of synthetic DNA by introducing a modelling framework and a dedicated experimental platform. In particular, we perform Monte Carlo simulations that combine a coarse grained description of the lipid bilayer with state of art analytical models for multivalent ligand–receptor interactions. Using density of state calculations, we derive the partition function in pairs of vesicles and compute the number of ligand–receptor bonds as a function of temperature. Numerical results are compared to microscopy and fluorimetry experiments on large unilamellar vesicles decorated by DNA linkers carrying complementary overhangs. We find that vesicle aggregation is suppressed when the total number of linkers falls below a threshold value. Within the model proposed here, this is due to the higher configurational costs required to form inter-vesicle bridges as compared to intra-vesicle loops, which are in turn related to membrane deformability. Our findings and our numerical/experimental methodologies are applicable to the rational design of liposomes used as functional materials and drug delivery applications, as well as to study inter-membrane interactions in living systems, such as cell adhesion.
1 Introduction
Ligand–receptor interactions play a crucial role in a large variety of biological processes, including cell adhesion and signalling.1 In biology, the selective nature of ligand–receptor interactions enables functional behaviours and responsiveness to environmental stimuli, which can be replicated in biomimetic materials where the interactions between the unit components are mediated by supramolecular ligand–receptor complexes.2 The eminent example is represented by systems of DNA-functionalised colloidal units,3–6 where the artificial DNA linkers can be designed to control phase behaviour7–13 and self-assembly kinetics,14–19 as well as to engineer biological probes.20–23A complete understanding of the complex emerging phenomena observed in multivalent interactions is only possible through a combination of experiments and numerical/theoretical analysis. Modelling multivalent interactions24 is however a challenging task, as it requires the calculation of ensemble averages over the many possible configurations of the supramolecular linker complexes.20,25 Analytical methods capable of capturing the resulting entropic effects have been recently developed.26–35 Such theories have been utilised to calculate effective potentials in DNA mediated interactions between solid26–31 and deformable particles,35–39 as well as to design superselective probes.20,25,32–35,40 Analytical models have however limited applicability to those biologically and technologically relevant scenarios where non-specific contributions significantly affect the interactions. Effects neglected by analytical models include steric repulsion between the linkers and the deformability of the interacting surfaces. The latter is a particularly crucial aspect when dealing with multivalent interactions between soft substrates such as biological membranes. Numerical approaches could provide a faithful description of specific and non-specific effects in multivalent interactions. However, in view of the large interval of relevant lengthscales, from the molecular scale of ligands/receptors to the micron scale of the interacting units, even coarse-grained models are unsuitable to simulate phase behaviour and material properties in ensembles of micron-sized multivalent objects.41 Overcoming the limitation of purely analytical and purely numerical approaches is a critical step towards the development of truly predictive theoretical methods to aid the design of synthetic multivalent materials and improve our understanding of emergent behaviours in multivalent biological systems. A suitable approach should be capable of describing simultaneously the behaviour of the individual ligand/receptor pairs and the global phase behaviour of the systems.
The validation of such multiscale theoretical framework requires dedicated experiments in which the global phase behaviour can be disentangled from that of the individual ligand/receptor pairs, and the effect of the latter on the former can be assessed as a function of the number and adhesive strength of the linkers.
In this work we investigate the self-assembly behaviour of a biomimetic system of DNA-functionalised lipid vesicles,18,35,36,42–44 where artificial DNA linkers play the role of ligands/receptors and membrane deformability can potentially affect the resulting multivalent interactions. DNA linkers can freely diffuse on the surface of the vesicles and form either intra-vesicle loops or inter-vesicle bridges, the latter being responsible for attractive interactions and driving vesicle aggregation. We study the response of the system to temperature changes, and clarify how the aggregation/melting transition of the liposomes is affected by the competition between loop and bridge formation and the non-selective free energy contributions related in turn to membrane deformability.
We propose a new “hybrid” framework to calculate the free energy of the interactions between such vesicles, that combines state-of-art analytical theories developed for solid particles29–31,35–39 with Monte Carlo simulations that account for configurational costs related to membrane deformability.
By exploiting a fully automated and programmable platform, we perform experiments that for the first time are capable of simultaneously monitoring the self-assembly state of the liposomes and the bound/unbound state of the DNA linkers through a combination of fluorescence microscopy and Förster resonance energy transfer (FRET) measurements.
In systems where the number of linkers per vesicle N is low, simulations are capable of quantitatively replicating the response to temperature changes observed in experiments, including the aggregation/melting temperature of large unilamellar vesicle (LUV) clusters and its correlation with the temperature-dependent fraction of formed DNA bonds. Such agreement is lost at high N, most likely due to the effects of linker–linker and linker–vesicle steric interactions, neglected by our current model. Our numerical results confirm the importance and the nature of the previously hypothesised entropic effects on the hybridisation free energy of surface-tethered linkers.36,37,39,45 In cases where linkers can diffuse on the surface of the substrates, such as DNA-tethers on lipid vesicles or ligands/receptors on cells,46 these entropic costs include the loss of translational freedom following the formation of a bond. Particularly severe are the effects experienced by linkers forming inter-vesicle bridges, which end up confined within the relatively small adhesion patch between the vesicles. With the present numerical method these contributions can be directly evaluated based on the observed size of the adhesion patch, and then compared to the overall configurational free energy costs evaluated via density of states calculations.36,39
Experiments and simulations demonstrate that these repulsive free energy contributions, combined with the competition between loop and bridge formation, have a substantial effect on self-assembly behaviour of DNA-functionalised vesicles: a minimum number of linkers Ndim is required to stabilise adhesion.11,12 If fewer linkers are present vesicles do not aggregate.11,12 The fair agreement between experimental and predicted value of the threshold number of linkers validates our methods as an useful tool to design biomimetic self-assembling systems featuring complex functionalities.
The paper is structured as follows. Section 2 reports on experimental methods. In Section 3 we present our modelling framework. In particular in Sections 3.2 and 3.3 we present respectively the analytical and numerical methods. The latter section illustrates how the two are combined. In Section 4 we discuss the simulations' outcomes for a large set of different system parameters (listed in Section 3.6) and perform a detailed comparison with experimental results.
2 Experimental methods
In this section we present our sample preparation protocols and experimental setup designed to provide a complete characterisation of the self-assembly behaviour of DNA-functionalised LUVs. In particular we can simultaneously monitor temperature dependent vesicle aggregation and the binding/unbinding state of the membrane-anchored DNA linkers in multiple samples using fully programmable and automated microscopy/fluorimetry apparatus. Experimental information can then be directly compared to numerical results to validate the assumptions and highlight the limitations of the numerical/theoretical framework described in Section 3.2.1 Experimental system
As sketched in Fig. 1(a), LUVs with diameter Dexp ≈ 400 nm are functionalised by hydrophobised DNA linkers featuring a cholesterol anchor partitioning within the lipid bilayer, a rigid double-stranded DNA (dsDNA) spacer of length![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 10 nm and a single-stranded DNA (ssDNA) sticky end. Membranes are in a fluid state, which enables cholesterol anchors to freely diffuse onto the vesicles' surface. On average, half of the overall 2N linkers present on each vesicle carry a sticky end a, the second half carry the complementary sequence a′. One linker type can bind to the other forming either inter-vesicle bridges or intra-vesicle loops, the latter being possible because each vesicle carries both types of linkers. Bridges are responsible for inter-vesicle adhesive forces that ultimately lead to aggregation of the LUVs. Sticky ends a and a′ are labelled with fluorophores Cy3 and Cy5 respectively, so that Förster resonance energy transfer (FRET) can be used to assess bond formation.
≈ 10 nm and a single-stranded DNA (ssDNA) sticky end. Membranes are in a fluid state, which enables cholesterol anchors to freely diffuse onto the vesicles' surface. On average, half of the overall 2N linkers present on each vesicle carry a sticky end a, the second half carry the complementary sequence a′. One linker type can bind to the other forming either inter-vesicle bridges or intra-vesicle loops, the latter being possible because each vesicle carries both types of linkers. Bridges are responsible for inter-vesicle adhesive forces that ultimately lead to aggregation of the LUVs. Sticky ends a and a′ are labelled with fluorophores Cy3 and Cy5 respectively, so that Förster resonance energy transfer (FRET) can be used to assess bond formation.
2.2 Sample preparation
LUVs are prepared from dioleoyl-sn-glycero-3-phosphocholine (DOPC, Avanti Polar Lipids) doped with 0.8 molar percent Marina Blue 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (DHPE, Life Technologies) for fluorescent imaging. Vesicles are prepared by extrusion in a 300 mM sucrose solution using a Mini Extruder (Avanti Polar Lipids) equipped with polycarbonate track-etched membranes with 400 nm pores (Whatman), as detailed in ref. 18.Hydrophobised DNA linkers are pre-hybridised from the ssDNA
(i) 5′–CGT GCG CTG GCG TCT GAA AGT CGA TTG CGAAAA–3′ [Cholesterol TEG]
(ii) 5′–GC GAA TCG ACT TTC AGA CGC CAG CGC ACGA [Sticky End] A–3′ Cy3/Cy5,
where bases marked in bold belong to the dsDNA rigid spacer and unpaired A bases highlighted in italic are included to provide flexibility. Hybridisation is carried out in TE buffer (10 mM Tris, 1 mM EDTA, Sigma) with 100 mM NaCl as detailed in ref. 35.
Samples are prepared by mixing a 10 μl extruded vesicle solution with 90 μl iso-osmolar solution containing TE buffer, 87 mM glucose, 100 mM NaCl and a variable concentration of pre-assembled DNA linkers spanning from 12.7 μM to 0.25 μM, equally divided between a and a′ linkers. The nominal number of DNA linkers per vesicles is calculated assuming that all linkers partition into the bilayer,47 that all the processed lipids form unilamellar vesicles with diameter of 400 nm, and that each lipid molecule contributes with 70 Å2 to the bilayer area.48 This estimate leads to a number of a and a′ linkers per vesicle between 71 ≤ N ≤ 3550. The assumption that all linkers partition onto the bilayer may breakup at high DNA density due to surface saturation, as discussed in Section 4.
For thermal processing and imaging, samples are injected into borosilicate glass capillaries (0.2 × 4 mm2 rectangular inner section, CM Scientific), protected with a droplet of mineral oil at both ends, and permanently sealed with epoxy glue (Araldite).
2.3 Temperature cycling and imaging
Imaging and fluorescence spectroscopy are carried out on a fully automated Nikon Eclipse Ti-E inverted epifluorescence microscope equipped with a Nikon PLAN APO 20 × 0.75 NA dry objective and a Point Grey Research Grasshopper-3 GS3-U3-23S6M-C camera. Temperature is controlled with a tailor made Peltier stage hosting 7 capillaries with samples at different linker concentration. Temperature is repeatedly ramped up and down between 80 °C (or 90 °C) and 0 °C in steps of 1 °C and a rate of 0.5 °C min−1, and measured with a precision <0.1 °C by a thermocouple located in close proximity of the capillaries.At each temperature step, the motorised stage is moved to sequentially image all samples, recording snapshots with different fluorescence excitation wavelength and emission windows. For these different combinations of monochromatic LED sources (Philips Lumileds LUXEON UV, LUEXON Z), quad band fluorescence filter set (Semrock LED-DA/FI/TR/Cy5-A) and exchangeable motorized emission filters (Semrock FF01-600/37-25, FF01-731/137-25) are used. Specifically: Marina Blue (quad band filter set, excitation LED LHUV-0380-0200 at 380 nm); Cy3–Cy3 (quad band filter set, emission filter FF01-600/37-25, excitation LED LXZ1-PM01 at 530 nm); Cy3–Cy5 (quad band filter set, emission filter FF01-731/137-25, excitation LED LXZ1-PM01 at 530 nm); Cy5–Cy5 (quad band filter set, emission filter FF01-731/137-25, excitation LED LXZ1-PD01 at 627 nm). A single snapshot for each fluorescence channel is recorded on each sample, imaging an area of 563 × 352 μm2 at a fixed height of a ≈8 μm from the bottom of the capillary. Dark frames where no excitation is used are acquired between each fluorescence image and used for background subtraction. All steps of the experiment are fully automated. A Perfect Focusing System (Nikon) enables correction for vertical drift.
2.4 Image analysis
Images collected on the Marina Blue channel are used for structural characterisation of vesicle aggregates, carried out as described in ref. 18. Briefly, Fourier analysis of the images enables the evaluation of a 2D projection of the samples' structure factor S(q), where q is the spatial frequency. The first moment of S(q) is then measured as an indicator of the aggregation state of the samples, going from high values for monomeric vesicles towards low values when aggregation takes place and S(q) develops a strong peak at low-q.Images in the Cy3–Cy3, Cy3–Cy5 and Cy5–Cy5 channels are used to assess the efficiency of FRET between donor and acceptor fluorophores attached to a and a′ sticky ends respectively. The average intensities of each channel ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) Cy3–Cy3,
Cy3–Cy3, ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) Cy3–Cy5, and
Cy3–Cy5, and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) Cy5–Cy5 are extracted from the images, and used to evaluate the (ratio)A
Cy5–Cy5 are extracted from the images, and used to evaluate the (ratio)A
 | (1) |
 , and the intensities
, and the intensities  and
and 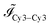 are measured in a reference sample that only contains Cy3 fluorophores. The (ratio)A is linearly dependent on the FRET efficiency.49 The Förster radius of the Cy3–Cy5 pair is ≈5–6 nm,50 therefore high FRET efficiency is expected in bound a–a′ pairs, where donor and acceptor are kept at ≈2–3 nm from each other. The probability of FRET between unbound linkers is comparatively small, although not fully negligible in samples with the high DNA coverage, where the average distance between unbound a–a′ linkers goes down to ≈11.9 nm. As a function of temperature, (ratio)A describes a sigmoidal curve from which the fraction of hybridised linkers ϕ(T) can be extracted as
are measured in a reference sample that only contains Cy3 fluorophores. The (ratio)A is linearly dependent on the FRET efficiency.49 The Förster radius of the Cy3–Cy5 pair is ≈5–6 nm,50 therefore high FRET efficiency is expected in bound a–a′ pairs, where donor and acceptor are kept at ≈2–3 nm from each other. The probability of FRET between unbound linkers is comparatively small, although not fully negligible in samples with the high DNA coverage, where the average distance between unbound a–a′ linkers goes down to ≈11.9 nm. As a function of temperature, (ratio)A describes a sigmoidal curve from which the fraction of hybridised linkers ϕ(T) can be extracted as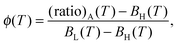 | (2) |
3 Modelling framework
3.1 Interacting large unilamellar vesicles (LUV)
Vesicles are modelled as triangulated surfaces [see Fig. 1(b)] as described previously.51,52 Following ref. 53–56 the vertices of the mesh are represented by hard spheres of diameter σ, taken as the unit length in our simulations. With the exception of the case described in Section 3.3.2, in this work we always simulate pairs of interacting vesicles. The Hamiltonian of two vesicles, each with Nv vertices is then given by | (3) |
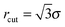 . vexcl(rij) is a hard core repulsion that constrains vertices i and j to stay at distance rij > σ. Note that vexcl acts also between vertices belonging to different vesicles.
. vexcl(rij) is a hard core repulsion that constrains vertices i and j to stay at distance rij > σ. Note that vexcl acts also between vertices belonging to different vesicles.
We distribute 2N implicit linkers, N of type a and N of type a′, over the Nv vertices of each vesicle in a way that no more than one linker is allowed on the same vertex (2N < Nv). Two free complementary linkers can react if their distance is smaller than L. In the case of DNA linkers, L is equal to twice the length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of the spacers connecting the sticky ends to the cholesterol anchors. Accordingly, the Hamiltonian associated to linker–linker interactions is given by
of the spacers connecting the sticky ends to the cholesterol anchors. Accordingly, the Hamiltonian associated to linker–linker interactions is given by
 | (4) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ves + ves + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) link. link. | (5) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) link is considered, analytical models used in our previous studies35,36 enable the calculation of the partition function of two interacting membranes, neglecting non-specific membrane–membrane interactions and configurational contributions associated to membrane deformation. These calculations adapted to the present system are given in Section 3.2. The hybrid numerical/analytical framework discussed in Section 3.3 combines analytical calculations with Monte Carlo methods to sample the non-specific contributions described by
link is considered, analytical models used in our previous studies35,36 enable the calculation of the partition function of two interacting membranes, neglecting non-specific membrane–membrane interactions and configurational contributions associated to membrane deformation. These calculations adapted to the present system are given in Section 3.2. The hybrid numerical/analytical framework discussed in Section 3.3 combines analytical calculations with Monte Carlo methods to sample the non-specific contributions described by ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ves (see eqn (5)) to the overall partition function Z, which is then used in Section 3.4 (see eqn (17)) to investigate vesicle dimerisation.
ves (see eqn (5)) to the overall partition function Z, which is then used in Section 3.4 (see eqn (17)) to investigate vesicle dimerisation.
3.2 Analytical modelling of multivalent interactions
Interactions between multivalent objects are strengthened by the combinatorial entropic contributions accounting for the many different ways of forming a given number of bonds starting from a set of linkers. The experimental system features identical vesicles functionalised by an equal number N of two complementary linkers, which can therefore form both inter-vesicle bridges and intra-vesicle loops [see Fig. 1(a)]. In this scenario, the contribution of![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) link (eqn (4)) to the partition function of two vesicles linked by nB bridges, taking two non interacting vesicles as reference, becomes36
link (eqn (4)) to the partition function of two vesicles linked by nB bridges, taking two non interacting vesicles as reference, becomes36 | (6) |
 | (7) |
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[1/(ρ⊖L3)], where ρ⊖ = 1 M is the standard concentration.35,36 More accurate configurational terms can be estimated accounting for variations in the distance between the two binding linkers. We leave such refinement to future investigations in which linkers will be simulated as explicit objects. Differently from ΔGB, ΔGL should also include an entropic cost ΔGconfiningL = −TΔSconfiningL of confining the otherwise diffusive linkers to within a short distance from each other.35–39 Including an analogous term ΔGconfiningB in ΔGB is not necessary, as confinement entropy is already accounted for by our simulation procedure that explicitly enables surface mobility in bridge-forming linkers (see Section 3.3.1). We estimate ΔGconfiningL = −kBT
log[1/(ρ⊖L3)], where ρ⊖ = 1 M is the standard concentration.35,36 More accurate configurational terms can be estimated accounting for variations in the distance between the two binding linkers. We leave such refinement to future investigations in which linkers will be simulated as explicit objects. Differently from ΔGB, ΔGL should also include an entropic cost ΔGconfiningL = −TΔSconfiningL of confining the otherwise diffusive linkers to within a short distance from each other.35–39 Including an analogous term ΔGconfiningB in ΔGB is not necessary, as confinement entropy is already accounted for by our simulation procedure that explicitly enables surface mobility in bridge-forming linkers (see Section 3.3.1). We estimate ΔGconfiningL = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(L2/A), where A is the area of a vesicle.35,36 In summary, we obtain
log(L2/A), where A is the area of a vesicle.35,36 In summary, we obtain | (9) |
In this work we combine multivalent partition functions, like the one in eqn (6) or (8), with Monte Carlo estimates of the configurational free energy costs of pairs of vesicles linked by nB inter-vesicle bridges. In our model such costs only depend on the number of bridges nB. In particular, the interaction free energy does not depend on the number of formed loops (see Section 3.3.3). For computational efficiency we therefore use a simplified system where only bridges are possible, which could be realised experimentally using two families of vesicles each carrying only one of the two complementary linkers. In this case the contribution to the partition function due to ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) link for vesicles with nB bridges and N linkers (per type) is simply given by ΩB(N,nB) (eqn (8)). In Section 3.3 we use Ω† (e.g. † = B or † = B, L) to tag the contribution to the partition function due to the selective part of a generic multivalent system.
link for vesicles with nB bridges and N linkers (per type) is simply given by ΩB(N,nB) (eqn (8)). In Section 3.3 we use Ω† (e.g. † = B or † = B, L) to tag the contribution to the partition function due to the selective part of a generic multivalent system.
3.3 Numerical estimate of configurational effects
In this section we explain our strategy to combine the analytical partition functions of interacting multivalent vesicles Ω† (with † = B or † = B, L, see Section 3.2) with the numerical calculation of the configurational costs due to non selective terms of the Hamiltonian (![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ves in eqn (5)) as estimated via Monte Carlo. These terms account for the deformation of the membranes following the formation of flat adhesion patches in the interacting vesicles, for the steric repulsion between membranes, as well as for the entropic costs of confining linkers forming bridges within the patch area. The role played by elastic and entropic terms in non-selective adhesion of vesicles with different morphologies has been extensively studied in the past.62–64 However a direct comparison with previous results is not straightforward in view of the many peculiarities of multivalent ligand/receptor interactions.29,60
ves in eqn (5)) as estimated via Monte Carlo. These terms account for the deformation of the membranes following the formation of flat adhesion patches in the interacting vesicles, for the steric repulsion between membranes, as well as for the entropic costs of confining linkers forming bridges within the patch area. The role played by elastic and entropic terms in non-selective adhesion of vesicles with different morphologies has been extensively studied in the past.62–64 However a direct comparison with previous results is not straightforward in view of the many peculiarities of multivalent ligand/receptor interactions.29,60
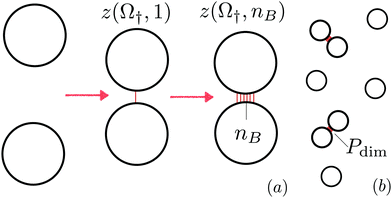
Fig. 2(a) sketches the thermodynamic path we employ for the simulations. First, as detailed in Section 3.3.2, we use a hit-or-miss algorithm to calculate the internal partition function z(Ω†,nB = 1) of two vesicles linked by a single bridge with respect to the reference state of two free vesicles. By definition, the internal partition function includes the contributions of all degrees of freedom but the centre of mass of the free/linked vesicles. In Section 3.3.3 we then use the results of Section 3.3.2 to calculate the internal partition function of vesicles featuring an arbitrary number (nB) of bridges z(Ω†,nB). In Section 3.3.1 we briefly outline our simulation algorithm.
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i of all possible complementary linkers that could potentially form a bond with i, eventually including the linker to which i is already bound. The selected linker has then a probability pfree of becoming (or remaining) free and a probability n(
i of all possible complementary linkers that could potentially form a bond with i, eventually including the linker to which i is already bound. The selected linker has then a probability pfree of becoming (or remaining) free and a probability n(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i)pbound of getting (or staying) connected to a randomly chosen partner from the list
i)pbound of getting (or staying) connected to a randomly chosen partner from the list ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i, which counts n(
i, which counts n(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i) elements. Consistently with eqn (4) and (5), the probabilities are defined as
i) elements. Consistently with eqn (4) and (5), the probabilities are defined as | (10) |
When studying systems of adhering vesicles (Section 3.3.3) we also attempt moves in which a vesicle is randomly chosen and rigidly translated along a random vector. The move is rejected if it causes two vesicles to overlap or a formed bridge to stretch beyond its maximum allowed bond-length L.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC cycles as defined in Section 3.3.1 and use the final configurations to estimate the internal partition function Q1 of two vesicles each featuring a single linker. In particular we choose Ntries = 250 random displacements between the centres of mass of the two vesicles (rj, j = 1,…,Ntries) uniformly sampled from the spherical shell of inner radius Rmin,i and outer radius Rmax,i. The radii Rmin,i and Rmax,i are chosen in a way to guarantee that all possible displacements between vesicle's centre of mass resulting in a linked configurations satisfy the condition Rmin,i < |r| < Rmax,i. Additionally a random rotation of the displaced vesicle around its centre of mass is performed. For each displacement and rotation, we loop over all the pairs of vertices belonging to different vesicles and count the number nbondsi of possible inter-particle bonds, with nbondsi = 0 if the two vesicles overlap. Q(1)i is then estimated as
000 MC cycles as defined in Section 3.3.1 and use the final configurations to estimate the internal partition function Q1 of two vesicles each featuring a single linker. In particular we choose Ntries = 250 random displacements between the centres of mass of the two vesicles (rj, j = 1,…,Ntries) uniformly sampled from the spherical shell of inner radius Rmin,i and outer radius Rmax,i. The radii Rmin,i and Rmax,i are chosen in a way to guarantee that all possible displacements between vesicle's centre of mass resulting in a linked configurations satisfy the condition Rmin,i < |r| < Rmax,i. Additionally a random rotation of the displaced vesicle around its centre of mass is performed. For each displacement and rotation, we loop over all the pairs of vertices belonging to different vesicles and count the number nbondsi of possible inter-particle bonds, with nbondsi = 0 if the two vesicles overlap. Q(1)i is then estimated as | (11) |
where 1/Nv2 accounts for the probability of finding one linker on a given node of the membrane and the volume v0,i encloses the displacement between the vesicles' centres of mass we sample, accounting for both changes in the absolute distance between the vesicles and rotations of one LUV around the other.
The final value of Q(1) is sampled using
 | (12) |
| z(Ω†,1) = Q(1)Ω†(N,1). | (13) |
The values of Q(1) for the systems considered in this work have been reported in Table 1.
| Vertices Nv | Linker length L/σ | Bending rigidity κ/kBT | Q 1/σ3 |
|---|---|---|---|
| 8004 | 3 | 20 | 0.15 |
| 4504 | 3 | 20 | 0.22 |
| 2004 | 3 | 20 | 0.40 |
| 4504 | 5 | 20 | 2.98 |
| 4504 | 10 | 20 | 67.14 |
| 4504 | 3 | 5 | 0.16 |
| 4504 | 3 | 30 | 0.23 |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB+1/
nB+1/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB, where
nB, where ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB+1 and
nB+1 and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB count the number of times the system visits states with nB + 1 and nB bridges respectively. Using z(Ω†,1) as calculated in Section 3.3.2 we then obtain
nB count the number of times the system visits states with nB + 1 and nB bridges respectively. Using z(Ω†,1) as calculated in Section 3.3.2 we then obtain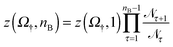 | (14) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB+1/
nB+1/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB is shown as a function of nB for a bridge-only model († = B) with different amounts of linkers N. Similar to what done in eqn (13), we factorise the internal partition function using the selective term Ω† and a configurational term indicated as
nB is shown as a function of nB for a bridge-only model († = B) with different amounts of linkers N. Similar to what done in eqn (13), we factorise the internal partition function using the selective term Ω† and a configurational term indicated as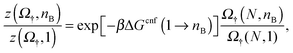 | (15) |
 | (16) |
3.4 Dimerisation probability
To study the melting transition of the DNA-functionalised vesicles we calculate the probability of forming liposome dimers starting from a dilute suspension of free vesicles [see Fig. 2(b)]. We start by evaluating the internal partition function of pairs of bound vesicles (Z) that is obtained by summing z(Ω†,nB) over all possible number of bridges | (17) |
| Pdim = (1 − Pdim)2ZcexpNA, | (18) |
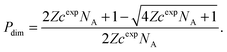 | (19) |
 | ||
Fig. 3 Evaluating configurational free energy in pairs of interacting vesicles from MC simulations. (a) Ratio ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB+1/ nB+1/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB between the number of times the system visits a configuration with nB + 1 bridges and one with nB bridges for different number of linkers (per type) N. Model parameters: ΔG0 = 0 kJ mol−1, Nv = 2004, and Ω† = ΩB. (b) Computed configurational free energy (1 → nB) as a function of nB for the same values of N as in panel (a). No significant dependence on N is observed (see inset). Note that accordingly to eqn (16) a different choice of ΔG0 for the calculation of nB between the number of times the system visits a configuration with nB + 1 bridges and one with nB bridges for different number of linkers (per type) N. Model parameters: ΔG0 = 0 kJ mol−1, Nv = 2004, and Ω† = ΩB. (b) Computed configurational free energy (1 → nB) as a function of nB for the same values of N as in panel (a). No significant dependence on N is observed (see inset). Note that accordingly to eqn (16) a different choice of ΔG0 for the calculation of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB+1/ nB+1/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) nB would produce identical ΔGcnf. nB would produce identical ΔGcnf. | ||
It is important to stress the portability of our method. In view of the universality of [eqn (16) and Fig. 3(b)], our procedure allows to calculate the internal partition function in pairs of vesicles at different temperatures or number of linkers N by re-weighting with the proper multivalent partition function (see eqn (15)), without the need of further MC simulations.
3.5 Other quantified observables
Besides the configurational contribution to the vesicle–vesicle interaction free energy ΔGcnf, and the vesicle dimerisation probability Pdim, we quantify the area Ap of the adhesion patch, and the number of formed intra-vesicle bridges and inter-vesicle loops.The adhesion patch between vesicles [see Fig. 1(b)] is defined as the region featuring vertices that could potentially bind to at least one vertex on the partner vesicle. Note that the exact position of the patch border depends on L. For numerical efficiency the patch area is once evaluated every 2500 MC steps. From the area Ap of the adhesion patch, we can evaluate the confining contribution to the configurational free energy of bridge formation as
 | (20) |
The average number of bridges is calculated as
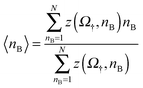 | (21) |
 | (22) |
 | (23) |
〈nB+L〉tot = Pdim〈nB+L〉dim + (1 − Pdim)2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) L L | (24) |
Vesicle dimerisation temperature is estimated by evaluating the temperature dependence of Pdim. Starting from T = 0 °C and incrementing T in steps of 1 °C, the dimerisation temperature is defined as the first point where Pdim drops below 0.5.
Similarly, the melting temperature of the DNA linkers is defined as the temperature above which less than 50% of the linkers are hybridised.
3.6 Simulated systems
Table 1 lists the parameters of the simulated systems. We explored the influence of vesicle size, the maximum distance between bound linkers L, and the bending rigidity of the membrane κ on different properties of interest. Simulation units are converted to physical units by comparing the diameter of the vesicles in experiments Dexp, with that of the simulated liposomes Dsim. In particular the relation Dsimσ = Dexp allows to convert the simulation unit length σ and the linkers' binding range Lexp = Lσ in physical units. In the system with Nv = 8004 and L = 3σ, using Dexp ≈ 400 nm we find σ = 9.1 nm.4 Results and discussion
4.1 Configurational free energy
In this section we discuss numerical estimates of the configurational contribution ΔGcnf(1 → nB) to the interaction free energy of pairs of liposomes linked by nB bridges, and disentangle components deriving from membrane deformation and steric repulsion from those caused by the confinement of bridge-forming linkers within the inter-vesicle adhesion patch. Fig. 4 shows the configurational free energy ΔGcnf(1 → nB) and the area Ap of the inter-vesicle adhesion patch as a function of the number of formed bridges at different vesicle size [(a) and (b)], linker length L [(c) and (d)], and membrane bending modulus κ [(e) and (f)]. In all cases, we find that ΔGcnf increases linearly with the number of bridges, and this is correlated with the formation of larger adhesion patches at higher nB. However the patch area is non-linear in nB with Ap that increases more rapidly for small number of bridges. Similar trends have been previously reported when studying adhesion between fluid vesicles and solid supports at different vesicle–substrate attraction.64,70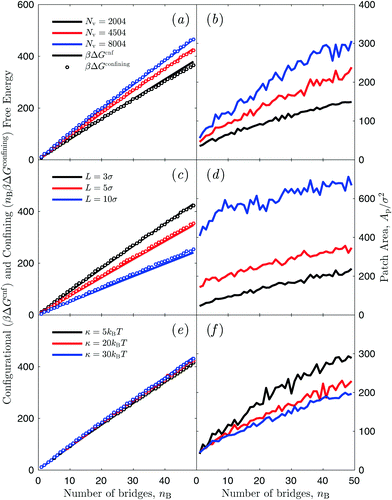 | ||
| Fig. 4 Simulated configurational free energy for the formation of vesicle dimers ΔGcnf(1 → nB) (left column) and area of the adhesion patch Ap (right column) as a function of the number of inter-vesicle bridges nB. (a and b) Effect of changing vesicle size (number of vertices in the triangulated mesh) Nv. (c and d) Effect of changing maximum bond length L. (e and f) Effect of changing bending modulus κ. Circles in the left column mark the confinement contribution ΔGconfiningB to ΔGcnf(1 → nB) evaluated using eqn (20) (multiplied by the number of bridges nB) and values of Ap shown in the right column. | ||
As discussed in Section 3.2, ΔGcnf implicitly includes the entropic cost ΔGconfiningB of confining each linker engaged in a bridge within the patch region. This term can be estimated using the measured patch area (right column of Fig. 4) and eqn (20), and it is shown in Fig. 4 (left column, circles). Interestingly, nBΔGconfiningB accounts for the entire configurational free-energy costs of binding a pair of vesicles, regardless of the simulation conditions tested in Fig. 4. Deviations of nBΔGconfiningB from ΔGcnf are difficult to quantify due to uncertainties in the estimation of Ap. From this observation we deduce that translational entropic terms hindering bridge formation are largely dominant over other contributions to ΔGcnf. In particular steric repulsion between the membranes, and membrane stretching following adhesion have negligible effect. Note that ΔGcnf accounts for the overall configurational free energy of the system, while ΔGconfiningB as derived in eqn (20) accounts for the contribution of a single linker, hence we compare ΔGcnf with nBΔGconfiningB.
Nonetheless, changing physical parameters of the vesicles causes changes in the area of the adhesion patch, and thereby in ΔGconfiningB and ΔGcnf. In Fig. 4(a) and (b) we explore the effect of changing vesicle size. The patch area increases with the number of vertices Nv, but the ratio L2Ap/A2 decreases, causing the configurational penalty for bridge formation to become more severe, effectively weakening the attraction between membranes. Similar considerations can be used to understand the results of Fig. 4(c) and (d) where we study the effect of changing the bond length L. Increasing L results in more stable bridges (see eqn (20)) and therefore in larger adhesion patches. However, especially for large L, the increase in patch area is also due to the fact that bridges made by longer tethers can explore a wider portion of the curved membrane region at the periphery of the adhesion patch. In Fig. 4(e) and (f) we test the effect of changing membrane bending modulus κ. In the range of values we tested, centred around the experimental bending modulus of DOPC bilayers κ ≈ 19kBT,71–73 we observe little effect on the patch size and thereby on the configurational free energy. This evidence confirms that contributions arising from the elastic deformation and the suppression of membrane thermal fluctuations are overwhelmed by the entropic terms related to bridge formation.62,63 Our findings are consistent with the observation that the effect of thermal fluctuations becomes negligible for liposomes in the size-range of LUVs.74
4.2 Vesicle aggregation and DNA hybridisation
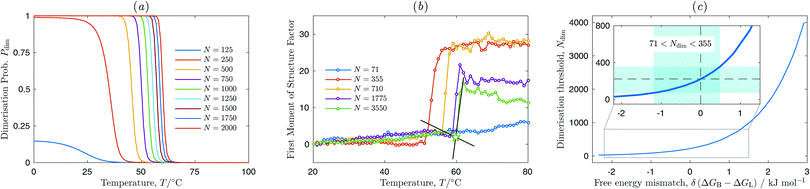
In this section we study temperature dependent self-assembly of vesicle suspensions by means of our model and experiments. We show that experiments and modelling agree on the fact that at low number of binders N self-assembly is suppressed. Numerically, self-assembly is characterised by means of the vesicle dimerisation probability Pdim (see Section 3.4). In experiments, we make use of the fully automated microscopy/fluorimetry platform described in Section 2.3 and characterise aggregation of vesicles through Fourier analysis of epifluorescence images and the binding/unbinding state of DNA linkers via FRET.For a meaningful comparison with experimental data we choose model parameters that better match the experimental ratio between vesicle diameter and linker length, in particular Nv = 8004 L = 3σ and κ = 20 (see Section 3.6). As done in experiments (see Fig. 1) we consider identical vesicles functionalised by two types of complementary linkers featuring intra-vesicle loops and inter-vesicle bridges († = L, B in Sections 3.2 and 3.3.3). Fig. 5(a) shows the calculated dimerisation probability as a function of temperature and the number of linkers per vesicle and type N. The Pdim(T) curves describe a sigmoidal shape, shifting towards higher temperature and becoming more sharp as the number of available linkers increases, a characteristic behaviour of multivalent interactions already observed in DNA functionalised solid particles.27 As N is decreased, Pdim(T) tends to converge to a low-temperature plateau smaller than 1, and eventually smaller than 0.5 for N = 125, effectively suppressing dimerisation. This is a unique characteristic of multivalent interactions featuring competition between loops and bridges,11,12 also confirmed by our experiments. Fig. 5(b) shows the experimental curves of the first moment of the structure factor as measured upon heating up vesicle samples with different N from low to high temperature. The step-like features mark the sharp melting of the aggregates. Also in experiments we observe a threshold value of N below which aggregation is suppressed. In samples with N = 177 partial self-assembly is observed in 2 out of 5 nominally identical repetitions, while the other 3 samples showed no aggregation, indicating that N = 177 is close to the threshold value for vesicle clustering. All samples with N = 71 showed no sign of aggregation, while all samples with N = 355 aggregated. The presence of a threshold value Ndim in the number of linkers, below which dimerisation does not take place, can be rationalised by observing that at low temperature, where the overall number of bonds (loops or bridges) is maximised, the driving force for vesicle adhesion is purely entropic and due to the combinatorial advantage of having a fraction of the linkers forming bridges.11,12 At low N such gain is not sufficient to overcome the repulsive configurational contributions to the free energy, thus vesicle adhesion becomes unfavourable. The agreement between the experimental and simulated value of Ndim is remarkable, particularly in view of the high sensitivity of this value to changes in the model parameters. To exemplify such sensitivity, in Fig. 5(c) we report the simulated Ndim as a function of a hypothetical unbalance δ(ΔGB − ΔGL) between the hybridisation free energy of forming loops and bridges (see eqn (9)), where δ(ΔGB − ΔGL) = 0 marks our original choice described in Section 3. A small bias of 3 kJ mol−1 between the two free energies produces a theoretical threshold value of Ndim ∼ 4000, more than one order of magnitude larger than the experimental value. In the inset of Fig. 5(c) we highlight how the experimentally determined Ndim can only be captured by simulations for uncertainties in the estimated ΔGB − ΔGL smaller than ±1 kJ mol−1. Note that an unbalance between ΔGB and ΔGL would also result from a wrong estimate of ΔGcnf. In this respect Fig. 5(c) certifies the accuracy of our model in conditions of low N.
In Fig. 6 we study the fraction of DNA strands engaged either in loops or bridges as a function of temperature, experimentally measured on the same systems of Fig. 5. Panel (a) reports simulation results obtained using eqn (24). Panel (b) shows the experimental FRET (ratio)A, linearly dependent on the FRET efficiency between the fluorophores on complementary linkers. The sigmoidal decrease of FRET efficiency marks the melting of the DNA bonds, while the low and high-temperature plateaux represent the regimes where all the linkers are bound or free, respectively. The fraction of hybridised linkers can therefore be easily estimated by fitting such plateaux with linear baselines as explained in Section 2.4 and shown in Fig. 6(b).35 Note however that for high DNA coverage (N = 3550, 1775), a second small drop in FRET efficiency is observed at high T (∼80 °C) as highlighted in the inset of in Fig. 6(b). In these samples DNA linkers are densely packed, and the average distance between them is comparable to the Förster radius of the Cy3–Cy5 pair, causing a non-zero chance of energy transfer also between unbound linkers. When the temperature is increased to ∼80 °C, the dsDNA spacers melt and the single-strands carrying the sticky ends and the fluorescent labels, no longer bound to the cholesterol anchors, are released in solution. The detachment of fluorophore-carrying DNA from the membranes causes the suppression of the small FRET signal ascribed to high-density coating. In samples where the double-transition is present the high-temperature baseline is chosen to fit the plateau observed before the final FRET-efficiency drop, which particularly for N = 3550 spans a relatively small temperature range, possibly leading to uncertainty in baseline determination. Similarly uncertainties are found in the samples with the lowest DNA coverage (N = 71) and thereby the lowest melting temperature, where the low-temperature plateau spans a small temperature range [see Fig. 6(b)]. The fraction of hybridised DNA linkers as extracted according to this procedure is shown in Fig. 6(c) as a function of temperature and N. The DNA melting temperature is extracted as the point where the fraction of hybridised DNA is equal to 0.5, determined via linear interpolation. Both simulation and experimental results show the broad melting transition typical of short oligomers.
 | ||
Fig. 6 Melting of DNA links. (a) Simulated fraction of formed DNA links (loops + bridges) as a function of temperature for systems with variable number of linkers per vesicle. Model parameters: Nv = 8004, L = 3σ. (b) Experimental FRET (ratio)A as a function of temperature. Solid lines indicate high- and low-temperature baselines fitted by straight lines (see Section 2.4). In the inset: a detail of the high temperature plateau in samples with high N showing a second drop in FRET efficiency at ∼80 °C that marks the disassembly of the dsDNA spacers connecting the linkers to the membranes (see Section 4.2). The curves are obtained averaging over 2 consecutive temperature ramps collected on heating and cooling. No hysteresis is observed. At high temperature ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) Cy3–Cy5 (see eqn (1)) becomes very small in samples with low DNA concentration and its detection is affected by background noise, e.g. sample autofluorescence. This causes the high temperature value of (ratio)A to increase for samples with low N. (c) Experimental fraction of formed DNA bonds extracted from the ramps of panel (b) as detailed in Section 2.4. Legend applies also to panel (b). Cy3–Cy5 (see eqn (1)) becomes very small in samples with low DNA concentration and its detection is affected by background noise, e.g. sample autofluorescence. This causes the high temperature value of (ratio)A to increase for samples with low N. (c) Experimental fraction of formed DNA bonds extracted from the ramps of panel (b) as detailed in Section 2.4. Legend applies also to panel (b). | ||
Fig. 7 summarises and compares the dimerisation/aggregation temperature of the vesicles and the melting temperature of DNA linkers, as computed by our simulations [panel (a)] and measured experimentally [panel (b)]. Simulations predict a linear increase as a function of N for both the DNA melting temperature and the vesicle dimerisation temperature. However, the slope of the two curves is different, with the vesicle dimerisation temperature increasing more sharply than the DNA melting temperature. As a result, a crossover temperature exists, above which the vesicles can dimerise even when less than 50% of the DNA bonds are formed, and below which more than 50% of the available linkers are needed for dimerisation. In Fig. 7(a) we also investigate the effect of uncertainties in the hybridisation free energy of the sticky ends ΔG0. For all results presented in this work, ΔG0 has been calculated using conventional nearest neighbours rules57–59 applied on the sticky-end sequences shown in Fig. 1(a), including also the attractive effect of the dangling bases (of type A) neighbouring the hybridising duplexes. However this modelling choice is far from being univocal. On the one hand, it has been demonstrated that the presence of inert DNA tails emanating from the duplexes, like the dsDNA spacers in the present system, can have substantial destabilising effect.18,75–77 On the other hand, Cy3 and Cy5 fluorophores have a stabilising effect, decreasing the hybridisation free energy by ≈2 kJ mol−1.78 The dashed lines in Fig. 7(a) exemplify the effect of including this attractive free energy contribution to the vesicle dimerisation and DNA melting temperatures. In both cases we observe a shift of about 10 °C, which demonstrates how sensitive the present results are to uncertainties in the estimation of ΔG0.
 | ||
| Fig. 7 Melting temperatures for DNA bonds and vesicle aggregation. (a) Simulated melting temperatures as a function of the number of linkers per vesicle (per linker type) N. Data shown and solid lines are obtained using hybridisation free energy between DNA sticky ends ΔG0 evaluated using nearest-neighbours thermodynamic rules on the sequences shown in Fig. 1(a).57–59 To produce dashed curves ΔG0 has been corrected with an attractive term (2 kJ mol−1) to account for the stabilising effect of Cy3 and Cy5 fluorophores.78 (b) Experimental melting temperatures obtained by averaging over 4 independent experiments. Errorbars indicate standard errors. | ||
Experimental data in Fig. 7(b) show that the DNA melting temperature and the vesicle aggregation temperature approach linear dependence on N only at low DNA coverage, and tend to plateau at high N. We ascribe this trend to the possible saturation of the lipid membranes when very high concentration of DNA linkers is added in solution. Saturation would result in an actual number of DNA linkers per vesicle smaller than the nominal value calculated as described in Section 2.2. High concentration of hydrophobised linkers may also promote the formation of stable DNA-cholesterol micelles, which would decrease the available number of linkers. As they approach the linear regime at low N, also the experimental curves for DNA melting temperature and vesicle aggregation temperature have a different slope, with the latter being more steep. The difference in slope is however less pronounced as compared to simulation results, which causes the vesicles aggregation temperature to reach lower values at high N. This discrepancy is possibly due to steric repulsion between linkers, neglected in simulations. In particular, the adhesion patch between two vesicles features an even higher linker concentration than the surrounding free-standing membrane due to the recruitment of bridge-forming linkers.36 Steric repulsion within the adhesion patch would therefore limit the number of possible bridges and weaken vesicle–vesicle adhesion.
A more insightful view in this effect is given by Fig. 8 where we compare the number of formed DNA bonds, including both loops and bridges, evaluated at the vesicle melting temperature. Simulation results [panel (a)] predict that the number of DNA bonds at vesicle melting does not depend on N for a broad range of model parameters. If steric interactions between the linkers are neglected, multivalent theories predict that the ratio between loops and bridges is independent on temperature or the total number of linkers, and determined only by vesicle geometry.36 Thus the constant trends in Fig. 8(a) imply that a fixed number of bridges is required to overcome entropic repulsion and bind vesicles to each other.
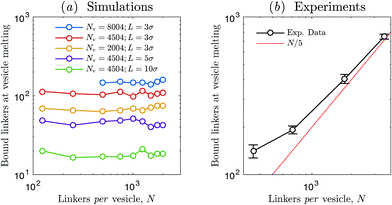 | ||
| Fig. 8 Fraction of formed DNA bonds evaluated at the melting temperature of vesicle aggregates as a function of the number of DNA linkers per vesicle N. (a) Simulation results. Curves display a constant trend in a broad range of model parameters (κ = 20kBT). (b) Experimental results. The number of formed DNA bonds at vesicle melting temperature is extracted by linear interpolation of curves of the type shown in Fig. 6(c). Data are averaged over 4 independent experiments. Errorbars indicate standard errors. The curve shows an increasing trend as a function of N, approaching a plateau at low N and a linear asymptote (N/5) at high N. | ||
Experiments predict an increase of the fraction of hybridised DNA at vesicle melting as a function of N, seemingly approaching a plateau at low N (compatibly with simulations) and a linear asymptote at high N. Since it is reasonable to argue that a fixed number of bridges is required to drive vesicle aggregation, we speculate that the observed trend may be caused by a dependence of the bridge/loop ratio on N. This could be again ascribed to steric repulsion between linkers within the crowded adhesion patch: although at high linker concentration the number of formed DNA bonds at vesicle melting is higher, excluded volume effects between linkers in the patch would result in a smaller fraction of bridges and a higher fraction of loops with respect to the ideal scenario in which linker–linker steric interactions are negligible.
5 Conclusions
Multivalent interactions are at the forefront of many applications in nanotechnology and underpin several functional behaviours in biology. A satisfactory understanding of all aspects of the problem is lacking, particularly in biologically relevant scenarios where substrate deformability couples with configurational free energy contributions and steric interactions. A numerical/theoretical framework validated by dedicated experiments and capable of assessing the consequences of such interplay is therefore of pivotal importance for biological and technological applications. Modelling multivalent interactions requires a significant coarse graining effort to bridge atomistic scales at which non-covalent bonds form with mesoscopic scales at which functionalised objects (vesicles, surfaces, polymers or nanoparticles) interact as a result of many possible reversible supramolecular linkages. Analytical theories have been developed to calculate the free energy of multivalent interactions.26,27,29–35 Considering a set of interacting multivalent objects, these methods attempt to enumerate all possible configurations of the supramolecular network of linkers mediating the interactions. The success of these theories enabled the development of efficient simulation schemes for characterising the phase behaviour of multivalent objects, coarse-grained as simple particles with effective pair interactions. Analytical multivalent theories, however, neglect non-selective interactions arising from particle deformability or excluded-volume effects between linkers.In this work we addressed some of the limitations of current modelling approaches to multivalent interactions, particularly the impossibility of accounting for deformable particles. Working on a system of soft liposomes functionalised by linkers made of synthetic DNA, we propose a method that combines state-of-art multivalent theories with Monte Carlo methods. In particular we used a triangulated model of the lipid bilayer together with free energy calculations to estimate the configurational free energy cost of having a given number of bridges formed between interacting vesicles. We clarify how such contributions are mainly due to the entropic penalty of confining bridge-forming linkers within the flat contact area formed between adhering deformable vesicles. We then characterise the response of pair of interacting vesicles to changes in temperature, and in particular the temperature-dependent dimerisation probability and the melting curves of DNA linkers. Simulation results are compared to experiments on DNA functionalised large unilamellar vesicles, where the temperature-dependent vesicle aggregation state and DNA hybridisation can be independently monitored by fluorescence microscopy and Förster resonant energy transfer thanks to a fully automated and programmable setup. Both simulations and experiments confirm that a minimum number of linkers per vesicle is required to overcome configurational entropic costs for membrane deformation and produce stable aggregation. We observe deviations between simulated and experimental trends at high density of the DNA linkers. We argue that this disagreement is caused by excluded volume effects between pairs of linkers and between the linkers and the membranes, neglected in the present contribution to maximise the portability of the model. These deviations deserve future investigation.
Our experimental and numerical results highlight the importance of configurational free energy costs arising from the deformability of objects interacting via multivalent interactions. This is an ubiquitous scenario in biological contexts, where deformable cells adhere to each other or to the extra-cellular matrix thorough membrane ligand/receptors, but also in bio-nanotechnology and nano-medicine, where multivalent synthetic probes are designed to selectively target cells. The novel numerical approach we developed to reach these conclusions combining state-of-art analytical modelling with Monte Carlo simulations provides a valuable tool for further investigations of specific biological and nano-technological problems including tissue dynamics, cell sorting, cell–cell and cell–substrate adhesion, tissue scaffolding, and designing multivalent probes for drug and gene delivery.
Acknowledgements
SJB and BMM are supported by the Université Libre de Bruxelles (ULB). JK, LP, LDM and PC acknowledge support from the EPSRC Programme Grant CAPITALS number EP/J017566/1. LDM acknowledges support from the Oppenheimer Fund, Emmanuel College Cambridge, the Leverhulme Trust and the Isaac Newton Trust through an Early Career Fellowship. AS thanks the Human Frontier Science Program and Emmanuel College Cambridge. BMM thanks Ignacio Rondini for contributing to the early stages of this work. Computational resources have been provided by the Consortium des équipements de Calcul Intensif (CECI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under Grant No. 2.5020.11. In compliance with the requirements of EPSRC a representative dataset underlying this publication is available for download at http://dx.doi.org/10.17863/CAM.1301.References
- N. J. Gay, M. F. Symmons, M. Gangloff and C. E. Bryant, Nat. Rev. Immunol., 2014, 14, 546–558 CrossRef CAS PubMed.
- E. Sackmann and A.-S. Smith, Soft Matter, 2014, 10, 1644–1659 RSC.
- C. A. Mirkin, R. C. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607 CrossRef CAS PubMed.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Nature, 1996, 382, 609 CrossRef CAS PubMed.
- L. Di Michele and E. Eiser, Phys. Chem. Chem. Phys., 2013, 15, 3115–3129 RSC.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 CrossRef PubMed.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nat. Mater., 2008, 451, 553–556 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, Nat. Mater., 2008, 451, 549–552 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, D. R. Breed, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- J. D. Halverson and A. V. Tkachenko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062310 CrossRef PubMed.
- S. Angioletti-Uberti, B. Mognetti and D. Frenkel, Nat. Mater., 2012, 11, 518–522 CrossRef CAS PubMed.
- W. B. Rogers and V. N. Manoharan, Science, 2015, 347, 639–642 CrossRef CAS PubMed.
- J. T. McGinley, I. Jenkins, T. Sinno and J. C. Crocker, Soft Matter, 2013, 9, 9119–9128 RSC.
- M. E. Leunissen, R. Dreyfus, F. C. Cheong, D. G. Grier, R. Sha, N. C. Seeman and P. M. Chaikin, Nat. Mater., 2009, 8, 590–595 CrossRef CAS PubMed.
- Q. Xu, L. Feng, R. Sha, N. C. Seeman and P. M. Chaikin, Phys. Rev. Lett., 2011, 106, 228102 CrossRef CAS PubMed.
- W. B. Rogers, T. Sinno and J. C. Crocker, Soft Matter, 2013, 9, 6412–6417 RSC.
- J. D. Halverson and A. V. Tkachenko, J. Chem. Phys., 2016, 144, 094903 CrossRef PubMed.
- L. Parolini, J. Kotar, L. Di Michele and B. M. Mognetti, ACS Nano, 2016, 10, 2392–2398 CrossRef CAS PubMed.
- Y. Wang, Y. Wang, X. Zheng, é. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Nat. Commun., 2015, 6, 7253 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10963–10968 CrossRef CAS PubMed.
- N. A. Licata and A. V. Tkachenko, Phys. Rev. Lett., 2008, 100, 158102 CrossRef PubMed.
- T. A. Taton, C. A. Mirkin and R. L. Letsinger, Science, 2000, 289, 1757–1760 CrossRef CAS PubMed.
- J.-M. Nam, C. S. Thaxton and C. A. Mirkin, Science, 2003, 301, 1884–1886 CrossRef CAS PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef.
- P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271–16284 CrossRef CAS PubMed.
- R. Dreyfus, M. E. Leunissen, R. Sha, A. V. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Phys. Rev. Lett., 2009, 102, 048301 CrossRef PubMed.
- R. Dreyfus, M. E. Leunissen, R. Sha, A. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041404 CrossRef PubMed.
- W. B. Rogers and J. C. Crocker, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15687–15692 CrossRef CAS PubMed.
- P. Varilly, S. Angioletti-Uberti, B. Mognetti and D. Frenkel, J. Chem. Phys., 2012, 137, 094108 CrossRef PubMed.
- S. Angioletti-Uberti, P. Varilly, B. Mognetti, A. Tkachenko and D. Frenkel, J. Chem. Phys., 2013, 138, 021102 CrossRef PubMed.
- L. Di Michele, S. J. Bachmann, L. Parolini and B. M. Mognetti, J. Chem. Phys., 2016, 144, 161104 CrossRef PubMed.
- N. B. Tito, S. Angioletti-Uberti and D. Frenkel, J. Chem. Phys., 2016, 144, 161101 CrossRef PubMed.
- H. Xu and D. E. Shaw, Biophys. J., 2016, 110, 218–233 CrossRef CAS PubMed.
- R. De Gernier, T. Curk, G. V. Dubacheva, R. P. Richter and B. M. Mognetti, J. Chem. Phys., 2014, 141, 244909 CrossRef PubMed.
- S. Shimobayashi, B. M. Mognetti, L. Parolini, D. Orsi, P. Cicuta and L. Di Michele, Phys. Chem. Chem. Phys., 2015, 17, 15615–15628 RSC.
- L. Parolini, B. M. Mognetti, J. Kotar, E. Eiser, P. Cicuta and L. Di Michele, Nat. Commun., 2015, 6, 5948 CrossRef CAS PubMed.
- L. Feng, L.-L. Pontani, R. Dreyfus, P. Chaikin and J. Brujic, Soft Matter, 2013, 9, 9816–9823 RSC.
- L.-L. Pontani, I. Jorjadze, V. Viasnoff and J. Brujic, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9839–9844 CrossRef CAS PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2014, 113, 128303 CrossRef PubMed.
- G. V. Dubacheva, T. Curk, R. Auzély-Velty, D. Frenkel and R. P. Richter, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5579–5584 CrossRef CAS PubMed.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Phys. Chem. Chem. Phys., 2016, 18, 6373–6393 RSC.
- M. Hadorn, E. Boenzli, K. T. Sørensen, D. De Lucrezia, M. M. Hanczyc and T. Yomo, Langmuir, 2013, 29, 15309–15319 CrossRef CAS PubMed.
- R. J. Banga, N. Chernyak, S. P. Narayan, S. T. Nguyen and C. A. Mirkin, J. Am. Chem. Soc., 2014, 136, 9866–9869 CrossRef CAS PubMed.
- P. A. Beales and T. K. Vanderlick, J. Phys. Chem. A, 2007, 111, 12372–12380 CrossRef CAS PubMed.
- M. E. Leunissen and D. Frenkel, J. Chem. Phys., 2011, 134, 084702 CrossRef PubMed.
- A.-S. Smith, K. Sengupta, S. Goennenwein, U. Seifert and E. Sackmann, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6906–6911 CrossRef CAS PubMed.
- I. Pfeiffer and F. Höök, J. Am. Chem. Soc., 2004, 126, 10224–10225 CrossRef CAS PubMed.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2006, 208, 193–202 CrossRef PubMed.
- R. M. Clegg, A. I. Murchie, A. Zechel and D. M. Lilley, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 2994–2998 CrossRef CAS.
- F. Yuan, L. Griffin, L. Phelps, V. Buschmann, K. Weston and N. L. Greenbaum, Nucleic Acids Res., 2007, 35, 2833–2845 CrossRef CAS PubMed.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef PubMed.
- A. Šarić and A. Cacciuto, Soft Matter, 2013, 9, 6677–6695 RSC.
- Y. Kantor, M. Kardar and D. R. Nelson, Phys. Rev. Lett., 1986, 57, 791–794 CrossRef CAS PubMed.
- J.-S. Ho and A. Baumgärtner, Europhys. Lett., 1990, 12, 295 CrossRef.
- A. Baumgärtner and J.-S. Ho, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 5747–5750 CrossRef.
- G. Gompper and D. M. Kroll, J. Phys.: Condens. Matter, 1997, 9, 8795 CrossRef CAS.
- J. SantaLucia, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465 CrossRef CAS.
- J. SantaLucia Jr and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef PubMed.
- R. M. Dirks, J. S. Bois, J. M. Schaeffer, E. Winfree and N. A. Pierce, SIAM Rev., 2007, 49, 65–88 CrossRef.
- J. Hu, R. Lipowsky and T. R. Weikl, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15283–15288 CrossRef CAS PubMed.
- G.-K. Xu, J. Hu, R. Lipowsky and T. R. Weikl, J. Chem. Phys., 2015, 143, 243136 CrossRef PubMed.
- R. Lipowsky and U. Seifert, Mol. Cryst. Liq. Cryst., 1991, 202, 17–25 CrossRef CAS.
- R. Lipowsky and S. Leibler, Phys. Rev. Lett., 1986, 56, 2541 CrossRef CAS PubMed.
- T. Gruhn and R. Lipowsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 011903 CrossRef PubMed.
- H. Noguchi, J. Phys. Soc. Jpn., 2009, 78, 041007 CrossRef.
- B. Li, N. Madras and A. D. Sokal, J. Stat. Phys., 1995, 80, 661–754 CrossRef.
- S. Caracciolo, B. M. Mognetti and A. Pelissetto, J. Chem. Phys., 2008, 128, 065104 CrossRef PubMed.
- B. M. Mladek and D. Frenkel, Soft Matter, 2011, 7, 1450–1455 RSC.
- P. Virnau and M. Müller, J. Chem. Phys., 2004, 120, 10925–10930 CrossRef CAS PubMed.
- G. Linke, R. Lipowsky and T. Gruhn, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 217–227 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- B. Sorre, A. Callan-Jones, J.-B. Manneville, P. Nassoy, J.-F. Joanny, J. Prost, B. Goud and P. Bassereau, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 5622–5626 CrossRef CAS PubMed.
- S. A. Rautu, D. Orsi, L. Di Michele, G. Rowlands, P. Cicuta and M. S. Turner, 2015, arXiv preprint, arXiv:1511.05064v1.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768 CrossRef CAS.
- L. Di Michele, B. M. Mognetti, T. Yanagishima, P. Varilly, Z. Ruff, D. Frenkel and E. Eiser, J. Am. Chem. Soc., 2014, 136, 6538–6541 CrossRef CAS PubMed.
- N. Srinivas, T. E. Ouldridge, P. Šulc, J. M. Schaeffer, B. Yurke, A. A. Louis, J. P. Doye and E. Winfree, Nucleic Acids Res., 2013, 41, 10641–10658 CrossRef CAS PubMed.
- C. Wang, J. H. Bae and D. Y. Zhang, Nat. Commun., 2016, 7, 10319 CrossRef CAS PubMed.
- B. G. Moreira, Y. You and R. Owczarzy, Biophys. Chem., 2015, 198, 36–44 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |