Open Access Article
Open Access ArticleWrinkles on a textile-embedded elastomer surface with highly variable friction†
K.
Suzuki
and
T.
Ohzono
*
Research Institute for Sustainable Chemistry, AIST, 1-1-1 Higashi, Tsukuba, 305-8565, Japan. E-mail: ohzono-takuya@aist.go.jp
First published on 24th June 2016
Abstract
Wrinkling of a soft elastomer surface capped by a relatively hard thin film or modified by some physical treatments to induce hardening has been widely studied for applications in fields such as low-cost micro-fabrication, optics and tribology. Here we show that a biaxial textile sheet embedded on the surface of an elastomer buckles and selectively forms anisotropic wrinkles when experiencing a compressive strain in the fibre axial direction. The wrinkles also possess a fine surface structure that originates from the periodic structure of the biaxial textile sheet. Depending on whether the surface is wrinkled or not, the unique frictional property due to which the friction on wrinkles significantly decreases by a factor of less than 0.1 because of the localized contact regions on the protrusions originating from the textile structure is shown.
Introduction
Surface wrinkles which are formed on deformable substrates1 because of buckling have been exploited in a variety of applications such as micropatterning,2 adjustable optics,3–5 colloid patterning,6–9 biological cell proliferation,10 metrology of thin films,11–13 flexible electronics,14 energy harvesting,15 controllable wetting and microfluidics,16,17 chiral gas sensing,18 and tribology.19–21 One of the characteristic features of wrinkled surfaces is their shape-tunability in response to changes in the applied strain.22,23 This property is particularly advantageous for the above-mentioned applications, as it will impart reversibility and tunability to the surface functions.Recently, mechanically durable wrinkles, which are formed on elastomers embedded with porous films, have been proposed, particularly toward tribological applications such as tunable friction.24 The commonly used mechanically fragile thin film, which is simply attached to the soft flat substrate, can be replaced with a gauche porous film embedded near its surface. This forms an interlocked interface between the film and the substrate, resulting in a reinforced wrinkled surface. The wrinkles indeed showed good tribological durability against, e.g., scratching and rubbing in dry conditions.25 In general, fibre-reinforced rubbers have been widely used whenever high strength is required in addition to flexibility such as in hoses, tires, and sealing materials. The biological cells also use a similar strategy to maintain their shapes, where the actin filaments and tubules form a network in the cytoplasm composing a cytoskeleton. However, it is noted that, in addition to the reinforcement effect, the embedded porous film primarily functions as a hard surface layer to form a wrinkled topography because of buckling instability, as the previous study shows.24
As another proof of concept for reinforcing the wrinkled surface, this study focuses on the formation of wrinkles on an elastomer surface that has a textile sheet embedded near the surface instead of the previously used self-organized porous film with a honeycomb-like structure.26 The textile sheet is more of a general material than the self-organized porous film, and thus is commercially available in large sizes at a low cost. Moreover, the textile sheet usually shows a perfect periodic pattern of pores on its lattice, which cannot be observed on a self-organized porous film. Such an irregular pattern and alignment of pores on the embedded self-organized porous film can easily create a disturbance in the wrinkle structure. Hence, using the present textile sheet, which has a perfect square lattice over the sample, may improve the ability to control the wrinkle structure. An anisotropic formation of wrinkles is particularly expected when a biaxial textile is used because it is well-known that the modulus along the fibre axis is much higher than that in other directions.27 Moreover, the effects of the fine structure of the textile sheet (such as periodically undulating fibres in proximity to the top surface) on the fine morphology of the sample surface (which has a smaller length than the wavelength of the wrinkle) can be predicted, along with the effect on tribological properties.
This paper describes the fabrication method and the characterization of wrinkles formed on a textile-embedded elastomer. In addition to the macroscopic wrinkled topography, the fine surface structures originating from the periodic structure of the plain weave fabric and the mechanical response to the uniaxial strain will also be studied. As a representative tribological property of the present surface, friction at low loads and slow sliding speed is investigated and a significant reduction of friction on the wrinkles with the fine structure is reported.
Experimental
Materials and fabrication
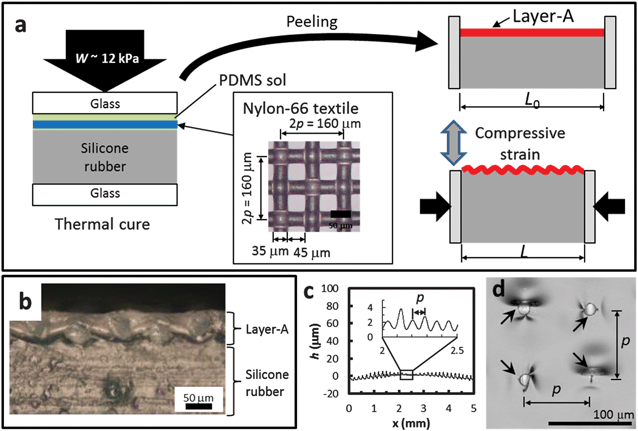
The fabrication method is summarized in Fig. 1a. A biaxial textile sheet, i.e. a plain weave fabric made of nylon-66 fibre (yarn) with a diameter of d = 35 μm (N-NO. 305), was obtained from AzOne (Japan). The periodicity of the warp and weft p is approximately 80 μm (Fig. 1a inset). This was used as a hard porous sheet to be embedded within a layer of a polydimethylsiloxane (PDMS) elastomer (Sylgard 184, Toray-Dow Corning; mixed monomer and curing agent = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w)). A portion of the textile sheet was placed on a flat glass plate, and the liquid precursor of PDMS was poured onto the sheet. A 5 mm-thick elastomeric silicone rubber base piece (Young's modulus Ebase ∼ 2 MPa, AzOne, Japan) was steadily pressed onto the sample with an interface pressure of W ∼ 12 kPa to squeeze out the excessive liquid precursor and smoothen out the textile sheet in a reproducible manner, after which it was cured at 80 °C for 3 h. The cured sample (in which the Young's modulus of the cured PDMS was EL ∼ 1.3 MPa24) was peeled from the glass substrate by using a base silicone rubber. The sample was uniaxially compressed in the lateral direction using a small vice to induce wrinkles on the surface (Fig. 1a). The applied compressive strain, which is defined as s = −(L − L0)/L0 (where L and L0 = 20 mm are the actual and original lengths of the sample, respectively), was changed to tune the depth and shape of the wrinkles. The surface topography and wrinkle patterns were characterized using a surface profiler (DEKTAK8, ULVAC), a laser microscope (VK-9710, KEYENCE) and an optical microscope (MZ8, Leica).
1 (w/w)). A portion of the textile sheet was placed on a flat glass plate, and the liquid precursor of PDMS was poured onto the sheet. A 5 mm-thick elastomeric silicone rubber base piece (Young's modulus Ebase ∼ 2 MPa, AzOne, Japan) was steadily pressed onto the sample with an interface pressure of W ∼ 12 kPa to squeeze out the excessive liquid precursor and smoothen out the textile sheet in a reproducible manner, after which it was cured at 80 °C for 3 h. The cured sample (in which the Young's modulus of the cured PDMS was EL ∼ 1.3 MPa24) was peeled from the glass substrate by using a base silicone rubber. The sample was uniaxially compressed in the lateral direction using a small vice to induce wrinkles on the surface (Fig. 1a). The applied compressive strain, which is defined as s = −(L − L0)/L0 (where L and L0 = 20 mm are the actual and original lengths of the sample, respectively), was changed to tune the depth and shape of the wrinkles. The surface topography and wrinkle patterns were characterized using a surface profiler (DEKTAK8, ULVAC), a laser microscope (VK-9710, KEYENCE) and an optical microscope (MZ8, Leica).
Friction measurements
The frictional force was measured using a pin-on-plate friction tester (IMC-9006, Imoto Machinery).21,25 Here, a spherical glass ball (R = 5.0 mm, surface roughness Ra ∼ 77 nm, Edmund) was used as the indenter and was tightly connected to a beam type load cell (WBJ-05N, Showa Measuring Instruments). The sample was held by a vice mounted on a linear sliding stage to allow for frictional sliding, with the alignment of the wrinkle grooves set perpendicular to the sliding direction unless otherwise stated.All experiments were conducted in air at a temperature of 25.0 °C ± 0.5 °C and a relative humidity of 30% ± 10%. The indenter and the sample surface were wiped with a cotton cloth soaked in acetone before measuring the friction each time. The sample began to slide 15 s after the indenter and the sample surface made contact, with the sliding speed of the linear stage fixed at 0.1 mm s−1. The applied normal force, P, during sliding was constantly kept within a range of 29.4 mN to 196.0 mN. The lower detection limit of the frictional force for the present system was 0.1 mN. The average kinetic friction force was calculated from the pulses of raw frictional force during sliding for a total distance of at least 20.0 mm under a specific set of conditions (e.g. applied strain s for wrinkling and normal load P during sliding); data from the first 3.0 mm of each run were omitted. Each friction test under a certain condition was repeated five times at different positions on the sample surface, and the averaged kinetic friction forces shown were the average of those multiple iterations.
The averaged static friction forces were also extracted from the initial data of the friction profiles. The maximum friction force value before the beginning of the sliding under a certain condition was extracted and averaged over multiple iterations.
Estimation of the apparent contact area
To evaluate the apparent contact between the indenter and the unwrinkled/wrinkled surfaces, a contact stamping method was utilized. The indenter surface was wiped with a cotton cloth soaked in a pink fluorescent ink (Promark pink, PB105T.13, Mitsubishi Pencil, Japan) to prepare the inked stamp. After drying for 1 min, the indenter was lightly placed on the surface of the samples and removed within 15 s. The trace of the ink on the surfaces was observed using a fluorescence microscope (BX-51, Olympus) with a filter set (excitation 460–490 nm, emission ∼510 nm) to examine the apparent contact regions. The experiment was repeated nine times to obtain the average value for area.Results and discussion
Characterization of the as-prepared sample
The cross-sectional image shown in Fig. 1b indicates that the textile sheet is embedded in the cured PDMS layer, referred to as layer-A in the present study. The average thickness of layer-A (DA) equals (60 μm ± 10 μm) ∼1.7d. The profile of the top surface shown in Fig. 1c indicates the small undulation with a periodicity identical to that of warp (or weft) p ∼ 80 μm and with an average depth of 1–6 μm, which is also noted in the cross-sectional image. This small undulation is assumed to have originated because of the pressure (W ∼ 12 kPa) applied during the sample preparation to fix the textile sheet between the glass plate and the silicone base and smooth it out over the sample area as follows.The pressure W should be supported only by the textile sheet and not by the uncured PDMS between the glass plate and the soft silicone base. More importantly, each intersection point between the warp and the weft, at which the actual thickness is the maximum (∼2d), is assumed to support the pressure. As the bulk modulus of nylon-66 is on the order of GPa, a depression of the soft silicone base (Ebase ∼ 2 MPa) at each intersection is plausible. When the pressure W is removed after the curing of PDMS, the silicone base tends to relax the deformation causing the intersection points to push upward and protrude in the normal direction of the surface, relative to the other position.
Assuming that the fibre can be roughly approximated as a sphere with a diameter of d at the intersection point, the relative depression D can be estimated using the Hertzian contact theory between a hard sphere with a radius r (=d/2 ∼ 17.5 μm) and a soft and elastic half-plane with a modulus Ebase (∼2 MPa), f = (4/3)EbaseD3/2r1/2, where f is the applied force.28 Here, f is estimated as the force applied on the single intersection point, which is located on each unit lattice of the textile with an area of p2 = 802 μm2. Thus, f can be calculated as Wp2 ∼ 0.077 mN, and D is estimated to be ∼3.6 μm by using the relation D = [(3/4)f/(Ebaser1/2)]2/3. This shows good consistency, considering the present rough estimation, with the depth of the small undulation on the top surface having an observed value of 1–6 μm. The result supports the hypothesis of this study about the origin of the small protrusions on the surface before wrinkling.
Evaluating the small undulations more carefully, slightly depressed parts were observed at the top of most of the intersection points. When magnified, the microscopic image indicates that the layer of PDMS skin on the intersection point was partially peeled by a diameter of 15–25 μm (Fig. 1d) and with a height difference of 50–80 nm at the edge, measured using a laser microscope. After peeling the sample, the corresponding flakes were indeed found on the glass plate used during curing. The result suggests that the adhesion of PDMS to the nylon-66 fibre was weaker than that to the glass plate, and only the very thin PDMS layer formed on the top of the intersection point was peeled away as flakes. Consequently, the surface of the sample is covered with PDMS, except at the intersection points, where the fibre surface is slightly exposed. These fine surface structures originate from the periodic structure of the textile sheet and are unique to the present system.
Characterization of the wrinkled sample
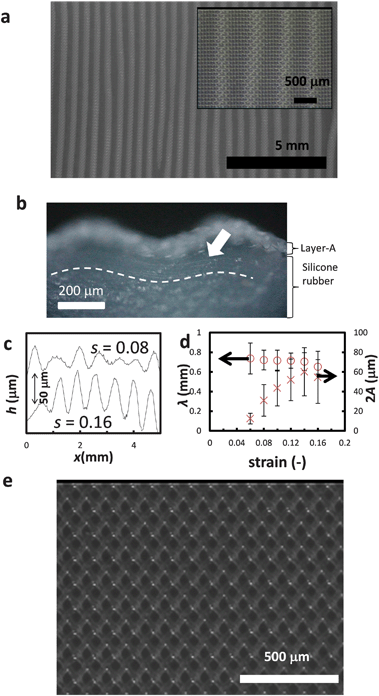
Wrinkles appear when uniaxial compression is applied in the fibre direction with (s > sc) ∼ 0.06, as shown in Fig. 2a. Although the shape of the wrinkle deviates from an ideal sinusoidal curve with a constant amplitude A, the two-dimensional (2D) image and surface profiles show that the wrinkle wavelength λ ∼ 0.7 mm ± 0.1 mm ranging over 9–10 yarns (Fig. 2a and c). The average wrinkle depth, 2A, increases with s in an inverse-quadratic manner (Fig. 2d), which is typical of a wrinkling system.1 It is noted that the initial shape recovers after releasing s, s = 0, indicating the typical property of the shape-tunable wrinkles.22 The striped pattern of the present wrinkles can be recognized by the naked eye even at s = 0, owing to the marginal delamination between the fibres and the PDMS matrix which partly occurs at the crests upon initial wrinkling. The thin air gaps between the fibres and the PDMS matrix scatter light, illuminating the crest parts (Fig. 2a). Although the air gaps continue to remain even after a sample has been wrinkled, this does not lead to critical failure of the wrinkle structure and the reversible shape-tunability is retained.Here we assume that the present wrinkling phenomenon can be qualitatively explained using the conventional model for the wrinkling of a flat surface layer supported by a soft substrate.1 This assumption is supported by the undulation observed within the soft substrate, silicone rubber (Fig. 2b), which is qualitatively expected from the model. Then, the bending rigidity of the effective hard layer of wrinkling in the present system can be estimated as follows. According to the conventional model, the wrinkle wavelength at the minimum buckling strain is expressed as λ0 = 2πH[(1 + νs)/6(1 − νf2)]1/3[Ef/Es]1/3, where H is the imaginary thickness of the effective hard layer, ν and E are Poisson's ratio and Young's modulus respectively, and indices “s” and “f” represent the silicone base substrate and the effective surface layer respectively. The effective bending rigidity can be calculated using the relation κ = λ03Es/[2(2π)3(1 + νs)] = EfH3/[12(1 − νf2)]. Putting the actual values λ0 ∼ λ ∼ 0.74 mm, Es ∼ Ebase ∼ 2 MPa, and νs ∼ 0.5 in the former relation, we find the value of κ to be ∼1.1 × 10−6 N m. Since the modulus of the PDMS (∼1 MPa) should be much smaller than that of the textile sheet, the estimated bending rigidity should be almost equal to that of the textile sheet.
Individually, κ of the textile sheet can be roughly estimated using a simple method, Technical Association of the Pulp and Paper Industry (TAPPI) UM409, in which the deflection (δ ∼ 4 ± 1 mm) of the sheet with a length (l ∼ 0.020 m) and the weight (w ∼ 28.5 g m−2) are related to κ as κ = g(wl4)/(8δ). The estimated κe ∼ 1.4 ± 0.4 × 10−6 N m, showing good agreement with κ ∼ 1.1 × 10−6 N m estimated from the observed wrinkle wavelength within the error range. This result supports that the textile sheet embedded within layer-A functions as the hard layer in the observed wrinkling.
When strain is applied in the direction of bias, 45° from the fibre axes, in contrast, the previously discussed wrinkles never formed even at the highest strain of s = 0.16 in the present study (Fig. 2e). To discuss this anisotropy and wrinkling which is dependent on the direction of compression, we focus on the anisotropy of the effective modulus of layer-A, the imaginary top layer. The effective modulus of the plain weave in the bias direction (Ebias) is known to be smaller than the one in the fibre axis direction by at least one order,27Ebias ≤ Ef/10, because of the fairly low shear modulus. The value of Ef can be estimated using the observed critical strain for wrinkling under compression in the fibre direction, sc ∼ 0.06, from Ef ∼ Es(2sc)−3/2 ∼ 50 MPa.29 Using this value, the critical strain for wrinkling in the bias direction sc-bias ∼ 0.5(Es/Ebias)2/3 ≥ 0.27, which has a much larger value than the one available in the present experiment. Consequently, the large anisotropy in the effective modulus of the textile sheet can lead to the clear anisotropy of the direction of wrinkling.
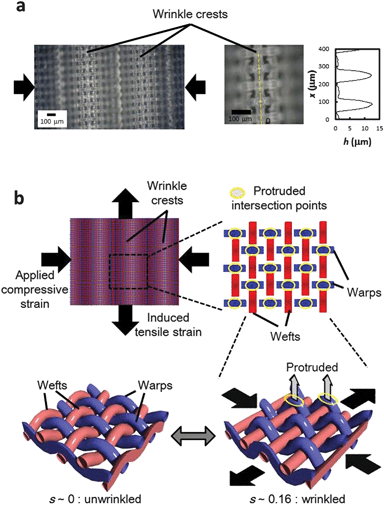
In the wrinkled state, the smaller fine structures, which are the undulation related to the intersection points of the textile sheet, also change as follows. The intersection points along the wrinkle crest alternatively protrude and the protruded points correspond to the fibres that align in the direction of compression, warp. The height difference between the neighbouring top parts of the warp and weft fibres along the crest is hw–w ∼ 10 μm (Fig. 3a).
The warps support the applied uniaxial compressive strain and buckle at a macroscopic scale with a periodicity of λ ∼ 0.7 mm. On the other hand, this also induces a tensile strain in the perpendicular direction to the compressive strain depending on the Poisson's ratio. This tensile strain is also exerted on weft fibres in the textile sheet. These weft fibres under tensile strain tend to become straight inducing, in contrast, further undulation with even greater bending in the warp fibres (see Fig. 3b). As a result, only those intersection points where the warp fibres overlap the weft fibres can undergo protrusion. This characteristic response of the general textile sheet to the uniaxial tensile strain in the fibre direction is assumed to be the reason for the observed alternative protrusions on the crest (Fig. 3). These protrusions will be generally available even in the case of non-plain textiles (e.g. textiles with other patterns and/or multi-axes). The reversible formation of the present fine structure with protrusions of warp fibres at the top of the crest is directly proportional to the reduction of friction on the wrinkled surface as described below.
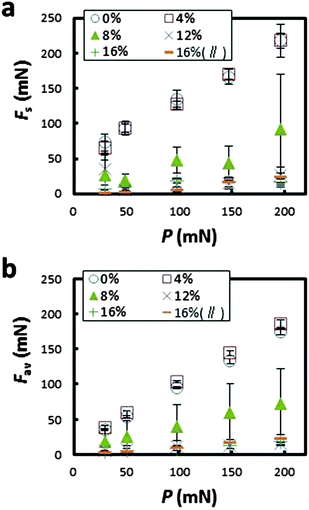
Frictional properties
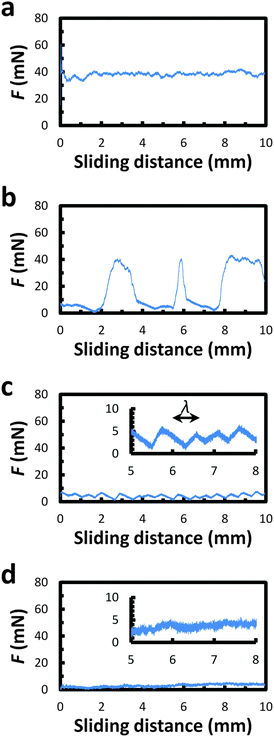
Representative friction signals are shown in Fig. 4. On unwrinkled surfaces (s = 0–0.04), apart from some random fluctuations the kinetic friction force is almost constant. In contrast, on wrinkles at s = 0.16, the kinetic friction force is greatly reduced and shows periodic fluctuations corresponding to the appearance of the wrinkles (∼0.7 mm). In the middle range of s (=0.08–0.12), depending on the position, both the high and low friction states are observed.The average kinetic friction force (Fav) for the various loads (P) is shown in Fig. 5a. The result clearly indicates that the kinetic friction force significantly decreases by a factor of ∼1/12 on the wrinkled surface (s = 0.12–0.16) compared to that on the unwrinkled surface (s = 0–0.04) over the present load range. In the case of the averaged static friction (Fig. 5b), the difference between those at s = 0–0.04 and s = 0.12–0.16 becomes slightly more apparent because the static frictions at s = 0–0.04 are slightly greater than the kinetic frictions over the present load range. Moreover, the sub-linear relationship found in both kinetic and static friction forces suggests that Amontons–Coulomb's law has failed slightly under the present experimental conditions. The large error bars at s = 0.08 originate from a situation that includes two frictional states: the high and low friction states, originating from the inhomogeneous wrinkled shape (Fig. 2b).
The periodic signal observed on the wrinkles in the low friction state, e.g. s = 0.16 (Fig. 4c), hints at the oscillatory frictional dynamics reported in the previous paper,21 in which the friction force periodically increases as the front side of the small indenter interlocks with each wrinkle crest and induces a large deformation, resulting in an increased average friction force on the wrinkles. However, with the present system using a larger indenter, the severe interlocking state should not appear. Hence, it only induces a small periodic oscillation reflecting the macroscopic wrinkle structure on the friction signal.
Additionally, the averaged friction force for the sliding in the direction parallel to the wrinkle grooves at s = 0.16 also shows low values (Fig. 5). In this case, the oscillatory frictional dynamics, which originated from the periodic undulation of wrinkles, disappears (Fig. 4d). Thus, in terms of tactile sensing, the surface will exhibit anisotropy because the shape of the frictional signal is significant. Meanwhile, the anisotropy dependent on the sliding direction in the averaged fictional force is less, since a significant variation in friction is observed independent of the sliding friction. A brief demonstration of the reversible tunability of friction in the present system is shown in the ESI† Movie 1.
In general, the kinetic friction force between rubber and a hard smooth surface depends mainly on the adhesive force at the area of contact.28,30 This simple relationship between friction F and the real contact area Ar, known as Bowden–Tabor's law, has a form, F ∝ σAr, where σ is the shear stress at rupture of adhesion and depends on the material at the area of contact. Based on this framework, Ar and σ for the present unwrinkled and wrinkled surfaces are discussed as follows.
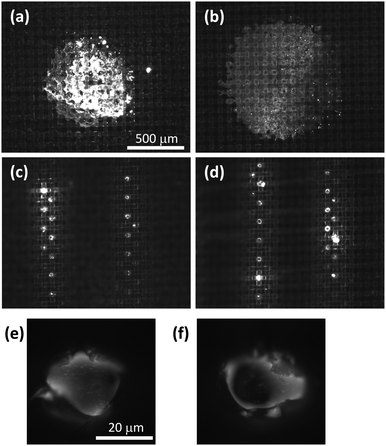
Here, the experimentally examined contact states are discussed. Fig. 6 shows the representative fluorescent images of the traces of contact on unwrinkled and wrinkled surfaces stamped at different loads (low P = 29.4 mN and high 196.0 mN). On the unwrinkled surface (Fig. 6a and b), the apparent contact area appears as a single circular region with averaged areas of 0.51 mm2 ± 0.20 mm2 and 0.87 mm2 ± 0.12 mm2 at P = 29.4 mN and 196.0 mN respectively. If the true contact area was identical to the observed one, a large stick–slip signal may appear as reported in the related systems.20,25 However, the present result displaying no such clear signal on the unwrinkled surface suggests that the small local stick–slip events occur randomly over the apparent contact area. This scenario becomes more likely when considering that the small undulation, with a periodicity ∼80 μm on the sample at s = 0 shown in Fig. 1c, produces a pressure gradient along with the undulation and/or makes partial real contacts. According to previous studies,25,31 this situation can suppress the large concurrent stick–slip event. Nevertheless, the average friction on an unwrinkled surface is much larger than that on the wrinkles probably because of the totally different contact state.
In striking contrast, the contact region on the wrinkled surface is limited to the alternatively protruding intersection points on top of the two neighbouring wrinkle crests (Fig. 6c–f), the exposed warp nylon-66 fibre, and the small surrounding area covered by PDMS, which appears as a ring-like brighter edge in the fluorescent images. The total apparent areas are estimated as 0.012 mm2 ± 0.004 mm2 and 0.013 mm2 ± 0.002 mm2 at P = 29.4 mN and 196.0 mN respectively. This significant reduction of the apparent contact area is probably the main reason for the greatly reduced friction, assuming that the true contact area in the Bowden–Tabor's law is qualitatively related to the apparent one, and that the shear strengths (σ) for both high and low friction states are of the same order of magnitude. This is estimated as follows.
The shear strength σ is expected to be monotonically related to the work of adhesion between the glass indenter and the surface material “x”, which is mainly PDMS at s = 0 or nylon-66 at s = 0.16 at a microscopic scale; Wad ∼ 2(γglassγx)1/2, where γ is the surface energy of the material mostly determined by the dispersion term.32 Thus, σunwrinkled ∝ Wad ∝ (γPDMS)1/2 at s = 0 and σwrinkled ∝ (γnylon-66)1/2 at s = 0.16. Considering that γPDMS ∼ 20 mN m−1 (ref. 33) and γnylon-66 ∼ 46 mN m−1 (ref. 34), σunwrinkled/σwrinkled ∼ 0.66. Thus, regarding the decreased friction observed on the wrinkled surface, this difference in shear strength contributes less.35 Consequently, the difference in contact state estimated due to the apparent contact area is probably the main reason for the observed frictional difference.
Previous studies20,25 investigated the effect of the sinusoidal shape of an elastomer surface (without any small protrusions present) on the friction, and a difference of ∼50% at the maximum was reported between the coefficients of friction for wrinkled surfaces and flat surfaces. Thus, the present significant reduction of friction on the wrinkled surface is mainly due to the induced protrusions of the warp fibres at the crests, which greatly reduces the contact area. Furthermore, the characteristic mechanical property of biaxial weaves,36 in which the warp fibres on the weft ones at the intersection points are protruded in response to the tensile strain in the weft fibre direction, is the key to producing the small protrusions only when the surface is wrinkled under uniaxial compressive strain.
Conclusions
A new class of shape-tunable wrinkles, which were formed on the surface of a textile-embedded elastomer in response to the applied uniaxial compressive strain, was studied for the first time. The embedded textile sheet functions as the hard layer, which buckles when a uniaxial strain is applied in the fibre direction. Since the effective modulus of the textile in the other (bias) directions is much lower than in the fibre direction, no wrinkle appears when strain is applied in the bias direction, showing a strong anisotropy of wrinkle formation. In addition to the sinusoidal shape of the wrinkles, small protrusions of the warp fibres appear at crests over the wrinkled surface. This originates because of the characteristic change in the shape of the warp fibres under the induced tensile strain in the weft fibre direction. The friction on the present wrinkles shows a significant reduction by a factor of ∼1/12 compared to that on the unwrinkled surface. This is probably due to a large reduction in the true contact area for the wrinkled surface with the small protrusions, which only supports the load during frictional sliding. However, future studies should investigate the frictional properties over a long duration (e.g. wear) and the dependence of friction on the sliding velocity and on the properties of the indenter (e.g. modulus and structures) for the sake of practical applications. The present system is believed to be encouraging as a unique switchable surface on which the friction coefficient is changeable between ∼1.0 and ∼0.1 under given conditions, and may lead to further creation of new tribological soft interfaces.Acknowledgements
This work was partly supported by the Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT) via Grants-in-Aid for Scientific Research on Innovative Areas (Grant No. 24120003). We thank Y. Nishihara and M. Chikamatsu for their assistance with topography measurements.Notes and references
- H. G. Allen, Analysis and Design of Structural Sandwich Panels, Pergamon, New York, 1969 RSC; J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310 RSC; R. Huang and Z. Suo, J. Appl. Phys., 2002, 91, 1135 CrossRef CAS; N. Bowden, S. Brittain, A. G. Evans, J. W. Hutchinson and G. M. Whitesides, Nature, 1998, 393, 146 CrossRef; F. Brau, H. Vandeparre, A. Sabbah, C. Poulard, A. Boudaoud and P. Damman, Nat. Phys., 2011, 7, 56 Search PubMed; F. Brau, P. Damman, H. Diamant and T. A. Witten, Soft Matter, 2013, 9, 8177 RSC; N. Uchida and T. Ohzono, Soft Matter, 2010, 6, 5792 RSC.
- P. J. Yoo and H. H. Lee, Phys. Rev. Lett., 2003, 91, 154502 CrossRef CAS PubMed; T. Okayasu, H.-L. Zhang, D. G. Bucknall and G. A. D. Briggs, Adv. Funct. Mater., 2004, 14, 1081 CrossRef.
- N. Bowden, W. T. S. Huck, K. E. Paul and G. M. Whitesides, Appl. Phys. Lett., 1999, 75, 2557 CrossRef CAS.
- T. Ohzono, K. Suzuki, T. Yamaguchi and N. Fukuda, Adv. Opt. Mater., 2013, 1, 374 CrossRef.
- P. Kim, Y. Hu, J. Alvarenga, M. Kolle, Z. Suo and J. Aizenberg, Adv. Opt. Mater., 2013, 1, 381 CrossRef.
- K. Efimenko, M. Rackaitis, E. Manias, A. Vaziri, L. Mahadevan and J. Genzer, Nat. Mater., 2005, 4, 293 CrossRef CAS PubMed.
- C. Lu, H. Möhwald and A. Fery, Soft Matter, 2007, 3, 1530 RSC.
- T. Ohzono, H. Monobe, N. Fukuda, M. Fujiwara and Y. Shimizu, Small, 2011, 7, 506 CrossRef CAS PubMed.
- T. Ohzono and J. Fukuda, Nat. Commun., 2012, 3, 701 CrossRef PubMed.
- X. Jiang, S. Takayama, X. Qian, E. Ostuni, H. Wu, N. Bowden, P. LeDuc, D. E. Ingber and G. M. Whitesides, Langmuir, 2002, 18, 3273 CrossRef CAS.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. Vanlandingham, H. C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3, 545 CrossRef CAS PubMed.
- A. J. Nolte, M. F. Rubner and R. E. Cohen, Macromolecules, 2005, 38, 5367 CrossRef CAS.
- R. Vendamme, T. Ohzono, A. Nakao, M. Shimomura and T. Kunitake, Langmuir, 2007, 23, 2792 CrossRef CAS PubMed.
- J. A. Rogers, ACS Nano, 2007, 1, 151 CrossRef CAS PubMed.
- W. H. Koo, S. M. Jeong, F. Araoka, K. Ishikawa, S. Nishimura, T. Toyooka and H. Takezoe, Nat. Photonics, 2010, 4, 222 CrossRef CAS.
- J. Y. Chung, J. P. Youngblood and C. M. Stafford, Soft Matter, 2007, 3, 1163 RSC.
- K. Khare, J. Zhou and S. Yang, Langmuir, 2009, 25, 12794 CrossRef CAS PubMed; T. Ohzono, H. Monobe, K. Shiokawa, M. Fujiwara and Y. Shimizu, Soft Matter, 2009, 5, 4658 RSC; H. Monobe, T. Ohzono, H. Akiyama, K. Sumaru and Y. Shimizu, ACS Appl. Mater. Interfaces, 2012, 4, 2212 Search PubMed.
- T. Ohzono, T. Yamamoto and J. Fukuda, Nat. Commun., 2014, 5, 3735 Search PubMed.
- E. P. Chan, E. J. Smith, R. C. Hayward and A. J. Crosby, Adv. Mater., 2008, 20, 711 CrossRef CAS.
- C. J. Rand and A. J. Crosby, J. Appl. Phys., 2009, 106, 064913 CrossRef.
- K. Suzuki, Y. Hirai and T. Ohzono, ACS Appl. Mater. Interfaces, 2014, 6, 10121 Search PubMed.
- T. Ohzono and M. Shimomura, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 132202 CrossRef; T. Ohzono and H. Monobe, J. Colloid Interface Sci., 2012, 369, 1 CrossRef PubMed.
- S. Yang, K. Khare and P.-C. Lin, Adv. Funct. Mater., 2010, 20, 2550 CrossRef CAS; C. Cao, H. F. Chan, J. Zang, K. W. Leong and X. Zhao, Adv. Funct. Mater., 2014, 26, 1763 CrossRef PubMed.
- T. Ohzono, Y. Hirai, T. Suzuki, M. Shimomura and N. Uchida, Soft Matter, 2014, 10, 7165 RSC.
- K. Suzuki, Y. Hirai, M. Shimomura and T. Ohzono, Tribol. Lett., 2015, 60, 24 CrossRef.
- H. Yabu, Y. Hirai and M. Shimomura, Langmuir, 2006, 22, 9760 CrossRef CAS PubMed; Y. Hirai, H. Yabu, Y. Matsuo, K. Ijiro and M. Shimomura, J. Mater. Chem., 2010, 20, 10804 RSC.
- A. K. Sengupta, D. De and B. P. Sarkar, Text. Res. J., 1972, 42, 268 CrossRef; M. Niwa, S. Kawabata and H. Kawai, J. Text. Mach. Soc. Jpn., 1969, 22, 14 Search PubMed.
- V. I. Popov, Contact Mechanics and Friction, Springer, Berlin, 2010 Search PubMed.
- H. Jian, et al. , Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15607 CrossRef PubMed.
- F. P. Bowden and D. Tabor, The friction and lubrication of solids, Clarendon Press, Oxford, 1950 Search PubMed.
- K. Brörmann, I. Barel, M. Urbakh and R. Bennewitz, Tribol. Lett., 2013, 50, 3 CrossRef.
- J. Israelachvili, Intermolecular & Surface Forces, Academic Press, San Diego, 1992 Search PubMed.
- M. K. Chaudhury, J. Adhes. Sci. Technol., 1993, 7, 669 CrossRef CAS.
- W. A. Zismann, in Contact Angle, Wettability and Adhesion, ed. F. M. Fowkes, Advances in Chemistry, American Chemical Society, Washington, DC, 1964, vol. 43 Search PubMed.
- Empirically, it is known that the adhesive force on the PDMS elastomer is often larger than the nylon-66. This is due to the difference in the true contact area to be raptured; the PDMS can make larger true contact area owing to the low modulus ∼2 MPa than that of nylon-66.
- As preliminary results, we have found that a 2/2 twill weave (fibre diameter of 30 μm, periodicity of 50 μm, N-NO. 508, AzOne, Japan) also exhibits significant frictional tunability similar to the present results found with the plain weave textile.
Footnote |
| † Electronic supplementary information (ESI) available: This movie shows the tunability of the frictional force on the present system. The object with a plain surface relatively large compared to that of the wrinkle periodicity (a button cell, CR2032, ∼3 g) is placed on the sample surface inclined by ∼20°. The reversible wrinkles are induced by applying compressive strain manually. The button cell starts sliding down when the surface is wrinkled because of the lowered (static) friction. See DOI: 10.1039/c6sm00728g |
| This journal is © The Royal Society of Chemistry 2016 |