Synthesis of colloidal microgels using oxygen-controlled flow lithography†
Harry Z.
An
a,
H. Burak
Eral
a,
Lynna
Chen
 b,
Michelle B.
Chen
c and
Patrick S.
Doyle
*a
b,
Michelle B.
Chen
c and
Patrick S.
Doyle
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: pdoyle@mit.edu
bDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 24th July 2014
Abstract
We report a synthesis approach based on stop-flow lithography (SFL) for fabricating colloidal microparticles with any arbitrary 2D-extruded shape. By modulating the degree of oxygen inhibition during synthesis, we achieved previously unattainable particle sizes. Brownian diffusion of colloidal discs in bulk suggests the out-of-plane dimension can be as small as 0.8 μm, which agrees with confocal microscopy measurements. We measured the hindered diffusion of microdiscs near a solid surface and compared our results to theoretical predictions. These colloidal particles can also flow through physiological microvascular networks formed by endothelial cells undergoing vasculogensis under minimal hydrostatic pressure (∼5 mm H2O). This versatile platform creates future opportunities for on-chip parametric studies of particle geometry effects on particle passage properties, distribution and cellular interactions.
1. Introduction
Controlled synthesis of non-spherical microparticles is an important problem in biomaterial design and drug delivery. Deviation from simple spherical symmetry in particle architecture dramatically improves the utility of these particles in a wide spectrum of biomedical applications, including multiplexed sensing and diagnostics of clinically relevant disease markers,1,2 mimicry of naturally occurring biological entities (such as red blood cells3–7 or platelets8,9), programmed encapsulation of drugs and imaging probes,10,11 followed by their systemic or targeted delivery in due course.In general, performance of designer particulate systems is the product of a complex interplay of material characteristics. This is especially true for microfabricated drug delivery vectors: modulating the size,12,13 shape,14 elasticity, and surface chemistry of the particles has been shown to delay internationalization by immune cells,12 influence intracellular trafficking,15,16 and prolong in vivo circulation.5,17
In order to elucidate a complete set of design criteria for maximizing selectivity at the cell and tissue levels, synthesis methods need to afford independent control over the physicochemical properties of the resulting particles. A variety of versatile top-down particle fabrication techniques have emerged in the past few decades, chief among them microfluidics,18 lithography,19 electrospraying,20 template stretching,21,22 or combinations thereof.23,24 However, not all techniques can freely access the material composition, particle architecture, or length scale (≤10 μm) relevant to biological assays, especially cellular uptake, and intravenous injections. For example, particles synthesized using droplet microfluidics are often restricted to spheres or deformations thereof due to surface energy minimization, with characteristic size ∼O (10 μm). Electrohydrodynamic jetting can be used to create many unique non-equilibrium particle structures. However, its ability to do so hinges heavily on prepolymer flow characteristics, which varies according to particle composition. Up to now, techniques for generating geometrically-complex, and structurally-anisotropic microparticles with size in the colloidal regime remain elusive.
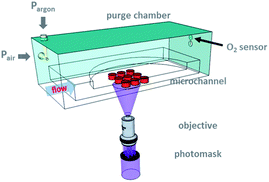
To ameliorate the experimental bottleneck on biocompatible colloidal microgel synthesis, we developed a modified flow lithography technique. This versatile method builds upon stop-flow lithography23 (SFL), which allows microparticles of any 2D-extruded, mask-defined shape to be patterned from UV-crosslinkable oligomer formulations in a semi-continuous fashion. During normal operation, oxygen, a polymerization inhibitor, rapidly diffuses through the PDMS sidewalls, and gives rise to lubricating layers of thickness δ above and below the particle. However, this fortuitous ability to easily create free-standing structures leads to other problems: δ limits the feature resolution of the technique to ∼2 μm in the out-of-plane direction.4 Furthermore, for particle synthesis using conventional SFL, the minimum in-plane feature resolution depends on the channel height. In particular, 5 μm diameter cylinders can only be synthesized using devices that are at least 10 μm tall.23 In this contribution, we control the inhibitory effects of ambient oxygen25via simple purge (Fig. 1). The improved experimental setup extends the particle synthesis capabilities of SFL to ∼5 μm in diameter (in-plane resolution) and sub-micron in height, simultaneously.
In this article, we substantiate the colloidal nature of the microparticles fabricated using oxygen-controlled SFL by examining their diffusion in bulk and near an interface. In the latter case, we constructed a simple argument based on Boltzmann statistics for estimating the hindered diffusion coefficient near a planar wall.
In addition, we perform proof-of-concept experiments showing the flow of polyethylene glycol (PEG)-based hydrogel colloids through multi-culture microfluidic vascular networks (μVNs) formed by human umbilical vein endothelial cells undergoing vasculogenesis.26 These self-organized, perfusable 3D μVNs were recently used to better understand extravasation events in tumor cell metastasis.27 The in vitro microvascular network platform is a very useful tool for systematically studying transport of microparticles in real time, with increased physiological relevance compared to microfluidics-based flow assays (similar to other bio-inspired experiments4,28).
2. Experimental
2.1 Materials
Solutions of poly(ethylene glycol) diacrylate (PEGDA, Mn = 700 g mol−1, Sigma Aldrich) and 2-hydroxy-2-methyl-1-phenyl-propan-1-one (Darocur® 1173, Sigma Aldrich) were used for particle synthesis. Methacryloxyethyl thiocarbamoyl rhodamine B (λex/λem = 548/570 nm, Polysciences) was used to label the gel particles for fluorescence imaging.2.2 Particle synthesis
The microfluidic devices were prepared by pouring polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) onto a 4 inch silicon wafer containing positive-relief SU-8 features. Procedures for device fabrication and assembly are discussed in detail elsewhere.29 The devices contain parallel rectangular channels 100 μm in width and 2 μm in height. Thickness over the synthesis section of each device was tuned between 1 to 3 mm by varying the amount of PDMS used. For synthesis experiments done in this work, a second layer of PDMS was poured near the inlet and outlet reservoirs to support modified pipette tips30 (used to inject prepolymer mixtures) and blunt needles (used to collect particles).All of the particles shown in this work were prepared using a modified stop-flow lithography (SFL) technique. The synthesis devices were placed inside a custom-made sealed chamber with multiple purge gas inlet and outlet apertures, and mounted on an inverted microscope (Axiovert 200, Zeiss). A prepolymer mixture consisting of 80% PEGDA, 15% photoinitiator and 5% fluorescent dye stock solution (1 mg mL−1 PEG200), by volume, was injected into a synthesis device using modified pipette tips (Molecular BioProducts) under moderate forcing pressure (∼4 psi). Concurrently, air and argon purge streams (DPG4000-30, Omega) were introduced into the chamber according to a predetermined calibration curve to achieve a targeted oxygen concentration, between 0% and 21%. The enclosed microfluidic device and prepolymer mixture were allowed to equilibrate with the exchanged gas mixture for up to 90 minutes, depending on the device thickness.
Colloidal microparticles were patterned by projecting mask-defined UV light from a Lumen 200 metal arc lamp (Prior Scientific, 100% setting, 1250 mW cm−2) through a wide excitation UV filter set (300–380 nm, 11000v2 UV, Chroma Technology) using a 20× objective. A shutter system (VS25, Uniblitz) interfaced with a custom-written Python automation script precisely controlled the duration of UV exposure (up to 250 ms). Microparticle formation was visualized using a cooled interline charge-coupled device camera (Clara, Andor).
Following polymerization, particles were transferred from the outlet reservoir of the microfluidic synthesis device to a clean 1.5 mL Eppendorf tube containing 750 μL PBST (1× phosphate buffered saline with 0.1% (v/v) Tween® 20). Particles were washed and re-suspended five times in PBST then stored at 4 °C until further characterization.
2.3 Particle characterization
The slides were transferred to an inverted microscope (Axiovert 200, Zeiss) equipped with an EC Plan Neofluar® objective (40×, NA = 0.75) and observed under fluorescence mode. Movies of up to 2500 frames were recorded using a cooled interline CCD camera (Clara, Andor) at a rate of 13.6 fps with an exposure time of 20 ms to minimize dynamic error. We used a public-domain MATLAB algorithm written by Kilfoil and coworkers31 to extract two-dimensional particle trajectories from the movies. To extract particle mobility, trajectories were averaged to obtain the unbiased mean-squared displacement (MSD), 〈ΔR(τ)〉 as a function of lag time, τ. The static error (![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) 2) due to camera noise was deduced from MSDs of immobilized discs at short lag time32 to be 10−4 μm2.
2) due to camera noise was deduced from MSDs of immobilized discs at short lag time32 to be 10−4 μm2.
2.4 Determination of oxygen concentration in purge chamber
The gas-phase oxygen concentration inside the purge chamber was monitored non-invasively using the RedEye™ oxygen sensing patches (FOXY, Ocean Optics) placed directly above the purge gas outlet (Fig. 1). The patches contain immobilized indicator dyes that quench in the presence of oxygen molecules. The degree of quenching correlates quantitatively with the partial pressure of oxygen (pO2) according to Stern–Volmer equation, t0/t = 1 + KSVpO2, where t0 and t is the fluorescence lifetime in the absence and presence of oxygen, respectively, KSV is the Stern–Volmer coefficient. Operational details of the oxygen sensing system were discussed previously.3Ambient oxygen concentration was varied from 0% to 20.9% by adjusting the relative flow rates of argon and air into the chamber, and was measured from a linear calibration curve. A 2-point calibration was performed prior to each sensing experiment. Typically, fluorescence lifetime decreased from 2.848 μs for 0% oxygen to 1.990 μs for 20.9% oxygen.
2.5 Numerical solutions of mass transport equations
The simulation results shown in Fig. 3 were obtained by numerically integrating the conservation equations for oxygen and unconverted oligomers using a custom-written script in Fortran 77. Eqn (6) and (7) were discretized into 500 uniform mesh elements along the channel height (z) direction between 0 (channel bottom) and 1 (channel top), and propagated in dimensionless time intervals of 10−6 for ≥104 steps.2.6 Particle flow experiments
The vasculogenesis flow devices (height = 100 μm) were molded in PDMS and permanently bonded to glass slides via oxygen plasma treatment. Device contains three parallel, spatially segregated gel regions. Each gel region is flanked by medium channels to provide adequate nutrients and gas exchange, and direct access to the openings of the vasculature. Human umbilical vein endothelial cells (HUVECs) were encapsulated in fibrin gels and cultured alongside human lung fibroblasts (HLFs). Two columns of equally spaced trapezoidal PDMS posts, one on either side of the central HUVEC gel region, were introduced to (1) enable uniform gel-fluidic interfaces, and (2) minimize spillage into medium channels during gel filling. HLFs prevent nascent vascular networks from regressing after ∼4 days under non-contact co-culture conditions. For detailed procedures for device assembly, cell culture, and gel filling, see ref. 26.To introduce colloidal particles into the microvascular networks, media from the reservoirs of the two channels flanking the endothelial cell channel was aspirated and 40 μL of the particle suspension containing ∼300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles per mL was deposited into one of the reservoirs connected to the central media channel. This creates a pressure drop of 5.2 mmH2O across the vascular network, drawing the particles into the vasculature.
000 particles per mL was deposited into one of the reservoirs connected to the central media channel. This creates a pressure drop of 5.2 mmH2O across the vascular network, drawing the particles into the vasculature.
Videos were recorded, under both fluorescence and DIC conditions simultaneously on an Olympus confocal microscope (10× objective, 2.4× optical zoom) at a frame rate of 0.33 fps. Composite images were created using ImageJ showing the outlines of the microvascular network and the particle trajectory.
After the flow experiment, vessels were fixed with 4% paraformaldehyde (Electron Microscopy Sciences) for 15 min, permeabilized with 0.01% Triton X (Sigma) and stained for actin using Alexa Fluor® 488 Phalloidin (Invitrogen) at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 dilution. Fluorescent confocal images (Olympus IX81) were then taken and processed using the IMARIS imaging software (Bitplane).
200 dilution. Fluorescent confocal images (Olympus IX81) were then taken and processed using the IMARIS imaging software (Bitplane).
3. Results and discussion
3.1 Modified stop-flow lithography
To synthesize sub-micron tall particles, we build upon the stop-flow lithography (SFL) technique introduced by Doyle and co-workers.23 In conventional SFL, pulses of mask-defined UV light are projected through a microscope objective to generate free-standing gel structures within a microfluidic device. The particles of height h are flanked above and below by lubricating layers of thickness, δ, which is normally ∼O (1 μm). The boundary of the inhibition layer is determined by the delicate balance between oxygen diffusion and consumption via the inhibition reaction with propagating oligomers. Therefore, in order to fabricate microgels with h ∼ δ, ways of controlling ambient oxygen concentration during synthesis needed to be explored. We note that the use of inert sheath flows is insufficient as the minimum gap height achievable is ∼2 μm (ref. 34) for any reasonable polymerization time due to diffusive mixing at the fluid interfaces.One facile method of exercising oxygen control is through the use of a purge chamber. A schematic of the modified flow lithography experimental setup is shown in Fig. 1. The chamber is made in-house and latches onto the microscope stage. During particle synthesis, oxygen concentration inside the chamber can be altered by passing air and argon (which contains 20.9% and 0% O2 by volume, respectively) in the desired proportions through the two purge gas inlet apertures. Placing the two nozzles at a right angle facilitates gas mixing. We maintain the flow rates of the purge gases for the duration of the experiment in order to prevent gas leakage through any microscopic cracks on the chamber walls (Fig. S1†).
Use of the purge chamber introduces an additional conditioning step in the normal experimental workflow. At the beginning of each synthesis experiment, a brief waiting period is required for (1) the individual purge gas streams to mix and (2) the microfluidic device and its contents to equilibrate with the air/argon mixture within the chamber. In practice, the former occurs more rapidly than the latter. We placed a RedEye™ oxygen sensor patch above the purge gas outlet to monitor the oxygen concentration in the gas phase (Fig. 1). The patch contains an immobilized dye molecule that quenches in the presence of O2. To make chamber oxygen readings, we point a bifurcated optical fiber (RE-BIFBORO-2) at the RedEye™ patch. The fiber directs a blue LED excitation light toward the patch, and excites the sensor dye. The red emitted signal is then collected by the optical probe and transmitted to a fluorometer, which measures the fluorescence lifetime, t. t is related to the partial pressure of oxygen by the well-known Stern–Volmer equation.35Fig. 2(b) shows the chamber oxygen concentration as a function of time for a range of air inlet pressures. In all cases, the oxygen concentration reached an equilibrium value approximately 1 minute after the onset of purge, indicating efficient gas mixing.
 | ||
| Fig. 2 Timescale comparison. (A) Thickness of the PDMS synthesis device determines the threshold response time (defined as the duration of continuous gas purge needed to reach equilibrium). The measured response time obeys a power-law trend, with exponent of 0.5 (a dashed line is drawn to guide the eye), which suggests a simple diffusion-based mechanism, with a characteristic coefficient ∼O (10−9) m2 s−1, typical of oxygen35 and argon36 diffusion through porous PDMS. (B) The amount of oxygen in the chamber for a range of air feed pressures: 0 psi (orange circles), 0.1 psi (blue circles), 0.5 psi (black circles), 1.0 psi (red circles). Pressure of the argon stream is fixed at 1 psi. Efficient mixing at the gas stream inlets result in short time lags (<1.5 min) until a final chamber oxygen concentration plateau is reached. (C) Equilibrium oxygen concentration in the purge chamber as a function of volume fraction of air introduced. The empirical measurements (red circles) made using the RedEye™ oxygen sensors are in excellent agreement with a simple model of high Re gas mixing derived from the Blasius correlation (dotted line, eqn (2) in text). | ||
A second time delay is associated with the synthesis device and the prepolymer solution flowing within the microchannel coming to equilibrium with the surrounding chamber gas mixture. Duration of the delay or response time is determined by the thickness of the PDMS layer above the synthesis microchannel. To demonstrate this, we assembled devices of varying PDMS thickness (the channel height stayed the same at 2 μm). The practical lower threshold (∼2 mm) is set by the minimum thickness necessary to reliably secure fluidic connections into the device inlet and outlet reservoirs. Using a canonical composition (80% v/v PEGDA700, and 15% v/v Darocur®1173, and 5% v/v rhodamine B), we synthesized cuboids of decreasing size in 2 μm tall channels under constant influx of pure argon (1.0 psi). Fig. 2(a) shows the time necessary for the smallest feature (5 μm square) to stick to the confining PDMS surfaces due to lack of oxygen inhibition near the channel periphery. The observed linear trend in log-log format, with a power-law slope of 0.5, is consistent with a simple diffusive mechanism, in which the PDMS layer above the synthesis device acts as the dominant barrier for mass transfer. We estimate the characteristic diffusion coefficient to be ∼O (10−9 m2 s−1), on par with the diffusivity of oxygen36 and argon37 through PDMS. In order to limit the overall equilibration time prior to synthesis to ∼5 min, we developed a tiered PDMS synthesis device (Fig. S2†) using a two-step curing process. First, we poured a thin layer (∼1 mm) of PDMS over the device wafer and partially cured in the oven at 65 °C for 25 min. Then, shortened pipette tips (200 μL) were used to shield the central synthesis portion of each device and allow a second layer of PDMS to coat only the inlet and outlet regions, where rapid gas transport is unessential. The sacrificial pipette tips (Fig. S2B†) were removed from the wafer once the PDMS fully cured after baking overnight at 65 °C.
Fabrication of free-standing gel particles using SFL requires non-zero oxygen concentrations in the purge chamber in order to avoid particle sticking. As such, we systematically calibrated the equilibrium chamber oxygen concentration for a wide range of air pressures using the RedEye™ sensor. The concentration measurements were collapsed using a simple model derived from the Blasius correlation for high Re flow in smooth pipes43 (Fig. 2(c)). This approach is justified since the Re for purge gas flow estimated using a typical pressure drop of 1 psi was >4000. Applying the Blasius equation, gas flow rate, Qi, where i stands for either air or argon, can be expressed as:
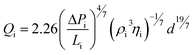 | (1) |
ΔP/L is the pressure drop per unit length of tubing, d is the nozzle diameter (∼1 mm), ρ and η are the density and kinematic viscosity, respectively. Therefore, setting Largon = Lair, the volume fraction of air introduced Qair/Qtotal is:
 | (2) |
3.2 Modeling of photopolymerization
The importance of controlling ambient oxygen concentration in enabling thin particle synthesis can be understood using a simple reaction-diffusion model. This one-dimensional description of particle formation in a microfluidic channel was first formulated by Dendukuri et al.25 It has since been adapted44 and further validated via experiments.3This model considers the spatial and temporal variation of dissolved oxygen concentration [O2] and un-crosslinked oligomers [M] within a prepolymer mixture between confining PDMS channel boundaries (z-direction). Using mass action kinetics, we can write the governing equations as:
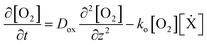 | (3) |
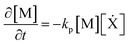 | (4) |
The RHS terms of eqn (3) correspond to oxygen diffusion through PDMS (with Dox as the diffusion coefficient) and reaction with propagating radical species, Ẋ (with rate constant ko), respectively. This model neglects the diffusion of oligomers due to their bulky size relative to that of oxygen. As a result, only the propagation reaction (with rate constant kP) contributes to the decrease in [M] over time. The two expressions are coupled via the inhibition reaction where oxygen quenches further polymerization by reacting with propagating radical species. [Ẋ] can be estimated by invoking the quasi-steady state approximation, and setting the rate of radical generation (ra) in a thin film of prepolymer at height z equal to the rate of consumption by the inhibition and termination reactions:
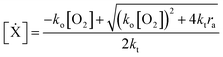 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ε[PI]z). ψ is the quantum yield of the initiating radical species. ε and [PI] is the molar extinction coefficient (at 365 nm) and concentration of the photoinitiator, respectively. Io is the incident light intensity. kt is the rate constant for the bimolecular termination reaction. For detailed derivation of the model equations and full reaction mechanism, see ref. 25.
exp(−ε[PI]z). ψ is the quantum yield of the initiating radical species. ε and [PI] is the molar extinction coefficient (at 365 nm) and concentration of the photoinitiator, respectively. Io is the incident light intensity. kt is the rate constant for the bimolecular termination reaction. For detailed derivation of the model equations and full reaction mechanism, see ref. 25.
The governing equations, eqn (3) and (4), can be non-dimensionalized using
| τ = tDox/H2, η = z/H |
| θ = [O2]/[O2]eq, ξ = [M]/[M]0 |
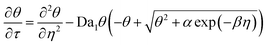 | (6) |
 | (7) |
Da1 and Da2 are Damkohler numbers. The former quantifies the relative rates of oxygen inhibition and oxygen diffusion, while the latter quantifies the relative rates of chain propagation and oxygen diffusion. We note that the expression for α differs from its counterpart in the original contribution by a factor of E, which denotes the energy content of a mole of photons at 365 nm (328 kJ mol−1).25 This conversion factor was not explicitly stated previously. However, we do so here to maintain dimensional consistency.
To computationally show the feasibility of creating thin particles by controlling the chamber oxygen concentration, we numerically integrated eqn (6) and (7) to obtain θ and ξ given the parameters listed in Table 1 and the following boundary conditions:
| θ(0, τ) = 1, θ(1, τ) = 1, θ(η, 0) = 1 |
| Parameter | Value | Units | Source |
|---|---|---|---|
| k p | 25 | m3 mol−1 s−1 | Ref. 38 |
| k t | 2.52 × 103 | m3 mol−1 s−1 | Ref. 38 |
| k o | 5 × 105 | m3 mol−1 s−1 | Ref. 39 |
| D ox | 2.84 × 10−11 | m2 s−1 | Ref. 40 |
| H | 2 | μm | Measured |
| I o | 1.25 × 104 | W m−2 | Measured |
| [PI] | 990 | mol m−3 | Calculated |
| ε | 1.6 | m3 mol−1 m−1 | Ref. 41 |
| [O2]eq | 1.5 | mol m−3 | Ref. 42 |
| φ | 0.6 | — | Ref. 41 |
In order to vary [O2] in the chamber, we assumed 1) the equilibrium dissolved oxygen concentration [O2]eq in the prepolymer mixture obeys Henry's law, with a proportionality constant kH of 140 L atm mol−1; and (2), [O2]eq = 1.5 mol m−3 under standard ambient conditions (20.9% O2). Simulation results for τ = 0.1 are shown in Fig. 3. Physically, this corresponds to ∼100 ms for a 2 μm tall device, similar to exposure times used during synthesis. Keeping the exposure time short helps to generate more uniform particles.45
 | ||
| Fig. 3 Steady state profiles of oxygen (θ) and unconverted monomer concentration (ξ) as a function of non-dimensionalized channel height (η). The results shown in (A) and (B) were obtained by numerically integrating eqn (6) and (7) using the parameter values listed in Table 1 for a range of ambient oxygen concentrations. Decreasing ambient O2 concentration leads to a reduction in oxygen penetration depth near the channel walls, where rapid oxygen diffusion prevents particle formation. Cross-linked structures start to grow from the channel center as θ and ξ fall below a critical threshold value (θc ∼ 10−3, ξc = 0.98) for gelation. Modulating the chamber [O2] allows particle height to approach the sub-micron regime. (C) A series of bright-field micrographs showing the change in height of 10 μm diameter discs for a range of chamber [O2] (noted in the upper left corner). Above ∼10%, no particles can be made, in agreement with model predictions. Scale bar is 5 μm. | ||
At high chamber oxygen concentrations (≥10%), transport of oxygen near the channel interfaces occurs rapidly and prevents particle formation. Here, we adopt the convention that gelation occurs when monomer conversion first reaches 2% (ξc = 0.98), similar to what was done previously.25 Below 10% O2, the propagation reaction dominates the inhibition reaction between radical species and dissolved oxygen. As a result, particles grow from the channel center, where the dissolved oxygen concentration is at a minimum, outward. The 10% O2 threshold satisfies the critical Da criterion for effective synthesis (Da ≥ 4) developed by Dendukuri et al.25
To confirm the validity of the simulations, we synthesized 10 μm discs in a 2 μm tall tiered microfluidic device under a range of chamber oxygen concentrations. We imaged the resulting gel structures in situ. When [O2] was above ∼10%, particle could not be made even using extended exposure durations (∼1 s), in agreement with model predictions. However, as [O2] in the purge chamber was decreased, discs formed according to the mask pattern with increasing height (Fig. 3(c)). A similar trend was qualitatively forecast by simulations (Fig. 3(b)). In practice, performing synthesis with chamber oxygen level below 4% is not ideal, as it leads to excessive particle sticking after ∼10 min of operation.
Synthesis of thinner particles in microfluidic channels with height H < 2 μm will be difficult for two reasons (1) the window of opportunity for effective synthesis is small (Da scales quadratically with H but only linearly with [O2]eq), and (2) the pressure drop needed to drive flow scales as H−3.46 Therefore, device modifications may be required to prevent channels from bursting.
3.3 Brownian motion of microparticles
Achieving the colloidal (or cellular) size regime is a necessary synthesis milestone for probing the interactions of designer microparticles with biological or biomimetic environments. It is well known that one of the hallmarks of colloidal objects is they undergo spontaneous, random walk when suspended in a viscous fluid. A common statistical measure for particle dynamics in an inherently stochastic process is mean-squared displacement (MSD), 〈ΔR2(τ)〉, calculated from particle trajectories:| 〈ΔR2(τ)〉 = 〈(R(t + τ) − R(t))2〉 | (8) |
| 〈ΔR2(τ)〉 = 4Diτ | (9) |
To demonstrate the colloidal nature of the microparticles generated using the modified SFL technique, we synthesized 5 μm and 8 μm diameter discs in the presence of 8.5% O2. These synthesis experiments would not be feasible without lowering the oxygen concentration in the vicinity of the synthesis microfluidic device. Rhodamine B was covalently conjugated to the hydrogel backbone during synthesis to facilitate particle tracking. We recorded the motion of the microdiscs at least 4 particle diameters away from the rigid bottom surface of the observation chamber. The experimental buffer solution was density-matched by adding 90% v/v deuterium oxide in order to prolong the observation period, in which the particles remain in the focal plane of the microscope objective. We did not observe any particle swelling after D2O addition. The choice to synthesize discs rather than more complex shapes enables the use of a public-domain algorithm to first locate the particles, then extract the particle trajectories, and finally calculate the MSDs47 (Fig. 4). Trajectories were constructed by linking of the brightness centroid locations of candidate particles found on at least 10 consecutive frames, until they fell out of focus. The resulting MSD curves are linear in τ, consistent with Brownian motion. The corresponding translational diffusivity coefficients in bulk (D∞) were calculated from lines of best fit to the data using eqn (9) (Table 2). The values of D∞ decrease as the size of the discs increase, as one would intuitively expect.
 | ||
| Fig. 4 Mean-square displacement 〈ΔR2〉 in bulk as a function of lag time, τ for various colloidal discs suspended in 90% v/v D2O. The MSD curves show a power-law slope of 1, which is consistent with Brownian motion, revealing the colloidal nature of these disc-shaped particles. For Brownian motion in 2-dimensions, 〈ΔR2〉 = 4Dτ, where D is the translational diffusivity. The value of h for each particle sample was calculated from eqn (11) given the diffusivity measurement. | ||

| r (μm) | r s (μm) | h (μm) | D ∞ (μm2 s−1) |
|---|---|---|---|
| 2.5 | 1.67 | 1.0 | 0.105 |
| 4 | 2.29 | 1.0 | 0.070 |
| 5 | 2.47 | 0.8 | 0.059 |
| 5 | 2.82 | 1.2 | 0.055 |
We can use the bulk diffusivity measurements to estimate the height of the colloidal particles. This method is valuable because the out-of-plane dimension of non-spherical colloids is often difficult to directly quantify using conventional optical microscopy techniques. In general, bulk diffusivities are affected by particle geometry and size. In the simplest case, translational diffusion coefficient, Ds, of a sphere is related to its radius, rs, by the Stokes–Einstein equation:
 | (10) |
For thin discoids, the bulk diffusivity, D∞, is a function of the aspect ratio, p = h/2r, where h is the height, and r is the radius of the disc. Hansen48 developed the following correlation that fits results from Monte Carlo simulations:
Ds/D∞=1.0304 + 0.0193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p + 0.0623(ln p + 0.0623(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p)2 + 0.0048(ln p)2 + 0.0048(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p)3 + 0.0017(ln p)3 + 0.0017(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p)4 p)4 | (11) |
To estimate the height of colloidal discs using eqn (10) and (11), we assumed the diameter of the particles to be the size of the mask pattern. This is a good assumption for two reasons: (1) the coefficient of variation for SFL is no more than a few percent,50 and (2) the high PEGDA concentration minimizes any swelling effects. High resolution confocal imaging of a 10 μm disc supports this assumption (Fig. 5(c)). Particle height calculated from diffusivity measurements and eqn (11) are shown in Table 2. Error introduced in h through the uncertainties in the bulk diffusivity measurement (±0.002 μm2 s−1) is less than 0.1 μm in all cases (Fig. S4†). We note that the 5 μm × 1 μm discs are the smallest particles synthesized to date using SFL.
While size and geometry of the in-plane feature is defined by the photomask, height of the particles can be tuned by adjusting the chamber oxygen concentration.3 And more importantly, sub-micron-tall particles can be generated by lowering the chamber O2 concentration close to the critical threshold of 10%. To show this, we synthesized 10 μm discs using 8% and 9.5% O2, and measured their bulk diffusivities in a 90% (v/v) D2O aqueous mixture (Fig. 4). We estimated the out-of-plane dimension of the particles to be 1.2 and 0.8 μm, respectively (Table 2).
To verify the latter result, a laser scanning confocal microscope equipped with a high numerical aperture oil immersion objective (NA = 1.3) was used to directly visualize the thinnest particle sample (10 μm × 0.8 μm discs). Confocal microscopy relies on point illumination through a pinhole to eliminate out-of-focus light in the region of interest (ROI) within the sample, resulting in increased optical resolution. Using an excitation wavelength appropriate for rhodamine B (568 nm), the in-plane resolution is ∼0.25 μm. The particles were immersed in 2% alginate solution to arrest their orientation, and imaged on the bottom surface. The image stack was assembled using ImageJ to construct the 3D structure of the microgels (Fig. 5(b)). Dimensions of the particle were gauged at full width at half-maximum (FWHM) from spatially-resolved intensity profiles (Fig. 5). Accordingly, the particle height was estimated to be ∼0.8 μm, in agreement with predictions made based on diffusivity measurements. Error introduced by Brownian motion during imaging acquisition is estimated to be ∼0.1 μm.
Next, we examine the Brownian motion of discoids near a planar solid surface. Studying the transport behaviour of non-spherical particles near physical boundaries has proven to be a difficult task both theoretically and experimentally. Analytical expressions from theoretical treatment of hindered diffusion are limited to the simplest particle geometries (i.e., spheres51 and discs). Techniques which are capable of creating exotic particle morphologies (i.e., lock–key particles,52 boomerangs,53etc.), have only recently been introduced.
To measure the hindered diffusion coefficients of discs experimentally, we suspended the particles in an aqueous buffer and allowed ample time for them to sediment to the bottom surface of the observation chamber prior to imaging. Up to 2500 frames were collected per movie in order to gather at least 20 000 particle trajectories in total and extract the in-plane translational diffusion coefficient, D0. Fig. 6 and Table 3 show MSDs and hindered diffusivities, respectively, in two different buffers. Unlike their bulk counterparts (Table 2), mobility of microparticles is reduced by as much as ∼80% owing to hydrodynamic interactions with the wall. For thin discs diffusing close to a wall, the preferred mode of motion is in the plane of the particle, parallel to the glass slide. Addition of 90% deuterium oxide by volume reduced the density mismatch (Δρ) between the aqueous buffer and the particles from 0.10 to 0.02 g mL−1. The particle density was estimated using the weighted sum of PEGDA and the photoinitiator densities to be 1.1 g mL−1. This assumes 100% conversion, and represents the density upper bound. As a result, the average gravitational height of the particles,
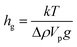 | (12) |
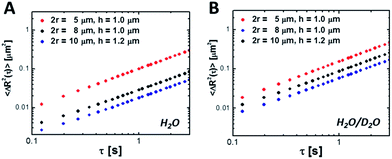 | ||
Fig. 6 Mean-square displacement 〈ΔR2〉 near a wall as a function of lag time, τ for various colloidal discs in (A) water and (B) a mixture of deuterium oxide and water (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by volume). 1 ratio by volume). | ||
| r (μm) | Buffer | h g (nm) | D 0 (μm2 s−1) | |
|---|---|---|---|---|
| Experiment | Model | |||
| 2.5 | H2O | 213.4 | 0.0285 | 0.0271 |
| 2.5 | D2O/H2O | 1067 | 0.0381 | 0.0814 |
| 4 | H2O | 83.3 | 0.0069 | 0.0056 |
| 4 | D2O/H2O | 416.7 | 0.0210 | 0.0199 |
| 5 | H2O | 44.5 | 0.0042 | 0.0029 |
| 5 | D2O/H2O | 266.7 | 0.0129 | 0.0093 |
In reality, the equilibrium separation distance between the particle and the surface continuously fluctuates as a result of thermal motion. It is difficult to isolate the dynamics of a particle sliding parallel to the glass slide from movement in the transverse direction without resorting to specialized techniques, such as total internal reflection microscopy.55 As a result, the experimentally-determined D0 values are in fact apparent diffusion coefficients that encompass the cumulative effect of sampling a range of gap heights on particle motion:
 | (13) |
Kim et al. derived an analytical expression for f(a), characterizing the edgewise translation of a thin circular plate parallel to an infinite plane:54
 | (14) |
At equilibrium, p(a) is the Boltzmann distribution, with hg as the average lubricating gap distance, where potential and thermal energies balance:
| p(a) ∝ exp(−a/hg) | (15) |
Substituting eqn (13) and (14) into eqn (15), we can calculate the hindered diffusivity as long as the particle dimensions are known a priori. This simple model contains no adjustable parameters, and captures the essential physics. It can predict D0 to within 25% when hg ≪ r (Table 3). This can be attributed, at least in part, to overestimating the conversion and therefore, particle density. As the separation distance grows, however, this model breaks down, as the colloidal discs can no longer be approximated as infinitely thin (Table 3, 2.5 μm radius discs in D2O/H2O). We note that a similar approach was used to understand the Brownian fluctuations of charge-stabilized colloidal spheres located near a flat plate.56 The close agreement between the model predictions and experimental data gave us confidence regarding the accuracy with which we estimated the particle dimensions using multiple particle tracking. This model can be used to guide the self-assembly of non-spherical particles near a solid boundary.
3.4 Flow of hydrogel colloids through microvascular networks
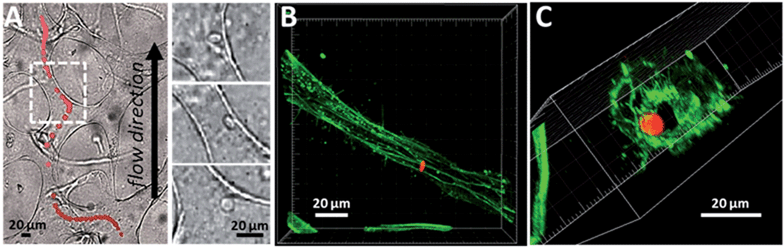
The ability of SFL to generate anisotropic colloidal particles allows us to begin to probe the flow behaviour of particles in a biological environment. Past experiments revealed interesting shape4 and elasticity5,7 induced passage properties, both in vitro and in vivo. A novel method for understanding particle flow characteristics involves the use of engineered, microfluidic vascular networks (μVNs). μVNs can be formed by endothelial cells (HUVECs) undergoing the process of vasculogenesis. In the presence of human lung fibroblasts, HUVECs gradually develop stable networks of interconnected, perfusable vessels after ∼4 days in non-contact cell culture.26 Phenotypic state of the network, such as the number of branches, and average diameter or length of the vessels, can be tuned by adjusting initial input parameters during cell culture (e.g., concentration of growth factors). To demonstrate the passage of fluorescent PEG-based colloids through μVNs, we flowed 10 μm × 1.2 μm discs by applying a small (∼5 mmH2O) hydrostatic driving pressure across the vascularized region on the microfluidic device. Particles entered the network via vessel openings to the adjacent medium channel (Fig. S5†), and navigated through by exploiting the path of least fluidic resistance. A representative particle trajectory through a portion of the network is shown in Fig. 7. The fluorescence signal from the candidate particle was isolated from consecutive frames of experimental movies (Video S1†) and superimposed on top of a bright-field image showing the layout of the microvessels in the ROI. To preserve mass conservation, particles accelerated (marked by the spreading of their fluorescence signals) when they encountered contractions, and vice versa. Importantly, particles do not adhere to the vessel walls (Fig. 7(a), right panel), showing signs of bio-inertness To clearly show the size of a representative vessel in 3D relative to that of a particle, we fluorescently stained for actin with Alexa Fluor® 488 phalloidin after the flow experiment and imaged a residual particle lingering in the lumen. These results demonstrate the feasibility of using μVNs as a useful tool to study particle passage properties. Future experiments may offer mechanistic insight on shape or size effects on particle flow that ultimately result in distribution patterns seen in animal studies.4. Conclusions
In summary, we have shown that controlling the oxygen concentration surrounding the synthesis microfluidic device allows us to synthesize colloidal particles using flow lithography. One of the key advantages of this technique is that geometry of the particles is mask-defined, and as a result, not limited to simple polygonal shapes. Morphologically-complex colloids are critical for efficient assembly of ordered functional materials. In addition, passage of non-spherical colloids through microfluidic vascular networks deserves further attention. This platform can be used to understand the effect of particle shape and deformability on passage properties in a physiological, yet controlled setting.Acknowledgements
HZA and LC are supported by the Institute for Collaborative Biotechnologies through grant W911NF-09-0001 from the U.S. Army Research Office. Additional support is provided by NSF grants CMMI-1120724 and DMR-1006147, and the Singapore MIT Alliance for Research and Technology SMART. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. HZA thanks Andrew Ryan for making the microscope purge chamber, Wendy Salmon for her assistance with confocal microscope training, Bashar Hamza, A. J. Aranyosi, and Octavio Hurtado for device microfabrication at the Charlestown Navy Yard Clean Room facility, and A. Wagner for helpful comments on the manuscript. MBC is supported by the National Science Foundation Graduate Fellowship.Notes and references
- K. W. Bong, S. C. Chapin and P. S. Doyle, Langmuir, 2010, 26, 8008 CrossRef CAS PubMed.
- R. L. Srinivas, S. C. Chapin and P. S. Doyle, Anal. Chem., 2011, 83, 9138 CrossRef CAS PubMed.
- H. Z. An, E. R. Safai, H. B. Eral and P. S. Doyle, Lab Chip, 2013, 13, 4765 RSC.
- R. Haghgooie, M. Toner and P. S. Doyle, Macromol. Rapid Commun., 2010, 31, 128 CAS.
- T. J. Merkel, S. W. Jones, K. P. Herlihy, F. R. Kersey, A. R. Shields, M. Napier, J. C. Luft, H. L. Wu, W. C. Zamboni, A. Z. Wang, J. E. Bear and J. M. DeSimone, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 586 CrossRef CAS PubMed.
- K. Chen, T. J. Merkel, A. Pandya, M. E. Napier, J. C. Luft, W. Daniel, S. Sheiko and J. M. DeSimone, Biomacromolecules, 2012, 13, 2748 CrossRef CAS PubMed.
- N. Doshi, A. S. Zahr, S. Bhaskar, J. Lahann and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21495 CrossRef CAS PubMed.
- C. L. Modery-Pawlowski, L. L. Tian, V. Pan, K. R. McCrae, S. Mitragotri and A. Sen Gupta, Biomaterials, 2013, 34, 526 CrossRef CAS PubMed.
- N. Doshi, J. N. Orje, B. Molins, J. W. Smith, S. Mitragotri and Z. M. Ruggeri, Adv. Mater., 2012, 24, 3864 CrossRef CAS PubMed.
- H. Z. An, M. E. Helgeson and P. S. Doyle, Adv. Mater., 2012, 24, 3838 CrossRef CAS PubMed.
- S. H. Kim, H. C. Shum, J. W. Kim, J. C. Cho and D. A. Weitz, J. Am. Chem. Soc., 2011, 133, 15165 CrossRef CAS PubMed.
- J. A. Champion, A. Walker and S. Mitragotri, Pharm. Res., 2008, 25, 1815 CrossRef CAS PubMed.
- T. J. Merkel, K. Chen, S. W. Jones, A. A. Pandya, S. M. Tian, M. E. Napier, W. E. Zamboni and J. M. DeSimone, J. Controlled Release, 2012, 162, 37 CrossRef CAS PubMed.
- J. A. Champion, Y. K. Katare and S. Mitragotri, J. Controlled Release, 2007, 121, 3 CrossRef CAS PubMed.
- P. Kolhar and S. Mitragotri, Adv. Funct. Mater., 2012, 22, 3759–3764 CrossRef CAS PubMed.
- J. W. Yoo, N. Doshi and S. Mitragotri, Macromol. Rapid Commun., 2010, 31, 142 CrossRef CAS PubMed.
- K. Herlihy, T. Merkel, H. Y. An, W. L. Lin and J. DeSimone, Nanotech Conference & Expo 2009, Vol. 2, Technical Proceedings, 2009, pp. 60 Search PubMed.
- H. C. Shum, A. R. Abate, D. Lee, A. R. Studart, B. G. Wang, C. H. Chen, J. Thiele, R. K. Shah, A. Krummel and D. A. Weitz, Macromol. Rapid Commun., 2010, 31, 108 CAS.
- J. P. Rolland, B. W. Maynor, L. E. Euliss, A. E. Exner, G. M. Denison and J. M. DeSimone, J. Am. Chem. Soc., 2005, 127, 10096 CrossRef CAS PubMed.
- S. Bhaskar, K. M. Pollock, M. Yoshida and J. Lahann, Small, 2010, 6, 404 CrossRef CAS PubMed.
- J. A. Champion, Y. K. Katare and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11901 CrossRef CAS PubMed.
- Y. P. Wang, T. J. Merkel, K. Chen, C. A. Fromen, D. E. Betts and J. M. DeSimone, Langmuir, 2011, 27, 524 CrossRef CAS PubMed.
- D. Dendukuri, S. S. Gu, D. C. Pregibon, T. A. Hatton and P. S. Doyle, Lab Chip, 2007, 7, 818 RSC.
- D. Dendukuri, D. C. Pregibon, J. Collins, T. A. Hatton and P. S. Doyle, Nat. Mater., 2006, 5, 365 CrossRef CAS PubMed.
- D. Dendukuri, P. Panda, R. Haghgooie, J. M. Kim, T. A. Hatton and P. S. Doyle, Macromolecules, 2008, 41, 8547 CrossRef CAS.
- J. A. Whisler, M. B. Chen and R. D. Kamm, Tissue Eng., Part C, 2013, 20(7), 543–552 CrossRef PubMed.
- M. B. Chen, J. A. Whisler, J. S. Jeon and R. D. Kamm, Integr. Biol., 2013, 5, 1262 RSC.
- H. Bow, I. V. Pivkin, M. Diez-Silva, S. J. Goldfless, M. Dao, J. C. Niles, S. Suresh and J. Y. Han, Lab Chip, 2011, 11, 1065 RSC.
- D. C. Appleyard, S. C. Chapin, R. L. Srinivas and P. S. Doyle, Nat. Protoc., 2011, 6, 1761 CrossRef CAS PubMed.
- K. W. Bong, S. C. Chapin, D. C. Pregibon, D. Baah, T. M. Floyd-Smith and P. S. Doyle, Lab Chip, 2011, 11, 743 RSC.
- V. Pelletier, N. Gal, P. Fournier and M. L. Kilfoil, Phys. Rev. Lett., 2009, 102, 188303 CrossRef PubMed.
- T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623 CrossRef CAS PubMed.
- H. B. Eral, V. Lopez-Mejias, M. O'Mahony, B. L. Trout, A. S. Myerson and P. S. Doyle, Cryst. Growth Des., 2014, 14, 2073 CAS.
- K. W. Bong, J. Xu, J. H. Kim, S. C. Chapin, M. S. Strano, K. K. Gleason and P. S. Doyle, Nat. Commun., 2012, 3, 805 CrossRef PubMed.
- D. B. Papkovsky and R. I. Dmitriev, Chem. Soc. Rev., 2013, 42, 8700–8732 RSC.
- H. Shiku, T. Saito, C. C. Wu, T. Yasukawa, M. Yokoo, H. Abe, T. Matsue and H. Yamada, Chem. Lett., 2006, 35, 234 CrossRef CAS.
- L. Brandao, L. M. Madeira and A. M. Mendes, J. Membr. Sci., 2007, 288, 112 CrossRef CAS PubMed.
- S. Kızılel, V. H. Pérez-Luna and F. Teymour, Macromol. Theory Simul., 2006, 15, 686 CrossRef PubMed.
- C. Decker and A. D. Jenkins, Macromolecules, 1985, 18, 1241 CrossRef CAS.
- H. Lin and B. D. Freeman, Macromolecules, 2006, 39, 3568 CrossRef CAS.
- L. Lecamp, P. Lebaudy, B. Youssef and C. Bunel, Polymer, 2001, 42, 8541 CrossRef CAS.
- M. D. Goodner and C. N. Bowman, Chem. Eng. Sci., 2002, 57, 887 CrossRef CAS.
- M. M. Denn, Process fluid mechanics, Prentice-Hall, Englewood Cliffs, N.J., 1980 Search PubMed.
- S. K. Suh, K. W. Bong, T. A. Hatton and P. S. Doyle, Langmuir, 2011, 27, 13813 CrossRef CAS PubMed.
- S. Park, D. Kim, S. Y. Ko, J. O. Park, S. Akella, B. Xu, Y. Zhang and S. Fraden, Lab Chip, 2014, 14, 1551 RSC.
- T. Gervais, J. El-Ali, A. Gunther and K. F. Jensen, Lab Chip, 2006, 6, 500 RSC.
- J. C. Crocker and B. D. Hoffman, Methods Cell Biol., 2007, 83, 141 CAS.
- S. Hansen, J. Chem. Phys., 2004, 121, 9111–9115 CrossRef CAS PubMed.
- A. Ortega and J. G. de la Torre, J. Chem. Phys., 2003, 119, 9914 CrossRef CAS PubMed.
- D. C. Pregibon, M. Toner and P. S. Doyle, Science, 2007, 315, 1393 CrossRef CAS PubMed.
- P. Huang and K. S. Breuer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 046307 CrossRef.
- S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575 CrossRef CAS PubMed.
- A. Chakrabarty, A. Konya, F. Wang, J. V. Selinger, K. Sun and Q. H. Wei, Phys. Rev. Lett., 2013, 111, 160603 CrossRef.
- M. U. Kim, K. W. Kim, Y. H. Cho and B. M. Kwak, Fluid Dynam. Res., 2001, 29, 137 CrossRef.
- S. G. Flicker, J. L. Tipa and S. G. Bike, J. Colloid Interface Sci., 1993, 158, 317 CrossRef CAS.
- M. A. Bevan and D. C. Prieve, J. Chem. Phys., 2000, 113, 1228 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01400f |
| This journal is © The Royal Society of Chemistry 2014 |