Crystal structure, magnetotransport properties, and electronic band structure of V_1−xTi_xSe₂ single crystals

Abstract

We fabricated full spectrum V_1−xTi_xSe₂ samples (0 ≤ x ≤ 1) and systematically studied their crystal structure and electrical properties and their band structure. Ti was found by X-ray diffraction to substitute for V atoms. Our results show that the electrical properties of V_1−xTi_xSe₂ are highly tunable, suggesting a promising application in future electronic devices. In addition, we have observed weak localization in VSe₂ and TiSe₂ single crystals, and the strength of weak localization can be modulated by the defect density. The charge density wave transition for both pure samples, TiSe₂ and VSe₂, is significantly suppressed by doping. Band structure calculations on a subset of V_1−xTi_xSe₂ compositions are in line with the experimental observations.

---

1. Introduction

Transition metal dichalcogenide materials (TMDs) are of fundamental interest for their electronic and optical properties, because of their two dimensional (2D) nature. Explorations of 2D transition-metal dichalcogenides have revealed numerous intriguing properties, such as layer-dependent tunable band gaps, direct-to-indirect band-gap crossovers, and tunable superconductivity by gate-controlled, pressure, or charge density waves (CDW), etc.^1–4 VSe₂ and TiSe₂ are typical TMD materials that have attracted much attention due to their van der Waals layered structures and rich variety of physical properties, including charge density waves, superconductivity, magnetoresistance (MR), etc.^5–11 For example, the origin of the charge-density-wave (CDW) transition occurred in TiSe₂ around 202 K.¹² VSe₂ has a CDW transition at around 110 K which is seen in the temperature dependent electrical transport and magnetic susceptibility measurements.^13,14 The CDW transition is also reported to be suppressed with decreasing thickness in nanoflakes of VSe₂.¹⁵ In addition, Weak localization (WL), a phenomenon first discovered in quantum physics, has become a method for determining the processes responsible for electron dephasing due to inelastic electron scattering or scattering by magnetic impurities. The weak localization effect introduced by defects has been reported in VSe₂ single crystals¹⁶ and polycrystalline TiSe₂ samples.¹⁷ In contrast to paramagnetism in bulk VSe₂, the ferromagnetic order was observed in monolayer VSe₂ at room temperature.¹⁸ The Kondo effect was reported in bulk VSe₂, probably due to the interstitial vanadium ions.¹⁹ When magnetic 3d transition metals (Co, Ni and Fe) are intercalated into TiSe₂, the Kondo effect is induced in the dilute limit.²⁰ So, the resistivity upturn and negative magnetoresistance in VSe₂ are still under debate. Some reports attributed them to the weak localization, while other reports attributed them to the Kondo effect.

In this manuscript, we study the evolution of the CDW and WL in VSe₂ and TiSe₂ single crystals. In order to systematically explore the intriguing properties of the CDW-bearing materials VSe₂ and TiSe₂, we doped VSe₂ with Ti to yield V_1−xTi_xSe₂. Ti was found to be doped on the V sites, based on the X-ray diffraction (XRD) patterns, and the structural and transport properties of V_1−xTi_xSe₂ (0 < x < 1) crystals were studied. The CDW transition for both pure samples, TiSe₂ and VSe₂, is significantly suppressed by doping. The weak localization was observed in bulk VSe₂ and TiSe₂ single crystals, where the weak localization can be modulated by different synthesis conditions. Band structure calculations on a subset of V_1−xTi_xSe₂ compositions are in line with the experimental observations. It is possible to see that the doping with Ti decreases the density of states at the Fermi energy (E_F). This is due to the intrinsically low contributions of Ti d states at the E_F when compared to the V 3d states (21 vs. 73 electrons per eV).

2. Experimental details

The V_1−xTi_xSe₂ (0 < x < 1) single crystal samples studied here were synthesized by a conventional solid-state method. Stoichiometric amounts of V, Ti, and Se powders were weighed, mixed, and loaded into a vacuum-sealed quartz tube. For the V_1−xTi_xSe₂ samples, the evacuated quartz tube was heated to 800 °C with a heating rate of 10 °C min⁻¹ and then kept at this temperature for 25 h. For the TiSe₂ samples, the evacuated quartz tube was heated to 700 °C or 800 °C with a heating rate of 10 °C min⁻¹ and then kept at this temperature for 25 h or 50 h. After that, the samples were slowly cooled to 400 °C for 30 h and 50 h, and then the furnace was shut down. The crystal structures of the samples were characterized by X-ray diffraction (XRD) (Cu Kα radiation). Transport measurements were performed by the standard four-probe technique using a Quantum Design physical properties measurement system. Magnetoresistance (MR) measurements were carried out in the temperature range from 2.0 to 300 K and at magnetic fields up to 8.0 T.

3. Results and discussion

All the V_1−xTi_xSe₂ samples were also prepared by using a solid state reaction. As shown in Fig. 1(a), the structural refinement analysis performed on the V_1−xTi_xSe₂ powdered samples confirmed the compounds to be in a single phase (space group P3̄m1) and have the same hexagonal crystal structure, implying that there were no traces of impurities, interstitial atoms and second phases in them and that there was successful substitution of Ti on V sites in the VSe₂ lattice. When x in V_1−xTi_xSe₂ increases, the (110) peaks shift to smaller 2θ values and the (00l) peaks shift to larger 2θ values, which is consistent with the fact that the lattice parameter a/b gradually increases and the lattice parameter c decreases in the solid solution region, as observed elsewhere. The fact that the lattice parameters track each other so well in the case is because the V_1−xTi_xSe₂ systems are structurally analogous. The lattice parameters a, b, and c as functions of the Ti doping concentration, x, are plotted in Fig. 1(c). The lattice parameters a and b show a linear increase, and c shows a linear decrease with the Ti doping level. The a and b parameters increase from 3.357 Å for x = 0 to 3.539 Å for x = 1, while the c parameter is reduced from 6.106 Å for x = 0 to 6.011 Å for x = 1, respectively. A summary of the refinement parameters, such as the lattice parameters, cell volumes, atomic positions, and R-factors of the V_1−xTi_xSe₂ samples, is listed in Table 1. Fig. 1(b) shows the XRD patterns of the V_1−xTi_xSe₂ (x = 0, 0.05, 0.1, 0.5, 0.6, 0.9, 1) single crystals, with all the diffraction peaks showing a good fit to the (00l) orientation and no other impurity peaks. All these samples have grown along the c-axis and have the same crystal structure.

Fig. 1 (a) Rietveld refinement results for characterization of lattice parameters. X-ray diffraction patterns and refined XRD patterns for all the V_1−xTi_xSe₂ bulks fabricated by a conventional solid-state method. (b) XRD patterns of V_1−xTi_xSe₂ single crystals. (c) Change in the lattice parameters of V_1−xTi_xSe₂ with Ti content x. The solid lines reflect the expected Vegard's law scaling of a, b, and c with x. Inset: the crystal structure of V_1−xTi_xSe₂.

Table 1 Values of the Rietveld refined parameters: lattice parameters, cell volume, atomic positions, and R-factors of the V_1−xTi_xSe₂ (x = 0, 0.05, 0.1, 0.5, 0.6, 0.9, 1) samples. R_p: profile reliability factor; R_wp: weighted profile reliability factor

Parameters		x = 0	x = 0.05	x = 0.1	x = 0.5	x = 0.6	x = 0.9	x = 1
a/b (Å)		3.3572	3.3665	3.3736	3.4645	3.4821	3.5358	3.5394
c (Å)		6.1067	6.0999	6.1005	6.0487	6.0359	6.0182	6.0118
V (Å^3)		59.6045	59.8709	60.1258	62.8304	63.3497	65.1439	65.2299
V/Ti	x	0	0	0	0	0	0	0
	y	0	0	0	0	0	0	0
	z	0	0	0	0	0	0	0
Se	x	0.3333	0.3333	0.3333	0.3333	0.3333	0.3333	0.3333
	y	0.6667	0.6667	0.6667	0.6667	0.6667	0.6667	0.6667
	z	0.2450	0.26009	0.25718	0.26042	0.26024	0.25691	0.2568
R p		5.51	8.32	7.21	5.30	4.87	7.12	5.21
R wp		7.82	10.71	10.63	7.35	7.01	9.60	7.53

---

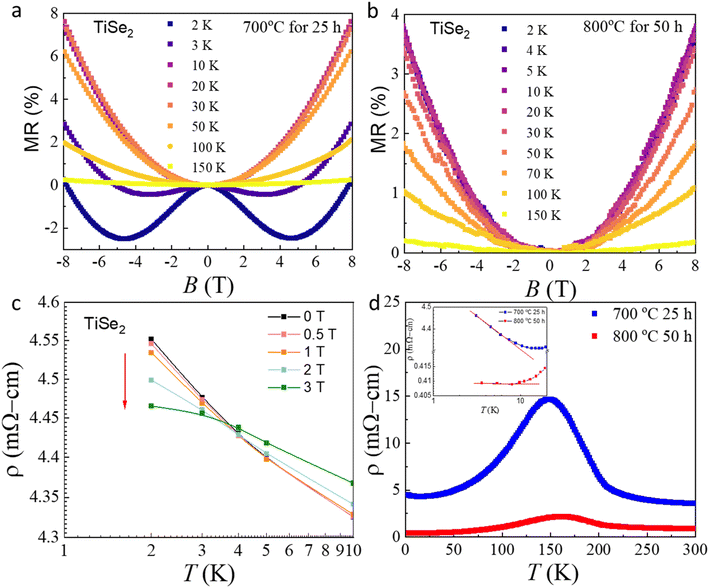
The transverse MR, defined as 100% × [ρ(B) − ρ(0)]/ρ(0), where ρ is the resistivity and B is the magnetic field, of the VSe₂ and TiSe₂ single crystals at different temperatures was measured with the magnetic field parallel to the c-axis. As shown in Fig. 2(a) and 3(a), the magnetoresistance (MR) in VSe₂ and TiSe₂ is very intriguing and extraordinary: it is negative at low fields, with a crossover to a positive MR at higher fields below 6 and 10 K, respectively, while a positive B-parabolic MR can be observed above 6 K and 10 K. The dominant effect here is just the classical MR due to the electrons deviating from the electric field direction because of the Lorentz force, MR α B². As shown in Fig. 2(b) and 3(c), an upturn in resistivity at temperatures below 6 K for VSe₂ and below 10 K for TiSe₂ have appeared, and low-temperature resistivity minima are usually caused by WL, the Kondo effect, or electron–electron interactions. Weak localization is a common physical mechanism that can induce negative magnetoresistance behavior, which generally occurs at small magnetic fields, and is most pronounced at low temperatures as well as perpendicular fields. The negative magnetoresistance due to weak localization is anisotropic and disappears when the magnetic field is parallel to the current direction. The negative magnetoresistance due to the Kondo effect is characterized by isotropy and has no relation to the direction of the magnetic field. This part of the experiment is confirmed in our previous work, ref. 17. The angular (θ) dependence of MR at 2 K was investigated, where θ = 0° corresponds to the magnetic field being perpendicular to the plane of the sample and θ = 90° corresponds to the magnetic field being parallel to the current. The results showed that the negative MR vanishes by tilting the magnetic field from perpendicular to parallel to the current. It is clear that the MR is anisotropic, suggesting that the negative MR is due to a weak-localization effect rather than the Kondo effect. The diffusion channel for electron–electron interference, in which the dominant effect comes from the splitting of the spin states by a magnetic field (or the Zeeman contribution), manifests itself in positive MR.¹⁶ So the electron–electron interactions can be ruled out. In addition, the WL and Kondo effect are sensitive to the field and will be suppressed in an applied magnetic field, while the e–e interactions are generally much less sensitive to the magnetic field. From Fig. 2(b) and 3(c), it is apparent that the resistivity upturn is suppressed by the magnetic field, and therefore, the e–e interactions can be safely ruled out, so the upturn in resistivity at low temperatures originates from the WL. The upturn is a signature of the weak localization effect, which is induced by defects in the VSe₂ and TiSe₂ single crystals.

Fig. 2 (a) Magnetoresistance (MR) measured at different temperatures for VSe₂ single crystals. (b) Logarithmic temperature dependence of the resistivity for VSe₂ single crystals in various fields at low temperature.

Fig. 3 Magnetoresistance (MR) for TiSe₂ single crystals grown at different temperatures and annealing times: (a) 700 °C for 25 h, (b) 800 °C for 50 h. (c) Logarithmic temperature dependence of the resistivity for TiSe₂ single crystals in various fields at low temperature. (d) ρ–T curves of TiSe₂ samples with post-annealing temperatures of 700 °C for 25 h and 800 °C for 50 h. Inset: logarithmic temperature dependence of the resistivity at low temperature. The solid red lines are only a guide to the eyes.

In order to explore weak localization in the TiSe₂ single crystal, we further investigated the defect-induced weak-localization by changing the defect density. As shown in Fig. 3(a) and (b), on changing the post-annealing temperature and time from 700 °C for 25 h to 800 °C for 50 h, followed by slow cooling to 400 °C for 30 h and 50 h, the resistivity of TiSe₂ decreases dramatically, where a larger resistivity (the blue curve) indicates more defects, as shown in Fig. 3(d). The bump in the ρ–T curve of both samples is the typical feature of a charge density wave. For comparison, the single crystal sample grown at 800 °C for 50 h does not show WL behaviour in MR (Fig. 3(b)), and there is no resistivity upturn in ρ–T at low temperature (See the inset in Fig. 3(d)), indicating that the defect-induced nature of the WL is further proved by the experimental results of the lower defect density.

Fig. 4(a) shows the ρ–T curves of samples with different Ti doping levels. The anomalies in the resistivity at 108 K and 175 K for VSe₂ and TiSe₂, respectively, are induced by the charge density wave transition, which is consistent with previous reports.^5,21,22 The resistance of a sample with any Ti doping level decreases as the temperature is reduced, indicating metallic behaviour. As with the lattice parameters, the resistivity also shows a systematic increase as the Ti doping level increases. In Fig. 4(b), the ρ–T curves are normalized by dividing by ρ (300 K). Despite the anomalous resistivity induced by the charge density wave transition, the resistivity of each sample shows an overall linear relationship with temperature. The linear portion of the resistivity is contributed by phonon scattering, which increases linearly with temperature. At low temperature, the phonon degrees of freedom are frozen. The contribution from impurity (and defect) scattering dominates in the ρ–T curves. The slope (dρ*/dT) and intercept (ρ₀) of each curve are plotted in Fig. 4(c), to reflect the relative strength of phonon scattering and defect scattering, respectively. The indicator of phonon scattering (dρ*/dT) is larger in pure VSe₂ and TiSe₂, and smaller in the doped samples. In contrast, the indicator of impurity scattering (ρ₀) is smaller in pure VSe₂ and TiSe₂, and larger in the doped samples. The smallest dρ*/dT and largest ρ₀ occurred in the V_0.5Ti_0.5Se₂ sample, indicating that it has the largest component of impurity scattering. This is consistent with the substitutional doping. In addition, Fig. 4(d) also displays the carrier density of VSe₂, V_0.5Ti_0.5Se₂, and TiSe₂ single crystals at various temperatures, respectively.

Fig. 4 Resistivity of V_1−xTi_xSe₂ single crystals. (a) The temperature dependence of the resistivity (ρ) for V_1−xTi_xSe₂. Inset: The ρ–T (black line: left axis) and dρ/dT–T (red line: right axis) curves for a VSe₂ single crystal. (b) The resistivity normalized to room temperature value for V_1−xTi_xSe₂. (c) Plots of the slope (dρ*/dT), where ρ* is ρ normalized by its 300 K value, and the intercept (ρ₀) of each curve. (d) The electron concentration (n) of the VSe₂, V_0.5Ti_0.5Se₂, and TiSe₂ single crystals as a function of temperature.

The density of state calculations performed in Fig. 5(a–n) show clearly that firstly the density of states at the Fermi energy for VSe₂ is significantly higher than the density of states of TiSe₂. Indicating a lower carrier concentration for TiSe₂, this matches our experimental results in Fig. 4. Secondly, a gradual decrease in the density of states at the Fermi energy is seen from Fig. 5(a–h); looking at the partial contributions we can see that the contributions are a result of the d orbitals from the V ion. The projected partial orbitals for Fig. 5(b) for VSe₂ show the orbitals are a majority dominated by V d_z² orbitals with other contributions in the order of greatest to lowest from d_xy, d_xz, d_x²−y², Se p orbitals(mostly from p_x and p_y) and d_yz. The majority contribution coming from the V d_z² decreases significantly in Fig. 5(d), (f) and (h) and is substituted by contributions from Ti d_z², but as we can see from the projected partial orbitals in TiSe₂ in Fig. 5(n) although the majority contribution still comes from the Ti d_z² orbitals the band has shifted to a higher energy and as a result, the overall contribution has decreased, hence as we increase the doping of Ti ions we are substituting the d orbitals of the V ion for smaller contributions of the d orbitals for the Ti ions decreasing the overall density of states as seen in Fig. 5(i)–(l).

Fig. 5 The partial density of states of the supercells (left column), and the vanadium and/or titanium orbital contributions (right column) of (a and b) pure VSe₂, (c and d) V_0.96Ti_0.04Se₂, (e and f) V_0.8Ti_0.2Se₂, (g and h) V_0.52Ti_0.48Se₂, (i and j) V_0.2Ti_0.8Se₂, (k and l)V_0.04Ti_0.96Se₂, and (m and n)pure TiSe₂.

Computational details: in this work, first-principles density functional theory (DFT) calculations^23,24 are performed using the Vienna Ab initio Simulation Package (VASP),²⁵ which incorporates the use of a plane-wave basis set. The external potential is given by the projector augmented-wave approximation.²⁶ The exchange correlation functional used to describe the exchange–correlation interactions was the general gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) formulation,²⁷ and a van der Waals (vdW) correction (DFT-D) as implemented by Grimme was added.²⁸ Energy calculations were performed with energy cut-off of 500 eV and a 5 × 5 × 11 Monkhorst pack k-point mesh to sample the Brillouin zone with a reciprocal spacing of 0.03 Å⁻¹. Our calculation results are from a 5 × 5 × 1 doped supercell, with the lattice parameters varied consistent with our XRD results. These lattices parameters are a = 3.3583 and c = 6.10902 Å for pure VSe₂, a = 3.38833 and c = 6.08146 Å for V_0.8Ti_0.2Se₂, a = 3.45831 and c = 6.04873 Å for V_0.5Ti_0.5Se₂, a = 3.51818 and c = 6.01938 Å for V_0.2Ti_0.8Se₂, and a = 3.53049 and c = 6.00935 Å for V_0.05Ti_0.95Se₂.

4. Conclusions

In conclusion, this work reports the weak localization in VSe₂ and TiSe₂ single crystals, and that the weak localization can be controlled by different growth conditions. The crystal structure and electrical properties and the band structure of a series of V_1−xTi_xSe₂ single crystals are systematically reported. The CDW transition for both pure samples, TiSe₂ and VSe₂, is significantly suppressed by doping. Band structure calculations on a subset of V_1−xTi_xSe₂ compositions are in line with the experimental observations.

Data availability

All the data have been presented in the article or file of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge support from the Australian Research Council (ARC) through the ARC Centre of Excellence in Future Low-Energy Electronics Technologies (FLEET, CE170100039) and the NCI Australia. Xiaolin Wang acknowledges support from an ARC Professorial Future Fellowship project (FT130100778). Zhi Li acknowledges support from ARC Discovery Projects (DE190100219, DP160101474, DP170104116, FT210100844). Lina Sang acknowledges support from The National Natural Science Foundation of China (52302339).

References

1. E. Morosan, H. W. Zandbergen, B. Dennis, J. Bos, Y. Onose, T. Klimczuk, A. Ramirez, N. P. Ong and R. J. Cava, Nat. Phys., 2006, 2, 544–550.
2. A. F. Kusmartseva, B. Sipos, H. Berger, L. Forro and E. Tutiš, Phys. Rev. Lett., 2009, 103, 236401.
3. E. Sajadi, T. Palomaki, Z. Fei, W. Zhao, P. Bement, C. Olsen, S. Luescher, X. Xu, J. A. Folk and D. H. Cobden, Science, 2018, 362, 922–925.
4. P. Huang, P. Zhang, S. Xu, H. Wang, X. Zhang and H. Zhang, Nanoscale, 2020, 12, 2309–2327.
5. J. S. Chen, J. K. Wang, S. V. Carr, S. C. Vogel, O. Gourdon, P. Dai and E. Morosan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045125.
6. M.-L. Mottas, T. Jaouen, B. Hildebrand, M. Rumo, F. Vanini, E. Razzoli, E. Giannini, C. Barreteau, D. Bowler and C. Monney, Phys. Rev. B, 2019, 99, 155103.
7. J. Yang, W. Wang, Y. Liu, H. Du, W. Ning, G. Zheng, C. Jin, Y. Han, N. Wang and Z. Yang, Appl. Phys. Lett., 2014, 105, 063109.
8. Y. I. Joe, X. Chen, P. Ghaemi, K. Finkelstein, G. de La Peña, Y. Gan, J. Lee, S. Yuan, J. Geck and G. MacDougall, Nat. Phys., 2014, 10, 421–425.
9. W. Yu, J. Li, T. S. Herng, Z. Wang, X. Zhao, X. Chi, W. Fu, I. Abdelwahab, J. Zhou and J. Dan, Adv. Mater., 2019, 31, 1903779.
10. S. Lee, J. Kim, Y. C. Park and S.-H. Chun, Nanoscale, 2019, 11, 431–436.
11. M. D. Watson, O. J. Clark, F. Mazzola, I. Marković, V. Sunko, T. K. Kim, K. Rossnagel and P. King, Phys. Rev. Lett., 2019, 122, 076404.
12. F. Di Salvo Jr, D. E. Moncton and J. V. Waszczak, Phys. Rev. B: Solid State, 1976, 14, 4321.
13. M. Bayard and M. Sienko, Anomalous, J. Solid State Chem., 1976, 19, 325.
14. A. H. Thompson and B. G. Silbernagel, Correlated, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 3420.
15. J. Yang, et al. , Appl. Phys. Lett., 2014, 105, 063109.
16. Q. Cao, F. F. Yun, L. Sang, F. Xiang, G. Liu and X. Wang, Nanotechnology, 2017, 28, 475703.
17. J. M. Moya, C. L. Huang, J. Choe, G. Costin, M. S. Foster and E. Morosan, Phys. Rev. Mater., 2017, 3, 084005.
18. M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289.
19. S. Barua, M. C. Hatnean, M. R. Lees and G. Balakrishnan, Sci. Rep., 2017, 7, 10964.
20. M. Sasaki, A. Ohnishi, T. Kikuchi, M. Kitaura, K.-S. Kim and H.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 224416.
21. F. J. Di Salvo, D. Moncton and J. Waszczak, Phys. Rev. B: Solid State, 1976, 14, 4321.
22. K. Terashima, T. Sato, H. Komatsu, T. Takahashi, N. Maeda and K. Hayashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 155108.
23. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
24. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
26. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
28. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta03663h

---