Optical study of Te₈ ring clusters: comparison with density functional theory and a step towards materials design using nanoporous zeolite space

Abstract

The Te₈ ring molecule (cluster) is poorly investigated due to the lack of experimental data. Here, we report an experimental and theoretical study of a regular array of oriented Te₈ rings formed in the ∼1.14 nm diameter cavities of zeolite LTA, which are arranged in a cubic lattice with a spacing of ∼1.2 nm. Single crystals of LTA with encapsulated tellurium (LTA-Te) were studied using Raman spectroscopy (RS) and optical absorption spectroscopy (OAS). The experimental LTA-Te spectra were found to be in agreement with those calculated using density functional theory (PBE0 hybrid functional and def2-TZVP basis sets) for the crown-shaped Te₈ ring molecule with D_4d symmetry. Using polarization–orientation RS, we show that the Te₈ rings are oriented by their major axes along the 4-fold axes of cubic LTA. We also show that the site symmetry of Te₈ in LTA-Te is lower than D_4d. Te₈ bond-bending modes are well described in the harmonic approximation, while bond-stretching modes are mixed due to the reduced ring symmetry and, probably, anharmonicity. Importantly, OAS data of LTA-Te display dependence on the Te₈ concentration, implying the interaction of the rings from neighbouring LTA cavities with the generation of the valence and conduction electron bands of such a cluster crystal.

---

Introduction

Tellurium (Te) belongs to the same group of the periodic table as oxygen (O), sulphur (S) and selenium (Se). Since its discovery at the end of the 18^th century, Te was widely used in metal alloys. Nowadays, Te and its compounds have become a real frontier of science and technology. They have found important applications in electronics, optoelectronics, photonics, phase-change materials, topological insulators, Li–Te batteries, thermoelectrics and solar cells.^1–6 However, elemental Te is mainly known in its chain form analogous to crystalline trigonal tellurium (t-Te) while it is nearly unknown in the ring form.

Zeolites provide a unique opportunity to form and accommodate uniform guest species in their cavities/channels where the species are oriented due to the crystalline nature of zeolites.^7–13 For example, only zeolites allowed obtaining polarized Raman spectra (RS) and optical absorption spectra (OAS) of isolated Te chains and rings.^7–11 Moreover, fabrication of such regular high-density Te species arrays can be considered as an important direction in the development of new functional materials, so-called cluster crystals.^14–16

Here, we study Te₈ rings regularly arranged in the large cavities of zeolite LTA. Importantly, we are using the polarization–orientation RS examination of zeolite single crystals. On one hand, this method can be considered as an alternative to X-ray diffraction (XRD) for the structural study of zeolite-confined clusters. On the other hand, it provides very useful information about the cluster properties and their interaction with zeolites. We also study the OAS spectra of Te₈ and demonstrate the effect of the interaction between Te₈ rings in neighboring cavities, which is important for the fabrication of real cluster crystals.

The idea of Te₈ ring formation in LTA cavities was proposed in ref. 17 where the only observed RS feature at ∼168 cm⁻¹ was assigned to the ring with an argument that its frequency is different from the dominant trigonal tellurium (t-Te) band frequency at ∼120.5 cm⁻¹.^18,19 However, this observation was not confirmed later. In ref. 20, the RS of LTA-Te microcrystalline powder was re-examined. A strong band at ∼182 cm⁻¹ and a weaker one at ∼45 cm⁻¹ were observed and attributed rather to Te₁₂ than to Te₈ since Te₈ requires a relatively strong symmetric bond-bending mode band at around 60 cm⁻¹, which was not clearly detected due to laser-induced band broadening, as was found later. The LTA-Te band at ∼62 cm⁻¹ accompanied by ∼182 cm⁻¹ and ∼45 cm⁻¹ bands was observed in ref. 21. This was a rather strong argument in favor of Te₈ ring formation in LTA cavities. The observed bands at ∼45, ∼62 and ∼182 cm⁻¹ look similar to the bending E₂ and A₁ mode bands and stretching A₁ mode bands of S₈ (∼153, ∼222, ∼480 cm⁻¹) and Se₈ (∼76, 111, 267 cm⁻¹) rings.²¹ The RS of another zeolite AFI with encapsulated tellurium (AFI-Te) showed similar bands at 41–47 cm⁻¹, 65 cm⁻¹ and 184 cm⁻¹.⁷ The bands were attributed to the Te₈ ring. However, no polarized RS study of LTA-Te single crystals has been performed yet, which could provide crucial evidence for Te₈ ring formation. Here, we present this evidence. Importantly, no other species but Te₈ was found in LTA-Te. This is beneficial for realizing the idea of cluster crystal formation.

Experimental and theoretical methods

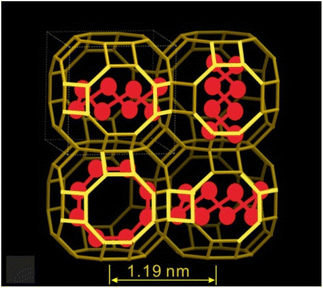
Synthetic zeolite LTA with the composition Na₁₂Al₁₂Si₁₂O₄₈ was used in this work. The crystal growth procedure for LTA is described in ref. 22. The sizes of the cubic LTA crystals were ∼20 μm along the edge of the cube. LTA has nearly spherical-shaped large cavities with a diameter of ∼1.14 nm, which are connected through narrow windows of ∼0.42 nm diameter (Fig. 1). The LTA cavities are arranged in a simple cubic lattice. The zeolite structures are accessible at the International Zeolite Association website https://www.iza-structure.org/IZA-SC/ftc_table.php.

Fig. 1 Schematic view of the LTA framework with Te₈ rings in large cavities.

Dehydration of zeolites in a vacuum was performed in Pyrex ampoules for several hours at t ∼ 550 °C. The design of the ampoules made it possible to add crystalline Te powder to the zeolite after dehydration without exposing the dehydrated samples to air. The subsequent adsorption of the Te vapour was carried out at t ∼ 550 °C for a few days until the brownish colour of the sample was saturated.

RS spectra of the LTA-Te single crystals were studied using a Renishaw micro-Raman spectrometer equipped with Semrock edge-filters and an Olympus micro-objective lens allowing an ∼1 μm focused laser probe size. A 633 nm wavelength line of the He–Ne laser and a 785 nm line of the light-emitting diode laser were used for RS excitation. Weak absorption of Te₈ at these wavelengths is beneficial for Te₈ compared to the non-absorbing LTA matrix for obtaining the cluster Raman signal with nearly no contribution of LTA. An additional measurement with 561 nm laser diode line excitation was performed using a Nanofinder-30 Raman/AFM system (Tokyo Instruments Inc.) specially designed for the maximal RS detection sensitivity around this wavelength, which allowed LTA-Te Raman measurement at relatively high Te₈ absorption and very low laser excitation power in order not to strongly heat or destroy the clusters. Moreover, a Nanofinder-30 (Tokyo Instruments Inc.) was equipped with a set of three volume Bragg grating notch filters (OptiGrate Co), allowing the detection of the Raman signal with frequencies down to ∼6 cm⁻¹. UV-visible OAS was performed using a Carl Zeiss micro-optical spectrometer with a light probe size of ∼5 μm. The samples were intentionally broken to minimize their optical density in the ultraviolet (UV) spectral range and placed in glycerol between two cover glasses to minimize surface light scattering.

The Te₈ RS, infrared (IR) spectra and OAS were simulated using density functional theory (DFT).^23–26 The structure and vibrational frequencies of Te₈ were computed using the hybrid PBE0 exchange–correlation functional²⁶ and the resolution-of-identity approximation for the Coulomb part (RI-J).²⁷ The def2-TZVP basis sets²⁸ together with the corresponding auxiliary basis sets²⁹ and small-core effective core potentials (ECPs)³⁰ were employed for Te. RS intensities were obtained in the double harmonic approximation using analytical derivatives of static electronic polarizabilities³¹ and analytical energy Hessians.^32,33 Calculations of static polarizability derivatives used the PBE0 functional and augmented def2-TZVPD basis sets.³⁴ IR spectra were computed in the double harmonic approximation from the analytical dipole and energy Hessians.^32,33 The vibrational frequencies were not scaled in this work. OAS was performed with time-dependent DFT (TDDFT)³⁵ using the PBE0 functional with the RI-J approximation³⁶ and def2-TZVPD basis sets. All calculations were performed with the Turbomole program package, version 7.5.^23,37

Structure and Raman and absorption spectra of single Te₈ rings via DFT calculations

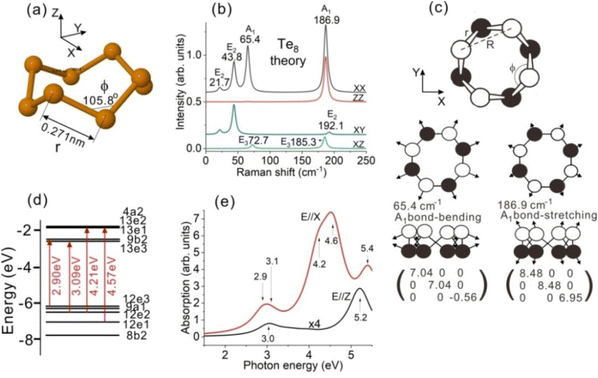
The calculated Te₈ (D_4d point group symmetry) ring structure is shown in Fig. 2(a). The bond length of Te₈ is r = 0.271 nm and the second neighbour distance is R = 0.432 nm, while its bond and dihedral angles are 105.8° and 101.2°, respectively. The obtained structure parameters are in agreement with previous DFT calculations.^38–42 The ring Z axis is directed along its 4-fold axis, while the X and Y axes lie in the molecule plane normal to the Z axis (Fig. 2(a)).

Fig. 2 Te₈ ring with the bond length r and angle ϕ (a); calculated Raman spectra of a single free-standing Te₈ ring for XX, ZZ, XY and XZ polarization configurations (b); Te₈ atomic displacements for A₁ bond-bending and A₁ bond-stretching modes with corresponding Raman tensors (c); Te₈ MO diagram with dominant MO contributions to the strongest optical transitions shown in red, all for E//X (d); and calculated Te₈ OAS including transitions with photon energies of <5.5 eV (e).

Theoretical point group analysis for the vibration modes of Te₈ is similar to that made for the S₈ molecule with a similar crown shape.⁴³ The Te₈ vibration irreducible representations (symmetries) with calculated frequencies and IR/Raman activities are shown in Table 1. The E₁ symmetry corresponds to the IR activity for the light polarized in the ring plane (E//X or E//Y), while the B₂ symmetry corresponds to the E//Z IR activity. Calculated Te₈ Raman intensities for different polarization configurations are equal to their squared Raman tensor components (XX, ZZ, XY, XZ) for each mode, which are determined by the corresponding atomic displacements and related molecular polarizability derivatives. The corresponding values in Table 1 are given in atomic units of 10⁻²e²a₀/E_h, where e, a₀ and E_h are the electron charge, Bohr radius and Hartree energy, respectively.

Table 1 Te₈ normal vibrations: symmetries, computed frequencies, IR intensities and Raman activities

Symmetry	Frequency (cm^−1)	IR intensity (km mol^−1)	Raman activity XX	Raman activity ZZ	Raman activity XY	Raman activity XZ
E2	21.7	0	−0.49	0	−2.08	0
	21.7	0	−2.08	0	0.49	0
E2	43.8	0	−4.38	0	−3.36	0
	43.8	0	3.36	0	−4.38	0
E1	56.9	0.524	0	0	0	0
	56.9	0.524	0	0	0	0
A1	65.4	0	−7.04	0.56	0	0
B2	68.6	0.128	0	0	0	0
E3	72.7	0	0	0	0	−1.86
	72.7	0	0	0	0	−0.86
B1	179.9	0	0	0	0	0
E3	185.3	0	0	0	0	−3.54
	185.3	0	0	0	0	−0.17
A1	186.9	0	−8.48	−6.95	0	0
E1	188.1	1.29	0	0	0	0
	188.1	1.29	0	0	0	0
E2	192.1	0	1.21	0	−1.05	0
	192.1	0	−1.05	0	−1.21	0

---

The calculated RS spectra of Te₈ for different polarization configurations, corresponding to the Raman tensor components from Table 1, are shown in Fig. 2(b). Raman bands are represented as Lorentz curves with the amplitudes corresponding to the calculated Raman activities and half-widths of 5 cm⁻¹ for all bands.

The dominant band in the calculated RS spectra of Te₈, displaying comparable XX and ZZ activities, corresponds to the A₁ symmetric bond-stretching mode at a frequency of 186.9 cm⁻¹. In contrast, the A₁ bond-bending mode at 65.4 cm⁻¹ displays high XX activity and nearly negligible ZZ activity. Fig. 2(c) shows atomic displacements and Raman tensors of these two A₁ modes, which explain the difference in their ZZ activities. One can consider the A₁ bond-stretching as a breathing mode since both in-plane and off-plane Te₈ dimensions expand and contract the in-phase, while the A₁ bond bending mode is an important instrument for Te₈ ring orientation determination.

The E₂ bond-bending mode at 43.8 cm⁻¹ is rather active in the XX and XY configurations, while inactive in the ZZ configuration. Similar but weaker activity is displayed by the E₂ torsion and stretching modes at 21.7 cm⁻¹ and 192.1 cm⁻¹, respectively. The E₃ bond-bending mode at 72.7 cm⁻¹ and the bond-stretching mode at 185.3 cm⁻¹ dominate in the XZ configuration spectrum.

In addition to the Te₈ Raman-active modes, there are several inactive modes: E₁ bond-bending at 56.9 cm⁻¹, B₂ bond-bending at 68.6 cm⁻¹, B₁ bond stretching at 179.9 cm⁻¹ and E₁ bond stretching at 188.1 cm⁻¹, which can become active when the ring D_4d symmetry is reduced. As we mentioned above, the E₁ and B₂ modes are IR-active.

The calculated partial molecular orbital (MO) diagram of Te₈ including the highest occupied MOs and the lowest unoccupied MOs is presented in Fig. 2(d). These MOs consist of combinations of Te 5p orbitals, as determined by Mulliken population analysis. The occupied orbitals correspond to Te lone pairs, while the unoccupied orbitals have antibonding character with respect to Te–Te bonds. The largest MO contributions to the allowed electronic transitions with photon energies <4 eV and the largest oscillator strengths are shown in red. It should be noted that the electron transition energies take into account excitonic effects. Therefore, the transition energies are less than the orbital energy differences of the dominant MO contributions. All these four transitions have E₁ symmetry, implying the polarization of light E//X.

There are also E//Z-allowed transitions of B₂ symmetry. However, their oscillator strengths appeared to be much lower than those of the strongest E//X transitions (Table 2). The calculated OAS spectra of Te₈ for polarizations of light E//X and E//Z are shown in Fig. 2(e). Allowed electronic transitions (E₁ for E//X and B₂ for E//Z) with photon energies of up to 5.5 eV were computed. Due to the difference in the oscillator strengths, the E//X absorption is stronger than the E//Z one. The E//X absorption is mainly represented by transitions at photon energies of ∼2.9, ∼3.1, ∼4.2, ∼4.6 and ∼5.4 eV, while the E//Z one is determined by transitions at photon energies of ∼3, ∼3.6, ∼4 and ∼5.2 eV. The corresponding absorption bands are approximated by the Lorentz curves with half-widths of ∼0.6 eV.

Table 2 Computed dipole-allowed electron transitions of Te₈

Symmetry	Photon energy (eV)	Oscillator strength
E1	2.90	0.104
B2	3.03	0.016
E1	3.09	0.053
B2	3.45	0.003
E1	3.53	0.001
B2	3.61	0.003
E1	3.89	0.012
B2	3.96	0.004
E1	4.11	0.006
E1	4.21	0.357
E1	4.35	0.002
E1	4.57	0.525
B2	5.21	0.071
E1	5.42	0.333
B2	5.77	0.008
E1	5.82	0.229
B2	5.94	0.002

---

Experimental polarized Raman spectra of LTA-Te single crystals

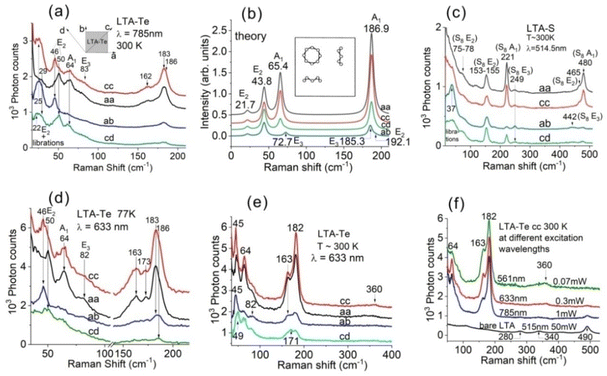
Using Te vapor adsorption, we obtained LTA-Te samples with Te loading densities of ∼3 and ∼8 atoms per cavity (at. per cav.). Unlike the RS of LTA-Se with different loading densities showing changes in the Se₈/Se₁₂ intensity ratio,⁴⁴ LTA-Te RS spectra did not show any qualitative dependence on the Te loading density except an increase in the Raman signal of the same bands with an increase in the Te density. This is a strong argument in favour of the formation of only one stable Te cluster in the LTA cavities.

RS spectra of LTA-Te with a loading density of ∼8 at. per cav. at an excitation wavelength of 785 nm are shown in Fig. 3(a). We performed measurements in four different polarization configurations: aa, cc, ab and cd (see the inset in Fig. 3(a)) similar to the polarization–orientation Raman study of LTA with sulphur LTA-S¹² and LTA with selenium LTA-Se.^12,44,45 Experimentally, we rotated the LTA-Te crystals in the ab plane with incident and scattered light polarizations (1) parallel and (2) perpendicular to each other. The procedure was described in detail earlier.¹² Theoretical RS spectra of LTA-Te for the aa, cc, ab and cd polarization configurations were obtained via summation of the Raman responses of three Te₈ rings in their three possible orientations in LTA crystals [Fig. 3(b)].

Fig. 3 LTA-Te Raman spectra of aa, cc, ab and cd polarization configurations at room temperature and 785 nm wavelength excitation with the inset schematically showing LTA-Te cubic crystals and the a, b, c and d axes (a); summation of the calculated Raman spectra of three Te₈ orientations in LTA (see the inset) for aa, cc, ab and cd polarization configurations (b); LTA-S Raman spectra of aa, cc, ab and cd polarization configurations (c); LTA-Te Raman spectra of aa, cc, ab and cd polarization configurations at T ∼ 77 K and 633 nm wavelength excitation (d); LTA-Te Raman spectra of aa, cc, ab and cd polarization configurations at room temperature and 633 nm wavelength excitation (e); and LTA-Te Raman spectra of the cc polarization configuration at different excitation wavelengths with the unpolarized spectrum of bare LTA (black curve) (f).

The experimental LTA-Te RS spectra display rather good correspondence with the calculated ones. Indeed, the bands at 162 cm⁻¹ and 183 cm⁻¹ can be assigned to the Te₈ E₃ and A₁ bond-stretching modes similar to the 442 cm⁻¹ and 480 cm⁻¹ bands of S₈ in LTA-S [Fig. 3(c)]. The correspondence between the experiment and theory looks especially good for the A₁ mode frequency (experimental: ∼183 cm⁻¹vs. theoretical: 186.9 cm⁻¹) and intensity (the strongest band in the spectrum). At first glance, the polarization dependence of its intensity also looks reasonable: the band is strong in aa and cc polarization configurations, while it is weak in ab and cd configurations as expected for the A₁ modes. Actually, as we have shown below, the situation is more complicated for the bond stretching modes due to a possible mode mixing effect but, in a rough approximation, the assignment of the 183 cm⁻¹ band to the A₁ bond-stretching mode looks reasonable.

Polarization dependencies of the LTA-Te bands in the Te₈ bond-bending mode region appear to be qualitatively similar to those of the bond-bending modes of S₈ ¹² [Fig. 3(c)] and Se₈ ^12,44,45 rings in LTA. Indeed, the 46–50 cm⁻¹ band polarization–orientation dependence is similar to that of the E₂ band at 74–76 cm⁻¹ or 77–79 cm⁻¹ of Se₈ ⁴⁵ and the E₂ band at 153–155 cm⁻¹ of S₈ [Fig. 3(c)]. The calculated Te₈ E₂ bond-bending mode frequency of 43.8 cm⁻¹ is in good agreement with the observed 46–50 cm⁻¹ band frequencies of LTA-Te. The splitting of the degenerate E₂ mode indicates structural distortion of Te₈ in LTA and therefore a reduced symmetry compared to the initial D_4d symmetry of the ring. For example, a slight reduction of the Te₈ symmetry from D_4d to C_4v would split the E₂ mode into B₁ and B₂ modes, active in XX and XY polarization configurations, respectively. This is exactly what we experimentally observed. Interestingly, the splitting of the Te₈ E₂ mode in LTA is very strong, ∼8.3%, in contrast to the weaker splitting of the corresponding E₂ modes of S₈, ∼ 1.3%, and Se₈, ∼ 2.6%.

The LTA-Te 64 cm⁻¹ band displays polarization dependence similar to the A₁ symmetric bond-bending mode band of S₈ at ∼221 cm⁻¹ [Fig. 3(c)] and the analogous band of Se₈ at ∼112 cm⁻¹.^12,44,45 The frequency of 64 cm⁻¹ is very close to the calculated frequency of 65.4 cm⁻¹ of the Te₈ A₁ bond-bending mode [Fig. 2(b); 3(b)]. The experimental 64 cm⁻¹ band is rather strong in the aa and cc polarization configurations and it is still not weak in the cd configuration, while the band completely disappears in the ab configuration. This is a consequence of the 2-dimensional character of the Raman tensor of this mode with only two strong diagonal tensor components in contrast to the rather 3-dimensional tensor of the A₁ bond-stretching mode [Fig. 2(c)]. Correspondingly, the single free-standing Te₈ A₁ bond-bending mode band is strong in the XX polarization configuration and negligibly weak in the ZZ configuration with the zero XY and XZ activities [Fig. 2(b)]. Theoretical calculation of this mode activity in the RS spectra of LTA-Te [Fig. 3(b)] is also in very good agreement with the experiment, namely high aa activity and no ab activity. This is a clear indication of the orientation of the Te₈ 4-fold axis along the 4-fold axis of LTA.

The experimental LTA-Te ∼ 83 cm⁻¹ band looks similar to the 248 cm⁻¹ E₃ bond-bending mode band of S₈ [Fig. 3(c)]. It can be attributed to the E₃ bond-bending mode of Te₈ with a calculated frequency of 72.7 cm⁻¹. The ∼29 cm⁻¹ band of LTA-Te can be attributed to the E₂ torsional mode of Te₈ with a calculated frequency of 21.7 cm⁻¹. A broad ∼25 cm⁻¹ band, probably, originates from the superposition of the second component of the E₂ torsional mode and the ring librations in the LTA cavity.

As we mentioned above, the bands of LTA-Te in the bond-stretching mode region require more detailed consideration. Fig. 3(d) shows LTA-Te RS in this region taken at temperature T ∼ 77 K and an excitation wavelength of 633 nm with better resolved bands due to their temperature-induced narrowing. Fig. 3(e) shows room temperature LTA-Te RS at the same excitation wavelength in a wider spectral range. Four bands at ∼163 cm⁻¹, ∼173 cm⁻¹, and ∼183 cm⁻¹ and its shoulder at ∼186 cm⁻¹ can be observed in Fig. 3(d). The shoulder is, probably, associated with the Te₈ E₂ bond-stretching mode (theoretical frequency of ∼192 cm⁻¹). Taking into account our preliminary assignment of the 182–183 cm⁻¹ and 162–163 cm⁻¹ bands to the Te₈ A₁ and E₃ modes, respectively, we have to attribute the 171–173 cm⁻¹ band to the forbidden B₁ (theoretical frequency of ∼180 cm⁻¹) mode which can be activated due to the reduced symmetry of Te₈ in the LTA cavity, and we found that the bands in the bond-stretching mode region can be mixed.

The band at 182–183 cm⁻¹ shows slightly stronger activity in the cc polarization configuration than that in the aa configuration, which is clearly seen in the room temperature RS of LTA-Te obtained by excitation with 633 nm light, as shown in Fig. 3(e). This can be associated with the mode mixing due to the reduced symmetry of the Te₈ rings. Interestingly, the 2^nd order Raman band of Te₈ can be recognized in the cc configuration spectrum at ∼360 cm⁻¹ [Fig. 3(e)]. An even stronger 2^nd order Raman band can be clearly seen at an excitation wavelength of 561 nm [Fig. 3(f), green curve] due to the resonant Raman enhancement. The band is very broad covering the spectral range from ∼300 cm⁻¹ to ∼375 cm⁻¹. Importantly, LTA bands do not contribute to the 2^nd order Raman band of Te₈ since even the strongest LTA band at ∼490 cm⁻¹ [Fig. 3(f), black curve] does not contribute to LTA-Te RS obtained by excitation with 561 nm light.

Summarizing this section, the polarization dependence of the A₁ bond-bending mode Raman band of Te₈ indicates the orientation of the ring by its 4-fold axis along the LTA 4-fold axis, while that of the E₂ bond-bending mode suggests a noticeable symmetry reduction of the ring from the ideal D_4d point group symmetry. Te₈ bond-stretching modes are mixed due to the ring symmetry reduction. The Raman bands at 162–163 cm⁻¹ and 171–173 cm⁻¹, probably, originate from the E₃ mode and formerly inactive B₁ mode while the Raman bands at 182–183 cm⁻¹ and 186 cm⁻¹ originate from the A₁ and E₂ modes of Te₈. The originally inactive E₁ bond-stretching mode may also contribute to the observed Raman bands.

Optical absorption spectra of LTA-Te single crystals

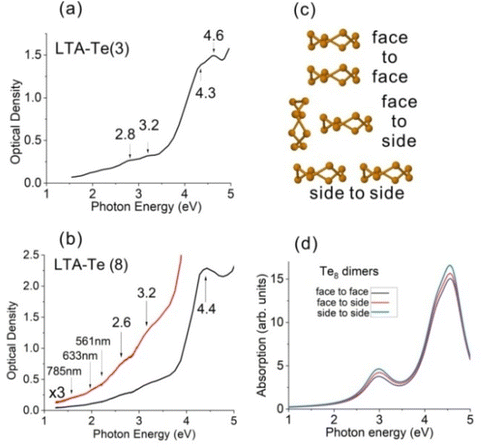
Fig. 4(a and b) show the OAS of LTA-Te with the loading densities of ∼3 atoms per cavity [LTA-Te(3)] and ∼8 atoms per cavity [LTA-Te(8)]. Absorption bands at ∼2.8 eV, 3.2 eV, 4.3 eV and 4.6 eV are observed in the OAS of LTA-Te(3), while absorption bands at ∼2.6 eV, 3.2 eV and 4.4 eV are observed in the OAS of LTA-Te(8). The spectra indicate that the energy band gap decreases when the Te loading density increases. Moreover, LTA-Te(8) bands look slightly broader than those of LTA-Te(3). In particular, the absorption band doublet at ∼4.3 eV and 4.6 eV, resolved in LTA-Te(3), looks like a single band at ∼4.4 eV.

Fig. 4 Experimental absorption spectra of LTA-Te(3) (a) and LTA-Te(8) (b); three Te₈ dimers considered for the calculation of the effect of ring interaction on the absorption spectrum (c); and calculated absorption spectra of the considered Te₈ dimers including transitions with photon energies of <5 eV (d).

First, the observed experimental OAS spectra of LTA-Te [Fig. 4(a and b)] appeared to be in nearly perfect agreement with the theoretical OAS spectra of Te₈ [Fig. 2(e)]. The agreement with theoretical OAS for a single Te₈ ring is especially good for LTA-Te(3) with approximately two rings per five cavities. We have to note that surface light scattering, which increases with the photon energy, contributes to the experimental spectra. In contrast, theoretical spectra do not include this effect and do not include high-energy transitions (>5.5 eV in Fig. 2(e)). This may produce an impression that the experimental and theoretical spectra are different. However, actually, they are very similar.

Secondly, differences between the OAS of LTA-Te(3) and LTA-Te(8) indicate a noticeable interaction between the Te₈ rings in neighbouring LTA cavities, in particular, for LTA-Te(8) with one ring per cavity. In Fig. 4(b), we show the spectral positions of the Raman excitation laser lines, clearly indicating rather strong absorption of LTA-Te(8) at a wavelength of 561 nm corresponding to the resonant Raman effect [Fig. 3(f)]. To avoid laser-induced heating/destruction of Te₈, we used a very low 561 nm laser power of ∼0.07 mW. At weaker LTA-Te absorption corresponding to wavelengths of 785 nm and 633 nm [Fig. 4(b)], we were able to use higher laser powers of ∼1 mW and ∼0.3 mW, respectively [Fig. 3(f)].

In order to examine a possible effect of the ring interaction on the OAS spectrum of LTA-Te, we theoretically considered three possible Te₈ ring dimers with a separation of ∼1.2 nm between the ring centres [Fig. 4(c)]. The corresponding calculated dimer OAS spectra are shown in Fig. 4(d). The effect of the ring interaction is indicated by the absorption enhancement with an increase in the ring interaction, which is the weakest in the “face-to-face” configuration and the strongest in the “side-to-side” configuration. Due to the inter-ring interaction, the unoccupied MOs of the Te₈ rings organize conduction bands of the LTA-Te cluster crystals, while the highest occupied MOs organize its valence band. The conduction and valence bands should be rather narrow. Therefore, a variety of non-linear electric conductance effects predicted for narrow semiconductor superlattice mini-bands⁴⁶ can be expected in the LTA-Te electric properties. A negative differential electric resistance of LTA-Te observed in ref. 47 confirms this.

Te₈ interaction with LTA and its librations vs. temperature

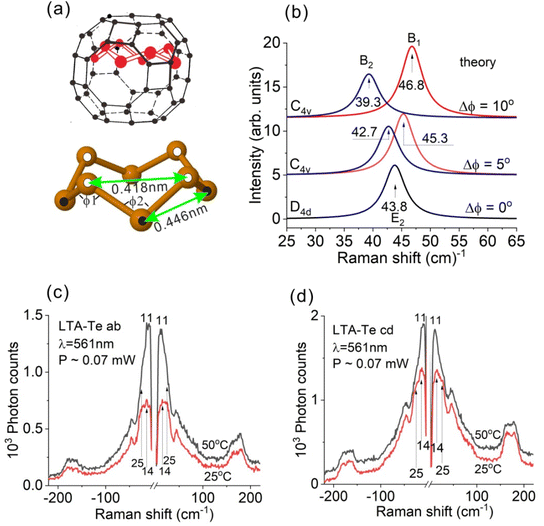
According to the calculated Te₈ structure [Fig. 2(a)], the diameter of the ring, including the van der Waals radius of ∼0.2 nm of the Te atom, is ∼1 nm, which is slightly smaller than the LTA large cavity diameter. Therefore, one can expect that the Te₈ ring is slightly shifted from the cavity center along the 4-fold LTA axis similar to the S₈ and Se₈ rings^12,44,45 but not as much as in the cases of S₈ and Se₈. This should cause Te₈ symmetry reduction from D_4d at least to C_4v [Fig. 5(a)]. We imposed the bond angle changes in order to simulate such structural distortion. The angles of type ϕ1 were enlarged while those of type ϕ2 were reduced. The second nearest neighbor distances R = 0.418 nm and 0.446 nm in Fig. 5(a) correspond to Δϕ = ϕ1 − ϕ2 = 5° (R = 0.432 nm for undisturbed Te₈).

Fig. 5 Te₈ ring shifted up from the centre of the LTA large cavity (top) with the C_4v structural distortion corresponding to the bond angle difference Δϕ = ϕ1 − ϕ2 = 5° (bottom), the white and black spots show Te atoms in the top and bottom layers, respectively (a); calculated RS spectra of the Te₈ (D_4d) E₂ bond-bending mode (black) and Te₈ (C_4v) B₁ (red) and B₂ (blue) bond-bending modes (b); and experimental low-frequency RS of LTA-Te at stage temperatures of ∼25 °C and ∼50 °C for ab (c) and cd (d) polarization configurations.

The experimentally observed splitting of the E₂ bond-bending mode [Fig. 3(a, d and e)] is, definitely, a sign of D_4d symmetry reduction. It is important to verify whether the observed E₂ mode splitting fits the ring structure distortion shown in Fig. 5(a) or not. Due to the Te₈ symmetry reduction from D_4d to C_4v, the E₂ bond-bending mode splits into B₁ and B₂ modes, displaying XX and XY Raman activities, respectively. We performed calculations of the B₁ and B₂ mode frequencies and intensities as a function of the distortion Δϕ. The results are shown in Fig. 5(b). The B₁ mode frequency increases while the B₂ mode frequency decreases with Δϕ. This corresponds well to our experimental observation for the E₂ bond-bending mode with the LTA-Te aa-active component frequency higher than that of the ab-active component. Thus, we conclude that the Te₈ structural distortion shown in Fig. 5(a) reasonably describes the experimentally observed splitting of the E₂ bond-bending mode of Te₈. However, even stronger symmetry reduction of Te₈ is possible.

As we mentioned in the Introduction, Raman polarization–orientation spectroscopy in application to the zeolite-confined cluster structure study can be considered in some sense as an alternative to XRD. Indeed, using Raman polarization–orientation spectroscopy, we can determine a type of cluster (molecule) and its orientation in a zeolite. Then we can suggest its possible location in the zeolite when we know its size. However, we can only guess what sort of interaction occurs between the Te atoms and the zeolite. For understanding this point, the XRD data would be very useful. However, a structural analysis of LTA-Te by XRD is rather difficult because Te is distributed statistically inside the cavities. The resulting scattering power of Te sites with partial occupancy is comparable to those of Na⁺ cations and water molecules filling spaces not occupied by Te.

The ∼20 micron size of LTA-Te is insufficient for single-crystal XRD, while powder XRD of zeolites with clusters is, definitely, not effective for the examination of the cluster structure. It shows that the zeolite filling with clusters or molecules causes just changes in the relative intensities of the XRD peaks like, for example, in ref. 48 and its ESI, where a number of different types of zeolites, including LTA, with/without sulphur clusters were examined using powder XRD. In contrast, XRD analysis of ∼65 micron size LTA single crystals containing sulphur clearly showed double S₈ ring cluster formation in each large cavity,⁴⁹ which is in agreement with the published RS results^12,50,51 and this work [Fig. 3(c)].

An XRD study of ∼60 micron size LTA-Te single crystals was performed in ref. 52. The XRD analysis suggested the interaction of Te atoms with the zeolite oxygen atoms and cations, while it showed low occupancy and high temperature factors for Te atomic sites. Therefore, the authors could not make any univocal conclusion about the Te cluster structure and they proposed several options including Te₈ rings.

Using the RS of LTA-Te, the interaction between the Te₈ ring and the zeolite can be probed via observation of the Te ring librations vs. temperature. Taking into account the S₈ libration frequency of ∼37 cm⁻¹ [Fig. 3(c)] and assuming approximately the same van der Waals interaction force with LTA for both S₈ and Te₈, we can roughly estimate the expected Te₈ room temperature libration frequency as ∼18.5 cm⁻¹ using the square root of the Te and S mass ratio, which is ∼2.

In the LTA-Te RS spectra obtained by excitation with 785 nm light, Te₈ librations, probably, contribute to the broad ∼22–25 cm⁻¹ band [Fig. 3(a)]. Instrumental limitations did not allow RS detection at frequencies <20 cm⁻¹ at this excitation wavelength. In contrast, such measurements were available at 561 nm light excitation. A weak point of this wavelength is that the corresponding Te₈ absorption and light-induced heating are not negligible.

Fig. 5(c and d) show the Stokes and anti-Stokes low-frequency RS of LTA-Te in ab and cd polarization configurations at ∼25 °C and ∼50 °C temperatures of the heat-controlling table. We roughly estimated the laser-induced heating from the Stokes/anti-Stokes intensity ratio as ∼20–30 °C, the value that should be added to the heating table temperature. In the RS taken at ∼25 °C table temperature, one can see a ∼25 cm⁻¹ band in combination with a ∼14 cm⁻¹ band for both configurations. The last band, definitely, originates from the Te₈ librations. With the increase of the table temperature to ∼50 °C, it shifts to a lower frequency of ∼11 cm⁻¹ and displays significant enhancement. This corresponds to the intensification of librations and the reduction of the ring interaction with LTA. The position of the ∼25 cm⁻¹ feature remains unchanged, confirming its origin from the internal torsional E₂ mode of Te₈.

Thus, the Te₈ libration amplitudes strongly increase with a moderate increase in the LTA temperature. This corresponds to a rather weak van der Waals interaction of Te₈ with LTA. At room temperature, the libration amplitudes are, probably, quite strong as well. This explains high temperature factors observed for Te sites,⁵² which complicates the XRD analysis of LTA-Te. In contrast, this effect does not cause any trouble for polarization–orientation Raman spectroscopy, which appears to be a very fruitful method of zeolite-confined cluster study providing information on the cluster structure with distortions, orientation and interaction with zeolites.

Conclusions

In summary, the electronic and vibrational properties of Te₈ rings were studied experimentally using Raman and absorption optical spectroscopy and theoretically using density functional theory. A good agreement is obtained between (1) the theoretical optical absorption and Raman spectra of isolated Te₈ and (2) those of Te₈ formed in the large cavities of the zeolite LTA. Owing to zeolite utilization, this is a big step in the experimental study of Te₈, which is limited by the fabrication of exotic compounds like Cs₃Te₂₂ ⁵³ or cluster registration in molecular beams.⁵⁴ Polarization–orientation Raman spectra of LTA-Te show that the rings are oriented by their major axes along the 4-fold axes of LTA. The observed splitting of the Te₈ bond-bending modes suggests the reduction of the ring D_4d symmetry in the LTA cavity. The bond-stretching modes demonstrate mixing due to the reduced symmetry of the ring and, probably, the essential anharmonicity of the vibrations. Even moderate heating of LTA-Te causes significant intensification of Te₈ librations in the LTA cavities, which corresponds to a rather weak van der Waals interaction between the ring and the zeolite. Experimental optical absorption spectra of LTA-Te display dependence on the Te loading density due to the electronic interaction of Te₈ from neighbouring cavities, which increases with an increase in the loading density. The effect is confirmed using DFT calculations of the absorption spectra of Te₈ dimers. The observed Te₈ ring–ring interaction is beneficial for the formation of cluster crystals with narrow electron bands and predicted non-linear electric properties. On the other hand, our results can be interesting in the sense of relationships with other inorganic 8-membered ring clusters such as Pd₈.⁵⁵

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank V. P. Petranovskii for LTA crystal synthesis and A. V. Fokin for the Te vapour adsorption procedure.

References

1. T. Chivers and R. S. Laitinen, Tellurium: A Maverick Among the Chalcogens, Chem. Soc. Rev., 2015, 44, 1725–1739,  10.1039/C4CS00434E.
2. Y. Liu, J. Wang, Y. Xu, Y. Zhu, D. Bigio and C. Wan, Lithium-Tellurium Batteries Based on Tellurium/Porous Carbon Composite, J. Mater. Chem. A, 2014, 2, 12201–12207,  10.1039/C4TA02075H.
3. T. Cao, R. Wang, R. E. Simpson and G. Li, Photonic Ge-Sb-Te phase change metamaterials and their applications, Prog. Quantum Electron., 2020, 74, 100299,  DOI:10.1016/j.pquantelec.2020.100299.
4. M. Z. Hasan and C. L. Kane, Topological Insulators, Rev. Mod. Phys., 2010, 82, 3045–3067,  DOI:10.1103/RevModPhys.82.3045.
5. S. Lin, W. Li, Z. Chen, J. Shen, B. Ge and Y. Pei, Tellurium as a high-performance elemental thermoelectric, Nat. Commun., 2016, 7, 10287,  DOI:10.1038/ncomms10287.
6. W. K. Metzger, S. Grover, D. Lu, E. Colegrove, J. Moseley, C. L. Perkins, X. Li, R. Mallick, W. Zhang, R. Malik, J. Kephart, C.-S. Jiang, D. Kuciauskas, D. S. Albin, M. M. Al-Jassim, G. Xiong and M. Gloeckler, Exceeding 20% efficiency with in situ group V doping in polycrystalline CdTe solar cells, Nat. Energy, 2019, 4, 837–845,  DOI:10.1038/s41560-019-0446-7.
7. V. V. Poborchii, A. V. Fokin and A. A. Shklyaev, Optical properties of extreme tellurium nanowires formed in subnanometer-diameter channels, Nanoscale Adv., 2023, 5, 220–227,  10.1039/d2na00590e.
8. V. N. Bogomolov, S. G. Romanov, S. V. Kholodkevich and L. S. Agroskin, The absorption spectra of single selenium and tellurium chains in dielectric matrix channels, Solid State Commun., 1983, 47, 181–182,  DOI:10.1016/0038-1098(83)90704-4.
9. V. V. Poborchii, Polarized Raman and optical absorption spectra of the mordenite single crystals containing sulphur, selenium or tellurium confined in the one-dimensional nanochannels, Chem. Phys. Lett., 1996, 251, 230–234,  DOI:10.1016/0009-2614(96)00045-0.
10. S.-I. Inoue, N. Koshizaki and T. Kodaira, Formation of Te nanowires in zeolite AFI and their polarized absorption spectra, Int. J. Mod. Phys. B, 2005, 19, 2817–2822,  DOI:10.1142/s0217979205031754.
11. T. Kodaira and T. Ikeda, The selective adsorption of tellurium in the aluminosilicate regions of AFI- and MOR-type microporous crystals, Dalton Trans., 2014, 43, 13979–13987,  10.1039/c4dt01028k.
12. V. V. Poborchii, Raman microprobe polarization measurements as a tool for studying the structure and orientation of molecules and clusters incorporated into cubic zeolites: S₈ and Se₁₂ rings in zeolite A, J. Chem. Phys., 2001, 114, 2707–2717,  DOI:10.1063/1.1339268.
13. V. N. Bogomolov, V. V. Poborchii and S. V. Kholodkevich, Size effects in the vibrational spectrum of 10 Å selenium particles, JETP Lett., 1985, 42, 517–520.
14. V. N. Bogomolov, Liquids in ultrathin channels (Filament and cluster crystals), Sov. Phys. Usp., 1978, 21, 77–83,  DOI:10.1070/PU1978v021n01ABEH005510.
15. G. D. Stucky and J. E. MacDougall, Quantum Confinement and Host/Guest Chemistry: Probing a New Dimension, Science, 1990, 247, 669–678,  DOI:10.1126/science.247.4943.669.
16. G. A. Ozin, Nanochemistry: Synthesis in diminishing dimensions, Adv. Mater., 1992, 4, 612–649,  DOI:10.1002/adma.19920041003.
17. V. N. Bogomolov, A. I. Zadorozhnii, V. I. Petranovskii, A. V. Fokin and S. V. Kholodkevich, Identification of a new tellurium modification – a Te₈ ring in small-diameter clusters, JETP Lett., 1979, 29, 373–375.
18. A. S. Pine and G. Dresselhaus, Raman Spectra and Lattice Dynamics of Tellurium, Phys. Rev. B: Solid State, 1971, 4, 356–371,  DOI:10.1103/PhysRevB.4.356.
19. V. V. Poborchii, V. A. Sachkov, A. A. Shklyaev, A. V. Fokin and P. I. Geshev, Photonic and phononic properties of oriented 5 nm diameter tellurium nanowires, J. Phys. Chem. Solids, 2024, 185, 111806,  DOI:10.1016/j.jpcs.2023.111806.
20. V. V. Poborchii, M. S. Ivanova, V. P. Petranovskii, Y. A. Barnakov, A. Kasuya and Y. Nishina, Raman and absorption spectra of the zeolites A and X containing selenium and tellurium in the nanopores, Mater. Sci. Eng., A, 1996, 217/218, 129–134,  DOI:10.1016/S0921-5093(96)10365-8.
21. V. V. Poborchii, Raman spectra of sulfur, selenium or tellurium clusters confined in nano-cavities of zeolite A, Solid State Commun., 1998, 107, 513–518,  DOI:10.1016/S0038-1098(98)00205-1.
22. V. P. Petranovskii, Y. Kiyozumi, N. Kikuchi, H. Hayamisu, Y. Sugi and F. Mizukami, The influence of mixed organic additives on the zeolite A and X crystal growth, Stud. Surf. Sci. Catal., 1997, 105, 149–156.
23. S. G. Balasubramani, et al., TURBOMOLE: Modular program suite for ab initio, quantum-chemical and condensedmatter simulations, J. Chem. Phys., 2020, 152, 184107,  DOI:10.1063/5.0004635.
24. D. Rappoport and F. Furche, Lagrangian approach to molecular vibrational Raman intensities using time-dependent hybrid density functional theory, J. Chem. Phys., 2007, 126, 201104,  DOI:10.1063/1.2744026.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
26. J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985,  DOI:10.1063/1.472933.
27. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary Basis Sets to Approximate Coulomb Potentials, Chem. Phys. Lett., 1995, 242, 652–660,  DOI:10.1016/0009-2614(95)00838-u.
28. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305,  10.1039/b508541a.
29. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065,  10.1039/B515623H.
30. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, Systematically Convergent Basis Sets with Relativistic Pseudopotentials. II. Small-Core Pseudopotentials and Correlation Consistent Basis Sets for the Post- d Group 16–18 Elements, J. Chem. Phys., 2003, 119, 11113–11123,  DOI:10.1063/1.1622924.
31. D. Rappoport and F. Furche, Lagrangian Approach to Molecular Vibrational Raman Intensities Using Time-Dependent Hybrid Density Functional Theory, J. Chem. Phys., 2007, 126, 201104,  DOI:10.1063/1.2744026.
32. P. Deglmann, F. Furche and R. Ahlrichs, An Efficient Implementation of Second Analytical Derivatives for Density Functional Methods, Chem. Phys. Lett., 2002, 362, 511–518,  DOI:10.1016/s0009-2614(02)01084-9.
33. P. Deglmann, K. May, F. Furche and R. Ahlrichs, Nuclear Second Analytical Derivative Calculations Using Auxiliary Basis Set Expansions, Chem. Phys. Lett., 2004, 384, 103–107,  DOI:10.1016/j.cplett.2003.11.080.
34. D. Rappoport and F. Furche, Property-Optimized Gaussian Basis Sets for Molecular Response Calculations, J. Chem. Phys., 2010, 133, 134105,  DOI:10.1063/1.3484283.
35. R. Bauernschmitt and R. Ahlrichs, Treatment of Electronic Excitations within the Adiabatic Approximation of Time Dependent Density Functional Theory, Chem. Phys. Lett., 1996, 256, 454–464,  DOI:10.1016/0009-2614(96)00440-x.
36. R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Calculation of Excitation Energies within Time-Dependent Density Functional Theory Using Auxiliary Basis Set Expansions, Chem. Phys. Lett., 1997, 264, 573–578,  DOI:10.1016/s0009-2614(96)01343-7.
37. Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. D. Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, TURBOMOLE: Today and Tomorrow, J. Chem. Theory Comput., 2023, 19, 6859–6890,  DOI:10.1021/acs.jctc.3c00347.
38. B. C. Pan, Geometric structures, electronic properties, and vibrational frequencies of small tellurium clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 085407,  DOI:10.1103/PhysRevB.65.085407.
39. J. Akola and R. O. Jones, Structure and dynamics in amorphous tellurium and Te_n, clusters: A density functional study, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134103,  DOI:10.1103/PhysRevB.85.134103.
40. H. H. Abdallah, Revisiting the Tellurium Clusters (Te_n; n = 2-8) using Ab initio Methods, Can. J. Phys., 2020, 98, 57–64,  DOI:10.1139/cjp-2019-0015.
41. V. S. Ghemud, H. A. S. Gol and A. Kshirsagar, How different are Te clusters - a first-principles study, J. Nanopart. Res., 2018, 20, 177,  DOI:10.1007/s11051-018-4274-7.
42. T. Sharma, R. Sharma, R. A. Tamboli and D. G. Kanhere, Ab initio investigation of structural and electronic properties of selenium and tellurium clusters, Eur. Phys. J. B, 2019, 92, 51,  DOI:10.1140/epjb/e2019-90491-5.
43. D. W. Scott, J. P. McCollough and F. H. Kruse, Vibrational Assignment and Force Constants of S8 from a Normal-Coordinate Treatment, J. Mol. Spectrosc., 1964, 13, 313–320,  DOI:10.1016/0022-2852(64)90079-7.
44. V. V. Poborchii and A. V. Fokin, Raman and optical absorption spectra of oriented Se₈ and Se₁₂ rings formed in zeolites: Dependence on the Se loading density, Microporous Mesoporous Mater., 2022, 338, 111954,  DOI:10.1016/j.micromeso.2022.111954.
45. V. V. Poborchii, V. P. Petranovskii, I. A. Glukhov and A. A. Fotiadi, Optical study of oriented double-Se8-ring clusters and luminescent Se₂⁻ anions in LTA at extremely high selenium loading density, Microporous Mesoporous Mater., 2023, 348, 112395,  DOI:10.1016/j.micromeso.2022.112395.
46. V. V. Bryksin and P. Kleinert, Microscopic theory of high-field miniband transport in semiconductor superlattices, J. Phys.: Condens.Matter, 1997, 9, 7403–7418,  DOI:10.1088/0953-8984/9/35/014.
47. Z. K. Tang and X.-R. Wang, Nonresonant electron tunneling in cluster superlattice of tellurium in zeolite, Appl. Phys. Lett., 1996, 68, 3449–3451,  DOI:10.1063/1.115789.
48. E. Han, Y.-G. Kim, H.-M. Yang, I.-H. Yoon and M. Choi, Synergy between Zeolite Framework and Encapsulated Sulfur for Enhanced Ion-Exchange Selectivity to Radioactive Cesium, Chem. Mater., 2018, 30, 5777–5785,  DOI:10.1021/acs.chemmater.8b02782.
49. K. Seff, The Crystal Structure of a Sulfur Sorption Complex of Zeolite 4A, J. Phys. Chem., 1972, 76, 2601–2605,  DOI:10.1021/j100662a023.
50. V. V. Poborchii, V. Petranovskii, I. A. Glukhov and A. A. Fotiadi, Single crystal polarization-orientation Raman spectroscopy of zeolite LTA with confined S3⁻ anions - High dielectric constant nanoporous material, Mater. Chem. Phys., 2024, 316, 129103,  DOI:10.1016/j.matchemphys.2024.129103.
51. V. N. Bogomolov, V. P. Petranovskii, V. V. Poborchii and S. V. Kholodkevich, Absorption, Raman and ESR spectra and the dielectric permittivity of NaA-S cluster crystals, Sov. Phys. Solid State, 1983, 25, 1415–1417.
52. W. T. Lim, J. S. Park, S. H. Lee, K. J. Jung and N. H. Heo, Synthesis of Tellurium Sorption Complexes in Fully Dehydrated and Fully Ca²⁺-exchanged Zeolites A and X and their Single-crystal Structures, Bull. Korean Chem. Soc., 2009, 30, 1274–1284,  DOI:10.5012/bkcs.2009.30.6.1274.
53. W. S. Sheldrick and M. Wachhold, Discrete crown-shaped Te₈ rings in Cs₃Te₂₂, Angew. Chem., Int. Ed. Engl., 1995, 34, 450–451,  DOI:10.1002/anie.199504501.
54. J. Becker, K. Rademann and F. Hensel, Electronic structure of selenium- and tellurium-clusters, Z. Phys. D: At., Mol. Clusters, 1991, 19, 233–235,  DOI:10.1007/BF01448300.
55. P. An, R. Anumula, C. Cui, Y. Liu, F. Zhan, Y. Tao and Z. Luo, A facile method to synthesize water-soluble Pd₈ nanoclusters unraveling the catalytic mechanism of p-nitrophenol to p-aminophenol, Nano Res., 2019, 12, 2589–2596,  DOI:10.1007/s12274-019-2491-8.

---