Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning-driven investigation of the structure and dynamics of the BMIM-BF4 room temperature ionic liquid†
Fabian
Zills
 a,
Moritz René
Schäfer
a,
Moritz René
Schäfer
 b,
Samuel
Tovey
b,
Samuel
Tovey
 a,
Johannes
Kästner
a,
Johannes
Kästner
 b and
Christian
Holm
b and
Christian
Holm
 *a
*a
aInstitute for Computational Physics, University of Stuttgart, 70569 Stuttgart, Germany. E-mail: holm@icp.uni-stuttgart.de
bInstitute for Theoretical Chemistry, University of Stuttgart, 70569 Stuttgart, Germany
First published on 19th March 2024
Abstract
Room-temperature ionic liquids are an exciting group of materials with the potential to revolutionize energy storage. Due to their chemical structure and means of interaction, they are challenging to study computationally. Classical descriptions of their inter- and intra-molecular interactions require time intensive parametrization of force-fields which is prone to assumptions. While ab initio molecular dynamics approaches can capture all necessary interactions, they are too slow to achieve the time and length scales required. In this work, we take a step towards addressing these challenges by applying state-of-the-art machine-learned potentials to the simulation of 1-butyl-3-methylimidazolium tetrafluoroborate. We demonstrate a learning-on-the-fly procedure to train machine-learned potentials from single-point density functional theory calculations before performing production molecular dynamics simulations. Obtained structural and dynamical properties are in good agreement with computational and experimental references. Furthermore, our results show that hybrid machine-learned potentials can contribute to an improved prediction accuracy by mitigating the inherent shortsightedness of the models. Given that room-temperature ionic liquids necessitate long simulations to address their slow dynamics, achieving an optimal balance between accuracy and computational cost becomes imperative. To facilitate further investigation of these materials, we have made our IPSuite-based training and simulation workflow publicly accessible, enabling easy replication or adaptation to similar systems.
Introduction
The application of machine learning in computational chemistry has started a revolution in material design and understanding. While the methods themselves have been developing gradually for more than a decade,1–5 it is only recently that the community has started to see breakthroughs in their applications to chemistry and materials science.6 This can be attributed to the development of advanced training strategies,7 improved accelerator hardware,8 and new model architectures.9 One family of materials that has been of great interest for years are room-temperature ionic liquids (RTILs). These molecular liquids find application in a diverse range of fields10 from battery technology,11 super-capacitors,12 carbon capture devices,13 biomass extraction,14 and many more.15–17 The potential to customize them for particular purposes has enabled their use in a wide range of applications. Their adaptability arises from the presence of cationic and anionic molecules, which can be modified to meet specific requirements. The large design space of RTILs make in silico studies an exciting endeavor. However, a significant obstacle is their complex and long-ranged interactions. Their treatment typically requires ab initio methods such as density functional theory (DFT), since classical approaches will struggle to capture all relevant effects. The highly viscous nature of RTILs results in slow dynamics, which are impossible to study using these levels of theory. However, with the development of machine-learned potentials (MLPs), these simulations have become tractable, as it is now possible to capture close to ab initio accuracy on near classical time and size-scales. RTILs possess a large configuration space, hence training of MLPs must be done with great care to not fall into unphysical configurations during deployment. Furthermore, DFT calculations need high accuracy to capture relevant interactions inside the materials which again incurs substantial computational cost. Moreover, careful attention must be paid to dispersion interactions.18In this work, we demonstrate our approach for the construction of an MLP for the RTIL 1-butyl-3-methylimidazolium tetrafluoroborate BMIM+BF4−. We train the model starting from a small number of configurations obtained from a classical trajectory and then perform a learning-on-the-fly (LotF) workflow to iteratively improve the MLP, thereby exploring a significant portion of configuration space. This approach allows us to overcome the use of extensive ab initio calculations, thus reducing the overall computation time. In order to assess the accuracy of the potential, we perform large-scale molecular dynamics (MD) simulations in the NPT and NVT ensembles and compare the resulting structures and dynamics to literature values. Our work demonstrates that, with state-of-the-art LotF strategies for MLPs approaches, it is feasible to study this complex family of materials to previously unseen accuracy. Comparable studies on RTILs by Shayestehpour and Zahn19 and Montes-Campos et al.20 showed that MLPs can reproduce experimental self-diffusivity. With our MLPs we can achieve similar accuracy, while using significantly less training data than the DeepMD21 based approach.
The paper is structured as follows. We first introduce the machine learning and training methods used within our study. We then present the results of the production simulations and compare them to literature values. Finally, we highlight open areas for continued research into the material before summarizing our work in the conclusion. In particular, we demonstrate how the inclusion of physically inspired terms, namely D3 dispersion corrections, can be used in hybrid models. These corrections compensate for missing long-range interactions, which play a crucial role in obtaining accurate densities.
Methods
Reference quantum chemistry method
All quantum chemistry calculations were performed using the CP2K software package22–25 at the DFT level. The exchange–correlation energy was approximated using the B97-3C functional.26,27 The electronic wavefunctions were expanded in an atom-centered TZVP-GTH basis set28 with GTH-PBE pseudopotentials.29–31 A cutoff of 800 Ry was used for the auxiliary plane wave basis. The parameters were adopted from Perlt et al.18 and are tailored for the description of ionic liquids.Dispersion correction
A good description of dispersion interactions is crucial, as they are known to play a significant role in imidazolium-based ionic liquids, due to hydrogen and alkyl chain interactions.18 During LotF, all DFT calculations were combined with the empirical D3 dispersion correction by Grimme et al.32 including Becke–Johnson damping.33 Initially, the correction was applied within CP2K with a cutoff of 8 Å and many body C9 terms. To investigate the effect of dispersion on MLP training and MD simulations, the dataset was recomputed without D3 correction. We utilize the performant Torch-DFTD34 implementation of the D3 method to obtain a corrected and uncorrected version of the data. We added the D3 parameters for the B97-3C functional from Brandenburg et al.26 to the Torch-DFTD package. Furthermore, we have extended the Atomic Simulation Environment (ASE) calculator provided by the package with an option to only rebuild the neighbor list when atomic displacements exceed a threshold value. This was set to 0.5 Å throughout this work and roughly doubled the inference speed of the Torch-DFTD ASE calculator.Machine learning potential
In this work, we utilize the Apax35 package for training Gaussian Moment Neural Networks (GMNNs).36,37 Similar to other MLPs, the nearsightedness of electronic matter38 is exploited to divide the total energy of a structure, S, into atomic contributions.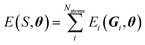 | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij.
ij.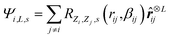 | (2) |
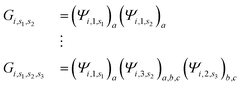 | (3) |
| Ei = σZi·NN(S) + μZi | (4) |
| Fi = −∇riE(S,θ) | (5) |
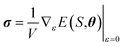 | (6) |
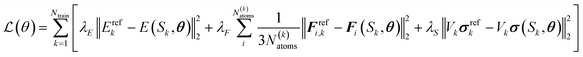 | (7) |
Throughout this work, we use 7 Gaussian functions for the radial grid and contract them down to 5 with rmin = 0.7 Å and rmax = 5.5 Å. The latter was increased to 6.0 Å for the final model. Neural networks with 2 hidden layers consisting of 512 units, respectively, were used for all models. Learning rates for β, the neural network, scaling and shifting parameters were independently set to 0.01, 0.005, 0.001 and 0.05, respectively. The batch size was set to 4 and the number of training epochs to 500 during the iterative training procedure and set to 1 and 2000 for the final models.
Learning-on-the-fly
An initial dataset was sampled from a trajectory generated using GROMACS 202142 with the OPLS-AA force field.43,44 A 5 ns simulation for 10 ion pairs at the density of 1.210 g cm−3 at 500 K was conducted. Starting with this trajectory, the entire LotF workflow was built using the Python package IPSuite.45,46 Within IPSuite, interfaces to MLP, DFT, and MD codes, in conjunction with analysis methods, are available. Initially, 100 datapoints were randomly selected for both the training and validation datasets, and subsequently, a first set of models was trained. We introduce the following notation for the iteration and number of models in the ensemble: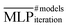 . Further, models for which the dispersion correction was learned implicitly are denoted by
. Further, models for which the dispersion correction was learned implicitly are denoted by 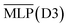 and hybrid models as
and hybrid models as 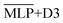 .
.
In order to obtain uncertainties for the predictions, an ensemble of two models was used throughout this work. During sampling simulations, the force uncertainty σ defined by eqn (8) was used as a stopping criterion with a threshold value of 0.5 eV Å−1.
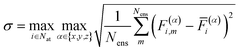 | (8) |
From then on, each new iteration starts with a trajectory driven by the MLP. At iteration 4, the model was able to simulate for 25 ps in the NVT ensemble at 298.15 K without triggering the stopping criterion. The dynamics were modified to enhance the sampling and encounter more informative configurations in subsequent iterations. For this purpose, temperature and density were modified during the simulation according to eqn (9), where Q denotes the modified quantity.
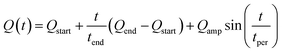 | (9) |
| It. | # | MD | T/K | Conditions |
|---|---|---|---|---|
| 0 | 500 | NVT | 500 | 1.210 g cm−3 |
| 1–4 | 4 × 50 | NVT, GeoOpt | 298.15 | 1.210 g cm−3 |
| 5–7 | 3 × 50 | NVT, GeoOpt | 230–500 | 1.210 g cm−3 |
| 8–10 | 3 × 50 | NVT | 298.15 | 0.992–1.499 g cm−3 |
| 11 | 20 | Conformers | — | 0.900 g cm−3 |
| 12 | 50 | NVT | 230–500 | 0.992–1.499 g cm−3 |
| 13 | 100 | NPT, VS | 300 | 1.0 atm, 0.151–1.661 g cm−3 |
| 14 | 50 | NPT | 300–500 | 1.0 atm |
| 15 | 100 | NPT | 200–300 | 1.0 atm |
| 16 | 105 | NPT, GeoOpt | 300 | 1.0 atm, — |
| 17 | 164 | NVT, NPT, GeoOpt | 500, 298.15 | 1.210 g cm−3, 1.0 atm, 0.900 g cm−3 |
This setup makes very few assumptions about the material under investigation. Material dependent parameters are the selected ranges for temperatures and densities and the DFT parameters. This allows for straightforward transfer to similar systems.
Production simulations
In order to obtain initial structures, we generated conformations of the ions using RDKit48 and PACKMOL49 to place them in a cubic box at a reduced density of 0.9 g cm−3. After a geometry optimization using FIRE51 as implemented in ASE,52 the simulation box was adjusted to the experimental densities.53 This was done for each temperature by continuously scaling the box size over the course of a 5 ps MD simulation.Simulations for radial distribution functions (RDFs) and diffusion coefficients calculations were performed using 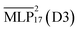 in the NVT ensemble using the Nosé–Hoover chain thermostat.54 Trajectories were simulated at temperatures T ∈ {283, 293, 313, 333, 353} K for n ∈ {8, 16, 32} pairs of BMIM+ and BF4− ions. The system was then equilibrated over 5 ps before a 20 ns production simulation using JaxMD55 was conducted. The density simulations were performed for n = 10 ion pairs at the same temperatures. The initial structures were equilibrated in the NVT ensemble for 200 ps and production simulations in the NPT were performed for 1 ns using the Nosé–Hoover chain thermostat54 with the Parrinello–Rahman barostat.56,57 While the JaxMD interface of Apax is significantly more performant than the ASE calculator, the utilization of Torch-DFTD for the hybrid
in the NVT ensemble using the Nosé–Hoover chain thermostat.54 Trajectories were simulated at temperatures T ∈ {283, 293, 313, 333, 353} K for n ∈ {8, 16, 32} pairs of BMIM+ and BF4− ions. The system was then equilibrated over 5 ps before a 20 ns production simulation using JaxMD55 was conducted. The density simulations were performed for n = 10 ion pairs at the same temperatures. The initial structures were equilibrated in the NVT ensemble for 200 ps and production simulations in the NPT were performed for 1 ns using the Nosé–Hoover chain thermostat54 with the Parrinello–Rahman barostat.56,57 While the JaxMD interface of Apax is significantly more performant than the ASE calculator, the utilization of Torch-DFTD for the hybrid 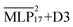 models necessitates the use of ASE. As such, all NPT simulations were performed with ASE. Confidence intervals for the simulated densities were obtained by applying the block averaging method.58 Additionally, ab initio molecular dynamics (AIMDs) at temperatures of 283 K and 353 K were performed. The simulation box was prepared analogously to the NVT production simulations, using
models necessitates the use of ASE. As such, all NPT simulations were performed with ASE. Confidence intervals for the simulated densities were obtained by applying the block averaging method.58 Additionally, ab initio molecular dynamics (AIMDs) at temperatures of 283 K and 353 K were performed. The simulation box was prepared analogously to the NVT production simulations, using 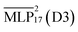 . Both simulations span 10 ps with 16 ion pairs and were performed using a Langevin thermostat. All simulations used a time step of 0.5 fs.
. Both simulations span 10 ps with 16 ion pairs and were performed using a Langevin thermostat. All simulations used a time step of 0.5 fs.
Results and discussion
Model evaluation
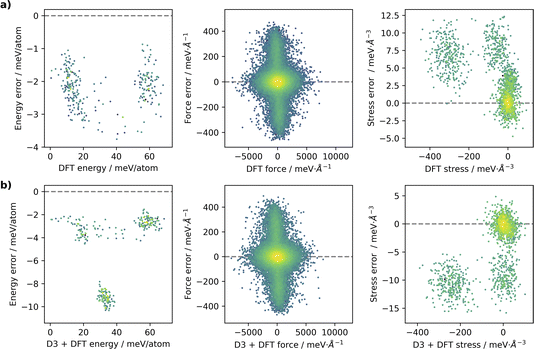
The MLPs were continuously evaluated against the validation dataset during the LotF cycles. A final evaluation of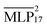 and
and 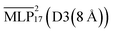 is shown in Fig. 1.
is shown in Fig. 1.
The 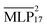 model is able to predict the DFT energies, forces and stress with mean absolute errors (MAEs) of 2.2 meV per atom, 48.0 meV Å−1 and 2.59 meV Å−3, respectively. Energy and stress prediction errors of the
model is able to predict the DFT energies, forces and stress with mean absolute errors (MAEs) of 2.2 meV per atom, 48.0 meV Å−1 and 2.59 meV Å−3, respectively. Energy and stress prediction errors of the 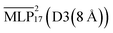 model have increased to 5.2 meV per atom and 2.99 meV Å−3. However, the quality of force predictions is essentially identical at an MAE of 48.0 meV Å−1. This is to be expected, as the tail of the dispersion interaction contributes a constant shift to energy and pressure.59 Overall, the accuracy of force predictions by models of the 17th LotF iteration almost reach chemical accuracy (43 meV Å−1), and were thus chosen for the subsequent production simulations.
model have increased to 5.2 meV per atom and 2.99 meV Å−3. However, the quality of force predictions is essentially identical at an MAE of 48.0 meV Å−1. This is to be expected, as the tail of the dispersion interaction contributes a constant shift to energy and pressure.59 Overall, the accuracy of force predictions by models of the 17th LotF iteration almost reach chemical accuracy (43 meV Å−1), and were thus chosen for the subsequent production simulations.
Another important aspect, crucial for the investigation of structural and dynamic properties of RTILs, is the inference time of the MLPs. An overview of different models on various system sizes is shown in Fig. 2. Whilst the hybrid MLP+D3 models are more accurate, they are not compatible with the JaxMD interface and thus running MD is 3.5 and 20 times slower using ASE. Compared to AIMD, simulations using 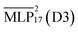 are ≈3000 times faster on 16 ion pairs and can be scaled to larger system sizes. Although the linear scaling of MLPs allows for investigations of large-scale systems, the maximum system size on a single GPU is restricted by the VRAM capacity. Within the current Apax implementation of GMNN, this is limited to approximately 330 ion pairs on an RTX 4090 GPU.
are ≈3000 times faster on 16 ion pairs and can be scaled to larger system sizes. Although the linear scaling of MLPs allows for investigations of large-scale systems, the maximum system size on a single GPU is restricted by the VRAM capacity. Within the current Apax implementation of GMNN, this is limited to approximately 330 ion pairs on an RTX 4090 GPU.
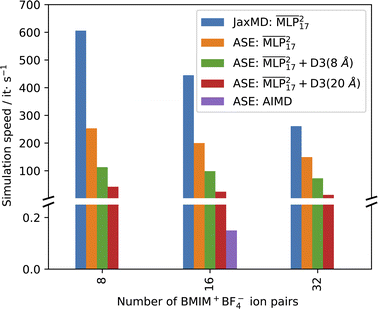 | ||
Fig. 2 Inference times of the original and hybrid  models for different system sizes on a single RTX 4090 GPU compared to AIMD simulations on 256 cores. models for different system sizes on a single RTX 4090 GPU compared to AIMD simulations on 256 cores. | ||
Structure
The structure of the RTIL was analyzed by calculating the RDF for all atom pairs in the NVT simulations. The RDFs obtained from the MLP simulations as well as the deviation from the AIMD results are displayed in Fig. 3.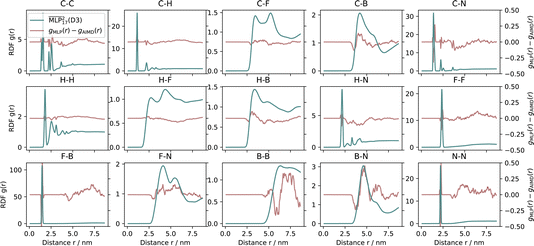 | ||
| Fig. 3 Comparison of RDFs at 353 K for 16 ion pairs of BMIM+BF4− from 20 ns MLP MD and 10 ps AIMD simulations. | ||
The RDFs are generally in good agreement with the reference AIMD simulations. This shows that inter- and intramolecular energies and forces are well predicted by the MLP. Differences between the RDFs of the MLP and AIMD can primarily be attributed to noise in the AIMD simulations caused by the short simulation times. The noticeable difference in the interatomic RDFs, especially the B–B RDF was further investigated by running 20 × 2.5 ps AIMD simulations at 353 K, starting at uniformly sampled configurations from the 20 ns MLP simulation. No significant energy jumps were observed in the AIMD trajectories, indicating that the MLP-obtained starting structures are also well equilibrated under the reference method. The energy over time of the trajectory is illustrated in Fig. S15.†
The combined RDF of the MLP and AIMD simulations is shown in Fig. 4. RDFs were computed using the MDSuite software60 over the entire trajectories with 1000 bins each. The smoothing of the B–B RDF can be explained by the long correlation time in the movement of the n-butyl chains, which are not captured in the short AIMD simulations. Fig. 5 shows how the distribution of the dihedral angles φ of the n-butyl chain changes over time. Some angles are only visited after 1 ns of simulation time. Furthermore, emergence of an equilibrated angle distribution is not even fully reached after 20 ns of MLP simulation.
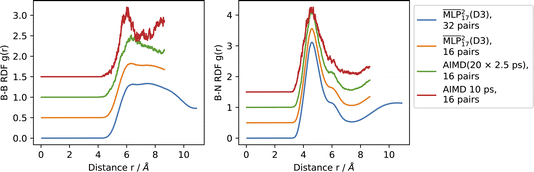 | ||
| Fig. 4 RDF of B–B and B–N pairs. The B–B RDF shows significant structure, which is smoothed out over the 20 ns. | ||
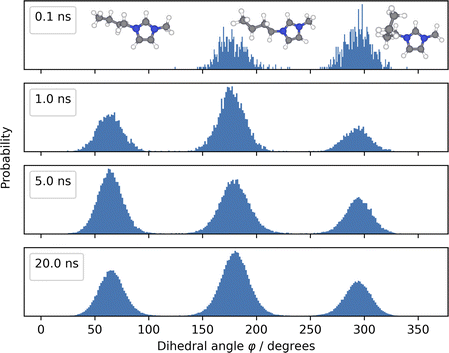 | ||
| Fig. 5 Dihedral angle distribution of an n-butyl chain in a single BMIM+ cation plotted over different simulation time scales. Molecules are visualized using the ZnDraw61 package. | ||
Dynamics
Diffusion coefficients were computed using the Einstein relation from the mean squared displacement of the H and B atoms in the NVT production simulations. The mean squared displacement was computed using a customized MDAnalysis62–65 toolkit integrated with IPSuite.46The results for the  are finite-size corrected using N ∈ {8, 16, 32} ion pairs.67,68 The diffusion coefficients for BF4− in Fig. 6 for the MLP and experiment are represented by the B atom, whilst the classical MD computes the self-diffusion from the center of mass of the ion. The diffusion coefficients for BMIM+ are computed from the H atoms and center of mass of the entire cation, respectively.
are finite-size corrected using N ∈ {8, 16, 32} ion pairs.67,68 The diffusion coefficients for BF4− in Fig. 6 for the MLP and experiment are represented by the B atom, whilst the classical MD computes the self-diffusion from the center of mass of the ion. The diffusion coefficients for BMIM+ are computed from the H atoms and center of mass of the entire cation, respectively.
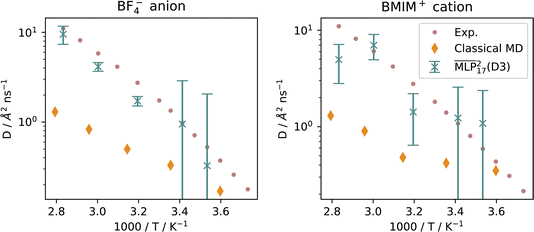 | ||
| Fig. 6 Arrhenius plot of the diffusion coefficients at different temperatures. Experimental values are taken from Hayamizu et al.,53 and results for classical MD are replicated from Bagno et al.66 | ||
The diffusion coefficients for BF4− shown in Fig. 6 at temperature above 313 K are in good agreement with the literature values. Below these temperatures, diffusion is underestimated by the MLP. The high viscosity of the RTIL at lower temperatures indicates that the MD simulations are not long enough to capture the long correlation times in the system.
It is noteworthy that the model yields good results, despite lacking explicit long-range electrostatic interactions, crucial for classical force fields.69 These findings are consistent with previous MLP studies of RTILs.19,20 However, the self-diffusion of the BMIM+ cation is less accurately captured in MD simulations using the MLP. While we demonstrate that the implicitly learned dispersion interactions of our 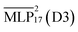 accurately describe the anion dynamics, a correct depiction of dispersion is particularly important for the cation, which exhibits the largest errors. It is possible that better agreement with experiment could be achieved if a hybrid model including an explicit dispersion term were used instead.
accurately describe the anion dynamics, a correct depiction of dispersion is particularly important for the cation, which exhibits the largest errors. It is possible that better agreement with experiment could be achieved if a hybrid model including an explicit dispersion term were used instead.
The results indicate that the MLP is capable of reproducing correct diffusion coefficients, drastically outperforming non-polarizable force fields. More work on learning inter-molecular interactions is required to remedy the remaining discrepancies. The errors for these observables obtained in this study are comparable to those of previous MLP-based works. However, our parameterization employed approximately 17 times fewer training configurations compared to Shayestehpour and Zahn,19 underscoring the advantages of the comprehensive LotF methodologies embedded within IPSuite, complemented by the efficiency of the Apax code.
Density
The ability of the MLP to reproduce experimental densities was investigated by computing the average density from MD simulations in an NPT ensemble at different temperatures. The experimental densities are taken from Hayamizu et al.53 We compare various GMNN models that were trained on dispersion corrected DFT and hybrid models with different D3 cutoffs in order to determine the most suitable setup. Fig. 7(a) shows the densities computed by the various models at 283 K. It is known that semi-local DFT does not properly capture dispersion interactions.70 Hence, the strong underestimation of the density by the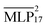 baseline is to be expected. Further, neither of the models trained on DFT+D3 at various dispersion cutoffs are able to capture the long range of the correction. We trained an additional model using an 8 Å radial cutoff. Unfortunately this model was not able to produce a stable simulation and increasing the cutoff further would incur a significant computational cost. The hybrid models come close to reproducing the experimental densities, with
baseline is to be expected. Further, neither of the models trained on DFT+D3 at various dispersion cutoffs are able to capture the long range of the correction. We trained an additional model using an 8 Å radial cutoff. Unfortunately this model was not able to produce a stable simulation and increasing the cutoff further would incur a significant computational cost. The hybrid models come close to reproducing the experimental densities, with 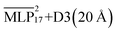 only slightly underestimating it.
only slightly underestimating it.
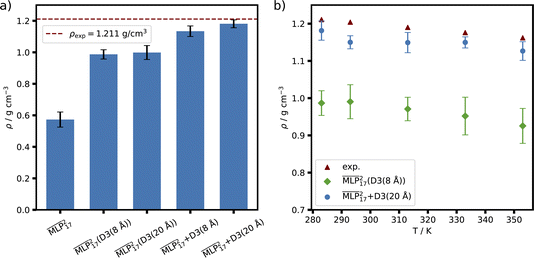 | ||
| Fig. 7 Densities obtained from NPT simulations in comparison to experimental values taken from Hayamizu et al.53 (a) Densities produced by models differing in the way the dispersion correction was learned or added for BMIM+BF4− at 283 K. (b) Comparison of densities across temperatures for three of these models. Error bars indicate 95% confidence intervals. | ||
The densities for the ionic liquid across various temperatures are displayed in Fig. 7(b). 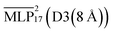 is also included as this was the model used to investigate the diffusion and structural properties. Across the range of temperatures
is also included as this was the model used to investigate the diffusion and structural properties. Across the range of temperatures 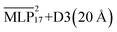 achieves errors below 5% and is in good agreement with experiment. The remaining deviations may be explained by errors in the stress tensor predictions and a too small cutoff for the dispersion correction. However, increasing the latter becomes quickly expensive as the addition of the 20 Å cutoff D3 correction slows the simulation down by about a factor of 10, as shown in Fig. 2.
achieves errors below 5% and is in good agreement with experiment. The remaining deviations may be explained by errors in the stress tensor predictions and a too small cutoff for the dispersion correction. However, increasing the latter becomes quickly expensive as the addition of the 20 Å cutoff D3 correction slows the simulation down by about a factor of 10, as shown in Fig. 2.
Summary and conclusion
We have presented an MLP for the RTIL BMIM+BF4− using a transferable LotF approach. The MLP generated by this semi-automatic procedure was able to reproduce structural properties compared to AIMD simulations and self-diffusion coefficients, as well as densities in good agreement with experimental values. We have shown that investigating structural and dynamic properties of the RTIL BMIM+BF4− using AIMD is difficult due to the long correlation times in the system, and therefore, MLPs provide a pathway to study these systems with high accuracy. Finding a good compromise between accuracy and speed is still crucial with MLPs, as long-range dispersion interactions play a significant role in the RTIL BMIM+BF4−. We have found that applying the dispersion correction terms post hoc to the MLP delivers the most accurate densities. However, developing efficient descriptions of long-range interactions remains one of the challenges for the application of MLPs. Nevertheless, the study of these RTILs is conducted at the performance and accuracy frontier of MLPs, demonstrating that, while recent research predominantly emphasizes accuracy enhancement, inference time is vital for performing simulations at significant system sizes and time scales.Data availability
The workflow notebook as well as all input files for the various software packages needed to reproduce the work presented here can be found at https://github.com/IPSProjects/BMIM-BF4.71 All data generated during the iterative training and production simulations are stored on an S3-object storage. It can be obtained by cloning the repository and executing dvc pull in the repository folder. Following the idea of Data as Code, models and simulation data can be loaded directly from the repository using the ZnTrack package.45 Further, the data can also be accessed on DaRUS https://doi.org/10.18419/darus-4086.Code availability
All software used throughout this work is publicly available. The Apax repository is available on Github at https://github.com/apax-hub/apax. IPSuite is available at https://github.com/zincware/IPSuite and can be installed from PyPi via pip install ipsuite.Author contributions
F. Zills and M. Schäfer’s contribution to the paper was conceptualization, methodology, investigation, software, validation, visualisation and writing – original draft. S. Tovey's contribution to the paper was conceptualization, methodology, supervision, writing – original draft. J. Kästner and C. Holm contributed in the fields of project administration, resources, supervision, funding acquisition and writing – review & editing.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
C. H., J. K., F. Z., and M. S. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the framework of the priority program SPP 2363, “Utilization and Development of Machine Learning for Molecular Applications – Molecular Machine Learning” Project No. 497249646. S. T. was supported by an LGF stipend of the state of Baden-Württemberg. Further funding through the DFG under Germany's Excellence Strategy – EXC 2075 – 390740016 and the Stuttgart Center for Simulation Science (SimTech) was provided. All authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant INST 35/1597-1 FUGG.References
- J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed
.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed
.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, Adv. Neural Inf. Process. Syst., 2022, 11423–11436 Search PubMed
.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning Local Equivariant Representations for Large-Scale Atomistic Dynamics, Nat. Commun., 2023, 14, 579 CrossRef CAS
.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed
.
- I. Batatia, et al., A Foundation Model for Atomistic Materials Chemistry, arXiv, 2023, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine Learning Force Fields, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS
.
- L. Deng, G. Li, S. Han, L. Shi and Y. Xie, Model Compression and Hardware Acceleration for Neural Networks: A Comprehensive Survey, Proc. IEEE, 2020, 108, 485–532 Search PubMed
.
- P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Machine-Learned Potentials for next-Generation Matter Simulations, Nat. Mater., 2021, 20, 750–761 CrossRef CAS PubMed
.
- G. Kaur, H. Kumar and M. Singla, Diverse applications of ionic liquids: A comprehensive review, J. Mol. Liq., 2022, 351, 118556 CrossRef CAS
.
- M. Kunze, S. Jeong, E. Paillard, M. Schönhoff, M. Winter and S. Passerini, New Insights to Self-Aggregation in Ionic Liquid Electrolytes for High-Energy Electrochemical Devices, Adv. Energy Mater., 2011, 1, 274–281 CrossRef CAS
.
- S. Pan, M. Yao, J. Zhang, B. Li, C. Xing, X. Song, P. Su and H. Zhang, Recognition of Ionic Liquids as High-Voltage Electrolytes for Supercapacitors, Front. Chem., 2020, 8 DOI:10.3389/fchem.2020.00261
.
- A. Krishnan, K. P. Gopinath, D.-V. N. Vo, R. Malolan, V. M. Nagarajan and J. Arun, Ionic Liquids, Deep Eutectic Solvents and Liquid Polymers as Green Solvents in Carbon Capture Technologies: A Review, Environ. Chem. Lett., 2020, 18, 2031–2054 CrossRef CAS
.
- T. G. Weldemhret, A. B. Bañares, K. R. M. Ramos, W.-K. Lee, G. M. Nisola, K. N. G. Valdehuesa and W.-J. Chung, Current Advances in Ionic Liquid-Based Pre-Treatment and Depolymerization of Macroalgal Biomass, Renewable Energy, 2020, 152, 283–299 CrossRef CAS
.
- A. Bera, J. Agarwal, M. Shah, S. Shah and R. K. Vij, Recent Advances in Ionic Liquids as Alternative to Surfactants/Chemicals for Application in Upstream Oil Industry, J. Ind. Eng. Chem., 2020, 82, 17–30 CrossRef CAS
.
-
Y. Kondo, T. Koyama, S. Sasaki, Y. Kondo, T. Koyama and S. Sasaki, Ionic Liquids - New Aspects for the Future, IntechOpen, 2013 Search PubMed
.
- A. A. M. Elgharbawy, M. Moniruzzaman and M. Goto, Facilitating Enzymatic Reactions by Using Ionic Liquids: A Mini Review, Curr. Opin. Green SustainableChem., 2021, 27, 100406 CrossRef CAS
.
- E. Perlt, P. Ray, A. Hansen, F. Malberg, S. Grimme and B. Kirchner, Finding the Best Density Functional Approximation to Describe Interaction Energies and Structures of Ionic Liquids in Molecular Dynamics Studies, J. Chem. Phys., 2018, 148, 193835 CrossRef
.
- O. Shayestehpour and S. Zahn, Efficient Molecular Dynamics Simulations of Deep Eutectic Solvents with First-Principles Accuracy Using Machine Learning Interatomic Potentials, J. Chem. Theory Comput., 2023, 19, 8732–8742 CrossRef CAS
.
- H. Montes-Campos, J. Carrete, S. Bichelmaier, L. M. Varela and G. K. H. Madsen, A Differentiable Neural-Network Force Field for Ionic Liquids, J. Chem. Inf. Model., 2022, 62, 88–101 CrossRef CAS PubMed
.
- L. Zhang, J. Han, H. Wang, W. Saidi, R. Car and W. E, End-to-End Symmetry Preserving Inter-atomic Potential Energy Model for Finite and Extended Systems, Adv. Neural Inf. Process. Syst., 2018, 31, 4436–4446 Search PubMed
.
- J. VandeVondele and J. Hutter, An Efficient Orbital Transformation Method for Electronic Structure Calculations, J. Chem. Phys., 2003, 118, 4365–4369 CrossRef CAS
.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS
.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC
.
- T. D. Kühne,
et al., CP2K: An Electronic Structure and Molecular Dynamics Software Package - Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152, 194103 CrossRef
.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, B97-3c: A Revised Low-Cost Variant of the B97-D Density Functional Method, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed
.
- A. D. Becke, Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS
.
- S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B, 1996, 54, 1703–1710 CrossRef CAS PubMed
.
- A. D. Becke, Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS
.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic Separable Dual-Space Gaussian Pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS
.
- M. Krack, Pseudopotentials for H to Kr Optimized for Gradient-Corrected Exchange-Correlation Functionals, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- S. Takamoto,
et al., Towards Universal Neural Network Potential for Material Discovery Applicable to Arbitrary Combination of 45 Elements, Nat. Commun., 2022, 13, 2991 CrossRef CAS
.
-
M. R. Schäfer, N. Segreto and F. Zills, apax-hub/apax: v0.3.0, 2024, DOI:10.5281/zenodo.10523139
.
- V. Zaverkin and J. Kästner, Gaussian Moments as Physically Inspired Molecular Descriptors for Accurate and Scalable Machine Learning Potentials, J. Chem. Theory Comput., 2020, 16, 5410–5421 CrossRef CAS PubMed
.
- V. Zaverkin, D. Holzmüller, I. Steinwart and J. Kästner, Fast and Sample-Efficient Interatomic Neural Network Potentials for Molecules and Materials Based on Gaussian Moments, J. Chem. Theory Comput., 2021, 17, 6658–6670 CrossRef CAS PubMed
.
- W. Kohn, Density Functional and Density Matrix Method Scaling Linearly with the Number of Atoms, Phys. Rev. Lett., 1996, 76, 3168–3171 CrossRef CAS
.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv, 2017, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- V. Zaverkin, D. Holzmüller, R. Schuldt and J. Kästner, Predicting properties of periodic systems from cluster data: A case study of liquid water, J. Chem. Phys., 2022, 156, 114103 CrossRef CAS PubMed
.
- O. T. Unke and M. Meuwly, PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- S. V. Sambasivarao and O. Acevedo, Development of OPLS-AA Force Field Parameters for 68 Unique Ionic Liquids, J. Chem. Theory Comput., 2009, 5, 1038–1050 CrossRef CAS PubMed
.
- B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, Revisiting OPLS Force Field Parameters for Ionic Liquid Simulations, J. Chem. Theory Comput., 2017, 13, 6131–6145 CrossRef CAS
.
- F. Zills, M. R. Schäfer, N. Segreto, J. Kästner, C. Holm and S. Tovey, Collaboration on Machine-Learned Potentials with IPSuite: A Modular Framework for Learning-on-the-Fly, J. Phys. Chem. B, 2024, 128(15), 3662–3676 CrossRef CAS
.
- F. Zills, M. R. Schäfer and N. Segreto, zincware/IPSuite: IPSuite v0.1.1, DOI:10.5281/zenodo.10069082.
- I.-B. Magdău, D. J. Arismendi-Arrieta, H. E. Smith, C. P. Grey, K. Hermansson and G. Csányi, Machine learning force fields for molecular liquids: Ethylene Carbonate/Ethyl Methyl Carbonate binary solvent, npj Comput. Mater., 2023, 9, 146 CrossRef
.
- G. Landrum, et al., rdkit/rdkit: 2023_03_2 (Q1 2023) Release, 2023, https://zenodo.org/record/8053810 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed
.
- V. Zaverkin, D. Holzmüller, I. Steinwart and J. Kästner, Exploring Chemical and Conformational Spaces by Batch Mode Deep Active Learning, Digital Discovery, 2022, 1, 605–620 RSC
.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural Relaxation Made Simple, Phys. Rev. Lett., 2006, 97, 170201 CrossRef
.
- A. H. Larsen,
et al., The Atomic Simulation Environment—a Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed
.
- K. Hayamizu, S. Tsuzuki, S. Seki and Y. Umebayashi, Multinuclear NMR Studies on Translational and Rotational Motion for Two Ionic Liquids Composed of BF4 Anion, J. Phys. Chem. B, 2012, 116, 11284–11291 CrossRef CAS PubMed
.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed
.
- S. S. Schoenholz and E. D. Cubuk, JAX, M.D. A framework for differentiable physics, J. Stat. Mech.: Theory Exp., 2021, 2021, 124016 CrossRef
.
- M. Parrinello and A. Rahman, Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- S. Melchionna, Constrained Systems and Statistical Distribution, Phys. Rev. E, 2000, 61, 6165–6170 CrossRef CAS PubMed
.
- A. Grossfield, P. N. Patrone, D. R. Roe, A. J. Schultz, D. Siderius and D. M. Zuckerman, Best Practices for Quantification of Uncertainty and Sampling Quality in Molecular Simulations [Article v1.0], Living J. Comput. Mol. Sci., 2019, 1, 5067 Search PubMed
.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: from Algorithms to Applications, Academic Press, Inc, 1st edn, 1996 Search PubMed.
- S. Tovey, F. Zills, F. Torres-Herrador, C. Lohrmann, M. Brückner and C. Holm, MDSuite: Comprehensive Post-Processing Tool for Particle Simulations, J. Cheminf., 2023, 15, 19 Search PubMed
.
- R. Elijošius, F. Zills, I. Batatia, S. W. Norwood, D. P. Kovács, C. Holm, G. Csányi, Zero Shot Molecular Generation via Similarity Kernels, arXiv, 2024, preprint, arXiv:2402.08708, DOI:10.48550/arXiv.2402.08708.
-
R. J. Gowers, et al., MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105 Search PubMed
.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed
.
- V. Calandrini, E. Pellegrini, P. Calligari, K. Hinsen and G. R. Kneller, nMoldyn - Interfacing Spectroscopic Experiments, Molecular Dynamics Simulations and Models for Time Correlation Functions, École thématique de la Société Française de la Neutronique, 2011, 12, 201–232 CrossRef
.
- P. de Buyl, Tidynamics: A Tiny Package to Compute the Dynamics of Stochastic and Molecular Simulations, J. Open Source Softw., 2018, 3, 877 CrossRef
.
- A. Bagno, F. D'Amico and G. Saielli, Computer Simulation of Diffusion Coefficients of the Room-Temperature Ionic Liquid [bmim][BF4]: Problems with Classical Simulation Techniques, J. Mol. Liq., 2007, 131–132, 17–23 CrossRef CAS
.
- I.-C. Yeh and G. Hummer, System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS
.
- E. J. Maginn, R. A. Messerly, D. J. Carlson, D. R. Roe and J. R. Elliot, Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0], LiveCoMS, 2019, 1, 6324 Search PubMed
.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed
.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Dispersion-Corrected Mean-Field Electronic Structure Methods, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed
.
- F. Zills and M. R. Schäfer, IPSProjects/BMIM-BF4: V1 Release, 2024, DOI:10.5281/zenodo.10797063.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00025k |
| This journal is © The Royal Society of Chemistry 2024 |