Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of collisions and uptake of alcohol molecules with hydrated nitric acid clusters†
Karolína
Fárníková
a,
Eva
Pluhařová
 *a,
Andrij
Pysanenko
*a,
Andrij
Pysanenko
 a,
Michal
Fárník
a,
Michal
Fárník
 *a,
Yihui
Yan
b and
Jozef
Lengyel
*a,
Yihui
Yan
b and
Jozef
Lengyel
 *b
*b
aJ. Heyrovský Institute of Physical Chemistry, v.v.i., Czech Academy of Sciences, Dolejškova 2155/3, 18223 Prague 8, Czech Republic. E-mail: eva.pluharova@jh-inst.cas.cz; michal.farnik@jh-inst.cas.cz
bLehrstuhl für Physikalische Chemie, TUM School of Natural Sciences, Technische Universität München, Lichtenbergstraße 4, 85748 Garching, Germany. E-mail: jozef.lengyel@tum.de
First published on 30th January 2024
Abstract
We investigate the collisions of different alcohol molecules with hydrated nitric acid clusters using a molecular beam experiment and molecular dynamics simulations. The uptake cross sections σp for the molecules evaluated from the experiment are in excellent agreement with the simulations. This suggests that (i) the nontrivial assumptions implemented in the evaluation procedure of the experimental data are valid, and (ii) the simulations describe correctly the major processes in the molecule–cluster collisions. We observe that σp decreases with the increasing alkyl chain length of the alcohol, and also with the branching of the molecules that have the same mass but different structures. These systematic trends can be rationalized based on the accessibility of the hydrophilic OH group, which decreases with the increasing chain length and steric hindrance. The observed trends and their interpretation differ significantly from the simple model of hard-sphere collisions. The obtained data shall be beneficial not only for the fundamental understanding of the molecule–cluster collisions, but also in the modelling of atmospheric new-particle formation and aerosol growth.
1 Introduction
Aerosol particles represent one of the most important, yet possibly the least known, components of our atmosphere. For example, they influence global climate by scattering radiation and forming clouds, promote heterogeneous reactions in the atmosphere, and have a negative impact on human health in polluted areas.1–6 About half of the aerosol particles that serve as cloud seeds in the atmosphere are generated through the nucleation and condensation of precursor gases in the process called new particle formation (NPF).7,8 Therefore, it is essential to understand the collisions between gas-phase molecules and clusters, particularly for comprehending the initial stages of NPF. Such processes can be investigated in molecular beam experiments, where the scattering and uptake of gas-phase molecules by the clusters in the beam take place.9–11 However, in order to understand and evaluate the experiments correctly, it is necessary to combine them with molecular dynamics simulations to obtain a detailed molecular-level insight into the collision processes, which is the main purpose of the present study.In our previous paper, we established a new approach for quantifying the uptake process of different molecules by hydrated nitric acid (NA) clusters (HNO3)M·(H2O)N.12 The clusters represent a prototypical example of the hydrated acid clusters. Despite sulfuric acid (SA) being the primary source of most NPF events,3 a recent theory13 suggested that NA can drive the early stages of the particle formation as efficiently as SA, and it is particularly relevant to the NPF events occurring in urban areas and in the cold upper troposphere.14 As oxidized derivatives of volatile organic compounds (OVOCs) are considered a key component of NPF,15–19 we have investigated their uptake on hydrated NA clusters.20 Our molecular beam experiment combined mass spectrometry of the clusters after the pickup of the molecules with the measurements of the cluster velocity. However, the evaluation of the uptake cross sections σp from the experimental data was based on simplifying assumptions about the molecule–cluster collisions. Here, we substantiate these assumptions using results from detailed molecular dynamics simulations of the collisions, which compare favorably with the new measured cross sections.
In the present study, we investigate the (HNO3)M·(H2O)N clusters that collide with different alcohol molecules: methanol (CH3OH), ethanol (CH3CH2OH), 1-propanol (CH3CH2CH2OH), isopropanol (CH3CH(OH)CH3), 1-butanol (CH3(CH2)2CH2OH), 2-butanol (CH3CH(OH)CH2CH3), isobutanol ((CH3)2CHCH2OH), tert-butanol ((CH3)3COH), and 1-pentanol (CH3(CH2)3CH2OH) (Fig. 1). They represent molecules with different chain lengths and species with different positions of the OH functional group in their structure. We intend to investigate how the uptake of the molecule depends on its chain length and on the position of the OH group, since it is apparently the moiety that anchors the molecule to the cluster upon the uptake.
The present alcohols are not only proxies of the OVOCs with varying structure, but they are also atmospherically relevant. They originate from various anthropogenic and biogenic sources.21,22 Methanol, ethanol and isopropanol have been detected in urban areas.23 In addition, other alcohols, e.g., hex-3-en-1-ol or 2-methyl-but-3-en-2-ol, which share structural motifs with the investigated isomers, are present above vegetation.24
First, we briefly describe the experiment and evaluation of the uptake cross sections σp from the measurements, which, however, have been extensively discussed elsewhere.12,20 Therefore, we concentrate on describing our molecular dynamics simulations in detail in the next section. We show the measured σp values and compare them with the calculated values. Finally, we discuss the uptake dependence on the length of the carbon chain (i.e., size, mass, and hydrophobicity) from methanol to 1-pentanol and also examine the steric effects in the different isomers of propanol and butanol. We conclude that the combination of the experiment with the simulations provides a detailed insight into the dynamics of the molecule–cluster collisions, and reliable uptake cross sections are derived.
2 Methods
2.1 Experiment
The experiments were performed in the cluster beam apparatus CLUB described in recent reviews9–11 and references cited therein. The clusters were produced by supersonic expansion through a 90 μm conical nozzle (30° opening angle, 2 mm long). The expansion conditions were similar to those in our previous experiments with the nitric acid clusters:12,20,25 65% nitric acid solution was heated in a reservoir placed in the source vacuum chamber to a temperature of TR ≈ 338 K and the vapor was carried by He buffer gas at a pressure of 2 bar to the nozzle attached directly to the reservoir. The nozzle was heated independently to a somewhat higher temperature of TN ≈ 348 K to prevent any condensation. Under these conditions, the mixed clusters (HNO3)M(H2O)N are generated with M ≈ 1–7 and N ≈ 1–16. About 2 cm downstream from the nozzle, the clusters passed through a skimmer (opening 0.8 mm in diameter) and entered the pickup chamber, which could be filled with the pickup gas at a controlled pressure Pp. The path-length of the beam in the pickup chamber was L = 17 cm.After passing through the pickup chamber, the clusters fly through two additional differentially pumped vacuum chambers and reach the next chamber with the reflectron time-of-flight (TOF) mass spectrometer. Here, after a flight path of about 150 cm, the clusters are ionized by 70 eV electrons. The electron gun repetition frequency is 10 kHz, and the ionization pulse is 5 μs long followed by 0.5 μs delay before the ions are extracted by a 2 kV pulse and subsequently accelerated by 8 kV into the time-of-flight region. After a flight path of about 95 cm, the ions are detected with a multichannel plate and the mass spectrum is recorded.
The methodology of the uptake cross section evaluation is described in ref. 12 and 20. After the pickup of molecules X, the mass spectra contain protonated ion series without and with the molecule (HNO3)m(H2O)nH+ and X·(HNO3)m(H2O)nH+, respectively. The pickup pressure Pp is adjusted so that on average the clusters undergo one collision in the pickup cell and the pickup of two molecules X is not observed. By measuring the cluster velocities, we have demonstrated that molecules X did not evaporate from the neutral X·(HNO3)M(H2O)N cluster upon ionization in our previous studies.12,20 Thus, the bare (HNO3)m(H2O)nH+ ions in the spectra originate from the clusters that undergo only non-sticking collisions in the pickup chamber. We integrate all the mass peaks corresponding to the X·(HNO3)m(H2O)nH+ ions yielding an integral IX, and all the (HNO3)m(H2O)nH+ ions yielding IC. The ratio f = IX/(IX + IC) corresponds to the pickup probability. On the other hand, the fraction of the collisions that lead to the uptake of a molecule can be expressed in terms of the uptake cross section as σp × L × np. This fraction corresponds to the above ratio f = σp × L × np, and using the expression for the pickup gas density np = Pp/(kB × T), the uptake cross section can be expressed as
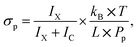 | (1) |
2.2 Calculations
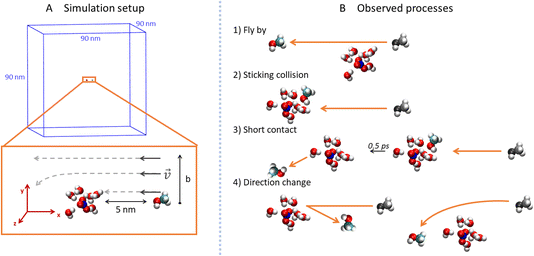
To explore the collisions of alcohol molecules with the nitric acid/water clusters, classical molecular dynamics simulations in the Gromacs 2020.3 program package26,27 were used. The AMBER99-based28 force field was employed with the partial atomic charges taken from various sources in the cases of the H3O+ cation,29 NO3− anion,30 and some of the alcohols.31 For 1-propanol, isopropanol, isobutanol and (2R)-butan-2-ol (just one enantiomer of the chiral alcohol was simulated, which is justified in the achiral environment), RESP atomic charges were determined by optimization at the HF/6-311G** level in the Gaussian16 program32 and then using the Antechamber program package.33 All parameter files are available from the national data repository at https://doi.org/10.48700/datst.jq7fm-k2x81. The SPC/E water model34,35 was used as in the recent study of the uptake cross section of water on pure water clusters.36For technical reasons, the open boundary conditions were mimicked by employing large cut-off values in a sizable periodic box.37 Specifically, the box dimensions were 90 × 90 × 90 nm3 (Fig. 2A) and the cutoff for the van der Waals and electrostatic interactions was 30 nm without the use of the PME method.38 The Newton’s equations of motion were propagated using the leap-frog algorithm with a 1 fs time-step and the LINCS algorithm39 was utilized to keep a constant length of the bonds containing hydrogen atoms.
In order to prepare various independent configurations of the HNO3·(H2O)6 cluster, we simulated this structure at 300 K maintained by Berendsen thermostat40 with a coupling constant of 0.2 ps for 2 ns. Then, 5 different structures were taken in 0.4 ns intervals (Fig. 1), which were used to calculate the theoretical uptake cross section of the nine alcohols. First, the cluster was rotated in 90° intervals, from 0 to 270° along the x, y and z axis with the origin being in the center of mass (COM) of the cluster. The same was done independently for the alcohol, which resulted in 4096 different initial conditions for one alcohol and one cluster for a given impact parameter b. Structures are available from the national data repository at https://doi.org/10.48700/datst.jq7fm-k2x81.
The impact parameter b was varied from 0 to 1 nm with steps of 0.2 nm, and the region between 0.3 nm to 0.6 nm was sampled with a 0.1 nm step size. In our setup (Fig. 2A), b equals the y-component of the COM distances of the alcohol and cluster which are aligned in the xy plane. The x-component of the initial distance between their COMs was 5 nm and the initial velocity of the alcohol was 1800 m s−1 in the −x direction. This velocity corresponded to the experimentally measured velocity of the cluster beam.12 Since the thermal velocity of the alcohol molecules in the pickup cell was randomly oriented, this initial velocity corresponded to the average relative velocity in the molecule–cluster collisions. The system was then propagated in a microcanonical ensemble for 20 ps in the double precision compilation of Gromacs, which ensures conservation of the total energy and momentum.
For each value of b, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 trajectories were collected and analyzed (Fig. 2B). If the final distance of the alcohol and the cluster is large and the y-position of the alcohol differs from the initial by less than 0.05 nm, we call the process fly-by (Fig. 2B1). In contrast, if the alcohol and the cluster are in contact (the distance between the COM of the alcohol and the COM of the ion pair is below 0.85 nm) at the end of the simulation, it is a sticking collision (Fig. 2B2). Next, short contact occurs if the alcohol and the cluster are separated at the end of the simulation, but stayed in contact for at least 0.5 ps (Fig. 2B3). Finally, a direction change takes place when the alcohol and the cluster were in contact for less than 0.5 ps or not at all (Fig. 2B4). The time evolution of the COM distances and their y-components for these processes are shown in the ESI (Fig. S6).†
480 trajectories were collected and analyzed (Fig. 2B). If the final distance of the alcohol and the cluster is large and the y-position of the alcohol differs from the initial by less than 0.05 nm, we call the process fly-by (Fig. 2B1). In contrast, if the alcohol and the cluster are in contact (the distance between the COM of the alcohol and the COM of the ion pair is below 0.85 nm) at the end of the simulation, it is a sticking collision (Fig. 2B2). Next, short contact occurs if the alcohol and the cluster are separated at the end of the simulation, but stayed in contact for at least 0.5 ps (Fig. 2B3). Finally, a direction change takes place when the alcohol and the cluster were in contact for less than 0.5 ps or not at all (Fig. 2B4). The time evolution of the COM distances and their y-components for these processes are shown in the ESI (Fig. S6).†
In addition to the processes described above, we also monitored water molecules. They can stay bound to the cluster or evaporate (their final distance from the COM of the cluster is above 1.5 nm). Interestingly, in a few cases we also observed evaporated water molecules sticking to the bounced alcohol.
3 Results
3.1 Measured relative uptake cross sections
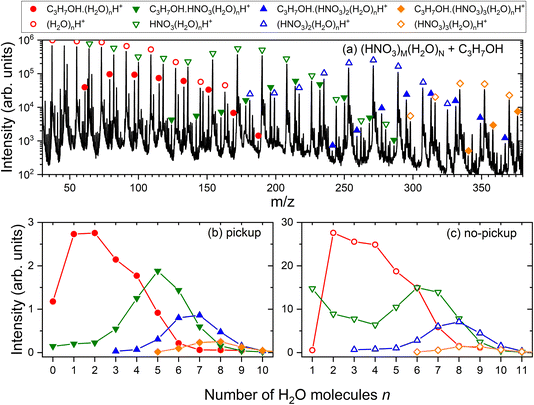
In the experiment, the mass spectra of (HNO3)M(H2O)N clusters with and without the uptake of molecules X in the pickup chamber were measured. The mass spectrum of pure (HNO3)M(H2O)N clusters recorded in the present study is shown in the ESI (Fig. S1a†) and the explanation of its shape and the individual protonated (HNO3)m(H2O)nH+ fragment ion series can be found in ref. 25 together with a detailed spectrum generated under very similar conditions (Fig. 1 in ref. 25). Briefly, the electron ionization of pure water in the clusters leads ultimately to the hydronium cation H3O+ and OH˙ radical, which leave the cluster.41,42 In the mixed clusters of the studied mean size, the hydronium ion is already generated in the neutral species by acid dissociation forming the H3O+⋯NO3− ion pair. The incoming electron can either ionize the nitrogen-containing species, resulting in (H2O)n−1H3O+ cluster ion fragments, or water leading to (HNO3)m(H2O)nH+. It was demonstrated12,20 that the mass spectrum after the pickup of molecules X exhibits a series of the same character shifted by the mass of the molecule, i.e., corresponding to the X·(HNO3)m(H2O)nH+ ions. Fig. 3a) illustrates this for the present case of the pickup of 1-propanol (X = CH3CH2CH2OH). The open symbols denote the (HNO3)m(H2O)nH+ series, which are present also in the pure (HNO3)M(H2O)N cluster mass spectra without any pickup. The full symbols denote the C3H7OH·(HNO3)m(H2O)nH+ series. The individual C3H7OH·(HNO3)m(H2O)nH+ and (HNO3)m(H2O)nH+ series are extracted in the bottom panels (b) and (c), respectively, as a function of the number of water molecules n. Further spectra for all picked-up molecules and the corresponding mass peak series are shown in the ESI (Fig. S1–S5).†As outlined in Section 2.1, the C3H7OH·(HNO3)m(H2O)nH+ series clearly originate from the uptake events, while the (HNO3)m(H2O)nH+ series correspond to the clusters undergoing non-sticking collisions in the pickup chamber. Thus, the uptake ratio f and the uptake cross section σp can be evaluated by integrating the series in Fig. 3b and c and using eqn (1).
The obtained uptake cross sections σp are summarized in Table 1 in comparison with the calculated values (discussed below). The absolute values of σp can be subjected to a systematic error due to the fact that the calculations are performed with one given cluster size, while the whole cluster size distribution is probed in the experiment. The cluster size in the calculations for (HNO3)M(H2O)N, M = 1 and N = 6, corresponds to the mean size obtained from the mass spectra. However, the neutral clusters might be larger due to cluster fragmentation after the electron ionization. Thus, the cluster size in the experiment is probably larger than the one used in the calculations. In addition, in the pickup experiment, the larger clusters contribute more to σp than the smaller ones, which can eventually pass through the pickup cell without collisions. Both these effects can lead to a bias of the calculated σp towards lower values with respect to the experiment. In Table 1, the experimental values are on average 1.5 times larger than the theoretical ones. Therefore, we normalize the σp values to the uptake cross section of methanol, yielding the relative cross sections. These values are in very good agreement with the calculations. Further possible sources of uncertainties and errors, which can affect our measured σp values, are mentioned in the ESI (Section 1.1).†
| Molecule | Absolute σp (Å2) | Relative | ||
|---|---|---|---|---|
| Exp. | Calc. | Exp. | Calc. | |
| Methanol | 75(11) | 41(7) | 1.00(15) | 1.00(17) |
| Ethanol | 48(7) | 25(3) | 0.64(9) | 0.61(8) |
| 1-Propanol | 47(10) | 34(5) | 0.63(13) | 0.82(11) |
| Isopropanol | 39(3) | 24(5) | 0.52(4) | 0.57(11) |
| 1-Butanol | 34(10) | 20(3) | 0.45(13) | 0.49(7) |
| 2-Butanol | 27(5) | 16(3) | 0.36(7) | 0.39(6) |
| Isobutanol | 25(5) | 13(2) | 0.33(7) | 0.32(6) |
| tert-Butanol | 16(3) | 13(2) | 0.21(4) | 0.32(6) |
| 1-Pentanol | 23(4) | 17(3) | 0.31(5) | 0.41(7) |
3.2 Calculated cross sections
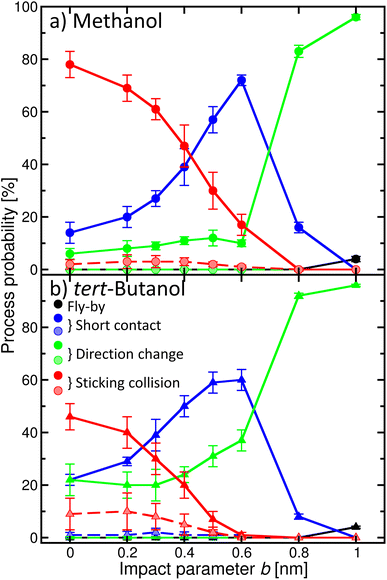
Once the alcohol molecule and the aqueous nitric acid water cluster approach each other, various processes can take place, as illustrated in Fig. 2. Their probability depends on the impact parameter b, which is exemplified in Fig. 4 for methanol (a) and tert-butanol (b). Results for other alcohols are available in the ESI (Fig. S7).† The most likely event when the centers of mass of the alcohol and the cluster are aligned (b = 0) is the sticking; its probability reaches nearly 80% for methanol (Fig. 4a), red solid line, full symbols). Sticking of this alcohol followed by water evaporation is much less probable (red dashed line, shaded symbols). The next process is short contact, i.e., the alcohol and the cluster were in contact for at least 0.5 ps, but then departed (blue). It is followed by a direction change, which differs from the previous situation by the time during which the alcohol and the cluster are close (green). As b increases, the probability of sticking decreases and short contact becomes the most likely process between ∼0.4–0.7 nm; then just the direction change dominates. It can happen either as a result of a collision or due to an attraction between the alcohol and the cluster, which leads to a curved trajectory without any contact (see Fig. 2). For the largest b investigated, fly-by without a significant change of the direction of the alcohol becomes possible. For the first three processes, we also monitor the evaporation of water molecules after the alcohol–cluster encounter. It is very rare for water evaporation to occur with the short contact and direction change processes, but more frequent during sticking collisions, yet it happens only in a few percent of cases.Comparison of methanol with tert-butanol (Fig. 4b) shows that the sticking is less likely (only 50% for b = 0) for the bulkier alcohol with a less accessible OH group. On the other hand, sticking with water evaporation is more likely than for methanol (10% for b = 0), and both the short contact and direction change processes are about twice as frequent. The dependence of the probability of individual processes on b is similar to methanol. The plots for other investigated alcohols (Fig. S7 in the ESI†) show that the trends are preserved and the actual values of the process probabilities lie between these two border lines.
In order to connect the simulations with experiment, we summed the sticking probabilities without and with water evaporation, because the summation of the experimental spectra yielding IX is performed over all peaks containing the alcohol molecule irrespective of the number of water molecules. The examples of the sticking probabilities for methanol and tert-butanol are plotted in Fig. 5. Results for other alcohols are shown in the ESI (Fig. S8).† To estimate the uptake cross sections, the sum of the two process probabilities Σp was integrated, R = ∫Σp db, and the obtained R was converted to the uptake cross section according to σcalp = πR2. The results are summarized in Table 1 together with the relative values with respect to methanol. This smallest investigated alcohol has the highest uptake cross section, followed by 1-propanol and ethanol. Isopropanol with a less accessible OH group has a lower σcalp than its isomer, the butanols have even lower values, and among them tert-butanol has the lowest uptake cross section. The σcalp of 1-pentanol is somewhat smaller than the one of 1-butanol, but almost equal to the one of 2-butanol and larger than σcalp of iso- and tert-butanol.
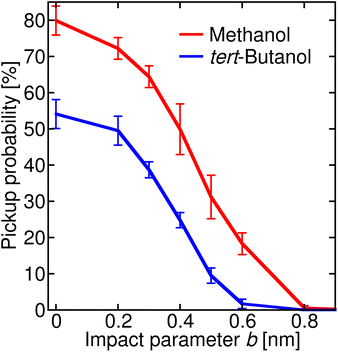 | ||
| Fig. 5 Sticking probability (with and without water evaporation added) as a function of the impact parameter b. The results for methanol are plotted in red, and for tert-butanol in blue. | ||
In addition, we quantified the amount of momentum p transferred from the incoming alcohol molecule to the cluster, and its dependence on the process (Fig. 6). Note that the p values are negative because the initial velocity of the alcohol has a negative sign in our coordinate system (see Fig. 2). If the alcohol sticks to the cluster, the whole object then moves with the initial momentum of the alcohol (red filled symbols). The transferred amount does not depend on b. If water evaporates (shaded symbols), the transferred momentum can be smaller. On the other hand, if the alcohol molecule bounces back with the velocity of opposite sign, the transferred momentum can be even larger than the initial momentum of the alcohol (green circle, for example, methanol b = 0 or 0.8 nm). However, it is not twice the initial value, as expected for an ideal elastic scattering in a hard-spheres collision. Other situations are accompanied by a smaller momentum transfer to the cluster, which can be further reduced due to the water evaporation. The calculated momentum transfer for the other alcohols are shown in the ESI (Fig. S9).†
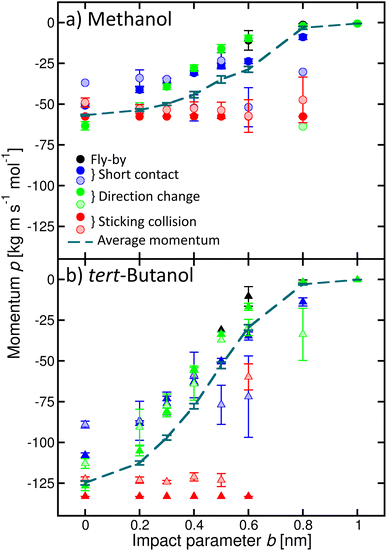 | ||
| Fig. 6 Momentum p transferred to the cluster for various processes as a function of the impact parameter b exemplified for methanol (a) and tert-butanol (b). Different colours and full and shaded symbols correspond to the different processes as in Fig. 4. The dashed line is the average momentum transferred to the cluster. | ||
4 Discussion
Fig. 7 compares the relative uptake cross sections of the investigated alcohols showing the experimental (a) and simulated (b) results. At first glance, the comparison between the experiment and theory is very favorable. In the experiment, the cross section decreases with the alkyl-chain length from methanol to ethanol and 1-propanol, which have nearly the same relative σp values slightly above 0.6, and further to 1-butanol and 1-pentanol with σp ≈ 0.45 and 0.3, respectively. The second and third groups of columns deal with the propanol and butanol isomers. They both show that the uptake decreases with the increasing steric hindrance of the OH group.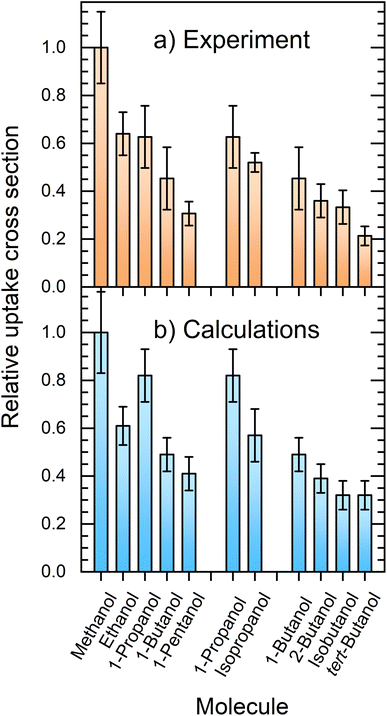 | ||
| Fig. 7 Comparison between the experimentally measured (a) and simulated (b) relative uptake cross sections σp. | ||
The experimental results and calculations show essentially the same qualitative trends and the relative uptake cross sections (normalized against methanol) are in good quantitative agreement. The obvious exception at first glance is 1-propanol, which has a higher simulated cross section σcalcp = 0.82(11) than the measured value of 0.63(13). The simulated value does not follow the above outlined decreasing trend with the alkyl-chain length observed in the experiment. Nevertheless, both values for 1-propanol still overlap within the corresponding error bars of the experiment and simulation. This is encouraging considering all the possible processes, sources of errors such as the approximate empirical force fields, and the experimental and evaluation procedures.
The qualitative agreement obtained for all the studied alcohols suggests that the assumptions involved in the evaluation of our experiment are justified, and that the experiment can deliver reliable relative uptake probabilities. On the other hand, the simulations provide unprecedented detailed insight into the collision processes, and obviously they are capturing all the major processes happening in the real collisions. Quantitatively, the calculated σcalcp values somewhat underestimate the experimental values by a factor of about 1.5 on average, as already mentioned in Section 3.1, where we also discuss a possible reason for this discrepancy: the larger average cluster size investigated in the actual experiment compared with the model (HNO3)1(H2O)6 cluster used in the simulations (see also Section 1.1 in the ESI†).
It is reassuring that our theoretical simulations describe correctly the observed qualitative trends in the uptake cross sections. Thus, it is justified to describe and analyze different processes in the simulations and interpret the observed trends. First, we focus on the decrease of σp with increasing the length of the alkyl chain. Assuming a spherical cluster of radius RC colliding with a spherical molecule of radius rM, the collision cross section shall be σc = π·(RC + rM)2. Thus, the longer chain molecules (larger rM) shall have a larger σc. These collision (geometrical) cross sections for the present molecules are calculated and given in Table 2. The cluster and molecule radii, RC and rM, respectively, were determined through volume calculations implemented in Gaussian using numerical Monte Carlo integration. To reduce the relatively large degree of error associated with this technique, we ran 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samplings with the tight convergence in the self-consistent field to estimate the molecular radius (rM(calc)). For selected molecules, we verified the calculated molecular radii with values (rM(exp)) derived from the viscosity η of the corresponding gas.43,44 For the evaluation of the cluster radius, the calculated geometries shown in Fig. 1 were considered to yield RC = 3.65 Å. Obviously, the collision cross sections σc in Table 2 show different trends than the measured and simulated σp in Table 1, suggesting that the treatment of the molecule–cluster collision as a hard spheres collision is oversimplified.
000 samplings with the tight convergence in the self-consistent field to estimate the molecular radius (rM(calc)). For selected molecules, we verified the calculated molecular radii with values (rM(exp)) derived from the viscosity η of the corresponding gas.43,44 For the evaluation of the cluster radius, the calculated geometries shown in Fig. 1 were considered to yield RC = 3.65 Å. Obviously, the collision cross sections σc in Table 2 show different trends than the measured and simulated σp in Table 1, suggesting that the treatment of the molecule–cluster collision as a hard spheres collision is oversimplified.
| Molecule | r M(exp) (Å) | r M(calc) (Å) | σ c (Å2) | Relative |
|---|---|---|---|---|
| Methanol | 2.34 | 2.33 | 112 | 1.00 |
| Ethanol | 2.77 | 2.65 | 125 | 1.11 |
| 1-Propanol | 3.16 | 2.87 | 133 | 1.19 |
| Isopropanol | 2.81 | 2.86 | 133 | 1.19 |
| 1-Butanol | 3.50 | 3.06 | 142 | 1.27 |
| 2-Butanol | — | 3.10 | 142 | 1.27 |
| Isobutanol | 3.10 | 3.08 | 142 | 1.27 |
| tert-Butanol | — | 3.06 | 141 | 1.26 |
| 1-Pentanol | 3.41 | 3.26 | 150 | 1.34 |
Assuming that the uptake probability is proportional to the collision cross section, we would expect a larger uptake cross section σp for the molecule with a longer chain as well. On the other hand, the collisions with larger impact parameters b contribute to the uptake cross section σp provided that the molecules are attracted to the cluster and attach to it. The heavier (longer chain) molecules can escape the attractive interaction due to their larger momentum in the collision, leading to just the direction change rather than to the uptake. More importantly, there is just one OH moiety in each molecule, by which it can attach to the cluster. For the longer chain molecules it is more difficult to approach the cluster in the right orientation for the molecule to anchor. Therefore, the longer chain molecules exhibit smaller σp values. In this respect, the other observed trend also makes sense: namely, in the more branched molecules isopropanol, 2-butanol, isobutanol and tert-butanol, the OH group is always more shielded in the collision by the CH2 and CH3 groups, and thus their uptake probabilities are smaller than the ones of the corresponding linear molecules. Thus, the present calculations together with the experiment demonstrate that the approximation of the uptake cross section σp by the collisions (geometrical) cross section σc would be a strong oversimplification leading to wrong conclusions. It is also worth noting that the absolute values of σc (Table 2) exceed significantly the calculated σp (Table 1). Since they are both evaluated for the cluster and molecules of the same theoretically calculated geometries, it once again proves that the molecule–cluster collisions cannot be simply approximated by the hard spheres if we want to understand the uptake processes. It would be illuminating to measure experimentally the uptake cross section dependence on the cluster size. However, it is not feasible within this study since it is difficult to control the cluster size distribution using expansion conditions for the present clusters, and it is even more problematic to determine their mean cluster size for the neutral species. Therefore, the demanding size dependence was also omitted from the calculations.
Our calculations also provide an important insight into the momentum transfer in the collisions. In our previous experiments, we have also measured the cluster velocities with and without the molecule uptake.12,20 We have observed that the momentum transferred to the clusters with the picked-up molecules did not quite correspond to the full momentum carried by the colliding molecule (in the cluster COM coordinate system). In our present simulations, we can see that the sticking collisions with water evaporation also lead to a smaller momentum transfer, which can even be significantly smaller for the larger scattering parameters. Also, we have observed in our previous velocity measurements that the non-sticking collisions lead on average to a relatively small momentum transfer. The present simulations confirm this observation qualitatively. Unfortunately, the velocity measurements could not be performed within the present measurements for experimental reasons; however, the momentum transfer measurements can be revisited in future experiments and compared to the present simulations.
5 Conclusions
We have investigated the uptake of nine different alcohols: methanol (CH3OH), ethanol (CH3CH2OH), 1-propanol (CH3CH2CH2OH), isopropanol (CH3CH(OH)CH3), 1-butanol (CH3(CH2)2CH2OH), 2-butanol (CH3CH(OH)CH2CH3), isobutanol ((CH3)2CHCH2OH), tert-butanol ((CH3)3COH), and 1-pentanol (CH3(CH2)3CH2OH) on hydrated nitric acid clusters (HNO3)M(H2O)N using a combination of our molecular beam experiment and molecular dynamics simulations. Both approaches show that the uptake cross section decreases with increasing alkyl chain length of the alcohol and also with the branching of the molecules that have the same mass but different structure (i.e., 1-propanol and isopropanol; 1-butanol, 2-butanol, isobutanol, and tert-butanol).The agreement between the experimental and simulated trends is reassuring and supports two major conclusions: (i) the non-trivial assumptions implemented in the evaluation procedure of the experimental mass spectra to yield the uptake cross sections are valid, and (ii) the simulations describe the major processes that happen during the molecule–cluster collisions. It allows us to rationalize the observed trends based on the accessibility of the hydrophilic OH group, which decreases with increasing the alkyl chain length and branching. These facts and interpretation differ significantly from a simple model of hard-sphere collisions. Molecular dynamics simulations revealed various processes taking place after the alcohol–cluster encounter, which can also be followed by the evaporation of water molecules. The accompanying momentum transfer calculations reveal further details of the collisions, which can be further tested in future experiments. The obtained data shall be beneficial not only for the fundamental understanding of molecule–cluster collisions, but also in the modeling and measurements of atmospheric new-particle formation and growth.
Author contributions
K. F. (theory): data curation, formal analysis, visualization, writing – review and editing; E. P. (theory): writing – original draft, supervision, conceptualization, methodology, validation; A. P. (experiment): data curation, formal analysis; M. F. (experiment): writing – original draft, supervision, conceptualization, methodology, validation, visualization, resources; Y. Y. (experiment): data curation, formal analysis, visualization; J. L. (experiment): writing – review and editing, methodology, validation, supervision, conceptualization, visualization, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Czech Science Foundation (GAČR) project no.: 21-07062S and 24-11390S and Deutsche Forschungsgemeinschaft (DFG) project no.: 442679477 (LE 4583/1-1). Computational resources were provided by the e-INFRA CZ project (ID: 90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic.Notes and references
- B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the Upper and Lower Atmosphere, Academic Press, San Diego, 2000 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: from Air Pollution to Climate Change, John Wiley & Sons Inc., Hoboken, NJ, 2016 Search PubMed.
- U. Pöschl, Angew. Chem., Int. Ed., 2005, 44, 7520–7540 CrossRef PubMed.
- C. E. Kolb and D. R. Worsnop, Annu. Rev. Phys. Chem., 2012, 63, 471–491 CrossRef CAS PubMed.
- C. George, M. Ammann, B. D’Anna, D. J. Donaldson and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4218–4258 CrossRef CAS PubMed.
- V. F. McNeill, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 427–444 CrossRef CAS PubMed.
- J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS.
- F. Yu and G. Luo, Atmos. Chem. Phys., 2009, 9, 7691–7710 CrossRef CAS.
- M. Fárník, J. Phys. Chem. Lett., 2023, 14, 287–294 CrossRef PubMed.
- M. Fárník, J. Fedor, J. Kočišek, J. Lengyel, E. Pluhařová, V. Poterya and A. Pysanenko, Phys. Chem. Chem. Phys., 2021, 23, 3195–3213 RSC.
- M. Fárník and J. Lengyel, Mass Spectrom. Rev., 2018, 37, 630–651 CrossRef PubMed.
- A. Pysanenko, J. Lengyel and M. Fárník, J. Chem. Phys., 2018, 148, 154301 CrossRef CAS PubMed.
- C. J. Bready, V. R. Fowler, L. A. Juechter, L. A. Kurfman, G. E. Mazaleski and G. C. Shields, Environ. Sci.: Atmos., 2022, 2, 1469–1486 CAS.
- M. Wang, W. Kong, R. Marten, X.-C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada, A. Kürten, T. Yli-Juuti, H. E. Manninen, S. Amanatidis, A. Amorim, R. Baalbaki, A. Baccarini, D. M. Bell, B. Bertozzi, S. Bräkling, S. Brilke, L. C. Murillo, R. Chiu, B. Chu, L.-P. D. Menezes, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, R. Guida, A. Hansel, V. Hofbauer, J. Krechmer, K. Lehtipalo, H. Lamkaddam, M. Lampimäki, C. P. Lee, V. Makhmutov, G. Marie, S. Mathot, R. L. Mauldin, B. Mentler, T. Müller, A. Onnela, E. Partoll, T. Petäjä, M. Philippov, V. Pospisilova, A. Ranjithkumar, M. Rissanen, B. Rörup, W. Scholz, J. Shen, M. Simon, M. Sipilä, G. Steiner, D. Stolzenburg, Y. J. Tham, A. Tomé, A. C. Wagner, D. S. Wang, Y. Wang, S. K. Weber, P. M. Winkler, P. J. Wlasits, Y. Wu, M. Xiao, Q. Ye, M. Zauner-Wieczorek, X. Zhou, R. Volkamer, I. Riipinen, J. Dommen, J. Curtius, U. Baltensperger, M. Kulmala, D. R. Worsnop, J. Kirkby and J. H. Seinfeld, Nature, 2020, 581, 184–189 CrossRef CAS PubMed.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. D. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- E. M. Dunne, H. Gordon, A. Kürten, J. Almeida, J. Duplissy, C. Williamson, I. K. Ortega, K. J. Pringle, A. Adamov, U. Baltensperger, P. Barmet, F. Benduhn, F. Bianchi, M. Breitenlechner, A. Clarke, J. Curtius, J. Dommen, N. M. Donahue, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, T. Jokinen, J. Kangasluoma, J. Kirkby, M. Kulmala, A. Kupc, M. J. Lawler, K. Lehtipalo, V. Makhmutov, G. Mann, S. Mathot, J. Merikanto, P. Miettinen, A. Nenes, A. Onnela, A. Rap, C. L. S. Reddington, F. Riccobono, N. A. D. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Simon, M. Sipilä, J. N. Smith, Y. Stozkhov, A. Tomé, J. Tröstl, P. E. Wagner, D. Wimmer, P. M. Winkler, D. R. Worsnop and K. S. Carslaw, Science, 2016, 354, 1119–1124 CrossRef CAS PubMed.
- I. Riipinen, T. Yli-Juuti, J. R. Pierce, T. Petäjä, D. R. Worsnop, M. Kulmala and N. M. Donahue, Nat. Geosci., 2012, 5, 453–458 CrossRef CAS.
- N. M. Donahue, I. K. Ortega, W. Chuang, I. Riipinen, F. Riccobono, S. Schobesberger, J. Dommen, U. Baltensperger, M. Kulmala, D. R. Worsnop and H. Vehkamäki, Faraday Discuss., 2013, 165, 91–104 RSC.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, M. Kulmala, D. R. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehm, Chem. Rev., 2019, 119, 3472–3509 CrossRef CAS PubMed.
- J. Lengyel, A. Pysanenko, K. Fárníková, E. Pluhařová and M. Fárník, J. Phys. Chem. Lett., 2020, 11, 2101–2105 CrossRef CAS PubMed.
- I. Colmenar, P. Martin, B. C. nas, S. Salgado, A. Tapia and I. Aranda, Atmos. Chem. Phys., 2020, 20, 699–720 CrossRef CAS.
- J. G. Calvert, A. Mellouki, J. J. Orlando, M. J. Pilling and T. J. Wallington, Mechanisms of Atmospheric Oxidation of the Oxygenates, Oxford University Press, New York, 2011 Search PubMed.
- H. T.-H. Nguyen, N. Takenaka, H. Bandow, Y. Maeda, S. T. de Oliva, M. M. Botelho and T. M. Tavares, Atmos. Environ., 2001, 35, 3075–3083 CrossRef CAS.
- R. Atkinson and J. Arey, Atmos. Environ., 2003, 37, 197–219 CrossRef.
- J. Lengyel, A. Pysanenko, J. Kočišek, V. Poterya, C. Pradzynski, T. Zeuch, P. Slavíček and M. Fárník, J. Phys. Chem. Lett., 2012, 3, 3096–3109 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, Solving Software Challenges for Exascale, Springer, Cham, Switzerland, 2015, pp. 3–27 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Noroozi and W. R. Smith, J. Chem. Inf. Model., 2021, 61, 4497–4513 CrossRef CAS PubMed.
- W. Jiang, T. Yan, Y. Wang and G. A. Voth, J. Phys. Chem. B, 2008, 112, 3121–3131 CrossRef CAS PubMed.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- S. Chatterjee, P. G. Debenedetti, F. H. Stillinger and R. M. Lynden-Bell, J. Chem. Phys., 2008, 128, 124511 CrossRef PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- M. Klíma, D. Celný, J. Janek and J. Kolafa, J. Chem. Phys., 2023, 159, 124302 CrossRef PubMed.
- L. Konermann, H. Metwally, R. G. McAllister and V. Popa, Methods, 2018, 144, 104–112 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- O. Maršálek, C. G. Elles, P. A. Pieniazek, E. Pluhařová, J. VandeVondele, S. E. Bradforth and P. Jungwirth, J. Chem. Phys., 2011, 135, 224510 CrossRef PubMed.
- O. Svoboda, D. Hollas, M. Ončák and P. Slavíček, Phys. Chem. Chem. Phys., 2013, 15, 11531–11542 RSC.
- R. S. Berry, S. A. Rice and J. Ross, Physical Chemistry, John Wiley & Sons, New York, 1980, p. 1259 Search PubMed.
- VDI-GVC, VDI-Wärmeatlas, Springer-Verlag, Berlin, Heidelberg, 2006, p. 1500 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Discussion of experimental errors and uncertainties in the absolute and relative pickup cross sections, mass spectra and ion series; analysis of selected collision trajectories, process probabilities, sticking probabilities, and momentum transfer. See DOI: https://doi.org/10.1039/d3fd00160a |
| This journal is © The Royal Society of Chemistry 2024 |