Lessons from recent theoretical treatments of Al–M bonds (M = Fe, Cu, Ag, Au) that capture CO2
S. M. Supundrika
Subasinghe
 and
Neal P.
Mankad
and
Neal P.
Mankad
 *
*
Department of Chemistry, University of Illinois Chicago, Chicago, IL 60607, USA. E-mail: npm@uic.edu
First published on 5th August 2024
Abstract
Complexes with Al–M bonds (M = transition metal) have emerged as platforms for discovering new reaction chemistry either through cooperative bond activation behaviour of the heterobinuclear unit or by modifying the properties of the M site through its interaction with the Al centre. Therefore, elucidating the nature of Al–M bonding is critical to advancing this research area and typically involves careful theoretical modelling. This Frontier article reviews selected recent case studies that included theoretical treatments of Al–M bonds, specifically highlighting complexes capable of cooperative CO2 activation and focusing on extracting lessons particular to the Al–M sub-field that will inform future studies with theoretical/computational components.
Introduction
As the area of heterobimetallic chemistry continues to attract attention,1–8 it is of importance to consider heterobinuclear complexes that feature earth's most abundant metal, aluminium. Indeed, studying complexes with direct Al–M bonds has become a frontier area of research with applications in areas such as catalysis9–12 and small molecule activation.13–20 As these applications continue to emerge, it becomes increasingly important to understand the nature of Al–M bonding itself. Canonically, heterobinuclear complexes pairing d-block elements with aluminium are viewed as featuring electropositive aluminium centres serving as donor atoms (aluminyl “metalloligands”) towards transition metal sites. According to this model, the unique reactivity of the transition metal site is imparted by this unconventional bond polarity vis á vis traditional coordination complexes with electronegative donor atoms. This bonding motif is certainly valid in some cases but may not be universal to all Al–M complexes.In this context, elucidating the electronic structures of Al–M bonds is critical. Because gaining this understanding will necessarily involve theoretical analysis, it is important to identify aspects of Al–M bonding that require special treatment theoretically.21 Lessons learnt from such case studies will inform future research in this frontier area. In this Frontier article, we briefly review selected recent cases to summarise some important lessons that have emerged. We have chosen to use Al–M complexes that capture CO2 as a venue. In the domain of anthropogenic greenhouse gases, carbon dioxide (CO2) stands out as the primary contributor to global warming.22 As atmospheric CO2 levels continue to rise, there is an increasing urgency for developing innovative strategies to capture and valorise CO2 to mitigate its environmental impact.23,24 Transition metal complexes have long been known to present promising pathways for CO2 capture due, in part to their ability to access multiple oxidation states during small-molecule activation.25,26 In addition to mononuclear and homobinuclear compounds, CO2 activation by heterobinuclear complexes, particularly those combining main group and transition metal systems, continues to be an area of focus dating back to seminal observations by Floriani.27,28 As discussed herein, our group and several others have recently studied CO2 activation with heterobinuclear complexes pairing d-block elements (e.g. Fe, Cu, Ag, Au) with aluminium.
Nucleophilic Al–M (M = coinage metal) complexes: covalent vs. polarised bonding
Initial discovery & assignment of nucleophilic Au(–I)
In an influential 2019 report,29 Hicks et al. synthesised (NON)Al–AuPtBu3 (1) by reacting the Al(I) nucleophile, K[Al(NON)], with the Au(I) complex, tBu3PAuI (Scheme 1). The resulting Al–Au bond was found to be the shortest on record (2.40 Å). The Al–N and Al–O bond distances in 1 being shorter than in the K[Al(NON)] precursor was attributed by the authors to 2e− oxidation of Al(I) to Al(III) during the formation of 1. However, contributions of molecular charge (i.e., transforming an anion to a neutral species) to these bond contractions were not considered at the time. The authors’ preliminary model for the short Al–Au interaction in 1 was that of a polarised Alδ+–Auδ− bond, i.e. resembling a strong [(NON)Al]+ ← [AuPtBu3]− dative interaction, based on the dramatically higher electronegativity of atomic Au (2.54) compared to atomic Al (1.61) on the Pauling scale. The implication that complex 1 contains a [AuPtBu3]− fragment, and thus a gold centre with formally Au(–I) (auride) character, was provocative since most sub-valent transition metal centres require stabilisation by strong π-acids like CO.30 | ||
| Scheme 1 Synthesis and reactivity of a nucleophilic Al–Au bond originally reported by Hicks et al.29 dipp = 2,6-di-iso-propylphenyl. | ||
The nature of the putatively Alδ+–Auδ− bond was investigated computationally in the same study using density functional theory (DFT), quantum theory of atoms in molecules (QTAIM), and natural orbitals for chemical valence (NOCV) calculations. QTAIM is a conceptual framework used in theoretical chemistry to understand the electronic structure of molecules through analysis of electron density distribution and topology.31,32 In this case, partial atomic charges were assigned from QTAIM calculations based on the integration of electron density over each atomic basin found within the overall density map. NOCV is a method that identifies the natural bond orbitals (NBOs,33i.e., localised wavefunctions resembling canonical Lewis structures) predominantly involved in chemical bonding.34 Like in QTAIM, the NOCV orbitals are derived from analysis of the total electron density of the molecule rather than from arbitrary basis functions sometimes used in standard DFT and NBO calculations.
Comparison of QTAIM partial atomic charges for 1 to those of its synthetic precursors indicated transfer of ∼1.6e− from [Al(NON)]− to [AuPtBu3]+ during Al–Au bond formation.29 The most significant Al/Au NOCV interaction in 1 compared to its synthetic precursor fragments was calculated to be a σ-bond assigned by the authors as Al-to-Au lone pair donation. These two observations were used to justify the formal 2e− oxidation of Al(I) to Al(III) and formal 2e− reduction of Au(I) to Au(–I) during formation of 1. However, one can argue that these analyses were biased because they relied on comparison of 1 to starting fragments defined by the theorists. In other words, the authors based their interpretations of NOCV and QTAIM calculations on comparison of 1 to its ionised fragments, [Al(NON)]− and [AuPtBu3]+. However, DFT calculations disclosed in the same study instead indicated that the lowest energy pathway (by 37–62 kcal mol−1)35 for Al–Au cleavage is not heterolytic but homolytic, i.e. to [Al(NON)]˙ and [AuPtBu3]˙ fragments.29 Thus, in contrast to the theoretical analyses described above and to use the authors’ own words written in the article's ESI, “the bonding interaction should rather be considered as a conventional covalent bond instead of a coordination or some other dative bond”. The further refinement of the bonding model for complex 1 as involving a highly covalent bond between formally Al(II) and Au(0) centres would emerge in later studies (see below).
Based on the observations above and the fact that the QTAIM charge at the Au centre in 1 was calculated to be quite negative (−0.82 au), the authors hypothesised that complex 1 would be nucleophilic at gold, in stark contrast to the typical electrophilic chemistry of molecular gold complexes. Addition of CO2 gas to 1 resulted in metallacarboxylate species 2 in which the Au centre is C-bound to CO2 (Scheme 1). This reaction outcome was used by the authors as further evidence for the presence of a nucleophilic centre with Au(–I) character in 1 that had added to the electrophilic carbon centre of CO2. However, soon afterwards, the same team as well as Liu et al. showed that CO2 inserts readily into corresponding Al–Ag, Al–Cu, and Al–Zn bonds (Fig. 1).36–39 These lighter analogues were calculated to feature significantly less Al–M polarisation and less accumulation of negative charge on the d-block metal; yet, they reacted as (or more) efficiently with CO2 as 1. In the most extreme case, an Al–Zn bond was calculated to accumulate positive charge of 1.26 au on Zn and still react with CO2 to form a metallcarboxylate species with a C-bound Zn centre.39 In other words, efficient CO2 activation to form AlO2C–M bonds does not correlate with nor require negative charge accumulation at M, thus negating the only experimental evidence for the presence of a nucleophilic Au(–I)-like ion in 1. Indeed, as later pointed out by Sorbelli et al.,35 even homobinuclear complexes (i.e., inherently apolar metal–metal bonds) efficiently insert CO2 to form analogous metallacarboxylate structures.
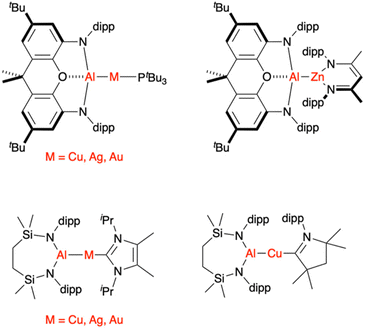 | ||
| Fig. 1 Selected Al–M bonds known to insert CO2 to form metallacarboxylates with C-bound M centres.29,36–39 dipp = 2,6-di-iso-propylphenyl. | ||
Re-interpretation as a covalent, nucleophilic Al–Au bond
In 2021, Sorbelli et al. revisited the computational analysis of 1 and its CO2 reactivity using DFT, extended transition state natural orbitals for chemical valence (ETS-NOCV), and charge displacement (CD) calculations.35 ETS-NOCV is a theoretical method that combines aspects of both transition state theory and NOCV analysis, essentially calculating changes in NOCV distributions occurring along a reaction coordinate.40 CD further partitions this data into partial atomic charge contributions from individual components of the molecule(s).41 Relatedly, the CD-NOCV method breaks down partial atomic charge density contributions that, together, comprise a covalent interaction.42In their report,35 the Sorbelli et al. disfavoured the nucleophilic auride model for 1, instead proposing that 1 contains a highly covalent Al–Au bond that, itself, serves as the nucleophilic electron pair towards CO2. The previous use of Pauling electronegativity values to formulate a polarised Alδ+–Auδ− bond was contradicted by noting that the ionisation energies of the [Al(NON)]˙ and [AuPtBu3]˙ fragments are calculated to be nearly identical (2.53 and 2.56 eV, respectively). The previous use of partial atomic charge calculations to support the Alδ+–Auδ− proposal was also called into question by noting that the partial atomic charge at Au in 1 varies from −0.83 to +0.22 au depending on the charge partitioning scheme used in the calculations.43
The overall CD-NOCV analysis of the Al–Au bond in 1 indicated only slight polarisation of 0.05e− towards the Au centre.35 This was partitioned into two charge fluxes, one from Au towards Al and the other from Al towards Au, that approximately counterbalanced each other (Fig. 2). Based on these observations and others, the authors assigned the Al–Au bond in 1 as involving formally Al(II) and Au(0) centres engaged in a bond with a high degree of covalency. Based on the bidirectional charge fluxes apparent by CD-NOCV, the authors also chose to describe the nature of 1 as “diradical-like” despite the calculated Al–Au bond energy of 83 kcal mol−1 precluding the formation of any radicals at standard conditions.35,44 Indeed, complete active space self-consistent field (CASSCF) calculations (known to be more accurate than DFT) later reported by Guo et al. indicated that the contributions of open-shell configurations are small and that the active electrons remain paired throughout the CO2 activation pathway.45 Thus, description of the chemistry of 1 as “diradical-like” is questionable, in our view.
 | ||
| Fig. 2 CD-NOCV curves for the interaction between [Al(NON)]˙ and [AuPtBu3]˙ fragments, with isodensity surfaces (1 me− a0−3) shown for the two main deformation densities contributing to Al–Au bonding (charge flux: red → blue). Image reproduced with permission from Sorbelli et al.35 | ||
In the 2021 study by Sorbelli et al., the reaction pathway for 1 and CO2 converting to 2 was calculated.35 The calculated mechanism is, effectively, a [2 + 2] cycloaddition involving the Al–Au σ-bonding pair and one of the CO2 π-bonding pairs, followed by rearrangement from κ1-to κ2-metallcarboxylate binding to aluminium. Interestingly, the calculated [2 + 2] transition state structure features the carbon centre of CO2 interacting with both Au and Al (M–C Mayer bond orders of 0.26 and 0.16, respectively), consistent with the Al–Au bond (and not a formal auride centre) acting as the nucleophilic electron pair. An analogous transition state geometry was calculated in 2022 by Guo et al. (Fig. 3), who also found that the Al–C interaction is even more significant at the transition state for the reaction of an Al–Cu analogue.45 ETS-NOCV calculations by Sorbelli et al. indicated that the major interaction during CO2 activation by 1 involves the transfer of electron density (0.33e−) from both Al and Au (specifically, from the Al–Au σ-bond region) to CO2 (specifically, its LUMO).35 Intrinsic bond orbital (IBO) calculations, which track changes in NBOs as a function of intrinsic reaction coordinate,46 were performed by Guo et al.45 The results (Fig. 4) agree with the results of Sorbelli et al. conceptually and are readily interpreted as involving flow of two reactive electron pairs: transformation of the Al–Au σ-bonding orbital into an Al–C σ-bonding orbital, and transformation of the CO2 π-bonding orbital into an Al–O σ-bonding orbital. Collectively, these computational models converge on the concept of the Al–Au σ-bond being the nucleophilic electron pair that adds to the CO2 carbon centre via a [2 + 2]-like transition state, with the C-bound rather than O-bound aurocarboxylate forming due to a secondary Lewis acid/base interaction between the Al site and the CO2 oxygen centre rather than being indicative of nucleophilic character at any individual atom within 1.
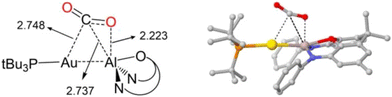 | ||
| Fig. 3 Calculated transition state for CO2 activation by 1.35,44,45 Image reproduced with permission from Guo et al.45 | ||
 | ||
| Fig. 4 IBO analysis of the reaction between 1 and CO2. Image reproduced with permission from Guo et al.45 | ||
Cooperative CO2 activation at a weak Al–Fe bond: frustrated radical pair behaviour
For about a decade (2012–2022), our group had studied (NHC)Cu–Fp complexes (NHC = N-heterocyclic carbene, Fp = FeCp(CO)2) with reactive Cu–Fe bonds.5,47,48 All physical and computational data indicated that such complexes contained polar Cuδ+–Feδ− bonds with Wiberg bond orders49 of <0.5 and with an accumulation of negative charge at the Fe centres.50–52 (Note that the proposed Cuδ+–Feδ− polarisation opposes the relative Pauling electronegativity values: Cu, 1.90; Fe, 1.83.) As such, depending on reaction conditions, we typically proposed either that (NHC)Cu–Fp complexes react as Fe(0) nucleophiles (akin to the auride proposal of Hicks et al. discussed above) or that they dissociate heterolytically to reveal [(NHC)Cu]+[Fp]− ion pairs with frustrated Lewis pair (FLP)53,54 behaviour.47,55–58In 2022, our group synthesised LAl(Me)Fp (3) by reacting the metallonucleophile, KFp, with the Al(III) β-diketiminate complex, LAl(Me)I (Scheme 2, L = HC[MeCNdipp]2−, dipp = 2,6-di-iso-propylphenyl).59 The resulting Al–Fe bond was found to be among the shortest on record (2.48 Å). Computational modelling revealed that the Al–Fe bond is significantly more covalent than the previously studied Cu–Fe systems, with a Wiberg bond order of >0.8 based on NBO calculations and with relatively less accumulation of negative charge at Fe according to theoretical QTAIM analysis. Moreover, whereas the heterolytic bond dissociation energy (BDE) of 3 to [LAlMe]+[Fp]− was calculated to be quite high (59 kcal mol−1), homolytic dissociation of 3 to the [LAlMe]˙/[Fp]˙ radical pair was calculated to be energetically accessible (25 kcal mol−1) at standard conditions. Thus, while the polar Cu–Fe bonds previously studied by our group were viewed as masked FLPs, the covalent Al–Fe bond in 3 can be regarded as a masked frustrated radical pair (FRP).60–62 Due to the covalent nature of the Al–Fe bond, oxidation state assignments have not been proposed in the literature for 3 and, arguably, are irrelevant to understanding chemical reactivity.
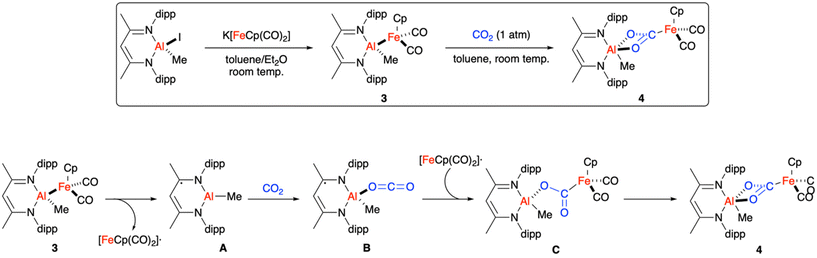 | ||
| Scheme 2 Synthesis and reactivity of a weak, covalent Al–Fe bond reported by Sinhababu et al.59 dipp = 2,6-di-iso-propylphenyl. | ||
Exposure of 3 to CO2 gas provided metallacarboxylate species 4 (Scheme 2).59 The mechanism for this transformation proposed by Sinhababu et al. is shown in Scheme 2. A reasonable pathway was calculated by DFT and, in accord with recent findings by Mears et al. on an Al–Cu system,21 required the use of dispersion corrections to the DFT functional along with the inclusion of all ligand substituents (as opposed to use of simplified models). In the proposed mechanism, spontaneous homolytic Al–Fe dissociation from 3 releases [Fp]˙ and forms [LAlMe]˙ intermediate A. While the [LAlMe]˙ formula would indicate an Al(II) formal oxidation state, DFT calculation of spin density indicated that A is better assigned as having an Al(III) centre bound to the 1e− reduced form of L. As such, the redox non-innocence of L must contribute significantly to the low homolytic BDE of 3. Coordination of CO2 to the Lewis acidic Al(III) site in A produces [LAl(Me)(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)]˙ intermediate B. Finally, net 2e− reduction of CO2 involves coupled delivery of 1e− from the non-innocent L ligand and 1e− from [Fp]˙ to generate κ1-metallacarboxylate C, which rearranges to κ2-isomer 4.
O)]˙ intermediate B. Finally, net 2e− reduction of CO2 involves coupled delivery of 1e− from the non-innocent L ligand and 1e− from [Fp]˙ to generate κ1-metallacarboxylate C, which rearranges to κ2-isomer 4.
In support of this mechanistic proposal, a synthetic model of B, namely [LAl(Me)(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)]˙, was isolated experimentally by replacing CO2 with benzophenone and characterised spectroscopically.59 An alternative mechanism involving heterolytic dissociation of 3 to the [LAlMe]+[Fp]− ion pair followed by FLP-like CO2 activation was ruled out based on the high heterolytic BDE calculated by DFT (see above) as well as FRP-like regioselectivity during ring opening of propylene oxide by 3.63 A concerted, [2 + 2]-like mechanism (such as that discussed in the previous section for 1 proposed by Sorbelli et al. and Guo et al.) involving direct engagement of CO2 with the covalent Al–Fe bond of 3 was ruled out based on the large and positive entropy of activation for CO2 insertion measured experimentally, as well as the fact that the Al–Fe homolytic BDE was computed to be lower than the [2 + 2] activation energy by ∼15 kcal mol−1.
CPh2)]˙, was isolated experimentally by replacing CO2 with benzophenone and characterised spectroscopically.59 An alternative mechanism involving heterolytic dissociation of 3 to the [LAlMe]+[Fp]− ion pair followed by FLP-like CO2 activation was ruled out based on the high heterolytic BDE calculated by DFT (see above) as well as FRP-like regioselectivity during ring opening of propylene oxide by 3.63 A concerted, [2 + 2]-like mechanism (such as that discussed in the previous section for 1 proposed by Sorbelli et al. and Guo et al.) involving direct engagement of CO2 with the covalent Al–Fe bond of 3 was ruled out based on the large and positive entropy of activation for CO2 insertion measured experimentally, as well as the fact that the Al–Fe homolytic BDE was computed to be lower than the [2 + 2] activation energy by ∼15 kcal mol−1.
Conclusions
Since heterobinuclear metal–metal bonds between p-block and d-block metals are historically less studied than metal–metal bonds between two d-block metals, it is unsurprising that frontier Al–M complexes like 1 and 3 would challenge traditional bonding paradigms, require careful iterations of interpretation and re-interpretation, and give rise to unconventional reaction pathways. As briefly reviewed here, complex 1 was originally assigned as having a polar Alδ+–Auδ− bond featuring a nucleophilic gold centre assigned as formally Au(–I). Subsequent re-evaluations led to reassignment as a covalently bonded, nucleophilic [Al–Au] unit best formulated as involving formal Al(II) and Au(0) centres. Lessons from the analysis of 1 and its reaction pathways informed studies of Al–Fe complex 3, which in turn provided additional lessons for the community to consider.When analysing the nature of Al–M bonds, certain trends may be emerging based on case studies presented here:
• Al–M bonds tend to be more covalent than analogous M–M bonds involving only d-block metals. This may be due to the stronger valence orbital overlap imparted by greater s/p character at aluminium relative to predominantly d character of a transition metal substitute.
• These covalent Al–M bonds are best analysed theoretically relative to their neutral (radical) fragments, even if they are synthesised from ionic precursors experimentally. Often, this is evident by comparing homolytic vs. heterolytic BDEs computationally.
• Atomic electronegativity values can be misleading since they do not necessarily reflect the properties of an atom in a molecular setting.
• Partial atomic charge calculations are method-dependent,43 making their absolute values sometimes misleading. It is more appropriate to focus on trends in partial atomic charges across a series of interrelated compounds.
• Al–M bonds can involve anomalously high levels of dispersion forces.21 Partly for this reason, it can be useful to base theoretical analyses on full molecules rather than truncated model systems.
Additionally, some lessons emerge from these case studies regarding the analysis of reaction pathways (e.g. CO2 activation):
• For CO2 activation by Al–M bonds, it is not necessary for there to be an accumulation of negative charge at M. Additionally, the formation of a C-bound metallacarboxylate does not necessarily imply that the M centre is, by itself, a nucleophilic site.
• For covalently bonded [Al–M] units, the assignment of oxidation states can be irrelevant or even misleading for interpreting reactivity behaviour. A parallel can be drawn to the Enemark–Feltham system for analysing covalent [M–NO]n units.64
• When making proposals about reaction mechanisms, it is more reliable to analyse changes in computed parameters over an entire reaction coordinate rather than focusing on the reactant Al–M bond itself.
• Where possible, one should measure experimental observables (e.g., activation parameters) reporting on the nature of a transition state to validate theoretical conclusions and help rule out alternative mechanisms.
Given the vibrant activity in the Al–M space, we expect new discoveries in small molecule activation and catalysis to continue emerging from studies of these fascinating metal–metal bonds. We hope that the brief reflection presented here will aid this research community as it continues to progress.
Author contributions
S. M. S. S. conceptualised the article and wrote the first draft. N. P. M. edited the manuscript and acquired funding.Data availability
No primary research results have been included and no new data were generated as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Grant DE-SC0021055.References
- J. Campos, Nat. Rev. Chem., 2020, 4, 696–702 CrossRef CAS PubMed.
- I. G. Powers and C. Uyeda, ACS Catal., 2017, 7, 936–958 CrossRef CAS.
- J. A. Chipman and J. F. Berry, Chem. Rev., 2020, 120, 2409–2447 CrossRef CAS PubMed.
- B. G. Cooper, J. W. Napoline and C. M. Thomas, Catal. Rev., 2012, 54, 1–40 CrossRef CAS.
- H.-C. Yu and N. P. Mankad, Synthesis, 2020, 1409–1422 Search PubMed.
- S. Sinhababu, Y. Lakliang and N. P. Mankad, Dalton Trans., 2022, 51, 6129–6147 RSC.
- R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111 CrossRef CAS.
- R. M. Charles and T. P. Brewster, Coord. Chem. Rev., 2021, 433, 213765 CrossRef CAS PubMed.
- R. P. Singh, S. Sinhababu and N. P. Mankad, ACS Catal., 2023, 13, 12519–12542 CrossRef CAS.
- N. Hara, K. Semba and Y. Nakao, ACS Catal., 2022, 12, 1626–1638 CrossRef CAS.
- Y.-X. Luan and M. Ye, Chem. Commun., 2022, 58, 12260–12273 RSC.
- Y. Nakao, Chem. Rev., 2021, 121, 327–344 CrossRef CAS PubMed.
- R. Y. Kong and M. R. Crimmin, Dalton Trans., 2021, 50, 7810–7817 RSC.
- N. Gorgas, A. J. P. White and M. R. Crimmin, J. Am. Chem. Soc., 2022, 144, 8770–8777 CrossRef CAS PubMed.
- N. Gorgas, A. J. P. White and M. R. Crimmin, Chem. Commun., 2022, 58, 10849–10852 RSC.
- B. Stadler, N. Gorgas, A. J. P. White and M. R. Crimmin, Angew. Chem., Int. Ed., 2023, 62, e202219212 CrossRef CAS PubMed.
- R. C. Cammarota and C. C. Lu, J. Am. Chem. Soc., 2015, 137, 12486–12489 CrossRef CAS PubMed.
- A. B. Thompson, D. R. Pahls, V. Bernales, L. C. Gallington, C. D. Malonzo, T. Webber, S. J. Tereniak, T. C. Wang, S. P. Desai, Z. Li, I. S. Kim, L. Gagliardi, R. L. Penn, K. W. Chapman, A. Stein, O. K. Farha, J. T. Hupp, A. B. F. Martinson and C. C. Lu, Chem. Mater., 2016, 28, 6753–6762 CrossRef CAS.
- B. J. Graziano, M. V. Vollmer and C. C. Lu, Angew. Chem., 2021, 133, 15214–15221 CrossRef.
- M. V. Vollmer, J. Ye, J. C. Linehan, B. J. Graziano, A. Preston, E. S. Wiedner and C. C. Lu, ACS Catal., 2020, 10, 2459–2470 CrossRef CAS.
- K. L. Mears, C. R. Stennett, E. K. Taskinen, C. E. Knapp, C. J. Carmalt, H. M. Tuononen and P. P. Power, J. Am. Chem. Soc., 2020, 142, 19874–19878 CrossRef CAS PubMed.
- J. Hansen and M. Sato, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16109–16114 CrossRef CAS PubMed.
- A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer, G. L. Waldrop, A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Chem. Rev., 2013, 113, 6621–6658 CrossRef CAS PubMed.
- M. D. Burkart, N. Hazari, C. L. Tway and E. L. Zeitler, ACS Catal., 2019, 9, 7937–7956 CrossRef CAS.
- A. Paparo and J. Okuda, Coord. Chem. Rev., 2017, 334, 136–149 CrossRef CAS.
- D. H. Gibson, Chem. Rev., 1996, 96, 2063–2096 CrossRef CAS PubMed.
- G. Fachinetti, C. Floriani and P. F. Zanazzi, J. Am. Chem. Soc., 1978, 100, 7405–7407 CrossRef CAS.
- S. Gambarotta, F. Arena, C. Floriani and P. F. Zanazzi, J. Am. Chem. Soc., 1982, 104, 5082–5092 CrossRef CAS.
- J. Hicks, A. Mansikkamäki, P. Vasko, J. M. Goicoechea and S. Aldridge, Nat. Chem., 2019, 11, 237–241 CrossRef CAS PubMed.
- V. R. Landaeta, T. M. Horsley Downie and R. Wolf, Chem. Rev., 2024, 124, 1323–1463 CrossRef CAS PubMed.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford University Press, Oxford, England, New York, 1994 Search PubMed.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355 CrossRef CAS PubMed.
- D. Sorbelli, L. Belpassi and P. Belanzoni, J. Am. Chem. Soc., 2021, 143, 14433–14437 CrossRef CAS PubMed.
- C. McManus, J. Hicks, X. Cui, L. Zhao, G. Frenking, J. M. Goicoechea and S. Aldridge, Chem. Sci., 2021, 12, 13458–13468 RSC.
- H. Liu, R. J. Schwamm, M. S. Hill, M. F. Mahon, C. L. McMullin and N. A. Rajabi, Angew. Chem., Int. Ed., 2021, 60, 14390–14393 CrossRef CAS PubMed.
- H.-Y. Liu, S. E. Neale, M. S. Hill, M. F. Mahon and C. L. McMullin, Dalton Trans., 2022, 51, 3913–3924 RSC.
- M. M. D. Roy, J. Hicks, P. Vasko, A. Heilmann, A.-M. Baston, J. M. Goicoechea and S. Aldridge, Angew. Chem., Int. Ed., 2021, 60, 22301–22306 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- G. Bistoni, L. Belpassi and F. Tarantelli, J. Chem. Theory Comput., 2016, 12, 1236–1244 CrossRef CAS PubMed.
- G. Bistoni, S. Rampino, F. Tarantelli and L. Belpassi, J. Chem. Phys., 2015, 142, 084112 CrossRef PubMed.
- M. Cho, N. Sylvetsky, S. Eshafi, G. Santra, I. Efremenko and J. M. L. Martin, ChemPhysChem, 2020, 21, 688–696 CrossRef CAS PubMed.
- D. Sorbelli, L. Belpassi and P. Belanzoni, Inorg. Chem., 2022, 61, 1704–1716 CrossRef CAS PubMed.
- X. Guo, T. Yang, Y. Zhang, F. K. Sheong and Z. Lin, Inorg. Chem., 2022, 61, 10255–10262 CrossRef CAS PubMed.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- N. P. Mankad, Chem. Commun., 2018, 54, 1291–1302 RSC.
- N. J. Leon, H.-C. Yu, T. J. Mazzacano and N. P. Mankad, Synlett, 2020, 125–132 CAS.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- M. K. Karunananda, F. X. Vázquez, E. E. Alp, W. Bi, S. Chattopadhyay, T. Shibata and N. P. Mankad, Dalton Trans., 2014, 43, 13661–13671 RSC.
- S. Banerjee, M. K. Karunananda, S. Bagherzadeh, U. Jayarathne, S. R. Parmelee, G. W. Waldhart and N. P. Mankad, Inorg. Chem., 2014, 53, 11307–11315 CrossRef CAS PubMed.
- U. Jayarathne, T. J. Mazzacano, S. Bagherzadeh and N. P. Mankad, Organometallics, 2013, 32, 3986–3992 CrossRef CAS.
- D. W. Stephan, Science, 2016, 354, aaf7229 CrossRef PubMed.
- A. R. Jupp and D. W. Stephan, Trends Chem., 2019, 1, 35–48 CrossRef CAS.
- M. K. Karunananda, S. R. Parmelee, G. W. Waldhart and N. P. Mankad, Organometallics, 2015, 34, 3857–3864 CrossRef CAS.
- S. R. Parmelee, T. J. Mazzacano, Y. Zhu, N. P. Mankad and J. A. Keith, ACS Catal., 2015, 5, 3689–3699 CrossRef CAS.
- M. K. Karunananda and N. P. Mankad, Organometallics, 2017, 36, 220–227 CrossRef CAS.
- D. R. Pye, L.-J. Cheng and N. P. Mankad, Chem. Sci., 2017, 8, 4750–4755 RSC.
- S. Sinhababu, M. R. Radzhabov, J. Telser and N. P. Mankad, J. Am. Chem. Soc., 2022, 144, 3210–3221 CrossRef CAS PubMed.
- M. Ju, Z. Lu, L. F. T. Novaes, J. I. Martinez Alvarado and S. Lin, J. Am. Chem. Soc., 2023, 145, 19478–19489 CrossRef CAS PubMed.
- L. Liu, L. L. Cao, Y. Shao, G. Ménard and D. W. Stephan, Chem, 2017, 3, 259–267 CAS.
- A. Dasgupta, E. Richards and R. L. Melen, Angew. Chem., Int. Ed., 2021, 60, 53–65 CrossRef CAS PubMed.
- S. Sinhababu, R. P. Singh, M. R. Radzhabov, J. Kumawat, D. H. Ess and N. P. Mankad, Nat. Commun., 2024, 15, 1315 CrossRef CAS PubMed.
- J. H. Enemark and R. D. Feltham, Coord. Chem. Rev., 1974, 13, 339–406 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |


