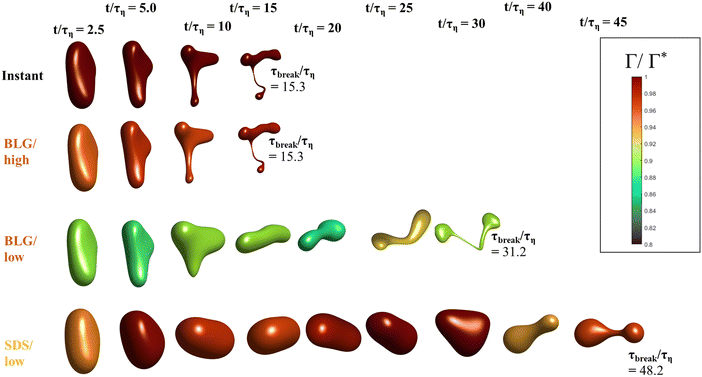Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Emulsifier adsorption kinetics influences drop deformation and breakup in turbulent emulsification
Andreas
Håkansson
 * and
Lars
Nilsson
* and
Lars
Nilsson

Department of Food Technology, Engineering and Nutrition, Lund University, Sweden. E-mail: andreas.hakansson@food.lth.se
First published on 14th November 2023
Abstract
Turbulent drop breakup is of large importance for applications such as food and pharmaceutical processing, as well as of substantial fundamental scientific interest. Emulsification typically takes place in the presence of surface-active emulsifiers (natural occurring and/or added). Under equilibrium conditions, these lower the interfacial tension, enabling deformation and breakup. However, turbulent deformation is fast in relation to emulsifier kinetics. Little is known about the details of how the emulsifier influences drop deformation under turbulent conditions. During the last years, significant insight in the mechanism of turbulent drop breakup has been reached using numerical experiments. However, these studies typically use a highly simplistic description of how the interface responds to turbulent stress. This study investigates how the limited exchange rate of emulsifier between the bulk and the interface influences the deformation process in turbulent drop breakup for application-relevant emulsifiers and concentrations, in the context of state-of-the-art single drop breakup simulations. In conclusion, if the Weber number is high or the emulsifier is supplied at a concentration giving an adsorption time less than 1/10th of the drop breakup time, deformation proceeds as if the emulsifier adsorbed infinitely fast. Otherwise, the limited emulsifier kinetics delays breakup and can alter the breakup mechanism.
1. Introduction
Turbulent emulsification is a fundamentally complex phenomenon where intermittent turbulent structures interact with a viscous interface,1–8 typically in the presence of surface-active emulsifiers (added or naturally occurring).6–8 The emulsifiers interact and modify the interface by several different mechanisms, each with its own timescale.9–14 Turbulent drop breakup is of considerable industrial interest for the processing of colloidal food systems such as emulsions,15–17 since it is the dominating mechanism in high-energy density emulsification devices such as high-pressure homogenizers and rotor-stator mixers.3,18–22Empirical investigations suggest that if the emulsifier is supplied at a sufficiently high concentration, turbulent drop breakup dominates the emulsification process and the resulting emulsion drop diameter is controlled by the physical properties of the two phases, the interfacial tension delivered by the emulsifier (γ) and the dissipation rate of turbulent kinetic energy of the flow (ε), as described by a Weber number, defined as the ratio between disruptive stress and the cohesive Laplace pressure. Assuming that the drop is large in comparison to the smallest eddies of the turbulence, the Weber number is given by,
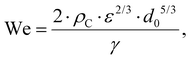 | (1) |
If the emulsifier concentration is below a critical limit, however, re-coalescence dominates28–32 and the emulsification process results in the drop diameter which is able to achieve a sufficiently high surface coverage. For an emulsifier soluble in the continuous phase, the critical concentration forming the demarcation between the two regimes is,6,7
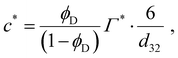 | (2) |
During the last decade, in addition to experimental single drop breakup visualization studies,14,33–38 substantial advances in understanding turbulent drop and bubble breakup has been reached using simulation-based techniques. These studies combine direct numerical simulation (DNS) with highly resolved interface tracking.10–12,39–46 The simulations based on DNS offer an unprecedented ability to describe the turbulent interaction free of modelling assumptions and at a high spatial and temporal resolution. However, from a colloidal chemistry perspective, the studies are based on rather crude descriptions of how the interface responds to stress and how this is related to the presence of an emulsifier. Typically, the interface is described using an interfacial tension, assumed to be uniform and constant in time. This is equivalent to assuming that the exchange of emulsifier between bulk and interface is infinitely fast,41i.e., as soon as the interface starts to deform due to a turbulent interaction, adsorption is fast enough to restore the original surface load instantly. Moreover, this implies that the state-of-the-art in these simulations neglect adsorption kinetics, and all effects of interfacial rheology. Some numerical studies have been performed including the Marangoni effects resulting from an uneven distribution of surface-active material, however only for a highly idealized system.47,48
It is problematic that the numerical literature on drop breakup relies on assuming an instantaneous emulsifier exchange, especially so in the studies including coalescence.42,43,49,50 However, assuming an instantaneous emulsifier exchange is also problematic when studying pure breakup, since the timescales of turbulent deformation and turbulently driven adsorption are generally considered to be similar.7,9 This suggests that adsorption often have difficulties keeping up with deformation, especially when considering larger polymeric emulsifiers [p. 82].9 When adsorption is not much faster than deformation, surface load decreases upon deformation, leading to an increase in interfacial tension, thus, increasing the drop's resistance to deformation. Moreover, the magnitude of this additional resistance to deformation differs between emulsifiers as characterized by their Gibbs elasticity,51,52
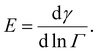 | (3) |
Furthermore, at least for low-molecular weight surfactants, with high interfacial mobility, localized deformation gives rise to spatial gradients in surface load driving additional restorative Marangoni flow. Protein emulsifiers, on the other hand, often display substantial effects of interfacial rheology such as interfacial shear and dilatational viscosity and interfacial shear and dilatational elasticity.53,54
From previous investigations, it is well known that the adsorption kinetics and interfacial rheology brought about by the properties imposed by the emulsifier is essential to understand coalescence,32,51,55 as well as to understand slow laminar deformation.56,57 The effect emulsifiers have on turbulent breakup (beyond the effect on the equilibrium value of the interfacial tension) is less well understood. One reason is that it is difficult-theoretically impossible, some argue19-to build an experimental system allowing direct visualization with high-speed imaging that correctly scales both adsorption/deformation timescales and hydrodynamics. Thus, simulation-based techniques are required to understand these phenomena.
The aim of the present contribution is to investigate how the limited exchange rate of emulsifier between the bulk and the interface influences the deformation process in turbulent drop breakup. Our focus is on settings corresponding to oil-in-water emulsions with application-relevant properties and concentrations of emulsifiers, in the context of state-of-the-art single drop breakup simulations. Application we aim to understand in the long run include processing of milk, mayonnaise, and dressings (food technology), and processing of intravenous emulsions (pharmaceutical technology).
In this first step it is assumed that the effect of the emulsifier is in lowering the interfacial tension in relation to the increase in surface load brough about by adsorption, as described by the adsorption kinetics and surface equation of state of the system. It is assumed that the emulsifier is surface active as soon as it arrives at the interface (neglecting unfolding/structural change processes sometimes necessary when arriving at the interface), that the effect of interfacial shear and/or dilatational viscosity does not have time to appear, and that the emulsifier distributes itself instantly across the interface (i.e., interfacial tension is assumed to be spatially homogeneous). Such an instant re-distribution across the interface has been argued to be a relevant assumption in (e.g., food) emulsification due to longitudinal waves acting to counter spatial gradients in surfactant concentrations.9 Under these assumptions, the dynamic effect of the emulsifier is described by a limited number of parameters (see Section 2.3). Thus, the general approach of this study is to analyse how drop deformation and breakup is influenced under application-relevant combinations of these parameters, using numerical drop breakup experiments as the methodological framework.
2. Theory and computational methods
2.1 Single drop breakup simulation methodology
Numerical breakup experiments have been used extensively in fluid mechanics literature to study turbulent breakup.10–12,40–48 A more comprehensive description of our methodology can be found elsewhere.40 In brief, we inject a single spherical drop into a cuboidal domain with periodic boundaries and containing a developed, forced, isotropic and homogeneous turbulence (Taylor Reynolds number, Reλ = 32). By solving the Navier–Stokes equations coupled to a MTHIC volume-of-fluid (VOF) scheme describing the interface42,58 the evolution of the flow-field and of the drop is followed with high temporal and spatial resolution (spatial resolution corresponding to 41 cells across the initial drop – see ref. 40 for a mesh-dependence study). The temporal resolution is 0.001τη, where τη denotes the Kolmogorov timescale of the turbulent flow,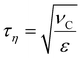 | (4) |
Note that the methodology entails solving for full two-way coupling between the continuous phase turbulent flow and the interface. The volume fraction of disperse phase is set low (1.7%) ensuring that drop filaments does not start interacting with other parts of the drop through the periodic boundaries.
Simulations are based on the CaNS implementation,59 which has been extensively tested and validated in previous studies. For emulsification under conditions like those investigated in the present study, good agreement has previously been found between simulations and high-speed breakup visualizations60 as well as between simulations and emulsification experiments.61
Traditionally, when neglecting emulsifier adsorption dynamics and interfacial rheology, three factors are expected to control breakup: the Weber number (We), the disperse to continuous phase viscosity ratio (μD/μC), and the disperse to continuous phase density ratio (ρD/ρC). Empirical studies also suggest that the ratio of the initial drop-diameter to the Kolmogorov length-scale (d0/η) plays a role, at least in the turbulent inertial regime.22,40 In the majority of the simulations in the present study, we set We = 5, μD/μC = 20, ρD/ρC = 0.9 and d0/η = 22. From an application perspective, this represents the smallest viscous oil drops breaking in an emulsification device.40 To compare the behaviour of small versus large drops, we also run a sequence of tests with We = 30, corresponding, approximately, to the behaviour of the largest drops entering an emulsification device.40,41
Note, however, that this direct translation of We to drop size is only possible when considering single emulsifier systems. The different emulsifiers studied (see Section 2.3) give rise to different value of the interfacial tension. Thus, We = 5 corresponds to a smaller drop diameter (in physical units) when considering an emulsifier with a higher interfacial pressure.
2.2 Modelling simultaneous adsorption and deformation/breakup
Under quiescent conditions, such as in a dynamic pendant drop experiment, adsorption is either diffusion controlled as described by a Ward–Tordai model62,63 or approximately ‘barrier-limited’, for example as described by a Langmuir–Hinshelwood model.62,64,65Turbulent emulsification is far from quiescent, however, and turbulent ‘eddies’ will lead to a substantial increase in the collision rate between drops, particles and/or molecules,66–68 leading to an increase in the effective adsorption rate.69 Assuming turbulent breakup to occur in the inertial regime (i.e., the drop diameter is large in comparison to the Kolmogorov length-scale of the turbulence), we model the adsorption rate as the collision rate between the emulsion drop (diameter d0) and a sphere with a volume-equivalent diameter of the emulsifier (dE), multiplied with an collision efficiency, taken to vary linearly with (1 − Γ/Γ*):64,68–71
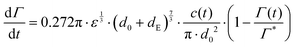 | (5) |
From the adsorption rate model in eqn (5) we define the adsorption timescale, τads, as the time required to reach a surface load of Γ = 0.99Γ*, following an instantaneous 5% increase in interfacial area (see Appendix A for derivation):
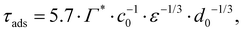 | (6) |
To integrate this adsorption model into the single drop deformation simulation framework outlines above (Section 2.1), a multi-scale modelling approach is used. Each drop is assumed to enter the emulsification device after a pre-emulsification stage; hence, it is in equilibrium with the emulsifier-solution having an initial surface load, Γ0, given by the equilibrium adsorption isotherm of the respective emulsifier (see Section 2.3). The DNS-framework is used for advancing the flow-field and the interface in time. Every Δt = 0.01τη (chosen sufficiently small not to influence how deformation evolves over time and representing approximately 10 time-steps in the DNS/VOF), the simulations are stopped, and the surface load in step k, Γk, is updated from mass conversion based on the adsorption rate (eqn (5))64
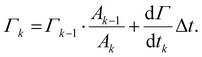 | (7) |
Depletion of emulsifier bulk concentration is described using a simple mass balance in the limit of a low volume-fraction of disperse phase,64
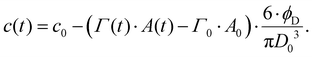 | (8) |
Note that this methodology allows for a time-varying interfacial tension but assumes that there are no spatial gradients in the surface load across the interface. Thus, once adsorbed, the emulsifiers are assumed to instantly spread across the interface. According to Walstra and Smulders9 this is a reasonable assumption for turbulent emulsification due to the redistributing effect of longitudinal waves.
2.3 Identification of realistic emulsifier parameters
Under the simplifying assumptions outlined above (Section 1), each emulsifier (in combination with a particular choice of disperse and continuous phases liquids) can be described by a limited number of parameters: the initial bulk concentration of the emulsifier (c0), the hydrodynamic diameter of the emulsifier/micelle (de), the equilibrium isotherm (describing the initial surface load corresponding to c0) and the surface equation of state (relating the interfacial tension to the surface load at each point in time). In particular, the surface equation of state includes information about the interfacial tension for the pure interface (γmax), the interfacial tension when the surface is fully covered (γmin), and the surface load corresponding to this ‘fully covered’ state (Γ*).As seen from the definition of We in eqn (1) (and from viscosity-corrected Kolmogorov–Hinze theory7,22–27), an emulsifier providing a lower interfacial tension will result in smaller drops. In this study, however, we want to compare the effect of different emulsifiers at the same Weber number (since We is the primary quantity controlling the turbulent deformation and breakup). Thus, since We is kept constant when comparing between emulsifiers, it is not the absolute value of the interfacial tension that matters but how much interfacial tension increases following a decrease in surface load from the initial value (which is typically equal to Γ* since the drop has been subjected to pre-emulsification in the presence of emulsifier at a concentration higher than the critical micelle concentration).
Fig. 1 displays normalized surface equations of state for three different emulsifier systems: (i) the non-ionic triblock copolymer Pluronic F-68 (F68) at the vegetable oil/water interface, (ii) the anionic low-molecular weight surfactant sodium dodecyl sulfate (SDS) at the dodecane/water interface; and (iii) the milk protein β-lactoglobulin (BLG) at the tetradecane/water interface. All three emulsifiers are soluble in the continuous aqueous phase, and commonly used as model emulsifiers for studying emulsification. (Physical properties, equilibrium adsorption isotherms, and surface equations of state are taken from literature and are summarized in Table 1.) The horizontal axis in Fig. 1 displays the normalized surface load, Γ/Γ*, indicating how close the surface load is to its maximum value. The vertical axis shows the interfacial tension scaled with its value when the surface load approaches Γ* (i.e., interfacial tension at ‘full coverage’).
 | ||
| Fig. 1 Interfacial tension (normalized to its minimum value, γmin, reached at full surface coverage) as a function of surface load (Γ/Γ*), based on literature data for SDS72,74 BLG73 and F68.64 | ||
| Triblock copolymer (F68) | Sodium dodecyl sulfate (SDS) | β-Lactoglobulin (BLG) | |
|---|---|---|---|
| Emulsion | Vegetable oil in water | Dodecane in water | Tetradecane in water |
| Temperature | 25 °C | 20 °C | 22 °C |
| Molecular weight of emulsifier (M) [kg mol−1] | 8.464 | 0.288 | 18.381,82 |
| Hydrodynamic diameter (dE) [nm] | 1279 (micelle) | 480 (micelle) | 783 (dimer) |
| Isotherm parameter (Γ*) [mol m−2−] | 1.4 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 64 |
5.2 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
0.11 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73 73 |
| Equilibrium adsorption isotherm | Langmuir isotherm64 | Two states model72 | Multiple-state model73,82,84 |
| Interfacial tension at Γ = 0(γmax) [mN m−1] | 19.664 | 51.372 | 51.373,84 |
| Interfacial tension at Γ = Γ*(γmin) [mN m−1] | 8.064 | 7.1872 | 20.673,82 |
| Surface equation of state | Szsyzkowski/Frumkin equation64 | Two states model72 | Multiple-state model73,82,84 |
| Critical micelle concentration (cCMC) [mol m−3] | 0.4864 | 8.372 | — |
| Technically relevant low conc. (clow) [mol m−3] | 2·cCMC | 2·cCMC | 1.7 |
| Technically relevant high conc. (chigh) [mol m−3] | 20·cCMC | 20·cCMC | 0.17 |
In Fig. 1, first, note that BLG and F68 result in similar normalized interfacial tension curves, despite that they correspond to two molecularly dissimilar emulsifiers (protein vs. non-ionic block copolymer) operating on two molecularly dissimilar disperse phase liquids (hydrocarbon vs. vegetable oil). More specifically, the rate at which the interfacial tension increases with a small decrease in surface load is similar near Γ ∼ Γ* for these two systems. The third system (SDS) gives rise to a substantially faster increase in interfacial tension when decreasing the surface load. This follows from that the Gibb's elasticity of the BLG and F68 are similar (90 and 88 mN m−1, as calculated from their surface equations of state and eqn (3)) and lower than for SDS (125 mN m−1). Also note that SDS can, if the surface load is substantially reduced, lead to a substantially larger relative increase in interfacial tension compared to its initial (nominal) value (factor 7 for SDS as compared to a factor 2.5 for BLG and F68).
In this study, we use the three emulsifier systems from Fig. 1 and Table 1 (F68, SDS and BLG) as illustrative cases to study how adsorption kinetics influences turbulent deformation and breakup. The choice of these three is based on (a) availability of high-quality experimental data and surface equations of states, (b) that these three represent the three main classes of emulsifiers found in food applications, and (c) that they allow us to investigate the effect of Gibbs elasticity.
Each emulsifier is investigated at two concentrations (‘high’ and ‘low’), chosen to be in the range relevant for emulsification applications. For BLG, the ‘high’ concentration is that achieved when preparing an emulsion with same BLG-concentration as in raw milk and ‘low’ is one tenth of this – which is still twice the concentration above which surface load is approximately independent of bulk concentration under equilibrium conditions.73 For F68 and SDS, ‘high’ concentration is 20 times the critical micelle concentration (CMC) and ‘low’ is a concentration twice the CMC (the ‘high’ concentration is still well below the aqueous solubility limit for the respective emulsifier).
Deformation gives rise to an expansion of the drop interface, which lowers the surface load and drives adsorption (through eqn (5)). Note that the adsorption rate is zero once the drop is fully covered by emulsifier (Γ = Γ*). However, deformation is typically not monotonic.10,40,45,75 For a relaxing drop, to which adsorption has taken place during deformation, this might lead to surface load increasing beyond the threshold/maximum surface load Γ* (typically the magnitude of the effect is small, i.e., Γ < 1.05Γ*). Since low-molecular weight surfactants typically adsorb reversibly, SDS was assumed to instantly desorb back to Γ = Γ* if this occurred. For the larger emulsifiers (F68 and BLG) adsorption is irreversible76,77 and Γ > Γ* is allowed in the simulations.
Using the numerical data on our three emulsifier systems, we can now see more quantitatively that the turbulently driven adsorption rate is substantially faster than both the Brownian/diffusion driven adsorption given by,71,78
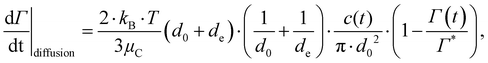 | (9) |
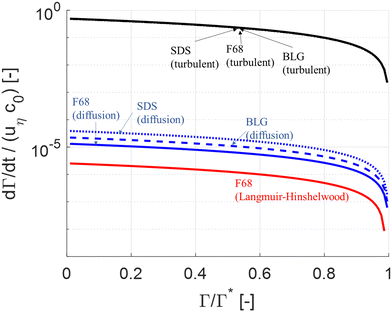 | ||
| Fig. 2 Comparison of (non-dimensionalized) adsorption rate as a function of surface load. Comparing turbulently driven adsorption (black line, eqn (5)) to Brownian diffusion driven transport (blue line78) and Langmuir–Hinshelwood limited adsorption (red line62,64). | ||
Note that diffusion is insignificant in comparison to turbulent driven adsorption despite that F68 is a relatively small polymer. Moreover, as seen in Fig. 2, the turbulently driven adsorption rate is almost independent of which emulsifier we consider since the velocity of the emulsion drop is the dominant factor driving drop-emulsifier collisions (i.e., since d0 + dE ∼ d0 in eqn (5)). For SDS turbulent adsorption is a factor 1.3 × 104 faster than diffusion and for BLG, the turbulent adsorption is a factor 2.0 × 104 faster than diffusion (at Γ = 0.95Γ*).
3. Results and discussion
3.1 Deformation and breakup neglecting emulsifier adsorption dynamics
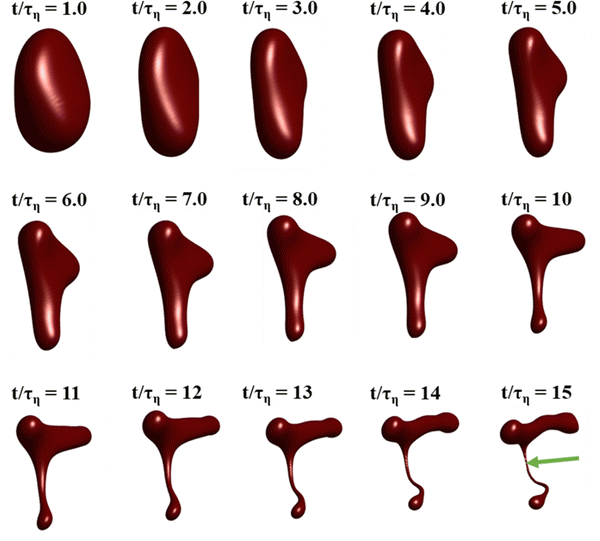
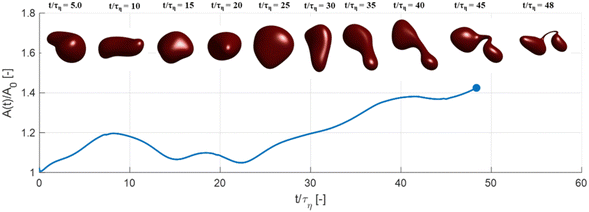
Fig. 3 displays how a We = 5 drop-based on the standard assumption of instant exchange of emulsifier between bulk and interface deforms in one example flow realization (data displayed as an iso-surface contour of VOF = 0.5, flow realization L, see drop library in ref. 41). The drop starts to deform directly upon injection and is rapidly flattened. Starting at t/τη = 5, a segment of the drop is further pulled out (downwards). As time progresses, this segment is deformed, forming a bulb at the end of the segment. Over time, the neck connecting the two is thinned out and the neck is critically deformed (i.e., deformed to the extent that breakup is now deterministic even if it was removed from the turbulence41) at τdef/τη = 9.9. Initial breakup (first detachment of a fragment85) occurs at τbreak/τη = 15.3.Fig. 4(A) displays the total interfacial area of the drop as a function of time, as a measure of the global extent of deformation, up to the point of initial breakup (marker). The drop deforms monotonously and has reached a value of 1.8 times the initial area when breaking, see black solid line (‘Instant’) in Fig. 4(A). Fig. 4(B) and (C) display the evolution of the normalized surface load and the normalized interfacial tension, respectively. Note how these are constant under the assumption of instant exchange of emulsifier between bulk and interface.
3.2 Effect of emulsifier dynamics on deformation
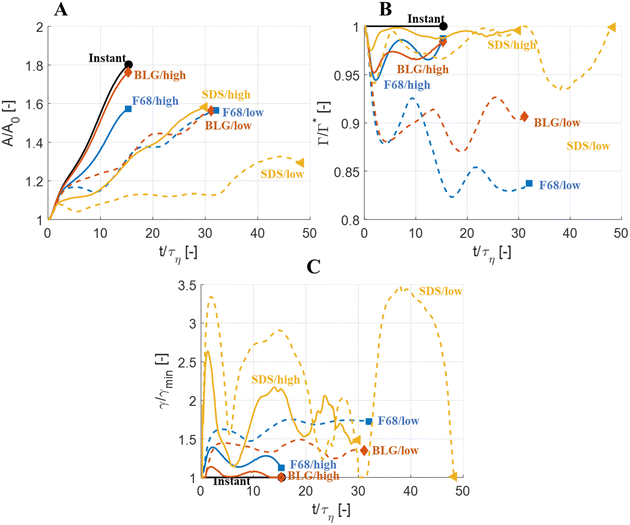
Fig. 5 displays drops injected in the same flow realization as in Fig. 3 (i.e., at the same Weber number and viscosity ratio) but when using dynamically adsorbing/desorbing emulsifiers at different concentrations to achieve these conditions. First note, that if the emulsifier concentration is sufficiently high (e.g., BLG/high in Fig. 5), the drop deformation is almost indistinguishable from that seen under instant exchange between bulk and interface (‘Instant’ in Fig. 5). Also note that BLG/high corresponds to using β-lactoglobulin as the emulsifier, under concentrations comparable to that in milk, i.e., we can achieve an adsorption rate independent deformation under conditions relevant in technical applications. The surface load does decrease initially due to the fast initial deformation as the drop encounters the turbulence (see drop colour-scale in Fig. 5 and plot in Fig. 4(B)). This also leads to an initial increase in interfacial tension of the drop (see Fig. 4(C)). However, with a high emulsifier concentration (BLG/high in Fig. 5), the adsorption rate is sufficiently fast to restore the surface load and, thus, lower the interfacial tension back to its initial value before deformation has ceased. Consequently, deformation and breakup are not limited by the adsorption under these conditions.If the emulsifier is used at a lower concentration, however, this significantly alters the deformation process, including morphology at breakup, deformation time and breakup time. This is exemplified by using the same emulsifier at the lower (but still technically relevant concentration), see ‘BLG/low’ in Fig. 5. With the lower concentration, the emulsifier adsorption is slower, and, thus, the surface load decreases more (reaching as low as Γ/Γ* = 0.88 at t/τη = 2.2), leading to a higher interfacial tension (γ/γmin = 1.4), decreasing the effective Weber number by 40%. This increase in interfacial tension brings an increased stabilization. Thus, the segment which is pulled out from the drop under conditions of instant adsorption (t/τη > 5, Fig. 3), is halted and relaxes back when the emulsifier concentration is too low (‘BLG/low’ in Fig. 5). Breakup is observed even at the lower concentration, but it occurs later (τbreak/τη = 31.2).
3.3 Emulsifier type and Gibbs elasticity
How susceptible the deformation process is to the emulsifier depend on which emulsifier is used. BLG and F68 behaves similarly (Fig. 4); when used at technically relevant ‘high’ concentrations (‘BLG/high’ and ‘F68/high’ in Fig. 4), the adsorption is fast enough to restore surface load and, consequently, breakup occurs at approximately the same time as when assuming instant exchange of emulsifier between bulk and interface. At the ‘low’ (but still technically relevant) concentrations, both BLG and F68 give rise to a delayed breakup, occurring at ∼31τη. To understand why these two emulsifiers behave similarly, it is also interesting to note that they give rise to similar Gibbs elasticities, i.e., the interfacial tension responds similarly to a small change in surface load (see eqn (3)).The low weight molecular emulsifier (SDS), however, is different. The adsorption rate is relatively high (as indicated by the relatively short adsorption time, even at the ‘low’ concentration for SDS), resulting in a high surface load (‘SDS/low’ in Fig. 5 and 4(B)). The higher Gibbs elasticity imposed by SDS (see Fig. 1), however, gives even a slight reduction in surface load a large impact on the interfacial tension (‘SDS/low’ in Fig. 4(C)). For the low SDS concentration case, the interfacial tension rapidly increases to 3.3 times its initial value, thus decreasing the effective Weber number encountered by the drop from 5 to 1.5. The high Laplace pressure causes the drop to quickly relax from the initial deformation (Fig. 5). Also note that deformation is delayed, even if using this high Gibbs elasticity emulsifier at a high concentration (SDS/high); despite that adsorption rapidly loads the expanding interface with new emulsifier, the slight and short-lived depletion of the adsorbed layer stabilizes the drop (Fig. 4).
The high Gibbs elasticity drop (‘SDS/low’) does eventually break, but it does so in a slow process. After the initial deformation has been halted by the high interfacial tension, it proceeds by deforming slowly (dA/dt is low in Fig. 4(A)). During this slow deformation, the drop continues to accumulate emulsifier through adsorption to the deformed interface–as the interface deforms, Γ/Γ* remains below one, resulting in a continuous driving force for adsorption, which increases the total adsorbed amount, Γ(t)·A(t), over time. Shortly after t/τη ∼ 30, some turbulent structures appear to interact more forcefully with the drop, increasing the deformation rate (see Fig. 4(A)). The drop is unable to break directly upon this extra stress (since interfacial tension increases rapidly in response, as seen in Fig. 4(C)). However, the turbulent structures allow the drop to relax in such a way so that it forms the necessary thinning neck, while simultaneously reducing its total interfacial area (cf.Fig. 4(A) and ‘SDS/low’ in Fig. 5). Due to the slow accumulation of emulsifier during the first 30τη, the drop can now achieve a relatively high surface load even in the critically deformed state (see colour-scale of ‘SDS/low’ in Fig. 5), allowing the drop to break.
3.4 Adsorption time
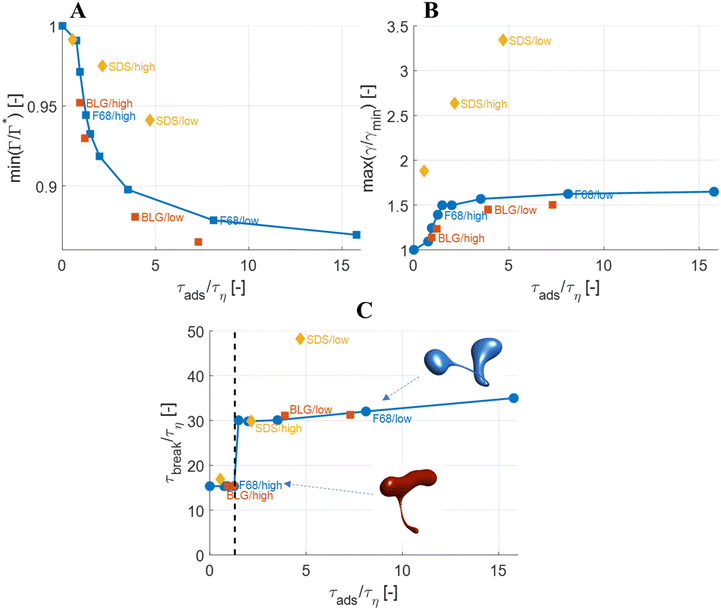
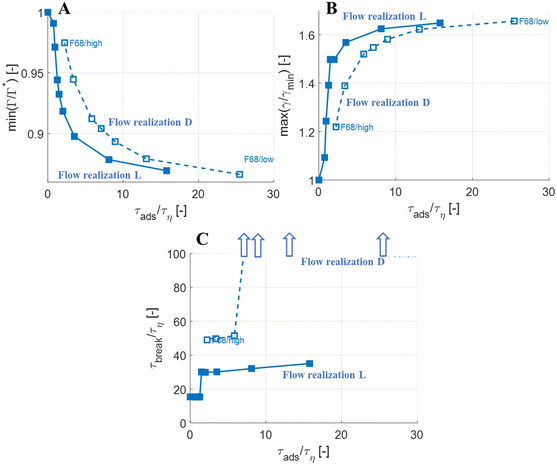
The observations on how emulsifier concentration influences the deformation process can be quantified in terms of adsorption time (cf.eqn (6)). Using the same emulsifier at a higher concentration reduces the adsorption time (i.e., by increasing c0 in eqn (6)). Fig. 6(A) displays the maximum reduction in surface load, min(Γ/Γ*), during the initial deformation (t < 10τη), comparing different emulsifiers and concentrations thereof, plotted versus the adsorption time imposed by using different emulsifier concentration. Starting with a single emulsifier (F68, blue squares), the shorter is the adsorption time, the smaller is the maximum reduction in the surface load. The curve shows a sigmoidal shape, approaching no depression in surface load if the adsorption time is short in comparison to the Kolmogorov timescale (τη), and levelling off at min(Γ/Γ*) ≈ 0.7 if adsorption time is long in comparison to τη. Note that if τads/τη > 5, the adsorption is sufficiently slow for adsorption to be negligible, and the surface load evolution is almost entirely determined by how fast the interface is deformed by the external turbulent stress. As before, BLG and F68 behaves similarly, with min(Γ/Γ*) falling approximately on the same master curve.The corresponding maximum increase in interfacial tension during the initial deformation, max(γ/γmin), can be seen in Fig. 6(B). Note that the two emulsifiers with approximately the same Gibbs elasticity (F68 and BLG) (disks and squares) fall approximately on the same curves in Fig. 6. The high interfacial elasticity emulsifier (SDS), however, gives a somewhat lower relative reduction in surface load at the same adsorption time (i.e., min(Γ/Γ*)), see Fig. 6(A), and a higher relative increase in interfacial tension (i.e., max(γ/γmin)), see Fig. 6(B).
The effect of emulsifier dynamics on breakup time can also be better understood in terms of adsorption time, see Fig. 6(C). Starting with BLG and F68 (low interfacial elasticity), the breakup time is approximately equal to that obtained by assuming instant exchange of emulsifier between bulk and interface if (and only if) τads < 1.4τη. This corresponds to an adsorption time that is less than 0.1 of the breakup time. Thus, if the emulsifier is used at a high-enough concentration so to achieve an adsorption time that is one order magnitude lower than the breakup time, the turbulent deformation process is independent of emulsifier dynamics. If not, there is a delay in breakup.
From previous investigations, it is well-known that using an emulsifier concentration less than the level indicated by eqn (2) makes turbulent coalescence dominate turbulent breakup.6,7,28–31 However, the critical concentration required to prevent coalescence is low unless using exceedingly high volume-fractions of disperse phase, i.e., ∼1/100 ccmc for F68 according to eqn (2). This is substantially lower than the concentration required to ensure that the deformation process is uninfluenced by the rate at which emulsifier is exchanged between bulk and interface.
3.5 Generalization across flow initializations
Turbulent flows are highly stochastic, and each drop subjected to it will take a different trajectory and interact with different turbulent structures.10,36,40,46,60 Looking at a larger collection of viscous drops (μD/μC = 20) subjected to conditions of We = 5, we see mainly two types of deformation processes:41 some drops-upon being injected in the turbulence-encounter sufficiently forceful turbulent stress to immediately go into a monotonous deformation that eventually leads to breakup (cf.Fig. 3). Other drops go through a stochastic number of oscillations before eventually reaching a deformation sequence that eventually break them (see Fig. 7 for an example). This behaviour has also been seen in similar investigations across a larger number of flow realizations in independent studies.11,45As a test of how the results from the investigations above generalize between flow realizations, Fig. 8 (open markers) displays the results of how maximum surface load suppression (Fig. 8(A)), minimum interfacial tension (Fig. 8(B)) and breakup time (Fig. 8(C)), depends on adsorption timescale, comparing the previously investigated flow realization leading to monotonous deformation (labelled ‘L’), to the flow realization in Fig. 7, leading to oscillatory behaviour (labelled ‘D’). Solid markers show results from the flow realization used in previous sections (‘L’). As seen in Fig. 8(A) and (B), the maximum initial reduction in surface load and the resulting maximum increase in interfacial tension is similar between the two flow realizations.
More interestingly, Fig. 8(C) displays how breakup time depends on the emulsifier concentration (via its effect on the imposed adsorption timescale), comparing the two flow realizations. As discussed above, for the previously discussed flow realization (‘L’), breakup is unaffected if emulsifier is supplied at a concentration to ensure that τads < 0.1τbreak (solid markers), and breakup is delayed if the emulsifier concentration is below this threshold. For the flow realization where breakup is preceded by oscillations (flow realization ‘D’, open markers in Fig. 8(A)), a similar effect is seen, but the delay is long enough to move it beyond the end-time in the simulations (corresponding, approximately, to the time spent in the emulsification device, t/τη ≈ 10040). In Fig. 8(C), these conditions where the imposed adsorption time is sufficiently long for drops not to break before t/τη ≈ 100 are illustrated using arrows. In terms of breakup time, this critical adsorption time required for fast exchange is longer for the second flow realization (τads < 0.14τbreak, as compared to τads < 0.11τbreak for the first flow realization), but of the same order of magnitude, τads < 0.1τbreak.
The results above suggest that for drops with We = 5, the assumption of an instant exchange of emulsifier between bulk and interface, which is imposed in the majority of previous numerical drop breakup studies, is only realistic if using an emulsifier concentration that is high enough to ensure that the adsorption time is a decade lower than the breakup time.
3.6 Effect at higher Weber number
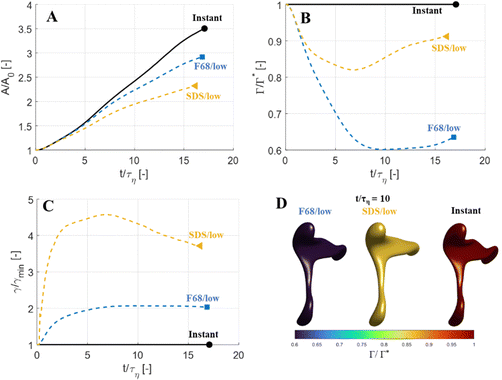
The focus thus far has been on low Weber numbers (e.g., characteristic of the smallest drops breaking in an emulsification device). For a large drop (illustrated here by We = 30), the adsorption dynamics has less of an effect on the deformation and breakup behaviour (Fig. 9). With a slowly adsorbing emulsifier, the drop deforms less than if adsorption was instant (Fig. 9(A)) but break at almost the same time (see markers in Fig. 9(A)). At low emulsifier concentrations (SDS/low and F68/low), the adsorption is slow, and the surface load decreases initially—for F68/low Γ/Γ* reaches as low as 0.6 (Fig. 9(B))—which leads to a large increase in interfacial tension (Fig. 9(C)). However, even with interfacial tension reaching 4.5 times higher than the equilibrium value at its peak (SDS/low, see Fig. 9(C)), the effective Weber number obtained by replacing the equilibrium value of interfacial tension with the time-dependent one from Fig. 9(C), is still large (We ≥ 11), indicating that the disruptive turbulent stresses still substantially outweigh the stabilizing Laplace pressure. The results even suggest that the high-We drop breaks marginally earlier if subjected to a slowly adsorbing emulsifier giving a high Gibbs elasticity (SDS/low breaks 0.8τη earlier than when assuming instant emulsifier exchange, Fig. 9(A)–(C)), most likely due to that the transient increase in interfacial tension hinders the excessive deformation in regions further from the neck which acts as a drain of turbulent kinetic energy (cf. ref. 44).The observation that large drops (i.e., drops with large We) are less sensitive to emulsifier dynamics, also explains why emulsification experiments see relatively little effect of emulsifier concentration on the drop size distribution beyond the concentration required to prevent coalescence during emulsification.7,28–30 Whereas a considerable amount of turbulent coalescence will drastically increase the number of large drops which shows up as a marked translation of the drop-size distribution and volume-based average diameters, a delay in the deformation process which only acts on small drops have less of an effect on the drop size distribution, thus making it more difficult to identify using emulsification experiments.
3.7 Non-uniform surface load, Marangoni stresses and interfacial rheology
In the present study, following Walstra and Smulders,9 it is assumed that once adsorbed to the interface, the emulsifiers distribute themselves evenly across the interface. However, the rate at which emulsifiers redistributes on the interface is not understood in detail. If redistribution over the interface is slower than the deformation/relaxation, this would lead to gradients in surface load (and, consequently, in interfacial tension) across the interface, which drives tangential Marangoni stresses that act by further pulling the interface together.51,52,55,56 Thus, surface load gradients will also act to delay the deformation process. Large emulsifiers such as proteins will generally require additional time, once arrived at the interface, to undergo the conformational changes (‘unfolding’) required to reach more energetically favourable conformations. This process can take several orders of magnitude longer than the time a drop spends in the turbulent zone of an emulsification device.86,87 Moreover, these emulsifiers typically give rise to interfacial rheology expected to further affect the deformation process.53,54 Since surface active material is typically present, both at drop and bubble interfaces during turbulent deformation and breakup in technically relevant and naturally occurring systems, further investigations continuing to include more of these phenomena in single drop breakups simulations is of great importance to advance the field as well as for advancing our understanding of turbulent drop and bubble breakup.4. Conclusions
If the Weber number is sufficiently high or if the emulsifier concentration is high enough to give an adsorption timescale which is a decade lower than the breakup time, then the breakup process is identical to that obtained when assuming instant exchange of emulsifier between bulk and interface (as in current state-of-the-art drop simulation literature). For a small drop (We = 5) with relatively high viscosity (μD/μC = 20), using a lower emulsifier concentration than this delays breakup. If the time spent in the turbulence is short enough, this delay can result in that the drop does not have time to break before exiting (as seen for the flow realization where the drop oscillates before entering the stage of critical deformation).Note that both these conditions (deformation not influenced by emulsifier dynamics and deformation delayed by emulsifier dynamics) are found within the span of technically relevant emulsifier concentrations.
The Gibbs elasticity imposed by the emulsifier plays an important role. For the emulsifier imposing a higher interfacial elasticity, the breakup is delayed longer when using a low emulsifier concentration. Moreover, for emulsifiers imparting higher Gibbs elasticity, breakup of limiting drops (i.e., drops with low Weber number) is only possible through a slow deformation process where emulsifier is accumulated allowing critical deformation to be reached without a rapid global increase in interfacial area. Thus, the kinetics imposed by the emulsifier does not only delay breakup but might also influence the mechanism of breakup.
Author contributions
AH: conceptualization, writing – original draft; methodology; analysis; visualization. LN: conceptualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Appendix A: adsorption time
Consider an emulsion drop in equilibrium with a continuous bulk concentration of emulsifier, c0, which is above the critical micelle concentration, CMC, so that the drop has a surface load Γ*. Assume that at t = 0 the drop is suddenly deformed so that its interfacial area increases by 5%. Since the deformation is too fast for adsorption to compensate, the surface load decreases to an amount given by mass conservation across the interface, i.e., Γ(t = 0) = Γ*/1.05.The time necessary for the surface load to increase to 99% of the critical surface load, denoted τads, can be obtained from integration of the adsorption rate (eqn (5)):
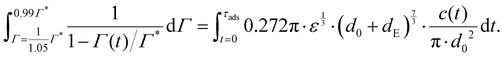 | (A.1) |
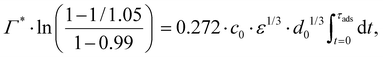 | (A.2) |
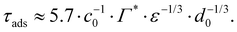 | (A.3) |
Acknowledgements
This study was funded by the Swedish Research Council, grant number 2018-03820.References
- F. Risso, The mechanisms of deformation and breakup of drops and bubbles, Multiphase Sci. Technol., 2000, 12, 1–50, DOI:10.1615/MultScienTechn.v12.i1.10.
- J. Solsvik, S. Tangen and H. A. Jakobsen, On the constitutive equations for fluid particle breakage, Rev. Chem. Eng., 2013, 29(5), 241–356, DOI:10.1515/revce-2013-0009.
- A. Håkansson, Emulsion formation by homogenization: Current understanding and future perspectives, Annu. Rev. Food Sci. Technol., 2019, 10, 239–258, DOI:10.1146/annurev-food-032818-121501.
- J. Baldyga and W. Podgórska, Drop break-up in intermittent turbulence: Maximum stable and transient sizes of drops, J. Chem. Eng., 1998, 76, 456–470, DOI:10.1002/cjce.5450760316.
- H. K. Foroushan and H. A. Jakobsen, On the dynamics of fluid particle breakage induces by hydrodynamic instabilities: A review of modelling approaches, Chem. Eng. Sci., 2020, 219, 115575, DOI:10.1016/j.ces.2020.115575.
- S. Tcholakova, N. Denkov and T. Danner, Role of surfactant type and concentration for the mean drop size during emulsification in turbulent flow, Langmuir, 2004, 20, 7444–7458, DOI:10.1021/la049335a.
- S. Tcholakova, N. D. Denkov and A. Lips, Comparison of solid particles, globular proteins and surfactants as emulsifiers, Phys. Chem. Chem. Phys., 2008, 10, 1608–1627, 10.1039/B715933C.
- T. F. Tadros, Emulsion Formation and Stability, Wiley-VCH, 2013 Search PubMed.
- P. Walstra and P. E. A. Smulders, Emulsion formation, in Modern aspects of emulsion science, ed. B. P. Binks, Royal Society of Chemistry, 1998 Search PubMed.
- A. Rivière, W. Mostert, S. Perrard and L. Deike, Sub-Hinze scale bubble production in turbulent bubble break-up, J. Fluid Mech., 2021, 917, A40, DOI:10.1017/jfm.2021.243.
- A. Vela-Martín and M. Avila, Deformation of drops by outer eddies in turbulence, J. Fluid Mech., 2021, 929, A38, DOI:10.1017/jfm.2021.879.
- A. Vela-Martín and M. Avila, Memoryless drop breakup in turbulence, Sci. Adv., 2022, 8(50), eabp9561, DOI:10.1126/sciadv.abp9561.
- R. Ni Deformation and breakup of bubbles and drops in turbulence, 2023. Manuscript under publication. https://arxiv.org/pdf/2305.18570.pdf.
- A. U. M. Masuk, A. K. R. Salibindla and R. Ni, Simultaneous measurements of deforming Hinze-scale bubbles with surrounding turbulence, J. Fluid Mech., 2021, 910, A21, DOI:10.1017/jfm.2020.933.
- D. J. McClements, Food emulsions: Principles, practices, and techniques, CRC Press, 2015 Search PubMed.
- D. J. McClements, Edible nanoemulsions: Fabrication, properties, and functional performance, Soft Matter, 2011, 7, 2297–2316, 10.1039/C0SM00549E.
- J. B. Aswathanarayan and R. R. Vittal, Nanoemulsions and their potential applications in food industry, Front. Sustain. Food Syst., 2019, 3, 95, DOI:10.3389/fsufs.2019.00095.
- M. Ashar, D. Arlov, F. Carlsson, F. Innings and R. Andersson, Single droplet breakup in a rotor-stator mixer, Chem. Eng. Sci., 2018, 181, 186–198, DOI:10.1016/j.ces.2018.02.021.
- F. Innings, L. Fuchs and C. Trägårdh, Theoretical and experimental analyses of drop deformation and break-up in a scale model of a high-pressure homogenizer, J. Food Eng., 2011, 103, 21–28, DOI:10.1016/j.jfoodeng.2010.09.016.
- K. Kelemen, S. Gepperth, R. Koch, H. J. Bauer and H. P. Schuchmann, On the visualization of droplet deformation and breakup during high-pressure homogenization, Microfluid. Nanofluid., 2015, 19, 1139–1158, DOI:10.1007/s10404-015-1631-z.
- B. Mutsch, F. J. Preiss, T. Dagenbach, H. P. Karbstein and C. J. Kähler, Scaling of droplet breakup in high-pressure homogenizer orifices. Part ii: Visualization of the turbulent droplet breakup, Chem. Eng., 2021, 5, 7, DOI:10.3390/chemengineering5010007.
- N. Vankova, S. Tcholakova, N. D. Denkov, I. Ivanov, V. D. Vulchev and T. Danner, Emulsification in turbulent flow 1. Mean and maximum drop diameters in inertial and viscous regimes, J. Colloid Interface Sci., 2007, 312, 363–380, DOI:10.1016/j.jcis.2007.03.059.
- J. T. Davies, Drop sizes of emulsions related to turbulent energy dissipation rates, Chem. Eng. Sci., 1985, 40, 839–842, DOI:10.1016/0009-2509(85)85036-3.
- R. V. Calabrese, T. P. K. Chang and P. T. Dang, Drop breakup in turbulent stirred tank contactors. Part I: Effect of dispersed-phase viscosity, AIChE J., 1986, 32(4), 657–666, DOI:10.1002/aic.690320416.
- A. N. Kolmogorov, On the breakage of drops in a turbulent flow, Dokl. Akad. Nauk, 1949, SSSR 66, 825–828 (Originally in Russian. Reprinted and translated in Selected Works of A. N. Kolmogorov, Volume 1: Mathematics and Mechanics, ed. V. M. Tikhomirov, 1991, pp. 339–343).
- J. O. Hinze, Fundamentals of the hydrodynamic mechanism of splitting in dispersion process, AIChE J., 1955, 1, 289–295, DOI:10.1002/aic.690010303.
- J. A. Boxall, C. A. Kohn, E. D. Sloan, A. K. Sum and D. T. Wu, Droplet size scaling of water-in-oil emulsions under turbulent flow, Langmuir, 2012, 28, 104–110, DOI:10.1021/la202293t.
- S. Mohan and G. Narsimhan, Coalescence of protein-stabilized emulsions in a high-pressure homogenizer, J. Colloid Interface Sci., 1997, 192(1), 1–15, DOI:10.1006/jcis.1997.5012.
- G. Narsimhan and P. Goel, Drop coalescence during emulsion formation in a high-pressure homogenizer for tetradecane-in-water emulsion stabilized by sodium dodecyl sulfate, J. Colloid Interface Sci., 2001, 238(2), 420–432, DOI:10.1006/jcis.2001.7548.
- L. Lobo, A. Svereika and M. Nair, Coalescence during emulsification. 1. Method development, J. Colloid Interface Sci., 2002, 253(2), 409–418, DOI:10.1006/jcis.2002.8560.
- L. Taisne, P. Walstra and B. Cabane, Transfer of oil between emulsion droplets, J. Colloid Interface Sci., 1996, 184(2), 378–390, DOI:10.1006/jcis.1996.0632.
- J. V. L. Henry, P. J. Fryer, W. J. Frith and I. T. Norton, Emulsification mechanism and storage instabilities of hydrocarbon in-water sub-micron emulsions stabilised with Tweens (20 and 80), Brij 96v and sucrose monoesters, J. Colloid Interface Sci., 2009, 338(1), 201–206, DOI:10.1016/j.jcis.2009.05.077.
- E. H. Herø, N. La Forgia, J. Solsvik and H. A. Jakobsen, Single drop breakage in turbulent flow: Statistical data analysis, Chem. Eng. Sci.: X, 2020, 8, 100082, DOI:10.1016/j.cesx.2020.100082.
- N. La Forgia, E. H. Herø and H. A. Jakobsen, High-speed image procssing of fluid particle breakage in turbulent flow, Chem. Eng. Sci.: X, 2021, 12, e100117, DOI:10.1016/j.cesx.2021.100117.
- C. D. Eastwood, L. Armi and J. C. Lasheras, The breakup of immiscible fluids in turbulent flows, J. Fluid Mech., 2004, 502, 309–333, DOI:10.1017/S0022112003007730.
- S. Galinat, L. Garrido Torres, O. Masbernat, P. Guiraud, F. Risso, C. Dalmazzone and C. Noik, Breakup of a drop in a liquid-liquid pipe flow through an orifice, AIChE J., 2007, 53(1), 56–68, DOI:10.1002/aic.11055.
- Y. Qi, S. Tan, N. Corbitt, C. Urbanik, A. K. R. Salibindla and R. Ni, Fragmentation in turbulence by small eddies, Nat. Commum., 2022, 13, 469, DOI:10.1038/s41467-022-28092-3.
- J. Vejražka, M. Zedníková and P. Stranovský, Experiments on breakup of bubbles in a turbulent flow, AIChE J., 2018, 64, 740–757, DOI:10.1002/aic.15935.
- A. E. Komrakova, D. Eskin and J. J. Derksen, Numerical study of turbulent liquid-liquid dispersions, AIChE J., 2015, 61, 2618–2633, DOI:10.1002/aic.14821.
- A. Håkansson and L. Brandt, Deformation and initial breakup morphology of viscous emulsion drops in isotropic homogeneous turbulence with relevance for emulsification devices, Chem. Eng. Sci., 2022, 253, 117599, DOI:10.1016/j.ces.2022.117599.
- A. Håkansson, M. Crialesi-Esposito, L. Nilsson and L. Brandt, A criterion for when an emulsion drop undergoing turbulent deformation has reached a critically deformed state, Colloids Surf., A, 2022, 648, 129213, DOI:10.1016/j.colsurfa.2022.129213.
- M. E. Rosti, F. De Vita and L. Brandt, Numerical simulations of emulsions in shear flows, Acta Mech., 2019, 230(2), 667–682, DOI:10.1007/s00707-018-2265-5.
- M. Crialesi-Esposito, M. E. Rosti, S. Chibbaro and L. Brandt, Modulation of homogeneous and isotropic turbulence in emulsions, J. Fluid Mech., 2021, 940, A19, DOI:10.1017/jfm.2022.179.
- M. Crialesi-Esposito, M. E. Rosti, S. Chibbaro and L. Brandt, The interaction of droplet dynamics and turbulence cascade, Commun. Phys., 2023, 6, 5, DOI:10.1038/s42005-022-01122-8.
- I. Roa, M.-C. Renoult, C. Dumochel and J. C. Brändle de Motta, Droplet oscillations in turbulent flow, Front. Phys., 2023, 11, 1173521, DOI:10.3389/fphy.2023.1173521.
- C. Shao, K. Luo, Y. Yang and J. Fan, Direct numerical simulation of droplet breakup in homogeneous isotropic turbulence: The effect of the Weber number, Int. J. Multiphase Flow, 2018, 107, 263–274, DOI:10.1016/j.ijmultiphaseflow.2018.06.009.
- G. Soligio, A. Roccon and A. Soldati, Effect of surfactant-laden droplets on turbulent, Phys. Rev. Fluids, 2020, 5, 073606, DOI:10.1103/PhysRevFluids.5.073606.
- G. Soligio, A. Roccon and A. Soldati, Coalescence of surfactant-laden drops by phase field method, J. Comput. Phys., 2018, 376, 1291–1311, DOI:10.1016/j.jcp.2018.10.021.
- L. Scarbolo, F. Bianco and A. Soldati, Coalescence and breakup of large droplets in turbulent channel flow, Phys. Fluids, 2015, 27, 073302, DOI:10.1063/1.4923424.
- S. Mukherjee, A. Safdari, O. Shardt, S. Kenjeres and H. E. A. Van den Akker, Droplet–turbulence interactions and quasi-equilibrium dynamics in turbulent emulsions, J. Fluid Mech., 2019, 878, 221–276, DOI:10.1017/jfm.2019.654.
- K. D. Danov, P. A. Kralchvsky and I. B. Ivanov, Dynamic processes in surfactant-stabilized emulsions, in Encycolpedic handbook of Emulsion Technology ed. J. Sjöblom, Marcel Dekker, 2001, pp. 621–659 Search PubMed.
- D. A. Edwards, H. Brenner and D. T. Wasan, Interfacial transport processes and rheology, Butterworth-Heinemann, 1995 Search PubMed.
- M. A. Bos and T. van Vliet, Interfacial rheological properties of adsorbed protein layers and surfactants: a review, Adv. Colloid Interface Sci., 2001, 91, 437–471, DOI:10.1016/S0001-8686(00)00077-4.
- B. S. Murray, Interfacial rheology of food emulsifiers and proteins, Curr. Opin. Colloid Interface Sci., 2002, 7, 426–431, DOI:10.1016/S1359-0294(02)00077-8.
- L. Y. Yeo, O. K. Matar, E. S. Perez de Ortiz and G. F. Hewitt, The dynamics of Marangoni-driven local film drainage between two drops, J. Colloid Interface Sci., 2001, 241, 233–247, DOI:10.1006/jcis.2001.7743.
- E. H. Lucassen-Reynders, Interfacial viscoelasticity in emulsions and foams, Food Struct., 1993, 12, 1–12 CAS.
- R. G. M. van der Sman and S. van der Graaf, Diffuse interface model of surfactant adsorption onto flat droplet interfaces, Rheol. Acta, 2006, 46, 3–11, DOI:10.1007/s00397-005-0081-z.
- S. Ii, B. Xie and F. Xiao, An interface capturing method with a continuous function: The THINC method on unstructured triangular and tetrahedral meshes, J. Comput. Phys., 2014, 259, 260–269, DOI:10.1016/j.jcp.2013.11.034.
- P. Costa, A fft-based finite-difference solver for massively-parallel direct numerical simulations of turbulent flows, Comput. Math. Appl., 2018, 76(8), 1853–1862 CrossRef.
- P. Olad, F. Innings and A. Håkansson, Turbulent drop breakup in a simplified high-pressure homogenizer geometry: A comparison of experimental high-speed visualization and numerical experiments based on DNS and interface tracking, Chem. Eng. Sci., 2023, 282, 119274 CrossRef CAS.
- F. Lewerentz, K. Pappas, B. Bergenståhl and A. Håkansson, The effect of disperse phase viscosity in the emulsification of a semi-dairy beverage–combining emulsification experiments and numerical single drop breakup simulations, Food Bioprod. Process., 2023, 138, 103–115, DOI:10.1016/j.fbp.2023.01.008.
- C.-H. Chang and E. I. Franses, Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms, Colloids Surf., A, 1995, 100, 1–45, DOI:10.1016/0927-7757(94)03061-4.
- Y. Scher, O. L. Bonomo, A. Pal and S. Reuveni, Microscopic theory of adsorption kinetics, Chem. Phys., 2023, 158(9), 094107, DOI:10.1063/5.0121359.
- S. N. Maindarkar, P. Bongers and M. A. Henson, Predicting the effects of surfactant coverage on drop size distributions of homogenized emulsion, Chem. Eng. Sci., 2013, 89, 102–114, DOI:10.1016/j.ces.2012.12.001.
- T. Miura and K. Seki, Diffusion influenced adsorption kinetics, J. Phys. Chem. B, 2015, 119, 10954–10961, DOI:10.1021/acs.jpcb.5b00580.
- M. Delichatsios and R. Probstein, Coagulation in turbulent flow: theory and experiment, J. Colloid Interface Sci., 1975, 51, 394–405, DOI:10.1016/0021-9797(75)90135-6.
- V. G. Levich, Physiochemical Hydrodynamics, Prentice Hall, 1962 Search PubMed.
- L. Wågberg and R. Hägglund, Kinetics of polyelectrolyte adsorption on cellulosic fibres, Langmuir, 2001, 17, 1096–1103, DOI:10.1021/la000629f.
- L. Nilsson, M. Leeman, K.-G. Wahlund and B. Bergenståhl, Competitive adsorption of a polydisperse polymer during emulsification: experiments and modeling, Langmuir, 2007, 23(5), 2346–2351, DOI:10.1021/la062483b.
- A. Håkansson, C. Trägårdh and B. Bergenståhl, Dynamic simulation of emulsion formation in a high pressure homogenizer, Chem. Eng. Sci., 2009, 64, 2915–2925, DOI:10.1016/j.ces.2009.03.034.
- N. B. Raikar, S. R. Bhatia, M. F. Malone, D. J. McClements and M. A. Henson, Predicting the effect of the homogenization pressure on emulsion drop-size distributions, Ind. Eng. Chem. Res., 2011, 50, 6089–6100, DOI:10.1021/ie101818h.
- S. Llamas, E. Santini, L. Liggieri, F. Salerni, D. Orsi, L. Cristofolini and F. Ravera, Adsorption of sodium dodecyl sulfate at water–dodecane interface in relation to the oil in water emulsion properties, Langmuir, 2018, 34, 5978–5989, DOI:10.1021/acs.langmuir.8b00358.
- J. Won, Dynamic and Equilibrium Adsorption Behaviour of β-lactoglobulin at the Solution/Tetradecane Interface: Effect of Solution Concentration, pH and Ionic Strength, PhD thesis Mathematisch-Naturwissenschaftlichen Fakultät, Universität Potsdam, Germany, 2016.
- T. Bui, H. Frampton, S. Huang, I. R. Collins, A. Striolo and A. Michaelides, Water/oil interfacial tension reduction – an interfacial entropy driven process, Phys. Chem. Chem. Phys., 2021, 23, 25075, 10.1039/D1CP03971G.
- F. Risso and J. Fabre, Oscillations and breakup of a bubble immersed in a turbulent field, J. Fluid Mech., 1998, 372, 323–355, DOI:10.1017/S0022112098002705.
- N. Källrot, M. Dahlqvist and P. Linse, Dynamics of polymer adsorption from bulk solution onto planar surfaces, Macromolecules, 2009, 42, 3641–3649, DOI:10.1021/ma900050a.
- R. Zajac and A. Chakrabarti, Statics and dynamics of homopolymer adsorption and desorption: A Monte Carlo study, J. Chem. Phys., 1996, 104, 2418–2437, DOI:10.1063/1.470937.
- M. Smoluchowski, Drei Vortrageüber Diffusion, Brownsche Molekular-bewegung und Koagulation von Kolloidteilchen, Phys. Z, 1916, 17, 585–599 Search PubMed.
- S. Costanzo, A. Di Sarno, M. D’Apuzzo, P. R. Avallone, E. Raccone, A. Bellissimo, F. Auriemma, N. Grizzuti and R. Pasquino, Rheology and morphology of Pluronic F68 in water, Phys. Fluids, 2020, 33, 043113, DOI:10.1063/5.0049722.
- G. Duplâtre, M. F. Ferreira Marques and M. da Craca Miguel, Size of sodium dodecyl sulfate micelles in aqueous solutions as studied by positron annihilation lifetime spectroscopy, J. Phys. Chem., 1996, 100, 16608–16612, DOI:10.1021/jp960644m.
- P. Walstra, T. J. Geurts, A. Noomen, A. Jellema and M. A. J. S. van Boekel, Dairy Technology, Marcel Dekker, 1999 Search PubMed.
- J. Y. Won, G. G. Gochev, V. Ulaganathan, J. Krägel, E. V. Aksenenko, V. B. Fainerman and R. Miller, Mixed adsorption mechanism for the kinetics of BLG interfacial layer formation at the solution/tetradecane interface, Colloids Surf., A, 2017, 519, 146–152, DOI:10.1016/j.colsurfa.2016.08.024.
- J. A. O’Mahony and P. F. Fox, Milk: An overview, in Milk Proteins, ed. H. Singh, M. Bland and A. Thompson, Elsevier, 2014 DOI:10.1016/B978-0-12-405171-3.00002-7.
- J. Y. Won, G. G. Gochev, V. Ulaganathan, J. Krägel, E. V. Aksenenko, V. B. Fainerman and R. Miller, Effect of solution pH on the adsorption of BLG at the solution/tetradecane interface, Colloids Surf., A, 2017, 519, 161–167, DOI:10.1016/j.colsurfa.2016.05.042.
- J. Solsvik, S. Maaß and H. A. Jakobsen, Definition of the single drop breakup event, Ind. Eng. Chem. Res., 2016, 55(10), 2872–2882, DOI:10.1021/acs.iecr.6b00591.
- J. Bergfreund, P. Bertsch and P. Fischer, Adsorption of proteins to fluid interfaces: Role of the hydrophobic subphase, J. Colloid Interface Sci., 2021, 584, 411–417, DOI:10.1016/j.jcis.2020.09.118.
- V. Mitropoulos, A. Mütze and P. Fischer, Mechanical properties of protein adsorption layers at the air/water and oil/water interface: A comparison in light of the thermodynamical stability of proteins, Adv. Colloid Interface Sci., 2014, 206, 95–206, DOI:10.1016/j.cis.2013.11.004.
| This journal is © The Royal Society of Chemistry 2023 |