Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine-learning based prediction of small molecule–surface interaction potentials†
Ian
Rouse
 * and
Vladimir
Lobaskin
* and
Vladimir
Lobaskin

School of Physics, University College Dublin, Belfield, Dublin 4, Ireland. E-mail: ian.rouse@ucd.ie
First published on 28th December 2022
Abstract
Predicting the adsorption affinity of a small molecule to a target surface is of importance to a range of fields, from catalysis to drug delivery and human safety, but a complex task to perform computationally when taking into account the effects of the surrounding medium. We present a flexible machine-learning approach to predict potentials of mean force (PMFs) and adsorption energies for chemical–surface pairs from the separate interaction potentials of each partner with a set of probe atoms. We use a pre-existing library of PMFs obtained via atomistic molecular dynamics simulations for a variety of inorganic materials and molecules to train the model. We find good agreement between original and predicted PMFs in both training and validation groups, confirming the predictive power of this approach, and demonstrate the flexibility of the model by producing PMFs for molecules and surfaces outside the training set.
1 Introduction
The interaction between a molecule and an adsorbent surface in a medium is crucial to a wide range of fields of chemistry, ranging from catalysis or drug development to the prediction of toxic effects of nanoparticles (NPs) in the human body.1–3 Given the high dimensionality of chemical space for both adsorbates and adsorbent surfaces, it is infeasible to experimentally characterise the binding affinity of even a fraction of potential binding partners, while a computational approach based around traditional molecular dynamics simulations would likewise require an impractical amount of time. Docking methods, meanwhile, offer a route to scan large numbers of molecules against target surfaces but are still not strongly developed for molecule–surface rather than molecule–protein systems and in the latter case are known to have significant limitations.4–6 Consequently, there is a need for alternative methods that allow for rapid evaluation of the binding affinity of molecules to surfaces and screening for optimal adsorbate–adsorbent pairs.On a physical level, the surface and the molecule of interest interact through multiple mechanisms that may include specific or non-specific (electrostatic and van der Waals) forces. In a medium, many-body effects involving solvent molecules might also play a significant role. The solvent mediates van der Waals and electrostatic interactions between the adsorbate and adsorbent and competes with the adsorbate for a place at the surface. Other many-body effects may include hydrophobic attraction between the adsorbent and adsorbate, resulting from the interplay of respective pairwise interactions. All these contributions to the interaction depend on the distance and orientation of the molecule relative to the surface. A full description of the surface–molecule system therefore comprises not only the coordinates of all atoms in the surface and the molecule, but also those of the medium and of the ensemble as a whole.
This complex system can be quantified in terms of a potential of mean force (PMF), which is defined as the free energy profile along a chosen coordinate known as the collective variable and generally obtained via atomistic molecular dynamics using enhanced sampling methods such as metadynamics.7–10 The procedure of PMF evaluation involves taking averages over all the remaining degrees of freedom of the medium and the molecule at each value of the collective variable. Thus, the resulting potential includes all the many-body effects and indirect interactions. This operation reduces the large number of degrees of freedom to a more manageable number, typically, a single distance h between the centre of mass (COM) of the adsorbate and the uppermost surface layer of atoms9,10 but loses information about the interaction energy at different molecule orientations. The average free energy of adsorption can be obtained from these PMFs according to
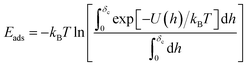 | (1) |
In principle, it would be possible to simply define a vector of distances h and energies U(h) and either develop a model to predict all of these at once, or to predict these recursively given a known starting point. Most points in the PMF, however, are strongly correlated to those immediately before or after, and so there is a high degree of redundancy if models are developed to predict each point individually. Sequence-based models, e.g. recurrent neural networks, suffer from the drawback that they typically scale unfavourably with the length of the sequence. The PMFs we are interested in typically cover a range of up to 1.5 nm from the surface at a resolution on the order of 0.02 nm and thus consist of hundreds of datapoints, which would require unfeasible amounts of memory for transformer based approaches or an exceedingly long runtime for long short-term memory network (LSTM) models.20 Thus, we seek a more compact representation of these potentials in order to allow for an efficient predictive model. We must also obtain a suitable set of descriptors to parameterise the surfaces and chemicals to be modelled. The more universal and closer these descriptors are to underlying physical properties relevant to adsorption, the more likely we can find a robust model which transfers outside of the training set to novel surfaces and chemicals. To ensure that the methodology is as widely applicable and can be used by as many research groups as possible, these descriptors should not rely on proprietary software and should be able to be calculated in a reasonable timeframe using a typical workstation rather than relying on high-performance computing clusters. Finally, we also require that the descriptors differentiate between different allotropes or crystal phases of the same material and different isomers of the same chemical, and at least potentially are able to describe atoms present in either structure even if they do not appear in the training set. This rules out the use of descriptors which are purely categorical or depend primarily on statistics averaged over atom counts, and suggests that we employ descriptors based on the three-dimensional structure of the compounds involved. Previously, it has been found that interaction potentials offer a useful basis for machine learning of binding affinities21 and we employ a similar approach. Training a model for the prediction of binding energies and, even more so, potentials presents a significant technical challenge as a variety of definitions is used in the literature for both the bound state and the distance between the molecule and the surface. Combining data from different sources requires a universal framework to allow a robust mapping of potential profiles and interaction descriptors onto each other. In the following, we describe the proposed procedure in detail.
Here, we present a generic methodology for the prediction of PMFs for small molecules interacting with planar and cylindrical surfaces. Our approach encodes the chemical identity of both the surface and the ligand in terms of their interaction potentials with a set of chemical probes. This representation depends on molecular dynamics forcefield parameters and atomic co-ordinates and as such represents both the component elements and the structure of surfaces and chemicals in a readily extendable manner. These potentials and the target PMFs are converted to a compact set of basis set expansion coefficients in terms of hypergeometric functions to minimise the amount of information required to represent them. We employ an artificial neural network implemented using TensorFlow,22 to convert this representation into the set of coefficients characterising the PMF in the same basis set, which provides a smooth analytic function describing the interaction of the small molecule and surface in the medium. The model is trained on results obtained via atomistic molecular dynamics for a range of small organic molecules adsorbing to carbonaceous, metallic, and metal oxide surfaces, with the methodology developed to handle PMFs obtained through multiple computational methods. The predicted PMFs and adsorption energies extracted from these are generally in good agreement with the input values in both training and validation sets. The trained models are incorporated into a suite of Python scripts to form the PMFPredictor Toolkit, which handles the parameterisation of new chemicals and surface structures and the generation of final sets of PMFs, together with scripts to convert chemicals generated using ACPYPE23 and surfaces generated using CHARMM-GUI Nanomaterial Modeller.24 The entire toolkit including a graphical interface for adding materials is available for download from GitHub25 and the current set of descriptors and predicted PMFs for over 100 small molecules with over 50 surfaces is archived on Zenodo.26
2 Methods
2.1 Overall scheme
Briefly, we discuss the overall methodology used for the prediction of PMFs with an overall workflow presented schematically in Fig. 1. We require a flexible means to represent both the material surfaces (hereafter just “surface”) and molecules of interest (“chemicals”) in a form that can be most easily processed into a PMF. We have investigated a number of possible descriptors for both, including those obtained via density functional theory, cheminformatics descriptors obtained via the MORDRED server, and machine learning embedding methods.27–29 The most successful has been the description of both surfaces and chemicals in terms of their interaction potentials with a set of probe molecules. Intuitively, it makes sense that these would be quite closely related to the PMF, since this itself is a form of interaction potential, and we demonstrate later that the PMF for a specific molecule–surface pair is not too dissimilar from that of the molecule–surface interaction potential for selected configurations. Moreover, these potentials can be calculated from the structures of the surface or chemical provided a molecular dynamics forcefield is available. For the set of PMFs used to construct the model, this is true for all surfaces and chemicals, and optimised forcefields e.g. INTERFACE30 are available to describe a wide range of further surfaces. Even if a highly accurate forcefield is not available, approximate parameters may be used to provide a first estimate of the binding affinity. To reduce the complexity of the input and output, we convert these potentials and the target PMF to a representation in terms of an expansion in terms of a basis set of functions constructed from powers of 1/r, similar to a classic multipole expansion and enabling the high-resolution potentials to be expressed as a small (20) set of expansion coefficients and a characteristic length scale. This basis set can be expressed in terms of hypergeometric functions and thus we refer to this as the hypergeometric expansion (HGE) method. Finally, a machine-learning-based model implemented in TensorFlow is trained to convert the input HGE coefficients describing the interaction potentials for the materials and chemicals into a set of output HGE coefficients describing the PMF. As a training set for this model, we employ PMFs calculated at Stockholm University describing the interactions of small organic molecules – primarily amino acid side chain analogues and lipid fragments – parameterised using the GAFF forcefield with face-centered cubic (FCC) gold (100), iron oxide, titanium dioxide in four combinations of crystal phase and surface, silica (amorphous and quartz), cadmium selenide, a variety of functionalised carbon nanotubes (CNTs) and graphene with varying numbers of sheets and surface oxidation, available for download at ref. 31 and calculated using methodology as described in ref. 11, 27 and 32. These are augmented with further PMFs calculated at University College Dublin (UCD) for FCC gold and silver (100), (110) and (111) surfaces, which include additional sugar molecules and use CHARMM parameters to describe the adsorbates.33–35 Lists of the small molecules and surfaces are provided in the ESI in Tables S1 and S4† respectively; see also Fig. S1† for structures of the small molecules. Our methodology is therefore designed to incorporate not only this wide range of structures, which covers cylindrical and planar geometries each with varying degrees of roughness and surface modification, but also different forcefields and conventions for the collective distance variable. The trained model is integrated into a pipeline of scripts which handle the generation of input potentials and output of final PMFs as shown in Fig. 1. Prediction of PMFs for novel chemicals can be achieved using their SMILES code as input to ACPYPE, with a wrapper script provided to convert this output to the format expected for the following script. Alternatively, if a structure and forcefield parameters are already known for this chemical, they can be manually converted to the input format. Novel surfaces likewise require a structure and set of forcefield parameters and we provide a wrapper for converting the output from the CHARMM-GUI Nanomaterial modeller tool to the required input format. We furthermore provide a GUI for convenient access to the set of scripts for generating new input and generating a set of predicted PMFs. Throughout, we use units of nm for distance and kJ mol−1 for energy, with the temperature T = 300 K assumed where relevant. We denote point–point distances by r, the distance from a point to a reference surface by d, and the PMF collective variable by h.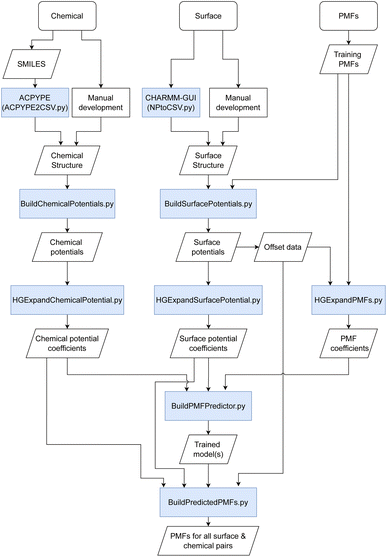 | ||
| Fig. 1 Schematic of the methodology used for the prediction of PMFs. Boxes shaded in blue indicate scripts provided in the toolkit to link different input/output stages together. | ||
2.2 Material and chemical definition
During the early development of the model, both the materials and chemicals were defined using a set of descriptors obtained from density functional theory and other methods, augmented with SMILES-based descriptors generated via the MORDRED28 web interface for chemicals, and further descriptors learnt during model training using an embedding technique. The correlation of the pre-specified descriptors with the adsorption energies was typically quite low, limiting the ability of the model to extrapolate to new materials. Better performance was found when using the embedding technique, but this cannot be applied to chemicals and materials outside the training set. This necessitated the development of descriptors more closely related to the adsorption properties of the chemicals in question. A further challenge is finding a representation of the surface structure of the material, e.g., representing the difference between different Miller indices and crystal structures or realisations of different random surfaces. Likewise, it is necessary to differentiate between different chemicals with the same empirical formula, e.g. the leucine and isoleucine side chain analogues. To overcome these issues and produce an input which is already similar to the desired output of a potential, we define the surfaces and chemicals in terms of a set of potentials representing their interactions with various probes representing atoms (see Table 1), a generic planar surface (for chemicals only) and small molecules, taking into account multiple possible orientations of the probe molecule relative to the surface or chemical in question. The atomic probes are selected to characterise three main axes: charge affinity, van der Waals affinity, and length scales by systematically varying the charge, and Lennard-Jones (LJ) ε and σ parameters, respectively. The small molecules here consist of water, comprising O and two HW atoms based on the TIP3P model of water, a rigid model of methane consisting of C and 4 HC atoms in a tetrahedral configuration based on the structure generated by ACPYPE, a six-membered ring of C atoms, and a line of C atoms consisting of either 3 (for surfaces) or 7 (for molecules) atoms, using the smaller set for surfaces for reasons of computational efficiency and to avoid edge effects. The resulting set of potentials include a representation of the spatial arrangement and chemical identity of all atoms present in the structure (chemical or surface) of interest, and can be calculated for new structures using Python scripts supplied in the repository.25| Label | σ [nm] | ε [kJ mol−1] | Charge [e] |
|---|---|---|---|
| C | 0.339 | 0.360 | 0 |
| K | 0.314 | 0.364 | 1 |
| Cl | 0.404 | 0.628 | −1 |
| C2A | 0.200 | 0.360 | 0 |
| C4A | 0.400 | 0.360 | 0 |
| CPlus | 0.339 | 0.360 | 0.5 |
| CMinus | 0.339 | 0.360 | −0.5 |
| CMoreLJ | 0.339 | 0.5 | 0 |
| CLessLJ | 0.339 | 0.2 | 0 |
| CEps20 | 0.339 | 20 | 0 |
| O* | 0.339 | 0.2 | 0 |
| HW* | 0.339 | 0.2 | 0 |
| HC* | 0.339 | 0.2 | 0 |
The potential describing the interaction between a structure and a probe is constructed from two components: the van der Waals potential in the LJ model and the electrostatic potential. We first consider the total LJ potential obtained by summation over all atoms in the structure, indexed i, with a point atom defined by parameters εp, σp employing standard mixing rules 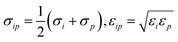 such that the potential is given by
such that the potential is given by
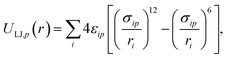 | (2) |
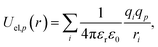 | (3) |
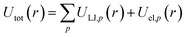 and evaluated on a grid of points corresponding to a single value of the reference distance d, taking d to be the height above a reference plane (defined later) for a planar structure, the radial distance from a reference surface for a cylindrical structure, or the distance from the COM for a chemical to points in a spherical grid, and where r in the above is a function of d. The resolution of the grid used for molecular probes is reduced slightly to compensate for the increased computational time required to evaluate multiple orientations of these. By evaluating the total potential at each point on the grid for a given value of d, we extract an effective free energy at this distance by averaging over multiple degrees of freedom according to
and evaluated on a grid of points corresponding to a single value of the reference distance d, taking d to be the height above a reference plane (defined later) for a planar structure, the radial distance from a reference surface for a cylindrical structure, or the distance from the COM for a chemical to points in a spherical grid, and where r in the above is a function of d. The resolution of the grid used for molecular probes is reduced slightly to compensate for the increased computational time required to evaluate multiple orientations of these. By evaluating the total potential at each point on the grid for a given value of d, we extract an effective free energy at this distance by averaging over multiple degrees of freedom according to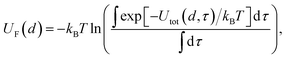 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ required for averaging over the surface of a sphere implicitly contained in dτ. The limits of integration for surfaces are chosen to cover a sufficiently large portion of the material surface to capture surface irregularities without approaching the boundaries, since for reasons of speed we do not implement periodic boundary conditions. In certain cases, e.g. charge–charge interactions at short range, the numerical evaluation of eqn (4) returns infinite results due to numerical overflow and in these cases we approximate UF(d) for that probe by the minimum value of the energy at that distance. Since eqn (4) is essentially a soft-minimum function, this does not lead to too significant an error and we find the resulting potentials remain smooth despite this approximation. We further record the minimum energy at each value of d for use as a further model input, i.e., eqn (4) evaluated in the limit T → 0.
θ required for averaging over the surface of a sphere implicitly contained in dτ. The limits of integration for surfaces are chosen to cover a sufficiently large portion of the material surface to capture surface irregularities without approaching the boundaries, since for reasons of speed we do not implement periodic boundary conditions. In certain cases, e.g. charge–charge interactions at short range, the numerical evaluation of eqn (4) returns infinite results due to numerical overflow and in these cases we approximate UF(d) for that probe by the minimum value of the energy at that distance. Since eqn (4) is essentially a soft-minimum function, this does not lead to too significant an error and we find the resulting potentials remain smooth despite this approximation. We further record the minimum energy at each value of d for use as a further model input, i.e., eqn (4) evaluated in the limit T → 0.
For chemicals, we generate an additional potential corresponding to the interaction between the chemical and an infinite slab of number density ρi,
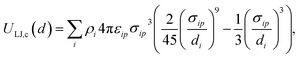 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, d
θ, d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, d
θ, d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and the normal vector defined by the COM of the molecule to this point, taking the slab to be infinite in the directions perpendicular to this vector, and extends infinitely outwards. In general, the number density can be estimated from the proportion of each type of atom in the material, the size of the atom, and the packing fraction ηi. Here, we assume that the slab consists of a single type of atom with the same LJ parameters as the carbon point probe. The volume per atom is given by
θ) and the normal vector defined by the COM of the molecule to this point, taking the slab to be infinite in the directions perpendicular to this vector, and extends infinitely outwards. In general, the number density can be estimated from the proportion of each type of atom in the material, the size of the atom, and the packing fraction ηi. Here, we assume that the slab consists of a single type of atom with the same LJ parameters as the carbon point probe. The volume per atom is given by  such that ρi = 6ηi/(πσi3), where ηi ≈ 0.74 as an upper bound of the volume fraction. The exact value of this density is not too significant in the present work as the same value is applied for all chemicals, but may play a role if further slab potentials are added.
such that ρi = 6ηi/(πσi3), where ηi ≈ 0.74 as an upper bound of the volume fraction. The exact value of this density is not too significant in the present work as the same value is applied for all chemicals, but may play a role if further slab potentials are added.
To demonstrate this procedure, we show the results obtained for a selection of atomic and molecular probes for the tryptophan side-chain analogue (TRPSCA) in Fig. 2, using both CHARMM and GAFF models for the molecule. In this case, we observe that the GAFF model is more strongly interacting overall, which is especially obvious for the interaction with a planar surface and with the potassium ion probe. The primary difference between the two forcefields appears to be the treatment of hydrogen atoms, which in the GAFF model are typically less strongly interacting with smaller values of both ε and σ than their equivalents in the CHARMM model, leading to an observable difference in the interaction with neutral atoms. We note also that the charge distribution in the CHARMM model for TRPSCA is more strongly weighted to certain atoms than in GAFF, as exemplified by the nitrogen atom (GAFF −0.1954e vs. CHARMM −0.5e) while maintaining overall neutrality.
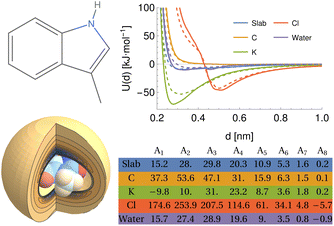 | ||
| Fig. 2 An overview of the procedure for obtaining a numerical representation of a given molecule demonstrated for the tryptophan side-chain analogue (TRPSCA). Left: 2D (top) and 3D (bottom) structure of TRPSCA, the latter shown with the potential arising by summing the LJ point–point potential over all atoms present in the molecule with a carbon atom probe. Atoms here are coloured according to their partial charge distribution and represented by spheres of radius σi/2. Top right: Potentials generated for a range of probes (see Table 1) using the GAFF (solid lines) and CHARMM (dashed lines) forcefields to describe TRPSCA. Bottom right: Array of hypergeometric expansion coefficients describing the potentials for the GAFF model of TRPSCA for use in machine-learning models. | ||
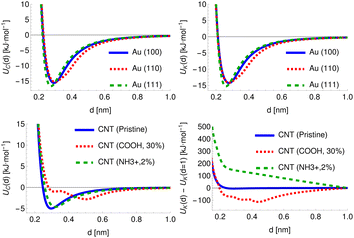
For chemicals, the potential can be defined relative to the COM, which provides a physically meaningful reference point and is straightforward to calculate. The surfaces, however, are infinite along at least one axis and may possess an arbitrary degree of surface roughness or modification. For the cylindrical structures, the distance for all provided PMFs is defined with respect to a fixed radius R = 0.75 nm. For the planar structures, however, the structure and all generated potentials can be freely translated along the axis perpendicular to the surface and thus the definition of distance is more arbitrary and we discuss later the multiple definitions of adsorbate–surface distance in use. To provide a fixed reference for these potentials, we generate the potential UC for the carbon point probe with the structure initially positioned such that the uppermost surface atom defines d′ = 0, locate the distance at which UC(d′) = 35 kJ mol−1 and translate the entire structure and all generated potentials by a distance Δs such that UC(d = 0.2 nm) = 35 kJ mol−1. This choice is largely arbitrary but provides a physically meaningful definition of the surface for amorphous or locally modified structures. The specific value is chosen to coincide with the typical value of PMFs for smooth planar surfaces at this distance. In general, the potential is sufficiently rapidly increasing in this region so that changes in the value of the energy chosen as a reference produce only very minor changes in the location chosen by this procedure. For FCC (100) metal surfaces, the required translation of the structure is very close to 0, e.g. Δs = 0.007 nm for Au (100), while for an amorphous carbon surface (c-amorph-2) we obtain Δs = 0.17 nm. We calculate the value which would be required for this translation for cylindrical NPs and find it is typically on the order of −0.03 nm. For consistency with the planar set, we apply this offset to the potentials initially generated with distance defined relative to the cylindrical axis and subtract R, such that again we have UC(d = 0.2 nm) = 35 kJ mol−1 to ensure a large cylindrical NP would produce the same set of descriptive potentials as a planar NP of the same material. In Fig. 3 we plot the carbon atom probe and potassium ion probe potentials generated for three gold surfaces and three carbon nanotubes: pristine, COOH modified (30% by weight) and NH3+ modified (2% by weight). As expected, the uncharged gold surfaces behave essentially identically for the two probes since these have very similar LJ parameters and differ only in terms of charge, but it can still be seen that the three surfaces themselves exhibit different interaction potentials, with the (110) surface showing a slightly wider attractive region and the (111) surface a deeper minimum compared to the (100) surface. These follow from the different surface morphologies: the FCC (110) surface exhibits ridges of atoms which effectively leads to the superposition of two potentials with slightly different distances to the minimum relative to a fixed surface, while the FCC (111) surface has a hexagonal structure and higher atomic density, leading to a minimum at approximately the same distance but of a greater depth. The CNTs, meanwhile, exhibit a stark difference between the charged and uncharged probes due to the strong charge–charge interaction present for the modified surfaces. Moreover, the high-density COOH modification produces a clear difference in the uncharged probe as well, with the CNT surface and functional groups producing two distinct minima at different distances relative to the CNT surface.
2.3 Overview of PMFs
The PMFs consist of tabulated data consisting of pairs of values of the surface separation distance (SSD) h from the nominal surface of the material to the COM of the adsorbate and the potential energy at this distance. In principle, the material surface is well-defined for materials with a smooth surface, e.g. FCC (100) crystals or planar forms of carbon, but not for materials with more complex structures, e.g. amorphous materials, FCC (110) crystals or CNTs modified with functionalised groups. Moreover, the exact choice of definition of h varies between methodologies, even within PMFs supplied by the same group. During data pre-processing, four main definitions of h were found to be in use: (1) the distance from the uppermost plane or CNT radius to the adsorbate COM, (2) the minimum distance between the adsorbate COM and all atoms in the material slab, (3) the distance between the COMs of the slab and of the adsorbate minus half the total slab width, and (4) the distance between the COM of the surface atoms and the COM of the adsorbate. These definitions coincide for some simple crystal structures but differ significantly for surfaces with more complex structures. In particular, definitions (2) and (4) do not produce a one-to-one mapping between the vertical height above an arbitrary plane drawn through the material and the proposed definition of h unless the adsorbate COM is above the highest atom. Consequently, the value of h is not necessarily a simple or unique function of the distance d considered in the previous sections. Indeed, even in the simplest case of an adsorbate at a distance d from a plane at a reference location d0, the distance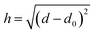 is only a single-valued function of d if d ≥ d0 at all times. If the adsorbate is permitted to sample regions d ≤ d0, i.e. inside the surface, then these will be mapped to the same set of values d as states outside the surface, regardless of if they represent high-energy overlaps, low-energy insertions, or a poorly defined surface plane. By inspection of some of the input PMFs, it appears that this has occurred for at least some of the FCC (110) surfaces, which exhibit local minima or attractive states at distances which would correspond to a substantial overlap between the solid surface and the adsorbate. We have attempted to filter these out where possible to ensure the model learns only examples from which it is reasonably certain that there is a one-to-one correlation between d and h.
is only a single-valued function of d if d ≥ d0 at all times. If the adsorbate is permitted to sample regions d ≤ d0, i.e. inside the surface, then these will be mapped to the same set of values d as states outside the surface, regardless of if they represent high-energy overlaps, low-energy insertions, or a poorly defined surface plane. By inspection of some of the input PMFs, it appears that this has occurred for at least some of the FCC (110) surfaces, which exhibit local minima or attractive states at distances which would correspond to a substantial overlap between the solid surface and the adsorbate. We have attempted to filter these out where possible to ensure the model learns only examples from which it is reasonably certain that there is a one-to-one correlation between d and h.
To account for the fact that there is potentially an arbitrary offset included in these definitions depending on the exact choice of the surface atoms, we compare the potential generated for rigid methane to the PMF for ALASCA for each of the surfaces and extract a translation distance required to move the potential onto the PMF. This is achieved by selecting the first point in the PMF with an energy under 50 kJ mol−1 and recording the distance of this point, then selecting the first point in the rigid methane potential with the same value of energy (i.e., 50 kJ mol−1 or the maximum recorded in the PMF) and recording the distance for this equivalent point. Since the rigid methane potential is defined at a known distance from the surface structure used to generate the potential, the distance ΔP between these points defines the PMF relative to the input structure. We apply this procedure to all the surfaces describing the training set of PMFs except for three specific cases. Firstly, for CdSe the alanine potential does not diverge at the surface as a consequence of the highly charged ions present in the structure, but since this has a smooth surface which can be assumed to coincide with the d = 0 plane no correction is applied to these PMFs. The Au FCC (110) PMF for alanine appears improperly converged in the region h ≤ 0.2 and so for the purposes of generating this alignment we employ the equivalent Ag FCC (110) PMF, which appears to be more consistent with the others and can be expected to be a suitable proxy due to the high similarities between these surfaces. Finally, the TiO2 anatase (100) PMF does not extend to sufficiently high values of U(h) and is not recorded close to the nominal surface, so in this case we perform the alignment at the lower value of U(h) = 17.5 kJ mol−1, which produces a result consistent with the other titania surfaces. To account for other possible differences, e.g. the absence of a one-to-one mapping for SSD types 2 and 4, we also provide the SSD class obtained from the available literature for that set of PMFs as a zero-indexed categorical variable s, e.g. SSD class 1 has s = 0. For SSD class 2 we provide the distance between the uppermost atom and the set of heavy atoms assumed to form the nominal surface as it is unclear where exactly the distance is defined from in the PMFs supplied for training, while, for SSD class 4 we provide the distance from the uppermost atom to the COM of the uppermost solid layer of carbon atoms.
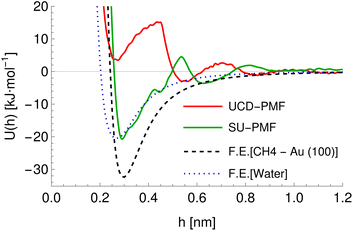
Further differences between methodologies also exist, which lead to different PMFs being calculated for the same system as can be seen for the ALASCA (methane)–gold (100) system in Fig. 4. Here, the Stockholm PMF gives a very strongly binding interaction, while the UCD PMF is essentially non-binding except for a local minimum at ca. 0.3 nm, which is binding with respect to the next local maximum. We plot the interaction potential generated for the GAFF model of methane for both to indicate the interaction potential expected in the absence of water while treating methane as a rigid molecule, which can be seen to be a much better match to the Stockholm PMF than to the UCD PMF. We posit that the difference arises due to the use of the CHARMM forcefield in the UCD simulations in place of the GAFF forcefield employed for the Stockholm set, the inclusion of solution ions in the UCD simulations which are excluded from some (but not all) Stockholm simulations and differences in the exact type of metadynamics and criteria used for convergence and post-processing. We observe similar effects for the remainder of the UCD (100) materials but typically no equivalent in the (110) and (111) structures, which are generally strongly binding to all chemicals. We note also that different Stockholm calculations vary in the method used to generate PMFs (MetaDF vs. AWT-MetaD) and the simulation timespan, although these are expected to be reasonably consistent.32 Furthermore, although both groups employ a TIP3P model of water, the SU PMFs set the ε parameter for the hydrogen atoms to 0 while the UCD PMFs use a non-zero value for consistency with the CHARMM forcefield. Finally, the PMFs for SU Au (100) surface were potentially generated using full amino acids rather than SCAs. For our purposes, we encapsulate these differences by ensuring the chemicals are described using the appropriate forcefield and by providing a categorical variable (the source variable) describing the methodology used to compute the PMF in four classes: Stockholm-no ions, Stockholm-ions, UCD-1 (110) and (111) surfaces, and UCD-2 (100) surfaces. We also include an additional variable ΔH representing the average distance between points in the input PMF to allow the model to compensate for the different resolutions at which PMFs are recorded, which reflects possible post-processing and computational differences.
2.4 Hypergeometric expansion of potentials
The tabulated PMFs and potentials describing the materials and chemicals typically contain on the order of hundreds of pairs of distances and energies, with no consistent choice of initial and final distances, number of points per PMF, or the spatial resolution employed. Consequently, any representation of these potentials must account for all these differences while discarding as little information as possible. Directly using these paired sequences as input and output for models would greatly inflate the amount of memory required and the amount of time required to train the model, since typically sequence based methods scale unfavourably with the length of the sequence. Downsampling of the potentials risks losing valuable information, especially considering many minima are quite narrow and exist near the short-range repulsion and so may be lost during downsampling, especially if naive averaging techniques are employed. Instead, we represent the entire potential in terms of the coefficients of a basis set expansion to preserve as much information as possible in a more compressed form. In this way, an entire PMF can be predicted in one step, with the output providing a smooth function which can be sampled at an arbitrary resolution. We exploit the underlying physical knowledge that the potentials represent interactions which are individually typically modelled using inverse powers of the distance r, e.g. the vdW potential r−6 and the Coulomb potential r−1, and that the potentials obey similar boundary conditions, i.e. they diverge for r → 0 and tend towards a constant which may be set equal to zero for r → ∞. To take advantage of this, we apply the Gram–Schmidt orthonormalisation method to the set of functions 1/ri to construct an orthonormal basis set of functions um(r),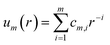 | (6) |
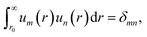 | (7) |
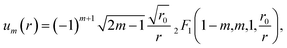 | (8) |
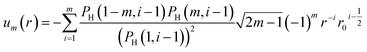 | (9) |
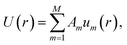 | (10) |
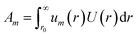 | (11) |
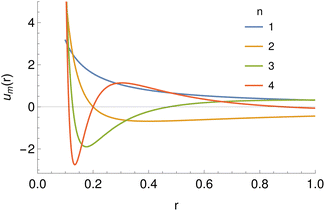 | ||
| Fig. 5 The basis set of functions based on hypergeometric functions used for the expansion of potentials, taking r0 = 0.1 and a range of values of the parameter n. | ||
2.5 ANN model for PMF prediction
In the previous sections, we have provided methodology for representing materials and chemicals of interest in terms of a set of coefficients describing their interaction potentials with probe molecules. These coefficient sets are similar to the feature maps produced by classification and image recognition neural networks, e.g. ResNet, while the remapping of the input potentials to an output potential is conceptually similar to translation and style transfer techniques implemented in various language and image models, again employing neural networks.38 Taking inspiration from this, we employ a neural network method and treat the set of chemical and surface potentials as a feature map and use an encoder approach to reduce this to a low-dimensional space employing both convolutional and fully-connected layers to produce multiple representations of the system. This encoder serves as an initial feature selection to determine the most relevant parts of the input data for the prediction of the PMF. These are combined with estimates of the energy at r0 and the minimum energy in the region h > r0 to produce a final encoded state, to which the inputs describing the particular PMF (r0, surface offset Δs, PMF offset ΔP, resolution ΔH, the source, SSD, and offset variables) are appended. The E(r0), Emin estimates are generated using fully-connected networks operating on values obtained from the set of input potentials including their minima and values at a fixed reference point and the categorical variables. These are sent directly as output for optimisation, and copies with back-propagation blocked are passed as input to the remainder of the network. To accelerate the training of the remainder of the network, we use a stochastic teacher forcing approach in which the true value is sent 50% of the time and the predicted value the remainder of the time, in either case applying noise and normalisation to produce a form useful for input. The PMF itself is generated through a multi-step approach. First, a set of expansion coefficients is generated using a small fully-connected network directly from the encoded state. During the development of the model, this was found to not produce a sufficiently accurate PMF and so it requires further refinement. We generate additional potentials by mixing together the input potentials, using the encoded state as the input to a small set of fully-connected layers to produce the mixing coefficients, one for each input potential. The weighted sum of the current set of potentials is passed through a non-linear activation layer to produce a new potential, which is appended to the list of known potentials. This procedure is repeated a small number of times with the newly created potentials appended to the list of input potentials to allow for the generation of more complex potentials. Additional potentials are generated by a convolution-transpose network from the encoded state, which starts from an initial set of three coefficients and up-scales these to take into account the sharing of information between neighbouring coefficients in a given potential. Another set of mixed potentials is generated from all these candidates and from this the initial output potential is generated. This output potential is then refined by multiplication by a matrix generated with coefficients computed from the input parameters independent of the structures in question, i.e., on r0 and the set of categorical variables. This final step is done to provide any necessary translation or transformation of the potential which is independent of the exact chemical identity. As is typical for neural networks, the number of free parameters is substantially higher than the number of data points and so we employ regularisation techniques, primarily dropout and Gaussian noise (both additive and multiplicative) to reduce the risk of overfitting.38Throughout the network, we generally use residual connections to accelerate learning and allow for additional layers to be added without decreasing the performance of the model.38 The coefficients describing the input potentials take both positive and negative values and vary over multiple orders of magnitude and we require that the model remains sensitive to small changes in coefficients with absolute values close to zero without clipping large values. We therefore employ an activation function of the form,
f(x) = b2 + sgn(x + b1)α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(|(x + b1)/α| + 1) log(|(x + b1)/α| + 1) | (12) |
The primary input is a value of r0 for the PMF and a set of HGE coefficients describing the interaction potentials of the chemicals and surfaces with a set of probes as discussed in Section 2.2. All input potentials are described using an expansion value of rp,0 = 0.2, which typically ensures that the entire region in which the potential is attractive is included. The value of these potentials at this point and the global minimum for each are passed as further input. We normalise r0 by transforming this to the log-domain and rescaling the resulting variable to have mean and variance of 0 and 1 respectively and pass this as a model input. The log-transformation is done to ensure that the model is sensitive to small variations in r0 at small values of this parameter, which significantly change the expansion coefficients. We assign further variables to account for differences in geometry and methodology used to generate the PMFs as discussed previously. In general, these categorical variables are encoded in the datasets using an integer and converted to a one-shot encoding by a pre-processing layer, then mapped from (0,1) to (−0.5,0.5). To ensure the network does not over-specialise to one particular category, a noise layer randomly perturbs these encodings during training by multiplying them by −1 with a probability of 0.1 and applying Gaussian noise. In total, the categorical values consist of the source variable defining general simulation properties, a second defining the shape (planar, cylindrical) and a third defining the convention used for the SSD (upper surface–COM, minimum atom–COM distance, adjusted centre slab–COM distance, surface COM–COM distance). For most input potentials, we provide only the free energy averages, with the potentials obtained from the minimum energy at each value of r used for the carbon atom, water and carbon ring potentials for both surfaces and chemicals, with methane-minimum additionally provided for surfaces. The goal of providing these minimum energy potentials is to enable the model to distinguish between a surface with high and low regions of binding affinity and a uniform surface of medium binding affinity, since both of these may have similar average free-energy potentials. Likewise, for chemicals this enables the model to learn differences between isotropic molecules and those with regions of high and low binding affinity or hydrophobicity.
To train the network, we employ the Adam optimiser with empirically adjusted learning rate and ε parameter39 for 50 epochs. During development of the model, we have explored a number of loss functions to overcome the issue of the different characteristic magnitudes of the various outputs (Ai, E0, Emin) and ensure the model does not specialise to one of these at the expense of the remaining outputs. In particular, we find that root-mean-square and related loss functions (Huber loss, MSE, absolute error) tend to over-emphasise the lower-order coefficients, primarily A1, and only gradually fit the higher-order coefficients. A further issue is the fact that the root-mean-square deviation between a predicted and target PMF as averaged over the entire PMF is weighted more strongly towards the h → 0 region in which the potential diverges towards positive infinity. In this region, a slight horizontal displacement of the PMF corresponds to a very large, but physically meaningless error, since large positive values correspond to essentially a zero probability for the adsorbate to be located there. The relative error, meanwhile, diverges for values of the potential close to 0 and so a loss function based on this value over-emphasises the long-range section, which again is of less physical interest. To overcome these issues, we define a loss function based on the Kullback–Leibler (KL) divergence,38 which measures the distance between a target probability density p(x) and an approximate one q(x),
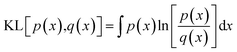 | (13) |
The PMF is related to the probability density f(h) for the position of a particle in that potential, f(h) = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−U(h)/kBT], where B is a normalisation constant to ensure the total probability integrated over the interval [0,δc] is equal to unity,
exp[−U(h)/kBT], where B is a normalisation constant to ensure the total probability integrated over the interval [0,δc] is equal to unity,
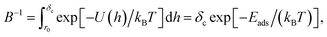 | (14) |
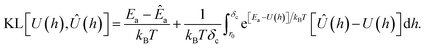 | (15) |
The first term in the above expression is simply the difference between the adsorption energy for the target and predicted PMFs, while the latter is a measure of the difference between the PMFs themselves with a weighting function exp[Ea − U(h)] applied. This weighting function is smaller where the target PMF takes large positive values and greater where the PMF is large and negative, reaching its peak in the most strongly binding regions. Thus, minimising this loss function helps to ensure that the PMF is most accurate in the physically relevant regions. The choice of kBT = 1 is used to ensure that the loss function remains relatively sharp towards minima, as during initial testing it was found that using a larger value corresponding to a physical temperature of T = 300 K reduced the accuracy of the model. We evaluate this loss numerically by sampling the PMFs generated for the target and predicted coefficients on a grid and approximating the integration by summation over these points. Formally, the KL loss is non-negative for all input functions and so can be directly used as a loss function by summation of this value over all PMFs in a batch, but in practice we use the mean-square value calculated over a batch to stabilise the training for values of the loss close to zero. We combine this loss with the mean-squared error for each of the Ai and the two values E0, Emin, weighting each of these by the variance for that output variable estimated from the training set to ensure that the optimisation treats each of these equally. Without this weighting, we find the training emphasises the fitting of the A1 parameter which typically varies over the widest range of values and thus has the largest mean-square error but controls only the coarse long-range behaviour of the output potentials. To counteract the unbalanced nature of the dataset, e.g. the high proportion of PMFs for planar surfaces compared to cylindrical surfaces, we assign sample weights to each PMF which are used during the evaluation of the loss function to ensure PMFs with rarer features contribute more to the training and avoid biasing the network towards the most common PMFs. These sample weights are generated based on several criteria. Each categorical variable contributes a factor to the weight proportional to the inverse of the frequency of that value, such that PMFs consisting of a category with few examples are weighted more strongly. The AGGLOMERATE clustering algorithm implemented in scikit-learn40 is used to assign sets of Ai values to clusters in order to identify PMFs with dissimilar features and weights are assigned based on the inverse frequencies of these. Finally, we also include a factor derived from the minimum of the PMF in the region h ≥ r0, normalised by the mean and standard deviation of the PMF minima in the entire training set. This ensures that the training algorithm weights especially strongly and weakly binding PMFs more in order to reproduce the correct behaviour at both extremes.
2.6 Generation of training data
For training purposes, it is advantageous to provide multiple sets of Ai values for each PMF and set of input potentials to increase the size of the dataset which is otherwise fairly limited. We therefore apply the HGE procedure to each PMF taking multiple values of r0 for each PMF to generate multiple sets of coefficients. This has the additional benefit of dealing with the issue that the PMFs are generally truncated at different minimum values of h by providing examples of the same PMF with different degrees of truncation, and further eliminates the need to choose a specific value for r0. During the expansion, we record both the actual value of U(r0) and the value obtained from the generated expansion, UH(r0). We discard results where |U(r0) − UH(r0)|2 ≥ 10 or where the error increases with increasing m since this indicates that the expansion has failed to converge. For each PMF we record the methane-to-alanine offset distance ΔP calculated for the surface in question as an additional parameter to allow the model to compensate for the unknown location of the surface used in the definition of the PMF. To increase the size of the training set we generate additional expansions in which we translate the PMFs by ΔP and a random value drawn from a zero-mean normal distribution with standard deviation σ = 0.1, again recording the final offset relative to the methane potential. Consequently, the initial PMF has a recorded offset of ΔP while translated PMFs have an offset typically in the interval (−0.1,0.1). These translated PMFs are further perturbed by small amounts of noise prior to applying the HGE for a given value of r0. Denoting a normal distribution of mean μ and standard deviation σ by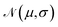 , these perturbations are random translations of the entire PMF by an additional small random amount
, these perturbations are random translations of the entire PMF by an additional small random amount 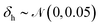 , multiplication of the energy values for the entire PMF by
, multiplication of the energy values for the entire PMF by 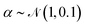 and the application of a small amount of additive noise
and the application of a small amount of additive noise 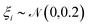 to each individual energy value in the PMF such that the noisy PMF is given by
to each individual energy value in the PMF such that the noisy PMF is given by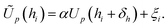 | (16) |
This procedure has the advantage of smoothing out some of the noise inherent in each PMF and reducing the risk of the neural network overfitting to the specific examples provided, and is essentially the one-dimensional equivalent of the typical image augmentation techniques of adding shot noise, randomly translating the images, and randomly adjusting the brightness of the entire image, all of which are known to improve both the training and validation of networks.38 Multiplication by α maps directly onto the coefficients of the modified PMF, Ãi = αAi, but the modifications in the perturbed coefficients due to translation or shot noise are much more difficult to express in terms of a simple transformation of the HGE coefficients. Thus, these transformations are pre-applied to the PMFs before expansion to generate four noise replicates at each value of r0 for each PMF. Compared to implementing these noise transformations directly in the network, this method has the benefit of producing a larger dataset to optimise over and thus smoothing out the loss function for an individual epoch. The downside of this method is that it increases the memory required for the dataset and does not produce a new random sample for each epoch. Thus, we also apply similar noise directly in the HGE domain implemented as Tensorflow layers for the sets of input potentials to provide new perturbations for every training epoch without an increase in the memory required for the training set while providing some protection against overfitting. Noise is additionally applied to all outputs as a form of label smoothing, again to reduce overfitting.
Due to the limited size of the available dataset, the majority of available PMFs were used for model development with a small number reserved for final testing. Some PMFs have been manually excluded due to being clear outliers for reasons which could not be resolved during model development, namely: AFUC, TRPSCA, and PHESCA for Au (100) UCD; ALASCA, CYSSCA, LYSSCA, and HIESCA, for Au (110) UCD; GLUSCA, BGLCNA and TYRSCA for Ag (100) UCD; ASPPSCA, LYSSCA and THRSCA for Ag (110). Typically, these exhibit either spurious maxima or minima, or appear to have allowed penetration of the molecule past the nominal surface. Predictions are still made for these PMFs and they are not excluded from the calculation of final train and test statistics. The Ag (100) and Au (100) PMFs are set to a separate methodology (UCD-2) due to their clear difference from the remaining UCD FCC metal PMFs, but otherwise treated normally. For the remaining PMFs, we have tested two variants of generating the training and validation sets. In the first variant, the sets of materials and chemicals (identified by SMILES code) are individually split into training and validation sets, with any PMF featuring a validation material or chemical excluded from the dataset used for training the model. This produces a total of four classes of PMF: training material–training chemical, training material–validation chemical, validation material–training chemical, and validation material–validation chemical. We manually assign the gold FCC (100) structure from both sources to the training set in order to provide the model with a comparison between the two sources for the same structure. Since the Stockholm-sourced gold PMFs typically exhibit a very strong binding energy, this has the further benefit of ensuring the model is valid over a wide range of interaction strengths. Likewise, the gold FCC (111) structure is manually assigned to the training set since this exhibits an even stronger binding energy and to ensure that the class of non-(100) UCD PMFs is represented. To generate the rest of the training set, we employ a clustering algorithm to identify broad classes of surfaces and chemicals and ensure the training set contains examples of all classes. To do so, we use the AGGLOMERATE clustering algorithm implemented in scikit-learn40 based on the coefficients describing the input potentials up to the 8th order, with a maximum of fifteen clusters allowed each for chemicals and materials. A randomly selected example from each cluster is assigned to the training set such that this covers as wide a variety of surfaces and chemicals as possible. The remainder of the training sets are chosen from all remaining materials and chemicals. For the materials, we generally find many clusters consist of a single example (e.g. CdSe, Fe2O3) while a large cluster contains almost all the CNTs. Depending on the exact parameters chosen, the FCC metals are either combined into a single cluster or separated into a group containing (100) and (111) surfaces and a second containing the (110) surface as a consequence of the roughness of the (110) surface compared to the other two. We train five variants of the model using different random splits generated in this way and demonstrate later that this produces acceptable results in most cases, but the set for which both material and chemical are excluded from the training set typically exhibits a number of mis-predictions. Thus, to produce reliable predictions and maximise the range of materials for which reliable predictions can be made, we employ a bootstrap aggregation (bagging) method. In this method, we again train ten variants of the model for fifty epochs each using the same architecture but each using a different dataset selected by random resampling from the set of all PMFs, with training and validation sets selected from these resampled sets at random. This bootstrap aggregation procedure is known to produce more reliable predictions in general and potentials in particular,17,41 ensures that there is a non-zero probability for all PMFs in the dataset to contribute to the final model, and has the additional benefit of providing estimates of the uncertainty of each prediction by comparing the output of each model. Typically, circa 500 distinct PMFs contribute to a given bootstrap replicate after the resampling and training–validation split. For reproducible results, the seed values used for the random number generation in Python, NumPy and Tensorflow are fixed based on the model type.
For final testing and comparison of the bootstrap ensemble, we use surfaces not employed in the development of the model (copper, iron and an additional amorphous carbon structure) and two additional small molecules calculated in the UCD set (beta-galactose, choline). The former is designed to assess the ability of the model to make predictions of the PMFs required for the operation of the United Atom adsorption model11 for new materials and is a key outcome of this work. The prediction of adsorption profiles for small molecules is of interest but due to the small amount of available data only limited testing of this functionality can be achieved here. Testing results reported were evaluated using the version of the model archived at ref. 26; all results shown in this work correspond to the model trained before prediction was performed for this test set. Full details of which potentials are supplied as input are provided in the model repository, as is the Python code used to generate the network and details on the training–validation splits.
2.7 Implementation
All scripts are implemented in Python 3 using primarily the NumPy, SciPy, Pandas, Tensorflow, and scikit-learn libraries.22,40 Calculation of potentials and training of the neural network are performed on a Dell Precision 7910 workstation with a Xeon CPU E5-2640 v4 running at 2.40 GHz. A training epoch on the noise-augmented dataset takes on the order of 20 to 30 minutes utilising the CPU only. Parameterising a new chemical takes on the order of a few minutes while each surface takes up to a few hours for one CPU core for the set of point probes, plus an extra hour for each molecular probe. Optimisation of this bottleneck remains a future goal, but we note that multiple surfaces may be parameterised simultaneously and that this remains substantially faster than direct computation of PMFs.3 Results
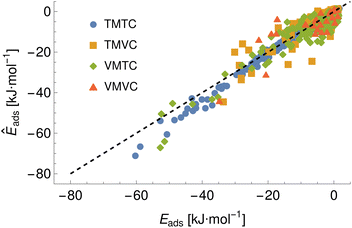
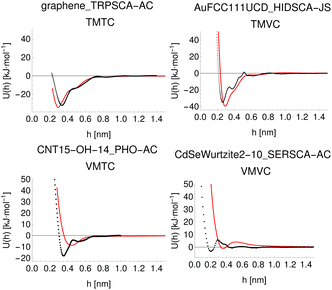
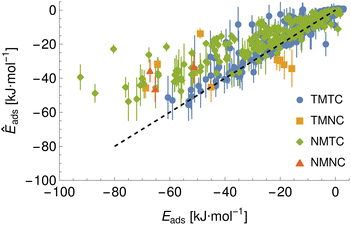
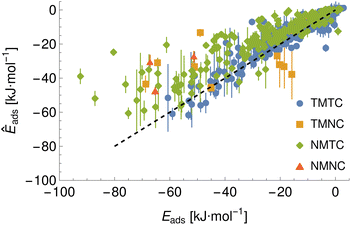
To demonstrate a typical output of the procedure for generating a numerical representation of a molecule, the low order coefficients for a set of probes to the tryptophan side chain analogue are presented in Fig. 2. Potentials for the full set of surfaces and chemicals and the HG expansion coefficients corresponding to the results presented here are archived at ref. 26. This repository also contains tabulated binding energies for all predicted PMFs using both ensemble methods. The code repository25 contains the most recent values reflecting any changes in the code or addition of new molecules or surfaces. All results in this section are obtained from the model checkpoints with lowest training loss, for which the validation loss is typically also a minimum.Given the large number of predicted PMFs and models, here we only present some examples and summary statistics, with the full set of predictions available for download at ref. 26 and results for selected materials and the testing chemicals available in the ESI.† For each model variant, we compute the PMFs, KL divergences, and binding energies at T = 300 K for all material–adsorbate pairs, matching simulation type and SSD parameters to the ones used for training the model and taking r0 to be as close to 0.2 as possible based on the input PMF. The results for one example model (cluster split, no bootstrapping, split ID 1) are plotted in Fig. 6 in comparison to the binding energies calculated for the original PMFs with the worst-performing predictions for each of the four classes in terms of KL divergences shown in Fig. 7. The agreement is generally quite good and we find a high correlation for both training and validation groups for this model. The poorly-performing PMFs can be seen to generally exhibit the correct structure aside from the PMF for phosphate binding to an OH modified CNT (VMTC class) capturing only the second, weaker adsorption and the horizontal translation of the CdSe–serine SCA PMF. This latter case is attributed to the fact that CdSe is in general non-binding and the same general structure is observed for the majority of the other PMFs for this surface, with SERSCA providing one of the few exceptions. This highlights the importance of employing a diverse training set to capture such outliers. In the ESI† we give summary statistics for the binding energy and KL divergence for groups of networks employing different random seeds and both split methodologies. We observe that there is a high degree of variability in the accuracy of the predictions for the cluster-based random splitting when attempting to predict materials from the validation set, with some splits producing very good results on unseen materials and others failing to converge. Two of the cluster-based splitting models (cluster-A-3, cluster-A-4) perform significantly worse on validation data and so are not used for further study. This likely relates to the highly heterogeneous nature of the set of materials, which may require further refinement of the cluster-based assignment of outliers to the training set. The bootstrap replicates generally exhibit more reliable validation scores (see Tables 2 and S5 in the ESI†) and so we recommend the use of results from the ensemble of these, but provide results for both ensembles excluding the two poorly performing cluster models.
| TMTC | TMNC | NMTC | NMNC | |
|---|---|---|---|---|
| Bootstrap correlation | 0.96 | 0.59 | 0.89 | 0.55 |
| Bootstrap R2 | 0.92 | 0.35 | 0.8 | 0.3 |
| Cluster correlation | 0.97 | 0.53 | 0.89 | 0.54 |
| Cluster R2 | 0.93 | 0.28 | 0.79 | 0.29 |
Final prediction of PMFs is achieved by averaging the PMFs generated from all ensemble members, which implicitly allows for all material–chemical pairs to feature in the training set. Thus, to validate this model, we must employ the (limited) data not otherwise used in the model development process. To test the ability to make predictions for new chemicals, we calculate PMFs for two extra molecules: 2-acetyl-2-deoxy-beta-D-galactosamine (BGALNA) and choline (CHOL), which are compared to the predicted PMFs generated for the FCC Au and Ag surfaces (UCD methodology, three surface indices, see Fig. S2† for BGALNA). Predictions for new surfaces are performed for an alternate amorphous carbon morphology c-amorph-3 and additional FCC metals Cu42 and Fe.43 We match the input parameters for prediction to those assumed for the style of PMF but do not calculate the alanine offset. The generated PMFs and adsorption energies are provided in the repository26 and binding energies extracted from these are presented in Fig. 8 and 9, with adsorption energies for the novel chemicals to FCC metals listed in the ESI in Table S6,† and energies for the training chemicals to the amorphous carbon surface in Table S7,† and to Cu (111) in Table S8.† We find a generally correct ranking for novel surfaces but worse agreement for novel chemicals. We attribute this discrepancy to the limited amount of data for novel chemicals and the noise and inconsistency in the target PMFs. In particular, BGALNA should be similar to BGLCNA but is found to differ significantly in metadynamics across surfaces despite the similar surface input potentials (Fig. S2†). CHOL is typically predicted reasonably accurately except to (111) faces, for which the predicted binding energy is much more favourable than that found through metadynamics, e.g. −34 vs. −16 kJ mol−1 for Ag (111). The reason for this is unknown but it appears consistent across the models (Fig. 8 and 9).
The methodology proposed here uses descriptors for the surfaces and chemicals which can be derived directly from their structure and forcefield parameters and so is conveniently extendable to new structures for both. To demonstrate the power of this approach, we use the trained model to make predictions for approximately one hundred additional small molecules taken from the ChemSpider database, making the selection based on those consisting of the “standard” elements for organic molecules and with total molecular mass of under 200 AMU, selecting the hundred most highly cited and discarding those already present in the dataset. Details of the full set are available in the ESI,† where we report the ChemSpider ID, SMILES code and a brief description of each molecule. To this set we add some short alkanes and alkenes for use in the construction of more complex molecules by a fragment-based approach, and caffeine as an example of a small molecule drug. These predictions are made for the materials in the development set and the surfaces used for testing, plus the (001) surfaces of platinum, cerium, chromium oxide (Cr2O3), tricalcium silicate, hydroxyapatite, a range of gold (001) surfaces with 5/25/50/75% of the surface atoms randomly removed to mimic weathering of the surface, and gold (001) surfaces modified with a dense rigid brush (100% grafting density) of either PEG or PE polymers.24 These latter two are less physically realistic in that they do not allow for motion of the brushes, but may be a reasonable first approximation to the potential which would be obtained for solid polymer NPs since the gold surface is sufficiently far away to not significantly contribute to the potentials. We generate a set of PMFs for all material–chemical pairs both matching the original parameters and a “canonical” set of PMFs using the parameters equivalent to Stockholm methodology with ions, SSD type 1, ΔH = 0.002, ΔP = 0, r0 = 0.2 nm. Both matched and canonical PMFs are included in the repository and the results for the GAFF parameterised biomolecules required for UnitedAtom11 are copied to a secondary archive for ease of access. Samples of the matched, canonical and metadynamics PMFs for this subset are shown in Fig. S3–S6 of the ESI† with all plots available in the repository.26
4 Discussion
The model and methodology proposed here allow for a cost-effective prediction of interactions for multiple classes of materials and chemicals. When trained on a sufficiently diverse set of materials and chemicals, they will be able provide a universal tool for a fast screening of adsorbates in silico. Yet, they are by no means definitive and further optimisation is possible, both for the selection of probes used to define the chemicals and surfaces, and the structure of the network used. In this work, we have attempted to develop a model that is robust enough to demonstrate the overall methodology while still remaining sufficiently flexible to make predictions for a wide range of surfaces and chemicals despite the inhomogeneity of the pool of input PMFs taken from different sources. Crucially, the input is generic enough that new surfaces and adsorbates can be defined without requiring any retraining of the model. The procedure used to parameterise chemicals and materials relies on the existence of a set of co-ordinates and suitable forcefield for the species in question, but provided these exist or can be obtained then the PMFs generated should be valid for a wide range of material surfaces, including high-order Miller indices, amorphous structures, or crystal planes with missing or adsorbed atoms. This is a consequence of the fact that the methodology relies on the construction of the free energy as a function of the distance from the surface and does not directly attempt to make predictions based on the exact structure or component atoms. Thus, as long as the input potentials are physically realistic and not too dissimilar from those in the training set, the output PMF should at least be a reasonable approximation to the one which would be obtained after performing metadynamics simulations with substantially less time investment. The potentials and HGE coefficients produced are themselves useful descriptors of materials for further use in advanced applications.A key challenge that we tried to answer in building the predictive model is the size and reliability of the dataset used to train it. Here, only a fairly limited number of materials and chemicals have been considered, and the training dataset lacks consistency in terms of the results for nominally the same surface and chemical, e.g. the differing PMFs provided for the Au (100) surface which in certain cases produce substantially different results between groups. Moreover, PMFs produced by the same group for closely related surfaces, e.g. Au (100) and Au (111), exhibit surprising differences despite nearly identical input structures (Fig. S2†). Since the exact reason for these inconsistencies is not known, we are limited to labelling the dataset by methodology, and it is further not known if these differences reflect genuine differences between the simulated systems or errors in the metadynamics calculations or associated metadata. Further complications arise due to the inconsistent definitions of the location of the surface and the definition of surface–adsorbate distance. Again, we have attempted to develop the methodology to compensate for this, but a more standardised definition would be beneficial for future work. Another small error has been introduced due to the use of an incorrect structure for the CHARMM parameterisation of GANSCA/GLUPSCA, but this impacts only six training PMFs and is compensated for by the GAFF version for other PMFs and so is unlikely to constitute a large source of error. Likewise, the SU Au (100) PMFs may have used different structures (full AA vs. SCA) and CdSe surface potentials were calculated using an incorrect crystal facet. These errors were not discovered until after model training, but as these two are assigned a different source variable the model implicitly will have been trained to circumvent these errors.
Despite these limitations, we generally find a good agreement between the adsorption energies predicted using the model presented here and those found through computationally demanding metadynamics simulations, even for materials not included in the training set. We observe that the model remains generally accurate for these new materials over the range of binding energies in the training set but has difficulty extrapolating to even more strongly binding materials. The limited data for testing new chemicals makes it difficult to evaluate whether this limit is responsible for the poor performance of chemicals in the testing set and this remains a topic for further study. The first testing chemical BGALNA is an epimer of the training chemical BGLCNA, yet exhibits significantly different metadynamics results (Fig S2†). The second testing chemical is correctly predicted by some members of the ensemble but not others, suggesting that this may require a larger ensemble or a greater proportion of training data in each ensemble member. For chemicals or surfaces for which no reference is available, we recommend inspection of the PMFs predicted by individual ensembles and the distribution of associated binding energies, under the assumption that if all ensemble members predict the same binding energy this is likely to be more reliable than if there is a significant spread.
For future use, the model may be fine-tuned for a specific material or chemical through use of transfer learning by generating PMFs for a limited number of examples and re-training the model using a very low learning rate for a small number of epochs.38 Based on the typical success of transfer learning it is likely that this would enable the model to make reliable predictions for novel structures within a much shorter period of time than would be necessary to generate a full set of PMFs. Even without this step, the predictions for materials similar to those in the training set are likely to be quite accurate given the generally good performance for the validation set, especially for perturbations of existing structures, e.g., introducing surface defects into an otherwise pristine structure or modifications of the charge of surface atoms. For organic molecules, ACPYPE and the CHARMM-GUI ligand generator provide well-tested means to generate the input structures and atomic parameters required for essentially arbitrary molecules. Provided that these molecules are similar to those in the training set, i.e., organic molecules with low formal charges and molecular masses under 200 amu, it is reasonable to assume that the predictions of the model will be at least approximately correct. At present, the model cannot accurately account for flexibility of input molecules, which may explain some limitations in the reliability of the model. We intend to improve this in future versions of the model by representing molecules as an ensemble of structures rather than the single structure currently used, similar to recent work on the SPICE dataset.44 This also offers the scope to expand the model to larger chemicals and flexible surfaces such as brushes.
5 Conclusions
We have developed a flexible framework for the prediction of PMFs of the interaction between small organic molecules and solid surfaces using a combination of atomistic properties and an artificial neural network. Our methodology represents complex input structures in terms of a universal expansion into basic interaction potentials which can be generated for new molecules and surfaces using their structures and molecular dynamics forcefield parameters. We find a generally good agreement between the target and predicted PMFs in both training and validation sets. Our model enables the rapid analysis of a complex surface in terms of its activity towards small molecules, with applications in catalysis, drug design and computational nanotoxicity.Author contributions
I. Rouse: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization. V. Lobaskin: conceptualization, methodology, resources, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank J. Subbotina, P. Mosaddeghi and A. Lyubartsev for providing details of the metadynamics simulations, and K. Kotsis, A. Colibaba and the members of QSAR Lab (Gdansk) for calculating nanomaterial descriptors used in development and for useful discussions. We acknowledge funding from EU Horizon 2020 grants no. 814572 (NanoSolveIT) and no. 101008099 (CompSafeNano).Notes and references
- D. Astruc, Chem. Rev., 2020, 120(2), 461–463 CrossRef CAS PubMed.
- M. Chamundeeswari, J. Jeslin and M. L. Verma, Environ. Chem. Lett., 2019, 17, 849–865 CrossRef CAS.
- X.-R. Xia, N. A. Monteiro-Riviere and J. E. Riviere, Nat. Nanotechnol., 2010, 5, 671–675 CrossRef CAS PubMed.
- G. Bitencourt-Ferreira and W. F. d. Azevedo, in Docking Screens for Drug Discovery, Springer, 2019, pp. 251–273 Search PubMed.
- Y.-C. Chen, Trends Pharmacol. Sci., 2015, 36, 78–95 CrossRef PubMed.
- M. O. Rodrigues, M. V. de Paula, K. A. Wanderley, I. B. Vasconcelos, S. Alves Jr and T. A. Soares, Int. J. Quantum Chem., 2012, 112, 3346–3355 CrossRef CAS.
- J. Kirkwood and F. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- B. Ensing, M. De Vivo, Z. Liu, P. Moore and M. L. Klein, Acc. Chem. Res., 2006, 39, 73–81 CrossRef CAS PubMed.
- E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. C, 2015, 119, 18126–18139 CrossRef CAS.
- V. Marinova and M. Salvalaglio, J. Chem. Phys., 2019, 151, 164115 CrossRef PubMed.
- D. Power, I. Rouse, S. Poggio, E. Brandt, H. Lopez, A. Lyubartsev and V. Lobaskin, Modell. Simul. Mater. Sci. Eng., 2019, 27, 084003 CrossRef CAS.
- D. Horinek, A. Serr, M. Geisler, T. Pirzer, U. Slotta, S. Q. Lud, J. A. Garrido, T. Scheibel, T. Hugel and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2842–2847 CrossRef CAS PubMed.
- M. Bertazzo, D. Gobbo, S. Decherchi and A. Cavalli, J. Chem. Theory Comput., 2021, 17, 5287–5300 CrossRef CAS PubMed.
- P. Gkeka, G. Stoltz, A. Barati Farimani, Z. Belkacemi, M. Ceriotti, J. D. Chodera, A. R. Dinner, A. L. Ferguson, J.-B. Maillet and H. Minoux, et al. , J. Chem. Theory Comput., 2020, 16, 4757–4775 CrossRef CAS PubMed.
- Q. Dong and S. Zhou, IEEE/ACM Trans. Comput. Biol. Bioinf., 2011, 8, 476–486 Search PubMed.
- Y. Min, Y. Wei, P. Wang, N. Wu, S. Bauer, S. Zheng, Y. Shi, Y. Wang, D. Zhao, J. Wu and J. Zeng, Predicting the protein–ligand affinity from molecular dynamics trajectories, arXiv, 2022, preprint, DOI:10.48550/arXiv.2208.10230.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed.
- S. Käser, L. I. Vazquez-Salazar, M. Meuwly and K. Töpfer, Neural Network Potentials for Chemistry: Concepts, Applications and Prospects, arXiv, 2022, preprint, DOI:10.48550/arXiv.2209.11581.
- D. Nasikas, E. Ricci, G. Giannakopoulos, V. Karkaletsis, D. N. Theodorou and N. Vergadou, Proceedings of the 12th Hellenic Conference on Artificial Intelligence, 2022 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Advances in neural information processing systems, 2017, vol. 30, pp. 5998–6008 Search PubMed.
- J. Pei, L. F. Song and K. M. Merz Jr, J. Chem. Theory Comput., 2020, 16, 5385–5400 CrossRef CAS PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, arXiv, 2015, preprint, https://www.tensorflow.org/.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 1–8 CrossRef PubMed.
- Y. K. Choi, N. R. Kern, S. Kim, K. Kanhaiya, Y. Afshar, S. H. Jeon, S. Jo, B. R. Brooks, J. Lee, E. B. Tadmor, H. Heinz and W. Im, J. Chem. Theory Comput., 2022, 18, 479–493 CrossRef CAS PubMed.
- I. Rouse, PMFPredictor-Toolkit, 2022, https://github.com/ijrouse/PMFPredictor-Toolkit Search PubMed.
- I. Rouse, Computed Surface and Chemical Potentials, Expansion Coefficients, Structures, Models and Results for the PMFPredictor Toolkit, 2022, DOI:10.5281/zenodo.7458499.
- I. Rouse, D. Power, E. G. Brandt, M. Schneemilch, K. Kotsis, N. Quirke, A. P. Lyubartsev and V. Lobaskin, Phys. Chem. Chem. Phys., 2021, 23, 13473–13482 RSC.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 1–14 Search PubMed.
- C. Guo and F. Berkhahn, Entity Embeddings of Categorical Variables, 2016 Search PubMed.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- A. Lyubartsev, E. Brandt and M. Saeedimasine, Adsorption Free Energies and Potentials of Mean-Force for Interactions between Amino Acids, Lipid Fragments, and Nanoparticles, 2020, DOI:10.5281/zenodo.4314912.
- M. Saeedimasine, E. G. Brandt and A. P. Lyubartsev, J. Phys. Chem. B, 2021, 125, 416–430 CrossRef CAS PubMed.
- J. Subbotina, United Atom Parameters for United Atom Multiscale Modelling of Bio–Nano Interactions of Zero-Valent Silver Nanoparticles, 2022, DOI:10.5281/zenodo.5846080.
- J. Subbotina, United Atom Parameters for United Atom Multiscale Modelling of Bio–Nano Interactions of Zero-Valent Gold Nanoparticles, 2022, DOI:10.5281/zenodo.6066434.
- J. Subbotina and V. Lobaskin, J. Phys. Chem. B, 2022, 126, 1301–1314 CrossRef CAS PubMed.
- W. R. Inc., Mathematica, Version 13.1, Champaign, IL, 2022, https://www.wolfram.com/mathematica Search PubMed.
- NIST Digital Library of Mathematical Functions, ed. F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl, and M. A. McClain, Release 1.1.6 of 2022-06-30, http://dlmf.nist.gov/ Search PubMed.
- K. P. Murphy, Probabilistic Machine Learning: an Introduction, MIT Press, 2022 Search PubMed.
- D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, 2014 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. K. Agrafiotis, W. Cedeno and V. S. Lobanov, J. Chem. Inf. Comput. Sci., 2002, 42, 903–911 CrossRef CAS PubMed.
- J. Subbotina, United Atom Parameters for United Atom Multiscale Modelling of Bio–Nano Interactions of Zero-Valent Copper Nanoparticles, 2022, DOI:10.5281/zenodo.6066480.
- P. Mosaddeghi, J. Subbotina and V. Lobaskin, Multiscale Modelling of Milk Proteins Interaction with Zero-Valent Iron Nanoparticles, 2022 Search PubMed.
- P. Eastman, P. K. Behara, D. L. Dotson, R. Galvelis, J. E. Herr, J. T. Horton, Y. Mao, J. D. Chodera, B. P. Pritchard, Y. Wang, G. D. Fabritiis and T. E. Markland, SPICE, A Dataset of Drug-like Molecules and Peptides for Training Machine Learning Potentials, 2022 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the material surfaces and small molecules parameterised for use in the machine learning model, tables of predicted binding energies for sample novel chemicals and surfaces. See DOI: https://doi.org/10.1039/d2fd00155a |
| This journal is © The Royal Society of Chemistry 2023 |