Exploring potential dual-stage attention based recurrent neural network machine learning application for dosage prediction in intelligent municipal management
Received
18th July 2022
, Accepted 21st December 2022
First published on 23rd January 2023
Abstract
Chemical demand prediction is important for water management and the environment. This study aimed to select and apply suitable data-driven models based on real-world big data for dosage prediction towards improved automated control of water treatment plant management. Coagulation is a prominent process in normal water treatment plants (WTP). The chemical reactions are complex and the amount of coagulant dosage required was affected by many factors which makes it difficult to determine the optimal dosage effectively. Additionally, the coagulant process is a typical non-linear, multi-variable, large time-delay, non-stationary, strong coupling and time-varying system. Accurately determining the amount of coagulant added has become one of the most significant challenges. Some studies build a prediction model that only uses current water quality parameters, the previous time sequences were ignored and lacked consideration of multivariate time series and multiple water quality parameters simultaneously, resulting in unsatisfactory prediction accuracy. This study not only takes current water quality parameters into account during the modelling but also considers historical time-series water quality features. We found that the attention-based encoder-decoder of the recurrent neural network framework is an effective model in the area of intelligent water management. In this paper, we studied real-world data with 4 different machine learning models. Compared to the other three potential competitive machine learning algorithm models (random forest, multiple linear regression, and long short term memory), the experiment results demonstrated the best performance for predictive analysis with a highest coefficient of determination (R2) of 0.9908 and lowest values of root mean squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) (1.2524%, 1.1263%, and 1.01%, respectively) in the DA_RNN algorithm. Consequently, this study provides a more reliable and accurate approach for forecasting wastewater coagulation dosage, which is pivotal in terms of the socio-economic aspects of wastewater management.
Water impact
Every cubic meter of water needs to consume about 13 g of chemicals in water processing and the dosage will change depending on design, water use, water quality, treatment process, etc. Based on multivariate time series and multiple water quality parameters, we built a deep learning model to improve dosage prediction accuracy in wastewater treatment plants, which saves resources and improves economic efficiency.
|
1. Introduction
Every day, the world needs to treat an incredible amount of wastewater (about 1 billion m3 per day of wastewater), with the development of society, the treatment load is expected to increase by 24% by 2030 and 50% by 2050.1 The chemicals usage varies from 1 to 13 g m−3 regarding the feeding management and real water quality (inlet status and outlet requirement) in a real wastewater treatment plant (WWTP).2 However, machine learning (ML) instead of relying on workers' experience is claimed to save chemicals in water management.3 The worldwide treatment wastewater market is expected to increase from 283.5 billion US dollars a year in 2021 to 465 in 2028,4 thus, the financial benefits of chemical saving are significant. The consumption of chemicals has also been greatly improved, which cause secondary pollution to the environment and waste huge amounts of energy resources. Considering applying ML in more accurate dosage demands requires understanding that coagulation is one of the most widespread water treatment methods,5 and the coagulant process is a typical non-linear, multi-variable, large time-delay, non-stationary, strong coupling, time-varying system.6,7 Meanwhile, the complexity of the coagulation chemical theory is affected by many factors (turbidity (TUR), pH value (PH), electrical conductivity (CON), flow rate, total phosphorus, total nitrogen, ammonia nitrogen (AN), chemical oxygen demand, etc.), which means it is difficult to accurately determine the amount of coagulant added.8 Data-driven solutions for maintenance or efficiency improvement have been proven to have a positive impact on social and environment aspects in real-world projects,9 with the advancement of data analytical tools and their interdisciplinary applications in environmental science and engineering, powerful computer-based ML and artificial neural networks (ANN) have shown great potential for prediction and optimization of process control for wastewater treatment.3,10,11
With the rapid development of ML algorithms, a favourable tool for precise dosing control is provided.12–15 Heddam16 proposed an extremely randomized tree, random forest (RF) and multiple linear regression (MLR) for predicting coagulant dosage in the Boudouaou drinking water treatment plant (DWPT). Wang17 combined a genetic algorithm-based and particle swarm optimization technique with regression model analyses implemented to optimize the coagulation dosage. Icke18 applied a self-learning feed-forward algorithm to improve chemical dosing accuracy and reduce energy consumption. Xu3 employed eight ML models to predict the chemical dosage WWTP and compared the performance of each model. Fang19 utilized the light gradient boosting machine algorithms to forecast dosage in WWPT, and relatively good results were achieved. Wang20 compared principal component regression (PCR), support vector regression (SVR) and long short-term memory (LSTM) neural networks to build predictive models, and the results show that the LSTM algorithm outperforms both PCR and SVR. However, the wastewater treatment process is a typical non-linear, multi-variable, time-lapse system involving complex removal mechanisms influenced by a multiplicity of factors such as coagulant types, properties and source water origin. Traditional machine learning algorithms under-perform when solving this kind of problem.
Artificial neural networks (ANN) have proven to be an effective way to solve various non-linear problems.21–25 Heddam26 and Hong27 adopted an adaptive neuro-fuzzy inference system model with pH, TUR, dissolved oxygen (DO), CON, and temperature as model input parameters for coagulant dosage in DWPT. Wadkar28 applied a cascade feeds forward neural network to predict coagulant dose. Haghiri29 used PH, temperature, alkalinity, and TUR as training parameters for the multi-layer perceptron model to determine the coagulation dosage in WWTP. Wu30 explored the effects of data normalization and inherent factors on the decision of optimal coagulant dosage in WWT by using the ANN algorithm. Wang31 used the Elman neural network (ENN) to predict coagulant dosage in the DWTP. Although these models have achieved better results compared to ML algorithms in dealing with nonlinear problems, nevertheless, these models were used to treat original data as discrete data, the water quality parameters of the previous time sequence information were ignored and were not transformed into a time series prediction problem, resulting in the prediction accuracy being not satisfactory.
The sewage treatment process is a continuous addition of drugs into the water stream and the collected data are the time sequence. Simply using the current water quality parameters to forecast dosage ignores the implied information of the time series. As a result, the aforementioned methods cannot reach accurate prediction results. The amount of coagulant required at the current time is not only related to the water quality parameters at the current time but also related to the water quality parameters at the previous time. Therefore, the problem of coagulant dosage can be solved by time series prediction. Recurrent neural network (RNN)32 is a kind of dealing with time series task neural network, LSTM33 is a special type of RNN that solves the vanishing gradient problem. Fang34 used the LSTM algorithm model to predict the dosage of coagulant in WWTP. Liu6 proposed a based-LSTM adjusting accumulated error automatically and time-consistent term to determine coagulant dosage in different data sources, better experimental results are obtained. Based on the RNN and attention mechanism,35 Qin36 proposed a dual-stage attention-based recurrent neural network (DA-RNN), which demonstrated great success in temporal forecasting, it seems the fitness of this model regarding the features of water quality is matched but it needs deeper research. Jing37 combined historical time-series data of COVID-19 with geographic and local factors in the DA-RNN model to predict COVID-19 cases, the model has better performance than support-vector-regression and the encoder–decoder network on the experimental datasets. Huang38 exactly forecasts wind power generation by historical power and wind speed information in DA-RNN. Liu39 proposed a dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction, the experimental results demonstrate that the model can be successfully used to develop expert or intelligent systems. Due to the successful performance of the DA-RNN model on other time series problems interdisciplinary applications, we attempt to apply it to more accurate predicted dosing control in the wastewater treatment process.
The main contributions are summarized as follows: (1) a detailed comprehensive review of the advantages and disadvantages of addition prediction methods in WWTP. (2) RNN-based models were able to capture the nonlinear and time sequence relationship between chemical dose and source water quality changes. (3) Not only current water quality parameters but also the historical time-series water quality feature data are taken into account to construct a multivariate time series prediction model. (4) Compared to three potential competitive algorithm models (RF, MLR, LSTM), experimental results demonstrate that the present work can be successfully used to predict coagulation in WWTP.
After the literature review, the remainder of this paper is organized as follows: in section 2, we present the wastewater treatment relevant materials and preliminary knowledge of the proposed method. The DA-RNN model for dosage prediction in WWT is presented in section 3 in detail. In section 4, the experimental design, assessment criteria, experimental results analysis, and analyzed parameter sensitivity were evaluated for model algorithm comparison purposes. To assess the predictive accuracy of the models, we also compared the predicted performance of RF, MLR, and LSTM methods, and the datasets were mathematically evaluated by calculating the following evaluation criteria: coefficient of determination (R2), root mean squared error (RMSE), mean relative error (MRE) and mean absolute percentage error (MAPE). Section 5 is the conclusion.
2. Materials and preliminary knowledge
2.1 Description of the wastewater treatment plant
Fig. 1 exhibits the partial process and DA-RNN unit of the WWTP. The raw water was textile printing and dyeing wastewater from a printing and dyeing mill in Jiaxing city of Zhejiang province, China. The stirring unit used polyaluminum chloride (PAC) as a coagulant and the DA-RNN unit installed here is to predict the optimal dosage for this process. Usually, the wastewater treatment process involves physical, chemical, and biological reactions that transform raw water into sewage discharge standards. Physical handling is first, the coarse grid is the first treatment procedure of sewage after influent, its purpose is to filter out large, suspended pollutants. After the coarse grid, the wastewater flows into the thin grid, by the coarse grid and the thin grid, most of the solid pollutants were removed. The pre-treated wastewater was pumped into the coagulation reaction pool. In the coagulation reaction pool, by adding coagulants in the sewage to destroy the stability of the colloid, the fine suspended particles and colloidal particles aggregate into larger particles and settle and separate from the wastewater. In this process, the wastewater characteristics including PH, TUR, CON and flow rate were measured by the sensor. Due to the factory being a constant temperature workshop, the wastewater temperature was stable, so we did not collect the temperature feature of the wastewater. The DA-RNN algorithm model is trained by four kinds of parameter characteristics and previous time sequence features, according to the water quality parameter input, the coagulant prediction algorithms will automatically adjust dosage volume to lower costs and optimizing chemical usage, thereby cutting the operating costs of the water treatment process. The mixer was employed to keep the liquor completely mixed in the coagulant reaction pool. Wastewater had a sufficient reaction of coagulation-flocculation and sedimentation in the integrative reactor, and the effluent of the super-stratum wastewater was poured into an aeration pool for the biological treatment stage. The electromagnetic valve at the bottom of the reactor was used for discharging the sludge.
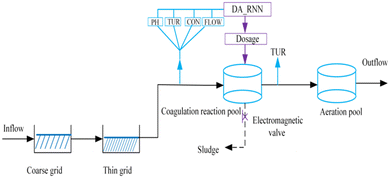 |
| | Fig. 1 Flow chart of the wastewater treatment process. | |
2.2 Data collection and characterization
To test the performance of different methods for coagulation dosage prediction, we collected every 5 min real-world data from the remote sensing data collector from the WWTP. The plant mainly needs to treat different dyeing and post-processing of fabrics because of the industrial needs for dyeing and post-processing of fabrics. The data collection period was from June 4 to September 27, 2019. The total data samples collected is 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 during the real operation period. Although the output data were collected daily as 24 hour pulses, there lacks some data due to missing data or interruptions. In this case, after cleaning the noisy data, 25
064 during the real operation period. Although the output data were collected daily as 24 hour pulses, there lacks some data due to missing data or interruptions. In this case, after cleaning the noisy data, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 effective data samples of the model test were analyzed. The raw water variables collected include the flow rate of the wastewater, the pH of the incoming wastewater, the electrical conductivity of the incoming wastewater, the turbidity of the incoming wastewater, and the coagulation dosages. The coagulation dosages were calibrated to the best possible performance. The ranges of the available online data and statistical properties of the data are presented in Table 1.
930 effective data samples of the model test were analyzed. The raw water variables collected include the flow rate of the wastewater, the pH of the incoming wastewater, the electrical conductivity of the incoming wastewater, the turbidity of the incoming wastewater, and the coagulation dosages. The coagulation dosages were calibrated to the best possible performance. The ranges of the available online data and statistical properties of the data are presented in Table 1.
Table 1 Statistical summary of raw HongHe water data
| Variable |
Unit |
Min |
Max |
Mean |
Variance |
| pH |
— |
6.80 |
7.76 |
7.34 |
0.04 |
| TUR |
NTU |
2.00 |
100 |
54.22 |
1396.97 |
| CON |
μs m−1 |
6.89 |
12.27 |
9.69 |
1.15 |
| Flow rate |
M3 s−1 |
2.90 |
3.11 |
2.90 |
0.01 |
2.3 Recurrent neural network
The recurrent neural network uses neurons with self-feedback, it employed sequential information to capture information about what has been calculated so far and can process an arbitrary length of time series data. Meanwhile, it performs the same task for every element of a sequence, with the output being dependent on the previous computations. Given an input sequence (x1,T = x1, x2, …, xt, …, xT) RNN by formula ht = f(ht−1, xt) the activity value ht of the hidden layer can be updated with feedback and h0 = 0, f(·) is a nonlinear function, it could be a feed-forward network. Theoretically, a fully connected RNN can approximate any non-linear dynamical system. When the input sequence is long, there will be gradient explosions and disappearance problems. To solve these problems, one of the most effective ways is to improve the cited gating mechanism. It can control the cumulative speed of information, including the selective addition of new information and selective forgetting of previously accumulated information. The long short-term memory (LSTM) cell is a famous instance of RNN.
2.4 Long short term memory
LSTM can effectively solve the problem of gradient explosion or disappearance of recurrent neural networks. LSTM network introduces a gating mechanism to control the path of information transmission. The specific structure of the LSTM unit is shown in Fig. 2. Each LSTM cell consists of an input gate it, forgotten gate ft, and output gate ot, they can be obtained by the eqn (1)–(3).| | 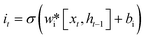 | (1) |
| | 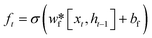 | (2) |
| | 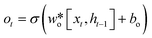 | (3) |
ct−1 is the memory unit of the previous moment, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) t is the candidate state obtained by nonlinear function by eqn (4)
t is the candidate state obtained by nonlinear function by eqn (4)| | 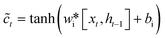 | (4) |
ht is the hidden state at the time t, which is defined as eqn (5)| | 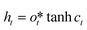 | (5) |
ct is the cell state at the time t, which is defined as eqn (6)| | 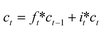 | (6) |
In the formula xt, is the input at the time t, ht−1 is the hidden state of the layer at time t – 1 or the initial hidden state at time 0, ot is the output gate, which controls how much ct outputs to the next hidden state ht, wi, wf, wf, wo are the weight matrices. bi, bf, bo, bc, bi are the bias vector, σ is the sigmoid function and * is the vector elements product.
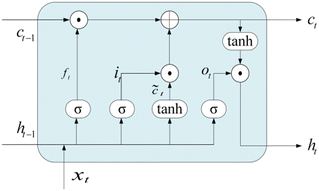 |
| | Fig. 2 The structure of the LSTM cell. | |
2.5 Attention encoder decoder
Based on LSTM or gated recurrent unit (GRU), encode-decoder networks40 have become popular due to their success in machine translation. The encoder extracts a fixed-length representation from a variable-length input sentence and the decoder generates a correct translation from this representation. Cho40 proposed an attention-based encoder–decoder network that employs an attention mechanism to select parts of hidden states across all the time steps. It solved the problem that their performance will deteriorate rapidly as the length of the input sequence increases. Inspired by some theories of human attention, Hübner41 posits that human behaviour is well-modelled by a two-stage attention mechanism. Qin36 proposed a novel dual-stage attention-based recurrent neural network (DA-RNN) to perform time series prediction, the challenge of features transferring from water quality in time series could possibly be addressed by this algorithm because they share similar feature characteristics but this needs more research.
3. Modelling approaches
Fig. 3 is the graphical illustration of the DA-RNN model for dosage prediction in WWTP. The model includes the input of data, the learning of the DA_RNN model and the output of predicted values of dosing. The input of data includes feature input and label input. Feature input that is input four driving series, i.e. x = (x1, x2, x3, x4)T = (x1, x2, …, xt) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) 4×T, there are representative PH, TUR, CON and flow rate, where T is the length of window size, use xk = (x1k, x2k, ·, xTk)T ∈
4×T, there are representative PH, TUR, CON and flow rate, where T is the length of window size, use xk = (x1k, x2k, ·, xTk)T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) T to represent a driving series of length T and employ xt = (xt1, xt2, xt3, xt4)T ∈
T to represent a driving series of length T and employ xt = (xt1, xt2, xt3, xt4)T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) 4 to denote a vector of four input series at time t. The label input that is given the previous values of the target series, i.e., (y1, y2, …, yt−1) with yt ∈
4 to denote a vector of four input series at time t. The label input that is given the previous values of the target series, i.e., (y1, y2, …, yt−1) with yt ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) , which are the values of dosing.
, which are the values of dosing.
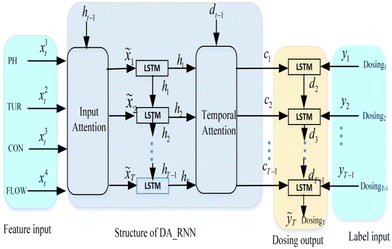 |
| | Fig. 3 Graphical illustration of DA-RNN to predict dosage for the wastewater treatment plant. | |
The model learning section contains two stages, in the first stage, a new attention mechanism was designed to adaptively extract the relevant driving series at each time step by referring to the previous encoder hidden state. The input attention layer calculates the attention weights αt for multiple feature time series xt conditioned on the previous hidden state ht−1 in the encoder and then feeds the computed ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) t into the encoder RNN layer. The calculation formula is as follows:
t into the encoder RNN layer. The calculation formula is as follows: ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) t = atTXt. In the second stage, a temporal attention mechanism is used to select relevant encoder hidden states across all time steps. The temporal attention system then calculates the attention weights based on the previous decoder hidden state dt−1 and represents the input information as a weighted sum of the encoder hidden states across all the time steps. The generated context vector ct is then used as an input to the decoder RNN layer.
t = atTXt. In the second stage, a temporal attention mechanism is used to select relevant encoder hidden states across all time steps. The temporal attention system then calculates the attention weights based on the previous decoder hidden state dt−1 and represents the input information as a weighted sum of the encoder hidden states across all the time steps. The generated context vector ct is then used as an input to the decoder RNN layer.
The predicted values of dosing are the output results. The DA_RNN model aims to learn a nonlinear mapping to the current value of the target series yT: ỹT = F(y1, …, yT−1, x1, …, xT). Where F(·) is the nonlinear mapping function we aim to learn by model training. The output ỹt of the last decoder cell is the predicted dosing result at time t.
4. Results and discussion
4.1 Experimental setup and parameter settings
Our experiment environment uses TensorFlow running as a backend and Keras API in Python3.7 version is used for model training and building. In this study, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 effective data samples were used for validation of the algorithmic model. Every sample of data input feature includes the PH, TUR, CON, flow rate, and the coagulation dosages of the predicted label. 70% of the dataset was divided into the training set, 20% of the dataset was used for the validation set and the remaining 10% of the dataset is used as a test set for evaluating the performance of the model prediction.
930 effective data samples were used for validation of the algorithmic model. Every sample of data input feature includes the PH, TUR, CON, flow rate, and the coagulation dosages of the predicted label. 70% of the dataset was divided into the training set, 20% of the dataset was used for the validation set and the remaining 10% of the dataset is used as a test set for evaluating the performance of the model prediction.| | 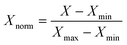 | (7) |
| | | X = (Xmax − Xmin) × Xnorm + Xmin | (8) |
Because the data collected by various sensors have different dimensions and magnitudes, to avoid the situation of slow model training speed and large training errors caused by different dimensions, in this paper, the input and output data are normalized by the method max-min. Convert the data to the range [0,1], data recovery will be carried out after the prediction. Max–min normalization formula as eqn (8). Xnorm is normalized data by eqn (7). X is original data, Xmax is the maximum value of the data and Xmin is the minimum value of the data.
In the experiment settings, the loss function used here is mean square error loss, the optimizer function we used the Adam method. In the activation function, we used the tanh function. The batch size is 64, the epoch is 50, and the size of hidden states for the encoder and hidden states for the decoder is 64.
4.2 Assessment criteria
To verify the reliability of different algorithms, we evaluated the performance of models by the coefficient of determination (R2), root mean squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). R2 is a mathematical calculation of the square of the correlation coefficient, also called the determination coefficient, as shown in the formula (9). It is an easy-to-calculate and very intuitive metric for measuring correlation. The corresponding value is between 0 and 1. The larger the value of R2, the better the performance of the model. RMSE is the square root of the ratio of the square sum of the deviation between the observed value and the true value to the number of observations, as shown in the formula (10). Its value is always non-negative, typically, a lower RMSE is better than a higher RMSE. MAE represents the average of absolute errors between predicted and observed values, as shown in formula (11), the error cancellations can be avoided and the actual prediction error can be accurately reflected. MAPE is used to measure the relative errors between the average test value and the real value on the test set, it is defined as formula (12). The smaller the MAPE, the better the accuracy of the prediction model.| | 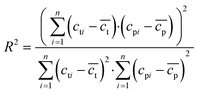 | (9) |
| | 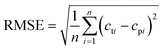 | (10) |
| | 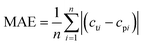 | (11) |
| | 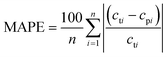 | (12) |
In the formula, n is the number of data, cti is the true value of the drug dosage at the ith sample point; cpi is the predicted value of the drug dosage at the ith sample point and is the average of the predicted results and the real results.
4.3 Experimental results and analysis
To verify the effectiveness of the DA-RNN for dosage prediction in WWTP, we compare the DA-RNN against three different algorithm models, which are RF, MLR and LSTM. Fig. 4 shows the comparison between the predicted coagulant dosage and the actual dosage in four algorithm models. Fig. 4 shows that the amount of dosing required fluctuates widely, there are no obvious specific patterns and it shows nonlinear and non-stationary characteristics. The red line represents the actual recorded dosage, and the green line represents the predicted coagulant dosage in the algorithm model. The DA-RNN algorithms model seems to be very suitable for dosage prediction because all evaluation metrics (R2 is 0.9908, RMSE is 1.2524, MAE is 1.1263, and MAPE is 1.01%) were better than the other 3 algorithms (see Table 2). As shown in Fig. 4(a), the predicted dosage and actual dosage are not perfectly matched and the coincidence of the two lines is relatively low (MAPE of RF is 8.29% compared to that of DA-RNN is 1.01%; the R2 is only 0.9082 compared to 0.9908 for DA-RNN). It shows that the RF algorithm performs poorly in the regression task of time series data. Besides, Fig. 4(b) shows that the coincidence of the two lines is relatively low (MAPE of MLR is about 3.19%, which is less than that of RF but double that of DA-RNN; the R2 is only 0.9174, although it is slightly better than the RF algorithm, it is still not best choice). Because of the complex characteristics of the coagulant–flocculant reaction, the relationship between coagulant dosage and sewage characteristics is also nonlinear, this shows that it is not suitable to solve the problem of nonlinear prediction with a linear model. Moreover, Fig. 4(c) presents the experimental results of the LSTM algorithm model, it is observed that the predictive performance is better than RF and MLR (for which MAPE is 1.76% compared to 8.29% and 3.19% of those two algorithms, separately). Additionally, the line of prediction dosage and actual dosage have a relatively high degree of overlap (MAPE of LSTM is 1.76%; the R2 is about 0.9627, but the RMSE 3.3871 is about double of that of the DA-RNN algorithm), and it demonstrated that the neural network algorithm has a strong nonlinear fitting ability and the LSTM algorithm has comparably higher efficiency to fit the time series model. Fig. 4(d) presents the experimental results of the DA-RNN algorithm model, the line of prediction dosage and actual dosage have an almost perfect overlap, there are only very few points of error, and the error values are quite small. It is shown that this algorithmic model has strong multivariate timing prediction capabilities, and good experimental results were obtained in these four algorithmic models.
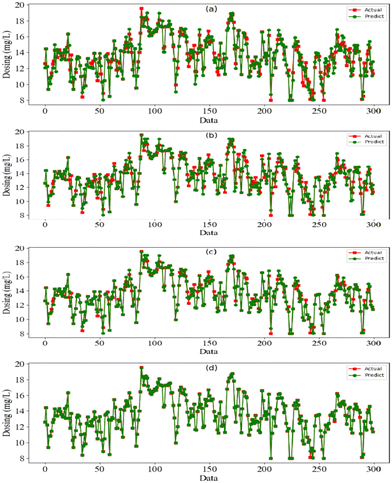 |
| | Fig. 4 The comparisons of the predicted and actual dosing in different models. (a) RF (b) MLR (c) LSTM and (d) DA-RNN. | |
Table 2 The results of the different models
| Model |
R
2
|
RMSE |
MAE |
MAPE |
| RF |
0.9082 |
9.6459 |
6.4793 |
8.29% |
| MLR |
0.9174 |
8.5686 |
5.3936 |
3.19% |
| LSTM |
0.9627 |
3.3871 |
2.2202 |
1.76% |
| DA-RNN |
0.9908 |
1.2524 |
1.1263 |
1.01% |
The scatter plot is an advantageous method in regression forecasting analysis. Corresponding to Fig. 4 and 5 presents the scatter plots of actual versus predicted values for the four algorithm models, RF, MLR, LSTM, and DA_RNN in turn. As shown in Fig. 5(a), there are many points outside the regression line, and the predicted value deviation is also relatively large. Fig. 5(b) is the same as Fig. 5(a). This indicated that RF and MLR algorithm performs poorly for dosage prediction in WWTP. In Fig. 5(c), a small number of predicted deviations was observed, and the margin of error seems acceptable. Viewing the whole picture, it is clear that the scatter plot is largely around the regression line, with only a very few forecast deviations. The result of the DA-RNN algorithm model achieved the best fitting degree in Fig. 5(d). It is shown that the DA-RNN algorithm presents a more reliable performance by using multi-variable time series prediction model than a single time-series model.
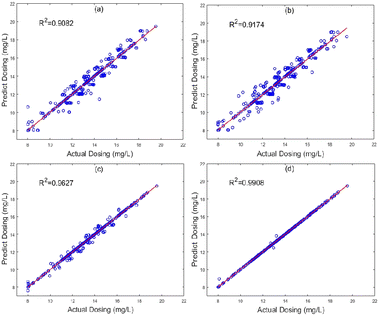 |
| | Fig. 5 The scatter diagram of the predicted and actual dosing in different models. (a) RF, (b) MLR, (c) LSTM and (d) DA-RNN. | |
The predicted results assessment criteria of different methods are listed in Table 2. From Table 2, the performance of each algorithm model can be compared more accurately by a quantitative evaluation index value. In the prediction result of the RF model, the value of R2 reached the lowest of 0.9082, and the value of RMSE, MAE, and MAPE obtained were the highest, 9.6459%, 6.4793%, and 8.29%, which performed worst in the four models. In the prediction result of the MLR model, the value of R2 is 0.9174, and the values of RMSE, MAE, and MAPE are 8.5686%, 5.3936%, and 3.19%, resulting in a prediction slightly better than the RF model. In the prediction result of the LSTM model, the value of R2 is 0.9627 and the values of RMSE, MAE, and MAPE are 3.3871%, 2.2202%, and 1.76%, compared with the RF model, which was improved by 0.0453, 5.1815%, 3.1734%, and 6.53%, respectively. Qualitative analysis of the predictions of the LSTM algorithm compared to RF and MLR showed a significant improvement in evaluation criteria, it shows that the LSTM algorithm is stronger than the RF algorithm and MLR algorithm when dealing with nonlinear predictions. In the prediction result of the DA-RNN model, the value of R2 reaches the highest value of 0.9908 and the values of RMSE, MAE, and MAPE obtained are the lowest at 1.2524%, 1.1263%, and 1.01%, respectively. Compared with the RF model, which was improved by 0.0826, 8.3953%, 5.353%, and 7.28%, respectively, all kinds of evaluation indicators have been greatly improved. Compared with LSTM, the same neural network model was improved by 0.0281, 2.1347%, 1.0939%, and 0.75%, respectively. By quantitative analysis, considering multivariate time series and multiple water quality parameters simultaneously in the DA-RNN algorithm model, experiments verify the effectiveness of model DA-RNN in WWT for predicting the coagulant dosage.
4.4 Comparison with existing methods
We compared the prediction result of the DA-RNN method with some existing methods, as shown in Table 3. In Table 3, we listed the location of data collection, algorithm model, input variable features and four kinds of evaluation metrics for each existing method. The regions cover many parts of the world and methods include ML and neural network methods. Salim-Heddam's16,26,44 experimental research regarded coagulation dosage prediction coagulant dosage rate in Boudouaou DWPT, Algeria. It used TUR, PH, DO, CON, and temperature as input variable features and RF, MLR, ANFIS, and RBFNN methods to conduct experimental research, respectively. The experimental result shows that the ANN methods prediction result is better than the traditional ML algorithm and consistent with our experimental results, which manifested that the neural network algorithm has a strong nonlinear prediction ability. Kim43 applied generalized regression neural network (GRNN) to determine the coagulant dosage at Bansong drinking WTP, and determined that the RMSE and R2 of the test data were 2.52% and 0.92. Wu42 used TUR, temperature, colour, and PH as input variables to construct the neural network model and discussed the data normalization, neurons of hidden layer and inherent-factor influence on experimental results. CD Jayaweera45 applied ELM to determine the coagulant dosage in Malaysia and obtained the R2 of the test data of 0.87. For the time series prediction model, to solve the shortcoming of the LSTM, Liu6 utilized automatically adjusting (AA) the cumulative error in training and adds a time-consistent (TC) in the loss function, abbreviated to the AATC_LSTM model, to guarantee stable prediction, which obtained good results. We use the most advanced time series prediction algorithm model DA_RNN, which has the best results so far.
Table 3 Performance comparison of the different existing methods
| Articles |
Location |
Method |
Input variables |
RMSE |
R
2
|
MAE |
MAPE |
| Salim Heddam26 |
Algeria |
ANFIS |
TUR, PH, DO, CON, temperature |
1.95 |
0.92 |
2.74 |
— |
| Guandu Wu42 |
Taiwan |
ANN |
TUR, temperature, colour, PH |
1.46 |
0.76 |
|
|
| Sadaf Haghiri29 |
Iran |
ANN |
PH, temperature, TUR |
|
0.85 |
|
|
| Kim43 |
South Korea |
GRNN |
TUR, temperature, PH, CON |
2.52 |
0.92 |
|
|
| Wang31 |
Suzhou |
ENN |
DO, PH, temperature, flow, TUR |
1.89 |
0.89 |
|
5.01 |
| Salim Heddam44 |
Algeria |
RBFNN |
TUR, PH, DO, temperature, CON |
3.05 |
0.90 |
|
|
| CD Jayaweera45 |
Malaysia |
ELM |
PH, TUR, color, alkalinity |
|
0.87 |
|
|
| Yiqun Liu6 |
Shanghai |
AATC_LSTM |
PH, DO, AN, CON, TUR |
1.81 |
0.90 |
|
3.63 |
| Salim Heddam16 |
Algeria |
RF |
PH, TUR, DO, temperature, CON |
5.63 |
0.66 |
4.28 |
|
| Salim Heddam16 |
Algeria |
MLR |
PH, TUR, DO, temperature, CON |
7.58 |
0.23 |
6.80 |
|
| Author |
Jiaxing |
DA_RNN |
TUR, PH, CON, flow |
1.25 |
0.99 |
1.12 |
1.01 |
4.5 Parameter sensitivity
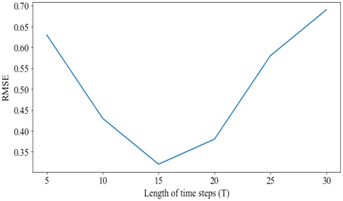
We plot the RMSE versus different lengths of time steps in the window T in Fig. 6. The influence of DA-RNN with the hyper-parameter and the length of time steps T was studied. We kept the others fixed when we vary T, by setting beach size and the size of hidden states to change the structure of the encoder-decode network. The corresponding RMSE was compared to different lengths of time steps in window T in Fig. 6. It is easily observed that the performance of DA-RNN will be worse when the length of time steps is too short or too long. DA-RNN usually achieves the best performance when T = 15, it demonstrated that the wastewater quality parameters within 15 minutes were useful for the prediction results. As a result, the dosage prediction changes irregularly but is highly related to both present and historical water quality data. This implied information from previous time series contributes to improving the accuracy of dosage prediction in WWTP.
 |
| | Fig. 6 RMSE vs. length of time steps T. | |
5. Conclusions
This paper has demonstrated the potential of deep neural network models for applications in coagulant dosage control in WWTPs. Compared to the fourth competitive artificial intelligence algorithm model (RF, MLR, LSTM, DA_RNN), RF and MLR are traditional ML methods, owing to the datasets with nonlinearity and time sequences, it did not achieve good experimental predicted results. LSTM and DA_RNN are deep neural network methods, they rely on the strong predictive and analytical ability of deep learning for nonlinearity and timing sequence, we transform the dosing prediction into a time series prediction problem, and the experimental results also demonstrated that the predictive power of these two methods is superior to RF and MLR methods. Compared with LSTM, which introduce two attention mechanisms, the DA-RNN can not only adaptively select the most relevant input features but can also capture the long-term temporal dependencies of a time series appropriately. Experimental results demonstrate that the DA-RNN algorithm model can obtain state-of-the-art prediction accuracy. In the meantime, we analyzed the effect of the sensitivity of the hyper-parameters and the length of time steps T on the predicted results. By using the DA RNN algorithm to accurately predict the dosage, we shed light on the optimization of wastewater treatment efficiency. This is pivotal concerning the socioeconomic aspects of wastewater management. Although the experimental results were satisfactory, many limitations should be addressed in the future to further warrant the successful application of neural networks algorithm for WWP prediction. The priority is a necessity to collect more data from different industry WWTPs to ensure the neural network's algorithms are generalized. The second is to optimize the computation time of the algorithm to guarantee real-time prediction. Finally, it is necessary to explore the application of more advanced algorithms in the dosing control of sewage treatment.
Author contributions
Conceptualization, X. F. and J. Z.; methodology X. F. J. Z. and L. Z.; software, X. F.; validation J. Z.; writing-original draft preparation by J. Z. and X. F.; writing-review and editing, J. Z.; supervision, J. Z.; project administration Z. Z. and J. Z.; proof-reading Z. S. and Y. L. All the authors have read and agreed to the published version of the manuscript.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. There are no conflicts to declare.
Acknowledgements
This work has been supported by the Zhejiang Province 2019 Key Research and Development Plan Project (Grant no. MY80), Science and Technology Innovation Development Fund Project by the 36th Research Institute of China Electronics Technology Group Corporation (Grant no. MK2101S). We also want to show great thanks to Honghe (Jiaxing) sewage treatment plant for providing the required data and the OEICDI fund (Grant no. B13041) for supporting research needs. Additionally, we would like to thank Special Funding for Post-doctoral Research Project support from RLSBJ Chongqing.
Notes and references
- M. Qadir, P. Drechsel, B. Jiménez Cisneros, Y. Kim, A. Pramanik, P. Mehta and O. Olaniyan, Global and regional potential of wastewater as a water, nutrient and energy source, Nat. Resour. Forum, 2021, 44, 40–51 CrossRef
 .
.
- J. Zang, M. Kumar and D. Werner, Real-world sustainability analysis of an innovative decentralized water system with rainwater harvesting and wastewater reclamation, J. Environ. Manage., 2021, 280, 111639 CrossRef CAS PubMed
 .
.
- Y. Xu, X. Zeng, S. Bernard and Z. He, Data-driven prediction of neutralizer pH and valve position towards precise control of chemical dosage in a wastewater treatment plant, J. Cleaner Prod., 2022, 348, 131360 CrossRef CAS
 .
.
- L. Tiseo, Water and wastewater treatment market size worldwide in 2020, with a forecast to 2028, Energy Environ., 2021, 5, 47 Search PubMed
 .
.
- A. Sonune and R. Ghate, Developments in wastewater treatment methods, Desalination, 2004, 167, 55–63 CrossRef CAS
 .
.
- Y. Liu, Y. He, S. Li, Z. Dong, J. Zhang and U. Kruger, An Auto-Adjustable and Time-Consistent Model for Determining Coagulant Dosage Based on Operators' Experience, IEEE Trans. Syst. Man. Cybern. Syst., 2019, 51, 5614–5625 Search PubMed
 .
.
- G. Muthuraman and S. Sasikala, Removal of turbidity from drinking water using natural coagulants, J. Ind. Eng. Chem., 2014, 20, 1727–1731 CrossRef CAS
 .
.
- B. Lamrini and E.-K. Lakhal, A survey of deep learning methods for WTP control and monitoring, Desalin. Water Treat., 2018, 15, 298–299 Search PubMed
 .
.
- J. Zang, M. Royapoor, K. Acharya, J. Jonczyk and D. Werner, Performance gaps of sustainability features in green award-winning university buildings, Build. Environ., 2022, 207, 108417 CrossRef
 .
.
- Q. V. Ly, V. H. Truong, B. Ji, X. C. Nguyen, K. H. Cho, H. H. Ngo and Z. Zhang, Exploring potential machine learning application based on big data for prediction of wastewater quality from different full-scale wastewater treatment plants, Sci. Total Environ., 2022, 832, 154930 CrossRef CAS PubMed
 .
.
- F. C. R. dos Santos, A. F. H. Librantz, C. G. Dias and S. G. Rodrigues, < b> Intelligent system for improving dosage control, Acta Sci., Technol., 2017, 39, 33–38 CrossRef
 .
.
- S. Amali, N.-E. E. L. Faddouli and A. Boutoulout, Machine learning and graph theory to optimize drinking water, Procedia Comput. Sci., 2018, 127, 310–319 CrossRef
 .
.
- C. M. Kim and M. Parnichkun, Prediction of settled water turbidity and optimal coagulant dosage in drinking water treatment plant using a hybrid model of k-means clustering and adaptive neuro-fuzzy inference system, Appl. Water Sci., 2017, 7, 3885–3902 CrossRef
 .
.
- F. Muharemi, D. Logofătu and F. Leon, Machine learning approaches for anomaly detection of water quality on a real-world data set, Journal of Information and Telecommunication, 2019, 3, 294–307 CrossRef
 .
.
- K. Zhang, G. Achari, H. Li, A. Zargar and R. Sadiq, Machine learning approaches to predict coagulant dosage in water treatment plants, Int. J. Syst. Assur. Eng. Manag., 2013, 4, 205–214 CrossRef
 .
.
-
S. Heddam, Extremely randomized tree: a new machines learning method for predicting coagulant dosage in drinking water treatment plant, Water Engineering Modeling and Mathematic Tools, 2021, pp. 475–489 Search PubMed
 .
.
- K.-J. Wang, P.-S. Wang and H.-P. Nguyen, A data-driven optimization model for coagulant dosage decision in industrial wastewater treatment, Comput. Chem. Eng., 2021, 152, 107383 CrossRef CAS
 .
.
- O. Icke, D. M. van Es, M. F. de Koning, J. J. G. Wuister, J. Ng, K. M. Phua, Y. K. K. Koh, W. J. Chan and G. Tao, Performance improvement of wastewater treatment processes by application of machine learning, Water Sci. Technol., 2020, 82, 2671–2680 CrossRef CAS PubMed
 .
.
- X. Fang, Z. Zhai, J. Zang and Y. Zhu, An Intelligent Dosing Algorithm Model for Wastewater Treatment Plant, J. Phys.: Conf. Ser., 2022, 2224, 012027 CrossRef
 .
.
- H. Wang, T. Asefa and J. Thornburgh, Integrating water quality and streamflow into prediction of chemical dosage in a drinking water treatment plant using machine learning algorithms, Water Sci. Technol.: Water Supply, 2022, 22, 2803–2815 CAS
 .
.
- A. J. León-Luque, C. L. Barajas and C. A. Peña-Guzmán, Determination of the optimal dosage of Aluminum Sulfate in the coagulation-flocculation process using an Artificial Neural Network, Int. J. Environ. Sci. Dev., 2016, 7, 346–350 CrossRef
 .
.
- A. S. Kote and D. V. Wadkar, Modeling of chlorine and coagulant dose in a water treatment plant by artificial neural networks, Eng. Technol. Appl. Sci. Res., 2019, 9, 4176–4181 CrossRef
 .
.
- N. Bekkari and A. Zeddouri, Using artificial neural network for predicting and controlling the effluent chemical oxygen demand in wastewater treatment plant, Manag. Environ. Qual., 2017, 30, 593–608 CrossRef
 .
.
- H. H. Loc, Q. H. Do, A. A. Cokro and K. N. Irvine, Deep neural network analyses of water quality time series associated with water sensitive urban design (WSUD) features, J. Appl. Water Eng. Res., 2020, 8, 313–332 CrossRef
 .
.
- G. O'Reilly, C. C. Bezuidenhout and J. J. Bezuidenhout, Artificial neural networks: applications in the drinking water sector, Water Sci. Technol.: Water Supply, 2018, 18, 1869–1887 Search PubMed
 .
.
- S. Heddam, A. Bermad and N. Dechemi, ANFIS-based modelling for coagulant dosage in drinking water treatment plant: a case study, Environ. Monit. Assess., 2012, 184, 1953–1971 CrossRef CAS PubMed
 .
.
- E. Hong, A. M. Yeneneh, T. K. Sen, H. M. Ang and A. Kayaalp, ANFIS based Modelling of dewatering performance and polymer dose optimization in a wastewater treatment plant, J. Environ. Chem. Eng., 2018, 6, 1957–1968 CrossRef CAS
 .
.
- D. V. Wadkar, R. S. Karale and M. P. Wagh, Application of cascade feed forward neural network to predict coagulant dose, J. Appl. Water Eng. Res., 2022, 10, 87–100 CrossRef
 .
.
- S. Haghiri, A. Daghighi and S. Moharramzadeh, Optimum coagulant forecasting by modeling jar test experiments using ANNs, Drinking Water Eng. Sci., 2018, 11, 1–8 CrossRef CAS
 .
.
-
Y. Wu, J. M. Hernández-Lobato and G. Zoubin, Dynamic covariance models for multivariate financial time series, International Conference on Machine Learning, 2013, pp. 558–566 Search PubMed.
- D. Wang, X. Chang and K. Ma, Predicting flocculant dosage in the drinking water treatment process using Elman neural network, Environ. Sci. Pollut. Res., 2022, 29, 7014–7024 CrossRef CAS PubMed
 .
.
-
W. Zaremba, I. Sutskever and O. Vinyals, Recurrent neural network regularization, arXiv, 2014, preprint, arXiv:1409.2329, DOI:10.48550/arXiv.1409.2329.
-
A. Graves, Long short-term memory, Supervised sequence labelling with recurrent neural networks, 2012, pp. 37–45 Search PubMed
 .
.
- X. Fang, Z. Zhai, R. Xiong, L. Zhang and B. Gao, LSTM-based Modelling for Coagulant Dosage Prediction in Wastewater Treatment Plant, J. Phys.: Conf. Ser., 2022, 2224, 23–27 Search PubMed
 .
.
-
D. Bahdanau, K. Cho and Y. Bengio, Neural machine translation by jointly learning to align and translate, arXiv, 2014, preprint, arXiv:1409.0473, DOI:10.48550/arXiv.1409.0473.
-
Y. Qin, D. Song, H. Chen, W. Cheng, G. Jiang and G. Cottrell, A dual-stage attention-based recurrent neural network for time series prediction, arXiv, 2017, preprint, arXiv:1704.02971, DOI:10.48550/arXiv.1704.02971.
- N. Jing, Z. Shi, Y. Hu and J. Yuan, Cross-sectional analysis and data-driven forecasting of confirmed COVID-19 cases, Appl. Intell., 2022, 52, 3303–3318 CrossRef PubMed
 .
.
- B. Huang, Y. Liang and X. Qiu, Wind power forecasting using attention-based recurrent neural networks: a comparative study, IEEE Access, 2021, 9, 40432–40444 Search PubMed
 .
.
- Y. Liu, C. Gong, L. Yang and Y. Chen, DSTP-RNN: A dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction, Expert Syst. Appl., 2020, 143, 113082 CrossRef
 .
.
-
K. Cho, B. Van Merriënboer, D. Bahdanau and Y. Bengio, On the properties of neural machine translation: Encoder-decoder approaches, arXiv, 2014, preprint, arXiv:1409.1259, DOI:10.48550/arXiv.1409.1259.
- R. Hübner, M. Steinhauser and C. Lehle, A dual-stage two-phase model of selective attention, Psychol. Rev., 2010, 117, 759 Search PubMed
 .
.
- G.-D. Wu and S.-L. Lo, Effects of data normalization and inherent-factor on decision of optimal coagulant dosage in water treatment by artificial neural network, Expert Syst. Appl., 2010, 37, 4974–4983 CrossRef
 .
.
- C. M. Kim and M. Parnichkun, MLP, ANFIS, and GRNN based real-time coagulant dosage determination and accuracy comparison using full-scale data of a water treatment plant, J. Water Supply: Res. Technol.--AQUA, 2017, 66, 49–61 CrossRef
 .
.
- S. Heddam, A. Bermad and N. Dechemi, Applications of radial-basis function and generalized regression neural networks for modeling of coagulant dosage in a drinking water-treatment plant: comparative study, J. Environ. Eng., 2011, 137, 1209–1214 CrossRef CAS
 .
.
- C. D. Jayaweera, M. R. Othman and N. Aziz, Improved predictive capability of coagulation process by extreme learning machine with radial basis function, J. Water Process Eng., 2019, 32, 100977 CrossRef
 .
.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ba,
Zhengang
Zhai
a,
Li
Zhang
a,
Ziyu
Shu
b and
Yuqi
Liang
c
*ba,
Zhengang
Zhai
a,
Li
Zhang
a,
Ziyu
Shu
b and
Yuqi
Liang
c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 during the real operation period. Although the output data were collected daily as 24 hour pulses, there lacks some data due to missing data or interruptions. In this case, after cleaning the noisy data, 25
064 during the real operation period. Although the output data were collected daily as 24 hour pulses, there lacks some data due to missing data or interruptions. In this case, after cleaning the noisy data, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 effective data samples of the model test were analyzed. The raw water variables collected include the flow rate of the wastewater, the pH of the incoming wastewater, the electrical conductivity of the incoming wastewater, the turbidity of the incoming wastewater, and the coagulation dosages. The coagulation dosages were calibrated to the best possible performance. The ranges of the available online data and statistical properties of the data are presented in Table 1.
930 effective data samples of the model test were analyzed. The raw water variables collected include the flow rate of the wastewater, the pH of the incoming wastewater, the electrical conductivity of the incoming wastewater, the turbidity of the incoming wastewater, and the coagulation dosages. The coagulation dosages were calibrated to the best possible performance. The ranges of the available online data and statistical properties of the data are presented in Table 1.
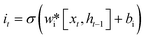
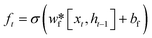
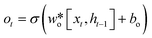
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) t is the candidate state obtained by nonlinear function by eqn (4)
t is the candidate state obtained by nonlinear function by eqn (4)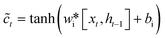
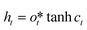
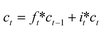
![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) 4×T, there are representative PH, TUR, CON and flow rate, where T is the length of window size, use xk = (x1k, x2k, ·, xTk)T ∈
4×T, there are representative PH, TUR, CON and flow rate, where T is the length of window size, use xk = (x1k, x2k, ·, xTk)T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) T to represent a driving series of length T and employ xt = (xt1, xt2, xt3, xt4)T ∈
T to represent a driving series of length T and employ xt = (xt1, xt2, xt3, xt4)T ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) 4 to denote a vector of four input series at time t. The label input that is given the previous values of the target series, i.e., (y1, y2, …, yt−1) with yt ∈
4 to denote a vector of four input series at time t. The label input that is given the previous values of the target series, i.e., (y1, y2, …, yt−1) with yt ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/i_char_e175.gif) , which are the values of dosing.
, which are the values of dosing.
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) t into the encoder RNN layer. The calculation formula is as follows:
t into the encoder RNN layer. The calculation formula is as follows: ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) t = atTXt. In the second stage, a temporal attention mechanism is used to select relevant encoder hidden states across all time steps. The temporal attention system then calculates the attention weights based on the previous decoder hidden state dt−1 and represents the input information as a weighted sum of the encoder hidden states across all the time steps. The generated context vector ct is then used as an input to the decoder RNN layer.
t = atTXt. In the second stage, a temporal attention mechanism is used to select relevant encoder hidden states across all time steps. The temporal attention system then calculates the attention weights based on the previous decoder hidden state dt−1 and represents the input information as a weighted sum of the encoder hidden states across all the time steps. The generated context vector ct is then used as an input to the decoder RNN layer.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 effective data samples were used for validation of the algorithmic model. Every sample of data input feature includes the PH, TUR, CON, flow rate, and the coagulation dosages of the predicted label. 70% of the dataset was divided into the training set, 20% of the dataset was used for the validation set and the remaining 10% of the dataset is used as a test set for evaluating the performance of the model prediction.
930 effective data samples were used for validation of the algorithmic model. Every sample of data input feature includes the PH, TUR, CON, flow rate, and the coagulation dosages of the predicted label. 70% of the dataset was divided into the training set, 20% of the dataset was used for the validation set and the remaining 10% of the dataset is used as a test set for evaluating the performance of the model prediction.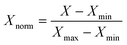
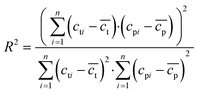
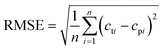
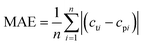
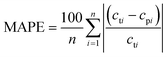


.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




