Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrogen evolution by polymer photocatalysts; a possible photocatalytic cycle†
Andrew W.
Prentice
 and
Martijn A.
Zwijnenburg
and
Martijn A.
Zwijnenburg
 *
*
Department of Chemistry, University College London (UCL), London, WC1H 0AJ, UK. E-mail: m.zwijnenburg@ucl.ac.uk
First published on 30th March 2021
Abstract
We propose, supported by ab initio calculations, a possible photocatalytic cycle for hydrogen evolution by a prototypical polymer photocatalyst, poly(p-phenylene), in the presence of a sacrificial electron donor. As part of that cycle, we also introduce a family of related sites on the polymer that in the absence of a noble metal co-catalyst can facilitate the evolution of molecular hydrogen when the polymer is illuminated. The bottlenecks for hydrogen evolution, electron transfer from the sacrificial electron donor and hydrogen–hydrogen bond formation, are discussed, as well as how they could potentially be improved by tuning the polymer properties and how they change in the presence of a noble metal co-catalyst.
1. Introduction
The depletion of fossil fuels, not to mention their detrimental effect on the environment and the ever-growing demand for energy, has led to development and application of low-CO2, in some instances CO2-free, renewable-energy sources such as bio-mass, solar, wind, tidal and geothermal.1–3 Solar energy is by far the most promising of the renewable sources as the hypothetical energy attained from incident light on 1% of the earth's surface at a 10% conversion efficiency (105 TW) considerably out-weighs the predicted energy demand for 2050.4 To put the importance of solar energy into perspective the cumulative upper bound energy output of bio-mass, wind, tidal and geothermal is one-fifth of that of the aforementioned solar energy output.The role of molecular hydrogen (H2) as an energy carrier has also been extensively studied and garnered significant interest in recent times because of the high energy content (141.9 MJ kg−1) when compared to other known fuels such as methane (55.5 MJ kg−1) and gasoline (47.5 MJ kg−1).5 However, the use of molecular hydrogen has been hindered by the difficulty of finding a renewable, low-cost, synthetic route, as well as a convenient way of subsequently storing the produced hydrogen. One possible synthetic route is photocatalytic water-splitting, see eqn (1), first demonstrated in the form of photoelectrolysis, using a TiO2 photoanode, by Fujishima and Honda in 1972.6
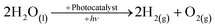 | (1) |
Traditionally, crystalline inorganic solids such as TiO2, SrTiO3, Ga2O3, GaN, Ge3N4 and Ta2O5 are employed as water-splitting photocatalysts.7–9 However, organic materials such as carbon nitrides, conjugated linear polymers, conjugated microporous polymers (CMPs) and covalent organic frameworks (COFs) have also been shown to be able to drive proton reduction, see eqn (2), and/or water oxidation, see eqn (3), in the presence of sacrificial electron donor (SED) and acceptor (SEA) species, respectively.10–12 Carbon nitride was the first organic material to evolve both hydrogen and oxygen in the presence of these sacrificial species,13,14 as well as the first organic material reported to perform overall water-splitting.15,16 Compared to their inorganic counterparts, organic photocatalysts have the advantage of facile tunability of the photocatalyst's properties through co-polymerisation and chemical functionalisation,17,18 as well as being based on generally more earth-abundant elements.
| 2H+(aq) +2e− → H2(g) | (2) |
| O2(g) + 4H+(aq) + 4e− → 2H2O(l) | (3) |
Despite a significant uptake of interest in organic materials the exact relationship between their (opto-)electronic/structural properties and the observed hydrogen (HER) and oxygen evolution reaction (OER) rates still remains far from clear.19 Previously, we demonstrated that empirically the variation in HER/OER rates between polymers can be described in terms of (i) the thermodynamic driving force for proton reduction and water oxidation, controlled by the ionisation potential (IP) and electron affinity (EA) of the neutral polymer, in both the ground state and in the presence of an excited electron–hole pair (exciton),20,21 (ii) the onset of light absorption and (iii) the dispersability of the polymer particles in suspension.18,22,23 The dispersability of a polymer probably depends both on the size (distribution) of the polymer particles in suspension and the inherent wettability of the polymer or the sidegroups present.24,25 Our empirical observations are in line with a classical semiconductor microscopic model where excitons formed through the absorption of light either (i) spontaneously fall apart and the free electrons and holes formed in the process reduce protons/SEAs and oxidize water/SEDs, respectively, or, more likely due to the large exciton binding energy relative to kBT in polymers, (ii) drive one of the two solution half-reactions and the remaining free electrons/holes the other.26,27 Transient spectroscopy of polymers under hydrogen evolution conditions25,28 indeed suggest the presence of electron polarons, i.e. self-trapped electrons, though the exact catalytic cycle, the nature of the sites responsible for HER/OER based on this semiconductor-like model, and the role played by (noble) metal co-catalysts, are less clear. McCulloch and co-workers demonstrated that upon removal of palladium from polymers prepared via Suzuki coupling the HER rates drop to effectively zero29,30 but other authors report HER by polymers that contain negligible noble metals or are prepared via a noble metal free route.31,32 Domcke, Sobolewski and co-workers have proposed an alternative micropscopic HER mechanism, based on ab initio calculations on hydrogen bonded pyridine,33 acridine,34 heptazine,35 and triazine–water complexes,36,37 which does not involve heterolytic exciton dissociation, and thus the formation of formally charged species. Instead, photon absorption induces an electron-driven proton transfer, i.e. proton-coupled electron transfer (PCET) or hydrogen atom transfer (HAT), from water to the photoexcited organic molecule, resulting in the formation of a hydrogenated organic molecule and a hydroxyl radical, essentially homolytic rather than heterolytic exciton dissociation, as two neutral open-shell species are generated. The evolution of molecular hydrogen can then proceed through a dark reaction involving the combination of two hydrogenated radicals or via absorption of another photon populating a bond dissociative pathway, either directly through vibronic coupling or excited state absorption.
Here we propose, supported by density functional theory (DFT) and correlated wavefunction calculations, a possible photocatalytic cycle for hydrogen evolution by a prototypical polymer photocatalyst, poly(p-phenylene) see Fig. 1, in the presence of triethylamine (TEA), a commonly used SED.38 We present a family of related sites on the polymer that in the absence of a noble metal co-catalyst can facilitate the evolution of molecular hydrogen when the polymer is illuminated. We discuss what can be learned from this cycle in regards to the bottlenecks for hydrogen evolution in the absence and presence of noble metal co-catalysts, and what polymer properties should be tuned to potentially increase the HER rate. Finally, we argue that the difference between heterolytic and homolytic exciton dissociation, for polymers with strongly bound excitons, might be smaller than expected and mostly depend if electron and proton transfer between a SED (or water) and the polymer is synchronous or not.
2. Computational details
2.1 Computational model
The poly(p-phenylene) polymer is described in this study as single p-phenylene (PPn) oligomers of different length n. These oligomers are then embedded in H2O or TEA to model a polymer strand near the polymer–H2O and polymer–TEA interface, respectively, where the chemistry takes place. The effect of solvent in these calculations is described by an implicit continuum solvation model, which recovers the main dielectric effect of solvation on the (electronic) properties of these relatively hydrophobic polymers. While essentially a minimal model of polymer particles, such an approach has been successfully used to calculate the potentials of charge carriers and excitons in polymers,18,20–23,25,28,39 and has been previously shown to predict accurate potentials when compared with available experimental photoelectron spectroscopy data.25,392.2 Density functional theory
All DFT40,41 calculations were performed with Gaussian 16 (Revision A.03)42 employing a polarisable continuum solvation model43–45 to account for the reaction field, specifically the integral equation formalism (IEF-PCM).46 In order to explore the excited state landscape we utilise the time-dependent extension to DFT (TD-DFT).47 All structures were confirmed as stationary points on the multi-dimensional potential energy surface and further validated to be local minima by analytic frequency calculations, displaying positive curvature along all vibrational modes. The (free) energy differences for all process considered are adiabatic, i.e. the structure of all species are the relevant local minima with the solvent fully equilibrated for each structure, this is also extended to the first singlet exited state (S1). However, for the vertical absorption profiles we use the non-equilibrium approach which only takes into account solvent polarization from the shift in electron density upon photoexcitation, maintaining the cavity shape which was optimal for the ground state density. As discussed above, we utilize either H2O (ε = 78.36) or TEA (ε = 2.38) PCM models to describe the effect of H2O/TEA on the properties of a polymer strand near the interface between a polymer and the SED solution, denoted herein as PPn–H2O or PPn–TEA, respectively. The free energy (G) is obtained via corrections to the electronic energy and calculated using the standard ideal gas, rigid rotor and harmonic oscillator statistical models to the translational, rotational and vibrational energy levels of the molecule at a temperature of 298.15 K. No free energy standard state corrections were applied by default as they would be small and only be relevant for reactions where either water, when discussing solvation in water, or TEA, when discussing solvation in TEA, is involved explicitly, or during steps where the number of reactant and product molecules differ. The B3LYP,48–50 CAM-B3LYP51 and MN15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 approximations to the exchange–correlation functional were used in conjunction with the cc-pVTZ basis set. To account for dispersion interactions we include Grimme's D3 dispersion correction53 to the B3LYP and CAM-B3LYP electronic energies and forces.
52 approximations to the exchange–correlation functional were used in conjunction with the cc-pVTZ basis set. To account for dispersion interactions we include Grimme's D3 dispersion correction53 to the B3LYP and CAM-B3LYP electronic energies and forces.
2.3 Second order algebraic diagrammatic construction
All second order Møller–Plesset (MP2) and algebraic diagrammatic construction [ADC(2)] calculations were performed using TURBOMOLE V7.4.1.54–60 Herein, all MP2/ADC(2) computations make use of the frozen core and resolution of the identity approximations,61,62 to reduce the computational expense. In addition, we also use the spin-component-scaled (SCS) approximation and exploit symmetry.63,64 All ground and excited state geometries were obtained using the cc-pVDZ basis set. We include the conductor-like screening model (COSMO)65 solely in the former calculations as gradients are not implemented within TURBOMOLE V7.4.1 for ADC(2) and compute the SCS-MP2 energy using the solvated Hartree–Fock (HF) molecular orbitals.66 Once again we use H2O and TEA implicit solvent models. For the adiabatic excitation energy a single point calculation using the larger cc-pVTZ basis set was then performed in which the correlated density of the ground or excited state is self consistent with the reaction field. For the vertical excitation spectra we once again use the cc-pVTZ basis set and the correlated density to generate the reaction field, computing the non-equilibrium response of each state.2.4 Coupled cluster theory
All single point coupled cluster singles and doubles (CCSD)67–69 calculations were performed with Gaussian 16 (Revision A.03)42 employing an IEF-PCM solvation model to describe a polymer strand near the polymer–H2O interface, as well as invoking the frozen core approximation. The effect of solvation when calculated using the HF or CCSD densities was found to be very similar, with the adiabatic excitation energy and electron affinity differing by 0.01 and 0.04 eV, respectively, as computed with the cc-pVDZ basis set. For excited states the equation of motion (EOM)70 extension to CCSD was employed. Taking into account the much larger computational cost of using the CCSD densities when calculating the effect of solvation, as this involves additional CCSD self-consistent cycles, we use the CCSD energy with HF solvation for all (EOM-)CCSD results we discuss below. These calculations use the larger cc-pVTZ basis set, with the neutral and excited state singlet PPn geometries obtained from SCS-MP2 and SCS-ADC(2), respectively. All other geometries were obtained from the DFT calculations using the B3LYP exchange–correlation functional.3. Results
3.1 Proposed photocatalytic cycle and overview of reactions
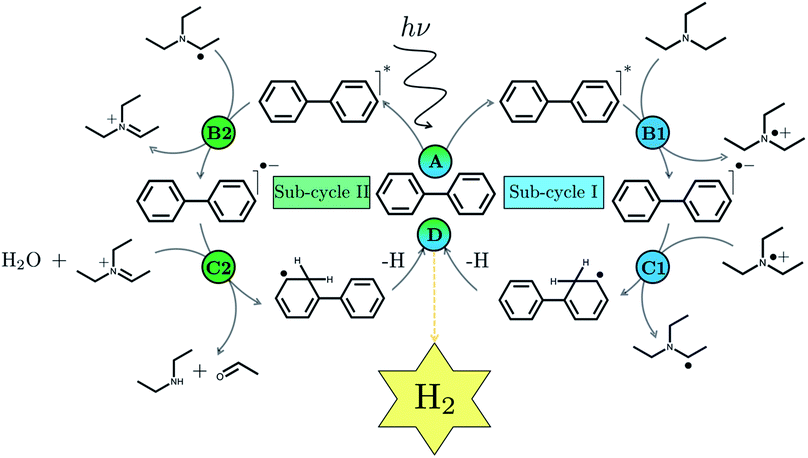
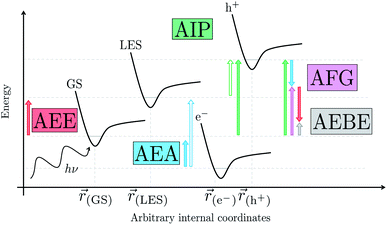
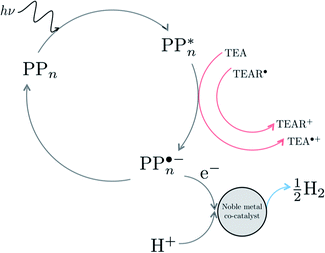
We begin with an overview of the proposed catalytic cycle, which is illustrated in Fig. 2. As the evolution of one molecule of H2 requires two electrons and because the oxidation of most SEDs to stable, i.e. non-charged closed shell, oxidation products involves two one-electron steps, the proposed cycle consists of two sub-cycles. Sub-cycle I (right-hand side of Fig. 2) involves the SED as the electron source, TEA in our case, and in sub-cycle II (left-hand side of Fig. 2) the dehydrogenated SED is the electron source. Together sub-cycles I and II produce one molecule of H2 from two photons of light.Initially, in both sub-cycle I and II, PPn undergoes excitation after absorption of a photon generating an exciton. After this vertical excitation into any excited singlet state with non-zero oscillator strength, the energy of which is defined as the vertical excitation energy (VEE), the system is expected to rapidly descend into the S1 state through internal conversion, in line with Kasha's rule, and then relax to the S1 minimum energy geometry 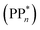 (step A, sub-cycle I and II). The energy difference between the structurally relaxed excited and ground state geometry is the adiabatic excitation energy (AEE) which is defined in eqn (4) and shown in Fig. 3 (red arrow).
(step A, sub-cycle I and II). The energy difference between the structurally relaxed excited and ground state geometry is the adiabatic excitation energy (AEE) which is defined in eqn (4) and shown in Fig. 3 (red arrow).
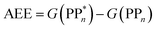 | (4) |
The overall oxidation pathway of TEA, in the presence of H2O, involves two one-electron oxidation and proton transfer steps ultimately resulting in the formation of diethylamine (DEA) and acetaldehyde (MeCHO). Electron transfer (ET) to the photoexcited PPn may thus either take place from TEA (step B1, sub-cycle I) or the dehydrogenated species TEAR˙ (step B2, sub-cycle II), see eqn (5).
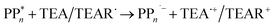 | (5) |
The thermodynamic nature of this ET step can be investigated in terms of a 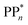 dependent and independent term, namely the adiabatic electron affinity (AEA) of
dependent and independent term, namely the adiabatic electron affinity (AEA) of 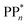 [AEA
[AEA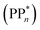 ] and the adiabatic ionisation potential (AIP) of TEA [AIP(TEA)] and that of TEAR˙ [AIP(TEAR˙)], see eqn (6), (7) and (8), respectively. These terms are shown schematically in Fig. 3 by the hollow blue, AEA, and solid green, AIP, arrows, respectively. For the ET step to be thermodynamically favourable the
] and the adiabatic ionisation potential (AIP) of TEA [AIP(TEA)] and that of TEAR˙ [AIP(TEAR˙)], see eqn (6), (7) and (8), respectively. These terms are shown schematically in Fig. 3 by the hollow blue, AEA, and solid green, AIP, arrows, respectively. For the ET step to be thermodynamically favourable the 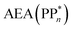 must be larger in magnitude than AIP(TEA) in sub-cycle I and larger than AIP(TEAR˙) in sub-cycle II, with a greater difference signifying more exothermic (exergonic) reactions.
must be larger in magnitude than AIP(TEA) in sub-cycle I and larger than AIP(TEAR˙) in sub-cycle II, with a greater difference signifying more exothermic (exergonic) reactions.
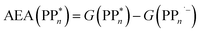 | (6) |
| AIP(TEA) = G(TEA˙+) − G(TEA) | (7) |
| AIP(TEAR˙) = G(TEAR+) − G(TEAR˙) | (8) |
The next step would involve the transfer of a proton (PT) for which we have multiple possible scenarios: (i) PT between TEA˙+ and PPn˙− (step C1, sub-cycle I), (ii) PT between TEAR+ and PPn˙− (step C2, sub-cycle II), as well as (iii) PT between TEA–H+ and PPn˙−. The final step of sub-cycle I and II would involve dehydrogenation of PPn–H˙, resulting in the formation of H2 for every 2 molecules of PPn–H˙ (step D), thus completing the proposed catalytic cycle. Microscopically, the source of the two hydrogen atoms in a given H2 molecule could be PPn–H˙ molecules produced in sub-cycle I and/or sub-cycle II, even if stoichiometry implies that on average one PPn–H˙ molecule should originate from each sub-cycle. Therefore, in the thermodynamic analysis which follows we assume that half a molecule of H2 is produced upon the completion of either sub-cycle I or II.
There are also a number of competing side-reactions to consider. Besides TEA–H+ acting as the proton source rather than TEA˙+ or TEAR+, TEA can deprotonate TEA˙+ to form TEA–H+ and TEAR˙, and PPn˙− and TEA˙+ can recombine regenerating PPn in the ground state and TEA. The latter reaction is the ground state back reaction where the energy gained by absorbing a photon gets lost in the form of heat rather than used productively.
Instead of sequential electron and proton transfer upon excitation of the polymer, concerted electron–proton transfer, and thus effectively hydrogen atom transfer, could take place, analogous to the mechanism discussed by Domcke and co-workers for water oxidation,33–37 see eqn (9) for an example involving PPn and TEA.
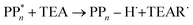 | (9) |
3.2 Excited state landscape
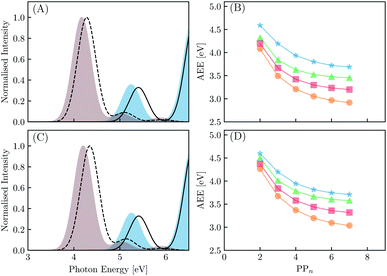
We begin with an exploration of the vertical absorption spectra as a function of increasing oligomer length using both TD-DFT and SCS-ADC(2). In order to reduce some of the computational strain we employ symmetry within the SCS-ADC(2) calculations, namely D2 and C2h for even and odd oligomer lengths, while in the TD-DFT equivalent no symmetry was enforced (i.e. C1). Despite being one of the simplest possible conjugated materials, it has been noted in previous studies that there is a disagreement between correlated wavefunction methods and TD-DFT when predicting the nature of the vertical excited states for small p-phenylene oligomers.71,72 This is discussed further within the ESI (see Section S1†). The simulated absorption spectra for the largest and smallest oligomers using CAM-B3LYP and SCS-ADC(2) are provided in Fig. 4(A) and (C) (see Section S2† for the peak broadening parameters and Fig. S2† for all other predicted absorption spectra). As expected, upon extension of the oligomer length a clear redshift of the lowest energy bright absorption band is observed. This lowest energy bright state corresponds to a 1ππ* transition and can be described by a single particle–hole transition from the highest occupied molecular orbital to the lowest unoccupied molecular orbital. The redshift with oligomer length is most prominent for B3LYP with the VEE changing from 4.87 to 3.53 eV (1.34 eV) for PP2–H2O to PP7–H2O. For SCS-ADC(2), CAM-B3LYP and MN15 we observe shifts of 5.40 to 4.28 eV (1.12 eV), 5.24 to 4.17 eV (1.07 eV) and 5.02 to 3.82 eV (1.20 eV), respectively. We observe a good agreement between both SCS-ADC(2) and CAM-B3LYP for the VEE of the optically bright state, with a maximum deviation of 0.16 eV. For B3LYP and MN15 the excitation energy of this absorption band is significantly underestimated when compared to the aforementioned methods. Upon switching from the high-dielectric H2O environment to low-dielectric TEA we observe a small increase in the VEE of the bright state, with a maximum blueshift of 0.08 eV.We now turn our attention to the S1 AEE for each oligomer length and theoretical method combination. As calculation of the vibrational frequencies when using ADC(2) and CCSD is computationally expensive we compare the AEE here in terms of electronic energies. The AEE for each oligomer length is shown in Fig. 4(B) and (D) for the case of PPn–H2O and PPn–TEA, respectively. As a result of structural relaxation of the oligomer and the response of the solvent to the S1 density, the AEE is significantly smaller than the VEE, this additional energy may potentially be dissipated to the environment as heat and thus lost. For SCS-ADC(2) when going from PP2–H2O to PP7–H2O the AEE decreased from 4.59 to 3.69 eV and from 4.32 to 3.45 eV for CAM-B3LYP. For B3LYP and MN15 the AEE ranged from 4.08 to 2.92 eV and from 4.20 to 3.20 eV, respectively. For PP2–H2O an AEE of 4.76 eV was calculated using CCSD on the SCS-MP2/ADC(2) geometries, 0.17 eV larger than the SCS-ADC(2) energy equivalent. For oligomers in the presence of TEA the DFT predicted AEE is once again blueshifted when compared to the higher dielectric environment, with a maximum blueshift of 0.18 eV, which was observed for PP2. The SCS-ADC(2) AEE on the other hand was essentially the same in both environments, maximum blueshift of 0.02 eV for PP6, which may be the result of neglecting the effect of solvation in the SCS-ADC(2) structural optimizations.
3.3 Exciton dissociation and electron transfer
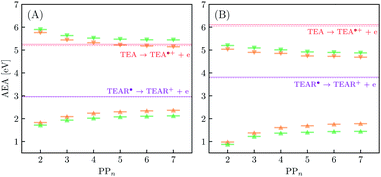
In inorganic materials the exciton binding energy (EBE) is normally a few tens of meV or less and excitons thus spontaneously dissociate into free-charge carriers. In contrast, the S1 exciton in polymer photocatalysts is normally still bound at room temperature as a result of the much larger EBE in organic conjugated materials,26,27 as well as the fact that excitons in polymers self-trap, i.e. localize by distorting the polymer geometry. As shown in Fig. 3 the adiabatic EBE (grey arrow), the EBE when also considering self-trapping and the formation of electron and hole polarons after exciton dissociation, can be obtained from the difference between the adiabatic fundamental gap (AFG) (pink arrow) and the AEE, where the former quantity itself is the difference between the AIP and AEA of the material. For PPn–H2O the adiabatic EBE is calculated to be approximately 0.4 eV for each of the exchange–correlation functionals considered, essentially independent of oligomer length (see Table S5†). However, for PPn–TEA the adiabatic EBE is predicted to be significantly larger, more than 1.2 eV for all oligomer lengths (see Table S6†). This increase can be attributed to the larger stabilization of the charged species in the high-dielectric environment, schematically shifting down the energy of the arbitrary h+ and e− potential energy surface in Fig. 3, thus providing smaller AIPs and larger AEAs, ultimately translating into smaller AFGs (see Tables S5 and S6†). As mentioned previously, the AEE is only slightly blueshifted in TEA therefore the increase in EBE is dominated by the difference of the AFG between both environments.We now turn our attention to the ET process from the SED to the photoexcited polymer. As discussed earlier the oxidation pathway of TEA means that this electron may come from this species directly (step B1, sub-cycle I) or from the TEAR˙ radical (step B2, sub-cycle II). As the oligomer length increases AEA(PP*) in-turn decreases, resulting in a lower thermodynamic driving force for this ET. For oligomers in the presence of H2O, ET when using TEA as the electron source is moderately favourable from a thermodynamic perspective (see Fig. 5(A)), with free energy values ranging from −0.65 eV for PP2 and −0.19 eV for PP7 when using CAM-B3LYP. For B3LYP and MN15 the dependence on oligomer length is similar, however, for PP6 and PP7 the ET is predicted to be slightly endergonic. Using CCSD the electronic energy difference of the ET process for PP2 was calculated to be −0.89 eV, more exothermic than that predicted by DFT (−0.52 eV and −0.61 eV for B3LYP and CAM-B3LYP, respectively). For ET involving TEAR˙ we predict that ET is highly exergonic for all oligomer lengths. For PPn–TEA the increased AIP of TEA coupled with the decreased AEA(PP*) values of the oligomer results in ET when using TEA as electron source being endergonic for all oligomer lengths (see Fig. 5(B)). Application of the standard state correction to the free energies would result in ET free energies which are 0.05 eV less positive therefore slightly reducing the endergonicity of ET in TEA (step B1, sub-cycle I). Once again ET from TEAR˙ is exergonic for all oligomer lengths, though with a lower driving force than in H2O.
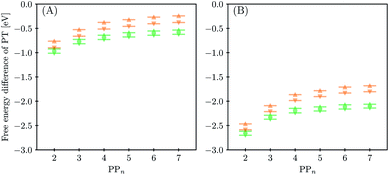
3.4 Proton transfer and H2 generation
The next step of the proposed catalytic cycle then involves the protonation of the one-electron reduced polymer (steps C1/C2 of sub-cycle I/II). The various proton sources have been outlined above in Section 3.1 and Fig. 2. For PP2–H2O to PP5–H2O, using B3LYP and CAM-B3LYP we have studied each unique adsorption site on the photocatalyst, see Fig. 1 for the labels of the non-equivalent carbon atoms. For all oligomer lengths we find that the lowest energy adsorption sites are those corresponding to aromatic –CH– sites with adsorption of the proton on the sites linking the phenyl units being considerably less favourable (see Table S7† for the specific free energy differences for each oligomer length). In terms of free energies all the different aromatic –CH– sites lie within 0.03 eV (<1 kcal mol−1), with the exception of the C2 position which was found to be upwards of 0.1 eV higher in energy. Therefore, in the discussion below and the reaction profiles which follow we only discuss the case for the C3 position, which was the lowest free energy adsorption site. As shown in Fig. 6, for oligomers PT is predicted to be exergonic with the driving force once again decreasing with increasing oligomer length. The PT step is far more exergonic near the polymer–TEA interface with B3LYP predicted PT free energies of −0.24 and −1.68 eV for PP7–H2O and PP7–TEA, respectively, when using TEA˙+ as the proton source. As PPn–H˙ is neutral both solvents will stabilize this species to a similar extent, therefore, the low-dielectric environment will essentially gain back the energy differential of the preceding ET step. The PT free energy is similar for the three proton sources considered, see Fig. 6(A) and (B) for the case of TEA˙+ and TEAR+ acting as the proton source, respectively, and Tables S5 and S6† for TEA–H+. Applying the standard state correction to the free energies for PT in H2O using TEAR+ as the proton source results in 0.10 eV more negative PT free energies, therefore increasing the exergonicity of this reaction (step C2, sub-cycle II). Using CCSD the reaction energetics, in terms of the electronic energies, for PP2–H2O are similar to that obtained with DFT with a PT energy of −0.96 eV when using TEA˙+ as the proton source for CCSD, which can be compared with −0.77 eV and −0.90 eV for B3LYP and CAM-B3LYP, respectively.The final step of the catalytic cycle then involves the regeneration of the original polymer from PPn–H˙ and the release of molecular hydrogen (step D, cycle I and II). We find in both environments that this reaction is considerably exergonic, DFT predicted hydrogen formation free energy of approximately −1.2 eV, and essentially does not change when going from PP2 to PP7 (see Tables S5 and S6†). We also observe no apparent difference between the reaction energetics for PPn–H2O and PPn–TEA. The hydrogen formation free energy increases by 0.08 eV to approximately −1.1 eV when applying standard state corrections. The H2 adsorption energy 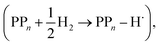 an often used descriptor for HER activity, is by definition the negative of the hydrogen formation free energy, and thus equals approximately 1.2 eV for PPn, corresponding to a hydrogen binding free energy (PPn–H˙ → PPn + H) of approximately 0.8 eV. The hydrogen binding energy calculated using CCSD for PP2–H2O, again in terms of the electronic energies, was found to be 1.35 eV, close to the DFT predicted values of 1.33 and 1.36 eV for B3LYP and CAM-B3LYP, respectively. The CCSD H2 adsorption energy was computed to be 1.00 eV, which too was extremely close to the B3LYP and CAM-B3LYP values of 1.06 and 1.01 eV, respectively. The H2 adsorption free energies for PPn lie in between those predicted for hydrogen adsorption on the nitrogen (0.7 eV) and sulphur atoms (2.0 eV) in benzothiadiazole based co-polymers,73 though are considerably larger than the lowest hydrogen absorption free energy predicted for organic materials (0.02 eV).74
an often used descriptor for HER activity, is by definition the negative of the hydrogen formation free energy, and thus equals approximately 1.2 eV for PPn, corresponding to a hydrogen binding free energy (PPn–H˙ → PPn + H) of approximately 0.8 eV. The hydrogen binding energy calculated using CCSD for PP2–H2O, again in terms of the electronic energies, was found to be 1.35 eV, close to the DFT predicted values of 1.33 and 1.36 eV for B3LYP and CAM-B3LYP, respectively. The CCSD H2 adsorption energy was computed to be 1.00 eV, which too was extremely close to the B3LYP and CAM-B3LYP values of 1.06 and 1.01 eV, respectively. The H2 adsorption free energies for PPn lie in between those predicted for hydrogen adsorption on the nitrogen (0.7 eV) and sulphur atoms (2.0 eV) in benzothiadiazole based co-polymers,73 though are considerably larger than the lowest hydrogen absorption free energy predicted for organic materials (0.02 eV).74
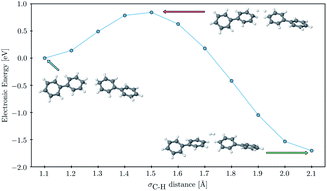
Finally, to probe the barrier to H2 evolution we performed a constrained optimization, starting from a fully optimized tail-to-tail cluster of two PP2–H˙–H2O molecules, where we step-by-step stretch the σC–H bonds decreasing the H–H distance. We keep the two phenyl rings furthest away from the forming H2 molecule fixed at all points along the scanning coordinate and take the hydrogen binding site as C1 rather than C3 as this allowed us to construct a reaction coordinate where the shortening of the hydrogen–hydrogen distance and the subsequent flattening of the two phenyl rings, on which the hydrogen atoms were adsorbed, were the only major structural changes. The result of this constrained optimization can be seen in Fig. 7. The approximate barrier height that we obtain in this way is 0.79 eV relative to the cluster of the two PP2–H˙ molecules, which serves as an upper estimate of the true barrier height for hydrogen evolution starting from two hydrogen atoms adsorbed on nearby polymer chains. As there are no formally charged species in this process, we would expect the barrier for PP2–TEA, and thus for oligomers near the polymer–TEA interface, to be similar to that predicted here for oligomers near the H2O interface. This value is significantly smaller than that predicted using a similar computational setup for the hydrogen evolution barrier from hydrogen adsorbed on the nitrogen atom of benzothiadiazole-fluorene based co-polymers (1.32 eV) in work by Pati and co-workers,73 but considerably larger than that measured experimentally for platinum (0.1–0.2 eV depending on the surface75).
4. Discussion
Fig. 8 shows the predicted B3LYP free energy profile starting from TEA and PPn, for sub-cycle I, producing TEAR˙ and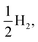 and for sub-cycle II, the subsequent oxidation of TEAR˙ to DEA and MeCHO and producing another
and for sub-cycle II, the subsequent oxidation of TEAR˙ to DEA and MeCHO and producing another 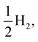 regenerating PPn at the end of each sub-cycle. Fig. 8(A) and (B) are the profiles for oligomers near the polymer–H2O interface (PPn–H2O) and (C) and (D) the profiles for the equivalent polymer–TEA case (PPn–TEA). See Fig. S3† for the corresponding profiles calculated with CAM-B3LYP. As can be seen, for both environments hydrogen evolution driven by the absorption of two photons, with the electrons provided by the overall oxidation of TEA, is thermodynamically favourable. In the case of oligomers near the polymer–H2O interface, both sub-cycles are downhill after excitation by light. The free energy profile for sub-cycle II is considerably steeper, as TEAR˙ is a stronger reductant than TEA (see Fig. 5(A)), while for sub-cycle I the top of the profile flattens for longer oligomers (see Fig. 8(A)), as the ET free energy tends towards 0, becoming slightly endergonic for PP6 and PP7. In the case of the CAM-B3LYP, free energy profile the flattening is not as apparent as the ET for large oligomer lengths is still exergonic. In contrast to the H2O case, for oligomers near the polymer–TEA interface, the first step of sub-cycle I after excitation is uphill by ∼1 eV, because ET from TEA to the polymer in TEA is endergonic (see Fig. 5(B)). Based on our calculations we cannot rule in or out that proton and electron transfer happens simultaneously via PCET or HAT rather than sequentially. If proton and electron transfer is coupled then that would have the largest effect for oligomers near the polymer–TEA interface as it would allow the mechanism to side-step the uphill ET step, making the free energy profile, just like for the polymer–H2O case, all downhill. We also have considered inverting the order of ET and PT steps, first transferring a proton to form PPn–H+ and TEAR− from
regenerating PPn at the end of each sub-cycle. Fig. 8(A) and (B) are the profiles for oligomers near the polymer–H2O interface (PPn–H2O) and (C) and (D) the profiles for the equivalent polymer–TEA case (PPn–TEA). See Fig. S3† for the corresponding profiles calculated with CAM-B3LYP. As can be seen, for both environments hydrogen evolution driven by the absorption of two photons, with the electrons provided by the overall oxidation of TEA, is thermodynamically favourable. In the case of oligomers near the polymer–H2O interface, both sub-cycles are downhill after excitation by light. The free energy profile for sub-cycle II is considerably steeper, as TEAR˙ is a stronger reductant than TEA (see Fig. 5(A)), while for sub-cycle I the top of the profile flattens for longer oligomers (see Fig. 8(A)), as the ET free energy tends towards 0, becoming slightly endergonic for PP6 and PP7. In the case of the CAM-B3LYP, free energy profile the flattening is not as apparent as the ET for large oligomer lengths is still exergonic. In contrast to the H2O case, for oligomers near the polymer–TEA interface, the first step of sub-cycle I after excitation is uphill by ∼1 eV, because ET from TEA to the polymer in TEA is endergonic (see Fig. 5(B)). Based on our calculations we cannot rule in or out that proton and electron transfer happens simultaneously via PCET or HAT rather than sequentially. If proton and electron transfer is coupled then that would have the largest effect for oligomers near the polymer–TEA interface as it would allow the mechanism to side-step the uphill ET step, making the free energy profile, just like for the polymer–H2O case, all downhill. We also have considered inverting the order of ET and PT steps, first transferring a proton to form PPn–H+ and TEAR− from  and TEA, and then transferring an electron to form PPn–H˙ and TEAR˙. This was, however, considerably worse from an energetic perspective. PT is strongly endergonic in that scenario (1.46 and 3.18 eV for PP2 near the polymer–H2O and polymer–TEA interface, respectively as predicted by B3LYP) and while ET would be more favorable (−2.79 and −4.63 eV, respectively), in this case there would even be an even greater free energy barrier to climb over, even in the case of the polymer–H2O interface, ruling out this order of events.
and TEA, and then transferring an electron to form PPn–H˙ and TEAR˙. This was, however, considerably worse from an energetic perspective. PT is strongly endergonic in that scenario (1.46 and 3.18 eV for PP2 near the polymer–H2O and polymer–TEA interface, respectively as predicted by B3LYP) and while ET would be more favorable (−2.79 and −4.63 eV, respectively), in this case there would even be an even greater free energy barrier to climb over, even in the case of the polymer–H2O interface, ruling out this order of events.
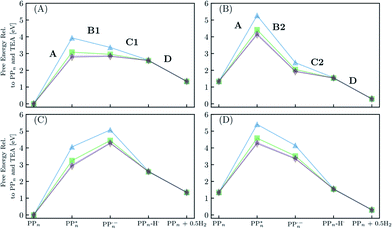 | ||
| Fig. 8 The predicted free energy profile for each step in H2O of sub-cycle I (A) and II (B). The predicted free energy profile for each step in TEA of sub-cycle I (C) and II (D). Data shown for n = 2 (blue triangles), 4 (green squares), 6 (purple stars) and 7 (brown diamonds), calculated using B3LYP and provided relative to PPn and TEA. The x-axis labels omit any reference to the SED or its degradation products. For the equivalent data calculated with CAM-B3LYP see Fig. S3.† | ||
From a thermodynamic perspective hydrogen evolution, and two-hole oxidation of TEA, is thus exergonic under illumination for both oligomers near the polymer–H2O and polymer–TEA interface. The uphill ET step for the case of the polymer–TEA interface, when oxidising TEA in sub-cycle I, gives rise to a thermodynamic barrier of ∼1 eV when the ET and PT steps are sequential, that would be absent in the case of concerted PCET/HAT. Illumination is essential as in the absence of the two-photon bias, nothing would happen as the ground state of the polymer, in contrast to its excited state counterpart, cannot extract an electron from TEA/TEAR˙. Poly(p-phenylene) is significantly hydrophobic resulting in the mixtures of H2O and TEA (and methanol), used experimentally as SEDs, phase-segregating in solution. Molecular dynamics simulations suggest that the environment close to the polymer is TEA-rich28 and as such the environment of the polymer will lie somewhere in between the two extreme cases in terms of the dielectric environment modeled here. This means, that if ET and PT are not concerted, there will likely be, besides the 0.79 eV barrier of the molecular hydrogen formation step, a free energy barrier due to the uphill ET-step with an activation energy somewhere between that predicted for the polymer–H2O and polymer–TEA interface. The ET step will also be competing with the ground-state back reaction where the electron is transferred back to TEA and the polymer returns to its electronic ground state, a process that due to fact that ground state adiabatic electron affinity is much smaller than its excited state counterpart is more exergonic than proton transfer. Other side reactions such as proton transfer between TEA˙+ and TEAR+ with TEA, would also be in competition with the polymer PT steps (see Table S8†). A polymer such as poly(p-phenylene), should thus be able to evolve hydrogen when illuminated but in practice the HER rates will be low due to a combination of the barriers and the back reaction.
Next we can investigate the effect of adding a noble metal co-catalyst such as platinum or palladium nanoparticles. Assuming that also in the presence of such a co-catalyst the exciton falls apart by accepting an electron from TEA/TEAR˙ when on the polymer, in line with the observation with a signal in transient absorption spectroscopy that has been assigned as arising from an electron polaron on the polymer,25,28 the effect of the co-catalyst is in this case mainly to lower the barrier for the molecular hydrogen formation step. See Fig. 9 for a possible cycle in the presence of a co-catalyst. Even in the presence of the co-catalyst the issue of the thermodynamic barrier due to the uphill ET step and the competing ground-state back reaction will remain. This combined with the fact that poly(p-phenylene) only starts absorbing light on the edge between visible and ultraviolet light might explain why even in the presence of platinum or palladium particles poly(p-phenylene) is experimentally not a very active hydrogen evolution photocatalyst.
The calculations also suggest that polymers with a more positive excited state electron affinity than poly(p-phenylene), i.e. more electron-poor polymers, probably will be more active. A positive shift in the excited state electron affinity will make ET in general more favorable, reducing the uphill nature of ET for the polymer–TEA interface limit and perhaps even making this step downhill. Ideally, a shift in the excited state electron affinity may be accompanied by a similar shift in the ground state electron affinity, making the ground state back reaction less favorable and reducing the optical gap of the polymer – the difference between the ground state and excited state adiabatic electron affinity is by definition equal to the adiabatic excitation energy20 – , allowing for the absorption of a larger part of the visible spectrum and thus the generation of more excitons. The ground state electron affinity, however, cannot become too positive as eventually this may impact the driving force for the PT step. Understanding how the barrier of the molecular hydrogen formation step can be lowered requires more work but in the first instance reducing the binding energy of the hydrogen atoms on the polymer might be a promising approach, which may again be linked with the polymer's ground state electron affinity.
Finally, as already mentioned above, the mechanism proposed by Domcke and co-workers,33–37 where the exciton on the polymer dissociates homolytically rather than heterolytically, i.e. by forming two neutral rather than two oppositely charged fragments, and a hydrogen atom is transferred between the molecule that gets oxidized and the polymer, is a special case of the mechanism discussed here. This assumes that electron and proton transfer happen simultaneously and that the proton and electron by definition come from the same source. Domcke and co-workers typically only consider water oxidation but it appears trivial to extend their mechanism to instances where the source of the electron and proton is a SED, such as TEA.
5. Conclusions
A potential photocatalytic cycle for hydrogen evolution by poly(p-phenylene), a prototypical polymer photocatalyst, in the presence of triethylamine as a sacrificial electron donor has been proposed and the thermodynamics of the cycle explored via ab initio calculations, using both density functional theory and correlated wavefunction methods. As part of the cycle a series of related sites on the polymer, the aromatic –CH– atoms, have been found to be able to adsorb hydrogen atoms and to facilitate hydrogen–hydrogen bond formation and thus molecular hydrogen evolution, albeit with a considerably larger barrier than for hydrogen evolution on noble-metals such as platinum.To evolve one molecule of H2 in the presence of TEA each of the two sub-cycles of the proposed catalytic cycle needs to be traversed. In the first sub-cycle TEA gets oxidized to TEAR˙, dehydrogenated TEA, with the polymer accepting this hydrogen atom, while in the second sub-cycle TEAR˙ gets oxidized to DEA and MeCHO. In each case, TEA or TEAR˙ transfers one electron and one proton to the polymer resulting in an adsorbed hydrogen atom. This electron and proton transfer can take place sequentially or synchronously. Finally, two hydrogen atoms adsorbed on adjacent or the same polymer chain combine to make molecular hydrogen. For polymer particles surrounded by H2O all steps are predicted to be downhill, however, for polymer particles surrounded by TEA, electron transfer from TEA to the polymer excited by the absorption of light is predicted to be uphill. Previous molecular dynamics simulations on similar types of hydrophobic polymers immersed in a mixture of H2O, TEA and methanol, used experimentally as reaction solution, show that the environment around the polymer becomes locally enriched in TEA, with the mixture phase-segregating. Therefore, under experimental conditions electron transfer from TEA is likely uphill and will form a thermodynamic barrier. Since experimental transient absorption spectroscopy suggests that even in the presence of noble metal co-catalysts electron transfer and exciton dissociation still takes place on the polymer, this thermodynamic barrier is also likely there in the presence of such co-catalysts. The thermodynamic barrier combined with the fact that poly(p-phenylene) only starts absorbing light on the edge between visible and ultraviolet light probably explains why even in the presence of platinum or palladium particles poly(p-phenylene) is not a very active hydrogen evolution photocatalyst.
Based on the proposed cycle, polymers that have more positive excited state and ground state electron affinity values than poly(p-phenylene) are likely more active. The positive shift in the excited state electron affinity reduces how uphill the electron transfer step is in the presence of TEA and thus under experimental conditions, while shifting the ground state electron affinity to more positive values reduces how thermodynamically favorable the undesired back reaction is, where after electron transfer to the excited polymer the electron is returned to TEA and the energy of the light absorbed dissipated in the form of heat.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We kindly acknowledge Prof. R. Godin, Dr M. A. Kochman, Prof. M. J. Porter, Dr M. Sachs and Dr R. S. Sprick for useful discussion and the Leverhulme Trust for funding (RPG-2019-209).References
- S. Shafiee and E. Topal, Energy Policy, 2009, 37, 181–189 CrossRef.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- S. Vijayavenkataraman, S. Iniyan and R. Goic, Renew. Sustain. Energy Rev., 2012, 16, 878–897 CrossRef.
- G. Centi and S. Perathoner, ChemSusChem, 2010, 3, 195–208 CrossRef CAS PubMed.
- P. Nikolaidis and A. Poullikkas, Renew. Sustain. Energy Rev., 2017, 67, 597–611 CrossRef CAS.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 1–17 Search PubMed.
- Q. Wang and K. Domen, Chem. Rev., 2020, 120, 919–985 CrossRef CAS PubMed.
- Z. Wang, C. Li and K. Domen, Chem. Soc. Rev., 2019, 48, 2109–2125 RSC.
- V. S. Vyas, V. W. H. Lau and B. V. Lotsch, Chem. Mater., 2016, 28, 5191–5204 CrossRef CAS.
- Y. Wang, A. Vogel, M. Sachs, R. S. Sprick, L. Wilbraham, S. J. Moniz, R. Godin, M. A. Zwijnenburg, J. R. Durrant, A. I. Cooper and J. Tang, Nat. Energy, 2019, 4, 746–760 CrossRef CAS.
- T. Banerjee, F. Podjaski, J. Kröger, B. P. Biswal and B. V. Lotsch, Nat. Rev. Mater., 2020, 168–190 Search PubMed.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- K. Maeda, X. Wang, Y. Nishihara, D. Lu, M. Antonietti and K. Domen, J. Phys. Chem. C, 2009, 113, 4940–4947 CrossRef CAS.
- J. Liu, Y. Liu, N. Liu, Y. Han, X. Zhang, H. Huang, Y. Lifshitz, S.-T. Lee, J. Zhong and Z. Kang, Science, 2015, 347, 970–974 CrossRef CAS PubMed.
- G. Zhang, Z.-A. Lan, L. Lin, S. Lin and X. Wang, Chem. Sci., 2016, 7, 3062–3066 RSC.
- J. X. Jiang, A. Trewin, D. J. Adams and A. I. Cooper, Chem. Sci., 2011, 2, 1777–1781 RSC.
- R. S. Sprick, C. M. Aitchison, E. Berardo, L. Turcani, L. Wilbraham, B. M. Alston, K. E. Jelfs, M. A. Zwijnenburg and A. I. Cooper, J. Mater. Chem. A, 2018, 6, 11994–12003 RSC.
- C. M. Aitchison, V. Andrei, D. Antón-García, U.-P. Apfel, V. Badiani, M. Beller, A. B. Bocarsly, S. Bonnet, P. Brueggeller, C. A. Caputo, F. Cassiola, S. T. Clausing, A. I. Cooper, C. E. Creissen, V. A. de la Peña O'Shea, W. Domcke, J. R. Durrant, M. Grätzel, L. Hammarström, A. Hankin, M. C. Hatzell, F. Karadas, B. König, M. F. Kuehnel, S. Lamaison, C.-Y. Lin, M. Maneiro, S. D. Minteer, A. R. Paris, E. Pastor, C. Pornrungroj, J. N. H. Reek, E. Reisner, S. Roy, C. Sahm, R. Shankar, W. J. Shaw, S. I. Shylin, W. A. Smith, K. Sokol, H. S. Soo, R. S. Sprick, W. Viertl, A. Vogel, A. Wagner, D. Wakerley, Q. Wang, D. Wielend and M. A. Zwijnenburg, Faraday Discuss., 2019, 215, 242–281 RSC.
- P. Guiglion, C. Butchosa and M. A. Zwijnenburg, J. Mater. Chem. A, 2014, 2, 11996–12004 RSC.
- C. Butchosa, P. Guiglion and M. A. Zwijnenburg, J. Phys. Chem. C, 2014, 118, 24833–24842 CrossRef CAS.
- Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063–9071 CrossRef CAS PubMed.
- C. B. Meier, R. Clowes, E. Berardo, K. E. Jelfs, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Chem. Mater., 2019, 31, 8830–8838 CrossRef CAS PubMed.
- Y. Bai, D. J. Woods, L. Wilbraham, C. M. Aitchison, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Mater. Chem. A, 2020, 8, 8700–8705 RSC.
- D. J. Woods, S. A. Hillman, D. Pearce, L. Wilbraham, L. Q. Flagg, W. Duffy, I. McCulloch, J. R. Durrant, A. A. Guilbert, M. A. Zwijnenburg, R. S. Sprick, J. Nelson and A. I. Cooper, Energy Environ. Sci., 2020, 13, 1843–1855 RSC.
- P. Guiglion, C. Butchosa and M. A. Zwijnenburg, Macromol. Chem. Phys., 2016, 217, 344–353 CrossRef CAS.
- H. Wang, S. Jin, X. Zhang and Y. Xie, Angew. Chem., Int. Ed., 2020, 59, 22828–22839 CrossRef CAS PubMed.
- M. Sachs, R. S. Sprick, D. Pearce, S. A. Hillman, A. Monti, A. A. Guilbert, N. J. Brownbill, S. Dimitrov, X. Shi, F. Blanc, M. A. Zwijnenburg, J. Nelson, J. R. Durrant and A. I. Cooper, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- J. Kosco, M. Sachs, R. Godin, M. Kirkus, L. Francas, M. Bidwell, M. Qureshi, D. Anjum, J. R. Durrant and I. McCulloch, Adv. Energy Mater., 2018, 8, 1802181 CrossRef.
- J. Kosco and I. McCulloch, ACS Energy Lett., 2018, 3, 2846–2850 CrossRef CAS.
- Z. Zhang, J. Long, L. Yang, W. Chen, W. Dai, X. Fu and X. Wang, Chem. Sci., 2011, 2, 1826–1830 RSC.
- C. Han, P. Dong, H. Tang, P. Zheng, C. Zhang, F. Wang, F. Huang and J.-X. Jiang, Chem. Sci., 2021, 12, 1796–1802 RSC.
- X. Liu, A. L. Sobolewski, R. Borrelli and W. Domcke, Phys. Chem. Chem. Phys., 2013, 15, 5957–5966 RSC.
- X. Liu, T. N. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. B, 2015, 119, 10664–10672 CrossRef CAS PubMed.
- J. Ehrmaier, T. N. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764 CrossRef CAS PubMed.
- J. Ehrmaier, M. J. Janicki, A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2018, 20, 14420–14430 RSC.
- W. Domcke, J. Ehrmaier and A. L. Sobolewski, ChemPhotoChem, 2019, 3, 10–23 CrossRef CAS.
- Y. Pellegrin and F. Odobel, C. R. Chim., 2017, 20, 283–295 CrossRef CAS.
- P. Guiglion, A. Monti and M. A. Zwijnenburg, J. Phys. Chem. C, 2017, 121, 1498–1506 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 1449–1458 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154122 CrossRef PubMed.
- TURBOMOLE V7.4.1 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, 1989–2007, since 2007, available from http://www.turbomole.com Search PubMed.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- C. Hättig, A. Hellweg and A. Köhn, Phys. Chem. Chem. Phys., 2006, 8, 1159–1169 RSC.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299–2324 CrossRef CAS.
- C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- C. Hättig, in Response Theory and Molecular Properties (A Tribute to Jan Linderberg and Poul Jørgensen), Academic Press, 2005, vol. 50 of Advances in Quantum Chemistry, pp. 37–60 Search PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 1999, 103, 9100–9108 CrossRef CAS.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer, J. Chem. Phys., 1988, 89, 7382–7387 CrossRef CAS.
- G. E. Scuseria and H. F. Schaefer, J. Chem. Phys., 1989, 90, 3700–3703 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- R. Fukuda and M. Ehara, Phys. Chem. Chem. Phys., 2013, 15, 17426–17434 RSC.
- V. Lukeš, A. J. A. Aquino, H. Lischka and H. F. Kauffmann, J. Phys. Chem. B, 2007, 111, 7954–7962 CrossRef PubMed.
- P. B. Pati, G. Damas, L. Tian, D. L. A. Fernandes, L. Zhang, I. B. Pehlivan, T. Edvinsson, C. M. Araujo and H. Tian, Energy Environ. Sci., 2017, 10, 1372–1376 RSC.
- G. Damas, C. F. N. Marchiori and C. M. Araujo, J. Phys. Chem. C, 2018, 122, 26876–26888 CrossRef CAS.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison between excited states predicted by TD-DFT and SCS-ADC(2), tabulated reaction free energies, adsorption free energies for different sites on the polymer and optimized structures of relevant species. See DOI: 10.1039/d1se00059d |
| This journal is © The Royal Society of Chemistry 2021 |