 Open Access Article
Open Access ArticleConceptual density functional theory based electronic structure principles
Debdutta
Chakraborty
 a and
Pratim Kumar
Chattaraj
a and
Pratim Kumar
Chattaraj
 *bc
*bc
aDepartment of Chemistry, KU Leuven, Celestijnenlaan 200F-2404, 3001 Leuven, Belgium
bDepartment of Chemistry, Indian Institute of Technology, Kharagpur 721302, West Bengal, India. E-mail: pkc@chem.iitkgp.ac.in; Fax: +91 3222 255303; Tel: +91 3222 283304
cDepartment of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
First published on 31st March 2021
Abstract
In this review article, we intend to highlight the basic electronic structure principles and various reactivity descriptors as defined within the premise of conceptual density functional theory (CDFT). Over the past several decades, CDFT has proven its worth in providing valuable insights into various static as well as time-dependent physicochemical problems. Herein, having briefly outlined the basics of CDFT, we describe various situations where CDFT based reactivity theory could be employed in order to gain insights into the underlying mechanism of several chemical processes.
1. Introduction
Ever since the proclamation by Dirac in 1929 that “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble,”1 a great deal of efforts have been devoted by researchers over the last several decades in order to develop suitable numerical methods to solve the Schrodinger equation for atoms and molecules which in turn can help to shed light on various physicochemical processes. To this end, the formulation of density functional theory (DFT) is widely accepted to be a major development.2–9 DFT provides a suitable theoretical alternative to ab initio wave-function based electronic structure methods albeit at a much cheaper computational cost. It is a well-established fact that for a system comprising N electrons and bound by an external potential v(r), the Hamiltonian (Ĥ) is completely defined by v(r) and N. Upon solving the Schrodinger equation for a known H, the many-electron wave function ψ(r1, r2…rN) could be obtained which can provide all the information about the system under consideration. The single-particle density ρ(r) could be obtained upon performing integration over the coordinates of (N − 1) electrons,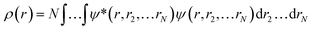 | (1) |
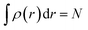 | (2) |
Therefore, it is evident that there exists a mapping in between v(r) and ρ(r). In the presence of an inverse mapping between ρ(r) and v(r), ρ(r) can determine v(r) which in turn can help to determine H and thus the many-electron wave function. Therefore, all the properties of the system could be evaluated. Hohenberg and Kohn4 proved that there indeed exists an inverse mapping between ρ(r) and v(r), thus paving the way to develop and interpret chemical processes based on DFT. Since ρ(r) is a 3 dimensional quantity as opposed to the many-electron wave-function, it is convenient to visualise and provide chemically intuitive interpretations of various processes under consideration.9 On the other hand, ρ(r) can help to provide classical interpretation of quantum mechanical processes. It is also possible to develop various theoretical models by making use of ρ(r). In this regard, conceptual density functional theory (CDFT), originally developed by Parr and collaborators,9–16 constitutes a prominent theoretical framework, where ρ(r) is utilised to define several reactivity descriptors, based on which chemical processes are interpreted and understood. The reactivity of a system is basically its potential to react to an action. It measures the response of the system when acted upon by a perturbation caused by another reactant, a reagent, catalyst, solvent, external electric/magnetic field, confinement, change in temperature/pressure, etc. As the Hamiltonian of the system is totally characterized by the number of electrons and the external potential, the variation in energy or density by changing N and/or v(r) is utilised in understanding reactivity. In order to better understand the conceptual genesis of Parr's theoretical formulations, one needs to consider the second Hohenberg–Kohn theorem. According to the second Hohenberg–Kohn theorem,4 the energy functional E[ρ] attains the minimum value for the true N-electron density for a given N and v(r) at the electronic ground state. Therefore, the density ρ(r) could be obtained via the variational optimization of the following Euler–Lagrange equation:
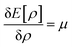 | (3) |
Herein, μ is the Lagrange multiplier associated with the normalization constraint (eqn (2)) and it is classified as the electronic chemical potential. Parr and co-workers proved that there exists a connection between μ and the thermodynamic chemical potential within a grand canonical ensemble at the zero temperature limit.17,18 Furthermore, it was proposed that μ is the negative of electronegativity (χ), which helped to establish a direct connection with chemical reactivity.17 One can consider the atoms in a molecule as a part of a grand canonical ensemble. In such a framework, the change in electron density could be analysed via DFT. At the electronic ground state, E[ρ] attains the minimum value. At a finite temperature for such a set of densities, the equilibrium state is characterized via the minimum Helmholtz free energy A[ρ] and grand potential functionals Ω[ρ] within the framework of canonical and grand canonical ensembles, respectively. The ground electronic state could be conceived as the zero temperature limit of the equilibrium state.9 These concepts lie at the heart of the formulation of CDFT. Since chemical reactions accompany the change and reorientation of electron densities, several global and local reactivity descriptors could be defined within the premise of CDFT, which in turn can help to understand various physicochemical processes.20,21 The backbone of CDFT is formed by these reactivity descriptors and associated electronic structure principles. The purpose of this review article is to introduce the general scientific community to these principles. Therefore, we do not intend to reiterate mathematical derivations and subtle technical issues within this article as exhaustive accounts are already available on these issues. Rather, the focus of this article is to highlight where and how one can employ these concepts to better understand a given chemical process. In the following sections of this article, we hope to outline the basic principles of CDFT and highlight various applications in static as well as time-dependent situations.
2. Global reactivity descriptors
As mentioned before, the Hamiltonian for a given system gets fixed upon specifying N and v(r). If a given system transforms from the ground electronic state to another, the energy change (up to the first order) associated with that process could be expressed as follows:9,19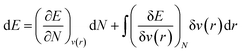 | (4) |
Making use of the Euler–Lagrange equation for a fixed v(r), one can arrive at the following expression:
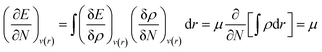 | (5) |
Herein, the Lagrange multiplier μ (electronic chemical potential) could be correlated with the corresponding thermodynamic quantity measuring the escaping tendency of an electron.9 Upon considering a finite difference approximation to eqn (5), one can arrive at the following expression:
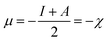 | (6) |
Here, χ, I and A represent the Mulliken electronegativity, ionization potential and electron affinity, respectively. Therefore, a direct connection with chemical reactivity could be established via this formulation. Upon employing further approximation by making use of Koopmans' theorem, one can arrive at the following expression:22,23
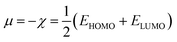 | (7) |
Therefore, it is possible to express χ in terms of the energies of the lowest unoccupied (ELUMO) and highest occupied (EHOMO) molecular orbitals. These quantities, i.e., χ and μ, are termed global reactivity descriptors as they can help to shed light on the reactivity of atoms, molecules and ions. Pearson introduced the concept of Hardness (η) within the premise of the hard–soft acid–base principle24,25 and it could be expressed as follows:26
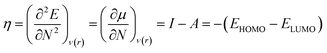 | (8) |
Softness (S)27 could be expressed as the reciprocal of hardness as follows:
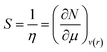 | (9) |
In general, the hardness of a system is associated with low polarizability as well as magnetizability. Parr et al. defined the electrophilicity index (ω)28,29 as follows:
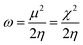 | (10) |
Here, ω is the measure of electrophilic power (bearing resemblance to classical electrostatics (=V2/R), where μ and η act as the potential (V) and resistance (R) respectively) of a system. Due to the discontinuity in energy versus N curves,18,30 different definitions for the aforementioned quantities exist for the cases of charge acceptance and depletion.31,32 Despite the limitations within the definitions of these quantities owing to the problem of this discontinuity, one can invoke the concept of atoms-in-a-molecule within the premise of a grand canonical ensemble at the zero temperature limit33–39 in order to alleviate any inconsistencies.37–40 Furthermore, one can also consider the isolated chemical entity as part of a larger system so that the aforementioned limitations in the definitions of the global reactivity descriptors could be eradicated.37–40 It should be noted that these global reactivity descriptors could be used to describe the reactivity as well as the stability of a given chemical entity. In order to understand the site selectivity, several local reactivity descriptors are defined, which will be mentioned in the following section.
3. Local reactivity descriptors
In order to understand the activity of a specific atomic site within a molecule, several local reactivity descriptors were developed by the researchers. Electron density itself is the most fundamental local reactivity descriptor and we can denote it as follows: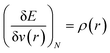 | (11) |
Drawing inspiration from the spirit of Fukui's frontier orbital theory,41,42 the Fukui function was developed and defined as follows:43,44
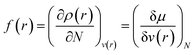 | (12) |
The Fukui function follows the normalization condition like the electron density. It also follows a cusp condition.45–47 Owing to the discontinuity in the electron density versus N curves, several Fukui functions are defined for different chemical reactivity situations (electrophilic, nucleophilic and radical attacks, respectively).43,44 One can employ the frozen core approximation in conjunction with a finite difference approximation, in order to arrive at the following expressions for the Fukui function for different chemical reactivity situations:
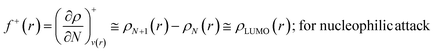 | (13) |
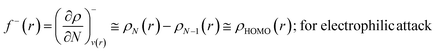 | (14) |
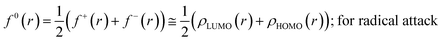 | (15) |
It could be seen from the aforementioned expressions that a direct connection could be drawn with Fukui's frontier orbital theory by defining the Fukui functions in this manner as these quantities are functions of frontier orbital density. The Fukui function assumes a rather large value in the cases where electron transfer is energetically favourable. In such situations, a concomitant large variation in the values of μ is observed thereby signifying greater chemical reactivity. In order to make these aforementioned quantities more convenient for chemical interpretations, the concept of atoms-in-a-molecule could be invoked and upon employing these formulations, one can arrive at the following condensed-to-atom variants of these quantities:48
| fK+ = qK(N + 1) − qK(N); for nucleophilic attack | (16) |
| fK− = qK(N) − qK(N − 1); for electrophilic attack | (17) |
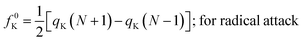 | (18) |
Here, qK represents the electron population of the atom within a molecule. In order to compute qK, one could carry out Mulliken population analysis or Hirshfeld population analysis. It was shown that while using the Mulliken population analysis, the values of the Fukui functions could turn out to be negative.49–51 So in general, Hirshfeld population analysis49–51 is usually performed in order to calculate qK, which is positive in most cases and thus the Fukui functions. There are, however, situations where negative Fukui functions are qualitatively important to decipher the nature of some chemical processes.52–55
We note, however, that these local reactivity descriptors are poor intermolecular reactivity descriptors even though they could be useful in order to decipher the intramolecular reactivity. When two molecules interact with each other in the long range, the concerned molecules cannot ‘sense’ the local reactivity variations in each other. At long intermolecular separations, primarily electrostatic interactions dictate the intermolecular interactions as compared to the orbital interactions. In these situations, instead of the Fukui functions, one could utilize other reactivity descriptors such as local softness sα(r)56 as well as philicity ω(r).57 By making use of the resolution of the identity associated with the normalization conditions for the Fukui functions, researchers have arrived at the following expressions for these two quantities:56,57
| sα(r) = Sfα(r); α ≡ −, +, 0 | (19) |
| ωα(r) = ωfα(r); α ≡ −, +, 0 | (20) |
Condensed-to-atom variants for the aforementioned quantities were also developed and they are expressed as follows:
| skα = SfKα; α ≡ −, +, 0 | (21) |
| ωkα = ωfKα; α ≡ −, +, 0 | (22) |
It has been shown that philicity could be utilized to understand nucleophile–electrophile interactions, whereas local softness can describe soft–soft interactions quite well. It was shown that one can arrive at the group quantities by summing over all condensed-to-atom quantities over the group of corresponding atoms.58,59 The various local reactivity descriptors such as sα(r), ωα(r), ρ(r) and f(r) could be evaluated by following appropriate variational methods.
Attempts have been made to define a local variant of hardness under certain conditions.60–62 Because of the inter-dependence of v(r) and ρ(r) within the premise of DFT, ambiguities arise63–65 for the simultaneous definition of local hardness and local softness when local hardness is described as follows:66,67
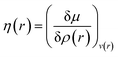 | (23) |
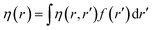 | (24) |
The hardness kernel could be expressed in the following way:
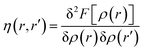 | (25) |
Here, F[ρ(r)] is the Hohenberg–Kohn universal functional. It should be noted that η(r) provides a measure of nuclear reactivity, whereas s(r) gives an estimate for the electronic reactivity.68,69
In addition to the aforementioned quantities, several other local reactivity descriptors are also utilized. Prominent examples among them include the gradient (∇ρ(r)) and Laplacian (∇2ρ(r)) of electron density,70 quantum potential,71,72 electron localization function,73 molecular electrostatic potential,74–77 multiphilic descriptor (Δω(r)),78 dual descriptors (Δf(r)),79–81etc. A local temperature Θ(r) has been developed82–86 by making use of the density and kinetic energy density within the realm of an ideal gas kinetic energy density approximation. This quantity has been also defined in the cases of time dependent situations as well as in the cases of the excited states having non-vanishing current density.87–91 Even though a condensed-to-atom variant of Θ(r) has been developed, such a condensation suffers from a mathematical drawback.92–98 As Θ(r) is non-linearly dependent on ρ(r), its condensation using the associated electron population becomes ad hoc. Attempts to define a local variant of hardness also suffer from this mathematical inexact formulation.99 Since all the aforementioned quantities ultimately depend on the employed density partitioning schemes, these quantities need to be employed with careful scrutiny in order to alleviate any unphysical behaviour. In general, during the course of hard–hard interactions, atomic charge dictates100 the nature of interaction and thus reactivity. Therefore, in such situations, local reactivity descriptors based on atomic charges can describe the reactivity quite well.101,102 On the other hand, when the nature of interaction is dominated by frontier orbitals which happens to be the case in the instances of soft–soft interactions, one could employ descriptors such as the Fukui function48 or the inter-molecular variants like s(r) and ω(r).
The aforementioned reactivity descriptors often obey some electronic structure principles. Thus, these reactivity descriptors are utilized in conjunction with these electronic structure principles. In the following sections, we intend to describe these principles, which in concomitance with the reactivity descriptors form the backbone of CDFT.
4. Electronic structure principles
The concept of electronegativity was introduced by Pauling.103 It measures the relative propensity of the electron donation or acceptance capacity of two interacting moieties. It has been argued that during the course of flow of electrons between two interacting moieties, the process continues until their electronegativity values get equalized.104–107 This is stated as Sanderson's electronegativity equalization principle. According to this principle, the final molecular electronegativity tends to equal the geometric mean of the electronegativity values of constituent atoms at the isolated state. During the course of formation of a complex such as X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y, from an acid X and base Y, the extent of charge transfer (ΔN) and energy change (ΔE) could be expressed as follows:26
Y, from an acid X and base Y, the extent of charge transfer (ΔN) and energy change (ΔE) could be expressed as follows:26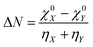 | (26) |
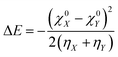 | (27) |
The aforementioned equations were originally proposed by Parr and Pearson. Since then, these equations have been invoked in various different contexts. These equations were utilized while seeking an analytical proof for the hard–soft acid–base principle (HSAB).108–116 They were also used while defining an electrophilicity index.117–119 However, this approach fails to take into account important factors such as entropy and solvent effects, electrostatic interaction, etc. and relies heavily on the effect of charge transfer.120 This approach also suffers from the derivative discontinuity problem.46–49 In order to alleviate these issues, efforts have been made by recasting this problem within the framework of a grand canonical ensemble.33–39 Statistical mechanical apparatus may be properly exploited in defining reactivity descriptors at a finite temperature.9 For example, the softness can alternatively be defined in terms of number fluctuations.56 It is to be noted that in order to overcome the derivative discontinuity problem in the energy functional (E[N, v]), the incorporation of temperature within the definition of E[N, v] was considered by Franco-Perez, Ayers, Gázquez and Vela.121–123 Within this approach, the premise of CDFT moves from the realm of canonical to a grand-canonical ensemble.33–39 Within the premise of temperature dependent CDFT, the average electronic energy and its derivatives become the crucial component. Due to the incorporation of finite temperature effects, the deviations in the various response functions are negligible from their zero temperature counterparts (within the temperature independent formulation). In addition, within the premise of temperature dependent CDFT, quantities like heat capacity (and its local variant) could be defined.122 Thus, energy transfer processes could be studied by making use of temperature dependent CDFT. The thermodynamic hardness and dual descriptor could also be defined by following temperature dependent CDFT.123 These constitute important formal developments in CDFT.
In addition to the difference in electronegativity, the hardness sum is also an important quantity which can help to understand electron transfer processes. The hardness measures the reluctance of a chemical entity for electron transfer.26 As the value of ΔE is always negative irrespective of the direction of electron transfer within a molecule, one needs to consider the ΔN values in order to understand the direction of the electron flow. In the cases of local reactivity descriptors, the condensed-to-atom variant of the Fukui function could be utilized in order to understand the direction of electron transfer.
In order to better understand the reactivity of a system, one needs to consider the concept of hardness as well, as electronegativity alone cannot describe the reactivity of chemical moieties. The concept of hardness was proposed by Pearson24,25 and the utility of this concept was demonstrated while trying to explain the nature of acid–base reactions through his HSAB principle as follows: “Hard acids prefer to coordinate with hard bases and soft acids prefer to coordinate with soft bases for both their kinetic and thermodynamic properties.” By following the definition of hardness viaeqn (8), the hard–soft nature of a large number of acids and bases could be corroborated nicely with available experimental trends. An important electronic structure principle concerning the hardness is termed the maximum hardness principle (MHP).124–130 According to the MHP, the following statement could be stated: “There seems to be a rule of nature that molecules arrange themselves so as to be as hard as possible.” There exist a number of processes where the validity of the MHP has been computationally proven. A few representative examples include the cases of various chemical reactions,131 molecular vibrations as well as internal rotations,132–137 Woodward–Hoffmann rules,138,139 time dependent situations,140 aromaticity,141 chaotic ionization from Rydberg states,142etc.
In view of the less magnetizability and polarizability of hard systems, two additional electronic structure principles namely the minimum magnetizability principle (MMP) and minimum polarizability principle (MPP) are formulated. According to the MPP,143 the following could be stated: “The natural direction of evolution of any system is towards a state of minimum polarizability (α)” whereas the MMP states that144,145 “A stable configuration/conformation of a molecule or a favourable chemical process is associated with a minimum value of the magnetizability (ξ).”
By making use of the η and μ values, the extremum values of electrophilicity (ω) could be calculated.146–148 It has been proposed that a minimum electrophilicity principle (MEP) might be operative in several cases.149–152 By drawing comparison with classical electrostatics, it has been argued153 that the MEP is inherently defined within the Maynard-Parr definition of ω. During the course of chemical reactions, extrema of ω occur at points where the following condition is satisfied:146–148
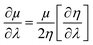 | (28) |
Herein, λ could be either a reaction coordinate for a chemical reaction or some internal degree of freedom for the cases of vibration or internal rotational processes. We note that η is always positive and μ is always negative because of the convex nature of energy. Therefore, electrophilicity achieves the extremum value, when the dependencies of η and μ on λ are opposed.
In addition to the aforementioned principles, it might be prudent to mention how the concept of entropy is defined and utilized within the realm of DFT. Considering an N electron system and assuming that it consists of N non-interacting particles under the influence of an effective potential veff(r,t), entropy density in a time-dependent situation is formulated within an average density framework as follows:87,154
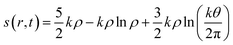 | (29) |
Herein, k is the Boltzmann constant, whereas θ represents a space-time dependent ‘temperature’. In order to define θ, the kinetic energy density is utilized as follows:
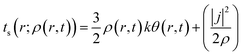 | (30) |
Here, j represents the current density. We note that by making use of information theory, one can arrive at eqn (29) as well. To this end, the Shannon entropy for the system could be expressed in terms of the density of the system and one could maximize it under certain constraints in order to arrive at eqn (29). The global entropy could be obtained by integrating eqn (29) over the whole space as follows:
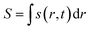 | (31) |
In several time-dependent situations, it was shown that in the cases where the processes are favourable, the entropy gets maximized and a maximum entropy principle remains operative in such situations.142,143 It should be noted that within the realm of CDFT, concepts derived from information theory155 could be utilized and suitable descriptors could be defined to provide several important insights. To this end, the utilization of information theory has provided physical insights into atoms-in-molecule theory.156 It has been shown that Shannon entropy, when expressed as a functional of ρ(r), can on its own describe coulombic moieties.157 The implication of this observation is profound. It could be argued that the Shannon entropy could turn out to be as important as ρ(r) and it could be utilized to explain several chemical processes. In this context, several other density functionals are also defined such as Onicescu information energy,158 Fisher information159 and Renyi entropy.160 The Kullback–Leibler information measure also contains meaningful information.89 Several important insights have been provided into many physicochemical processes (such as the steric effect, aromaticity, etc.) by employing these concepts.161–165 The information conservation principle could be utilized to quantify important reactivity descriptors such as electrophilicity, nucleophilicity and regioselectivity.
There are several reactions associated with a change in spin multiplicity. Spin dependent reactivity descriptors have been derived.166–168 The above-mentioned quantities are separately defined for up and down spins. Related chemical potential, spin potential and different types of hardnesses are made use of.
5. Reactivity descriptors within time dependent situations
Runge and Gross showed169 that it is possible to extend DFT as developed by Hohenberg and Kohn, to time-dependent situations. They proved that there exists a one-to-one correspondence between the time-dependent external potential vext(r,t) and time-dependent density ρ(r,t) in the cases of a many-electron moiety evolving from a given initial state. All the time dependent properties of a given system are unique functionals170 of time-dependent density ρ(r,t) and the current density j(r,t). The set of time dependent Kohn–Sham equations could be expressed as follows: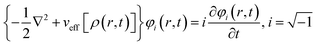 | (32) |
Here,
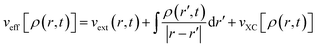 | (33) |
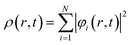 | (34) |
Inspired by the work of Madelung on quantum fluid dynamics,171 a different route could be considered in order to evaluate ρ(r,t) and j(r,t). This approach is termed quantum fluid density functional theory (QFDFT).87–89 Within this framework, a generalized nonlinear Schrodinger equation (GNLSE) is solved to study the temporal evolution of a system and this GNLSE could be expressed as follows:
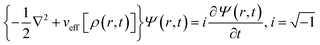 | (35) |
Here,
| Ψ(r,t) = ρ1/2(r,t)exp(iξ(r,t)) | (36) |
| j(r,t) = [Ψre∇Ψim − Ψim∇Ψre] = ρξ | (37) |
It should be noted that the Hohenberg–Kohn theorems have been further developed in order to incorporate the effects of external electric and magnetic fields.172 In this formulation, the kinetic energy operator, within the time dependent Kohn–Sham equations, would include a term arising from the vector potential. Furthermore, j(r,t) and veff[ρ(r,t)] would include terms arising from both vector and scalar potentials. These additional terms arise in order to incorporate the effects of external time-dependent electric and magnetic fields. These additional terms are also taken care of within the QFDFT framework.
The time dependent variants of both global and local reactivity descriptors could be defined so that these quantities could be evaluated within the time dependent scenario.143,173 To this end, the chemical potential μ(t) could be defined by making use of j(r,t) and ρ(r,t) within eqn (3). One, however, needs to define a suitable time-dependent energy functional. Time-dependent hardness η(t) could be calculated via the time-dependent variants of eqn (23)–(25). Therefore, it becomes possible to evaluate the time-dependent electrophilicity ω(t) by making use of η(t) and μ(t) viaeqn (10).
Having outlined the basics of CDFT, in the following sections we intend to provide an overview of processes where CDFT turns out to be very useful in understanding various physicochemical processes.
6. Electronic structure principles under special conditions
Before we describe the utility of CDFT in understanding several special physicochemical processes, it might be prudent to briefly state a few general trends vis-à-vis chemical reactivity as observed within the purview of CDFT. Firstly, we consider the case of reactivity of atoms across the periodic table. In general, along a given period, hardness increases whereas it decreases along a given group.174 This fact is in conformity with the MHP. Similarly, electrophilicity,175 polarizability175 and magnetizability144,145 increase along a group whereas the values of these quantities decrease along a period. These facts are in accordance with principles such as the MEP, MMP and MPP. Therefore, the utility of global reactivity descriptors in explaining chemical reactivity becomes quite evident from the aforementioned facts. One can utilize the radial distribution function of philicity,176i.e., 4πr2ω(r), in order to retrieve the characteristic features of the electronic shell structure much like the plot of 4πr2ρ(r). One can define the following cusp condition for ω(r) from that of f(r). We note that for all r in a molecule, ω remains a constant and thus the following equation could be derived:45,46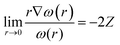 | (38) |
Utilizing eqn (38), one could construct a map of ω(r), which in turn can help to find the nuclei within a molecule as well as the loci of atoms and thus help to shed light on the atoms-in-molecule picture.
Similarly, global and local reactivity descriptors could be utilized to understand the change in reactivity and stability associated with the changes in molecular vibration and internal rotation. We note that due to the changes in molecular vibration and internal rotation, the electron density distribution within a molecule also changes. In general,132–136 within a minimum energy configuration and/or conformation, the hardness value becomes maximum, whereas polarizability tends to attain the minimum value. In a number of cases, electrophilicity attains the minimum value in the corresponding situations. In order to understand the nature of the extremals in ω, one may consider the characteristics of the first and second order derivatives of this quantity with respect to a generalized reaction coordinate (λ).146–148 One can differentiate both sides of eqn (10) with respect to λ as follows:
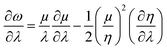 | (39) |
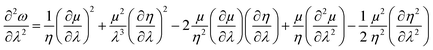 | (40) |
One could infer from the expressions stated above that ω would be an extremum when η and μ attain the respective extrema. Even though this criterion is a sufficient condition, it does not always have to be a necessary condition. During the course of molecular vibrations and internal rotations, the local reactivity descriptors also exhibit characteristic oscillations.133–136
In order to analyse the reaction between an electrophile and nucleophile, one can utilise local and global electrophilicities. An electrophile would have a larger ω value as compared to a nucleophile and as a result of this difference, they will be drawn towards each other. Once these moieties come in close proximity to one another, several other local reactivity descriptors could be utilized to understand the nature of interaction between them. It should be noted that during the course of the interaction between the electrophile and nucleophile, the sites having the largest local electrophilicity and nucleophilicity values would primarily dictate the process. Since 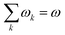 , local philicity values at the concerned atomic sites govern the corresponding global reactivity trend.
, local philicity values at the concerned atomic sites govern the corresponding global reactivity trend.
In order to analyse the nature of cycloaddition reactions, CDFT based reactivity descriptors have been utilized by several research groups. To this end, the difference in electrophilicity (Δω) between a diene and a dienophile could be employed. It has been suggested177–179 that in the cases when the Δω is small between a diene–dienophile pair, the reaction mechanism follows a concerted pathway, and that the reaction could be primarily understood by considering the properties of the concerned frontier orbitals. Therefore, these types of reactions occur as a result of soft–soft interactions. In the cases when the Δω is large for a diene–dienophile pair, the reactions proceed via a polar and step-wise mechanism. These reactions are primarily charge-controlled and thus could be classified as an example of hard–hard interactions. These trends could be understood by employing philicity also.180 Electrophilicity has been utilized in order to understand the salient features of acidity/basicity concepts as defined by the Lewis and Brønsted–Lowry models.181,182 Similarly, electrophilicity has been employed in order to understand several concepts prevalent in organic chemistry, details of which could be found elsewhere.20 We state another prominent example where the utility of the electrophilicity concept could help to elucidate many facets of organic reactions. Maynard and co-workers showed28 that there exists a connection between electrophilicity and kinetic behaviour. Thus, this concept could be employed to understand chemical kinetics. Parr et al. developed29 the concept of electrophilicity by employing an energy minimization criterion. Therefore, one could gain insights into the thermodynamic stability of a given system under consideration. In this context, the variations in electrophilicity along the intrinsic reaction coordinate (IRC) of several reactions have been analysed in great detail.146–148 In these cases, the minimum electrophilicity principle remains operative. In order to understand this observation, one could make use of eqn (39) and (40). For the minimum energy configurations, the following conditions hold: 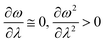 , whereas for the transition states the corresponding conditions could be stated as follows:
, whereas for the transition states the corresponding conditions could be stated as follows: 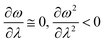 .
.
Local reactivity descriptors demonstrate opposite trends for bond breaking and bond making processes. They tend to intersect at some point along the IRC, in the cases of several reactions.140,141 In the cases of thermoneutral reactions, these intersection points coincide with the saddle points within the potential energy surfaces. Therefore, by employing the outlined method, one can locate the transition states. In accordance with a reactivity based Hammond's postulate, the intersection points succeed the transition states in the cases of exothermic reactions, whereas these points precede the transition states in the cases of endothermic reactions.183,184 In a number of exothermic reactions, it has been proven151–153 that the least electrophilic moiety lies in the product side. The average electrophilicity value generally decreases in these cases as we move from the reactant to the product's end. This observation could be classified as an outcome of the MEP. In general, for a favourable reaction, the ΔηProduct−Reactant value should be a positive quantity, whereas Δα,E,ωProduct−Reactant should be a negative quantity.185–187
6.1. Change in chemical reactivity indices in the presence of solvents
Since the reactivity of systems varies as we move from a gas phase to a solution phase, it is extremely important to know how the CDFT based reactivity descriptors behave in such situations. Lipinski and co-workers considered a homogeneous polar medium using a virtual charge based model in order to understand the changes in the hardness and electronegativity of some bonded moieties.188 They have showed that upon increasing the solvent polarizability, the hardness of ions decreases, whereas the electronegativity increases and decreases, respectively, in the cases of anions and cations. However, the molecular level hardness and electronegativity exhibited only minor variations as a function of the solvent effects. According the models considered by Pearson189 in the cases of hydration, neutral molecules become less hard upon solvation. Anions and cations, on the other hand, become poorer electron donors and acceptors (so more and less electronegative, respectively) respectively upon hydration. Sivanesan et al.190 analysed the changes in the Fukui function in going from a gas to a water solvent phase in the cases of several organic molecules and they showed that in general the propensity of nucleophilic and electrophilic attacks increases in moving from a gas to a solvent phase. The change in electrophilicity upon solvation was analysed in several studies.191–194 It has been suggested that solvation enhances the electrophilic power of neutral electrophilic moieties, whereas the opposite effect seemingly operates in the cases of charged and ionic electrophiles. Upon solvation, the insertion energy could be approximated by the changes in Δη and Δμ. While the former was shown to be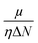 times the solvation energy, the latter quantity was shown to be twice the solvation energy. Therefore, the changes in electrophilicity are linearly correlated with the solvation energy. The global electrophilicity is much more sensitive to solvation effects as compared to its local counterpart and thus it could be utilized to understand changes in chemical reactivity.
times the solvation energy, the latter quantity was shown to be twice the solvation energy. Therefore, the changes in electrophilicity are linearly correlated with the solvation energy. The global electrophilicity is much more sensitive to solvation effects as compared to its local counterpart and thus it could be utilized to understand changes in chemical reactivity.
6.2. Change in chemical reactivity indices in the presence of an external field
In order to understand how a many-electron system behaves in the presence of an external perturbation, both perturbative and variational methods were adopted.195–198 We note that the external perturbation might originate from the presence of another molecule or one could utilize electromagnetic radiation in order to perturb the system under consideration. Numerical results199 have shown that ω and μ are much more prone to getting affected by some external field as compared to η. Local reactivity descriptors are much more susceptible to changes as a function of the strength of the external fields as compared to their global counterparts.QFDFT87,88 has been utilized extensively in order to understand the changes in CDFT reactivity descriptors as a function of external perturbation. The temporal evolution of reactivity descriptors has been analysed therein. In the presence of a low-intensity field, in-phase oscillations in the time evolution of μ have been observed, whereas one needs to employ a much higher intensity field in order to observe analogous behaviour in the case of η.199 The competition between the axial external field and spherical nuclear Coulomb field could be nicely demonstrated with this approach. Furthermore, the chaotic dynamics of Rydberg atoms in the cases of ionization was analysed in these studies.142
In addition to external fields, ion-atom collision dynamics was also analysed within the QFDFT framework. We highlight only the salient features herein.200 The time dependent μ-profile clearly demonstrates the three scattering regions during the course of the reactive collisions. It was shown that the hardness is maximized and the polarizability is minimized in the interaction region. These results are in accordance with the time dependent variants of the MHP and MPP. The changes in ω resembled the corresponding case of μ. Herein, the MEP was not observed to be operative in the sense that we have discussed in the preceding sections in the cases of static situations. The time dependent variant of the HSAB principle was proven in these studies. Insight was provided into the regioselectivity of some reactions as well.
6.3. Change in chemical reactivity indices in a confined environment
Confined quantum systems exhibit fascinating changes in their physicochemical properties as compared to their counterparts in the free state, details of which could be found elsewhere.201–212 In order to understand the effect of confinement on the reactivity of atoms and ions, the Hartree–Fock–Slater equation has been considered in order to obtain a self-consistent field (SCF) electronic wave function. In order to impose the effect of confinement, Dirichlet boundary conditions have been imposed on the electronic wave function. The CDFT based reactivity descriptors have been analysed from this SCF wave function.206,207 As one imposes the effect of confinement, systems become harder. The polarizability decreases monotonically as the confinement radius is reduced. It is suggested that electronegativity is not very sensitive to the effect of confinement. In the case of ω, a similar behaviour has been noted. It is suggested that as we keep increasing the effect of confinement, systems tend to become less polarizable and harder. Under these conditions, systems also become more difficult to excite.Utilizing the theoretical framework of QFDFT, simultaneous effects of confinement and electronic excitations have been analyzed.208–212 Upon increasing the degree of confinement, hardness increases both in the ground and the excited electronic states. Polarizability decreases as compared to the free atom due to the effect of confinement. As expected from the MPP, in both confined as well as unconfined states, the excited state polarizability is higher as compared to that in the ground state. Chattaraj et al. proved the validity of the HSAB principle in the cases of atoms and hydrogen molecules exposed to an external magnetic field in the confined state.
In order to show some representative plots for the time evolution of some reactivity descriptors discussed above during the course of atom–field interaction as well as during collisional processes, we have presented Fig. 1–5 for the purpose of illustration.
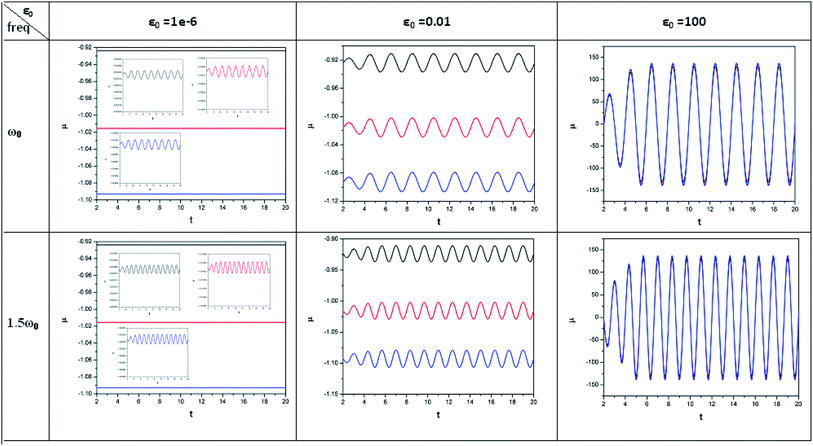 | ||
| Fig. 1 Time evolution of chemical potential (μ, in a.u.) when a helium atom in the ground state is placed in an intense laser field (amplitude = 10−6, 0.01 and 100 a.u.). Black line (length of the cylinder = 6 a.u.) represents the unconfined system, and red line (length of the cylinder = 4.8 a.u.) and blue line (length of the cylinder = 4.2 a.u.) represent confined systems (radius of the cylinder = 4.2025 a.u.); ω0 = π. (Reproduced from ref. 208 with permission from the [PCCP Owner Societies] copyright [2012]). | ||
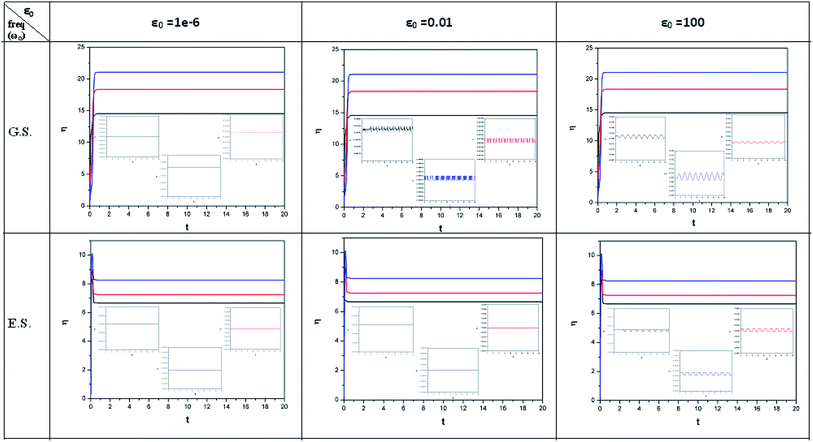 | ||
| Fig. 2 Time evolution of chemical hardness (η, in a.u.) when a helium atom in the ground state (G.S.) and excited state (E.S.) is placed in an intense laser field. See the Fig. 1 caption for further details (reproduced from ref. 208 with permission from the [PCCP Owner Societies] copyright [2012]). | ||
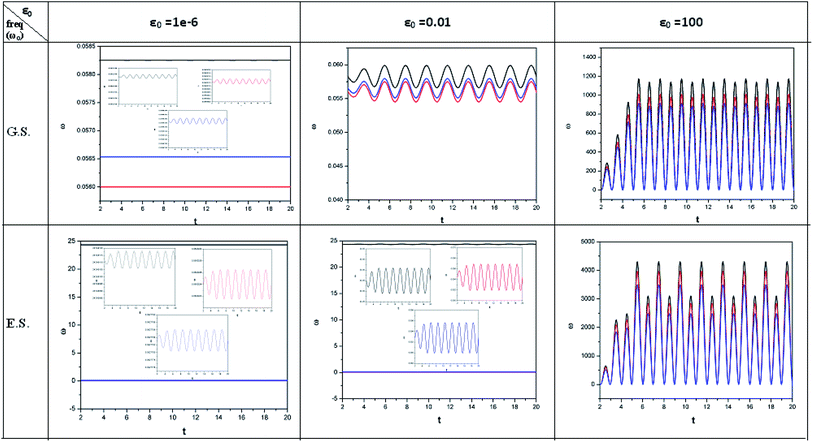 | ||
| Fig. 3 Time evolution of the electrophilicity index (ω, in a.u.) when a helium atom in the ground state (G.S.) and excited state (E.S.) is placed in an intense laser field. See the Fig. 1 caption for further details (reproduced from ref. 208 with permission from the [PCCP Owner Societies] copyright [2012]). | ||
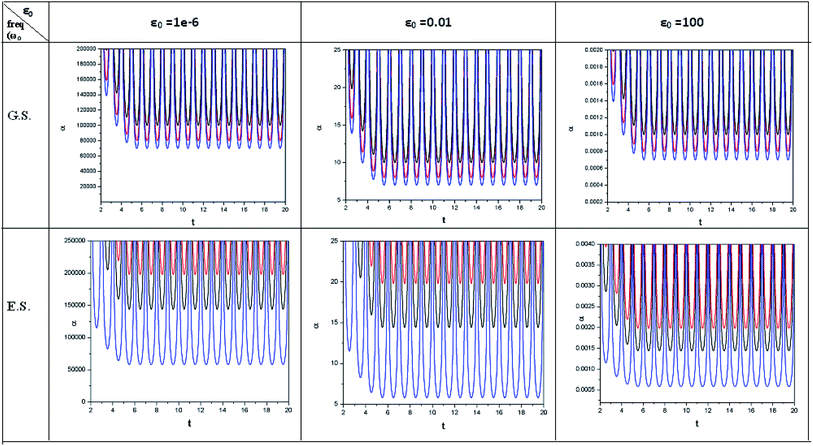 | ||
| Fig. 4 Time evolution of polarizability (α, in a.u.) when a helium atom in the ground state (G.S.) and excited state (E.S.) is placed in an intense laser field. See the Fig. 1 caption for further details (reproduced from ref. 208 with permission from the [PCCP Owner Societies] copyright [2012]). | ||
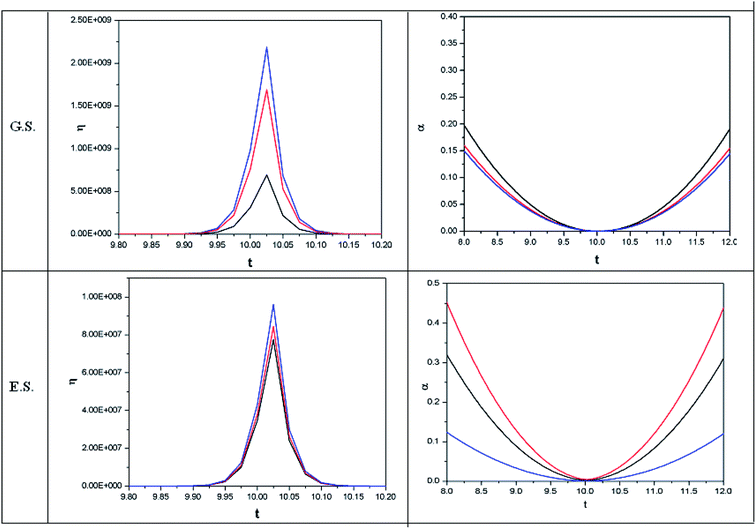 | ||
| Fig. 5 Time evolution of hardness (η, in a.u.) and polarizability (α, in a.u.) during a collision process between a proton and helium atom in the ground state and excited state. See the Fig. 1 caption for further details (reproduced from ref. 208 with permission from the [PCCP Owner Societies] copyright [2012]). | ||
Several important insights have been provided by Morell and co-workers on the excited state properties of several chemical systems as well.213,214
6.4. Change in chemical reactivity indices upon electronic excitation
As any system becomes more reactive upon excitation, it is expected from the MHP and MPP that it will be softer and more polarizable in its excited state than in the ground state. It has been explicitly demonstrated to be the case in the case of atoms, molecules and ions.215,216 In a two-state ensemble also systems become softer and more polarizable when the contribution from the excited state increases in the complexion of this ensemble.215,216 A favorable collision occurs when a hard projectile hits a target in its ground state rather than in the excited state where it is softer and more polarizable, as is expected from the HSAB principle.200 These features are valid in a confined environment as well and a suitable choice of simultaneous application of confinement and excitation during ion–atom collision and atom–field interaction can bring back the ground state behavior of a corresponding free state.208,209,217 As electrophilicity is a composite reactivity descriptor, it shows the validity of the MEP when both chemical potential and hardness behave properly. It has been argued that the excited state reactivity may be understood by analyzing the change in the electron density distribution upon electronic excitation218,2196.5. Quantitative structure–toxicity relationship
Electrophilicity and its local counterpart have been shown to be important descriptors of cytotoxicity.220–223 A small number of descriptors can provide robust quantitative structure–toxicity relationship (QSTR) models. A multiple linear regression analysis has also highlighted that when they are used in conjunction with other popular descriptors like hydrophobicity, useful QSTR models are generated which in turn will help screening the initial drug targets saving time and money. The robustness of the models is analyzed by employing multilayer perceptron neural networks.224,2256.6. Aromaticity
The relative and absolute hardness could be utilized in order to understand the stability of aromatic molecules. In view of the fact that both hardness and aromaticity provide means to understand the stability and reactivity of a system, the correlation between them could be intriguing. Nucleus independent chemical shift (NICS)226 values could be utilized in order to understand the aromatic or anti-aromatic properties of a molecule. An aromaticity descriptor could be defined as follows:227Yaromatic = Ymolecule − Yreference; Y = E, α, ω, η. The reference molecule could be either the corresponding localized molecule or it could be a corresponding open chain system. Aromatic molecules possess a positive228,229ηaromatic value, whereas the other descriptors mentioned above possess negative values, according to the CDFT based electronic structure principles as discussed above. In the cases of anti-aromatic molecules, these trends are reversed. A number of all-metal and non-metal molecules and their aromatic behaviour have been analyzed by following these criteria.230–233 Aromaticity can drive a system towards its stable structure as can be understood through the dynamical variants of the CDFT based electronic structure principles.234 They are also helpful in understanding the aromaticity of compounds of multivalent superatoms.235 Recently, a similar approach has been adopted in explaining the stability of metal clusters.2367. Conclusion
Based on the discussions stated in this article, we can say that CDFT could be utilized in several physicochemical contexts. Global and local reactivity descriptors can help to shed light on stability, reactivity, dynamics, etc. Global reactivity descriptors are connected with several electronic structure principles and thus are very important. Local reactivity descriptors can help to provide insights into site selectivity. Despite a lot of computational evidence in support of CDFT, it is necessary, formally, to understand why and how CDFT works. To this end, more mathematical analysis is needed especially to highlight the domain of applicability of these electronic structure principles.237 This in turn can increase the predictive power of CDFT going beyond its usual interpretive value.Author contributions
PKC supervised all of the relevant research work emanating from his research group . He worked out the overall plan of this review article as well. DC wrote the first draft of this article.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
P. K. C. thanks DST, New Delhi for the J. C. Bose National Fellowship (grant number SR/S2/JCB-09/2009) and his students and collaborators whose work is presented in this paper.References
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1929, 123, 714 CAS
.
- L. H. Thomas, Proc. Cambridge Philos. Soc., 1927, 23, 542 CrossRef CAS
.
- E. Fermi, Z. Phys., 1928, 48, 73 CrossRef CAS
.
- P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, 864 CrossRef
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef
.
- B. Y. Tong and L. J. Sham, Phys. Rev., 1966, 144, 1 CrossRef CAS
.
- T. Ziegler, Chem. Rev., 1991, 91, 651 CrossRef CAS
.
-
The Single Particle Density in Physics and Chemistry, ed. N. H. March and B. M. Deb, Academic Press, London, 1987 Search PubMed
.
-
R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989 Search PubMed
.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974 CrossRef CAS
.
-
P. W. Ayers and W. Yang, Density Functional Theory, in Computational Medicinal Chemistry for Drug Discovery, ed., P. Bultinck, H. de Winter, W. Langenaeker and J. P. Tollenaere, Dekker, New York, 2003, p. 571 Search PubMed
.
- R. G. Parr and W. T. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701 CrossRef CAS PubMed
.
-
P. K. Chattaraj and R. G. Parr, Density Functional Theory of Chemical Hardness, in Chemical Hardness, Structure and Bonding, ed., K. D. Sen and D. M. P. Mingos, Springer-Verlag, Berlin, 1993, p. 11 Search PubMed
.
-
P. K. Chattaraj, A. Poddar and B. Maiti, Chemical Reactivity and Dynamics within a Density-based Quantum Mechanical Framework, in Reviews In Modern Quantum Chemistry: A Celebration of the Contributions of Robert Parr, ed., K. D. Sen, World Scientific, Singapore, 2002, p. 871 Search PubMed
.
-
P. K. Chattaraj, S. Nath and B. Maiti, Reactivity Descriptors, in Computational Medicinal Chemistry for Drug Discovery, ed., J. Tollenaere, P. Bultinck, H. D. Winter and W. Langenaeker, Marcel Dekker, New York, 2003, p. 295 Search PubMed
.
- U. Sarkar and P. K. Chattaraj, J. Phys. Chem. A, 2021, 125, 2051 CrossRef CAS PubMed
.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801 CrossRef CAS
.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz Jr, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS
.
- S. K. Ghosh and B. M. Deb, Phys. Rep., 1982, 52, 1 CrossRef
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793 CrossRef CAS PubMed
.
-
Chemical Reactivity Theory: A Density Functional View, ed. P. K. Chattaraj, Taylor & Francis/CRC Press, Florida, 2009 Search PubMed
.
- R. G. Pearson, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8440 CrossRef CAS PubMed
.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef
.
-
R. G. Pearson, Chemical Hardness: Applications from Molecules to Solids, Wiley-VCH, Weinheim, 1997 Search PubMed
.
-
R. G. Pearson, Hard and Soft Acids and Bases, Dowden, Hutchinson & Ross, Stroudsberg, PA, 1973 Search PubMed
.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512 CrossRef CAS
.
- W. T. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723 CrossRef CAS PubMed
.
- A. T. Maynard, M. Huang, W. G. Rice and D. G. Covell, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11578 CrossRef CAS PubMed
.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922 CrossRef CAS
.
- P. W. Ayers, J. Math. Chem., 2008, 43, 285 CrossRef CAS
.
- P. W. Ayers and R. G. Parr, J. Am. Chem. Soc., 2000, 122, 2010 CrossRef CAS
.
- J. L. Gazquez, A. Cedillo and A. Vela, J. Phys. Chem. A, 2007, 111, 1966 CrossRef CAS PubMed
.
- E. P. Gyftopoulos and G. N. Hatsopoulos, Proc. Natl. Acad. Sci. U. S. A., 1965, 60, 786 CrossRef PubMed
.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS
.
- Y. K. Zhang and W. T. Yang, Theor. Chem. Acc., 2000, 103, 346 Search PubMed
.
- M. Franco-Perez, P. W. Ayers, J. L. Gazquez and A. Vela, J. Chem. Phys., 2017, 147, 094105 CrossRef PubMed
.
- M. H. Cohen and A. Wasserman, J. Phys. Chem. A, 2007, 111, 2229 CrossRef CAS PubMed
.
- P. K. Chattaraj, G. H. Liu and R. G. Parr, Chem. Phys. Lett., 1995, 237, 171 CrossRef CAS
.
- P. K. Chattaraj, A. Cedillo and R. G. Parr, Chem. Phys., 1996, 204, 429 CrossRef CAS
.
- A. Cedillo, P. K. Chattaraj and R. G. Parr, Int. J. Quantum Chem., 2000, 77, 403 CrossRef CAS
.
-
K. Fukui, Theory of Orientation and Stereoselection, Springer, Berlin, 1973 Search PubMed
.
- K. Fukui, Science, 1982, 218, 747 CrossRef CAS PubMed
.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049 CrossRef CAS
.
- P. W. Ayers and M. Levy, Theor. Chem. Acc., 2000, 103, 353 Search PubMed
.
- P. K. Chattaraj, A. Cedillo and R. G. Parr, J. Chem. Phys., 1995, 103, 7645 CrossRef CAS
.
- P. K. Chattaraj, A. Cedillo and R. G. Parr, J. Chem. Phys., 1995, 103, 10621 CrossRef CAS
.
- P. W. Ayers and A. Nagy, J. Chem. Phys., 2007, 126, 144108 CrossRef PubMed
.
- W. Yang and W. J. Mortier, J. Am. Chem. Soc., 1986, 108, 5708 CrossRef CAS PubMed
.
- D. E. P. Vanpoucke, P. Bultinck and I. Van Driessche, J. Comput. Chem., 2013, 34, 405 CrossRef CAS PubMed
.
- P. Bultinck, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed
.
- P. W. Ayers, R. C. Morrison and R. K. Roy, J. Chem. Phys., 2002, 116, 8731 CrossRef CAS
.
- P. W. Ayers, Phys. Chem. Chem. Phys., 2006, 8, 3387 RSC
.
- J. Melin, P. W. Ayers and J. V. Ortiz, J. Phys. Chem. A, 2007, 111, 10017 CrossRef CAS PubMed
.
- E. Echegaray, C. Cardenas, S. Rabi, N. Rabi, S. Lee, F. H. Zadeh, A. Toro-Labbe, J. S. M. Anderson and P. W. Ayers, J. Mol. Model., 2013, 19, 2779 CrossRef CAS PubMed
.
- E. Echegaray, S. Rabi, C. Cardenas, F. H. Zadeh, S. Lee, J. S. M. Anderson, A. Toro-Labbe and P. W. Ayers, J. Mol. Model., 2014, 20, 2162 CrossRef PubMed
.
- W. T. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723 CrossRef CAS PubMed
.
- P. K. Chattaraj, B. Maiti and U. Sarkar, J. Phys. Chem. A, 2003, 107, 4973 CrossRef CAS
.
- R. Parthasarathi, J. Padmanabhan, M. Elango, V. Subramanian and P. K. Chattaraj, Chem. Phys. Lett., 2004, 394, 225 CrossRef CAS
.
- F. De Proft, S. B. Liu and R. G. Parr, J. Chem. Phys., 1997, 107, 3000 CrossRef CAS
.
- M. K. Harbola, P. K. Chattaraj and R. G. Parr, Isr. J. Chem., 1991, 31, 395 CrossRef CAS
.
- P. K. Chattaraj, D. R. Roy, P. Geerlings and M. Torrent-Sucarrat, Theor. Chem. Acc., 2007, 118, 923 Search PubMed
.
- P. W. Ayers and R. G. Parr, J. Chem. Phys., 2008, 128, 184108 CrossRef PubMed
.
- T. Gal, Theor. Chem. Acc., 2012, 131, 1223 Search PubMed
.
- T. Gal, P. Geerlings, F. De Proft and M. Torrent-Sucarrat, Phys. Chem. Chem. Phys., 2011, 13, 15003 RSC
.
- R. Cuevas-Saavedra, N. Rabi and P. W. Ayers, Phys. Chem. Chem. Phys., 2011, 13, 19594 RSC
.
- M. Berkowitz, S. K. Ghosh and R. G. Parr, J. Am. Chem. Soc., 1985, 107, 6811 CrossRef CAS
.
- S. K. Ghosh and M. Berkowitz, J. Chem. Phys., 1985, 83, 976 Search PubMed
.
- F. De Proft, S. Liu and P. Geerlings, J. Chem. Phys., 1998, 108, 7549 CrossRef CAS
.
- B. G. Baekelandt, J. Chem. Phys., 1996, 105, 4664 CrossRef CAS
.
-
R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed
.
-
P. R. Holland, The Quantum Theory of Motion, Cambridge University Press, Cambridge UK, 1993 Search PubMed
.
-
Quantum Trajectories, ed. P. K. Chattaraj, Taylor and Francis, CRC Press, Florida, 2010 Search PubMed
.
- B. Silvi and A. Savin, Nature, 1994, 371, 683 CrossRef CAS
.
- J. S. Murray and P. Politzer, Theor. Chim. Acta, 1987, 72, 507 CrossRef CAS
.
- S. R. Gadre, S. A. Kulkarni and I. H. Srivastava, J. Chem. Phys., 1992, 96, 5253 CrossRef CAS
.
- A. M. Koster, C. Kolle and K. Jug, J. Chem. Phys., 1993, 99, 244 CrossRef
.
- G. Naray-Szabo and G. G. Ferenczy, Chem. Rev., 1995, 95, 829 CrossRef CAS
.
- J. Padmanabhan, R. Parthasarathi, M. Elango, V. Subramanian, B. S. Krishnamoorthy, S. Gutierrez-Oliva, A. Toro-Labbé, D. R. Roy and P. K. Chattaraj, J. Phys. Chem. A, 2007, 111, 9130 CrossRef CAS PubMed
.
- C. Morell, A. Grand and A. Toro-Labbé, J. Phys. Chem. A, 2005, 109, 205 CrossRef CAS PubMed
.
- C. Morell, A. Grand and A. Toro-Labbé, Chem. Phys. Lett., 2006, 425, 342 CrossRef CAS
.
- F. De Proft, P. W. Ayers, S. Fias and P. Geerlings, J. Chem. Phys., 2006, 125, 214101 CrossRef PubMed
.
- S. K. Ghosh, M. Berkowitz and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 8028 CrossRef CAS PubMed
.
- R. G. Parr, K. Rupnik and S. K. Ghosh, Phys. Rev. Lett., 1986, 56, 1555 CrossRef CAS PubMed
.
- P. W. Ayers, R. G. Parr and A. Nagy, Int. J. Quantum Chem., 2002, 90, 309 CrossRef CAS
.
- P. W. Ayers and A. Nagy, J. Chem. Phys., 2007, 126, 144108 CrossRef PubMed
.
- P. W. Ayers, Chem. Phys. Lett., 2007, 438, 148 CrossRef CAS
.
- B. M. Deb and P. K. Chattaraj, Phys. Rev. A, 1989, 39, 1696 CrossRef CAS PubMed
.
- B. M. Deb, P. K. Chattaraj and S. Mishra, Phys. Rev. A, 1991, 43, 1248 CrossRef CAS
.
- P. K. Chattaraj, Int. J. Quantum Chem., 1992, 41, 845 CrossRef CAS
.
- B. K. Dey and B. M. Deb, Int. J. Quantum Chem., 1995, 56, 707 CrossRef CAS
.
- P. K. Chattaraj, S. Sengupta and A. Poddar, Int. J. Quantum Chem., 1998, 69, 279 CrossRef CAS
.
- P. K. Chattaraj and S. Giri, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2009, 105, 13 RSC
.
- J. S. M. Anderson, P. W. Ayers and J. I. Rodriguez Hernandez, J. Phys. Chem. A, 2010, 114, 8884 CrossRef CAS PubMed
.
- A. Nagy, R. G. Parr and S. B. Liu, Phys. Rev. A, 1996, 53, 3117 CrossRef CAS PubMed
.
- T. Gal and A. Nagy, Mol. Phys., 1997, 91, 873 CrossRef CAS
.
- A. Nagy, Int. J. Quantum Chem., 2017, 117, 25396 CrossRef
.
- L. Cohen, J. Chem. Phys., 1984, 80, 4277 CrossRef CAS
.
- L. Cohen, J. Chem. Phys., 1979, 70, 788 CrossRef CAS
.
- S. Saha and R. K. Roy, J. Phys. Chem. B, 2007, 111, 9664 CrossRef CAS PubMed
.
- P. K. Chattaraj, J. Phys. Chem. A, 2001, 105, 511 CrossRef CAS
.
- J. Melin, F. Aparicio, V. Subramanian, M. Galván and P. K. Chattaraj, J. Phys. Chem. A, 2004, 108, 2487 CrossRef CAS
.
- A. Hocquet, A. Toro-Labbé and H. Chermette, J. Mol. Struct.: THEOCHEM, 2004, 686, 213 CrossRef CAS
.
-
L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1960 Search PubMed
.
- R. T. Sanderson, Science, 1951, 114, 670 CrossRef CAS
.
- R. T. Sanderson, J. Chem. Educ., 1954, 31, 238 CrossRef CAS
.
- R. T. Sanderson, Science, 1955, 121, 207 CrossRef CAS PubMed
.
- R. G. Parr and L. J. Bartolotti, J. Am. Chem. Soc., 1982, 104, 3801 CrossRef CAS
.
- P. K. Chattaraj, H. Lee and R. G. Parr, J. Am. Chem. Soc., 1991, 113, 1855 CrossRef CAS
.
- P. W. Ayers, J. Chem. Phys., 2005, 122, 141102 CrossRef PubMed
.
- P. W. Ayers, R. G. Parr and R. G. Pearson, J. Chem. Phys., 2006, 124, 194107 CrossRef PubMed
.
- P. W. Ayers, Faraday Discuss., 2007, 135, 161 RSC
.
- P. K. Chattaraj and P. W. Ayers, J. Chem. Phys., 2005, 123, 086101 CrossRef PubMed
.
- P. K. Chattaraj, P. W. Ayers and J. Melin, Phys. Chem. Chem. Phys., 2007, 9, 3853 RSC
.
- P. K. Chattaraj and P. V. R. Schleyer, J. Am. Chem. Soc., 1994, 116, 1067 CrossRef CAS
.
- P. K. Chattaraj, B. Gomez, E. Chamorro, J. Santos and P. Fuentealba, J. Phys. Chem. A, 2001, 105, 8815 CrossRef CAS
.
- R. G. Pearson and P. K. Chattaraj, Chemtracts: Inorg. Chem., 2009, 21, 1 Search PubMed
.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065 CrossRef CAS PubMed
.
- P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107, PR46 CrossRef CAS
.
- P. K. Chattaraj, S. Giri and S. Duley, Chem. Rev., 2011, 111, PR43 CrossRef PubMed
.
- J. Goodisman, J. Chem. Phys., 2007, 127, 066101 CrossRef PubMed
.
- J. L. Gázquez, M. Franco-Perez, P. W. Ayers and A. Vela, Int. J. Quantum Chem., 2019, 119, e25797 CrossRef
.
- M. Franco-Perez, P. W. Ayers and J. L. Gázquez, Theor. Chem. Acc., 2016, 135, 199 Search PubMed
.
- M. Franco-Perez, J. L. Gázquez, P. W. Ayers and A. Vela, Acta Phys.-Chim. Sin., 2018, 34, 683 Search PubMed
.
- R. G. Pearson, J. Chem. Educ., 1987, 64, 561 CrossRef CAS
.
- R. G. Parr and P. K. Chattaraj, J. Am. Chem. Soc., 1991, 113, 1854 CrossRef CAS
.
- R. G. Pearson, Acc. Chem. Res., 1993, 26, 250 CrossRef CAS
.
- P. W. Ayers and R. G. Parr, J. Am. Chem. Soc., 2000, 122, 2010 CrossRef CAS
.
- R. G. Pearson and W. E. Palke, J. Phys. Chem., 1992, 96, 3283 CrossRef CAS
.
- M. Torrent-Sucarrat, J. M. Luis, M. Duran and M. Sola, J. Am. Chem. Soc., 2001, 123, 7951 CrossRef CAS PubMed
.
- M. Torrent-Sucarrat, J. M. Luis, M. Duran and M. Sola, J. Chem. Phys., 2002, 117, 10561 CrossRef CAS
.
- T. K. Ghanty and S. K. Ghosh, J. Phys. Chem., 1996, 100, 12295 CrossRef CAS
.
- P. K. Chattaraj, P. Fuentealba, P. Jaque and A. Toro-Labbé, J. Phys. Chem. A, 1999, 103, 9307 CrossRef CAS
.
- P. K. Chattaraj, S. Nath and A. B. Sannigrahi, J. Phys. Chem., 1994, 98, 9143 CrossRef CAS
.
- G. I. Cárdenas-Jirón and A. Toro-Labbé, J. Phys. Chem., 1995, 99, 12730 CrossRef
.
- G. I. Cárdenas-Jirón, J. R. Letelier and A. Toro-Labbé, J. Phys. Chem. A, 1998, 102, 7864 CrossRef
.
- S. Gutiérrez-Oliva, J. R. Letelier and A. Toro-Labbé, Mol. Phys., 1999, 96, 61 CrossRef
.
- P. K. Chattaraj, S. Gutierrez-Oliva, P. Jaque and A. Toro-Labbe, Mol. Phys., 2003, 101, 2841 CrossRef CAS
.
- P. K. Chattaraj, P. Fuentealba, B. Gomez and R. Contreras, J. Am. Chem. Soc., 2000, 122, 348 CrossRef CAS
.
- F. De Proft, P. K. Chattaraj, P. W. Ayers, M. Torrent-Sucarrat, M. Elango, V. Subramanian, S. Giri and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 595 CrossRef CAS PubMed
.
- P. K. Chattaraj and S. Sengupta, J. Phys. Chem., 1996, 100, 16126 CrossRef CAS
.
- P. K. Chattaraj, D. R. Roy, M. Elango and V. Subramanian, J. Mol. Struct.: THEOCHEM, 2006, 759, 109 CrossRef CAS
.
- P. K. Chattaraj and S. Sengupta, J. Phys. Chem. A, 1999, 103, 6122 CrossRef CAS
.
- P. K. Chattaraj and S. Sengupta, J. Phys. Chem. A, 1997, 101, 7893 CrossRef CAS
.
- A. Tanwar, S. Pal, D. R. Roy and P. K. Chattaraj, J. Chem. Phys., 2006, 125, 056101 CrossRef PubMed
.
- P. K. Chattaraj, T. V. S. Arun Murthy, S. Giri and D. R. Roy, J. Mol. Struct.: THEOCHEM, 2007, 813, 63 CrossRef CAS
.
- P. K. Chattaraj, P. Pérez, J. Zevallos and A. Toro-Labbé, J. Phys. Chem. A, 2001, 105, 4272 CrossRef CAS
.
- E. Chamorro, P. K. Chattaraj and P. Fuentealba, J. Phys. Chem. A, 2003, 107, 7068 CrossRef CAS PubMed
.
- R. Parthasarathi, M. Elango, V. Subramanian and P. K. Chattaraj, Theor. Chem. Acc., 2005, 113, 257 Search PubMed
.
- P. K. Chattaraj, D. R. Roy and S. Giri, Comput. Lett., 2007, 3, 223 Search PubMed
.
- S. Pan, M. Sola and P. K. Chattaraj, J. Phys. Chem. A, 2013, 117, 1843 CrossRef CAS PubMed
.
- P. K. Chattaraj and S. Giri, Ind. J. Phys., 2007, 81, 871 CAS
.
- S. Noorizadeh and E. Shakerzadeh, J. Mol. Struct.: THEOCHEM, 2008, 868, 22 CrossRef CAS
.
- P. Chaquin, Chem. Phys. Lett., 2008, 458, 231 CrossRef CAS
.
- P. K. Chattaraj, E. Chamorro and P. Fuentealba, Chem. Phys. Lett., 1999, 314, 114 CrossRef CAS
.
- S. B. Sears, R. G. Parr and U. Dinur, Isr. J. Chem., 1980, 19, 165 CrossRef CAS
.
- R. F. Nalawajski and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8879 CrossRef PubMed
.
- A. Nagy, Chem. Phys. Lett., 2013, 556, 355 CrossRef CAS
.
- O. Onicescu, C. R. Acad. Sci., 1966, 263, 841 Search PubMed
.
- R. A. Fischer, Math. Proc. Cambridge Philos. Soc., 1925, 22, 700 CrossRef
.
-
A. Renyi, in Proceedings of fourth Berkeley symposium on mathematical statistics and probability, University of California Press, Berkeley, CA, 1960, vol. 1, p. 547 Search PubMed
.
-
(a) S. B. Liu, J. Chem. Phys., 2007, 126, 244103 CrossRef PubMed
; (b) S. B. Liu, Acta Phys.-Chim. Sin., 2016, 32, 98 Search PubMed
.
- J. Wu, D. Yu, S. Liu, C. Rong, A.-G. Zhong, P. K. Chattaraj and S. Liu, J. Phys. Chem. A, 2019, 123, 6751 CrossRef CAS PubMed
.
- X. Y. Zhou, C. Y. Rong, T. Lu, P. P. Zhou and S. B. Liu, J. Phys. Chem. A, 2016, 120, 3634 CrossRef CAS PubMed
.
- S. B. Liu, C. Rong and T. Lu, J. Phys. Chem. A, 2014, 118, 3698 CrossRef CAS PubMed
.
- B. Wang, C. Rong, P. K. Chattaraj and S. B. Liu, Theor. Chem. Acc., 2019, 138, 124 Search PubMed
.
- M. Galván, A. Vela and J. L. Gázquez, J. Phys. Chem., 1988, 92, 6470 CrossRef
.
- T. K. Ghanty and S. K. Ghosh, J. Am. Chem. Soc., 1994, 116, 3943 CrossRef CAS
.
- J. Garza, R. Vargas, A. Cedillo, M. Galván and P. K. Chattaraj, Theor. Chem. Acc., 2006, 115, 257 Search PubMed
.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS
.
- A. K. Dhara and S. K. Ghosh, Phys. Rev. A, 1987, 35, 442 CrossRef CAS PubMed
.
- E. Madelung, Z. Phys., 1926, 40, 322 CrossRef
.
- S. K. Ghosh and A. K. Dhara, Phys. Rev. A, 1988, 38, 1149 CrossRef CAS PubMed
.
- P. K. Chattaraj and B. Maiti, J. Phys. Chem. A, 2004, 108, 658 CrossRef CAS
.
- R. G. Parr and Z. Zhou, Acc. Chem. Res., 1993, 26, 256 CrossRef CAS
.
- P. K. Chattaraj and B. Maiti, J. Chem. Educ., 2001, 78, 811 CrossRef CAS
.
- P. K. Chattaraj, B. Maiti and U. Sarkar, J. Phys. Chem. A, 2003, 107, 4973 CrossRef CAS
.
- P. Peréz, L. R. Domingo, M. J. Aurell and R. Contreras, Tetrahedron, 2003, 59, 3117 CrossRef
.
- P. W. Ayers, C. Morell, F. De Proft and P. Geerlings, Chem.–Eur. J., 2007, 13, 8240 CrossRef CAS PubMed
.
- P. Geerlings, P. W. Ayers, A. Toro-Labbe, P. K. Chattaraj and F. De Proft, Acc. Chem. Res., 2012, 45, 683 CrossRef CAS PubMed
.
- W. Benchouk and S. M. Mekelleche, J. Mol. Struct.: THEOCHEM, 2008, 1, 862 Search PubMed
.
- K. Gupta, D. R. Roy, V. Subramanian and P. K. Chattaraj, J. Mol. Struct.: THEOCHEM, 2007, 812, 13 CrossRef CAS
.
- P. W. Ayers, Theor. Chem. Acc., 2001, 106, 271 Search PubMed
.
- P. K. Chattaraj and D. R. Roy, J. Phys. Chem. A, 2005, 109, 3771 CrossRef CAS PubMed
.
- P. K. Chattaraj and D. R. Roy, J. Phys. Chem. A, 2006, 110, 11401 CrossRef CAS PubMed
.
- P. K. Chattaraj, D. R. Roy, M. Elango and V. Subramanian, J. Phys. Chem. A, 2005, 109, 9590 CrossRef CAS PubMed
.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, J. Chem. Educ., 2007, 84, 354 CrossRef CAS
.
- Y. Xia, D. Yin, C. Rong, Q. Xu, D. Yin and S. Liu, J. Phys. Chem. A, 2008, 112, 9970 CrossRef CAS PubMed
.
- J. Lipinski and L. Komorowski, Chem. Phys. Lett., 1996, 262, 449 CrossRef CAS
.
- R. G. Pearson, J. Am. Chem. Soc., 1986, 108, 6109 CrossRef CAS
.
- D. Sivanesan, R. Amutha, V. Subramanian, B. U. Nair and T. Ramasami, Chem. Phys. Lett., 1999, 308, 223 CrossRef CAS
.
- P. Pérez, A. Toro-Labbé and R. Contreras, J. Am. Chem. Soc., 2001, 123, 5527 CrossRef PubMed
.
- P. K. Chattaraj, P. Pérez, J. Zevallos and A. Toro-Labbé, J. Mol. Struct.: THEOCHEM, 2002, 580, 171 CrossRef CAS
.
- L. Meneses, P. Fuentealba and R. Contreras, Chem. Phys. Lett., 2006, 433, 54 CrossRef CAS
.
- J. Padmanabhan, R. Parthasarathi, U. Sarkar, V. Subramanian and P. K. Chattaraj, Chem. Phys. Lett., 2004, 383, 122 CrossRef CAS
.
- P. W. Ayers and R. G. Parr, J. Am. Chem. Soc., 2001, 123, 2007 CrossRef CAS PubMed
.
- P. Fuentealba and A. Cedillo, J. Chem. Phys., 1999, 110, 9807 CrossRef CAS
.
- P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quantum Chem., 2005, 101, 520 CrossRef CAS
.
- P. W. Ayers and J. Melin, Theor. Chem. Acc., 2007, 117, 371 Search PubMed
.
- P. K. Chattaraj and B. Maiti, J. Phys. Chem. A, 2001, 105, 169 CrossRef CAS
.
- P. K. Chattaraj and B. Maiti, J. Am. Chem. Soc., 2003, 125, 2705 CrossRef CAS PubMed
.
- D. Chakraborty and P. K. Chattaraj, J. Phys. Chem. A, 2019, 123, 4513 CrossRef CAS PubMed
.
- D. Chakraborty and P. K. Chattaraj, J. Comput. Chem., 2018, 39, 151 CrossRef CAS PubMed
.
- D. Chakraborty, R. Das and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2017, 19, 23373 RSC
.
- D. Chakraborty and P. K. Chattaraj, Chem. Phys. Lett., 2015, 621, 29 CrossRef CAS
.
- Chemical Reactivity in Confined Systems: Theory, Modelling and Applications, ed. P. K. Chattaraj and D. Chakraborty, John Wiley & Sons, Oxford, UK, in press Search PubMed.
- P. K. Chattaraj and U. Sarkar, J. Phys. Chem. A, 2003, 107, 4877 CrossRef CAS
.
- P. K. Chattaraj and U. Sarkar, Chem. Phys. Lett., 2003, 372, 805 CrossRef CAS
.
- U. Sarkar, M. Khatua and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2012, 14, 1716 RSC
.
- M. Khatua and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2013, 15, 5588 RSC
.
- M. Khatua, S. Pan and P. K. Chattaraj, J. Chem. Phys., 2014, 140, 164306 CrossRef PubMed
.
- M. Khatua, U. Sarkar and P. K. Chattaraj, Eur. Phys. J. D, 2014, 68, 22 CrossRef
.
- M. Khatua, U. Sarkar and P. K. Chattaraj, Int. J. Quantum Chem., 2015, 115, 144 CrossRef CAS
.
- F. Guegan, T. Pigeon, F. De Proft, V. Tognetti, L. Joubert, H. Chermette, P. W. Ayers, D. Luneau and C. Morell, J. Phys. Chem. A, 2020, 124, 633 CrossRef CAS PubMed
.
- C. Morell, V. Labet, A. Grand, P. W. Ayers, F. De Proft, P. Geerlings and H. Chermette, J. Chem. Theory Comput., 2009, 5, 2274 CrossRef CAS PubMed
.
- P. K. Chattaraj and A. Poddar, J. Phys. Chem. A, 1998, 102, 9944 CrossRef CAS
.
- P. K. Chattaraj and A. Poddar, J. Phys. Chem. A, 1999, 103, 8691 CrossRef CAS
.
- P. Fuentealba, Y. Simon-Manso and P. K. Chattaraj, J. Phys. Chem. A, 2000, 104, 3185 CrossRef CAS
.
- P. K. Chattaraj and A. Poddar, J. Phys. Chem. A, 1999, 103, 1274 CrossRef CAS
.
- P. K. Chattaraj, S. Sengupta and A. Poddar, J. Mol. Struct.: THEOCHEM, 2000, 501, 339 CrossRef
.
- D. R. Roy, R. Parthasarathi, B. Maiti, V. Subramanian and P. K. Chattaraj, Bioorg. Med. Chem., 2005, 13, 3405 CrossRef CAS PubMed
.
- J. Padmanabhan, R. Parthasarathi, V. Subramanian and P. K. Chattaraj, Chem. Res. Toxicol., 2006, 19, 356 Search PubMed
.
- D. R. Roy, U. Sarkar, P. K. Chattaraj, A. Mitra, J. Padmanabhan, R. Parthasarathi, V. Subramanian, S. Van Damme and P. Bultinck, Mol. Diversity, 2006, 10, 119 CrossRef CAS PubMed
.
- D. R. Roy, N. Pal, A. Mitra, P. Bultinck, R. Parthasarathi, V. Subramanian and P. K. Chattaraj, Eur. J. Med. Chem., 2007, 42, 1365 CrossRef CAS PubMed
.
- R. Pal, G. Jana, S. Sural and P. K. Chattaraj, Chem. Biol. Drug Des., 2019, 93, 1083 CrossRef CAS PubMed
.
- G. Jana, R. Pal, S. Sural and P. K. Chattaraj, Int. J. Quantum Chem., 2020, 120, e26097 CrossRef CAS
.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. V. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317 CrossRef CAS PubMed
.
- P. K. Chattaraj, D. R. Roy, M. Elango and V. Subramanian, J. Mol. Struct.: THEOCHEM, 2006, 759, 109 CrossRef CAS
.
- Z. Zhou, R. G. Parr and J. F. Garst, Tetrahedron Lett., 1988, 29, 4843 CrossRef CAS
.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1989, 111, 7371 CrossRef CAS
.
-
Aromaticity and Metal Cluster, ed. P. K. Chattaraj, Taylor & Francis/CRC Press, Florida, 2009 Search PubMed
.
- D. Yu, C. Rong, T. Lu, P. Geerlings, F. De Proft, M. Alonso and S. B. Liu, Phys. Chem. Chem. Phys., 2020, 22, 4715 RSC
.
- D. Yu, T. Stuyver, C. Rong, M. Alonso, T. Lu, F. De Proft, P. Geerlings and S. B. Liu, Phys. Chem. Chem. Phys., 2019, 21, 18195 RSC
.
- D. Yu, C. Rong, T. Lu, P. K. Chattaraj, F. De Proft and S. B. Liu, Phys. Chem. Chem. Phys., 2017, 19, 18635 RSC
.
- S. Mondal and P. K. Chattaraj, Chem. Phys. Lett., 2014, 593, 128 CrossRef CAS
.
- P. K. Chattaraj and S. Giri, J. Phys. Chem. A, 2007, 111, 11116 CrossRef CAS PubMed
.
- S. Bakhsh, X. Liu, Y. Wang, L. He and X. Ren, J. Phys. Chem. A, 2021, 125, 1424 CrossRef CAS PubMed
.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. W. Ayers, Theor. Chem. Acc., 2020, 139, 36 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2021 |


