Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum tunneling during interstellar surface-catalyzed formation of water: the reaction H + H2O2 → H2O + OH†
Thanja
Lamberts
 *,
Pradipta Kumar
Samanta
,
Andreas
Köhn
and
Johannes
Kästner
*,
Pradipta Kumar
Samanta
,
Andreas
Köhn
and
Johannes
Kästner

Institute for Theoretical Chemistry, University of Stuttgart, Stuttgart, Germany. E-mail: lamberts@theochem.uni-stuttgart.de; Tel: +49 (0)711 685 64833
First published on 8th November 2016
Abstract
The final step of the water formation network on interstellar grain surfaces starting from the H + O2 route is the reaction between H and H2O2. This reaction is known to have a high activation energy and therefore at low temperatures it can only proceed via tunneling. To date, however, no rate constants are available at temperatures below 200 K. In this work, we use instanton theory to compute rate constants for the title reaction with and without isotopic substitutions down to temperatures of 50 K. The calculations are based on density functional theory, with additional benchmarks for the activation energy using unrestricted single-reference and multireference coupled-cluster single-point energies. Gas-phase bimolecular rate constants are calculated and compared with available experimental data not only for H + H2O2 → H2O + OH, but also for H + H2O2 → H2 + HO2. We find a branching ratio where the title reaction is favored by at least two orders of magnitude at 114 K. In the interstellar medium this reaction predominantly occurs on water surfaces, which increases the probability that the two reactants meet. To mimic this, one, two, or three spectator H2O molecules are added to the system. Eley–Rideal bimolecular and Langmuir–Hinshelwood unimolecular rate constants are presented here. The kinetic isotope effects for the various cases are compared to experimental data as well as to expressions commonly used in astrochemical models. Both the rectangular barrier and the Eckart approximations lead to errors of about an order of magnitude. Finally, fits of the rate constants are provided as input for astrochemical models.
Introduction
In the dense and cold regions of the interstellar medium (ISM), water is known to be formed on the surface of dust grains via sequential hydrogenation of O, O2, or O3. The full water surface reaction network consists of ∼15 reactions and depending on density, temperature and H, H2, and O abundance of the interstellar region, different reaction pathways towards the formation of water are important.1,2 In regions with the highest density, the absolute amount of oxygen becomes sufficiently high for the following reaction pathway to contribute significantly to the formation of H2O and OH:The final step in this reaction route is known to have a large activation barrier in the gas phase, see Baulch et al.3 and references therein. It has also been studied experimentally in the solid phase at low temperatures and a kinetic isotope effect was found.4 This indicates the importance of tunneling which allows it to be efficient even at 15 K. Note that the surface reaction takes place in an environment that consists predominantly of water molecules. Since the H2O2 molecule can partake in several hydrogen bonds, it is expected that there is an influence of the surface on the course of the reaction. Another important influence of the surface is the increased concentration of reactants as well as heat dissipation of the exothermicity of the reaction. Furthermore, the gas-phase detections and non-detections of H2O2 in a diverse sample of sources5–7 gave rise to the conclusion that the production of peroxide and therefore the gas-phase detectability is very sensitive to temperature. The surface destruction of peroxide was taken into account by rescaling the reaction rate according to experimental data.6,8 Quantitatively rescaling a rate is, however, not trivial for a reaction that is deeply embedded within a reaction network.
There are two reactions possible between H and H2O2: the first, (R1), where the O–O bond is broken and a second, (R2), where an H-atom is abstracted.
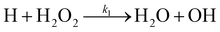 | (R1) |
 | (R2) |
Here, we present a theoretical study of the reactions (R1) and (R2) within the concept of studying reactions on a surface that proceed via tunneling. Calculations are performed using a DFT functional and basis set combination that is benchmarked to single-reference and multireference coupled-cluster single-point energies as outlined in Sections 2.1 and 3.1. Rate constants are calculated with instanton theory which is briefly described in Section 2.2. We give activation barriers and rate constants for three different cases: the gas-phase reaction (Section 3.2), the reaction with several spectator H2O molecules (small clusters) to mimic a surface related to a bimolecular reaction (Section 3.3), and the reaction with the same small clusters related to a unimolecular reaction (Section 3.4). Previous studies have focused only on the pure gas-phase reaction, did not take into account the differences between hydrogenation and deuteration, have not benchmarked their DFT functional, neglected tunneling and/or calculated rate constants only down to 200 K.9–11 Finally we explain how the calculated reaction rate constants can be implemented in astrochemical models (Section 4) and give more general conclusions (Section 5).
Methods
Electronic structure
The core system is small (19 electrons) and could be well treated by high-accuracy methods, but the actual focus is a reaction on a surface of water molecules and hence the method of choice to describe the electronic structure is density functional theory (DFT). A suitable functional and basis set needs to describe the interaction between atomic hydrogen and hydrogen peroxide, as well as between water molecules. We perform a benchmark study for the activation and reaction energies of reactions (R1) and (R2) with respect to two coupled cluster methods. The first benchmark method is spin-orbital based (unrestricted) coupled-cluster theory with singles, doubles, and perturbative triples clusters (UCCSD(T))12–14 and explicitly-correlated geminal functions (UCCSD(T)-F12)15,16 employing a restricted Hartree–Fock (RHF) reference function and the cc-pVTZ17 or cc-pVTZ-F1218 basis set. To test for multireference character, the internally contracted multireference coupled-cluster method, again with singles, doubles, and perturbative triples clusters (icMRCCSD(T)) was used.19,20 These computations were carried out with a cc-pVTZ basis set.17 A complete active space self-consistent field (CASSCF) reference was used for this method. The CAS used for H2O2, the transition state, H2O, OH, and HO2 are (6e,6o), (7e,7o), (4e,4o), (3e,3o), and (5e,5o). The active space was chosen to describe the unpaired electron and all bonding and antibonding sigma orbitals of the system. These benchmark computations were carried out for single geometries, as obtained from DFT computations optimized on MPW1B95/MG3S21,22 and M05-2X/MG3S22,23 levels for reactions (R1) and (R2), respectively. This choice of functional is based on finding the best match to coupled cluster energetics. Data are given in Section 3.1.Additionally, the reaction energies are also compared to the high-accuracy extrapolated ab initio thermochemistry (HEAT) theoretical model that has been shown to go beyond CCSD(T) methods in accuracy.24
For the benchmark, we follow the approach of Ellingson et al.10 and construct a set of commonly or previously10,11 used functionals (BHLYP,25–27 B3LYP,25,27,28 PBE0,29,30 PWB6K,31 MPW1B95,21 M05-2X23) in combination with the basis sets def2-TZVPD32,33 and MG3S.22,34 The MG3S basis set is equivalent to 6-311+G(3d2f,2df,2p) for H and O atoms.
All geometry optimizations are performed using DL-find35 within the Chemshell36,37 framework and NWChem versions 6.3 and 6.6.38 The single energy points are calculated with Molpro39 for UCCSD(T) and UCCSD(T)-F12 and GeCCo19 for icMRCCSD(T). VMD version 1.9.240 and wxMacMolPlt version 7.741 are used for visualization.
Reaction rate constants
The hydrogenation reactions are initially modeled in the gas phase. To investigate the influence of the surface more specifically, we added one, two, or three water molecules to the previously optimized structures and re-optimized the resulting configuration. Reaction rate constants are calculated using instanton theory42–60 which has been shown to provide accurate tunneling rates down to very low temperature and is increasingly used to predict rate constants.56,58,61–83Instanton theory treats the quantum effects of atomic movements by Feynman path integrals. The main tunneling path, the instanton, is described by a closed Feynman path, which connects the reactant and product valleys of the potential energy surface. The instanton represents the tunneling path with the highest statistical weight at a given temperature. It is located by a Newton–Raphson optimization scheme.56,57 A semiclassical approximation results in the rate constants. More details on our implementation of instanton theory are given elsewhere.56,57 Rotational and translational partition functions were approximated by their classical analogues (J-shifting approximation), which is generally accepted as a good approximation at the temperature scale considered here. In bimolecular cases, the product of the partition functions of the separated reactants was used, in unimolecular cases, the partition function of the encounter complex. The Feynman paths were discretized to 60 images. Instanton theory is applicable below the crossover temperature Tc, which is defined as
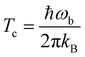 | (1) |
First, we consider the pure gas-phase reaction. This may not be very relevant in terms of astrochemistry, but it is important to understand the simplest case first. In the gas phase, a hydrogen atom can approach the molecule on both oxygen atoms, since they are equivalent. In other words, the rate constants need to be multiplied with a rotational symmetry factor. The symmetry factor used here is 2, resulting from the pointgroup C2 for the hydrogen peroxide molecule.84 Concerning the surface reaction, there are typically two reaction mechanisms taken into consideration: the Eley–Rideal (ER) and the Langmuir–Hinshelwood (LH) processes. The ER mechanism describes one species to be adsorbed on the surface and the other approaching from the gas phase, i.e., an overall bimolecular reaction. For the LH mechanism both species are adsorbed on the surface, approach each other via diffusion and form an encounter complex of H and H2O2 on the surface. This encounter, or pre-reactive, complex can then decay to yield the reaction products in a unimolecular process. Moreover, to extend the results to the solid phase it is key to realize that rotational motion on the surface is restricted. Therefore, rate constants calculated for both ER and LH mechanisms need to keep the rotational partition function constant between the reactant and transition state. Moreover, the surface structure breaks the gas-phase symmetry, hence no symmetry factor is required.
For astrochemical modelers to be able to easily implement the calculated rate constants, we fitted these to the rate expression85
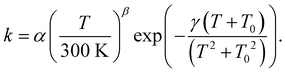 | (2) |
Results and discussion
Here we first present the results of the DFT benchmark (Section 3.1) and subsequently give the results for the three cases of the reaction that we study: the gas-phase reaction (Section 3.2), the bimolecular Eley–Rideal reaction (Section 3.3), and the unimolecular Langmuir–Hinshelwood reaction (Section 3.4). All values for the rate constants are given in the ESI.†DFT benchmark
Table 1 gives an overview of the activation and reaction energies without zero-point energy (ZPE) corrections for reactions (R1) and (R2). All DFT calculations comprise full geometry optimizations and all stationary points were verified by their appropriate number of imaginary frequencies, i.e., zero for the reactants/products and one for the transition states. The coupled cluster values are single-point energies on MPW1B95/MG3S and M05-2X/MG3S levels for reactions (R1) and (R2). Finally, reaction energies have also been calculated with the use of atomization energies computed with the HEAT-456QP protocol (as tabulated in Harding et al.24).| Method reference | H + H2O2 → H2O + OH | H + H2O2 → HO2 + H2 | |||
|---|---|---|---|---|---|
| Activation energy | Reaction energy | Activation energy | Reaction energy | ||
| UCCSD(T)-F12/cc-pVTZ-F12 | 15, 16 and 18 | 25.5 | −299.3 | 39.4 | −66.6 |
| UCCSD(T)/cc-pVTZ | 12–14 and 17 | 27.7 | −294.3 | 39.6 | −69.8 |
| icMRCCSD(T)/cc-pVTZ | 17, 19 and 20 | 24.9 | −292.2 | 38.3 | −70.9 |
| HEAT-456QP | 24 | −297.7 | −66.5 | ||
| BHLYP/def2-TZVPD | 25–27, 32 and 33 | 27.2 | −331.4 | 27.6 | −89.2 |
| B3LYP/def2-TZVPD | 25, 27, 28, 32 and 33 | 10.8 | −299.3 | 7.3 | −90.3 |
| B3LYP/MG3S | 22, 25, 27 and 28 | 11.2 | −300.2 | 8.1 | −88.1 |
| PBE0/def2-TZVPD | 29, 30, 32 and 33 | 20.7 | −288.0 | 17.3 | −74.4 |
| PBE0/MG3S | 22, 29 and 30 | 21.4 | −289.0 | 18.1 | −72.3 |
| PWB6K/MG3S | 22 and 31 | 36.0 | −307.5 | 35.4 | −74.2 |
| MPW1B95/MG3S | 21 and 22 | 26.5 | −291.8 | 23.7 | −76.7 |
| M05-2X/MG3S | 22 and 23 | 45.9 | −303.3 | 39.7 | −68.5 |
CCSD(T) results are commonly used in computational chemistry as a gold standard for activation and reaction energies. This is, however, valid only for species where a single reference wavefunction is a good approximation. We found values of the T1 and D1 diagnostics of 0.022 and 0.062 (R1) and 0.031 and 0.109 (R2) in our CCSD(T)-F12 calculations. Therefore, additional tests with the icMRCCSD(T) method seemed important. The icMRCCSD(T) method translates the accuracy of CCSD(T) to multireference cases and has been successfully applied to predicting barriers of reactions.86 An estimate of the multireference effects can be obtained from the results of icMRCCSD(T) and UCCSD(T) calculations using the cc-pVTZ basis. The computations indicate, that multireference effects only slightly lower the activation energy (−2.8 kJ mol−1 for (R1) and −1.3 kJ mol−1 for (R2)). We hence conclude that the multireference character of the transition state is not pronounced. This can also be seen from the contributions of the main configurations to the CASSCF wavefunction for the transition states. These are (a) a doubly occupied bonding sigma orbital with a singly occupied orbital and (b) a doubly occupied anti-bonding sigma orbital with again the singly occupied orbital. For reaction (R1) the probabilities are 0.93 and 0.03, for reaction (R2) they are 0.94 and 0.02 for configurations (a) and (b) respectively. In both cases the bonding and anti-bonding sigma orbitals are similar, albeit with different geometries for the two reactions. The orbital corresponding to the unpaired electron has contributions mainly from 1s orbital of the incoming hydrogen atom and the 2pz orbital of one of the oxygen atoms. The corresponding figures of the three orbitals for both reactions are given in the ESI.†
Comparing the coupled cluster values to those obtained with DFT, it is clear that the barrier of reaction (R1) is best described by the combination MPW1B95/MG3S and reaction (R2) by M05-2X/MG3S, which is in full agreement with previous findings.10 The slight overestimation of the barrier can result in an underestimation of the calculated reaction rate constants, but we will show that the spread in the activation energies resulting from the interaction with spectator H2O molecules is much larger. The need for using two different functionals for the O–O bond breaking and H-abstraction reactions is somewhat dissatisfactory from a purist's point of view. At present, however, our choice is dictated by the absence of any practical functional that is good as describing both reaction paths.10 The issue is alleviated to some degree by the fact that the two processes take place on different parts of the potential energy surface.
As we will outline in Section 3.2 the main focus of the paper is on reaction (R1) and therefore we focus our attention concerning the description of dispersive interactions on this reaction only. The functional MPW1B95 has been shown to have a good performance for hydrogen bonding and weak interaction calculations.21 Therefore it is not obvious if an empirical dispersion correction should be applied additionally. We have tested the performance of the MPW1B95/MG3S combination with and without a D3 correction91 for the H2O dimer, trimer, and tetramer as well as for the interaction energy between H2O2 and H2O. We find that without additional correction the interaction energies differ from the CCSD(T)-F12 single points by ±1.6–4.3%, whereas with D3 correction they differ by ±5.3–7.4%. Since a good description of the H2O surface and the binding between H2O2 and such a surface is important for our astrochemical application, we will not use an additional dispersion correction.
Gas-phase reaction
Fig. 1 shows the bimolecular reaction rate constants calculated for reactions (R1) and (R2) for the pure gas-phase situation. Note that the black curve has been calculated with the MPW1B95/MG3S combination and the red curve with M05-2X/MG3S following earlier statements.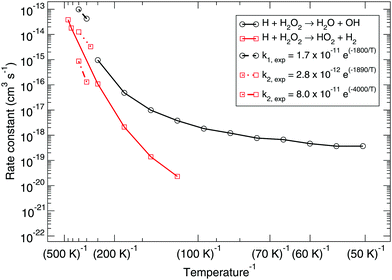 | ||
| Fig. 1 Gas-phase branching ratio: calculated bimolecular reaction rate constants k1 and k2 for reactions (R1) and (R2), respectively, in the gas phase compared to recommended expressions derived from gas-phase experiments.87–90 | ||
Instanton theory is not applicable above the crossover temperature, which are 275 and 463 K for (R1) and (R2) respectively. This is why the two curves are cut off at the higher temperature range. From the figure the rate constants calculated at the highest temperatures can be compared to the expressions summarized by Baulch et al.3 based on experimental and modeling work.87–90 These expressions are recommended down to 280 or 300 K and a reasonably good correspondence to our calculated values can be seen.
Already at a temperature of 114 K the difference between the rate constants of (R1) and (R2) is more than two orders of magnitude. This can be explained by the much higher activation energy, despite the fact that tunneling might be expected to dominate H-abstraction at low temperatures more than the breaking of the O–O bond. Therefore, we exclude it from further investigation, i.e., the branching ratio (R1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (R2) at lower temperature is at least 100
(R2) at lower temperature is at least 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fig. 3 shows the instanton paths at 114 K for both reactions. The path essentially shows the delocalization of the atoms involved in the reaction. This deviates from the classical picture of overcoming a barrier and visualizes tunneling through a barrier. The lower the temperature, the more delocalization is usually visible, since tunneling then plays a larger role.
1. Fig. 3 shows the instanton paths at 114 K for both reactions. The path essentially shows the delocalization of the atoms involved in the reaction. This deviates from the classical picture of overcoming a barrier and visualizes tunneling through a barrier. The lower the temperature, the more delocalization is usually visible, since tunneling then plays a larger role.
Several possible isotopic substitutions can be made: O vs.18O and H vs. D. In Fig. 2 the resulting rate constants for such substitutions are depicted. Firstly, changing the oxygen atom to a heavier isotope results in a lowering of the rate constant by a factor 1.4 at 50 K, because the O–O bond needs to be broken. In Fig. 3 it is visible why: the oxygen atoms are somewhat delocalized as well, meaning that they take part in the tunneling process. Exchanging a protium for a deuterium on the peroxide molecule has a similar small effect, i.e., decreasing the rate constant by a factor 1.3 at 50 K. However, for the hydrogen that approaches the peroxide and is to be added to the oxygen there is a strong kinetic isotope effect of a factor 229 at 50 K, see Table 3, again visualized by strong delocalization.
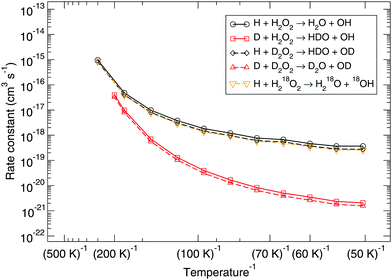 | ||
| Fig. 2 Gas-phase kinetic isotope effect: bimolecular reaction rate constants for reaction (R1) and isotope substituted analogues. Note that the curves for the reactions H + D2O2 → HDO + OD and H + H218O2 → H218O + 18OH overlap. | ||
 | ||
| Fig. 3 Instanton path for reaction (R1) (O–O bond breaking, left) and (R2) (H-abstraction, right) at 114 K. | ||
Eley–Rideal surface reaction mechanism
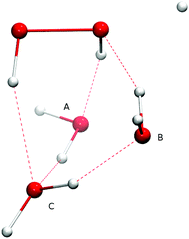
The Eley–Rideal reaction mechanism in surface chemistry corresponds to a reaction between one reactant that is adsorbed on a surface, and a second reactant that approaches directly from the gas-phase, hence to a bimolecular reaction between the adsorbate–surface system and the incoming atom. In our case, the adsorbate is the H2O2 molecule, the incoming atom is the H atom, and the surface is represented by spectator H2O molecules. The opposite case where H is pre-adsorbed and peroxide comes in from the gas phase is much less likely given the low H2O2 gas-phase abundance in the ISM.Adding one (A or B), two (A and B), or three (A, B, and C) spectator water molecules, as depicted in Fig. 4, helps to elucidate the effect of the interaction between the water surface and the reactants. In Fig. 4, a transition structure with three added water molecules is shown, including their hydrogen bonded structure and respective labeling. Table 2 summarizes the activation energies for the reaction between hydrogen peroxide and protium or deuterium. Adding water molecules to the reactive site indeed has an influence on the activation energies, which consequently span a range between 25.1 and 32.5 kJ mol−1. The activation energy seems to correlate with the O–O and O–H (incoming) distances in the transition state: the higher the activation energy, the larger the O–O and the smaller the O–H bond lengths, i.e., the later the transition state is.
| E a bimol. | E a unimol. | T C | |
|---|---|---|---|
| H + H2O2 → H2O + OH | |||
| Gas | 27.6 | 26.6 | 275 |
| 1H2O: A | 25.1 | 24.2 | 264 |
| 1H2O: B | 29.9 | 283 | |
| 2H2O: A, B | 27.9 | 26.8 | 274 |
| 3H2O: A, B, C | 32.6 | 30.4 | 288 |
| D + H2O2 → HDO + OH | |||
| Gas | 26.2 | 25.6 | 222 |
| 2H2O: A, B | 26.4 | 25.7 | 221 |
| 3H2O: A, B, C | 31.0 | 29.6 | 234 |
The corresponding reaction rate constants are presented in Fig. 5. Here, rate constants are calculated keeping the rotational partition function constant and without a symmetry factor. Therefore, the black curves without water have been recalculated and differ from those in Fig. 1 and 2. Correlating the five curves to their respective activation energies we can see that the higher the barrier, the lower the rate constant, as can be expected. The spread at the lowest temperature, 50 K, is about 1.5 orders of magnitude. However, all curves do seem to follow the same trend, which indicates that the way the reaction proceeds it not altered by the presence of water molecules. This means that although hydrogen bonds can and are formed, the influence thereof lies only in the height of the activation energy. The rate constants seem to level off around a value of 10−19 cm3 s−1 at 50 K.
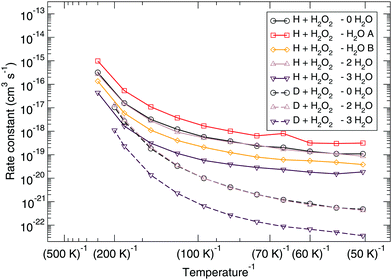 | ||
| Fig. 5 Eley–Rideal mechanism: bimolecular reaction rate constants for reaction (R1) surrounded by various spectator H2O molecules and isotope substituted analogues. Note that the curves for the reactions D + H2O2 – 0H2O and D + H2O2 – 2H2O overlap. | ||
Again, the same correspondence between the activation energy and rate constant is found for the deuterated reactions. Furthermore, a similar spread in the rate constants is observed at 50 K. The ratios between the reaction rate constants for hydrogenation and deuteration of H2O2 for the ER and LH rate constants are summarized in Table 3. This ratio is defined here as the kinetic isotope effect, ϕKIE,
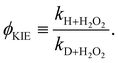 | (3) |
| T (K) | ER bimol. | LH unimol. | ||||
|---|---|---|---|---|---|---|
| Gas | 2H2O | 3H2O | Gas | 2H2O | 3H2O | |
| 179 | 6.0 | 4.9 | 7.2 | 3.8 | 4.7 | 8.2 |
| 139 | 17 | 13 | 23 | 11 | 14 | 27 |
| 114 | 36 | 26 | 50 | 24 | 30 | 64 |
| 97 | 58 | 53 | 87 | 39 | 56 | 120 |
| 84 | 91 | 87 | 146 | 63 | 84 | 215 |
| 74 | 117 | 128 | 204 | 85 | 130 | 326 |
| 66 | 169 | 148 | 266 | 127 | 176 | 461 |
| 59 | 169 | 176 | 269 | 133 | — | 510 |
| 54 | 199 | 202 | 306 | 163 | 340 | — |
| 50 | 229 | 202 | 522 | 197 | — | 1194 |
Langmuir–Hinshelwood surface reaction mechanism
The Langmuir–Hinshelwood reaction mechanism assumes two already adsorbed species on the surface that find each other via diffusion, sit next to each other, i.e., form a pre-reactive complex, and then attempt a reaction. This is thus related to a unimolecular reaction starting out from the encounter complex; note the different units.Table 2 gives the activation energies for the reactions with respect to this encounter complex. It is clear from the small differences in the barriers between the first and the second column of the table that the interaction between the hydrogen atom and the H2O2 (+ (H2O)n) system is very weak. In fact the interaction energies are slightly positive, 1–2 kJ mol−1. This could be caused by the poor description of the van der Waals interaction by DFT, however, even an additional D3 correction leaves the interaction energies positive. The result is that at lower temperatures the rate constants become more noisy. This weak interaction of the H atoms shows that it is not trivial to define an encounter complex, since most likely one should take an ensemble of possible configurations into account. This will be dealt with in a future study.
The reaction rate constants are presented in Fig. 6. Again the rotational partition function has been kept constant. Furthermore, a similar trend as for the ER bimolecular case can be observed, with a spread of about an order of magnitude. The rate constants seem to level off around a value of 2 × 104 s−1 at 50 K.
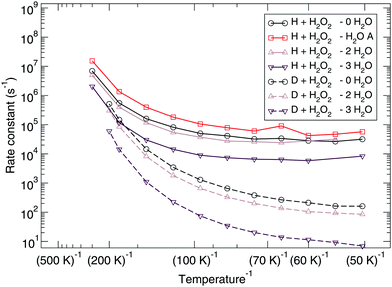 | ||
| Fig. 6 Langmuir–Hinshelwood mechanism: unimolecular reaction rate constants for reaction (R1) surrounded by various spectator H2O molecules and isotope substituted analogues. | ||
Experimentally, under ultra-high vacuum conditions, it is assumed that the LH mechanism plays the dominant role. Early work by Miyauchi et al.,92 Ioppolo et al.,93 Cuppen et al.94 already specifically mentions the role of the reaction H + H2O2 → H2O + OH within the water network, but it was only by Oba et al.4 that the reaction and the role of tunneling were explored to a greater detail. In their paper, they show a clear kinetic isotope effect between hydrogenation and deuteration of H2O2 and also of D2O2. Since experimentally it is not possible to determine the amount of H/D atoms residing on the surface, the reported ϕKIE's are based on effective rate constants and have a value of approximately 50. A more exact treatment would have to include the exact H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D flux ratio as well as diffusion and recombination rates. Our low-temperature ϕKIE is at least a factor of four higher, which is caused by the fact that the theoretical ϕKIE is based solely on the rate constant for the reactions, excluding any additional effects. Since the longer lifetime of D atoms on the surface with respect to that of H atoms on the surface indeed is expected to lower the kinetic isotope effect, the agreement to experiments is actually reasonable. Note that in the unimolecular case, the addition of spectator molecules strongly influences the kinetic isotope effect, the reason for this is at present unclear.
D flux ratio as well as diffusion and recombination rates. Our low-temperature ϕKIE is at least a factor of four higher, which is caused by the fact that the theoretical ϕKIE is based solely on the rate constant for the reactions, excluding any additional effects. Since the longer lifetime of D atoms on the surface with respect to that of H atoms on the surface indeed is expected to lower the kinetic isotope effect, the agreement to experiments is actually reasonable. Note that in the unimolecular case, the addition of spectator molecules strongly influences the kinetic isotope effect, the reason for this is at present unclear.
Implementation in astrochemical models
The rate constants that are presented in this work can be used as input for astrochemical models. To that purpose, we have fitted rate constants to eqn (2) with fitting parameters α, β, γ, and T0. The values of these parameters are given in Table 4. Note that in all cases, we used the pure gas-phase geometries, i.e. without spectator molecules, but calculated the ER and LH rate constants keeping the rotation partition function constant. In Fig. 5 we showed that the rate constants without spectator molecules lie nicely within the range spanned by the various geometries and can thus be interpreted as an average value. The full spread is about 1–1.5 orders of magnitude and therefore the exact values of the rate constant fits should be considered to have an uncertainty of approximately a factor 5. We stress here that in astrochemical grain–surface reaction modeling this accuracy is in fact quite sufficient. Uncertainties of that order can even be found in gas-phase reaction networks although these are typically better constrained.95| Parameter | Gas | ER | LH |
|---|---|---|---|
| H + H2O2 → H2O + OH | |||
| α (cm3 s−1 s) | 1.92 × 10−12 | 2.74 × 10−13 | 1.51 × 1010 |
| β | 2.54 | 2.61 | 0.86 |
| γ (K) | 1660 | 1630 | 1750 |
| T 0 (K) | 180 | 180 | 180 |
| D + H2O2 → HDO + OH | |||
| α (cm3 s−1 s) | 1.09 × 10−12 | 2.76 × 10−13 | 8.37 × 109 |
| β | 2.65 | 2.69 | 1.19 |
| γ (K) | 1615 | 1600 | 1625 |
| T 0 (K) | 125 | 125 | 125 |
As outlined above, this reaction can, in principal, take place both in the gas phase and on a (water) surface. As a result of the low interstellar abundances of H2O2 in the gas phase, the gas-phase route is unlikely. A gas-phase hydrogen atom could directly strike a reaction partner that is adsorbed to a water or grain surface, as in a bimolecular process. However, the timescales involved in dark cloud chemistry are large enough for a hydrogen atom to scan the surface and eventually meet an H2O2 molecule. Therefore, unimolecular rate constants have a direct correspondence to the process as it occurs in the interstellar medium. For the sake of completeness we provide fit parameters for all three possibilities.
The rate constants presented here are not directly comparable to the expressions commonly used in astrochemical modelling. Usually in such models the tunneling probability, Ptunn., is described by the rectangular barrier approximation
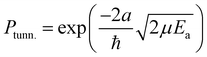 | (4) |
| RLH,react. = Preact.Rdiffusion. | (5) |
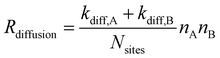 | (6) |
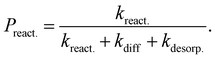 | (7) |
| Instanton | Eckart | Rect. barrier | |
|---|---|---|---|
| ER | 197 | 27 | 6945 |
| LH | 229 | 60 | 7033 |
Fig. 7 and 8 show a comparison of the rate constants as calculated with harmonic transition state theory (incl. ZPE), with an Eckart approximation, and with the instanton method. These figures again indicate that any correspondence between the Eckart approximation and instanton rates is only fortuitous, compare the ER bimolecular D + H2O2 rate constants (which overlaps with the instanton curve) with those for the LH unimolecular H + H2O2 case. More generally speaking, Eckart rate constants are likely to underestimate the true value and show a wrong low-temperature behavior.
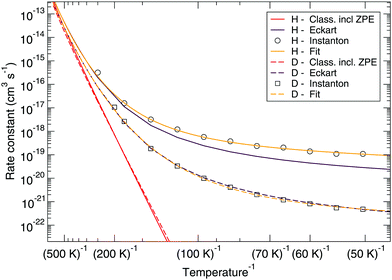 | ||
| Fig. 7 Eley–Rideal mechanism: comparison between rate constants calculated with transition state theory including quantized vibrations, the Eckart approximation, and instanton theory. The fit to eqn (2) is also shown. | ||
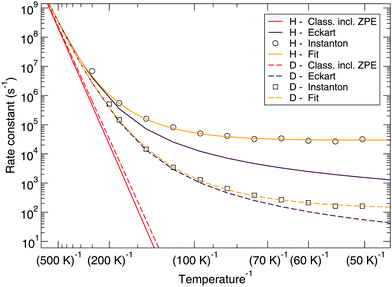 | ||
| Fig. 8 Langmuir–Hinshelwood mechanism: comparison between rate constants calculated with transition state theory including quantized vibrations, the Eckart approximation, and instanton theory. The fit to eqn (2) is also shown. | ||
Conclusion
With the study of the reaction between atomic hydrogen and hydrogen peroxide the final step of the water formation sequence starting from molecular oxygen is further quantified. In particular, attention is paid to the low-temperature behavior, the kinetic isotope effect, and the influence of spectator water molecules mimicking an icy grain surface.Specifically,
• prior to calculating rate constants the method of choice (DFT) has been benchmarked to single-reference and multireference coupled cluster single-point energies for the stationary points on the potential energy surface,
• a branching ratio between the rate constants for O–O bond breaking, (R1), and H-abstraction, (R2), of at least 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was established at a temperature of 114 K,
1 was established at a temperature of 114 K,
• rate constants that apply to the gas-phase, surface Eley–Rideal, and surface Langmuir–Hinshelwood mechanisms are now available down to 50 K,
• the 50 K results, or an extrapolation down to at least 30 K via the fitted expression eqn (2) (Table 4), can be used as a reasonable guess for even lower-temperature surface processes thanks to the rate constants leveling off with decreasing temperature,
• quantitative agreement with experimental gas-phase data and qualitative agreement with the experimental surface kinetic isotope effects is found,
• the addition of spectator molecules indeed influences on the reaction rate constant and kinetic isotope effect, mainly by influencing the transition state structure, which leads to a change in the activation energy of the reaction,
• general trends such as the asymptotic behavior of the curves, don't seem to be strongly affected by the addition of spectator molecules, but it is important to note that the surface aids in bringing the two reactants together and allows for heat dissipation of the exothermicity,
• a comparison between the rectangular barrier approximation, the Eckart approximation, and instanton rate constants shows that both approximations leads to large errors (more than an order of magnitude).
The quantification of the reaction rate constants for H(D) + H2O2 → H2O(HDO) + OH can help to constrain the HDO/H2O ratio in the ice. Note that the high ϕKIE's of more than 200 (Table 3) indicate that a high abundance of H2O2 results in a decrease of the HDO/H2O ratio. Furthermore it is of aid to elucidate the H2O2 abundance on surfaces.
Acknowledgements
TL and JK are financially supported by the European Union's Horizon 2020 research and innovation programme (grant agreement no. 646717, TUNNELCHEM). PKS and AK would like to thank the German Research Foundation (DFG) for financial support of the project within the Cluster of Excellence in Simulation Technology (EXC 310/2) at the University of Stuttgart. Jan Meisner and Sonia Álvarez Barcia are acknowledged for their help and discussions in various stages of the project.References
- H. M. Cuppen and E. Herbst, Astrophys. J., 2007, 668, 294–309 CrossRef CAS.
- T. Lamberts, X. de Vries and H. M. Cuppen, Faraday Discuss., 2014, 168, 327–347 RSC.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, T. Murrells, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnartz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef CAS.
- Y. Oba, K. Osaka, N. Watanabe, T. Chigai and A. Kouchi, Faraday Discuss., 2014, 168, 185–204 RSC.
- P. Bergman, B. Parise, R. Liseau, B. Larsson, H. Olofsson, K. M. Menten and R. Güsten, Astron. Astrophys., 2011, 531, L8 CrossRef.
- B. Parise, P. Bergman and K. Menten, Faraday Discuss., 2014, 168, 349–367 RSC.
- R. Liseau and B. Larsson, Astron. Astrophys., 2015, 583, A53 CrossRef.
- F. Du, B. Parise and P. Bergman, Astron. Astrophys., 2012, 538, A91 CrossRef.
- K. Koussa, M. Bahri, N. Jaïdane and Z. Ben Lakhdar, THEOCHEM, 2006, 770, 149–156 CrossRef.
- B. A. Ellingson, D. P. Theis, O. Tishchenko, J. Zheng and D. G. Truhlar, J. Phys. Chem. A, 2007, 111, 13554–13566 CrossRef CAS PubMed.
- V. Taquet, P. S. Peters, C. Kahane, C. Ceccarelli, A. López-Sepulcre, C. Toubin, D. Duflot and L. Wiesenfeld, Astron. Astrophys., 2013, 550, A127 CrossRef.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106–3107 CrossRef CAS.
- M. J. O. Deegan and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326 CrossRef CAS.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2012, 136, 204107 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918 CrossRef CAS.
- B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384–1388 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305 CrossRef CAS.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110 CrossRef CAS.
- M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2015.1, a package of ab initio programs, 2015, see http://www.molpro.net Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- B. M. Bode and M. S. Gordon, J. Mol. Graphics Modell., 1998, 16, 133–138 CrossRef CAS PubMed.
- J. Langer, Ann. Phys., 1967, 41, 108–157 CAS.
- J. S. Langer, Ann. Phys., 1969, 54, 258–275 CAS.
- W. H. Miller, J. Chem. Phys., 1975, 62, 1899–1906 CrossRef CAS.
- C. G. Callan and S. Coleman, Phys. Rev. D: Part. Fields, 1977, 16, 1762–1768 CrossRef.
- S. Coleman, Phys. Rev. D: Part. Fields, 1977, 15, 2929–2936 CrossRef.
- E. Gildener and A. Patrascioiu, Phys. Rev. D: Part. Fields, 1977, 16, 423–430 CrossRef.
- I. Affleck, Phys. Rev. Lett., 1981, 46, 388–391 CrossRef.
- S. Coleman, Nucl. Phys. B, 1988, 298, 178–186 CrossRef.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- One-Dimensional Models, ed. V. A. Benderskii, D. E. Makarov and C. A. Wight, John Wiley & Sons, Inc., 1994, pp. 55–95 Search PubMed.
- M. Messina, G. K. Schenter and B. C. Garrett, J. Chem. Phys., 1995, 103, 3430–3435 CrossRef CAS.
- J. O. Richardson and S. C. Althorpe, J. Chem. Phys., 2009, 131, 214106 CrossRef PubMed.
- M. Kryvohuz, J. Chem. Phys., 2011, 134, 114103 CrossRef PubMed.
- S. C. Althorpe, J. Chem. Phys., 2011, 134, 114104 CrossRef PubMed.
- J. B. Rommel, T. P. M. Goumans and J. Kästner, J. Chem. Theory Comput., 2011, 7, 690–698 CrossRef CAS PubMed.
- J. B. Rommel and J. Kästner, J. Chem. Phys., 2011, 134, 184107 CrossRef PubMed.
- M. Kryvohuz, J. Phys. Chem. A, 2014, 118, 535–544 CrossRef CAS PubMed.
- Y. Zhang, J. B. Rommel, M. T. Cvitaš and S. C. Althorpe, Phys. Chem. Chem. Phys., 2014, 16, 24292–24300 RSC.
- J. O. Richardson, J. Chem. Phys., 2016, 144, 114106 CrossRef PubMed.
- S. Chapman, B. C. Garrett and W. H. Miller, J. Chem. Phys., 1975, 63, 2710–2716 CrossRef CAS.
- G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124–1127 CrossRef CAS PubMed.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- G. Mills, G. K. Schenter, D. E. Makarov and H. Jónsson, Chem. Phys. Lett., 1997, 278, 91–96 CrossRef CAS.
- W. Siebrand, Z. Smedarchina, M. Z. Zgierski and A. Fernández-Ramos, Int. Rev. Phys. Chem., 1999, 18, 5–41 CrossRef CAS.
- Z. Smedarchina, W. Siebrand, A. Fernández-Ramos and Q. Cui, J. Am. Chem. Soc., 2003, 125, 243–251 CrossRef CAS PubMed.
- T. Qian, W. Ren, J. Shi, W. E and P. Sheng, Physica A, 2007, 379, 491–502 CrossRef.
- S. Andersson, G. Nyman, A. Arnaldsson, U. Manthe and H. Jónsson, J. Phys. Chem. A, 2009, 113, 4468–4478 CrossRef CAS PubMed.
- T. P. M. Goumans and S. Andersson, Mon. Not. R. Astron. Soc., 2010, 406, 2213–2217 CrossRef CAS.
- S. Andersson, T. P. M. Goumans and A. Arnaldsson, Chem. Phys. Lett., 2011, 513, 31–36 CrossRef CAS.
- T. P. M. Goumans, Mon. Not. R. Astron. Soc., 2011, 415, 3129–3134 CrossRef CAS.
- T. P. M. Goumans, Mon. Not. R. Astron. Soc., 2011, 413, 2615–2620 CrossRef CAS.
- T. P. M. Goumans and J. Kästner, Angew. Chem., Int. Ed., 2010, 49, 7350–7352 CrossRef CAS PubMed.
- H. Jónsson, Proc. Natl. Acad. Sci. U. S. A., 2010, 108, 944–949 CrossRef PubMed.
- J. Meisner, J. B. Rommel and J. Kästner, J. Comput. Chem., 2011, 32, 3456–3463 CrossRef CAS PubMed.
- T. P. M. Goumans and J. Kästner, J. Phys. Chem. A, 2011, 115, 10767–10774 CrossRef CAS PubMed.
- D. M. Einarsdóttir, A. Arnaldsson, F. Óskarsson and H. Jónsson, Lect. Notes Comput. Sci., 2012, 7134, 45–55 Search PubMed.
- J. B. Rommel, Y. Liu, H.-J. Werner and J. Kästner, J. Phys. Chem. B, 2012, 116, 13682–13689 CrossRef CAS PubMed.
- M. Kryvohuz and R. A. Marcus, J. Chem. Phys., 2012, 137, 134107 CrossRef CAS PubMed.
- J. Kästner, Chem. – Eur. J., 2013, 19, 8207–8212 CrossRef PubMed.
- S. Álvarez-Barcia, J. R. Flores and J. Kästner, J. Phys. Chem. A, 2014, 118, 78–82 CrossRef PubMed.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 158–168 CrossRef.
- J. Meisner and J. Kästner, Angew. Chem., Int. Ed., 2016, 55, 5400–5413 CrossRef CAS PubMed.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 CrossRef.
- J. Zheng and D. G. Truhlar, Phys. Chem. Chem. Phys., 2010, 12, 7782–7793 RSC.
- Y. A. Aoto and A. Kohn, Phys. Chem. Chem. Phys., 2016, 18, 30241 RSC.
- E. Albers, K. Hoyermann, H. Wagner and J. Wolfrum, Symp. (Int.) Combust., [Proc.], 1971, 13, 81–88 CrossRef.
- R. Klemm, W. Payne and L. Stief, Int. J. Chem. Kinet. Symp., 1975, 1, 61–72 Search PubMed.
- R. R. Baldwin and R. W. Walker, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 140–154 RSC.
- D. Lee and S. Hochgreb, Int. J. Chem. Kinet., 1998, 30, 385–406 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- N. Miyauchi, H. Hidaka, T. Chigai, A. Nagaoka, N. Watanabe and A. Kouchi, Chem. Phys. Lett., 2008, 456, 27–30 CrossRef CAS.
- S. Ioppolo, H. M. Cuppen, C. Romanzin, E. F. van Dishoeck and H. Linnartz, Astrophys. J., 2008, 686, 1474–1479 CrossRef CAS.
- H. M. Cuppen, S. Ioppolo, C. Romanzin and H. Linnartz, Phys. Chem. Chem. Phys., 2010, 12, 12077–12088 RSC.
- V. Wakelam, F. Selsis, E. Herbst and P. Caselli, Astron. Astrophys., 2005, 444, 883–891 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp06457d |
| This journal is © the Owner Societies 2016 |