Open Access Article
Open Access ArticleUnlocking the potential of open-tunnel oxides: DFT-guided design and machine learning-enhanced discovery for next-generation industry-scale battery technologies†
Joy
Datta
a,
Nikhil
Koratkar
b and
Dibakar
Datta
 *a
*a
aDepartment of Mechanical and Industrial Engineering, New Jersey Institute of Technology (NJIT), Newark, NJ 07052, USA. E-mail: dibakar.datta@njit.edu; Tel: +1 973 596 3647
bDepartment of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, New York 12180, USA
First published on 25th March 2024
Abstract
Lithium–ion batteries (LIBs) are ubiquitous in everyday applications. However, lithium (Li) is a limited resource on the planet and, therefore, not sustainable. As an alternative to lithium, earth-abundant and cheaper multivalent metals such as aluminum (Al) and calcium (Ca) have been actively researched in battery systems. However, finding suitable intercalation hosts for multivalent-ion batteries is urgently needed. Open-tunneled oxides represent a specific category of microparticles distinguished by the presence of integrated one-dimensional channels or nanopores. This work focuses on two promising open-tunnel oxides: niobium tungsten oxide (NTO) and molybdenum vanadium oxide (MoVO). The MoVO structure can accommodate a larger number of multivalent ions than NTO due to its larger surface area and different shapes. Specifically, the MoVO structure can adsorb Ca, Li, and Al ions with adsorption potentials ranging from around 4 to 5 eV. However, the adsorption potential for hexagonal channels of Al ions drops to 1.73 eV due to the limited channel area. The NTO structure exhibits an insertion/adsorption potential of 4.4 eV, 3.4 eV, and 0.9 eV for one Li, Ca, and Al, respectively. Generally, Ca ions are more readily adsorbed than Al ions in both MoVO and NTO structures. Bader charge analysis and charge density plots reveal the role of charge transfer and ion size in the insertion of multivalent ions such as Ca and Al into MoVO and NTO systems. Exploring open-tunnel oxide materials for battery applications is hindered by vast compositional possibilities. The execution of experimental trials and quantum-based simulations is not viable for addressing the challenge of locating a specific item within a large and complex set of possibilities. Therefore, it is imperative to conduct structural stability testing to identify viable combinations with sufficient pore topologies. Data mining and machine learning techniques are employed to discover innovative transition metal oxide materials. This study compares two machine learning algorithms, one utilizing descriptors and the other employing graphs to predict the synthesizability of new materials inside a laboratory setting. The outcomes of this study offer valuable insights into the exploration of alternative naturally occurring multiscale particles that exhibit promising potential for the utilization of multivalent ions in battery-related contexts.
1. Introduction
Rechargeable batteries, specifically secondary batteries, play a critical role in enabling the electrification of automobiles and the storage of energy from renewable sources such as wind and solar.1–3 However, the rising costs of rare-earth lithium have prompted a shift towards multivalent ions, such as aluminum, calcium, magnesium, and zinc. These ions are being investigated as substitutes for lithium–ion battery systems due to their abundant nature1–8 and reduced degradation9 concerns. Consequently, a host material capable of withstanding the mechanical stresses induced by the insertion of multivalent ions is imperative for establishing multivalent-ion batteries as viable and competitive alternatives to lithium–ion batteries.The selection of the active material's particle size used in the anode and cathode is crucial in affecting battery performance.10,11 Traditionally, microparticles have been used in the industry due to their higher volumetric energy density, high mass loading, better scalability, and lower cost.12 Nevertheless, microparticles encounter mechanics, thermodynamics, and kinetics challenges, all of which nanoparticles can solve.13–15 Nanoparticles exhibit enhanced cycle stability over microparticles. Their smaller size allows for more uniform intercalation than microparticles, improving fracture toughness and fatigue life for electrode materials.16–20 Notably, nanoparticles also exhibit superior fast-charging capabilities. Their small size drastically reduces diffusion length, enabling faster charging and discharging ability.21,22 Furthermore, nanoparticles' limited compositional range makes them less conducive to the co-existence of distinct phases within nanostructures. Consequently, phase transitions occur more swiftly in nanostructures, releasing the excess free energy generated from lattice mismatch and high surface area.23–25
Nanostructures, however, come with their distinct set of drawbacks. For instance, the large surface area of nanostructures leads to extensive electrolyte decomposition. Consequently, the solid electrolyte interphase (SEI) layer forms early in the battery cycle, resulting in low first-cycle coulombic efficiency.26–30 Additionally, achieving an industrial standard (20–30 mg cm−2) high mass loading (20–30 mg cm−2) proves problematic with nanostructures.31,32 Nanostructure-based batteries also suffer from low volumetric capacity, significantly limiting their utility in stationary and grid storage applications.19,33,34 Moreover, the synthesis cost of nanostructures is higher, and the manufacturing process generates substantial chemical waste.35–38
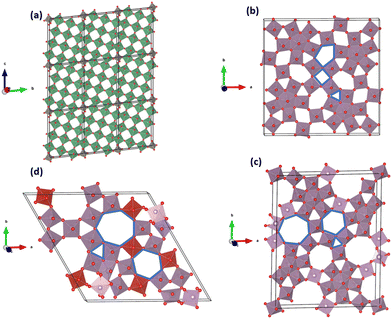
Multiscale particles (MP) embody nanoscale attributes within microscale particles, effectively combining characteristics of both micro and nanostructures,13 potentially yielding the best of both worlds. These particles can be synthesized as engineered multiscale particles (E-MP) or multiscale particles with natural nano-porosity (N-MP). However, manufacturing cost and scalability pose significant challenges for E-MPs.3,32 On the other hand, micro-particles based on open-tunnel oxides, such as niobium tungsten oxide (NTO) and molybdenum vanadium oxide (MoVO), embody naturally formed nanoscale channels, endowing them with exceptionally fast ion diffusion abilities.39,40 N-MP family members display unique characteristics, exemplified by niobium tungsten oxide structures like Nb12WO33, Nb16W5O55, and Nb18W16O93.41,42 For example, Nb12WO33 is a wadsley-roth type crystallographic shear structure composed of (3 × 4) size of MO6 (M = Nb, W) octahedral block.42 These octahedral blocks share edges around the corner, forming open channel-like structures, as shown in Fig. 1a. Kocer et al.41 investigated density functional theory (DFT) to identify Li insertion sites and scrutinized lattice contraction in the Nb12WO33 structure during high Li concentration, enhancing cycle stability. MoVO structures (Fig. 1b–d) can have different polymorphs – orthorhombic (MoV2O8), trigonal (MoV3O6), and tetragonal (MoVO5). Furthermore, these structures feature additional tunnels like hexagonal, heptagonal, pentagonal, and rectangular varieties.39
A thorough analysis of diverse materials is required to improve our understanding of open-tunnel oxide materials. The goal of this research is to uncover previously unknown chemicals that have the potential to surpass current ones. Pursuing an optimal solution through experimental trial and error is improbable, given the extensive range of possible material compositions and stoichiometries. This difficulty is compounded by complex and not fully understood reaction mechanisms.43–45 Hence, selecting the most appropriate candidate from the myriad options becomes a challenge akin to finding a ‘needle in a haystack’.9 Given the limited availability of known open-tunnel oxides with suitable pore sizes for accommodating multiply charged ions, a comprehensive exploration of new compounds becomes imperative.
Transition metal oxides (TMOs), especially at the nanoscale, possess distinctive structural characteristics essential for a wide range of applications.46 Nanotechnology enables precise control of TMO nanostructures, resulting in customized sizes and shapes with excellent surface area-to-volume ratios.47 Utilizing machine learning models trained on transition metal oxide (TMO) characteristics can aid in investigating various open tunnel oxides found in nature, drawing from knowledge and design concepts obtained from TMO nanostructures. Tunnel-structured transition metal oxides (TMOs) constitute a crucial subgroup of TMOs with open channels enabling fast ion transport, including open tunnel oxides.48 Thus, a thorough understanding, and utilization of TMO-based oxide material training data provides critical insights for uncovering and investigating novel open tunnel oxide materials. This undertaking may encompass the study of binary, ternary, quaternary, quinary, and senary-based families of transition metal oxides (TMOs), a task laden with challenges due to the vast array of potential structures stemming from diverse combinations of elements and stoichiometries.49 The number of attainable materials reaches millions by varying the elements and stoichiometric ratios, rendering experimental exploration infeasible. Before selecting stable configurations with acceptable pore architectures for intercalating multiply charged ions, it is critical to analyze the structural stability of potential TMOs to assure their synthesizability.49
To forecast the structural stability of TMOs, a DFT-based energy hull diagram can be constructed by evaluating the formation energy across all conceivable stoichiometric ratios.9 However, the computationally intensive nature of this procedure is exacerbated by the intricate crystal structures and substantial unit cells of TMOs. Furthermore, addressing the “Needle in a Haystack” conundrum using DFT poses challenges due to the multitude of potential multivalent ion insertion sites and the potential for cation disorder.50–52 Molecular modeling employing the MD method presents a possible approach for exploring TMO crystal structures. Nonetheless, this approach hinges on the availability of a suitable interatomic potential, a requirement frequently unmet for oxide materials, constraining the MD method's capacity to explore all feasible combinations of TMO crystal structures. Furthermore, the reliability of the interatomic potential rests on data derived from DFT, which is not without limitations.53
In recent years, deep learning algorithms such as graph neural networks (GNNs) have surfaced as a cost-effective avenue for predicting formation energy and band gap while establishing correlations between structure and properties.54–57 Compared to traditional methods, machine learning (ML) boasts two distinct advantages: compactness and the ability to predict the properties of numerous compounds within seconds without requiring substantial processing power. ML relies exclusively on information garnered from DFT and experimental techniques. Several databases, such as the materials project database (MPD),58 open quantum materials database (OQMD),59 automatic flow for materials discovery (AFLOW),60 and inorganic crystal structure database (ICSD),61 provide the necessary crystal structure data for training and testing, as well as the corresponding property data that is utilized for the application of ML models.
Descriptor-based and GNN-based approaches have demonstrated strong predictive capabilities for material property forecasts.56,62,63 A “descriptor” comprises a numerical vector, employed as input for ML models in materials science, and encompasses diverse choices like coulomb matrix,64 sine coulomb matrix,65 atom-centered symmetry functions,66 smooth overlap of atomic orbitals,67 and orbital field matrix.68 In contrast, GNNs represent a category of deep learning techniques tailored to operate on graph structures. The GNNs are extensively utilized in graph analysis because of their exceptional performance and interpretability. Multiple GNNs such as materials graph network (MEGNet),56 atomistic line graph neural network (ALIGNN),69 continuous graph neural networks (CGNN),70 global attention based graph convolutional neural networks (GATGNN),55 have exhibited strong prediction capabilities about material structures.
In contrast to the research mentioned above conducted with lithium (Li), there currently needs to be more available literature about the incorporation of multivalent ions, such as aluminum (Al) and calcium (Ca), into NTO or MoVO systems. In addition to that, we are extending our study from DFT-based investigations into a ML-focused approach, explicitly aiming to predict the formation energy of naturally occurring TMO. Our whole contribution to this work is organized in two interconnected sections –
1. We investigated the insertion of Ca, Al, and Li into trigonal structures (MoV3O6) that feature a variety of hexagonal, heptagonal, and triangular channels, thereby assessing their adsorption potential. Expanding our analysis, we also explored NTO (Nb12WO33) systems, enabling a comparison of the adsorption capabilities between NTO and MoVO structures. Moreover, we examined the influence of multivalent ion size and charge density on insertion potentials.
2. The preceding section utilized DFT to investigate certain TMOs recognized as stable and experimentally synthesizable. However, the potential number of stable TMOs is infinite, rendering it impossible to conduct DFT calculations for all possible combinations. In this section, we adopt a machine learning approach to identify potential stable TMOs by predicting their formation energy. To accomplish this, we used the MPD to compile an inorganic crystal structure dataset for TMOs. Using this dataset, we trained CNNs and GNNs to predict these materials' formation energy. The test dataset compared both models' performance. Once trained, these ML models allow experimentalists to estimate the synthesizability of unknown crystal structures. Furthermore, akin to the previous section, the predicted stable TMOs can be considered for further exploration via DFT studies in future investigations.
2. Methods
2.1 DFT calculation
We employed DFT for structural optimization, utilizing the vienna ab initio simulation package (VASP)71 in conjunction with the projector augmented wave (PAW)72 method. The Perdew−Burke−Ernzerhof (PBE)73 formulation of the generalized gradient approximation (GGA) represents the exchange–correlation function. We employed an energy cut-off of 520 eV to represent the plane wave basis set. The k-point grid was utilized for Brillouin zone sampling. For molybdenum vanadium oxide (MoVO) and niobium tungsten oxide (NTO) structure, we employed 4 × 4 × 1 and 1 × 4 × 5 k-point grid, respectively. To relax the MoVO and NTO structures, we selected a force tolerance of 0.02 eV Å−1 and an energy-stopping criterion of 10−6 eV Å−1.The adsorption potential (V) is calculated as:
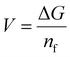 | (1) |
| ΔG = ΔEf + PΔVf − TΔSf | (2) |
| ΔEf = ΔEXnG − (nEx + Eg) | (3) |
2.2 Machine learning approach
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 inorganic structures of TMO-based compositions. It encompasses binary, ternary, quaternary, quinary, and senary TMO compositions. We utilize rigorous approaches to assess the structural characteristics of transition metal oxides (TMOs) in our dataset. We evaluated the void space of the 8098 training data structures using the VoronoiNN approach.76 Among these, 6500 structures had a void space larger than 0.5, suggesting a considerable number with significant empty spaces. This discovery indicates the capacity of the material to host ions or molecules, especially in situations where empty space is advantageous, such as in multivalent ion battery applications. We obtained packing fraction data from the MPD to evaluate the level of porosity. 6190 structures have a packing fraction below 0.5, suggesting that most of them have low packing fractions and a significant level of porosity.9 Materials with reduced packing fractions may have advantageous characteristics for ion diffusion and storage, which are essential for effective multivalent ion battery applications. The data distribution of these TMOs is illustrated in Fig. 2a. We selectively picked the transition metal data due to its relevance in the battery material industry. Notably, there are over 4000 datapoints for quaternary-based TMOs, while binary TMOs are the least represented, with only 313 datapoints (Fig. 2a).
123 inorganic structures of TMO-based compositions. It encompasses binary, ternary, quaternary, quinary, and senary TMO compositions. We utilize rigorous approaches to assess the structural characteristics of transition metal oxides (TMOs) in our dataset. We evaluated the void space of the 8098 training data structures using the VoronoiNN approach.76 Among these, 6500 structures had a void space larger than 0.5, suggesting a considerable number with significant empty spaces. This discovery indicates the capacity of the material to host ions or molecules, especially in situations where empty space is advantageous, such as in multivalent ion battery applications. We obtained packing fraction data from the MPD to evaluate the level of porosity. 6190 structures have a packing fraction below 0.5, suggesting that most of them have low packing fractions and a significant level of porosity.9 Materials with reduced packing fractions may have advantageous characteristics for ion diffusion and storage, which are essential for effective multivalent ion battery applications. The data distribution of these TMOs is illustrated in Fig. 2a. We selectively picked the transition metal data due to its relevance in the battery material industry. Notably, there are over 4000 datapoints for quaternary-based TMOs, while binary TMOs are the least represented, with only 313 datapoints (Fig. 2a).
 | ||
| Fig. 2 Data distribution of TMO based oxide material: (a) number of data present concerning the number of TMOs material compositions, (b) overview of binary TMOs, (c) overview of ternary-based TMOs, (d) training and testing data distribution for the ML model. In (b) and (c), the green color represents the considered material, and red color depicts the ruled-out material from our list. Areas without color in (c) represent the third element in ternary-based TMOs. (b) Shows the binary-based TMOs, where all transitional metals should be present, except for oxygen (O). (c) Represents ternary-based TMOs. In (c), multicomponent materials on TMO consist of elements from any element group except group 1 alkali metals, aligning with our focus on multivalent ions. For example, quaternary-based TMOs follow the format WsArBmOn. Here, W represents any metal from the periodic table, excluding monovalent metals. A represents any metal from the periodic table. B represents the transition metal. The s, r, m, and n, denote the stoichiometry ratio.9 In our ML model, we allocated 80% of our randomly selected data to the training dataset, while the remaining 20% constitutes the testing dataset. | ||
The dataset was retrieved from MP database utilizing the application programming interface (API) with the Matminer77 and python materials genomics (pymatgen)78 libraries in Python. Each data entry is associated with an ICSD ID, ensuring that these crystal structures are also present in the MP and ICSD databases. It is worth noting that the MP database includes a subset of naturally synthesizable ICSD materials.78,79
In this work, we have selected the magpie descriptor and X-ray diffraction pattern for our CNN input data. The descriptor simplifies feature extraction for supplementary applications by transforming these properties into a one-dimensional vector representation. The robust magpie descriptor technique82,83 allows for the calculation of various material properties, including physical, chemical, electrical, ionic, and fundamental characteristics.
The descriptor leverages a statistical analysis of the material's electrical structure, elemental composition, stoichiometric and elemental properties. Also, as part of its electronic structure properties, the descriptor contains information about electronic configuration, such as the typical proportion of electrons from each element's s, p, d, and f valences. The magpie descriptor has widespread applicability across numerous material science fields and can considerably improve the effectiveness and efficiency of materials research. The magpie features on pymatgen78 library python with 132 dimensions represent a crystal structure's material properties.
Another descriptor is X-ray diffraction pattern, which plays a pivotal role in the experimental technique for determining the crystal structure of synthesized materials. It provides valuable insights into the atomic arrangement throughout the lattice. In the present dataset, we readily access XRD data from the MP Database58 and incorporate it as one of the structure-based descriptors in this study. Previous work by Aguiar et al.84 demonstrated using XRD descriptors for classifying the space group of crystal structures.
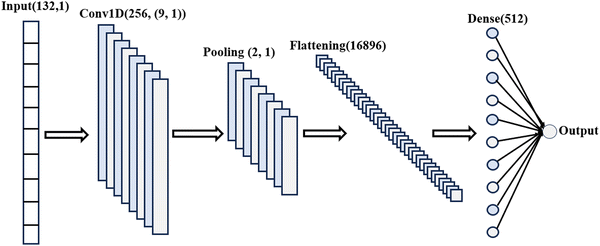
To incorporate XRD descriptors into our ML model for this study, we utilize the featurization tools provided by the Matminer library.77 The XRD featurizer transforms atomic positions into a one-dimensional (1D) array, effectively capturing essential crystal structure and phase information. The entire CNN architecture is depicted in Fig. 3. We applied ReLU activation function after the convolutional layer and dropout after average pooling operation and dense operation to avoid overfitting.
To select the optimal hyperparameters, we employed Bayesian optimization using the keras tuner library available in keras.85–87 Bayesian optimization has demonstrated remarkable effectiveness in determining the optimal hyperparameters for predicting material properties.88,89 Our technique involved dividing our datapoints into several subsets for the purposes of training and validation. More precisely, we employed an 80–20 division, allocating 80% of the data for training the model and reserving 20% of this training data for validation purposes during the hyperparameter tuning stage. The utilization of this validation set was crucial in fine-tuning the model's hyperparameters using Bayesian optimization. The best hyperparameters were determined by evaluating the root mean square error (RMSE) on the validation dataset.
2.2.3.1 MEGNet. The MEGNet framework, stands for materials graph network, is an implementation of graph networks for universal machine learning in materials science developed by DeepMind.56 The MEGNet architecture is constructed by stacking multiple MEGNet blocks. This architecture incorporates a dense layer that takes in three attributes: atomic state, binding state, and global state. The vectors are subsequently reduced and concatenated. MEGNet is essentially a sequence of update operations, facilitating the transformation from the initial graph G = (E, V, u) to the updated graph G* = (E*, V*, u*). The MEGNet structure comprises a series of MEGNet blocks that process atomic, binding, and global states, followed by vector reduction, concatenation, and update operations.
The MEGNet framework has been highly accurate in predicting molecular and crystalline properties using GNNs that can learn from the underlying structure of materials, including atoms, bonds, and crystal lattices. One of the main advantages of using GNNs is their ability to capture complex relationships among various atoms and their spatial arrangements.
2.2.3.2 DeeperGATGNN. DeeperGATGNN is an advanced GNN model designed to predict the properties of inorganic molecules.90 Building upon the successful GATGNN model,55 DeeperGATGNN addresses the challenge of over-smoothing, which limits the depth of the network. This limitation is overcome by incorporating additive skip-connections and differentiable group normalization (DGN) layers. The architecture of DeeperGATGNN comprises augmented graph attention (AGAT) layers, DGN operators, skip connections, a global attention layer, global pooling, and fully connected hidden layers. Through extensive experiments, DeeperGATGNN demonstrates superior performance compared to existing methods in predicting inorganic materials' properties. Furthermore, it provides interpretability by highlighting each atom's contribution. DeeperGATGNN represents a significant advancement in inorganic materials property prediction by effectively extracting inter-atomic-dependent features and overcoming the over-smoothing limitation.
2.2.3.3 ALIGNN. The ALIGNN model69 utilizes edge-gated graph convolution91 to update the atomistic bond graph and its corresponding line graph. This model consists of two main parts: the bond graph and line graph. In bond graph, atoms are considered as nodes, and bonds are represented as edges, following a similar approach to the two models described earlier. The line graph, however, presents bonds as nodes, and edges connect pairs of bonds that share a common atom. This variant of graph convolution allows for aggregation of features from bond pairs and effective updates to atom and bond representations.
ALIGNN derives the atomistic line graph from the atomistic graph to incorporate angular information. Every node in the line graph corresponds to an edge in the original graph, representing interatomic bonds. The initial edge characteristics in the line graph are obtained through a radial basis function (RBF) expansion of the bond angle cosines. ALIGNN collects more details of atomic structure by incorporating angle information, improving its capacity to predict material properties.
The primary goal of ALIGNN is to develop a model that captures the complex interactions between atoms and bonds in crystal structures. By leveraging edge-gated graph convolution and incorporating angular information through the atomistic line graph, ALIGNN improves the accuracy of material property predictions. It provides a comprehensive representation of the atomic system, facilitating efficient information propagation between the atomistic bond graph and its line graph. This results in the effective capture of crucial features that influence material properties, particularly in crystals.69
3. Results and discussion
3.1 DFT analysis of adsorption potential and charge density
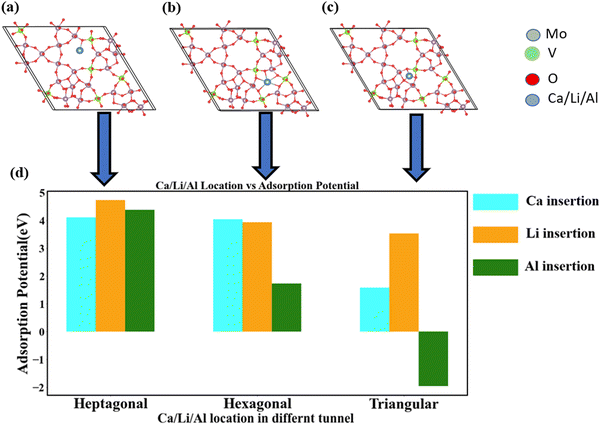
We inserted Ca into trigonal MoVO structures, specifically targeting three different types of channels: heptagonal, hexagonal, and triangular shapes.11 These channels contain 7-, 6-, and 3-membered rings, respectively. Identifying the most stable ion position within these channels is crucial. For this purpose, we strategically inserted Ca at various locations within the hexagonal and heptagonal tunnels, assessing the most stable position by comparing the energy of the optimized structures. The heptagonal and hexagonal channels have dimensions of approximately 5–6 Å, which are five times larger than the Ca ion (Ca2+),39 making them well-suited for the intercalation of Ca, as depicted in Fig. S1(b)–(f) (ESI†).Given the limited space within the triangular tunnel, it can only accommodate a single Ca ion. To facilitate a clearer evaluation of the difference in adsorption potential, we inserted 2 Ca ions into both the heptagonal and hexagonal tunnels. For a single Ca ion, the heptagonal and hexagonal tunnels exhibited nearly equivalent adsorption favorability of 4 eV (Fig. S1b, c and g, ESI†). Subsequently, we explored the insertion of 2 Ca ions into the heptagonal and hexagonal tunnels. In this case, the adsorption potential for the heptagonal and hexagonal channels is 3.06 eV and 2.07 eV, respectively. Consequently, the heptagonal channel emerged as the more favorable choice for Ca insertion compared to the other channels.
Given that Li has smaller charge density (Table 1) and size compared to Ca, we conducted a similar study using Li to investigate the influence of charge density and particle size. In this investigation, we explored the insertion of Li into both heptagonal and hexagonal channels, allowing Li to reposition itself to achieve the most optimized structure.
| Ion name | Heptagonal 1 ion | Hexagonal 1 ion | Trigonal 1 ion | Heptagonal 2 ion | Hexagonal 2 ion | |
|---|---|---|---|---|---|---|
| Charge transfer (e per atom) | Ca | 1.08 | 1.57 | 1.42 | 1.22 | 1.25 |
| Li | 0.55 | 0.69 | 0.63 | 0.38 | 0.46 | |
| Al | 1.28 | 1.04 | 1.65 | 1.06 | 1.26 |
For the insertion of a single Li atom, the highest adsorption potential was observed within the heptagonal tunnel (4.73 eV, Fig. S2a and f, ESI†). Conversely, the lowest adsorption potential was found in the triangular channel (3.53 eV, Fig. S2c and f, ESI†). Fig. S2f (ESI†) illustrates that even after introducing 2 Li atoms into both the heptagonal and hexagonal channels, the adsorption potential remains relatively high. The adsorption potential for the heptagonal and hexagonal channels is 4.22 eV and 3.46 eV, respectively. Consequently, the atomic size plays a significant role in enhancing the adsorption potential for 2 Li atoms (Fig. S2f, ESI†).
Al was introduced using the same intercalation process to assess the channels’ comparative capabilities. However, when considering triangular channels (Fig. S3c, ESI†), Al could not be successfully inserted due to an unfavorable adsorption potential of −1.95 eV (Fig. S3f, ESI†). The highest adsorption favorability for a single Al atom is observed within the heptagonal channel (4.39 eV, Fig. S3f, ESI†). In contrast, the adsorption potential within the hexagonal tunnel is less than 50% compared to the heptagonal channel (Fig. S3f, ESI†). A larger channel size favors Al to achieve this high adsorption potential for the heptagonal channel (Fig. S3f, ESI†), which has 1.5 times more area in comparison with hexagonal channel. In the case of hexagonal channels, the ability to accommodate 2 Al atoms proved challenging because of low adsorption favorability (0.66 eV, Fig. S3f, ESI†).
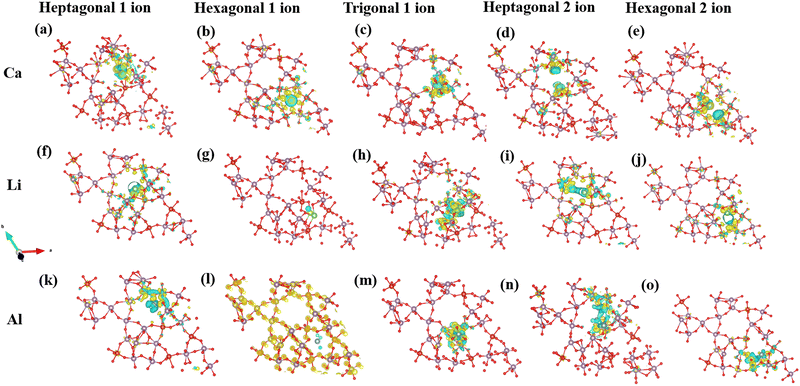
Fig. 4 presents a performance comparison of the adsorption capabilities of Ca, Li, and Al. Notably, Li exhibits the highest adsorption ability across various channel shapes. Ca demonstrates a nearly equivalent intercalation ability to Li, despite having a larger particle size compared to both Li and Al. However, as the channel dimensions decrease from heptagonal to triangular, Al exhibits a significantly poorer adsorption potential compared to Li and Ca (Fig. 4(d)). This discrepancy can be primarily attributed to Al's notably high charge density (Table 1).
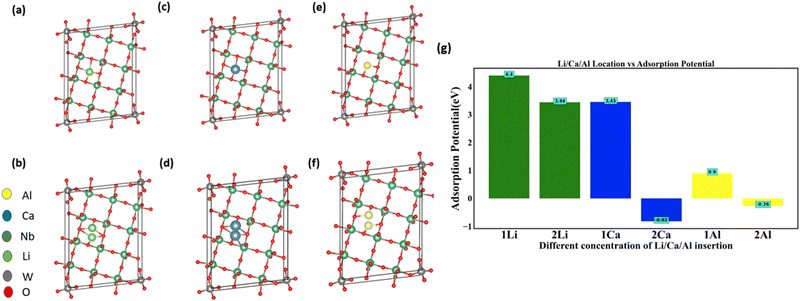
Another multiscale particle with naturally occurring nanochannels is the NTO-based structure, with one of its family members being Nb12WO33.41,42 Similar to MoVO structures, we computed the adsorption potential for the insertion of Li, Ca, and Al insertion into NTO using DFT. In Nb12WO33, there is a single rectangular-shaped channel available for insertion. We inserted Li, Ca, and Al into those channels at various concentrations (Fig. 5a–f). For the insertion of 1 and 2 Li atoms, the adsorption potential (Fig. 5g) is 4.4 eV and 3.44 eV, respectively. In contrast, 2 Ca and 2 Al atoms insertion into the channel resulted in the adsorption potential of −0.82 eV and −0.26 eV, respectively (Fig. 5g). However, insertion favorability of 2 Ca and 2 Al is positive for the MoVO structure because heptagonal and hexagonal channels have areas of 41.67 Å2 and 27.19 Å2, respectively. However, for NTO, the area is only 15.36 Å2. These results indicate that channel area and charge density of cation (Table 2) play an important factor for adsorption favorability. Our results indicate that inserting multivalent ions into the MoVO structure is more advantageous as compared to NTO.
| Ion name | 1 Ion | 2 Ions | |
|---|---|---|---|
| Charge transfer (e per atom) | Ca | 1.36 | 1.13 |
| Li | 0.22 | 0.26 | |
| Al | 1.53 | 3.01 |
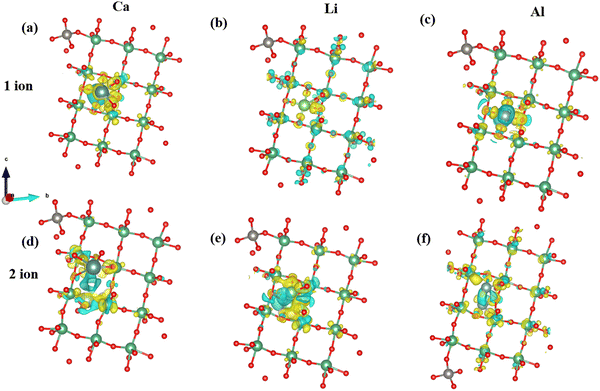
To gain a comprehensive understanding of the charge distribution within the MoVO and NTO structures, we conducted Bader charge analysis and computed the charge density difference (Δρ).92
| Δρ = ρA+B − (ρA + ρB) | (4) |
ρ A indicates the charge density of the MoVO/NTO crystal structures, while ρB represents the density of the cation. The Bader charge analysis has determined the number of charge transfers between cations and MoVO structures. Table 1 displays the results, showing that when 1 Al ion is inserted into a triangular channel, there is a charge transfer of 1.65 e per atom, which is higher than other cations. The charge density plot in Fig. 6 illustrates the relationship between charge accumulation and depletion. In Fig. 6m, Al ions exhibit the weakest interactions with all cations at these positions. Consequently, the negative adsorption potential observed in Fig. S3 and S4 (ESI†) can be attributed to the lowest ionization of Al ion and MoVO structure at the triangular channel.
When contemplating the transfer of two ions, the charge transfer exhibits distinct characteristics owing to dipole–dipole interactions. These interactions can disturb the electronic structure of the atoms engaged in the exchange, causing modifications in electron density distribution. The redistribution of charges significantly impacts the overall transfer of charge, as alterations in electron density directly influence the kinetics of charge transfer. Consequently, the charge transfer efficiency is lower for transferring two ions in the MoVO structure compared to sharing a single ion.
Charge transfer for NTO structures is highest for 1 Al ion (Table 2). Consequently, the adsorption potential is lowest for a single ion insertion (Fig. 5g). Concerning two ions insertion, Ca exhibits the highest charge transfer relative to other cations (Table 2). Introducing two ions can elicit cooperative phenomena and facilitate a more extensive redistribution of charges inside the NTO structure. This can lead to more robust interactions with the host material and higher charge transfer compared to a scenario involving only a single ion. Consequently, the insertion of two Ca ions has the lowest potential for adsorption. In a broader context, our charge investigations reveal a negative correlation between the potential for adsorption and the extent of charge transfer within the NTO structure. An increase in charge transfer is inversely proportional to the degree of adsorption (Fig. 7) in the NTO structure.
3.2 ML approach for discovering intercalation hosts
We trained our input data using a CNN model that incorporates XRD patterns and magpie descriptors. In the process, we conducted an exhaustive search for optimal hyperparameters, encompassing various aspects such as the best convolutional layer, dense layer, number of nodes in each dense layer, learning rate, dropout rate, and optimizers. For magpie descriptors, the optimal architecture comprises a single convolution layer and one dense layer with 512 nodes. Conversely, when utilizing XRD featurizers, the best configuration entails two convolution layers and three dense layers with 512, 512, and 32 nodes, respectively. For both featurizers, we applied 1D average pooling to reduce spatial dimensionality of the input signal while retaining the essential features. We selected the ReLu activation function to accomplish the desired CNN outcomes. To mitigate overfitting, dropout rates ranging from 0.5 to 0.3 were implemented after each convolutional layer and dense layers.We evaluated the validation dataset results for all two input data types to choose the best hyperparameters. In our research, we employ the commonly used RMSE metric for assessing prediction accuracy in predictive modeling. RMSE provides a numerical representation of the typical “distance” between model-predicted values and actual values, with lower RMSE values indicating a closer match to the data.
The RMSE values for the 2026 test dataset for 1-dimensional magpie descriptors and 1-dimensional XRD pattern are 0.25 eV per atom (see Fig. 8b) and 0.56 eV per atom (see Fig. 8a), respectively. Fig. 8 displays the trendline between the actual and predicted values for the two descriptors. The x-axis in this scattering plot represents the actual formation energies, while the y-axis represents the predicted formation energies. The scatter plot in Fig. 8 demonstrates the low variability or dispersion of predicted development forces compared to the calculated values. The dark data points in the graph represent the TMO materials with actual formation energies falling within the silicon range of −4.5 to 1.5 eV. Consequently, based on the 1-dimensional CNN model using these descriptors, magpie descriptors prove to be the more effective input data featurization approach for predicting the TMO-based formation energies (see Fig. 8).
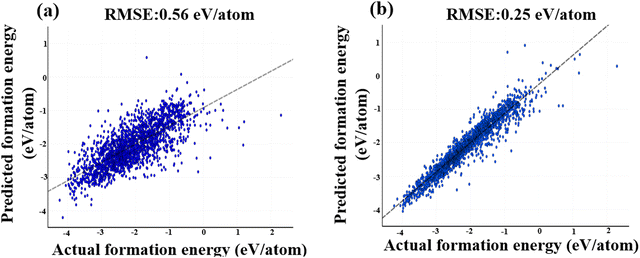 | ||
| Fig. 8 Visualization of CNN-based model predictions, showcasing the relationship between actual and predicted values using two distinct featurization methods: (a) XRD patterns, and (b) magpie descriptors. As evident from Fig. 8(b), the magpie descriptors resulted in predictions that exhibited sparser and less pronounced deviations from the actual values, in contrast to the other featurization method. | ||
In our pursuit of more accurate material property predictions, we explored the use of crystal-based graph conversion as our input data. For this purpose, we leveraged the MEGNet model, equipped with carefully selected parameters: a batch size of 32, a learning rate of 0.00075, and an L2 regularization coefficient of 0.001. We conducted training for 300 epochs, keeping these parameters56 consistent. Initially, we employed a cutoff radius of 5 Å to capture crystal structure interactions. However, recognizing the potential significance of long-range interactions, we expanded the cutoff radius to 6 Å to investigate their effects.
Interestingly, this modification did not yield a significant improvement in the model's performance. The system's predicted properties may be primarily influenced by short-range interactions, with long-range interactions playing a negligible role in this context. Furthermore, we employed an elemental embedding of 16 and selected three blocks to optimize the model's generalization capabilities. Although we experienced with different block numbers, ranging from 3 to 5, there is no substantial improvement in performance.
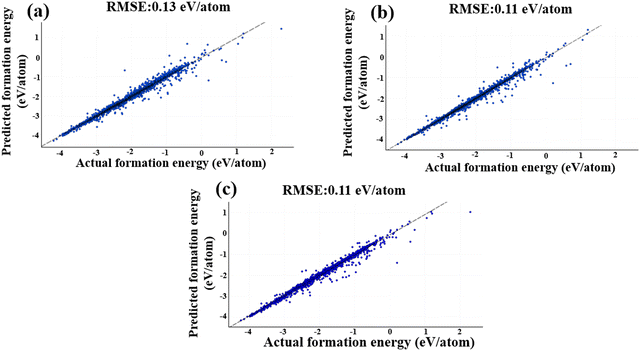
Fig. 9 illustrates the MEGNet model's performance, using the same test dataset as the descriptor data, achieving an RMSE value of 0.13 eV per atom. This represents a significant improvement compared to the Magpie descriptors, where the RMSE value was 0.25 eV per atom. The performance of the MEGNeT model is visualized in Fig. 9(a).
As we considered the number of graph convolutional layer, it's important to note that an excessive increase in layers can lead to over-smoothing issues. DeeperGATGNN applies DGN and skip connections for training the data. Our implementation utilized a learning rate of 0.005 and batch size of 100. The model architecture consists of multiple layers, including a single pre-fully connected layer, several graph convolution layers, and no post fully connected layer. The model employs a “global_add_pool” pooling mechanism for effective global information aggregation and follows an “early” pooling order. The DeeperGATGNN model employs a graph representation with a maximum atomic interaction radius of 12 Å and a maximum of 12 neighboring atoms per atom, effectively capturing local atomic connectivity.
All training data underwent 300 epochs of training. To determine the optimal number of GNN layers, we studied with 10, 15 and 20 layers. Other parameters adhered to the default settings of DeeperGATGNN.90 Surprisingly, the best test RMSE value of 0.11 eV per atom was obtained with 10 GNN layers, beyond which the performance began to deteriorate, resulting in an RMSE value of 0.13 eV per atom for 15 and 20 GNN layers. This decline in performance can be attributed to the excessive increase in learning parameters when utilizing a larger number of GNN layers, which can hinder model performance, particularly with a limited training dataset. Fig. 9b presents the performance of the DeeperGATGNN model.
In this study, we introduced the ALIGNN model, which leverages cutting-edge technology and complex algorithms to extract significant characteristics and properties of individual atoms within the molecular structure. This model comprises four alignment layers and four graph convolutional layers, with input features spanning 92-dimensional atomic attributes, 80 interatomic bond features, and 40 triplet input features.69 As a result of the inconclusive outcomes observed when experimenting with different cutoff radius values, we decided to utilize the default value of 8 Å in the ALIGNN model, which permits the inclusion of up to 12 adjacent atoms per atom.69
By encoding the molecular structure into a lower-dimensional space using an embedding feature size of 64, the ALIGNN model efficiently extracts essential structural information and aligns molecular graphs. The inclusion of hidden features, set at 256, empowers the model to learn intricate patterns and representations effectively. For the ALIGNN model, the test RMSE is 0.11 eV per atom, underlining its exceptional predictive capabilities. Fig. 9c represents the exemplary performance of the ALIGNN model.
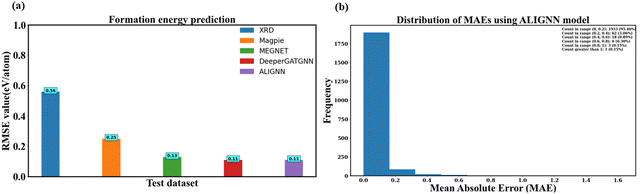
Fig. 10a compares RMSE values between human-crafted descriptors and the GNN model. Notably, human-crafted descriptors appear to encompass critical structure–property relationships. Magpie descriptors stand out as the best performing, with an RMSE value of 0.25 eV per atom. However, the best RMSE value is obtained from ALIGNN and DeeperGATGNN models, both exhibiting an RMSE value of 0.11 eV per atom. This represents a remarkable 56% improvement in human-crafted descriptors. ALIGNN, in particular, emerges as the top-performing model, achieving this exceptional RMSE value with fewer convolutional layers.
In contrast, the DeeperGATGNN model necessitates a more intricate hyperparameter optimization process, consuming computational resources, and time. ALIGNN distinguishes itself as the sole three-GNN model investigated in this study, preserving atom representations (one-body), bond representations (two-body), and bond angle representations (three-body). This distinguishing feature holds immense promise for capturing and portraying the periodic correlations inherent in crystal formations, thereby making a significant contribution to the field.
Fig. 10b illustrates the distribution of mean absolute error (MAE) using ALIGNN. The analysis reveals that nearly 95% of the test samples (1933 instances) exhibit an error below 0.2 eV per atom, and half of the data showcases an error below this threshold. The overall average error, represented as the MAE, stands at approximately 0.05 eV per atom. Fig. 10b provides a quantitative assessment of our model's performance, indicating that in 98.52% of cases, the model accurately predicts the formation energy/atom with an error below 0.40 eV per atom.
However, the ALIGNN model exhibits limitations in predicting the formation energy per atom for three specific structures (mp-690844, mp-1191949, mp-27873), as indicated by their higher MAE values exceeding 1. Upon detailed analysis, it becomes apparent that the graph representation employed by the ALIGNN model may not fully encapsulate the intricacies of interactions within these structures, leading to more pronounced prediction errors. One noteworthy observation from these cases is that ALIGNN primarily focuses on explicitly encoding three-body interactions. However, including higher-order n-body interactions (where n is greater than or equal to 4) could enhance the predictive capability of the ALIGNN model. Various studies in GNN have explored the incorporation of n-body interactions for diverse applications.93–96
4. Conclusions
We conducted first-principles calculations involving the insertion of both monovalent (Li) and multivalent (Ca, Al) species into multiscale oxide particles, characterized by one-dimensional nanochannels, exemplified by NTO and MoVO structures. A comparison of the adsorption potential of Ca, Li, and Al ions shows that the MoVO structure is more favorable to accommodate multivalent ions than NTO. The larger channel areas and different shapes of available channels, such as hexagonal, heptagonal, and triangular shapes, make MoVO a superior intercalation host for multivalent ions when compared to NTO structures.The results from Bader charge analysis and charge density plots have unveiled that Al ions exhibit the lowest insertion favorability for both MoVO and NTO structures, primarily due to Al's substantial charge transfer to these materials. Meanwhile, Ca ions demonstrate adsorption behavior akin to monovalent Li ions but encounter challenges when inserted into the smaller channels of NTO structures, particularly when accommodating 2 Ca ions. Hence, it becomes evident that channel dimension, ion size, and ion charge density collectively play pivotal roles in the insertion of ions into MoVO and NTO structures. This deep understanding of ion insertion processes is critical for exploring materials with improved ion storage.
To lay the groundwork for future material screening methodologies, we gathered an extensive dataset of TMOs from the ICSD. The dataset has diverse structural compositions with empty spaces and nanochannels resembling those seen in NTO and MoVO structures, such open-tunnel oxides. In our research employing GNNs, we explored various methods for representing graphs. The ALIGNN and DeeperGATGNN models outperformed conventional descriptors, highlighting the effectiveness of graph-based representations in predicting formation energy. Based on these results, we aim to employ ML algorithms to forecast the stability of additional promising open-tunneled oxide materials for more efficient multivalent-ion batteries.
In the future, our focus will be on inverse machine learning (IML), a method that enables the creation of new crystal structures from TMOs.9,97 IML combined with our ML model holds great promise for predicting materials with specific characteristics including porosity, tunnel structure, formation energy, and conductivity (Fig. S3, ESI†).9 The generative adversarial network (GAN) represents a potential approach IML, having successfully generated novel crystal structures with specific properties, expanding the scope of materials that can be developed beyond current databases.97
Structures generated by IML can undergo further screening using our ML models to forecast stability, electronic and ionic conductivity, and pore sizes. By integrating ML with IML, we can effectively explore a wide variety of material parameters, leading to the identification of robust, conductive, and structurally strong intercalation hosts for multivalent-ion batteries. This approach simplifies the practical process of material screening, thereby advancing state-of-the-art materials for energy storage solutions.
Author contributions
D. D. and N. K. conceived the project. J. D. performed all work and wrote the manuscript with D. D. and N. K. All authors approved the final version of the manuscript.Data availability
Data can be obtained by requesting the corresponding author.Code availability
Code for extracting the data and its training model is available on GitHub (https://github.com/joy1303125/Graph-vs.-Descriptor-Approaches-for-Natural-Transition-Metal-Oxide-Discovery), providing researchers in the field with a valuable resource. Restrictions apply to the availability of the simulation codes, which were used under license for this study.Conflicts of interest
The authors have no conflicts of interest to declare. All authors have seen and agree with the contents of the manuscript and there is no financial interest to report. We certify that the submission is original work and is not under review at any other publication.Acknowledgements
The work is supported by National Science Foundation (NSF) (Award Number # 2126180, # 2126178, #2237990). Authors acknowledge Advanced Cyberinfrastructure Coordination Ecosystem: Service & Support (ACCESS) for the computational facilities (Award Number – DMR180013).References
- H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Mg Rechargeable Batteries: An on-Going Challenge, Energy Environ. Sci., 2013, 6(8), 2265–2279 RSC.
- G. A. Elia, K. Marquardt, K. Hoeppner, S. Fantini, R. Lin, E. Knipping, W. Peters, J. Drillet, S. Passerini and R. Hahn, An Overview and Future Perspectives of Aluminum Batteries, Adv. Mater., 2016, 28(35), 7564–7579 CrossRef CAS PubMed.
- J. Muldoon, C. B. Bucur and T. Gregory, Quest for Nonaqueous Multivalent Secondary Batteries: Magnesium and Beyond, Chem. Rev., 2014, 114(23), 11683–11720 CrossRef CAS PubMed.
- R. J. Gummow, G. Vamvounis, M. B. Kannan and Y. He, Calcium-ion Batteries: Current State-of-the-art and Future Perspectives, Adv. Mater., 2018, 30(39), 1801702 CrossRef PubMed.
- A. Ponrouch and M. R. Palacin, On the Road toward Calcium-Based Batteries, Curr. Opin. Electrochem., 2018, 9, 1–7, DOI:10.1016/j.coelec.2018.02.001.
- N. R. Niloy, M. I. Chowdhury, M. A. H. Shanto, J. Islam and M. M. Rhaman, Multiferroic Bismuth Ferrite Nanocomposites as a Potential Photovoltaic Material, IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2021, vol. 1091, p. 12049 Search PubMed.
- M. A. H. Shanto, M. I. Chowdhury, A. B. Antu, N. R. Niloy, N. Alam, M. A. Ullah and M. S. Anowar, MXene Based Heterostructures for Electrode Materials of Batteries: A Review, IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2022, vol. 1225, p. 12018 Search PubMed.
- B. S. Vishnugopi, Mesoscale Physics of Electrified Interfaces with Metal Electrodes, Purdue University, 2023 Search PubMed.
- A. S. Lakhnot, R. A. Panchal, J. Datta, V. Mahajani, K. Bhimani, R. Jain, D. Datta and N. Koratkar, Intercalation Hosts for Multivalent-Ion Batteries, Small Struct., 2022, 2200290, 2200290, DOI:10.1002/sstr.202200290.
- S. Chu, Y. Cui and N. Liu, The Path towards Sustainable Energy, Nat. Mater., 2017, 16(1), 16–22 CrossRef PubMed.
- S. Chu and A. Majumdar, Opportunities and Challenges for a Sustainable Energy Future, Nature, 2012, 488(7411), 294–303 CrossRef CAS.
- M. S. Whittingham, History, Evolution, and Future Status of Energy Storage, Proc. IEEE, 2012, 100, 1518–1534 CAS.
- R. Jain, A. S. Lakhnot, K. Bhimani, S. Sharma, V. Mahajani, R. A. Panchal, M. Kamble, F. Han, C. Wang and N. Koratkar, Nanostructuring versus Microstructuring in Battery Electrodes, Nat. Rev. Mater., 2022, 7(9), 736–746, DOI:10.1038/s41578-022-00454-9.
- J. Datta, D. Datta and V. Sharma, Transferable and Robust Machine Learning Model for Predicting Stability of Si Anodes for Multivalent Cation Batteries, J. Mater. Sci., 2023, 58(27), 11085–11099, DOI:10.1007/s10853-023-08705-y.
- K. G. Naik, B. S. Vishnugopi, J. Datta, D. Datta and P. P. Mukherjee, Electro-Chemo-Mechanical Challenges and Perspective in Lithium Metal Batteries, Appl. Mech. Rev., 2023, 75(1), 10802 CrossRef.
- W. Qi, J. G. Shapter, Q. Wu, T. Yin, G. Gao and D. Cui, Nanostructured Anode Materials for Lithium-Ion Batteries: Principle, Recent Progress and Future Perspectives, J. Mater. Chem. A, 2017, 5(37), 19521–19540 RSC.
- J. Graetz, C. C. Ahn, R. Yazami and B. Fultz, Highly Reversible Lithium Storage in Nanostructured Silicon, Electrochem. Solid-State Lett., 2003, 6(9), A194 CrossRef CAS.
- X. H. Liu, L. Zhong, S. Huang, S. X. Mao, T. Zhu and J. Y. Huang, Size-Dependent Fracture of Silicon Nanoparticles during Lithiation, ACS Nano, 2012, 6(2), 1522–1531 CrossRef CAS PubMed.
- M. A. H. Shanto, N. R. Niloy, R. Islam, M. I. Chowdhury, M. M. Abrar and S.-A. Imam, Effect of Channel Length and Dielectric Constant on Carbon Nanotube FET to Evaluate the Device Performance, 2020 4th International Conference on Electronics, Materials Engineering & Nano-Technology (IEMENTech), IEEE, 2020, pp. 1–4 Search PubMed.
- M. S. Uddin, R. A. Mayanovic and M. Benamara, On the Synthesis and Characterization of Bimagnetic CoO/NiFe2O4 Heterostructured Nanoparticles, AIP Adv., 2023, 13(2), 025314 CrossRef CAS.
- Y. Tang, Y. Zhang, W. Li, B. Ma and X. Chen, Rational Material Design for Ultrafast Rechargeable Lithium-Ion Batteries, Chem. Soc. Rev., 2015, 44(17), 5926–5940 RSC.
- P.-C. Tsai, B. Wen, M. Wolfman, M.-J. Choe, M. S. Pan, L. Su, K. Thornton, J. Cabana and Y.-M. Chiang, Single-Particle Measurements of Electrochemical Kinetics in NMC and NCA Cathodes for Li-Ion Batteries, Energy Environ. Sci., 2018, 11(4), 860–871 RSC.
- E. Madej, F. La Mantia, W. Schuhmann and E. Ventosa, Impact of the Specific Surface Area on the Memory Effect in Li-Ion Batteries: The Case of Anatase TiO2, Adv. Energy Mater., 2014, 4(17), 1400829 CrossRef.
- A. Van der Ven and M. Wagemaker, Effect of Surface Energies and Nano-Particle Size Distribution on Open Circuit Voltage of Li-Electrodes, Electrochem. Commun., 2009, 11(4), 881–884 CrossRef CAS.
- X. Guo, B. Song, G. Yu, X. Wu, X. Feng, D. Li and Y. Chen, Size-Dependent Memory Effect of the LiFePO4 Electrode in Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2018, 10(48), 41407–41414 CrossRef CAS PubMed.
- K. Xu, Electrolytes and Interphases in Li-Ion Batteries and Beyond, Chem. Rev., 2014, 114(23), 11503–11618 CrossRef CAS PubMed.
- C. Keller, A. Desrues, S. Karuppiah, E. Martin, J. P. Alper, F. Boismain, C. Villevieille, N. Herlin-Boime, C. Haon and P. Chenevier, Effect of Size and Shape on Electrochemical Performance of Nano-Silicon-Based Lithium Battery, Nanomaterials, 2021, 11(2), 307 CrossRef CAS PubMed.
- S. Y. Lai, K. D. Knudsen, B. T. Sejersted, A. Ulvestad, J. P. Mæhlen and A. Y. Koposov, Silicon Nanoparticle Ensembles for Lithium-Ion Batteries Elucidated by Small-Angle Neutron Scattering, ACS Appl. Energy Mater., 2019, 2(5), 3220–3227 CrossRef CAS.
- P. Hundekar, S. Basu, X. Fan, L. Li, A. Yoshimura, T. Gupta, V. Sarbada, A. Lakhnot, R. Jain and S. Narayanan, In Situ Healing of Dendrites in a Potassium Metal Battery, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(11), 5588–5594 CrossRef CAS PubMed.
- L. Li, Z. Li, A. Yoshimura, C. Sun, T. Wang, Y. Chen, Z. Chen, A. Littlejohn, Y. Xiang and P. Hundekar, Vanadium Disulfide Flakes with Nanolayered Titanium Disulfide Coating as Cathode Materials in Lithium-Ion Batteries, Nat. Commun., 2019, 10(1), 1764 CrossRef.
- F. Wang, R. Robert, N. A. Chernova, N. Pereira, F. Omenya, F. Badway, X. Hua, M. Ruotolo, R. Zhang and L. Wu, Conversion Reaction Mechanisms in Lithium Ion Batteries: Study of the Binary Metal Fluoride Electrodes, J. Am. Chem. Soc., 2011, 133(46), 18828–18836 CrossRef CAS PubMed.
- I. A. Courtney, W. R. McKinnon and J. R. Dahn, On the Aggregation of Tin in SnO Composite Glasses Caused by the Reversible Reaction with Lithium, J. Electrochem. Soc., 1999, 146(1), 59 CrossRef CAS.
- Z. Karkar, T. Jaouhari, A. Tranchot, D. Mazouzi, D. Guyomard, B. Lestriez and L. Roué, How Silicon Electrodes Can Be Calendered without Altering Their Mechanical Strength and Cycle Life, J. Power Sources, 2017, 371, 136–147 CrossRef CAS.
- Y.-K. Sun, S.-M. Oh, H.-K. Park and B. Scrosati, Micrometer-Sized, Nanoporous, High-Volumetric-Capacity LiMn0.85Fe0.15PO4 Cathode Material for Rechargeable Lithium-Ion Batteries, Adv. Mater., 2011, 23(43), 5050–5054 CrossRef CAS PubMed.
- S.-K. Jung, I. Hwang, D. Chang, K.-Y. Park, S. J. Kim, W. M. Seong, D. Eum, J. Park, B. Kim and J. Kim, Nanoscale Phenomena in Lithium-Ion Batteries, Chem. Rev., 2019, 120(14), 6684–6737 CrossRef PubMed.
- G. Berckmans, M. Messagie, J. Smekens, N. Omar, L. Vanhaverbeke and J. Van Mierlo, Cost Projection of State of the Art Lithium-Ion Batteries for Electric Vehicles up to 2030, Energies, 2017, 10(9), 1314 CrossRef.
- X. Fan, Y. Zhu, C. Luo, L. Suo, Y. Lin, T. Gao, K. Xu and C. Wang, Pomegranate-Structured Conversion-Reaction Cathode with a Built-in Li Source for High-Energy Li-Ion Batteries, ACS Nano, 2016, 10(5), 5567–5577 CrossRef CAS PubMed.
- K.-F. Hsu, S.-Y. Tsay and B.-J. Hwang, Synthesis and Characterization of Nano-Sized LiFePO 4 Cathode Materials Prepared by a Citric Acid-Based Sol–Gel Route, J. Mater. Chem., 2004, 14(17), 2690–2695 RSC.
- A. S. Lakhnot, K. Bhimani, V. Mahajani, R. A. Panchal, S. Sharma and N. Koratkar, Reversible and Rapid Calcium Intercalation into Molybdenum Vanadium Oxides, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(30), e2205762119 CrossRef CAS PubMed.
- A. S. Lakhnot, T. Gupta, Y. Singh, P. Hundekar, R. Jain, F. Han and N. Koratkar, Aqueous Lithium-Ion Batteries with Niobium Tungsten Oxide Anodes for Superior Volumetric and Rate Capability, Energy Storage Mater., 2020, 27, 506–513, DOI:10.1016/j.ensm.2019.12.012.
- C. P. Koçer, K. J. Griffith, C. P. Grey and A. J. Morris, Cation Disorder and Lithium Insertion Mechanism of Wadsley-Roth Crystallographic Shear Phases from First Principles, J. Am. Chem. Soc., 2019, 141(38), 15121–15134, DOI:10.1021/jacs.9b06316.
- R. J. Cava, D. W. Murphy and S. M. Zahurak, Lithium Insertion in Wadsley-Roth Phases Based on Niobium Oxide, J. Electrochem. Soc., 1983, 130(12), 2345–2351, DOI:10.1149/1.2119583.
- M. Aykol, J. H. Montoya and J. Hummelshøj, Rational Solid-State Synthesis Routes for Inorganic Materials, J. Am. Chem. Soc., 2021, 143(24), 9244–9259 CrossRef CAS PubMed.
- J. R. Chamorro and T. M. McQueen, Progress toward Solid State Synthesis by Design, Acc. Chem. Res., 2018, 51(11), 2918–2925 CrossRef CAS PubMed.
- D. Turnbull and B. Vonnegut, Nucleation Catalysis, Ind. Eng. Chem., 1952, 44(6), 1292–1298 CrossRef CAS.
- S. R. Meher, Transition Metal Oxide-Based Materials for Visible-Light-Photocatalysis, Nanostructured Materials for Visible Light Photocatalysis, Elsevier, 2022, pp. 153–183 Search PubMed.
- S. Banerjee, B. De, P. Sinha, J. Cherusseri and K. K. Kar, Applications of Supercapacitors, 2020, vol. 300 DOI:10.1007/978-3-030-43009-2_13.
- C. N. R. Rao and G. V. S. Rao, Transition Metal Oxides:: Crystal Chemistry, Phase Transition, and Related Aspects, 1974 Search PubMed.
- A. S. Lakhnot, R. A. Panchal, J. Datta, V. Mahajani, K. Bhimani, R. Jain, D. Datta and N. Koratkar, Intercalation Hosts for Multivalent-Ion Batteries, Small Struct., 2023, 4(4), 2200290 CrossRef CAS.
- E. Rudberg, E. H. Rubensson and P. Sałek, Kohn− Sham Density Functional Theory Electronic Structure Calculations with Linearly Scaling Computational Time and Memory Usage, J. Chem. Theory Comput., 2011, 7(2), 340–350 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for Density Functional Theory, Chem. Rev., 2012, 112(1), 289–320 CrossRef CAS PubMed.
- P. Verma and D. G. Truhlar, Status and Challenges of Density Functional Theory, Trends Chem., 2020, 2(4), 302–318 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, Statistical Variances of Diffusional Properties from Ab Initio Molecular Dynamics Simulations, npj Comput. Mater., 2018, 4(1), 1–9 CrossRef CAS.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301, DOI:10.1103/PhysRevLett.120.145301.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Graph Convolutional Neural Networks with Global Attention for Improved Materials Property Prediction, Phys. Chem. Chem. Phys., 2020, 22(32), 18141–18148 RSC.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31(9), 3564–3572 CrossRef CAS.
- M. F. bin Noor, N. Yasmin and T. Besara, Machine Learning in High-Entropy Alloys: Phase Formation Predictions with Artificial Neural Networks, Futur. Sustain., 2023, 02, 47–58, DOI:10.55670/fpll.fusus.2.1.5.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): Assessing the Accuracy of DFT Formation Energies, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, AFLOW: An Automatic Framework for High-Throughput Materials Discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- F. Karlsruhe, Inorganic Crystal Structure Database, URL https://http//icsd.fiz-karlsruhe.de. Acessed 2014, 12 Search PubMed.
- A. Seko, A. Togo and I. Tanaka, Descriptors for Machine Learning of Materials Data, arXiv, 2017, preprint, arXiv:1709.01666 DOI:10.48550/arXiv.1709.01666.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, DScribe: Library of Descriptors for Machine Learning in Materials Science, Comput. Phys. Commun., 2020, 247, 106949, DOI:10.1016/j.cpc.2019.106949.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. Von Lilienfeld, Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning, Phys. Rev. Lett., 2012, 108(5), 1–5, DOI:10.1103/PhysRevLett.108.058301.
- F. A. Faber, A. Lindmaa, O. A. Von Lilienfeld and R. Armiento, Machine Learning Energies of 2 Million Elpasolite (ABC2D6) Crystals, Phys. Rev. Lett., 2016, 117(13), 2–7, DOI:10.1103/PhysRevLett.117.135502.
- J. Behler, Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials, J. Chem. Phys., 2011, 134(7), 74106 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(18), 184115 CrossRef.
- T. L. Pham, H. Kino, K. Terakura, T. Miyake and K. Tsuda, Machine Learning Reveals Orbital Interaction in Materials, Sci. Technol. Adv. Mater., 2017, 6996, 1–2, DOI:10.1080/14686996.2017.1378060.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for Improved Materials Property Predictions, npj Comput. Mater., 2021, 7(1), 185 CrossRef.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Generalized Gradient Approximation for the Exchange-Correlation Hole of a Many-Electron System, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(23), 16533 CrossRef CAS PubMed.
- D. Datta, J. Li and V. B. Shenoy, Defective Graphene as a High-Capacity Anode Material for Na- and Ca-Ion Batteries, ACS Appl. Mater. Interfaces, 2014, 6(3), 1788–1795, DOI:10.1021/am404788e.
- R. Mukherjee, A. V. Thomas, D. Datta, E. Singh, J. Li, O. Eksik, V. B. Shenoy and N. Koratkar, Defect-Induced Plating of Lithium Metal within Porous Graphene Networks, Nat. Commun., 2014, 5, 3710 CrossRef CAS PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials, Microporous Mesoporous Mater., 2012, 149(1), 134–141 CrossRef CAS.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Matminer: An Open Source Toolkit for Materials Data Mining, Comput. Mater. Sci., 2018, 152, 60–69, DOI:10.1016/j.commatsci.2018.05.018.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, The Materials Application Programming Interface (API): A Simple, Flexible and Efficient API for Materials Data Based on REpresentational State Transfer (REST) Principles, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- C. Rao and Y. Liu, Three-Dimensional Convolutional Neural Network (3D-CNN) for Heterogeneous Material Homogenization, Comput. Mater. Sci., 2020, 184, 109850 CrossRef.
- S. M. Azimi, D. Britz, M. Engstler, M. Fritz and F. Mücklich, Advanced Steel Microstructural Classification by Deep Learning Methods, Sci. Rep., 2018, 8(1), 2128 CrossRef PubMed.
- F. Faber, A. Lindmaa, O. Anatole von Lilienfeld and R. Armiento, Crystal Structure Representations for Machine Learning Models of Formation Energies, Int. J. Quantum Chem., 2015, 115(16), 1094–1101 CrossRef CAS.
- L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Big Data of Materials Science: Critical Role of the Descriptor, Phys. Rev. Lett., 2015, 114(10), 105503 CrossRef PubMed.
- J. A. Aguiar, M. L. Gong and T. Tasdizen, Crystallographic Prediction from Diffraction and Chemistry Data for Higher Throughput Classification Using Machine Learning, Comput. Mater. Sci., 2020, 173, 109409, DOI:10.1016/j.commatsci.2019.109409.
- A. Gulli and S. Pal, Deep Learning with Keras, Packt Publishing Ltd, 2017 Search PubMed.
- T. O’Malley, E. Bursztein, J. Long, F. Chollet, H. Jin and L. Invernizzi, Keras Tuner. Retrieved May 2019, 21, 2020.
- F. K. Chollet, Available Online: Https://Keras.Io (Accessed on 14 August 2019).© 2019 by the Authors. Licens. MDPI, Basel, Switzerland. This Artic. is an open access Artic. Distrib. under terms Cond. Creat. Commons Attrib. (CC BY) Licens. (https://http//creativecommons.org/licenses/by/4.0/) 2015.
- W. M. Czarnecki, S. Podlewska and A. J. Bojarski, Robust Optimization of SVM Hyperparameters in the Classification of Bioactive Compounds, J. Cheminform., 2015, 7(1), 1–15, DOI:10.1186/s13321-015-0088-0.
- K. Stergiou, C. Ntakolia, P. Varytis, E. Koumoulos, P. Karlsson and S. Moustakidis, Enhancing Property Prediction and Process Optimization in Building Materials through Machine Learning: A Review, Comput. Mater. Sci., 2023, 220, 112031 CrossRef CAS.
- S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Scalable Deeper Graph Neural Networks for High-Performance Materials Property Prediction, Patterns, 2022, 3(5), 100491 CrossRef PubMed.
- V. P. Dwivedi, C. K. Joshi, A. T. Luu, T. Laurent, Y. Bengio and X. Bresson, Benchmarking Graph Neural Networks, 2020 Search PubMed.
- R. F. W. Bader, Atoms in Molecules, Acc. Chem. Res., 1985, 18(1), 9–15, DOI:10.1021/ar00109a003.
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. C. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, The Design Space of E(3)-Equivariant, Atom-Centered Interatomic Potentials, arXiv, 2022, preprint, arXiv:2205.06643 DOI:10.48550/arXiv.2205.06643.
- T. Hsu, T. A. Pham, N. Keilbart, S. Weitzner, J. Chapman, P. Xiao, S. R. Qiu, X. Chen and B. C. Wood, Efficient and Interpretable Graph Network Representation for Angle-Dependent Properties Applied to Optical Spectroscopy, npj Comput. Mater., 2022, 8(1), 151 CrossRef CAS.
- C. Morris, G. Rattan and P. Mutzel, Weisfeiler and Leman Go Sparse: Towards Scalable Higher-Order Graph Embeddings, Adv. Neural Inf. Process. Syst, 2020, 33, 21824–21840 Search PubMed.
- H. Maron, O. Litany, G. Chechik and E. Fetaya, On Learning Sets of Symmetric Elements, International conference on machine learning, PMLR, 2020, pp. 6734–6744 Search PubMed.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, Generative Adversarial Networks for Crystal Structure Prediction, ACS Cent. Sci., 2020, 6(8), 1412–1420 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00014e |
| This journal is © The Royal Society of Chemistry 2024 |