Integrative studies of ionic liquid interface layers: bridging experiments, theoretical models and simulations

Abstract

Ionic liquids (ILs) are a class of salts existing in the liquid state below 100 °C, possessing low volatility, high thermal stability as well as many highly attractive solvent and electrochemical capabilities, etc., making them highly tunable for a great variety of applications, such as lubricants, electrolytes, and soft functional materials. In many applications, ILs are first either physi- or chemisorbed on a solid surface to successively create more functional materials. The functions of ILs at solid surfaces can differ considerably from those of bulk ILs, mainly due to distinct interfacial layers with tunable structures resulting in new ionic liquid interface layer properties and enhanced performance. Due to an almost infinite number of possible combinations among the cations and anions to form ILs, the diversity of various solid surfaces, as well as different external conditions and stimuli, a detailed molecular-level understanding of their structure–property relationship is of utmost significance for a judicious design of IL–solid interfaces with appropriate properties for task-specific applications. Many experimental techniques, such as atomic force microscopy, surface force apparatus, and so on, have been used for studying the ion structuring of the IL interface layer. Molecular Dynamics simulations have been widely used to investigate the microscopic behavior of the IL interface layer. To interpret and clarify the IL structure and dynamics as well as to predict their properties, it is always beneficial to combine both experiments and simulations as close as possible. In another theoretical model development to bridge the structure and properties of the IL interface layer with performance, thermodynamic prediction & property modeling has been demonstrated as an effective tool to add the properties and function of the studied nanomaterials. Herein, we present recent findings from applying the multiscale triangle “experiment–simulation–thermodynamic modeling” in the studies of ion structuring of ILs in the vicinity of solid surfaces, as well as how it qualitatively and quantitatively correlates to the overall ILs properties, performance, and function. We introduce the most common techniques behind “experiment–simulation–thermodynamic modeling” and how they are applied for studying the IL interface layer structuring, and we highlight the possibilities of the IL interface layer structuring in applications such as lubrication and energy storage.

---

Rong An

Rong An received her PhD degree in Chemical Engineering from Nanjing Tech University, China, in 2013. She then worked as a postdoc researcher in Chemical and Biomolecular Engineering at North Carolina State University from 2013 to 2015. She joined School of Materials Science and Engineering/Herbert Gleiter Institute of Nanoscience, at Nanjing University of Science and Technology since 2015. Her current position is an Associate Professor. Her research interests include ionic liquid-solid interations, interface and surface science, liquid-solid interfacial phenomena, ionic liquid-based lubrication and energy storage, etc.

Nanhua Wu

Nanhua Wu received her Dual-PhD degree in Chemical Engineering from Nanjing Tech University, China, in 2019, and Luleå University of Technology, Sweden in 2020, respectively. She joined School of Petrochemical Engineering at Changzhou University since 2020. Her current position is an Associate Professor. Her research interests focus on the modeling of interfacial molecular thermodynamics in the area of catalysis, ionic liquids, membrane, etc.

Aatto Laaksonen

Aatto Laaksonen is a Professor of Physical Chemistry at Stockholm University (SU), PhD in 1981 (SU), PDF Daresbury Laboratory (UK) in 1982 with Vic Saunders and at IBM Poughkeepsie/Kingston (USA) from 1983 to 1985 with Enrico Clementi, Sabbatical at Dalhousie University 1993–1995 (Canada) with Rod Wasylishen. He is a visiting professor at JAERI 2002, 2005 (Japan), at Cagliari University 2008, 2009, 2011, 2015 (Italy), at Nanjing Tech University 2018-present (China), Petru Poni Institute 2018-present (Romania) and Luleå University of Technology 2020-present. His research focuses on multiscale modelling/simulations, model development in materials sciences and green chemical engineering.

Faiz Ullah Shah

Faiz Ullah Shah is an Associate Professor in Chemistry of Interfaces at Luleå University of Technology, Sweden. In 2011, he obtained his PhD degree in Chemistry from Luleå University of Technology, Sweden. Since 2013, he is leading a research group of PhD students, postdoctoral researchers and master students. His research is focused on the development of halogen-free ionic liquids and electrolytes for various energy related applications including batteries and supercapacitors. He has co-authored more than 80 research articles and is a co-inventor of eight patents.

Xiaoyan Ji

Xiaoyan Ji is a full Professor in Division of Energy Science at Luleå University of Technology, Sweden. She received her PhD degree in Chemical Engineering from Nanjing Tech University, China, in 2000 with 20+ years experience of research and development in the area of Chemical Engineering and Energy Engineering. Her research work is from theoretical modeling to technology developing, process simulating and integrating. Up to now, as a first author or main contributor, she has published 200+ journal articles.

Harald Fuchs

Harald Fuchs is a Chair-Professor of Experimental Physics at the University of Münster, Germany. He spent from 1984 to 1985 a post-doctoral year with IBM Research Laboratory Zurich in the group of G. Binnig and H. Rohrer. He is the founder of the Center for nanotechnology in Münster and its scientific director. His research focuses on nanoscale science and nanotechnology, ranging from scanning probe microscopy to self-organized nanostructure fabrication, on-surface chemical reactions, and nano-bio systems. He is an elected member of the German National Academy of Science ‘Leopoldina’, the German National Academy of Science and Engineering ‘acatech’, and the ‘TWAS’.

---

1. Introduction

Ionic liquids (ILs) are a class of salts existing in the liquid state below 100 °C, while many of them are liquids already at room temperature. As salts, their ions (organic or inorganic) form relatively short-lived ion pairs. They possess unique properties of great technological interest, such as negligible vapor pressure, nonflammability, high thermal and chemical stability, wide liquid range and electrochemical window, high ionic conductivity, and more, all with a rational molecular designability for a great variety of applications due to their rich diversity of physical and chemical properties.^1–3 Although the first IL, ethylammonium nitrate (EAN), was discovered more than a century ago, they have caught much attention from both the academic and industrial communities during the last two decades. The potential energy-related applications are solar and fuel cells, high-temperature heat transfer fluids, carbon capture and utilization, and biomass processing. In addition, the particularly interesting is their tribological applications as electrically conductive lubricants for modern electric vehicles^4,5 and electrolytes for energy storage devices such as batteries and supercapacitors, due to their excellent electrochemical performance in general.^6–14

ILs in a variety of recent applications are often used in direct contact with solid surfaces or embedded in pores and constraint spaces,^2,3 as the function of ILs at surfaces is considerably different and improved from that of bulk ILs. This is due to the altered property of ILs by forming well-defined interfacial layers with well-tunable structures.^2,3,6,7,15 The ion structuring of the near-(solid) surface ILs is determined by a variety of attractive interactions ranging from short-range van der Waals forces to long-range electrostatic forces, and hydrogen bonding, etc.,^2,16,17 depending on the surface properties (material, chemistry, roughness, curvature, etc.),^3,16,18,19 the nature of ILs,^6,20,21 as well as external conditions.^7,22,23 Ion arrangements of the ILs in direct contact or close vicinity can be precisely controlled by fine-tuning the ILs and adapting the solid materials at the interfaces. For example, imidazolium-based ILs at the surface exhibit a dramatic shift towards a more ordered solid-like phase below a threshold thickness. This is related to the metallic nature of the underlying materials, i.e., more metallic surfaces facilitating the phase shift.¹⁸ The ILs with cations/anions having a longer alkyl chain exhibit well-pronounced “…cation–cation–anion–anion…” bilayer structures induced by van der Waals forces, rather than alternating cation–anion monolayer structures by electrostatic forces in shorter-chained ILs.^6,21,24 External stimuli can play a critical role in the ion structuring of the IL interface layer. For example, charged surfaces^1,25 can create fairly dense ion layers next to the surface, while decaying exponentially into the bulk IL.²⁶ In this way, the tailorable ion structures of the IL interface layer largely determine their properties and performance.^27,28 Considering the excessively large number of possible ILs (estimated to ∼10¹⁸) as well as the great diversity of available solid surfaces and external conditions and stimuli, theoretical modeling is critically important to bridge the interfacial structure and properties/performance of the IL interface layer and to provide a quantitative understanding of the structure–property relationships, which is a prerequisite for the design of ILs with properties tailored for targeted applications.

Many experimental techniques have been used to study the ion structuring of the IL interface layer.^2,23,29 Among them, surface force apparatus (SFA)^30–34 and atomic force microscopy (AFM)^{17,25,33,35,36} have emerged as more important experimental tools for detailed investigations due to their accuracy and atomic resolution. In parallel, molecular simulations, such as molecular dynamics (MD) and Monte Carlo (MC), have been widely used to investigate the structures of the IL interface layer.^23,37 There is no doubt that it is important to combine simulation and modeling with advanced experimental techniques to interpret and clarify the IL structure at the microscopic level, as well as to predict the properties. But even further, to better bridge the experiments and simulations is to include modern thermodynamic property & prediction modeling in the constellation to create a powerful multiscale triangle. We will call it here simply for “thermodynamic modeling” (TDM) although it may mean different things depending on the subfield of research. We intend to stress that during the last decades, and thermodynamic modeling has continuously become more accurate and predictive but also contains more molecular features. Thermodynamic models have been traditionally based on their fundamental principles and mathematical rules with collected reference data of thermodynamic and transport properties to describe the behavior of substances and systems. It has been always used exclusively in chemical and process engineering. Thermodynamic models rely much on the use of a large variety of equations of state (EOS) starting from the van der Waals equation. Classical density functional theory (DFT) is a highly powerful TDM method for equilibrium properties (free energy, phase behavior, etc), suitable for inhomogeneous systems and phase transitions. It can predict TM properties for complex chain-like fluids like polymers and ILs. Many TDM methods can also take molecular information from both experiments and molecular modeling and simulations, which has become a powerful and general tool alongside molecular simulations. At its best, it provides the means to couple the microscopic description of matter with macroscopic properties and function of the real world. Molecular simulations (MD & MC) as such can give thermodynamic quantities after applying statistical mechanics in the analysis, but the particle-based simulations can only take us to the mesoscale from where many orders of magnitude remain to the macroscale, and to get there continuum models are needed, or alternatively thermodynamic modeling. Therefore, the combination of experiments, molecular simulations, and thermodynamic modeling as a “tripod” is an ideal multi-scale tool. This integrated bottom-up/top-down approach has been used for homogeneous and bulk systems, but as a general tool, it can be applied to study the heterogeneous systems and interfaces between bulk and surfaces. The use of the triangle can provide a more comprehensive understanding. It is a way to perform verification and validation of the findings and test hypotheses. But after all, it gives a good insight into these complex systems of IL interface layers and allows predictive capabilities. It is an ultimate synergetic approach. We have collected the recent advances from literature where this approach, as a whole or partially, is used for IL interface layers to find how their nanostructure affects their properties and then makes use in different applications.

Excellent reviews have already been published from the aspects of experiments and/or molecular simulations, to reveal the IL interface layer structuring and their properties.^{1–4,23,25,29,38} However, molecular thermodynamic models have been developed to describe melting temperature,^39–41 gas adsorption⁴² of confined nano-phases, surface wetting,^39,43,44etc., but for ILs, most of them are used for predicting the bulk characteristics.^45–50 To the best of our knowledge, no reviews have been reported to include even the research on thermodynamic models in the studies of IL interface layers. Not to mention a systematic survey on the ion structuring and the associating properties of the IL interface layer as well as their structure–property relationships. The main motivation behind this review is to introduce and highlight the development and application of multiscale triangle “experiment–simulation–thermodynamic modeling” to study the IL interface layer structures and properties, representing many exciting challenges while being of paramount^2,3,29 importance from both the scientific and applied perspectives.

This review is organized as follows. We introduce the multi-scale the “experiment–simulation–thermodynamic modeling” triangle and how it can be applied on the studies of IL interface layers in Section 2. In Section 3 we detail the studies of mono- and bilayer structuring of ILs on surfaces using the triangle. Structure–property relationships of IL interface layers are collected in Section 4. Among many applications of IL interface layers, we choose to present those connected to tribology and lubrication as well as energy storage in Section 5. Summary and future outlook are given finally in Section 6.

2. Structure–property relationships of ionic liquids interface layer by “experiment–simulation–thermodynamic modeling” tool

Several findings in literature have demonstrated a clear effect of the ion structuring of IL interface layers on the overall properties and performance in different applications, and for the IL-based lubricants and electrolytes in particular. For example, more ordered IL layers in the vicinity of a solid surface can both increase the friction^51–53 and reduce it.^52,54,55 In the case of electrolytes, the ordered ion packing of ILs can enhance the charge storage performance,⁶ while the structuring of ILs can slow down the capacitive process.⁵⁶ These different responses observed in these properties due to the structures of ILs can be given completely by different interpretations.

2.1 Overview of various techniques to study interface layer ionic liquids and their applications

Relevant experimental investigations, such as sum frequency generation vibrational spectroscopy (SFG), high-energy reflection and scattering using X-rays and neutrons, nuclear magnetic resonance (NMR), X-ray photoelectron spectroscopy (XPS), quartz crystal microbalance (QCM), surface-force apparatus (SFA), and atomic force microscopy (AFM), have been carried out to reveal detailed structures of IL interface layers. In studies of ion nano-structuring of ILs at solid interfaces, SFA (Fig. 1a, left) and AFM (Fig. 1b, left) are the most extensively utilized experimental techniques to unveil the intrinsic mechanism behind IL–solid interfacial phenomena at the nanoscale, as a layering structure of IL interface layers is resistive against an external pressing force to a certain extent.^57–60 Thus, the force-sensitive techniques, i.e., SFA and/or AFM have been naturally employed to directly probe the layering structures of the interfaces, allowing for the ion structure to be visualized to obtain not only the number and thickness of layering structures but also the force that each layer can resist. Together with molecular simulation (Fig. 1c), these tools have provided molecular insights on the microstructural changes of ILs at solid interfaces, i.e., how the ion self-assembly underpins much of their complex chemical and physical behavior. It is crucial to note that the local structural features of ILs are correlated strongly with their properties,²⁷ and a detailed understanding of how the ion structuring of the IL interface layer at the molecular level affects their properties is a prerequisite for the design of ILs with properties tailored for targeted applications.²⁸ In this respect, thermodynamic modeling (Fig. 1d) plays an essential role in relating the structure–property of the IL interface layer, allowing the judicious design of IL–solid interfaces for task-specific applications.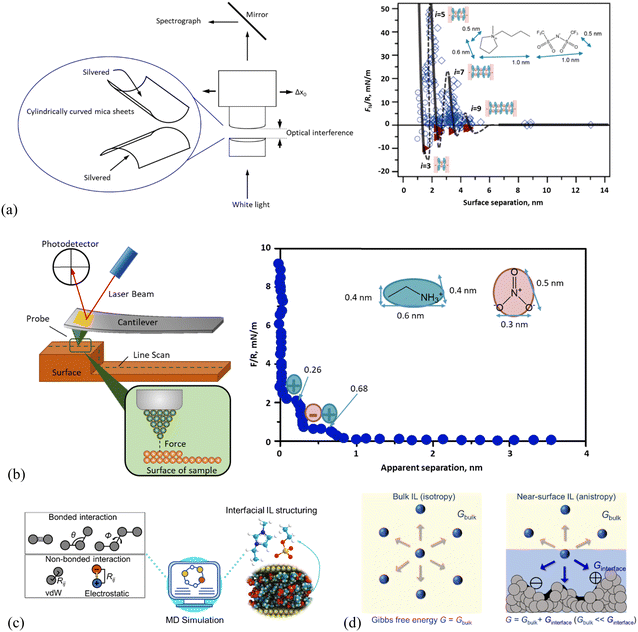

Fig. 1 Schematic presentation of the working principle in (a) surface force apparatus (SFA) and a typical SFA-measured force curve for [C₄C₁Pyrr][NTf₂] confined between mica sheets, adapted from ref. 51 with permission from RSC, copyright 2013, (b) atomic force microscopy (AFM) and AFM-measured normal force curve for EAN on mica with a 5 μm-radius silica colloid probe. Adapted from ref. 73 with permission from RSC, copyright 2016. In the right panel of (a), open diamonds and circles indicate points measured on approach and retraction of the surfaces, respectively. Filled triangles in (a) indicate points measured from the jump-apart of the surfaces from an adhesive minimum. i means the number of ion layers. The lines are a guide to the eye to show the oscillatory nature of the forces, with solid lines through measured regions and dashed lines through the regions inaccessible to measurement due to the jump-in from the previous energy barrier. (c) Molecular dynamics (MD) simulation method for detailing the structure and dynamics of the ionic liquid interface layer. Adapted from ref. 74 and 75 with permissions from Wiley, copyright 2022, and MDPI, copyright 2019. (d) Molecular thermodynamics modeling, here in quantitatively describing bulk and ionic liquid interface layer via Gibbs free energy (G). The solid surface in contact with the IL (right panel) shows varying nanostructured features, and/or chemical heterogeneities, and/or surface charges.

2.1.1 Surface force apparatus. Among advanced experimental instruments, the sensitive SFA can be used to detect the force within small atomic separations, enabling an accurate detection of tiny changes in the surface structure and separation with a sensitivity within a distance resolution of 1 Å.⁶¹ SFA has been extensively used to detect the attractive van der Waals and repulsive electrostatic “double-layer” forces, hydrophobic forces, hydration forces, oscillatory (solvation or structural) forces, viscous forces, steric interactions, capillary and adhesion forces, friction and lubrication forces, etc.^62–65 As one of the most commonly used tools for measuring molecular forces of interfacial ILs, SFA exhibits a high normalized force sensitivity down to 10⁻⁶–10⁻⁷ N m⁻¹. The loading force in SFA is large enough to enable the last few ion layers to be squeezed out from the surfaces, allowing the study of interaction behavior related to surface-induced ion layering.⁶⁶ SFA has been used to reveal structural and dynamic properties of ILs with a molecular resolution, being particularly important for emerging applications where ILs, in general, are confined into narrow pores or form thin films on the surface. It should be also pointed out that SFA is usually applied to measure the interaction forces between two (semi)transparent curved samples with a low surface roughness in a crossed-cylinder geometry. Fig. 1(a), (right panel) shows a typical force profile measured by SFA for 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₄C₁Pyrr][NTf₂]) confined between mica sheets, with an oscillatory function. Such oscillatory force profiles are observed because the IL is structured in ordered layers between two surfaces. The oscillatory forces are caused by the sequential squeeze-out of ionpair layers, observed as repulsive and attractive walls at specific separation values, corresponding to a configuration with an integral number of ion layers (i = 3, 5, 7, 9, cf. the inset scheme in Fig. 1a, right).^49,51

2.1.2 Atomic force microscopy. AFM is another powerful tool to allow highly sensitive measurements of interactions and provide microstructural mapping at interfaces from microscopic to (sub-)nanoscopic scale.⁶⁷ The AFM measurements consist of probe–sample interaction forces (Fig. 1b, left). They do not only reflect the probe–sample separation but depend also on the material properties of both the probe and sample.^68,69 Unlike SFA, AFM allows the use of various types of substrates including both transparent and non-transparent surfaces.⁶⁶ AFM can trace the ion structuring of ILs adjacent to solid surfaces with a sensitivity of 10⁻³ and 10⁻⁶ N m⁻¹ for tip and colloidal probes, respectively. The AFM-detected normal force–distance curves (force curves) and the lateral nanoscale friction force enable us to reveal the interactions and structural information of IL interface layers across the normal and lateral directions, respectively. The normal force curves provide direct insight into the ion layering at the IL–solid interfaces in studies of the periodicity of these structuring ion layers at solid substrates.^60,70–72 For example, as illustrated in Fig. 1(b), (right panel), typical AFM-measured forces normalized by the probe radius (F/R) exhibits distinct force steps at two different separations for EAN IL on mica surfaces with a silica colloid probe. The step size of the force curve at a larger separation of ∼5 Å is consistent with the ionpair size of EAN. While the step at the shortest separation is only 2.5–3 Å, less than the size of EAN ionpair, corresponding to the size of the electrostatically interacting cations on the negatively charged mica surface.⁷³

2.1.3 Molecular dynamics simulations. As one of the computational techniques, molecular dynamics (MD) simulation⁷⁶ is an essential tool for providing molecular-scale insight into the structure–property relationships of condensed phase ionic systems.⁷⁷ Its principle is to solve the equations of motion for the atoms in molecular systems from solids to complex solutions of biological material, thereby allowing for simulating the behavior of atoms and molecules over time.⁷⁸ It can model both equilibrium and non-equilibrium systems of any types made of particles. Over several decades, owing to advances in computer hardware and software as well as the development of new molecular mechanical (MM) force fields and simulation methods, MD exists as classical MM or quantum mechanical (QM) or hybrid QM/MM. MD simulations (Fig. 1c) can provide detailed information about the structure and dynamics of the IL interface layer,⁷⁴ as well as the interactions between ILs and the surrounding environment, such as solvent molecules or substrate surfaces.^1,3,29,79,80 Simulating the interfacial region of ILs involves the creation of a computational model that accurately represents the bulk properties while capturing the distinct features of the interface. Typically, a periodic simulation cell is employed to mimic the infinite nature of the system, and appropriate force field parameters are assigned to describe the interactions between ions.⁸¹ Analyzing MD simulation results provides a comprehensive understanding of the interfacial phenomena in ILs. Parameters such as ion density profiles,⁸² orientational order,⁸³ and intermolecular forces offer detailed insights into the organization and dynamics of IL ions at the interface. By examining the spatial distribution of ions, researchers can discern the structure of the interfacial region and elucidate the effects of surface properties on the ion arrangement.^84–86 Additionally, time-dependent properties, such as diffusion coefficients and residence times, contribute to characterizing the mobility and transport mechanisms of ILs near the interface.⁸⁷ The results of MD simulations can also be combined with experiments to provide a more comprehensive understanding of the interfacial IL behavior and theoretical guidelines for model development, leading to important insights into the design and optimization of IL-based materials and processes.^82,88,89 However, there exist problems in performing MD simulations, in particular, ILs have often conjugated rings, and the electrons there get delocalized. It is therefore difficult to create reliable force fields, and thus ad hoc type of scaling is used for the atomic charges to dilute them. And as the force fields are developed for ILs in bulk, it is unsure that such developed force fields will work correctly at surfaces. In addition, the obtained value from MD is mainly used to explain the complex structure and dynamics for which no other methods can be used on the molecular level.

2.1.4 Thermodynamic modeling. With thermodynamic modeling (TDM), researchers can screen an extensive large number of potential IL structures in a rational way, thereby discovering ILs with properties tuned for a given application. TDM is closely connected to experimental and/or computational findings, and it has been successful in predicting the properties of the bulk ILs.^45–50 TDM in general can be spitted into two groups, one is based on the Gibbs free energy and the other is based on the classical density functional theory (abbreviated as DFT). For the first group, only a very few studies have been conducted on ILs at interfaces. For example, gas adsorption on the ILs immobilized on porous solid supports and computing the Gibbs free energy of the gas adsorptive process.⁴² Here, the Gibbs free energy (G) calculations was extended to the nano-micro interface by: G = G_bulk + G_interface, where G_bulk is the Gibbs free energy of the bulk ILs, and G_interface is the contribution from interface ILs. In the absence of solid surfaces, the property of the bulk IL is homogeneous and isotropic (Fig. 1d, left panel), and G = G_bulk. After introducing solid substrates, the IL interface layer becomes anisotropic, and G_interface can become dominating (Fig. 1d, right panel), i.e., G_interface ≫ G_bulk.⁴² Modeling G_interface is the key to extending molecular TDM to be applicable at interfaces. G_interface is closely related to the size or thickness, surface energy of ILs at solid surfaces as well as the properties of the contacting solid surfaces,⁴⁰ and the acquism of G_interface often requires molecular parameters, which are not always easy to obtain.^41,42 There are some attempts to acquire them by combining AFM and computer simulations.^90–92 To the best of our knowledge, very scarce efforts have been devoted to the structure of ILs interface layer from the molecular thermodynamic viewpoint, some of which calculated the entropy change and vibrational spectrum of CO₂ in various imidazolium ILs at Ag(111) electrodes with the two-phase thermodynamics free energy method. And the potential of mean force for CO₂ across the interfacial ILs was obtained further based on the free-energy analysis using the umbrella sampling method.⁹³ The calculated entropy or free energy in interfacial ILs can be correlated to the behavior of IL interface layers, including density, viscosity, diffusion, etc., and can serve as the key indicators in designing functional ILs for high-performance applications such as energy storage devices.⁹⁴ Thus, molecular thermodynamic models provide only thermodynamic properties, and the structuring layering of interfacial ILs cannot be obtained directly from them.

DFT is another powerful and efficient theoretical tool to model the structuring layers of interfacial ILs and their properties⁹⁵ by minimizing the grand potential.^95,96 In general, DFT is developed based on any equation of state (EOS),⁹⁷ while for ILs, owing to their complexicity, the EOS based on statistical associating fluid theory (SAFT) is preferred, which have been intensively developed to study the properties of ILs.⁹⁸ To present the layering structures and properties of the interfacial ILs, an external potential is needed to consider the strongly assymetruic interactions between ILs and the solid surface.⁹⁹ DFTs have been intensively developed to study the properties such as gas adsorption isotherms in metal organic frameworks,^100,101 partition and selectivity of IL mixtures in porous electrodes,¹⁰² surfactant and polyelectrolyte on rock surface for selecting appropriate polyelectrolytes suitable for different reservoirs,¹⁰³ interfacial layering of ILs,¹⁰⁴ interfacial structure and differential capacitance of IL–graphite interface,¹⁰⁵etc. Meanwhile, further development has been conducted and extended to the dimention more than one, as well as complex structures including the surface roughness and heterogeneity. In developing DFT, those based on third-order thermodynamic perturbation theory of Feynman-Hibbs-corrected Mie potentials and using the modified fundamental measure theory were recently reported.¹⁰⁶ Perturbed chain-SAFT-based DFT was employed to study the selective adsorption of mixed ILs confined in rough slit pores of electrodes, where the Helmholtz energy functional of the DFT model accounts for the hard-sphere, the dispersive, and the electrostatic correlation interactions among ILs ions.¹⁰² To accelate the computation speed, different althorighms have been combined and integrated into DFT. For example, the Chebyshev pseudospectral collocation method was integrated into DFT to efficiently describe the density profile of the IL–CO₂ system inside electroneutral nanopores.⁹⁸ This Chebyshev pseudo-spectral collocation method was combined with Anderson mixing algorithm to accelerate the interative process, to study the effects of temperature, pressure, pore size, and pore shape on the gas solubility in the ILs confined inside silica nanopores.¹⁰⁷ A two-dimensional DFT model was used to investigate the distribution and partition behavior of imidazolium-based Ls in slit nanopores with rough surfaces, where the Helmholtz free-energy functionals were used to account for the excluded-volume effect and chain formation.¹⁰⁸ While it should be addressed that most of studies is limited to the systems other than ILs. In summary, DFT has become a fantastic tool for characterizing the ion distribution of the ILs at the interface,^109,110 while obtaining the external function still remains a challenge.

2.2 Quantized friction and nano-structuring of interface layer ionic liquids seen in AFM and SFA

Studies of AFM nano-frictional response allow the variations in friction force with a normal load to be correlated with the interfacial IL structure.^{20,53,55,73,111–116} AFM-measured nanoscale friction force offers a unique insight into the nano-structures of ILs at the interface. Few studies are reported on the phenomenon of ‘quantized friction’, in which the friction coefficient can be indexed by the number of layers of the IL film at solid surfaces, providing valuable insight into the overall interface structure of ILs.⁶⁵ For example, as shown in Fig. 2(a), for ethylammonium nitrate (EAN) on mica at room temperature, two distinct regimes in a quantized manner can be obtained. One is for loosely ordered ion layers obtained at smaller normal loads <20 nN and another for highly ordered ion layers at higher loads larger than 20 nN.⁷³ While for 1-(4-hydroxybutyl)pyridinium bis(trifluoromethanesulfonyl)imide ([HOC₄Py][NTf₂]) at the mica surface, a three-regime quantized nanofriction feature with two critical normal forces (breakpoints) at 12 and 81 nN was detected (Fig. 2(b)).¹¹⁷ (1) The first breakpoint (12 nN) means when the normal force is larger than 12 nN, and the AFM probe should have reached the boundary regime, where a strongly adsorbed cation boundary layer resists getting “squeezed out” and the friction force increases monotonously with a normal load. (2) The second breakpoint is detected at a normal force of 81 nN, indicating a rupture of an additional layer. However, the adsorbed cation-enriched boundary layer should have not been completely squeezed out, resulting in direct contact between the AFM probe and mica. Further, the Infrared spectra can demonstrate that strong stabilizing H-bonding among the [HOC₄Py]⁺ cations is formed in a bilayer cation structure. This structure is similar to that observed by Mao et al.,⁶ which is more difficult to squeeze out. (3) The first [HOC₄Py]⁺ cation layer is shaved away when the normal load is >81 nN due to the destruction of the H-bonds between the two cation layers, and only the final cation layer remains to prevent a direct probe–mica surface contact (cf. the inset scheme in Fig. 2b).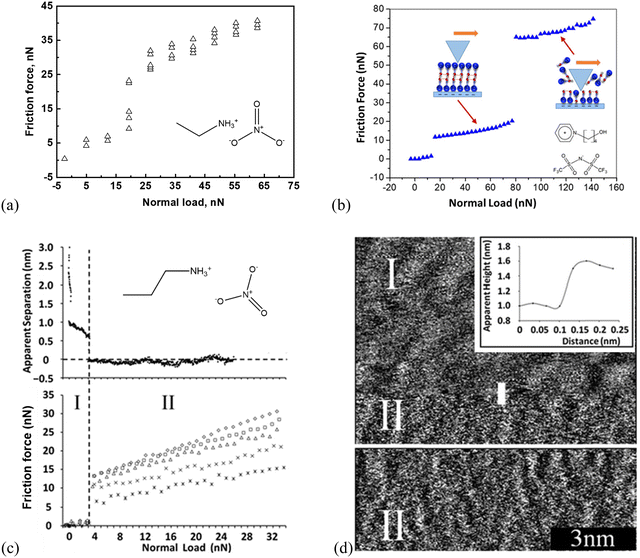

Fig. 2 Friction-load plots obtained by a (a) colloid silica probe with a radius of 3.4 μm in EAN, adapted from ref. 73 with permission from RSC, copyright 2016, and (b) sharp AFM silicon probe in [HOC₄Py][NTf₂] supported by mica at room temperature. Reproduced from ref. 117 with permission from ACS, copyright 2020. (c) Top: Apparent separation between a mica surface and the silica colloid probe (diameter ∼5 μm) as a function of normal load for the mica–PAN system. Bottom: Friction force as a function of normal load for various sliding velocities using silica colloid probe. Stars: 5 μm s⁻¹, crosses: 10 μm s⁻¹, triangles: 20 μm s⁻¹, squares: 30 μm s⁻¹, diamonds: 40 μm s⁻¹. Reproduced from ref. 111 with permission from RSC, copyright 2013. (d) Sharp AFM tip images of the PAN–mica interface. The inset is a section analysis for the sharp AFM probe moving from regime I to II. Reproduced from ref. 111 with permission from RSC, copyright 2013.

Propylammonium nitrate (PAN) on a mica surface shows a two-distinct-layering frictional behavior (Fig. 2c, bottom), in which the silica colloid probe slides along either an upper layer (I) or the innermost layer (II).¹¹¹ More specifically, as shown in Fig. 2c, the approaching force curve (top) demonstrates the quantized frictional regimes I and II, exhibiting two discrete jumps at large separations (II) and two subsequent ion layers (I). The friction force (bottom) jumps abruptly from ∼1 to 7–13 nN, revealing that the AFM colloid probe moves from the contact with the upper ionic liquid interface layer (I) to the innermost layer, closer to the surface (II). The corresponding topographic images further confirm the upper ion layer (I). It has a distinct, undulating structure with a periodicity of about 1 nm and is evocative of its bulk nanostructures (Fig. 2d). After the sharp AFM probe jumps inward to the innermost layer (II), a “worm-like” morphology is observed, and the height difference between the regimes I and II is around 0.5 nm (Fig. 2d). This is consistent with both the step size in the force curve (Fig. 2c, top) and the PAN ion pair diameter (∼0.56 nm).

With SFA, a layered ion structuring and quantized friction behavior are simultaneously observed in the dicationic IL, 1,10-bis(3-methylimidazolium)decane di[bis(trifluoromethylsulfonyl)]-imide ([C₁₀(C₁Im)₂][NTf₂]₂) confined by the mica surfaces (Fig. 3a). The measured friction F_S appears extremely low when the film thickness (separation) D > 3.2 nm, while F_S increases linearly with the normal force F_N. This is because F_N increases sufficiently to expel a further ion-pair layer of the IL, decreasing the separation D to 2.4 nm. When the normal force is increased further to squeeze another ion pair layer out with a separation D of 1.6 nm, the value of F_S is larger and increases with a steeper gradient.

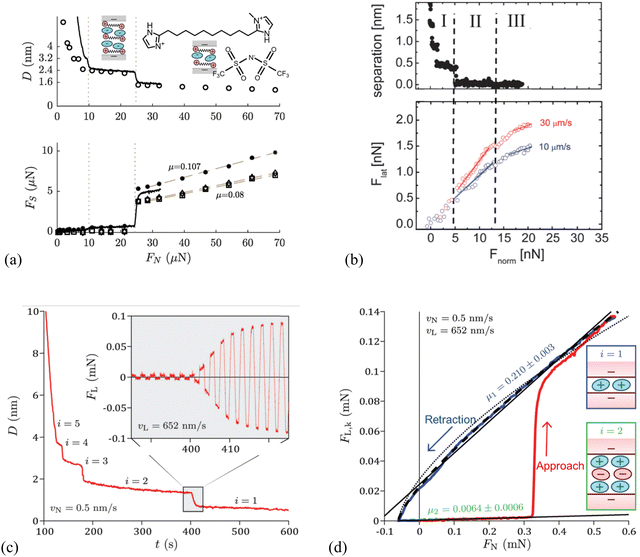Fig. 3 (a) Top: Surface separation D as a function of normal force F_N during friction measurements by SFA for the dicationic IL, 1,10-bis(3-methylimidazolium)decane di[bis(trifluoromethylsulfonyl)]-imide, shortened as [C₁₀(C₁Im)₂][NTf₂]₂. The continuous line corresponds to an approach performed while shearing continuously at a velocity of 470 nm s⁻¹, whereas the circles represent the distances at which shear measurements were performed during a stepped approach. Bottom: Kinetic friction force F_S as a function of F_N, for a continuous approach while shearing at a velocity of 470 nm s⁻¹ (solid line), and for measurements in the stepped approach (markers). The squares, diamonds, and asterisks represent measurements at a shearing velocity of 470, 105, and 52 nm s⁻¹, respectively. Reproduced from ref. 118 with permission from ACS, copyright 2019. (b) Top: Separation D versus normal force F_norm of EAN at mica surfaces measured by an AFM silica colloid probe with a diameter of 20.8 μm, and bottom: lateral force F_latversus normal force F_norm at sliding velocities of 10 and 30 μm s⁻¹. Dashed vertical lines denote the divisions between Intervals I, II, and III. Solid lines denote linear fits to increasing load data from which friction coefficients μ are obtained. Reproduced from ref. 119 with permission from RSC, copyright 2012. SFA measurements for 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₄C₁Pyrr][NTf₂]), when moving the top surface with the piezoelectric tube at a normal velocity v_N = 0.5 nm s⁻¹ and a lateral velocity v_L = 652 nm s⁻¹: reproduced from ref. 65 with permission from RSC, copyright 2020. (c) Temporal evolution of the apical distance D on full approach. The inset shows the temporal evolution of the lateral friction force F_L during the squeeze-out transition from layer i = 2 to layer i = 1. (d) Kinetic friction F_L,k as a function of load FN on full approach (in red) then retraction from layer i = 1 (in blue).

It should be mentioned that the magnitude and gradient of F_S are weakly dependent on the shearing velocity, e.g., slow velocity results in large F_S on the layer with a separation of 1.6 nm, while the friction coefficient μ shows a very weak velocity dependence. Apparently, Fig. 3(a) reveals a quantized friction behavior, in which discontinuities occur in friction as the molecular layers of the IL are squeezed out and the friction coefficient μ depends on the number of confined ion layers.¹¹⁸Fig. 3(b) shows a nano-frictional force response of EAN at mica surfaces with an AFM silica colloid probe, which can be decomposed into 3 linear regions, i.e., Intervals I, II and III, each having a distinct slope. As the applied normal load F_norm is increased, the apparent separation decreases from >2 to 0.4 nm as 4 weak ion pair layers are ruptured, and then remains almost constant up to 5 nN load (Interval I). The friction force F_lat increases linearly with the normal load over the same loading range and is independent of the sliding velocity. When the load exceeds 5 nN with the apparent separation decreasing to 0.1 nm (Interval II), only a single confined layer remains, consisting mostly of cations adsorbed to mica for neutralizing the surface charge. A break is observed in the friction data in Interval II, which is most noticeable at a higher sliding velocity. The resulting friction coefficient, which is defined by the gradient of the lateral vs. normal loads based on Amontons’ law, depends strongly on the velocity in Interval II, and is smaller than that obtained in Interval I for thicker confined films at lower normal load. A final transition to Interval III is observed due to the structural transition of the ion layers when the normal load is further increased above 13 nN, corresponding to a separation decreasing to zero, and the friction coefficient is further reduced compared with that in Interval II and independent of the velocity.¹¹⁹

Similar quantized friction phenomena have also been found in other investigations performed by AFM¹²⁰ and SFA⁶⁵ in which the friction coefficient is clearly indexed by the number of ions composing the IL film. Confining the 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₄C₁Pyrr][NTf₂]) between mica surfaces forms a structured film responding to shear in a pronounced quantized way (Fig. 3c).⁶⁵ This friction response has been determined by SFA more precisely, comprehensively and rapidly, based on the simultaneous application of normal and lateral motions to the surfaces. Fig. 3(c) shows temporal evolutions of the apical distance D and lateral friction force F_L in which the apical distance varies by 0.64 nm in 10 s, associating with about four shearing cycles (inset). The amplitude of F_L is observed to increase continuously during the squeeze-out transition from layer i = 2 to i = 1. The extracted average lateral friction force during the creep stage for each shearing period is identified as the kinetic friction force F_L,k, and the resulting friction coefficient μ is clearly indexed by the number of ions of the IL film, which is the signature of the quantized friction phenomenon (Fig. 3d). In layer i = 2 (retraction branch in green) where the film is composed of two cation layers and one anion layer, the friction coefficient μ is 0.0064 ± 0.0006. While the value of friction coefficient is almost two orders of magnitude larger in layer i = 1, which is composed of only a monolayer of cations (μ = 0.210 ± 0.003, retraction branch in blue) than that in layer i = 2, and a transition happens at a load F_N = 0.33 mN between the two regimes.

2.3 Electrically controlled friction and nano-structuring of interface layer ionic liquids

The IL lubrication at solid–liquid interfaces can be well-controlled via electrical polarization of the sliding surfaces to regulate the interface layer ion structural features.²³ Urbakh's group elucidated the connection between the charge effect on the structure of the IL layers and their lubricating properties using MD simulation, in which, the friction force varies with the surface charge density through ordering the interface ions layer and switching between anion and cation layers in contact with substrate surfaces. They found that large surface charge densities are beneficial to the reduction of friction coefficient and strong interaction between the ionic layers and surfaces to prevent the ‘‘squeeze-out’’ of ILs under high pressure.⁸¹ In particular, the [C₂MIM][NTf₂] IL confined between charged surfaces has recently been found to be less compressible than that confined between neutral surfaces, favoring the use of charged surfaces over neutral ones for the lubrication by sustaining loads of several GPa.¹²¹

Interestingly, the friction force of imidazolium ILs is found to feature a nonmonotonic behavior with surface charge at high normal loads of ∼200 and 300 MPa, showing a maximum at a specific charge density (Fig. 4a). This maximum results from the interplay between the increase of the roughness of the energy landscape with surface charge and the shift of the slippage plane from the solid–liquid interface to the interior of the lubricating IL film (cf. inset illustrations, Fig. 4a).¹²² A previous simulation by Urbakh's group¹²³ also showed that the variation of the friction force with the surface charge density is determined by the regime of motion of the confined [BMIM][BF₄] IL between the graphite substrate and tip, depending on the strengths of the ion–substrate and ion–tip interactions (Fig. 4b). In the case of the weak ion–substrate interaction (ε_is = 0.23 kJ mol⁻¹, Fig. 4b, blue), the friction as a function of surface charge density has a minimum for the uncharged graphite surface and increases by an order of magnitude with the surface charging of either sign. This friction feature here is related to the shift of the slippage plane, where the frictional energy dissipation mainly occurs at the IL–graphite interface in the case of weak ion–substrate interaction. In comparison, most ions stick to the graphite substrate surface when the IL ions interact strongly with the graphite substrate, and the slippage occurs at the IL–tip interface. Thus, the friction has a maximum for the uncharged graphite substrate and decreases with increasing the charge of any sign, for the strong ion–substrate interaction (ε_is = 70 kJ mol⁻¹, Fig. 4b, red).

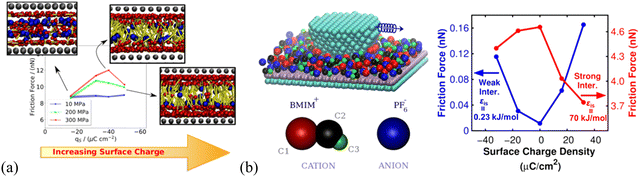Fig. 4 (a) Dependence of the friction force of [C₆MIM][BF₄] on the surface charge and normal load applied on the slabs, using non-equilibrium MD simulation. Insets are the front views of the confined ILs at 300 MPa next to the moving wall for different charge densities. The three beads in the charged head group of the cation are represented as red spheres. The blue spheres represent the anion and the cation aliphatic tails are colored in yellow. Reproduced from ref. 122 with permission from ACS, copyright 2020. (b) Friction force as a function of graphite surface charge density calculated for two ion–substrate interactions: ε_is = 0.23 kJ mol⁻¹, where slippage occurs at the interface between the [BMIM][BF₄] IL layer and the substrate, and ε_is = 70 kJ mol⁻¹, where slippage takes place mainly at the interface between the tip and the IL layer. Here, the simulations are performed for the uncharged tip and similar results can also be obtained for a negatively charged tip. Reproduced from ref. 123 with permission from ACS, copyright 2018.

The responses of 1-butyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate ([BMIM]FAP) and 1-hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate ([HMIM]FAP) to the variation of surface potentials at Au(111) are the same, i.e., all are more lubricating at negative potentials than neutral surfaces while poorly lubricating at positive surfaces (Fig. 5a, left and middle panels).¹²⁴ This reveals that the imidazolium-enriched layer is more lubricating than the mixed layer, followed by the [FAP]⁻ anion-enriched layer (inset illustration in Fig. 5a, left). The negative surface potential induces the cations of the ILs to orient with charged groups towards the surface such that the alkyl tails form a well-defined sliding plane.¹¹⁴ The poorest lubricity appears in the [FAP]⁻ anion enriched layer at positive potentials because of the disordered coil morphology of the anions producing a rough sliding plane,¹²⁵ and the weak interaction of the anion with the Au(111) surface due to the larger size and more delocalized charge.^114,124 The mixed cation–anion layer formed at the neutral surface reveals a lubricity in between. It is found in Fig. 5(a) that the lubricity can be altered by changing the cation alkyl chain length at negative potentials and neutral surfaces, in which the long chain facilitates the interfacial lubricity. In comparison, the response of the friction force in 1-butyl-3-methylimidazolium iodide ([BMIM]I) to surface potential is completely different from that in the ILs with [FAP]⁻ anion. A higher friction is observed in [BMIM]I at a more negatively charged Au(111) surface (Fig. 5a, right), because of the spherical shape and localized charge of I-anions, allowing the strong ion adsorption to form a smooth, well-ordered surface plane. Thus, the interfacial lubrication at IL–solid interfaces can be well-tuned by modifying the composition and structure of the interface layer ions through varying the applied voltages.

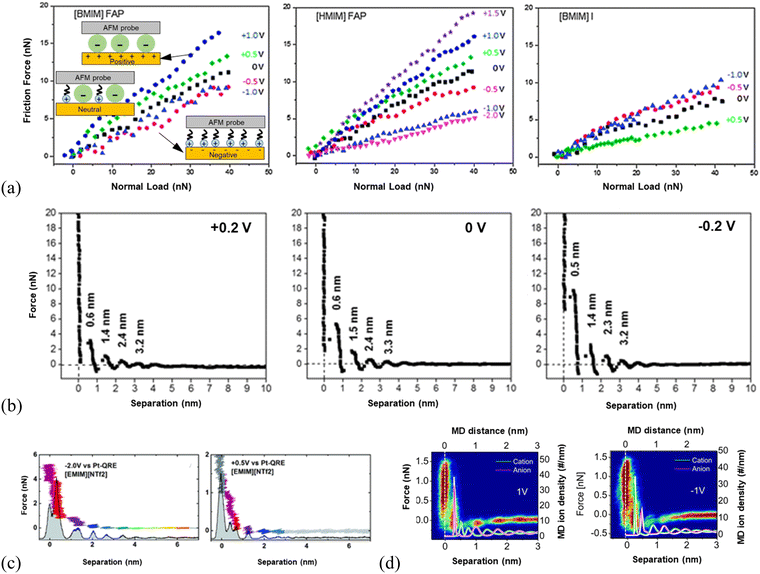Fig. 5 (a) Friction force versus normal load as a function of surface potential for [BMIM]FAP (left), [HMIM]FAP (middle) and [BMIM]I (right) at Au(111) surfaces, with silica AFM probes. Reproduced from ref. 54 with permission from RSC, copyright 2013. (b) A comparison of the AFM force-separation curves of [Py_1,4][TFSA] at Au(111) under varying surface potentials. Reproduced from ref. 126 with permission from RSC, copyright 2018. (c) AFM normal force as a function of the tip-sample separation in [EMIM][NTf₂] for electrical potentials of −2 V (left) and +0.5 V (right) at Au(100) surfaces. The histogram underlying the force curve represents the probability of finding the tip at a given distance to the sample during approach. The colors serve as a guide to the eye to compare equal molecular layers in the panels. Reproduced from ref. 127 with permission from RSC, copyright 2017. (d) Comparison of AFM force curves with MD simulations of [EMIM][NTf₂] cation and anion positions at positively (left) and negatively (right) polarized graphite surfaces. The white line denotes the position of the graphite surface. Reproduced from ref. 72 with permission from ACS, copyright 2013.

AFM approaching force curves have shown that the distinctiveness of the ion layering of interface layer ILs varies with the applied surface potential.² For example, the force required to rupture the ion layer of [Py_1,4][TFSA] (1-butyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl)amide) adjacent to Au(111) surface was found to vary with the applied surface potential. The rupturing force of the innermost ion layer is 10, 6, and 3 nN for the IL at −0.2, 0, and +0.2 V, respectively (Fig. 5b), indicating an increase in the strength of ion adsorption at more negative surface potentials, corresponding to a relatively strong near-surface structure.¹²⁶ For the AFM probe approaching [EMIM][NTf₂] (1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide) on a negatively polarized Au(100) surface (left, Fig. 5c), the force curves revealed a more pronounced layering of the IL compared to that at the positive surface (right, Fig. 5c). The layering structure of the ionic liquid interface can be further recognized in the underlying histogram of the probability of finding the tip at a given distance.¹²⁷ A detailed picture of the molecular ordering of [EMIM][NTf₂] at the charged graphite⁷² and [BMIM][NTf₂] at the charged silica surface¹²⁸ has also been demonstrated by both AFM experiments and MD simulations, which is comparable to the configuration of cations and anions at charged Au(100) surfaces.¹²⁷ As shown in the comparison of AFM force curves overlaid with the ion density curves by simulation in the left panel of Fig. 5(d), the ion layer of [EMIM][NTf₂] closest to the positively biased graphite surface matches the calculated position of the first anion layer. While at −1 V, the first layer is detected as the strongly bound cation layer, which balances the negative surface charge in accordance with the simulations.⁷² Thus, the charge at the surface induces the ordering of ILs into layers of alternating charge, which would favor the lubrication of ILs at solid surfaces.

To briefly summarize, the nano-frictional properties of ionic liquid interface layer, particularly, the ‘quantized friction’ phenomenon observed by either AFM or SFA does depend strongly on the ILs nano-structuring. The dependence of nanofriction on the ion nanostructures of interface layer ILs can be influenced by external stimuli, such as the electrical potential, but is mostly being studied qualitatively, and the quantitative description of the relationship between interfacial ILs nanostructure and properties has not yet been developed.

2.4 Structure–property relationships for interface layer ionic liquids

Thermodynamic modeling analysis reveals a wealth of information of the microscopic structure and mechanisms. It can be used to provide quantitative structure–property relationships (Fig. 6a), highly important in all design and engineering of ILs. Still, reliable interaction parameters for the molecular thermodynamic modeling is demanding (Fig. 6a) and requires reliable and accurate experimental data.^129,130 Molecular simulations are the best tools to verify and validate the feasibility of the experimentally derived interaction parameters (Fig. 6a).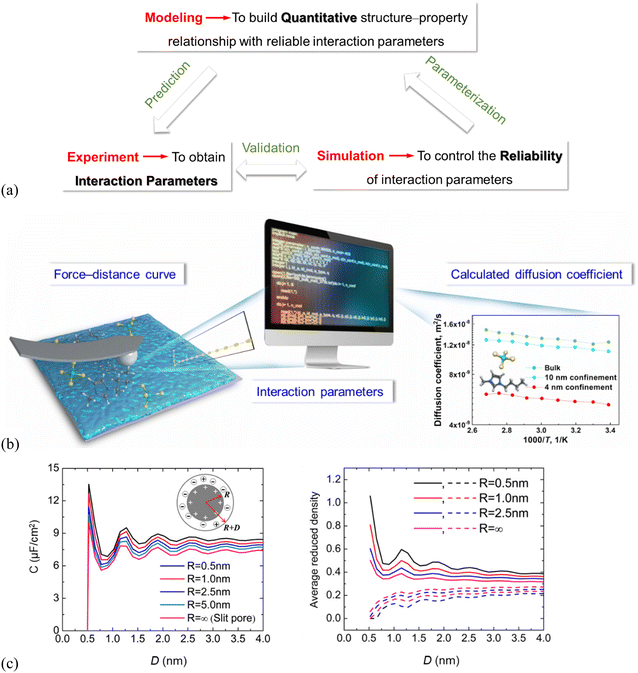

Fig. 6 (a) Multiscale–triangle “experiment–simulation–thermodynamic modeling” technique enabling structure–property relationships. (b) Schematic illustration showing interaction parameters derived from CP–AFM-measured force–distance curves, which can be used in simulations to calculate temperature–dependent diffusion coefficients of the nano-porous SiO₂ confined IL (4, 10 nm pore size) and for ILs in the bulk. Adapted from ref. 90 with permission from RSC, copyright 2022. (c) Left: DFT-predicted overall integral capacitance (C) of room-temperature ILs vs. thickness (D) for spherical shells of different inner radii (R), right: average densities of counterions (solid lines) and co-ions (dashed lines) inside the spherical shell at different thicknesses. The surface electrical potential is ψ₀ = 1.5 V. Reproduced from ref. 109 with permission from ACS, copyright 2016.

There are recently only a few studies to derive interaction parameters directly from experiments. The force curves of IL systems, measured by using SFA and AFM, show typically an oscillatory behavior, indirectly containing information about the number density distribution of the IL cations/anions on the solid substrate. Amano, et al.⁹² did transform their high-resolution AFM-measured force curves into the number density distributions to estimate the hydration structure of liquids at the muscovite mica (001) surface, but only for the molecular liquid region. Wei, et al.^131,132 recently proposed an experimental approach with colloid probe AFM (CP–AFM) to quantify the molecular interactions of imidazolium-based ILs with charged SiO₂ surfaces.^90,91 The CP–AFM-measured adhesion force offers a direct measure of the IL interactions with SiO₂, which can be used to fit the interaction parameters for the molecular simulations (Fig. 6b).⁹⁰ The CP–AFM-derived interaction parameters are further used in MD simulations to compute the temperature–dependent diffusion coefficient of the ILs confined in cylindrically porous SiO₂ with varying pore size (4, 10 nm, cf.Fig. 6b) and compared with those measured experimentally by Nuclear Magnetic Resonance (NMR) spectroscopy, confirming the reliability of the AFM-quantified molecular interactions. An enhanced diffusion rate in ILs at elevated temperatures was observed by simulations for the bulk ILs as well as the confined ones in cylindrically porous SiO₂ with 4 and 10 nm pores, in agreement with that in NMR measurements. However, the diffusion coefficients in the bulk and confined ILs calculated in simulations based on these AFM-quantified interaction parameters are 1–3 orders of magnitude higher than those measured by NMR. The main reason for the much faster diffusion obtained in the simulation is the complete neglecting of the electrostatic interactions as the cation and anion are considered as an ion pair and the charges are simply switched off. Also, the surface topologies of the nano-porous SiO₂ used for NMR measurements are complex in comparison with the SiO₂ model in simulations. Thus, the MD simulation with CP–AFM-derived interaction parameters succeeds in predicting the trends of diffusion coefficients, but fails in reproducing the NMR-measured values. This demonstrates the need for considering the cation/anion charges and surface complexities in deriving the interaction parameters for both simulations and experiments.⁹⁰ The lack of accurate interaction parameters is, due to the rather limited number of studies, still being reported in using thermodynamic modeling analysis to quantitatively predict the properties of the interface layer ILs, although the modeling is expected to greatly improve the quantification of the structure–property relationships.

The interaction parameters⁴² were also reported to be derived from molecular simulations and thermodynamic modeling⁴¹ by describing the substrate effect on the Gibbs free energy of the supported metal nanoparticles, to quantify CO₂ absorption working capacity of the supported imidazolium-based ILs. The thermodynamic modeling was performed to describe the Gibbs free energy of CO₂ in the supported ILs, so that the CO₂ solubility could be quantitatively predicted in the supported ILs.⁴² The interface layer ILs increase the CO₂ solubility compared to the bulk ILs. This can be explained by dividing the Gibbs free energy into three parts, i.e., the terms for bulk, IL–CO₂ interface, and IL–substrate interface. The CO₂ solubility increases in the IL–substrate interface. DFT studies show a qualitative correlation between the differential capacitance of electric double layers in ILs at electrode surfaces and the interfacial ion layering structure.^95,109 The left panel in Fig. 6(c) shows the oscillatory dependence of overall capacitance (C) of room-temperature ILs for spherical shells of varied inner radii (i.e. pore size, R) and thickness (D), which is consistent with those in average densities of the IL-counterions inside the spherical shells (Fig. 6c, right). This can be explained because a smaller inner core radius results in more counterions inside the pore leading to a larger capacitance.¹⁰⁹

Wang, et al. used the colloid probe AFM to demonstrate that the phosphonium-based IL (trihexyltetradecyl-phosphonium bis(salicylato)borate) ([P_6,6,6,14][BScB]) with a long cation chain prefers to form stiffer ion layers at the charged gold surface with a “…cation–cation–anion–anion…” bilayer structure through van der Waals interactions among the nonpolar long alkyl tails of the cations. The formed bilayer structure of this IL exhibits an enhanced capacitance than the monolayer of the IL with a shorter chain, as the excess ions packed in the bilayer structure promote the IL to reach bulk electroneutrality over a shorter distance, enhancing the capacitance.²¹ Similar enhanced charge storage performance was reported earlier in the bilayer ILs with long amphiphilic chains at electrified surfaces by Yang et al.⁹⁶ and Mao et al.⁶ For the latter, they found that a surface-active IL, 1-butyl-3-methylimidazolium 1,4-bis(2-ethylhexoxy)-1,4-dioxobutane-2-sulfonate([C₄C₁Im][AOT]) with a long anion chain exhibits significant and competing van der Waals interactions owing to the non-polar surfactant tails, leading to unusual bilayer ion structure and displaying optimum electrocapacitive performance. These but still qualitative findings on structure–property relationship of interface layer ILs further suggest that there is an urgent need to develop generalized thermodynamic models, based on accurate molecular parameters to quantitatively describe the interfacial ILs nanostructure and properties.

3. “Experiment–simulation–thermodynamic modeling” studies on nano-structuring of interface layer ionic liquids

3.1 Monolayer and bilayer structures of interface layer ionic liquids by experimental techniques

Monolayer. ILs containing short (or no) alkyl chains form layered structures at charged surfaces, consisting of alternating cation–anion monolayers.^65,133–135 For example, typical AFM force curves presented in Fig. 7(a) show pronounced cation–anion monolayers for the 1-ethyl-3-methylimidazolium acetate ([C₂mim]Ac) IL on mica with a Si₃N₄ probe.⁷¹ In general, when the probe moves towards the IL, it cannot first interact with the IL over a long distance, and then a sudden jump in the force is observed at a separation of ∼1.81 nm caused by the probe penetration of the ion layer. When the probe then moves closer to the mica surface to a separation of ca. 1.27 nm, the probe penetrates additional ion layer. After further approaching the surface probe, the probe penetrates yet another ion layer at a separation of ca. 0.64 nm, and finally, it will be in contact with the mica surface (at 0 nm). A series of distinct “push-throughs” can be observed at discrete separations due to the AFM probe rupturing successive IL interface layer of [C₂mim]Ac. Three distinct segments are observed in the approach part of the force curves, each segment being associated with an ion layer, approximately corresponding to the physical size of [C₂mim]Ac at the mica surface. The magnitude of the force required to rupture each layer increases as the AFM probe moves closer to the surface, suggesting that ordering into layers decays further from the substrate as the molecular structure approaches that of bulk EAN. On retraction, the AFM probe jumps from contact to a separation of ∼1.81 nm which is associated with three ion layers, as observed for [C₂mim]Ac.

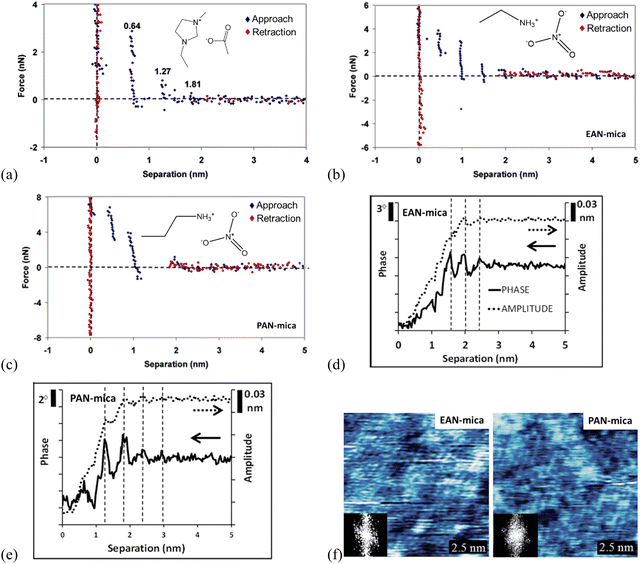Fig. 7 (a) Force curves for a Si₃N₄ AFM probe approaching and retracting from a mica surface in [C₂mim]Ac. The separation distances for each ion layer prior to a push-through are given on the plot. Reproduced from ref. 71 with permission from ACS, copyright 2007. Force curves for an AFM Si₃N₄ probe approaching and retracting (b) EAN-, (c) PAN-mica interfaces. Reproduced from ref. 71 with permission from ACS, copyright 2007. Typical amplitude (dotted) and phase (solid) data recorded as an oscillating AFM probe approaches a mica substrate immersed in (d) EAN, and (e) PAN. Topographic images of (f) EAN and PAN innermost ion layers adsorbed to a mica surface and the inset show the 2D Fourier transforms by dynamic mode AFM. The x-axis in (d) and (e) measures the extension of the AFM Z piezo. Reproduced from ref. 35 with permission from RSC, copyright 2015.

AFM force curves in Fig. 7(b) and (c) compare the ion layering in ILs of different sizes, in which the longer-chained propylammonium nitrate (PAN) exhibits fewer ion layers than the shorter ethylammonium nitrate (EAN) on mica, due to the higher molecular flexibility of PAN.⁷¹ Meanwhile, the force profiles oscillate periodically with the characteristic oscillation length corresponding to the physical dimension of the ion pair for the ILs confined between Si₃N₄ probes and mica. The magnitude of the force required to rupture each ion layer increases as the probe moves closer to the surface for both EAN and PAN, suggesting that the layers closer to the mica are more ordered, with decreasing ordering into layers further from the mica substrate. A stronger attractive interaction of the longer PAN with mica is detected, and the force steps in PAN are not vertical like those in EAN, suggesting the detected ion layers in PAN are more compressible.

Combining with the dynamic mode AFM, the 3-dimensional ion ordering of ILs at solid interfaces can be captured further.³⁵ In the dynamic mode AFM, the cantilever can oscillate close to or at resonance frequency and the cantilever oscillation alters as the height changes, to adjust the probe-surface distance. This allows a simultaneous detection of the structure in both lateral and normal directions to obtain 3-dimensional information on the ion ordering at solid interfaces.¹³⁶ With the dynamic mode AFM, the phase and amplitude of EAN and PAN at mica surfaces are measured as a function of the separation, revealing clearly layered ion structures in the normal direction (Fig. 7d and e), although the steps tend to be less distinct in the amplitude than in the phase data.³⁵ For both EAN and PAN, the phase and amplitude are constant when the probe-surface separation is greater than 3 nm, indicating that the AFM probe is insensitive to the bulk ILs. While as the separation is decreased below 3 nm, the phase and amplitude decrease as a consequence of the confining effect of the probe and mica substrate. The obtained phase and amplitude signals exhibit periodic oscillations as the probe moves closer to the mica, and the oscillation periods in EAN and PAN in Fig. 7(d) and x1(e) are the same as the step sizes in AFM force curves (Fig. 7b and c), respectively. The magnitude of the oscillations increases closer to the surface due to a more pronounced ion ordering and enhanced confinement near the surface. The oscillations in PAN are more intense than EAN due to the longer alkyl chains of PAN, producing stronger solvophobic segregation. In the lateral direction, the topographic images of the IL-mica innermost layer obtained by the dynamic mode AFM (Fig. 7f) exhibit a regular lattice structure. The insets 2D Fourier transforms show a hexagonal symmetry of the lattice with a repeated spacing of 0.5 nm, which is in agreement with that of the mica lattice, as a consequence that the cations are electrostatically bound to mica-charged sites.

Bilayer. By increasing the alkyl chain length and hence the amphiphilicity of the cation/anion, the positive charge places at one end of the ion and a non-polar chain to the other end can self-assemble to form lamellar ion bilayers under confinement.^{6,96,137–141} The chemistry and geometry of the cation headgroup play a pivotal role in determining both the chain length, at which the segregation of non-polar and polar domains occur and lead to a bilayer architecture. For example, the interfacial layering of two amphiphilic ILs has been investigated via SFA, possessing differently long cations sharing the same anion, i.e., 1-butlyl-3-methylimidazoliym bis(trifluoronmenthylsuldonyl)imide, [C₄C₁im][NTf₂], and 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide, [C₆C₁im][NTf₂] confined between negatively charged mica sheets.¹³⁷ As shown in Fig. 8, both ILs show distinct oscillatory forces with alternating repulsive and attractive regions of increasing amplitude with a decreasing separation D. However, the period of the oscillations is different, where six oscillations are observed in the shorter-chain [C₄C₁im][NTf₂] corresponding to alternating cation–anion monolayers (Fig. 8a). In comparison, four oscillations with a much greater repeat distance are observed in the longer-chained [C₆C₁im][NTf₂] due to the formation of cation bilayer (cf.Fig. 8b, insets). Because the longer [C₆C₁im] cation is distinctly amphiphilic with the positive charge at the headgroup and a non-polar tail, the aggregation of these non-polar chains, with neutralizing layers of anions adjacent to the cationic headgroups, results in the bilayer structure of [C₆C₁im] cations. The more amphiphilic nature of the [C₆C₁im] cation causes self-assembly into tail-to-tail cation bilayers at the mica surface, which could be driven by the need to sequester the hydrocarbon chains away from the ionic regions.

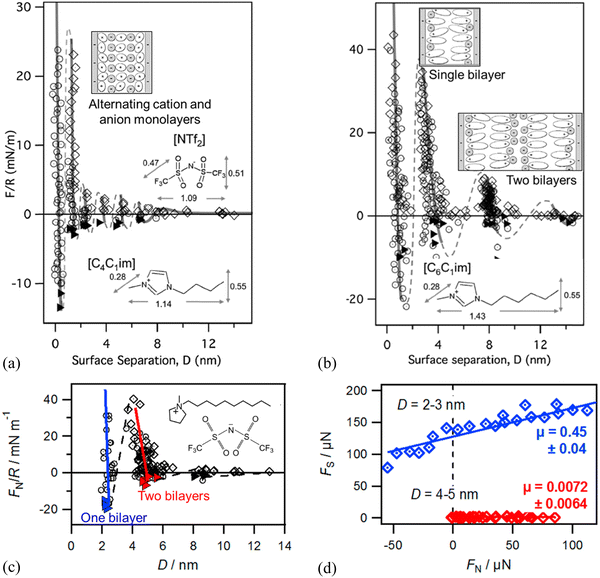Fig. 8 SFA-measured normal force (F) between two negatively charged mica surfaces (normalized by the mica curvature, R) versus film thickness (D) for (a) [C₄C₁im][NTf₂] and (b) [C₆C₁im][NTf₂]. The lines are a guide to the eye to show the oscillatory nature of the forces. The insets show ion orientations and molecular structure of differently lengthened cations and the anion. Reproduced from ref. 137 with permission from RSC, copyright 2011. (c) SFA-measured normal force F_N/R versus D showing sequential squeeze-out of bilayers of [C₁₀C₁Pyrr][NTf₂] between two mica sheets. Open diamonds and circles show data measured upon approach and retraction of the surfaces, respectively, and adhesive minima are marked as filled triangles. The inset shows the molecular structure of [C₁₀C₁Pyrr][NTf₂]. Reproduced from ref. 138 with permission from ACS, copyright 2013. (d) SFA-measured friction force F_Sversus F_N measured for one and two bilayers of [C₁₀C₁Pyrr][NTf₂]. Solid lines are linear fits in (d) to obtain friction coefficient μ (slope) following Amontons’ law. Reproduced from ref. 142 with permission from ACS, copyright 2014.

The dynamic friction force was also measured by SFA across one and two bilayers of 1-decyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₁₀C₁Pyrr][NTf₂]) confined between two mica sheets (Fig. 8c and d).¹⁴² As shown in Fig. 8(d), the friction force versus normal load measured by SFA gives a low friction coefficient μ = 0.0072 ± 0.0064 for a film of 5.0 nm consisting of two bilayers, which corresponds to two bilayers in the red regime in Fig. 8(c). When the IL film is squeezed down to one bilayer with a film thickness of 2.4 nm corresponding to one bilayer (blue regime in Fig. 8c), it becomes very sticky with a concomitant abrupt increase in friction and a high friction coefficient of μ = 0.45 ± 0.04 (Fig. 8d). The friction for the two bilayers in [C₁₀C₁Pyrr][NTf₂] is lower than that for any of those alternating cation–anion monolayers (9, 7, 5, and 3 ion monolayers)⁵¹ in shorter-chained [C₄C₁Pyrr][NTf₂], whereas the friction for one bilayer is higher than that for any of the monolayer regimes.

3.2 Monolayer and bilayer structures – molecular simulations & thermodynamic modeling

Monolayer. The ionic liquid interface layer nano-structuring affects strongly the properties of interfacial ILs.^143–149 For a deeper understanding of the distribution and nanostructure of interfacial ILs, several theoretical studies have been recently performed.^{122,150–158} For example, MD simulations were carried out to investigate the nanostructure of [BMIM][PF₆] at the graphite surface,¹⁵⁹ in which, the ion mass densities of the interface layer IL exhibit damped oscillations. More distinct oscillations were observed in the mass density of [BMIM][PF₆] with alternating cationic and anionic mono-layering features when the graphite surface is negatively charged.¹⁶⁰Fig. 9(a) shows the concentration profiles of imidazolium rings and anions of [BMIM][PF₆], depending on the distance to the negatively charged graphite surface, in which the maxima of the ring concentrations coincide with the minima of the anion concentrations and vice versa.¹⁶⁰ The oscillatory behavior with an alternating cation–anion monolayer structuring feature was also observed in both 1-ethyl-3-methylimidazolium dicyanamide ([C₂mim][dca]) and N-butyl-N-methylpyrrolidinium dicyanamide ([C₄myr][dca]) at charged graphene interfaces, as shown in Fig. 9(b).¹⁴⁹ Another MD simulation work found the oscillatory ion layers of the [BMIM][PF₆] IL in a 2.8 nm-wide carbon layer forming three distinct regions, i.e., a compact layer closest to the carbon surface with a pronounced ion density peak, thereafter a subcompact layer at the position further away from the surface, and then a central layer with non-significant density peak of ions at a greater distance from the surface.¹⁶¹ This finding from simulations was also confirmed in a recent experimental work, in which the ion layering of interface ILs is associated closely with the layered nanoscale friction.⁵³

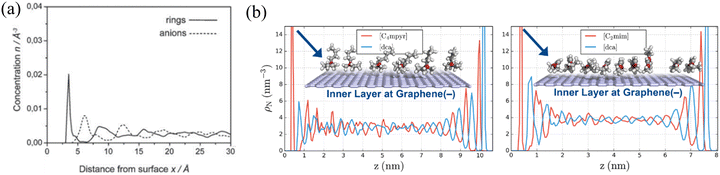Fig. 9 (a) The concentration profiles of imidazolium rings and anions of [BMIM][PF₆] in the vicinity of the negatively charged graphite surface. Reproduced from ref. 160 with permission from RSC, copyright 2019. (b) Partial density profiles of 1-ethyl-3-methylimidazolium dicyanamide ([C₂mim][dca]) and N-butyl-N-methylpyrrolidinium dicyanamide ([C₄myr][dca]) at both charged graphene surfaces. Reproduced from ref. 149 with permission from RSC, copyright 2017.

Classical density functional theory (DFT) has been employed to characterize and predict the IL interface layer nano-structuring.^{95,96,109,110}Fig. 10 presents DFT predictions of the ionic distributions, the local mean electrical potential (φ(z)), and the integrated local charge density (q(z)) for three different ILs (symmetric IL with cation and anion of the same size in Fig. 10(a), asymmetric IL with a larger cation than the anion in Fig. 10(b), and asymmetric IL with a smaller cation than the anion in Fig. 10c) at charged surfaces.¹⁰⁴ Distinctive multiple alternating layers of cations and anions were observed near the charged surface beyond 10 times the ionic diameter (Fig. 10a, top). The observed alternative monolayer ion structuring is concomitant with strong charge inversion (or ‘‘over screening’’) as shown by the oscillatory distributions of the local mean electric potential and the integrated charge density (Fig. 10a, bottom). Fig. 10(b) shows that an increase in the cation size results in a significant reduction of both the anion contact density and the magnitudes of charge oscillations, although the number of oscillatory layers remains largely unchanged. The reduced contact density and the magnitudes of charge oscillations are because of the weakened electrostatic effect by the larger cations near the surface due to the enhanced cation excluded volume. While the reduction of the cation size strengthens the electrostatic interactions, reduces the number of ionic layers at the surface, and makes the layering structure less distinctive (Fig. 10c). The less distinctive layering structure in the IL with a smaller cation calculated by DFT in Fig. 10(c) seems to contradict the SFA experimental results in Fig. 8(a) and (b) where 6 oscillatory layers were observed in the IL with the smaller [C₄C₁im]⁺ cation but only 4 oscillations for the larger [C₆C₁im]⁺ cation. However, it is noteworthy that the longer-chained [C₆C₁im][NTf₂] exhibits a distinct amphiphilicity with the positive charge at the headgroup and a non-polar tail, which can induce a strong van der Waals force, resulting in a “…cation–cation–anion–anion…” bilayering structure. However, in the DFT calculations, the ILs were assumed to be spherical particles or segments, implying that they are non-amphiphilic. Therefore, in SFA measurements, the larger amphiphilic [C₆C₁im][NTf₂] exhibits less oscillations than those of the smaller [C₄C₁im][NTf₂], but still showing a more distinctive layering structure with a much greater repeat distance, in agreement with the DFT predictions.

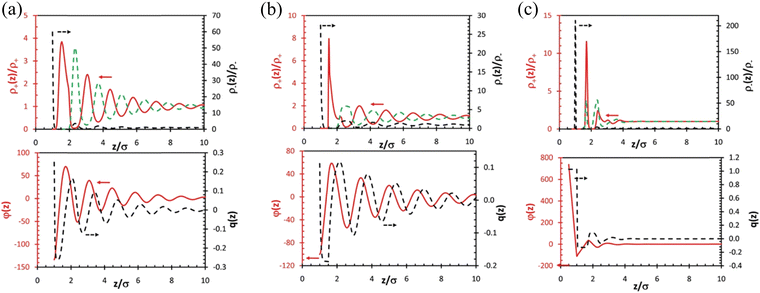Fig. 10 (a) Top: DFT-predicted distributions of cations (red solid line) and anions (black dashed line) for a symmetric IL (σ₊ = σ_–= σ) near a charged surface with reduced charge density Qσ²/e = 0.25. The green dashed line represents the anion density beyond the first layer plotted using the same scale of that for the cation density (left axis). Bottom: The reduced mean electric potential, φ(z), and the integrated charge distribution function, q(z), near the electrode. (b) The same as (a) but for an IL with asymmetric ionic size (σ₊ = 1.5σ, σ_–= σ). (c) The same as (a) but for an IL with asymmetric ionic size (σ₊ = 0.5σ, σ_–= σ). Reproduced from ref. 104 with permission from RSC, copyright 2011. σ₊ and σ_– represent the size of cation and anion, respectively.

Bilayer. A Landau–Ginzburg-like functional for the total free energy was developed to predict the structure of the electrical double layer of solvent-free ILs at the electrode surface.¹⁶² This model captures over-screening alternative monolayer ion structures at a small voltage of 0.26 V (Fig. 11a, left panel),¹⁶² similar to the earlier experimental finding.²⁶ While increasing the voltage gradually to 2.6 V suppresses over-screening in favor of the crowding of counterions near the electrode, namely bilayer ion structures as shown in the middle panel of Fig. 11(a). The predicted double-layer capacitance versus potential by this Landau–Ginzburg-type model (Fig. 11a, right panel)¹⁶² is in very close agreement with the simulation result.¹⁶³ At a higher voltage, the first counterion layer attains the maximum density with a second layer of excess co-ions (Fig. 11a, middle panel). The co-ion-rich layer next to the first counterion layer has a lower density, but is still larger than the bulk phase, and the formed bilayer IL structure is beneficial to the improvement of the capacitance.¹⁶⁴

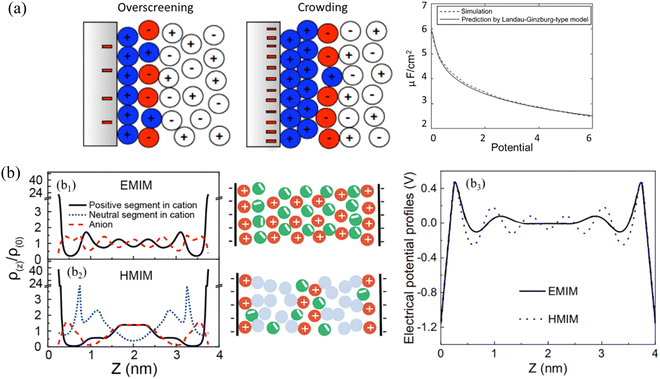Fig. 11 (a) Structure of the IL double layer (in color) predicted by Landau–Ginzburg-type continuum theory at a moderate voltage of 0.26 V (left), and a high voltage of 2.6 V (right). Right panel: Comparison of double-layer differential capacitance obtained from Landau–Ginzburg-type model (solid curve) and simulation (dashed curve). Reproduced from ref. 162 with permission from APS, copyright 2011. (b) b₁ and b₂: DFT-predicted density profiles (left) and schematics (middle) of anions (red dashed line), the positive (black solid line) and neutral (blue dotted line) segments of cations inside a negatively charged nanopore at the electrical surface potential of –ψ for ILs containing (b₁) 1-methyl-3-ethylimidazolium ([EMIM]⁺) and (b₂) 1-methyl-3-hexylimidazolium ([HMIM]⁺) cations. b₃: Electrical potential profiles inside a negative nanopore at the electrical surface potential of –ψ for ILs containing [EMIM]⁺ (blue dotted line) and [HMIM]⁺ (black solid line). Reproduced from ref. 96 with permission from Elsevier, copyright 2020.

Aided by DFT, the alternative cation–anion monolayer structure for the symmetrical IL containing 1-methyl-3-ethylimidazolium ([EMIM]⁺) within a negatively charged pore (–ψ) can be seen in Fig. 11(b₁). While the addition of a long chain into the cation, i.e., the IL containing 1-methyl-3-hexylimidazolium ([HMIM]⁺, cf.Fig. 11b₂), disrupts the mono-layering of ions that is normally seen for a symmetrical IL in Fig. 11(b₁). In the IL with a long [HMIM]⁺ cation chain (Fig. 11b₂), the van der Waals force will dictate the arrangement of ions, forming a new layer of neutral segments, so that bilayer IL structuring occurs. As a result, the electrical potential profiles of the first layer are more balanced in the IL with a longer [HMIM]⁺ cation than those of the symmetric IL system with a [EMIM]⁺ cation, and the oscillation of charge smooths for the longer IL (Fig. 11b₃).⁹⁶ Despite the years of active research and the significant efforts of theorists and simulators, the studies on the ILs interface layer with the combination of modeling and simulation are still fairly lacking.¹⁶⁵ Vaganova et al.¹⁶⁶ proposed an approach that combines DFT and MD simulations to study the behavior of pure methane, ethane and carbon dioxide and their binary mixtures in slit-like carbon nanopores, showing a good agreement between the structures obtained by theory and simulation. This approach consists of two principal steps: a DFT calculation of fluid composition and density distribution in a nanopore under specified thermodynamic conditions and an MD simulation of the confined system with obtained characteristics. Malpica-Morales et al.¹⁶⁷ combined machine learning techniques with DFT to reconstruct the external potential which accounts for the interaction of the many-particle system with an external field and thus affects the density distribution. This combination accurately infers the density profile of the many-particle system, probably serve as a prototype for studying a wide variety of applications, especially for ILs interface layering behavior. Here are a few examples just for quanlitative validation between modeling and simulation: electrolyte perturbed-chain SAFT-DFT model was developed to describe the behavior of the imidazolium-based IL and CO₂–IL mixture confined in silica nanopores, in which an ionic functional was proposed for electrostatic free-energy contribution. The DFT model predicting long-range oscillatory density profiles of ILs confined in silica slit and cylindrical pores agree well with those predicted by molecular simulation.¹⁶⁸ The strong oscillations of ionic density profiles and the local electrostatic potential were predicted by DFT to describe the double layer structure of an IL at an electrode surface using a dimer model, which was confirmed further by simulation.¹⁶⁹ DFT-based MD simulations were conducted to study the interface between graphene and 1-ethyl-3-methyl-imidazolium tetrafluoroborate IL to examine the ions arrangement at variable surface charge densities.¹⁷⁰

3.3 Combined atomic force microscopy & simulations

AFM studies have been combined with MD simulations to examine the distinct effect of the addition of salts into ILs at solid interfaces on the cation–anion monolayers.⁷ In Fig. 12(a), neat IL, i.e., N-methyl-N-propylpyrrolidinium bis(fluorosulfonyl)imide ([C₃mpyr][FSI]) gives rise to five oscillations at gold surfaces in the approaching force curve, with the step period of 0.60 nm, being consistent with the size of the cation–anion pair. The solvation force, required to squeeze-out a layer, increases closer to the surface as the ordering of the layered ions is enhanced. In contrast, with the addition of 50 mol% NaFSI in the [C₃mpyr][FSI] IL (Fig. 12b), the ion structure is significantly changed stepwise. A considerable decrease is observed in the solvation force, indicating that the reduced force to rupture each ion layer, due to the weakening of the ion–ion association caused by NaFSI salt. The observed shift of the step position in Fig. 12(b) suggests that the dimensions of ion packing have been changed by NaFSI, attributed to the Na⁺ altering the chemical composition of the inner ion layers.⁷ The presented ion number density profiles show around five peaks for the [C₃mpyr][FSI] IL system without NaFSI salt, agreeing well with the AFM results (Fig. 12a). With the addition of 50 mol% NaFSI salt, the number of peaks in the density profiles of both cations and anions reduces to three, again reproducing the change observed in the AFM measurements (Fig. 12b). The height of the first sharp peak for the IL cation reduces as the salt is added, whereas that of the [FSI]⁻ increases, suggesting a growth in the number of anions in the innermost layer.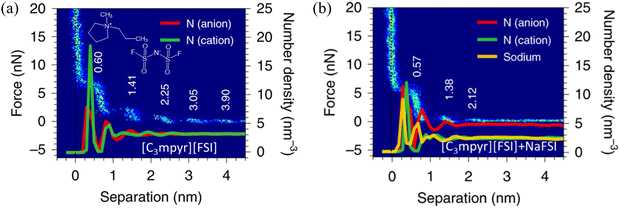

Fig. 12 AFM-measured force curves and MD-calculated ion number density profiles of the [C₃mpyr][FSI] IL (a) without and (b) with an addition of 50 mol% NaFSI on gold electrodes at open circuit potential (OCP). Reproduced from ref. 7 with permission from Springer, copyright 2020.

To reveal the molecular origin of the experimentally detected ionic layers in the amphiphilic IL at solid surfaces, Mao et al.⁶ compared the different ion structures of non-amphiphilic (Fig. 13a) and amphiphilic (Fig. 13b) ILs at graphite surfaces through the combination of the atomistic molecular dynamics (MD) simulation and AFM force curves. The conventional non-amphiphilic 1-butyl-3-methylimidazolium tetrafluoroborate ([C₄C₁Im][BF₄]) and amphiphilic 1-butyl-3-methylimidazolium 1,4-bis(2-ethylhexoxy)-1,4-dioxobutane-2-sulfonate ([C₄C₁Im][AOT]) are compared. The latter IL, i.e., [C₄C₁Im][AOT], is amphiphilic because it possesses a special anion [AOT]⁻ with a negative charge located at one end of the ion (polar head) and a bulky branched di-chain hydrocarbon group at the other end (non-polar tail). The left panels of Fig. 13(a) and (b) show the ion number density (ρ_N) profiles of [C₄C₁Im][BF₄] and [C₄C₁Im][AOT], respectively, obtained from MD simulations at charged graphite surfaces with applied potentials (U) of ±2 V. The non-amphiphilic [C₄C₁Im][BF₄] IL exhibits a lamellar structure of alternating charges, persisting for around 8 ion layers (Fig. 13a). While for the amphiphilic [C₄C₁Im][AOT], it is interesting that the surface-induced charge-alternating structure only persists for around two ion layers, with the first peak showing a much larger ρ_N (Fig. 13b) relative to that of [C₄C₁Im][BF₄].

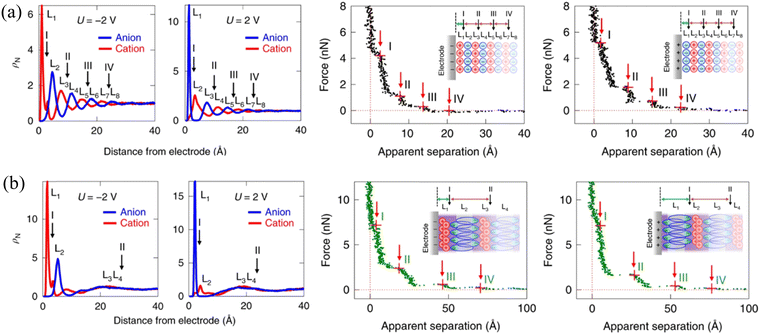Fig. 13 Ion number density profiles obtained from MD simulations (left) and typical AFM force curves (right) of (a) non-amphiphilic [C₄C₁Im][BF₄] and (b) amphiphilic [C₄C₁Im][AOT] on negatively and positively charged graphite electrodes. Reproduced from ref. 6 with permission from Springer, copyright 2019. Insets in AFM force curves are schematics of hypothesized ion arrangements of the ILs at charged graphite surfaces. Red arrows with I, II, III and IV in the force curves indicate the possible positions corresponding to the AFM push-through locations, corresponding to the black arrows marked positions in ion number density profiles from MD.

AFM force curves in the right panels of Fig. 13(a) and (b) demonstrate the alternating cation–anion molecular layering in [C₄C₁Im][BF₄] and unusual interfacial ion distribution in the amphiphilic [C₄C₁Im][AOT] that have been observed in MD simulations. The separation between steps for [C₄C₁Im][AOT] is 22–24 Å (right, Fig. 13b), which is three to four times larger than those for [C₄C₁Im][BF₄] (6–7 Å), corresponding to the physical dimension of an ion pair of [C₄C₁Im]⁺ and [BF₄]⁻ (right, Fig. 13a). The presented unusual interfacial ion distribution in the amphiphilic [C₄C₁Im][AOT] results from the significant van der Waals interactions among the non-polar surfactant tails in the anion. At a positively charged electrode surface, the polar heads of anions [AOT]⁻ are electrostatically attracted to the interface, whereas the non-polar tails orientate outward, in close proximity to the non-polar tails of the next anion layer. A bilayer thus forms in parallel to the positively charged surface, with a neutralizing cation layer adjacent to the anionic polar heads. Near a negatively charged surface, the innermost ion layer is enriched in cations, fully neutralizing the adjacent anionic bilayer, and resulting in a larger separation (right, Fig. 13b, inset). In contrast, the distribution of most cations and anions in the non-amphiphilic [C₄C₁Im][BF₄] is dominated by the Coulombic interactions, forming ‘neutral aggregates’ (right, Fig. 13a, inset) with the characteristic separation of an ion-pair dimension. Similar “…anion–anion–cation–cation…” bilayer structure has also been observed in the amphiphilic phosphonium-based IL trihexyltetradecyl-phosphonium bis(salicylato)borate ([P_6,6,6,14][BScB]).²¹ The observed bilayer structure of the amphiphilic ILs, allowing the excess ions to pack at charged surfaces, facilitates the improvement of the capacitive energy storage capability.^6,21,96

4. How interface layer ionic liquid nano-structuring enables lubrication and energy storage

ILs exhibit many attractive properties in proximity to solid surfaces, and can form well-defined ion layers at interfaces where the composition, structure, dynamics, etc. are tunable. A large volume of work has appeared over the past few years to witness the growth of ILs in the vicinity of solid surfaces for engineering and electrochemical applications, especially in lubrication and energy storage.^{4–7,12,15,29,38,171}

4.1 Lubrication and friction reduction

ILs can lead to a better friction reduction than conventional molecular lubricants, because they can form a robust boundary film better resisting the squeeze-out at heavy loads. ILs self-assemble to ordered ion layers near the surface exhibiting strong interactions with surfaces.³⁰ The interface ion layering of ILs simply plays a pivotal role in improving the lubricating efficiency at IL–solid interfaces.^2,171 A super-lubrication with a super-low friction coefficient (μ) of 0.001 at pressures up to 78 MPa has been observed at varying sliding velocities by AFM in imidazolium ILs at graphite surfaces even without electric field regulation (Fig. 14a).²⁰ The ordered striped structure driven by the “atomic-locking” effect between carbon atoms on the alkyl chain of ILs and graphite unveils the hidden structural feature of IL ions dominating this extreme lubrication. Taking the imidazolium IL, [C₁₈mim][NTf₂] as an example, it is obvious that the IL self-assembles into smooth films (Fig. 14b) with a thickness of ∼0.5 nm corresponding to a monolayer IL with the imidazole ring lying flat on the surface. A well-ordered striped structure with a periodicity of about 6 nm has been observed in the high-resolution image (Fig. 14c), with bright striped regions representing the self-assembled ILs on the surface. In combination with simulation, the alternate ordered and disordered ionic regions are recognized, where a head-to-head structure pattern is shown with two different configurations of the imidazole ring arranged alternately in the same column (Fig. 14d). The cross-sectional profiles from AFM experiment and simulation in Fig. 14(e) indicate that the length of one period of this head-to-head ion structure can be divided into three regions, in which, regions I, II, and III correspond to imidazole rings, anions, and alkyl chains, respectively. The height difference between the experiment and simulation is attributed mainly to the out-of-plane flexibility of the warped imidazole rings, which are deformed and pushed closely to the graphite surface under the sliding AFM tip.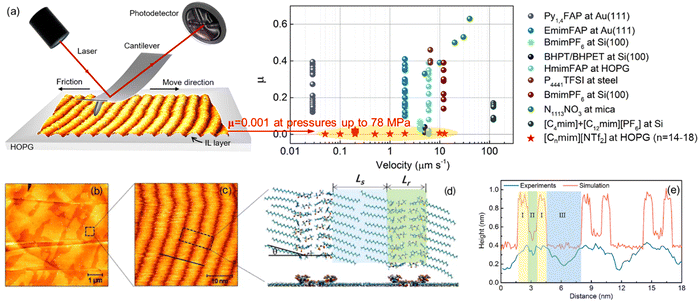

Fig. 14 (a) Friction coefficient (μ) of various ILs obtained by AFM experiments. (b)–(e) Typical AFM images and simulation results of [C₁₈mim][NTf₂] on the HOPG surface: (b) topography image of [C₁₈mim][NTf₂] and (c) a close-up view of the fine structure. (d) Top and side views of arrangements for cations and anions obtained by simulation, L_s and L_r represent the lengths of the alkyl chain and anion region, respectively, and graphite surface is now shown here. (e) Comparison of cross-sectional profiles in the experiment (black line in (c)) and simulation. Reproduced from ref. 20 with permission from ACS, copyright 2022.

Despite great progress in the fundamental understanding of the ion layering of ILs at solid surfaces and the friction through various advanced techniques, the influence of the layering structure of ILs on friction is still controversial. The layering structures of 1-hexyl-3-methylimidazolium tris(pentafluoroethyl) trifluorophosphate ([HMIM][FAP]) and trihexyl-(tetradecyl)phosphonium bis(trifluoromethane)sulfonamide ([P_6,6,6,14][TFSI]) confined between a sharp AFM Si probe and a stainless steel surface are compared by AFM force curves together with the friction force (Fig. 15a).⁵² The force curves of [HMIM][FAP] (Fig. 15a, left) exhibit more ion layers near the surface than [P_6,6,6,14][TFSI], because the bulkiness of the [P_6,6,6,14]⁺ cation in [P_6,6,6,14][TFSI] weakens the electrostatic interaction with the anion and results in the weaker structure. Therefore, the sliding AFM probe expels the weak ionic liquid interface layer structure of [P_6,6,6,14][TFSI] with minimal energy loss and low friction (Fig. 15a, right). A quantized friction feature is observed in the IL, 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₄C₁Pyrr][NTf₂]), confined between two mica sheets in a SFA, as shown in Fig. 15(b). Each of the quantized friction regimes follows an approximately linear friction vs. normal load relationship, and the resulting gradient, i.e., the friction coefficient μ increases as the layering ion pairs become thinner. This is attributed to the greater degree of interlocking of the layers closer to the surface, which are more ordered, with a greater ion excess concentration. These more ordered and densely packed ion layers result in a ‘stronger inter-layer attraction for the same value of contact area and a greater barrier for unlocking the surfaces to allow shear’.⁵¹ A higher friction force, as a result of a stronger layering structure of IL ions at the surface, has also been found by AFM in the imidazole-based ILs on the surfaces of mica and carbon.^53,113,172 It is apparent that the strongly structured ion layers of the interface layer IL result in a higher friction, because of more dissipated energy, and a higher friction is required by breaking the stronger interlayer bonds.

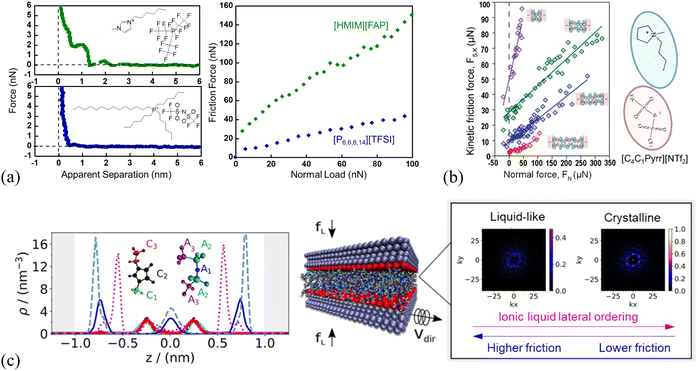Fig. 15 (a) AFM force curves (left) and friction force vs. normal load (right) of [HMIM][FAP] and [P_6,6,6,14][TFSI] on the stainless steel surface. Reproduced from ref. 52 with permission from ACS, copyright 2017. (b) Kinetic friction force F_S,kvs. the normal load F_N measured for different numbers of ion layers of the IL 1-butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide ([C₄C₁Pyrr][NTf₂]) confined between mica surfaces in a SFA. Reproduced from ref. 51 with permission from RSC, copyright 2013. (c) Left: Number density profiles of the [C₂MIM][NTf₂] IL confined between two positively charged slabs (+32 μC cm⁻²) under a load of 400 MPa using the nonequilibrium MD simulations. The color of the line corresponds to that of each group in the IL (see legend). Middle: The slabs confining the IL, with a normal load, f_L, and the top slab moving along the y direction at a constant velocity, V_dir, with a fixed lower slab. Right: 2D structure factor S_m(k_x, k_y) for the layer 2 and 3 in the first 3 ion layers of the confined [C₂MIM][NTf₂] nearest to the slab surface, showing the ion crystalline ordering. k_x and k_y represent the wave-vectors in x and y directions, and the bright spots indicate the formation of 2D crystalline structures. Layer 1 corresponds to the anion-rich layer next to the fixed wall, layer 2 to the adjacent cation-rich layer, and layer 3 to the anion-rich layer in the middle of the IL film. Reproduced from ref. 173 with permission from ACS, copyright 2020.

However, Atkin's group^54,55 found a different ion ordering dependence of the friction, where more ordered IL layers lead to a smoother sliding plane, resulting in a smaller friction, and this is further demonstrated by simulation findings.¹⁷³ With atomistic nonequilibrium molecular dynamics (NEMD) simulations, the friction is observed to vary with the ion layering structure of imidazolium ILs at surfaces, in which these ILs feature the lower friction forces for the more ordered ion layers (Fig. 15c).^23,173 As shown in Fig. 15c (left panel), the number density profiles of 1-ethyl-3-methyl-imidazolium bis-(trifluoromethylsulfonyl)imide ([C₂MIM][NTf₂]) between two positively charged slabs under a load of 400 MPa exhibit 5 ionic layers. The characteristic alternating charge structure of the IL under confinement is clearly observed. With the time-averaged 2D structure factor S_m(k_x, k_y),¹⁷³ the ion crystalline ordering is observed for the first 3 ion layers of the confined [C₂MIM][NTf₂] nearest to the slab surface (right panel, Fig. 15c). Layer 1 corresponds to the anion-rich layer next to the fixed wall which is not shown in Fig. 15c, layer 2 to the adjacent cation-rich layer, and layer 3 to the anion-rich layer in the middle of the IL film. The appeared well-defined bright spots in layer 3 of [C₂MIM][NTf₂] (right panel, Fig. 15c), are indicative of crystalline order throughout the confined IL film induced by the positive charged slab surface, while the structure of layer 2 is clearly disordered liquid-like. The observed crystalline ordering of the IL ions is closely related to the friction forces, in which ordered ion structures are weakly commensurate or incommensurate with the slab structure facilitating the decrease of the friction. Thus, there is a controversy over the correlation between the ion ordering of ILs and the friction at IL–solid interfaces, which needs further investigation.

4.2 Making use of nano-structuring of interface layer ionic liquids in energy storage

Conventional organic solvent-based electrolytes have a number of limitations including flammability, unsatisfactory electrochemical stability, thermal instability, and decomposition of the salts that are adversely affecting the overall performance and service life of energy storage devices.¹⁷⁴ IL-Based electrolytes are considered as promising alternative electrolytes with great potential to overcome the drawbacks associated with these conventional electrolytes.¹⁷⁵ ILs have a combination of properties making them appropriate electrolytes for energy storage devices. Some of these properties include non-flammability, negligible vapor pressure, chemical, thermal and electrochemical stabilities, inherent ionic conductivity, and wide electrochemical stability windows up to 6.0 V.^176–178 In the case of batteries, the energy storage is based on faradaic reactions and the voltage corresponds to the redox couple, however, energy is stored through compression of IL ions along the electrode surfaces in the case of an electric double-layer capacitor. In the latter, energy storage occurs via physical separation by the ions under the influence of applied electric potential, and no chemical reactions are involved.

We focus on the interfacial structuring of ILs as electrolytes in electric double-layer capacitors, where an electric double layer (EDL) is formed in contact with electrode surfaces, i.e., the ILs screen charged surfaces by the formation of bound layers and diffuse electric double layers containing dissociated ions. As illustrated in Fig. 16(a),¹⁷⁹ the dissociated IL ions of the opposite signs are accumulated on the surface of carbon electrodes as a result of the applied negative potentials and the amount of ions is proportional to the applied potential. The resulting local Coulombic rearrangements of the IL ions at negatively charged carbon electrode surfaces are responsible for the energy storage performance. Apparently, the nature of the electrode can affect the structure of the EDL and thus plays a key role in the differential capacitance of the supercapacitors.¹⁸⁰ For example, Su et al.¹⁸¹ functionalized gold electrode surfaces by –COOH and –NH₂ groups to adjust surface chemistry and control the ion structuring of [BMIM][PF₆] IL, strongly influencing the capacitance process of the IL. With in situ colloid probe AFM detection of nano-friction and torsional resonance frequency at the IL–electrode interfaces, they observed stiffer ion layers on the Au–COOH surface than on Au–NH₂, demonstrating more ordered ion layers on the –COOH-terminated Au surface. The strength of the ion layering on the Au–COOH surface is facilitated by the π–π⁺ stacking interaction between the delocalized π⁺ electrons from the imidazolium ring of the [BMIM]⁺ and the localized π electrons from the sp² carbon on the –COOH group. On the contrary, the weaker IL–surface interactions on the Au–NH₂ surface lead to aggregating IL droplets and are unable to induce a strong templating effect on the IL ions. The resulting uniform structuring ion layers of the IL at Au–COOH speed up the capacitive process and make the electrochemical response more sensitive (Fig. 16b). With MD simulations, Vatamanu et al. observed a noticeable improvement in the capacitive storage of the IL by increasing the curvature of the electrode, as an effectively larger volume of the ILs interface layer allows more counterions per surface area in contrast to a flat surface, leading to an increased capacitance.¹⁸²

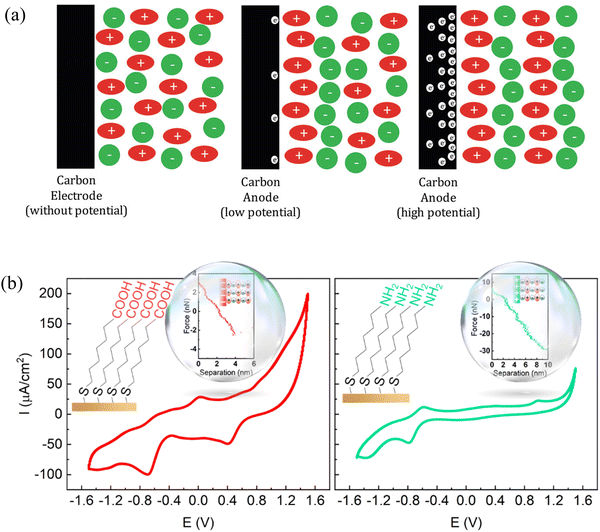Fig. 16 (a) Schematic of the carbon electrode–IL interface in electric double-layer capacitors showing local ordering transitions of IL ions caused by varying surface potentials. Adapted from ref. 179 with permission from RSC, copyright 2018. (b) Cyclic voltammetry curves of [BMIM][PF₆] on the surface of –COOH and –NH₂ terminated gold electrodes. The inset circles showing the colloid probe AFM obtained ion structuring of the IL at the functionalized electrode surfaces. Reproduced from ref. 181 with permission from ACS, copyright 2023.

Besides, the chemical structure of the IL has a direct influence on the ion distribution near the charged electrode to affect the differential capacitance of the supercapacitors. For example, the imidazolium cations of ILs, which get chemisorbed on metals such as Ag and Au, were found to result in voltage-mediated structural transitions and large peaks in capacitance profiles.^183–185 MD simulations were performed to compare differential capacitance profiles of [BMIM][BF₄] and [BMIM][TFSI] at graphene electrodes, which exhibit similar camel-shaped capacitance profiles with two peaks on either side of a minimum centered at the potential of zero charge (left panel, Fig. 17).¹⁸⁶ However, their capacitance profiles at large absolute voltages are different, where the differential capacitance begins to decrease at both positive and negative polarizations for [BMIM][BF₄], but only at positive polarization for [BMIM][TFSI]. The different capacitive behavior at the positively polarized carbon electrode surface is due to the different anions restructuring of [BMIM][BF₄] and [BMIM][TFSI] within the inner layer adjacent to the electrode surface (cf. middle and right panels in Fig. 17).

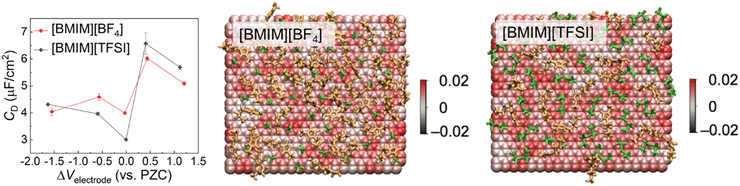Fig. 17 Left: Differential capacitance “C_D” of [BMIM][BF₄] and [BMIM][TFSI] electrolytes at graphene electrode as a function of electrode potential (ΔV_electrode), plotted relative to the potential of zero charge. Snapshots of [BMIM][BF₄] (middle) and [BMIM][TFSI] (right) electrolytes near the electrode surface at approximately +1.6 V relative to PZC (potential of zero charge). Orange: [BMIM]⁺ cation; green: [BF₄]⁻ (middle panel) and [TFSI]⁻ (right panel) anions. The color bar on the right indicates the value of image charges on each atom of the graphene electrode. Reproduced from ref. 186 with permission from ACS, copyright 2021.

Recent studies have demonstrated that IL electrolytes comprising structural analogous anions have different modes of interactions with carbon electrode surfaces, leading to different capacitive performances on the same carbon electrode.^175,187 For example, the IL containing non-aromatic tetrahydrofuran-2-carboxylate anion [HFuA]⁻ with delocalized electrons has shown somewhat tilted orientation on the surface of graphene associated with the best capacitive performance as compared with the other two ILs containing aromatic anions, 2-furoate [FuA]⁻ and thiophene-2-carboxylate [TpA]⁻ anions. The configurations of [P₄₄₄₄]⁺ cation (Fig. 18a and e), [FuA]⁻ (Fig. 18b and f), [HFuA]⁻ (Fig. 18c and g), and [TpA]⁻ (Fig. 18d and h) anions at electrified graphene electrodes with a surface charge density of 10 μC cm⁻² are shown in Fig. 18. The tetra(n-butyl)phosphonium [P₄₄₄₄]⁺ cation exhibited random distributions near the surface with no specific coordination with the graphene electrode. The aromatic anions, [FuA]⁻ and [TpA]⁻, exhibited perpendicular distributions to the positively charged graphene electrode resulting in very strong surface interactions that might need a large voltage to break the interfacial structures. This was the main reason that the [P₄₄₄₄][FuA] and [P₄₄₄₄][TpA] ILs have provided relatively lower capacitances than the [P₄₄₄₄][HFuA] IL.¹⁸⁸

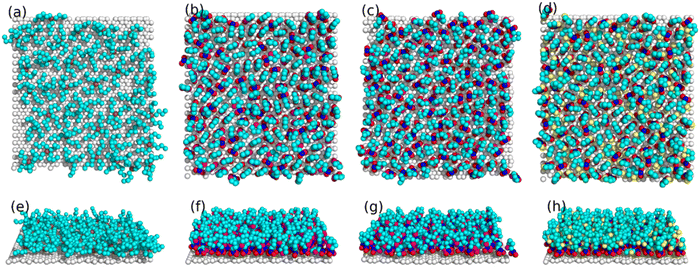Fig. 18 Ion configures of [P₄₄₄₄]⁺ (a) and (e) cation in cation-cathode interfacial region, and of [FuA]⁻ (b) and (f), [HFuA]⁻ (c) and (g), and [TpA]⁻ (d) and (h) anions in anion-anode interfacial region. The lower panels correspond to the side-views of the top-view configurations shown in upper panels. Adapted from ref. 188 with permission from Elsevier, copyright 2022.

5. Summary and outlook

We have reviewed recent studies of the multifaceted layering behavior of ionic liquids at a variety of different surfaces, studied by experiments, molecular simulations, and thermodynamic modeling methods. Ionic liquid interface-layered nanostructures are important in numerous applications. The ordered surface structures after embedding them on surfaces and in constrained spaces greatly enhance many of IL properties, from those observed in bulk. They provide a convenient platform for novel innovations within sensor, electrode, battery, capacitor, and lubricant technologies. There are several research methods and strategies to study IL interface layers. We have chosen to survey more closely three highly powerful methodologies. First, advanced experimental techniques for surface analysis: surface force apparatus (SFA) and atomic force microscopy (AFM). SFA provides detailed and highly accurate information about interaction forces (attractive and repulsive) between surfaces in a controlled manner in a variety of mediums. AFM with its very sharp tip at the end of a cantilever scans the surface using different modes. It can visualize the topography and morphology of ILs on a solid surface at an atomistic resolution. It provides information about structure, arrangements, organization, thickness, elasticity, and friction, etc. Although fundamentally and operationally different, they can give similar and complementary information. Second, Molecular simulations, and in particular molecular dynamics (MD), which is invaluable to studying the structure, thermodynamics, and dynamics of any type of molecular system, from solid metals to large biological systems in realistic environments and conditions. MD can be performed from first-principles to classical atomistic and coarse-grained mesoscopic systems at and out of equilibrium, including all possible hybrid methods among them. It is an ideal tool for studying ILs on different surfaces of constrained spaces. Third, thermodynamics provides an incredible and complete toolbox to study matter in its all possible states both at equilibrium and non-equilibrium. Already van der Waals gave us the first thermodynamic model which inspired to a wealth of state functions. Although thermodynamics works well without molecular degrees of freedom and is best for macroscopic matter, it can take molecular information from both experiments and simulations. Thermodynamics is highly useful for surface studies providing quantities like adsorption isotherms, solvation-free energies, phase equilibria, activity coefficients, surface/interface tension to mention a few. Many of these quantities can also be calculated from MD simulations or obtained experimentally.

As all methods operate on their specific resolutions (molecular or material) and scales (length, time, etc.) providing results and data on properties of what they are designed to do, it is preferable to combine several of them. This is also normally done in the characterization of newly synthesized materials. Designing new materials and products with specifically tailored properties starting from molecular building blocks requires connecting ten orders of magnitude in the length scale. This is impossible using any single method or methodology. It can only be done using different multi-scale strategies. Multi-scale modeling, both “from bottom-up” and “from top-down” has been developed during the last two decades based on several strategies to connect and couple the scales. By writing this review our idea was to propose a strategy for multi-scale studies by using a triangle made of (1) advanced experimental tools, (2) MD simulations, and (3) thermodynamic modeling. The latter is an essential tool in chemical engineering. However, it has developed rapidly during the last decades and can be connected as a complementary tool with both experiments and molecular simulations. Therefore, it works well as a bridge between (1) and (2). We will demonstrate it for interfacial ILs. Mainly, because it is our own area of research but also because they are among the most complicated molecular systems due to all molecular interactions are there in concert. However, the modeling for ILs interface layers is somewhat scarce, which inspires and promotes us to perform it now, especially to build a multi-scale methodology by integrating modeling with experiments and simulations. Therefore, there is an urgent need to bridge theoretical modeling, simulation and advanced experimental tools to qualitatively and quantitatively study the ILs interface layer to enable the judicious design of IL–solid interfaces with appropriate properties for task-specific applications.

Experimental, molecular simulation, and thermodynamic modeling studies of the IL interface layer have shown different subtle responses of the overall properties and performance to the ion structuring for the interface layer ILs, but being tied to completely different interpretations. The combination of experimental techniques and/or computational simulations and/or thermodynamic modeling analysis is one important route to build up the quantitative structure–property relationship of interface layer ILs to deeply understand the mechanism in the ILs-based applications, and identify the proper ILs for specific solid interfaces with targeted properties/performance, and is seen in just a few other scenarios, such as CO₂ adsorption⁴² with supported ILs.

However, establishing any quantitative structure–property relationships of interface layer ILs requires more research. The property/performance of ILs at solid surfaces is a complex function of the characteristics of the contacting surfaces, the nature of the IL, and external stimuli. Thus, the picture emerging now is that a large number of potential IL cations and anions are available, which provides enormous scope for scientific innovations, meaning that the use of ILs often results in reduced efficiencies or deviations from expected behavior. Using solid surfaces with a wide variety of adjustable properties further imposes challenges in identifying an optimum IL for any given solid surface in any specific application. Therefore, a good understanding and control of the chosen ILs, their structuring and ion dynamics when interacting with the solid surfaces, and how they are affected by the external conditions are needed to create assemblies for applications like boundary lubrication and high-performance energy storage devices. It is highly important to achieve an atomic-scale understanding of the molecular origin of the interface layer ILs behavior, providing quantitative structure–property relationships for exquisite control of functional IL–solid interfaces.

Theoretical studies, including computational simulations and thermodynamic modeling, can help in identifying the conditions that lead to optimal performance by achieving quantitative structure–property relationships of interface layer ILs. Nevertheless, the key problem in these theoretical studies is that the interaction parameters must be accurately introduced as an input to the model, and acquiring these ‘inputs’ experimentally is challenging. A colloid probe AFM-based methodology was proposed to attempt to quantify the molecular interactions of imidazolium-based ILs with SiO₂ surfaces, in which, the AFM-measured adhesion force offers a direct measure of the IL interactions with the solid SiO₂, that can be used to fit interaction parameters for theoretical calculations.^90,91 However, the applicability and reliability of these derived interaction parameters still need to be validated.

The translation of ILs interface layer structuring to applications would also be of interest. When considering IL-based applications such as lubrication and energy storage, the corresponding properties/performance, i.e., friction and capacitance, are expected to be controllable at will. Although some of the properties are imposed by external conditions (e.g., temperature and potential) and the specific properties of surfaces (e.g. nanostructure and chemical heterogeneity), ILs themselves offer a vast parameter space in terms of their chemical compositions, which can be further diversified using solvents and additives.²³ Therefore, it will be necessary to fully characterize the role of surface characteristics, nature of ILs, and external stimuli to build up the quantitative structure–property relationship. Previous exploration in molecular liquids at solid surfaces, combined the AFM experiment and thermodynamics modeling to find that the nanofriction coefficient, μ, is a function of three dimensionless parameters reflecting the intermolecular forces involved and the structure of the solid substrate according to the following equation: μ = 0.0079·ρ_s·Δ_s·σ_ls², where ρ_s is the atomic density of the solid, Δ_s is the spacing between layers of solid atoms, and σ_ls is the molecular diameter that characterizes the liquid–solid interaction.⁴³ This quantitative description cannot be extended straightforwardly to ILs and complex solid interfaces, but, at least, it demonstrates the possibility of building up quantitative structure–property relationships.

Detailed scenarios for solving these problems lie beyond the scope of this review. The exploration of building up quantitative structure–property relationships of interface layer ILs is only in its infancy, and there is still a lot of work for physicists and chemists to do to realize this quantification and guide for screening the best ILs-based lubricants and electrolytes. We hope that this review will motivate further work and enable the multiscale–triangle “experiment–simulation–thermodynamic modeling” in building up quantitative structure–property relationships for guidance in the virtual design of IL-based applications.

Abbreviations

[C4C1Pyrr][NTf2]	1-Butyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide
[C10C1Pyrr][NTf2]	1-Decyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide
[C4C1im][NTf2]	1-Butlyl-3-methylimidazoliym bis(trifluoronmenthylsuldonyl)imide
[C6C1im][NTf2]	1-Hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide
[C2mim]Ac	1-Ethyl-3-methylimidazolium acetate
EAN	Ethylammonium nitrate
PAN	Propylammonium nitrate
[C4C1Im][BF4]	1-Butyl-3-methylimidazolium tetrafluoroborate
[C4C1Im][AOT]	1-Butyl-3-methylimidazolium 1,4-bis(2-ethylhexoxy)-1,4-dioxobutane-2-sulfonate
[C3mpyr][FSI]	N-Methyl-N-propylpyrrolidinium bis(fluorosulfonyl)imide
[HMIM][FAP]	1-Hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate
[P6,6,6,14][TFSI]	Trihexyl-(tetradecyl)phosphonium bis(trifluoromethane)sulfonamide
[HOC4Py][NTf2]	1-(4-Hydroxybutyl)pyridinium bis(trifluoromethanesulfonyl)imide
[P6,6,6,14][BScB]	Trihexyltetradecylphosphonium bis(salicylato)borate
[C2MIM][NTf2]	1-Ethyl-3-methyl-imidazolium bis-(trifluoromethylsulfonyl)imide
[Py1,4][TFSA]	1-Butyl-1-methylpyrrolidinium bis(trifluoromethylsulfonyl)amide
[BMIM]FAP	1-Butyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate
[HMIM]FAP	1-Hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate
[BMIM]I	1-Butyl-3-methylimidazolium iodide
[EMIM][NTf2]	1-Ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide
[C2mim][dca]	1-Ethyl-3-methylimidazolium dicyanamide
[C4myr][dca]	N-Butyl-N-methylpyrrolidinium dicyanamide
[P4444][FuA]	Tetra(n-butyl)phosphonium furan-2-carboxylate
[P4444][TpA]	Tetra(n-butyl)phosphonium thiophene-2-carboxylate
[P4444][HFuA]	Tetra(n-butyl)phosphonium tetrahydrofuran-2-carboxylate

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors are grateful to the funding by the China Postdoctoral Science Foundation and the National Natural Science Foundation of China (Grant No. 21838004, 22108015, 21978134). X. J. thanks the financial support from the Swedish Research Council (Grant No. 2020-03899), STINT (Grant No. CH2019-8287), and Horizon-EIC, Pathfinder challenges (Grant No. 101070976). F. U. S gratefully acknowledges the financial support from the Swedish Research Council (Grant No. 2018-04133). A. L. acknowledges Kempe Foundation project (Grant No. SMK21-0011), Swedish Research Council (Grant No. 2019-03865) and European Union's Horizon Europe research and innovation programme under grant agreement No 101086667, project BioMat4CAST.

References

1. M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036.
2. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
3. S. Zhang, J. Zhang, Y. Zhang and Y. Deng, Chem. Rev., 2017, 117, 6755–6833.
4. M. Cai, Q. Yu, W. Liu and F. Zhou, Chem. Soc. Rev., 2020, 49, 7753–7818.
5. F. Zhou, Y. Liang and W. Liu, Chem. Soc. Rev., 2009, 38, 2590–2599.
6. X. Mao, P. Brown, C. Červinka, G. Hazell, H. Li, Y. Ren, D. Chen, R. Atkin, J. Eastoe, I. Grillo, A. A. H. Padua, M. F. Costa Gomes and T. A. Hatton, Nat. Mater., 2019, 18, 1350–1357.
7. D. A. Rakov, F. Chen, S. A. Ferdousi, H. Li, T. Pathirana, A. N. Simonov, P. C. Howlett, R. Atkin and M. Forsyth, Nat. Mater., 2020, 19, 1096–1101.
8. A. Eftekhari, Energy Storage Mater., 2017, 9, 47–69.
9. K. L. Van Aken, M. Beidaghi and Y. Gogotsi, Angew. Chem., Int. Ed., 2015, 54, 4806–4809.
10. P. F. R. Ortega, G. A. dos Santos Jr., J. P. C. Trigueiro, G. G. Silva, N. Quintanal, C. Blanco, R. L. Lavall and R. Santamaría, J. Phys. Chem. C, 2020, 124, 15818–15830.
11. M. Forsyth, L. Porcarelli, X. Wang, N. Goujon and D. Mecerreyes, Acc. Chem. Res., 2019, 52, 686–694.
12. S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dincă, A. A. Kornyshev and G. Feng, Nat. Mater., 2020, 19, 552–558.
13. M. Chen, J. Wu, T. Ye, J. Ye, C. Zhao, S. Bi, J. Yan, B. Mao and G. Feng, Nat. Commun., 2020, 11, 5809.
14. X. Wang, M. Salari, D.-E. Jiang, J. Chapman Varela, B. Anasori, D. J. Wesolowski, S. Dai, M. W. Grinstaff and Y. Gogotsi, Nat. Rev. Mater., 2020, 5, 787–808.
15. M. Radiom, Curr. Opin. Colloid Interface Sci., 2019, 39, 148–161.
16. R. Futamura, T. Iiyama, Y. Takasaki, Y. Gogotsi, M. J. Biggs, M. Salanne, J. Ségalini, P. Simon and K. Kaneko, Nat. Mater., 2017, 16, 1225–1232.
17. R. An, A. Laaksonen, M. Wu, Y. Zhu, F. U. Shah, X. Lu and X. Ji, Nanoscale, 2022, 14, 11098–11128.
18. J. Comtet, A. Niguès, V. Kaiser, B. Coasne, L. Bocquet and A. Siria, Nat. Mater., 2017, 16, 634–639.
19. A. Sheehan, L. A. Jurado, S. N. Ramakrishna, A. Arcifa, A. Rossi, N. D. Spencer and R. M. Espinosa-Marzal, Nanoscale, 2016, 8, 4094–4106.
20. Y. Lu, Y. Wang, F. Huo, W. Chen, M. Ma, W.-L. Ding, H. He and S. Zhang, ACS Nano, 2022, 16, 16471–16480.
21. T. Wang, L. Li, F. Zhang, Z. Dai, F. U. Shah, W. Wang, F. Xu and R. An, Phys. Chem. Chem. Phys., 2022, 24, 25411–25419.
22. T. Sun, Y. Lu, J. Lu, H. Dong, W. Ding, Y. Wang, X. Yang and H. He, J. Phys. Chem. Lett., 2022, 13, 7113–7120.
23. F. Bresme, A. A. Kornyshev, S. Perkin and M. Urbakh, Nat. Mater., 2022, 21, 848–858.
24. J. Yang, C. Lian and H. Liu, Chem. Eng. Sci., 2020, 227, 115927.
25. R. Hayes, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2010, 12, 1709–1723.
26. M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428.
27. Y. Hu and X. Peng, Structure and Bonding, in Structures and Interactions of Ionic Liquids, ed. S. Zhang, J. Wang, X. Lu and Q. Zhou, Springer-Verlag Berlin, Heidelberg, 2014, vol. 151.
28. E. J. Maginn, Acc. Chem. Res., 2007, 40, 1200–1207.
29. Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877.
30. S. Perkin, T. Albrecht and J. Klein, Phys. Chem. Chem. Phys., 2010, 12, 1243–1247.
31. U. Raviv and J. Klein, Science, 2002, 297, 1540–1543.
32. A. M. Smith, A. A. Lee and S. Perkin, Phys. Rev. Lett., 2017, 118, 096002.
33. Y. Wang and L. Li, Langmuir, 2020, 36, 2743–2756.
34. L. R. Griffin, K. L. Browning, S. M. Clarke, A. M. Smith, S. Perkin, M. W. A. Skoda and S. E. Norman, Phys. Chem. Chem. Phys., 2017, 19, 297–304.
35. A. Elbourne, K. Voïtchovsky, G. G. Warr and R. Atkin, Chem. Sci., 2015, 6, 527–536.
36. S. Zhou, K. S. Panse, M. H. Motevaselian, N. R. Aluru and Y. Zhang, ACS Nano, 2020, 14, 17515–17523.
37. J. P. de Souza, K. Pivnic, M. Z. Bazant, M. Urbakh and A. A. Kornyshev, J. Phys. Chem. B, 2022, 126, 1242–1253.
38. Y. Zhou and J. Qu, ACS Appl. Mater. Interfaces, 2017, 9, 3209–3222.
39. K. E. Gubbins, Y. Long and M. Śliwinska-Bartkowiak, J. Chem. Thermodyn., 2014, 74, 169–183.
40. N. Wu, X. Ji, L. Li, J. Zhu and X. Lu, Chem. Eng. Sci., 2021, 229, 116164.
41. N. Wu, X. Ji, R. An, C. Liu and X. Lu, AIChE J., 2017, 63, 4595–4603.
42. N. Wu, X. Ji, W. Xie, C. Liu, X. Feng and X. Lu, Langmuir, 2017, 33, 11719–11726.
43. R. An, L. Huang, Y. Long, B. Kalanyan, X. Lu and K. E. Gubbins, Langmuir, 2016, 32, 743–750.
44. R. An, L. Huang, K. P. Mineart, Y. Dong, R. J. Spontak and K. E. Gubbins, Soft Matter, 2017, 13, 3492–3505.
45. G. Yu, Z. Wei, K. Chen, R. Guo and Z. Lei, AIChE J., 2022, 68, e17575.
46. K. Paduszyński and U. Domańska, J. Phys. Chem. B, 2012, 116, 5002–5018.
47. T. Zhou, H. Shi, X. Ding and Y. Zhou, Chem. Eng. Sci., 2021, 229, 116076.
48. Y. Huang, X. Zhang, X. Zhang, H. Dong and S. Zhang, Ind. Eng. Chem. Res., 2014, 53, 11805–11817.
49. I. I. I. Alkhatib, D. Bahamon, A. Al Hajaj and L. F. Vega, Ind. Eng. Chem. Res., 2022, 61, 12190–12207.
50. X. Liu, Y. Chen, S. Zeng, X. Zhang, S. Zhang, X. Liang, R. Gani and G. M. Kontogeorgis, AIChE J., 2020, 66, e16794.
51. A. M. Smith, K. R. J. Lovelock, N. N. Gosvami, T. Welton and S. Perkin, Phys. Chem. Chem. Phys., 2013, 15, 15317–15320.
52. P. K. Cooper, C. J. Wear, H. Li and R. Atkin, ACS Sustainable Chem. Eng., 2017, 5, 11737–11743.
53. R. An, X. Qiu, F. U. Shah, K. Riehemann and H. Fuchs, Phys. Chem. Chem. Phys., 2020, 22, 14941–14952.
54. H. Li, M. W. Rutland and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 14616–14623.
55. H. Li, M. W. Rutland, M. Watanabe and R. Atkin, Faraday Discuss., 2017, 199, 311–322.
56. R. Atkin, N. Borisenko, M. Drueschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, Phys. Chem. Chem. Phys., 2011, 13, 6849–6857.
57. C. Rodenbücher, K. Wippermann and C. Korte, Appl. Sci., 2019, 9, 2207.
58. Y.-X. Zhong, J.-W. Yan, M.-G. Li, X. Zhang, D.-W. He and B.-W. Mao, J. Am. Chem. Soc., 2014, 136, 14682–14685.
59. X. Zhang, Y.-X. Zhong, J.-W. Yan, Y.-Z. Su, M. Zhang and B.-W. Mao, Chem. Commun., 2012, 48, 582–584.
60. J. M. Black, M. Zhu, P. Zhang, R. R. Unocic, D. Guo, M. B. Okatan, S. Dai, P. T. Cummings, S. V. Kalinin, G. Feng and N. Balke, Sci. Rep., 2016, 6, 32389.
61. J. Marra and J. J. B. Israelachvili, Biochemistry, 1985, 24, 4608–4618.
62. U. Raviv and J. Klein, Science, 2002, 297, 1540–1543.
63. J. Klein, Nature, 1980, 288, 248–250.
64. J. Klein and P. Luckham, Nature, 1982, 300, 429–431.
65. R. Lhermerout and S. Perkin, Phys. Chem. Chem. Phys., 2020, 22, 455–466.
66. L. Xiang, J. Zhang, L. Gong and H. Zeng, Soft Matter, 2020, 16, 6697–6719.
67. D. Alsteens, H. E. Gaub, R. Newton, M. Pfreundschuh, C. Gerber and D. J. Müller, Nat. Rev. Mater., 2017, 2, 17008.
68. R. García and R. Pérez, Surf. Sci. Rep., 2002, 47, 197–301.
69. H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152.
70. R. Hayes, N. Borisenko, M. K. Tam, P. C. Howlett, F. Endres and R. Atkin, J. Phys. Chem. C, 2011, 115, 6855–6863.
71. R. Atkin and G. G. Warr, J. Phys. Chem. C, 2007, 111, 5162–5168.
72. J. M. Black, D. Walters, A. Labuda, G. Feng, P. C. Hillesheim, S. Dai, P. T. Cummings, S. V. Kalinin, R. Proksch and N. Balke, Nano Lett., 2013, 13, 5954–5960.
73. N. Hjalmarsson, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2016, 18, 9232–9239.
74. M. Dong, K. Zhang, X. Wan, S. Wang, S. Fan, Z. Ye, Y. Wang, Y. Yan and X. Peng, Small, 2022, 18, 2108026.
75. M. Aminpour, C. Montemagno and J. A. Tuszynski, Molecules, 2019, 24, 1693.
76. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017.
77. D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, Jr., B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995.
78. D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, 2002.
79. B. Xin and J. Hao, Chem. Soc. Rev., 2014, 43, 7171–7187.
80. S. Baldelli, Acc. Chem. Res., 2008, 41, 421–431.
81. O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, Sci. Rep., 2015, 5, 7698.
82. Y. Wang, C. Wang, Y. Zhang, F. Huo, H. He and S. Zhang, Small, 2019, 15, 1804508.
83. G. Saielli, J. Phys. Chem. B, 2016, 120, 2569–2577.
84. C. Qian, Y. Wang, H. He, F. Huo, N. Wei and S. Zhang, J. Phys. Chem. C, 2018, 122, 22194–22200.
85. G. Jin, X. Song, Q. Gao, Y. Zhang, Y. Chen, X. Lu and Y. Zhu, Ind. Eng. Chem. Res., 2022, 61, 3754–3765.
86. R. An, G. Zhou, Y. Zhu, W. Zhu, L. Huang and F. U. Shah, Adv. Mater. Interfaces, 2018, 5, 1800263.
87. X. Zhong, Z. Fan, Z. Liu and D. Cao, J. Phys. Chem. B, 2012, 116, 3249–3263.
88. Y. Wang, J. Liu, X. Yuan, M. Wang, Y. Nie, S. Zhang and H. He, Chem. Eng. J., 2023, 455, 140370.
89. Y. Lu, Y. Wang, F. Huo, W. Chen, M. Ma, W.-L. Ding, H. He and S. Zhang, ACS Nano, 2022, 16, 16471–16480.
90. Y. Wei, Z. Dai, Y. Dong, A. Filippov, X. Ji, A. Laaksonen, F. U. Shah, R. An and H. Fuchs, Phys. Chem. Chem. Phys., 2022, 24, 12808–12815.
91. Y. Wei, Y. Dong, X. Ji, F. Ullah Shah, A. Laaksonen, R. An and K. Riehemann, J. Mol. Liq., 2022, 350, 118506.
92. K.-i Amano, Y. Liang, K. Miyazawa, K. Kobayashi, K. Hashimoto, K. Fukami, N. Nishi, T. Sakka, H. Onishi and T. Fukuma, Phys. Chem. Chem. Phys., 2016, 18, 15534–15544.
93. Y. Wang, C. Qian, F. Huo, B. Xu, H. He and S. Zhang, AIChE J., 2021, 67, e17060.
94. M. Wang, Y. Wang, T. Zhang, Y. Xia and H. He, AIChE J., 2023, 69, e18222.
95. D.-e Jiang, D. Meng and J. Wu, Chem. Phys. Lett., 2011, 504, 153–158.
96. J. Yang, C. Lian and H. Liu, Chem. Eng. Sci., 2020, 227, 115927.
97. P. Rehner, G. Bauer and J. Gross, Ind. Eng. Chem. Res., 2023, 62, 5347–5357.
98. Y. Sun, X. Lu, G. Shen and X. Ji, Ind. Eng. Chem. Res., 2021, 60, 9269–9285.
99. G. Shen, X. Lu and X. Ji, Fluid Phase Equilib., 2014, 382, 116–126.
100. M. Zhou, J. Wang, J. Garcia, Y. Liu and J. Wu, Ind. Eng. Chem. Res., 2021, 60, 17016–17025.
101. X. Wu, Z. Cao, X. Lu and W. Cai, Chem. Eng. J., 2023, 459, 141612.
102. G. Shen, H. Yang, Y. Hu, X. Zhang, F. Zhou, H. Li and K. Hong, Nanomaterials, 2022, 13, 1–13.
103. J. Cheng, J. Xu, J. Yang, W. Lv, C. Lian and H. Liu, Chem. Eng. Sci., 2022, 261, 117957.
104. J. Wu, T. Jiang, D.-E. Jiang, Z. Jin and D. Henderson, Soft Matter, 2011, 7, 11222–11231.
105. G. Shen, Y. Sun, Y. Wang, X. Lu and X. Ji, J. Mol. Liq., 2020, 310, 113199.
106. M. Hammer, G. Bauer, R. Stierle, J. Gross and Ø. Wilhelmsen, J. Chem. Phys., 2023, 158, 104107.
107. Y. Sun, Z. Dai, G. Shen, X. Lu, X. Ling and X. Ji, Front. Chem., 2022, 9, 801551.
108. G. Shen, D. Zhang, Y. Hu, X. Zhang, F. Zhou, Y. Qian, X. Lu and X. Ji, J. Chem. Phys., 2022, 157, 014701.
109. C. Lian, D.-E. Jiang, H. Liu and J. Wu, J. Phys. Chem. C, 2016, 120, 8704–8710.
110. A. L. Frischknecht, D. O. Halligan and M. L. Parks, J. Chem. Phys., 2014, 141, 054708.
111. A. Elbourne, J. Sweeney, G. B. Webber, E. J. Wanless, G. G. Warr, M. W. Rutland and R. Atkin, Chem. Commun., 2013, 49, 6797–6799.
112. H. Li, Y. Zhang, S. Jones, R. Segalman, G. G. Warr and R. Atkin, J. Colloid Interface Sci., 2022, 606, 1170–1178.
113. R. An, Y. Wei, X. Qiu, Z. Dai, M. Wu, E. Gnecco, F. U. Shah and W. Zhang, Friction, 2022, 10, 1893–1912.
114. J. Sweeney, F. Hausen, R. Hayes, G. B. Webber, F. Endres, M. W. Rutland, R. Bennewitz and R. Atkin, Phys. Rev. Lett., 2012, 109, 155502.
115. H. Li, R. J. Wood, M. W. Rutland and R. Atkin, Chem. Commun., 2014, 50, 4368–4370.
116. X. Qiu, L. Lu, Z. Qu, J. Liao, Q. Fan, F. U. Shah, W. Zhang and R. An, Friction, 2022, 10, 268–281.
117. H. Li, T. Niemann, R. Ludwig and R. Atkin, J. Phys. Chem. Lett., 2020, 11, 3905–3910.
118. C. S. Perez-Martinez and S. Perkin, Langmuir, 2019, 35, 15444–15450.
119. O. Werzer, E. D. Cranston, G. G. Warr, R. Atkin and M. W. Rutland, Phys. Chem. Chem. Phys., 2012, 14, 5147–5152.
120. J. Hoth, F. Hausen, M. H. Müser and R. Bennewitz, J. Phys.: Condens. Matter, 2014, 26, 284110.
121. S. Di Lecce, A. A. Kornyshev, M. Urbakh and F. Bresme, Phys. Chem. Chem. Phys., 2021, 23, 22174–22183.
122. S. Di Lecce, A. A. Kornyshev, M. Urbakh and F. Bresme, ACS Appl. Mater. Interfaces, 2020, 12, 4105–4113.
123. K. Pivnic, O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, J. Phys. Chem. C, 2018, 122, 5004–5012.
124. R. Atkin, N. Borisenko, M. Drüschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, Phys. Chem. Chem. Phys., 2011, 13, 6849–6857.
125. T. Waldmann, H.-H. Huang, H. E. Hoster, O. Höfft, F. Endres and R. J. Behm, ChemPhysChem, 2011, 12, 2565–2567.
126. V. Hoffmann, G. Pulletikurthi, T. Carstens, A. Lahiri, A. Borodin, M. Schammer, B. Horstmann, A. Latz and F. Endres, Phys. Chem. Chem. Phys., 2018, 20, 4760–4771.
127. G. Krämer, F. Hausen and R. Bennewitz, Faraday Discuss., 2017, 199, 299–309.
128. F. Federici Canova, M. Mizukami, T. Imamura, K. Kurihara and A. L. Shluger, Phys. Chem. Chem. Phys., 2015, 17, 17661–17669.
129. A. Moradzadeh, M. H. Motevaselian, S. Y. Mashayak and N. R. Aluru, J. Chem. Theory Comput., 2018, 14, 3252–3261.
130. F. Uhlig, J. Zeman, J. Smiatek and C. Holm, J. Chem. Theory Comput., 2018, 14, 1471–1486.
131. S. Zimmermann, W. Klauser, J. Mead, S. Wang, H. Huang and S. Fatikow, Nano Res., 2019, 12, 389–396.
132. J. Erath, S. Schmidt and A. Fery, Soft Matter, 2010, 6, 1432–1437.
133. R. Lhermerout and S. Perkin, Phys. Rev. Fluid, 2018, 3, 014201.
134. M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679.
135. M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224.
136. Y. F. Dufrêne, T. Ando, R. Garcia, D. Alsteens, D. Martinez-Martin, A. Engel, C. Gerber and D. J. Müller, Nat. Nanotechnol., 2017, 12, 295–307.
137. S. Perkin, L. Crowhurst, H. Niedermeyer, T. Welton, A. M. Smith and N. N. Gosvami, Chem. Commun., 2011, 47, 6572–6574.
138. A. M. Smith, K. R. J. Lovelock, N. N. Gosvami, P. Licence, A. Dolan, T. Welton and S. Perkin, J. Phys. Chem. Lett., 2013, 4, 378–382.
139. A. M. Smith, K. R. J. Lovelock and S. Perkin, Faraday Discuss., 2013, 167, 279–292.
140. B. Yoo, J. K. Shah, Y. Zhu and E. J. Maginn, Soft Matter, 2014, 10, 8641–8651.
141. A. A. d Freitas, K. Shimizu, A. M. Smith, S. Perkin and J. N. C. Lopes, J. Chem. Phys., 2018, 148, 193808.
142. A. M. Smith, M. A. Parkes and S. Perkin, J. Phys. Chem. Lett., 2014, 5, 4032–4037.
143. Y. Shen, X. X. He and F. R. Hung, J. Phys. Chem. C, 2015, 119, 24489–24500.
144. M. Rouha and P. T. Cummings, Phys. Chem. Chem. Phys., 2015, 17, 4152–4159.
145. O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, J. Phys. Chem. Lett., 2015, 6, 3998–4004.
146. J. Jiang, D. P. Cao, D. E. Jiang and J. Z. Wu, J. Phys. Chem. Lett., 2014, 5, 2195–2200.
147. Y. L. Wang, A. Laaksonen and Z. Y. Lu, Phys. Chem. Chem. Phys., 2013, 15, 13559–13569.
148. X. J. Zhong, Z. Fan, Z. P. Liu and D. P. Cao, J. Phys. Chem. B, 2012, 116, 3249–3263.
149. S. Begić, E. Jónsson, F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2017, 19, 30010–30020.
150. C. Wang, C. Qian, Z. Li, N. Wei, N. Zhang, Y. Wang and H. He, Ind. Eng. Chem. Res., 2020, 59, 8028–8036.
151. Y. Zhang and P. T. Cummings, ACS Appl. Mater. Interfaces, 2019, 11, 42680–42689.
152. N. Vucemilovic-Alagic, R. D. Banhatti, R. Stepic, C. R. Wick, D. Berger, M. U. Gaimann, A. Baer, J. Harting, D. M. Smith and A. S. Smith, J. Colloid Interface Sci., 2019, 553, 350–363.
153. C. Qian, B. Ding, Z. W. Wu, W. L. Ding, F. Huo, H. Y. He, N. Wei, Y. L. Wang and X. P. Zhang, Ind. Eng. Chem. Res., 2019, 58, 20109–20115.
154. Y. L. Wang, F. Huo, H. Y. He and S. J. Zhang, Phys. Chem. Chem. Phys., 2018, 20, 17773–17780.
155. A. Ruzanov, M. Lembinen, P. Jakovits, S. N. Srirama, I. V. Voroshylova, M. Cordeiro, C. M. Pereira, J. Rossmeisl and V. B. Ivanistsev, Phys. Chem. Chem. Phys., 2018, 20, 10275–10285.
156. S. J. Zhang, Y. L. Wang, H. Y. He, F. Huo, Y. M. Lu, X. C. Zhang and K. Dong, Green Energy Environ., 2017, 2, 329–330.
157. Y.-L. Wang, M. Golets, B. Li, S. Sarman and A. Laaksonen, ACS Appl. Mater. Interfaces, 2017, 9, 4976–4987.
158. J. N. Neal, D. J. Wesolowski, D. Henderson and J. Wu, J. Chem. Phys., 2017, 146, 174701.
159. S. Maolin, Z. Fuchun, W. Guozhong, F. Haiping, W. Chunlei, C. Shimou, Z. Yi and H. Jun, J. Chem. Phys., 2008, 128, 134504.
160. S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590.
161. Z. Dai, Y. You, Y. Zhu, S. Wang, W. Zhu and X. Lu, J. Phys. Chem. B, 2019, 123, 6857–6869.
162. M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102.
163. M. V. Fedorov and A. A. Kornyshev, Electrochim. Acta, 2008, 53, 6835–6840.
164. M. Chu, M. Miller and P. Dutta, ACS Cent. Sci., 2016, 2, 175–180.
165. S. Kondrat, G. Feng, F. Bresme, M. Urbakh and A. A. Kornyshev, Chem. Rev., 2023, 123, 6668–6715.
166. M. Vaganova, I. Nesterova, Y. Kanygin, A. Kazennov and A. Khlyupin, Chem. Eng. Sci., 2022, 250, 117383.
167. A. Malpica-Morales, P. Yatsyshin, M. A. Durán-Olivencia and S. Kalliadasis, J. Chem. Phys., 2023, 159, 104109.
168. G. Shen, A. Laaksonen, X. Lu and X. Ji, J. Phys. Chem. C, 2018, 122, 15464–15473.
169. L. B. Bhuiyan, S. Lamperski, J. Wu and D. Henderson, J. Phys. Chem. B, 2012, 116, 10364–10370.
170. H. Ers, M. Lembinen, M. Mišin, A. P. Seitsonen, M. V. Fedorov and V. B. Ivaništšev, J. Phys. Chem. C, 2020, 124, 19548–19555.
171. S. Perkin, Phys. Chem. Chem. Phys., 2012, 14, 5052–5062.
172. B. Wang, C. Moran, D. Lin, H. Tang, E. Gage and L. Li, ACS Appl. Nano Mater., 2019, 2, 5260–5265.
173. S. Di Lecce, A. A. Kornyshev, M. Urbakh and F. Bresme, ACS Nano, 2020, 14, 13256–13267.
174. F. Larsson, P. Andersson, P. Blomqvist and B.-E. Mellander, Sci. Rep., 2017, 7, 1–13.
175. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250.
176. S. Che, R. Dao, W. Zhang, X. Lv, H. Li and C. Wang, Chem. Commun., 2017, 53, 3862–3865.
177. M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239.
178. G. A. Giffin, J. Mater. Chem. A, 2016, 4, 13378–13389.
179. M. Antonietti, X. Chen, R. Yan and M. Oschatz, Energy Environ. Sci., 2018, 11, 3069–3074.
180. M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872.
181. Y. Su, T. Wang, F. Zhang, J. Huang, Z. Zhu, F. U. Shah, F. Xu and R. An, Langmuir, 2023, 39, 8463–8474.
182. J. Vatamanu, Z. Hu, D. Bedrov, C. Perez and Y. Gogotsi, J. Phys. Chem. Lett., 2013, 4, 2829–2837.
183. N. García Rey and D. D. Dlott, J. Phys. Chem. C, 2015, 119, 20892–20899.
184. Y.-Z. Su, Y.-C. Fu, J.-W. Yan, Z.-B. Chen and B.-W. Mao, Angew. Chem., Int. Ed., 2009, 48, 5148–5151.
185. M. Urushihara, K. Chan, C. Shi and J. K. Nørskov, J. Phys. Chem. C, 2015, 119, 20023–20029.
186. Y.-J. Tu and J. G. McDaniel, J. Phys. Chem. C, 2021, 125, 20204–20218.
187. F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818–12826.
188. I. A. Khan, Y.-L. Wang and F. U. Shah, J. Energy Chem., 2022, 69, 174–184.

---

Footnote

† Rong An and Nanhua Wu contributed equally to this work.

---