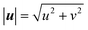Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing conversion using diffusio-osmosis from patterned catalytic surfaces
Aura
Visan
,
Jeffery A.
Wood
 and
Rob G. H.
Lammertink
and
Rob G. H.
Lammertink
 *
*
Soft Matter, Fluidics and Interfaces, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands. E-mail: r.g.h.lammertink@utwente.nl
First published on 1st March 2024
Abstract
An inhomogeneous catalyst surface leads to concentration gradients along this surface, which can generate diffusio-osmotic flows. The magnitude of this surface flow and the extent to which it impacts the catalytic conversion is numerically investigated and depends foremost on the reaction kinetics of the system and the surface-species interactions expressed via the diffusio-osmotic mobility. We present general scaling laws based on the reaction kinetics and interaction potential between chemical species and the catalytic surface, captured in a single parameter. We further investigate the optimal catalyst coverage in order to maximize the benefit of these surface flows.
Keywords: Diffusio-osmosis; Catalysis; Transport; Enhancement.
1 Introduction
There is a constant effort to produce increasingly more active catalysts. However, an improvement in the catalyst activity does not necessarily translate into a corresponding increase in chemical conversion. Mass transfer may become limiting very close to the catalyst surface, where diffusion is still the dominating transport mechanism. Mass transfer needs to be enhanced in order to benefit from these more active catalyst, especially in this near surface region. Active methods include increasing flow rates to reduce the boundary layer thickness. Passive mixing can result from, for example, buoyancy driven flow due to (thermal or concentration) density differences generated by the catalytic conversion which can also help to reduce boundary layer thicknesses. Another possible approach to enhance near-surface transport that we want to exploit is diffusio-osmotic flows.Diffusio-osmotic flows, i.e. surface flows generated by concentration gradients, were first described by Derjaguin in 1947.1 In the presence of concentration gradients parallel to the surface, osmotic pressure differences develop within the interfacial layer where the interaction potential spans. The diffuse part of this interfacial layer is mobile, leading to an osmotic flow parallel to the surface. In the case of charged species, an additional driving force comes from the contrast in diffusivity of the corresponding ions, generating an induced electric field. A large body of work has been dedicated to validate and further develop theoretical descriptions.2–26
Many of these studies relied on externally imposed concentration gradients. Except for particular designs (e.g. pores connecting large reservoirs21), immobilised surfaces that pump the solution by diffusio-osmosis relax concentration gradients and this results in a decay in driving force. However, sustained driving forces can be achieved using reactive systems. As an early example, Smith and Prieve10 investigated the instantaneous rate of deposition of latex particles by diffusio-phoresis on a dissolving stainless steel surface, driven by the addition of acid and oxidising agents. Recently, numerical and theoretical investigations regarding a uniformly active catalytic surface indicate the existence of an instability region.27,28 Such spontaneous wall-driven flows affect the distribution of the reactive species and with that the overall conversion.
A few experimental examples of in situ driven diffusio-osmosis by non-uniform reactive surfaces29–32 have been reported for transport in microfluidics. The most common system is the redox decomposition of H2O2 on Pt/Au alternating surfaces.33–41 The uneven distribution of protons leads to a strong electric field which sets the charged electric double layer in motion, driving fluid flow.
Here, we describe more generally diffusio-osmotic flows generated by surface reactivity contrast that is not pinned to a particular chemistry. We purposely minimize the number of parameters to the surface reactivity and diffusio-osmotic mobility, to explore their impact. We thus do not include the very details of specific species interactions with the active catalytic surface and generate a contrast purely based on local active and inactive regions. In this manner, the concentration gradients can now extend in-plane creating the condition for the diffusio-osmotic flow.
To explore the potential impact on the catalytic by patterning the catalyst using an irreversible first-order reaction, we explore the general features of the diffusio-osmotic flow generated by patterned catalytic surfaces. The influence of the characteristic dimensions of the system are investigated, namely the active and inactive spacing and total catalyst coverage and we also explore the influence of catalytic rate parameters different reaction kinetics and diffusio-osmotic mobilities (parameter quantifying the interaction potential between the chemical species and the catalytic surface) to identify the potential of the induced flow to impact the conversion. Scaling laws for the surface velocity and Sherwood number (Sh) on reaction rate constant and mobility are derived to illustrate the potential benefit of diffusio-osmotic enhanced catalytic conversion.
2 Results and discussion
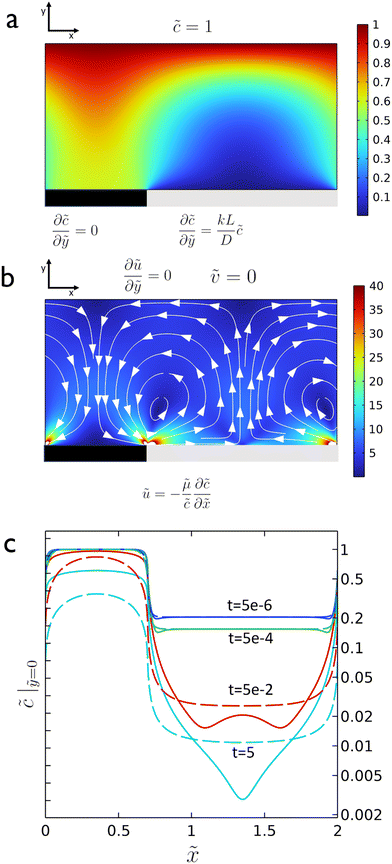
As the reaction proceeds and the depletion zone forms, the solute influx leads to significant gradients along the surface which initiates the diffusio-osmotic flow (Fig. 1a and b). Once the flow sets in, it transports fresh solution from the inactive region towards the catalyst region. Due to the symmetry of the system, diffusio-osmotic slip is generated in both directions. The inward flows extend halfway across the catalyst towards the middle of the active region and diverge upwards giving rise to two mirrored vortex structures. This mixing of the otherwise stagnant boundary layer replenishes the catalyst surface and, consequently, increases the reaction rate. The impact of diffusio-osmotic flow on enhancing interfacial transport depends on the size and dynamics of the vortex region with respect to the thickness of the diffusion-dominated stagnant layer. It follows that the vortex size should match this height, so it can reach the reservoir and replenish the catalyst surface with fresh solution. This prescribes an optimum 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 aspect ratio, as the vortex is half the size of the periodic catalyst pattern due to the symmetry of the system.
2 aspect ratio, as the vortex is half the size of the periodic catalyst pattern due to the symmetry of the system.
Intuitively, one would imagine that replenishing the surface of the catalyst with fresh solution will diminish the concentration gradient such that the diffusio-osmotic slip will limit its own driving force. However, comparing the transient concentration profiles for the slip and no-slip scenarios, there is an obvious reinforcement in the relative gradient development due to the osmotic flow. Fig. 1c presents the surface concentration profiles for a scenario where the surface flow is absent (uDO = 0, dashed lines) and where it is present (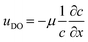 , continuous lines, with μ the diffusio-osmotic mobility). The steeper gradients are a result of the diffusio-osmotic flow along the active surface. This allows for a simplified description of the transport and reaction of chemical species along the catalyst, which we will provide next.
, continuous lines, with μ the diffusio-osmotic mobility). The steeper gradients are a result of the diffusio-osmotic flow along the active surface. This allows for a simplified description of the transport and reaction of chemical species along the catalyst, which we will provide next.
To illustrate the concept of self-reinforcing catalytic-induced surface flow, we developed an analytical expression for a 1D system encompassing a diffusio-osmotic flow along a catalyst surface. For this, we will ignore the diffusive and advective contributions in the wall-normal direction, and only describe the x direction transport and reaction. We describe the surface flow along a reactive surface by an advection–diffusion–reaction mass balance (eqn (1)). The equation represents a solute mass balance which assumes a steady state between the diffusio-osmotic flow along this surface and diffusion that supply the reactant and the reaction that consumes it. In steady state this becomes:
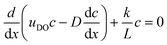 | (1) |
The diffusio-osmotic flow uDO (eqn (11)) is a function of the reactant concentration and its gradient, both a function of x, which leads to the following differential equation:
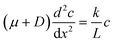 | (2) |
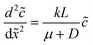 | (3) |
Taking ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) = 1 at
= 1 at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0 and d
= 0 and d![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) /d
/d![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0 at
= 0 at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 1 (note that we thus consider only the x-direction, describing one half of the active catalyst patch), we obtain the following expression that estimates the surface concentration along the catalyst patch:
= 1 (note that we thus consider only the x-direction, describing one half of the active catalyst patch), we obtain the following expression that estimates the surface concentration along the catalyst patch:
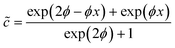 | (4) |
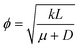 . We can see that ϕ describes a reaction to transport rate ratio, similar to the Thiele modulus, however, including the effect of diffusio-osmosis. Based on eqn (4) and (11), we can express the diffusio-osmotic velocity along the catalyst patch and can see how this velocity depends on the reaction and transport constants included in ϕ.
. We can see that ϕ describes a reaction to transport rate ratio, similar to the Thiele modulus, however, including the effect of diffusio-osmosis. Based on eqn (4) and (11), we can express the diffusio-osmotic velocity along the catalyst patch and can see how this velocity depends on the reaction and transport constants included in ϕ.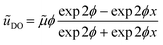 | (5) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) the dimensionless mobility (μ/D). For values of ϕ ≫ 1, the fraction in eqn (5) approaches 1 for small x, which gives a relative concentration gradient
the dimensionless mobility (μ/D). For values of ϕ ≫ 1, the fraction in eqn (5) approaches 1 for small x, which gives a relative concentration gradient 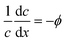 . In our example, the slope of log(c) versus x for the numerical data equals −4.47 (Fig. 1c). This is slightly lower compared to the analytical prediction of the slope, −ϕ = −5.06, that was used in this example. This can be explained by the wall-normal transport that is ignored in this analytical model. The analytically derived relative gradient can be regarded as the maximum driving force that is relaxed by transversal mass transport. For high reaction rates, i.e. large ϕ, the concentration gradients will deepen and consequently increase the diffusio-osmotic flow. We also see that for increasing mobility, ϕ will reduce and with that the concentration gradient along the surface. The enhanced diffusio-osmotic flow transports more reactant across the catalyst surface, increasing the reaction rate as the catalyst is in contact with a higher reactant concentration.
. In our example, the slope of log(c) versus x for the numerical data equals −4.47 (Fig. 1c). This is slightly lower compared to the analytical prediction of the slope, −ϕ = −5.06, that was used in this example. This can be explained by the wall-normal transport that is ignored in this analytical model. The analytically derived relative gradient can be regarded as the maximum driving force that is relaxed by transversal mass transport. For high reaction rates, i.e. large ϕ, the concentration gradients will deepen and consequently increase the diffusio-osmotic flow. We also see that for increasing mobility, ϕ will reduce and with that the concentration gradient along the surface. The enhanced diffusio-osmotic flow transports more reactant across the catalyst surface, increasing the reaction rate as the catalyst is in contact with a higher reactant concentration.
These expressions can be used to determine the average dimensionless concentration and diffusio-osmotic velocity along a patch, which gives an insight into the degree of reaction enhancement possible with diffusio-osmosis as well as the magnitude of the induced DOF velocity.
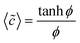 | (6) |
〈ũDO〉 = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(cosh log(cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) ϕ) | (7) |
We can analyze the effect of diffusio-osmosis on the catalytic reaction rate, through the reactant concentration profile along the catalyst surface. Most relevant is the reaction rate enhancement by the diffusio-osmotic flow, which we can directly quantify through the average concentration along the catalyst patch, 〈![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 〉 relative to the average concentration for the case of only diffusive transport (ũ = 0).
〉 relative to the average concentration for the case of only diffusive transport (ũ = 0).
In Fig. 2, the direct relation is plotted between ϕ and the ratio of average concentration on the catalyst patch, 〈![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 〉 for the case with and without diffusio-osmosis, which is proportional to the reaction rate enhancement. For values of ϕ between 0.5 and 10, we can expect a substantial enhancement of the reaction rate due to the diffusio-osmotic flow. For lower values of ϕ, the reaction is too sluggish to benefit from any mass transport enhancement. At higher values of ϕ the concentration along the surface approaches zero and the reaction is depleting the reactant severely.
〉 for the case with and without diffusio-osmosis, which is proportional to the reaction rate enhancement. For values of ϕ between 0.5 and 10, we can expect a substantial enhancement of the reaction rate due to the diffusio-osmotic flow. For lower values of ϕ, the reaction is too sluggish to benefit from any mass transport enhancement. At higher values of ϕ the concentration along the surface approaches zero and the reaction is depleting the reactant severely.
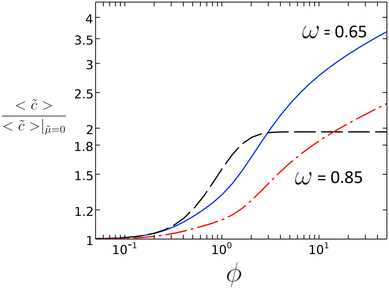 | ||
Fig. 2 Reaction rate enhancement vs. ϕ for ω = 0.65 and ω = 0.85 with ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) = 2.82 from 2D simulations along with the value determined from the 1D scaling law (dashed black line). = 2.82 from 2D simulations along with the value determined from the 1D scaling law (dashed black line). | ||
In order to enhance the reaction rate, the mobility should be substantial enough to reduce the value of ϕ such that higher average concentration (reaction rate) values are obtained. As illustrated in Fig. 3a, the reaction rate can be greatly enhanced vs. the case without diffusio-osmotic transport. At the same time, even with using less catalyst (ω < 1) it is possible to achieve a higher conversion of material as illustrated in Fig. 3b where an increase in conversion is obtained at a coverage of ∼0.65. The specific optimum coverage for a given system would vary depending on the nature of the reaction rate, diffusio-osmotic mobilities, etc. The optimum in active catalyst fraction, ω, can be understood as follows. For a too-short catalyst patch, the depletion of reactant will be limited, which reduces the generated gradient. For a too-long catalyst patch, or too-short inactive patch, the generated vortex will be slanted, which reduces its effectiveness. These results highlight the potential of intentionally introducing non-active patches in order to achieve not just higher fluxes to but also overall higher conversions at reaction surfaces even with less catalytic surface area.
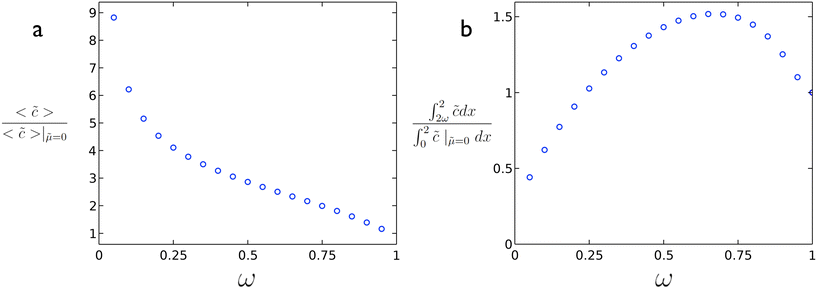 | ||
Fig. 3 (a) Reaction rate enhancement vs. ω and (b) extent of conversion vs. ω for ϕ = 5.07 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) = 2.82 from 2D simulations. = 2.82 from 2D simulations. | ||
We want to make a final note regarding the configuration of the system. Until now, we have described the system as a diffusion-dominated boundary layer close to a catalytic surface. By a common engineering practice, this boundary layer is considered stagnant while encompassing all bulk mass transfer resistances such that the bulk solution at the top boundary is considered perfectly mixed. We made this decision to preserve a general framework.
3 Conclusion
We propose a new context for reaction-induced diffusio-osmosis, i.e. enhancing chemical reaction rate by geometric patterning of the catalyst surface. The reactivity contrast designed by alternating active and inactive regions generates in-plane gradients that drive a steady diffusio-osmotic flow. While the details of our numerical model may need to be adjusted for particular catalytic reactions, the approach is not pinned to a certain chemistry.We use a numerical model based on a first-order reaction rate to study the structure of the diffusio-osmotic flow. We have quantified its development and dependency on the catalytic chemistry, i.e. reaction kinetics and interaction potential between chemical species and catalytic surface (expressed through the mobility parameter). Diffusio-osmosis is initiated by the contrast in reactivity and develops along the catalyst due to a self-reinforcing mechanism. The flow parallel to the catalyst surface introduces a concentration gradient which is the sustaining driving force that depends on both reaction kinetics and mobility. A simplified theoretical model is able to predict the degree of reaction rate enhancement, based on reaction rate constant, mobility, diffusivity, and characteristic length, all captured in a single parameter 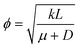 . Based on this fundamental understanding we introduce criteria to dimension the catalyst patch according to the chemistry. Specific chemistries, with known reaction kinetics and interaction potentials (i.e. mobilities), can now be tested against this predictive model.
. Based on this fundamental understanding we introduce criteria to dimension the catalyst patch according to the chemistry. Specific chemistries, with known reaction kinetics and interaction potentials (i.e. mobilities), can now be tested against this predictive model.
4 Model
For our system, we first consider a 2D periodic domain where a first-order reaction is assumed to take place on a catalytically active patch in a larger domain for conversion of methylene blue as an arbitrary solute. Momentum and mass transport are solved numerically for a two-dimensional domain of height L and width 2L consisting of a solution of an arbitrary chemical which is consumed at the catalytic surface and replenished by the top reservoir. We assume an otherwise stagnant boundary layer that will now be mixed by the induced osmotic flow. As such, the characteristic dimension of this system concerns the boundary layer thickness, or stagnant film thickness. This thickness depends on design and operation parameters and sets the typical size of the catalyst structure accordingly. The domain is periodic in the x direction. The width represents the period of a repeating pattern consisting of an alternating active and inactive region, with a reactive fraction (active area over total area) equal to ω. The domain was chosen for better visualisation in order to encompass 2 vortexes instead of 1 vortex which would represent the basic symmetry of the system, while keeping the aspect ratio of the vortex near unity.The system is governed by the Stokes and the continuity equations for fluid dynamics where the inertial term is neglected due to small Re numbers (here between 10−4 and 10−1) and the species conservation equation for mass transport which includes advection and diffusion. These equations (in dimensionless form) are:
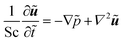 | (8) |
| ∇·ũ = 0 | (9) |
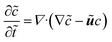 | (10) |
The Schmidt number is Sc = ν/D0, where ν is the kinematic viscosity of water, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t/t0 is dimensionless time where t0 = L2/D0 is the diffusion time scale with D0 = 4.6 × 10−10 m2 s−1 the diffusivity of methylene blue42 and
= t/t0 is dimensionless time where t0 = L2/D0 is the diffusion time scale with D0 = 4.6 × 10−10 m2 s−1 the diffusivity of methylene blue42 and ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) = p/(μD0/L2) is the pressure. The dimensionless velocity ũ is obtained with respect to the diffusion velocity ũ = uL/D0, where the height of the boundary layer is L = 5.00 × 10−4 m.
= p/(μD0/L2) is the pressure. The dimensionless velocity ũ is obtained with respect to the diffusion velocity ũ = uL/D0, where the height of the boundary layer is L = 5.00 × 10−4 m. ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) = c/c0 is the dimensionless concentration, where c0 is the bulk concentration which sets the top boundary condition.
= c/c0 is the dimensionless concentration, where c0 is the bulk concentration which sets the top boundary condition.
The upper boundary condition is set to full slip in the x direction and no velocity in the y direction. The active and inactive regions of the solid surface are defined by the diffusio-osmotic slip, uDO, which acts along the surface in x-direction only.
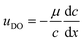 | (11) |
The diffusio-osmotic (phoretic) mobility μ is the prefactor of the diffusio-osmotic slip, describing the effective motion of a fluid with respect to a relative concentration gradient. This mobility is quantified via the zeta potential in case of charged species and can be written as follows:2,4,5
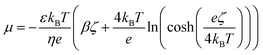 | (12) |
For the species transport, the reservoir boundary condition is defined by a fixed bulk concentration, c = 1. The boundary condition for the catalyst surface is represented by the normalised surface flux which is a pseudo-homogeneous first-order reaction rate, 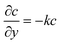 , with surface reaction rate constant k (m s−1). The inactive region has a no flux boundary condition,
, with surface reaction rate constant k (m s−1). The inactive region has a no flux boundary condition, 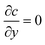 . The left and right boundaries are set as periodic, with equal concentration and flux continuity for each boundary. The governing equations were solved using Finite Element Analysis in COMSOL Multiphysics 5.3 with a relative tolerance of 0.01. P2 + P1 discretization (second-order Lagrange elements for velocity and first-order elements for pressure) was used to solve the Stokes equations and second-order Lagrange elements for the species conservation equation. The simulations were performed using an unstructured mesh with triangular elements. The mesh was refined near the walls and intersection points and mesh independence was obtained by successive refinement. The complete mesh consisted of approximately 180
. The left and right boundaries are set as periodic, with equal concentration and flux continuity for each boundary. The governing equations were solved using Finite Element Analysis in COMSOL Multiphysics 5.3 with a relative tolerance of 0.01. P2 + P1 discretization (second-order Lagrange elements for velocity and first-order elements for pressure) was used to solve the Stokes equations and second-order Lagrange elements for the species conservation equation. The simulations were performed using an unstructured mesh with triangular elements. The mesh was refined near the walls and intersection points and mesh independence was obtained by successive refinement. The complete mesh consisted of approximately 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements.
000 elements.
We chose a catalytic example from literature to illustrate the induced flow conversion enhancement. Yang et al. reports the photocatalytic degradation of methylene blue by poly-o-phenylenediamine modified TiO2 with pH dependent kinetics that vary between k = 5.5 × 10−5 and 1.9 × 10−4 m s−1.43 The pH dependent zeta potential of TiO2 is reported between ζ = 100 and ζ = −150 mV.44 To avoid any bias we select an intermediary value for kinetics (k = 9 × 10−5 m s−1) and an average zeta potential (ζ = −75 mV) that is characteristic for metal oxides at low electrolyte concentrations. The diffusivity contrast gives a β = −0.65 (based on D+ = 4.3 × 10−10 m2 s−1 and D− = 2.03 × 10−9 m2 s−1)45 which sets the mobility to μ = 1.298 × 10−9 m2 s−1. The optimal reactive fraction, ω, is 0.65 and will be rationalised later on. Further studies preserve these characteristics while varying one parameter at a time. The example concerns realistic values for the mentioned parameters to benchmark the effect. We extend the study to report a range around these values in order to investigate their relative influence and preserve the generality of this mechanism.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the government of the Netherlands. Rob Lammertink acknowledges the Vici project STW 016.160.312, financed by the Netherlands Organisation for Scientific Research (NWO).Notes and references
- B. V. Derjaguin, G. Sidorenkov, E. Zubashchenko and E. Kiseleva, Kinetic Phenomena in the boundary layers of liquids 1. the capillary osmosis, Prog. Surf. Sci., 1993, 43, 138–152 CrossRef.
- B. V. Derjaguin, S. S. Dukhin and M. M. Koptelova, Capillary osmosis through porous partitions and properties of boundary layers of solutions, J. Colloid Interface Sci., 1972, 38, 584–595 CrossRef.
- B. Derjaguin, S. Dukhin and A. Korotkova, Diffusiophoresis in electrolyte solutions and its role in the Mechanism of the formation of films from caoutchouc latexes by the ionic deposition method, Prog. Surf. Sci., 1993, 43, 153–158 CrossRef.
- J. L. Anderson, M. E. Lowell and D. C. Prieve, Motion of a particle generated by chemical gradients Part 1. Non-electrolytes, J. Fluid Mech., 1982, 117, 107 CrossRef CAS.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, Motion of a particle generated by chemical gradients. Part 2. Electrolytes, J. Fluid Mech., 1984, 148, 247 CrossRef CAS.
- J. L. Anderson, Effect of nonuniform zeta potential on particle movement in electric fields, J. Colloid Interface Sci., 1985, 105, 45–54 CrossRef CAS.
- M. C. Fair and J. L. Anderson, Electrophoresis of nonuniformly charged ellipsoidal particles, J. Colloid Interface Sci., 1989, 127, 388–400 CrossRef CAS.
- J. L. Anderson and D. C. Prieve, Diffusiophoresis Caused by Gradients of Strongly Adsorbing Solutes, Langmuir, 1991, 7, 403–406 CrossRef CAS.
- J. L. Anderson, Colloid Transport By Interfacial Forces, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- R. E. Smith and D. C. Prieve, Accelerated deposition of latex particles onto a rapidly dissolving steel surface, Chem. Eng. Sci., 1982, 37, 1213–1223 CrossRef CAS.
- J. P. Ebel, J. L. Anderson and D. C. Prieve, Diffusiophoresis of Latex Particles in Electrolyte Gradients, Langmuir, 1988, 4, 396–406 CrossRef CAS.
- P. O. Staffeld and J. A. Quinn, Diffusion-induced banding of colloid particles via diffusiophoresis 1. Electrolytes, J. Colloid Interface Sci., 1989, 130, 69–87 CrossRef CAS.
- W. J. Lechnick and J. A. Shaeiwitz, Measurement of diffusiophoresis in liquids, J. Colloid Interface Sci., 1984, 102, 71–87 CrossRef CAS.
- W. J. Lechnick and J. A. Shaeiwitz, Electrolyte concentration dependence of diffusiophoresis in liquids, J. Colloid Interface Sci., 1985, 104, 456–470 CrossRef CAS.
- M. M. J. Lin and D. C. Prieve, Electromigration of latex induced by a salt gradient, J. Colloid Interface Sci., 1983, 95, 327–339 CrossRef CAS.
- P. O. Staffeld and J. A. Quinn, Diffusion-induced banding of colloid particles via diffusiophoresis 2. Non-Electrolytes, J. Colloid Interface Sci., 1989, 130, 88–100 CrossRef CAS.
- M. Kosmulski and E. Matuevi, Solvophoresis of latex, J. Colloid Interface Sci., 1992, 150, 291–294 CrossRef CAS.
- M. Elimelech and C. R. O'Melia, Effect of electrolyte type on the electrophoretic mobility of polystyrene latex colloids, Colloids Surf., 1990, 44, 165–178 CrossRef CAS.
- B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, Osmotic manipulation of particles for microfluidic applications, New J. Phys., 2009, 11, 075022 CrossRef.
- B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, Boosting migration of large particles by solute contrasts, Nat. Mater., 2008, 7, 785–789 CrossRef.
- A. Siria, P. Poncharal, A. L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Giant osmotic energy conversion measured in a single transmembrane boron nitride nanotube, Nature, 2013, 494, 455–458 CrossRef CAS PubMed.
- J. S. Paustian, C. D. Angulo, R. Nery-Azevedo, N. Shi, A. I. Abdel-Fattah and T. M. Squires, Direct measurements of colloidal solvophoresis under imposed solvent and solute gradients, Langmuir, 2015, 31, 4402–4410 CrossRef CAS PubMed.
- R. Nery-Azevedo, A. Banerjee and T. M. Squires, Diffusiophoresis in Ionic Surfactant Gradients, Langmuir, 2017, 33, 9694–9702 CrossRef CAS PubMed.
- M. Shen, F. Ye, R. Liu, K. Chen, M. Yang and M. Ripoll, Chemically driven fluid transport in long microchannels, J. Chem. Phys., 2016, 145, 124119 CrossRef.
- S. Michelin, T. D. Montenegro-Johnson, G. De Canio, N. Lobato-Dauzier and E. Lauga, Geometric pumping in autophoretic channels, Soft Matter, 2015, 11, 5804–5811 RSC.
- M. Yang and M. Ripoll, A self-propelled thermophoretic microgear, Soft Matter, 2014, 10, 1006–1011 RSC.
- S. Michelin, S. Game, E. Lauga, E. Keaveny and D. Papageorgiou, Spontaneous onset of convection in a uniform phoretic channel, Soft Matter, 2019, 16, 1259–1269 RSC.
- Y. Chen, K. L. Chong, L. Liu, R. Verzicco and D. Lohse, Instabilities driven by diffusiophoretic flow on catalytic surfaces, J. Fluid Mech., 2021, 919, A10 CrossRef CAS.
- H. Zhang, K. Yeung, J. S. Robbins, R. A. Pavlick, M. Wu, R. Liu, A. Sen and S. T. Phillips, Self-powered microscale pumps based on analyte-initiated depolymerization reactions, Angew. Chem., Int. Ed., 2012, 51, 2400–2404 CrossRef CAS.
- V. Yadav, H. Zhang, R. Pavlick and A. Sen, Triggered “on/off” micropumps and colloidal photodiode, J. Am. Chem. Soc., 2012, 134, 15688–15691 CrossRef CAS PubMed.
- Y. Hong, M. Diaz, U. M. Córdova-Fteueroa and A. Sen, Light-driven titanium-dioxide-based reversible microfireworks and micromotor/micropump systems, Adv. Funct. Mater., 2010, 20, 1568–1576 CrossRef CAS.
- R. Niu, P. Kreissl, A. T. Brown, G. Rempfer, D. Botin, C. Holm, T. Palberg and J. De Graaf, Microfluidic pumping by micromolar salt concentrations, Soft Matter, 2017, 13, 1505–1518 RSC.
- T. R. Kline, W. F. Paxton, Y. Wang, D. Velegol, T. E. Mallouk and A. Sen, Catalytic micropumps: Microscopic convective fluid flow and pattern formation, J. Am. Chem. Soc., 2005, 127, 17150–17151 CrossRef CAS PubMed.
- J. L. Moran and J. D. Posner, Electrokinetic locomotion due to reaction-induced charge auto-electrophoresis, J. Fluid Mech., 2011, 680, 31–66 CrossRef CAS.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, Catalytically induced electrokinetics for motors and micropumps, J. Am. Chem. Soc., 2006, 128, 14881–14888 CrossRef CAS PubMed.
- A. A. Farniya, M. J. Esplandiu, D. Reguera and A. Bachtold, Imaging the proton concentration and mapping the spatial distribution of the electric field of catalytic micropumps, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef.
- A. A. Farniya, M. J. Esplandiu and A. Bachtold, Sequential tasks performed by catalytic pumps for colloidal crystallization, Langmuir, 2014, 30, 11841–11845 CrossRef.
- S. M. Davidson, R. G. H. Lammertink and A. Mani, A Predictive Model for Convective Flows Induced by Surface Reactivity Contrast, Phys. Rev. Fluids, 2017, 053701, 1–16 Search PubMed.
- S. Ebbens, D. A. Gregory, G. Dunderdale, J. R. Howse, Y. Ibrahim, T. B. Liverpool and R. Golestanian, Electrokinetic effects in catalytic platinum-insulator Janus swimmers, EPL, 2014, 106, 1–5 Search PubMed.
- D. A. Gregory and S. J. Ebbens, Symmetrical Catalytically Active Colloids Collectively Induce Convective Flow, Langmuir, 2018, 34, 4307–4313 CrossRef CAS PubMed.
- A. A. Ashaju, J. A. Wood and R. G. H. Lammertink, Electrocatalytic reaction-driven flow, Phys. Rev. Fluids, 2021, 6, 044004 CrossRef.
- N. Miložič, M. Lubej, U. Novak, P. Žnidaršič-Plazl and I. Plazl, Evaluation of Diffusion Coefficient Determination using a Microfluidic Device, Chem. Biochem. Eng. Q., 2014, 28, 215–223 CrossRef.
- C. Yang, W. Dong, G. Cui, Y. Zhao, X. Shi, X. Xia, B. Tang and W. Wang, Highly efficient photocatalytic degradation of methylene blue by P2ABSA-modified TiO2 nanocomposite due to the photosensitization synergetic effect of TiO2 and P2ABSA, RSC Adv., 2017, 7, 23699–23708 RSC.
- P. Leroy, C. Tournassat and M. Bizi, Influence of surface conductivity on the apparent zeta potential of TiO2 nanoparticles, J. Colloid Interface Sci., 2011, 356, 442–453 CrossRef CAS.
- D. G. Leaist, The effects of aggregation, counterion binding, and added sodium chloride on diffusion of aqueous methylene blue, Can. J. Chem., 1988, 66, 2452–2457 CrossRef CAS.
| This journal is © Institute of Process Engineering of CAS 2024 |