Open Access Article
Open Access ArticleHydrogen and oxygen evolution reactions on single atom catalysts stabilized by a covalent organic framework†
Ilaria
Barlocco
,
Giovanni
Di Liberto
 * and
Gianfranco
Pacchioni
* and
Gianfranco
Pacchioni

Dipartimento di Scienza dei Materiali, Università degli Studi di Milano Bicocca, Via R. Cozzi 55 (20125), Milano, Italy. E-mail: giovanni.diliberto@unimib.it
First published on 9th May 2023
Abstract
Single Atom Catalysts (SACs) bridge homo- and heterogenous catalysis and are promising for several chemical processes of interest, including water splitting. SACs can form reaction adducts that do not likely form on conventional metal catalysts. Besides the typical supporting matrices made by carbon-based materials, Covalent Organic Frameworks (COFs) are gaining attention because of the possibility to design the hosting cavity to stably bind the active metal site. We performed a density functional theory (DFT) study of a set of SACs made by transition metal atoms embedded in a recently synthesized COF material. We explored their reactivity in Hydrogen and Oxygen Evolution Reactions (HER and OER, respectively). SACs@COF can form several intermediates with no counterpart on the classical metal electrodes, with important implications on the reaction mechanism. The results are useful for the design of novel catalytic materials and for the identification of interpretative/predictive activity descriptors.
1. Introduction
Single atom catalysis is a relatively new frontier bridging the two worlds of homogeneous and heterogenous catalysts.1–6 In a single atom catalyst (SAC), transition metal (TM) atoms are dispersed atomically in a solid matrix. The atomic dispersion allows in principle maximization of the active phase, and tailoring of the activity by playing with the local environment.7–9 Both aspects are of paramount importance for the development of a new generation of catalytic materials with high activity and limited amounts of precious materials.SACs can be considered analogs of coordination chemistry compounds,8,10,11 and the TM atom embedded in a solid matrix can bind and activate molecular species. The reactivity is sensitive to the local coordination and to the nature of the ligand atoms of the support.7,8,12 This hallmark of SACs has intriguing potential implications in catalysis, since the reactivity can be substantially different from that of conventional catalysts based on extended metal surfaces.13,14 Typical supports of SACs are 2D materials such as graphene, nitrogen-doped graphene, carbon nitride, MoS2 and MXenes.2,15–25
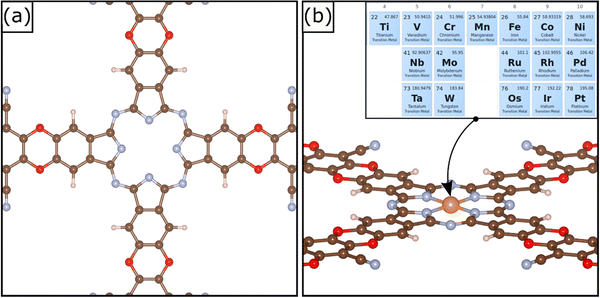
A relatively novel family of supports is that of Covalent Organic Frameworks (COF), porous crystalline polymers.26–28 COFs are periodic frameworks of organic building blocks held together by covalent interactions. They are characterized by cavities of tunable size depending on the nature of the composing blocks.29 The possibility to rationally design the cavity size and its symmetry allows one to engineer the local environment with atomistic precision. The cavities can be used to stabilize atomically dispersed metal species. Therefore, COFs are excellent templates for SACs. Several examples of COFs used to stabilize TM atoms have been reported in the literature. For instance, Meng et al. prepared a two-dimensional COF with optimal sensing response to several gas phase molecules.30 A similar framework was synthetized by Yue et al. and successfully applied for CO2 reduction in aqueous media.31 A detailed review of 2D COFs was published recently by Guan et al.32 2D COFs have also stimulated several computational screening studies.33,34 A recent example of a supporting matrix for SACs is a COF material shown in Fig. 1; this was obtained through the combination of metallophthalocyanine and pyrazine.34,35 The crystalline structure is characterized by a pore able to host a TM atom coordinated by four in plane nitrogen atoms, Fig. 1. This arrangement is reminiscent of that of porphyrins and nitrogen-doped graphene,7,36 and therefore it is expected to be able to strongly bind the active phase, thus preventing sintering. This system has been successfully synthetized and applied for CO2 reduction.35 A recent screening study was performed aiming at unveiling promising SACs for N2 electroreduction.34
In this work we performed a systematic computational study of SACs made by a series of 3d, 4d, and 5d TM atoms (Fig. 1) and their reactivity in Hydrogen Evolution (HER) and Oxygen Evolution (OER) reactions, the two fundamental chemical processes of the electrochemical water splitting. Given the steadily growing number of computational studies on SACs it is important to underline the main novelty of the present study. We will show that the chemistry of SACs supported on COF is complex and reminiscent of coordination chemistry, since several intermediates can form in analogy with previous studies on carbon-based materials.13,14,37,38 These intermediates differ from those usually found on metal electrodes, and therefore are classified as “unconventional”. Including also the unconventional intermediates in the study of the reactivity is of primary importance to predict new catalysts, find universal descriptors, or attempt comparisons with experiments. The thermodynamic stability of the relevant reaction intermediates and the catalytic implications are also discussed.
2 Computational details
The calculations have been done within the framework of density functional theory (DFT) as implemented in the VASP package.39–42 The PBE parametrization of the exchange and correlation functional was used.43 To consider the self-interaction error inherent to standard GGA functionals, we adopted the DFT+U approach.44,45 PBE + U allows one to reproduce with acceptable accuracy the Gibbs free energies of water splitting intermediates computed at the PBE0 level (hybrid functional) for a wide series of SACs embedded in a carbon-based support with a similar local coordination to that of the COF investigated in this work.46 The working U-correction term is reported in Table 1 and its origin has been discussed elsewhere.46,47 The core electrons were treated with the Projector Augmented Method (PAW) and the valence electrons were expanded on a set of plane waves with a kinetic energy cutoff of 400 eV.48,49 The threshold criteria for the convergence of electronic energies of forces of the ions were set to 10−5 eV and 10−2 eV Å−1 respectively. Dispersion forces have been included by means of the Grimme's D3 scheme.50 The sampling of the reciprocal space was reduced to the gamma point because of the large cell size.51 The unit cell of the COF matrix was fully relaxed. After including the metal atom, as well as for each reaction intermediate, the atomic coordinates of were fully reoptimized keeping fixed the lattice constants. This represents a reasonable approximation, since it usually leads to negligible errors.47| TM | E ad/eV | Magnetization/μB | q(M)/|e| | U 46,47,70/eV |
|---|---|---|---|---|
| Ti | −10.46 | 1.05 | 1.85 | 2.58 |
| V | −10.13 | 2.37 | 1.51 | 2.72 |
| Cr | −9.36 | 3.55 | 1.32 | 2.93 |
| Mn | −8.24 | 3.44 | 1.36 | 3.06 |
| Fe | −8.93 | 2.02 | 1.04 | 3.29 |
| Co | −9.27 | 1.05 | 1.09 | 3.42 |
| Ni | −9.46 | 0.00 | 0.98 | 3.40 |
| Nb | −11.12 | 1.28 | 1.89 | 2.02 |
| Mo | −9.27 | 2.86 | 1.61 | 2.30 |
| Ru | −9.51 | 1.66 | 1.16 | 2.79 |
| Rh | −9.26 | 0.90 | 1.03 | 3.04 |
| Pd | −8.39 | 0.00 | 0.75 | 3.33 |
| Ta | −11.98 | 1.04 | 2.00 | 1.87 |
| W | −11.17 | 2.33 | 1.77 | 2.08 |
| Os | −9.98 | 1.54 | 1.05 | 2.51 |
| Ir | −10.34 | 0.73 | 0.90 | 2.74 |
| Pt | −10.58 | 0.00 | 0.79 | 2.95 |
The reaction Gibbs free energies were obtained by adopting the seminal thermochemistry approach of Norskov and co-workers:52–56
| ΔG = ΔH − TΔS + ΔEZPE |
ΔH is obtained from calculated DFT energies. The entropic contribution at 298 K of gas phase species (TΔS) is taken from International Tables and that of solid-state systems is neglected.52,53,56 This assumption can be improved by estimating the entropy of adsorbates by means of the partition function formalism. However, this contribution is often small (about 0.1–0.2 eV), and therefore can be neglected.37 ΔEZPE is the zero-point energy correction that was evaluated in a harmonic fashion by allowing to vibrate all the atoms of the reaction intermediates and the metal.37 Tables S1 and S2 (ESI†) report the main working quantities adopted.
Of course, other effects can be relevant in modeling the reaction, in particular pH-dependence and solvation effects should be considered to provide quantitative predictions.57–65 Nevertheless, the purpose of this work is to assess the overall ability of SACs stabilized at COF to catalyze HER and OER and to analyze the similarities or differences that TM atoms embedded in COFs present compared to other supporting matrices with similar local structure, such as N-doped graphene or carbon nitride. In this respect, models that do not include solvation effects can provide a first assessment. The role of the solvent will be specifically addressed in future studies.
3 Results and discussion
The reference COF material is made by a 2D periodic arrangement of building blocks and stacking of different nanosheets along the third dimension, similarly to what occurs in graphene-based and carbon nitride materials. A common approximation is to model the systems with a single nanosheet.66,67 The optimized lattice parameters of the COF structure are a = 20.318 Å and b = 20.318 Å. The TM atoms are stably embedded in the matrix with a square planar coordination, Fig. 1. The adsorption of the metal atom in the cavity leads to SACs with very strong binding energies, see Table 1. The atomic-like character of the TM atoms is shown by the net magnetization on several TM atoms, Table 1.68 We observe that the binding energies of the TM atoms are larger, in absolute value, than those of the same species on N-doped graphene or carbon nitride.14,46 For instance, Co has a binding energy to COF of −9.27 eV, while it binds to N–Gr and C3N4 by −7.79 eV and −3.34 eV, respectively. Similarly, the binding energy of Pt is −10.58 eV in COF, to be compared with −7.99 eV (N–Gr) and −2.79 eV (C3N4). Table S3 (ESI†) reports the metal binding energies in the COF compared with that of other carbon-based materials. This suggests that COFs may be good candidates in stabilizing the TM atoms and avoid diffusion and sintering. On the other side, this result can imply a lower reactivity of the SAC towards adsorbates, based on the bond order conservation principle.693.1 Hydrogen evolution
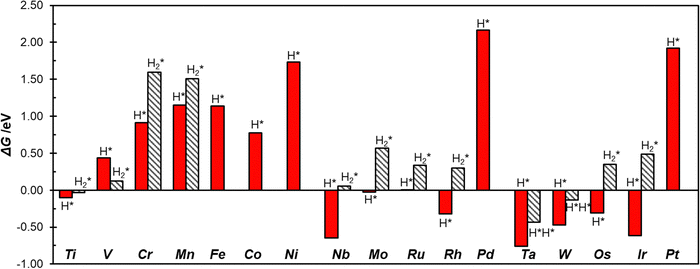
To study the activity of SACs@COF in HER we adsorbed a hydrogen atom on the TM active site. Fig. 2 shows an example of local geometry of the adducts, and Table 2 reports the calculated Gibbs free energies and structural parameters. The high stability of the SACs discussed above often reflects in a moderate reactivity towards hydrogen as shown by the fact that most of the SACs considered exhibit positive free energies of adsorption. Of course, there are differences, and the nature of the TM has a primary effect. For instance, among 3d elements only Ti can form H* species with a negative ΔG. Some atoms, see e.g. Mo@COF and Ru@COF, bind H* with ΔG ∼ 0 eV, which is close to the ideal value according to the classical Norskov's model (the catalyst binds H not too strongly nor too weakly). Heavy metals such as Rh@COF (−0.32 eV) and Ir@COF (−0.61 eV) bind H* more strongly and could also exhibit some activity according to Norskov's model. On the contrary, noble metal atoms such as Ni, Pd, and Pt are expected to be inert, since the ΔG > 1.5 eV is very far from the ideal condition for high reactivity (ΔG ∼ 0 eV). Overall, Fig. S1 (ESI†) shows a general trend where 4d and 5d TMs are more reactive than 3d ones, forming more stable H* species. | ||
| Fig. 2 (a) Example of local geometry of H*, (b) example of local geometry of a dihydrogen complex H2* and (c) example of local geometry of a dihydride complex H*H* on TM@COF. | ||
| TM | ΔGH/eV | d TM–H/Å | ΔGH2/eV | d H–H/Å | d TM–H/Å |
|---|---|---|---|---|---|
| Ti | −0.10 | 1.71 | −0.03 | 0.78 | 2.04 |
| V | 0.44 | 1.67 | 0.12 | 0.78 | 1.99 |
| Cr | 0.91 | 1.61 | 1.59 | 0.82 | 1.77 |
| Mn | 1.15 | 1.53 | 1.51 | 0.80 | 1.79 |
| Fe | 1.14 | 1.47 | — | — | — |
| Co | 0.77 | 1.41 | — | — | — |
| Ni | 1.73 | 1.40 | — | — | — |
| Nb | −0.65 | 1.80 | 0.06 | 0.82 | 2.02 |
| Mo | −0.03 | 1.70 | 0.57 | 0.88 | 1.90 |
| Ru | 0.01 | 1.59 | 0.34 | 0.75 | 2.82 |
| Rh | −0.32 | 1.50 | 0.30 | 0.76 | 2.33 |
| Pd | 2.16 | 1.83 | — | — | — |
| Ta | −0.76 | 1.76 | −0.43 | 1.88 | 1.77 |
| W | −0.47 | 1.70 | −0.13 | 1.77 | 1.71 |
| Os | −0.31 | 1.60 | 0.35 | 0.75 | 3.15 |
| Ir | −0.61 | 1.53 | 0.49 | 0.77 | 2.18 |
| Pt | 1.92 | 1.61 | — | — | — |
The picture becomes more interesting when one considers two hydrogen atoms binding simultaneously to the TM. Recently we have shown that these are stable species, with strong analogies with coordination chemistry compounds, and that they need to be accounted for when SACs are involved in HER.13,38 The formation of dihydrogen complexes can be considered the first step of hydrogenation reactions, or, viceversa, the last before step before the release of molecular hydrogen to the gas-phase in HER. In a dihydrogen complex (H2*), the H–H bond length is slightly elongated with respect that of the free H2 molecule, while in dihydride complexes (H*H*) the H–H bond is completely broken,71–74Table 2. Ti@COF, V@COF, and W@COF form dihydrogen complexes nearly thermoneutral with respect to the H2 molecule and the free catalyst, with ΔG = −0.03 eV, 0.12 eV, and −0.13 eV respectively. Cr@COF and Mn@COF can potentially form a dihydrogen complex, which is however a local minimum along the potential energy surface, given the positive Gibbs free energies. In some cases, see W@COF and Ta@COF, the complex displays dihydride character (H*H*), Table 2.71–74 In particular, the formation of H*H* on W@COF is nearly thermoneutral with respect to the free H2 molecule. Finally, there are SACs that do not form dihydrogen complexes.
The importance to consider all the intermediates, including the double hydrogen complexes, to predict the catalytic activity of SACs becomes apparent looking at the case of Mo@COF. If one considers the formation of the H* intermediate only (classical model), then the catalyst is predicted to be ideal (ΔG ∼ 0 eV); but if one considers also the formation of the H2* complex, this is predicted to be a poor catalyst due to the positive free adsorption energy (ΔG = 0.57 eV, Table 2). This means that the reaction implies an additional step, which is usually neglected if the analysis is limited to the single H adsorption.
Fig. 3 shows the calculated Gibbs free energies of single hydrogen, H*, and double hydrogen, H2*/H*H*, intermediates, where one can observe that Ti@COF and Ru@COF bind the intermediates nearly ideally (ΔG ∼ 0 eV). These systems could potentially have a good activity in the HER. Also, we checked for a possible relation between the free energy of adsorption of H* and that of H2*/H*H*, but we did not find clear correlations, Fig. S2 (ESI†). This shows that it is not easy to find scaling relationships for SACs involved in HER due to their complex chemistry.14,38
3.2 Oxygen evolution
We now discuss the reactivity of TM@COF in the Oxygen Evolution Reaction (OER). On metal electrodes the reaction is commonly assumed to proceed via consecutive reactions involving one electron transfer at the time, as reported below.| * + H2O → OH* + H+ + e− | (1) |
| OH* → O* + H+ + e− | (2) |
| O* + H2O → OOH* + H+ + e− | (3) |
| OOH* → O2 + * + H+ + e− | (4) |
Table 3 reports the calculated Gibbs free energies for each of these intermediates that we classify as “conventional” since these are the species that are usually taken into account in the discussion of the mechanism of the OER. Starting from the initial step, OH* formation, eqn (1), we observe that the nature of the metal largely affects the stability of the species. For instance, Ti@COF and W@COF bind OH* strongly. Ir@COF, Rh@COF, Mn@COF, Fe@COF, and Co@COF bind OH* with a free energy ∼1.2 eV, the ideal value for an OER catalyst. Some metals, Ni@COF, Pd@COF, and Pt@COF, are very weakly reactive due to the too large and positive ΔG. A similar result is obtained when looking at the O* intermediate, eqn (2), where we observe a quite broad scenario, ranging from very reactive species, such as Ti@COF, and W@COF to rather inert ones such as Ni@COF, Pd@COF, Pt@COF.
| M | ΔGOH/eV | ΔGO/eV | ΔGOOH/eV | ΔGOHOH/eV | ΔGOHO/eV | ΔGη1/eV | ΔGη2/eV |
|---|---|---|---|---|---|---|---|
| Ti | −1.51 | −1.46 | — | −1.02 | 0.81 | 1.27 | 1.25 |
| V | −0.60 | −0.76 | — | 0.86 | 1.47 | — | — |
| Cr | 1.62 | 1.89 | 4.88 | 3.11 | 4.46 | 4.53 | 4.87 |
| Mn | 1.27 | 2.15 | 4.96 | 3.16 | 4.96 | 4.71 | 4.76 |
| Fe | 1.54 | 2.53 | 4.36 | 3.72 | 5.47 | 5.12 | — |
| Co | 1.70 | 3.44 | 4.75 | 5.00 | 6.65 | 4.99 | — |
| Ni | 2.40 | 4.60 | 5.45 | — | — | — | — |
| Nb | −2.03 | 2.30 | — | −1.78 | −1.97 | 0.96 | −0.02 |
| Mo | −0.05 | −0.86 | 3.09 | 0.41 | 0.54 | 3.69 | 0.76 |
| Ru | 0.62 | 1.31 | 3.79 | 2.91 | 4.29 | 4.38 | 5.73 |
| Rh | 1.14 | 2.97 | 4.49 | 4.24 | 5.88 | 4.63 | 7.76 |
| Pd | 2.73 | 4.94 | — | — | — | — | — |
| Ta | −1.92 | −2.28 | — | −2.23 | −2.08 | 0.46 | −0.19 |
| W | −0.81 | −1.68 | — | −0.48 | −0.45 | 1.95 | −0.43 |
| Os | 0.49 | 0.90 | 3.64 | 2.38 | 3.05 | 4.24 | 4.10 |
| Ir | 1.04 | 2.16 | 4.38 | 3.79 | 5.20 | 4.61 | 6.83 |
| Pt | 2.63 | 4.84 | — | — | — | — | — |
The next intermediate is OOH*, eqn (3). For some systems, such as Ti@COF and V@COF, we did not detect its formation although both OH* and O* species are quite stable. Interestingly, we detected the formation of a related species where the O–OH bond is completely broken, resulting in an OH* O* intermediate (Table 3) bound to the catalyst with both oxygen atoms. The formation of such unconventional intermediate has been previously predicted on other SACs supported on carbon-based materials.14
The role of unconventional intermediates for the OER on SACs has been emphasized only recently, and their formation opens interestingly new routes for the catalyst optimization. Furthermore, they are indicative of how complex is the chemistry of SACs.13,14 In general, once OH* adsorbs to the catalyst, the system can bind another water molecule, resulting in the formation of a OH*OH* intermediate:13
| OH* + H2O → OH*OH* + H+ + e− | (5) |
This species is competitive with O*, since it implies the release of two electrons starting from the clean catalyst. Similarly, the OH*O* species discussed above is competitive with the OOH* intermediate:
| OH*OH* → OH*O + H+ + e− | (6) |
Finally, before the release of the free oxygen molecule to the gas-phase, SACs can form stable peroxo or superoxo complexes with O2:
| OH*O* → O2* + H+ + e− | (7) |
In these dioxygen species, if the O–O bond distance is only slightly elongated from that of the free O2 molecule (1.25 Å) the system can be classified as a superoxo complex (η1) (1.25–1.35 Å); when the O–O bond length is larger (1.35–1.45 Å), the system is classified as a peroxo complex. Eventually, in the case of a complete O–O bond breaking, one is in the presence of a dioxo complex, O*O*. In these last two cases the TM is bound via two M–O bonds in to the intermediate (η2). Fig. 4 reports some examples of the structure of different oxygenate intermediates adsorbed on SACs@COF. It must be mentioned that the picture can be even more complex if one considers that intermediates binding with two ligands can be attached to the metal both in syn- and anti- configurations.14 However, the latter case will unlikely release the product. We decided to restrict the present study to syn- intermediates since the scope of this work is to investigate the reactivity of SACs supported on a COF.
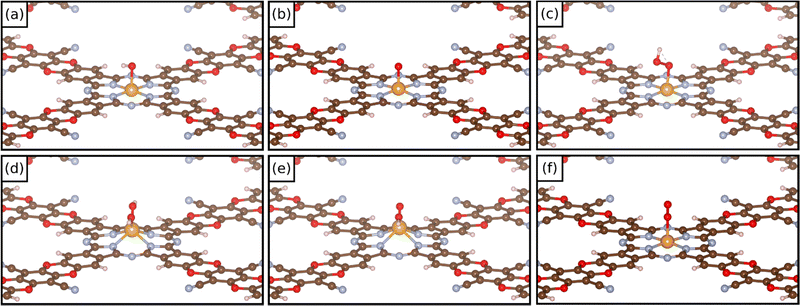 | ||
| Fig. 4 Examples of the structure of (a) OH*, (b) O*, (c) OOH*, (d) OH*OH*, (e) OH*O*, and (f) O2* intermediates on COF-based SACs. | ||
The OH*OH* intermediate is more stable than the O* only in the case of Ta@COF, thus, this is the species that is expected to form. The remaining metals bind O* more strongly than OH*OH*, so that the latter is only a local minimum along the potential energy surface.
In the next step, the OH*O* intermediate is the global minimum for several metals such as Cr@COF, Mn@COF, Mo@COF, and Os@COF, indicating that these systems are not expected to form the “conventional” OOH* species. Interestingly, Ta@COF and W@COF form only the OH*O* complex, showing that for these two systems the conventional path is clearly prevented.
Several systems form a stable dioxygen complex before they release O2 to the gas-phase. Table S4 (ESI†) reports the calculated O–O bond distances. In particular, a superoxo complex, η1, is found on Cr@COF, Mn@COF, Fe@COF, Co@COF, Ru@COF, Rh@COF and Ir@COF. On the contrary, Ti@COF leads to a peroxo adduct, η2. On Nb@COF, Mo@COF, Ta@COF, W@COF and Os@COF the O–O bond is completely broken, leading to a O*O* dioxocomplex. Interestingly, the Ni-triad, Ni@COF, Pd@COF, and Pt@COF, is unreactive. In particular, Ni forms weakly bounds conventional intermediates only, and Pd@COF, and Pt@COF are not able to bind neither OOH* nor OH*O* species.
These results show that most SACs involve the formation of at least one unconventional intermediate. In this respect, the classical path for OER is not the preferred one except for Fe@COF, Co@COF, and Ni@COF, Table 3. This result is consistent with previous calculations indicating that on SACs the OER follows a path characterized by the formation of unconventional intermediates, typical of coordination compounds.14 We also observe that the formation of unconventional intermediates can cause some protrusion of about 0.1 Å of the metal atom from the plane of the 2D COF to stabilize the adduct.14
Of the relatively large number of systems considered, only Fe@COF, Co@COF, Rh@COF and Ir@COF seem to exhibit interesting catalytic activity associated to a relatively small overpotential, around 0.5–0.6 eV. This is similar to the best overpotential expected with conventional catalysts.56,75Fig. 5 shows the corresponding Gibbs free energy profiles where it is possible to appreciate the most likely reaction path. The Gibbs free energy profiles are reported assuming to work at an applied voltage of 1.23 V, corresponding to the working condition of an ideal catalyst. This allows to gain some insight about the presence and extent of overpotentials as well as on the nature of the limiting potential of the reaction.56,75
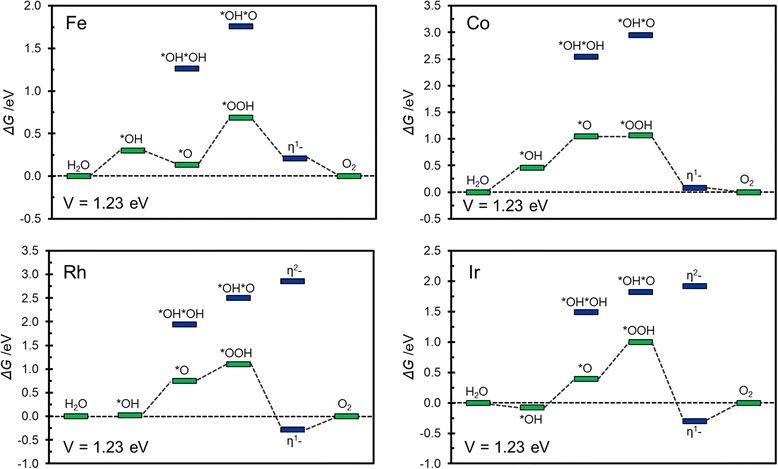 | ||
| Fig. 5 Gibbs free energy profile at V = 1.23 V for Fe@COF, Co@COF, Rh@COF, and Ir@COF SACs. In green and blue are reported conventional and unconventional intermediates respectively. | ||
Conclusions
In this work we performed a computational study of a set of single atom catalysts consisting of transition metal atoms embedded in a recently prepared Covalent Organic Framework. The catalytic activity was investigated for the two semi-reactions of water splitting, i.e. the Hydrogen Evolution and the Oxygen Evolution Reactions.The TM atoms are strongly bound to the COF structures, with positive consequences on the expected thermodynamic stability of the catalysts but the potentially negative effects on their reactivity (more stable species are usually less reactive). In this respect, the nature of the metal is of primary importance to determine the final reactivity and the stability of the reaction intermediates. Out of 17 SACs considered, four are predicted to be rather good for the HER (Ti@COF, W@COF, Ru@COF, Rh@COF); another four exhibit appreciable activities in OER (Fe@COF, Co@COF, Ir@COF, and Rh@COF). From this it emerges that only Rh@COF is, in principle, a good catalyst for both HER and OER. Future work is planned to verify if these conclusions hold true also for the same systems in a water environment.
The other relevant conclusion is that SACs@COF form several unconventional intermediates in both HER and OER and that these species can be more stable than the classical HER and OER adducts. This derives from the fact that SACs are analogs of coordination chemistry compounds and as such they exhibit a rich and complex chemistry. The formation of non-classical intermediates can affect both the thermodynamics and the kinetics of the HER and OER processes. Neglecting the formation of these species in the computational screening of new catalytic systems can result in totally unreliable predictions. Further work will be dedicated in the future to the investigation of more complex syn- and anti-adsorbates for relevant electrochemical reactions, as well as the role of solvation.
Author contributions
Dr Ilaria Barlocco: data simulation, revision and discussion. Dr Giovanni Di Liberto: supervision, revision and discussion. Prof. Gianfranco Pacchioni: supervision, funding acquisition, revision and discussion. The manuscript was written through contributions of all authors.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Livia Giordano for useful discussions. Access to the CINECA supercomputing resources was granted via ISCRAB. We also thank the COST Action 18234 supported by COST (European Cooperation in Science and Technology).References
- A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- S. K. Kaiser, Z. Chen, D. Faust Akl, S. Mitchell and J. Pérez-Ramírez, Chem. Rev., 2020, 120, 11703–11809 CrossRef CAS PubMed.
- M. A. Bajada, J. Sanjosé-Orduna, G. Di Liberto, S. Tosoni, G. Pacchioni, T. Noël and G. Vilé, Chem. Soc. Rev., 2022, 51, 3898–3925 RSC.
- H. Xu, Y. Zhao, Q. Wang, G. He and H. Chen, Coord. Chem. Rev., 2022, 451, 214261 CrossRef CAS.
- S. Tosoni, G. Di Liberto, I. Matanovic and G. Pacchioni, J. Power Sources, 2023, 556, 232492 CrossRef CAS.
- M. B. Gawande, P. Fornasiero and R. Zbořil, ACS Catal., 2020, 10, 2231–2259 CrossRef CAS.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, ChemCatChem, 2022, 14, e202200611 CrossRef CAS.
- X. Li, H. Rong, J. Zhang, D. Wang and Y. Li, Nano Res., 2020, 13, 1842–1855 CrossRef CAS.
- C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2019, 3, 1800376 CrossRef.
- C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421 CrossRef PubMed.
- J. Wang, C. Y. Fan, Q. Sun, K. Reuter, K. Jacobi, M. Scheffler and G. Ertl, Angew. Chem., Int. Ed., 2003, 42, 2151–2154 CrossRef CAS PubMed.
- C. Asokan, H. V. Thang, G. Pacchioni and P. Christopher, Catal. Sci. Technol., 2020, 10, 1597–1601 RSC.
- L. Zhong and S. Li, ACS Catal., 2020, 10, 4313–4318 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, J. Catal., 2023, 417, 351–359 CrossRef CAS.
- Z. Lin, M. Escudero-Escribano and J. Li, J. Mater. Chem. A, 2022, 10, 5670–5672 RSC.
- N. Cheng, S. Stambula, D. Wang, M. N. Banis, J. Liu, A. Riese, B. Xiao, R. Li, T.-K. Sham, L.-M. Liu, G. A. Botton and X. Sun, Nat. Commun., 2016, 7, 13638 CrossRef CAS PubMed.
- W. Qiao, W. Xu, X. Xu, L. Wu, S. Yan and D. Wang, ACS Appl. Energy Mater., 2020, 3, 2315–2322 CrossRef CAS.
- G. Vilé, G. Di Liberto, S. Tosoni, A. Sivo, V. Ruta, M. Nachtegaal, A. H. Clark, S. Agnoli, Y. Zou, A. Savateev, M. Antonietti and G. Pacchioni, ACS Catal., 2022, 12, 2947–2958 CrossRef.
- G. Di Liberto, S. Tosoni, L. A. Cipriano and G. Pacchioni, Acc. Mater. Res., 2022, 3, 986–995 CrossRef CAS.
- D. Van Dao, L. A. Cipriano, G. Di Liberto, T. T. D. Nguyen, S.-W. Ki, H. Son, G.-C. Kim, K. H. Lee, J.-K. Yang, Y.-T. Yu, G. Pacchioni and I.-H. Lee, J. Mater. Chem. A, 2021, 9, 22810–22819 RSC.
- D. Van Dao, G. Di Liberto, H. Ko, J. Park, W. Wang, D. Shin, H. Son, Q. Van Le, T. Van Nguyen, V. Van Tan, G. Pacchioni and I.-H. Lee, J. Mater. Chem. A, 2022, 10, 3330–3340 RSC.
- Y. Chen, S. Ji, C. Chen, Q. Peng, D. Wang and Y. Li, Joule, 2018, 2, 1242–1264 CrossRef CAS.
- H. Fei, J. Dong, D. Chen, T. Hu, X. Duan, I. Shakir, Y. Huang and X. Duan, Chem. Soc. Rev., 2019, 48, 5207–5241 RSC.
- M. D. Hossain, Z. Liu, M. Zhuang, X. Yan, G.-L. Xu, C. A. Gadre, A. Tyagi, I. H. Abidi, C.-J. Sun, H. Wong, A. Guda, Y. Hao, X. Pan, K. Amine and Z. Luo, Adv. Energy Mater., 2019, 9, 1803689 CrossRef.
- J. Deng, H. Li, J. Xiao, Y. Tu, D. Deng, H. Yang, H. Tian, J. Li, P. Ren and X. Bao, Energy Environ. Sci., 2015, 8, 1594–1601 RSC.
- C. Lin, L. Zhang, Z. Zhao and Z. Xia, Adv. Mater., 2017, 29, 1606635 CrossRef PubMed.
- Z. Li, N. Huang, K. H. Lee, Y. Feng, S. Tao, Q. Jiang, Y. Nagao, S. Irle and D. Jiang, J. Am. Chem. Soc., 2018, 140, 12374–12377 CrossRef CAS PubMed.
- C. A. Trickett, A. Helal, B. A. Al-Maythalony, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Nat. Rev. Mater., 2017, 2, 17045 CrossRef CAS.
- V. Hasija, S. Patial, P. Raizada, A. Aslam Parwaz Khan, A. M. Asiri, Q. Van Le, V.-H. Nguyen and P. Singh, Coord. Chem. Rev., 2022, 452, 214298 CrossRef CAS.
- Z. Meng, R. M. Stolz and K. A. Mirica, J. Am. Chem. Soc., 2019, 141, 11929–11937 CrossRef CAS PubMed.
- Y. Yue, P. Cai, K. Xu, H. Li, H. Chen, H.-C. Zhou and N. Huang, J. Am. Chem. Soc., 2021, 143, 18052–18060 CrossRef CAS PubMed.
- Q. Guan, G.-B. Wang, L.-L. Zhou, W.-Y. Li and Y.-B. Dong, Nanoscale Adv., 2020, 2, 3656–3733 RSC.
- J. Wang, J. Wang, S. Qi and M. Zhao, J. Phys. Chem. C, 2020, 124, 17675–17683 CrossRef CAS.
- J. Wang, Z. Zhang, Y. Li, Y. Qu, Y. Li, W. Li and M. Zhao, ACS Appl. Mater. Interfaces, 2022, 14, 1024–1033 CrossRef CAS PubMed.
- M. Lu, M. Zhang, C. Liu, J. Liu, L. Shang, M. Wang, J. Chang, S. Li and Y. Lan, Angew. Chem., 2021, 133, 4914–4921 CrossRef.
- J. P. Collman, R. R. Gagne, C. Reed, T. R. Halbert, G. Lang and W. T. Robinson, J. Am. Chem. Soc., 1975, 97, 1427–1439 CrossRef CAS PubMed.
- L. A. Cipriano, G. Di Liberto and G. Pacchioni, ACS Catal., 2022, 11682–11691 CrossRef CAS.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, J. Am. Chem. Soc., 2021, 143, 20431–20441 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Adv. Theory Simul., 2022, 2200513 CrossRef.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, ACS Catal., 2022, 5846–5856 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- J. K. Norskov and C. H. Christensen, Science, 2006, 312, 1322 LP–1323 CrossRef PubMed.
- Y. Sha, T. H. Yu, B. V. Merinov, P. Shirvanian and W. A. Goddard, J. Phys. Chem. Lett., 2011, 2, 572–576 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. M. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed.
- F. Calle-Vallejo, R. F. de Morais, F. Illas, D. Loffreda and P. Sautet, J. Phys. Chem. C, 2019, 123, 5578–5582 CrossRef CAS.
- P. Gono, F. Ambrosio and A. Pasquarello, J. Phys. Chem. C, 2019, 123, 18467–18474 CrossRef CAS.
- A. Bouzid, P. Gono and A. Pasquarello, J. Catal., 2019, 375, 135–139 CrossRef CAS.
- G. Di Liberto, F. Maleki and G. Pacchioni, J. Phys. Chem. C, 2022, 126, 10216–10223 CrossRef CAS.
- L. Giordano, B. Han, M. Risch, W. T. Hong, R. R. Rao, K. A. Stoerzinger and Y. Shao-Horn, Catal. Today, 2016, 262, 2–10 CrossRef CAS.
- G. Di Liberto and L. Giordano, Electrochem. Sci. Adv., 2023, e2100204 Search PubMed.
- S. Rojas-Carbonell, K. Artyushkova, A. Serov, C. Santoro, I. Matanovic and P. Atanassov, ACS Catal., 2018, 8, 3041–3053 CrossRef CAS.
- F. Maleki, G. Di Liberto and G. Pacchioni, ACS Appl. Mater. Interfaces, 2023, 15, 11216–11224 CrossRef CAS PubMed.
- V. Dao, L. A. Cipriano, S.-W. Ki, S. Yadav, W. Wang, G. Di Liberto, K. Chen, H. Son, J.-K. Yang, G. Pacchioni and I.-H. Lee, Appl. Catal., B, 2023, 330, 122586 CrossRef CAS.
- J. Wang, Z. Zhang, Y. Li, Y. Qu, Y. Li, W. Li and M. Zhao, ACS Appl. Mater. Interfaces, 2022, 14, 1024–1033 CrossRef CAS PubMed.
- M. T. Greiner, T. E. Jones, S. Beeg, L. Zwiener, M. Scherzer, F. Girgsdies, S. Piccinin, M. Armbrüster, A. Knop-Gericke and R. Schlögl, Nat. Chem., 2018, 10, 1008–1015 CrossRef CAS PubMed.
- E. Shustorovich, Surf. Sci. Rep., 1986, 6, 1–63 CrossRef CAS.
- I. V. Solovyev, P. H. Dederichs and V. I. Anisimov, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 16861–16871 CrossRef CAS PubMed.
- G. J. Kubas, Acc. Chem. Res., 1988, 21, 120–128 CrossRef.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS PubMed.
- R. H. Crabtree, Acc. Chem. Res., 1990, 23, 95–101 CrossRef CAS.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00162h |
| This journal is © The Royal Society of Chemistry 2023 |