Locally varying formation of nanoclusters across a low-intensity ultra-short laser spot†
Niklas
Osterloh
a,
Tianluo
Pan
ab and
Karina
Morgenstern
 *a
*a
aRuhr-Universität Bochum, Physical Chemistry I, Universitätsstr. 150, D-44801, Bochum, Germany. E-mail: karina.morgenstern@rub.de; Tel: +49-234-32-25529
bShenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology, Shenzhen, 518055, China
First published on 28th October 2022
Abstract
Ultra-short laser illumination is an intriguing tool for engineering material by light. It is usually employed at or above the ablation threshold. Practical applications profit from tailoring surface properties, for instance, by structural changes to the surface layer of an irradiated target. A target-orientated restructuring of surfaces on the nanoscale is much less explored. In particular, an intrinsic intensity variation across a laser spot has not yet been considered or employed. We image the unexpected nanoscale clusters formed on the Cu(111) surface upon illumination of a Cu sample far below its ablation threshold by femtosecond laser light, employing a specifically-developed multi-scale approach. We unravel that these clusters vary significantly in size and shape across the micrometer-scale 400 nm 50 fs laser spot (repetition rate: 250 kHz). There are three qualitatively different regions separated by sharp changes. The observations highlight the importance of local fluence for specific types of nanoclusters. Ultra-short laser illumination represents a non-trivial interplay between photo-thermal and electron-induced mechanisms, transport of heat and electrons, and material properties, which we discuss for identifying the underlying principles. Our study demonstrates that a multitude of as yet unconsidered processes are involved in the tailoring of nanoscale materials by ultra-short laser light.
New conceptsWhile material processing by high-intensity ultra-fast lasers is well-established, even used industrially, it is a topic of current research on how the interaction between the light and the material causes the changes on the nanoscale. Our results falsify a well-established assumption that a 50 fs laser illumination of a few mJ cm−2 fluence leaves a metal surface unperturbed. By observing a laser-treated surface with the high spatial resolution of a scanning tunneling microscope at low temperatures below 10 K, where all thermal motion is frozen, we reveal nanoscale clusters formed from material ejected from the bulk to the surface. Moreover, the laser-induced nanoclusters vary qualitatively across the laser spot. This local variation on the microscale has been mostly ignored so far, both in research and application of nanoclusters. We propose to utilize the low-intensity femtosecond laser illumination for tailored nanocluster design. |
1 Introduction
Ultra-short laser irradiation drives materials into new states of matter far from equilibrium. The ultra-short laser light causes structural modifications, impossible under equilibrium conditions,2,3 yielding unique bulk structures4 and surface properties,5–7 defining the material's behavior for, e.g., catalysis,2 friction,5,8,9 or coating.10 For further examples, see recent reviews covering fundamental aspects as ultrafast spectroscopic probes and their future and11 ultrafast laser structuring of materials12 or more applied topics as 3D laser-writing of dielectrics13 and surface functionalization14 by ultrafast laser light.While the lattice stays cold during the absorption of ultrashort laser light, electron temperatures reach several thousand Kelvin.1 An understanding of such non-equilibrium processes behind the induced structural modifications is of utmost importance for practical applications, such as nanoablation and photo-lithography,15,16 and at the cutting edge of condensed matter physics and material science17,18 because it elucidates the non-equilibrium material properties.19 The energy densities to alter the surface structure by femtosecond laser pulses are commonly above the ablation threshold, where the purely thermal process is governed by the energy coupling between the excited electrons and the cold lattice.16 This threshold is, e.g., 400 mJ cm−2 at 355 nm20 and 240 mJ cm−2 at 532 nm21 for the here investigated copper.
On the other hand, the field of femtochemistry, where reactions of surface-adsorbed molecules are initiated by ultra-short laser pulses,22 employs considerably lower fluences of the order of mJ cm−2. Femtochemical reactions are interpreted based on unaltered surfaces. However, a Cu surface was structurally modified at an illumination fluence of 60 mJ cm−2 (400 nm), below the ablation thresholds at similar wavelengths and only an order of magnitude larger than those employed in femtochemistry.23 These changes were revealed by X-ray diffraction, a method that averages across a ∼3 mm2 area. The missing local view of such surface restructuring is a prerequisite to revealing the true nature of ultrafast laser-induced changes. Other explored effects of the interaction of femtosecond laser light with matter are, e.g. femtosecond laser-induced photodynamic assembly,24in situ anisotropic laser printing,25 or the optical response of nanostructures.26 These might profit from a local view on surface restructuring by femtosecond laser light.
In this article, we use scanning tunneling microscopy (STM) to reveal nanoclusters formed on a Cu(111) surface by ultra-short laser pulses at unexpected low fluences below the ablation threshold. The clusters vary qualitatively and abruptly across the laser spot. Their non-equilibrium origin is discussed to assess the underlying mechanisms.
2 Methods
The experiments were performed with a home-built low-temperature (5 K) STM of the beetle-type in an ultra-high vacuum (UHV) chamber (base pressure ≤ 2 × 10−10 mbar) with standard facilities for sample preparation.27The Cu(111) sample is prepared by repeated cycles of Ne+ sputtering for 45 min (1.3 keV, 1.5 μA at 3 × 10−5 mbar) and annealing at 650 °C for 5 min. The impurity level at the surface is below 0.1% ML after this preparation procedure.
The STM features the possibility to guide a femtosecond laser beam into the tip-sample region, as described in detail elsewhere.27 The laser light is focused in situ, i.e., within the He cryostat that surrounds the STM head, below the STM tip to an elliptical spot of 13.5 μm × 11.0 μm, measured at 1/e2 of a photo-electron signal.
Laser pulses with a repetition rate of 250 kHz from a commercial laser (RegA 9050 from Coherent) are frequency-doubled in a Beta-Barium-Borate (BBO) crystal to 400 nm. The 400 nm pulse width is around 50 fs at the sample surface, as measured in an in situ auto-correlation experiment. Here, we use a power of (12.7 ± 0.3) mW with 97% p-polarized light at the surface. Both values are determined in a parallel set-up outside the UHV chamber, mimicking the path of the laser to the tip-sample region. For an absorption in Cu of 72% for p-polarized 400 nm light at an incident angle of 65°, the absorbed fluence is (7.6 ± 0.4) mJ cm−2.28
An experiment starts by recording an STM image of the pristine surface. Then, the tip is retracted from the scanned area and the incoming laser light as far as possible without moving the scanner head. The sample is subsequently illuminated for 40 s, corresponding to a train of 107 laser pulses. After illumination, the tip is re-approached to scan the same spot on the surface.
The usual scanning range of low-temperature STMs is quite limited, to 1 μm × 1 μm in our case. We increase this range by one order of magnitude by moving the ramp that supports the tip in slip-stick motion by approximately half its maximum scan range (400 nm) followed by recording several partly overlapping STM images of 0.3 μm × 0.3 μm.
All images are recorded at a tunneling current of 100 pA and a voltage of 228 mV. Large-scale images are recorded at a lower resolution of (1.2 nm × 1.2 nm)/pixel than small-scale images, recorded at a higher resolution of (0.3 nm × 0.3 nm)/pixel. For image analysis, the program WSxM is used.29
3 Results and discussion
We propose to use low-intensity femtosecond laser light for a targeted restructuring of metal surfaces on the nanoscale based on scanning tunneling microscopy (STM), a technique for which we developed a protocol to combine nanoscale resolution to μm ranges. We demonstrate the approach for nanoclusters formed on a Cu(111) surface by ultra-short laser pulses in a fluence range where femtochemistry is performed. The fluence is thus considerably lower than that in23 and far below the ablation threshold. We discover not only nanocluster formation at low energy density but also a substantial variety of these changes across the laser spot. Based on this unprecedented local view, we discuss the non-equilibrium origin of the nanoclusters to assess their underlying formation mechanisms, which can be used for a targeted restructuring of metal surfaces on the nanoscale by femtosecond laser light.3.1 Surface changes below the ablation threshold
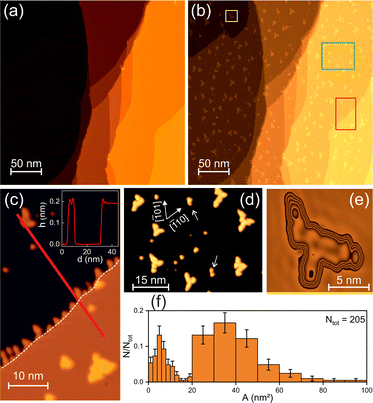
Illuminating a pristine Cu(111) surface (Fig. 1a), as detailed in the methods section, at a fluence that is more than two orders of magnitude below the ablation threshold of Cu, leads to unexpected substantial structural changes consisting of clusters of various sizes and shapes (Fig. 1b). The additional material must be ejected from the bulk because (a) the tip remains unaltered, (b) there are no holes in the surface, (c) the step edges have not retracted (cf. dashed line in Fig. 1c), and (d) all additional structures have the height of intrinsic Cu steps (Fig. 1c). Thus, the illumination creates interstitials within the bulk and induces their diffusion to the surface and on it to form islands, a process distinctly different from the melting and recrystallization process suggested earlier.23While the overall triangular shape of the islands reflects the symmetry of the fcc(111) surface, their outline is quite irregular with branches along the three 〈110〉 directions (Fig. 1c–e), a shape reminiscent of kinetically-limited dendritic islands resulting from low-temperature metal-on-metal growth.30,31 In contrast to such grown dendrites, two island types with significantly different sizes coexist here (Fig. 1d). We define islands by the sharp minimum in the histogram in Fig. 1f at 16 nm2 as “small” and “large”. The large islands are dendritic, and the small islands are more compact, at an average size of (34 ± 1) nm2 and (5.4 ± 0.5) nm2, respectively. The differences in size and shape point to two separate formation mechanisms. Higher resolution images reveal that the large islands consist of smaller subunits (Fig. 1e), at an average size of (6.3 ± 1.6) nm2, comparable to the average size of the small islands. Thus, small islands formed in earlier laser pulses are induced to diffuse in subsequent laser pulses to agglomerate to large dendritic islands through a hit-and-stick mechanism (see arrows in Fig. 1d). A comparable agglomeration has recently been proven in time-lapsed sequences of thermal growth of water on Ag(111).32
3.2 Local variation in island size and shape
To explore the dependence of the surface restructuring on local fluence, we developed a protocol to record a series of images across a sizable part of the Gaussian-shaped laser spot in two perpendicular directions (Fig. 2). On the micro-scale, the clusters vary quantitatively and qualitatively. Quantitatively, the coverage decreases with increasing distance from the origin, following a power law with an exponent of roughly five (θ ∝ F4.9±0.6, Fig. 2, inset), indicative of a similar interstitial-fluence dependence. The exponent is in the typical range of 233 to 15,34 as observed in power law yield dependencies in femtochemistry, giving the first indication of a non-equilibrium process.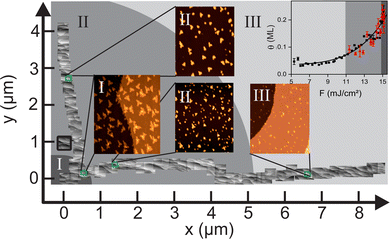 | ||
| Fig. 2 Micrometer-scale imaging across the laser spot: 90 adjacent STM images covering a range of 8.5 μm in the x direction and 4.1 μm in the y direction. The origin is set to the image of the highest coverage. Different regions are marked in different shades of gray and by roman numerals. The enlarged images represent examples for the three regions. The black square marks the position of the image in Fig. 1b. Inset in the upper right corner: Coverage θ vs. local fluence F in x (black squares) and y direction (red triangles) with fit of θ ∝ Fc yielding c = (4.9 ± 0.6). | ||
Since the local coverage correlates to the number of created interstitials, a similar non-linear relationship should hold for the dependence of their amount on local fluence. Despite a monotonous change in interstitial formation and coverage, the number of islands changes non-monotonously. It increases from region III to II following the increase in the coverage. However, it decreases from region II to I despite a further coverage increase, accompanied by a qualitative change in the island geometry. The few islands in the region I are predominantly large and dendritic; in region II, small compact and large dendritic islands coexist (cf.Fig. 1f); in region III, the small compact islands dominate (Fig. 2). Island area histograms in Fig. 3 reflect these differences in island sizes.
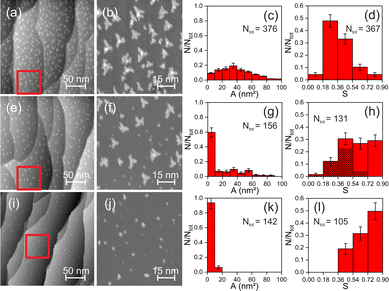
3.3 Fluence-dependent regions
We present one example for each of the three regions identified from these dependencies (Fig. 3). The large variety of dendritic islands (Fig. 3a and b) in the region I leads to a broad distribution of island sizes up to 100 nm2 with a weak maximum at approximately 33 nm2 (Fig. 3c). Though around 10% of the islands are in the range defined as small, these relate to the broad equilibrium distribution of dendritic islands. The area histogram of the more uniform circular islands in the region III (Fig. 3i and j) is much sharper, with all islands smaller than 20 nm2. Thereby more than 90% are within the region defined above as small (Fig. 3k). The area histogram in the region II, where both types of islands coexist (Fig. 3e and f), can be considered a superposition of those in the other two regions (Fig. 3g). In this region, 67% of the islands smaller than 20 nm2 echo the small islands in the region III. The size distribution of the remaining islands in region II is as broad as that for the dendritic islands in region I. We multiply the ratio of the island area A to the square of the perimeter P by 4π to capture the different shapes of the islands. In this definition, S = 4π·(A/P2) has a value of 1 for a perfectly circular island.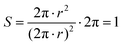 . The more dendritic a cluster is the lower its S value. For instance, the shape value of the cluster shown in Fig. 1e is, at 0.29, only one-third of that for a circular one. The histogram of these shape values in the region I is asymmetric, with its maximum at a comparable value of 0.27 (Fig. 3d), corresponding thus mainly to dendritic clusters. The shape value histogram of the region III displays considerably higher values, with more than 80% of the clusters with values above 0.54 (Fig. 3l), indicating small, compact ones. The lack of shape values below 0.36 is consistent with the absence of large, dendritic clusters. The shape value histogram from the region II displays no distinct maximum with an equal distribution of shape values between 0.36 and 0.90. Existing smaller S values reflect the coexistence of dendritic and more compact clusters (Fig. 3h). However, separating the shape values for small and large clusters reveals that this histogram is not a simple superposition of those in the regions I and III. While the shape value distribution of the small clusters mostly resembles that of clusters in the region III, the shape value distribution of the dendritic clusters in the region II differs distinctly from that in the region I. The shape values of the large clusters in the region II are distributed around a maximum of S = 0.45, while they lie around S = 0.27 lower in the region I. Therefore the large clusters in the regions I and II differ in shape.
. The more dendritic a cluster is the lower its S value. For instance, the shape value of the cluster shown in Fig. 1e is, at 0.29, only one-third of that for a circular one. The histogram of these shape values in the region I is asymmetric, with its maximum at a comparable value of 0.27 (Fig. 3d), corresponding thus mainly to dendritic clusters. The shape value histogram of the region III displays considerably higher values, with more than 80% of the clusters with values above 0.54 (Fig. 3l), indicating small, compact ones. The lack of shape values below 0.36 is consistent with the absence of large, dendritic clusters. The shape value histogram from the region II displays no distinct maximum with an equal distribution of shape values between 0.36 and 0.90. Existing smaller S values reflect the coexistence of dendritic and more compact clusters (Fig. 3h). However, separating the shape values for small and large clusters reveals that this histogram is not a simple superposition of those in the regions I and III. While the shape value distribution of the small clusters mostly resembles that of clusters in the region III, the shape value distribution of the dendritic clusters in the region II differs distinctly from that in the region I. The shape values of the large clusters in the region II are distributed around a maximum of S = 0.45, while they lie around S = 0.27 lower in the region I. Therefore the large clusters in the regions I and II differ in shape.
We use contour plots to visualize the transition between the regions by displaying area and shape value histograms for all images shown in Fig. 2. In contour plots, the relative abundances N/Ntot are converted into colors (Fig. 4).
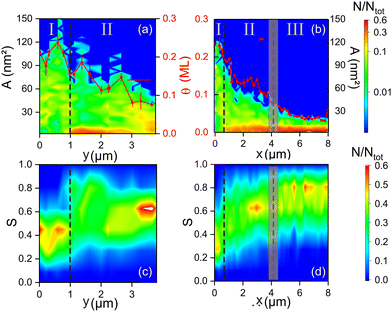 | ||
| Fig. 4 Variation of area and shape value histograms along y (a and c) and x (b and d) in the coordinate system defined in Fig. 2 on the false colour scale given on the right-hand side: (a and b) area histograms on logarithmic N/Ntot scale. Red squares: Coverage θ (right axis), vertical lines across the data points mark the range of local coverages on these images. (c and d) shape value histograms on a linear N/Nges scale. The dashed lines separate the regions marked on top of the images. | ||
Apart from compression due to the ellipticity of the laser beam on the surface, the clusters follow similar trends in both directions. The coverage decreases (Fig. 4a and b, red data points), the fraction of small clusters increases (Fig. 4a and b), and the maximum of S shifts to higher values (Fig. 4c and d). Despite the smooth change in fluence across a laser spot, some features change abruptly. From the regions I to II, the number of small clusters increases sharply (Fig. 4a and b, at the dashed line). An accompanying sharp change in shape value (Fig. 4c and d) results from an absence of small clusters and a shift of the shape values of the large clusters from an average value of ∼0.35 to a higher average of ∼0.55. A (less abrupt) discontinuity between the regions II and III is best observable in the x direction (Fig. 4d). The maximum of the shape value histograms in the region II at S ≈ 0.62 is fading out when approaching this discontinuity, while a new maximum at S ≈ 0.81 starts to grow at it.
We relate disparate clusters in the three regions to distinct processes at other local fluences. At the lowest fluence in the region III, the adatoms form small, compact clusters. Thus, adatom diffusion is induced by the fluence in the region III but the small clusters are stationary in laser pulses following their creation. The higher fluence in the region II is sufficient to induce diffusion of these small clusters, leading to their agglomeration into dendritic clusters. As small clusters hardly exist in region I and the shape of the dendritic clusters is more fractal, a third process triggers the formation of the dendritic clusters in the region I, adding to the processes leading to the formation of small clusters in the region III (adatom diffusion) and large clusters in the region II (small cluster diffusion). The smaller shape value S suggests that the clusters in the region I are formed from smaller particles than the large clusters in the region II, possibly adatoms. Thus, either the small clusters do not agglomerate or are not stable at the higher fluence of the region I.
3.4 Excitation mechanism
To explain the three processes, we discuss the excitation mechanisms behind the observed nanocluster formation. In general, the processes can be driven either by the laser-excited electrons or thermally by the increased temperature of the lattices after electron–phonon equilibration.22 For forming small clusters, the adatoms must diffuse over the surface. The diffusion might be induced thermally during the transient increase of the surface temperature after the laser pulse. The maximum phonon temperature is estimated to ∼135 K, employing the two-temperature model for the parameters used here.22 It stays for ∼100 ps above a temperature of 90 K. For the thermal adatom diffusion energy barrier of 0.04 eV,35 each adatom moves around once every second pulse, calculated as before.36,37 This scenario implies sufficient thermal mobility to form the observed small clusters in the region III during the pulses following the adatom creation.The diffusivity of small clusters, consisting of up to 100 atoms, is several orders of magnitude lower than that of single adatoms,38,39 excluding a significant thermal diffusion during the transiently elevated phonon temperature. It implies an electron-induced process. We propose that the small clusters are excited as an entity, similar to adsorbed molecules in femtochemical reactions.22 The long lifetime of an excited state of a small cluster in the large projected band gap of Cu(111) may aid the subsequent diffusion, similar to the anti-bonding states of Cs/Cu(111).40 It explained the coexistence of small and large clusters in the region II: some small clusters move far enough to form larger clusters, while others don’t. Such mobility should increase with laser fluence across the region II, reflected in a decrease in the number of small clusters by the approach towards the region I (Fig. 4a and b).
The sudden absence of small clusters in the region I implies a threshold fluence for an additional process. We propose that a second, energetically higher excited quantum state of the small clusters is accessible by the hotter electrons, leading to the destruction of the small clusters. The resulting fragments, possibly single adatoms, form the more dendritic clusters in the region I with their smaller shape value S.
The primary result of this study is the unexpected nanoclusters formed in the mJ cm−2 fluence range, far below the laser ablation threshold. As the highest phonon temperature of 135 K is far below the thermal melting temperature of Cu, at 1357 K, melting and recrystallization of23 cannot explain it. The question arises of how the interstitials form. A single photon of ∼3.1 eV carries sufficient energy to break the bonds of bulk Cu atoms (calculated vacancy formation energy of 1.33 eV).41 However, its energy cannot be converted directly for this purpose as it is absorbed by the electron system.42 Instead, excited electrons and holes are formed. Neither an excited electron nor the corresponding hole can transfer its whole energy to a single atom via scattering because of momentum conservation. Thus, another process must be responsible for creating bulk interstitials. We discuss two scenarios. The interstitials might be created before the conversion of the excitation into delocalized electron Bloch waves. Or, they might be created after these Bloch waves got relocalized. Short-lived excitons in d-band metals offer a pathway for the first scenario. The absorbed photon energy remains for a few femtoseconds localized in such bound electron–hole pair.43 If the exciton recombined within its short lifetime, it could transfer its entire energy to one individual atom in a radiation-less process to overcome the interstitial formation energy. The second scenario of Bloch wave localization demands breaking the crystal symmetry. We propose that the formation of initial interstitials is initiated by electrons or holes localizing at intrinsic defects or even at an emerging defect as suggested recently.44 In subsequent laser pulses, the thus created interstitials serve as additional defects for localization. This effect is called incubation in laser ablation studies. It relates to ablation thresholds which reduce with the number of laser pulses.45–48 The processes to explain this phenomenon include plastic deformations49 due to heat accumulation50 and laser-induced defect accumulation.51 These mechanisms may contribute to lower the damage threshold or to the variation of the absorption length so that the deposited energy is increased during trains of laser irradiation.52 Cases for which heat accumulation cannot describe the experimental result are successfully modeled in an extended defect model.53 This model attributes the lowering of the threshold to the accumulation of long-lived optically active defects, which increase absorption locally (e.g. roughening due to the ejection of atoms and clusters far below the macroscopic ablation threshold fluence54 or void formation55). We suggest that similar processes operate in our case. However, the threshold decrease saturates typically at around 1000 pulses,56 a pulse train that is not accessible in our experiment but will hopefully be approached in the future.
4 Conclusion
In conclusion, we unveiled the importance of the local fluence for nanoclusters formed across the spot of an ultrafast laser by extending the size range of local imaging for a fundamental understanding of photo-induced processes. The local view revealed that the surface is altered severely by ultrashort laser pulses with fluences orders of magnitudes below the ablation threshold. At least two non-thermal processes are involved in the nanocluster formation, the interstitial formation and surface diffusion of Cu clusters on Cu(111). Those processes result from not yet considered energy transfers upon ultra-short laser excitation. The perceptions of the underlying physics recast our understanding of the interaction of matter with ultra-short lasers. Understanding these non-equilibrium processes may be used in future to control and thus tailor material properties by ultra-short laser light. Furthermore, recognizing a transient surface structuring during a femtochemical reaction may change our view of surface femtochemistry.Author contributions
Niklas Osterloh: investigation, methodology, validation, formal analysis, writing, visualization; Tianluo Pan: investigation, methodology, writing – review and editing; Karina Morgenstern: conceptualization, supervision, resources, data curation, writing – review and editing, visualization, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) project MO 960/25-1 and under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV.Notes and references
- E. G. Gamaly and A. V. Rode, Physics of ultra-short laser interaction with matter: from phonon excitation to ultimate transformations, Prog. Quantum Electron., 2013, 37, 215–323 CrossRef.
- L. Jiang, A. Wang, B. Li, T. H. Cui and Y.-F. Lu, Electrons dynamics control by shaping femtosecond laser pulses in micro/nanofabrication: modeling, method, measurement and application, Light: Sci. Appl., 2018, 7, 17134 CrossRef CAS.
- M. Z. Mo, Z. Chen, R. K. Li, M. Dunning, B. B. L. Witte, J. K. Baldwin, L. B. Fletcher, J. B. Kim, A. Ng, R. Redmer, A. H. Reid, P. Shekhar, X. Z. Shen, M. Shen, K. Sokolowski-Tinten, Y. Y. Tsui, Y. Q. Wang, Q. Zheng, X. J. Wang and S. H. Glenzer, Heterogeneous to homogeneous melting transition visualized with utrafast electron diffraction, Science, 2018, 360, 1451–1455 CrossRef CAS.
- X. Wen, B. Zhang, W. Wang, F. Ye, S. Yue, H. Guo, G. Gao, Y. Zhao, Q. Fang, C. Nguyen, X. Zhang, J. Bao, J. T. Robinson, P. M. Ajayan and J. Lou, 3D-printed silica with nanoscale resolution, Nat. Mater., 2021, 20, 1506–5015 CrossRef CAS PubMed.
- P. Fan, R. Pan and M. Zhong, Ultrafast laser enabling hierachical structures for versatile superhydrophobitcity with enhanced Cassie-Baxter stability and durability, Langmuir, 2019, 35, 16693–16711 CrossRef CAS.
- A. H. A. Lutey, L. Gemini, L. Romoli, G. Lazzini, F. Fuso, M. Faucon and R. Kling, Towards laser-textured antibacterial surfaces, Sci. Rep., 2018, 8, 10112 CrossRef PubMed.
- D. Hu, Y. Lu, Y. Cao, Y. Zhang, Y. Xu, W. Li, F. Gao, B. Cai, B.-O. Guan, C.-W. Qiu and X. Li, Laser-splashed three-dimensional plasmonic nanovolcanoes for steganography in angular anisotropy, ACS Nano, 2018, 12, 9233–9239 CrossRef CAS PubMed.
- J. Israelachvili, N. Maeda, K. J. Rosenberg and M. Akbulut, Effects of sub-Angstrom (pico-scale) structure of surfaces on adhesion, friction, and bulk mechanical properties, J. Mater. Res., 2005, 20, 1952–1972 CrossRef CAS.
- X. Zhang and J. Jia, Frictional behaviour of micro/nanotextured surfaces investigated by atomic force microscope: a review, Surf. Rev. Lett., 2015, 22, 1530001 CrossRef CAS.
- D. J. O'Connor, B. A. Sexton and R. S. C. Smart, Surface analysis methods in materials science, Springer; Berlin, 2nd edn, 2003 Search PubMed.
- J. Lloyd-Hughes, P. M. Oppeneer, T. Pereira dos Santos, A. Schleife, S. Meng, M. A. Sentef, M. Ruggenthaler, A. Rubio, I. Radu and M. Murnane, et al., The 2021 ultrafast spectroscopic probes of condensed matter roadmap, J. Phys.: Condens. Matter, 2021, 33, 353001 CrossRef CAS.
- R. Stoian and J.-P. Colombier, Advances in ultrafast laser structuring of materials at the nanoscale, Nanophotonics, 2020, 9, 4665–4688 CrossRef.
- M. Chambonneau, D. Grojo, O. Tokel, F. Ö. Ilday, S. Tzortzakis and S. Nolte, In-volume laser direct writing of silicon - challenges and opportunities, Laser Photonics Rev., 2021, 15, 2100140 CrossRef.
- M. Liu, M.-T. Li, S. Xu, H. Yang and H.-B. Sun, Bioinspired superhydrophobic surfaces via laser-structuring, Front. Chem., 2020, 8, 835 CrossRef CAS PubMed.
- B. Öktem, I. Pavlov, S. Ilday, H. Kalayciogglu, A. Rybak, S. Yavas,M. Erdogan and F. Ömer Ilday, Nonlinear laser lithography for indefinitely large-area nanostructuring with femtosecond pulses, Nat. Photonics, 2013, 7, 897–901 CrossRef.
- K. Sugioka and Y. Cheng, Ultrafast lasers-reliable tools for advanced materials processing, Light: Sci. Appl., 2014, 3, e149 CrossRef CAS.
- A. M. Lindenberg, J. Larsson, K. Sokolowski-Tinten, K. J. Gaffney, C. Blome, O. Synnergren, J. Sheppard, C. Caleman, A. G. MacPhee, D. Weinstein and D. P. Lowney, et al., Atomic-scale visualization of inertial dynamics, Science, 2005, 308, 392–395 CrossRef CAS.
- Y. Terada, S. Yoshida, O. Takeuchi, H. Shigekawa and H. Laser-combined, scanning tunnelling microscopy for probing ultrafast transient dynamics, J. Phys.: Condens. Matter, 2005, 22, 264008 CrossRef PubMed.
- C. Wang, H. Huo, M. Johnson, M. Shen and E. Mazur, The thresholds of surface nano-/micro-morphology modifications with femtosecond laser pulse irradiations, Nanotechnology, 2010, 21, 075304 CrossRef PubMed.
- P. Lorenz, M. Himmerlich, M. Ehrhardt, E. Bez, K. Bogdanowicz, M. Taborelli and K. Zimmer, Secondary electron yield reduction of copper after 355 nm ultrashort pulse laser ablation, Lasers Manuf. Mater. Process., 2022, 9, 135–150 CrossRef.
- D. Bajek, S. Wackerow, D. A. Zanin, L. Baudin, K. Bogdanowicz, E. Garcia-Tabares Valdivieso, S. Calatroni, B. Di Girolamo, M. Sitko, M. Himmerlich, M. Taborelli, P. Chiggiato and A. Abdolvand, Role of surface microgeometries on electron escape probability and secondary electron yield of metal surfaces, Sci. Rep., 2020, 10, 250 CrossRef CAS.
- C. Frischkorn and M. Wolf, Femtochemistry at metal surfaces: nonadiabatic reaction dynamics, Chem. Rev., 2006, 106, 4207–4233 CrossRef CAS PubMed.
- R. Li, O.-A. Ashour, H. E. Elsayed-Ali and P. M. Rentzepis, Femtosecond laser induced structural dynamics and melting of Cu (111) single crystal. An ultrafast time-resolved x-ray diffraction study, J. Appl. Phys., 2017, 121, 055102 CrossRef.
- H. Wang, Y.-L. Zhang, H. Xia, Q.-D. Chen, K.-S. Lee and H.-B. Sun, Photodynamic assembly of nanoparticles towardsdesignable patterning, Nanoscale Horiz., 2016, 1, 201–211 RSC.
- Y. Zhang, L. Shi, D. Hu, S. Chen, S. Xie, Y. Lu, Y. Cao, Z. Zhu, L. Jin, B.-O. Guan, S. Roggec and X. Li, Full-visible multifunctional aluminium metasurfaces by in situ anisotropic thermoplasmonic laser printing, Nanoscale Horiz., 2019, 4, 601–609 RSC.
- Q. Xiao, B. Ma, X. Fei, D.-W. Liu, X.-P. Zhai, X.-Y. Li, M.-J. Xiao, Y. Peng, Q. Wang and H.-L. Zhang, Unveiling the dimension-dependence of femtosecond nonlinear optical properties of tellurium nanostructures, Nanoscale Horiz., 2021, 6, 918–927 RSC.
- M. Mehlhorn, H. Gawronski, L. Nedelmann, A. Grujic and K. Morgenstern, An instrument to investigate femtochemistry on metal surfaces in real-space, Rev. Sci. Instrum., 2007, 78, 033905 CrossRef PubMed.
- S. Babar and J. H. Weaver, Optical constants of Cu, Ag, and Au revisited, Appl. Opt., 2015, 54, 477–481 CrossRef CAS.
- I. Horcas, R. Fernandez, J. M. Gomez-Rodriguez, J. Colchero, J. Gomez-Herrero and A. M. Baro, WSXM: A software for scanning probe microscopy and a tool for nanotechnology, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- H. Brune, Microscopic view of epitaxial metal growth: nucleation and aggregation, Surf. Sci. Rep., 1998, 31, 125–229 CrossRef.
- C. Sprodowski and K. Morgenstern, Temperature-dependent change of the fractal dimension of Cu dendrites on Cu(111), New J. Phys., 1998, 22, 063055 CrossRef.
- S. Heidorn, K. Lucht, C. Bertram and K. Morgenstern, Preparation dependent orientation of crystalline ice islands on Ag(111), J. Phys. Chem. B, 2018, 122, 479–484 CrossRef.
- M. Bonn, S. Funk, Ch Hen, D. N. Denzler, C. Stampfl, M. Scheffler, M. Wolf and G. Ertl, Phonon versus electron-mediated desorption and oxidation of CO on Ru(0001), Science, 1999, 285, 1042–1045 CrossRef CAS PubMed.
- H. Ueba, M. Hayashi, M. Paulsson and B. N. J. Persson, Adsorbate hopping via vibrational-mode coupling induced by femtosecond laser pulses, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113408 CrossRef.
- N. Knorr, H. Brune, M. Epple, A. Hirstein, M. A. Schneider and K. Kern, Long-range adsorbate interactions mediated by a two-dimensional electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115420 CrossRef.
- M. Mehlhorn, J. Carrasco, A. Michaelides and K. Morgenstern, Local Investigation of femtosecond laser induced dynamics of water nanoclusters on Cu(111), Phys. Rev. Lett., 2009, 103, 026101 CrossRef PubMed.
- M. Mehlhorn, H. Gawronski and K. Morgenstern, Diffusion and dimer formation of molecules induced by femtosecond laser pulses, Phys. Rev. Lett., 2010, 104, 076101 CrossRef PubMed.
- J. Yang, W. Hu, J. Tang and M. Xu, Long-time scale molecular dynamics study of diffusion dynamics of small Cu clusters on Cu(111) surface, J. Phys. Chem. C, 2008, 112, 2074–2078 CrossRef CAS.
- M. O. Jahma, M. Rusanen, A. Karim, I. T. Koponen, T. Ala-Nissila and T. Rahman, Diffusion and submonolayer island growth during hyperthermal deposition on Cu(100) and Cu(111), Surf. Sci., 2005, 598, 246–252 CrossRef CAS.
- H. Petek, M. J. Weida, H. Nagano and S. Ogawa, Real-time observation of adsorbate atom motion above a metal surface, Science, 2000, 288, 1402–1404 CrossRef CAS.
- T. Korhonen, M. J. Puska and R. M. Nieminen, Vacancy-formation energies for fcc and bcc transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 9526–9532 CrossRef CAS PubMed.
- J. Hohlfeld, S. S. Wellershoff, J. Güdde, U. Conrad, V. Jahnke and E. Matthias, Electron and lattice dynamics following optical excitation of metals, Chem. Phys., 2000, 251, 237–258 CrossRef CAS.
- X. Cui, C. Wang, A. Argondizzo, S. Garrett-Roe, B. Gumhalter and H. Petek, Transient excitons at metal surfaces, Nat. Phys., 2014, 10, 505–509 Search PubMed.
- S. Kretschmer, T. Lehnert, U. Kaiser and A. V. Krasheninnikov, Formation of defects in two-dimensional MoS2 in the transmission electron microscope at electron energies below the knock-on threshold: the role of electronic excitations, Nano Lett., 2020, 20, 2865–2870 CrossRef CAS PubMed.
- Y. Jee, M. F. Becker and R. M. Walser, Laser-induced damage on single-crystal metal surfaces, J. Opt. Soc. Am. B, 1988, 5, 648–659 CrossRef CAS.
- K.-H. Leitz, B. Redlingshöfer, Y. Reg, A. Otto and M. Schmidt, Metal ablation with short and ultrashort laser pulses, Phys. Procedia, 2011, 12, 230–238 CrossRef CAS.
- F. Di Niso, C. Gaudioso, T. Sibillano, F. P. Mezzapesa, A. Ancona and P. M. Lugara, Influence of the repetition rate and pulse duration on the incubation effect in multiple-shots ultrafast laser ablation of steel, Phys. Procedia, 2013, 41, 698–707 CrossRef.
- O. Armbruster, A. Naghilou and M. Kitzler, Wo. Kautek, Spot size and pulse number dependence of femtosecond laser ablation thresholds of silicon and stainless steel, Appl. Surf. Sci., 2017, 396, 1736–1740 CrossRef CAS.
- P. T. Mannion, J. Magee, E. Coyne, G. M. O'Connor and T. J. Glynn, The effect of damage accumulation behaviour on ablation thresholds and damage morphology in ultrafast laser micro-machining of common metals in air, Appl. Surf. Sci., 2004, 233, 275–287 CrossRef CAS.
- C. Gaudioso, G. Giannuzzi, A. Volpe, P. M. Lugara, I. Choquet and A. Ancona, Incubation during laser ablation with bursts of femtosecond pulses with picosecond delays, Opt. Express, 2018, 26, 3801–3813 CrossRef.
- G. Raciukaitis, M. Brikas, P. Gecys and M. Gedvilas, Accumulation effects in laser ablation of metals with high-repetition-rate lasers, Proc. SPIE, 2008, 7005, 70052L CrossRef.
- B. Neuenschwander, B. Jaeggi, M. Schmid, A. Dommann, A. Neels, T. Bandi and G. Hennig, Factors controlling the incubation in the application of ps laser pulses on copper and iron surfaces, Proc. SPIE, 2013, 8607, 86070D CrossRef.
- A. Naghilou, O. Armbruster, M. Kitzler and W. Kautek, Merging spot size and pulsenumber dependence of femtosecond laser ablation thresholds: modeling and demonstration with high impact polystyrene, J. Phys. Chem. C, 2015, 119, 22992–22998 CrossRef CAS.
- A. Borowiec and H. K. Haugen, Subwavelength ripple formation on the surfaces of compound semiconductors irradiated with femtosecond laser pulses, Appl. Phys. Lett., 2003, 82, 4462–4464 CrossRef CAS.
- C. Wu, M. S. Christensen, J.-M. Savolainen, P. Balling and L. V. Zhigilei, Generation of subsurface voids and a nanocrystalline surface layer in femtosecond laser irradiation of a single-crystal Ag target, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 035413 CrossRef.
- F. Di Niso, C. Gaudioso, T. Sibillano, F. P. Mezzapesa, A. Ancona and P. M. Lugara, Role of heat accumulation on the incubation effect in multi-shot laser ablation of stainless steel at high repetition rates, Opt. Express, 2014, 22, 12200–12210 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00386d |
| This journal is © The Royal Society of Chemistry 2023 |