Open Access Article
Open Access ArticleCharge transport properties of ideal and natural DNA segments, as mutation detectors
Marilena
Mantela
 ,
Konstantinos
Lambropoulos
,
Konstantinos
Lambropoulos
 and
Constantinos
Simserides
and
Constantinos
Simserides
 *
*
Department of Physics, National and Kapodistrian University of Athens, Panepistimiopolis, Zografos, GR-15784 Athens, Greece. E-mail: mmantela@phys.uoa.gr; klambro@phys.uoa.gr; csimseri@phys.uoa.gr
First published on 7th February 2023
Abstract
DNA sequences of ideal and natural geometries are examined, studying their charge transport properties as mutation detectors. Ideal means textbook geometry. Natural means naturally distorted sequences; geometry taken from available databases. A tight-binding (TB) wire model at the base-pair level is recruited, together with a transfer matrix technique. The relevant TB parameters are obtained using a linear combination of all valence orbitals of all atoms, using geometry, either ideal or natural, as the only input. The investigated DNA sequences contain: (i) point substitution mutations – specifically, the transitions guanine (G) ↔ adenine (A) – and (ii) sequences extracted from human chromosomes, modified by expanding the cytosine–adenine–guanine triplet [(CAG)n repeats] to mimic the following diseases: (a) Huntington's disease, (b) Kennedy's disease, (c) Spinocerebellar ataxia 6, (d) Spinocerebellar ataxia 7. Quantities such as eigenspectra, density of states, transmission coefficients, and the – more experimentally relevant – current–voltage (I–V) curves are studied, intending to find adequate features to recognize mutations. To this end, the normalised deviation of the I–V curve from the origin (NDIV) is also defined. The features of the NDIV seem to provide a clearer picture, being sensitive to the number of point mutations and allowing to characterise the degree of danger of developing the aforementioned diseases.
1 Introduction
DNA is the repository of genetic information in organisms. Each DNA double helix strand consists of a sugar-phosphate backbone connecting bases: purines [adenine (A), guanine (G)] and pyrimidines [thymine (T), cytosine (C)]. A purine (G or A) of one strand is joined with a pyrimidine (C or T) of the other strand via (three or two) hydrogen bonds, respectively. G is normally bonded with C, and A with T, unless a mutation occurs, e.g., a transition (interchange of purines, A ↔ G, or of pyrimidines, C ↔ T) or a transversion (interchange purine ↔ pyrimidine).1–4 The structure of DNA favours the overlap of the electron density of adjacent bases, which, besides stabilising the double helix, creates a nearly one-dimensional π-pathway along which charge transfer and transport are possible. The term transfer implies that a carrier, created (e.g. a hole by oxidation or an extra electron by reduction) or injected at a specific location, moves to more favourable sites, without application of external gradient (e.g. temperature gradient or voltage). The term transport implies the application of an external gradient. In this work, we consider electrodes between which voltage is applied. Experimental studies aiming to understand the properties and mechanisms of charge transfer and transport along DNA span over than two decades.5–7 The most experimentally relevant quantities for charge transfer and transport are the transfer rates and the current–voltage curves, respectively. Charge movement along DNA is usually studied within two main frameworks: (i) incoherent or thermal hopping, (ii) coherent tunnelling or both.8–10 The term tunnelling implies quantum mechanical tunnelling through the sequence. The coherent mechanism is expected to be dominant in the low temperature regime.11 In thermal hopping, the carrier is localized and exchanges energy with the environment, hence it can travel longer than via the coherent mechanism. However, the presence of the two mechanisms is not mutually exclusive.9,12,13 It is probable that long-range hole transfer in DNA proceeds via the incoherent multistep mechanism: a hole moves by hopping between neighbouring sites, but holes could be localized on a single base or spread over a number of bases, especially in sequences containing consecutive homobases.14 In this work, coherent charge transport is studied.Charge transfer and transport through the aromatic base-pair stack depends on the electronic coupling between adjacent bases. Therefore, e.g. distortions15,16 affect charge transfer and transport. Also, deviations in that stacking, e.g., through base modifications, insertions, or protein binding, can be electrically observed. DNA charge transfer and transport has been used to detect changes in DNA, like lesions, mismatches, mutations, binding proteins, protein activity, even reactions under weak magnetic fields.17 Charge transfer and transport properties and long-range oxidation of DNA provide an understanding of its biological role and reveal potential nano-applications, such as nanosensors, nanocircuits, and molecular wires.18–20 In the context of biomedicine, these properties can be used to detect pathogenic mutations at early stage. For example, the pairing of non-complementary bases leads to point mutations which are potentially harmful to the development of organisms (carcinogenesis). Each DNA sequence has a unique electronic signature, which may be useful for identifying a mutant DNA molecule.21,22 Thus, charge transfer and transport can bring valuable information about sequencing. It is expected that these properties can be further employed to design electronic circuits as diagnostic tools.
Considering the above, this work focuses on charge transport along DNA molecules, using the Tight-Binding (TB) method, together with the transfer matrix technique, to solve the time-independent Schrödinger equation and finally obtain I–V curves. We study double-stranded DNA molecules, the ends of which are connected to electrodes, focusing on: (1) both ideal and natural geometries. (2) Two types of mutations: (i) point substitution mutations, specifically, transitions G ↔ A, and (ii) sequences extracted from segments of human chromosomes, modified by expanding the CAG triplet to mimic the following diseases: (a) Huntington's disease, (b) Kennedy's disease, (c) Spinocerebellar ataxia 6, (d) Spinocerebellar ataxia 7. Physical quantities such as eigenspectra, density of states, transmission coefficients, and current–voltage curves are obtained. The parameters used to describe the molecular electronic structure of nucleic acid bases and extract the on-site energies and the interaction integrals used in the recruited TB wire model were obtained from the linear combination of atomic orbitals (LCAO) method, considering the molecular wave function as a linear combination of all valence orbitals of all atoms, i.e., 2s, 2px, 2py, 2pz orbitals for C, N, and O atoms and 1s orbital for H atoms.
The novel features of this work compared to state of the art include the following: (1) Ideal and natural DNA geometries are compared. (2) Known mutations are examined, and mutated sequences, either containing point substitution mutations (G ↔ A transitions) or extracted from human chromosomes and modified by expanding the CAG triplet to mimic diseases, are compared to unmutated ones. (3) The potential use of physical quantities related to charge transport as mutation detectors is investigated. (4) The normalised deviation of the I–V curve from the origin (NDIV), which seems to be a useful quantity for that purpose, is defined.
The rest of this article is organized as follows: Section 2 includes a description of the employed methods; the studied sequences and genetic disorders are listed in Section 3; in Section 4, results for various physical quantities are presented and discussed; finally, Section 5 contains our conclusions and some reflections on perspectives.
2 Methods
TB is an approach to the calculation of the electronic structure of materials which assumes that the systems orbitals are tightly bound at the sites they belong. When the overlap of neighbouring sites' orbitals is small, the system's state can be expressed as a superposition of the states corresponding to isolated sites. The system's eigenspectra are distributed relatively close to the opposite of the ionization energies of isolated sites because the interaction with neighbouring sites is relatively limited. TB is semi-empirical; specifically, two sets of parameters are needed for its application: (a) the on-site energies of the orbitals at each site, and (b) the interaction integrals that quantify the coupling between orbitals belonging to neighbouring sites. Although the terms hopping or transfer integrals or parameters are usually used, the term interaction integral or parameter is generic, not reminiscent of the nature of carrier movement or specific problem. The simplicity of TB makes it appropriate to obtain analytical and numerical results with minimal computational cost, in contrast to ab initio techniques. Additionally, given an appropriate parametrization, TB can handle the effects induced by the variation of DNA sequences, hence any given segment can be treated within TB. On the other hand, ab initio methods such as Density Functional Theory (DFT) and Hartree–Fock Crystal Orbital (HFCO) theory, cannot do so in a straightforward manner, due to computational limitations23 and underlying theoretical assumptions,24,25 respectively.In the present work, the so-called “wire model” variant of the TB method is employed. For double-stranded DNA, the wire model is essentially a description at the base-pair level, i.e., the DNA polymer is considered as a wire, composed of successive base pairs (or monomers). The parameters required for the wire model description are the on-site energies of the base pairs and the interaction integrals between successive base pairs. In order to produce the required on-site energies, the Linear Combination of Atomic Orbitals (LCAO) method was employed, considering the molecular wave function as a linear combination of all valence orbitals, i.e., of the 2s, 2px, 2py, 2pz orbitals for C, N, and O atoms and the 1s orbital for H atoms. A novel parameterization was used, initially introduced in ref. 26. As for the interaction integrals, a Slater–Koster two-centre interaction form27 was employed, using Harrison-type expressions,28,29 with slightly modified factors relative to the original ones.26 These parameters have been calibrated by comparing our LCAO predictions for the ionization and excitation energies of heterocycles with those obtained from the Ionization Potential Equation of Motion Coupled Cluster with Singles and Doubles (IP-EOMCCSD)/aug-cc-pVDZ level of theory and the Completely Renormalized Equation of Motion Coupled Cluster with Singles, Doubles, and non-iterative Triples (CR-EOMCCSD(T))/aug-cc-pVDZ level of theory, respectively (vertical values), as well as with experimental data.30
The problem to be solved, i.e., the time-independent or time-dependent Schrödinger equation of the polymer, is reduced to a system of coupled algebraic equations or differential equations of first order, respectively. For example, the time-independent TB system of equations, from which the eigenenergies, E, are obtained, for a DNA segment within the wire model, reads
| Eψn = Enψn + tn−1,nψn−1 + tn,n+1ψn+1, ∀n = 1, 2, …, N, | (1) |
 | (2) |
 | (3) |
3 Studied sequences and genetic disorders
Genetic disorders occur when a mutation affects an organism's genes or when the organism has the wrong amount of genetic material. Carrying the mutation does not necessarily mean that the organism will end up with a disease. There are many types of disorders, including single-gene, multifactorial and chromosomal ones. This work focuses on single-gene genetic disorders, i.e., changes or mutations that occur in the DNA sequence of a single gene and are otherwise known as monogenetic disorders.Point substitutional mutations are common; the G-T mismatch mutation alone occurs about once in every 104–105 base pairs. Cell viability and health are highly dependent on keeping the mutation rate small. The high fidelity of DNA replication is established and secured by an enzyme, the replicative polymerase, though several mechanisms: (1) sensing proper geometry of the correct base pair, (2) slowing down catalysis in case of a mismatch, and (3) partitioning the mismatched primer to exonuclease active site.31 However, the performance of polymerases is not error-free: it is estimated31–33 that, even after proofreading, the overall fidelity of DNA synthesis lays in the range of one wrong nucleotide incorporated per 103–105. Besides, DNA replication is constantly challenged by internal and external factors, non-canonical DNA structures, and complex DNA sequences.31
Another category of DNA mutations related to several diseases is the short tandem repeat (STR) expansions or microsatellites.34,35 These are small sections of DNA, usually 2–6 nucleotides long, repeated at a defined region. At least 6.77% of the human genome is comprised of these repetitive DNA sequences.35 Large STR expansions are potentially pathogenic, setting the ground for several neurological diseases. In fact, 37 of the already known STR genes that can cause disease when expanded, exhibit primary neurological presentations.35 In neurological STR diseases, ‘CAG’ repeat expansions code for the amino acid glutamine. When expanded, they create polyglutamine tract expansions, which are thought to alter and expand the transcribed protein, creating insoluble protein aggregates within neuronal cells. This can cause perturbations in intracellular homeostasis and cell death.36
Two categories of DNA polymers are examined in this work: (i) sequences that contain point substitution mutations (specifically, transitions involving G ↔ A exchange), of both ideal and natural geometries, replacing the out-of-ring atoms that are different between A and G, while ensuring that the number of hydrogen bonds is correct, and (ii) sequences of ideal geometry extracted from segments of human chromosomes, subsequently modified by a CAG triplet expansion [(CAG)n repeats], to mimic four selected STR diseases, namely, (a) Huntington's disease, (b) Kennedy's disease, (c) Spinocerebellar ataxia 6, (d) Spinocerebellar ataxia 7. The number of pathogenic repeats, i.e., CAG triplets, in Huntington's disease, is np = 36–250, located in exon 1 of HTT gene, chromosome 4.35,37,38 In spinal and bulbar muscular atrophy of Kennedy (Kennedy's disease), np = 38–68, located in exon 1 of AR gene, chromosome X.35,39–41 In spinocerebellar ataxia 6, np = 19–33, located in exon 47 of CACNA1A gene, chromosome 19.35,42,43 In spinocerebellar ataxia 7, np = 34–460, located in exon 1 of ATXN7 gene, chromosome 3.35,44,45
In summary, the protocol to implement mutations in this study is the following: (i) for transitions involving G ↔ A exchange, of both ideal and natural geometries, the out-of-ring atoms that are different between A and G are replaced, while ensuring that the number of hydrogen bonds is correct. (ii) For all diseases with the same triplet motif, (CAG)n, we keep 9 base pairs at the start and 9 base pairs at the other end of the sequence (primers). Of course, primers are different for each disease, but they only contain 18 base pairs altogether, which is not a large number when dealing with a sequence of 180 or 300 base pairs. Of course, the procedure used in the present work could be ameliorated in future studies.
4 Results and discussion
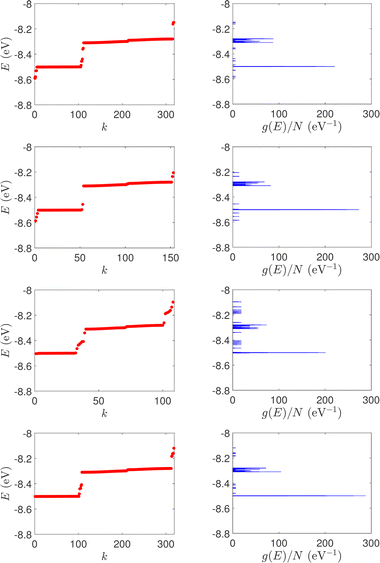
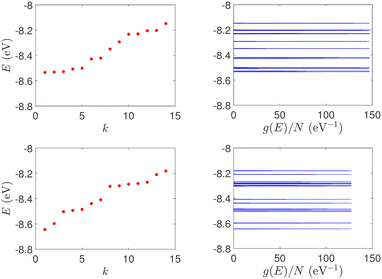
Section 4.1 is devoted to eigenenergies and densities of states, Section 4.2 to transmission coefficients and Section 4.3 to current (I)–voltage (V) curves, where the normalised deviation of the I–V curve from the origin (NDIV) is introduced. In this work, we focus on charge transport through the highest occupied molecular orbitals (HOMOs).For DNA segments of ideal geometry, the base pairs are not distorted; they are separated and twisted by 3.4 Å and 36°, respectively, relative to the double helix growth axis. The geometries of the natural sequences G14 and A15 have been extracted from Bioinformatics (RCSB) Protein Data Bank (https://www.rcsb.org) [accession numbers 4WZW and 6VAA, respectively], from the original ref. 46 and 47, respectively.
The on-site energies and interaction integrals for all sequences were calculated using all valence orbitals of all atoms, according to the procedure described in ref. 26. For ideal sequences, the on-site energies are EA–T = −8.49 eV for the A–T base pair, and EG–C = −8.30 eV for the G–C base pair.26 In Table 1, the energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the two B-DNA base pairs, A–T and G–C, are shown. The bases constituting these base pairs are slightly deformed relative to their geometry in gas phase. Table 1 also contains the HOMO and LUMO energies of these slightly deformed bases. These levels are of π and π* character, unless otherwise stated. The on-site energy of the mismatched A–C base pair was calculated, as well. Its HOMO value is EA–C = −8.43 eV, i.e., very close to the one of the A–T base pair. The HOMO and LUMO interaction integrals between successive base pairs of ideal geometry, without mismatches, calculated with the method described in ref. 26, using all valence orbitals of all atoms, are listed in Table 2. Mutations and distortions change the values of interaction integrals; this effect is included in present work, using the same method.26
| Base or base pair | E H | E L |
|---|---|---|
| A | −8.50 | −4.19 |
| T | −9.12 | −4.30 |
| G | −8.31 | −4.12 |
| −4.43 (σ*) | ||
| C | −8.67 | −4.11 |
| A–T | −8.49 | −4.31 |
| −4.43 (σ*) | ||
| G–C | −8.30 | −4.14 |
| −4.43 (σ*) | ||
| A–C | −8.43 | −4.23 |
| GG, CC | GC | CG |
|---|---|---|
| 116 | 10 | 75 |
| (92(σ*), 2) | (2(σ*), 19) | (1(σ*), 9) |
| AA, TT | AT | TA |
|---|---|---|
| 38 | 50 | 37 |
| (22) | (1) | (2) |
| AG, CT | TG, CA | AC, GT | TC, GA |
|---|---|---|---|
| 37 | 28 | 16 | 142 |
| (11(σ*), 11) | (2(σ*), 9) | (1(σ*), 1) | (3(σ*), 6) |
| GAm | AmG | AmAm |
|---|---|---|
| 130 | 31 | 36 |
| (89(σ*), 8) | (90(σ*), 20) | (90(σ*), 25) |
Observation: the HOMO (LUMO) of a base pair is very close to the highest HOMO (lowest LUMO) of its constituent bases,48cf.Table 1. Hence, studying charge transport through HOMOs within the TB wire model (as done here), it is practically easier to examine purine substitution mutations; given that purines have higher HOMOs than pyrimidines, this substitution has a substantial effect on the base pair on-site energy. This generates an important diagonal disorder to the TB wire model Hamiltonian matrix, in addition to the always-present off-diagonal disorder caused by the modification of interaction parameters.
4.1 Eigenspectra and density of states
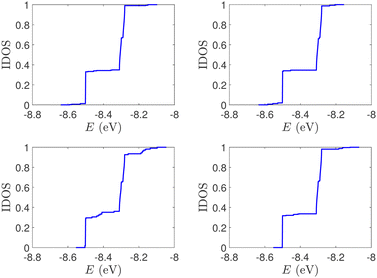
The term eigenspectra is used to describe the whole set of eigenenergies. The eigenspectra of the studied sequences were calculated by numerical diagonalisation of the Hamiltonian matrices, which, within the TB wire model, are real, tridiagonal and symmetric matrices.48,49 A quantity used to describe the energy structure of a given system is the density of states (DOS), which shows the number (NE) of states that can be occupied by electrons per energy (E) interval, namely,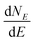 . A useful equivalent definition is
. A useful equivalent definition is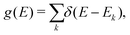 | (4) |
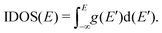 | (5) |
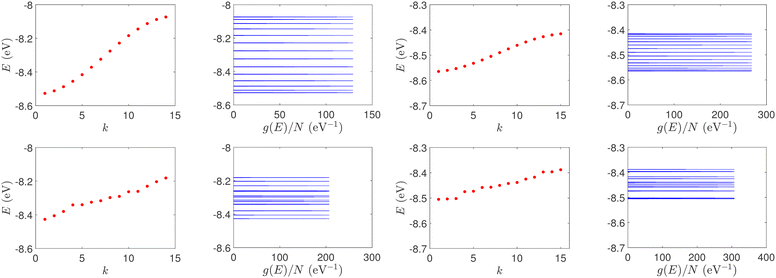 | ||
| Fig. 1 Eigenspectra and DOS of unmutated DNA homopolymers. Upper panels: Ideal, lower panels: natural, left panels: G14, right panels: A15. The geometries of the natural sequences G14 and A15 have been extracted from the Bioinformatics (RCSB) Protein Data Bank (https://www.rcsb.org) [accession numbers 4WZW and 6VAA, respectively] from the original ref. 46 and 47, respectively. k is the eigenenergy index. | ||
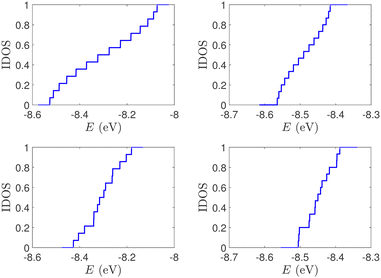 | ||
| Fig. 2 Normalized IDOS of the unmutated DNA sequences depicted in Fig. 1. Upper panels: Ideal, lower panels: natural, left panels: G14, right panels: A15. | ||
(i) Point substitution mutations. The transition G ↔ A occurs by introducing A instead of G in G… polymers: the pyrimidine strand still contains only cytosines, but in the purine strand guanines are replaced by adenines. Hence, the replaced base pairs are A–C, instead of G–C. When such mismatches are introduced, the respective interaction integrals are modified, according the procedure described above, i.e., using the input geometry and LCAO with all valence orbitals of all atoms.26 The eigenspectra and the corresponding DOS for the studied ideal and natural G14 sequences with 7 A–C mismatch mutations, randomly positioned in the sequence, are presented in Fig. 3. The corresponding normalised IDOS can be found in Fig. 4. In other words, the purine strand contains 7 G and 7 A randomly distributed, while the pyrimidine strand still contains 14 C. Comparing Fig. 1 with Fig. 3, it can be observed that, apart from the increased irregularity of the mutated sequences, there is roughly a movement of the mean value of eigenenergies from around EG–C towards around EA–C (cf.Table 1). It can be observed that the number of levels close to EA–C is increased. In particular, the natural mutated sequence displays a high density of levels closer to both EG–C and EA–C. This can also be understood by inspecting the IDOS, i.e., by comparing Fig. 2 with Fig. 4.
 | ||
| Fig. 3 Eigenspectra and DOS of G14 sequences with 7 randomly positioned A–C mismatch mutations. The purine strand contains 7 G and 7 A, distributed randomly, while the pyrimidine strand contains 14 C. Upper panels: Ideal polymers, lower panels: natural polymers. This figure can be compared with the left part of Fig. 1. | ||
 | ||
| Fig. 4 Normalized IDOS of G14 sequences with 7 randomly positioned A–C mismatch mutations. The purine strand contains 7 G and 7 A, distributed randomly, while the pyrimidine strand contains 14 C. Left panel: Ideal polymer, right panel: natural polymer. This figure can be compared with the left part of Fig. 2. | ||
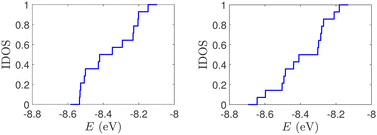
(ii) Short tandem repeat (STR) expansions. Four important cases of STR expansions are examined: (a) Huntington's disease, (b) Kennedy's disease, (c) Spinocerebellar ataxia 6, (d) Spinocerebellar ataxia 7. The complete sequences, including primers,50 used in these examples are: (a) Huntington's disease: AAGTCCTTC(CAG)100CAACAGCCG, (b) Kennedy's disease: CTGCTGCTG(CAG)45CAAGAGACT, (c) Spinocerebellar ataxia 6: GGGCCCCCG(CAG)30GCGGTGGCC, (d) Spinocerebellar ataxia 7: GCCGCCCGG(CAG)100CCGCCGCCT. The eigenspectra and corresponding DOS for the studied sequences with STR expansion mutations are presented in Fig. 5. Two subbands occur around the on-site energies, EG–C = −8.30 eV and EA–T = −8.49 eV, in addition to scattered features, due to the presence of primers. The corresponding normalised IDOS can be found in Fig. 6.
4.2 Transmission coefficient
Charge transport properties are studied under the assumption that the DNA sequences of interest lie on sites n = 1, 2, …, N, and are connected with two semi-infinite homogeneous metallic electrodes (leads), acting as carrier baths, which lie on sites (−∞, 0] ∪ [N + 1, +∞). The leads are described by properly chosen on-site energies and interaction parameters. In this work, left and right electrodes are assumed to be identical. The electrodes energy spectrum is given by the dispersion relation51E = Em + 2tm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(qa), where Em is the on-site energy of the electrodes, tm is the interaction integral between the electrodes sites, and a is the lattice constant. The electrodes' band lies in the energy interval [Em − 2|tm|, Em + 2|tm|]. Hence, the energy center and bandwidth of the electrodes are Em and 4|tm|, respectively. It should be noted that the nature of the mobile charges (holes or electrons) depends upon factors such as the availability of states, their filling, and the alignment to the Fermi levels of the leads.52 Here, the nature of the leads is not specified. However, we use HOMO levels, and it is assumed that Em is either equal to EG–C or EA–T: for ideal or natural G…, Em = EG–C; for ideal or natural A…, Em = EA–T; for G… sequences containing A–C mutations, Em = EG–C; for diseases, the value Em = EG–C is still used. If the lead is modelled as a homogeneous system with one electron per site, then the band is half-filled, the electrodes are metallic, and the Fermi level of the electrodes, EFm, is identified with the on-site energy of the electrodes, Em. In this article, the value |tm| = 0.5 eV is assumed, so that the leads' bandwidth contains all the eigenstates of the studied sequences; cf., Fig. 1–6.
cos(qa), where Em is the on-site energy of the electrodes, tm is the interaction integral between the electrodes sites, and a is the lattice constant. The electrodes' band lies in the energy interval [Em − 2|tm|, Em + 2|tm|]. Hence, the energy center and bandwidth of the electrodes are Em and 4|tm|, respectively. It should be noted that the nature of the mobile charges (holes or electrons) depends upon factors such as the availability of states, their filling, and the alignment to the Fermi levels of the leads.52 Here, the nature of the leads is not specified. However, we use HOMO levels, and it is assumed that Em is either equal to EG–C or EA–T: for ideal or natural G…, Em = EG–C; for ideal or natural A…, Em = EA–T; for G… sequences containing A–C mutations, Em = EG–C; for diseases, the value Em = EG–C is still used. If the lead is modelled as a homogeneous system with one electron per site, then the band is half-filled, the electrodes are metallic, and the Fermi level of the electrodes, EFm, is identified with the on-site energy of the electrodes, Em. In this article, the value |tm| = 0.5 eV is assumed, so that the leads' bandwidth contains all the eigenstates of the studied sequences; cf., Fig. 1–6.
The details of the lead-DNA interface are rather complex;11 the coupling of the sequence with the edge electrode sites is described by the effective interaction integrals tcL(R). The choice of appropriate parameters is important, since the quality of the contact plays a crucial role in charge transport;53 in fact, it defines the optimum transport profile.11,54 For periodic sequences, the coupling strength 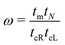 and coupling asymmetry
and coupling asymmetry 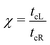 have been defined previously.54 The ideal coupling condition, which is definable only in periodic cases, is |ω| = 1. The symmetric coupling condition is |χ| = 1. In periodic cases, the ideal and symmetric coupling condition, ω = 1 = χ, leads to the most enhanced transmission.54 Here, tcL and tcR are chosen from the ideal and symmetric coupling conditions of periodic cases of ideal homopolymers, G… and A…, i.e., when dealing with G… or A…, tN is chosen as equal either to tGG = 0.116 eV or to tAA = 0.038 eV, according to our TB parametrization.26 This procedure results in tcL = tcR = 0.24 eV for G… and 0.14 eV for A…. In natural homopolymers G…, the value tcL = tcR = 0.24 eV is still used. In natural homopolymers A…, the value tcL = tcR = 0.14 eV is still used. For A–C mismatches in G… as well as for diseases, the value tcL = tcR = 0.24 eV is still used.
have been defined previously.54 The ideal coupling condition, which is definable only in periodic cases, is |ω| = 1. The symmetric coupling condition is |χ| = 1. In periodic cases, the ideal and symmetric coupling condition, ω = 1 = χ, leads to the most enhanced transmission.54 Here, tcL and tcR are chosen from the ideal and symmetric coupling conditions of periodic cases of ideal homopolymers, G… and A…, i.e., when dealing with G… or A…, tN is chosen as equal either to tGG = 0.116 eV or to tAA = 0.038 eV, according to our TB parametrization.26 This procedure results in tcL = tcR = 0.24 eV for G… and 0.14 eV for A…. In natural homopolymers G…, the value tcL = tcR = 0.24 eV is still used. In natural homopolymers A…, the value tcL = tcR = 0.14 eV is still used. For A–C mismatches in G… as well as for diseases, the value tcL = tcR = 0.24 eV is still used.
The transmission coefficient at zero bias, T(E), is a useful quantity for the description of charge transport properties; it refers to the probability that a carrier transmits through the sequence's eigenstates. To compute T(E), a transfer matrix formalism51,54,55 is used. After some manipulations, the analytical form of T(E) can be expressed as:51
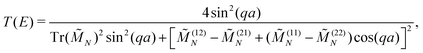 | (6) |
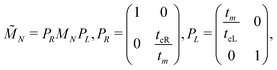 | (7) |
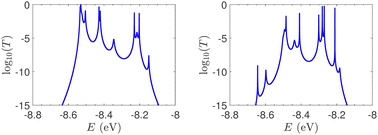
T(E) for the studied ideal and natural unmutated DNA sequences, G14 and A15, are presented in Fig. 7. In ideal periodic segments, it is expected from theory54 that full transmission (T(E) = 1) occurs at specific energies, at least N − 1 in number. This is actually the case in the upper panels of Fig. 7 (not all peaks are seen clearly at this scale). Natural sequences have a significantly less symmetric profile, and significantly reduced overall transmission, as expected, since in this case neither the on-site energies nor the interaction integrals are identical, i.e., in natural homopolymers, both diagonal and off-diagonal disorder are present.
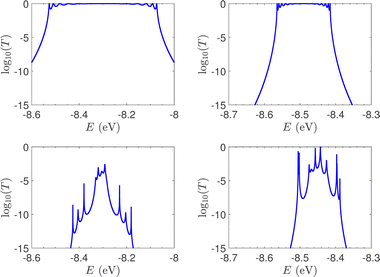 | ||
| Fig. 7 The log10(T(E)) of the studied unmutated DNA sequences. Upper panels: Ideal polymers. There are N − 1 peaks with full transmission (left) and N peaks with full transmission (right). Theory54 guarantees at least N − 1 peaks. Lower panels: Natural polymers. Left: G14, right: A15. | ||
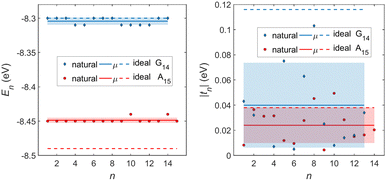
In Fig. 8, the on-site energies (left) and absolute values of the interaction integrals (right) are depicted, together with their mean values, μ, and standard deviations, σ, for the natural G14 and A15 sequences whose transmission is shown in the lower panels of Fig. 7. The corresponding values of ideal sequences are also shown, for reference. The mean values and standard deviations (μ, σ) of the on-site energies, which account for diagonal disorder, are ≈(−8.304 eV, 0.005 eV) for G14 and (−8.449 eV, 0.004 eV) for A15, while, those of the magnitude of the interaction integrals, which account for off-diagonal disorder, are (0.040 eV, 0.034 eV) for G14 (0.024 eV, 0.014 eV) for A15. In terms of coefficients of variation, 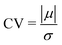 , diagonal disorder is small and of comparable magnitude between G14 and A15, i.e., ≈0.06% and 0.05%, respectively. On the other hand, off-diagonal disorder is much larger, i.e., ≈85.00% and 58.33%, respectively. Clearly, off-diagonal disorder is more pronounced in G14. This explains qualitatively the smaller transmission peaks G14 displays compared to A15 (cf., bottom panels of Fig. 7). Notice that |tn| was used to assess the off-diagonal disorder, since the spectrum of tridiagonal, irreducible, real, symmetric matrices (as all matrices studied here are, within the wire model) does not depend on the signs of their off-diagonal entries.56
, diagonal disorder is small and of comparable magnitude between G14 and A15, i.e., ≈0.06% and 0.05%, respectively. On the other hand, off-diagonal disorder is much larger, i.e., ≈85.00% and 58.33%, respectively. Clearly, off-diagonal disorder is more pronounced in G14. This explains qualitatively the smaller transmission peaks G14 displays compared to A15 (cf., bottom panels of Fig. 7). Notice that |tn| was used to assess the off-diagonal disorder, since the spectrum of tridiagonal, irreducible, real, symmetric matrices (as all matrices studied here are, within the wire model) does not depend on the signs of their off-diagonal entries.56
 | ||
| Fig. 8 TB parameters for the natural G14 and A15 polymers whose transmission is shown in the lower panels of Fig. 7. Left: On-site energies, En. Right: Absolute values of interaction parameters, |tn|. Blue (G14) diamonds and red (A15) circles represent the values of the parameters at each site, continuous lines their mean values, μ, and shaded areas include the region μ ± σ, where σ is the standard deviation. The values of parameters for ideal polymers are shown in dashed lines, for reference. | ||
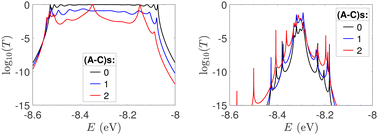
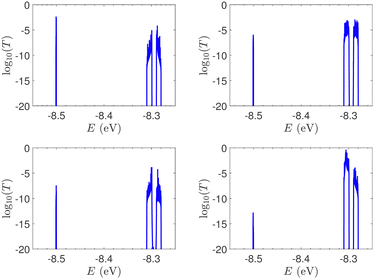
In Fig. 9, the effect of including zero, one, and two A–C mismatches, randomly distributed in the sequence, is shown, for ideal and natural G14 segments. Transmission coefficients, T(E), are depicted in log-scale. The randomly positioned mismatches are placed at the same sites for both ideal and natural sequences. [log10(T(E)) for zero A–C mismatch mutations is also shown in the left panels of Fig. 7.] The values of 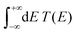 (which act as a measure of the overall transmission) for the three ideal cases are: 0.3856 eV, 0.0430 eV, and 0.0237 eV for 0, 1, and 2 (A–C) mismatches, respectively. Hence, in ideal cases, inclusion of more mismatches decreases transmission, because the sequence homogeneity – in terms of on-site energies and interaction integrals – is deteriorated. On the other hand, for the three natural cases, the values of the integrals are 1.0651 × 10−5 eV, 3.0247 × 10−4 eV, and 2.2113 × 10−4 eV, respectively. However, a natural sequence with no mismatches, is already inhomogeneous; there is no homogeneity to be lost by inserting (A–C) mismatches, since the sequences are already disordered. Therefore, it is difficult to characterize natural sequences based only upon T(E).
(which act as a measure of the overall transmission) for the three ideal cases are: 0.3856 eV, 0.0430 eV, and 0.0237 eV for 0, 1, and 2 (A–C) mismatches, respectively. Hence, in ideal cases, inclusion of more mismatches decreases transmission, because the sequence homogeneity – in terms of on-site energies and interaction integrals – is deteriorated. On the other hand, for the three natural cases, the values of the integrals are 1.0651 × 10−5 eV, 3.0247 × 10−4 eV, and 2.2113 × 10−4 eV, respectively. However, a natural sequence with no mismatches, is already inhomogeneous; there is no homogeneity to be lost by inserting (A–C) mismatches, since the sequences are already disordered. Therefore, it is difficult to characterize natural sequences based only upon T(E).
T(E) for ideal and natural G14 sequences with seven randomly positioned A–C mismatch mutations are presented in Fig. 10. Fig. 10 can therefore be compared with the left column of Fig. 7. When seven mutations are included, i.e., 50% of the total number of monomers, the polymer becomes a random binary sequence. The influence of the inclusion of A–C monomers can be observed; there are some lightly conducting states closer to EA–C; cf., Table 1. However, since Em is aligned with EG–C, this effect is small.
T(E) for the studied DNA sequences of ideal geometries with STR expansion mutations are presented in Fig. 11. As their DOS suggest (cf.Fig. 5), these sequences display narrow regions close to EG–C and EA–T within which transmission is allowed. The relative contribution of each region, as well as the overall transmission profile, are different for each sequence, allowing for distinct current–voltage curves, as it is shown below.
4.3 Current–voltage curves
The I–V curves of the DNA sequences have been calculated using the Landauer–Büttiker formalism.57–59 A constant bias voltage was applied, Vb, between the leads, which induces a linear potential energy drop, Ub = −eVb, from one to the other edge of the DNA sequence. Thus, the transmission coefficient becomes bias-dependent. The leads' chemical potential takes the form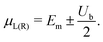 | (8) |
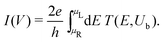 | (9) |
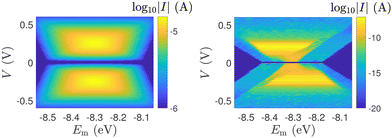
In Fig. 12, the absolute value of the current in logarithmic scale, log10|I|, is demonstrated as a function of both the leads on-site energy, Em, and the applied voltage between the leads, V, for both ideal (left) and natural (right) G14 polymers. It is evident that the electrode's on-site energy plays a crucial role in the shape and magnitude of the current–voltage curves. A general trend for homopolymers is that larger currents occur when Em is closer to the monomer's on-site energy. The I–V curves of the studied ideal and natural unmutated DNA sequences are shown in Fig. 13, assuming Em = EG–C for G14 and Em = EA–T for A15. The left panels of Fig. 13 are a subset of Fig. 12, for Em = EG–C = −8.3 eV.
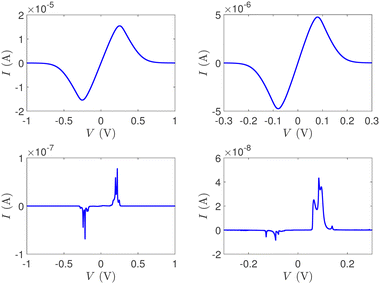 | ||
| Fig. 13 The I–V curves of the studied unmutated DNA sequences. Upper: Ideal polymers, lower: natural polymers, left: G14 (with Em = EG–C), right: A15 (with Em = EA–T). | ||
The order of magnitude of the I–V curves and their shape varies dramatically when many mutations are included. Hence, another physical magnitude that could be used to characterise the I–V curves was devised; this is the normalised deviation of the I–V from the origin, defined as
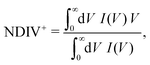 | (10) |
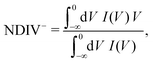 | (11) |
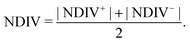 | (12) |
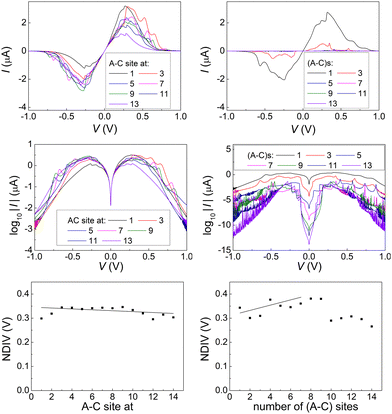
Fig. 14 and 15 display I–V related diagrams of the studied ideal and natural G14 DNA sequences, respectively, with one A–C mismatch mutation of varying position (left columns) and with varying number of randomly distributed A–C mismatch mutations (right columns). The rows contain the I–V curves, the log10|I| − V curves (i.e., in logarithmic |I| scale), and the newly introduced quantity, i.e., the normalised deviation of the I–V from the origin, NDIV. It can be seen that, for ideal segments, generally the I–V curves do not vary significantly with the position of a single A–C mismatch in the sequence (≈half an order of magnitude); for natural segments, the position of the mismatch affects the current more significantly (some orders of magnitude). The variation of the I–V curves becomes much more significant with increasing the number of A–C mismatches (many orders of magnitude). As a particular example, the I–V curves of the studied ideal (left) and natural (right) DNA sequences with 7 randomly positioned A–C mismatch mutations, are presented in Fig. 16.
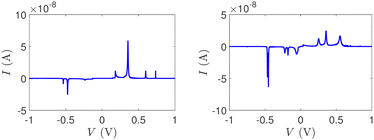 | ||
| Fig. 16 The I–V curves of the studied DNA sequences, initially G14, but with 7 A–C mismatch mutations, randomly inserted in the sequence. Left: Ideal polymers, right: natural polymers. | ||
In ideal sequences with one A–C mismatch of varying position, the NDIV remains almost constant; its slope versus the A–C site position is close to zero. Hence, the NDIV is insensitive to the position of a point substitution mutation. However, in ideal sequences with increasing number of A–C mismatch mutations, the NDIV does not remain constant; its slope versus the number of A–C mismatch mutations is positive, until the number of (A–C)s becomes equal to the number of (G–C)s. After that point, the number of (A–C)s becomes larger than the number of (G–C)s, i.e., mutations become dominant, and a further increase of the number of (A–C)s stabilises the NDIV. Hence, the NDIV is sensitive to the increase of the number of point substitution mutations. In natural sequences, the situation is similar, but with pronounced slopes, especially when an increasing number of A–C mismatch mutations is introduced. Therefore, the NDIV is a useful quantity to characterise these sequences.
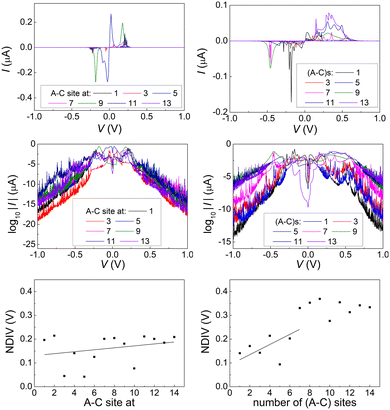
In Fig. 17 and 18, the I–V related diagrams of the studied DNA sequences (ideal geometry) with STR expansion mutations are presented. For all studied cases, changes in the I–V curves become more pronounced with increasing the number of STR expansion mutations (i.e., the number of CAG repeats). The respective NDIV display significant but almost monotonous variations, and can, therefore, be used to evaluate the number of (CAG) repeats in a sequence. This behaviour of the NDIV versus the number of CAG repeats suggests that it can be used to characterise the grade of danger for developing the studied diseases.
5 Conclusion and perspectives
The present work focused on to the effect of two types of mutations [(i) point substitution transitions, particularly guanine ↔ adenine, and (ii) cytosine–adenine–guanine triplet expansions], on the charge transport properties of DNA sequences. The following physical quantities were studied: eigenspectra, density of states, transmission coefficients, current–voltage curves. Both ideal (textbook geometry) and natural (naturally distorted, geometry from databases) sequences were considered. A tight-binding wire model was recruited for charge transport, in conjunction with a transfer matrix technique. However, the on-site energies and interaction parameters for that TB wire model were obtained by another TB LCAO utilizing all valence orbitals, capable of treating any given geometry. Our results point to the following conclusions:(1) All the aforementioned physical quantities possess interesting features that allow to distinguish between mutated and unmutated sequences.
(2) However, the most experimentally relevant quantities are the I–V curves. Their characteristics are significantly altered when mutations are introduced, and conclusions cannot be drawn in a straightforward manner.
(3) Since both the order of magnitude and the shape of the I–V curves varies when mutations are introduced, another physical quantity to characterise the I–V curves was introduced. i.e., the normalised deviation of the I–V from the origin (NDIV).
(4) In ideal sequences with one A–C mismatch of varying position, the NDIV remains almost constant: its slope versus the mismatch position is close to zero.
(5) In ideal sequences with increasing number of A–C mismatch mutations, the NDIV does not remain constant: its slope versus the number of A–C mismatch mutations is positive, until the number of (A–C)s becomes equal to the number of (G–C)s. After that point, since the number of (A–C)s becomes larger than the number of (G–C)s, a further increase of the number of (A–C)s stabilises the situation, as expected.
(6) In natural sequences, the NDIV is similar but with pronounced slopes, especially when an increasing number of A–C mismatch mutations is introduced. Hence, NDIV is a useful quantity to characterise these sequences.
(7) Although dramatic changes in the I–V curves occur for all studied cases of STR expansions, as the number of CAG repeats increases, NDIV shows significant but almost monotonous variation, and can, therefore, be used to evaluate the number of (CAG) repeats in the sequence. Therefore, the NDIV can be used to characterise the grade of danger for developing the studied diseases.
(8) Overall, the NDIV is generally insensitive to the position of a point mutation, but rather sensitive to the number of point mutations and STR expansion mutations.
The recruitment of specific natural geometries in this work for type (i) sequences does not imply their association with the studied diseases i.e. with type (ii) sequences. These geometries were used to demonstrate the expected differences between the electrical behaviour of ideal and distorted conformations. However, it should be noted that the TB protocol with all valence orbitals used here26 can be easily employed to sequences of arbitrary geometry.
Transitions with C ↔ T exchange have not been included in this work, because their effects could not be properly grasped within the wire model. These mutations could be studied within the extended ladder model,48i.e. a TB description at the single-base level; this will be hopefully done in the future.
Transitions are more likely than transversions (purine ↔ pyrimidine interchange), because it is easier to substitute a single ring by another single ring than a double ring for a single ring or vice versa. Hence, careful geometry optimization is necessary to study transversions. This will also be hopefully done in the future.
Another category of mutations is germline mutations,60i.e. a gene change in a reproductive cell that becomes incorporated into the DNA of every cell in the body of the offspring. This way, the mutation can be passed from parent to offspring, and is, therefore, hereditary. This could be also the subject of a future study.
The vibrational and large-scale dynamical flexibility of DNA has not been taken into account in this work. However, the presented methodology could be applied in a straightforward manner on top of snapshots extracted by Molecular Dynamics simulations.16 This could be another future perspective.
All diseases studied here have the same triplet motif, i.e., (CAG)n, between 9 base pairs at the start and 9 base pairs at the other end of the sequence (primers). Of course, primers are different for each disease, but they only contain 18 base pairs altogether, which is not a large number when dealing with a sequence of 180 or 300 base pairs. Under these conditions, it is not safe to draw direct conclusions regarding the identity of the disease. This issue could be possibly tackled by including larger primers, which would produce much more distinctive DOS or IDOS features and allow for sequence recognition. However, this exceeds the scope of the present study, which has the aim to demonstrate the possibility of mutation detection using the TB model. The treatment discussed above could be included in a future work.
Another perspective would be to consider, e.g., a 300 base-pair sequence and change both the number of repetitions n and the length of primers, while keeping the number of total base pairs (e.g., 300) constant. This is a different perspective that will hopefully be included in a future work. Such an alternative perspective has been previously adopted to study the Huntington's disease within a TB model, but off-diagonal disorder (the fact that interaction integrals are not identical) was not taken into account.61
Finally, a general comment: the interplay between periodicity and aperiodicity in biology62 is a vast area of extreme interest to us; novel methods must be devised to explore it.
Author contributions
Conceptualization, C. S.; methodology, C. S., K. L., M. M.; software, M. M., K. L.; validation, C. S., K. L., M. M.; formal analysis, M. M., K. L.; investigation, C. S., M. M., K. L.; resources, C. S., M. M., K. L.; data curation, M. M.; writing – original draft preparation, M. M.; writing – review and editing, C. S., K. L., M. M.; visualization, M. M., K. L.; supervision, C. S.; project administration, C. S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Georgia Thodi of Laboratory of Prenatal and Neonatal Screening, Neoscreen Ltd, Athens, Greece, for providing information about the sequences utilized in this work. M. Mantela wishes to thank the State Scholarships Foundation (IKY): This research is co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning” in the context of the project “Strengthening Human Resources Research Potential via Doctorate Research” (MIS-5000432), implemented by the State Scholarships Foundation (IKY).References
- Z. Yang and A. D. Yoder, J. Mol. Evol., 1999, 48, 274–283 CrossRef CAS PubMed.
- I. Keller, D. Bensasson and R. A. Nichols, PLoS Genet., 2007, 3, 1–7 CrossRef PubMed.
- A. Stoltzfus and R. W. Norris, Mol. Biol. Evol., 2015, 33, 595–602 CrossRef PubMed.
- D. M. Lyons and A. S. Lauring, Mol. Biol. Evol., 2017, 34, 3205–3215 CrossRef CAS PubMed.
- D. Porath, A. Bezryadin, S. de Vries and C. Dekker, Nature, 2000, 403, 635–638 CrossRef CAS PubMed.
- J. C. Genereux and J. K. Barton, Chem. Rev., 2010, 110, 1642–1662 CrossRef CAS PubMed.
- K. L. Jiménez Monroy, N. Renaud, J. Drijkoningen, D. Cortens, K. Schouteden, C. van Haesendonck, W. J. Guedens, J. V. Manca, L. D. A. Siebbeles, F. C. Grozema and P. H. Wagner, J. Phys. Chem. A, 2017, 121, 1182–1188 CrossRef PubMed.
- D. Rawtani, B. Kuntmal and Y. Agrawal, Front. Life Sci., 2016, 9, 214–225 CrossRef CAS.
- B. Giese, J. Amaudrut, A.-K. Köhler, M. Spormann and S. Wessely, Nature, 2001, 412, 318–320 CrossRef CAS PubMed.
- A. Landi, A. Capobianco and A. Peluso, J. Phys. Chem. Lett., 2020, 11, 7769–7775 CrossRef CAS PubMed.
- E. Maciá, F. Triozon and S. Roche, Phys. Rev. B, 2005, 71, 113106 CrossRef.
- M. Bixon, B. Giese, S. Wessely, T. Langenbacher, M. E. Michel-Beyerle and J. Jortner, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11713–11716 CrossRef CAS PubMed.
- L. Xiang, J. L. Palma, C. Bruot, V. Mujica, M. A. Ratner and N. Tao, Nat. Chem., 2015, 7, 221–226 CrossRef CAS PubMed.
- A. Capobianco, T. Caruso, A. M. D'Ursi, S. Fusco, A. Masi, M. Scrima, C. Chatgilialoglu and A. Peluso, J. Phys. Chem. B, 2015, 119, 5462–5466 CrossRef CAS PubMed.
- A. Capobianco, A. Velardo and A. Peluso, J. Phys. Chem. B, 2018, 122, 7978–7989 CrossRef CAS PubMed.
- M. Mantela, A. Morphis, K. Lambropoulos, C. Simserides and R. Di Felice, J. Phys. Chem. B, 2021, 125, 3986–4003 CrossRef CAS PubMed.
- T. J. Zwang, E. C. M. Tse and J. K. Barton, ACS Chem. Biol., 2018, 13, 1799–1809 CrossRef CAS PubMed.
- F. D. Lewis and M. R. Wasielewski, Pure Appl. Chem., 2013, 85, 1379–1387 CrossRef CAS.
- C. H. Wohlgamuth, M. A. McWilliams and J. D. Slinker, Anal. Chem., 2013, 85, 8634–8640 CrossRef CAS PubMed.
- R. G. Endres, D. L. Cox and R. R. P. Singh, Rev. Mod. Phys., 2004, 76, 195–214 CrossRef CAS.
- S. R. Rajski, B. A. Jackson and J. K. Barton, Mutat. Res., 2000, 447, 49–72 CrossRef CAS PubMed.
- C.-T. Shih, Y.-Y. Cheng, S. A. Wells, C.-L. Hsu and R. A. Römer, Comput. Phys. Commun., 2011, 182, 36–38 CrossRef CAS.
- Y. Liu, X. Ren and L. He, J. Chem. Phys., 2019, 151, 215102 CrossRef PubMed.
- A. Bende, F. Bogár and J. Ladik, Solid State Commun., 2011, 151, 301–305 CrossRef CAS.
- F. Bogár, A. Bende and J. Ladik, Phys. Lett. A, 2014, 378, 2157–2162 CrossRef.
- M. Mantela, C. Simserides and R. Di Felice, Materials, 2021, 14, 4930 CrossRef CAS PubMed.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524 CrossRef CAS.
- W. A. Harrison, Electronic Structure and the Properties of Solids: the Physics of the Chemical Bond, Dover, New York, 2nd edn, 1989 Search PubMed.
- W. A. Harrison, Elementary Electronic Structure, World Scientific, River Edge, NJ, 1999 Search PubMed.
- M. Mantela, A. Morphis, M. Tassi and C. Simserides, Mol. Phys., 2016, 114, 709–718 CrossRef CAS.
- A. Bebenek and I. Ziuzia-Graczyk, Curr. Genet., 2018, 64, 985–996 CrossRef CAS PubMed.
- T. A. Kunkel and K. Bebenek, Annu. Rev. Biochem., 2000, 69, 497–529 CrossRef CAS PubMed.
- A. K. Showalter and M.-D. Tsai, Biochemistry, 2002, 41, 10571–10576 CrossRef CAS PubMed.
- H. Dashnow, M. Lek, B. Phipson, A. Halman, S. Sadedin, A. Lonsdale, M. Davis, P. Lamont, J. S. Clayton, N. G. Laing, D. G. MacArthur and A. Oshlack, Genome Biol., 2018, 19, 121 CrossRef PubMed.
- S. R. Chintalaphani, S. S. Pineda, I. W. Deveson and K. R. Kumar, Acta Neuropathol. Commun., 2021, 9, 98 CrossRef PubMed.
- I. H. Kratter and S. Finkbeiner, Neuron, 2010, 67, 897–899 CrossRef CAS PubMed.
- M. E. MacDonald, C. M. Ambrose, M. P. Duyao, R. H. Myers, C. Lin, L. Srinidhi, G. Barnes, S. A. Taylor, M. James, N. Groot, H. MacFarlane, B. Jenkins, M. A. Anderson, N. S. Wexler, J. F. Gusella, G. P. Bates, S. Baxendale, H. Hummerich, S. Kirby, M. North, S. Youngman, R. Mott, G. Zehetner, Z. Sedlacek, A. Poustka, A.-M. Frischauf, H. Lehrach, A. J. Buckler, D. Church, L. Doucette-Stamm, M. C. O'Donovan, L. Riba-Ramirez, M. Shah, V. P. Stanton, S. A. Strobel, K. M. Draths, J. L. Wales, P. Dervan, D. E. Housman, M. Altherr, R. Shiang, L. Thompson, T. Fielder, J. J. Wasmuth, D. Tagle, J. Valdes, L. Elmer, M. Allard, L. Castilla, M. Swaroop, K. Blanchard, F. S. Collins, R. Snell, T. Holloway, K. Gillespie, N. Datson, D. Shaw and P. S. Harper, Cell, 1993, 72, 971–983 CrossRef PubMed.
- P. McColgan and S. J. Tabrizi, Eur. J. Neurol., 2018, 25, 24–34 CrossRef CAS PubMed.
- P. Fratta, T. Collins, S. Pemble, S. Nethisinghe, A. Devoy, P. Giunti, M. G. Sweeney, M. G. Hanna and E. M. Fisher, Neurobiol. Aging, 2014, 35, 443.e1–443.e3 CrossRef CAS PubMed.
- G. Kuhlenbäumer, W. Kress, E. B. Ringelstein and F. Stögbauer, J. Neurol., 2001, 248, 23–26 CrossRef PubMed.
- A. R. L. Spada, E. M. Wilson, D. B. Lubahn, A. E. Harding and K. H. Fischbeck, Nature, 1991, 352, 77–79 CrossRef PubMed.
- J. Sequeiros, S. Seneca and J. Martindale, Eur. J. Hum. Genet., 2010, 18, 1188–1195 Search PubMed.
- O. Zhuchenko, J. Bailey, P. Bonnen, T. Ashizawa, D. W. Stockton, C. Amos, W. B. Dobyns, S. H. Subramony, H. Y. Zoghbi and C. C. Lee, Nat. Genet., 1997, 15, 62–69 CrossRef CAS PubMed.
- C. Cagnoli, G. Stevanin, C. Michielotto, G. Gerbino Promis, A. Brussino, P. Pappi, A. Durr, E. Dragone, M. Viemont, C. Gellera, A. Brice, N. Migone and A. Brusco, J. Mol. Diagn., 2006, 8, 128–132 CrossRef CAS PubMed.
- G. David, N. Abbas, G. Stevanin, A. Dürr, G. Yvert, G. Cancel, C. Weber, G. Imbert, F. Saudou, E. Antoniou, H. Drabkin, R. Gemmill, P. Giunti, A. Benomar, N. Wood, M. Ruberg, Y. Agid, J.-L. Mandel and A. Brice, Nat. Genet., 1997, 17, 65–70 CrossRef CAS PubMed.
- C. Qiu, K. L. McCann, R. N. Wine, S. J. Baserga and T. M. T. Hall, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18554–18559 CrossRef CAS PubMed.
- R. Wang, S. Wang, A. Dhar, C. Peralta and N. P. Pavletich, Nature, 2020, 580, 278–282 CrossRef CAS PubMed.
- K. Lambropoulos, M. Chatzieleftheriou, A. Morphis, K. Kaklamanis, R. Lopp, M. Theodorakou, M. Tassi and C. Simserides, Phys. Rev. E, 2016, 94, 062403 CrossRef CAS PubMed.
- K. Lambropoulos, M. Chatzieleftheriou, A. Morphis, K. Kaklamanis, M. Theodorakou and C. Simserides, Phys. Rev. E, 2015, 92, 032725 CrossRef CAS PubMed.
- N. H. G. R. Institute, Primers, https://www.genome.gov/genetics-glossary/Primer, A primer, as related to genomics, is a short single-stranded DNA fragment used in certain laboratory techniques, such as the polymerase chain reaction (PCR). In the PCR method, a pair of primers hybridizes with the sample DNA and defines the region that will be amplified, resulting in millions and millions of copies in a very short timeframe, Primers are also used in DNA sequencing and other experimental processes.
- K. Lambropoulos and C. Simserides, Phys. Rev. E, 2019, 99, 032415 CrossRef CAS PubMed.
- D. Porath, G. Cuniberti and R. Di Felice, in Charge Transport in DNA-Based Devices, ed. G. Schuster, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 183–228 Search PubMed.
- E. Macia Barber, Aperiodic Structures in Condensed Matter: Fundamentals and Applications, CRC Press, 1st edn, 2008 Search PubMed.
- K. Lambropoulos and C. Simserides, J. Phys. Commun., 2018, 2, 035013 CrossRef.
- K. Lambropoulos and C. Simserides, Phys. Chem. Chem. Phys., 2017, 19, 26890–26897 RSC.
- M. Mantela, K. Lambropoulos, M. Theodorakou and C. Simserides, Materials, 2019, 12, 2177 CrossRef CAS PubMed.
- R. Landauer, IBM J. Res. Dev., 1957, 1, 223–231 Search PubMed.
- M. Buttiker, IBM J. Res. Dev., 1988, 32, 317–334 Search PubMed.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, 1995 Search PubMed.
- G. Thodi, F. Fostira, R. Sandaltzopoulos, G. Nasioulas, A. Grivas, I. Boukovinas, M. Mylonaki, C. Panopoulos, M. B. Magic, G. Fountzilas and D. Yannoukakos, BMC Cancer, 2010, 10, 544 CrossRef CAS PubMed.
- R. G. Sarmento, R. N. O. Silva, M. P. Madeira, N. F. Frazao, J. O. Sousa and A. Macedo-Filho, Braz. J. Phys., 2018, 48, 155–159 CrossRef CAS.
- E. Maciá, J. Phys.: Condens. Matter, 2022, 34, 123001 CrossRef PubMed.
| This journal is © the Owner Societies 2023 |