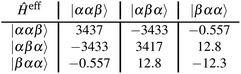Open Access Article
Open Access ArticleCalculation of exchange couplings in the electronically excited state of molecular three-spin systems†
Michael
Franz
 a,
Frank
Neese
b and
Sabine
Richert
a,
Frank
Neese
b and
Sabine
Richert
 *a
*a
aInstitute of Physical Chemistry, University of Freiburg, Albertstraße 21, 79104 Freiburg, Germany. E-mail: sabine.richert@physchem.uni-freiburg.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany
First published on 19th September 2022
Abstract
Photogenerated molecular three-spin systems, composed of a chromophore and a covalently bound stable radical, are promising candidates for applications in the field of molecular spintronics. Through excitation with light, an excited doublet state and a quartet state are generated, whereby their energy difference depends on the exchange interaction JTR between the chromophore triplet state (T) and the stable radical (R). In order to establish design rules for new materials to be used in molecular spintronics devices, it is of great importance to gain knowledge on the magnitude of JTR as well as the factors influencing JTR on a molecular level. Here, we present a robust and reliable computational method to determine excited state exchange couplings in three-electron-three-centre systems based on a CASSCF/QD-NEVPT2 approach. The methodology is benchmarked and then applied to a series of molecules composed of a perylene chromophore covalently linked to various stable radicals. We calculate the phenomenological exchange interaction JTR between chromophore and radical, which can be compared directly to the experiment, but also illustrate how the individual exchange interactions Jij can be extracted using an effective Hamiltonian that corresponds to the Heisenberg–Dirac–Van-Vleck Hamiltonian. The latter procedure enables a more detailed analysis of the contributions to the exchange interaction JTR and yields additional insight that will be invaluable for future design optimisation.
1 Introduction
Molecular spintronics is an emerging interdisciplinary research field that has attracted an increasing amount of attention in recent years since it may allow the development of nanoscale devices with improved performance or new functionalities.1–3 One of the greatest challenges in the field is to find new materials that have suitable properties to enable an efficient generation, transport and storage of spin information.Molecular systems are promising since modern synthesis allows molecules to be tailored with atomic precision. Furthermore, molecular systems have sharply defined electronic states, the manipulation of which could bring functionalities which are not necessarily accessible in the case of solids.4–6 If the desired properties for a possible application are known, suitable molecular systems can thus be developed. However, in order to establish design guidelines for the development of such materials, it is important to know how the material's properties can be influenced, specifically the exchange interaction between spin centres.
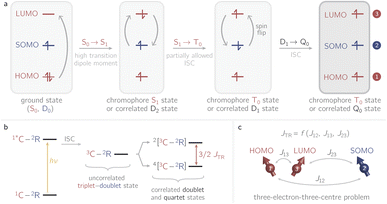
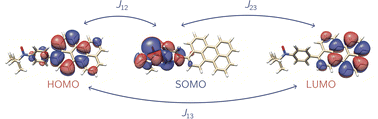
Recently it has been shown that photogenerated molecular three-spin systems, composed of an organic chromophore covalently linked to a stable radical, may be ideal candidates to explore the factors governing spin communication on a molecular level.6–9 The photophysical processes taking place in these systems after light excitation are summarised in Fig. 1.
The chromophore is excited to its first excited singlet state S1 by absorption of light. This transition corresponds to the HOMO–LUMO transition of the chromophore and exhibits a high transition dipole moment. In the presence of the radical, the triplet ground state T0 of the chromophore may then be generated by radical-enhanced intersystem crossing (EISC).10 The requirement for this partially allowed transition is the formation of a correlated doublet state between the chromophore and the stable radical, rather than the coexistence of two isolated systems with different spin multiplicities. The chromophore S1 → T0 transition can then be seen as a D2 → D1 transition, which is spin-allowed. Finally, the Q0 state can be generated by intersystem crossing from the D1 state.11–14
If the exchange interaction JTR between the chromophore triplet and the radical doublet surpasses all other magnetic interactions in the system significantly, the molecular system is said to be in the strong coupling regime.13,14 Depending on the sign of JTR, the quartet state Q0 may be lower in energy than the excited doublet state D1 and vice versa. The energetic order of the doublet and quartet states (sign of JTR) as well as the magnitude of JTR will determine the magnetic properties of the system and therefore its suitability for different applications. Consequently, to guide the design of these highly modular molecular three-spin systems, detailed knowledge of the factors governing the interaction between the triplet and radical spin centres will be essential.
Experimentally, the excited state exchange interaction in such systems is frequently difficult to determine. Transient electron paramagnetic resonance (EPR) spectroscopy can be used for this purpose, but a reliable value for JTR can only be obtained as long as JTR is smaller or of the same order of magnitude as other magnetic interactions in the system.15,16 Once the strong coupling regime is reached, where pure quartet and doublet states are formed, the magnitude of JTR has no influence any more on the shape of the transient EPR spectrum and only a lower bound for JTR is obtained. Experimental data is thus only available for a small subset of the hitherto investigated systems and it seems natural to take recourse to computational methods that allow systematic studies on the properties of these materials to be performed.
In this work, we present a robust computational method for the prediction of the exchange interactions JTR in photoexcited chromophore−radical systems. The approach, based on a CASSCF/NEVPT2 calculation, is generally applicable for any three-spin system and suitable for molecules up to a size of about 250 atoms.
The methodology is applied to a series of perylenes covalently attached to different stable radicals and the trends in JTR are carefully analysed. Further, we illustrate how the phenomenological exchange interaction JTR can be decomposed into three individual exchange interactions Jij (cf.Fig. 1) by using an effective Hamiltonian that corresponds to the Heisenberg–Dirac–Van-Vleck Hamiltonian.17,18 This approach enables a more detailed analysis of the factors influencing the magnetic properties of such systems and will be used as a predictive tool to establish guidelines for the optimisation of the design of molecular three-spin systems. Our results further indicate that most of the perylene−radical systems are antiferromagnetically coupled and that the symmetry of the magnetic orbitals is likely to be one of the main factors determining the sign of JTR.
2 Theory
There are different approaches to calculate the exchange interactions. One of the most popular approaches is broken symmetry DFT, which is a single-determinant method.19–22 The exchange coupling constants are estimated by only using the energy of the high spin determinant and the energy of the broken symmetry determinant. If the Yamaguchi approach is applied, also the expectation value of the total spin 〈S2〉 is required.23The disadvantage of this method is that an appropriate functional has to be found for a specific problem in order to compute reliable results, which makes this method unsystematic.24 In addition, the BS-DFT method delivers unphysical spin densities that require projection methods to be used before physical observables can be calculated.25
Unfortunately, not every system can be benchmarked, since it is frequently not possible to determine the exchange interactions experimentally. As such, BS-DFT can only be applied to electronic ground states, or a limited number of excited states that would not face variational collapse during the self-consistent field optimisation. TD-DFT does not alleviate the problem, since it cannot deal with complex spin couplings. However, it is noteworthy that a certain subset of open shell states can be addressed by the spin-flip TD-DFT method.26,27
Hence, the calculation of exchange interactions is most rigorously addressed theoretical by using genuinely multi-determinantal methods to calculate the ground- and possibly also excited states.18
Commonly used methods of this type include the CASSCF (complete active space self-consistent field) and CASCI (complete active space configuration interaction) methods.18,28–33 Both methods have in common that the orbitals are divided into three sub-classes: the internal orbitals, which are occupied exactly twice, the external orbitals, which are not occupied, and the active orbitals, which can have any occupation number between zero and two. In the subspace of the active orbitals, a full configuration interaction is carried out, yielding a qualitatively correct wavefunction if the active space is properly chosen.
If quantitatively accurate results are required, it is necessary to also account for dynamic electron correlation. Very precise values for the exchange interactions can for instance be achieved with multi-reference configuration interaction (MRCI) methods such as DDCI (difference dedicated configuration interaction) or broken symmetry coupled cluster (BS-CC) methods.24,32,34 However, since the computational effort is very high, MRCI or CC methods can only be applied to very small molecules. Furthermore, MRCI methods are subject to size-consistency errors, which have a strong influence on the calculated exchange interactions for any larger systems.35–37
An alternative to the mentioned approaches are multi-reference perturbation theory methods such as NEVPT2 (n-electron valence state perturbation theory)38,39 or CASPT2 (complete active space perturbation theory),40 which are less computationally expensive but underestimate the exchange interactions by 60–80% with a minimal active space in comparison to multi-reference CI methods such as DDCI3.41 Nevertheless, multi-reference perturbation theory methods provide part of the dynamic electron correlation, which leads to better results than a simple CASCI or a CASSCF calculation.18,24,42 However, based on the analysis of Calzado, Malrieu and co-workers, it is to be expected that a number of physical effects that are relevant for the correct description of exchange couplings will only occur at higher orders of perturbation theory.43,44
2.1 Choice of the molecules and method
The motivation for this study was the determination of the excited state exchange couplings in a series of perylene-based molecules as shown in Fig. 2. In this series, perylene is covalently bound to seven different radicals, which are commonly used in experimental studies on molecular three-spin systems.45–54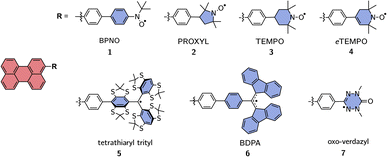 | ||
| Fig. 2 Investigated series of perylene derivatives covalently linked to various, commonly used, stable radicals. | ||
The goal was to determine the influence of the nature of the radical on the magnitude of the exchange interaction(s) and to verify whether systematic trends can be identified.
Perylene was chosen as a representative example for a choromophore since its photophysics is well-known, it is highly photostable and can be substituted easily following established protocols.55 With regard to the computational effort, perylene-based systems are relatively easy to calculate due to the small size and rigidity of the chromophore, which is convenient when wanting to compare a large number of molecules. We also examined a second series of molecules, which contains only perylene–BPNO and perylene–BDPA structures, but with linkers of different lengths. This second series is shown in the ESI† and allows us to comment on the influence of the linker length on JTR.
In order to find a suitable computational procedure, we started by calculating the exchange interaction JTR for two previously investigated perylene diimide (PDI) derivatives, which are linked to BPNO radicals,48 using different approaches, including restricted open-shell CIS (ROCIS) and CASSCF with and without a QD-NEVPT2 correction. The structures are shown in Fig. 3 and only differ with respect to the orientation of the BPNO substituent attached to the imide position of PDI (meta vs. para). Experimentally, a change in sign of JTR between the para- and meta structures is suggested, inferred from an inverted spin polarisation of the central line (mS = +1/2 ↔ −1/2 transition) in the transient EPR spectra of the formed quartet states.13,48 Since quartet state formation was observed, also a lower bound for JTR of ∼0.4 cm−1 can be given, assuming that JTR is about ten times larger than the zero-field-splitting of a PDI triplet state of ∼1100 MHz.56,57
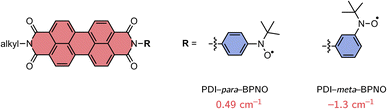 | ||
| Fig. 3 Structures of the perylene diimide derivatives used for benchmarking and calculated values of JTR using CASSCF/QD-NEVPT2. | ||
For the comparison of the different computational approaches, the structures were optimised at the B3LYP/def2-TZVP level of theory.58–60 We used the quasi-restricted orbitals from DFT calculations for the active space selection in CASSCF calculations, whereby the active space was defined by the chromophore HOMO/LUMO, and the radical SOMO. For the CASSCF/QD-NEVPT2 and ROCIS calculations the def2-TZVP basis set was used. Further computational details are given below.
The experimentally observed sign and change in sign of JTR between the para- and meta structures could be reproduced with the CASSCF/QD-NEVPT2 calculation, showing that the results using this method are qualitatively correct. The ROCIS calculations were judged less reliable since they predicted a ferromagnetic coupling for both structures. Using CASSCF/QD-NEVPT2, a JTR value of 0.49 cm−1 was calculated for PDI–para–BPNO, while for PDI–meta–BPNO a value of −1.3 cm−1 was obtained.
Unfortunately, it is more difficult to judge the agreement regarding the calculated magnitude of JTR, since no accurate experimental reference values are available. In the above-mentioned experimental study, |JTR| was estimated to be larger than 3 cm−1 for both the meta and para compounds based on structural comparisons with a number of different biradical compounds for which J could be determined.48 Assuming that this estimate is correct, this would imply that the CASSCF/QD-NEVPT2 calculation underestimates JTR by roughly a factor of six which is in line with theoretical studies predicting an underestimation of the exchange coupling by up to an order of magnitude.41
Although JTR is underestimated, the correct prediction of the sign, sign change and trend is highly promising. In addition, any higher-level methods (e.g. MRCI) that could likely yield more accurate results would be computationally unfeasible for molecules of the considered size. Consequently, we settled on the use of CASSCF/(quasi-degenerate)-NEVPT2 for the calculation of the exchange interactions in the perylene series (cf.Fig. 2).61 The individual exchange interactions can then be extracted from the ab intio Hamiltonian in the subspace of neutral determinants. The exact procedure is discussed in the following.
2.2 Decomposition of the phenomenological exchange interaction JTR
The magnetic interactions in a quantum mechanical system can be described by the Heisenberg–Dirac–Van-Vleck Hamiltonian:62–64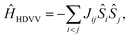 | (1) |
| ĤHDVV = −J12Ŝ1Ŝ2 − J23Ŝ2Ŝ3 − J13Ŝ1Ŝ3. | (2) |
Applying the three-electron-three-centre HDVV-Hamiltonian on the neutral determinants, the Hamiltonian can be written in its matrix representation as follows:17
Diagonalisation gives the eigenvectors, which are the |Q0〉, |D1〉 and |D2〉 states (with mS = 1/2), and the eigenvalues, which are the energies of these states.17
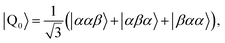 | (3) |
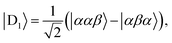 | (4) |
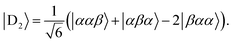 | (5) |
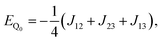 | (6) |
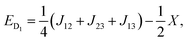 | (7) |
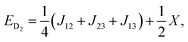 | (8) |
| X = (J212 + J213 + J223 − J12J13 − J12J23 − J13J23)1/2. | (9) |
As can be seen from eqn (6–8), there are only two linearly independent energy differences, which are defined by three independent constants. As a consequence, it is not possible to calculate the J-couplings only by the energy differences of the eigenstates without any further assumptions. But assumptions could be made on the basis of the structure/symmetry.17
Assuming that the exchange interaction between the HOMO-electron of the chromophore and the electron of the stable radical J12 equals the exchange interaction between the LUMO-electron of the chromophore and the electron of the stable radical J23, one can define:
| JTR = J12 = J23. | (10) |
If J13 ≥ JTR, then the energy difference between the states Q0 and D1 can be expressed as:
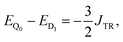 | (11) |
| E(S) − E(S − 1) = −J·S. | (12) |
Unfortunately, these assumptions are not necessarily fulfilled and could lead to a erroneous description of JTR. Instead we will define JTR as:
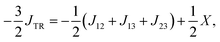 | (13) |
In order to extract the individual exchange interactions, an effective ab initio Hamiltonian has to be constructed that corresponds directly to the HDVV-Hamiltonian. Using this approach, one has to project the target states onto a model space, which consists of the neutral determinants |ααβ〉, |αβα〉 and |βαα〉. Then, the projected wavefunctions need to be orthonormalised, such that an effective Hamiltonian can be constructed with the obtained orthonormal wavefunctions.17,18,65
From the ab initio calculation, the states φi and the corresponding energies Ei are obtained using the Schrödinger equation within the Born–Oppenheimer approximation:
| Ĥφi = Eiφi. | (14) |
Then, the target states φi need to be projected onto the model space S using the projection operator ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) S, which is defined as:
S, which is defined as:
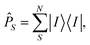 | (15) |
Application of the projection operator on the target states φi gives the projected states φS,i:
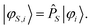 | (16) |
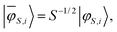 | (17) |
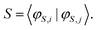 | (18) |
With the orthonormal basis at hand, the matrix elements of the effective Hamiltonian are calculated using:
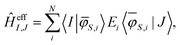 | (19) |
Now, the matrix elements of the obtained effective Hamiltonian can be compared directly with the HDVV-Hamiltonian, which allows for the estimation of J12, J13, and J23. The quality of the effective ab initio Hamiltonian can be verified by estimating the shift of the single diagonal elements compared to the diagonal elements of the model Hamiltonian. If the shift remains constant between the single diagonal elements, the Hamiltonian model describes the investigated system well.
3 Computational details
All structures were optimised at the B3LYP/def2-SVP level of theory.58,59,67 The structures shown in Fig. 2, except for the tetrathiaryl trityl compound and the BDPA compound, were also optimised at the B3LYP/def2-TZVP level of theory,60 in order to estimate the influence of the quality of the structure on the exchange interactions.After every geometry optimisation, a frequency calculation was carried out to verify that the optimisation converged to the ground state structure. All optimisations were carried out using the Gaussian 16 program.68
For the selection of the active space, a TD-DFT calculation with the RIJCOSX approximation was performed for every structure at the CAM-B3LYP/def2-TZVP level of theory using the ORCA 5.0.3 program.69,70 Using the results from the TD-DFT calculation, the orbitals defining the three-electron-three-centre problem were determined. We considered the energetically lowest possible transition, which shows the strongest transition dipole moment. Typically, this excited state is composed of transitions within the HOMO/LUMO orbitals of the chromophore and the SOMO of the stable radical and is related to the HOMO–LUMO transition of the chromophore. The photophysical mechanism on which the selection of the active orbitals is based is also illustrated in Fig. 1.
For the calculation of the excited states, which were used to construct the effective Hamiltonian, we carried out a state averaged CASSCF(3,3) calculation with a QD-NEVPT2 calculation on top, in order to account for dynamic electron correlation. The calculations were sped up by the RI-JK approximation for the coulomb and exchange integrals.71 As starting orbitals we used the orbitals obtained from the TD-DFT calculation. The optimised active orbitals were localised by a Foster-Boys localisation,72 which allows for an easier interpretation of the excited states. All excited state calculations were also performed using the ORCA 5.0.3 program.
Regarding the choice of the active space, we would like to point out here, that, in studying such systems, it is important to first understand the nature of the low-lying excited states by carefully assessing their orbital contributions. Initially, this may involve a limited amount of trial and error. However, once the relevant orbitals for the state of interest have been established, we are of the school of thought that the smallest active space that leads to a qualitatively correct description of these states is the preferred one.
4 Results and discussion
In this section, we will first focus on the phenomenological exchange coupling constant JTR of eqn (13), the value of which can be obtained almost directly from the ab initio calculation.We will then consider the individual exchange interactions J12, J13, and J23 extracted from the effective Hamiltonian, which corresponds to the HDVV-Hamiltonian. The methodology is presented taking the perylene–BPNO radical as an example. The individual exchange interactions of the remaining compounds of our series can be found in the ESI†.
4.1 Calculation of JTR
Fig. 4 shows the calculated exchange couplings JTR for all compounds of the series. The values are shown for the optimisation performed using the def2-SVP basis set. The calculations on the structures optimised using a larger basis set (def2-TZVP) provide very comparable results for all structures. With the exception of the perylene–TEMPO compound, a slightly smaller absolute value is predicted for JTR using def2-TZVP. The corresponding values can be found in the ESI†.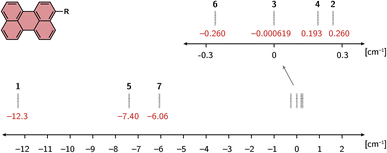 | ||
| Fig. 4 Calculated exchange interactions JTR for all molecules of the perylene series, optimised using the def2-SVP basis set. | ||
As can be seen from Fig. 4, a relatively strong dependence of the exchange interaction on the radical type is predicted. The absolute values of the computed exchange interaction |JTR| range from close to zero (e.g.perylene–TEMPO) to >10 cm−1 for perylene–BPNO. Most perylene−radical systems are antiferromagnetically coupled. Only the perylene–proxyl system and the perylene–eTEMPO system are ferromagnetically coupled. Interestingly, both of these radicals are asymmetric towards the chromophore−radical bonding axis, which is not the case for the remaining antiferromagnetically coupled compounds. This suggests that the symmetry of the magnetic orbitals might be crucial for the resulting sign (and magnitude) of the exchange interaction JTR. Compared to the influence of symmetry, the extent of electron delocalisation appears to play a minor role when visually comparing the tetrathiaryl compound and the BDPA compound, or the proxyl compound and the TEMPO compound.
As shown in the ESI,† a dependence on the linker length can also be observed, whereby a larger linker length causes a reduction in the exchange interaction. This trend is to be expected from the exponential distance dependence of exchange interactions since the main effect of a longer linker will be the increase in distance between the interacting spin centres. An exception would only occur here if the radical electron were also delocalised over the linker, which is conceivable, since the energy difference between the linker HOMO and the radical SOMO decreases with increasing linker length, making the mixing of these orbitals more likely.
4.2 Extraction of the individual exchange interactions
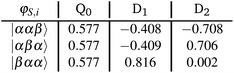
In order to better understand the rather large differences in magnitude and sign of the calculated exchange interactions JTR within the perylene series and to be able to interpret them in a meaningful way, it is advisable to consider the individual contributions to JTR. We will illustrate the procedure using the perylene–BPNO system as an example.First, the target states of the ab initio calculation will be projected onto the subspace of the neutral determinants and normalised (see also section 5 in the ESI† for additional details and an excerpt of the corresponding output file). We obtain:
The projected target states are not necessarily orthogonal, consequently a Löwdin orthogonalisation is applied on these states using eqn (17). The states are then renormalised, which gives the orthonormalised states:
The quality of the orthonormalisation can be verified by simply calculating the overlap matrix S. The off-diagonal elements of S should ideally be zero, or at least close to zero.
For the calculation of the effective ab initio Hamiltonian, we need to consider the calculated energies of the target states, whereby we will set the energy of the Q0 state to zero.
Using the coefficients of the target states and their energies, the effective Hamiltonian can be constructed according to eqn (19), which can also be represented as:
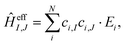 | (20) |
All values are given in cm−1. Now the individual exchange couplings can be extracted from this effective Hamiltonian, since it has a one-to-one correspondence to the Heisenberg–Dirac–Van-Vleck Hamiltonian. The following exchange couplings are obtained:
It should again be mentioned, that the subscripts refer to the predefined spin centres. Fig. 5 shows a visualisation of the corresponding localised spin centres. In the case of the perylene–BPNO system, the size of the individual exchange interactions can be explained by such a visualisation of the spin centres in a relatively straightforward manner. Electrons from spin centres that are closer together show a larger exchange interaction compared to those that are farther away. By visual analysis of the orbitals, without numerical considerations, it can be stated that J12 will likely be larger in magnitude than J23. The interpretation of the sign of the individual exchange interactions, on the other hand, is more difficult. However, as already noted above, the sign is likely to depend on the symmetry of the individual spin centres.
We would like to emphasise here, that the orbitals shown in Fig. 5 are their localised representations. In order to ensure a consistent assignment of the spin centres for all molecules in our series, the spin centres were not assigned according to their occupancy number but according to their orbital compositions, which allows for a better comparison.
The advantage of the decomposition method is that we are now in a position that allows us to better analyse and understand the different contributions to the exchange interaction JTR, their individual importance and how we can modify them, if necessary. If J13 ≥ JTR, then we can approximately express JTR as the average of J12 and J23:
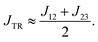 | (21) |
As a consequence, if we want to modify the exchange interaction JTR, we have to focus mainly on J12 and J23. In order for the exchange interaction JTR to become minimal, J12 and J23 must either trivially approach zero or they must cancel each other out. However, in order for the exchange interaction JTR to be maximised, J12 and J23 must either have the same sign or one of the two exchange interactions must be significantly larger. The latter can presumably be achieved by lowering the molecular symmetry, e.g. by appropriate asymmetric substitution.
5 Conclusions
To our knowledge, this is the first study dealing with the problem of calculating the exchange interaction JTR in the excited state of molecular three-spin systems, which turned out not to be an easy task. For example, the frequently used broken symmetry DFT method would fail on such systems, since they cannot be sufficiently described with a single ground state determinant. Furthermore, high-level methods as for example the DDCI3 method are only feasible for very small structures and therefore not applicable for the molecules investigated here. We have found a robust method that is relatively fast and easy to apply while providing reliable trends for the exchange interaction in excited triplet−doublet systems.We could show that most of the investigated excited perylene−radical systems are predicted to be antiferromagnetically coupled, whereby asymmetric chromophore−radical systems (regarding the chromophore−radical bonding axis) exhibit a ferromagnetic coupling. By extracting the individual exchange couplings using an effective Hamiltonian that corresponds to the Heisenberg–Dirac–Van-Vleck Hamiltonian, we could analyse the phenomenological exchange interaction JTR in more detail. We showed that the exchange interaction JTR can be expressed as the average of the two chromophore–radical exchange interactions (J12 and J23). As a consequence, any future optimisation of JTR should mainly focus on controlling these two contributions.
Future investigations in our group will focus on the decomposition of the individual exchange couplings, which are still effective parameters. From this decomposition we will get valuable information on the direct exchange and the kinetic exchange contributions,18,43,73 which is needed in order to understand the signs of the individual exchange interactions. Further, we will examine the symmetry of the magnetic orbitals and its influence on the exchange interactions.
Data availability
The data supporting the findings of this study are available within the article and in the ESI†.Author contributions
Quantum chemical calculations, investigation, methodology, formal analysis, data validation and visualisation, original draft writing, review and editing M. F.; Supervision, review and editing of the manuscript F. N.; Conceptualisation, project administration, funding acquisition, supervision, original draft writing, review and editing S. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) − Project number 417643975 (S. R.). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster). F. N. would like to thank the Max Planck society for financial support.Notes and references
- M. Shiraishi and T. Ikoma, Phys. E, 2011, 43, 1295–1317 CrossRef.
- A. R. Rocha, V. M. Garcia-Suarez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335–339 CrossRef CAS.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- A. Cornia and P. Seneor, Nat. Mater., 2017, 16, 505–506 CrossRef CAS PubMed.
- S. J. van der Molen, R. Naaman, E. Scheer, J. B. Neaton, A. Nitzan, D. Natelson, N. Tao, H. van der Zant, M. Mayor and M. Ruben, et al. , Nat. Nanotechnol., 2013, 8, 385–389 CrossRef.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson III, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Feedman and D. D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed.
- M. Mayländer, S. Chen, E. R. Lorenzo, M. R. Wasielewski and S. Richert, J. Am. Chem. Soc., 2021, 143, 7050–7058 CrossRef.
- S. M. Harvey and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 15508–15529 CrossRef CAS PubMed.
- A. L. Buchachenko and V. L. Berdinsky, Chem. Rev., 2002, 102, 603–612 CrossRef CAS PubMed.
- Y. Teki, Chem.–Eur. J., 2020, 26, 980–996 CrossRef CAS PubMed.
- K. Ishii, J. Fujisawa, A. Adachi, S. Yamauchi and N. Kobayashi, J. Am. Chem. Soc., 1998, 120, 3152–3158 CrossRef CAS.
- Y. Kandrashkin and A. van der Est, Chem. Phys. Lett., 2003, 379, 574–580 CrossRef CAS.
- Y. E. Kandrashkin and A. van der Est, J. Chem. Phys., 2004, 120, 4790–4799 CrossRef CAS.
- M. S. Asano, K. Ishizuka and Y. Kaizu, Mol. Phys., 2006, 104, 1609–1618 CrossRef CAS.
- H. Moons, E. Goovaerts, V. P. Gubskaya, I. A. Nuretdinov, C. Corvaja and L. Franco, Phys. Chem. Chem. Phys., 2011, 13, 3942–3951 RSC.
- D. Reta, I. P. R. de Moreira and F. Illas, J. Chem. Theory Comput., 2016, 12, 3228–3235 CrossRef CAS PubMed.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. De Graaf and N. Guihery, Chem. Rev., 2014, 114, 429–492 CrossRef PubMed.
- R. Caballol, O. Castell, F. Illas, I. P. R. de Moreira and J.-P. Malrieu, J. Phys. Chem. A, 1997, 101, 7860–7866 CrossRef.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef.
- F. Neese, J. Phys. Chem. Solids, 2004, 65, 781–785 CrossRef.
- K. Yamaguchi, H. Fukui and T. Fueno, Chem. Lett., 1986, 4, 625–628 CrossRef.
- G. Singh, S. Gamboa, M. Orio, D. A. Pantazis and M. Roemelt, Theor. Chem. Acc., 2021, 140, 1–15 Search PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef.
- Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- T. Steenbock, L. L. M. Rybakowski, D. Benner, C. Herrmann and G. Bester, J. Chem. Theory Comput., 2022, 18, 4708–4718 CrossRef CAS PubMed.
- E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS.
- K. Fink, R. Fink and V. Staemmler, Inorg. Chem., 1994, 33, 6219–6229 CrossRef CAS.
- A. Lunghi and F. Totti, Inorganics, 2016, 4, 28 CrossRef.
- M. Nishino, S. Yamanaka, Y. Yoshioka and K. Yamaguchi, J. Phys. Chem. A, 1997, 101, 705–712 CrossRef.
- O. Castell and R. Caballol, Inorg. Chem., 1999, 38, 668–673 CrossRef.
- J.-B. Rota, C. J. Calzado, C. Train and V. Robert, J. Chem. Phys., 2010, 132, 154702 CrossRef PubMed.
- J. Cabrero, C. de Graaf, E. Bordas, R. Caballol and J.-P. Malrieu, Chem.–Eur. J., 2003, 9, 2307–2315 CrossRef.
- E. R. Davidson and D. W. Silver, Chem. Phys. Lett., 1977, 52, 403–406 CrossRef.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef.
- E. R. Davidson, in The World of Quantum Chemistry, ed. R. Daudel and B. Pullman, Reidel, Dordrecht, 1974, pp. 17–30 Search PubMed.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef.
- K. Anderson and B. O. Roos, in Modern Electronic Structure Theory, ed. D. Yarkony, World Scientific, Singapore, 1995, pp. 55–109 Search PubMed.
- M. Spivak, C. Angeli, C. J. Calzado and C. de Graaf, J. Comput. Chem., 2014, 35, 1665–1671 CrossRef PubMed.
- C. de Graaf, C. Sousa, I. P. R. de Moreira and F. Illas, J. Phys. Chem. A, 2001, 105, 11371–11378 CrossRef.
- C. J. Calzado, J. Cabrero, J.-P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 2728–2747 CrossRef.
- C. J. Calzado, J. Cabrero, J.-P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 3985–4000 CrossRef.
- M. T. Colvin, A. L. Smeigh, E. M. Giacobbe, S. M. M. Conron, A. B. Ricks and M. R. Wasielewski, J. Phys. Chem. A, 2011, 115, 7538–7549 CrossRef PubMed.
- O. Nolden, N. Fleck, E. R. Lorenzo, M. R. Wasielewski, O. Schiemann, P. Gilch and S. Richert, Chem.–Eur. J., 2021, 27, 2683–2691 CrossRef.
- M. Mayländer, P. Gilch, M. R. Wasielewski, Y. Qiu, L. Bancroft, S. Richert, M. Franz, O. Nolden and S. Chen, Chem. Sci., 2022, 13, 6732–6743 RSC.
- E. M. Giacobbe, Q. Mi, M. T. Colvin, B. Cohen, C. Ramanan, A. M. Scott, S. Yeganeh, T. J. Marks, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2009, 131, 3700–3712 CrossRef.
- K. Katayama, M. Hirotsu, I. Kinoshita and Y. Teki, Dalton Trans., 2012, 41, 13465–13473 RSC.
- Y. Teki, M. Nakatsuji and Y. Miura, Mol. Phys., 2002, 100, 1385–1394 CrossRef.
- M. Imran, M. Taddei, A. A. Sukhanov, L. Bussotti, W. Ni, P. Foggi, G. G. Gurzadyan, J. Zhao, M. Di Donato and V. K. Voronkova, ChemPhysChem, 2022, 23, e202100912 CrossRef PubMed.
- S. Takeuchi, K. Ishii and N. Kobayashi, J. Phys. Chem. A, 2004, 108, 3276–3280 CrossRef.
- M. L. Kirk, D. A. Shultz, P. Hewitt, D. E. Stasiw, J. Chen and A. van der Est, Chem. Sci., 2021, 12, 13704–13710 RSC.
- M. L. Kirk, D. A. Shultz, P. Hewitt, J. Chen and A. van der Est, J. Am. Chem. Soc., 2022, 144, 12781–12788 CrossRef PubMed.
- F. Lewitzka, H. G. Löhmannsröben, M. Strauch and W. Lüttke, J. Photochem. Photobiol., A, 1991, 61, 191–200 CrossRef.
- Z. E. X. Dance, Q. Mi, D. W. McCamant, M. J. Ahrens, M. A. Ratner and M. R. Wasielewski, J. Phys. Chem. B, 2006, 110, 25163–25173 CrossRef PubMed.
- R. Carmieli, T. A. Zeidan, R. F. Kelley, Q. Mi, F. D. Lewis and M. R. Wasielewski, J. Phys. Chem. A, 2009, 113, 4691–4700 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef PubMed.
- W. Heisenberg, Original Scientific Papers/Wissenschaftliche Originalarbeiten, Springer, 1985, pp. 580–597 Search PubMed.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1926, 112, 661–677 Search PubMed.
- J. H. Van Vleck, Theory of Electric and Magnetic Susceptibilities, Clarendon Press, Oxford, 1932 Search PubMed.
- F. Illas, I. P. R. de Moreira, C. De Graaf and V. Barone, Theor. Chem. Acc., 2000, 104, 265–272 Search PubMed.
- J. Des Cloizeaux, Nucl. Phys., 1960, 20, 321–346 CrossRef.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2022, e1606 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef.
- C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470 CrossRef PubMed.
- S. F. Boys, Rev. Mod. Phys., 1960, 32, 296 CrossRef CAS.
- F. Neese, L. Lang and V. G. Chilkuri, in Topology, Entanglement, and Strong Correlations. Modeling and Simulation, ed. E. Pavarini and E. Koch, Forschungszentrum Jülich, Jülich, 2020, vol. 10, ch. 4 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc04701b |
| This journal is © The Royal Society of Chemistry 2022 |