Open Access Article
Open Access ArticleOrganic radicals with inversion of SOMO and HOMO energies and potential applications in optoelectronics
Sitthichok
Kasemthaveechok
 a,
Laura
Abella
a,
Laura
Abella
 b,
Jeanne
Crassous
b,
Jeanne
Crassous
 a,
Jochen
Autschbach
a,
Jochen
Autschbach
 *b and
Ludovic
Favereau
*b and
Ludovic
Favereau
 *a
*a
aUniv Rennes, CNRS, ISCR – UMR 6226, F-35000 Rennes, France. E-mail: ludovic.favereau@univ-rennes1.fr
bDepartment of Chemistry, University at Buffalo, State University of New York, Buffalo, New York 14260, USA. E-mail: jochena@buffalo.edu
First published on 8th July 2022
Abstract
Organic radicals possessing an electronic configuration in which the energy of the singly occupied molecular orbital (SOMO) is below the highest doubly occupied molecular orbital (HOMO) level have recently attracted significant interest, both theoretically and experimentally. The peculiar orbital energetics of these SOMO–HOMO inversion (SHI) organic radicals set their electronic properties apart from the more common situation where the SOMO is the highest occupied orbital of the system. This review gives a general perspective on SHI, with key fundamental aspects regarding the electronic and structural factors that govern this particular electronic configuration in organic radicals. Selected examples of reported compounds with SHI are highlighted to establish molecular guidelines for designing this type of radical, and to showcase the potential of SHI radicals in organic spintronics as well as for the development of more stable luminescent radicals for OLED applications.
Introduction
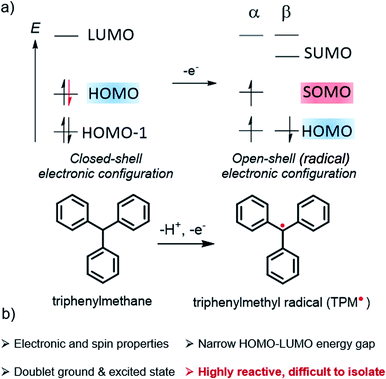
Organic radicals form a particular class of materials exhibiting an open-shell electronic structure with one or more unpaired electrons (Fig. 1). Radical compounds are often considered as highly sensitive, and they usually react quickly via dimerization, hydrogen abstraction, or other degradation mechanisms. With the continuous development of organic chemistry and the deeper experimental and theoretical understanding of the parameters controlling molecular reactivity, a number of stable or persistent organic open-shell compounds have been isolated and investigated. As a result of their specific (photo-)reactivity, radicals have continued to attract significant interest in chemistry and biochemistry, notably playing a central role in many enzymatic reactions as well as in vivo imaging.1–3 Organic π-conjugated radicals are also the subject of intense research in materials science because of their electron spin, making them innovative alternatives for the basis of next-generation optoelectronics, for instance, in organic field-effect transistors (OFETs),4–6 organic light-emitting diodes (OLEDs), or organic magnets.4,5,7–27 Furthermore, these molecular materials also provide fundamental insights about the nature of chemical bonds and their delocalization in open-shell systems, in addition to their other features such as narrow HOMO–LUMO energy gaps, low-lying doubly-excited states, or redox amphoterism.4,10,12,13,15,28,29In the popular molecular orbital (MO) description of electronic structure, as widely adopted in chemistry and related fields,30 an unpaired electron means the set of MOs includes a singly occupied molecular orbital (SOMO, Fig. 1), that is, an occupied α spin (‘spin-up’ ↑) or β spin (‘spin-down’ ↓) orbital without a matching occupied opposite-spin (β or α) counterpart with the same or very similar spatial behaviour (spatial function). The spatial function is what defines the two-colored isosurface plots seen in research articles and textbooks for depictions of MOs; the SOMO spatial function and the unpaired spin are of course intimately connected to the radical properties.
For the radical in Fig. 1, the α and β spin components of the HOMO are assumed to have matching spatial functions, and are therefore grouped as a spin pair. Likewise, the SOMO and its unoccupied spin counterpart, which we label SUMO for convenience, are assumed to have matching spatial functions, but only one of them is occupied. As drawn, the figure reflects the fact that in spin-unrestricted MO self-consistent field (SCF) calculations, the α and β spin orbitals may have different energies, even if their spatial functions match closely. This is the case, in particular, for the SOMO–SUMO pair.
Since the pioneering works of Thiele and Chichibabin on open-shell hydrocarbons,31–33 significant efforts have been directed toward understanding the structural and electronic factors that may lead to an increased stability of radical systems. When discussing this crucial aspect, it is important to differentiate between the terms stable and persistent for quantifying the reactivity of a radical by using the advice of Ingold, who wrote that34 “[…] the word stable should only be used to describe a radical so persistent and so unreactive to air, moisture, etc., under ambient conditions that the pure radical can be handled and stored in the lab with no more precautions than would be used for the majority of commercially available organic chemicals”. Thus, most long-lived radicals deserve to be labeled persistent, and few rise to the level of stable.
The challenge for chemists is to design organic radicals that are as persistent as possible, to investigate their specific properties in depth, and to take advantage of these properties in optoelectronic and other types of applications. To reach this objective, an old and rather simple approach is to introduce bulky substituents to prevent dimerization or reaction with molecular oxygen, for instance. This strategy is often quite efficient to increase the kinetic stability of a radical compound. Another approach involves the delocalization of the unpaired electron along a molecular backbone, which reduces the accumulation of spin density at certain atoms and tends to increase the overall radical stability. Very recently, Paton et al. proposed a quantitative description of the term stability for radicals based on a combination of thermodynamic and kinetic factors,35 which can be related to the aforementioned delocalization and steric protection approaches, respectively.
In addition to gaining fundamental insight regarding the reactivity of organic radicals, investigations of these species have also furnished a better understanding of how the presence of unpaired electrons influences the optical, electronic and magnetic properties of a molecule. For instance, the ground state of a mono-radical and its lowest excited state, accessible via spin-allowed processes, are of spin-doublet nature,36,37 which can offer new opportunities for optoelectronic applications and especially in OLED technology.14,16,17,38–41 Considered as a curiosity for a long time, this type of luminescence is currently attracting strong interest because doublet radicals do not give rise to dark triplet states, unlike classical fluorescent organic emitters with closed-shell electronic configuration (Fig. 2). Accordingly, radicals offer the potential to reach a theoretical internal quantum efficiency (IQE) of 100% in OLEDs, whereas the IQE is ca. 25% for classical fluorophore compounds. Furthermore, the nanosecond luminescence lifetime of radicals is highly beneficial for display applications, in comparison to the microseconds found for thermally activated delayed fluorescence (TADF) materials.37,42 In the latter process, the reverse intersystem crossing rate, illustrated by the dashed arrow from T1 to S1 in Fig. 2, is low and often competes with non-radiative quenching, causing poor device efficiency at high brightness levels.43
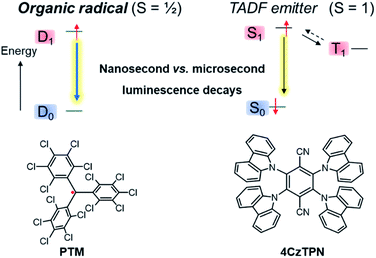 | ||
| Fig. 2 Comparison of the emission process of the organic radical emitter per-chlorotriphenylmethyl PTM (left) and the TADF emitter 2,3,5,6-tetra(9H-carbazol-9-yl)terephthalonitrile, 4CzTPN (right).44 | ||
Beyond mono-radicals, the design of organic molecules containing at least two interacting unpaired electrons, such as diradicals, is of particular interest, because of the multiplicity of the spin states and their energetic ordering, which is related to the strength of the interaction between the unpaired electrons.7,45,46 For example, in the case of a di-radical the stability of the triplet vs. an open-shell singlet spin state becomes important. Different accessible spin states provide a molecular system with switchable magnetic properties, and the possibility of a high-spin ground state,45–47 which is desirable for molecular-scale spin information processing and memory devices. Polymeric radicals have also been investigated, with recent examples displaying high conductivity properties48 as well as high spin multiplicity.49
One typical feature of an organic mono-radical is that the SOMO has higher energy than the doubly occupied MOs in the ground-state electronic configuration (Fig. 1). This is associated with the aufbau rule, by which orbitals are occupied by up to two electrons (counting a pair of α and β orbitals with matching (identical or very similar) spatial functions as a single orbital in this context) from low to high orbital energy. This concept is extremely useful in chemistry for rationalizing the electronic structure and reactivity of molecules. However, it is important to note that a change in the electronic configuration, for example from ionisation or electron reduction of a molecule, or an excitation, impacts all orbitals of the system. In other words, the spatial functions (orbital shapes) as well as the orbital energies change in response to a change in the electron configuration. This means the ‘ladder of MOs’ of a system is not rigid.30,50,51 For example, changes in the inter-orbital repulsion must be considered when assessing the relative stability of different alternative electron configurations. A case in point is the 3d–4s inversion of filling order for neutral first-transition row atoms: the partially filled 3d shell in the atomic ground states is energetically below the singly or doubly occupied 4s,52 in apparent violation of the aufbau rule.
Recently, a violation of the aufbau rule has also been claimed for certain organic radicals. These systems possess an electronic configuration in which the energy of the SOMO is below the HOMO level (Fig. 3). This SOMO–HOMO inversion (SHI), alternatively referred to as SOMO–HOMO conversion or a quasi-closed-shell configuration, has generated widespread interest, both theoretically and experimentally, to rationalize and understand the consequences of the peculiar electronic structure of this class of open-shell systems.23,50,53–57 SHI has been investigated in organic spin-polarized donor systems as a route toward high-spin diradicals,18,58–62 and also in the case of luminescent radicals where SHI was associated with a significant increase of photostability.38 Coote, Corminboeuf et al. summarized various theoretical aspects related to the characterization of this phenomenon with molecular examples of SHI in 2015.50 Very recently, Abe et al. exhaustively surveyed the reported compounds in which SHI has been identified.55 Given the strong attention that SHI organic radicals have received again recently, it appears timely to review the synthetic challenge to obtain SHI in open-shell compounds, as well as some important new theoretical insight regarding the occurrence of SHI and its impact on the molecular optoelectronic and magnetic properties.
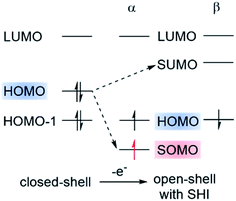 | ||
| Fig. 3 Schematic representation of the electronic configuration found in organic radicals with SOMO–HOMO inversion (SHI). Figure adapted with permission from ref. 53. Copyright 2021 American Chemical Society. | ||
In this short review, our objective is to give the readers a general perspective on SHI, with key fundamental aspects regarding the electronic and structural factors that govern this particular electronic configuration in organic radicals. We first introduce some basic considerations regarding SHI and explain why the ‘non-aufbau’ designation is somewhat imprecise in the context of spin-unrestricted SCF MO calculations. We then present the current theoretical understanding of the electronic factors that govern SHI in organic radicals, along with selected examples of reported compounds illustrating these findings. This is followed by a description of the common features exhibited by the SHI radicals reported in the literature, based on what is known about the key parameters responsible for SHI, along with a discussion of the (actual or postulated) consequences of this electronic configuration on the molecular properties of radicals, especially their (photo)stability. We hope that this work will not only provide a general view of the current state-of-the-art, but will also identify new opportunities for future research directions.
SOMO–HOMO inversion (SHI): basic considerations
Strictly speaking, the electron orbitals calculated for many-electron systems, and their energies, are not observable. However, the orbitals acquire meaning via approximations. For example, per Koopmans' theorem, the vertical ionization potential (IP) is up to a sign approximately equal to εH, with the latter being the HOMO energy from a Hartree–Fock (HF) calculation. Similarly, the LUMO is approximately associated with electron attachment (EA = electron affinity). In Kohn–Sham density functional theory (DFT), IP = −εH, holds exactly, as long as the functional is exact. This is often referred to as Janak's theorem; for a critique see ref. 63. In practice, with approximate functionals, DFT HOMO and LUMO energies may differ considerably, numerically, from the IP and EA, although procedures are available to establish these numerical relationships very closely.64,65 Koopmans' and Janak's theorem and their relation to electron removal or addition are also fundamentally related to Fukui functions and associated concepts describing the reactivity of a molecule.66 Therefore, as chemists know well, the orbitals of a molecule provide important qualitative, and sometimes even quantitative, information about its physico-chemical properties. Regarding SHI, for a reliable assignment by calculations the presence or absence of SHI should be robust, i.e., not sensitive to the chosen electronic structure approximations such as the functional used in DFT calculations.As mentioned, SHI has been associated with a non-aufbau electronic configuration similar to what has been reported for metal complexes67–69 and certain types of high-spin restricted open-shell HF calculations.70 We reiterate that in spin-unrestricted MO theory, that is, in spin-unrestricted HF or DFT SCF calculations, matching α- and β-spin MOs may have different energies. ‘Matching’ means the spatial functions are the same, or very similar.† For the reported SHI molecules, the SUMO is above the HOMO in energy in such calculations. Therefore, there is no unoccupied spin orbital energetically below the highest occupied spin orbital, the aufbau rule is not technically violated, and the non-aufbau designation should probably be avoided unless there is actually a 'hole below the Fermi level'.71 Nonetheless, of course, SHI is very intriguing. As depicted in Fig. 3, the general illustration of SHI is that the HOMO pair of matching spin orbitals is higher in energy than the SOMO, and below the corresponding β-spin hole represented by the SUMO.
This electronic configuration sets the electronic properties of these radicals apart from the more common situation where the SOMO is the highest occupied orbital of the system. While it is not always obvious to relate the electronic configuration of a molecule to its thermodynamic stability and other properties, what is clear is that when SHI is present, further oxidation of the molecular system will most likely produce an open-shell di-radical instead of a closed-shell configuration. This is because, per Koopmans' or Janak's theorem, further ionization of the radical will be from its HOMO. This specific reactivity has been successfully used to produce an organic diradical with a triplet ground-state,72 resulting from the oxidation of a monoradical with SHI electronic configuration (vide infra). Also, the energetic inversion of the SOMO and HOMO has been recently associated with a certain gain of chemical and/or photophysical stability for organic radicals,73,74 thus potentially offering a complementary approach to the two classical ones for stabilizing radicals (i.e. shielding the unpaired electrons with bulky substituents, or enhancing their delocalization over the molecular backbone10,11,75–79). Complementing these molecular material applications, organic radicals with SHI have recently been claimed as key intermediates for regiospecific reaction of C(sp3)H-amination and photocatalytic allylation, providing alternative directions for organic synthesis.80,81
Design strategies for SHI radicals
Numerous molecular systems have been reported to show SHI. However, a clear understanding of the electronic factors that lead to this specific electronic configuration has been lacking. Pioneering work related to this aspect started in the 90 s with the contributions of Sugimoto,82 Sawaki83 and Sugawara,84–88 who explored SHI electronic configurations in organic compounds implying highly persistent and localized radicals. For instance, Sugawara and co-workers developed several molecular systems combining an electron donor unit and a pendent radical, named spin-polarized donor, with SHI configuration and potentially spin-polarized current conduction.18 The investigated design of these compounds was mainly based on the nitronyl nitroxide radical unit functionalized by different organic electron donor fragments (Fig. 4), in a way that the two parts weakly interact electronically with each other. Based on a structure–properties relationship study, Sugawara et al. identified important structural and electronic factors that favor SHI in the spin-polarized donors, involving notably the electron donor strength of the fragment bearing the HOMO level, and the torsion angle between the latter and the radical unit (Fig. 4).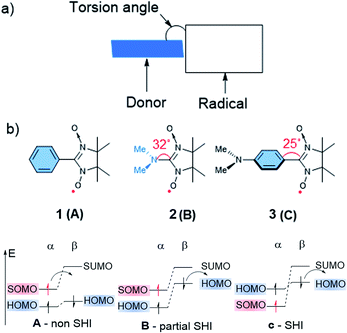 | ||
| Fig. 4 (a) Schematic illustration of the Sugawara spin-polarized donor structure. (b) Nitronyl nitroxide radical 1, 2, and 3 with corresponding torsion angles between the radical and donor fragments in degrees with schematic illustration of the corresponding electronic configuration. Figures adapted with permission from ref. 59. Copyright 2000 American Chemical Society. | ||
As illustrated in Fig. 4, three possible scenarios can be considered for these donor-radicals, resulting in different electronic configurations:59
- (A) When a weak electron donor unit is connected to the radical, such as for example a benzene unit in phenyl nitronyl nitroxide 1, the α-SOMO is higher in energy than the HOMO, resulting in a common open-shell molecular orbital arrangement with the SOMO being the highest occupied orbital.
- (B) In the case of dimethylamino nitronyl nitroxide 2, increasing the donor strength of the organic donor unit results in an α-SOMO that is higher in energy than the α-HOMO, but lower in energy than the β-HOMO. The energetic splitting between the α-HOMO and β-HOMO arises from a non-equivalent electronic repulsion between the latter two and the α-SOMO, as evidenced by spin-unrestricted calculations. Thus, this electronic configuration affords what we may call partial SHI, where oxidation would likely occur from the β-HOMO instead of the α-SOMO.
- (C) Decreasing the electronic interaction between the donor and radical units while keeping the donor strength character of the organic donor unit results in a complete SHI electron configuration, where both α- and β-HOMO energy levels become higher in energy than the α-SOMO. For instance, p-aminophenyl nitronyl nitroxide 3 displays this kind of electronic configuration.
Interestingly, the two latter types of design should give a diradical with a triplet ground-state upon one-electron oxidation of the donor unit in accordance with Hund's first rule, and because of the non-disjoint connection of the resulting two SOMOs, following Borden and Davidson.89 Experimentally, this kind of specific reactivity can be characterized using electrochemical methods, electron paramagnetic resonance (EPR) and magnetometry measurements (vide infra).
Having these preliminary molecular guidelines in mind, we recently embarked on a computational study with the aim of understanding the electronic factors that govern SHI in already reported mono-radicals. The findings were then applied to identify potential SHI candidates ‘in silico’.53 Prior calculations already indicated that SHI might be less uncommon than once thought,57 especially for small systems or spatially compact (localized) SOMOs, hinting at the important role of intra vs. inter-orbital electron repulsion discussed in the following. Analysis of various contributions to the MO energies individually, along with selected electron repulsion integrals (ERIs) for the frontier MOs, was carried out. The SHI analysis starts out with a closed-shell parent (CS), which is analogous to the radical but has one additional electron. Initially, the CS parent is in its equilibrium structure (CS//CS). The radical is then formed in three steps:
(i) Removal of an electron without letting the MOs or structure relax: CS//CS → ![[R with combining tilde]](https://www.rsc.org/images/entities/char_0052_0303.gif) //CS.
//CS.
(ii) MO relaxation via SCF: ![[R with combining tilde]](https://www.rsc.org/images/entities/char_0052_0303.gif) //CS → R//CS.
//CS → R//CS.
(iii) The radical adopts its own equilibrium structure: R//CS → R//R.
Step (i) is key and typically already establishes SHI. Based on the analysis, the preconditions in the CS system for formation of an SHI radical are as follows: (a) the CS HOMO energy is balanced by a large self-Coulomb repulsion (i.e., the repulsion between the α and β spin component of the HOMO) and a strongly stabilizing negative electron–nucleus attraction. The former can be tuned via the spatial compactness of the moiety on which the MO is localized, and the latter by inductive effects from substituents or substitution of carbon with electronegative heteroatoms, for example. As noted later, bonding vs. antibonding character of an MO may also be a factor in the energetic balance. (b) The HOMO self-Coulomb repulsion in the CS system is considerably larger than the repulsion between the HOMO and other occupied frontier orbitals (HOMO − 1, in particular). This is the reason why many of the known SHI radicals have spatially disjoint HOMO and SOMO: when the MOs are disjoint, their mutual Coulomb repulsion is relatively weak, favouring SHI in the presence of condition (a).
The main effect from removing an occupation from the CS HOMO, to form the radical, is then a strong stabilization of the orbital's remaining occupied spin component, from the loss of the self-Coulomb repulsion according to condition (a), whereas HOMO − 1 and potentially other occupied frontier MOs are far less stabilized because of condition (b). The SOMO ends up below one or several pairs of matching spin orbitals. The energy of the SUMO still contains the Coulomb repulsion with the SOMO, and therefore it remains high in energy.
In a nutshell, the formation of an SHI radical is likely to occur when the electrons in the HOMO of the CS parent repel each other strongly, while the repulsion between the HOMO and other occupied frontier MOs is much weaker. Then, the SHI is driven by the loss of a considerable amount of repulsive energy upon removing one of the HOMO occupations. In a design approach that starts with a radical moiety already, connecting the latter with an electron donor group that has a lower IP, while keeping the electronic interaction between the two units relatively weak, likewise seems to represent an efficient way of creating SHI radicals, as illustrated in Fig. 4.
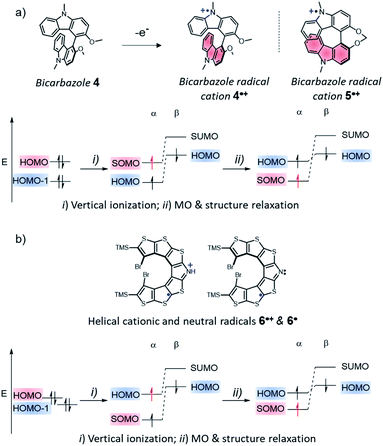
A counter example of the crucial role of step (i) in establishing SHI is the case of a system composed of two identical fragments with limited electronic interaction, in which one fragment is then oxidized. A representative example of that system if the case of the bicarbazole radical cation 4˙+ (Fig. 5 and vide infra),74 a system with a CS parent composed of two identical carbazole fragments, which we recently reported as the first enantiopure chiral SHI monoradical.74 In the CS parent system, the HOMO and HOMO − 1 are essentially in-phase and out-of-phase (+/−) linear combinations of individual carbazole fragment frontier orbitals, with Coulomb ERIs within and between HOMO and HOMO − 1 being nearly the same. The vertical ionization of dimer 4 does not immediately afford an SHI system. For such a design and presumably related ones, such as in bridged bicarbazole radical cation 5˙+, a significant distortion of the molecular structure upon oxidation is required for the occurrence of SHI (step (ii) in Fig. 5a), causing the HOMO and SOMO to localize on separate fragments. Nonetheless, key to understand the occurrence of SHI in a radical is the electrostatic repulsion among the frontier orbitals, before and after the radical formation.
Another type of SHI radical can be also identified, in which the HOMO and SOMO are spatially overlapping. This scenario is exemplified by the radical aza-thia[7]helicene derivatives 6˙+ and 6˙ reported by Rajca et al. in 2016 (Fig. 5b and vide infra).56 In this system, as revealed by our previous computational analysis, the HOMO and HOMO − 1 of the CS parent are effectively degenerate, and they both have strong—but sufficiently different—self-Coulomb repulsions. Moreover, there is a large Coulomb ERI between these two orbitals because they strongly overlap spatially. As for the SHI radical design mentioned first (Fig. 4), the ionization of the CS parent 6 induces the loss of a particularly large self-Coulomb ERI and results directly in SHI. Although significant orbital and structure relaxation also occurs, because of the spatial overlap of the HOMO and SOMO, the loss of the larger of the two Coulomb repulsion terms in the total energy favours the SHI ground-state configuration of the radical, and may likewise induce SHI in systems with similar orbital energetic characteristics.
To summarize thus far, calculations have uncovered electronic factors resulting in organic radicals with SHI and furthermore shown that the SOMO–HOMO energy gap in a multifragment SHI radical can be tuned via optimizing the HOMO energies of the precursor molecules (see ref. 53). While a clear molecular design to obtain SHI radical has been identified by the work of Sugawara et al., the recent results obtained on bicarbazole and aza-thia[7]helicene derivatives indicate that other strategies may be also relevant to obtain SHI radicals. Accordingly, further investigations are currently needed to rationalize these new approaches and provide new molecular guideline strategies. In the following sections, we discuss selected examples of organic SHI radicals, in which some common features can be identified with the ones illustrated by these theoretical results.
(i) SHI radical with a radical fragment weakly interacting with an electron donor unit
As mentioned, one of the strategy to design SHI organic radical relies on the functionalization of a radical unit by a secondary electron donor unit with a lower ionization potential (IP) while ensuring spatially disjoint HOMO and SOMO.An example of this design is detailed in Fig. 6 with compounds developed by Li, Brédas, Friend, and coworkers as doublet emitters for OLED applications.38 The chemical structure of these neutral radicals are based on the known luminescent tris(2,4,6-trichlorophenyl)methyl (TTM) radical,27,90,91 functionalized by either a phenyl-phenothiazine (PPTA) or a carbazole unit (3NCz) as donor groups. These organic neutral radicals can be readily prepared by one-electron oxidation of the corresponding anions, obtained via deprotonation of the hydrogenated precursors HTTM–PPTA and HTTM–3NCz, and represent an interesting comparison between a system with SHI (TTM–PPTA, 7) vs. without (TTM–3NCz, 8).
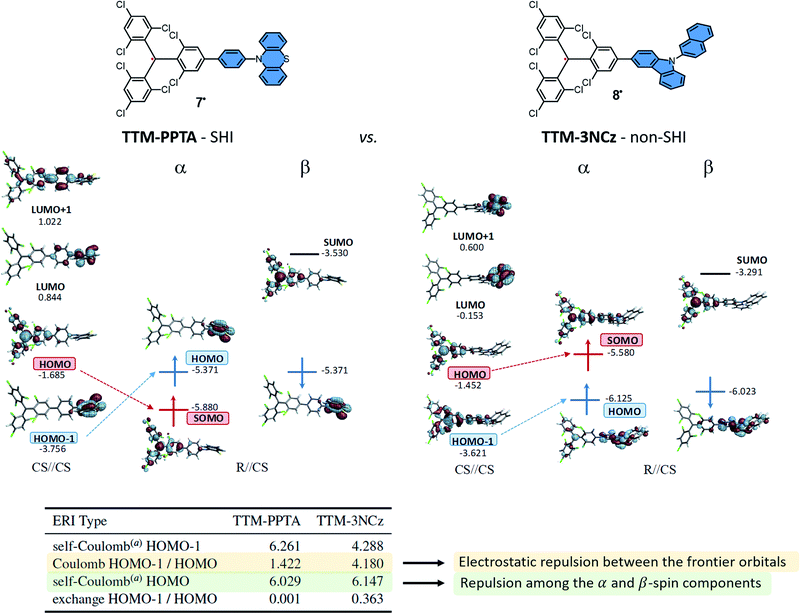 | ||
| Fig. 6 Orbital energies (in eV) and isosurfaces (0.030 a.u.) of selected MOs of the TTM–PPTA, 7 and TTM–3NCz, 8 systems. See the text for a description of the CS//CS and R//CS labelling. The vertical dimension of the figure is associated with the orbital energy; however, as in other figures herein, the energy scales are drawn qualitatively and are not aligned. The table provides selected Coulomb and exchange electron repulsion integrals (ERIs, in eV) for the corresponding closed-shell parent systems. aCoulomb repulsion between the α- and β-spin component of the MO. Figures adapted with permission from ref. 53. Copyright 2021 American Chemical Society. | ||
Using cyclic voltammetry (CV), ultraviolet photoelectron spectroscopy (UPS), EPR and computational methods, it was shown that the SHI electronic configuration can be obtained when there is not too strong electronic coupling between the neutral radical and the electron donor unit, as already mentioned, which in some cases goes along with near-orthogonal conjugated π systems. Accordingly, in TTM–PPTA the SOMO remains mainly localized on the triphenylmethyl radical moiety, and lies below the HOMO found mostly on the phenothiazine fragment. For this molecular design, i.e. a persistent radical weakly interacting with an electron donor unit, SHI is typically established in step (i) in the theoretical analysis (vide supra). As depicted in Fig. 6, both the release of the energetic repulsion between the α- and β-spin components of the HOMO in the CS of TTM–PPTA and the limited electrostatic repulsion between HOMO and HOMO − 1 are the key factors to obtain SHI. For TTM–3NCz, the stronger electronic interaction between the HOMO and HOMO − 1 disfavors the occurrence of SHI and ultimately leads to a classical organic radical electron configuration, with the SOMO higher in energy than the HOMO.
Another interesting finding of Li, Brédas, Friend, et al. was that the photostability of the luminescent radical with SHI was nearly five orders of magnitude higher than of PTM alone, and up to four orders of magnitude higher than similar radical derivatives without SHI reported in the literature.17,38 This effect was attributed to the SHI as well as the charge-transfer nature of the excited-state of the radical promoted by the presence of the carbazole unit, limiting some photodegradation reactions.
As already discussed, Sugawara et al. applied this strategy to construct a variety of spin-polarized donors based on amino groups, pyrrole, and other tetrathiafulvalene derivatives,61,92–104 and showed that this type of compounds can exhibit coexisting conductivity and magnetism, as illustrated with molecules 9a, b, resulting from a combination of the bis-ethylenedithio-tetraselenafulvalene (ESBN) donor and the nitronyl nitroxide (NN) radical (Fig. 7).72,101,105
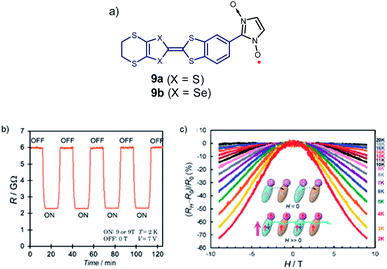 | ||
| Fig. 7 (a) Example of spin-polarized donors 9 where both magnetic and spin conductivity properties co-exist. (b) Magnetic switching of resistance of 9b at constant voltage. (c) Temperature-dependence of the ratio of magnetoresistance of 9b at a bias voltage of 7 V. Reprinted figures with permission from ref. 101. Copyright 2008 by the American Physical Society. | ||
In 2008, Nishihara et al. found that SHI can also be induced in organometallic complexes, by using the coordination of a platinum(II) ion by a dithiolate organic radical ligand (tempodt 10a, Fig. 8).106 Whereas the latter, composed of a (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO) fragment, displays the SOMO as its highest occupied orbital, Pt(II) complex 10, with 4,4′-di-tert-butyl-2,2′-bipyridyl as the ancillary ligand, shows an SHI configuration. The authors attributed this effect to an antibonding interaction of the highest doubly occupied MO of the tempodt ligand and the HOMO of Pt(tBubpy)2+, which raises the energy of the resulting HOMO in complex 10 above the SOMO. Furthermore, strong on-site Coulomb repulsion of the SOMO and its weak interaction with the HOMO, exclusively localized on the dithiolate ligand, were considered as decisive factors in obtaining SHI. These conclusions were supported by CV measurements, UV-vis spectroscopy, EPR, and DFT calculations. Interestingly, oxidation of the complex using the ferrocenium chemical oxidant resulted in the formation of dimer 102·2PF6 (Fig. 8). A clear triplet signal in the ESR spectrum, arising from the hyperfine coupling between the radical center and the nitrogen nucleus, indicated the presence of a nitroxide radical within the dimeric product, confirming that the removal of the electron involves the HOMO and not the SOMO of the complex. Nishihara et al. further investigated this approach using different metal ions such as nickel(II), gold(I), and palladium(II),107–109 likewise showing SHI electron configurations.
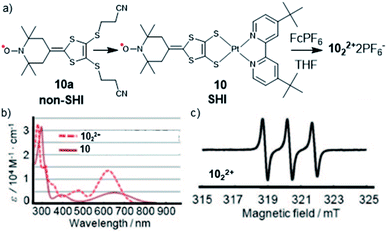 | ||
| Fig. 8 (a) Molecular structures of radical ligand tempodt 10a, platinum–tempodt complex 10, with the formation of the dimerized complex 1022+ and (b) the UV-vis spectra of 10 and 1022+; (c) EPR spectrum of 1022+. Figures adapted with permission from ref. 106. Copyright 2008 American Chemical Society. | ||
Following a similar direction, Coote et al. highlighted a potential consequence of SHI on the resulting chemical stability of the radical.110 The authors used distonic radical anions based on either stable diallyl or nitroxide radical units, linked via sigma bonds to a carboxylate group in which the HOMO has higher energy than the radical's SOMO (Fig. 9). Based on experimental and theoretical evidence, the authors found that the anion stabilizes the radical moiety and that the electronic configuration can be switched between aufbau and non-aufbau by protonation of the anionic group (Fig. 9). It was furthermore suggested that such a mechanism of stabilization also operates in nucleic acid radicals because of the presence of sulfate and phosphate groups, thus preventing undesirable radical reactivity.
 | ||
| Fig. 9 Molecular orbital configurations of the carboxy-aminoxyl radical in both anionic 11˙ and neutral 11H+ forms. | ||
Coote et al. expanded their investigations to other distonic radical anions and found that the stabilization effect diminishes in polar solvents,111 and even disappears in water, as also experimentally confirmed a year later by Lucarini et al. using bond dissociation energy measurments.112
In 2019, Kusamoto, Nishihara et al. reported another example of an SHI radical showing the radical site switching with the acidity of the medium,113 based on a similar molecular design as the radical emitters developed by Friend, Brédas and Li et al. (Fig. 6),38i.e., a donor–acceptor radical, using triphenylamine (TPA) as the electron donating unit and a molecular analogue of the TTM radical with the phenyl ring replaced by 3,5-dichloro-4-pyridyl (12, Fig. 10). In neutral conditions, 12 shows SHI with the SOMO being located mainly on the triaryl radical unit and the HOMO localized on the triaryl amine donor fragment, as shown by DFT calculations. Upon titration with trifluoroacetic acid (or with B(C6F5)5 as a lewis acid), protonation of the pyridine moiety occurs and induces an increase of the intramolecular charge transfer (ICT) occurring from the neutral donor to the radical unit. This results in a significant bathochromic shift in the UV-vis-IR absorption spectrum, as well as quenching of the radical luminescence, while keeping the SHI electron configuration. Moreover, an excess of acid (>200 eq.) triggers an intramolecular electron transfer from the trisarylamine to the radical center, affording a possibility to switch between TPA–[RH]˙+ and [TPA]˙+–RH.
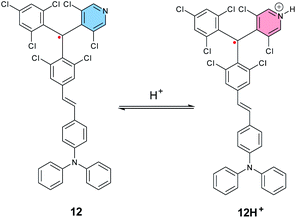 | ||
| Fig. 10 Molecular structures of tris(2,4,6-trichlorophenyl)-methyl radical, PyBTM 12, and [TPA–RH+]˙, 12H+. | ||
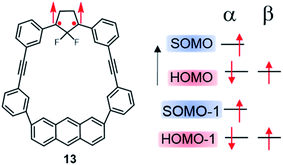
More recently, Abe, et al. investigated theoretically the electron configurations of diradical compounds based on a macrocycle composed of an anthracene and a 2,2-difluorocyclopentane diradical unit, linked together by two diphenylethyne fragments (13, Fig. 11).114,115 In this molecule, the HOMO is mainly localized on the anthracyl unit, with little electronic interaction with the SOMO and SOMO − 1 found on the 1,3-diphenylcyclopentane. Both the presence of the anthracene fragment and fluorine atoms within the cyclopentane unit were shown to be important factors to establish SHI, by raising the energy of the HOMO and stabilizing the SOMO and SOMO − 1, respectively.
(ii) SHI radicals from symmetric dimer compounds
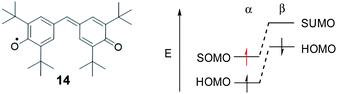
While the SHI concept has been popularized in the last decade (with the term of spin-polarized donor, vide supra), it is important to mention the work of Kinoshita et al. reported in 1987, on the galvinoxyl radical 14 (Fig. 12).116 Interested in the possibility of designing intermolecular ferromagnetism in organic materials, the team studied the orbital energies of the galvinoxyl radical using spin-unrestricted calculations and demonstrated that partial SHI occurs in the system, attributed to a difference of spin polarisation of the α and β spin component of the HOMO. These results also suggested that the oxidation of a radical with this kind of electronic configuration may favor the formation of a triplet diradical by selective oxidation involving the β-spin component of the HOMO.117–119Compound 14 can be therefore considered as an SHI precursor, based on a molecular dimer design, which has been mentioned already in the context of bicarbazole radical cations 4˙+ and 5˙+ (Fig. 5 and 13).74 The investigation of these radical systems allowed us to explore the SHI in chiral radical molecular systems and provide new insights regarding its impact on the stability of organic radicals. Photophysical (UV-vis-NIR absorption), chiroptical (ECD, electronic circular dichroism) and electrochemical characterization of the neutral bicarbazole system and its radical cationic form revealed high chemical stability for unprotected carbazole axial radical 4˙+, in comparison to unstable helical 5˙+, and in striking contradiction to the known polymerization reactivity of unprotected oxidized carbazole in the 3 and 6 positions (Fig. 13).120 Interestingly, both 4˙+ and 5˙+ exhibit SHI, indicating that such an electronic configuration is not a sufficient prerequisite to provide radical stability. Our experimental and theoretical results rather suggest that in addition to SHI, the electronic coupling between the radical center and the electron-rich unit on which the HOMO is centered plays a crucial role in the radical reactivity. In 4˙+ and 5˙+, this aspect depends on the dihedral angle between the carbazole moieties, which is governed by the axial and helical chirality of the bicarbazole systems.
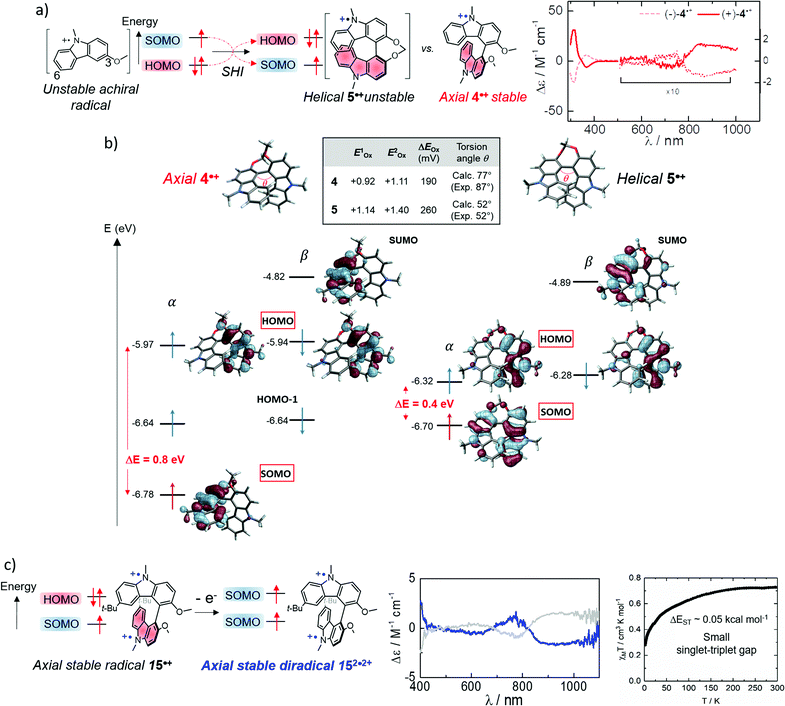 | ||
| Fig. 13 (a) Axially and helically chiral SHI cationic bicarbazole monoradicals 4˙+ and 5˙+, and orbital comparison with their common non-SHI cationic carbazole radical precursor, with the near IR circular dichroism of (+) and (−)-4˙+ (counter anions are omitted for clarity); (b) calculated orbital energies (in eV) and isosurfaces (±0.030) of frontier molecular orbitals computed for monoradicals 4˙+ (left) and 5˙+ (right). The HOMO–SOMO energy differences are averaged over the highest occupied spin orbital energies. Oxidation potentials and separation of the two first oxidation potentials in V vs. SCE, theoretical (calc.) and experimental (exp.) dihedral angles between the carbazole fragments; (c) schematic illustration of the electronic configuration of diradical 152˙2+ obtained upon oxidation of SHI radical 15˙+, near IR circular dichroism of (+) and (−)-152˙2+ in acetonitrile at 298 K, and its magnetic susceptibility (χMT vs. T). Figures adapted with permission from ref. 74. Copyright 2020 American Chemical Society. | ||
Furthermore, the persistence of 4˙+ provided an interesting opportunity to generate the corresponding chiral diradical. Oxidation of the remaining HOMO of sterically protected monoradical 15˙+ gave chiral diradical 152˙2+ with intense near-infrared (NIR) circular dichroism (Fig. 13). The radical's ground-state spin multiplicity appeared to be the low-spin singlet. This result was theoretically rationalized by a relatively weak interaction between the two SOMOs being each localized on one carbazole unit and ultimately favoring the singlet ground state. This work represents one of the rare examples of organic chiral radicals displaying SHI in which the corresponding chiroptical properties have also been investigated.
With the growing interest in chirality as a property of molecular materials,121–125 it has recently emerged that combining the attractive electronic/spin properties of an organic radical with a chiral organic π-conjugated system may give rise to molecular architectures with unique magnetic and chiroptic-electronic features, such as absorption of near infrared (NIR) circularly polarized (CP) light,56,79,126–134 radical CP luminescence (CPL),135,136 and possibly enhanced spin-filtering properties.137 However, designing organic chiral open-shell chromophores remains a formidable challenge, owing to the aforementioned high chemical reactivity and poor configurational stability that is typical of radicals.138 As for achiral radical systems, shielding the unpaired electrons with bulky substituents, or enhancing their delocalization over the molecular backbone have been used to overcome these issues.10,11,75–79 While these approaches can be efficient, they often require additional synthetic steps and may preclude significant interaction between the unpaired electron and the chiral molecular system, thus precluding efficient intermolecular interactions for charge and spin transport applications.19 In this context, the design of atropisomeric systems such as the C2-symmetric bicarbazole one depicted in Fig. 13 represents a potential strategy to obtain persistent and configurationally stable chiral radical. It is however important to note that some of the other SHI radicals described in this review are also chiral, such as the PTM and PTM derivatives, albeit without sufficient configurational stability at room temperature.136
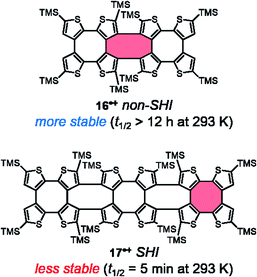
Although no chiroptical properties were reported for the radicals thiophene-based double helices 16 and 17, developed by Rajca et al. in 2021, they also represent interesting examples of chiral radicals of the symmetric-dimer type, in which SHI is present only for radical cation 17˙+ (Fig. 14).139,140 The cationic monoradicals 16˙+ and 17˙+ showed high persistence at 193 K (half-lives exceeding 24 hours). However, at room temperature in dichloromethane solution, radical 17˙+ showed much less stability than 16˙+ (t1/2 < 5 minutes vs. >12 hours in 17˙+). This result is in contradiction with the aforementioned findings for SHI vs. non-SHI radicals in terms of stability.38,74,110 The authors of ref. 140 therefore suggested that the steric hindrance brought by the peripheral TMS-thiophene units in 16˙+ plays a decisive role in stabilizing the unpaired electron. In fact, the spin density in 16˙+ is mostly localized in the center of the molecule whereas for 17˙+, it is also delocalized in the peripherical thiophene fragments (highlighted in red, Fig. 14).
SHI in a dimer molecular design was also theoretically investigated in cationic azulene radical by Mazaki et al. in 2019,141 and more recently by Casado, Nakamura et al. in 2021.23 Interestingly, in the latter report, the authors explored spiro-conjugated systems with the ability to adopt SHI in both anionic and cationic radical forms (Fig. 15).
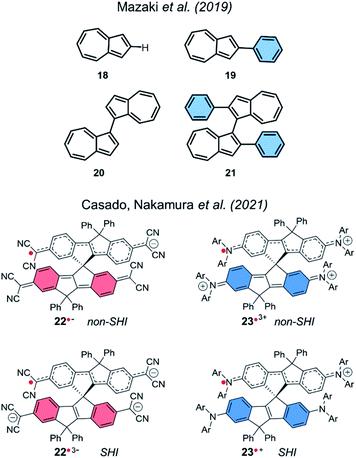 | ||
| Fig. 15 Azulenes 18–19 and dimers of azulene 20–21 (top), and spiroconjugated systems 22–23 (bottom). | ||
Using UV-vis-NIR absorption spectroscopy and DFT calculations, the team characterized a SHI for the radical trisanion of the quinoidal derivative 22˙3− and for the radical cation 23˙+. This report highlights a new design strategy for obtaining SHI open-shell systems based on spiro-conjugation and spiro-functionalization.
(iii) SHI radicals with spatially overlapping HOMO and SOMO
The first aza-thia[7]helicene radicals displaying SHI, 6˙ and 6˙+[PF6]−, represent interesting examples of this class of open-shell systems. Here, the HOMO and SOMO strongly overlap spatially (Fig. 16). Nonetheless, the difference in the intra- vs. inter-orbital repulsion upon formation of the radical must also be considered as the determining factor to favor the SHI electronic configuration in the radical (vide supra).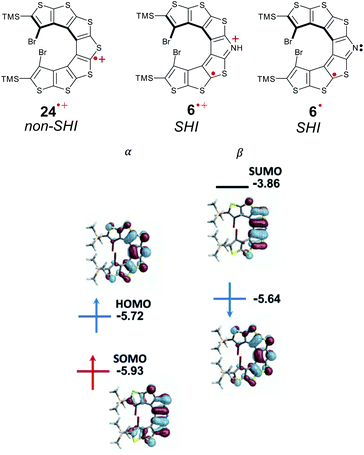 | ||
| Fig. 16 Chemical structures of cationic radicals thia[7]helicene 24˙+[PF6]− and aza-thia[7]helicene 6˙+[PF6]−, and neutral aza-thia[7]helicene 6˙. Orbital energies (in eV) and isosurfaces (±0.030 a.u.) of selected MOs of 7˙. Figures adapted with permission from ref. 53. Copyright 2021 American Chemical Society. | ||
Following previous work on thia[7]helicene 24˙+,142 Rajca et al. replaced the central thiophene ring by a pyrrole unit, for the potential generation of helical nitrogen-centered neutral and cationic radicals, 6˙ and 6˙+[PF6]−, respectively (Fig. 16). Starting from the NH precursor, the corresponding radical cation, 6˙+[PF6]− was generated using a chemical oxidant in dichloromethane solution at low temperature (233 K). EPR measurements confirmed the open-shell electron configuration, with a broad I = 1 triplet with 14N-hyperfine splitting, aN = 0.23 mT, and isotropic g = 2.005. The team also generated the neutral aminyl radical 6˙, either by oxidizing the anion precursor, or via an in situ deprotonation of the NH group of 6˙+[PF6]− using an inorganic base. The half-lives of these radicals were characterized in a mixture of dichloromethane/acetonitrile, reaching up to 8 h at 293 K. Based on cyclic voltammetry experiments and DFT calculations, Rajca et al. showed that for both radicals the SOMO is energetically below the HOMO, and that SHI can be maintained even in polar solvents such as dimethyl sulfoxide and water, in contrast with previous cases reported by Coote and Lucarini.111,112
Interestingly, the thia[7]helicene radical 24˙+[PF6]− without SHI has a weaker persistence with a half-life of ∼15–20 min at room temperature, showing the importance of the pyrrole ring in 6 for increasing the stability of the corresponding neutral and cationic open-shell compounds. While a significant racemization barrier of about 35 kcal mol−1 was determined by DFT calculations, no chiroptical properties of this chiral organic radical were reported.56
In 2021, Abe, Antol, et al. reported another example of this type of molecular design, based on carbene derivatives displaying SHI.54 Based on theoretical calculations, it was shown that triplet carbenes included in a cycloparaphenylene (CPP) scaffold have SOMO energy levels below the HOMO of the CPP ring (Fig. 17). This electronic configuration is found for the ring composed of four phenyl units (25), whereas in larger carbene-CPP derivatives (5 to 10 phenyl units), the HOMO lies energetically in between the two SOMOs. This inversion, upon increasing the ring size, was explained by a simultaneous destabilization of the HOMO localized on the π-orbitals of the CPP ring and a stabilization of the SOMO within the σ-orbital of the carbene via an increase of the carbene angle, θc (Fig. 17). SHI also occurs in simpler carbenes such as 26. The two aromatic rings stabilizing the carbene unit are structurally constrained, confirming the importance of the carbene angle (θc, Fig. 17). This result is particularly interesting given the extensive research on carbene chemistry, ranging from reactive intermediates to catalysis and material applications.
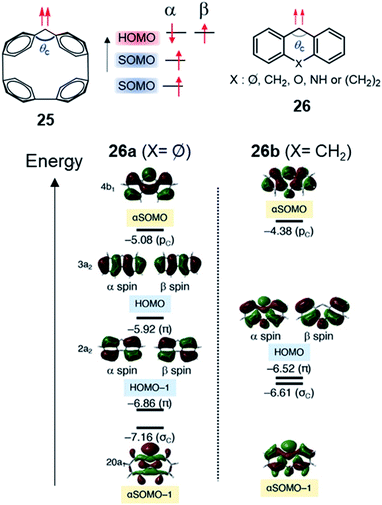 | ||
| Fig. 17 Top: triplet carbenes included in a cycloparaphenylene (CPP) scaffold 25 and 2,2-difluorocyclopentane diradical 26 (left) showing SHI; with corresponding molecular orbital diagrams for 26a and 26b. Figure reprinted with permission from ref. 54. Copyright 2021 by the American Chemical Society. | ||
Conclusions and outlook
In this review, we have described a specific class of organic radicals, showing an energetic inversion of the singly occupied molecular orbital (SOMO) and the highest doubly occupied molecular orbital (HOMO), namely organic SHI radicals. We first discussed the basic features of organic radicals in terms of electronic structure, stability, optical, and photophysical properties, related to the presence of an unpaired electron. We then focused the discussion on SHI organic radicals and gave some considerations regarding this particular electronic configuration in relation to the aufbau rule. We also discussed several examples of organic SHI radicals based on neutral nitroxide, triphenylmethyl and carbene units, cationic carbazole derivatives and anionic spiroconjugated systems, and described structural and electronic design rules that govern the occurrence of SHI. Along with experimental evidence, theory has brought important insights regarding the key parameters leading to SHI, for example in terms of the electrostatic repulsion among the frontier orbitals and between the α and β spin components of a given MO.This review also highlighted various specific features of SHI organic radicals, such as the postulated relationship between SHI and thermodynamic stability or photostability, which remains to be proven conclusively. The degree of ‘energetic isolation’ of the unpaired orbital in SHI radicals, when it is below the HOMO, means the HOMO instead of the SOMO defines the Fukui reactivity function in leading order. This opens the opportunity to relate electronic structure and reactivity directly with the SHI character of a system. Moreover, SHI radicals can be viewed as promising intermediates to form triplet ground state diradicals upon further oxidation of the HOMO level.
Merging the peculiar features of radical compounds and SHI with a chiral π-conjugated system is also currently attracting interest because of the potential of designing specific interactions with circularly polarized (CP) light143–145 as well as magneto-chiral effects146,147 and in the context of the chirality-induced-spin-selectivity.148–150
All these aspects appear particularly relevant for designing organic molecular materials with tailored spin properties, which are of high fundamental interest and may eventually offer new opportunities in organic spintronic and optoelectronic applications, both as semi-conductors,18,19 or as efficient radical emitters.27,38
Fundamental questions remain yet to be fully addressed, notably regarding the relationships between SHI and radical stability, as well as other desirable radical properties that are not present in classical organic radicals. Future joined experimental and theoretical works will be aimed at teasing out these differences. We hope that this review highlights new opportunities for future research directions in organic radicals.
Author contributions
JA and LF co-wrote the manuscript and conceived the theoretical and experimental studies underlying a subset of the findings reported in the article, with comments and advices from JC. SK and LA designed figures and performed original research reviewed herein.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. F. and J. C. acknowledge the Ministère de l'Enseignement supérieur, de la Recherche et de l'Innovation, the Centre National de la Recherche Scientifique (CNRS). L. F. thanks the French National Research Agency (ANR, OChiRaLec project, ANR-21-CE07-0019-01) and the European Research Council (ERC, grant agreement number: 101041516—SHIFUMI—ERC starting grant (StG)) for financial support. J. A. thanks the National Science Foundation (CHE-1855470) for financial support of the theoretical component of our joint research.Notes and references
- J. H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef PubMed.
- B. B. Williams and H. J. Halpern, Biomedical EPR – Part A: Free Radicals, Metals, Medicine and Physiology, Springer US, 2005 Search PubMed.
- G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Angew. Chem., Int. Ed., 2015, 54, 11770–11774 CrossRef CAS.
- Z. Zeng, X. Shi, C. Chi, J. T. L. Navarrete, J. Casado and J. Wu, Chem. Soc. Rev., 2015, 44, 6578–6596 RSC.
- Z. X. Chen, Y. Li and F. Huang, Chem, 2021, 7, 288–332 CAS.
- G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. Ponce Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Nat. Chem., 2016, 8, 753–759 CrossRef CAS PubMed.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed.
- S. Kumar, Y. Kumar, S. K. Keshri and P. Mukhopadhyay, Magnetochemistry, 2016, 2, 42 CrossRef.
- X. Hu, W. Wang, D. Wang and Y. Zheng, J. Mater. Chem. C, 2018, 6, 11232–11242 RSC.
- T. Y. Gopalakrishna, W. Zeng, X. Lu and J. Wu, Chem. Commun., 2018, 54, 2186–2199 RSC.
- K. Kato and A. Osuka, Angew. Chem., Int. Ed., 2019, 58, 8978–8986 CrossRef CAS PubMed.
- Y. Ni, T. Y. Gopalakrishna, H. Phan, T. Kim, T. S. Herng, Y. Han, T. Tao, J. Ding, D. Kim and J. Wu, Nat. Chem., 2020, 12, 242–248 CrossRef CAS PubMed.
- C. Liu, Y. Ni, X. Lu, G. Li and J. Wu, Acc. Chem. Res., 2019, 52, 2309–2321 CrossRef CAS PubMed.
- Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 CrossRef CAS PubMed.
- X. Gu, T. Y. Gopalakrishna, H. Phan, Y. Ni, T. S. Herng, J. Ding and J. Wu, Angew. Chem., Int. Ed., 2017, 56, 15383–15387 CrossRef CAS PubMed.
- X. Ai, Y. Chen, Y. Feng and F. Li, Angew. Chem., Int. Ed., 2018, 57, 2869–2873 CrossRef CAS PubMed.
- X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Nature, 2018, 563, 536–540 CrossRef CAS PubMed.
- T. Sugawara and M. M. Matsushita, J. Mater. Chem., 2009, 19, 1738–1753 RSC.
- T. Sugawara, H. Komatsu and K. Suzuki, Chem. Soc. Rev., 2011, 40, 3105–3118 RSC.
- D. Yuan, W. Liu and X. Zhu, Chem, 2021, 7, 333–357 CAS.
- Y. Tan, N. C. Casetti, B. W. Boudouris and B. M. Savoie, J. Am. Chem. Soc., 2021, 143, 11994–12002 CrossRef CAS PubMed.
- S. Kimura, R. Matsuoka, S. Kimura, H. Nishihara and T. Kusamoto, J. Am. Chem. Soc., 2021, 143, 5610–5615 CrossRef CAS PubMed.
- S. M. Rivero, R. Shang, H. Hamada, Q. Yan, H. Tsuji, E. Nakamura and J. Casado, Bull. Chem. Soc. Jpn., 2021, 94, 989–996 CrossRef.
- I. Ratera, J. Vidal-Gancedo, D. Maspoch, S. T. Bromley, N. Crivillers and M. Mas-Torrent, J. Mater. Chem. C, 2021, 9, 10610–10623 RSC.
- C. Shu, M. Pink, T. Junghoefer, E. Nadler, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2021, 143, 5508–5518 CrossRef CAS PubMed.
- A. Calzolari, A. Rajca and M. B. Casu, J. Mater. Chem. C, 2021, 9, 10787–10793 RSC.
- J. M. Hudson, T. J. H. Hele and E. W. Evans, J. Appl. Phys., 2021, 129, 180901 CrossRef CAS.
- Y. Teki, Chem.–Eur. J., 2020, 26, 980–996 CrossRef CAS PubMed.
- Y. Ni and J. Wu, Tetrahedron Lett., 2016, 57, 5426–5434 CrossRef CAS.
- J. Autschbach, Quantum Theory for Chemical Applications: From Basic Concepts to Advanced Topics, Oxford University Press, 2020 Search PubMed.
- L. K. Montgomery, J. C. Huffman, E. A. Jurczak and M. P. Grendze, J. Am. Chem. Soc., 1986, 108, 6004–6011 CrossRef CAS PubMed.
- J. Thiele and H. Balhorn, Ber. Dtsch. Chem. Ges., 1904, 37, 1463–1470 CrossRef.
- A. E. Chichibabin, Chem. Ber., 1907, 40, 1810 CrossRef.
- D. Griller and K. U. Ingold, Acc. Chem. Res., 1976, 9, 13–19 CrossRef CAS.
- S. Sowndarya S. V., P. C. S. John and R. S. Paton, Chem. Sci., 2021, 12, 13158–13166 RSC.
- X. K. Chen, D. Kim and J. L. Bredas, Acc. Chem. Res., 2018, 51, 2215–2224 CrossRef CAS.
- M. Godumala, S. Choi, M. J. Cho and D. H. Choi, J. Mater. Chem. C, 2019, 7, 2172–2198 RSC.
- H. Guo, Q. Peng, X.-K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J.-L. Brédas and F. Li, Nat. Mater., 2019, 18, 977–984 CrossRef CAS PubMed.
- A. Abdurahman, T. J. H. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Nat. Mater., 2020, 19, 1224–1229 CrossRef CAS.
- Y. Teki, Chem.–Eur. J., 2020, 26, 980–996 CrossRef CAS.
- K. Kato, S. Kimura, T. Kusamoto, H. Nishihara and Y. Teki, Angew. Chem., Int. Ed., 2019, 58, 2606–2611 CrossRef CAS PubMed.
- X. Liang, Z. L. Tu and Y. X. Zheng, Chem.–Eur. J., 2019, 25, 5623–5642 CrossRef CAS PubMed.
- Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020 CrossRef CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- A. Rajca, Chem. Rev., 1994, 94, 871–893 CrossRef CAS.
- N. M. Gallagher, A. Olankitwanit and A. Rajca, J. Org. Chem., 2015, 80, 1291–1298 CrossRef CAS PubMed.
- A. Rajca, A. Olankitwanit and S. Rajca, J. Am. Chem. Soc., 2011, 133, 4750–4753 CrossRef CAS PubMed.
- Y. Joo, V. Agarkar, S. H. Sung, B. M. Savoie and B. W. Boudouris, Science, 2018, 359, 1391–1395 CrossRef CAS PubMed.
- A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505 CrossRef CAS PubMed.
- G. Gryn'ova, M. L. Coote and C. Corminboeuf, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 440–459 Search PubMed.
- J. Autschbach, J. Chem. Educ., 2012, 89, 1032–1040 CrossRef CAS.
- M. P. Melrose and E. R. Scerri, J. Chem. Educ., 1996, 73, 498 CrossRef CAS.
- L. Abella, J. Crassous, L. Favereau and J. Autschbach, Chem. Mater., 2021, 33, 3678–3691 CrossRef CAS.
- R. Murata, Z. Wang, Y. Miyazawa, I. Antol, S. Yamago and M. Abe, Org. Lett., 2021, 23, 4955–4959 CrossRef CAS PubMed.
- R. Murata, Z. Wang and M. Abe, Aust. J. Chem., 2021, 74, 827 CrossRef CAS.
- Y. Wang, H. Zhang, M. Pink, A. Olankitwanit, S. Rajca and A. Rajca, J. Am. Chem. Soc., 2016, 138, 7298–7304 CrossRef CAS PubMed.
- A. Kumar and M. D. Sevilla, J. Phys. Chem. B, 2018, 122, 98–105 CrossRef CAS PubMed.
- A. Izuoka, M. Hiraishi, T. Abe, T. Sugawara, K. Sato and T. Takui, J. Am. Chem. Soc., 2000, 122, 3234–3235 CrossRef CAS.
- H. Sakurai, A. Izuoka and T. Sugawara, J. Am. Chem. Soc., 2000, 122, 9723–9734 CrossRef CAS.
- J. Nakazaki, I. Chung, M. M. Matsushita, T. Sugawara, R. Watanabe, A. Izuoka and Y. Kawada, J. Mater. Chem., 2003, 13, 1011–1022 RSC.
- H. Komatsu, R. Mogi, M. M. Matsushita, T. Miyagi, Y. Kawada and T. Sugawara, Polyhedron, 2009, 28, 1996–2000 CrossRef CAS.
- M. Souto, C. Rovira, I. Ratera and J. Veciana, CrystEngComm, 2017, 19, 197–206 RSC.
- E. J. Baerends, Mol. Phys., 2020, 118, e1612955 CrossRef.
- R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS.
- J. Autschbach and M. Srebro, Acc. Chem. Res., 2014, 47, 2592–2602 CrossRef CAS PubMed.
- R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1995 Search PubMed.
- B. L. Westcott, N. E. Gruhn, L. J. Michelsen and D. L. Lichtenberger, J. Am. Chem. Soc., 2000, 122, 8083–8084 CrossRef CAS.
- M. J. Bialek and L. Latos-Grazynski, Inorg. Chem., 2016, 55, 1758–1769 CrossRef CAS PubMed.
- A. Idec, M. Pawlicki and L. Latos-Grazynski, Inorg. Chem., 2017, 56, 10337–10352 CrossRef CAS PubMed.
- K. R. Glaesemann and M. W. Schmidt, J. Phys. Chem. A, 2010, 114, 8772–8777 CrossRef CAS PubMed.
- O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2004, 120, 8364–8372 CrossRef CAS PubMed.
- T. Sugawara, H. Komatsu and K. Suzuki, Chem. Soc. Rev., 2011, 40, 3105–3118 RSC.
- H. Guo, Q. Peng, X. K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J. L. Bredas and F. Li, Nat. Mater., 2019, 18, 977–984 CrossRef CAS.
- S. Kasemthaveechok, L. Abella, M. Jean, M. Cordier, T. Roisnel, N. Vanthuyne, T. Guizouarn, O. Cador, J. Autschbach, J. Crassous and L. Favereau, J. Am. Chem. Soc., 2020, 142, 20409–20418 CrossRef CAS.
- W. Wang, L. Wang, S. Chen, W. Yang, Z. Zhang and X. Wang, Sci. China: Chem., 2018, 61, 300 CrossRef CAS.
- N. Gallagher, H. Zhang, T. Junghoefer, E. Giangrisostomi, R. Ovsyannikov, M. Pink, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2019, 141, 4764–4774 CrossRef CAS PubMed.
- T. Kanetomo, K. Ichihashi, M. Enomoto and T. Ishida, Org. Lett., 2019, 21, 3909–3912 CrossRef CAS PubMed.
- B. Tang, J. Zhao, J.-F. Xu and X. Zhang, Chem. Sci., 2020, 11, 1192–1204 RSC.
- C. Shu, H. Zhang, A. Olankitwanit, S. Rajca and A. Rajca, J. Am. Chem. Soc., 2019, 141, 17287–17294 CrossRef CAS PubMed.
- R. Zhao, K. Fu, Y. Fang, J. Zhou and L. Shi, Angew. Chem., Int. Ed., 2020, 59, 20682–20690 CrossRef CAS.
- E. Levernier, K. Jaouadi, H.-R. Zhang, V. Corcé, A. Bernard, G. Gontard, C. Troufflard, L. Grimaud, E. Derat, C. Ollivier and L. Fensterbank, Chem.–Eur. J., 2021, 27, 8782–8790 CrossRef CAS PubMed.
- T. Sugimoto, S. Yamaga, M. Nakai, K. Ohmori, M. Tsujii, H. Nakatsuji, H. Fujita and J. Yamauchi, Chem. Lett., 1993, 22, 1361–1364 CrossRef.
- K. Ishiguro, M. Ozaki, N. Sekine and Y. Sawaki, J. Am. Chem. Soc., 1997, 119, 3625–3626 CrossRef CAS.
- S. Matsumiya, A. Izuoka, T. Sugawara, T. Taruishi and Y. Kawada, Bull. Chem. Soc. Jpn., 1993, 66, 513–522 CrossRef CAS.
- R. Kumai, M. M. Matsushita, A. Izuoka and T. Sugawara, J. Am. Chem. Soc., 1994, 116, 4523–4524 CrossRef CAS.
- R. Kumai, H. Sakurai, A. Izuoka and T. Sugawara, Mol. Cryst. Liq. Cryst., 1996, 279, 133–138 CrossRef CAS.
- H. Sakurai, R. Kumai, A. Izuoka and T. Sugawara, Chem. Lett., 1996, 25, 879–880 CrossRef.
- J. Nakazaki, M. M. Matsushita, A. Izuoka and T. Sugawara, Tetrahedron Lett., 1999, 40, 5027–5030 CrossRef CAS.
- W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587–4594 CrossRef CAS.
- D. Velasco, S. Castellanos, M. López, F. López-Calahorra, E. Brillas and L. Juliá, J. Org. Chem., 2007, 72, 7523–7532 CrossRef CAS PubMed.
- Z. Cui, A. Abdurahman, X. Ai and F. Li, CCS Chem., 2020, 2, 1129–1145 CrossRef CAS.
- J. Nakazaki, I. Chung, M. M. Matsushita, T. Sugawara, R. Watanabe, A. Izuoka and Y. Kawada, J. Mater. Chem., 2003, 13, 1011–1022 RSC.
- J. Nakazaki, I. Chung, R. Watanabe, T. Ishitsuka, Y. Kawada, M. M. Matsushita and T. Sugawara, Internet Electron. J. Mol. Des., 2003, 2, 112–127 CAS.
- I. Matsumoto, I. Ciofini, P. P. Laine and Y. Teki, Chemistry, 2009, 15, 11210–11220 CrossRef CAS PubMed.
- Y. Orimoto, F. L. Gu, J. Korchowiec, A. Imamura and Y. Aoki, Theor. Chem. Acc., 2009, 125, 493–501 Search PubMed.
- A. Ito, R. Kurata, Y. Noma, Y. Hirao and K. Tanaka, J. Org. Chem., 2016, 81, 11416–11420 CrossRef CAS PubMed.
- J. Nakazaki, Y. Ishikawa, A. Izuoka, T. Sugawara and Y. Kawada, Chem. Phys. Lett., 2000, 319, 385–390 CrossRef CAS.
- A. Izuoka, M. Hiraishi, T. Abe, T. Sugawara, K. Sato and T. Takui, J. Am. Chem. Soc., 2000, 122, 3234–3235 CrossRef CAS.
- M. h. Chahma, K. Macnamara, A. van der Est, A. Alberola, V. Polo and M. Pilkington, New J. Chem., 2007, 31, 1973 RSC.
- M. M. Matsushita, H. Kawakami, Y. Kawada and T. Sugawara, Chem. Lett., 2007, 36, 110–111 CrossRef CAS.
- M. M. Matsushita, H. Kawakami, T. Sugawara and M. Ogata, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195208 CrossRef.
- H. Komatsu, M. M. Matsushita, S. Yamamura, Y. Sugawara, K. Suzuki and T. Sugawara, J. Am. Chem. Soc., 2010, 132, 4528–4529 CrossRef CAS PubMed.
- J. Guasch, L. Grisanti, V. Lloveras, J. Vidal-Gancedo, M. Souto, D. C. Morales, M. Vilaseca, C. Sissa, A. Painelli, I. Ratera, C. Rovira and J. Veciana, Angew. Chem., Int. Ed., 2012, 51, 11024–11028 CrossRef CAS PubMed.
- H. Douib, M. Puget, Y. Suffren, F. Pointillart, K. Bernot, B. Le Guennic, O. Cador, A. Gouasmia and L. Ouahab, Dyes Pigm., 2017, 145, 285–293 CrossRef CAS.
- T. Sugawara and M. M. Matsushita, J. Mater. Chem., 2009, 19, 1738–1753 RSC.
- T. Kusamoto, S. Kume and H. Nishihara, J. Am. Chem. Soc., 2008, 130, 13844–13845 CrossRef CAS PubMed.
- T. Kusamoto, S. Kume and H. Nishihara, Angew. Chem., Int. Ed., 2010, 49, 529–531 CrossRef CAS PubMed.
- H.-B. Zhao, Y.-Q. Qiu, C.-G. Liu, S.-L. Sun, Y. Liu and R.-S. Wang, J. Organomet. Chem., 2010, 695, 2251–2257 CrossRef CAS.
- X. Zhang, S. Suzuki, M. Kozaki and K. Okada, J. Am. Chem. Soc., 2012, 134, 17866–17868 CrossRef CAS PubMed.
- G. Gryn'ova, D. L. Marshall, S. J. Blanksby and M. L. Coote, Nat. Chem., 2013, 5, 474 CrossRef PubMed.
- G. Gryn'ova and M. L. Coote, J. Am. Chem. Soc., 2013, 135, 15392–15403 CrossRef PubMed.
- P. Franchi, E. Mezzina and M. Lucarini, J. Am. Chem. Soc., 2014, 136, 1250–1252 CrossRef CAS PubMed.
- A. Tanushi, S. Kimura, T. Kusamoto, M. Tominaga, Y. Kitagawa, M. Nakano and H. Nishihara, J. Phys. Chem. C, 2019, 123, 4417–4423 CrossRef CAS.
- Z. Wang, R. Murata and M. Abe, ACS Omega, 2021, 6, 22773–22779 CrossRef CAS PubMed.
- Z. Wang, R. Akisaka, S. Yabumoto, T. Nakagawa, S. Hatano and M. Abe, Chem. Sci., 2021, 12, 613–625 RSC.
- K. Awaga, T. Sugano and M. Kinoshita, Chem. Phys. Lett., 1987, 141, 540–544 CrossRef CAS.
- K. Awaga, T. Sugano and M. Kinoshita, Chem. Phys. Lett., 1986, 128, 587–590 CrossRef CAS.
- K. Awaga, T. Sugano and M. Kinoshita, J. Chem. Phys., 1986, 85, 2211–2218 CrossRef CAS.
- K. Awaga, T. Sugano and M. Kinoshita, Solid State Commun., 1986, 57, 453–456 CrossRef CAS.
- K. Karon and M. Lapkowski, J. Solid State Chem., 2015, 19, 2601–2610 CAS.
- L. E. MacKenzie and P. Stachelek, Nat. Chem., 2021, 13, 521–522 CrossRef CAS PubMed.
- L. Frederic, A. Desmarchelier, L. Favereau and G. Pieters, Adv. Funct. Mater., 2021, 31, 2010281 CrossRef CAS.
- J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 0045 CrossRef CAS.
- S. H. Yang, R. Naaman, Y. Paltiel and S. S. P. Parkin, Nat. Rev. Phys., 2021, 3, 328–343 CrossRef.
- X. B. Shang, L. Wan, L. Wang, F. Gao and H. Y. Li, J. Mater. Chem. C, 2022, 10, 2400–2410 RSC.
- A. Ueda, H. Wasa, S. Suzuki, K. Okada, K. Sato, T. Takui and Y. Morita, Angew. Chem., Int. Ed., 2012, 51, 6691–6695 CrossRef CAS PubMed.
- B. D. Gliemann, A. G. Petrovic, E. M. Zolnhofer, P. O. Dral, F. Hampel, G. Breitenbruch, P. Schulze, V. Raghavan, K. Meyer, P. L. Polavarapu, N. Berova and M. Kivala, Chem.–Asian J., 2017, 12, 31–35 CrossRef CAS PubMed.
- M. V. Ivanov, K. Thakur, A. Bhatnagar and R. Rathore, Chem. Commun., 2017, 53, 2748–2751 RSC.
- Y. C. Hsieh, C. F. Wu, Y. T. Chen, C. T. Fang, C. S. Wang, C. H. Li, L. Y. Chen, M. J. Cheng, C. C. Chueh, P. T. Chou and Y. T. Wu, J. Am. Chem. Soc., 2018, 140, 14357–14366 CrossRef CAS PubMed.
- Y. Inoue, D. Sakamaki, Y. Tsutsui, M. Gon, Y. Chujo and S. Seki, J. Am. Chem. Soc., 2018, 140, 7152–7158 CrossRef CAS PubMed.
- M. Narita, T. Teraoka, T. Murafuji, Y. Shiota, K. Yoshizawa, S. Mori, H. Uno, S. Kanegawa, O. Sato, K. Goto and F. Tani, Bull. Chem. Soc. Jpn., 2019, 92, 1867–1873 CrossRef CAS.
- R. Prince, Š. Tomáš, R. Michel, H. Daniel, N. Markus, B. Martin and J. Michal, Angew. Chem., Int. Ed., 2016, 55, 1183–1186 CrossRef PubMed.
- P. Ravat, T. Solomek, D. Haussinger, O. Blacque and M. Juricek, J. Am. Chem. Soc., 2018, 140, 10839–10847 CrossRef CAS PubMed.
- C. Shen, G. Loas, M. Srebro-Hooper, N. Vanthuyne, L. Toupet, O. Cador, F. Paul, J. T. L. Navarrete, F. J. Ramirez, B. Nieto-Ortega, J. Casado, J. Autschbach, M. Vallet and J. Crassous, Angew. Chem., Int. Ed., 2016, 55, 8062–8066 CrossRef CAS PubMed.
- P. Mayorga-Burrezo, V. G. Jimenez, D. Blasi, T. Parella, I. Ratera, A. G. Campana and J. Veciana, Chem.–Eur. J., 2020, 26, 3776–3781 CrossRef CAS PubMed.
- P. M. Burrezo, V. G. Jimenez, D. Blasi, I. Ratera, A. G. Campana and J. Veciana, Angew. Chem., Int. Ed., 2019, 58, 16282–16288 CrossRef PubMed.
- S. Shil, D. Bhattacharya, A. Misra and D. J. Klein, Phys. Chem. Chem. Phys., 2015, 17, 23378–23383 RSC.
- J. S. J. Tan and R. S. Paton, Chem. Sci., 2019, 10, 2285–2289 RSC.
- S. Zhang, X. Liu, C. Li, L. Li, J. Song, J. Shi, M. Morton, S. Rajca, A. Rajca and H. Wang, J. Am. Chem. Soc., 2016, 138, 10002–10010 CrossRef CAS PubMed.
- A. Rajca, C. Shu, H. Zhang, S. Zhang, H. Wang and S. Rajca, Photochem. Photobiol., 2021, 97, 1376–1390 CrossRef CAS PubMed.
- T. Tsuchiya, Y. Katsuoka, K. Yoza, H. Sato and Y. Mazaki, ChemPlusChem, 2019, 84, 1659–1667 CrossRef CAS PubMed.
- J. K. Zak, M. Miyasaka, S. Rajca, M. Lapkowski and A. Rajca, J. Am. Chem. Soc., 2010, 132, 3246–3247 CrossRef CAS PubMed.
- J. R. Brandt, X. Wang, Y. Yang, A. J. Campbell and M. J. Fuchter, J. Am. Chem. Soc., 2016, 138, 9743–9746 CrossRef CAS PubMed.
- P. Josse, L. Favereau, C. Shen, S. Dabos-Seignon, P. Blanchard, C. Cabanetos and J. Crassous, Chem.–Eur. J., 2017, 23, 6277–6281 CrossRef CAS PubMed.
- Y. Yang, R. C. da Costa, M. J. Fuchter and A. J. Campbell, Nat. Photonics, 2013, 7, 634 CrossRef CAS.
- K. Ishii, S. Hattori and Y. Kitagawa, Photochem. Photobiol. Sci., 2020, 19, 8–19 CrossRef CAS PubMed.
- M. Atzori, G. Rikken and C. Train, Chem.–Eur. J., 2020, 26, 9784–9791 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- A. K. Mondal, M. D. Preuss, M. L. Ślęczkowski, T. K. Das, G. Vantomme, E. W. Meijer and R. Naaman, J. Am. Chem. Soc., 2021, 143, 7189–7195 CrossRef CAS PubMed.
- D. H. Waldeck, R. Naaman and Y. Paltiel, APL Mater., 2021, 9, 040902 CrossRef CAS.
Footnote |
| † Spin-unrestricted SCF calculations may not always produce the SOMO and SUMO with obviously matching spatial functions, even if spin contamination is not severe. The orbitals produced by standard SCF calculations are called ‘canonical’. We have previously noted cases where an α-spin SOMO matching the appearance of a β-spin SUMO was represented by a linear combination of occupied α-spin canonical MOs. |
| This journal is © The Royal Society of Chemistry 2022 |