Oriented internal electrostatic fields: an emerging design element in coordination chemistry and catalysis

Abstract

The power of oriented electrostatic fields (ESFs) to influence chemical bonding and reactivity is a phenomenon of rapidly growing interest. The presence of strong ESFs has recently been implicated as one of the most significant contributors to the activity of select enzymes, wherein alignment of a substrate's changing dipole moment with a strong, local electrostatic field has been shown to be responsible for the majority of the enzymatic rate enhancement. Outside of enzymology, researchers have studied the impacts of “internal” electrostatic fields via the addition of ionic salts to reactions and the incorporation of charged functional groups into organic molecules (both experimentally and computationally), and “externally” via the implementation of bulk fields between electrode plates. Incorporation of charged moieties into homogeneous inorganic complexes to generate internal ESFs represents an area of high potential for novel catalyst design. This field has only begun to materialize within the past 10 years but could be an area of significant impact moving forward, since it provides a means for tuning the properties of molecular complexes via a method that is orthogonal to traditional strategies, thereby providing possibilities for improved catalytic conditions and novel reactivity. In this perspective, we highlight recent developments in this area and offer insights, obtained from our own research, on the challenges and future directions of this emerging field of research.

---

Alexander B. Weberg

Alex Weberg received his bachelor's degree in chemistry from Macalester College in 2015 under the supervision of Professor Paul Fischer. In 2015, he joined Professor Neil Tomson's research group at the University of Pennsylvania where he studied the impacts of internal electrostatic fields in metal complexes and received his PhD in 2021. Alex is currently a postdoctoral researcher in Professor Eric Schelter's group at the University of Pennsylvania where he is studying critical metal separations chemistry.

Ryan P. Murphy

Ryan Murphy received his bachelor's degree in chemistry from Colgate University in 2018 under the supervision of Professor Matthew Buck. He joined Professor Neil Tomson's research group at the University of Pennsylvania in 2018, where he currently investigates the impacts of internal electrostatic fields on small molecule activation in metal complexes.

Neil C. Tomson

Neil Tomson received a B.A. in Chemistry in 2004 from Grinnell College (Prof T. Andrew Mobley) and a PhD in 2009 from the University of California, Berkeley (Profs John Arnold and Robert G. Bergman). He held post-doctoral positions at the Max Planck Institute for Bioinorganic Chemistry (now Chemical Energy Conversion; Prof Dr Karl Wieghardt) and Los Alamos National Laboratory (Prof James M. Boncella) before joining the faculty at the University of Pennsylvania in 2015. His awards include Glenn T. Seaborg and Director's Post-doctoral Fellowships at LANL, a 2017 NIH MIRA Award for Early-Stage Investigators, and a 2019 NSF CAREER Award.

---

Introduction

The incorporation of internal electrostatic fields into transition metal complexes is a new and rapidly developing design strategy that is being used both for rationally impacting chemical reactivity patterns and for modulating the physical characteristics of metal complexes.^1–7 This article aims to use a brief overview of the field to support our perspective that electrostatic effects in molecular complexes are poised to provide an entirely new paradigm for synthetic chemists to use when constructing molecules with tailor-made functions. In the following text, we first briefly summarize the nature of electrostatic fields and provide a glimpse into how tangential areas of study have applied these concepts to chemical reactivity. The work then describes recent examples of electrostatic effects that are associated with homogeneous transition metal complexes and concludes with a statement on our view of the field's future trajectory. For those interested in a broader understanding of electric field effects on chemical reactions and structure, we refer the reader to a recently published book that covers an extensive list of topics that derive from the same principles discussed herein.⁷

Electric fields (EFs) are central to the study of atomic physics and chemistry. EFs describe the attractive forces between electrons and protons – a concept at the heart of atomic structure and chemical bonding. Electric field lines (Fig. 1) are often used as qualitative depictions of an EF that illustrate the direction of the force vectors within the field. The arrows of the EF lines are defined, according to the chemistry convention, as the direction that a negative test charge would be pushed if placed into the field (i.e. negative to positive unless otherwise specified).

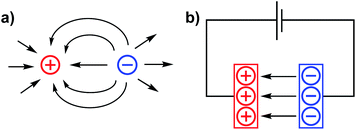Fig. 1 Electric field lines for (a) point charges of opposite sign in close proximity, and (b) separated anodic and cathodic plates of a capacitor.

In the case of an EF generated by charged species that are not changing in position with respect to time, the field can be simplified to the description of an electrostatic field (ESF).¹ In this case, the laws of electrostatic effects can be described by Coulomb's law (eqn (1)), which describes the force that an electrically charged particle, q₁, exerts on another charged particle, q₂, at a distance of r:

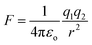where ε represents the permittivity of the medium. Rearrangement of eqn (1) 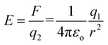yields eqn (2), which defines the electrostatic field, E, as the force per unit of charge at each point in space:

Since electrons bear negative charges, their positions in space and their associated energies should be susceptible to the presence of ESFs. In this way, the incorporation of internal or external ESFs into chemical reactions provides a promising new avenue for imposing control over reaction outcomes and increasing reaction efficiencies through the stabilization of key transition states. To showcase how electrostatic fields have been used in systems that might be considered molecular-adjacent, we will first highlight select examples of the study of electrostatic effects in enzymes and on surface-tethered molecular compounds. These case studies provide clear evidence that oriented electric fields have demonstrable impacts on chemical reactivity profiles.

ESFs in non-homogeneous systems

The contribution of ESFs to enzyme function was first proposed and studied by Warshel⁸ and has gained traction in enzymology as a key structural feature for some enzymes.^9–12 A particularly dramatic and well-studied example, reported by Boxer and co-workers, involves ketosteroid isomerase (KI), an enzyme that catalyzes the transformation of sterols into hormonally-active ketosteroids.⁹ The authors studied the enolization of 5-androstene-3,17-dione (Fig. 2), which is known to undergo the same isomerization mechanism in aqueous solution as in the enzyme, thereby allowing for a direct measure of the catalytic effect imparted by the wildtype enzyme (18 kcal mol⁻¹).^13–17 Importantly, the lengthening of the C=O bond in 5-androstene-3,17-dione during the rate-limiting enolization transformation (Fig. 2) corresponds with an increased dipole moment associated with the bond. Since the transition state for this process is expected to have a larger dipole moment along the C–O bond axis than the starting material, the presence of an opposing ESF would selectively stabilize the transition state, thereby contributing to the catalytic effect of the enzyme.

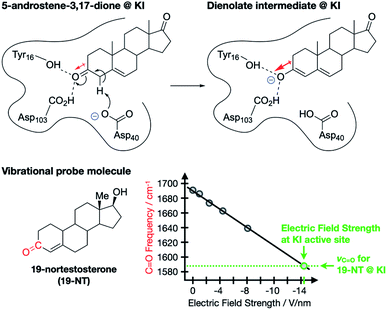Fig. 2 Enolization reaction of 5-androsten-3,17-dione occurring at the active site of ketosteroid isomerase (KI).^9,11 Red arrows indicate dipole moments associated with the C=O and C–O bonds. 19-nortestosterone was used as a vibrational probe for measuring local ESF strengths via Stark spectroscopy.

To test this hypothesis, Boxer and co-workers used vibrational Stark spectroscopy to quantify the magnitude of the ESF at this position for KI and several KI mutants. Doing so required the use of a vibrational probe molecule with a known (or obtainable) Stark tuning rate that would bind irreversibly to the active site of the enzyme and provide a distinct vibrational signature. These requirements were satisfied with 19-nortestosterone, and wild-type KI was found to impart an ESF strength of 14.4(6) V nm⁻¹ on its C=O bond, while various mutations led to subdued ESF strengths. Crucially, a linear correlation between enzyme catalytic performance and ESF strength was established for KI and its mutants, suggesting that ESFs play a dominant role in the enzyme's catalytic abilities. Using the measured ESF strength from wild-type KI, the authors estimated that the presence of ESFs in the active site of KI accounts for 72% of the total catalytic effect of this enzyme. Accumulated work in this area of enzymology similarly corroborates that enzymatic activity is generally impacted by strong, local electrostatic effects of this type.^{10,11,18–24}

Outside the area of enzymology, a range of work has been published studying the effects of ESFs on chemical structure and reactivity, including (i) the generation of bulk, external ESFs between parallel electrode plates,^25–27 (ii) the study of radical species and their electrostatic stabilization by ESFs,^28–32 and (iii) computational studies probing how selectivity of organic reactions can be manipulated through incorporation of charged functional groups or cation–π interactions.^33–42

The pioneering work of the Shaik group laid the foundation for the accepted use of bulk external electric fields for catalysis.^1,7,43–45 In 2010, Shaik and co-workers computationally predicted that even with neutral molecules (dienes and dienophiles), bond forming rate enhancements can be achieved through application of properly aligned ESFs.⁴⁴ In their study, the authors showed that varying the alignment and magnitude of computationally-generated ESFs led not only to changes in the predicted rates for Diels–Alder reactions, but also affected the predicted exo/endo selectivity of various reaction products. Several years later, Darwish, Ciampi, Diez-Perez, and Coote experimentally verified the Shaik predictions in a groundbreaking 2016 report through use of a scanning tunnelling microscopy (STM) “break junction” approach.²⁷ In their experiments, the authors tethered dienes to an STM tip, which was brought into close contact (ca. 1 nm) to dienophiles tethered to a flat gold surface (Fig. 3a). An ESF was generated through application of a potential bias across the junction, the magnitude and sign of which were systematically modulated. Importantly, this experimental setup allowed for a high level of control over the orientation of the ESFs with respect to the substrate molecules. The frequency of chemical events was monitored by counting spikes in current, indicating a junction spanned by the Diels–Alder product. Accordingly, a five-fold increase in the reaction frequency was found to occur when an ESF was applied from dienophile to diene (depicted with an arrow in Fig. 3b). It was postulated that this field orientation stabilizes a minor resonance form of the transition state in which an anionic charge is positioned on the diene and a cationic charge is positioned on the dienophile (Fig. 3b). Computational analysis of the reaction qualitatively corroborated the experimental findings.

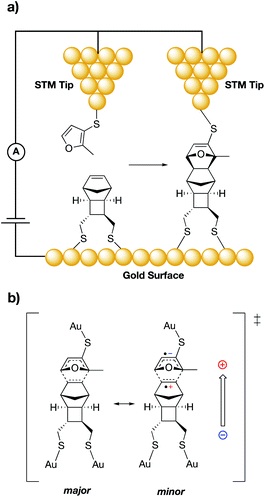Fig. 3 (a) Experimental set-up for the Darwish, Ciampi, Diez-Perez and Coote study of the Diels–Alder reaction between an STM tip and a gold surface.²⁷ (b) Resonance structures of a proposed Diels–Alder reaction transition state; the minor resonance contributor (right) can be stabilized by a properly aligned ESF (shown with an arrow).

In 2013, Kanan and co-workers found success in applying bulk ESFs to effect control over the products formed in the (porphyrin)Rh-catalyzed intramolecular reactions of 1-diazo-3,3-dimethyl-5-phenylhex-5-en-2-one (Fig. 4).²⁶ Bulk ESFs were generated through application of a potential bias across electrode plates. The Rh porphyrin catalyst was tethered to the electrode surface, orienting the catalyst with respect to the direction of the applied field. In the absence of a potential bias, the ratio of the insertion product (a) to the cyclopropanation product (b) was found to be ca. 1 : 10 (Fig. 4). This ratio increased as a voltage was applied (1.0 : 6.3 at −5 V), indicating a greater coulombic stabilization of the zwitterionic transition state associated with the formation of product a as compared with the “noncharged” transition state associated with the formation of product b (Fig. 4). Even larger changes to the a : b product ratio were observed upon decorating the electrode surface with additional charged functionalities (1.9 : 1.0 at −5 V), the results of which represent an 8-fold change in product selectivity due to the presence of ESFs.

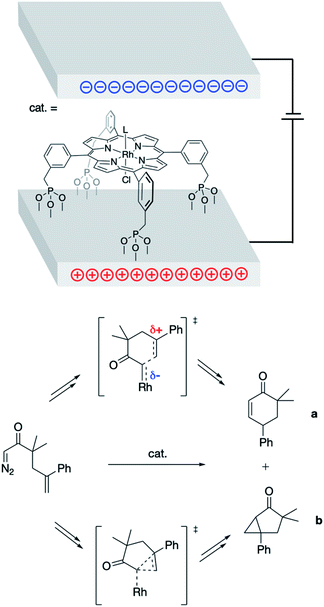Fig. 4 Parallel electrode plates used to impose external ESFs during the Rh porphyrin-catalyzed rearrangement of 1-diazo-3,3-dimethyl-5-phenylhex-5-en-2-one into products a and b.²⁶ Key transition states associated with the formation of a and b, which are inequivalently (de)stabilized by the presence of ESFs, are shown.

The examples outlined above beautifully demonstrate how ESFs can be harnessed to directly impact chemical reactivity through transition state (de)stabilization and selectivity control. These techniques, however, require tedious modifications to substrate and/or catalyst in order to properly align the ESFs in orientations that will impart desired reactivity. Additionally, the strength of the ESFs are limited by the dielectric breakdown of the solvent medium, which generally occurs at field strengths between 0.01–0.1 V nm⁻¹,⁴⁶ which is ca. 2 orders of magnitude smaller than ESFs present within enzyme active sites (as discussed above).^9–11

ESFs in homogeneous metal complexes

Homogeneous inorganic chemistry is a field that has the potential to benefit tremendously from the incorporation of rationally oriented internal ESFs. Charged groups can be positioned in the secondary coordination spheres of metal complexes through direct incorporation into the ligand scaffolds, then investigated for their ability to promote small molecule binding and/or reactivity. This strategy has the advantages of (a) maintaining a high degree of control over the positions and orientations of the charged moieties and (b) enforcing small distances between the charges and the substrate molecules, which is important for imparting strong ESFs (eqn (1) and (2)) while avoiding dielectric breakdown of the solvent media. As will be described throughout this perspective, the pursuit of harnessing internal electrostatic interactions to impart productive reactivity has recently become a burgeoning subfield of homogeneous inorganic chemistry.

Valence manifold tuning with through-space electrostatic effects

A central challenge to proving out the impact of intramolecular, through-space electrostatic effects on the valence manifolds of transition metal complexes comes in disentangling through-space effects from inductive effects. Modifications that introduce charged residues may alter the electron donating/withdrawing capability of the ligand, which would be expected to have more classical effects on the metal center's valence manifold. The research described in this section has been used to illustrate the ability of through-space electrostatic effects to tune the redox properties and valence orbital energies within metal complexes in a manner that is orthogonal to traditional primary coordination sphere effects. We note that while numerous examples are known of tightly bound Lewis acids impacting the properties of metal centers,^47–54 these will not be discussed below, since their through-space electrostatic effects cannot be fully disentangled from traditional Lewis acid effects.

In 2017 the Yang group reported a series of cobalt complexes bound by a novel N,N′-ethylene-bis(salicylimine) (salen)-based ligand containing a macrocyclic crown ether moiety in the secondary coordination sphere, in which they positioned charges in the form of alkali or alkaline earth metals (Na⁺, K⁺, Ca²⁺, Sr²⁺, and Ba²⁺) (Fig. 5a).⁵⁵ In this seminal study, the authors discovered large anodic shifts in the Co^II/Co^I redox couples as compared to the analogous Co^II complex bound by the salen ligand derivative with methoxy group substitution in place of the crown ether functionality. Only minor deviations from the parent complex were observed in the UV-vis and IR spectra for these compounds, and the primary coordination spheres of the complexes were found to be similar upon examination of their solid-state structures. These observations led the authors to conclude that the large shifts in the Co^II/Co^I redox couples were not a result of inductive effects upon coordination of the Lewis acidic metals to the secondary coordination spheres. Instead, the shifting redox couples of the Co^II complexes were found to correlate most closely with the calculated electric field potentials imparted by the alkali/alkaline earth metals, thereby implicating internal ESFs in anodically shifting the redox couples.

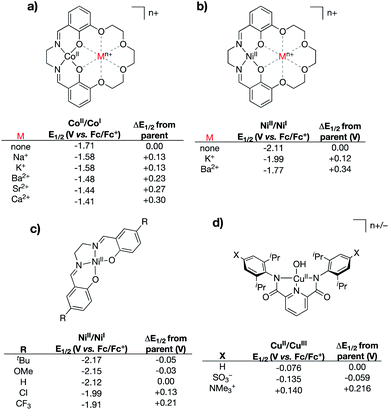Fig. 5 Various complexes that have been used to delineate inductive vs. electrostatic effects.^55–57 For (a) and (b) “none” indicates the salen complex containing methoxy group substitution at the 3-positions of the salen rings in place of the crown ether functionality.

In 2018, the Yang and Alexandrova groups published a synthetic/computational study using the same crown ether-modified salen ligand system.⁵⁶ In this study, the authors coordinated the ligand to Ni^II and positioned both monocationic (K⁺) and dicationic (Ba²⁺) metals within the pendant crown ethereal moiety (Fig. 5b). Compared to the analogous complex bearing salen with methoxy substitution in place of the crown ether, the Ni^II/Ni^I redox couples were found to shift to more positive potentials as the charge in the secondary coordination sphere was increased (120 mV shift for K⁺, 340 mV shift for Ba²⁺). The Ni^II/Ni^I redox couples and UV-vis spectral features for this series of compounds were compared to those of an analogous series of Ni^II complexes bound by salen ligands containing substitution at the 5-positions of the salen aromatic rings (–CF₃, –Cl, –^tBu, and –OMe) (Fig. 5c). Despite shifts in UV-vis spectral features being smaller for the complexes containing charged metals in the secondary coordination spheres (indicating smaller inductive changes), the measured shifts in the Ni^II/Ni^I redox couples were found to be significantly larger, indicating that electrostatic effects (as opposed to inductive effects) were the primary driver associated with the anodically shifting potentials. Computational analysis of the complexes containing K⁺ and Ba²⁺ in the secondary coordination spheres indicated that the valence orbitals were uniformly stabilized via incorporation of the main group ion; the degree of stabilization was found to be dependent on the magnitude of the charge of the ion.

The Tolman group reported a series of bis(carboxamide)pyridine ligands in which distal charges (both cationic and anionic) were positioned in the secondary coordination spheres of the ligands via incorporation of charged functional groups (–NMe₃⁺ and –SO₃⁻) at the 4-positions of the carboxamide aryl rings (Fig. 5d).⁵⁷ Cupric hydroxide complexes bound by these ligands, and by the parent ligand (without charges in the secondary sphere), were synthesized. Notably, the resulting series of complexes displayed similar solid-state geometries, as indicated by X-ray crystallography, as well as remarkably similar UV-vis and EPR spectra, suggesting that the primary coordination spheres of the complexes are minimally affected by the distal charges. However, evaluation of the electrochemical properties of these complexes revealed notable changes in the (formally) Cu^II/Cu^III redox couples, wherein the (–NMe₃⁺)-substituted complex exhibited the most anodic redox potential (140 mV vs. Fc/Fc⁺), while the (–SO₃⁻)-substituted complex exhibited the most cathodic redox potential (−135 mV vs. Fc/Fc⁺). This study, in combination with Yang's studies discussed above, highlight how appropriately positioned charges can impart through-space coulombic interactions that either stabilize or destabilize electron transfer involving transition metal complexes.

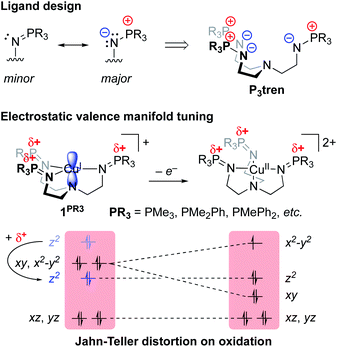
Our group recently reported a series of trigonal pyramidal Cu^I complexes bound by a new series of tren-based tripodal tris(phosphinimine) ligands (Fig. 6) containing cationic pseudo charges in the secondary coordination spheres.⁵⁸ The phosphinimine moieties within the ligand frameworks are best described by a zwitterionic resonance picture, in which there exists anionic charge on nitrogen and cationic charge on phosphorous, resulting in substantial amounts of cationic potential being localized in the secondary coordination spheres of the complexes (Fig. 7). The presence of these charges were calculated to induce ESF force vectors between 3–12 V nm⁻¹ at ca. 2.2 Å from Cu along the canonical z-axes, oriented away from Cu. To assess the impacts of the unique charge distribution within these complexes, we turned to density functional theory (DFT) to compute their valence manifolds. The a₁-symmetric d_z² orbital (HOMO-2) of each of these complexes were found to be uniquely stabilized in energy as compared to those of literature analogs containing isostructural primary coordination spheres. Importantly, the degree of the d_z² stabilization was found to correlate with both the amount of cationic potential contained in the secondary coordination spheres of the complexes and with the strength of the z-axis-oriented ESFs. This correlation implicates the cationic charges emanating from the phosphonium residues in the secondary coordination spheres of the phosphinimine ligands as directly impacting the d-orbitals of the Cu^I complexes. The Cu^I/Cu^II redox couples measured for these complexes were found to be highly cathodic, with the most reducing analog (PR₃ = PMe₃) being the most reducing isolated Cu^I complex reported to date (−780 mV vs. Fc/Fc⁺). These highly cathodic potentials were found to be an indirect consequence of the internal ESFs: the electrostatic stabilization of the a₁ orbitals in these complexes resulted in unique (as compared to the isostructural literature analogs analyzed in this study) 2 : 1 : 2 d-orbital splitting patterns. These splitting patterns were found to induce classic Jahn–Teller distortions upon oxidation to Cu^II, which subsequently provided an additional thermodynamic driving force (estimated to be ∼6 kcal mol⁻¹ for PR₃ = PMe₃) for electron transfer, thereby shifting the Cu^I/Cu^II redox couples to more negative potentials.

Fig. 6 Ligand design strategy and application of a series of phosphinimine-substituted tren ligands (P₃tren) and their Cu^I coordination complexes. ESFs emanating from the phosphonium residues in the secondary coordination spheres stabilize the a₁-symmetric d_z² orbital, resulting in unique 2 : 1 : 2 d-orbital splitting patterns that lead to Jahn–Teller distortions on oxidation to Cu^II.

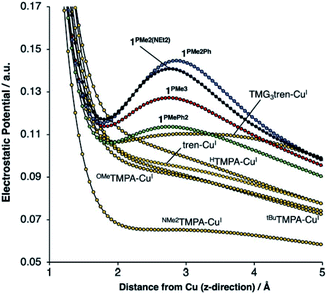Fig. 7 DFT-calculated electrostatic potential maps along the canonical z-axes for various copper(I) complexes. Reproduced from ref. 57 with permission from the Royal Society of Chemistry.

The Holland group recently reported an iron amido complex bound by an SCS pincer ligand (Fig. 8).⁵⁹ Most notable for the present discussion was their observation of an interesting result when trying to computationally reproduce the Mössbauer parameters for a bis(trimethylsilyl)amido complex that featured an outersphere [K(18-crown-6)(thf)₂]⁺ counterion (Fig. 8). The exclusion of the counterion in the DFT calculations resulted in poor modelling of the ⁵⁷Fe Mössbauer parameters, and inclusion of K⁺ without 18-crown-6 also performed poorly. Only when the full counterion was included in the calculation were they able to achieve a satisfactory fit. When K⁺ was encapsulated by 18-crown-6, the authors calculated a Löwdin charge of −0.06 on potassium, as compared to a charge of +0.99 at potassium in the ether-free species. This suggests that the distribution of cationic charge throughout the [K(18-crown-6)(thf)₂]⁺ ion and its associated effect on the metal center is critical to the electronic structure at Fe. The through-space electrostatic interaction changes the ordering and orbital energies of the valence manifold, stabilizing d_z² in the presence of the K⁺ (Fig. 8).

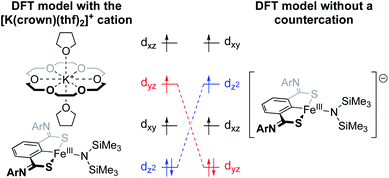Fig. 8 Valence manifold tuning at an Fe^III amido complex supported by an SCS pincer ligand.⁵⁹ The full [K(crown)(thf)₂]⁺ ion was found to be critical for reproducing experimental observables.

Molecular electrostatic effects in small molecule activation and catalysis

One of the major motivations behind tuning the properties of a metal center is to target specific reactivity. Metal complexes with ligand scaffolds containing charged moieties have been shown to take advantage of both changes to the metal center and the stabilization of reactive intermediates to demonstrate control and selectivity during catalysis. Thus, the works described in this section illustrate research that demonstrates ways in which electrostatic effects impact catalytic processes in various subfields of chemistry.

Electrocatalytic CO₂ and O₂ reduction. The subfield of CO₂ reduction electrocatalysis has recently experienced great improvements through the incorporation of internal ESFs. In 2016, Savéant and co-workers reported a series of iron tetraphenylporphyrin complexes containing either cationic (–NMe₃⁺) or anionic (–SO₃⁻) functional group substitutions at the ortho- or para-positions of the porphyrin phenyl rings (Fig. 9a).⁶⁰ In this study, the authors found that the iron complex containing cationic charges in closest vicinity to the CO₂ binding site (the ortho-substituted analog) was by far the most successful CO₂ reduction electrocatalyst, displaying both decreases in catalytic overpotential and increases in turnover frequencies (TOFs). This catalyst was found to outperform all other reported CO₂ reduction electrocatalysts, and the authors proposed a through-space coulombic stabilization of an intermediate Fe : CO₂ adduct as being operative in its catalytic success (Fig. 9b). Key to this postulation, the authors also reported a series of iron tetraphenylporphyrin complexes in which inductive effects were modulated through the perfluorination of various numbers of prophyrin phenyl groups (monokis-, bis-, and tetrakis-pentafluorophenyl groups on porphyrin) (Fig. 9c). A linear trend between TOF and catalytic overpotential was established across this series; however, the complexes containing charged residues deviated from this trend, displaying larger-than-expected TOFs for –NMe₃⁺ functionalization and smaller-than-expected TOFs for –SO₃⁻ functionalization, thereby suggesting that the differences observed in the electrocatalytic performances of the ammonium/sulfate-substituted complexes were independent of conventional inductive effects.

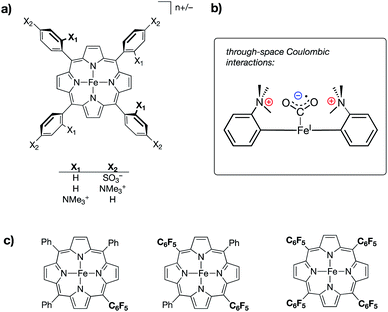Fig. 9 (a) Iron tetraphenylporphyrin-based CO₂ reduction electrocatalysts containing either cationic (–NMe₃⁺) or anionic (–SO₃⁻) substituents at different positions on the porphyrin phenyl rings;⁶⁰ (b) schematic of a proposed through-space coulombic interaction between cationic ammonium groups on the tetraphenylprophyrin ligand and a bound CO₂˙⁻ molecule; and (c) a series of iron tetraphenylporphyrin complexes in which inductive effects were systematically modulated through incorporation of pentafluorophenyl substituents.

Following the work by Savéant, several reports of CO₂ reduction electrocatalysts containing charged functional groups have been reported (Fig. 10),^61–67 with all showing that the incorporation of second sphere cationic charges results in enhanced electrocatalytic CO₂ reduction. Strong support for these catalytic improvements as being electrostatic in nature was provided by Mayer and co-workers in a publication featuring experimental and computational analysis of small molecule (CO₂, O₂, and CH₃COO⁻) binding to the Savéant iron tetraphenylporpyrin complex containing –NMe₃⁺ substitution at the ortho-positions of the phenyl rings.⁶⁸ In this study, the authors measured acetate and dioxygen equilibrium binding constants and computationally evaluated interactions between the bound small molecules and the ammonium groups in the secondary coordination sphere. Acetate binding was experimentally found to be inhibited in solvents with higher dielectric constants or in the presence of high concentrations of electrolyte, thereby implicating the permittivity of the reaction medium as influencing the electrostatic effects as predicted by Coulomb's law (eqn (1) and (2). DFT evaluation of rotamers of the CO₂˙⁻ and O₂˙⁻ adducts were undertaken, in which the distal oxygen atoms of these small molecules were directed either towards, or away from, the ammonium groups in the secondary coordination sphere. These calculations revealed that through-space coulombic interactions with the –NMe₃⁺ groups led to a stabilization for the CO₂-bound species (−5.5 kcal mol⁻¹ when the oxygens were directed toward the ammonium groups) and to a slight destabilization for the O₂-bound species (+1.1 kcal mol⁻¹ when the distal oxygen was directed toward an ammonium group). The results of this study showcase the stabilizing effect that charged moieties can have on CO₂ reduction/binding and lend support to the assertion that through-space electrostatic effects productively contribute to catalysis in the systems depicted in Fig. 10.

Fig. 10 Examples of charge incorporation into the secondary coordination spheres of CO₂ reduction electrocatalysts.^61–67

Mayer and co-workers recently reported the electrocatalytic oxygen reduction reaction (ORR) using a Fe^III electrocatalyst bound by the tetraporphyrin ligand reported by Savéant (Fig. 11).^69–72 The authors found no catalytic improvement over other iron porphyrin electrocatalysts, corroborating the study discussed above in which O₂ binding was (nearly) unaffected by the presence of cationic groups in the secondary coordination sphere.⁶⁸ Previous studies with iron porphyrin ORR electrocatalysts established scaling relationships between log(TOF_max) and effective overpotential under various reaction conditions, wherein changes in acid concentration, acid pK_a, O₂ concentration, or catalyst E_1/2 values led to increases in log(TOF_max) at the expense of effective overpotential, or vice versa.⁶⁹ For the Fe^III electrocatalyst studied by Mayer, however, modulating the identity of the buffer solution led to an unprecedented inverse scaling relationship between log(TOF_max) and effective overpotential. The cause of this phenomenon was found to relate to buffer anion (carboxylate) binding to the catalyst, which was strongly enhanced by the presence of the cationic charges in the secondary coordination sphere. This binding of the buffer conjugate base resulted in changes to the E_1/2 values of the iron catalyst (cathodic shifts with increasing buffer pK_a), which synergistically combined with the established scaling relationship of buffer acidity to result in an unprecedentedly efficient ORR electrocatalyst (low effective overpotential and high TOF_max).

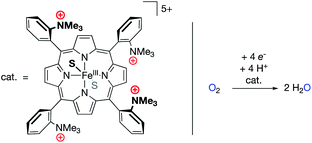Fig. 11 An oxygen reduction reaction (ORR) electrocatalyst with pendant –NMe₃⁺ units in the secondary coordination sphere.^69,70

Biomimetic (heme)Fe oxo reaction selectivity. In 2004, Shaik and co-workers computationally studied the impacts of applying external ESFs in the vicinity of Compound I, the iron-oxo porphyrin active site of cytochrome P450 enzymes.⁷³ In nature, Compound I is capable of both hydroxylating strong C–H bonds and epoxidizing C=C bonds, which has prompted widespread interest from the biochemistry and synthetic chemistry communities alike.^73,74 In their study, Shaik and co-workers found that the application of computationally generated ESFs of varying magnitude and orientation were capable of impacting the electronic structure of Compound I, which in turn led to the (de)stabilization of transition states toward the aforementioned reactivity. The authors found that the selectivity for hydroxylation vs. epoxidation could be rationally adjusted through incorporation of appropriately oriented external ESFs. Shaik and co-workers later showed that similar results could be obtained with nonheme iron oxo complexes when ESFs were oriented along the Fe=O bond axis.⁷⁵

Following in the wake of the Shaik predictions, the Groves group reported the synthesis of an oxyferryl porphyrin radical–cation complex, designed as a mimic of Compound I, that contained cationic pyridinium substitutions around the periphery of the complex (Fig. 12a).⁷⁶ The complex was shown to undergo kinetically fast C–H hydroxylation reactions, as compared with literature analogs. In a related 2017 publication, Groves and co-workers reported a ferric hydroxide complex bound by a porphyrazine ligand containing charged pyridinium substitutions around the periphery of the ligand (Fig. 12b).⁷⁷ This ferric hydroxide complex was found to undergo hydrogen atom abstraction reactions to form the corresponding ferrous aqua complex, the O–H bond dissociation energy (BDE) of which was estimated to be 84 kcal mol⁻¹. Again, incorporating charges into the ligand structure was found to drastically increase the rates for these reactions, with hydrogen atom transfer (HAT) rates for this complex being 5–6 orders of magnitude greater than those of other reported ferric hydroxide complexes.

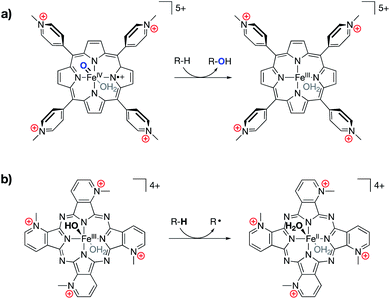Fig. 12 (a) An iron oxo complex shown to engage in fast C–H hydroxylation chemistry,⁷⁶ and (b) an Fe^III hydroxide complex shown to engage in unprecedentedly fast HAT reactivity with C–H bonds.⁷⁷

In a recent computational study, Shaik and co-workers characterized the fast kinetics observed in Groves' systems through the lens of electrostatic effects.⁴³ The authors performed DFT analysis on C–H activation reactions using both the Groves complexes and “uncharged” analogs in which the cationic pyridinium groups were replaced with neutral pyridine residues. Using their recently-developed “TITAN” code,⁷⁸ the authors calculated the ESF strengths along the Fe=O bonds of the Groves complexes. Computationally generated ESFs of equal magnitudes were then imposed along the Fe=O bond axes of the “uncharged” analogs, resulting in calculated transition states that closely reproduced the geometries and energies of the transition states calculated for the Groves complexes. These results implicated ESFs emanating from the charged pyridinium moieties in these complexes as being the dominant contributor to the overall catalytic effect. In a related study, Shaik and coworkers applied this approach to C–H activation in metal-free systems, wherein radical (de)stabilizations in the presence of distonic charges were almost perfectly reproduced by computationally-generated ESFs.⁷⁹

Oxidative addition and cross coupling reactions. The use of salt additives in palladium-catalyzed cross coupling reactions have been shown to impact kinetics and/or reaction efficiencies.^80–84 However, interpretations of the manner in which these salt additives lead to the observed reaction outcomes are varied. The Shaik group recently published a computational study demonstrating the ability of ESFs to sensitively tune transition state barriers associated with the rate-limiting oxidative addition steps in these reactions.⁴⁵ Oxidative addition involves charge transfer from metal to substrate throughout the reaction coordinate, which the authors reasoned should be susceptible to the presence of a properly aligned external ESF. As such, the authors found that external ESFs aligned along the vector of net charge transfer (the “reaction axis”) were able to lower transition state energies, ultimately leading to changes in the reaction mechanisms. Importantly, these calculations shed light on the role of salt additives in cross coupling reactions through comparision of the oxidative addition potential energy surfaces with and without the presence of an outer-sphere chloride anion (Fig. 13a and b). When a chloride anion was included in the calculation (non-covalently bound to the phosphine ligands, as had been previously established),^85,86 the transition state was found to be stabilized by ca. 9 kcal mol⁻¹. Using the TITAN code, the authors calculated the magnitude of the ESF emanating from the chloride to be 3.6 V nm⁻¹. Incorporating an external field of this magnitude into the calculation in the absence of chloride produced a transition state that was nearly identical, in both geometry and energy, to that in the presence of chloride (Fig. 13b and c), thereby implicating the ESF generated by the chloride as being the dominant factor in stabilizing the oxidative addition transition state.

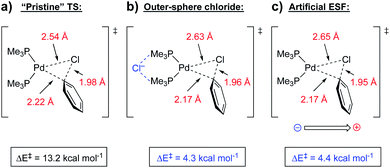Fig. 13 Oxidative addition transition states for (a) reaction without the presence of a chloride anion, (b) with the presence of a non-covalently bound chloride anion, and (c) with an artificial oriented ESF (3.6 V nm⁻¹) in place of the chloride anion.⁴⁵

Other ESF-impacted reactivity. Using their previously-reported salen-based ligand containing a crown ether functionality, the Yang group, in 2018, reported the aerobic oxidation and oxygenation of cyclohexene using Fe^III catalysts containing either K⁺ or Ba²⁺ tethered in the secondary coordination sphere (Fig. 14).⁸⁷ In previous studies with salen-Fe^III catalyst derivatives, only complexes with sufficiently oxidizing Fe^III/Fe^II redox couples (more anodic than −0.27 V vs. Fc/Fc⁺) were found to catalyze this reaction.⁸⁸ The Fe^III/Fe^II redox couples for the salen-Fe^II catalysts containing K⁺ or Ba²⁺ in the secondary coordination spheres are more cathodic than the threshold that is thought to be needed for C–H oxidation (−0.71 V and −0.57 V respectively), but both complexes were found to be competent catalysts for the transformation of cyclohexene to cyclohexanol/cyclohexanone in the presence of O₂. Evidence was provided for an established radical-chain mechanism as being operative in this system, wherein oxidation of an organic hydroperoxide complex by the Fe^III catalyst is rate limiting.^88–90 The authors speculated that the redox-innocent metals (K⁺ or Ba²⁺) tethered in the secondary coordination spheres of the catalysts interact with the lone pairs of the organic hydroperoxide to promote electron transfer. Additionally, these complexes exhibited unprecedented stability to water during catalysis, the degree to which scaled with the magnitude of charge (Ba²⁺ > K⁺). This study further highlights the orthogonal nature between primary and secondary coordination sphere effects on reactivity; the cationic charges in the secondary coordination spheres of the catalysts not only impacted the redox potentials but were also found to be integral in stabilizing key transition states and/or intermediates on the proposed catalytic cycle.

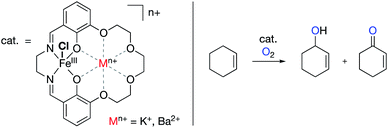Fig. 14 Aerobic oxygenations of cyclohexene using Yang's Fe^III salen catalyst with redox innocent metals tethered in the secondary coordination spheres.⁸⁷

Recently, the Yang group explored electrostatic effects on C–H activation for a series of manganese nitride complexes supported by their salen-based ligand scaffold.⁹¹ By varying the charge in the crown ether moity from Na⁺ to Eu³⁺, the reduction potentials of the complexes were found to shift anodically by upwards of 730 mV compared to the analogous non-crown salen manganese nitrido species. However, increasing the charge was shown to decrease the basicity of the manganese(v) nitride species, resulting in relatively consistent bond dissociation free energies across the series. Upon exploring the oxidation of dihydroxyanthracene with the Mn^VI nitride species, they observed increasing yields of anthracene as the magnitude of the cationic charge was increased. The authors postulated that this observation was due, in part, to the inhibition of a competing N–N coupling reaction to generate N₂ due to intermolecular repulsion between complexes, thereby allowing more of the Mn^VI nitride to perform C–H oxidation (Fig. 15). This result mirrored their previous studies,⁹² whereby complexes with the most cationic charge in the secondary coordination sphere had the smallest k₂ rate constants associated with N₂ formation, despite being the most oxidizing complexes. These results are counter to what had previously been observed with salen-bound Mn^V nitride complexes,⁹³ wherein complexes with more cathodic Mn^V/Mn^IV redox couples displayed slower rates of N₂ formation, suggesting that ESFs in the secondary coordination sphere inhibit the N–N coupling reaction.

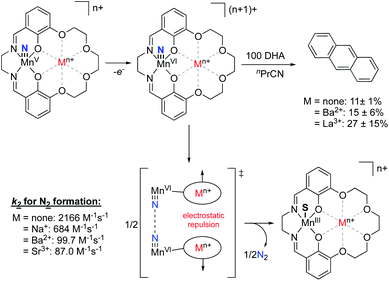Fig. 15 Mn^V nitride complexes that were shown to display inverse scaling relationships between Mn^V/Mn^IV redox potentials and the rate of N₂ release upon oxidation.^87,91

Recently, the Anderson group reported a modified version of methyldiphenyl phosphine in which the methyl group was functionalized with a trifluoroborate unit (Fig. 16). The inductive and electrostatic properties of this unique, anionic phosphine were studied through its use as a ligand on nickel/rhenium and through the formation of a phosphine selenide.⁹⁴ This latter species was studied in detail, and analysis of its ¹J_PSe NMR coupling constants in a variety of solvents revealed a dramatic dependence on the solvent dielectric constant. Since the R₃P=Se interaction exhibits significant ylidic character in the form of R₃P⁺–Se⁻, the impact of the solvent dielectric on ¹J_PSe suggested that local ESFs emanating from the borate group impact the ground state of the molecule. Computational analysis predicted that the borate residue exerted an effective Boltzmann weighted electric field of −0.107 V nm⁻¹ that was oriented parallel to the P–Se bond. Importantly, upon application of a computational external electric field of this magnitude on Se=PPh₂Et, identical changes (within error) to ¹J_PSe were computed. The electrostatic effects imparted by this borate-functionalized phosphine were further suggested to enhance the reactivity of the ligand's transition metal complexes, enabling faster C–F bond borylation of various substrates as compared to neutral phosphines.

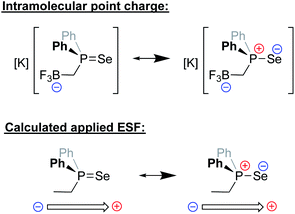Fig. 16 Top: major resonance contributors to the ground state of a novel phosphine selenide architecture bearing an appended –BF₃⁻ unit.⁹⁴ Bottom: the computational use of a point charge near a neutral varient (–Et) of the phosphine was needed to mimic experimental observables for the properties of the phosphine selenide.

Intermolecular electrostatic interactions in homogeneous systems

As with the previously-discussed Mn–nitride (Yang) and oxidative addition studies (Shaik), electrostatic interactions have been harnessed intermolecularly, either between complexes or between complexes and their counter-ions, to modulate reactivity and reaction selectivity. Although not an exhaustive collection, several recent and well-characterized examples of this class of electrostatic effect are briefly highlighted in this section.

In 2014, Kanan and co-workers reported regioselective control of Au^I-catalyzed aryl alkynyl sulfide rearrangements to dihydrobenzothiepinones using electrostatic anion–cation pairing in the catalysts (Fig. 17).^95,96 In this system, the ratio of the resulting regioisomers were found to change depending on (a) the dielectric constant (ε) of the reaction solvent and (b) the identity of the counter anion (SbF₆⁻, PF₆⁻, BF₄⁻, or BAr^F₄⁻) employed. The authors used DFT analysis to evaluate the electronic structures of the transition states for the two regioisomers studied in these reactions (a and b in Fig. 17) and discovered that differences in the dipole moments of the transition states between the two regioisomers was dependent on the identity of substitution at the 3-positions of the aryl rings. In almost all cases, the dipole of the transition state associated with the formation of regioisomer b was calculated to be larger than that of the transition state associated with the formation of regioisomer a. Importantly, Δρ values for the various substrates were found to correlate with the experimentally determined differences in regioselectivity in high polarity vs. low polarity solvents (dichloromethane, ε = 8.93 vs. toluene, ε = 2.38). These results are consistent with an electrostatic interaction between the counter-anion and the dipole of the reaction's transition state to affect the ultimate regioselectivity of the reaction. In low polarity solvents, regioisomer b is electrostatically favored over regioisomer a; however, in higher polarity solvents (ε ≥ 8) the cation–anion pairing is quenched, and regioisomer b becomes less-favored or disfavored as compared to regioisomer a. Consistent with this model, when larger anions (BAr^F₄⁻) were employed, little to no difference in regioselectivity was observed upon varying the dielectric of the solvent medium, indicating that the larger structure of BAr^F₄⁻ prevents close contact between the anionic charge and the bound substrate, thereby disallowing electrostatic influence on regioselectivity.

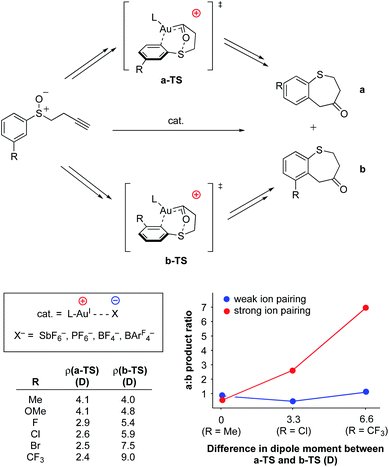Fig. 17 Au^I-catalyzed rearrangement of aryl alkynyl sulfides to dihydrobenzothiepinones.^95,96 The regioselectivity of the reaction was found to be dependent on the amount and distribution of charge density accumulated within the transition state.

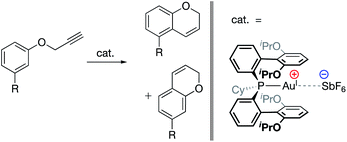Fig. 18 Au^I-catalyzed hydroarylation reaction in which product regioselectivity is modulated via electrostatic interaction between the cationic Au^I complex and the SbF₆ counteranion.⁹⁷ Substrate substitution: R = Cl, Br, I, OTf, Me, 3,4-(CH₂)₃, OMs, OMe, and OAc.

Similarly, in 2017, Kanan and co-workers reported a Au^I-catalyzed hydroarylation reaction in which the regioselectivity of the products was modulated via interaction with the catalysts' SbF₆⁻ counteranions (Fig. 18).⁹⁷ Experimental modulation of the solvent dielectric was again found to substantially skew the ratio of regioisomers observed to form, the trends of which were reproduced computationally. DFT analysis of the transition states indicated large differences between the charge distributions for different regioisomers, suggesting that electrostatic interactions with the counteranion led to inequivalent stabilization of the transition states for the two isomers, ultimately leading to electrostatically determined regioselectivity for the reaction.

Ahlquist, Zhang, Wang and co-workers recently reported alterations to the known 2,2′-bipyridine-6,6′-dicarboxylate (dba)-bound ruthenium water oxidation catalyst (WOC) in which cationic (N-methylpyridinium) and/or anionic (–SO₃⁻) functional groups were incorporated into the axial donor ligands of the catalysts (Fig. 19a–c).⁹⁸ The authors found that water oxidation using either a Ru-dba catalyst containing both cationic and anionic charges (Fig. 19a) or a mixture of a Ru-dba catalyst containing two cationic charges with a Ru-dba catalyst containing two anionic charges (Fig. 19b and c) led to improvements in catalytic performance by over an order of magnitude. Previous studies on dba-bound ruthenium WOC catalysts had established that the intermolecular coupling of two Ru^V=O units to form a “pre-reactive dimer” – the species immediately precedes O–O bond formation – is rate limiting.^99,100 In the present study, intermolecular electrostatic attraction between two catalyst monomers was found to provide an additional driving force for formation of the pre-reactive dimer, thereby leading to larger TOFs for catalysis (Fig. 19d). The authors employed a variety of techniques, including NMR, electrical conductivity, small-angle X-ray scattering, and cryotransmission electron microscopy experiments, in conjunction with DFT and molecular dynamics calculations, to characterize the intermolecular electrostatic interactions at play during catalysis.

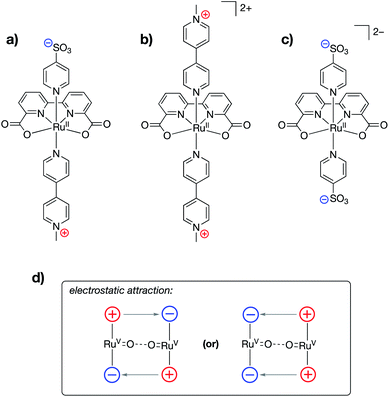Fig. 19 Ruthenium water oxidation catalysts containing (a) both cationically and anionically charged pyridyl ligands, (b) cationically charged pyridyl ligands, and (c) anionically charged pyridyl ligands. (d) Schematic showing how various combinations of complexes shown in (a), (b), and (c) may be used to ease the formation of the pre-reactive dimer complex.⁹⁸

In the Tolman study discussed above (Fig. 5d) the cupric hydroxide complexes bound by the charge-modified bis(carboxamide)pyridine ligands were chemically oxidized to formally Cu^III–OH complexes, which were subsequently shown to abstract hydrogen atoms from 9,10-dihydroanthracene.⁴⁴ BDEs for the resulting cupric aqua complexes were measured in both organic and aqueous media, and the complex containing cationic charges in the secondary coordination sphere was found to have slightly stronger O–H bonds than the complex containing anionic charges in the secondary coordination sphere (91–91.5 kcal mol⁻¹vs. 87–91 kcal mol⁻¹ respectively). Despite the modest increase in the thermodynamic driving force for hydrogen atom abstraction by the Cu^III–OH complex containing cationic charges, the kinetics for HAT with this complex were over two orders of magnitude slower than that of the Cu^III–OH complex containing anionic charges. The discrepancy between thermodynamics and kinetics in this case was found to result from tight ion pairing between the –NMe₃⁺ groups and the bulky tetrakis(3,5-bis(trifluoromethyl)phenyl)borate anions in the secondary coordination sphere, which sterically crowded the complex active site, thereby resulting in an attenuated rate for HAT.

Finally, work from our group found a direct correlation between the thermal stability of cupric superoxide complexes and the magnitude of cationic electrostatic potential in the secondary coordination sphere.¹⁰¹ In this study, we designed a series of tris(phosphinimine) ligands in which the steric profile was held constant, while the electronics and electrostatic properties of the ligands were systematically altered (Fig. 20). Despite the established precedent for strongly donating ligands stabilizing cupric superoxide complexes,¹⁰² in this case, the weakest electron donor ligand (PMe₂Ph–X = PMe₂Ph–CF₃) resulted in the most stable cupric superoxide complex due the larger magnitude of cationic electrostatic potential imparted by the ligand. This result established the impact of ESFs as being more important to cupric superoxide stability than conventional electronic effects. Analysis of kinetic parameters associated with the thermal decompositions of these complexes at elevated temperatures (−50–25 °C) revealed there to be nearly identical activation energies of decomposition across the series of complexes despite dramatic differences in their decomposition rates. Kinetic analyses also indicate there is a second order dependence on the amount of copper present in the decomposition of the superoxide species. These observations suggest that intermolecular electrostatic repulsion plays a role in slowing the rate of decomposition, presumably by disfavoring the formation of dicupric-μ-1,2-peroxide complexes (Fig. 20).

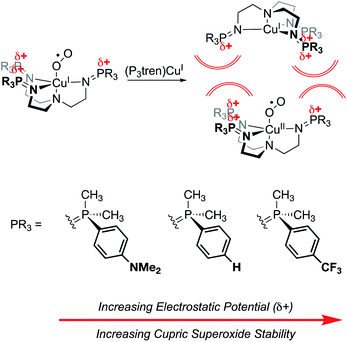Fig. 20 Cupric superoxide complexes supported by P₃tren ligands are affected by electrosteric repulsion, whereby increasing the charge in the secondary coordination sphere enhances the thermal stability of the Cu^II : O₂˙¹⁻ unit by preventing the formation of a bridging 1,2 peroxide.¹⁰¹

Conclusions and outlook

The examples given above lead to the undeniable view that electrostatic effects may be harnessed for impacting the construction, stability, and reaction profiles of transition metal complexes. This exciting development constitutes an entirely new paradigm for synthetic chemists to leverage in the search for molecular systems with improved physical properties and reaction selectivities. What's more, these electrostatic effects can be incorporated in such a wide variety of contexts. Examples range from oriented external electric fields, which apply a homogeneous field to a bulk material, to the inclusion of multiple charged residues within a single molecule that work in unison to create an effective field at a particular reaction site. Molecular electric field effects have also been used to modulate reduction potentials while maintaining the valence manifold structure of the metal center or, alternatively, to selectively alter the valence manifolds of metal centers, leading to classical ligand-field effects without the need for changes to the primary coordination sphere about the metal. Finally, an exciting use of electrostatic effects is emerging around the development of system that use intermolecular electrostatic interactions to switch reactivity on and off, promising, among other eventualities, the development of unique methods for independently tuning the steric profile and the nuclearity of a catalyst.

While electrostatic effects have been studied, to some degree, for decades in enzymatic systems, it is only within the past 10 years that their application to molecular transition metal complexes has started to gain traction. The field still has much to learn about when and how electric fields impact the chemistry occurring at metal centers. One challenge is simply synthetic. What are effective design strategies for creating soluble complexes that contain charged moieties? How important is the location of the charge, and how rigidly must it be held in place? An expanded library of suitable ligands will undoubtedly propel the field forward. The novelty of this field also greatly enhances the importance of fundamental research. Any new instance of peripheral charges playing a role in tuning valence electronic structure, transition state or intermediate stabilizations, and/or small molecule activation/catalysis will represent a valuable contribution that will help to shape the future understanding of these phenomena. While decoupling the contributions of electronics, sterics, and electrostatics to the properties and/or reactivity profiles of complexes can be challenging, we believe that the works outlined in this perspective showcase diverse and creative ways of isolating ESF effects in homogeneous metal complexes and lay the groundwork for future work in this area.

Examples of research surrounding the impacts of ESFs on homogeneous inorganic systems are rapidly increasing. Impressive improvements to catalytic systems have already taken shape; however, a give-and-take relationship between fundamental and applied research will continue to be important in the future. There is much room for contributions from synthetic, computational, and physical chemists, and our group is excited to partake in the field's growth and evolution over the coming years.

Author contributions

All authors contributed to writing, making figures, and editing this manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the National Institute of General Medical Sciences of the National Institutes of Health (award number R35GM128794), the Vagelos Institute for Energy Science and Technology (graduate fellowship for ABW), and the University of Pennsylvania for financial support.

References

1. S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098.
2. S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145.
3. S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, J. Am. Chem. Soc., 2020, 142, 12551–12562.
4. F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, ACS Catal., 2018, 9, 5153–5174.
5. S. Ciampi, N. Darwish, H. M. Aitken, I. Diez-Pérez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164.
6. N. G. Léonard, R. Dhaoui, T. Chantarojsiri and J. Y. Yang, ACS Catal., 2021, 11, 10923–10932.
7. S. Shaik and T. Stuyver, Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, Royal Society of Chemistry, 2021.
8. A. Warshel, P. K. Sharma, K. Mitsunori, X. Yun, L. Hanbin and O. M. Hm, Chem. Rev., 2006, 106, 3210–3235.
9. S. D. Fried, S. Bagchi and S. G. Boxer, Science, 2014, 346, 1510–1514.
10. M. G. Romei, C.-Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79.
11. S. D. Fried and S. G. Boxer, Annu. Rev. Riochem., 2017, 86, 387–415.
12. E. T. Novelli, J. T. First and L. J. Webb, Biochemistry, 2018, 57, 6356–6366.
13. R. M. Pollack, Bioorg. Chem., 2004, 32, 341–353.
14. S.-F. Wang, F. S. Kawahara and P. Talalay, J. Biol. Chem., 1963, 238, 576–585.
15. B. Zeng, P. L. Bounds, R. F. Steiner and R. M. Pollack, Biochemistry, 1992, 31, 1521–1528.
16. A. Kuliopulos, A. S. Mildvan, D. Shortle and P. Talalay, Biochemistry, 1989, 28, 149–159.
17. B. Zeng and R. M. Pollack, J. Am. Chem. Soc., 1991, 113, 3838–3842.
18. M. W. Shi, S. P. Thomas, V. R. Hathwar, A. J. Edwards, R. O. Piltz, D. Jayatilaka, G. A. Koutsantonis, J. Overgaard, E. Nishibori, B. B. Iversen and M. A. Spackman, J. Am. Chem. Soc., 2019, 141, 3965–3976.
19. S. Ye, C. Riplinger, A. Hansen, C. Krebs, J. M. Bollinger and F. Neese, Chem.–Eur. J., 2012, 18, 6555–6567.
20. P. Schyman, W. Lai, H. Chen, Y. Wang and S. Shaik, J. Am. Chem. Soc., 2011, 133, 7977–7984.
21. A. Morgenstern, M. Jaszai, M. E. Eberhart and A. N. Alexandrova, Chem. Sci., 2017, 8, 5010–5018.
22. D. Bím and A. N. Alexandrova, ACS Catal., 2021, 11, 6534–6546.
23. D. Bím and A. N. Alexandrova, Chem. Sci., 2021, 12, 11406–11413.
24. M. Strajbl, A. Shurki, M. Kato and A. Warshel, J. Am. Chem. Soc., 2003, 125, 10228–10237.
25. C. F. Gorin, E. S. Beh and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 186–189.
26. C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, J. Am. Chem. Soc., 2013, 135, 11257–11265.
27. A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91.
28. M. Klinska, L. M. Smith, G. Gryn'ova, M. G. Banwell and M. L. Coote, Chem. Sci., 2015, 6, 5623–5627.
29. G. Gryn'ova and M. L. Coote, Aust. J. Chem., 2017, 70, 367–372.
30. K. Zhang, B. B. Noble, A. C. Mater, M. J. Monteiro, M. L. Coote and Z. Jia, Phys. Chem. Chem. Phys., 2018, 20, 2606–2614.
31. L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2018, 140, 766–774.
32. L. Zhang, Y. B. Vogel, B. B. Noble, V. R. Gonales, N. Darwish, A. L. Brun, J. J. Gooding, G. G. Wallace, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2016, 138, 9611–9619.
33. M. T. Blyth, B. B. Noble, I. C. Russell and M. L. Coote, J. Am. Chem. Soc., 2020, 142, 606–613.
34. M. T. Blyth and M. L. Coote, J. Org. Chem., 2019, 84, 1517–1522.
35. N. S. Hill and M. L. Coote, Aust. J. Chem., 2019, 72, 627–632.
36. N. S. Hill and M. L. Coote, J. Am. Chem. Soc., 2018, 140, 17800–17804.
37. L.-J. Yu and M. L. Coote, J. Phys. Chem. A, 2019, 123, 582–589.
38. H. M. Aitken and M. L. Coote, Phys. Chem. Chem. Phys., 2018, 20, 10671–10676.
39. M. C. Holland, S. Paul, W. B. Schweizer, K. Bergander, C. Mck-Lichtenfeld, S. Lakhdar, H. Mayr and R. Gilmour, Angew. Chem., Int. Ed., 2013, 52, 7967–7971.
40. D. A. DiRocco, E. L. Noey, K. N. Houk and T. Rovis, Angew. Chem., Int. Ed., 2012, 51, 2391–2394.
41. G. Xiao, G. A. Cintron-Rosado, D. A. Glazier, B.-m. Xi, C. Liu, P. Liu and W. Tang, J. Am. Chem. Soc., 2017, 139, 4346–4349.
42. S. Yamada, Chem. Rev., 2018, 118, 11353–11432.
43. T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., Int. Ed., 2020, 59, 7915–7920.
44. R. Meir, H. Chen, W. Lai and S. Shaik, ChemPhysChem, 2010, 11, 301–310.
45. J. Joy, T. Stuyver and S. Shaik, J. Am. Chem. Soc., 2020, 142, 3836–3850.
46. G. U. Bublitz and S. G. Boxer, Annu. Rev. Phys. Chem., 1997, 48, 213–242.
47. V. F. Oswald, J. L. Lee, S. Biswas, A. C. Weitz, K. Mittra, R. Fan, J. Li, J. Zhao, M. Y. Hu, E. E. Alp, E. L. Bominaar, Y. Guo, M. T. Green, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2020, 142, 11804–11817.
48. Y. Gao, M. Pink and J. M. Smith, J. Am. Chem. Soc., 2022, 144, 1786–1794.
49. M. E. Carroll, B. Pinter, P. J. Carroll and D. J. Mindiola, J. Am. Chem. Soc., 2015, 137, 8884–8887.
50. S. Hong, F. F. Pfaff, E. Kwon, Y. Wang, M.-S. Seo, E. Bill, K. Ray and W. Nam, Angew. Chem., Int. Ed., 2014, 53, 10403–10407.
51. S. Kundu, E. Miceli, E. Farquhar, F. F. Pfaff, U. Kuhlmann, P. Hildebrandt, B. Braun, C. Greco and K. Ray, J. Am. Chem. Soc., 2012, 134, 14710–14713.
52. L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2017, 139, 2435–2442.
53. E. Y. Tsui and T. Agapie, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10084–10088.
54. J. A. Buss, D. G. VanderVelde and T. Agapie, J. Am. Chem. Soc., 2018, 140, 10121–10125.
55. A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718.
56. K. Kang, J. Fuller, A. H. Reath, J. W. Ziller, A. N. Alexandrova and J. Y. Yang, Chem. Sci., 2019, 10, 10135–10142.
57. D. Dhar, G. M. Yee and W. B. Tolman, Inorg. Chem., 2018, 57, 9794–9806.
58. A. B. Weberg, S. P. McCollom, L. M. Thierer, M. R. Gau, P. J. Carroll and N. C. Tomson, Chem. Sci., 2021, 12, 4395–4404.
59. K. L. Skubi, R. X. Hooper, B. Q. Mercado, M. M. Bollmeyer, S. N. MacMillan, K. M. Lancaster and P. L. Holland, Inorg. Chem., 2022, 61, 1644–1658.
60. I. Azcarate, C. Costentin, M. Robert and J. M. Savéant, J. Am. Chem. Soc., 2016, 138, 16639–16644.
61. H. Rao, L. C. Schmidt, J. Bonin and M. Robert, Nature, 2017, 548, 74–77.
62. S. Sahu, P. L. Cheung, C. W. Machan, S. A. Chabolla, C. P. Kubiak and N. C. Gianneschi, Chem.–Eur. J., 2017, 23, 8619–8622.
63. S. Sung, D. Kumar, M. Gil-Sepulcre and M. Nippe, J. Am. Chem. Soc., 2017, 139, 13993–13996.
64. M. Zhu, D.-T. Yang, R. Ye, J. Zeng, N. Corbin and K. Manthiram, Catal. Sci. Technol., 2019, 9, 974–980.
65. S. Sung, X. Li, L. M. Wolf, J. R. Meeder, N. S. Bhuvanesh, K. A. Grice, J. A. Panetier and M. Nippe, J. Am. Chem. Soc., 2019, 141, 6569–6582.
66. M. Wang, K. Torbensen, D. Salvatore, S. Ren, D. Joulie, F. Dumoulin, D. Mendoza, B. Lassalle-Kaiser, U. Isci, C. P. Berlinguette and M. Robert, Nat. Commun., 2019, 10, 1–8.
67. W. Nie, D. E. Tarnopol and C. C. L. McCrory, J. Am. Chem. Soc., 2021, 143, 3764–3778.
68. D. J. Martin, S. I. Johnson, B. Q. Mercado, S. Raugei and J. M. Mayer, Inorg. Chem., 2020, 59, 17402–17414.
69. D. J. Martin, C. F. Wise, M. L. Pegis and J. M. Mayer, Acc. Chem. Res., 2020, 53, 1056–1065.
70. D. J. Martin, B. Q. Mercado and J. M. Mayer, Sci. Adv., 2020, 6, 1–7.
71. D. J. Martin and J. M. Mayer, J. Am. Chem. Soc., 2021, 143, 11423–11434.
72. D. J. Martin, B. Q. Mercado and J. M. Mayer, Inorg. Chem., 2021, 60, 5240–5251.
73. S. Shaik, S. P. de Visser and D. Kumar, J. Am. Chem. Soc., 2004, 126, 11746–11749.
74. I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253–2278.
75. H. Hirao, H. Chen, M. A. Carvajal, Y. Wang and S. Shaik, J. Am. Chem. Soc., 2008, 130, 3319–3327.
76. S. R. Bell and J. T. Groves, J. Am. Chem. Soc., 2009, 131, 9640–9641.
77. H. Gao and J. T. Groves, J. Am. Chem. Soc., 2017, 139, 3938–3941.
78. T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, J. Comput. Chem., 2020, 41, 74–82.
79. T. Mondal, S. Shaik, H. Kenttämaa and T. Stuyver, Chem. Sci., 2021, 4800–4809.
80. C. Amatore and A. Jutand, Acc. Chem. Res., 2000, 33, 314–321.
81. C. Amatore, M. Azzabi and A. Jutand, J. Am. Chem. Soc., 1991, 113, 8375–8384.
82. L. Huang, L. K. G. Ackerman, K. Kang, A. M. Parsons and D. J. Weix, J. Am. Chem. Soc., 2019, 141, 10978–10983.
83. G. T. Achonduh, N. Hadei, C. Valente, S. Avola, C. J. O'Brien and M. G. Organ, Chem. Commun., 2010, 46, 4109–4111.
84. S. Shekhar and J. F. Hartwig, Organometallics, 2007, 26, 340–351.
85. L. J. Gooßen, D. Koley, H. Hermann and W. Thiel, Chem. Commun., 2004, 2141–2143.
86. S. Kozuch, C. Amatore, A. Jutand and S. Shaik, Organometallics, 2005, 24, 2319–2330.
87. T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574.
88. A. Böttcher, M. W. Grinstaff, J. A. Labinger and H. B. Gray, J. Mol. Catal. A: Chem., 1996, 113, 191–200.
89. A. Böttcher, E. R. Birnbaum, M. W. Day, H. B. Gray, M. W. Grinstaff and J. A. Labinger, J. Mol. Catal. A: Chem., 1997, 117, 229–242.
90. M. W. Grinstaff, M. G. Hill, J. A. Labinger and H. B. Gray, Science, 1994, 264, 1311–1313.
91. N. G. Léonard, T. Chantarojsiri, J. W. Ziller and J. Y. Yang, J. Am. Chem. Soc., 2022, 144, 1503–1508.
92. T. Chantarojsiri, A. H. Reath and J. Y. Yang, Angew. Chem., Int. Ed., 2018, 57, 14037–14042.
93. R. M. Clarke and T. Storr, J. Am. Chem. Soc., 2016, 138, 15299–15302.
94. M. L. Kelty, A. J. McNeese, J. W. Kurutz, A. S. Filatov and J. S. Anderson, Chem. Sci., 2022, 13, 4377–4387.
95. V. M. Lau, C. F. Gorin and M. W. Kanan, Chem. Sci., 2014, 5, 4975–4979.
96. V. M. Lau, C. F. Gorin and M. W. Kanan, Chem. Sci., 2015, 6, 3268.
97. V. M. Lau, W. C. Pfalzgraff, T. E. Markland and M. W. Kanan, J. Am. Chem. Soc., 2017, 139, 4035–4041.
98. J. Yi, S. Zhan, L. Chen, Q. Tian, N. Wang, J. Li, W. Xu, B. Zhang and M. S. G. Ahlquist, J. Am. Chem. Soc., 2021, 143, 2484–2490.
99. D. W. Shaffer, Y. Xie, D. J. Szalda and J. J. Concepcion, Inorg. Chem., 2016, 55, 12024–12035.
100. S. Zhan, R. Zou and M. S. G. Alhlquist, ACS Catal., 2018, 8, 8642–8648.
101. A. B. Weberg, S. P. McCollom and N. C. Tomson, ChemRxiv, 2022 DOI:10.26434/chemrxiv-2022-63pfg , this content is a preprint and has not been peer-reviewed.
102. C. X. Zhang, S. Kaderli, M. Costas, E. Kim, Y. M. Neuhold, K. D. Karlin and A. D. Zuberbuhler, Inorg. Chem., 2003, 42, 1807–1824.

---