Bayesian based reaction optimization for complex continuous gas–liquid–solid reactions†
Runzhe
Liang‡
,
Xiaonan
Duan‡
,
Jisong
Zhang
 * and
Zhihong
Yuan
*
* and
Zhihong
Yuan
*
State Key Laboratory of Chemical Engineering, Department of Chemical Engineering, Tsinghua University, Beijing 100084, China. E-mail: jiszhang@tsinghua.edu.cn; zhihongyuan@mail.tsinghua.edu.cn
First published on 18th October 2021
Abstract
In recent years, self-optimization strategies have been gradually utilized for the determination of optimal reaction conditions owing to their high convenience and independence from researchers' experience. However, most self-optimization algorithms still focus on homogeneous reactions or simple heterogeneous reactions. Investigations on complex heterogeneous gas–liquid–solid reactions are rare. Based on the Nelder–Mead simplex method and Bayesian optimization, this work proposes a reaction optimization framework for optimizing complex gas–liquid–solid reactions. Three gas–liquid–solid reactions including the hydrogenations of nitrobenzene, 3,4-dichloronitrobenzene, and 5-nitroisoquinoline are investigated, respectively. Reaction parameters (temperature, hydrogen pressure, liquid flow rate, and gas flow rate) are optimized. Compared with the traditional OVAT method, the proposed Bayesian based optimization algorithm exhibits remarkable performance with higher yields (0.998, 0.991 and 0.995, respectively) and computational efficiency.
Introduction
Gas–liquid–solid reactions, such as hydrogenation, oxidation and carbonylation, are widely used in the petroleum,1,2 agrochemical,3 fine chemical4–6 and pharmaceutical industry.7,8 The optimization of gas–liquid–solid reaction parameters (temperature, pressure, reaction time, etc.) is important to improve the reaction performance and to obtain target products with high purity. Traditionally, chemists are accustomed to evaluating the effects of reaction variables and designing experiments based on their knowledge, which is labour intensive and time-consuming.9–11 Additionally, gas–liquid–solid reactions are complicated by many factors, such as wetting efficiency, liquid holdup,12 complex mass and heat transfer,8 increasing the difficulty of the traditional experience based optimization method. Needless to say, the global optimality cannot be guaranteed.In contrast, automated optimization based on proper algorithms for designing optimal experiments, which was firstly proposed in the 20th century, has shown excellent performance. Recently, a self-optimization framework combining flow reactors, process analytics, and optimization algorithms without human intervention has been proposed as an effective approach to improving the experimental efficiency.13 Owing to the limitations of reagent cost and optimization time, obtaining satisfactory results via fewer experiments is preferred for reaction optimization. It should be pointed out that the traditional optimization algorithms based on derivative information are difficult to be applied to this situation since the objective function is a black-box and gradient information is unavailable for optimization. Therefore, it is necessary to develop new optimization algorithms for the rapid determination of optimal reaction conditions in flow.
In general, reaction optimization algorithms can be divided into two categories at present: local optimization algorithms and global optimization algorithms.14 Initially, local optimization algorithms were developed from the improvement of several direct search methods and surface response models, such as the Nelder–Mead simplex algorithm15–20 and design of experiments (DoE),18,21–28 and great performance has been achieved in practice. For instance, Fath et al. (2020) developed a self-optimizing framework based on the Nelder–Mead and DoE methods for the optimization of a homogeneous condensation reaction.18 This work systematically compared these two methods and analysed the influence of different factors in detail. Cortes-Borda et al. (2018) presented an autonomous flow reactor combining an optimization algorithm derived from the Nelder–Mead and golden section search methods for the homogeneous synthesis of carpanone.19 The autonomous self-optimization system allowed fast and efficient optimization of the chemical steps leading to carpanone. Although the general applicability of these methods has been proved via different reactions,17–28 researchers still focus on homogeneous reactions or simple gas–liquid reactions, and studies on the optimization of complex gas–liquid–solid reactions are rare. Indeed, for complex gas–liquid–solid reactions, there appear multiple local optima due to their complex response surface. It is difficult for local optimization algorithms to avoid getting stuck in the convergence of the local optimum, so their applications to complex chemical processes are blocked.
Global optimization algorithms, such as stable noisy optimization by branch and fit (SNOBFIT),29 have been gradually proposed for reaction optimization since the beginning of this century. In recent years, global optimization has received extensive attention. For example, Clayton et al. (2020) utilized the SNOBFIT algorithm for the autonomous optimization of multi-step reaction–extraction processes.30 The selective extraction of one amine was achieved with an optimum separation of 90%. This methodology was also utilized to optimize the homogeneous synthesis of N-benzyl-α-methylbenzylamine. Hall et al. (2021) developed an autonomous system to optimize the experimental conditions of a liquid–solid reaction based on the SNOBFIT algorithm.31 Furthermore, researchers also have applied machine learning based global optimization methods for chemical reactions. Shields et al. (2020) employed Bayesian optimization for a palladium-catalysed direct arylation reaction and performed systematic comparisons with human decisions.32 Häse et al. (2018) developed a Bayesian optimizer named Phoenics and applied it to the Belousov–Zhabotinsky reaction.33 Zhou et al. (2017) optimized homogeneous organic synthesis reactions in microdroplets with deep reinforcement learning.34 The optimal reaction conditions were determined in 30 min and a better understanding of the reaction parameters was reached.
Clearly, the aforementioned global optimization algorithms have only touched upon homogeneous reactions or simple liquid–solid reactions. Note that global optimization usually needs several experimental results for initialization so that the convergence is slow, to some extent. In detail, compared with that for local optimization, the number of experiments needed for global optimization may be obviously higher. More systematic and practical investigations on flexible and adaptable optimization algorithms are therefore required to tackle potential obstacles to enable the common usage of global optimization for complex reactions.
To address the aforementioned challenges, a continuous reaction optimization platform based on the Nelder–Mead simplex method and Bayesian optimization algorithm is developed for optimizing complex continuous gas–liquid–solid reaction systems in this paper. The hydrogenations of nitrobenzene, 3,4-dichloronitrobenzene and 5-nitroisoquinoline are selected as the model reactions due to their wide applications in dyes, pigments and active pharmaceutical ingredients.35–37 Specifically, Bayesian optimization is combined with the Nelder–Mead simplex method to strengthen each other's metrics so that the shortcomings of the requirement of initialization can be properly overcome. The proposed optimization approach is then integrated with a continuous flow system to optimize multiple variables (temperature, liquid flow rate, hydrogen pressure, gas flow rate) to determine the optimal reaction conditions with the purpose of achieving satisfactory yields.
Materials and methods
Chemicals
The reactants nitrobenzene (C6H5NO2, 99.9%), 3,4-dichloronitrobenzene (C6H3Cl2NO2, 99%), and 5-nitroisoquinoline (C9H6N2O2, 98%) were purchased from Aladdin-Holdings Group, Zhejiang Dibang Chemical Co. Ltd, and Shanghai Bide Pharmaceutical Technology Co. Ltd, respectively, and used without any purification. Methanol (CH3OH, 99.9%) and tetrahydrofuran (C4H8O, 99%) as solvents were purchased from Aladdin-Holdings Group and Shanghai Titan Technology Co. Ltd. Hydrogen (H2, 99.9%) and nitrogen (N2, 99.9%) were supplied by the Beijing Beiwen Gas Manufacturing Plant. The diameters of palladium/alumina catalysts (Pd/Al2O3, 0.5 wt%, spherical), nickel/silica catalysts (Ni/SiO2, 20 wt%, amorphous), platinum/carbon particle catalysts (Pt/C, 5 wt%, spherical) and alumina spheres were all in the range of 400–500 μm. All the catalysts and alumina spheres were acquired from the Dalian Institute of Chemical Physics.Experimental setup
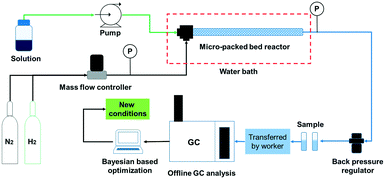
The schematic of the continuous flow system is shown in Fig. 1. The solution was delivered by a plunger pump at flow rates ranging from 0.2 mL min−1 to 2.0 mL min−1 (Ou Shi Sheng (Beijing) Technology Co. Ltd.). Hydrogen and nitrogen gas flows from regulated cylinders were fed via a mass flow controller (Beijing Sevenstar Electronics Co. Ltd.) at flow rates ranging from 10 to 50 sccm. The solution was premixed with the gas in a T-mixer prior to entering the reactor. Two pressure transducers (resolution: 0.01 MPa) were installed at upstream and downstream positions of the micro-packed bed reactor (length: 24.3 cm, inner diameter: 3.3 mm, outer diameter: 6.35 mm) respectively to allow for online monitoring of the system pressure, and no pressure drop was observed in the experiments. A commercially available frit (pore size of 20 μm and thickness of 1.6 mm) was installed at the exit of the reactor to support the fixed-bed particles and no powder was collected after installing the frit during the experiments. The reactor and two coils were immersed in a water bath to control the reaction temperature. The system pressure was set to the required value using a backpressure regulator.The reactant was prepared at a specific concentration in the solvent and the reactor was fully packed with the catalysts. The micro-packed bed reactor was prewetted with the solvent and H2 was transported into the reactor at the required flow rate. Then, the liquid flow rate was set to the required value as the system pressure gradually increased while simultaneously raising the system temperature. After waiting for at least three times the liquid residence time,9,10 a sample was collected and transferred manually to an offline gas chromatograph (Agilent, GC-8860) for analysis. Detailed information on the GC analysis and sample chromatograms is provided in the ESI† (section 1 and section 2). The analytical results were transferred into a computer and next the reaction conditions were generated using the Bayesian based optimization algorithm. To avoid the influence of catalyst deactivation on the optimization results, the catalyst activity for the hydrogenation of nitrobenzene, 3,4-dichloronitrobenzene and 5-nitroisoquinoline was evaluated under the same conditions (60 °C, 2 MPa, 20 sccm and 0.3 mL min−1) and compared with that of the fresh catalysts every 3 h. If the main product yield decreased by more than 3%, the catalyst would be replaced by a fresh catalyst.
Optimization methodology
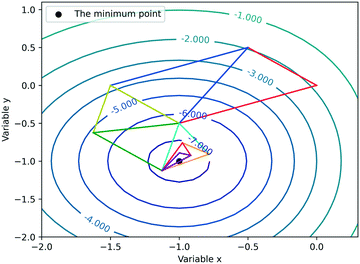
In this work, the Nelder–Mead simplex method and Bayesian optimization are combined for the optimization of gas–liquid–solid reactions. The Nelder–Mead simplex method, proposed firstly in 1965, is a classical direct search approach which depends on the comparison of function values at the (n + 1) vertices of a general simplex (where n is the number of variables), followed by the replacement of the vertex with the lowest value by another point.15 Each time an experiment is carried out (after constructing the initial simplex), the vertex with the lowest yield would be abandoned, and a new experiment point will be subsequently proposed to drive the simplex to move towards the optimum. To make this approach more flexible, the new search vertex should be obtained via geometric transformation. In other words, the shape of the simplex varies iteratively during the optimization. The simplex adapts itself to the local landscape, and contracts into the final optimum. Fig. 2 depicts an example of how the Nelder–Mead simplex method iteratively converges to the local optimum of a given response function.Bayesian optimization, an uncertainty-guided response surface method used for the optimization of computationally expensive objective functions, was firstly proposed for machine learning to assist practitioners in optimizing model hyperparameters.32,38,39 In fact, reaction optimization has many similarities with hyperparameter tuning of machine learning. The objective function is essentially a black-box for researchers; the cost of acquiring values of the objective function is expensive; the value of the objective function can be subject to noise, etc. Therefore, Bayesian optimization for reaction optimization has raised chemists' interest in recent years.
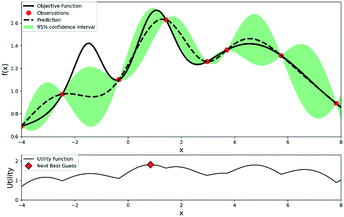
The procedures for Bayesian optimization can be described as follows: firstly, initial experimental results are required for the initialization of the Bayesian optimizer, which usually can be collected by DoE or at random. A probabilistic surrogate model is then generated from the initial experimental results to predict the expectation and uncertainty of each point. An acquisition function will help chemists maximize the expected utility of candidate experiments and make a trade-off between exploration and exploitation of reaction space. Exploration searches regions with high uncertainties, while exploitation focuses on the parts with high prediction expectations. After maximizing the acquisition function, a new experiment point will be proposed to carry out a new experiment. The experimental dataset will be expanded, and a more accurate surrogate model will be retrained. This process continues iteratively until a satisfactory reaction yield is obtained or the experimental budgets are depleted. An illustration of Bayesian optimization is shown in Fig. 3.
As a method based on the response surface, the performance of the surrogate model represents the prediction accuracy of the optimizer. Note that only when the estimation of the surrogate model for expectation and variance is close enough to the real response surface can its efficiency be recognized. For continuous domains, a Gaussian process (GP) can be used for training tasks under the assumption that the experimental noise follows a Gaussian distribution. Meanwhile, kernel functions for GP represent the covariance of observations. The Matérn kernel is a very flexible class of stationary kernels which have been commonly used for Gaussian processes.40 In this investigation, a Gaussian process model with the Matérn52 kernel is employed for the construction of the surrogate model.
Moreover, the selection of various acquisition functions is also crucial for desirable optimization performance. There are several functions extensively used for tuning hyperparameters in machine learning, such as the probability of improvement (PI), expected improvement (EI), upper confidence bound (UCB), etc.41–45 In this work, EI, as one of the most frequently used acquisition functions, is selected to balance exploration and exploitation.
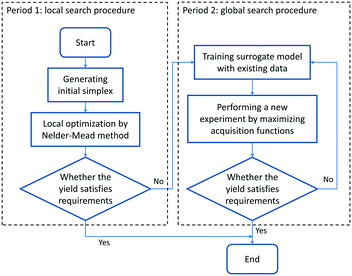
Due to the requirement of generating an initial probabilistic surrogate model, several initial experiments need to be conducted for the Bayesian optimizer. Much more initial experimental results are consequently required under higher optimization dimensions. Therefore, Bayesian optimization is actually excessively complicated when the response surface is relatively simple, which can be dealt with local optimization methods, for instance, when the response surface is convex and monotonous. To improve the performance of optimization and make the reaction optimization algorithm more flexible and adaptable, Bayesian optimization combined with the Nelder–Mead simplex method for chemical reactions is proposed in this work, which is depicted in Fig. 4. The optimization procedure can be divided into two periods. In the first period, the Nelder–Mead simplex method is employed for the preliminary exploration of the local optimum and providing initial experimental results for initializing the Bayesian optimizer. The initial simplex is located in the center of the reaction space, and it occupies 20 percent of the reaction space (which means the size of the start simplex corresponds to 20% in each parameter direction). The number of experiments carried out in this period is set as about 3 times the optimization variables for searching the local optimum (for example, if there are three optimization variables to be optimized, nine experiments conducted by the Nelder–Mead simplex method will be performed, and subsequent experiments should be conducted by Bayesian optimization). If the yield obtained in this period has satisfied the requirements, the optimization process will be terminated directly; otherwise, the second period will begin. The Bayesian optimizer can warm-up from the experimental data obtained in the first period. The information near the local optimum provides convenience for the Bayesian optimizer to precisely describe the response surface, in order to converge to the global optimum faster. Also, the Bayesian optimizer can further analyse the experimental noise, ensuring the stability and accuracy of optimization performance.
Results and discussion
In order to examine the performance of the proposed Bayesian based optimization approach, a comparison with the changing one variable at a time (OVAT) method and pure Bayesian optimization (initial experimental results collected by DoE) is presented. As a grid search method, OVAT has been regarded as one of the most frequently used methods for reaction optimization because of its simplicity and convenience. On the premise that optimization variables are irrelevant, OVAT explores the impact of each variable on the reaction yield, respectively, to finally find the highest yield. As reported by Zhang et al.,12 a bypass flow (representing the effect of the inner wall) will occur when the ratio of the bed diameter to the particle diameter is below 10. However, the difference of the pressure drop is lower than 0.014 MPa when the ratio varies from 6 to 10, which is much smaller than the reaction pressure (1.0–3.0 MPa). Besides, liquid holdup is independent of diameter-to-particle ratios, even when the ratio is below 10 due to the dominant surface tension suppressing the wall effect. Hence, the effect of the inner wall on the flow hydrodynamics and gas–liquid–solid mass transfer can be ignored in our experiments and reproducible implementation of the reactions in the fixed bed reactor could be achieved.To fairly compare the performance of different reaction optimization algorithms, two evaluation indices are introduced for quantitative analysis: the highest yield found (HYF) and average loss (AL). The highest yield found is defined as the highest yield obtained in all experiments that have been carried out. It is desirable that a higher HYF can be achieved by efficient optimization algorithms with limited experimental budgets.
| HYF = max(Y) | (1) |
Single experiment loss refers to the difference between the highest yield which can be reached (including experiments completed and not carried out) and the yield of the current experiment. The higher the loss, the lower the “efficiency” of this experiment. Average loss corresponds to the average value of all experiment losses completed, and represents the efficiency of the optimization algorithm:
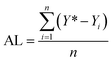 | (2) |
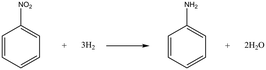
Case I: hydrogenation of nitrobenzene
The simple gas–liquid–solid reaction, hydrogenation of nitrobenzene, is firstly selected to examine the performance of the proposed method. The chemical reaction equation for the hydrogenation of nitrobenzene is depicted in Scheme 1. The reaction has high selectivity and almost no by-products can be observed in the reaction.The proposed approach, OVAT method and pure Bayesian optimization are all employed for optimizing reaction conditions. Three variables are selected for the optimization: temperature (30–50 °C), pressure (0.5–2.5 MPa), and liquid flow rate (0.6–1.6 ml min−1). 0.5 wt% Pd/Al2O3 catalysts (0.34 g, diluted with 1.36 g alumina spheres) are utilized for the experiments and the detailed information about the experimental conditions is summarized in the ESI† (section 4). The results indicate that all algorithms can easily achieve satisfactory yields. Including the initial reaction results (to generate the initial simplex), the proposed approach successfully achieves a yield of 0.997 within only 7 experimental budgets, and all the reaction yields obtained in the local optimization stage exceed 0.99. Considering that the obtained yield can be close enough to 100% with a local search procedure, it is almost impossible to significantly improve the yield with a global search procedure. Therefore, the proposed approach terminates in advance. In contrast, since each variable needs to be explored separately, the OVAT method carries out 16 experiments in total, with the highest yield being 0.985. Although a satisfactory yield is also obtained with the OVAT method, more experiments are required compared with the proposed approach. In other words, the OVAT method calls for higher reagent cost and more experiment time. For pure Bayesian optimization, a high yield of 0.997 can be achieved at the 9th experiment. The result is basically consistent with the proposed method, but a few more experiments are required.
Fig. 5 shows the HYF and AL associated with the different optimization methods for the hydrogenation of nitrobenzene. It can be clearly found from Fig. 5a that the red line representing the proposed approach is much shorter than the blue line representing the OVAT method and the green line representing Bayesian optimization. Such a comparison means that fewer experiments are required to achieve the desired yield following the suggestions from the proposed Bayesian based reaction optimization. Additionally, in Fig. 5b, the red line lies below the blue one and the green one with a much lower value. This shows that more satisfactory yields are obtained by the proposed approach. After the generation of the initial simplex, the rapid reduction of the value for the red line indicates that a local optimum (maybe the global optimum as well) has been found and the optimizer attempts to exploit regions nearby.
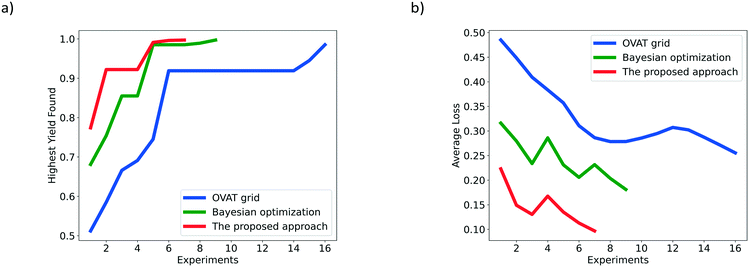 | ||
| Fig. 5 Comparison of the OVAT method, Bayesian optimization and the proposed Bayesian based approach for the hydrogenation of nitrobenzene based on a) HYF and b) AL. | ||
Although all the algorithms have identified the corresponding satisfactory yield, the proposed approach shows the best performance in terms of optimization speed and efficiency. In addition, since the reaction is relatively simple and the influence of variables is basically monotonous (to our knowledge, a higher temperature, higher pressure, and lower liquid flow rate are preferred for the production of aniline), the proposed approach adapts itself to a simpler form and searches for the target in the local optimization stage. The requirement of a large number of initial experiments for training the probabilistic surrogate model can essentially be avoided.
Case II: hydrogenation of 3,4-dichloronitrobenzene
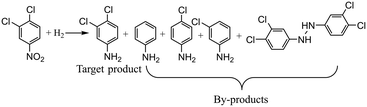
The second gas–liquid–solid reaction is the hydrogenation of 3,4-dichloronitrobenzene which has complex reaction pathways.46 For the hydrogenation of 3,4-dichloronitrobenzene, the reduction of 3,4-dichloronitrobenzene occurs via consecutive hydrogenation to a nitroso compound and hydroxylamine which could be further hydrogenated into 3,4-dichloroaniline, and the nitroso and hydroxylamine intermediates can also condense to form azoxy compounds. Besides, dehalogenation can possibly occur at any step during the reaction pathways and several by-products (aniline, m-chloroaniline, p-chloroaniline) would be detected in the samples. The reaction equation is shown in Scheme 2 with the main by-products detected during experiments, and detailed information about the reaction mechanism is depicted in the ESI† (section 3).The involved variables and their constraints for servicing the optimization of the hydrogenation of 3,4-dichloronitrobenzene conducted by different optimization methods are as follows: temperature (40–80 °C), pressure (1.0–3.0 MPa), and liquid flow rate (0.2–0.4 ml min−1). 20 wt% Ni/SiO2 catalysts are employed for the reaction and the detailed information about the reaction conditions can be found in the ESI† (section 4).
The HYF and AL of the different optimization methods for the hydrogenation of 3,4-dichloronitrobenzene are shown in Fig. 6. The number of experiments suggested by the proposed approach, OVAT method and pure Bayesian optimization is 18, 15 and 18, respectively. The highest yield achieved by the proposed approach is 0.991, which is higher than those of the traditional OVAT method (0.986) and pure Bayesian optimization (0.983). Fig. 6a shows that the highest yields of the proposed approach, OVAT method and Bayesian optimization are actually obtained at the 15th, 7th and 15th experiment, respectively. In spite of a few more experiments being required for the proposed approach, this method exhibits adaptable performance for the investigation of the influence of reaction parameters, and finally finds the highest yield by comparison. After the local optimization period, the highest yield obtained cannot meet requirements so the global search procedure will begin to seek for higher yields. With the information explored in the local optimization stage, a probabilistic surrogate model with excellent performance can be trained which accelerates the determination of the global optimum. In fact, the highest yield of 0.991 can be successfully obtained under two different conditions by the proposed approach, while the OVAT method carries out only one experiment whose yield exceeds 0.98. The three highest yields obtained by the proposed approach, OVAT method and Bayesian optimization are listed in Table 1. It can be also observed from the optimization results that the relevance of decision variables is negligible for this reaction. The results indicate that a high temperature and low liquid flow rate favour the dechlorination process which may result in the accumulation of chloroaniline. Meanwhile, incomplete conversion may occur at a low temperature, low hydrogen pressure and high flow rate since the 3,4-dichloronitrobenzene and azoxy compounds cannot be further hydrogenated into 3,4-dichloroaniline owing to low catalytic activity and insufficient residence time. Therefore, to obtain higher yields, a lower hydrogen pressure and higher liquid flow rate are preferred when the temperature is higher, and a higher hydrogen pressure, lower liquid flow rate and lower temperature can also lead to satisfactory results. For the lack of the ability to identify correlations, the traditional OVAT method can only focus on several modest conditions; for example, the temperature is recommended as 60 °C.
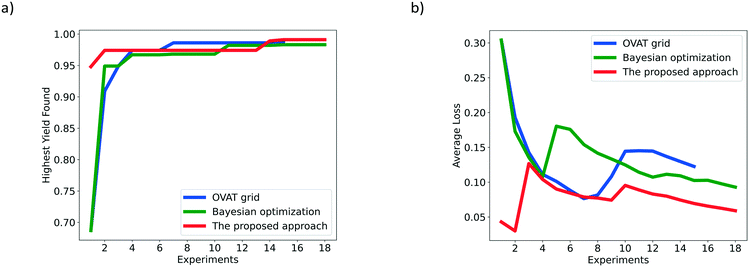 | ||
| Fig. 6 Comparison of the OVAT method, Bayesian optimization and the proposed Bayesian based approach for the hydrogenation of 3,4-dichloronitrobenzene based on a) HYF and b) AL. | ||
| Optimization method | Temperature/°C | Hydrogen pressure/MPa | Liquid flow rate/(mL min−1) | Yield |
|---|---|---|---|---|
| The proposed approach | 70.5 | 2.5 | 0.22 | 0.991 |
| 80.0 | 2.0 | 0.31 | 0.991 | |
| 60.4 | 2.2 | 0.20 | 0.989 | |
| OVAT method | 60.0 | 2.0 | 0.25 | 0.986 |
| 60.0 | 3.0 | 0.30 | 0.968 | |
| 60.0 | 2.0 | 0.20 | 0.967 | |
| Pure Bayesian optimization | 52.7 | 1.9 | 0.22 | 0.983 |
| 53.3 | 1.7 | 0.23 | 0.982 | |
| 59.0 | 1.7 | 0.34 | 0.980 |
Besides, as shown in Fig. 6b, the average loss of the proposed approach is much lower than that of the OVAT method, indicating that more satisfactory results are obtained by the proposed approach, which is consistent with the reaction results where almost all yields obtained in the global optimization stage are over 0.95. In contrast, most results obtained by the OVAT method are lower than 0.93, validating the superiority of the proposed approach.
Case III: hydrogenation of 5-nitroisoquinoline
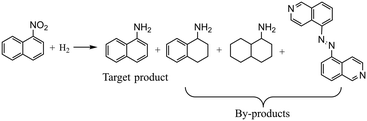
For the hydrogenation of 5-nitroisoquinoline, the reaction mechanism is similar to that of the hydrogenation of 3,4-dichloronitrobenzene. The hydrogenation of 5-nitroisoquinoline proceeds via several competitive ways, including consecutive reduction of the nitro group to nitroso and hydroxylamine compounds, and the condensation of nitroso and hydroxylamine compounds into an azoxy compound prior to the generation of 5-aminoisoquinoline. Besides, the target product 5-aminoisoquinoline could be further hydrogenated to 5-aminotetrahydroisoquinoline and 5-aminoperhydroisoquinoline, increasing the difficulty to obtain high yields.47 The reaction equation is shown in Scheme 3 with the main by-products detected during experiments, and the reaction mechanism is depicted in the ESI† (section 3). To prove the general capability of the proposed Bayesian based optimization method, four decision variables are considered: temperature (40–80 °C), pressure (1.0–3.0 MPa), liquid flow rate (0.2–1.2 ml min−1), and gas flow rate (15–30 ml min−1). Besides, 5 wt% Pt/C catalysts are used for the hydrogenation of 5-nitroisoquinoline and detailed experimental conditions are given in the ESI† (section 4).The complexity of optimization increases with the increase of decision variables. As shown in Fig. 7a, 59 experiments for the hydrogenation of 5-nitroisoquinoline are conducted in total. The proposed Bayesian based optimization approach needs only 15 experiments to achieve the highest yield of 0.995, while OVAT and Bayesian optimization ask for 24 and 20 experiments respectively with the highest yields obtained lower than 0.995. Similar to the above two cases, nearly each experiment suggested by the proposed optimization achieves a higher yield than its counterparts suggested by OVAT and Bayesian optimization. Indeed, the yields of all experiments suggested by the proposed approach exceed 0.975. Besides, the experimental results illustrate that 5-aminoisoquinoline is prone to further reduction to 5-aminotetrahydroisoquinoline under the conditions of high hydrogen pressure and temperature. And, the azoxy compound would accumulate at a low temperature, low hydrogen pressure and high flow rate owing to the insufficient catalytic activity. Additionally, Fig. 7b displays the AL of the proposed approach, OVAT method and pure Bayesian optimization, and the AL of the proposed approach is significantly lower than that of the others, which suggests the remarkable efficiency of the proposed Bayesian based optimization method.
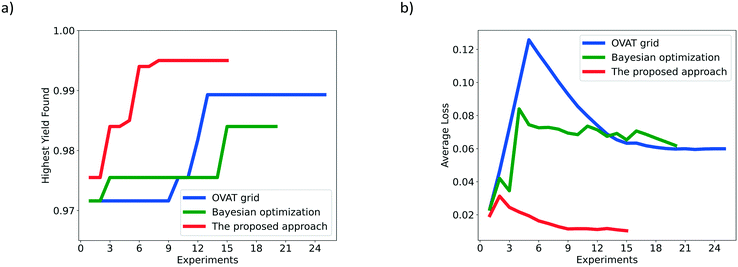 | ||
| Fig. 7 Comparison of the OVAT method, Bayesian optimization and the proposed Bayesian based approach for the hydrogenation of 5-nitroisoquinoline based on a) HYF and b) AL. | ||
The three highest yields obtained by the proposed approach, OVAT method and pure Bayesian optimization respectively are also listed in Table 2. For the OVAT method, the liquid flow rate is considered as an essential variable which has a significant impact on the yield and a number of experiments are carried out to find the optimal flow rate. However, only one variable can be changed at a time for the OVAT method so correlations of variables cannot be set up. In other words, the OVAT method cannot guarantee global optimality. In contrast, the proposed Bayesian based optimization exhibits better performance. In addition, parameter combinations with obvious differences have been found by the proposed approach with a high yield (for instance, temperature: 55.0 °C, hydrogen pressure: 2.3 MPa, liquid flow rate: 0.75 mL min−1, gas flow rate: 23.8 mL min−1versus temperature: 40.2 °C, hydrogen pressure: 1.3 MPa, liquid flow rate: 0.57 mL min−1, gas flow rate: 15.4 mL min−1), which suggests multiple local optima may exist and the surface response is relatively complex.
| Optimization method | Temperature/°C | Hydrogen pressure/MPa | Liquid flow rate/(mL min−1) | Gas flow rate/(mL min−1) | Yield |
|---|---|---|---|---|---|
| The proposed approach | 55.0 | 2.3 | 0.75 | 23.8 | 0.995 |
| 52.5 | 2.5 | 0.83 | 25.7 | 0.995 | |
| 40.2 | 1.3 | 0.57 | 15.4 | 0.994 | |
| OVAT method | 60.0 | 2.0 | 0.90 | 20.0 | 0.989 |
| 60.0 | 2.0 | 0.80 | 20.0 | 0.982 | |
| 60.0 | 2.0 | 0.60 | 20.0 | 0.976 | |
| Pure Bayesian optimization | 40.0 | 2.4 | 0.30 | 26 | 0.984 |
| 40.0 | 1.2 | 0.20 | 26 | 0.976 | |
| 40.0 | 2.8 | 0.20 | 27 | 0.975 |
In summary, the performance of the proposed Bayesian optimization method is obviously more desirable than that of the OVAT method and pure Bayesian optimization. Guided by the proposed approach, explicit optimization directions are shown and more beneficial conditions can be achieved, resulting in the improvement of experimental efficiency and the reduction of reactant cost.
Conclusions
In this work, a continuous reaction optimization platform based on the Bayesian optimization algorithm was developed for the rapid determination of the optimal reaction conditions for complex gas–liquid–solid reactions. The hydrogenations of nitrobenzene, 3,4-dichloronitrobenzene, and 5-nitroisoquinoline were investigated. The highest yield found (HYF) and average loss (AL) were proposed as the evaluation indices for comparing the proposed Bayesian based optimization approach and the traditional OVAT method and pure Bayesian optimization. Briefly speaking, the proposed approach is superior to OVAT and Bayesian optimization. Higher yields with fewer experimental budgets were obtained by utilizing the proposed Bayesian based optimization method. Moreover, Bayesian based optimization showed higher efficiency since the experimental conditions provided by the Bayesian optimizer tended to correspond to higher yields, while the OVAT method was apt to search the reaction space regions with low yields.The examinations on the three gas–liquid–solid reactions showed that the proposed Bayesian based optimization algorithm was an effective approach for optimizing complex gas–liquid–solid reactions. Needless to say, it can liberate chemists from tedious and labour-intensive reaction optimization processes. Furthermore, Bayesian based reaction optimization reduces the dependence on prior knowledge and enables chemists to focus on other significant issues such as the identification of precise mechanisms. Integration of the proposed optimization with online analysis instruments for the construction of a fully automated self-optimization system for complex reactions is under investigation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support from the National Natural Science Foundation of China (21991103, 22022809) for this work.Notes and references
- F. Pinto, S. Martins, M. Gonçalves, P. Costa, I. Gulyurtlu, A. Alves and B. J. A. E. Mendes, Appl. Energy, 2013, 102, 272–282 CrossRef CAS.
- X.-B Gong, Int. Biodeterior. Biodegrad., 2012, 70, 89–95 CrossRef CAS.
- A. Brennführer, H. Neumann and M. Beller, Angew. Chem., Int. Ed., 2009, 48, 4114–4133 CrossRef.
- S. Tadepalli, R. Halder and A. Lawal, Chem. Eng. Sci., 2007, 62, 2663–2678 CrossRef CAS.
- S. K. Tanielyan, S. R. More, R. L. Augustine and S. R. Schmidt, Org. Process Res. Dev., 2017, 21, 327–335 CrossRef CAS.
- S. E. Davis, M. S. Ide and R. J. Davis, Green Chem., 2013, 15, 17–45 RSC.
- J. S. Quesnel and B. A. Arndtsen, J. Am. Chem. Soc., 2013, 135, 16841–16844 CrossRef CAS PubMed.
- A. Faridkhou, J.-N. Tourvieille and F. Larachi, Chem. Eng. Process.: Process Intesif., 2016, 110, 80–96 CrossRef CAS.
- J. Tu, L. Sang, H. Cheng, N. Ai and J. Zhang, Org. Process Res. Dev., 2019, 24, 59–66 CrossRef.
- F. Xu, J. Chen, X. Xie, P. Cheng, Z. Yu and W. Su, Org. Process Res. Dev., 2020, 24, 2252–2259 CrossRef CAS.
- P. Loos, H. Alex, J. Hassfeld, K. Lovis, J. Platzek, N. Steinfeldt and S. Hübner, Org. Process Res. Dev., 2015, 20, 452–464 CrossRef.
- J. Zhang, A. R. Teixeira, L. T. Kögl, L. Yang and K. F. Jensen, AIChE J., 2017, 63, 4694–4704 CrossRef CAS.
- B. J. Reizman and K. F. Jensen, Acc. Chem. Res., 2016, 49, 1786–1796 CrossRef CAS.
- A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, React. Chem. Eng., 2019, 4, 1545–1554 RSC.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7(4), 308–313 CrossRef.
- V. Cerdà, J. L. Cerdà and A. M. Idris, Talanta, 2016, 148, 641–648 CrossRef PubMed.
- M. A. Bezerra, Q. O. dos Santos, A. G. Santos, C. G. Novaes, S. L. C. Ferreira and V. S. de Souza, Microchem. J., 2016, 124, 45–54 CrossRef CAS.
- V. Fath, N. Kockmann, J. Otto and T. Röder, React. Chem. Eng., 2020, 5(7), 1281–1299 RSC.
- D. Cortes-Borda, E. Wimmer, B. Gouilleux, E. Barre, N. Oger and L. Goulamaly, et al. , J. Org. Chem., 2018, 83(23), 14286–14299 CrossRef CAS.
- N. Vasudevan, E. Wimmer, E. Barré, D. Cortés-Borda, M. Rodriguez-Zubiri and F. Felpin, Adv. Synth. Catal., 2020, 363(3), 791–799 CrossRef.
- F. Galvanin, R. Marchesini, M. Barolo, F. Bezzo and M. Fidaleo, Chem. Eng. Res. Des., 2016, 105, 107–119 CrossRef CAS.
- M. Poroch-Seritan, S. Gutt, G. Gutt, I. Cretescu, C. Cojocaru and T. Severin, Chem. Eng. Res. Des., 2011, 89(2A), 136–147 CrossRef CAS.
- A. Echtermeyer, Y. Amar, J. Zakrzewski and A. Lapkin, Beilstein J. Org. Chem., 2017, 13, 150–163 CrossRef CAS PubMed.
- B. J. Reizman and K. F. Jensen, Org. Process Res. Dev., 2012, 16(11), 1770–1782 CrossRef CAS.
- O. W. Gooding, Curr. Opin. Chem. Biol., 2004, 8(3), 297–304 CrossRef CAS PubMed.
- P. M. Murray, F. Bellany, L. Benhamou, D.-K. Bučar, A. B. Tabor and T. D. Sheppard, Org. Biomol. Chem., 2016, 14(8), 2373–2384 RSC.
- S. Ko, X. Tang, F. Gao, Y. Zhou, R. Zhang and Y. Liu, et al. , J. Chem. Technol. Biotechnol., 2021, 96(10), 2965–2975 CrossRef CAS.
- A. Shahmohammadi and R. T. Bonnecaze, Chem. Eng. Res. Des., 2020, 160, 74–88 CrossRef CAS.
- W. Huyer and A. Neumaier, ACM Trans. Math. Softw., 2008, 35, 9 CrossRef.
- A. D. Clayton, L. A. Power, W. R. Reynolds, C. Ainsworth, D. R. J. Hose and M. F. Jones, et al. , J. Flow Chem., 2020, 10, 199–206 CrossRef.
- B. L. Hall, C. J. Taylor, R. Labes, A. F. Massey, R. Menzel, R. A. Bourne and T. W. Chamberlain, Chem. Commun., 2021, 57, 4926–4929 RSC.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani and J. I. M. Alvarado, et al. , Nature, 2021, 590(7844), 89–96 CrossRef CAS.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4(9), 1134–1145 CrossRef.
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3(12), 1337–1344 CrossRef CAS PubMed.
- R. S. Downing, P. J. Kunkeler and H. Van Bekkum, Catal. Today, 1997, 37, 121–136 CrossRef CAS.
- D. J. Dale, P. J. Dunn, C. Golightly, M. L. Hughes, P. C. Levett, A. K. Pearce, P. M. Searle, G. Ward and A. S. Wood, Org. Process Res. Dev., 2000, 4, 17–22 CrossRef CAS.
- Y. Xu, M. A. Celik, A. L. Thompson, H. Cai, M. Yurtsever, B. Odell, J. C. Green, D. M. Mingos and J. M. Brown, Angew. Chem., Int. Ed., 2009, 48, 582–585 CrossRef CAS.
- G. Luo, Netw. Model. Anal. Health Inform. Bioinform., 2016, 5, 18 CrossRef.
- M. Feurer and F. Hutter, Automated Machine Learning: Methods, Systems, Challenges, 2019, pp. 3–33 Search PubMed.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104(1), 148–175 Search PubMed.
- H. J. Kushner, J. Basic Eng., 1964, 86(1), 97–106 CrossRef.
- J. Mockus, V. Tiesis and A. Zilinskas, in Toward Global Optimization, 1978, vol. 2, pp. 117–129 Search PubMed.
- N. Srinivas, A. Krause, S. Kakade and M. Seeger, in Proc. Int. Conf. Mach. Learn., 2010, pp. 1015–1022 Search PubMed.
- B. Shahriari, Z. Wang, M. W. Hoffman, A. Bouchard-Côté and N. de Freitas, in Proc. NIPS Workshop Bayesian Optim., 2014 Search PubMed.
- M. W. Hoffman, E. Brochu and N. de Freitas, in Proc. Conf. Uncertainty Artif. Intell., 2011, pp. 327–336 Search PubMed.
- X. Duan, J. Yin, A. Feng, M. Huang, W. Fu, W. Xu, Z. Huang and J. Zhang, J. Flow Chem., 2021 DOI:10.1007/s41981-021-00200-2.
- X. Duan, X. Wang, X. Chen and J. Zhang, Org. Process Res. Dev., 2021, 25, 2100–2109 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Further description of the experimental procedure, including analysis methods, reaction pathways, and optimization routes, is provided. See DOI: 10.1039/d1re00397f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |