Steric hindrance in the on-surface synthesis of diethynyl-linked anthracene polymers

Abstract

Hybrid sp–sp² structures can be efficiently obtained on metal substrates via on-surface synthesis. The choice of both the precursor and the substrate impacts on the effectiveness of the process and the stability of the formed structures. Here we demonstrate that using anthracene-based precursor molecules on Au(111) the formation of polymers hosting sp carbon chains is affected by the steric hindrance between aromatic groups. In particular, by scanning tunneling microscopy experiments and density functional theory simulations we show that the de-metalation of organometallic structures induces a lateral separation of adjacent polymers that prevents the formation of ordered domains. This study contributes to the understanding of the mechanisms driving the on-surface synthesis processes, a fundamental step toward the realization of novel carbon-based nanostructures with perspective applications in nanocatalysis, photoconversion, and nano-electronics.

---

1 Introduction

Carbon exhibits the unique capability of forming a tremendous variety of nanostructures of different size, dimensionality, and other properties.¹ After the advent of graphene, research was devoted to the production of graphene nanoribbons, with the target of opening up a bandgap by exploiting lateral confinement effects.² Bottom-up fabrication^3,4 turned out to be a viable alternative to etching graphene edges,⁵ unzipping of carbon nanotubes,⁶ or exploiting lithographic methods.⁷

The bottom-up synthesis process requires an extremely fine control of the structures down to the atomic scale. The on-surface synthesis approach allows the fabrication of carbon nanostructures by promoting chemical reactions directly on a metal surface, and enables the use of in situ surface-science characterization techniques.^8–11 In particular, scanning tunneling microscopy (STM) and atomic force microscopy give access to the atomic-scale and molecular imaging of the structure and arrangement of the sample with unprecedented capability, thus opening a way to the controlled fabrication of atomically-precise, well-defined nanostructures.¹²

By playing with π-conjugated molecular precursors used as the building units in the on-surface synthesis process, a number of different systems has been realized so far, including one-dimensional (1D) and two-dimensional (2D) polymeric structures supported on metal surfaces.^13–15 More recently this approach has been extended to peculiar carbon structures involving combined sp–sp² hybridization by exploiting the dehalogenative homocoupling reaction of precursor molecules with ethynyl groups.^16–19 1D linear structures (i.e. sp–sp² carbon polymers) and 2D sp–sp² carbon networks (i.e. graphdiynes) have been synthesized on metal surfaces and investigated.²⁰

The on-surface synthesis process has been unveiled in detail as well as the structural, electronic and vibrational properties of these systems. Such properties have been shown to be affected by the metal substrate mainly through charge-transfer processes and structural distortions imposed to adapt the carbon network to the periodicity of the underlying metal surface.^18,19,21

Nonetheless, the choice of the precursor was demonstrated to be the primary aspect in the control of the on-surface synthesis process.^22,23 The rational design of the precursor molecules allows one – for example – to exploit their side functionality to control the order and symmetry of the polymers, and the steric hindrance of chemical groups to steer the molecular assembly.^24–26 Topologically non-trivial properties have been unveiled on π-conjugated polymers made by laterally assembling acene monomers, as a function of the number of the aromatic rings. In particular moving from anthracene- to pentacene-based polymers, a change from insulating to metallic behavior is expected, due to a topological phase transition.²⁷ Most of these investigations focus mainly on the single wire or polymer or on the single molecular bond,^27,28 while paying less attention to the polymer–polymer interaction and to the overall self-assembly on the metal surface. Due to the complex on-surface synthesis process involving different steps from dehalogenation to homocoupling, the self-assembling behavior is non trivial, and it can be affected by different aspects which are still unexplored.

In the present paper, we report a combined theoretical and experimental investigation of anthracene-based polymers synthesized on Au(111) and characterized by in situ STM.

Through the deposition of 9,10-di(bromoethynyl)anthracene on Au(111) followed by thermal annealing we obtain densely-packed organometallic polymers (i.e. with Au adatoms bridging the ethynyl groups) as first stage and homocoupled diethynyl-linked anthracene polymers ([–C₂–ANT–C₂–]_n) at high temperature. Upon the release of the Au bridging atoms we assist to a sideward distancing and bending of adjacent polymers resulting in a more disordered structure.

By means of density-functional-theory (DFT) calculations we demonstrate that this transition – from close-packed domains to disordered polymers – is due to the polymer–polymer interaction and in particular to the steric hindrance of lateral aromatic rings of adjacent molecules. This effect, caused by the shortening of the homocoupled diethynyl chain due to the removal of the Au atom, is also responsible of a different registry of anthracene units of neighboring chains. Moreover, electronic-structure results show that the interaction with the substrate determines the metallic character of both the organometallic and homocoupled polymers.

As a result we show that the overall behavior of the on-surface synthesized system emerges from a nontrivial interplay between intermolecular effects and polymer–substrate interaction. A deep understanding of such mechanisms is mandatory to engineer novel systems with ad hoc structure and electronic properties.

2 Results and discussion

2.1 STM experiments

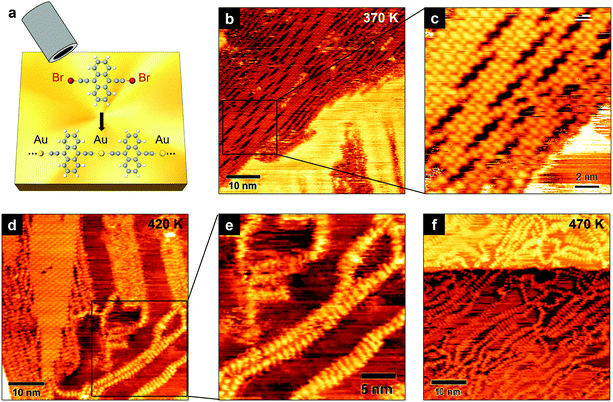
We have achieved the on-surface synthesis of 1D ethynyl-linked anthracene polymers on Au(111) through the deposition of the precursor molecule shown in Fig. 1a. The molecular assembly into longer chains occurs on Au(111) at room temperature (RT) via a three-fold process:¹⁹ (i) adsorption and diffusion on the surface (ii) debromination reaction (cleavage of C–Br bonds), and (iii) coupling of ethynyl chains to gold adatoms.

The resulting structures are 1D organometallic polymers, consisting in gold-mediated ethynyl chains linked to anthracene ([–Au–C₂–ANT–C₂–]_n). We imaged these structures after a mild annealing of the sample at 370 K, which favors the desorption of possible impurities coming from the evaporation and allows us to acquire more stable STM images. Fig. 1b shows the organometallic polymers at a relatively large scale. They tend to arrange themselves in compact domains with many chains running almost parallel to each other. The packing of adjacent chains in ordered domains is interposed by voids (Fig. 1c) which may occur periodically, suggesting the possibility that the packing of the linear structures could be hindered by internal forces.

Fig. 1 (a) Schematic representation of the synthesis process: precursor molecules are evaporated onto the Au(111) surface (top half of the image), which catalyzes the debromination and the coupling of monomers into an organometallic polymer. (b) 50 × 50 nm² STM image acquired after annealing at 370 K, showing the formation of ordered domains of packed organometallic chains (0.5 V, 0.2 nA). (c) Higher resolution image of the region inside the box in (b). (d) STM image acquired after annealing at 420 K, showing the coexistence of compact domains and isolated linear structures (1 V, 0.2 nA). The latter are shown at higher resolution in (e). (f) STM image acquired after annealing at 470 K, showing the disordered arrangement of isolated chains (1.7 V, 0.3 nA).

By increasing the annealing temperature to 420 K (Fig. 1d), the compact domains coexist with more isolated linear structures (Fig. 1e). As we will discuss below, these chains have a different structure compared to those forming the ordered domains. Also, the fuzzier imaging suggests that these chains have a higher mobility on the Au surface. After annealing at 470 K (Fig. 1f), we observe only disordered chains, suggesting that a thermally activated mechanism induces the closely-packed organometallic polymers to gradually convert into linear structures randomly arranged on the Au surface.

By means of high-resolution STM measurements, here we focus on the structure of the polymeric chains packed in compact domains and the isolated ones observed in the sample annealed at 470 K.

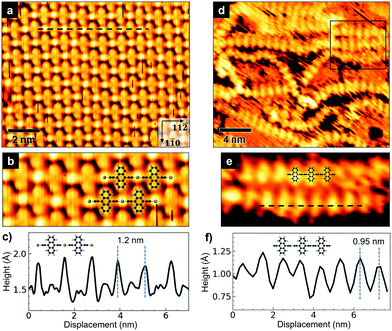
The STM image in Fig. 2a shows a portion of a well-ordered domain, observed in the sample annealed at 420 K. The organometallic chains are oriented along the [112̄] direction of the substrate. The bright spots alternating with the anthracene units along a single chain are produced by the gold atoms which mediate the coupling (see the model structure in Fig. 2b). Evidently, the well-oriented domains of organometallic chains are packed in such a way that the anthracene units come close to the gold adatoms of the adjacent linear molecules. The periodicity along the chain is 12 ± 0.3 Å (Fig. 2c); the average distance between adjacent chains along the [11̄0] direction is 8.4 ± 0.3 Å.

Fig. 2 (a) Molecular-scale STM image showing the linear organometallic chains packed in a well-oriented domain (0.5 V, 0.2 nA). (b) Close-up on adjacent organometallic chains, whose structure is highlighted by the superimposed ball and stick model. (c) Height profile along the chain axis, specifically along the dashed line in (a). (d) STM image showing disordered chains after annealing at 470 K (0.7 V, 0.2 nA). The black frame highlights adjacent chains whose anthracene units are nearly aligned in a side-by-side arrangement. (e) Molecular-scale STM image of a single homocoupled chain (1.7 V, 0.3 nA). (f) Height profile along the dashed line in (e), over the homocoupled chain.

Fig. 2d shows disordered chains observed after annealing at 470 K. There is no evidence of the gold spot between successive [–C₂–ANT–C₂–] monomers (Fig. 2e), a sign that gold adatoms have been released and the coupling between ethynyl terminal groups has occurred. This transformation is accompanied by a shortening of the periodicity along the chains, which reduces to 9.5 ± 0.3 Å (Fig. 2f). Also, the anthracene units of nearby chains are no longer in the alternating configuration of organometallic chains, but rather they tend to arrange themselves in a side-by-side configuration (see framed region in Fig. 2d) and – more importantly – they are spaced farther apart than in the ordered structure. A minimum distance of about 17 Å can be estimated when two or more chains are close together, such as in the framed region of Fig. 2d.

The tighter in-chain packing of the anthracene units produces a looser lateral packing of the polymeric chains, due to steric hindrance.

2.2 Theoretical structural models

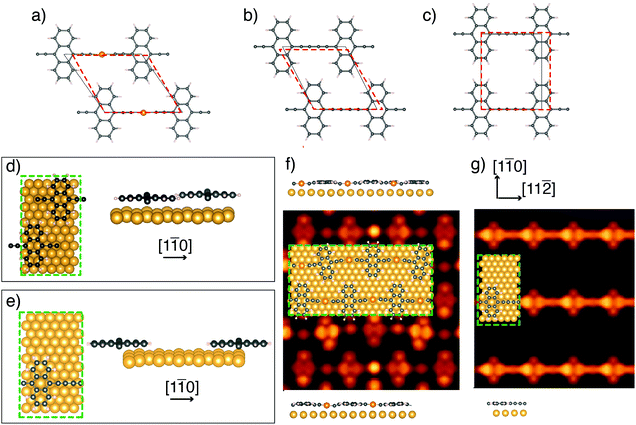
In order to obtain an insight into the formation mechanism of homocoupled [–C₂–ANT–C₂–]_n structures we perform DFT calculations aimed to characterize the different stages of the on-surface-synthesis process.

As a preliminary step we investigate, via structural relaxation, the optimal periodicity and stacking of the linear organometallic compounds in an ideal freestanding 2D array configuration, before and after the release of the gold linking atom. The resulting equilibrium structural models are reported in Fig. 3a–c. This figure additionally reports the unit cell adapted to the closest-matching periodicity of Au(111) (red dashed) compared to the relaxed unit cell of the freestanding model system (gray solid).

Fig. 3 Relaxed unit cells (solid gray) for the freestanding [–Au–C₂–ANT–C₂–]_n (a) and [–C₂–ANT–C₂–]_n in the staggered (b) and aligned configuration (c). The best fitting to Au-substrate-compatible periodic cell is reported by red dashed lines. (d) and (e): the two possible configurations for [–C₂–ANT–C₂–]_n on Au(111) and the related structural relaxation of the anthracene units. (f) and (g): the simulated STM images and the relaxed structures of [–Au–C₂–ANT–C₂–]_n and [–C₂–ANT–C₂–]_n on Au(111).

The relaxed freestanding [–Au–C₂–ANT–C₂–]_n forms organometallic chains with a spacing of 12.09 Å between successive anthracene units and a spacing of 9.19 Å between parallel linear structures (horizontal and vertical size of the gray cell of Fig. 3a, respectively).

The agreement between the calculated periodicity along the horizontal direction and the measured one has to be taken with care because it refers to a freestanding system compared to the adsorbed one. Actually, considering the usual over-estimate of the lattice constant by DFT-GGA this result suggests that the [–Au–C₂–ANT–C₂–]_n structures are strained upon adsorption on gold to adapt themselves to the underlying substrate.

The periodicity extracted from the STM (12 ± 0.3 Å) is compatible with the formation of a molecular superstructure commensurate with Au. Considering the experimental uncertainty the commensurability can be assumed with a mismatch relative to an Au supercell ranging between 0.5% and 5%, being these values referred to the two extremes of the experimental uncertainty for the measured periodicity.

The matching with the gold substrate (a^exp_Au = 4.078 Å) can hence be achieved by considering a supercell formed by 7 Au unit cell vectors along the [112̄] direction (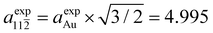 Å) and 6 unit cell vectors along the [11̄ 0] direction (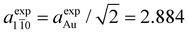 Å) (green rectangle in Fig. 3f) that accommodates two adjacent chains with three [–Au–C₂–ANT–C₂–]_n monomer units each.

In the theoretical description of the molecular overlayer adsorbed on Au we exploit the same supercell re-scaled to the theoretical lattice constant of Au (a^th_Au = 4.21 Å). Reporting this choice to the hexagonal unit-cell of the freestanding polymer (red dashed in Fig. 3a), the unit-cell lattice vectors (modulus 7/3a_112̄ and 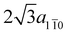, respectively) are slightly compressed with respect to the freestanding equilibrium model and the angle between them is reduced from 125° to 120°. Consequently, the separation between successive anthracene units and between parallel polymers is slightly reduced (−0.47% along the [112̄] direction and −1.6% along the [11̄0], respectively). The energy cost for matching amounts to 3 meV per monomer for the freestanding system, neglecting the structural relaxation due to the interaction with the substrate.

Fig. 3f reports the top view and side view of the relaxed geometries of [–Au–C₂–ANT–C₂–]_n on Au(111) and the simulated STM images for filled states (integration in the 0.5 eV-wide interval immediately below the Fermi energy) at a constant distance of 2 Å above the average height of the molecular layer. The structural relaxation performed for [–Au–C₂–ANT–C₂–]_n leads to a partial in-plane bending of the linear chains which is driven by the preference of the Au atoms in the chain to sit at a hollow position (see ball and stick model in Fig. 3f). Such bending cannot be detected in the high-resolution STM images reported in Fig. 2a and b. This feature might in fact be partially due to the forced matching to the underlying Au substrate periodicity imposed in the calculation, which is also affected by the 3% discrepancy between the experimental and the DFT-simulated lattice spacing of gold. It is quite possible that a longer supercell in the [112̄] direction compatible with a smaller strain of the polymer might produce smaller or even no bending.

The side view of the two linear fragments of parallel chains belonging to the unit cell (top and bottom of Fig. 3f) shows an overall modulation of the linear structures, with anthracene units lying farther from the surface (distances ranging from 2.84 Å to 2.92 Å) than the diethynyl chains that are pulled down toward the surface due to the small distance (Δz = 2.42 Å) between the gold adatom and the gold surface underneath. The STM simulation displays bright spots in correspondence of gold adatoms in the chain, in agreement with the experiments, and bright regions in correspondence of the external rings of anthracene.

For [–C₂–ANT–C₂–]_n we consider two possible configurations: the staggered one (Fig. 3b) which is the ground state for the 2D freestanding crystal of this polymer, and the aligned one (Fig. 3c) which has been chosen as representative of the arrangement observed in the STM images. In the first one the relaxed unit-cell vectors (black in Fig. 3b) form an angle of 116.7° and measure 9.52 Å in the horizontal direction and 10.59 Å in the rotated one. In the aligned configuration, the equilibrium unit cell is a rectangle with vector lengths 9.53 Å and 11.52 Å in the horizontal and vertical direction, respectively (black in Fig. 3c). It is worth noting that the most relevant aspect of the this configuration is that the separation between the linear chains, and consequently between adjacent anthracene units, is larger than in the staggered one. Small deviations from the orthogonality of the cell vectors, as observed in the experiment, would not change the considerations reported below. The freestanding staggered stacking turns out to be more stable than the aligned one by 35 meV per monomer.

The actual commensurability of [–C₂–ANT–C₂–]_n with Au(111) is weakly supported by the experimental measurements. Indeed the mismatch between the periodicity extracted from STM along the [112̄] direction and the closest length of an Au supercell vector (2 × a^exp_112̄ = 9.99 Å) is in the range 2–7%, considering the experimental error bar. We also notice that the overall disordered arrangement of the molecules plays against the formation of a large-scale commensurate superstructure. Nevertheless, by restricting our attention to the local order we assume a matching with 2 Au(111) unit cells along the [112̄] direction and 6 unit cells along the [11̄0] (6 × a^exp_11̄0 = 17.3 Å), in close agreement with the lengths extracted from STM. Such an assumption allows us to perform periodic-cell theoretical calculations, in order to understand the driving force governing the arrangement of the molecular chains upon demetalation.

In fact, this choice allows us to perform the DFT simulations of [–C₂–ANT–C₂–]_n adsorbed on Au(111) surface in both the staggered and the aligned configuration using the same supercell (green in Fig. 3d and e).

This superstructure includes 1 monomer in the aligned configuration, as in the experiments, and 2 monomers in the staggered one-which is taken as comparison being the most stable structure in the freestanding case.

The matching with the underlying Au substrate introduces in both cases a significant strain along the [112̄] direction (8.4% and 8.3% tensile strain in the staggered and aligned cases, respectively) which is necessary to fit the structure with 2 Au(111) cell vectors. The energy cost associated to such expansion of the polymer amounts to ∼1.9 eV per monomer. To obtain a mismatch lower than 1% also in this case, a unit cell including 6 monomer units fitting 11 Au(111) cell vectors would be required, which lies outside the limits of our computational setup.

Along the [11̄0] direction the staggered configuration matches 3× the Au lattice spacing with a 5.5% compression. This compression is associated to a small energy of 8 meV per monomer, since no covalent bond is compressed and adjacent chains can interpenetrate to some extent. The adapted unit cells is reported in Fig. 3b.

Differently, for the aligned configuration the periodicity observed in the STM images is larger than in the equilibrium freestanding system that would closely match 4 Au lattice spacing along the [11̄0] direction (3.3% strain, 1 meV per monomer energy cost – red dashed line in Fig. 3c).

We verified that a further expansion of the cell vector along [11̄0] to match the experimental periodicity and fit 6 Au(111) unit-cell vectors along the [11̄0] direction (see the frame in Fig. 2d) has a reasonably small cost, of the order of 30 meV per monomer in the freestanding system. By comparing the total DFT energy per [–C₂–ANT–C₂–]_n unit on Au(111) in the similarly strained configurations of Fig. 3d and e, we obtain an energy gain of 0.47 eV per monomer for the aligned configuration relative to the staggered one.

On the basis of these results and of the information extracted from the STM images, we can infer that the formation of [–C₂–ANT–C₂–]_n polymer on the Au(111) surface is made difficult by the steric hindrance of the anthracene units depending on the reduction of their distance induced by the release of the gold adatom.

This steric effect prevents the [–C₂–ANT–C₂–]_n polymers from packing in ordered domains after their formation. Indeed a certain degree of lateral order takes place only in less densely packed regions of the surface (Fig. 2d) where the separation of the linear chains is possible, leading to partly ordered structures resembling the aligned arrangement of Fig. 3c.

As a further test we perform an additional calculation for a 2D network of freestanding anthracene-based monomers (not linked by the terminal ethynyl groups), arranged analogously as in Fig. 3b, where the spacing between molecular rows in the vertical direction (referring to the figure) is fixed to the value observed in the experiments for [–Au–C₂–ANT–C₂–]_n (8.4 Å along [11̄0] direction) and varying the side-by-side separation of anthracene units.

We find an increase of energy for approaching anthracene units, with an energy cost of 0.5 eV when the periodicity along [112̄] is 9.50 Å, as in the experiment. The agreement with the calculation performed for the adsorbed system confirms that the driving mechanism governing the rearrangement of the molecular chains is the molecule–molecule repulsion while the substrate acts as a template.

The calculated adsorption energy, obtained as:

E_ads = (E_tot − E_mon − E_sub),

where E_tot, E_mon and E_sub are the (per monomer) energy of the adsorbed system, of the freestanding relaxed polymer, and of the 2 × 6 gold substrate, respectively, amounts to −8.32 eV for the [–Au–C₂–ANT–C₂–]_n on Au(111). For the [–C₂–ANT–C₂–]_n polymer on Au(111) it is −4.32 eV per monomer for the staggered configuration and −4.79 eV per monomer for the aligned one, confirming that the [–C₂–ANT–C₂–]_n polymers are more weakly bound to the surface and the inter-molecular distance is larger compared to the equilibrium freestanding case.

The two models considered for [–C₂–ANT–C₂–]_n on Au(111) show relevant differences in the relaxed geometry of the anthracene units: in the staggered configuration the steric hindrance induces a bending of the external aromatic rings of one anthracene unit in the cell (side view in Fig. 3d).

In contrast, in the aligned configuration the molecules preserve the planar geometry (see the side view in Fig. 3e), thus confirming the absence of steric hindrance. Moreover, the average height of the polymers above the substrate top layer is larger in the staggered configuration (2.77 Å) than in the aligned one (2.71 Å).

We have performed the STM simulation for the model with aligned molecules, with the same setup as in Fig. 3f. In agreement with experiments, the bright spot at the center of the diethynyl chain disappears, due to the absence of the gold adatom. Both the chain and the anthracene units are imaged with similar brightness.

2.3 Electronic properties

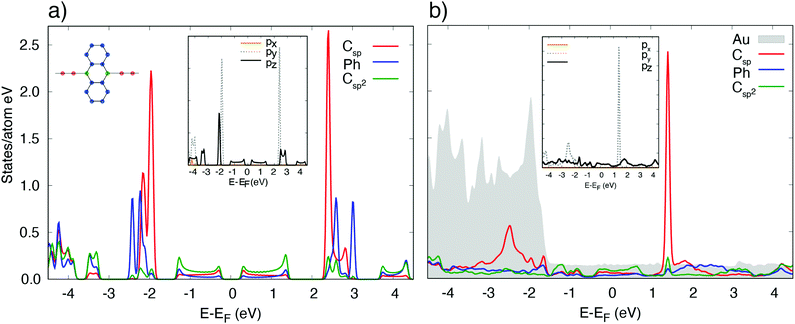
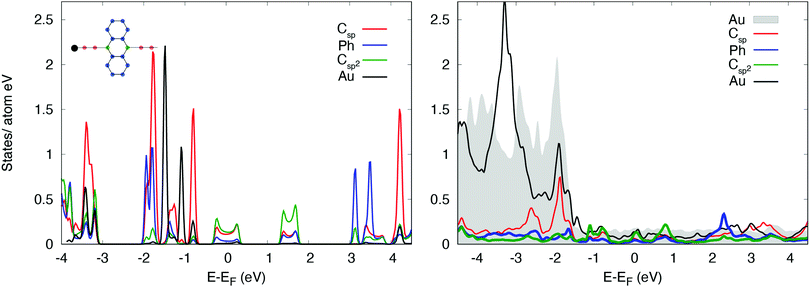
The calculated projected density of states (PDOS) of [–C₂–ANT–C₂–]_n/Au(111) is reported in Fig. 4. Below the Fermi level the PDOS exhibits similar contributions coming from the lateral aromatic rings, ethynyl chain and sp² carbon atoms at the edge of anthracene, as color-coded in the sketched molecule.

Fig. 4 Projected density of states of (a) freestanding [–C₂–ANT–C₂–]_n, and (b) [–C₂–ANT–C₂–]_n/Au(111) in the aligned configuration. The contributions of different groups of atoms in the polymer, namely sp carbon atoms in the chain (red), sp² carbon atoms linking the chain to the anthracene unit (green) and external phenyl rings (blue) are resolved (see also the color code in the inset). Grey shadow: Density of states projected on the Au substrate. Insets: The same density of states projected over the individual components of the p orbitals of the sp carbon atoms in the ethynyl chain. x indicates the [11̄0] direction, y is the [112̄] direction, and z is the direction perpendicular to the surface. Each individual PDOS is normalized to the number of atoms of the relevant kind.

The insets report the projected states on the ethynyl chain resolved by component: features at the Fermi level have a mainly p_z character; p_x states are mostly out of the energy range considered; p_y states, orthogonal to the chain direction, exhibit two peaked features at −2.5 and 1.2 eV that originate from the π-bonds formed between sp carbon atoms, and are relatively weakly affected by the hybridization with the substrate.²⁹ A comparison with the PDOS of the freestanding polymer evidences that the states at the Fermi level of [–C₂–ANT–C₂–]_n/Au(111) originate from a shift of the unoccupied DOS of the freestanding molecule to lower energy: this shift is associated to a mild charge transfer to the polymer, which we evaluate in 0.12 electrons per monomer.

In particular, the largest amount of charge (0.10 e per monomer) is transferred to the anthracene unit while sp chain acquires only 0.02 electrons.

Accordingly, we find a similar depletion of charge in Au surface layer (−0.005 e per Au, −0.11 e per surface layer).

The most relevant effect of the interaction between the polymer and the substrate is that the polymer acquires a metallic character, despite a hint of the energy gap is still visible just below the Fermi level, although reduced to 0.2 eV compared to the 0.4 eV of the freestanding polymer.

Hybridization with the d states of the substrate takes place via the p_z and p_y states of the sp chain below −1.5 eV and via the states of the aromatic ring in the same energy range which have p_z character.

The interaction between the organometallic [–Au–C₂–ANT–C₂–]_n and the substrate is stronger, due to the linking Au atom. The charge transfer to the molecule amounts to 0.25 electrons per monomer, mainly directed to the anthracene and the diethynyl chain. On the contrary, the Au adatom in the chain transfers 0.13 electrons to the surface layer. The PDOS's of [–Au–C₂–ANT–C₂–]_n, reported in Fig. 5, show the metallic character of the freestanding [–Au–C₂–ANT–C₂–]_n system which is mainly due to a charge transfer from sp carbon atoms to the bridging Au resulting into a shift of the HOMO states at the Fermi level. A shrink of the pristine HOMO–LUMO bands is also observed resulting in a larger gap just above the Fermi level. When the system is adsorbed on Au(111) the strong hybridization with the substrate produces a deformation of the features and the disappearence of any reminiscence of the original gap of [–C₂–ANT–C₂–]_n. Indeed, the PDOS of the Au adatom in the chain strongly overlaps with the substrate, giving rise to peaked structures in correspondence to the d bands of the Au surface and a broad continuum of states in the energy range of the s band of the substrate.

Fig. 5 Projected density of states of (a) freestanding [–Au–C₂–ANT–C₂–]_n, and (b) [–Au–C₂–ANT–C₂–]_n/Au(111). The contributions of different groups of atoms in the polymer, namely sp carbon atom in the ethynyl chain (red), sp² carbon atoms linking the chain to the anthracene unit (green), Au linking atom (black) and external phenyl rings (blue) are resolved (see also the color code in the inset). Grey shadow: Density of states projected on the Au substrate. Each individual PDOS is normalized to the number of atoms of the relevant kind. The PDOS of the Au linking atom has been divided for a factor 5.

3 Experimental

3.1 Synthesis of 9,10-di(bromoethynyl)anthracene

All reagents and solvents were purchased from Merck and used without additional purification. 9,10–diethynylanthracene was synthesized as previously reported in the literature.³⁰¹H and ¹³C nuclear magnetic resonance (NMR) spectra were recorded by using a Bruker Avance DRX-400 or a Bruker Avance DRX-300 spectrometer in CDCl₃ (Cambridge Isotope Laboratories, Inc.) as solvent. Mass spectra (MS) were obtained by means of an Advion expression CMS L01 instrument with an atmospheric-pressure chemical ionization source (APCI).

65.5 mg of 9,10-diethynylanthracene (0.289 μmol) were dissolved in 6 mL of acetone. Under stirring 123.8 mg of N-bromosuccinimide (1.2 equiv.) and 12.0 mg of AgNO₃ (0.06 equiv.) were added, then the stirring was maintained for 4 hours in the dark. The solvent was removed in vacuum and the crude product was purified by flash column chromatography (SiO₂, eluent: n-hexane gradient to n-hexane/CH₂Cl₂ 9 : 1). 46.4 mg of pure product were obtained (41.8% yield). ¹ H NMR (400 MHz, CDCl₃, 20): δ = 8.63 (m, 4H), 7.66 (m, 4H); ¹³ C NMR (300 MHz, CDCl₃, 20): δ = 132.61, 127.23, 126.77, 118.10, 77.06, 62.07. MS (APCI⁺): m/z (%): 384.6 (100) [M + H]⁺.

3.2 On-surface synthesis and STM

All experiments were conducted in an UHV system (base pressure 10⁻¹¹ mbar) composed of two interconnected chambers for sample preparation and STM characterization. Au(111)/mica substrates (Mateck) were cleaned by cycles of Ar⁺ sputtering (1 keV) and annealing at 700 K.

The precursor in powder form was deposited on Au(111) at RT from an effusion cell (Dr Eberl–MBE Komponenten) heated at 370 K. STM measurements were acquired at RT with an Omicron microscope, using homemade electrochemically etched W tips.

Typical measurement parameters were in the range 0.5–2 V for bias voltage and 0.1–0.3 nA for set-point current (the specific values for the reported STM images are stated in the captions).

3.3 Theory

We perform DFT calculations with the generalized gradient approximation (GGA) in the PBE form,³¹ and including van der Waals interactions between the organic overlayer and the substrate via a DFT-D2 Grimme potential.³² We use the approach implemented in the SIESTA code³³ that relies on norm-conserving pseudopotentials and an atomic–orbitals basis set. The simulated STM images are obtained in the Tersoff-Hamann approach.³⁴

We adopt a double-zeta basis set with polarization orbitals and a mesh-cutoff of 400 Ry for the kinetic-energy value that sets the real-space grid.

We relax the organic layers and the first substrate layer until the forces reach the tolerance value of 0.04 eV Å⁻¹. We use a 4 × 4 sampling of the Brillouin zone for the freestanding polymers; for the calculations on Au we use a 2 × 6 sampling for [–Au–C₂–ANT–C₂–]_n and a 7 × 6 sampling for [–C₂–ANT–C₂–]_n.

Along the z direction the slab includes three layers of Au substrate, the molecular overlayer and ∼85 Å of vacuum.

4 Conclusions

We demonstrate here the possibility to obtain hybrid sp–sp² carbon structures via on-surface synthesis reaction on a Au(111) substrate by starting from a 9,10-di(bromoethynyl)anthracene. The final product of the process are polymeric chains where the anthracene units are alternating with the ethynyl chains. The STM images indicate that the on-surface polymerization reaction proceeds through an organometallic polymer intermediate state arranged in compact and well-aligned rows. However, the elimination of the gold adatoms leads to poorly-ordered assemblies of the purely organic [–C₂–ANT–C₂–]_n polymer.

DFT simulations performed for different structural models, for both freestanding and Au-adsorbed polymers allow us to identify the steric hindrance between anthracene units as the main reason for the separation between the chains leading to their disordered arrangement. The repulsion between the electronic clouds of adjacent molecules arises due to the shrinking of the polymer upon the release of the gold adatoms, combined with the periodicity constraints induced by the interaction with the substrate. These results demonstrate the influence of the choice of the precursor on the properties of the final structures, confirming an interplay of both the molecule-molecule and molecule–substrate interaction in the on-surface synthesis process. Understanding this aspect would pave the way to the design and synthesis of new sp–sp² hybrid carbon nanostructures with potential application in various fields. The possibility to control both their structural and the electronic properties would be indeed a fundamental achievement to develop the potential of such systems as new materials for nano-electronics, photovoltaics, thermoelectrics, energy storage, and catalysis.²⁰

Author contributions

Conceptualization, SA, AOB, GF, CSC; Investigation, SA, FT, AR, GF; Resources, AOB, AB, CSC; Visualization, SA, FT, AR; writing – original draft, SA, AR; writing – review & editing, SA, FT, AR, AOB, ALB, AB, NM, GO, GF, CSC. All authors discussed the research while this was performed, and have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

F. T., A. R., A. L. B. and C. S. C. acknowledge funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program ERC Consolidator Grant (ERC CoG2016 EspLORE grant agreement no. 724610, website: http://www.esplore.polimi.it). S. A., G. F., N. M., and G. O. acknowledge CINECA for the use supercomputing facilities under the agreement with UNITECH-INDACO and Barcelona Supercomputing Center for the access to the Nasertic cluster of the Red Española de Supercomputacion (grant FI-2021-2-0047). N. M. acknowledges support from the grant PRIN2017 UTFROM of the Italian Ministry of University and Research.

Notes and references

1. A. Hirsch, Nat. Mater., 2010, 9, 868–871.
2. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
3. J. Jinming Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473.
4. Y.-C. Chen, D. G. de Oteyza, Z. Pedramrazi, C. Chen, F. R. Fischer and M. F. Crommie, ACS Nano, 2013, 7, 6123–6128.
5. S. S. Datta, D. R. Strachan, S. M. Khamis and A.-T.-C. Johnson, Nano Lett., 2008, 8, 1912–1915.
6. L. Y. Jiao, L. Zhang, X. R. Wang, G. Diankov and H. J. Dai, Nature, 2009, 458, 877–880.
7. S. Achilli, G. F. Tantardini and R. Martinazzo, Phys. Chem. Chem. Phys., 2014, 16, 17610–17616.
8. Q. Shen, H.-Y. Gao and H. Fuchs, Nano Today, 2017, 13, 77–96.
9. P. Ruffieux, S. Wang, B. Yang, C. Sanchez-Sanchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Möllen and R. Fasel, Nature, 2016, 531, 489–492.
10. C. Steiner, J. Gebhardt, M. Ammon, Z. Yang, A. Heidenreich, N. Hammer, A. Görling, M. Kivala and S. Maier, Nat. Commun., 2017, 8, 1–11.
11. S. Clair and D. G. de Oteyza, Chem. Rev., 2019, 119, 4717–4776.
12. C.-H. Shu, M.-X. Liu, Z.-Q. Zha, J.-L. Pan, S.-Z. Zhang, Y.-L. Xie, J.-L. Chen, D.-W. Yuan, X.-H. Qiu and P.-N. Liu, Nat. Commun., 2018, 9, 2322.
13. R. Zuzak, A. Jančařík, A. Gourdon, M. Szymonski and S. Godlewski, ACS Nano, 2020, 14, 13316–13323.
14. G. Galeotti, F. D. Marchi, E. Hamzehpoor, O. MacLean, M. R. Rao, Y. Chen, L. Besteiro, D. Dettmann, L. Ferrari, F. Frezza, P. Sheverdyaeva, R. Liu, A. Kundu, P. Moras, M. Ebrahimi, M. Gallagher, F. Rosei, D. Perepichka and G. Contini, Nat. Mater., 2020, 19, 874–880.
15. A. Basagni, F. Sedona, C. A. Pignedoli, M. Cattelan, L. Nicolas, M. Casarin and M. Sambi, J. Am. Chem. Soc., 2015, 137, 1802–1808.
16. Q. Sun, B. V. Tran, L. Cai, H. Ma, X. Yu, C. Yuan, M. Stöhr and W. Xu, Angew. Chem., 2017, 129, 12333–12337.
17. X. Yu, L. Cai, M. Bao, Q. Sun, H. Ma, C. Yuan and W. Xu, Chem. Commun., 2020, 56, 1685–1688.
18. A. Rabia, F. Tumino, A. Milani, V. Russo, A. Li Bassi, S. Achilli, G. Fratesi, G. Onida, N. Manini and Q. Sun, et al. , Nanoscale, 2019, 11, 18191–18200.
19. A. Rabia, F. Tumino, A. Milani, V. Russo, A. L. Bassi, N. Bassi, A. Lucotti, S. Achilli, G. Fratesi, N. Manini, G. Onida, Q. Sun, W. Xu and C. S. Casari, ACS Appl. Nano Mater., 2020, 3, 12178–12187.
20. F. Yan, L. Yuxin, Q. Lu, X. Yurui and L. Yuliang, Chem. Soc. Rev., 2022, 51, 2681–2709.
21. S. Achilli, A. Milani, G. Fratesi, F. Tumino, N. Manini, G. Onida and C. S. Casari, 2D Mater., 2021, 8, 044014.
22. Z. Xu, T. Kojima, W. Wang, K. Kaushik, A. Saliniemi, T. Nakae and H. Sakaguchi, Mater. Chem. Front., 2017, 2, 775–779.
23. S. Wang, Z. Li, P. Ding, C. Mattioli, W. Huang, Y. Wang, A. Gourdon, Y. Sun, M. Chen, L. Kantorovich, K. Yang, F. Rosei and M. Yu, Angew. Chem., 2021, 60, 17435–17439.
24. S. Clair and D. G. de Oteyza, Chem. Rev., 2019, 119, 4717–4776.
25. T. Wang and J. Zhu, Surf. Sci. Rep., 2019, 74, 97–240.
26. F. Xiang, Y. Lu, Z. Wang, H. Ju, G. Di Filippo, C. Li, X. Liu, X. Leng, J. Zhu, L. Wang and M. A. Schneider, J. Phys. Chem. C, 2019, 123, 23007–23013.
27. B. Cirera, A. Sánchez-Grande, B. de la Torre, J. Santos, S. Edalatmanesh, E. Rodríguez-Sánchez, K. Lauwaet, B. Mallada, R. Zbořil, R. Miranda, O. Gröning, P. Jelínek, N. Martín and D. Ecija, Nat. Nanotechnol., 2020, 15, 437–443.
28. S. Kawai, O. Krejčí, A. S. Foster, R. Pawlak, F. Xu, L. Peng, A. Orita and E. Meyer, ACS Nano, 2018, 12, 8791–8796.
29. G. Fratesi, S. Achilli, N. Manini, G. Onida, A. Baby, A. Ravikumar, A. Ugolotti, G. P. Brivio, A. Milani and C. S. Casari, Materials, 2018, 11, 2556.
30. A. M. Goudappagouda, V. C. Wakchaure, K. C. Ranjeesh, C. A. R. Abhai and S. S. Babu, Chem. Commun., 2017, 53, 7072–7075.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
33. J. M. Soler, E. Artacho, J. D. Gale, A. Garca, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
34. J. Tersoff and D. R. Hamman, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805.

---