Open Access Article
Open Access ArticleThe solvation structure, transport properties and reduction behavior of carbonate-based electrolytes of lithium-ion batteries†
Tingzheng
Hou
 *ab,
Kara D.
Fong
*ab,
Kara D.
Fong
 bc,
Jingyang
Wang
bc,
Jingyang
Wang
 ae and
Kristin A.
Persson
ae and
Kristin A.
Persson
 *ad
*ad
aDepartment of Materials Science and Engineering, University of California Berkeley, 210 Hearst Mining Building, Berkeley, California 94720, USA
bEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720, USA
dThe Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
eMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA. E-mail: kapersson@lbl.gov
First published on 17th September 2021
Abstract
Despite the extensive employment of binary/ternary mixed-carbonate electrolytes (MCEs) for Li-ion batteries, the role of each ingredient with regards to the solvation structure, transport properties, and reduction behavior is not fully understood. Herein, we report the atomistic modeling and transport property measurements of the Gen2 (1.2 M LiPF6 in ethylene carbonate (EC) and ethyl methyl carbonate (EMC)) and EC-base (1.2 M LiPF6 in EC) electrolytes, as well as their mixtures with 10 mol% fluoroethylene carbonate (FEC). Due to the mixing of cyclic and linear carbonates, the Gen2 electrolyte is found to have a 60% lower ion dissociation rate and a 44% faster Li+ self-diffusion rate than the EC-base electrolyte, while the total ionic conductivities are similar. Moreover, we propose for the first time the anion–solvent exchange mechanism in MCEs with identified energetic and electrostatic origins. For electrolytes with additive, up to 25% FEC coordinates with Li+, which exhibits a preferential reduction that helps passivate the anode and facilitates an improved solid electrolyte interphase. The work provides a coherent computational framework for evaluating mixed electrolyte systems.
1 Introduction
The composition of the electrolytes for commercialized lithium ion batteries (LIBs) has been well identified.1 Although the formulation differs between scenarios, the prototype employs a carbonate-based electrolyte with cyclic carbonates (e.g., ethylene carbonate (EC), and propylene carbonate (PC)), linear carbonates (e.g., ethyl methyl carbonate (EMC), diethyl carbonate (DEC), and dimethyl carbonate (DMC)) and lithium salts (e.g., LiPF6, and lithium bis(trifluoromethanesulfonyl)imide (LiTFSI)). The cyclic carbonates with high dielectric constant possess a higher relative solvating ability.2 The lithium salt cations and anions dissociate, fully or partially, and are solvated by the solvent molecules, which enables Li+ transport. The linear carbonates serve to mitigate the viscosity and lower the melting point. Moreover, the reduction reactions of electrolytes crucially lead to the spontaneous formation of an electrically insulating and ionically conductive solid electrolyte interphase (SEI) between anode and electrolyte in the initial cycles.3 Hence, the key descriptors for electrolyte performance lie in three major categories: the solvation behavior, the transport properties, and the electrochemical reduction/oxidation behavior.Extensive efforts have been devoted to understanding the solvation and transport property of non-aqueous electrolytes. Instrumental measurements including infrared spectroscopy (IR),4–6 and Raman7,8 have been utilized to determine the ion-solvent coordinating states. However, conventional spectroscopic methods are not without limitations for binary or ternary mixed-carbonate electrolytes (MCEs), since it is difficult to quantitatively deconvolute the overlapping peaks of different carbonate species, the overtone peaks, and the accompanied Fermi resonance effects, especially when solvents share the same functional groups.2,9 In addition, because of the possible difference in spectroscopic sensitivity between the coordinated and uncoordinated states of solvent moieties, the scaling of peak area integrals is required to obtain the actual molar ratio of species,10 which could introduce additional error and hinders straightforward quantitative interpretation. Most recently, an internally referenced diffusion-ordered spectroscopy (IR-DOSY) technique has been introduced to determine the solvation state of individual solvents in binary electrolyte systems, which may help overcome the limitation of conventional vibrational spectroscopy.2,11 As an alternative approach, computational methods including ab initio molecular dynamics (AIMD)12–14 and classical molecular dynamics (MD)15–19 simulations have shown satisfying results in modeling the solvation and transport behaviors. Recent studies9,20 reported MD simulations of 1.0 and 1.2 M LiPF6 in EC, revealing detailed solvation structures of the single-solvent electrolyte where cations and anions are mostly dissociated and uncorrelated. As a result, the ionic conductivity can be directly estimated by the Nernst–Einstein (NE) equation with the assumption that ions are fully dissociated without any interactions.21 However, in MCEs, the NE equation is not applicable because of significant correlated ion motions.22,23 Despite the approximate treatment of the correlated term of conductivity proposed by Borodin et al.,24–26 the ionic conduction mechanism, including the contribution from multimeric species, of MCEs is not completely understood. Most recently, Fong et al.27,28 demonstrated a rigorous methodology for analyzing transport properties in electrolytes, including Green–Kubo (GK) relations for the total conductivity and transference number. This approach will be used herein to enable a comprehensive study of transport in MCEs.
The electrochemical reactivity of electrolytes determines the voltage window of batteries. More importantly, constructing a stable and efficient SEI intrinsically formed by electrolytes is among the most effective strategies to achieve superior cycling performance.29,30 While EC has been long recognized as the major component that regulates the anode SEI,31–33 recent findings indicate that linear carbonates with a theoretically lower reduction potential could also facilitate the SEI formation.34 Furthermore, with the intensive studies on emerging Li metal and Si anode materials, electrolyte additives as minor species (e.g. fluoroethylene carbonate (FEC)) are recruited in novel electrolyte design to enhance the strength and stability of the SEI film.35,36 Consequently, in order to understand the macroscopic electrochemical performance, a comprehensive molecular-level investigation of MCEs is of great significance to deconvolute the influence of individual species and identify possible synergetic effects.
In this work, we report the atomic-scale modeling and transport property measurements of a binary MCE, Gen2 electrolyte (1.2 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (w/w 3
EMC (w/w 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7)), along with EC-base electrolyte (1.2 M LiPF6 in EC), GenF electrolyte (Gen2 + 10 mol% FEC), and ECF electrolyte (EC + 10 mol% FEC), to decipher the different roles of anion, cyclic carbonate, linear carbonate, and additive. Detailed static and dynamic solvation structure information is obtained from MD simulations. Self-diffusion coefficients, ionic conductivity, residence times are computed to characterize the transport properties. Using MD-obtained solvation structures as input, the electrostatic potential, solvent exchange energy, and reduction potential calculations are conducted using quantum chemistry to fully depict the solvation structure and its influence on the reduction behavior of electrolytes. The quantitative atomistic modeling of MCEs provides new insights into conventional carbonate electrolytes and novel electrolyte design.
7)), along with EC-base electrolyte (1.2 M LiPF6 in EC), GenF electrolyte (Gen2 + 10 mol% FEC), and ECF electrolyte (EC + 10 mol% FEC), to decipher the different roles of anion, cyclic carbonate, linear carbonate, and additive. Detailed static and dynamic solvation structure information is obtained from MD simulations. Self-diffusion coefficients, ionic conductivity, residence times are computed to characterize the transport properties. Using MD-obtained solvation structures as input, the electrostatic potential, solvent exchange energy, and reduction potential calculations are conducted using quantum chemistry to fully depict the solvation structure and its influence on the reduction behavior of electrolytes. The quantitative atomistic modeling of MCEs provides new insights into conventional carbonate electrolytes and novel electrolyte design.
2 Methodology
2.1 Molecular dynamics (MD) simulations
MD simulations were performed using LAMMPS (Large Scale Atomic/Molecular Massively Parallel Simulator).37 A non-polarizable force field model was employed, which is defined by the following potential functions:| Etotal(rN) = Ebonded + Enonbonded | (1) |
| Ebonded = Ebonds + Eangles + Edihedrals (+Eimpropers) | (2) |
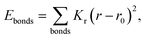 | (3) |
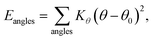 | (4) |
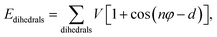 | (5) |
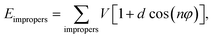 | (6) |
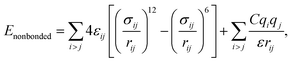 | (7) |
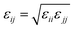 and σij = (σii + σjj)/2 are used. The bonded interactions (bonds, angles, dihedrals, and impropers) were modeled as harmonic functions, and the nonbonded included van der Waals interactions and Coulombic forces. The dihedral term accounts for the dihedral torsion of four consecutive bonded atoms, whereas the improper term accounts for the dihedral torsion of three atoms centered around a fourth atom. The bonded and non-bonded parameters for EC, EMC, and FEC were obtained from the OPLS-AA force fields (Optimized Potentials for Liquid Simulations All Atom),38,39 while those for PF6− are taken from Lopes et al.40 and Li+ from Jensen et al.41 The partial atomic charges were fitted using the RESP method.42,43 Long-range electrostatic interactions were handled by the particle–particle particle-mesh (PPPM) solver with a grid spacing of 0.1 nm. A cutoff distance of 1.5 nm was used for electrostatic and 12–6 Lennard–Jones interactions. The molecules were initially packed randomly in a cubic box using PACKMOL44 (Fig. S1 in ESI†). The force field is further benchmarked against experimental properties and quantum chemistry (see ESI†).
and σij = (σii + σjj)/2 are used. The bonded interactions (bonds, angles, dihedrals, and impropers) were modeled as harmonic functions, and the nonbonded included van der Waals interactions and Coulombic forces. The dihedral term accounts for the dihedral torsion of four consecutive bonded atoms, whereas the improper term accounts for the dihedral torsion of three atoms centered around a fourth atom. The bonded and non-bonded parameters for EC, EMC, and FEC were obtained from the OPLS-AA force fields (Optimized Potentials for Liquid Simulations All Atom),38,39 while those for PF6− are taken from Lopes et al.40 and Li+ from Jensen et al.41 The partial atomic charges were fitted using the RESP method.42,43 Long-range electrostatic interactions were handled by the particle–particle particle-mesh (PPPM) solver with a grid spacing of 0.1 nm. A cutoff distance of 1.5 nm was used for electrostatic and 12–6 Lennard–Jones interactions. The molecules were initially packed randomly in a cubic box using PACKMOL44 (Fig. S1 in ESI†). The force field is further benchmarked against experimental properties and quantum chemistry (see ESI†).
All simulation box consists of 1500 solvent molecules in EC-base (1500 EC), ECF (1350 EC, 150 FEC), Gen2 (504 EC, 996 EMC), and GenF (454 EC, 896 EMC, 150 FEC). A salt concentration of 1.2 M was made by adding 126 LiPF6 into EC-base/ECF and 166 LiPF6 into Gen2/GenF, respectively. The initial configuration was minimized by a conjugated-gradient energy minimization scheme employing a convergence criterion of 1.0 × 10−4. The electrolytes were then equilibrated for 5 ns in the isothermal–isobaric ensemble (constant NPT) using the Parrinello–Rahman barostat to maintain a pressure of 1 bar and a temperature of 298 K with a time constant of 1 ps. An annealing process was conducted to further guarantee that all systems are melted and to avoid local configuration confinement. All systems were heated from 298 K to 400 K for 1 ns, and maintained at 400 K for 2 ns, and subsequently annealed from 400 to 298 K in 2 ns. Finally, production runs of 60 ns were conducted in the canonical ensemble (NVT) under Nose–Hoover thermostats with a time constant of 1 ps at 298 K. The simulation time was long enough to sample adequately the Fickian (diffusive) regime of all systems.9 At least four independent duplicate runs were performed for each electrolyte in order to estimate the statistical uncertainties.
The solvation structure and transport properties analysis of the MD trajectories utilizes the MDAnalysis45 python package. The detailed population of species and solvent-specific solvation numbers are listed in Tables S1 and S2, respectively.†
The self-diffusion coefficients for Li+, PF6−, EC, EMC, and FEC were extracted from the MD simulation by analysis of the mean square displacement (MSD, (δr)2) over time.46 The slope of the linear regime in the MSD was obtained for each simulation duration of 1 ns and averaged over at least 10 ns of the production runs to obtain:
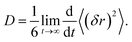 | (8) |
The ionic conductivity is related to the electrical current autocorrelation function (ECACF) via the following Green–Kubo relation:
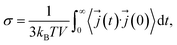 | (9) |
![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) (t) is the electrical current given by
(t) is the electrical current given by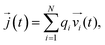 | (10) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i is the velocity of species i.
i is the velocity of species i.
As with the self-diffusivity, the ionic conductivity can also be computed using the following formally equivalent Einstein expression:
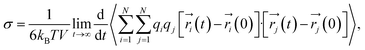 | (11) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i(t) is the coordinates of species i at time t. As is the case with diffusion coefficient calculations, a mathematically rigorous analysis of the conductivity requires the term enclosed in the angular brackets of eqn (11) to be linear in time. The simulations performed here all reached the linear regime as with the diffusion coefficient analysis above. Results from four representative simulations of the EC-base electrolyte are shown in Fig. S3 (see ESI†) to demonstrate this linear behavior for both self-diffusion coefficients and ionic conductivities calculation.
i(t) is the coordinates of species i at time t. As is the case with diffusion coefficient calculations, a mathematically rigorous analysis of the conductivity requires the term enclosed in the angular brackets of eqn (11) to be linear in time. The simulations performed here all reached the linear regime as with the diffusion coefficient analysis above. Results from four representative simulations of the EC-base electrolyte are shown in Fig. S3 (see ESI†) to demonstrate this linear behavior for both self-diffusion coefficients and ionic conductivities calculation.
The residence times of Li+-X pairs (Li+-EC, Li+-EMC, Li+-FEC, and Li+-PF6−) are calculated by computing the lifetime correlation function:47
| PLi+-X(t) = 〈HLi+-X(t)·HLi+-X(0)〉 | (12) |
The reported values and uncertainties of the total ionic conductivity, self-diffusion coefficient, residence time, population of solvation species, and solvent-specific coordination number are estimated by calculating the mean, and standard deviation of the quantities obtained from the four independent 60 ns duplicates.
2.2 Quantum chemical calculations
The anion solvent exchange energy and electrostatic potential were calculated using B3LYP-D3(BJ)/6-311+g(d,p)48–50//B2PLYPD3/def2TZVP51,52 level of theory with implicit solvent model IEF-PCM(UFF,Acetone)53,54 in Gaussian 16.55 Quasi-harmonic entropy and enthalpy correction with a cutoff frequency of 100 cm−1 was applied as suggested by Grimme et al.56 using the GoodVibes57 program. For the electronic contributions, it is assumed that the first and higher excited states are entirely inaccessible. For the entropy contributions, it is assumed that the implicit solvent model together with explicit solvent molecules is sufficiently accurate for modeling the free energy change of a molecule from an ideal gas to a solution phase. The calculated free energy includes the entropy contributions resulting from the translational, electronic, rotational, and vibrational motion.The adiabatic reduction potentials for the representative solvation structures were calculated at IEF-PCM(UFF,Acetone)/B3LYP-D3/6-31+g(d,p) level of theory using the following function58
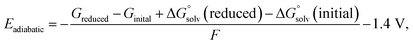 | (13) |
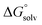 are the corresponding free energies of solvation with both implicit and explicit solvents considered, and F is the Faraday constant. The zero-point energy (ZPE) corrections were considered in the calculation while the basis set superposition error (BSSE) energy was neglected.59 A standard-state correction60 was considered to account for the different concentrations of the non-solvated species, which resulted in the addition of a correction constant RT
are the corresponding free energies of solvation with both implicit and explicit solvents considered, and F is the Faraday constant. The zero-point energy (ZPE) corrections were considered in the calculation while the basis set superposition error (BSSE) energy was neglected.59 A standard-state correction60 was considered to account for the different concentrations of the non-solvated species, which resulted in the addition of a correction constant RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.47/M) to
ln(24.47/M) to 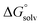 , where R is the gas constant, T is temperature, 24.47 is the molar volume in liter for ideal gas under 1 atm and 298.15 K, and M is the effective concentration of the species that are free of Li solvation. This effective concentrations of EC, EMC, and PF6− are 1.36, 3.66, and 0.2857, respectively, as computed from the MD simulation of the Gen2 electrolyte. A dielectric constant (ε) of 20.493 (Acetone) was adopted, which is similar to the reported value of 19. Geometries were allowed to relax after the electron transfer. Subtraction of 1.4 V accounts for the conversion from the absolute electrochemical scale to the commonly used Li/Li+ potential scale in order to compare predicted values with experimental data using the same reference electrode. An additional factor of 0.1–0.2 V for graphite intercalation or 0.3–0.4 V for Si anode Li insertion should be subtracted if the reference electrode is changed to these specific systems. The experimental reduction potentials are computed from the full cell differential capacity (dQ/dV) curve.61 The cells using graphite anodes were reported to be charged to 3.5 V during the formation cycle. This full cell voltage is set to be 0 V with respect to the graphite anode. For example, if the reduction peak is at 3.2 V, then the reduction potential of the reduced species will be 0.3 V (vs. graphite) or 0.45 V (vs. Li/Li+).
, where R is the gas constant, T is temperature, 24.47 is the molar volume in liter for ideal gas under 1 atm and 298.15 K, and M is the effective concentration of the species that are free of Li solvation. This effective concentrations of EC, EMC, and PF6− are 1.36, 3.66, and 0.2857, respectively, as computed from the MD simulation of the Gen2 electrolyte. A dielectric constant (ε) of 20.493 (Acetone) was adopted, which is similar to the reported value of 19. Geometries were allowed to relax after the electron transfer. Subtraction of 1.4 V accounts for the conversion from the absolute electrochemical scale to the commonly used Li/Li+ potential scale in order to compare predicted values with experimental data using the same reference electrode. An additional factor of 0.1–0.2 V for graphite intercalation or 0.3–0.4 V for Si anode Li insertion should be subtracted if the reference electrode is changed to these specific systems. The experimental reduction potentials are computed from the full cell differential capacity (dQ/dV) curve.61 The cells using graphite anodes were reported to be charged to 3.5 V during the formation cycle. This full cell voltage is set to be 0 V with respect to the graphite anode. For example, if the reduction peak is at 3.2 V, then the reduction potential of the reduced species will be 0.3 V (vs. graphite) or 0.45 V (vs. Li/Li+).
The energy decomposition analysis based on absolutely localized molecular orbitals within an implicit solvent model (ALMO-EDA(solv))62–64 were performed using Q-Chem 5.2.0,65 B3LYP-D3(BJ)/6-311+g(d,p)48–50 level of theory, and an implicit solvent model IEF-PCM(UFF,ε = 19.0).53,54
The ALMO-EDA(solv) method partitions the total binding energy (EB) of two clusters into contributions from permanent electrostatics (ELEC), Pauli repulsion (PAULI), dispersion (DISP), polarization (POL), and charge transfer (CT):
| E(s)B = ΔE(s)ELEC + ΔE(s)PAULI + ΔE(s)DISP + ΔE(s)POL + ΔE(s)CT, | (14) |
| ΔE(s)ELEC = ΔE(0)ELEC + ΔEelSOL, | (15) |
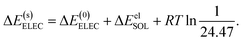 | (16) |
2.3 Ionic conductivity measurement
Ionic conductivities of the four electrolytes were measured by Mettler Toledo SevenCompact Cond meter S230, which is equipped with a 4-electrode Pt conductivity probe (Mettler Toledo, InLab 710). The probe was calibrated with a standardized 12.88 mS cm−1 potassium chloride (KCl) solution (Mettler Toledo). After the successful calibration of the instrument, the ionic conductivities of the four electrolytes were measured in an Ar-filled glove box (O2, H2O <0.1 ppm) at a temperature range of 29–35 °C, and corrected to 25 °C by a linear correction regime. The error of the conductivity meter and the linear correction is estimated as no more than 0.2 mS cm−1. The amount of the salt and solvents used for the electrolyte preparation and the measured conductivities are shown in Tables S3 and S4, respectively.†3 Results and discussion
3.1 Solvation structure of the Gen2 and EC-base electrolytes
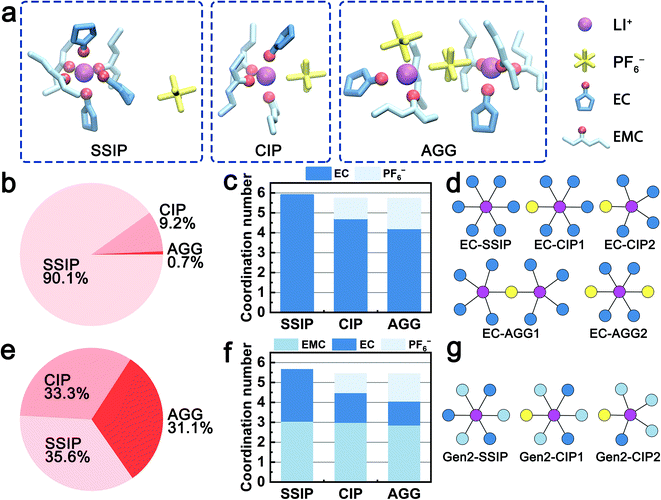
The solvation structures obtained from the MD simulations are categorized into three species, i.e., solvent-separated ion pairs (SSIP), contact ion pairs (CIP), and aggregates (AGG). Fig. 1a shows examples of the three species in the Gen2 electrolyte that are extracted from MD trajectories. For all the three species, both EC and EMC are observed in the first solvation shell and coordinate with Li+ ions via the carbonyl oxygen. Fig. 1b and e quantitatively compare the ratios of the three species in the EC-base and Gen2 electrolytes. In the EC-base electrolyte, the majority (90.1%) of Li+ are dissociated (SSIP), while in the Gen2 electrolyte, a much smaller proportion (35.6%) of SSIP species was observed, with CIP and AGG species contributing 33.3% and 31.3%, respectively. The low ion dissociation rate of the Gen2 electrolyte agrees well with previous experimental results using conductivity measurement66 and FTIR spectroscopy,5 as well as simulation results using non-polarizable18 and polarizable force field.25 This can be attributed to the reduced permittivity of the Gen2 electrolyte as a result of mixing EC (ε = 90) and EMC (ε = 2.96).1 Using nodes and vertices expression, we plotted the 2D topology graphs of the majority solvation structures observed in the EC-base and Gen2 electrolyte, as presented in Fig. 1d and g and S2 (see ESI†). It should be noted that, while the EC-base electrolyte has a much higher SSIP ratio than the Gen2 electrolyte, more than half of AGG in the Gen2 electrolyte are charged species (19% out of 31%), which narrows the population gap of ionically conductive species between the EC-base and Gen2 electrolyte. However, the bulky and sluggish AGG species are expected to diffuse slower and cannot transport Li+ as efficiently as SSIP species.2The coordination numbers in the two electrolytes are systematically analyzed. In average, the total solvent coordination number in the Gen2 electrolyte is 4.7, with 1.8 EC and 2.9 EMC, corresponding to an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC relative solvating power (Χ) of 1.59, which is the ratio between the coordination percentage of EC and the coordination percentage of EMC.11 The result is in excellent agreement with the IR-DOSY experiments reporting a solvent coordination number of 4.64 and an EC
EMC relative solvating power (Χ) of 1.59, which is the ratio between the coordination percentage of EC and the coordination percentage of EMC.11 The result is in excellent agreement with the IR-DOSY experiments reporting a solvent coordination number of 4.64 and an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC relative solvating power of 1.42 in 1
EMC relative solvating power of 1.42 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (molar ratio) LiPF6
4 (molar ratio) LiPF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC
EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC electrolyte.2 Furthermore, we have computed the detailed solvent-specific coordination numbers for the three species (Fig. 1c and f). For both the EC-base and Gen2 electrolyte, the total number of coordinating solvent molecules decreases from about 6 to 4 when Li+ ions are engaged in higher degrees of ion association (SSIP to AGG). Notably, in the Gen2 electrolyte, only the coordination number of EC decreases (from 2.6 to 1.2 with an increased degree of ion association) when PF6− enters the solvation sheath while that of EMC is preserved (about 3). This trend is confirmed by anion–solvent exchange free energy calculations (Table 1; Fig. S5 in ESI†). Three exchange reactions from a SSIP species (3 EC and 3 EMC) to CIP species with varying number of EC and EMC were calculated using MD obtained structures. The reaction replacing a Li+-coordinated EC with a PF6− exhibits the largest free energy gain, while the reaction replacing a Li+-coordinated EMC with a PF6− is energetically unfavored, which is in good agreement with the MD statistics. Therefore, the EC molecules are preferentially desolvated when Li+ coordinates with PF6−. To fully understand the different exchange mechanisms of EC and EMC, we rationalize the phenomena in terms of electrostatic repulsion in the following sections.
EMC electrolyte.2 Furthermore, we have computed the detailed solvent-specific coordination numbers for the three species (Fig. 1c and f). For both the EC-base and Gen2 electrolyte, the total number of coordinating solvent molecules decreases from about 6 to 4 when Li+ ions are engaged in higher degrees of ion association (SSIP to AGG). Notably, in the Gen2 electrolyte, only the coordination number of EC decreases (from 2.6 to 1.2 with an increased degree of ion association) when PF6− enters the solvation sheath while that of EMC is preserved (about 3). This trend is confirmed by anion–solvent exchange free energy calculations (Table 1; Fig. S5 in ESI†). Three exchange reactions from a SSIP species (3 EC and 3 EMC) to CIP species with varying number of EC and EMC were calculated using MD obtained structures. The reaction replacing a Li+-coordinated EC with a PF6− exhibits the largest free energy gain, while the reaction replacing a Li+-coordinated EMC with a PF6− is energetically unfavored, which is in good agreement with the MD statistics. Therefore, the EC molecules are preferentially desolvated when Li+ coordinates with PF6−. To fully understand the different exchange mechanisms of EC and EMC, we rationalize the phenomena in terms of electrostatic repulsion in the following sections.
| Anion–solvent exchange reaction | ΔG (kJ mol−1) |
|---|---|
| Li+-(EMC)3(EC)3 + PF6− → Li+-(EMC)3(EC)2PF6− + EC | −9.5 |
| Li+-(EMC)3(EC)3 + PF6− + EMC → Li+-(EMC)4(EC)1PF6− + 2EC | −6.7 |
| Li+-(EMC)3(EC)3 + PF6− → Li+-(EMC)2(EC)3PF6− + EMC | 1.7 |
3.2 Anion–solvent exchange mechanism
Analogous to the nucleophilic substitution reactions, “exit-entry” type and “entry-exit” type are considered two hypothetic mechanisms when the PF6− exchanges with the solvent molecule (Fig. 2a). The anion and solvent molecule exchange with the “exit-entry” type mechanism following two steps: (1) the leaving solvent/anion separates with the Li+ (exit), (2) the incoming anion/solvent coordinates with the Li+ (entry); and vice versa for the “entry-exit” type. In order to reveal the exchange mechanism, the coordination numbers of EC and EMC before and after each CIP–SSIP transition event (set as 0 ps) are extracted from the trajectories and averaged over all such events (Fig. 2b). When PF6− exits the first solvation shell (upper panel), the solvation structure changes from CIP to SSIP. The average EC coordination number with Li+ is above 2.1 before the transition, which is higher than the bulk average of all CIP species (1.5). This indicates that PF6− is more probable to leave the solvation shell when more EC molecules are coordinated. After PF6− separates with Li+ ions at 0 ps, the coordination numbers of both EC and EMC gradually increase to the bulk average of SSIP in about 100–200 ps, suggesting that the exchange is predominantly an “exit-entry” type. Likewise, when PF6− enters the solvation sheath (lower panel), the solvation structure changes from SSIP to CIP. The coordination number of EC as well as the total coordination number before the event is about 0.6 lower than the bulk average of SSIP. The coordination number of EC drops even further from −100 ps to 0 ps. This indicates that PF6− preferentially associates with Li+ ions that have less EC coordinated and a “vacant” coordination site. Subsequently, the coordination numbers of both EC and EMC remain almost unchanged after the PF6− coordination. Therefore, the “exit-entry” type mechanism is expected to dictate the anion–solvent exchange in both directions. To the best of our knowledge, this has not been previously reported.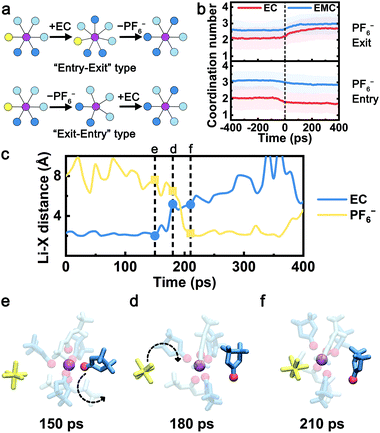 | ||
| Fig. 2 The anion–solvent exchange mechanism. (a) Node graph representations of two types of anion–solvent exchange mechanism, the “entry-exit” type and the “exit-entry” type. (b) The coordination numbers of EC and EMC as a function of time before and after each “PF6− exit” or “PF6− entry” event. The time of each event happens is set as 0 ps, and the coordination numbers are averaged over all such events. The light-colored area denotes the extent of standard deviation. (c–f) Sample trajectory of EC-PF6− exchange in the Gen2 electrolyte. (c) Li+-X (X = carbonyl O in EC or F in PF6−) distance as a function of time. The snapshots of the sampled Li+ solvation shell at (d) 150 ps, (e) 180 ps, and (f) 210 ps of the time slice. The color scheme is the same as Fig. 1a. The non-exchanging coordinated molecules are set as transparent for clarity. | ||
To further visualize the anion–solvent exchange process, a 400 ps long trajectory in the Gen2 electrolyte with an EC-PF6− exchange event is exhibited as an example in Fig. 2c–f. At time 150 ps, the central Li+ coordinates with the highlighted EC solvent. Next, the EC molecule starts to leave the Li+ solvation shell, and an undercoordinated Li+ solvation structure is captured at 180 ps. Subsequently, the PF6− enters the solvation shell to coordinate with Li+, and a CIP structure is formed at 210 ps. The duration of the sampled exchange event is less than 100 ps, which agrees with the observation in the lower panel of Fig. 2b.
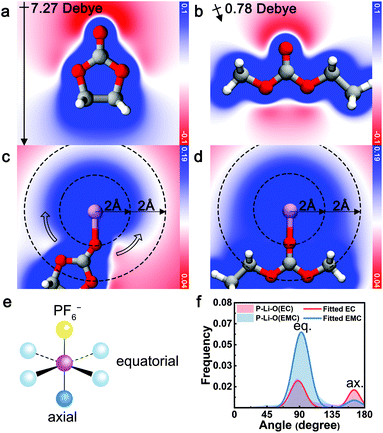
The electrostatic repulsion, arising from the high dipole moment of EC and the negative charge of PF6− is identified as the origin of the exclusive relationship between EC and PF6−. As a measure of the interaction between charge and dipole, electrostatic potential analysis was conducted with contour maps across the carbonyl plane. As illustrated in Fig. 3a and b, uncoordinated EC exhibits a large molecular polarization (7.27 Debye, calculated) while the dipole of EMC is mostly canceled out (0.78 Debye, calculated). When EC coordinates with Li+ ([Li+EC], Fig. 3c), a gradient of electrostatic potential is yielded along the circumference direction around Li+ (hollow arrow). In contrast, the electrostatic potential around EMC-coordinated Li+ ([Li+EMC]) is almost evenly distributed and more positive at the same radial distance (Fig. 3d). A more negative electrostatic potential near [Li+EC] indicates greater relative electrostatic repulsion between EC and PF6−, compared to [Li+EMC]. To quantify this electrostatic interaction, we performed energy decomposition analysis based on absolutely localized molecular orbitals within an implicit solvent model (ALMO-EDA(solv))62 on the binding energy of [Li+EC]⋯[PF6−] (Eb1) and [Li+EMC]⋯[PF6−] (Eb2), respectively (Fig. S7 in ESI;† ellipsis denotes the binding of two clusters). The difference in the attractive terms between Eb1 and Eb2 is found to be 63% contributed by the electrostatic interaction (Fig. S8 in ESI†). This dominancy of the electrostatic term verifies the arguments that the exclusive relationship between EC and PF6− mainly originates from electrostatic repulsion. Interestingly, the repulsive interaction even regulates the angular distribution of coordinating species as manifested in MD trajectories (Fig. 3e and f). Considering a model octahedral CIP solvation structure with four equatorial coordination sites and one axial coordination site with respect to PF6−, in an unbiased situation, the likelihood ratio of solvent molecules occupying the two types of sites is 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. By fitting the distribution of angle P–Li–O (P = P in PF6−, O = carbonyl O in EC and EMC) of CIP species with a binormal distribution, we observe a clear trend that the axial site is favored by EC, whereas EMC exhibits a higher probability for occupying the equatorial sites. The trend is consistent with the repulsive electrostatic interaction between EC and PF6− as elucidated by the quantum chemistry calculations. Note that PF6− can be either monodentate or bidentate, which leads to a deviation from 180° for the axial binding site.
1. By fitting the distribution of angle P–Li–O (P = P in PF6−, O = carbonyl O in EC and EMC) of CIP species with a binormal distribution, we observe a clear trend that the axial site is favored by EC, whereas EMC exhibits a higher probability for occupying the equatorial sites. The trend is consistent with the repulsive electrostatic interaction between EC and PF6− as elucidated by the quantum chemistry calculations. Note that PF6− can be either monodentate or bidentate, which leads to a deviation from 180° for the axial binding site.
The impact of the anion–solvent exchange mechanism on the electrochemical performance of electrolytes is two-fold. First, the exchange mechanism is likely to impact the SEI formation. When the electrolyte reacts with the anode surface to form the SEI, the reaction products depend on the starting reactants as well as their immediate solvation environment. The preferential substitution between EC and PF6− anion indicates a lower fraction of EC in solvation structures where Li+ coordinates with PF6−. Meanwhile, for this small fraction of EC in CIPs and AGGs, it is likely that EC and PF6− are separated by a larger angle. In contrast, positively charged SSIPs contain more EC than the bulk average, which preferentially move to the anode surface due to electrostatic and concentration gradients. Therefore, the EC-PF6− exchange influences both the neighbor distance between EC and PF6− within a solvation structure as well as the distribution of solvation species near the anode surface, which in turn impacts the composition of starting reactants, the environment of intermediate fragments, and ultimately the final products of SEI formation reactions. Secondly, the exchange mechanism enhances our understanding of salt dissociation and ionic conduction phenomena. With the “exit-entry” mechanism, a free PF6− does not coordinate with Li+ until an EC molecule exits the SSIP. Thus, the rate of ion pair formation is governed by the relatively long residence time of EC molecules in the Li+ solvation shell (6.4 ns as calculated in Section 3.4). In contrast, in the “entry-exit” mechanism PF6− may directly attack the solvation shell of an SSIP and associate with Li+, similar to a nucleophilic SN2 reaction. This identified mechanism may thus be significant in promoting the long-lived presence of SSIPs, which screen the electrostatic interaction between Li+ and PF6− and enable uncorrelated cation and anion flux.
3.3 Solvation structure of the GenF and ECF electrolytes
The influence of the electrolyte additive on the solvation structure of electrolytes was studied. Two model electrolytes (ECF and GenF electrolyte) are created by adding 10 mol% of FEC to the EC-base and Gen2 electrolyte. As shown in Fig. 4a and c, comparing with the EC-base and Gen2 electrolytes, the ECF and GenF electrolytes exhibit similar population distributions, despite that the SSIP ratio in the GenF electrolyte is slightly higher than that of Gen2. Likewise, in terms of the anion–solvent exchange behavior, electrolytes with FEC exhibit a similar trend as their base electrolytes (Fig. 4b and d). The average Li+ coordination number with EMC remains about 3 for all species, while the FEC coordination number to Li+ decreases along with EC when forming CIP and AGG in the GenF electrolyte. We hypothesize that the large dipole moment of FEC (6.44 Debye, calculated), which is comparable with that of the structurally analogous EC, is responsible for a similar repulsive interaction with PF6− as compared to EC.9 Moreover, fluorination is reported to cause large decreases in the solvating ability of fluorinated carbonate.2 On average, FEC exhibits a coordination number of 0.23 in both ECF and GenF electrolytes, corresponding to an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FEC molar ratio and an EC
FEC molar ratio and an EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC
EMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FEC molar ratio of 24
FEC molar ratio of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 7
1 and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the solvation shell. This less than 10% of FEC in the Li+ first solvation shell signifies its weaker solvating ability compared to EC and EMC, consistent with experimental observations.2,67 However, the fact that still a considerable portion (23%, if assuming single FEC coordination) of Li+ are coordinated with at least one FEC, is crucial for the reduction behavior of electrolytes with the FEC additive, as discussed below.
1 in the solvation shell. This less than 10% of FEC in the Li+ first solvation shell signifies its weaker solvating ability compared to EC and EMC, consistent with experimental observations.2,67 However, the fact that still a considerable portion (23%, if assuming single FEC coordination) of Li+ are coordinated with at least one FEC, is crucial for the reduction behavior of electrolytes with the FEC additive, as discussed below.
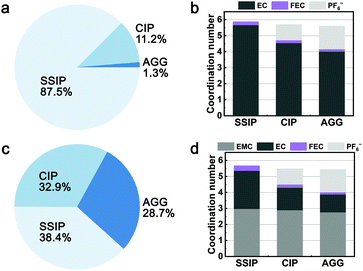 | ||
| Fig. 4 The population and species-specific coordination number of SSIP, CIP, and AGG in (a and b) the ECF electrolyte and (c and d) the GenF electrolyte. | ||
3.4 Transport properties
To evaluate the properties of the four model electrolytes, we consider not only the coordination environments but also the transport properties governing the Li+ diffusion and ionic conduction. In order to quantify the average time length of ion association, the residence times (τij) of Li+-EC, Li+-EMC, Li+-FEC, and Li+-PF6− in the four model electrolytes were computed by fitting the pair lifetime correlation function (Fig. 5a). The residence times of Li+-solvent pairs decrease in the order of EMC, EC, and FEC. A similar trend was found in previous theoretical calculations that DMC exhibits a longer residence time over EC with respect to Li+.16 Notably, the fitted RESP partial charges on the carbonyl oxygen of each solvent molecule decrease in the same order. We surmise that the partial charge of the coordinating atom rather than the donor number of the coordinating solvent is the decisive factor of the kinetic barrier of desolvation, which further determines the residence times. The residence times of Li+-PF6− in the Gen2 and GenF electrolytes are about 6 ns while those in EC and ECF electrolytes are less than 4 ns. The trend indicates that the Li+-PF6− pair coordinates with each other for a longer period of time in the presence of linear carbonates. Therefore, our solvation structure and residence time analysis have demonstrated that, with linear carbonates, the coordinated species (CIP and AGG) are more favored both spatially and temporally.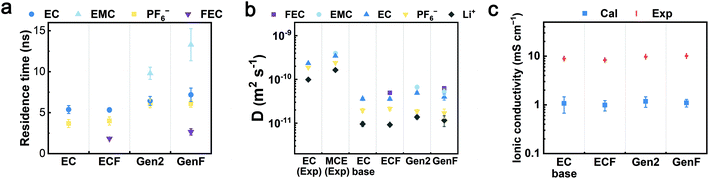 | ||
Fig. 5 Transport properties of the EC-base, ECF, Gen2, and GenF electrolytes. (a) The residence times (τij) of EC-Li+, EMC-Li+, FEC-Li+, and PF6−-Li+ pairs in the EC-base, ECF, Gen2, and GenF electrolytes. (b) The calculated self-diffusion coefficients of electrolyte species (EC, EMC, FEC, PF6−, and Li+) in the EC-base, ECF, Gen2, and GenF electrolytes. Experimental values for EC (1 M LiPF6 in EC), and MCE (1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC 1 DEC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (mol.)) at 298 K are taken from the literature.66 (c) The experimental (Exp) and calculated (Cal) ionic conductivity at 298 K. 2 (mol.)) at 298 K are taken from the literature.66 (c) The experimental (Exp) and calculated (Cal) ionic conductivity at 298 K. | ||
Furthermore, the self-diffusion coefficients were calculated using the slope of the mean square displacement (MSD) and compared to experiments (Fig. 5b and S3a in ESI†). In contrast to the EC-base and ECF electrolytes, MCEs (the Gen2 and GenF electrolytes) exhibit a greater self-diffusion coefficient for all species, as linear carbonates are less viscous. While it is well-known that the non-polarizable force field employed here underestimates the diffusivity, the calculated self-diffusion coefficients are in fair agreement with the experimental trends.66 It should be noted that scaling the point charges in non-polarizable force fields is an effective approach to account for the electronic polarizations that screen solvent-ion and ion–ion interactions.23,68,69 For a mixed carbonate electrolyte (e.g., Gen2), MD simulations using a non-polarizable force field can obtain a similar diffusivity and ionic conductivity as experiments by scaling the default ionic charges (±1) of Li+ and PF6− with a factor of 0.8, as demonstrated in our recent work.70 A less used approach is to scale the point charge of solvent molecules to modulate the solvent polarity.71,72
Thus far, we have shown that MCEs exhibit a higher diffusivity, while the EC-base and ECF electrolytes exhibit a higher ion dissociation rate and a higher ratio of ionic conducting species.
Based on the above understanding of the ion solvation and diffusion, the ionic conductivities were rigorously computed using GK relations and experimentally measured using conductivity meter, as shown in Fig. 5c and S3b (see ESI†). All four electrolytes exhibit similar calculated ionic conductivity values, within an order of magnitude. Interestingly, the significantly higher salt association of the Gen2 electrolyte does not lead to significantly lower ionic conductivity, which is attributed to the improved viscosity and self-diffusion properties. This trend is consistent with our experimentally obtained values (9.8 mS cm−1 for Gen2, 8.9 mS cm−1 for EC-base). In contrast, conventional ionic conductivity calculations using the Nernst–Einstein equation overestimate the ionic conductivity of the Gen2 and GenF electrolyte by more than 40% (Fig. S9 in ESI†). Hence, for highly associated mixed carbonate electrolytes, a rigorous calculation using Green–Kubo relations is important for obtaining a correct trend of the ionic conductivity. Notably, the inclusion of linear carbonates is essential for the practical operation of batteries at low temperature.1 Furthermore, as shown in Fig. 5b, the addition of 10% FEC slightly decreases the self-diffusion coefficients of other species, due to the high viscosity of FEC (4.1 cP, 298 K), as compared with EC (1.9 cP, 313 K) and EMC (0.65 cP, 298 K).73,74 As a result, the ionic conductivity of the ECF is slightly lower than that of the EC-base electrolyte for both experimental and calculated results. In contrast, the ionic conductivities of the Gen2 and GenF electrolytes are almost equal, on account of the slightly higher SSIP ratio in the GenF electrolyte that helps compensate for the decrease in diffusivity. The observation agrees with previous experimental results that the ionic conductivity of 1 M LiPF6 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (vol%) EC/PC/EMC remains similar when adding 2 vol% FEC at room temperature.75
3 (vol%) EC/PC/EMC remains similar when adding 2 vol% FEC at room temperature.75
3.5 Reduction behavior of each solvent ingredient
Given that the reduction reactions of electrolytes regulate the anode SEI formation and further influence the cycling performance of batteries, the reduction behavior of electrolytes was investigated by quantum chemical calculations. The initial step of reduction reactions and the corresponding reduction potentials of single EC, EMC, and FEC coordinated Li+ structures, as well as two full solvation structures obtained from the MD trajectory were computed and compared to experiments (Table 2; Fig. S6 in ESI†). The reduction potential decreases with the order of FEC, EC, and EMC, in agreement with the reported experimental results61,76,77 and previous theoretical calculations.78 Even as an additive (10%), FEC coordinates with Li+ (Fig. 4) and exhibits a high reduction potential (0.3 V higher than EC). Thus, FEC will be preferentially reduced in the early SEI formation using ECF and GenF in full cells, setting the stage for further SEI formation reactions, aging, and anode passivation.79 Moreover, FEC is expected to improve the SEI composition, through increased production of LiF and oligomeric components derived by FEC reduction.80,81 Even though the additive may slightly affect the conductivity as discussed above, the overall effect of FEC additive is beneficial for the cycling performance and capacity retention, especially for Li metal anode35 and Si anode applications.36 Furthermore, as noted by Horowitz et al.82 and Shi et al.,34 for reduction reactions specifically at the electrolyte–electrode interface, the interaction of the solvated species with the electrodes is another important factor governing the reduction behavior of electrolytes.The interaction between solvated species with Li metal and silicon anodes is especially sensitive to the surface conditions of the specific materials. The electrochemical and mechanical evolution of the Li metal surface is a highly complex, out-of-equilibrium reaction cascade, where the resulting composite surface film can reduce electronic charge transfer to the electrolyte,83 and its inorganic components including Li2O, Li2CO3, LiOH, Li2S, and LiF, along with organic components depending on manufacturing and storage conditions are all believed to influence the SEI layer composition and functionality.83,84 Similarly, almost all silicon surfaces exhibit a native oxide or sub-oxide layer that reacts irreversibly during the initial electrochemical cycles.85 While the reduction of linear carbonate is believed to be fully suppressed by EC on graphite anode,86,87in situ spectroscopic experiments have shown evidence of preferential reduction of linear carbonates (e.g., DMC) on the native silicon oxide film of non-lithiated silicon anode.34 Balbuena et al. have found that the reduction mechanism of EC and FEC is highly dependent on the surface termination of the Si surface, as well as the degree of lithiation of the surface.88,89 Moreover, it is reported that FEC exhibits a higher affinity towards the silicon surface than EC, and forms an ordered, up-right orientation, which may promote SEI formation and Li diffusion.90,91 Most recently, artificial surface coating with the appropriate binder,92 oxide layer,93 and Mg metal94 have been used to alter the interfacial interactions and reactions between the Si anode and electrolytes for achieving a stable SEI that minimizes side reactions and sustains efficient cycling. Finally, water contamination has been reported to cause detrimental parasitic reactions that affect the formation, evolution, and properties of the SEI.95 In addition, the hydrolysis of LiPF6 creates hydrofluoric acid, leading to a pitted and inhomogeneous SEI structure.96 Therefore, we note the importance of considering specific surface conditions as well as possible impurities when investigating the interfacial reactions between anodes and electrolytes.
4 Conclusions
In summary, the solvation structure, transport properties, and reduction behavior of four prototype electrolytes (EC-base, ECF, Gen2, and GenF) were investigated using classical MD simulations, quantum chemistry, and transport property measurements. While the LiPF6 salt in the EC-base electrolyte is mostly dissociated, the Gen2 electrolyte exhibits a much higher degree of ion association (>30% CIP, >30% AGG). Interestingly, and non-intuitively, in the Gen2 electrolyte, the coordination number of EC with Li+ decreases when PF6− enters the first solvation shell. We here identify electrostatic repulsion between the highly polarizable EC and the negative charged anion PF6−, as responsible for the phenomenon. We also reveal an anion–solvent exchange mechanism as “entry-exit” type, providing a dynamic perspective of ion transport in electrolytes. Furthermore, in contrast to the EC-base electrolyte, the Gen2 electrolyte exhibits greater self-diffusion coefficients, due to the lower viscosity of the linear carbonates. Therefore, although the Gen2 electrolyte exhibits more aggregates and bulky conductive species, the overall ionic conductivities of the Gen2 and EC-base electrolyte are very similar, as verified by experimental measurements. A considerable portion of the FEC additive in the ECF and GenF electrolyte is found to coordinate with Li+ in the first solvation shell, with a minor impact on the transport properties. Finally, the reduction potentials of Li+ coordinated solvent molecules are found to decrease in the order of FEC, EC, and EMC. The preferential reduction of the FEC additive is deemed beneficial for the early onset passivation of the anode surface and facilitates an improved composition of SEI. We believe our modeling of mixed carbonate electrolytes elucidates the atomistic origin of energy-storage relevant properties of this class of commercially relevant battery electrolytes, and provides a paradigm of computational property evaluation in novel electrolyte design.Author contributions
T. H. conducted the MD simulations and quantum chemical calculations. K. D. F. developed the theory and algorithms of the transport property analysis. J. W. performed the ionic conductivity measurements. All authors participated in data analyses and discussion. T. H., K. D. F, J. W., K. A. P. co-wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by the U.S. Department of Energy's Vehicle Technologies Office under the Silicon Electrolyte Interface Stabilization (SEISta) Consortium directed by Brian Cunningham and managed by Anthony Burrell. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. A portion of the research was performed using computational resources sponsored by the Department of Energy's Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory. The authors would like to thank Dr Julian Self for the helpful discussion on anion solvation exchange energy calculations.Notes and references
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- C.-C. Su, M. He, R. Amine, T. Rojas, L. Cheng, A. T. Ngo and K. Amine, Energy Environ. Sci., 2019, 12, 1249–1254 RSC.
- X. B. Cheng, R. Zhang, C. Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed.
- C. Liang, K. Kwak and M. Cho, J. Phys. Chem. Lett., 2017, 8, 5779–5784 CrossRef CAS PubMed.
- R. T. Pekarek, A. Affolter, L. L. Baranowski, J. Coyle, T. Hou, E. Sivonxay, B. A. Smith, R. D. McAuliffe, K. A. Persson, B. Key, C. Apblett, G. M. Veith and N. R. Neale, J. Mater. Chem. A, 2020, 8, 7897–7906 RSC.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, J. Phys. Chem. C, 2015, 119, 14038–14046 CrossRef CAS.
- M. G. Giorgini, K. Futamatagawa, H. Torii, M. Musso and S. Cerini, J. Phys. Chem. Lett., 2015, 6, 3296–3302 CrossRef CAS.
- J. L. Allen, O. Borodin, D. M. Seo and W. A. Henderson, J. Power Sources, 2014, 267, 821–830 CrossRef CAS.
- T. Hou, G. Yang, N. N. Rajput, J. Self, S.-W. Park, J. Nanda and K. A. Persson, Nano Energy, 2019, 64, 103881 CrossRef CAS.
- N. Chapman, O. Borodin, T. Yoon, C. C. Nguyen and B. L. Lucht, J. Phys. Chem. C, 2017, 121, 2135–2148 CrossRef CAS.
- C. C. Su, M. He, R. Amine, Z. Chen and K. Amine, Angew. Chem., Int. Ed. Engl., 2018, 57, 12033–12036 CrossRef CAS PubMed.
- O. Borodin, M. Olguin, P. Ganesh, P. R. Kent, J. L. Allen and W. A. Henderson, Phys. Chem. Chem. Phys., 2016, 18, 164–175 RSC.
- X. Zhang and D. G. Kuroda, J. Chem. Phys., 2019, 150, 184501 CrossRef PubMed.
- Z. K. Tang, J. S. Tse and L. M. Liu, J. Phys. Chem. Lett., 2016, 7, 4795–4801 CrossRef CAS PubMed.
- I. Skarmoutsos, V. Ponnuchamy, V. Vetere and S. Mossa, J. Phys. Chem. C, 2015, 119, 4502–4515 CrossRef CAS.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Phys. Chem. C, 2011, 116, 1114–1121 CrossRef.
- M. J. Boyer, L. Vilciauskas and G. S. Hwang, Phys. Chem. Chem. Phys., 2016, 18, 27868–27876 RSC.
- Y. Shim, Phys. Chem. Chem. Phys., 2018, 20, 28649–28657 RSC.
- N. Yao, X. Chen, X. Shen, R. Zhang, Z. H. Fu, X. X. Ma, X. Q. Zhang, B. Q. Li and Q. Zhang, Angew. Chem., Int. Ed. Engl., 2021, 60, 21473–21478 CrossRef CAS PubMed.
- B. Ravikumar, M. Mynam and B. Rai, J. Phys. Chem. C, 2018, 122, 8173–8181 CrossRef CAS.
- A. France-Lanord and J. C. Grossman, Phys. Rev. Lett., 2019, 122, 136001 CrossRef CAS PubMed.
- C. M. Tenney and R. T. Cygan, J. Phys. Chem. C, 2013, 117, 24673–24684 CrossRef CAS.
- H. Liu and E. Maginn, J. Chem. Phys., 2011, 135, 124507 CrossRef PubMed.
- O. Borodin, W. Gorecki, G. D. Smith and M. Armand, J. Phys. Chem. B, 2010, 114, 6786–6798 CrossRef CAS PubMed.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2009, 113, 1763–1776 CrossRef CAS PubMed.
- O. Borodin, G. D. Smith and P. Fan, J. Phys. Chem. B, 2006, 110, 22773–22779 CrossRef CAS PubMed.
- K. D. Fong, J. Self, K. M. Diederichsen, B. M. Wood, B. D. McCloskey and K. A. Persson, ACS Cent. Sci., 2019, 5, 1250–1260 CrossRef CAS PubMed.
- K. D. Fong, H. K. Bergstrom, B. D. McCloskey and K. K. Mandadapu, AIChE J., 2020, 66 Search PubMed.
- X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, J. G. Zhang and Q. Zhang, Adv. Sci., 2016, 3, 1500213 CrossRef PubMed.
- Y. X. Yao, X. Chen, C. Yan, X. Q. Zhang, W. L. Cai, J. Q. Huang and Q. Zhang, Angew. Chem., Int. Ed. Engl., 2021, 60, 4090–4097 CrossRef CAS PubMed.
- G. R. V. Zhuang, K. Xu, H. Yang, T. R. Jow and P. N. Ross, J. Phys. Chem. B, 2005, 109, 17567–17573 CrossRef CAS PubMed.
- Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708–11718 CrossRef CAS PubMed.
- C. R. Yang, Y. Y. Wang and C. C. Wan, J. Power Sources, 1998, 72, 66–70 CrossRef CAS.
- F. Shi, P. N. Ross, G. A. Somorjai and K. Komvopoulos, J. Phys. Chem. C, 2017, 121, 14476–14483 CrossRef CAS.
- X.-Q. Zhang, X.-B. Cheng, X. Chen, C. Yan and Q. Zhang, Adv. Funct. Mater., 2017, 27, 1605989 CrossRef.
- X. Chen, X. Li, D. Mei, J. Feng, M. Y. Hu, J. Hu, M. Engelhard, J. Zheng, W. Xu, J. Xiao, J. Liu and J.-G. Zhang, ChemSusChem, 2014, 7, 549–554 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- J. N. C. Lopes and A. A. H. Padua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef CAS.
- K. P. Jensen and W. L. Jorgensen, J. Chem. Theory Comput., 2006, 2, 1499–1509 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- N. N. Rajput, V. Murugesan, Y. Shin, K. S. Han, K. C. Lau, J. Chen, J. Liu, L. A. Curtiss, K. T. Mueller and K. A. Persson, Chem. Mater., 2017, 29, 3375–3379 CrossRef CAS.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2020, 53, 9503–9512 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- J. Tomasi, B. Mennucci and E. Cances, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- S. Grimme, Chemistry, 2012, 18, 9955–9964 CrossRef CAS PubMed.
- G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, F1000Research, 2020, 9 Search PubMed.
- T. R. Jow, K. Xu, O. Borodin and M. Ue, Electrolytes for Lithium and Lithium-Ion Batteries, 2014 Search PubMed.
- W. Ding, X. Lei and C. Ouyang, Int. J. Quantum Chem., 2016, 116, 97–102 CrossRef CAS.
- W. Cui, Y. Lansac, H. Lee, S. T. Hong and Y. H. Jang, Phys. Chem. Chem. Phys., 2016, 18, 23607–23612 RSC.
- J. Xia, R. Petibon, D. Xiong, L. Ma and J. R. Dahn, J. Power Sources, 2016, 328, 124–135 CrossRef CAS.
- Y. Mao, M. Loipersberger, K. J. Kron, J. S. Derrick, C. J. Chang, S. M. Sharada and M. Head-Gordon, Chem. Sci., 2021, 12, 1398–1414 RSC.
- P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079 RSC.
- Y. Mao, D. S. Levine, M. Loipersberger, P. R. Horn and M. Head-Gordon, Phys. Chem. Chem. Phys., 2020, 22, 12867–12885 RSC.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2014, 113, 184–215 CrossRef.
- K. Hayamizu, J. Chem. Eng. Data, 2012, 57, 2012–2017 CrossRef CAS.
- T. T. Hagos, B. Thirumalraj, C. J. Huang, L. H. Abrha, T. M. Hagos, G. B. Berhe, H. K. Bezabh, J. Cherng, S. F. Chiu, W. N. Su and B. J. Hwang, ACS Appl. Mater. Interfaces, 2019, 11, 9955–9963 CrossRef CAS PubMed.
- V. Chaban, Phys. Chem. Chem. Phys., 2011, 13, 16055–16062 RSC.
- I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626 RSC.
- A. J. Ringsby, K. D. Fong, J. Self, H. K. Bergstrom, B. D. McCloskey and K. A. Persson, J. Electrochem. Soc., 2021, 168, 080501 CrossRef CAS.
- M. I. Chaudhari, J. R. Nair, L. R. Pratt, F. A. Soto, P. B. Balbuena and S. B. Rempe, J. Chem. Theory Comput., 2016, 12, 5709–5718 CrossRef CAS PubMed.
- H. Gudla, C. Zhang and D. Brandell, J. Phys. Chem. B, 2020, 124, 8124–8131 CrossRef CAS PubMed.
- L. Xia, B. Tang, L. Yao, K. Wang, A. Cheris, Y. Pan, S. Lee, Y. Xia, G. Z. Chen and Z. Liu, ChemistrySelect, 2017, 2, 7353–7361 CrossRef CAS.
- K. Hagiyama, K. Suzuki, M. Ohtake, M. Shimada, N. Nanbu, M. Takehara, M. Ue and Y. Sasaki, Chem. Lett., 2008, 37, 210–211 CrossRef CAS.
- L. Liao, X. Cheng, Y. Ma, P. Zuo, W. Fang, G. Yin and Y. Gao, Electrochim. Acta, 2013, 87, 466–472 CrossRef CAS.
- J. Xia, R. Petibon, A. Xiao, W. M. Lamanna and J. R. Dahn, J. Electrochem. Soc., 2016, 163, A1637–A1645 CrossRef CAS.
- L. Ma, S. L. Glazier, R. Petibon, J. Xia, J. M. Peters, Q. Liu, J. Allen, R. N. C. Doig and J. R. Dahn, J. Electrochem. Soc., 2016, 164, A5008–A5018 CrossRef.
- O. Borodin, X. Ren, J. Vatamanu, A. von Wald Cresce, J. Knap and K. Xu, Acc. Chem. Res., 2017, 50, 2886–2894 CrossRef CAS PubMed.
- Y. B. Yohannes, S. D. Lin and N.-L. Wu, J. Electrochem. Soc., 2017, 164, A3641–A3648 CrossRef CAS.
- I. A. Shkrob, J. F. Wishart and D. P. Abraham, J. Phys. Chem. C, 2015, 119, 14954–14964 CrossRef CAS.
- E. Markevich, G. Salitra and D. Aurbach, ACS Energy Lett., 2017, 2, 1337–1345 CrossRef CAS.
- Y. Horowitz, H. L. Han, P. N. Ross and G. A. Somorjai, J. Am. Chem. Soc., 2016, 138, 726–729 CrossRef CAS PubMed.
- E. P. Kamphaus, S. Angarita-Gomez, X. Qin, M. Shao, M. Engelhard, K. T. Mueller, V. Murugesan and P. B. Balbuena, ACS Appl. Mater. Interfaces, 2019, 11, 31467–31476 CrossRef CAS PubMed.
- Z. Liu, Y. Qi, Y. X. Lin, L. Chen, P. Lu and L. Q. Chen, J. Electrochem. Soc., 2016, 163, A592–A598 CrossRef CAS.
- J. Nanda, G. Yang, T. Z. Hou, D. N. Voylov, X. Li, R. E. Ruther, M. Naguib, K. Persson, G. M. Veith and A. P. Sokolov, Joule, 2019, 3, 2001–2019 CrossRef CAS.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon, 2016, 105, 52–76 CrossRef CAS.
- D. Aurbach, B. Markovsky, A. Shechter, Y. EinEli and H. Cohen, J. Electrochem. Soc., 1996, 143, 3809–3820 CrossRef CAS.
- K. Leung, S. B. Rempe, M. E. Foster, Y. Ma, J. M. Martinez del la Hoz, N. Sai and P. B. Balbuena, J. Electrochem. Soc., 2013, 161, A213–A221 CrossRef.
- J. M. Martinez de la Hoz, K. Leung and P. B. Balbuena, ACS Appl. Mater. Interfaces, 2013, 5, 13457–13465 CrossRef CAS PubMed.
- Y. Horowitz, H. L. Han, F. A. Soto, W. T. Ralston, P. B. Balbuena and G. A. Somorjai, Nano Lett., 2018, 18, 1145–1151 CrossRef CAS PubMed.
- Y. Horowitz, H. G. Steinruck, H. L. Han, C. Cao, I. I. Abate, Y. Tsao, M. F. Toney and G. A. Somorjai, Nano Lett., 2018, 18, 2105–2111 CrossRef CAS PubMed.
- K. L. Browning, R. L. Sacci, M. Doucet, J. F. Browning, J. R. Kim and G. M. Veith, ACS Appl. Mater. Interfaces, 2020, 12, 10018–10030 CrossRef CAS PubMed.
- M. Schnabel, E. Arca, Y. Ha, C. Stetson, G. Teeter, S.-D. Han and P. Stradins, ACS Appl. Energy Mater., 2020, 3, 8842–8849 CrossRef CAS.
- Z. Li, C. Stetson, G. Teeter, A. Norman, Y. Ha, B. J. Tremolet de Villers, Z. Huey, P. Walker, S.-D. Han, S. C. DeCaluwe, C.-S. Jiang, A. K. Burrell and A. Zakutayev, ACS Appl. Energy Mater., 2020, 3, 11534–11539 CrossRef CAS.
- Y. Ha, C. Stetson, S. P. Harvey, G. Teeter, B. J. Tremolet de Villers, C. S. Jiang, M. Schnabel, P. Stradins, A. Burrell and S. D. Han, ACS Appl. Mater. Interfaces, 2020, 12, 49563–49573 CrossRef CAS PubMed.
- X. Cui, F. Tang, Y. Zhang, C. Li, D. Zhao, F. Zhou, S. Li and H. Feng, Electrochim. Acta, 2018, 273, 191–199 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The MD simulation box, detailed solvation structure population, linear diffusion behavior, sample trajectories, optimized solvation structures, binding energy decomposition, experimental measurement raw data, ionic conductivity calculating using conventional method, validation of the force field, and force field data of EC, EMC, FEC, and LiPF6. See DOI: 10.1039/d1sc04265c |
| This journal is © The Royal Society of Chemistry 2021 |