Open Access Article
Open Access ArticleMC2 (M = Y, Zr, Nb, and Mo) monolayers containing C2 dimers: prediction of anode materials for high-performance sodium ion batteries†
Zhanzhe
Xu
a,
Xiaodong
Lv
*bcd,
Wenyue
Gu
a and
Fengyu
Li
 *a
*a
aSchool of Physical Science and Technology, Inner Mongolia University, Hohhot, 010021, China. E-mail: fengyuli@imu.edu.cn
bCAS Key Laboratory of Magnetic Materials and Devices, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, China. E-mail: lvxiaodong@nimte.ac.cn
cZhejiang Province Key Laboratory of Magnetic Materials and Application Technology, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, China
dGanjiang Innovation Academy, Chinese Academy of Sciences, Ganzhou 341000, People's Republic of China
First published on 24th September 2021
Abstract
Seeking novel high performance anode materials for sodium ion batteries (SIBs) is an attractive theme in developing energy storage devices. In this work, by means of density functional theory computations, we predicted a family of MC2 (M = Y, Zr, Nb, and Mo) monolayers containing C2 dimers to be promising anode materials for SIBs. The stability, electronic structure, and adsorption/diffusion/storage behavior of sodium atoms in MC2 (M = Y, Zr, Nb, and Mo) monolayers were explored. Our computations revealed that Na adsorbed MC2 (M = Y, Zr, Nb, and Mo) monolayers show metallic characteristics that give rise to excellent electrical conductivity and Na mobility with low activation energies for diffusion (0.21, 0.04, 0.20, and 0.22 eV, respectively) in these materials, indicative of a high charge/discharge rate. In addition, the theoretical capacities of Na-adsorbed on YC2, ZrC2, NbC2, and MoC2 monolayers are 478, 697, 687, and 675 mA h g−1, respectively, higher than that of commercial graphite (284 mA h g−1), and the open-circuit voltages are moderate (0.11–0.25 V). Our results suggest that MC2 (M = Y, Zr, Nb, and Mo) monolayers have great potential to serve as anode materials for SIBs.
1. Introduction
The global demand for advanced energy storage and conversion technologies, especially electrochemical energy technologies, is growing rapidly. Among them, rechargeable batteries, such as lithium-ion batteries (LIBs), are widely used in mobile electronic and electrified vehicles.1–3 However, LIBs can meet the tough demands of energy storage and conversion applications, yet the limited abundance (only 20 ppm) and expensiveness of lithium are not the best choices for application in large-scale energy storage systems and sustainability.4,5 Fortunately, sodium-ion batteries (SIBs) were confirmed as low-cost alternatives to lithium-ion batteries (LIBs) in energy storage applications, on account of the natural abundance, high energy density and similar intercalation chemistry to lithium, suggesting that some mature technologies in LIBs can be translated to SIBs, and SIBs are promising candidates for next generation rechargeable batteries.6Cathode materials with high electrochemical performance for SIBs have been extensively studied experimentally and theoretically, such as layered transition metal oxide compounds, polyanionic compounds, Prussian blue analogues, and sodium-based layered materials.7,8 However, anode materials matching well LIB systems are not suitable for SIBs due to the bigger ionic radius and the higher redox potential of Na+ ions vs. Li+. For instance, graphite is not available in SIBs, because the interlayer distance of graphite is too small to accommodate sodium, leading to a larger mismatched layer spacing and poor capacity.9,10 Thus, the design and exploration of suitable electrode materials for SIBs are greatly desired.
In recent years, two-dimensional (2D) materials as electrodes have attracted great attention due to their excellent properties, including good mechanical flexibleness, rich active sites, large exposed surface area for electrochemical processes, and expanded interlayer spacing.11,12 For example, transition metal chalcogenides (TMDs),13–15 oxides (TMOs),16,17 borides (MBenes),18,19 transition metal carbides or nitrides (MXenes),20,21 and main group binary compounds (B2S, BN2, SiS, SnP3, etc.)22–25 have been theoretically and experimentally explored as anode materials. Among these materials, 2D MXenes have experienced rapid development as anode materials after the successful exfoliation of Ti3C2 nanosheets in 2011,26 due to their superior electrical conductivity, high performance rate, and high specific capacities.27–30 So far, metal-rich 2D MXene-based materials (i.e. Ti2C,31 V2C,32 Nb2C,33 Mo2C,34 Cr2C,35 Mn2C,36etc.) have been extensively studied as anode materials for LIBs and SIBs. However, the major problems with MXenes are surface functionalization and metal atoms exposed on the surface commonly to suppress sodium adsorption, which largely reduce the storage capacity and the performance of batteries.21
In this regard, Wang et al.37 proposed a novel carbon-rich 2D metal carbide (MC), namely TiC2 monolayer, which consists of unique C2 dimers (Fig. 1a) and exhibits high structural stability. The Li capacity, open-circuit voltage (OCV), and diffusion barrier were calculated to be 622 mA h g−1, 0.96 V, and 0.11 eV, respectively, indicating that the TiC2 monolayer is a promising anode material for LIBs. Subsequently, other transition metal carbide (VC2,38,39 TaC2,40 MnC2,41 ScC2,42 and WC2 (ref. 43)) monolayers with a similar configuration were also theoretically investigated as LIB and SIB anode materials. In particular, Zhao et al.44 found that an FeC2 monolayer containing isolated C2 dimers with ferromagnetic and half-metallic properties was possible to be synthesized by chemically exfoliating the bulk counterpart of ThFeC2.
Therefore, the proposal of C-rich MC2 monolayers may offer a new strategy for the rational design of 2D anode materials for SIBs. In this work, four C2-containing MC2 (M = Y, Zr, Nb and Mo) monolayers were systematically explored by means of DFT computations. According to our calculations of cohesive energy, phonon dispersion, first-principles molecular dynamics (FPMD) stimulation, mechanical parameters, and sodium adsorption/diffusion/capacity, the four examined monolayers were confirmed to exhibit great thermodynamic, dynamic, thermal, and mechanical stability, excellent electronic conductivity and outstanding electrode performance as a SIB anode material. In particular, the ZrC2 monolayer exhibits superior electrochemical performance with high theoretical storage capacity (699 mA h g−1) and small diffusion energy barriers (0.04 eV) for Na atoms.
2. Computational methods
In this study, the structural relaxation and performance calculations were based on density functional theory (DFT) methods within the Vienna ab initio simulation package (VASP).45–47 The general gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE) exchange and correlation functional and a plane wave basis set with an energy cut-off of 500 eV were employed.48,49 Monkhorst–Pack meshes50 of 11 × 11 × 1 and 5 × 5 × 1 k-points were used to sample the two-dimensional Brillouin zone for the unit cell and supercell relaxation and electronic structure calculations, respectively. An inter-layer vacuum space of 20 Å was used to avoid the interactions of mirror images in adjacent layers. All the structures are fully relaxed until the convergence tolerances for the energy and force on each atom were less than 1.0 × 10−5 eV and 0.02 eV Å−1, respectively. All the atomic structures and charge density distributions were visualized by using the VESTA package.51The dynamic stability of MC2 (M = Y, Zr, Nb, and Mo) monolayers was evaluated by recording the phonon spectrum with the PHONOPY code52 on the basis of density functional perturbation theory (DFPT). Thermal stabilities were assessed by performing first-principles molecular dynamics (FPMD) simulations (a 4 × 4 × 1 supercell, 96 atoms) in the NVT ensemble lasting for 5 ps with a time step of 1 fs at room temperature (300 K), and the temperature was controlled by the Nosé–Hoover method.53 By using the climbing-image nudged elastic band (CI-NEB) approach,54,55 the diffusion energy barrier and the minimum energy pathways of Na atom diffusing on MC2 (M = Y, Zr, Nb, and Mo) monolayers were calculated. The charge distribution and transfer were analyzed by the Bader charge method.56
3. Results and discussion
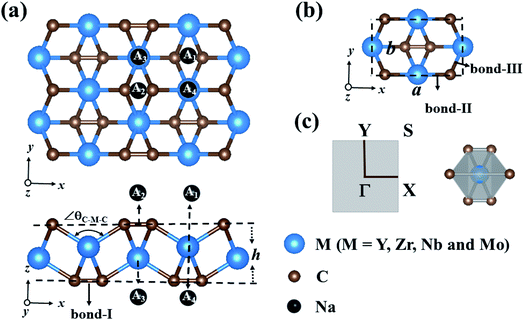
3.1 Geometric structure of the MC2 (M = Y, Zr, Nb, and Mo) monolayers
The optimized structures of MC2 (M = Y, Zr, Nb, and Mo) monolayers are displayed in Fig. 1a. From the top view, these monolayers exhibit a rectangular lattice with the space group Pmmn symmetry, where carbon atoms are in the form of C2 dimers, and each unit cell contains two M atoms and four C atoms (Fig. 1b). From the side view, the crystal structure of the MC2 (M = Y, Zr, Nb, and Mo) monolayers possesses a tetra-layer structure with two M layers sandwiched between two C layers, in which each M atom bonds with six neighboring C atoms, while each C atom is shared by one C of the same C2 dimer and three adjacent M atoms, forming an edge-shared MC6 octahedral structure without M atoms exposed on the surface (Fig. 1c).Table 1 summarizes the optimized structural parameters of MC2 (M = Y, Zr, Nb, and Mo) monolayers, including the lattice constants (a and b), bond lengths of C–C (bond I), M–C (bond II along the x axis and bond-III along the y axis) and thickness (h), and the evolution trend was plotted for different MC2 monolayers with transition metal atoms (M) from Y → Mo (Fig. S1 and S2†). The lattice constants (4.84 ≤ a ≤ 5.80 Å and 3.01 ≤ b ≤ 4.28 Å) are close to those of VC2 (a = 4.62 Å and b = 3.28 Å),38 FeC2 (4.54 Å and 2.89 Å),44 and ScC2 (5.39 Å and 4.12 Å).42 The remarkable feature we can see is that structural parameters, such as lattice constants (a and b), bond lengths M–C (dM–C) and bond angle (∠θC–M–C), decrease from 5.77 to 4.84 Å (4.45 to 3.03 Å), 2.39 to 2.03 Å (2.51 to 2.26 Å) along the x (y)-direction and 138.14° to 119.28° from Y → Mo (Fig. S3†), mainly originating from the decrease of the atomic radius from Y to Mo. However the others, including bond lengths C–C (dC–C) and thickness (h), increase (1.30 to 1.37 Å and 1.81 to 2.60 Å) from Y → Mo, respectively. The latter increasing trend could be understood by the electronegativity difference between the transition metal (Y → Mo) and carbon, which are strongly correlated with the structural properties.57,58 YC2 has the highest electronegativity difference (1.33 on the Pauling scale), while MoC2 possesses the lowest (0.39 on the Pauling scale), the angles of M–C–M (∠θM–C–M) gradually decrease, resulting in an increase in the dC–C and thickness of 2D MC2 from Y to Mo (Fig. S3†). Note that the C–C distances of C2 dimers are in the range of 1.30–1.37 Å, which are shorter than that in the Ti8C12 cage and MXenes with the C–C distances in the range of 1.40–3.35 Å,59–61 implying stronger C–C bonding in C2 dimers.
| System | a | b | Bond-I | Bond-II | Bond-III | ∠θC–M–C | h | E coh |
|---|---|---|---|---|---|---|---|---|
| YC2 | 5.77 | 4.45 | 1.30 | 2.39 | 2.51 | 138.14° | 1.81 | −7.40 |
| ZrC2 | 5.31 | 3.92 | 1.34 | 2.21 | 2.33 | 128.23° | 2.07 | −7.99 |
| NbC2 | 4.96 | 3.54 | 1.34 | 2.08 | 2.26 | 119.74° | 2.26 | −7.98 |
| MoC2 | 4.84 | 3.03 | 1.37 | 2.03 | 2.27 | 119.28° | 2.60 | −7.48 |
3.2 Stabilities of the MC2 (M = Y, Zr, Nb, and Mo) monolayers
Prior to exploring the physical properties and evaluating the probability of experimental synthesis of the MC2 (M = Y, Zr, Nb, and Mo) monolayers, we firstly verified their thermodynamic, dynamic, thermal, and mechanical stabilities and investigated the underlying mechanisms for their stabilities.First, we examined the thermodynamic stability by calculating their cohesive energy (Ecoh), which is defined as Ecoh = (EMC2 − nEM − mEc)/(n + m), in which EMC2 and EM/Ec are the energies of the MC2 monolayer and a free M/C atom, respectively, and n/m is the number of M/C atoms in one unit cell. According to this definition, a more negative Ecoh value indicates a better thermodynamic stability of the structure. The computed Ecoh values for MC2 (M = Y, Zr, Nb, and Mo) monolayers are −7.40, −7.99, −7.98, and −7.48 eV per atom, respectively, lower than that of the TiC2 monolayer (−6.59 eV),37 VC2 monolayer (−7.15 eV),38 ScC2 monolayer (−6.33 eV),42 and the synthesized Ti2C62 (6.18 eV per atom) MXene, all of which are demonstrated to be structurally and thermodynamically stable according to the first principles calculations or experimentally. Thus, the four MC2 (M = Y, Zr, Nb, and Mo) monolayers have solid thermodynamic stability.
Second, the dynamic stability of the MC2 (M = Y, Zr, Nb, and Mo) monolayers was evaluated by calculating their phonon dispersions, which are shown in Fig. S4.† All of them are dynamically stable as confirmed by the absence of imaginary phonon modes in the entire Brillouin zone. In particular, the highest frequencies for the dynamically stable monolayers (40.25–49.59 THz) are higher or comparable to those of the ScC2/ScN2 monolayer (50/38 THz),42 VC2 (∼43 THz),38 and the recently proposed TaC2 monolayer (42 THz),40 suggesting strong M–C bonding in these MC2 nanosheets.
Third, FPMD simulations were performed to assess their thermal stability at room temperature (300 K), and the structures after annealing at 300 K for 5 ps are presented in Fig. S5a–d.† Neither bond breakage nor structural distortion can be noted, and then we conclude that the YC2, ZrC2, NbC2 and MoC2 monolayers possess excellent thermal stabilities at room temperature.
Finally, we assessed the mechanical stability of the MC2 (M = Y, Zr, Nb, and Mo) monolayers by calculating their elastic constants using the finite distortion method.63 Mechanically, a stable 2D structure should meet the Born–Huang criteria64,65 given by C11C22 − C122 > 0 and C66 > 0. The calculated values of elastic constants fully satisfy these criteria (shown in Table 2), demonstrating that the MC2 (M = Y, Zr, Nb, and Mo) monolayers are also mechanically stable.
| System | C 11 | C 12 | C 22 | C 66 | Y x | Y y | ν x | ν y |
|---|---|---|---|---|---|---|---|---|
| YC2 | 79.33 | 22.17 | 32.21 | 16.51 | 64.07 | 26.01 | 0.69 | 0.28 |
| ZrC2 | 107.71 | 34.95 | 49.15 | 27.00 | 82.86 | 37.81 | 0.71 | 0.32 |
| NbC2 | 158.97 | 40.90 | 55.50 | 42.85 | 128.82 | 44.98 | 0.74 | 0.26 |
| MoC2 | 180.44 | 43.76 | 82.01 | 47.97 | 157.09 | 71.40 | 0.53 | 0.24 |
| TiC2 (ref. 37) | 140.58 | 25.10 | 70.52 | 16.19 | 131.17 | 66.04 | 0.59 | 0.21 |
To gain insights into the bonding nature and stabilizing mechanism, we calculated the electron localization functions (ELFs) of MC2 (M = Y, Zr, Nb, and Mo) monolayers. The ELF is an effective tool for characterizing chemical bonding and can reflect the electron localization in the system.66 Generally, the ELF value near zero (blue) denotes a low electron density area, whereas the ELF values of 1.0 (red) and 0.5 (green) represent the perfect localization and the free electron-gas, respectively. As shown in Fig. S6,† in the ELF maps of the (001) and (010) slices we can see that the region between M and C atoms in all the MC2 monolayers is in the green color corresponding to an ELF of around 0.5, indicating fully delocalized electron distribution, which well shared and delocalized electrons make robust connection between the M and C atoms, and the Bader charge analysis revealed that the each M (M = Y, Zr, Nb, and Mo) atom transfers 1.85, 1.81, 1.73, and 1.15 e− per atom to the C2 dimer, respectively, similar to the value of 1.80/1.50 e− for TiN2/C2,37 1.74/1.71 e− for ScC2/N2,42 and 1.85 e− for YN2 (ref. 67) monolayers, indicating ionic interactions between M and C atom. While, the C2 dimer exhibits strong covalent bond characteristics, the results are in agreement with previous studies that the formation of the C2 dimer plays an important role in stabilizing metal 2D structures. As a consequence, the coexistence of ionic and covalent bonding is mainly responsible for the structural stability.
3.3 Mechanical and electronic properties of the MC2 (M = Y, Zr, Nb, and Mo) monolayers
Having confirmed the stability of the MC2 (M = Y, Zr, Nb, and Mo) monolayers, the mechanical properties, including Young's modulus Y(θ) and Poisson's ratio ν(θ), were investigated. The angle-dependent in-plane Y(θ) and ν(θ) were estimated by using the following equation:68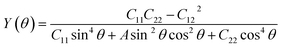 | (1) |
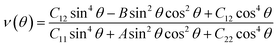 | (2) |
Based on the above equations, we plotted Y(θ) and ν(θ) with the variation of angle θ (Fig. 2). The Y(θ) of Y/Zr/Nb/MoC2 monolayers decreases from a maximum value of 64.07/82.86/128.82/157.09 N m−1 along the x direction to a minimum value of 26.01/37.81/44.98/71.40 N m−1 along the y direction, reflecting their high mechanical anisotropy. However, the Y(θ) of the TiC2 monolayer decreases from a maximum value of 131.17 N m−1 in the x direction to a minimum value of 55 N m−1 at about θ = 46°, which is consistent with a previous report.37 Compared with other well-known 2D materials, strikingly, our calculated Y along x and y directions of these C2-containing monolayers are comparable to the value of MoS2 (122 N m−1),69 silicene (61.7 N m−1) and germanene (44 N m−1),70 but smaller than that of graphene (341.60 N m−1)71 and hexagonal h-BN (271 N m−1),72 implying high flexibility for these monolayers. The modest mechanical properties are beneficial for the charge–discharge process of rechargeable ion batteries.
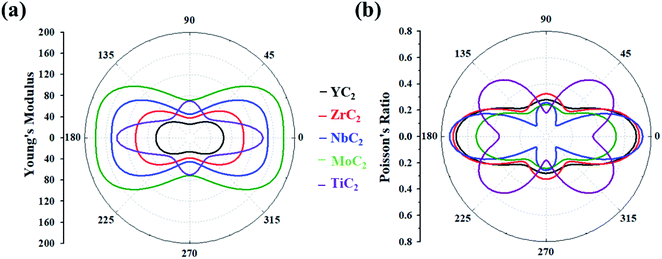 | ||
| Fig. 2 (a) Young's modulus and (b) Poisson's ratio of the MC2 (M = Y, Zr, Nb, Mo and Ti) monolayers as a function of the in-plane angle θ, and θ = 0° corresponds to the x-axis. | ||
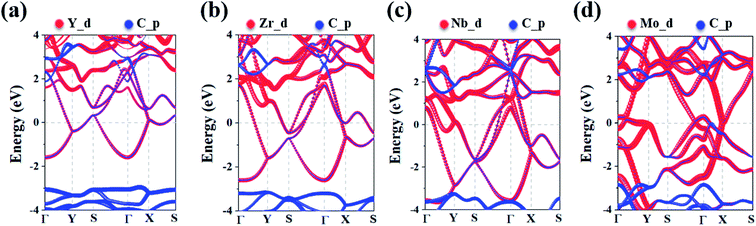
To analyze the electronic properties of the MC2 (M = Y, Zr, Nb, and Mo) monolayers, the atom-projected electronic band structure and partial density of states (PDOS) were carefully investigated (as shown in Fig. 3 and S7†). The results showed that all considered monolayers exhibit metallic character, as indicated by the partially occupied bands crossing the Fermi level in the Brillouin zone. The orbital analysis suggested that the bands near the Fermi level are dominated by the M_d orbitals, while the C_p orbitals make minor contribution by hybridizing with the M–d states, which is in line with the electrons transferred from M to C atoms based on the Bader charge analysis, as shown in Fig. S6.† The metallic nature of MC2 (M = Y, Zr, Nb, and Mo) monolayers indicates the advantage in electrical conductivity, which is highly desirable for high performance of electrode materials.
3.4 Na adsorption and diffusion on the MC2 (M = Y, Zr, Nb, and Mo) monolayers
The development of sodium ion batteries (SIBs) is often hindered by the limited choice of anode materials. The modest mechanical properties and metallic feature of the examined MC2 (M = Y, Zr, Nb, and Mo) monolayers facilitate our investigation on their potential application as SIB anode materials.The adsorption behavior between metal atoms and 2D materials closely correlates with the anode performance. Thus, we firstly examined the energy-preferred adsorption sites for a single Na atom on the surface of MC2 (M = Y, Zr, Nb, and Mo) monolayers with a 2 × 2 × 1 supercell. Four high symmetry adsorption sites were considered, namely A1 (where Na sits over the midpoint of the bottom C–C bond), A2 (where Na sits over the midpoint of the top C–C bond), A3 (where Na sits over the M atom and interacts with four top C atoms) and A4 (where Na sits over the M atom and interacts with two top C atoms) sites, as shown in Fig. 1a. After full relaxation, the energetically most favorable adsorption sites for Na on MC2 (M = Y, Zr, Nb, and Mo) monolayers were identified by calculating their adsorption energy (Eads), which is defined as:
| Eads = Etot − EMC2 − ENa | (3) |
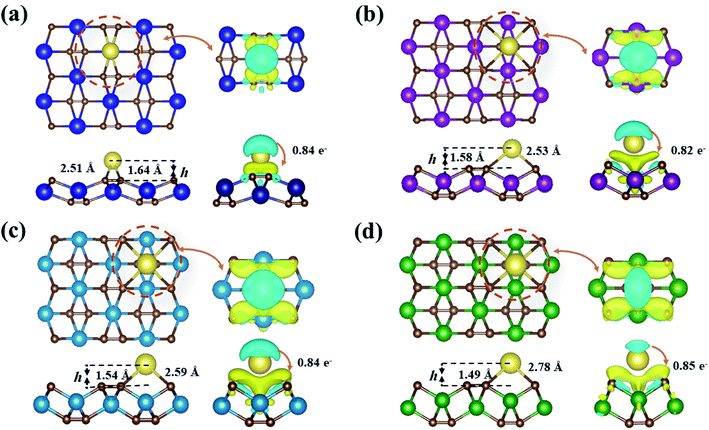
Almost all the investigated MC2 monolayers can effectively adsorb Na atoms, as indicated by the negative Eads values (Fig. 4). Except for the YC2 monolayer, on which the most stable adsorption site of Na is the A3 site (Eads = −1.55 eV), the Na's energy-favorable site on the other three MC2 (M = Zr, Nb, and Mo) monolayers is A1 with an Eads of −1.67, −2.45 and −2.95 eV, respectively, in agreement with the preferred adsorption site on TiC2 (A1),37 VC2 (A1),38 and ScC2 (A3).42 In addition, the A1 (A3 and A4) site is the Na's second favorable adsorption site on the YC2 (ZrC2/NbC2 and MoC2) monolayer. The difference of the most preferred Na adsorption site is due to the shorter Na–C bond lengths (dNa–C) formed between Na and C at the A3 (A1) site than those at the A1 (A3) site on YC2 (ZrC2, NbC2, and MoC2): 2.51 vs. 3.54/3.70 Å (2.53 vs. 2.61, 2.59 vs. 2.62, and 2.78 vs. 2.81 Å). Among the four examined monolayers, Na has the strongest/weakest interaction with the MoC2/YC2 monolayer, which can be understood by the gradually increasing distance between the adsorbed Na and the MC2 monolayer (from 1.49 Å on MoC2 to 1.64 Å on YC2, as shown in Fig. 5).
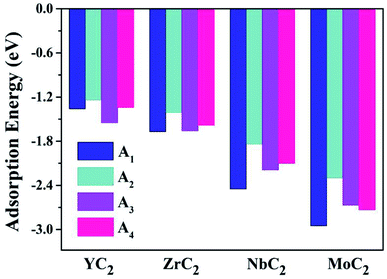 | ||
| Fig. 4 The adsorption energies of a single Na atom on the (M = Y, Zr, Nb, and Mo) monolayer at the four examined adsorptions sites A1, A2, A3 and A4. | ||
Fig. 5 presents the fully optimized structures for the Na-adsorbed YC2 monolayer at the site A3 and MC2 (M = Zr, Nb, and Mo) monolayers at the site A1, respectively. For Na-adsorbed Y/Zr/Nb/MoC2 monolayers, the Na–C bond length is 2.51/2.53/2.59/2.78 Å, and the adsorption height (h), i.e., the vertical distance between the top-layer carbon and Na atom is 1.64/1.58/1.54/1.49 Å. Obviously, the MC2 monolayer with a larger atomic number (smaller atomic radii) from Y → Mo has a lower adsorption height (h); however, the Na–C bond length and adsorption energy (Eads) are inversely proportional to the atomic radii.
To better understand the physical mechanism of the adsorption process, we investigated the charge transfer process between a single Na atom adsorbed on the MC2 (M = Y, Zr, Nb, and Mo) monolayers by using the charge density difference using the following formula,
| Δρ = ρtot − ρMC2 − ρNa | (4) |
Metal mobility was another significant factor in the design and selection of effective anode materials, which are directly linked to the charge–discharge rates of rechargeable batteries. Thus, we further investigated the diffusion of Na on the MC2 (M = Y, Zr, Nb, and Mo) monolayers (Fig. 6). For the YC2 monolayer (Fig. 6b), since A3 is the energetically most favorable site among the four adsorption sites (A1, A2, A3, and A4), three representative possible diffusion pathways were considered: path-I (A3–A1–A3), where Na migrates from an A3 to another A3 by crossing an A1 site, marked by red arrows; path-II (A3–A4–A3), where Na migrates from an A3 to another A3 by crossing an A4 site, marked by blue arrows; path-III (A3–A2–A3), where Na migrates from an A3 to another A3 by crossing an A2 site, marked by black arrows. For the Zr/Nb/MoC2 monolayers (Fig. 6d, f and h), similarly, there are three diffusion pathways with both starting and ending sites at A1: path-I (A1–A3–A1), path-II (A1–A2–A1), and path-III (A1–A4–A1), marked by red, blue and black arrows, respectively.
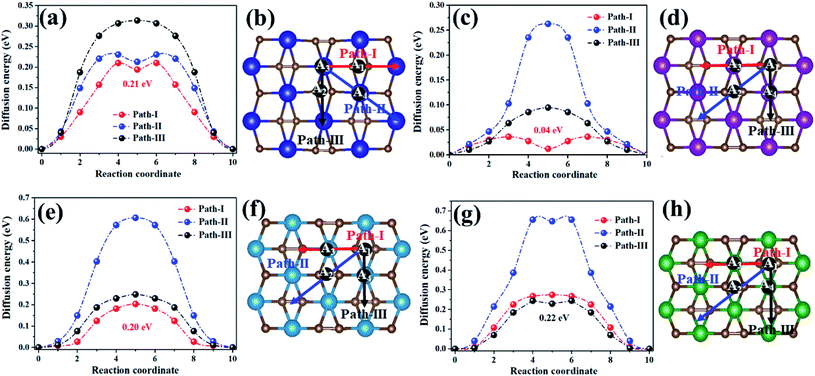 | ||
| Fig. 6 The energy profile (left plane) and diffusion pathways (right plane) of Na diffusing on theYC2 (a and b), ZrC2 (c and d), NbC2 (e and f), and MoC2 (g and h) monolayers. | ||
The energy profiles for Na diffusion over MC2 (M = Y, Zr, Nb, and Mo) monolayers along the examined diffusion pathways are illustrated in Fig. 6a, c, e and g. Obviously, Na diffusing along path-I has the lowest diffusion barrier (Ed) on the YC2 (Ed = 0.21 eV), ZrC2 (Ed = 0.04 eV), and NbC2 (Ed = 0.20 eV) monolayers, while on the MoC2 monolayer, path-III has the smallest diffusion barrier of 0.22 eV. Actually, the energy-favored diffusion route is Na migration from the most energy-preferred site to another crossing the second energy-preferred site on the four monolayers. Since the second lowest adsorption site on MoC2 is A4, the Na diffusion path with the smallest barrier is path-III instead of path-I on the other three monolayers. The corresponding diffusion lengths of Na along the minimum energy pathways on the four MC2 monolayers are given in Fig. S9,† and the diffusion length of Na on MC2 monotonically increases with the lattice constant from the MoC2 to the YC2 monolayer. Note that the Na diffusion barriers on the four MC2 monolayers are all lower than that on borophene (0.32 eV),73 Ti3C4 (0.35)74 and MoS2 (0.28 eV),75 and the lowest Ed value of 0.04 eV on the ZrC2 monolayer is comparable with the Ed on ScC2 (0.05 eV)42 and Ti3C2 (0.096),76 as shown in Table 3, indicating their excellent charge–discharge rate. Compared with the reported TiC2 monolayer as a promising anode for LIBs,37 the Na diffusing along path-I has the lowest diffusion barrier on TiC2 (Ed = 0.19 eV, Fig. S10†), and the Ed is comparable with the values on Y/Nb/MoC2 monolayers (0.20–0.22 eV), but higher than that on the ZrC2 monolayer (0.04 eV). Thus, as for SIB anode materials, compared to the TiC2 monolayer, ZrC2 distinguishes itself among the four examined MC2 (M = Y, Zr, Nb, and Mo) monolayers, since it has the lowest Na diffusion barrier and high Na capacity comparable to that of TiC2. Overall, from the perspective of Na diffusion behavior, anode materials with low energy barriers and short diffusion pathway lengths are suitable for SIBs.
| Theoretical specific capacity | Diffusion barrier | References | |
|---|---|---|---|
| YC2 | 478 | 0.21 | This work |
| ZrC2 | 699 | 0.04 | This work |
| NbC2 | 687 | 0.20 | This work |
| MoC2 | 675 | 0.22 | This work |
| TiC2 | 727 | 0.19 | This work |
| Ti3C2 | 352 | 0.096 | 78 |
| Ti3C4 | 560 | 0.35 | 74 |
| ScC2 | 777 | 0.05 | 42 |
| Sc2C | 362 | 0.012 | 81 |
| Nb2C | 271 | 0.015 | 33 |
| Mo2C | 132 | 0.015 | 34 |
| MoC | 284.2 | 0.09 | 82 |
| MoS2 | 146 | 0.28 | 75 |
| Phosphorene | 315.52 | 0.30 | 80 |
| Na2Mn3O7 | 166.1 | 0.16 | 7 |
3.5 Theoretical storage capacity and open-circuit voltage
2D materials as anode materials display a lot of attractive properties; besides mechanical flexibility, excellent electrical conductivity, and lower diffusion energies, they also have the ability to adsorb multilayer Na atoms and exhibit high capacity.77,78 Inspired by these properties, we expect that the predicted MC2 (M = Y, Zr, Nb, and Mo) monolayers can be used as anodes for SIBs with high storage capacity. Here, the two important descriptors, namely storage capacity (C) and average open-circuit voltage (OCV), were calculated to determine the performance of the SIBs based on the charge–discharge mechanism.The OCV can be evaluated from the following common half-cell reaction of the charge/discharge process:
| MC2 + xNan+ + xne− ↔ NaxMC2 | (5) |
| OCV = −Eave/xne | (6a) |
| Eave = (ENaxMC2 − EMC2 − xENa-bulk)/x | (6b) |
| C = xmax × F/MMC2 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801 mA h mol−1), and MMC2 is the molar weight of MC2 (M = Y, Zr, Nb, and Mo).
801 mA h mol−1), and MMC2 is the molar weight of MC2 (M = Y, Zr, Nb, and Mo).
Then the maximum storage capacity of Na atoms on MC2 (M = Y, Zr, Nb, and Mo) monolayers was evaluated by adding Na atoms to the surface gradually. As mentioned above, the most stable adsorption sites for Na on the four monolayers have been determined: the first layer of Na interaction at the A3 site for YC2 and the A1 site for Zr/Nb/MoC2, respectively; when the adsorption positions of the first layer are completely occupied, the subsequently added Na atoms form a second and a third adsorption layer. In addition, for the different sodium concentrations on the MC2 monolayer, the most stable configurations for each concentration, we considered by calculating their formation energy (Ef) of NaxMC2 (M = Y, Zr, Nb, and Mo) compounds with respect to the MC2 monolayer and Na bulk phase as the references (Fig. S11†).79
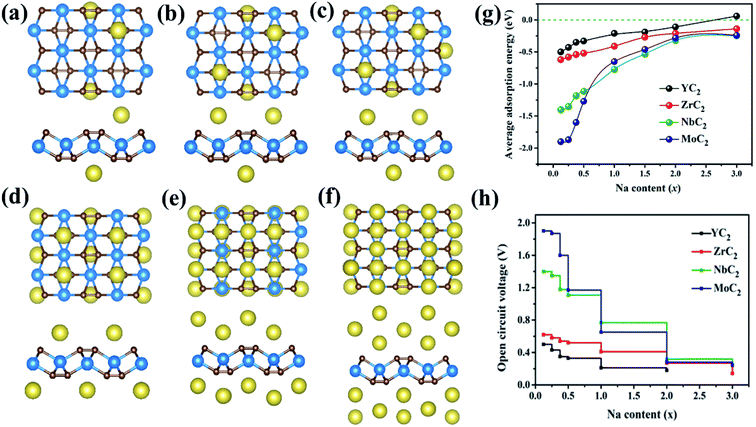
Here, based on the MC2 monolayer, taking the process of successive adsorption of Na atoms on the NbC2 monolayer as an example, adding a Na atom at site A1 on one surface of NbC2 results in a low-limit chemical formula NaxNbC2 (x = 0.125, Fig. 5c). Our computations showed that Na atoms tend to bond to both surfaces of the NbC2 monolayer when occupying the A1 site (Fig. S12–S14†). When the A1 sites of both surfaces were all occupied, Na atoms start to occupy the A3 sites in the second layer (Fig. S15†). Thus, the several possible configurations with both surfaces exposed to Na atoms were carefully considered for NaxNbC2 systems with higher x values (x = 0.25, 0.375, 0.5, 1, 2, 3), and the most stable configurations for each concentration are shown in Fig. 7a–f. The same approach was used to construct NaxYC2, NaxZrC2, and NaxMoC2 systems.
The average adsorption energy decreases with the increase of Na concentration (x), indicating the decreased thermodynamic stability of NaxMC2 (Fig. 7g), which can be attributed to the repulsive interaction between Na atoms, thus making more adsorption more difficult. For the Zr/Nb/MoC2 monolayer, the first Na-adsorption layer is formed by placing Na at the most favorable sites (A1) on both sides with an Eave of −0.41/−0.77/−0.65 eV (the composite is NaZrC2/NaNbC2/NaMoC2), suggesting the feasibility of adsorbing the second Na layer. The Eave of the second Na layer with Na adsorbing at site A3 (A4 for MoC2) is −0.27/−0.32/−0.28 eV and the corresponding configurations are Na2ZrC2, Na2NbC2, and Na2MoC2. When adding the third Na-layer on both sides with site A4 (A3 for MoC2), the Eave is −0.14/−0.25/−0.24 eV and the composites are Na3ZrC2, Na3ZrC2, and Na3MoC2. However, for the YC2 monolayer, in the first Na-layer Na atoms are adsorbed at the most favorable sites (A3) on both sides, and the Eave is −0.21 eV (the chemical formula is NaYC2). The Eave of the second layer with Na atoms locating at site A1 is −0.11 eV and the corresponding configuration is Na2YC2. The third Na-layer with Na atom adsorption at site A4 on both sides has an Eave of 0.06 eV, which implies that only the two adsorption layers of Na atoms are stable on the YC2 monolayer. Thus, we can conclude that the three (two) layers of Na atoms can be stably adsorbed on the Zr/Nb/MoC2 (YC2) monolayer.
Based on the above results, we estimated the maximum capacity (C) and open-circuit voltage (OCV) of Na atoms adsorbed on the MC2 (M = Y, Zr, Nb, and Mo) monolayers with the chemical stoichiometry of Na2YC2, Na3ZrC2, Na3NbC2, and Na3MoC2 (Fig. 7h). The corresponding values of maximum capacity (C) for SIBs are 478, 699, 687, and 675 mA h g−1, respectively. The MC2 (M = Y, Zr, Nb, and Mo) monolayers have much larger theoretical specific capacity in comparison to other electrode materials for SIBs, such as Ti3C2 (352 mA h g−1),76 phosphorene (315.52 mA h g−1),80 Sc2C (362 mA h g−1),81 Nb2C (271 mA h g−1),33 MoS2 (146 mA h g−1),75 MoC (248.2 mA h g−1)82 and Na-based layered materials (Na2Mn3O7, 166.1 mA h g−1),7 as shown in Table 3. We also estimated the Na capacity on the TiC2 monolayer and found that the TiC2 monolayer can adsorb two Na layers with the final formula of Na2TiC2, and the corresponding maximum specific capacity was then determined to be 727.29 mA h g−1, higher than that of the Y/Zr/Nb/MoC2 monolayer. Thus, as for SIB anode materials, compared to the TiC2 monolayer, ZrC2 distinguishes itself among the four examined MC2 (M = Y, Zr, Nb, and Mo) monolayers, since it has the lowest Na diffusion barrier and high Na capacity comparable to that of TiC2.
In addition, the OCV values are 0.11, 0.18, 0.25 and 0.24 V, which can avoid the dendrite formation of Na metal during the charge–discharge process due to satisfying the requirement of 0.1–1.0 eV for SIB anode materials.83 At the same time, the values are rather low and comparable to or slighter larger than that of 2D materials Mo2C (0.166 V),34 Ti3C2 (0.137 V),78 and NiC3 (0.17 V).84 The OCV values are low for Na atoms to be adsorbed on MC2 (M = Y, Zr, Nb, and Mo) nanosheets, which are beneficial for increasing and operating voltage and safety in practical applications.
Then, we examined the geometries of the MC2 (M = Y, Zr, Nb, and Mo) monolayers upon Na adsorption to evaluate the expansion in volume. The changes of the lattice constant and volume for the host sheets with interacted Na atoms are listed in Table S1.† Compared with the bare sheets, the expansions of the lattice and volume for the maximum Na concentrations are less than 8% and 10%, respectively, comparable to or much smaller than the lattice changes of the FeSe monolayer (5.50%)71 and the volume expansion of graphite (10%)85 and Na-based bulk electrode material NaTiF4 (13%),7 implying good cycling stability.
Finally, we explored the stability of the examined four C2-containing MC2 (M = Y, Zr, Nb, and Mo) monolayers under high concentration Na adsorption, by carrying out the FPMD stimulations of Na2YC2, Na3ZrC2, Na3NbC2, and Na3MoC2 monolayers for 5 ps at 300 and 500 K, respectively. No bond breakage or atomic structure reconstruction was observed, indicating that the 2D MC2 (M = Y, Zr, Nb, and Mo) materials are still stable under the maximum coverage of sodium. Overall, we conclude that the good structural stability of MC2 (M = Y, Zr, Nb, and Mo) sheets endows them with great potential as high-performance anode materials for SIBs.
4. Conclusions
In summary, based on first-principles calculations, we proposed four C2-containing monolayers (MC2, M = Y, Zr, Nb, and Mo) and systematically investigated the structural stability, mechanical and electronic properties, as well as the performance as anode materials for SIBs. Our results show that the MC2 (M = Y, Zr, Nb, and Mo) monolayers possess high cohesive energy and good dynamic, thermal and mechanical stability, and have metallic properties with excellent electronic conductivities. When used as battery electrodes for adsorbing Na atoms, the YC2 and Zr/Nb/MoC2 monolayers can adsorb two and three layers of Na atoms with the final formula of Na2YC2 and Na3ZrC2/Na3NbC2/Na3MoC2, respectively, and the corresponding maximum specific capacities (open circuit-voltage) were calculated to be 478 (0.11) and 699 (0.18)/687 (0.25)/675 (0.24) mA h g−1 (V), respectively. Taking advantage of containing C2 dimers, the MC2 (M = Y, Zr, Nb, and Mo) monolayers show superior stability and have high Na capacity due to the higher content of C. In addition, Na atoms show fast diffusion on the MC2 (M = Y, Zr, Nb, and Mo) monolayers with low diffusion barriers (0.21, 0.04, 0.20 and 0.22, respectively), indicating excellent rate capability. In view of the superior properties, such as good electronic conductivity, fast Na diffusion, low OCV, and high theoretical Na storage capacity, MC2 (M = Y, Zr, Nb, and Mo) monolayers become promising anode materials for SIBs.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (11964024), the “Grassland Talents” project of Inner Mongolia autonomous region (12000-12102613), the Young Scientific Talent Development Project (10000-21221505) and the Training Program of Innovation and Entrepreneurship for Undergraduates of Inner Mongolia University (201812236).References
- B. Scrosati, Electrochim. Acta, 2000, 45, 2461–2466 CrossRef CAS
.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC
.
- E. Fan, L. Li, Z. Wang, J. Lin, Y. Huang, Y. Yao, R. Chen and F. Wu, Chem. Rev., 2020, 120, 7020–7063 CrossRef CAS PubMed
.
-
R. S. Carmichael, Practical Handbook of Physical Properties of Rocks and Minerals, CRC Press, Boca Raton, FL, 1989 Search PubMed
.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed
.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901 RSC
.
- X. Zhang, Z. Zhang, S. Yao, A. Chen, X. Zhao and Z. Zhou, npj Comput. Mater., 2018, 4, 13 CrossRef
.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, Angew. Chem., Int. Ed., 2015, 54, 3431–3448 CrossRef CAS PubMed
.
- Y. Wen, K. He, Y. Zhu, F. Han, Y. Xu, I. Matsuda, Y. Ishii, J. Cumings and C. Wang, Nat. Commun., 2014, 5, 4033 CrossRef CAS PubMed
.
- P. Ge and M. Fouletier, Solid State Ionics, 1988, 28, 1172–1175 CrossRef
.
- Y. Bahari, B. Mortazavi, A. Rajabpour, X. Zhuang and T. Rabczuk, Energy Storage Mater., 2021, 35, 203–282 CrossRef
.
- J. Lin, T. Xu, F. Han and G. Yang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1437 Search PubMed
.
- X. Huang, Z. Zeng and H. Zhang, Chem. Soc. Rev., 2013, 42, 1934–1946 RSC
.
- R. Lv, J. A. Robinson, R. E. Schaak, D. Sun, Y. Sun, T. E. Mallouk and M. Terrones, Acc. Chem. Res., 2015, 48, 56–64 CrossRef CAS PubMed
.
- K. Tu, F. Li and Z. Chen, J. Mater. Res., 2016, 31, 878–885 CrossRef CAS
.
- L. Wang and T. Sasaki, Chem. Rev., 2014, 114, 9455–9486 CrossRef CAS PubMed
.
- F. Li, C. R. Cabrera and Z. Chen, J. Mater. Chem. A, 2014, 2, 19180–19188 RSC
.
- J. Jia, Bi. Li, S. Duan, Z. Cui and H. Gao, Nanoscale, 2019, 11, 20307–20314 RSC
.
- Z. Guo, J. Zhou and Z. Sun, J. Mater. Chem. A, 2017, 5, 23530–23535 RSC
.
- X. Tang, X. Guo, W. Wu and G. Wang, Adv. Energy Mater., 2018, 8, 1801897 CrossRef
.
- Q. Tang, Z. Zhou and P. Shen, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS PubMed
.
- S. Lei, X. Chen, B. Xiao, W. Zhang and J. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 28830–28840 CrossRef CAS PubMed
.
- T. Zhang, Y. Ma, B. Huang and Y. Dai, ACS Appl. Mater. Interfaces, 2019, 11, 6104–6110 CrossRef CAS PubMed
.
- S. Karmakar, C. Chowdhury and A. Datta, J. Phys. Chem. C, 2016, 120, 14522–14530 CrossRef CAS
.
- C. S. Liu, X. Yang, J. Liu and X. J. Ye, ACS Appl. Mater. Interfaces, 2018, 1, 3850–3859 CAS
.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultmman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed
.
- O. Mashtalir, M. Naguib and V. N. Mochalin, Nat. Commun., 2013, 4, 1716 CrossRef PubMed
.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CrossRef CAS PubMed
.
- Y. X. Yu, J. Phys. Chem. C, 2016, 120, 5288–5296 CrossRef CAS
.
- Q. Meng, J. Ma, Y. Zhang, Z. Li, C. Zhi, A. Hu and J. Fan, Nanoscale, 2018, 10, 3385–3392 RSC
.
- S. Zhao, W. Kang and J. Xue, J. Phys. Chem. C, 2014, 118, 14983–14990 CrossRef CAS
.
- J. Hu, B. Xu, C. Ouyang, S. A. Yang and Y. Yao, J. Phys. Chem. C, 2014, 118, 24274–24281 CrossRef CAS
.
- J. Hu, B. Xu, C. Ouyang, Y. Zhang and S. A. Yang, RSC Adv., 2016, 6, 27467–27474 RSC
.
- Q. Sun, Y. Dai, Y. Ma, T. Jing, W. Wei and B. Huang, J. Phys. Chem. Lett., 2016, 7, 937–943 CrossRef CAS PubMed
.
- Z. Xu, X. Lv, J. Chen, L. Jiang, Y. Lai and J. Li, Phys. Chem. Chem. Phys., 2017, 19, 7807–7819 RSC
.
- Y. Zhou and X. Zu, Electrochim. Acta, 2017, 235, 167–174 CrossRef CAS
.
- T. Zhao, S. Zhang, Y. Guo and Q. Wang, Nanoscale, 2016, 8, 233–242 RSC
.
- J. Xu, D. Wang, R. Lian, X. Gao, Y. Liu, G. Yury, G. Chen and Y. Wei, J. Mater. Chem. A, 2019, 7, 8873–8881 RSC
.
- B. Zhang, W. Zhang, Q. Meng, L. Fan and Q. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 1606–1613 RSC
.
- T. Yu, S. Zhang, F. Li, Z. Zhao, L. Liu, H. Xu and G. Yang, J. Mater. Chem. A, 2017, 5, 18698–18706 RSC
.
- B. Zhang, Q. Zhang and Y. Bai, J. Phys.: Condens. Matter, 2018, 30, 17 Search PubMed
.
- H. Huang, H.-H. Wu, C. Cui, B. Huang and T.-Y. Zhang, J. Mater. Chem. A, 2019, 7, 8897–8904 RSC
.
- C. Tang, X. Wang, H. Yao and L. Fu, Mater. Today Commun., 2020, 25, 101587 CrossRef CAS
.
- T. Zhao, J. Zhou, Q. Wang, Y. Kawazoe and P. Jena, ACS Appl. Mater. Interfaces, 2016, 8, 26207–26212 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- K. Albe and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1271–1276 CrossRef
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef
.
- N. Li, Y. Li, X. Zhu, C. Huang, J. Kai and J. Fan, J. Phys. Chem. C, 2020, 124, 14978–14986 CrossRef CAS
.
- Y. Li, D. B. Putungan and S. Lin, Phys. Lett. A, 2018, 38, 2781–2786 CrossRef
.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed
.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed
.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed
.
- S. Wang, J.-X. Li, Y.-L. Du and C. Cui, Comput. Mater. Sci., 2014, 83, 290–293 CrossRef CAS
.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef
.
- J. Wang, S. Yip, S. R. Phillpot and D. Wolf, Phys. Rev. Lett., 1993, 71, 4182–4185 CrossRef CAS PubMed
.
- Z. Wu, E. Zhao, H. Xiang, X. Hao, X. Liu and J. Meng, Phys. Rev. B: Conders. Matter. Phys., 2007, 76, 054115 CrossRef
.
- A. Savin, R. Nesper, S. Wengert and T. F. Fassler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS
.
- S. Gong, C. Zhang, S. Wang and Q. Wang, J. Phys. Chem. C, 2017, 121, 10258–10264 CrossRef CAS
.
- V. Wang and W. T. Geng, J. Phys. Chem. C, 2017, 121, 10224 CrossRef CAS
.
- C. R. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035423 CrossRef
.
- B. Mortazavi, O. Rahaman, M. Makaremi, A. Dianat, G. Cuniberti and T. Rabczuk, Phys. E, 2017, 87, 228–232 CrossRef CAS
.
- Q. Peng, C. Liang, W. Ji and S. De, Phys. Chem. Chem. Phys., 2013, 15, 2003–2011 RSC
.
- K. H. Michel and B. Verberck, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224301 CrossRef
.
- B. Mortazzvi, A. Dianat, O. Rahaman, G. Guniberti and T. Rabczuk, J. Power Sources, 2016, 329, 456–461 CrossRef
.
- Q. Meng, A. Hu, C. Zhi and J. Fan, Phys. Chem. Chem. Phys., 2017, 19, 29106–29113 RSC
.
- M. Mortazavi, C. Wang, J. Deng, V. B. Shenoy and N. V. Medhekar, J. Power Sources, 2014, 268, 279–286 CrossRef CAS
.
- D. Er, J. Li, M. Naguib, Y. Gogotsi and V. B. Shenoy, ACS Appl. Mater. Interfaces, 2014, 6, 11173–11179 CrossRef CAS PubMed
.
- T. Yu, S. Zhang, F. Li, Z. Zhao, L. Liu, H. Xu and G. Yang, J. Mater. Chem. A, 2017, 5, 18698–18706 RSC
.
- X. Lv, F. Li, J. Gong, J. Gu, S. Lin and Z. Chen, Phys. Chem. Chem. Phys., 2020, 22, 8902–8912 RSC
.
-
(a) T. Bo, P. F. Liu, J. Xu, J. R. Zhong, Y. B. Chen, O. Eriksson, F. W. Wang and B. T. Wang, Phys. Chem. Chem. Phys., 2018, 20, 22168–22178 RSC
; (b) T. Bo, P. F. Liu, J. Xu, J. R. Zhong, F. W. Wang and B. T. Wang, Phys. Chem. Chem. Phys., 2019, 21, 5178–5188 RSC
.
- A. Sibari, A. Marjaoui, M. Lakhal, Z. Kerrami, A. Kara, M. Benaissa, A. Ennaoui, M. Hamedoun, A. Benyoussef and O. Mounkachi, Sol. Energy Mater. Sol. Cells, 2018, 180, 253–257 CrossRef CAS
.
- X. Lv, W. Wei, Q. Sun, L. Yu, B. Huang and Y. Dai, ChemPhysChem, 2017, 18, 1627–1634 CrossRef CAS PubMed
.
- Y. Yu, Z. Guo, Q. Peng, J. Zhou and Z. Sun, J. Mater. Chem. A, 2019, 7, 12145–12153 RSC
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- C. Zhu, X. Qu, M. Zhang, J. Wang, Q. Li, Y. Geng, Y. Ma and Z. Su, J. Mater. Chem. A, 2019, 7, 13356–13363 RSC
.
- J. Vetter, P. Novák, M. R. Wagner, C. Veitb, K.-C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammmouche, J. Power Sources, 2005, 147, 269–281 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Lattice constants of the MC2 monolayers; bond length and thickness of the MC2 monolayers; the calculated phonon spectra of the MC2 monolayers; the FPMD simulations at the end of 5 ps at 300 K; the electronic localization function (ELF) of the MC2 monolayers; the partial density of states (TDOS and PDOS) of the MC2 monolayers; the partial density of states (PDOS) of Na-adsorbed MC2 monolayers; the variation of the path-I diffusion lengths of Na on the MC2 monolayers with the lattice constants of MC2; the energy profile (left plane) and diffusion pathways (right plane) of Na diffusing on the TiC2 monolayer; the formation energy (Ef) of NaxMC2 with respect to MC2 monolayers and Na bulk bcc metal; the configurations and their optimized adsorption energies (eV) for NaxNbC2; the side views of the Na-intercalated MC2 monolayer at the end of 5 ps FPMD simulations at 300 and 500 K, respectively. See DOI: 10.1039/d1na00422k |
| This journal is © The Royal Society of Chemistry 2021 |