Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of cooperative CO2 adsorption in diamine-appended variants of the metal–organic framework Mg2(dobpdc)†
Jeffrey D.
Martell‡§
a,
Phillip J.
Milner‡¶
 a,
Rebecca L.
Siegelman||
a,
Rebecca L.
Siegelman||
 a and
Jeffrey R.
Long
a and
Jeffrey R.
Long
 *abc
*abc
aDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: jrlong@berkeley.edu
bDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720, USA
cMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 31st March 2020
Abstract
Carbon capture and sequestration is a key element of global initiatives to minimize anthropogenic greenhouse gas emissions. Although many investigations of new candidate CO2 capture materials focus on equilibrium adsorption properties, it is also critical to consider adsorption/desorption kinetics when evaluating adsorbent performance. Diamine-appended variants of the metal–organic framework Mg2(dobpdc) (dobpdc4− = 4,4′-dioxidobiphenyl-3,3′-dicarboxylate) are promising materials for CO2 capture because of their cooperative chemisorption mechanism and associated step-shaped equilibrium isotherms, which enable large working capacities to be accessed with small temperature swings. However, the adsorption/desorption kinetics of these unique materials remain understudied. More generally, despite the necessity of kinetics characterization to advance adsorbents toward commercial separations, detailed kinetic studies of metal–organic framework-based gas separations remain rare. Here, we systematically investigate the CO2 adsorption kinetics of diamine-appended Mg2(dobpdc) variants using a thermogravimetric analysis (TGA) assay. In particular, we examine the effects of diamine structure, temperature, and partial pressure on CO2 adsorption and desorption kinetics. Importantly, most diamine-appended Mg2(dobpdc) variants exhibit an induction period prior to reaching the maximum rate of CO2 adsorption, which we attribute to their unique cooperative chemisorption mechanism. In addition, these materials exhibit inverse Arrhenius behavior, displaying faster adsorption kinetics and shorter induction periods at lower temperatures. Using the Avrami model for nucleation and growth kinetics, we determine rate constants for CO2 adsorption and quantitatively compare rate constants among different diamine-appended variants. Overall, these results provide guidelines for optimizing adsorbent design to facilitate CO2 capture from diverse target streams and highlight kinetic phenomena relevant for other materials in which cooperative chemisorption mechanisms are operative.
Introduction
Steadily rising atmospheric CO2 levels and the associated increase in average global temperatures have created an urgent need to curb anthropogenic CO2 emissions.1 While long-term solutions to this challenge necessitate a shift to renewable energy sources, fossil fuels will continue to supply a major portion of global energy in the near future.2 One proposed strategy to mitigate atmospheric CO2 emissions in the short term is carbon capture and sequestration from major point sources, such as power plants.3 To realize this strategy, carbon capture materials are needed that possess high selectivities and CO2 capacities, as well as minimal energy requirements for CO2 desorption. Rapid kinetics to bind and release CO2 are also critical, because they can dictate bed utilization and thus impact the cost and efficiency of a carbon capture process.4Aqueous solutions of organic amines are a mature CO2 capture technology, but they suffer from numerous drawbacks. For example, solutions with relatively low amine concentrations are necessary to minimize corrosive effects, thereby decreasing the solution CO2 absorption capacities and increasing the energy required to heat the absorbent during temperature-swing cycling.5 As a result, the implementation of aqueous amine scrubbers in a power plant places a parasitic load of 25–30% on the net power output.6 Furthermore, aqueous amine solutions are prone to thermal and oxidative degradation.3 As an alternative, porous solid adsorbents have been proposed as capture materials, owing to their lower heat capacities and high surface areas, which create the potential for high adsorption capacities and more efficient adsorption–desorption cycling. Nevertheless, many of these solid adsorbents fail to capture CO2 selectively from humid gas streams.7
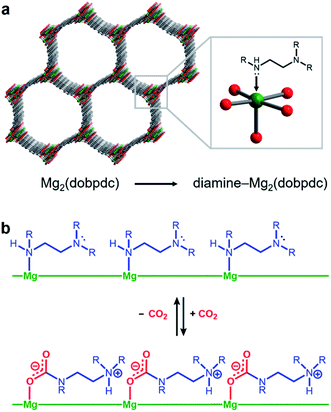
Amine-functionalized solid adsorbents combine the advantages of aqueous amine solutions and porous solid adsorbents. Examples of these materials include amine-functionalized silicas,8–11 porous polymers,12,13 zeolites,14,15 and metal–organic frameworks.16–20 Owing to their high crystallinity and chemical adjustability, metal–organic frameworks possess ordered structures that can be tailored with respect to pore size, shape, and chemical environment. In particular, amine functionalities can be incorporated within the organic linkers of these materials, both during framework synthesis21 or through post-synthetic modification.16–20,22 Additionally, the high internal surface areas accessible with metal–organic frameworks can allow for rapid diffusion of CO2 through the pores.23 Diamine-appended variants of the metal–organic framework Mg2(dobpdc)24–31 (dobpdc4− = 4,4′-dioxidobiphenyl-3,3′-dicarboxylate) represent a particularly promising class of amine-functionalized frameworks, as they readily adsorb CO2 through a chemically-specific, cooperative mechanism (Fig. 1).25 Here, the metal-bound amine reacts covalently with CO2 to generate a carbamate while the pendent amine is concomitantly protonated. This process propagates through the material to yield chains of ammonium carbamate stabilized through ionic interactions along the pore axis. As a result of this unique capture mechanism, diamine-appended variants of Mg2(dobpdc) exhibit step-shaped CO2 adsorption profiles, which give rise to large CO2 cycling capacities that are accessible with relatively small temperature swings.25 Importantly, by varying the metal cation,25 diamine,26–28 or organic linker,28 the adsorption step position can be tuned in pressure by over five orders of magnitude (from ∼10−5 to ∼1 bar at 40 °C) to enable the precise targeting of specific CO2 separation conditions. Moreover, these materials have also been shown to maintain high CO2 working capacities after 1000 adsorption/desorption cycles under humid gas streams.27
While the thermodynamics of CO2 capture in diamine-appended variants of Mg2(dobpdc) are promising for numerous carbon capture applications, the kinetics also play a crucial role in the practical application of these materials. For porous solid adsorbents, small-scale breakthrough experiments are often used to simulate a fixed-bed adsorption process. In these experiments, shaped particles of the adsorbent are packed into a column, a CO2-containing gas stream is fed through the inlet, and the outlet composition and flow rate are measured as a function of time until CO2 “breaks through.” Multiple kinetic parameters can influence the performance of an adsorbent in a fixed bed, including interparticle, intraparticle, and micropore diffusional resistances, as well as potential reaction limitations for amine-based chemisorption of CO2. Critically, the overall CO2 adsorption kinetics must be sufficiently fast to maximize bed utilization in the process. Promising initial results have been obtained for diamine-appended Mg2(dobpdc) variants in gram-scale breakthrough experiments for CO2 capture from simulated coal flue gas (15% CO2 in N2) under both dry and humid conditions.27 In addition, rapid cycle times have been employed for diamine-appended Mg2(dobpdc) variants in simulated temperature-swing experiments under 15% CO2 with a pure CO2 purge, and here cycle times were limited only by the temperature ramp rate of the thermogravimetric analyzer.27,28
Given the promise of diamine-appended Mg2(dobpdc) for CO2 capture applications, a detailed analysis of the kinetics of CO2 adsorption in these materials is necessary for optimal process implementation. Toward this end, we herein utilize thermogravimetric analysis (TGA) to systematically investigate the dry CO2 adsorption kinetics in diamine-appended variants of Mg2(dobpdc) under a range of adsorption conditions. Our results demonstrate the influence of adsorption temperature, CO2 concentration, and diamine structure on the rate of adsorption. On the basis of these correlations, we conclude with guidelines for the optimization of adsorbent structure and process parameters in CO2 capture applications.
Results and discussion
Experimental setup for a thermogravimetric assay to study CO2 adsorption kinetics
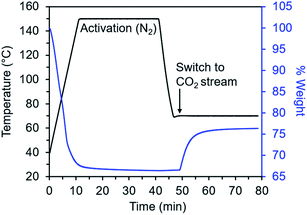
Diamine-appended variants of Mg2(dobpdc) were synthesized using our previously reported procedure.26 Specifically, methanol-solvated Mg2(dobpdc) was soaked in a 20% (v/v) toluene solution of the diamine of interest, and subsequent filtration, washing with toluene, and activation yielded adsorbents with one diamine per metal site. To ensure internal consistency for this study, all experiments were performed with the same batch of Mg2(dobpdc). The rod-shaped crystallites in this batch exhibited an aspect ratio of ∼10 and were heterogeneous in size, with widths ranging from ∼60 nm to >1 μm (Fig. S1†). Measurements in this study were carried out on as-synthesized diamine–Mg2(dobpdc) samples in powder form; future studies will explore adsorption/desorption kinetics in structured forms of these materials.We developed a TGA assay at atmospheric pressure to evaluate the CO2 adsorption kinetics of diamine-appended Mg2(dobpdc). In this assay, samples were first activated in the TGA furnace under flowing N2 to remove any captured CO2, solvent, or excess diamine present in the pores. Next, samples were cooled to a temperature of interest, the gas flow was switched to a CO2-containing stream, and the change in mass was monitored as a function of time (Fig. 2). Because N2 adsorption is negligible at and above room temperature in these materials,26,27 we approximated that all mass increase was due to CO2 adsorption. In addition, mass changes due to buoyancy effects upon switching the gas stream from N2 to CO2 were negligible compared to the mass of CO2 adsorbed by the standard sample size of 3 mg of diamine–Mg2(dobpdc) used in this work (Fig. S2†).
This TGA-based assay, which has been reported for fundamental kinetics characterization of other solid CO2 adsorbents,11,32–35 is advantageous given its simple setup, the small sample mass requirement, and the fact that adsorbents can be activated in situ and rapidly tested under many temperatures and partial pressures of CO2. However, this assay also has some limitations. For example, because TGA detects gas adsorption through a change in sample mass, it cannot discriminate between CO2, H2O, and N2 adsorption (although, as mentioned above, N2 adsorption is negligible for diamine-appended Mg2(dobpdc) variants under the conditions relevant for CO2 chemisorption). As a result, determining CO2 adsorption kinetics under humid conditions remains challenging, and here we discuss only dry adsorption/desorption kinetics profiles. In addition, the first few points of kinetics data from a TGA experiment are obscured by exchange of the initial gas in the furnace with the CO2-containing stream in adsorption experiments or the N2 purge stream in desorption experiments.
As has been previously noted,11 differences in flow rate and sample mass can also greatly affect TGA adsorption kinetics profiles. For example, in the case of m-2-m–Mg2(dobpdc) (m-2-m = N,N′-dimethylethylenediamine), we found that the sample mass has a substantial impact on adsorption kinetics from a simulated coal flue gas stream of 15% CO2 in N2,36 with larger samples displaying slower overall adsorption kinetics (Fig. S3†). Therefore, to maintain consistency across all samples in this study, we used a sample mass of 3 mg and ensured the powder was evenly distributed across the surface of the TGA pan. Also consistent with previous reports, faster adsorption kinetics were observed with faster flow rates (Fig. S3†). This flow rate effect could be due to the time required to completely exchange the initial gas in the furnace and/or to the observed kinetics being influenced by a mass transfer resistance related to diffusion. As a result, the kinetics of adsorption presented in this work likely represent lower bounds on the intrinsic adsorption kinetics of these materials. For the fastest flow rates tested (>100 mL min−1), adsorption was essentially complete within the first few data points collected on the TGA, making it difficult to quantitatively compare the kinetics among different adsorbents under these conditions. We therefore used a consistent flow rate of 25 mL min−1 for all experiments to facilitate quantitative comparisons among the diamine-appended variants. Under these conditions, a consistent delay of 19 s was observed before the sample mass increased, after switching the TGA valving to the analysis gas. This delay time corresponds to the time required for CO2 to reach the sample in the TGA furnace. Additionally, given a flow rate of 25 mL min−1, we approximate that at least 14–23 s are required at temperatures ranging from 120 to 30 °C for complete exchange of gases in the TGA furnace, beyond the initial 19 s delay (Table S1†). By accounting for these considerations in the measurements detailed below, we were able to compare the effects of temperature, CO2 partial pressure, and diamine structure on the CO2 adsorption kinetics of these materials.
Adsorption kinetics and temperature dependence for m-2-m–Mg2(dobpdc)
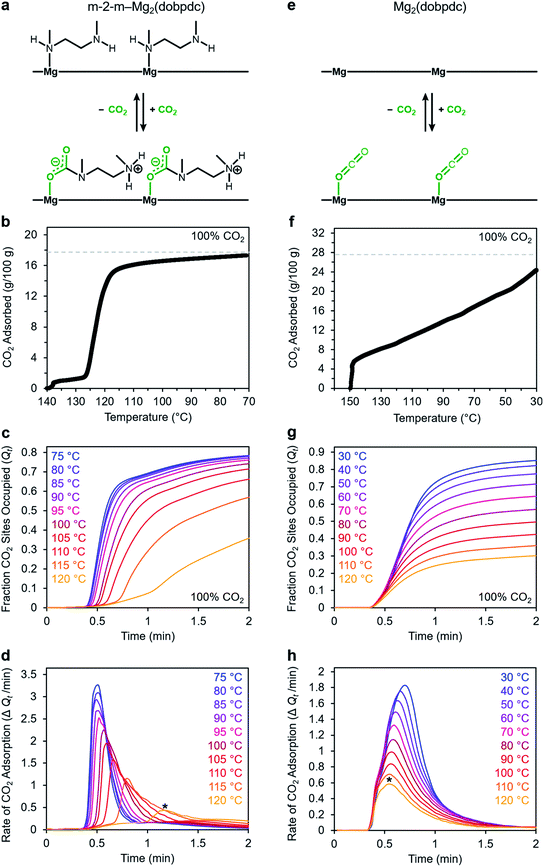
We utilized our optimized TGA assay to characterize the CO2 adsorption kinetics of m-2-m–Mg2(dobpdc), the first reported diamine-appended variant of Mg2(dobpdc),24 at selected temperatures. Extensive gas adsorption, structural, and spectroscopic data have been previously reported for this material,24–26 and an overview of the adsorption mechanism is shown in Fig. 3a. We first investigated the CO2 adsorption kinetics of m-2-m–Mg2(dobpdc) from a pure CO2 stream at atmospheric pressure over a range of temperatures below the adsorption step temperature (Tstep) of 127 °C,26 defined here as the onset of the step-shaped adsorption isobar (Fig. 3b). Rapid uptake of CO2 was observed below Tstep, as is evident in a plot of fraction of diamine sites occupied (Qt) vs. time (Fig. 3c). Interestingly, adsorption of CO2 is faster at lower temperatures and follows an inverse Arrhenius behavior (Fig. 3d). Such inverse Arrhenius behavior has been observed previously for a polyethylenimine-appended mesoporous silica11 and amine-functionalized carbon nanotubes,37 whereas normal Arrhenius behavior has been observed for other amine-appended solid adsorbents.34,35,38 Our results suggest that although the equilibrium capacity of m-2-m–Mg2(dobpdc) is relatively insensitive to temperature below Tstep,26 lower adsorption temperatures promote more rapid saturation with CO2. A more in-depth discussion of this phenomenon is provided below (see “Inverse Arrhenius behavior”).In addition to this inverse Arrhenius behavior, we also observed an induction period between the time at which the mass begins to increase, which corresponds to CO2 first entering the furnace, and the time associated with the fastest rate of CO2 uptake (Fig. 3d). This effect is particularly pronounced at temperatures close to Tstep. To elucidate whether the observed induction period is intrinsic to the CO2 adsorption kinetics of m-2-m–Mg2(dobpdc) or is an artifact of the experimental setup, we investigated CO2 adsorption in the bare framework material with no appended diamines, Mg2(dobpdc) (Fig. 3e and f). In Mg2(dobpdc), CO2 binds to open metal coordination sites exposed upon solvent removal from the framework, leading to a typical Langmuir adsorption profile (Fig. 3e).24 Importantly, because CO2 adsorption in Mg2(dobpdc) does not involve a chemical reaction, the adsorption kinetics are likely diffusion-limited. Consistently, Mg2(dobpdc) reaches its equilibrium CO2 adsorption capacity within a similarly short time for all temperatures examined (Fig. 3g and h), with the maximum rate of adsorption occurring at earlier times as the temperature is increased, in stark contrast to the behavior exhibited by m-2-m–Mg2(dobpdc). For example, at 120 °C, approximately 51 s elapses before the maximum rate of adsorption is achieved in m-2-m–Mg2(dobpdc), whereas the maximum rate is reached in only 14 s for bare Mg2(dobpdc) under the same conditions (see asterisks in Fig. 3d and h). Note that comparison of the absolute rate of adsorption is complicated by the lower equilibrium capacity of Mg2(dobpdc) at the low partial pressures present in the TGA furnace during the initial mixing period (Fig. S4†). Furthermore, the apparent kinetics of Mg2(dobpdc) include competition of N2 and CO2 for the same binding sites, and thus CO2 adsorption requires displacement of any adsorbed N2 molecules. Nevertheless, only a small fraction of metal sites (∼2–10%) is expected to be occupied by N2 under the conditions examined here, based on previously reported N2 adsorption isotherms for the isoreticular smaller-pore framework material Mg2(dobdc).39
In addition to the marked differences in the kinetics of CO2 adsorption, the bare framework Mg2(dobpdc) and amine-appended m-2-m–Mg2(dobpdc) also exhibit distinct trends in their variable–temperature equilibrium CO2 adsorption capacities (Qe). Whereas the CO2 saturation capacity of m-2-m–Mg2(dobpdc) is similar across nearly all temperatures investigated, decreasing only near Tstep (Fig. 3b), the capacity of Mg2(dobpdc) varies substantially with temperature (Fig. 3f). This difference arises due to the different adsorption profiles of these two materials and is best demonstrated through a van't Hoff plot (Fig. 4a). To quantify the kinetics in these two materials while accounting for variations in equilibrium capacity, we also analyzed the percent of adsorption complete (Qt/Qe) vs. time (Fig. 4b and c). This analysis again reveals that adsorption is faster at lower temperatures for m-2-m–Mg2(dobpdc), with induction periods observed at temperatures close to Tstep. In contrast, the adsorption profiles are similar at all temperatures for Mg2(dobpdc), with the highest temperatures exhibiting the fastest initial progress toward equilibrium. Overall, these findings corroborate that the chemisorptive mechanism operational in m-2-m–Mg2(dobpdc) leads to an unusual induction period that is not observed in the physisorptive mechanism in Mg2(dobpdc).
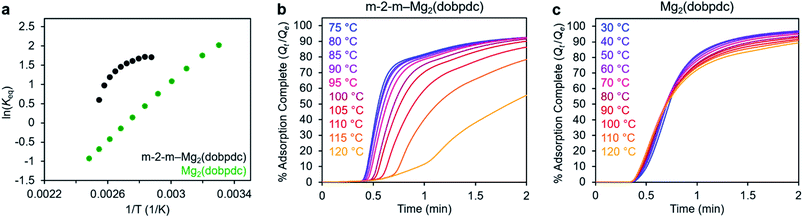 | ||
| Fig. 4 (a) Van't Hoff plot depicting the equilibrium CO2 adsorption capacity with varying temperature for m-2-m–Mg2(dobpdc) and Mg2(dobpdc) from a 100% CO2 stream (based on the data shown in Fig. 3c and g). Keq is defined as Qe/[(Qmax − Qe)pCO2], where Qe is the equilibrium adsorption capacity, Qmax is the theoretical maximum CO2 adsorption capacity, and pCO2 is the partial pressure of CO2, defined as p/p0, with p = p0 = 1 atm. We note that this van't Hoff analysis assumes an equilibrium exchange. Although the chemisorbed CO2 in saturated ammonium carbamate chains does not appreciably exchange with free CO2,52 the changes in adsorption capacity for m-2-m–Mg2(dobpdc) at temperatures below the step are likely due primarily to CO2 physisorption, which should be reversible. The enthalpy of CO2 adsorption, Δh, can be estimated for bare Mg2(dobpdc) based on the slope of a linear fit to the data points (Fig. S7†). (b) and (c): plots of % adsorption complete (Qt/Qe) vs. time corresponding to the data shown in Fig. 3c and g, respectively. Adsorption was monitored for 30 min (b) or 10 min (c) to confirm mass equilibration, but only the first 2 min of adsorption are shown. | ||
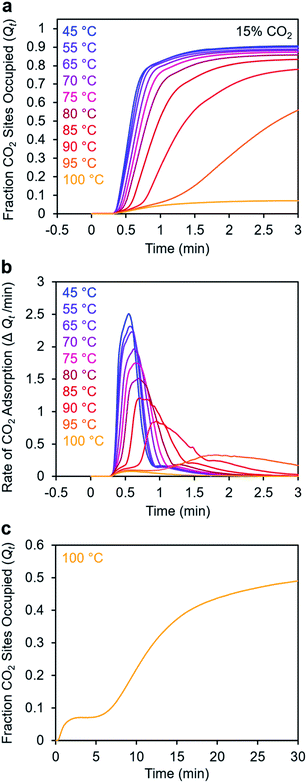
To further understand the induction period exhibited by m-2-m–Mg2(dobpdc), we characterized the adsorption kinetics from a 15% CO2 stream (Fig. 5), corresponding to the approximate partial pressure of CO2 in coal flue gas.36 In this case, the investigated temperature range (45–100 °C) is lower than that used in the experiments with 100% CO2 (75–120 °C), reflecting the lower adsorption step temperature under 15% CO2 (102 °C) compared to 100% CO2 (127 °C) (Fig. S8†). At temperatures below 75 °C, adsorption was nearly complete in less than 1 min. At temperatures near Tstep, however, the induction period was even more pronounced than in the analogous experiments with 100% CO2 (Fig. 5bvs.Fig. 3d). The effect was particularly dramatic at 100 °C (Fig. 5c)—a small amount of CO2 was rapidly adsorbed (6% of the diamine sites occupied within 1 min), followed by a period of 4 min during which almost no additional adsorption occurred. After 5 min, the rate of CO2 adsorption accelerated, and a substantial CO2 occupancy was ultimately reached, corresponding to occupation of approximately half of the diamine sites. The fast capture of CO2 at ∼6% of the m-2-m sites, as shown in Fig. 5c, is consistent with the previous finding that m-2-m–Mg2(dobpdc) adsorbs a small amount of CO2 even at pressures below the step.24,25 Spectroscopic studies indicate that this pre-step chemisorption arises due to ammonium carbamate species that form without metal–amine insertion.7 We hypothesize that the pre-step ammonium carbamate species forms rapidly, followed by slower cooperative adsorption of additional CO2via the formation of metal-bound ammonium carbamate chains. Qualitatively similar results were obtained using a 5% CO2 stream, for which the induction period is even more pronounced (Fig. S6†).
Taken together, these results suggest that the sigmoidal kinetics profile of m-2-m–Mg2(dobpdc) is directly related to its cooperative CO2 adsorption mechanism. This material exhibits a high degree of cooperativity in equilibrium gas adsorption isotherms, with its Hill coefficient of ∼11 indicating that, from a thermodynamic standpoint, capturing one CO2 molecule facilitates the adsorption of subsequent CO2 molecules.25 The pronounced sigmoidal kinetics profile exhibited by m-2-m–Mg2(dobpdc) likewise suggests that initial capture of a CO2 molecule also enhances the adsorption kinetics of subsequent CO2 molecules. Similar sigmoidal kinetic profiles have been reported previously for autocatalytic40 and autoinductive41 chemical reactions. While a recent TGA-based assay previously revealed that a polyethylenimine-appended mesoporous silica also exhibited sigmoidal CO2 adsorption kinetics,11 amine-impregnated clays did not exhibit sigmoidal uptake kinetics when evaluated using comparable TGA equipment and procedures.34 These precedents establish that not all amine-based CO2 adsorbents exhibit sigmoidal kinetics. As noted in a recent study,42 a long induction period is undesirable for implementation in a practical process because it can lead to lower bed utilization. Specifically, in breakthrough experiments simulating direct air capture with m-2-m–Mg2(dobpdc), it was found that after rapid partial breakthrough of CO2, the CO2 concentration at the outlet decreased before full breakthrough eventually occurred, consistent with a delayed onset of adsorption.42 Hence, it is critical to identify appropriate diamine variants and/or CO2 adsorption conditions that minimize this induction period (see below).
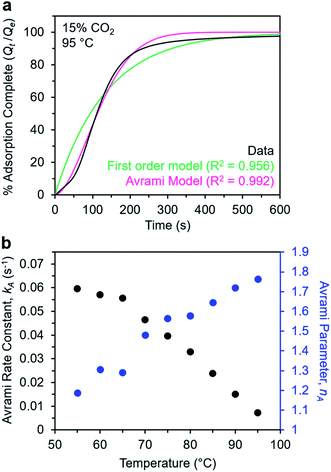
Avrami model of the adsorption kinetics of m-2-m–Mg2(dobpdc)
We next sought to model the CO2 adsorption kinetics of m-2-m–Mg2(dobpdc) from a gas stream of 15% CO2 in N2. The fraction of sites occupied at time t (Qt) was fit at each temperature using either a pseudo-first order model (eqn (1)) or Avrami's kinetics model (eqn (2)), which was originally developed to model nucleation-growth kinetics43 and has recently found application as a model for chemisorption in an amine-appended mesoporous silica.11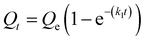 | (1) |
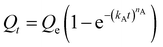 | (2) |
Note that in both models, the constant partial pressure of CO2 (P/P0 = 0.15) is embedded in the rate constant k1 or kA, respectively, and that nA in the Avrami model is also likely a function of P/P0. As expected, a pseudo-first order model using rate constant k1 (eqn (1)) failed to capture the induction period at temperatures near Tstep (Fig. 6a). In contrast, the Avrami model fits the data well, particularly for temperatures just below the step. We attribute the deviation from the model in the first 1.5 min to incomplete gas mixing in the furnace and to pre-step chemisorption, as discussed above. This model incorporates the Avrami parameter, nA, as well as the Avrami rate constant, kA, to produce sigmoidal kinetics profiles, with larger nA values leading to longer induction periods. For example, nA = 2 corresponds to the sigmoidal kinetics profile of the growth of a one-dimensional crystal.44,45
A plot of the Avrami rate constant kAvs. T, which is useful for visualizing trends in these data, is presented in Fig. 6b. This plot indicates that the Avrami rate constant becomes progressively larger with decreasing temperature, reflecting the inverse Arrhenius behavior of m-2-m–Mg2(dobpdc) (Fig. 6b). At temperatures below 70 °C, the slope of kAvs. T substantially decreases, possibly due to the intrinsic properties of the material or to instrumentation limitations associated with the high rate of adsorption at these colder temperatures. Unexpectedly, kAvs. T follows a linear trend from 70 to 95 °C, inconsistent with standard Arrhenius behavior (see “Inverse Arrhenius Behavior” below). Notably, the x-intercept of this plot (kA = 0) should correspond to Tstep; indeed, the x-intercept of a linear fit to the high-temperature data (70–95 °C) of 100 °C is close to the step temperature determined by cooling a sample of m-2-m–Mg2(dobpdc) under 15% CO2 (102 °C; see Fig. S8 and Table S2†). In addition, the parameter nA progressively decreases from an initial value of 1.7 at 95 °C to a value close to 1 at the lowest temperature of 55 °C, reflecting the longer induction periods near Tstep. Therefore, the parameters from these Avrami fits successfully reflect the experimental observations of slower CO2 adsorption kinetics (smaller kA) and longer induction periods (larger nA) at high temperatures close to the step temperature in m-2-m–Mg2(dobpdc). The smaller values of nA at lower temperatures reflect shorter induction periods and demonstrate an advantage of maintaining a buffer between the adsorption temperature and the step temperature.
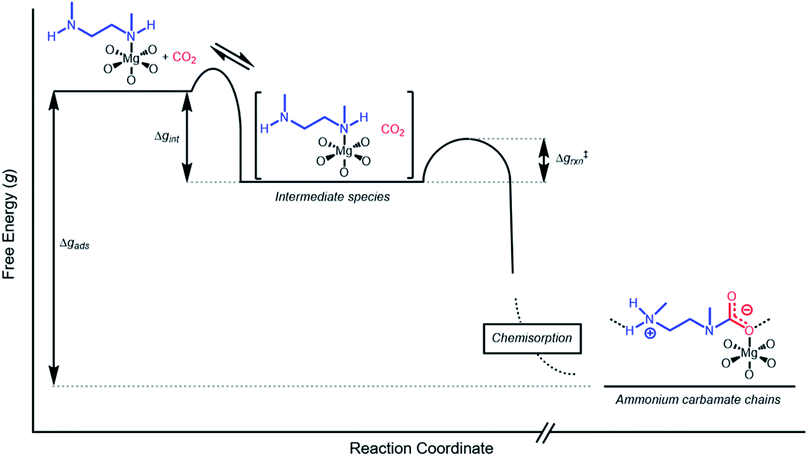
Inverse Arrhenius behavior
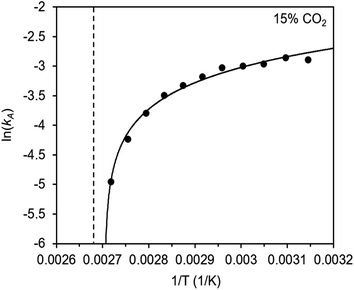
The inverse Arrhenius behavior observed here can be rationalized using a reaction coordinate diagram derived from several previous investigations of reactions with apparent negative activation energies (Fig. 7).40,46–49 In general, inverse Arrhenius behavior requires the reversible formation of an intermediate species with equilibrium constant Keq that (i) is lower in energy than the reactant(s), with energy difference Δgint; and (ii) proceeds to product formation through a transition state, with kinetic barrier Δg‡rxn, that is also lower in free energy than the reactant(s), such that |Δg‡rxn| < |Δgint| (see Fig. 7). In addition, the product formation must be an effectively irreversible process, with negligible conversion back to the intermediate species under the reaction conditions. This scenario leads to inverse Arrhenius behavior because the rate of product formation is dependent on the concentration of the intermediate species. Critically, for an adsorption process, this key intermediate species is thermodynamically disfavored at higher temperatures due to the greater entropic penalty associated with removing CO2 from the gas phase. In other words, increasing the temperature drives the intermediate species back toward the reactant(s) more than it promotes overcoming the barrier to form the product. In m-2-m–Mg2(dobpdc), reversible adsorption of CO2 to form a labile intermediate, such as a physisorbed or weakly chemisorbed species, likely precedes an exothermic rate-determining chemisorption step. The final product of chemisorption is an ammonium carbamate chain,26 which forms with a thermodynamic free energy change of Δgads. However, C–N bond formation, proton transfer, and metal–oxygen bond formation must all occur between the starting material and the final ammonium carbamate chains; the number of steps in this reaction pathway and the rate-determining step remain points of ongoing investigation. Nevertheless, the temperature dependence of the kinetics of CO2 adsorption in m-2-m–Mg2(dobpdc) is consistent with an overall mechanistic model involving the reversible formation of an entropically disfavored, CO2-bound intermediate followed by a rate-determining chemisorption step. A similar model can be invoked to explain the observed inverse Arrhenius behavior of CO2 adsorption in other amine-functionalized adsorbents.11,37To further understand the behavior of m-2-m–Mg2(dobpdc), we constructed an Arrhenius plot using the Avrami rate constants given in Fig. 6b. As expected, ln(kA) increases with 1/T (Fig. 8), and the sharp curvature occurring near 1/Tstep is consistent with the unusually linear behavior of kAvs. T near Tstep (Fig. 6b). The data can be fit well using a logarithmic function with a vertical asymptote corresponding to ∼97 °C, close to the Tstep of 102 °C (see Fig. S8†). The steeper slope of the Arrhenius plot near 1/Tstep indicates that the temperature dependence of the rate of adsorption in m-2-m–Mg2(dobpdc) is greatest close to Tstep.
While the reaction coordinate diagram in Fig. 7 accounts for the inverse Arrhenius behavior of CO2 adsorption in m-2-m–Mg2(dobpdc), it does not necessarily predict the extreme curvature of the Arrhenius plot near 1/Tstep. Because cooperative CO2 adsorption does not occur above Tstep, the Arrhenius plot for the cooperative adsorption process should deviate to −∞ upon approaching Tstep from low to high temperature. Discontinuities have previously been observed in linear Arrhenius plots when a phase change occurs at a specific temperature in an enzyme.50 However, the curvature exhibited in the Arrhenius plot of m-2-m–Mg2(dobpdc) is unusual and suggests a progressive decrease in the adsorption kinetics as T → Tstep. The curved Arrhenius plot can potentially be explained by considering the entropy change in the reaction coordinate diagram in Fig. 7, as has been previously described.51 Moving from left to right along the reaction coordinate in Fig. 7 corresponds to a significant decrease in degrees of freedom as gaseous CO2 is immobilized and the initially dynamic diamines are locked into ammonium carbamate chains. As the temperature increases, the entropic penalty for immobilizing CO2 increases and ultimately outweighs the enthalpic favorability of adsorption when T exceeds Tstep. Accordingly, the kinetic barrier of the rate-determining chemisorption step should become increasingly large at higher temperatures, consequently slowing the reaction kinetics. Therefore, increasing the temperature towards Tstep imposes two compounding deleterious entropic effects on the rate of adsorption in m-2-m–Mg2(dobpdc): it thermodynamically disfavors the formation of the intermediate species (as discussed above), and it increases the magnitude of the rate-limiting kinetic barrier. Together, these effects can potentially explain the observed progressively slower adsorption kinetics and resulting curved Arrhenius plot as T approaches Tstep. Determining the identity of the intermediate species and elucidating the mechanism of the rate-limiting chemisorption process remain active areas of investigation.
A structure–property kinetics relationship using a panel of ethylenediamine analogues
To determine the generalizability of these characteristics for m-2-m–Mg2(dobpdc) to other diamine-appended frameworks, we evaluated the kinetics of CO2 adsorption from a gas stream of 15% CO2 in N2 by a panel of Mg2(dobpdc) variants appended with structurally-diverse alkylethylenediamines. Notably, frameworks with 1°,3° alkylethylenediamines26 displayed minimal adsorption at temperatures ≥40 °C (Fig. S12†) and thus were not investigated further. In contrast, rate constants could be determined for frameworks appended with 1°,1°; 1°,2°; and 2°,2° amines (see Fig. 9). We note that the diamines N-isopropylethylenediamine (i-2) and N,N′-diethylethylenediamine (e-2-e) exhibit two-step adsorption behavior,28 and thus their kinetic profiles are complex at temperatures at which both steps are operative. As a result, Fig. 9 depicts only the temperatures under which the less thermodynamically favorable step is not operative for these two diamine-appended frameworks.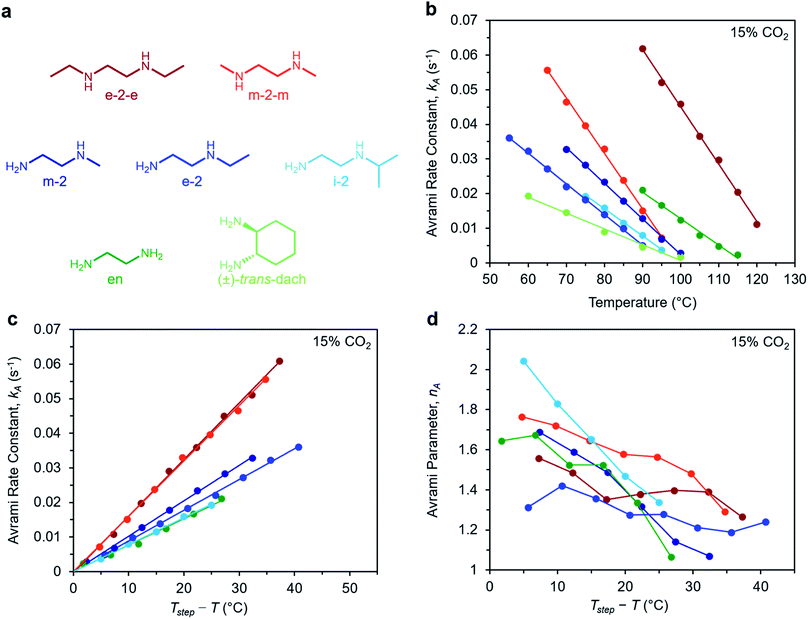 | ||
| Fig. 9 Rate constants and Avrami parameters for 15% CO2 adsorption by diamine-appended Mg2(dobpdc) variants. (a) Structures of diamines evaluated. The color scheme corresponds to the plots in (b)–(d). (b) Plot of Avrami rate constant (kA) vs. T for diamine-appended variants. Colored lines depict linear fits to the data. Linear regression data are shown in Fig. S26.† (c) Plot of kA data vs. Tstep − T, where T is the experimental adsorption temperature and Tstep is the adsorption step temperature (Tstep values correspond to the x-intercepts of the linear fits in (b)). (d) Plot of Avrami parameter (nA) vs. T for diamine-appended variants of Mg2(dobpdc). The x axis units are the same as in (c). Note that panels (c) and (d) do not contain data for (±)-trans-dach–Mg2(dobpdc) because it was not possible to approximate Tstep based on the linear fit shown in (b); see Fig. S19–20.† | ||
A similar overall sigmoidal kinetic profile was observed for all ethylenediamine variants in Fig. 9, consistent with our previous findings that these materials capture CO2 by the same mechanism.26,52 In each case, kA increases with decreasing temperature, indicative of inverse Arrhenius behavior, as observed for m-2-m–Mg2(dobpdc) (Fig. S13–S18†). Furthermore, all of the variants exhibit linear plots of kAvs. T (Fig. 9b) and curved Arrhenius plots that could be fit by logarithmic functions (Fig. S13–S18†), suggesting that the complex behavior characterized for m-2-m–Mg2(dobpdc) represents a general feature of these materials. In Fig. 9b, the linear fits to the kAvs. T data yield different x intercepts for each diamine-appended framework, reflecting their different adsorption step temperatures. The x-intercepts all match closely to step temperatures determined by cooling the frameworks under 15% CO2 (Fig. S8–S11 and Table S2†), except in the case of (±)-trans-dach–Mg2(dobpdc), for which the kAvs. T plot deviates from linearity at high temperatures (Fig. S20†).
The differences in adsorption step temperatures complicate comparisons between materials because the free energy change associated with CO2 adsorption (Δgads) is different for each material at a constant temperature. To account for this difference, we also plotted kAvs. Tstep − T to scale the x-intercepts of the linear fits to zero (Fig. 9c). Note that we do not consider Tstep − T to be a physically meaningful metric of chemical potential—rather, this plot is only intended to help visualize differences among diamine-appended frameworks. Importantly, the linear fits to the data in the corresponding plots all exhibit distinct slopes, reflecting variability in the extent to which decreasing the temperature below Tstep increases the CO2 adsorption kinetics. For practical applications, a steep slope in Fig. 9c is desirable to enable fast adsorption kinetics even at temperatures just below the step. In the plot of nAvs. Tstep − T (Fig. 9d), nA generally becomes smaller with decreasing temperature. Most of the materials exhibit values of nA between 1.3 and 1.8 at temperatures close to the step, decreasing to ∼1 at the lowest temperatures. Materials with smaller values of nA show less pronounced induction periods and are therefore preferable for implementation in a process.
Interestingly, the steepest slopes were observed for frameworks appended with the 2°,2° diamines m-2-m and e-2-e.24–26 These variants are notable for having weak metal–amine bonds, which serve to increase |Δhads| for CO2 and facilitate CO2 insertion, thus likely contributing to their fast adsorption kinetics.26 Despite these desirable kinetics properties, the weak metal–amine bonds lead to diamine volatilization under humid conditions, particularly at the high temperatures necessary for desorption under a pure CO2 stream.53,54 The second-fastest kinetics were found for variants of Mg2(dobpdc) functionalized with the 1°,2° diamines N-methylethylenediamine (m-2), N-ethylethylenediamine (e-2), and i-2.26,28,55 We previously determined that the primary amine preferentially binds to the metal site and reacts with CO2, which may account for the slower adsorption kinetics in these materials compared to those functionalized with 2°,2° diamines.26 However, this effect also bestows 1°,2° diamine-appended variants with enhanced stability toward diamine loss.26,28 The compounds with the least sterically-encumbered 1°,2° diamines exhibit slightly faster kinetics, as indicated by steeper slopes in the plots of kAvs. T (Fig. 9c). Overall, these results suggest a tradeoff between stability and adsorption kinetics for frameworks appended with 1°,2° diamines compared to those bearing 2°,2° diamines.
Finally, we studied the behavior of Mg2(dobpdc) variants appended with the 1°,1° diamines ethylenediamine (en) and (±)-trans-diaminocyclohexane (dach),26,29,31,56 which have previously been shown to exhibit significant adsorption/desorption hysteresis and unit cell contraction upon CO2 adsorption.56 Interestingly, the CO2 adsorption kinetics of en–Mg2(dobpdc) are extremely similar to those of i-2–Mg2(dobpdc)—the 1°,2° variant with the slowest CO2 adsorption kinetics—while (±)-trans-dach–Mg2(dobpdc) exhibits much slower kinetics. In addition, (±)-trans-dach–Mg2(dobpdc) displays an unusually high nA of ∼3 at temperatures close to the step, corresponding to a very long induction period (Fig. S19–S21†). As with the other diamines, the adsorption kinetics in (±)-trans-dach–Mg2(dobpdc) become much faster and the induction periods become much shorter at lower temperatures (nA = 1.3 at 60 °C; see Fig. S21†), and use of a fast flow rate (100 mL min−1) also shortens the induction period for this material (Fig. S22†). One possible explanation for the large nA value and slower overall kinetics of (±)-trans-dach–Mg2(dobpdc) is the unit cell contraction that occurs upon CO2 adsorption in conjunction with crystallographically characterized ion-pairing interactions between neighboring ammonium carbamate chains in the ab plane.56 Intriguingly, nA = 3 for the Avrami model corresponds to the growth of a crystal in two dimensions, whereas nA = 2 corresponds to growth in one dimension.44,45 Accordingly, cooperative CO2 adsorption in (±)-trans-dach–Mg2(dobpdc) may be akin to two-dimensional sheet growth, whereas cooperative CO2 capture by the other variants may be more akin to one-dimensional chain growth. Elucidating the potential correlation between ab plane contraction and the CO2 adsorption kinetics for 1°,1° diamine–Mg2(dobpdc) variants remains a subject of investigation.
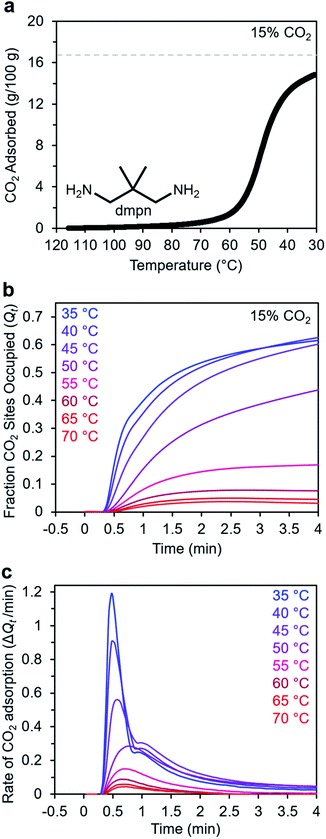
Adsorption kinetics of 2,2-dimethyl-1,3-diaminopropane–Mg2(dobpdc)
In addition to ethylenediamines, Mg2(dobpdc) has also been appended with diaminopropanes to yield cooperative adsorbents.27 For example, dmpn–Mg2(dobpdc) (dmpn = 2,2-dimethyl-1,3-diaminopropane) has a favorable adsorption step temperature for CO2 capture from coal flue gas and maintains a high working capacity over 1000 cycles under humid conditions.27 Notably, the complex CO2 chemisorption mechanism in dmpn–Mg2(dobpdc) ultimately leads to the formation of carbamic acids interacting with ammonium carbamates, and this material exhibits a mixture of ∼4 chemisorbed species in the early stages of CO2 adsorption.52 Given this complexity and the promising attributes of dmpn–Mg2(dobpdc) for implementation in practical processes, we sought to investigate its adsorption kinetics from a gas stream of 15% CO2 in N2.Consistent with previous findings, the 15% CO2 adsorption isobar for this material exhibits a step around 60 °C that is more broad than those of other diamine–appended Mg2(dobpdc) variants, reflecting its complex adsorption mechanism (Fig. 10a).27,52 Similarly, the kinetics profile of dmpn–Mg2(dobpdc) is distinct from that of the other diamine-appended variants (Fig. 10b and c), with no induction period observed even at temperatures close to the adsorption step. At all temperatures below 55 °C, dmpn–Mg2(dobpdc) exhibits a very rapid initial uptake, followed by slower uptake until reaching equilibrium. This unusual curve shape results in Avrami fits with small nA (∼0.4–0.7) and kA (∼0.003–0.006 s−1) values (Fig. S23†). The fastest initial uptake in dmpn–Mg2(dobpdc) occurs at 35 °C—the lowest temperature investigated—but only up to an occupancy of ∼0.6, after which the kinetics slow (Fig. S24†). We note that this slower adsorption at low temperatures and high occupancies was not observed in a comparable temperature range for the other diamine-appended variants, but a similar effect was reported previously in “molecular basket” polyamine-appended mesoporous silicas.10 Overall, the lack of induction period for dmpn–Mg2(dobpdc) is promising for implementation in a CO2 capture process.
Desorption kinetics
Desorption kinetics are also a critical consideration for the practical use of an adsorbent. In a typical fixed-bed process, adsorption and desorption stages are operated simultaneously using a minimum of two beds. As a consequence, fast desorption kinetics are desirable to minimize cycle times. In a simulation of the desorption conditions typical of a temperature swing adsorption process, we previously demonstrated that CO2 can be desorbed from diamine-appended Mg2(dobpdc) under a humidified stream of pure CO2 within less than 10 min, as limited by the heating rate of the TGA furnace.27,28 Alternatively, the introduction of dry N2 as a purge gas can be used to simulate the application of a concentration- or vacuum-swing process. Because diamine-appended Mg2(dobpdc) variants can maintain high CO2 capacities under pure CO2 even at relatively high temperatures, these materials can be heated under CO2 to a temperature of interest and allowed to equilibrate, after which the gas stream can be switched to dry N2 and the decrease in mass can be monitored.We utilized this dry N2 desorption assay to compare the desorption kinetics of dmpn–Mg2(dobpdc) and m-2-m–Mg2(dobpdc) (Fig. 11). At the highest temperature investigated for each material (70 and 110 °C for dmpn and m-2-m, respectively), nearly all of the CO2 was desorbed within 1.5 min, and decreasing the desorption temperature progressively decreased the rate of desorption. For each adsorbent, the initial Qt values varied with temperature, consistent with the isobaric adsorption profiles, and the larger Qt values at colder temperatures can be attributed to CO2 physisorption. Overall, desorption from dmpn–Mg2(dobpdc) occurs in a lower temperature range compared to desorption from m-2-m–Mg2(dobpdc), reflecting the lower desorption step temperature for the dmpn variant of 93 °C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 compared to 134 °C for m-2-m,26 as determined from dry 100% CO2 desorption isobars collected using a ramp rate of 1 °C min−1.
27 compared to 134 °C for m-2-m,26 as determined from dry 100% CO2 desorption isobars collected using a ramp rate of 1 °C min−1.
As shown in Fig. S25,† the desorption kinetics for dmpn–Mg2(dobpdc) and m-2-m–Mg2(dobpdc) fit well to the Avrami model across multiple temperatures. For both materials, desorption is initially slow, but is accelerated after some CO2 has been desorbed. Interestingly, the desorption kinetics behavior of dmpn–Mg2(dobpdc) differs from its adsorption kinetics behavior. While this material exhibits no induction period for adsorption (nA ∼0.5), a substantial induction period was observed for desorption (nA ∼2 for many of the conditions tested; see Fig. S25†). These dissimilar kinetics profiles may result from dmpn–Mg2(dobpdc) exhibiting a mixture of approximately four chemisorbed species in the early stages of CO2 adsorption, while a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ammonium carbamates:carbamic acids is formed following saturation with CO2 and long equilibration times.52
1 mixture of ammonium carbamates:carbamic acids is formed following saturation with CO2 and long equilibration times.52
Conclusions
The foregoing results describe a systematic investigation into the CO2 adsorption kinetics of diamine-appended variants of the metal–organic framework Mg2(dobpdc) using a TGA-based assay. Sigmoidal kinetics profiles were observed for all of the materials that exclusively form ammonium carbamate chains upon CO2 adsorption, which we attribute to their cooperative adsorption mechanism. While these adsorbents exhibit long induction periods at temperatures near the adsorption step, the kinetics of adsorption can be accelerated and the length of the induction period minimized by decreasing the adsorption temperature. Additionally, the diamine structure can be optimized to yield adsorption thermodynamics and kinetics that are most favorable for a target gas separation involving CO2. Finally, no induction period was observed for the material dmpn–Mg2(dobpdc), which adsorbs CO2via a mixed ammonium carbamate/carbamic acid mechanism. Thus, accessing new chemisorption products within the diamine-appended materials may give rise to advantageous changes in kinetics as well as thermodynamics. Overall, this study provides key guidelines for utilizing diamine-appended variants of Mg2(dobpdc) in CO2 separations and should prove more broadly useful for the design of new chemisorptive adsorbents for carbon capture applications.Conflicts of interest
The authors declare the following competing financial interest: J. R. L. has a financial interest in Mosaic Materials, Inc., a start-up company working to commercialize metal–organic frameworks for gas separations, including CO2 capture applications. The University of California, Berkeley has applied for a patent on some of the materials discussed herein, on which J. R. L., P. J. M., and R. L. S. are listed as inventors.Acknowledgements
We acknowledge ExxonMobil Research and Engineering Company for funding the initial synthesis and characterization of dmpn–Mg2(dobpdc) as part of a carbon capture research project. Characterization of dmpn–Mg2(dobpdc) was supported by the U.S. Department of Energy (DoE) under the National Energy Technology Laboratory (NETL) grant FWP-00006194. All other aspects of the research were supported in the early stages by the Center for Gas Separations Relevant to Clean Energy Technologies, an Energy Frontier Research Center supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award DE-SC0001015, and in later stages by the U.S. DoE, Office of Science, Office of Basic Energy Sciences under Award DE-SC0019992. We thank the Miller Institute for Basic Research in Science for postdoctoral fellowship support of J.D.M and the National Institutes of Health for support of P.J.M. through a postdoctoral fellowship (GM120799). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We further thank Kristen Colwell for obtaining SEM images, Dr T. David Harris for insightful comments, and Dr Katie Meihaus for editorial assistance.References
- J. Rogelj; D. Shindell; K. Jiang; S. Fifita; P. Forster; V. Ginzburg; C. Handa; H. Kheshgi, S. Kobayashi and E. Kriegler, Mitigation Pathways Compatible with 1.5 °C in the Context of Sustainable Development, in Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, 2018 Search PubMed.
- R. B. Jackson, C. Le Quéré, R. M. Andrew, J. G. Canadell, G. P. Peters, J. Roy and L. Wu, Warning Signs for Stabilizing Global CO2 Emissions, Environ. Res. Lett., 2017, 12(11), 110202 CrossRef.
- M. E. Boot-Handford, J. C. Abanades, E. J. Anthony, M. J. Blunt, S. Brandani, N. Mac Dowell, J. R. Fernandez, M.-C. Ferrari, R. Gross and J. P. Hallett, et al., Carbon Capture and Storage Update, Energy Environ. Sci., 2014, 7(1), 130–189 RSC.
- R. T. Yang, Adsorber Dynamics: Bed Profiles and Breakthrough Curves, in Gas Separation by Adsorption Processes, Butterworth-Heinemann, Boston, 1987, ch. 5, pp. 141–200 Search PubMed.
- A. S. Bhown and B. C. Freeman, Analysis and Status of Post-Combustion Carbon Dioxide Capture Technologies, Environ. Sci. Technol., 2011, 45(20), 8624–8632 CrossRef CAS PubMed.
- M. Ramezan, T. J. Skone, N. Y. Nsakala, G. N. Liljedahl, L. E. Gearhart, R. Hestermann and B. Rederstorff, Carbon Dioxide Capture from Existing Coal-Fired Power Plants, Natl. Energy Technol. Lab. DOENETL Rep., 2007, no. 401/110907 Search PubMed.
- J. A. Mason, T. M. McDonald, T.-H. Bae, J. E. Bachman, K. Sumida, J. J. Dutton, S. S. Kaye and J. R. Long, Application of a High-Throughput Analyzer in Evaluating Solid Adsorbents for Post-Combustion Carbon Capture via Multicomponent Adsorption of CO2, N2, and H2O, J. Am. Chem. Soc., 2015, 137(14), 4787–4803 CrossRef CAS PubMed.
- O. Leal, C. Bolívar, C. Ovalles, J. J. García and Y. Espidel, Reversible Adsorption of Carbon Dioxide on Amine Surface-Bonded Silica Gel, Inorg. Chim. Acta, 1995, 240(1), 183–189 CrossRef CAS.
- M. R. Mello, D. Phanon, G. Q. Silveira, P. L. Llewellyn and C. M. Ronconi, Amine-Modified MCM-41 Mesoporous Silica for Carbon Dioxide Capture, Microporous Mesoporous Mater., 2011, 143(1), 174–179 CrossRef CAS.
- X. Ma, X. Wang and C. Song, “Molecular Basket” Sorbents for Separation of CO2 and H2S from Various Gas Streams, J. Am. Chem. Soc., 2009, 131(16), 5777–5783 CrossRef CAS PubMed.
- E. R. Monazam, L. J. Shadle, D. C. Miller, H. W. Pennline, D. J. Fauth, J. S. Hoffman and M. L. Gray, Equilibrium and Kinetics Analysis of Carbon Dioxide Capture Using Immobilized Amine on a Mesoporous Silica, AIChE J., 2013, 59(3), 923–935 CrossRef CAS.
- Y. Yang, C. Y. Chuah and T.-H. Bae, Polyamine-Appended Porous Organic Polymers for Efficient Post-Combustion CO2 Capture, Chem. Eng. J., 2019, 358, 1227–1234 CrossRef CAS.
- W. Lu, J. P. Sculley, D. Yuan, R. Krishna, Z. Wei and H.-C. Zhou, Polyamine-Tethered Porous Polymer Networks for Carbon Dioxide Capture from Flue Gas, Angew. Chem., 2012, 124(30), 7598–7602 CrossRef.
- C. Kim, H. S. Cho, S. Chang, S. J. Cho and M. Choi, An Ethylenediamine-Grafted Y Zeolite: A Highly Regenerable Carbon Dioxide Adsorbent via Temperature Swing Adsorption without Urea Formation, Energy Environ. Sci., 2016, 9(5), 1803–1811 RSC.
- F. Su, C. Lu, S.-C. Kuo and W. Zeng, Adsorption of CO2 on Amine-Functionalized Y-Type Zeolites, Energy Fuels, 2010, 24(2), 1441–1448 CrossRef CAS.
- A. Demessence, D. M. D'Alessandro, M. L. Foo and J. R. Long, Strong CO2 Binding in a Water-Stable, Triazolate-Bridged Metal–Organic Framework Functionalized with Ethylenediamine, J. Am. Chem. Soc., 2009, 131(25), 8784–8786 CrossRef CAS PubMed.
- T. M. McDonald, D. M. D'Alessandro, R. Krishna and J. R. Long, Enhanced Carbon Dioxide Capture upon Incorporation of N,N′-Dimethylethylenediamine in the Metal–Organic Framework CuBTTri, Chem. Sci., 2011, 2(10), 2022–2028 RSC.
- S. Choi, T. Watanabe, T.-H. Bae, D. S. Sholl and C. W. Jones, Modification of the Mg/DOBDC MOF with Amines to Enhance CO2 Adsorption from Ultradilute Gases, J. Phys. Chem. Lett., 2012, 3(9), 1136–1141 CrossRef CAS PubMed.
- P.-Q. Liao, X.-W. Chen, S.-Y. Liu, X.-Y. Li, Y.-T. Xu, M. Tang, Z. Rui, H. Ji, J.-P. Zhang and X.-M. Chen, Putting an Ultrahigh Concentration of Amine Groups into a Metal–Organic Framework for CO2 Capture at Low Pressures, Chem. Sci., 2016, 7(10), 6528–6533 RSC.
- L. A. Darunte, A. D. Oetomo, K. S. Walton, D. S. Sholl and C. W. Jones, Direct Air Capture of CO2 Using Amine Functionalized MIL-101(Cr), ACS Sustainable Chem. Eng., 2016, 4(10), 5761–5768 CrossRef CAS.
- Z. Wang and S. M. Cohen, Postsynthetic Covalent Modification of a Neutral Metal−Organic Framework, J. Am. Chem. Soc., 2007, 129(41), 12368–12369 CrossRef CAS PubMed.
- H.-L. Jiang, D. Feng, T.-F. Liu, J.-R. Li and H.-C. Zhou, Pore Surface Engineering with Controlled Loadings of Functional Groups via Click Chemistry in Highly Stable Metal–Organic Frameworks, J. Am. Chem. Soc., 2012, 134(36), 14690–14693 CrossRef CAS PubMed.
- J. Liu, Y. Wang, A. I. Benin, P. Jakubczak, R. R. Willis and M. D. LeVan, CO2/H2O Adsorption Equilibrium and Rates on Metal−Organic Frameworks: HKUST-1 and Ni/DOBDC, Langmuir, 2010, 26(17), 14301–14307 CrossRef CAS PubMed.
- T. M. McDonald, W. R. Lee, J. A. Mason, B. M. Wiers, C. S. Hong and J. R. Long, Capture of Carbon Dioxide from Air and Flue Gas in the Alkylamine-Appended Metal–Organic Framework mmen-Mg2(dobpdc), J. Am. Chem. Soc., 2012, 134(16), 7056–7065 CrossRef CAS PubMed.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocella, F. Giordanino, S. O. Odoh and W. S. Drisdell, et al., Cooperative Insertion of CO2 in Diamine-Appended Metal-Organic Frameworks, Nature, 2015, 519(7543), 303–308 CrossRef CAS PubMed.
- R. L. Siegelman, T. M. McDonald, M. I. Gonzalez, J. D. Martell, P. J. Milner, J. A. Mason, A. H. Berger, A. S. Bhown and J. R. Long, Controlling Cooperative CO2 Adsorption in Diamine-Appended Mg2(dobpdc) Metal–Organic Frameworks, J. Am. Chem. Soc., 2017, 139(30), 10526–10538 CrossRef CAS PubMed.
- P. J. Milner, R. L. Siegelman, A. C. Forse, M. I. Gonzalez, T. Runčevski, J. D. Martell, J. A. Reimer and J. R. Long, A Diaminopropane-Appended Metal–Organic Framework Enabling Efficient CO2 Capture from Coal Flue Gas via a Mixed Adsorption Mechanism, J. Am. Chem. Soc., 2017, 139(38), 13541–13553 CrossRef CAS PubMed.
- P. J. Milner, J. D. Martell, R. L. Siegelman, D. Gygi, S. C. Weston and J. R. Long, Overcoming Double-Step CO2 Adsorption and Minimizing Water Co-Adsorption in Bulky Diamine-Appended Variants of Mg2(dobpdc), Chem. Sci., 2018, 9(1), 160–174 RSC.
- W. R. Lee, S. Y. Hwang, D. W. Ryu, K. S. Lim, S. S. Han, D. Moon, J. Choi and C. S. Hong, Diamine-Functionalized Metal–Organic Framework: Exceptionally High CO2 Capacities from Ambient Air and Flue Gas, Ultrafast CO2 Uptake Rate, and Adsorption Mechanism, Energy Environ. Sci., 2014, 7(2), 744–751 RSC.
- W. R. Lee, H. Jo, L.-M. Yang, H. Lee, D. W. Ryu, K. S. Lim, J. H. Song, D. Y. Min, S. S. Han and J. G. Seo, et al., Exceptional CO2 Working Capacity in a Heterodiamine-Grafted Metal–Organic Framework, Chem. Sci., 2015, 6(7), 3697–3705 RSC.
- H. Jo, W. R. Lee, N. W. Kim, H. Jung, K. S. Lim, J. E. Kim, D. W. Kang, H. Lee, V. Hiremath and J. G. Seo, et al., Fine-Tuning of the Carbon Dioxide Capture Capability of Diamine-Grafted Metal–Organic Framework Adsorbents Through Amine Functionalization, ChemSusChem, 2017, 10(3), 541–550 CrossRef CAS.
- A. Heydari-Gorji and A. Sayari, CO2 Capture on Polyethylenimine-Impregnated Hydrophobic Mesoporous Silica: Experimental and Kinetic Modeling, Chem. Eng. J., 2011, 173(1), 72–79 CrossRef CAS.
- A. D. Ebner, M. L. Gray, N. G. Chisholm, Q. T. Black, D. D. Mumford, M. A. Nicholson and J. A. Ritter, Suitability of a Solid Amine Sorbent for CO2 Capture by Pressure Swing Adsorption, Ind. Eng. Chem. Res., 2011, 50(9), 5634–5641 CrossRef CAS.
- E. R. Monazam, L. J. Shadle and R. Siriwardane, Equilibrium and Absorption Kinetics of Carbon Dioxide by Solid Supported Amine Sorbent, AIChE J., 2011, 57(11), 3153–3159 CrossRef CAS.
- J. Wang, L. A. Stevens, T. C. Drage and J. Wood, Preparation and CO2 Adsorption of Amine Modified Mg–Al LDH via Exfoliation Route, Chem. Eng. Sci., 2012, 68(1), 424–431 CrossRef CAS.
- E. J. Granite and H. W. Pennline, Photochemical Removal of Mercury from Flue Gas, Ind. Eng. Chem. Res., 2002, 41(22), 5470–5476 CrossRef CAS.
- Q. Liu, J. Shi, S. Zheng, M. Tao, Y. He and Y. Shi, Kinetics Studies of CO2 Adsorption/Desorption on Amine-Functionalized Multiwalled Carbon Nanotubes, Ind. Eng. Chem. Res., 2014, 53(29), 11677–11683 CrossRef CAS.
- R. Serna-Guerrero and A. Sayari, Modeling Adsorption of CO2 on Amine-Functionalized Mesoporous Silica. 2: Kinetics and Breakthrough Curves, Chem. Eng. J., 2010, 161(1), 182–190 CrossRef CAS.
- J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Evaluating Metal–Organic Frameworks for Post-Combustion Carbon Dioxide Capture via Temperature Swing Adsorption, Energy Environ. Sci., 2011, 4(8), 3030–3040 RSC.
- M. Quaranta, T. Gehring, B. Odell, J. M. Brown and D. G. Blackmond, Unusual Inverse Temperature Dependence on Reaction Rate in the Asymmetric Autocatalytic Alkylation of Pyrimidyl Aldehydes, J. Am. Chem. Soc., 2010, 132(43), 15104–15107 CrossRef CAS PubMed.
- S. P. Mathew, M. Klussmann, H. Iwamura, J. Wells, H. David, A. Armstrong and D. G. Blackmond, A Mechanistic Rationalization of Unusual Kinetic Behavior in Proline-Mediated C–O and C–N Bond-Forming Reactions, Chem. Commun., 2006, 41, 4291–4293 RSC.
- L. A. Darunte, T. Sen, C. Bhawanani, K. S. Walton, D. S. Sholl, M. J. Realff and C. W. Jones, Moving Beyond Adsorption Capacity in Design of Adsorbents for CO2 Capture from Ultradilute Feeds: Kinetics of CO2 Adsorption in Materials with Stepped Isotherms, Ind. Eng. Chem. Res., 2019, 58(1), 366–377 CrossRef CAS.
- M. Avrami, Kinetics of Phase Change. I General Theory, J. Chem. Phys., 1939, 7(12), 1103–1112 CrossRef CAS.
- G. Ruitenberg, A. K. Petford-Long and R. C. Doole, Determination of the Isothermal Nucleation and Growth Parameters for the Crystallization of Thin Ge2Sb2Te5 Films, J. Appl. Phys., 2002, 92(6), 3116–3123 CrossRef CAS.
- S. Ranganathan and M. Von Heimendahl, The Three Activation Energies with Isothermal Transformations: Applications to Metallic Glasses, J. Mater. Sci., 1981, 16(9), 2401–2404 CrossRef CAS.
- M. Oliveberg, Y. J. Tan and A. R. Fersht, Negative Activation Enthalpies in the Kinetics of Protein Folding, Proc. Natl. Acad. Sci. U. S. A., 1995, 92(19), 8926 CrossRef CAS PubMed.
- R. A. Moss, L. Wang, M. Zhang, C. Skalit and K. Krogh-Jespersen, Enthalpy versus Entropy in Chlorocarbene/Alkene Addition Reactions, J. Am. Chem. Soc., 2008, 130(17), 5634–5635 CrossRef CAS.
- K. N. Houk, N. G. Rondan and J. Mareda, Theoretical Studies of Halocarbene Cycloaddition Selectivities: A New Interpretation of Negative Activation Energies and Entropy Control of Selectivity, Tetrahedron, 1985, 41(8), 1555–1563 CrossRef CAS.
- M. Mozurkewich and S. W. Benson, Negative Activation Energies and Curved Arrhenius Plots. 1. Theory of Reactions over Potential Wells, J. Phys. Chem., 1984, 88(25), 6429–6435 CrossRef CAS.
- J. A. Biosca, F. Travers and T. E. Barman, A Jump in an Arrhenius Plot Can Be the Consequence of a Phase Transition: The Binding of ATP to Myosin Subfragment 1, FEBS Lett., 1983, 153(1), 217–220 CrossRef CAS.
- D. G. Truhlar and A. Kohen, Convex Arrhenius Plots and Their Interpretation, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(3), 848–851 CrossRef CAS.
- A. C. Forse, P. J. Milner, J.-H. Lee, H. N. Redfearn, J. Oktawiec, R. L. Siegelman, J. D. Martell, B. Dinakar, L. B. Porter-Zasada and M. I. Gonzalez, Elucidating CO2 Chemisorption in Diamine-Appended Metal–Organic Frameworks, J. Am. Chem. Soc., 2018, 140(51), 18016–18031 CrossRef CAS.
- I. Luz, M. Soukri and M. Lail, Synthesis of Fluidized CO2 Sorbents Based on Diamine Coordinated to Metal–Organic Frameworks by Direct Conversion of Metal Oxides Supported on Mesoporous Silica, Chem.–Eur. J., 2018, 24(42), 10612–10616 CrossRef CAS.
- W. Liang, P. M. Bhatt, A. Shkurenko, K. Adil, G. Mouchaham, H. Aggarwal, A. Mallick, A. Jamal, Y. Belmabkhout and M. Eddaoudi, A Tailor-Made Interpenetrated MOF with Exceptional Carbon-Capture Performance from Flue Gas, Chem, 2019, 5(4), 950–963 CAS.
- W. R. Lee, J. E. Kim, S. J. Lee, M. Kang, D. W. Kang, H. Y. Lee, V. Hiremath, J. G. Seo, H. Jin and D. Moon, et al., Diamine-Functionalization of a Metal–Organic Framework Adsorbent for Superb Carbon Dioxide Adsorption and Desorption Properties, ChemSusChem, 2018, 11(10), 1694–1707 CrossRef CAS.
- J. D. Martell, L. B. Porter-Zasada, A. C. Forse, R. L. Siegelman, M. I. Gonzalez, J. Oktawiec, T. Runčevski, J. Xu, M. Srebro-Hooper and P. J. Milner, et al., Enantioselective Recognition of Ammonium Carbamates in a Chiral Metal–Organic Framework, J. Am. Chem. Soc., 2017, 139(44), 16000–16012 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01087a |
| ‡ These authors contributed equally to this work. |
| § Present address: University of Wisconsin–Madison, Department of Chemistry, 1101 University Avenue, Madison, WI 53706, United States. |
| ¶ Present address: 328 Baker Laboratory, Cornell University, Ithaca, NY 14853, United States. |
| || Present address: DuPont de Nemours, Inc. 200 Powder Mill Rd, Wilmington, DE 19803, United States. |
| This journal is © The Royal Society of Chemistry 2020 |