Multiple magnetic relaxation pathways in T-shaped N-heterocyclic carbene-supported Fe(I) single-ion magnets†
Yin-Shan
Meng
ac,
Zhengwu
Ouyang
b,
Mu-Wen
Yang
 c,
Yi-Quan
Zhang
c,
Yi-Quan
Zhang
 d,
Liang
Deng
d,
Liang
Deng
 *b,
Bing-Wu
Wang
*b,
Bing-Wu
Wang
 *c and
Song
Gao
*c and
Song
Gao
 *c
*c
aState Key Laboratory of Fine Chemicals, Dalian University of Technology, 2 Linggong Rd., Dalian 116024, P. R. China
bState Key Laboratory of Organometallic Chemistry, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, 345 Lingling Road, Shanghai 200032, P. R. China. E-mail: deng@sioc.ac.cn
cBeijing National Laboratory for Molecular Sciences, Beijing Key Laboratory for Magnetoelectric Materials and Devices, Peking University, Beijing 100871, 100871 P. R. China. E-mail: wangbw@pku.edu.cn; gaosong@pku.edu.cn
dJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, P. R. China
First published on 7th March 2019
Abstract
The magnetic properties of the T-shaped three-coordinate complexes, namely, [(sIMes)2Fe(THF)][BPh4] (1, sIMes: 1,3-bis(2′,4′,6′-trimethylphenyl)-imidazolin-2-ylidene) and [(cyIMes)2Fe(THF)][BPh4] (2, cyIMes: 1,3-bis(2′,4′,6′-diethylphenyl)-4,5-(CH2)4-imidazol-2-ylidene) and quasi-linear two-coordinate complexes [(sIDep)2Fe][BArF4] (3, sIDep: 1,3-bis(2′,6′-diethylphenyl)-imidazolin-2-ylidene; ArF: 3,5-di(trifluoromethyl)phenyl) and [(cyIDep)2Fe][BArF4] (4, cyIDep: 1,3-bis(2′,6′-diethylphenyl)-4,5-(CH2)4-imidazol-2-ylidene) were studied. Magnetic characterization indicated the unquenched first-order angular momentum and large zero-field splitting. AC susceptibility measurements showed that the T-shaped three-coordinate Fe(I) complexes exhibited field-induced relaxation of magnetization. The Direct, resonant quantum tunneling, and Raman processes were observed and contributed to the determination of the overall magnetic relaxations.
Introduction
Single-molecule magnets (SMMs) are one type of discrete molecules that can show slow magnetic relaxation and/or magnetic hysteresis under a blocking temperature (TB).1,2 The magnetic bistability of SMMs has triggered increasingly active research in the field of molecular magnetism and materials chemistry. This remarkable physical property also makes SMMs potential materials for high-density information storage at the pure molecular level.3–5 To achieve this goal, one needs to enhance the blocking temperature and spin reversal barrier so as to meet the applicable demand. For transition metal-based SMMs, the spin reversal barrier has a great impact on the relaxation of the magnetization from the +Ms to −Ms state and has been previously rationalized by Ueff = |D|S2 for integer spin systems (Ueff = |D|(S2 − 1/4) for half-integer spin systems), where D is the zero-field splitting (ZFS) parameter and S is the ground spin number.1 Considerable efforts have been put forward in understanding the factors that influence the key parameters, especially in enhancing the ground spin number.6,7 However, the Ueff values are still within tens of wavenumbers despite the fact that the ground spin numbers have reached a huge value.8,9 It was rationalized that the ZFS parameter D is approximately proportional to the inverse of S2, restricting the attempts of increasing Ueff by solely increasing the S value.10,11 Researchers began to pay attention to mononuclear SMMs after the discovery of the lanthanide-based single-ion magnet (SIM) TbPc2 reported by Ishikawa et al.12 This is because SIMs represent a simple system in understanding the factors that influence magnetic anisotropy and magnetic relaxation. In the past decade, enormous numbers of SIMs, especially those based on 4f-block ions, have been reported, some of which exhibit ultrahigh energy barriers and blocking temperatures.7,13–19 Compared to the lanthanide-based SIMs, the reported 3d-block SIMs20–23 appear to be less competitive due to the smaller ground spin number and quenched first-order orbital momentum. For these transition metal-based SIMs, the orbital angular momentum originates from the contributions from the excited states (second-order effect), and the spin reversal barrier is related to the zero-field splitting (ZFS) parameter and ground spin number. This status did not change until Long and co-workers reported the two-coordinate Fe(I) complex that exhibited Ueff of 226 cm−1 and typical hysteresis.24 More recently, Gao and co-workers introduced M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N multiple bonds into the Co(II) systems, reaching a record Ueff value of 413 cm−1 and TB of 9.5 K under a field-sweeping rate of 700 Oe s−1.25 These remarkable achievements suggest that 3d-block compounds can also behave as high-performance SIMs and would be as good as 4f-based SIMs under a suitable ligand field. Further joint experiment-theory studies demonstrated that in the one-spin carrier systems that contain 3d-block ions, maintaining the first-order orbital angular momentum is essential to achieve large magnetic anisotropy comparable to that of 4f-ion-based compounds.26,27 In the case of unquenched first-order orbital momentum, the energy splitting of 3d-block SIMs can be best described by the total angular momentum J. The conservation of the first-order orbital angular momentum can be controlled by the chemical modification of the coordination environment such as the coordination number, atoms and geometry. In particular, the low-coordinate species (coordination number less than 4) among the big family of 3d-block mononuclear compounds were brought to attention since they favored degenerate ground state orbitals, which in turn resulted in the minimal quenching of the orbital angular momentum and thereby the first-order spin–orbit coupling. It has been demonstrated that the first-order orbital angular momentum is almost quenched in the five- and six-coordinate complexes,28 where the observed ZFS originates from second-order spin–orbit coupling.20,21 Besides, the novel structures and chemical properties of the low-coordinate 3d complexes have also stimulated the synthetic study in small-molecule activation and catalysis.29–33
N multiple bonds into the Co(II) systems, reaching a record Ueff value of 413 cm−1 and TB of 9.5 K under a field-sweeping rate of 700 Oe s−1.25 These remarkable achievements suggest that 3d-block compounds can also behave as high-performance SIMs and would be as good as 4f-based SIMs under a suitable ligand field. Further joint experiment-theory studies demonstrated that in the one-spin carrier systems that contain 3d-block ions, maintaining the first-order orbital angular momentum is essential to achieve large magnetic anisotropy comparable to that of 4f-ion-based compounds.26,27 In the case of unquenched first-order orbital momentum, the energy splitting of 3d-block SIMs can be best described by the total angular momentum J. The conservation of the first-order orbital angular momentum can be controlled by the chemical modification of the coordination environment such as the coordination number, atoms and geometry. In particular, the low-coordinate species (coordination number less than 4) among the big family of 3d-block mononuclear compounds were brought to attention since they favored degenerate ground state orbitals, which in turn resulted in the minimal quenching of the orbital angular momentum and thereby the first-order spin–orbit coupling. It has been demonstrated that the first-order orbital angular momentum is almost quenched in the five- and six-coordinate complexes,28 where the observed ZFS originates from second-order spin–orbit coupling.20,21 Besides, the novel structures and chemical properties of the low-coordinate 3d complexes have also stimulated the synthetic study in small-molecule activation and catalysis.29–33
Inspired by the work of two-coordinate Fe(I) SIMs [K(crypt-222)][Fe(C(SiMe3)3)2],24 we turned our interests to the low-coordinate transition metal complexes. Fe(I)-Based compounds were chosen since the half-integer spin character conserves the degeneracy of the ground state according to the Kramers Theory,34 thus minimizing the quantum tunneling of magnetization (QTM) within ground doublet under zero field. The stabilization of low-coordinate transition complexes is challenging and necessitates bulky ligands. For low-coordinate Fe(I) complexes, the bidentate β-diketiminate ligands bearing large N-aryl substituents were proved to be valid in stabilizing the Fe(I) ions.35,36 In addition, bulky ligands such as [(tBu2PCH2SiMe2)2N]−,37 [(Dipp)2C(cis-2,6-Me2NC5H8)]− (Dipp = 2,6-diisopropylphenyl),38 [N(SiMe3)(Dipp)]−, [N(SiMe3)2]−, imidazol-2-ylidenes (N-heterocyclic carbene) and cyclic alkylaminocarbenes (cAACs)39,40 were also applied in obtaining the three- and two-coordinate Fe(I) complexes. Compared to the synthetic works, the magnetic studies about their single-molecule magnet properties are still scarce. To date, only two of the two-coordinate and one of the three-coordinate Fe(I) complexes have been reported for showing SIM properties.41,42 In this work, we demonstrated an interesting example, where the three-coordinate [(cAAC)2FeCl] complex exhibited slow magnetic relaxation under 500 Oe dc field, while this was not shown by its two-coordinate counterpart [(cAAC)2Fe][B(C6F5)4]. We proposed the multiple bonding character, especially π bonding, to be one possible reason. Previously, we have utilized NHC as supporting ligands and obtained a series of low-coordinate Fe complexes with the valence states ranging from I to IV.33,43 Unlike the cAAC ligands with good π-accepting ability, N-heterocyclic carbenes are good σ-donating ligands with relatively weak π-accepting ability.44–47 We have also investigated the influence of the coordination number on the magnetic properties of the NHC-supported Fe(I) complexes. Herein, using the NHC ligands, the three-coordinate Fe(I) complexes [(sIMes)2Fe(THF)][BPh4] (1, sIMes: 1,3-bis(2′,4′,6′-trimethylphenyl)-imidazolin-2-ylidene) and [(cyIMes)2Fe(THF)][BPh4] (2, cyIMes: 1,3-bis(2′,4′,6′-diethylphenyl)-4,5-(CH2)4-imidazol-2-ylidene) and two-coordinate complexes [(sIDep)2Fe][BArF4] (3, sIDep: 1,3-bis(2′,6′-diethylphenyl)-imidazolin-2-ylidene; ArF: 3,5-di(trifluoromethyl)phenyl) and [(cyIDep)2Fe][BArF4] (4, cyIDep: 1,3-bis(2′,6′-diethylphenyl)-4,5-(CH2)4-imidazol-2-ylidene) were prepared. The structural and magnetic properties were characterized and discussed in detail (Fig. 1).
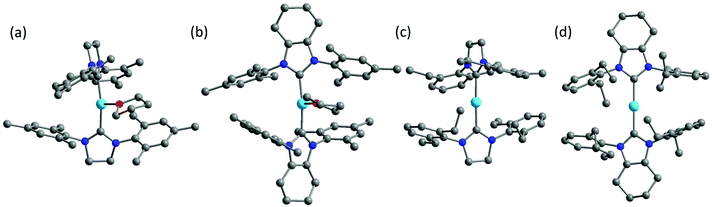 | ||
| Fig. 1 Molecular structures of 1–4 (a–b). The co-crystalized solvent molecules, counter ions and hydrogens were omitted for clarity. Color code: C, grey; N, blue; O, red; Fe, sky blue. | ||
Results and discussion
Structural characterization
The syntheses of the three-coordinate NHC–Fe(I) complexes were performed using the corresponding NHC ligands and Fe(II) salts by a reduction reaction with excess KC8 in a THF solution. The two-coordinate NHC–Fe(I) species were obtained via the salt elimination reaction. The complexes were all air- and moisture-sensitive but could be well maintained under an inert atmosphere in the crystalline form. Their valence and spin states were characterized by 57Fe Mössbauer spectroscopy, indicating the high-spin character of Fe(I) (S = 3/2).48 X-ray diffraction study revealed that complexes 1, 2 and 4 crystallized in the monoclinic space group except for complex 3, which crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table S1†). The selected bond lengths and angles are listed in Table 1. The three-coordinate 1 and 2 possessed slightly distorted T-shaped structures. Complex 3 and 4 exhibited the rare two-coordinate homoleptic NHC-supported Fe(I) structures with quasi-linear alignment of the C–Fe–C core. The Fe–C average bond lengths were nearly identical for them (from 1.972(4) Å to 2.000(6) Å). Complexes 1 and 2 presented larger angles of C–Fe–C (169.1(1)° for 1 and 164.5(1)° for 2) due to the additionally coordinated THF molecule. Another significant difference lies in the dihedral angle, α, formed by the imidazole planes. It is worth noting that although 1 and 2 exhibited the same IMes moieties around the Fe(I) center, they possessed different dihedral angles of 77.8(3)° and 55.9(3)°, respectively. Further structural comparison indicated that the interactions between the methyl groups on the wingtip and Fe(I) were almost the same. These results suggest that the dihedral angle is dominated by the crystal packing interaction. This difference is more obvious when we refer to 3 (74.0(3)°) and 4 (14.3(3)°). The nearest intermolecular Fe⋯Fe distances were all above 10 Å, suggesting that the intermolecular interaction would be considerably weak.
(Table S1†). The selected bond lengths and angles are listed in Table 1. The three-coordinate 1 and 2 possessed slightly distorted T-shaped structures. Complex 3 and 4 exhibited the rare two-coordinate homoleptic NHC-supported Fe(I) structures with quasi-linear alignment of the C–Fe–C core. The Fe–C average bond lengths were nearly identical for them (from 1.972(4) Å to 2.000(6) Å). Complexes 1 and 2 presented larger angles of C–Fe–C (169.1(1)° for 1 and 164.5(1)° for 2) due to the additionally coordinated THF molecule. Another significant difference lies in the dihedral angle, α, formed by the imidazole planes. It is worth noting that although 1 and 2 exhibited the same IMes moieties around the Fe(I) center, they possessed different dihedral angles of 77.8(3)° and 55.9(3)°, respectively. Further structural comparison indicated that the interactions between the methyl groups on the wingtip and Fe(I) were almost the same. These results suggest that the dihedral angle is dominated by the crystal packing interaction. This difference is more obvious when we refer to 3 (74.0(3)°) and 4 (14.3(3)°). The nearest intermolecular Fe⋯Fe distances were all above 10 Å, suggesting that the intermolecular interaction would be considerably weak.
| Complex | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a Dihedral angle between the two planes of the five-membered rings of the carbene ligands. b The shortest Co⋯C distance between Fe(I) center and the carbon atoms on the N-wingtip. c Nearest distance between adjacent Fe(I) ions. | ||||
| Fe–C | 1.975(3)–1.984(4) | 1.990(3)–1.992(3) | 1.972(4)–1.988(4) | 1.996(6)–2.000(6) |
| Fe–O | 2.149(3) | 2.173(2) | — | — |
| C–Fe–C | 169.1(1) | 164.5(1) | 175.8(2) | 178.0(2)–178.9(2) |
| C–Fe–O | 94.7(1)–102.1(1) | 97.7(1)–97.9(1) | — | — |
| α | 77.8(3) | 55.9(3) | 74.0(3) | 14.3(3) |
| Fe⋯Cb | 3.32(1) | 3.34(1) | 3.19(1) | 3.34(1) |
| Fe⋯Fec | 13.69(1) | 10.93(1) | 12.52(1) | 12.52(1) |
Magnetic analysis
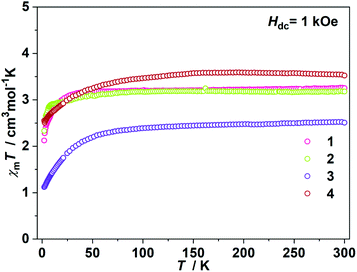
The direct current (dc) magnetic susceptibilities were first collected from 2 K to 300 K under 1 kOe applied field (Fig. 2). At an ambient temperature, the χmT values for 1–4 were 3.25, 3.18, 3.52 and 2.51 cm3 mol−1 K, respectively, which were comparable to those of the reported two- and three-coordinate Fe(I) complexes. The χmT values were all higher than the spin-only value for S = 3/2 (χmT: 1.875 cm3 mol−1 K). Upon cooling, the χmT values for 1 and 2 remained nearly constant from 300 K to 50 K. For complex 1, the χmT values declined gradually to 2.33 cm3 mol−1 K. For complex 2, the χmT values underwent rapid decrease below 10 K. The temperature dependences of the magnetic susceptibilities for 3 and 4 were very different. The χmT value of 4 was much larger than that of 3, indicating more first-order orbital angular momentum contribution. At 2 K, the variable-field-variable-temperature magnetization plots of 1–4 represent non-superimposition character and are far from saturation, demonstrating significant magnetic anisotropy (Fig. S1†). Attempts using the following spin Hamiltonian H = μBg·B·S + D[Sz2 − S(S + 1)/3] + E[Sx2 − Sy2] to simultaneously fit the susceptibility and magnetization data were unsuccessful due to the significant first-order angular momentum contribution.Alternating current (ac) susceptibility measurements revealed that complexes 1 and 2 showed weak frequency dependence of ac susceptibilities (Fig. S2†). No peaks of out-of-phase signals were observed possibly due to the fast quantum tunneling of magnetization within the ground state. As an applied field can suppress the QTM process, an optimized dc field of 2 kOe was applied. For complex 1, both the in-phase (χ′m) and out-of-phase (χ′′m) signals exhibited strong frequency and temperature dependence (Fig. 3a and b). The χ′′m peaks for 100 Hz and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz were 2.5 K and 6 K, respectively. The frequency-dependent ac susceptibilities were plotted as an Argand diagram and fitted with the generalized Debye model (Table S2, Fig. S3a†). Below 3 K, the distribution of relaxation times α′ (0.19–0.11) was larger than that from 3.5 K (0.07) to 6 K (0.03), suggesting that there might be multiple relaxation pathways for the spin reversal process. Above 4.5 K, the ln
000 Hz were 2.5 K and 6 K, respectively. The frequency-dependent ac susceptibilities were plotted as an Argand diagram and fitted with the generalized Debye model (Table S2, Fig. S3a†). Below 3 K, the distribution of relaxation times α′ (0.19–0.11) was larger than that from 3.5 K (0.07) to 6 K (0.03), suggesting that there might be multiple relaxation pathways for the spin reversal process. Above 4.5 K, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus 1/T plots show linearity, which can be fitted by the Arrhenius law ln
τ versus 1/T plots show linearity, which can be fitted by the Arrhenius law ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ = ln
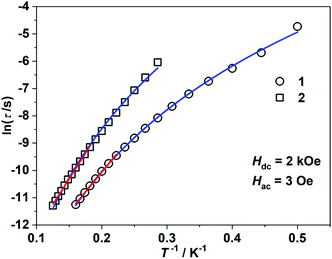
τ = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ0 + Ueff/(kBT) (τ0: pre-exponential factor). The fitted Ueff and τ0 values are 29(3) K and 1.29(0.03) × 10−7 s, respectively, falling in the typical range for the field-induced 3d-SIMs (Fig. 4).20,21 In consideration of the much smaller Ueff value than the value of 2|D| and the curvature of ln
τ0 + Ueff/(kBT) (τ0: pre-exponential factor). The fitted Ueff and τ0 values are 29(3) K and 1.29(0.03) × 10−7 s, respectively, falling in the typical range for the field-induced 3d-SIMs (Fig. 4).20,21 In consideration of the much smaller Ueff value than the value of 2|D| and the curvature of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus 1/T plots at a low-temperature region, the spin–phonon relaxation is not the Orbach process; some other relaxation processes should play a part. In addition, the ln
τ versus 1/T plots at a low-temperature region, the spin–phonon relaxation is not the Orbach process; some other relaxation processes should play a part. In addition, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus 1/T plots can be well fitted by applying the power law ln
τ versus 1/T plots can be well fitted by applying the power law ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ = ln(1/C) + n
τ = ln(1/C) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/T). The obtained n value is 5.6(0.04), suggesting that the second-order Raman process should be responsible for magnetization relaxation. The second-order Raman process involves one phonon causing a virtual transition from one of the ground states to an excited state, followed by another virtual transition induced by the second phonon, due to which the magnetic ion returns from an excited state to the other ground state.49,50 Notably, it involves a much weaker coupling mechanism than that for the first-order one. For complex 2, the out-of-phase components (χ′′m) showed typical frequency dependence in the temperature range from 2 K to 8 K (Fig. 3c and d). The linear region of ln
ln(1/T). The obtained n value is 5.6(0.04), suggesting that the second-order Raman process should be responsible for magnetization relaxation. The second-order Raman process involves one phonon causing a virtual transition from one of the ground states to an excited state, followed by another virtual transition induced by the second phonon, due to which the magnetic ion returns from an excited state to the other ground state.49,50 Notably, it involves a much weaker coupling mechanism than that for the first-order one. For complex 2, the out-of-phase components (χ′′m) showed typical frequency dependence in the temperature range from 2 K to 8 K (Fig. 3c and d). The linear region of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus 1/T plots above 5.5 K was fitted by the Arrhenius law, giving Ueff of 38(5) K and τ0 of 1.15(0.05) × 10−7 s. The power law fitting provided the n value of 6.23(0.07) with C of 0.21(0.04) s−1 K−n. In terms of the magnetic relaxation behaviors, complexes 1 and 2 were similar to the reported three-coordinate [(cAAC)2FeCl].42 The under-barrier behavior suggested that the relaxation process was not Orbach dominated. For two-coordinate 3 and 4, both of them exhibited no frequency dependence of χ′m and χ′′m components either in the absence of or under the applied dc field (Fig. S4 and S5†).
τ versus 1/T plots above 5.5 K was fitted by the Arrhenius law, giving Ueff of 38(5) K and τ0 of 1.15(0.05) × 10−7 s. The power law fitting provided the n value of 6.23(0.07) with C of 0.21(0.04) s−1 K−n. In terms of the magnetic relaxation behaviors, complexes 1 and 2 were similar to the reported three-coordinate [(cAAC)2FeCl].42 The under-barrier behavior suggested that the relaxation process was not Orbach dominated. For two-coordinate 3 and 4, both of them exhibited no frequency dependence of χ′m and χ′′m components either in the absence of or under the applied dc field (Fig. S4 and S5†).
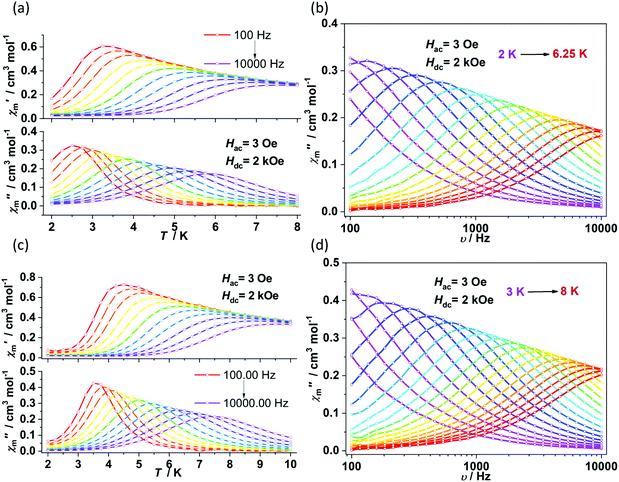 | ||
| Fig. 3 Temperature and frequency dependence of ac susceptibilities for 1 (a and b) and 2 (c and d) under 2 kOe dc field. | ||
To further investigate the multiple relaxation pathways in complexes 1 and 2, field-dependent ac susceptibilities were obtained at specified temperatures. As can be seen in Fig. 5a, the resonant peaks of χ′′m components move to a lower frequency region upon initially increasing the external field. Then, the resonant peaks move to a higher frequency region. The strong field dependence of the relaxation times indicates that there must be field-related relaxation pathways involved in the spin-phonon relaxations. For Kramers ions, the field-dependent relaxation processes include the Direct and QTM terms, which can be formalized as AH2T and B1/(1 + B2H2), respectively.51 The Direct process-determined relaxation rate is proportional to the square of the field, while the QTM rate slows down upon increasing the field. As a result, there would be a maximum of relaxation times due to their competition in the τ versus magnetic field profile. This is also consistent with the observation that the relaxation times reach a plateau under the applied field of 1–2 kOe for complex 1 (Fig. 5b and Fig. S6†). Therefore, eqn (1) was used to fit the field-dependent relaxation time plots, where the first, second and third terms represent the Direct process, QTM process and field-independent contributions from the Orbach and Raman processes, respectively.
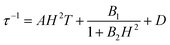 | (1) |
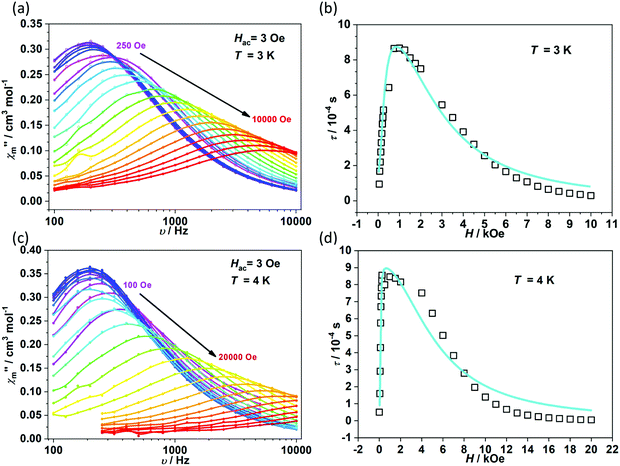 | ||
| Fig. 5 Field dependence of out-of-phase components (χ′′m) for 1 (a) and 2 (c). Field dependence of extracted relaxation times τ (b for 1 and d for 2). The sky blue colored solid lines represent the fitting using eqn (1). | ||
The τ versus field plots collected at 3 K and 4 K for complex 1 can be fitted with the listed parameters in Table 2, confirming that both QTM and Direct processes play a significant part. Complex 2 also exhibits multiple relaxation pathways in the measured temperature range (Fig. 5c and d; Fig. S7 and S8†). It can be seen that the coefficient A varies in a narrow range between 10−5 and 10−6 s−1 Oe−2 K−1 for both 1 and 2. The coefficients B1 and B2 show fluctuations over several orders. The multiple relaxation pathways are not uncommon in Non-Kramers systems, as reported in two-coordinate Fe(II) (S = 2) SIMs.52 However, it is rare to observe the Direct process in the Kramers systems as the transition element is largely cancelled in the ground Kramers doublet. The observed Direct process might be due to the mixing of the ground doublets and excited states, which opens the relaxation pathway under the applied dc field.
| Complex | Temperature (K) | D (s−1) | A (s−1 Oe−2 K−1) | B 1 (s−1) | B 2 (Oe−2) |
|---|---|---|---|---|---|
| a Contributions from field-independent relaxation processes. The values in bracket represent the standard errors. | |||||
| 1 | 3 | 973.7 (38.8) | 3.81 × 10−5 (3.4 × 10−6) | 5.51 × 103 (1.2 × 103) | 8.72 × 10−5 (2 × 10−5) |
| 4 | 5823 (105) | 6.90 × 10−5 (3.1 × 10−6) | 1.93 × 104 (3.4 × 103) | 2.56 × 10−4 (6.6 × 10−5) | |
| 2 | 3 | 36.8 (4.8) | 2.35 × 10−6 (6.3 × 10−7) | 2.97 × 105 (4.2 × 104) | 2.86 × 10−1 (1.4 × 10−1) |
| 4 | 1083 (50) | 9.46 × 10−6 (1.1 × 10−6) | 9.28 × 106 (8.6 × 106) | 1.50 (0.81) | |
| 5 | 4861 (182) | 1.69 × 10−5 (1.9 × 10−6) | 3.92 × 104 (4.9 × 10−4) | 2.21 × 10−3 (3.2 × 10−4) | |
For transition metal-based SIMs, it is supposed that low-coordinate, axially symmetric and weak ligand fields are preferred for conserving orbital angular momentum. It is interesting that although the three-coordinate complexes 1 and 2 bear lower axial symmetry than 3 and 4, the former complexes exhibit SIM property under an appropriate dc field. The introduction of an additional ligand, tetrahydrofuran, in 1 and 2 would reinforce the ligand field splitting, as also reflected in the calculated low-lying spin–orbit energy levels (Tables S4 and S5†). One can note that the energy separation between the ground and excited orbital states is only 1000 cm−1 and will have an influence largely on the calculated zero-field splitting (Tables S4 and S5†). However, it should be mentioned that the accurate result relies on fully evaluating the NHC–Fe(I) bond by taking more related orbitals into the ab initio calculations, which is beyond the ability of our current hardware. Concerning the specificity of the homoleptic C–Fe–C core and NHC–Fe(I) multiple bonds, we speculate that the dihedral angle plays the predominant role in determining the zero-field splitting. The detailed structural analysis revealed that there is no short contact between the wingtip groups and the central Fe(I) ion. Thus the rotation of NHC ligands along the Fe–C bond can occur freely in the solutions but is restricted in the solid state by the surrounding counter ions and other molecules. This is more obvious in complexes 3 and 4, for which the different dihedral angles lead to opposite D values (Tables S4 and S5†). Previous reports have also suggested that the change in the dihedral angle and the distortion from the specified geometry can change the magnitude and even the sign of the D value.53,54 Also, the π bonding nature would reduce the overall axial symmetry and introduce transverse components, thereby leading to the disappearance of SIM behavior.42
Conclusions
In summary, we reported the magnetic characterization of T-shaped three-coordinate NHC-supported Fe(I) complexes as well as the corresponding two-coordinate species. The dynamic magnetic study revealed that three-coordinate NHC–Fe(I) exhibited field-dependent relaxation of magnetization behavior. The relaxation involved multiple pathways including Direct, QTM and Raman processes. The two-coordinate NHC–Fe(I) complexes could not exhibit SIM behaviors under any applied fields. The change in the dihedral angle of the NHC planes drastically influenced the electronic structure and zero-field splitting, therefore leading to different magnetic behaviors. The ab initio calculations also reflected the change in the zero-field splitting parameter D of the four complexes. This study reveals that there is much more complexity for low-coordinate 3d-block single-ion magnets, and we still need further comprehensive investigation on this issue.Experimental section
The synthesis of air- and/or moisture-sensitive compounds was carried out in an Argon-filled glovebox. The solvents were dried in a solvent purification system, transferred under vacuum, and stored in the glovebox. Complexes 1, 3 and 4 were synthesized according to previously reported methods.48 Unless otherwise noted, all starting materials were commercially available and were used without further purification. Elemental analysis was performed by the Analytical Laboratory of Shanghai Institute of Organic Chemistry (CAS).2: The synthetic procedure of 2 was similar to that of compound 1. The cyIMes (688 mg, 2.5 mmol) was slowly added to the suspension of [Fe(tmeda)Cl2]2 (298 mg, 0.60 mmol) in THF (15 mL). The mixture was stirred for 2 h. After removal of the volatiles, THF (15 mL) was added to the residue and the mixture was stirred for several minutes. Potassium graphite (476 mg, 3.5 mmol) was then added to the suspension at room temperature. The color of the mixture turned into red-purple. The mixture was stirred for 4 min and then quickly filtered through diatomaceous earth. NaBPh4 (402 mg, 1.2 mmol) was added to the filtrate immediately. The mixture was stirred for 30 min and then filtered through diatomaceous earth to afford an orange-red solution. After removal of the volatiles, the residue was washed sequentially with n-hexane (15 mL) and Et2O (15 mL) and then dissolved in THF/Et2O (15 mL, 4/1) to afford an orange-red solution. After the solution was allowed to stand at −25 °C for several days to facilitate recrystallization, 2 was obtained as a red crystalline solid (544 mg).
X-ray crystallography
A single crystal of 2 was coated with mineral oil and mounted on a Bruker APEX CCD-based diffractometer equipped with an Oxford low-temperature apparatus. Cell parameters were retrieved with the SMART software and refined using SAINT software on all reflections. Data integration was performed with SAINT, which corrects for Lorentz polarization and decay. Absorption correction was applied using SADABS.55 Space group was assigned unambiguously by the analysis of symmetry and systematic absences determined by XPREP. The structure was solved and refined using SHELXTL.56 Metal and first coordination sphere atoms were located from direct-methods E-maps. Non-hydrogen atoms were found in alternating difference Fourier synthesis and least-squares refinement cycles and during final cycles were refined anisotropically. CCDC 1882118 contains the supplementary crystallographic data for 2. CCDC 1426589, 1426588 and 1426587† contain the supplementary crystallographic data for 1, 3 and 4, respectively, which can be found in our previous work.48Magnetic measurement
Direct current susceptibility experiment was performed on a Quantum Design MPMS XL-5 SQUID magnetometer on a polycrystalline sample. Alternating current susceptibility measurement with frequencies ranging from 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz was performed on Quantum Design PPMS on a polycrystalline sample. All dc susceptibilities were corrected for diamagnetic contribution from the sample holder, N-grease and diamagnetic contributions from the molecule using Pascal's constants.
000 Hz was performed on Quantum Design PPMS on a polycrystalline sample. All dc susceptibilities were corrected for diamagnetic contribution from the sample holder, N-grease and diamagnetic contributions from the molecule using Pascal's constants.
Theoretical calculations
Orca 3.03 calculations57 were performed with the difference-dedicated configuration interaction (DDCI3)58 method. The spin–orbit coupling (SOC) operator used was the efficient implementation of the multicenter spin–orbit mean-field (SOMF) concept developed by Heß et al.59 The spin–spin contributions (SSC) to the D values were also included although they are very small for our complex. The first CASSCF calculation with seven 3d electrons in the ten Fe(I) 3d-based orbitals (CAS(7, 10)) was performed on complexes 1–4 and then, we carried out DDCI358 on top of the CAS(7, 10) reference states. All calculations were performed with triple-ζ with one polarization function TZVP60 basis set for all atoms. Tight convergence criteria were used in order to ensure that the results are well converged with respect to technical parameters. Complete-active-space self-consistent field (CASSCF) using MOLCAS 7.8 program package was performed on the model structures of complexes 1–4.61 For the first CASSCF calculation, the basis sets for all atoms are atomic natural orbitals from the MOLCAS ANO-RCC library: ANO-RCC-VTZP for magnetic center ion FeI; VTZ for close C, N, O and atoms; VDZ for distant atoms. The calculations employed the second-order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set. The active electrons in 10 active spaces included all seven 3d electrons, and the mixed spin-free states are 50 (all from 10 quadruplets; all from 40 doublets).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21571008, 21621061, 21725104, 21290171 and 21801037), National Key R&D Program of China (2017YFA0206301, 2017YFA0204903 and 2018YFA0306003), and the Fundamental Research Funds for the Central Universities, China.Notes and references
- D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press on Demand, 2006 Search PubMed.
- S. Gao and M. Affronte, Molecular nanomagnets and related phenomena, Springer, 2015 Search PubMed.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421 CrossRef CAS PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- M. Murrie, Chem. Soc. Rev., 2010, 39, 1986–1995 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926–4929 CrossRef CAS PubMed.
- S. Kang, H. Zheng, T. Liu, K. Hamachi, S. Kanegawa, K. Sugimoto, Y. Shiota, S. Hayami, M. Mito, T. Nakamura, M. Nakano, M. L. Baker, H. Nojiri, K. Yoshizawa, C. Duan and O. Sato, Nat. Commun., 2015, 6, 5955 CrossRef PubMed.
- O. Waldmann, Inorg. Chem., 2007, 46, 10035–10037 CrossRef CAS PubMed.
- F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Phys. Chem. B, 2004, 108, 11265–11271 CrossRef CAS.
- L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905 RSC.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381–2389 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef PubMed.
- M. K. Thomsen, A. Nyvang, J. P. S. Walsh, P. C. Bunting, J. R. Long, F. Neese, M. Atanasov, A. Genoni and J. Overgaard, Inorg. Chem., 2019, 58, 3211–3218 CrossRef CAS PubMed.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- M. M. Rodriguez, E. Bill, W. W. Brennessel and P. L. Holland, Science, 2011, 334, 780–783 CrossRef CAS PubMed.
- J. S. Anderson, J. Rittle and J. C. Peters, Nature, 2013, 501, 84 CrossRef CAS PubMed.
- P. L. Holland, Acc. Chem. Res., 2008, 41, 905–914 CrossRef CAS PubMed.
- P. P. Power, Chem. Rev., 2012, 112, 3482–3507 CrossRef CAS PubMed.
- J. Cheng, L. Wang, P. Wang and L. Deng, Chem. Rev., 2018, 118, 9930–9987 CrossRef CAS PubMed.
- H. Kramers, Proc. Natl. Acad. Sci. U. S. A., 1930, 33, 959 CAS.
- J. M. Smith, A. R. Sadique, T. R. Cundari, K. R. Rodgers, G. Lukat-Rodgers, R. J. Lachicotte, C. J. Flaschenriem, J. Vela and P. L. Holland, J. Am. Chem. Soc., 2006, 128, 756–769 CrossRef CAS PubMed.
- M. M. Rodriguez, B. D. Stubbert, C. C. Scarborough, W. W. Brennessel, E. Bill and P. L. Holland, Angew. Chem., Int. Ed., 2012, 51, 8247–8250 CrossRef CAS PubMed.
- M. J. Ingleson, B. C. Fullmer, D. T. Buschhorn, H. Fan, M. Pink, J. C. Huffman and K. G. Caulton, Inorg. Chem., 2008, 47, 407–409 CrossRef CAS PubMed.
- K. P. Chiang, C. C. Scarborough, M. Horitani, N. S. Lees, K. Ding, T. R. Dugan, W. W. Brennessel, E. Bill, B. M. Hoffman and P. L. Holland, Angew. Chem., Int. Ed., 2012, 51, 3658–3662 CrossRef CAS PubMed.
- V. Lavallo, Y. Canac, C. Präsang, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2005, 44, 5705–5709 CrossRef CAS PubMed.
- F. E. Hahn and M. C. Jahnke, Angew. Chem., Int. Ed., 2008, 47, 3122–3172 CrossRef CAS PubMed.
- C. G. Werncke, P. C. Bunting, C. Duhayon, J. R. Long, S. Bontemps and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2015, 54, 245–248 CrossRef CAS PubMed.
- P. P. Samuel, K. C. Mondal, N. Amin Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer and L. Ungur, J. Am. Chem. Soc., 2014, 136, 11964–11971 CrossRef CAS PubMed.
- Z. Mo and L. Deng, Coord. Chem. Rev., 2017, 350, 285–299 CrossRef CAS.
- A. Liske, K. Verlinden, H. Buhl, K. Schaper and C. Ganter, Organometallics, 2013, 32, 5269–5272 CrossRef CAS.
- H. Jacobsen, A. Correa, A. Poater, C. Costabile and L. Cavallo, Coord. Chem. Rev., 2009, 253, 687–703 CrossRef CAS.
- O. Back, M. Henry-Ellinger, C. D. Martin, D. Martin and G. Bertrand, Angew. Chem., Int. Ed., 2013, 52, 2939–2943 CrossRef CAS PubMed.
- K. L. Fillman, J. A. Przyojski, M. H. Al-Afyouni, Z. J. Tonzetich and M. L. Neidig, Chem. Sci., 2015, 6, 1178–1188 RSC.
- Z. Ouyang, J. Du, L. Wang, J. L. Kneebone, M. L. Neidig and L. Deng, Inorg. Chem., 2015, 54, 8808–8816 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970, pp. 554, 564–567 Search PubMed.
- R. Carlin, Magnetochemistry, Springer-Verlag, Berlin, 1986 Search PubMed.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- Y.-S. Meng, Z. Mo, B.-W. Wang, Y.-Q. Zhang, L. Deng and S. Gao, Chem. Sci., 2015, 6, 7156–7162 RSC.
- Y.-Y. Zhu, Y.-Q. Zhang, T.-T. Yin, C. Gao, B.-W. Wang and S. Gao, Inorg. Chem., 2015, 54, 5475–5486 CrossRef CAS PubMed.
- G. M. Sheldrick, SADABS, Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Germany, 1996 Search PubMed.
- G. M. Sheldrick, SHELXTL 5.10 for Windows NT: Structure Determination Software Programs, Bruker Analytical X-ray systems, Inc., Madison, WI, 1997 Search PubMed.
- N. Frank, ORCA–an ab initio, density functional and semiempirical program package, Version 3.03, Max-Planck institute for bioinorganic chemistry: Mülheim an der Ruhr, Germany, 2015 Search PubMed.
- J. Miralles, O. Castell, R. Caballol and J.-P. Malrieu, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1426587–1426589. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9qi00073a |
| This journal is © the Partner Organisations 2019 |