An electric-field-dependent drop selector†
Jinlong
Yang
a,
Dehui
Wang
a,
Hailong
Liu
 b,
Linxian
Li
c,
Longquan
Chen
d,
Hong-Ren
Jiang
*e and
Xu
Deng
b,
Linxian
Li
c,
Longquan
Chen
d,
Hong-Ren
Jiang
*e and
Xu
Deng
 *a
*a
aInstitute of Fundamental and Frontier Sciences, University of Electronic Science and Technology of China, Chengdu, China. E-mail: dengxu@uestc.edu.cn
bSchool of Energy and Power Engineering, Jiangsu University, Zhenjiang, China
cMing Wai Lau Centre for Reparative Medicine, Karolinska Institute, Hong Kong, China
dSchool of Physics, University of Electronic Science and Technology of China, Chengdu, China
eInstitute of Applied Mechanics, National Taiwan University, Taipei, 106, Taiwan. E-mail: hrjiang@iam.ntu.edu.tw
First published on 25th February 2019
Abstract
Drop manipulation on hydrophobic surfaces is of importance in lab-on-a-chip applications. Recently, superhydrophobic surface-assisted lab-on-a-chips have attracted significant attention from researchers due to their advantages of contamination resistance and low adhesion between the drop and the surface during manipulation. However, control over both static and dynamic interactions between a drop and a superhydrophobic surface has been rarely achieved. In this study, we designed an electric-field-dependent liquid-dielectrophoresis force to manipulate a drop on a superhydrophobic surface. This type of control has been found to be fast in response, bio-friendly, convenient, repeatable, and energy efficient. Moreover, the adhesion force and rebounding for both the static and the dynamic interactions between the drop and the surface under an electric field have been explored. It was found that the adhesion force could be reversibly tuned three-fold without breaking the Cassie–Baxter state. Rebounding experiments showed a close to linear relation between energy dissipation and the applied voltage. This relation was used to tune the on-demand behaviors of a drop on a surface in a proof-of-concept experiment for drop sorting. This electric-field-dependent drop manipulation may have potential applications in digital microfluidics, micro-reactors and advanced lab-on-a-drop platforms.
1. Introduction
Control over the interactions of drops on surfaces is essential for not only the basic understanding of various processes, ranging from daily life to cooling and coating,1–3 but also a variety of viable applications such as in digital microfluidics.4–7 Recently, due to their excellent liquid-repellence, superhydrophobic surfaces have received significant attention as a promising substrate for controlling the behaviors of drops.8–11 In recent years, the dynamic behaviour, including rebounding, jumping, self-cleaning, and cooling, and the interactions between the drop and the superhydrophobic surface have been extensively studied;12–15 however, these surfaces have constant wetting properties over a certain period of time that restrict the real-time tunable wettability of these surfaces after fabrication. In practical applications, such as in digital microfluidics, active control of the wettability is more desirable. Although extensive studies have been reported on superhydrophobic surfaces with static wetting properties, dynamic and reversible control over the wettability of these surfaces have been less often studied.To actively control the interactions between the drop and the surface, which are mainly determined by the wettability of the surface, the development of adaptive and intelligent superhydrophobic surfaces is desired. Extensive strategies, including regulations of chemical composition and structural roughness16–19 and external stimulation to conquer the energy barrier,20–24 have been reported to design and fabricate smart surfaces with adjustable wettability. Compared to the passive method of changing the surface properties, external stimulation is of significant value for actively controlling the drop behavior in the process. Heat,24,25 light,22,26 pH,24 magnetic field,23,27 and electric field21,28–30 have been commonly used as external stimuli in the regulation of surface wettability. Among them, electrowetting, generated from an electric field, stands out due to its reliability, high efficiency, and fast response.21,29–31 Through the movement of free charge, electrowetting modulates the contact angle and thus actuates the drop. The variation of the contact angle (φ) in response to the applied voltage (U) is generally described by the Young–Lippmann equation (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ = cos
φ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φeq + CU2/2γ).30 Herein, φeq is the equilibrium contact angle at zero voltage, C is the capacitance per unit area, and γ is the surface tension of the liquid. With good stability in the modulation of the contact angle, electrowetting has been widely applied in applications such as in electronic displays, adaptive optical lenses, and microfluidics;32–34 despite the merits of electrowetting, the requirement of conducting liquids and the direct contact between the liquid and electrodes may limit the applications of electrowetting, especially in the dynamic manipulation of liquid drops. Therefore, it is highly desirable to fabricate customized surfaces with the ability to statically and dynamically realize the on-demand behaviors of drops.
φeq + CU2/2γ).30 Herein, φeq is the equilibrium contact angle at zero voltage, C is the capacitance per unit area, and γ is the surface tension of the liquid. With good stability in the modulation of the contact angle, electrowetting has been widely applied in applications such as in electronic displays, adaptive optical lenses, and microfluidics;32–34 despite the merits of electrowetting, the requirement of conducting liquids and the direct contact between the liquid and electrodes may limit the applications of electrowetting, especially in the dynamic manipulation of liquid drops. Therefore, it is highly desirable to fabricate customized surfaces with the ability to statically and dynamically realize the on-demand behaviors of drops.
Recently, dielectrowetting has been proposed and demonstrated under different conditions mainly for contact angle actuation.28,35–37 In the case of interdigitated finger electrodes underneath an insulating layer, dielectrowetting employs a non-uniform electric field, which penetrates the layer until the liquid drop, to generate a liquid-dielectrophoresis (L-DEP) force by the polarization of neutral matter.35,36 Unlike electrowetting, dielectrowetting is independent of the liquid conductivity and thus can be used to control the contact angle of the drop in a number of applications in microfluidics.28,36,38 However, compared to the extensive studies reported on contact angle manipulation on a smooth hydrophobic surface, few studies have been attempted to exploit dielectrowetting on a superhydrophobic surface.
In this study, we report an intelligent superhydrophobic surface with on-demand adjustable wettability controlled by dielectrowetting. An electric-field-dependent L-DEP force was harnessed to control the interaction between the drop and the superhydrophobic surfaces. Taking advantages of the superhydrophobic surface and dielectrowetting, we showed that both the adhesion force and the rebounding of the drop could be efficiently tuned on a superhydrophobic surface by the actuation voltage of 0–49 V. To demonstrate the possible applications of dielectrowetting on superhydrophobic surfaces, we have demonstrated a proof-of-concept experiment of drop sorting, which may have potential applications in digital microfluidics, micro-reactors and advanced lab-on-a-drop platforms.
2. Experimental
2.1. Design of the superhydrophobic interdigitated array (IDA) chips
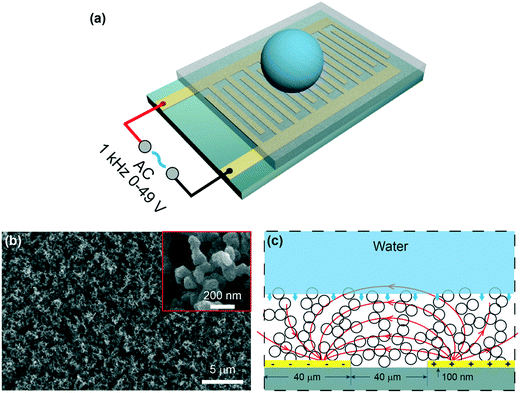
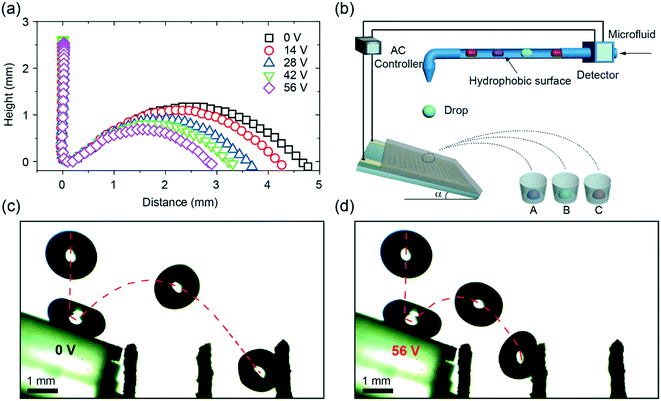
The schematic of the experimental setup is shown in Fig. 1a. An IDA chip (MECART, China) was coated with a superhydrophobic coating, which was made by chemical vapor deposition of silica on candle soot followed by fluorination as previously reported.8 Briefly, candle soot, consisting of carbon particles, was finely deposited on the chip by holding the substrate above the flame of a paraffin candle. The soot layer was then coated by a silica shell via chemical vapor deposition (CVD) using tetraethoxysilane (Sigma Aldrich, 98%) and an aqueous ammonia solution (TCI, 28%). After the silica shell was coated, the carbon core was removed by plasma. To reduce the surface energy, the surface was coated with trichloro(1H,1H,2H,2H-perfluorooctyl)silane (Sigma Aldrich, 97%) by CVD. The superhydrophobic surface featured the water apparent contact angle of 166° ± 1° and a roll-off angle less than 5°. The IDA chip was constructed by 25 sets of interdigitated gold finger electrodes with a thickness of 100 nm on the silicon substrate (6 × 4 mm). Both the width and spacing of the electrodes were 40 μm. Then, a superhydrophobic coating with a thickness of 10 μm was integrated on the chip (Fig. S1†). The morphology of the superhydrophobic surface was characterized by a scanning electron microscope (FEI, Inspect F50, Japan). The coating featured nano-sized particles with an outer radius of ∼60 nm and porosity with an average pore space of ∼1 μm (Fig. 1b).2.2. Generation of the electric field
To generate a non-uniform electric field between the finger electrodes, alternating current (AC) voltages were supplied to the circuit (Fig. 1a and c), allowing deeper penetration of the electric field into the liquid than the DC voltages.28 A sinusoidal signal was generated at the frequency of 1 kHz by a function generator (Tektronix, AWG 520, USA) and amplified by an amplifier (NF corporation, HSA4011, Japan). Voltages (root-mean-square values) ranging from 0 to 49 V were used throughout the experiments. When a voltage was applied, a highly localized electric field (Fig. 1c) was generated above the electrodes.36,39 Note that the dielectrowetting system is open circuit, and thus, the current is negligible; this makes the device energy efficient.2.3. Adhesion force, apparent contact angle, and roll-off angle measurement
The adhesion force (Fa) was measured using a high-sensitivity microelectromechanical balance system (Data-Physics, K100C, Germany). A 3 μL deionized (DI) water drop was suspended on a needle (0.5 mm in outer diameter), which was connected to a force sensor. The superhydrophobic IDA chip was placed on a horizontal table underneath the drop. During the measurement of the adhesion force, the IDA chip was slowly moved upward such that it contacted the water drop and then moved down at the constant speed of 0.02 mm s−1; during this process, the balancing force gradually increased to its maximum and then sharply reduced to zero. The maximum force before detachment was marked as the adhesion force. The apparent contact angle (φa) and roll-off angle (φr) were measured via the Data-Physics OCA 50 contact angle system using a 5 μL water drop. All the experiments were conducted at ambient temperature and repeated at least three times.2.4. Drop rebounding experiments
The superhydrophobic IDA chip was positioned on a horizontal stage. A 3 μL water drop impacted the superhydrophobic surface, and the velocity (v) changed from 0.2 to 0.4 m s−1; moreover, the corresponding Weber number (We = ρDv2/γ) changed from 1 to 4, where ρ, D and γ are the density, diameter and surface tension of the droplet, respectively. The impact process was investigated using a high-speed camera (Photron, Fastcam, Japan) at 5000 fps. The obtained videos were further processed using the custom-programmed MATLAB (Math_Works Inc., USA) algorithm.2.5. Simulation of the electric field
Simulation of the electric field was conducted using the commercial software COMSOL Multiphysics (Version 5.3a). The dimensions used in the simulation were exactly the same as those used in the fabrication (Fig. 1c, Fig. S2†). A vertical plane at the center of the water drop was selected as the computational domain (please refer to Fig. S2† for details of the simulation). The physical properties of the materials used in the simulation are summarized in Table S1.†3. Results and discussion
3.1. Manipulation of the static interaction between the drop and the surface under an electric field
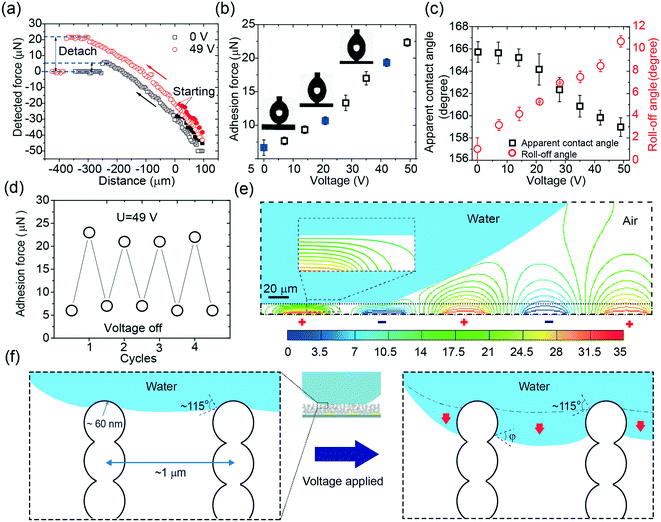
To demonstrate the capacity of the device to control the adhesion force (Fa), we first measured Fa in response to a series of voltages. A schematic of the adhesion force measurement can be found in Fig. 2a and Video S1.† The adhesion force at zero voltage was around 7 μN, consistent with the small adhesion force on superhydrophobic surfaces reported in other studies.8 The adhesion force monotonically increased when the voltage was elevated and reached almost three-fold at 49 V (Fig. 2b). The images in Fig. 2b show a comparison of the drop profiles upon detachment at the voltages of 0 V, 21 V, and 42 V. The force exerted on the droplet is reflected by the shape of the drop. Without voltage, the drop slightly deformed; this indicated a small hysteresis of the interaction between the drop and the surface. By increasing the applied voltage, the detaching force as well as the detaching distance increased; this was indicated by the deformation of the drop. Although there was a significant increase in the adhesion force, the apparent contact angle (φa) only slightly decreased from 166° at 0 V to 159° at 49 V (Fig. 2c). This monotonic increase in the adhesion force and slight decrease in the apparent contact angle suggested that the adhesion force could be modulated from 7 μN to 21 μN by a relatively low voltage, i.e., 49 V. The roll-off angles in response to the voltage (Fig. 2c) followed the same trend of the adhesion force curve, reaching a maximum value close to 11° at the voltage of 49 V. This was not unexpected since the increasing L-DEP force derived from the electric field contributed to the growth of the roll-off angle, namely, the hysteresis of the contact angle. Notably, the manipulation of the adhesion force under the applied voltage was reversible (Fig. 2d); this enabled the device to repeatedly regulate the adhesion force in practical applications.During the manipulation of the adhesion force, the electric field was mostly confined on the drop surface due to the exponential decay in the water phase.36 We confirmed this by simulating the electric field with a drop sitting on a superhydrophobic surface (Fig. 2e). The electric field was highly confined inside the porous structure and hardly penetrated inside the drop; this was is in accordance with the findings reported in the literature.36,40 Since the drop only touched the surface by a small area and the electric field only affected the air-liquid surface of the trapped liquid at the contact area, a negligible electric field penetrated the drop. This merit could be used to manipulate a drop with fragile loading in potential applications such as in handling mammalian cells or proteins.40
To illustrate local wetting in response to an electric field, a drop trapping model is shown in Fig. 2f. The superhydrophobic surface can be considered as aligned pillars of silica-coated soot particles.8,41 The nano-sized particles feature an outer radius (r) of ∼60 nm and an average pore space (dp–p) of ∼1 μm.41 At zero voltage, because of surface roughness and low surface energy, the drop only touched the top of the nanospheres, and a small adhesion force was observed (Fig. 2b and f). The force (Fas) required to pull a single nanosphere out of the air–liquid interface can be estimated from eqn (1).41,42
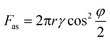 | (1) |
| Fa ∼ Fasl/dp−p | (2) |
Herein, Da is the drop diameter of the contact area before detachment, which can be measured by analyzing the images obtained upon the detachment of the drop. The measured diameters in response to voltage can be found in Fig. S3.† The diameter versus voltage curve features a relatively fast increase, followed by a plateau once the voltage exceeds 21 V. Thus, it can be predicted that the increase in the adhesion force originates from the increase of the local adhesion force and/or the detaching area. The contact angle on the nanosphere decreased as the applied voltage increased, which had the same tendency on a smooth flat surface.36 However, rather than being confined in two dimensions in the case of a flat surface, a portion of the drop penetrated inside the structure at elevated voltages in the case of a porous surface (Fig. 2f).
Although φ significantly reduced, the surface maintained the Cassie–Baxter state, which could be predicted from the Cassie–Baxter equation.
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φa = f1(cos φa = f1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ + 1) − 1 φ + 1) − 1 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φa and cos
φa and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ at zero voltage by eqn (3). Since φa = 166° and φ = 115° at zero voltage, f1 was calculated as 0.05.
φ at zero voltage by eqn (3). Since φa = 166° and φ = 115° at zero voltage, f1 was calculated as 0.05.
Based on the abovementioned analysis, we could establish a relation between the L-DEP force and the adhesion force. The L-DEP force results in two effects: it makes the contact line slide down along the nanospheres (reducing the contact angle) or leads to the spreading of the drop on the surface (increasing the detaching area). Both the effects increase the contact area between the liquid and the surface; this results in an increase in the adhesion force. Although there was a significant increase in the adhesion force, the surface retained its superhydrophobicity because the drop did not transition to the Wenzel state. The energy barrier required to overcome the transition was not reached since a limited voltage was applied. With the reduction of the contact angle on the nanospheres by the L-DEP force, the drop transitioned to a metastable Cassie–Baxter state. This metastable state will, however, collapse if the liquid further advances and completely covers the particles at higher voltages; this leads to a thoroughly wetted interface (the Wenzel state). For practical actuations, it is important to determine the maximum reversible adhesion force under an electric field. The breaking of the Cassie–Baxter state can be estimated from a completely immersed particle, i.e., φ = 0°. From eqn (1) and (2), the theoretical maximum adhesion force on a single particle was estimated to be 27 nN, and the corresponding adhesion force was around 35 μN supposing that the contact area at detachment remained unchanged. This is the maximum adhesion force that can be reached by an electric field in the metastable Cassie–Baxter state. However, the nanospheres in reality are mostly randomly arranged with inhomogeneous heights and positions; this makes the maximum adhesion force smaller than the predicted value.
3.2. Manipulation of the dynamic interaction between the drop and the surface under an electric field
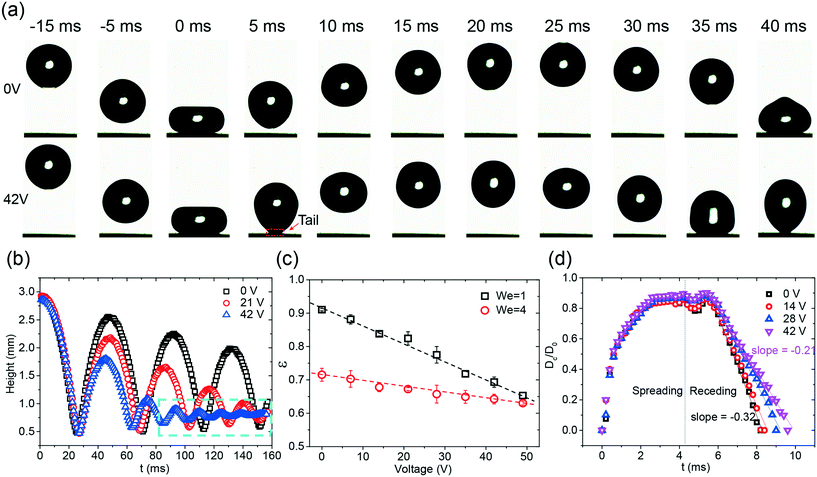
Taking advantage of the effective adhesion force modulation under an electric field, active control of the dynamic behavior, i.e., the rebounding of the drop, of the drop was realized on the superhydrophobic surface. The images of the rebounding drops, as depicted in Fig. 3a, demonstrate the influence of the electric field on the drop impact. In this case, the impact velocity of the drop was 0.2 m s−1, and the corresponding We was equal to unity. Without the applied voltage, after the drop released, the drop impacted the surface and smoothly rebounded (Video S2†); this was consistent with the results reported in other studies.8 When a voltage (i.e. 42 V) was applied to the chip, the chip became sticky to the drop. A tail was observed during the rebounding process (Fig. 3a, Video S2†). This sticky effect indicated that an attracting force was exerted on the drop during the impact.To quantify the effect of the electric field on drop rebounding, the time series of the rebounding drops was analyzed by the trajectories of the drop centroid (Fig. 3b). Without an external field, the drop rebounded several times, and the amplitude of rebounding slightly decreased with an increase in the number of rebounding cycles; this indicated that a small amount of energy dissipated during the impact. When the applied voltage was increased, the amplitude in each corresponding rebounding cycle as well as the period of that cycle decreased. The drop only rebounded twice in the case of 42 V. Note that the small oscillation at 42 V represents the oscillation of the drop rather than the rebounding (Fig. 3b, Video S2†). The reduction of the amplitude indicated that an increasing amount of energy was lost during rebounding at elevated voltages.
To quantify the energy loss, the coefficient of restitution (ε = vr/v) in the first rebounding was measured (Fig. 3c). Herein, vr is the velocity directly after rebounding. Because the impacting velocity would change the coefficient of restitution, two different initial heights, i.e. 3 mm and 9 mm, were tested in the experiments (Videos S2 and S3†). The corresponding We is equal to 1 and 4. The rebounding of a drop on a superhydrophobic coating has been previously studied.12,13 The higher coefficient of restitution at the lower initial height agrees with the previous study.12 For We = 1, ε significantly decreased from 0.91 at 0 V to 0.65 at 49 V. When We increased to 4, a smaller effect of the electric field on the energy dissipation was observed. ε decreased only by 0.05, namely, from 0.7 to 0.65, when a voltage of 49 V was applied. Notably, the decreasing speeds of ε in both cases are close to constants, indicated by the dashed line shown in Fig. 3c. The monotonic reduction of ε indicates that the variation of the electric field is an ideal method to tune the drop rebounding.
To verify the effect of the electric field on the rebounding, we further investigated the contact diameter ratio (Cr = Dc/D0) at the first rebounding at various voltages ranging from 0 V to 42 V. Herein, Dc is the contact diameter of the drop, and D0 is the diameter of the impacting drop. The contact diameter of the drop reflects the energy dissipation of the impacting drop in the spreading and retraction dynamics. As shown in Fig. 3d, the electric field imposes a relatively small influence on the spreading stage. The curves obtained at different voltages are almost identical. However, the retraction dynamics show a pronounced dependence on the applied voltage; this is reflected by the change in the retraction speed. The slope increased from −0.33 to −0.21 when the voltage was increased from 0 V to 42 V. The conclusions drawn from Fig. 3d are at least threefold. First, the small influence of the electric field on the spreading phase indicates that the L-DEP force only occurs once the drop interacts with the porous-structured surface. This finding is not unexpected since the electric field highly confines itself inside the superhydrophobic coating and decays fast while penetrating above. This is in accordance with the findings obtained via the adhesion force analysis. Second, the growing retraction rate with the increasing voltage indicates that a higher adhesion force is imposed on the liquid surface during the receding phase. The accumulative effect of the electric field leads to an increase in the contact time and a reduction of vr. This outcome is finally reflected by the decrease in the rebounding high; this makes the variation of the electric field an effective method for tuning the drop rebounding. Third, the imposed force is found to be uniform along the surface; this is reflected by the close to constant retraction rate. This uniform effect ensures a consistent response in the drop rebounding, making this electric-field-based tuning of the drop rebounding a reliable method.
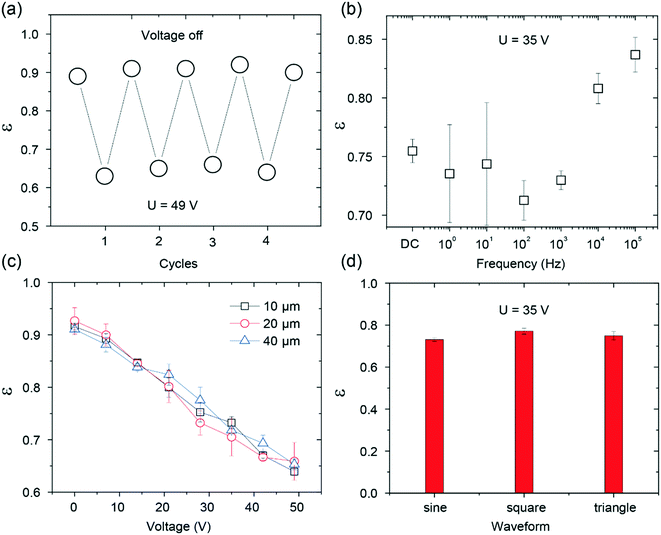
For practical applications, it is important to consider the reversible response as well as the experimental conditions in the electric-field-dependent tuning of the drop rebounding (Fig. 4). Similar to the reversible effect of the electric field on the adhesion force, the rebounding of the drop was also found to be repeatable (Fig. 4a). The experimental conditions, such as the width of electrodes, the frequency of the applied voltages, and the type of waveforms, could have an influence on the rebounding.28,43 To verify this, we investigated the rebounding coefficient under different conditions. The results are summarized in Fig. 4b–d. The rebounding coefficient versus voltage curve for different widths of the electrodes and waveforms are almost identical; this indicates that the width of the electrodes and the type of the waveforms have negligible effects on the rebounding. On the other hand, the rebounding was sensitive to the frequency of the waveform. High-energy dissipation was found when the frequency was below 1 kHz. The frequency-dependent effect is in line with the results reported in the literature.43 However, large errors were found when the frequency was below 100 Hz. This finding is not unexpected since the contact time of the drop on the superhydrophobic surface is close to 10 ms, and a frequency below 100 Hz indicates that the rebounding finishes within a single period. The change in the voltage magnitude introduces large deviations in the measured coefficient of restitution. Thus, the results reported herein were obtained under the following conditions: the electrode width of 40 μm, sinusoidal waveform, and the frequency of 1 kHz.
3.3. Demonstration of the drop selector
To demonstrate the applications of dielectrowetting on the superhydrophobic surface, we performed a proof-of-concept experiment of drop sorting. A drop of water was released into a tilted superhydrophobic coating with IDA electrodes. The slope of the surface was optimized to 20° (Fig. S4†). We showed that even relatively small voltages (0–56 V) applied to the IDA could significantly change the jumping distance (Fig. 5a). Based on the monotonic relation between the jumping distance and the applied voltage, a collecting device was added to separate different drops with different jumping distances (Fig. 5b). The time-lapsed images of drop rebounding on an electric-field-controlled tilted superhydrophobic IDA chip (Fig. 5c and d) show the capacity of this device to separate the drops. Without the applied voltage, the drop jumped at a certain distance and finally fell into a channel placed in front of the chip. In contrast, the jumping distance of the drop significantly decreased at the voltage of 56 V, and the drop fell into another channel closer to the chip. A video, demonstrating the reproducibility of the separating drops, can be found in Video S4.† Due to the fast response, the small amplitude of the voltage, the non-contact of electrodes, and the superhydrophobic property of the system, the device can easily be applied to biological samples in diverse applications.4. Conclusion
Herein, we proposed a new method to actively control the behaviors of a drop on a superhydrophobic surface by dielectrowetting at low voltages. The adhesion force and the coefficient of restitution curve were measured to elucidate the static and dynamic interactions between the drop and the surface. The adhesion force range can be reversibly tuned in the order of 15 μN at the voltage of 49 V. The modulation of the adhesion force can be easily extended to applications in digital microfluidics such as in transferring the drops, guiding the drop movement, and trapping the drops at desired places. We also demonstrated a contactless and fast response strategy to tune the drop rebounding dynamics. A monotonic relation between the coefficient of restitution and the voltage was established and used in a proof-of-concept drop selector. This low voltage response and all superhydrophobic condition by dielectrowetting may enable new applications in lab-on-drop platforms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Limei Xu (University of Electronic Science and Technology of China) for sharing the equipment. This work was supported by the Ministry of Science and Technology, Taiwan, under Grant NSC 103-2112-M-002-008-MY3. X. D. acknowledge the funding supported provided by the National Natural Science Foundation of China (21603026) and supported by Max-Planck-Gesellschaft (Max Planck Partner Group UESTC-MPIP).References
- L. Mishchenko, B. Hatton, V. Bahadur, J. A. Taylor, T. Krupenkin and J. Aizenberg, ACS Nano, 2010, 4, 7699–7707 CrossRef CAS PubMed.
- D. B. van Dam and C. Le Clerc, Phys. Fluids, 2004, 16, 3403–3414 CrossRef CAS.
- A. L. Yarin, Annu. Rev. Fluid Mech., 2006, 38, 159–192 CrossRef.
- X. Yang, J. Song, H. Zheng, X. Deng, X. Liu, X. Lu, J. Sun and D. Zhao, Lab Chip, 2017, 17, 1041–1050 RSC.
- M. Abdelgawad and A. R. Wheeler, Adv. Mater., 2009, 21, 920–925 CrossRef CAS.
- S. Ghosh, R. Lagraauw, S. Otten, A. Pit, C. Berendsen, J. Zeegers, D. Van Den Ende and F. Mugele, Nat. Commun., 2014, 5, 3559 CrossRef PubMed.
- J. Seo, S.-K. Lee, J. Lee, J. S. Lee, H. Kwon, S.-W. Cho, J.-H. Ahn and T. Lee, Sci. Rep., 2015, 5, 12326 CrossRef PubMed.
- X. Deng, L. Mammen, H.-J. Butt and D. Vollmer, Science, 2012, 335, 67–70 CrossRef CAS PubMed.
- Z. Chu and S. Seeger, Chem. Soc. Rev., 2014, 43, 2784–2798 RSC.
- C. Schlaich, Y. Fan, P. Dey, J. Cui, Q. Wei, R. Haag and X. Deng, Adv. Mater. Interfaces, 2018, 5, 1701536 CrossRef.
- J. Song, D. Zhao, Z. Han, W. Xu, Y. Lu, X. Liu, B. Liu, C. J. Carmalt, X. Deng and I. P. Parkin, J. Mater. Chem. A, 2017, 5, 14542–14550 RSC.
- X. Deng, F. Schellenberger, P. Papadopoulos, D. Vollmer and H.-J. Butt, Langmuir, 2013, 29, 7847–7856 CrossRef CAS.
- B. Zhao, X. Wang, K. Zhang, L. Chen and X. Deng, Langmuir, 2016, 33, 144–151 CrossRef PubMed.
- S. Lin, B. Zhao, S. Zou, J. Guo, Z. Wei and L. Chen, J. Colloid Interface Sci., 2018, 516, 86–97 CrossRef CAS PubMed.
- J. Song, M. Gao, C. Zhao, Y. Lu, L. Huang, X. Liu, C. J. Carmalt, X. Deng and I. P. Parkin, ACS Nano, 2017, 11, 9259–9267 CrossRef CAS PubMed.
- H. E. Jeong, M. K. Kwak and K. Y. Suh, Langmuir, 2010, 26, 2223–2226 CrossRef CAS PubMed.
- Y. Lai, X. Gao, H. Zhuang, J. Huang, C. Lin and L. Jiang, Adv. Mater., 2009, 21, 3799–3803 CrossRef CAS.
- J. Li, Z. Jing, F. Zha, Y. Yang, Q. Wang and Z. Lei, ACS Appl. Mater. Interfaces, 2014, 6, 8868–8877 CrossRef CAS PubMed.
- J. Li, Y. Hou, Y. Liu, C. Hao, M. Li, M. K. Chaudhury, S. Yao and Z. Wang, Nat. Phys., 2016, 12, 606 Search PubMed.
- S. Pan, R. Guo and W. Xu, Soft Matter, 2014, 10, 9187–9192 RSC.
- L. Heng, T. Guo, B. Wang, L.-Z. Fan and L. Jiang, J. Mater. Chem. A, 2015, 3, 23699–23706 RSC.
- J. Wang, W. Gao, H. Zhang, M. Zou, Y. Chen and Y. Zhao, Sci. Adv., 2018, 4, eaat7392 CrossRef PubMed.
- X. Hong, X. Gao and L. Jiang, J. Am. Chem. Soc., 2007, 129, 1478–1479 CrossRef CAS PubMed.
- Z. Cheng, H. Lai, M. Du, S. Zhu, N. Zhang and K. Sun, Soft Matter, 2012, 8, 9635–9641 RSC.
- X. Yao, J. Ju, S. Yang, J. Wang and L. Jiang, Adv. Mater., 2014, 26, 1895–1900 CrossRef CAS PubMed.
- X. Liu, M. Cai, Y. Liang, F. Zhou and W. Liu, Soft Matter, 2011, 7, 3331–3336 RSC.
- Y. Huang, B. B. Stogin, N. Sun, J. Wang, S. Yang and T. S. Wong, Adv. Mater., 2017, 29, 1604641 CrossRef PubMed.
- H. Geng, J. Feng, L. M. Stabryla and S. K. Cho, Lab Chip, 2017, 17, 1060–1068 RSC.
- M. E. Kavousanakis, N. T. Chamakos, K. Ellinas, A. Tserepi, E. Gogolides and A. G. Papathanasiou, Langmuir, 2018, 34, 4173–4179 CrossRef CAS PubMed.
- L. Chen and E. Bonaccurso, Adv. Colloid Interface Sci., 2014, 210, 2–12 CrossRef CAS PubMed.
- J. Heikenfeld and M. Dhindsa, J. Adhes. Sci. Technol., 2008, 22, 319–334 CrossRef CAS.
- R. A. Hayes and B. J. Feenstra, Nature, 2003, 425, 383 CrossRef CAS PubMed.
- B. Berge and J. Peseux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 159–163 CrossRef CAS.
- A. R. Wheeler, Science, 2008, 322, 539–540 CrossRef CAS PubMed.
- A. Edwards, C. Brown, M. Newton and G. McHale, Curr. Opin. Colloid Interface Sci., 2017, 36, 28–36 CrossRef.
- G. McHale, C. V. Brown, M. I. Newton, G. G. Wells and N. Sampara, Phys. Rev. Lett., 2011, 107, 186101 CrossRef CAS PubMed.
- D. Baratian, R. Dey, H. Hoek, D. van den Ende and F. Mugele, Phys. Rev. Lett., 2018, 120, 214502 CrossRef PubMed.
- S. Xu, H. Ren and S.-T. Wu, J. Phys. D: Appl. Phys., 2013, 46, 483001 CrossRef.
- A. Russell, W. Hsieh, K. Chen and J. Heikenfeld, Langmuir, 2014, 31, 637–642 CrossRef PubMed.
- S. L. Freire and B. Tanner, Langmuir, 2013, 29, 9024–9030 CrossRef CAS PubMed.
- M. Ye, X. Deng, J. Ally, P. Papadopoulos, F. Schellenberger, D. Vollmer, M. Kappl and H.-J. Butt, Phys. Rev. Lett., 2014, 112, 016101 CrossRef PubMed.
- A. Scheludko, B. Toshev and D. Bojadjiev, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 2815–2828 RSC.
- T. B. Jones, J. D. Fowler, Y. S. Chang and C.-J. Kim, Langmuir, 2003, 19, 7646–7651 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc01403e |
| This journal is © The Royal Society of Chemistry 2019 |