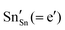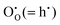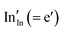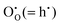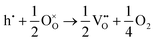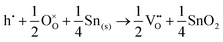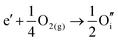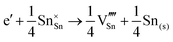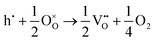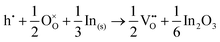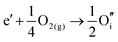Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect formation in In2O3 and SnO2: a new atomistic approach based on accurate lattice energies
Qing
Hou
 *a,
John
Buckeridge
*a,
John
Buckeridge
 a,
Tomas
Lazauskas
a,
Tomas
Lazauskas
 a,
David
Mora-Fonz
a,
David
Mora-Fonz
 b,
Alexey A.
Sokol
b,
Alexey A.
Sokol
 a,
Scott M.
Woodley
a,
Scott M.
Woodley
 a and
C. Richard A.
Catlow
*a
a and
C. Richard A.
Catlow
*a
aKathleen Lonsdale Materials Chemistry, Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: qing.hou.16@ucl.ac.uk; c.r.a.catlow@ucl.ac.uk
bDepartment of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
First published on 22nd October 2018
Abstract
We present a consistent interatomic force field for indium sesquioxide (In2O3) and tin dioxide (SnO2) that has been derived to reproduce lattice energies and, consequently, the oxygen vacancy formation energies in the respective binary compounds. The new model predicts the dominance of Frenkel-type disorder in SnO2 and In2O3, in good agreement with ab initio defect calculations. The model is extended to include free electron and hole polarons, which compete with charged point defects to maintain charge neutrality in a defective crystal. The stability of electrons and instability of holes with respect to point defect formation rationalises the efficacy of n-type doping in tin doped indium oxide (ITO), a widely employed transparent conducting oxide in optoelectronic applications. We investigate the clustering of Sn substitutional and oxygen interstitial sites in ITO, finding that the dopants substitute preferentially on the cation crystallographic d site in the bixbyite unit cell, in agreement with experiment. The force field described here provides a useful avenue for the investigation of the defect properties of extended transparent conducting oxide systems, including solid solutions.
1. Introduction
The combination of high optical transparency and high electrical conductivity in transparent conducting oxides (TCOs) results in the class of materials being widely used in many fields, including solar cells, liquid crystal displays, electrochromic plating and smart windows.1–3 The most commonly used n-type TCO materials are SnO2 and In2O3, which tend to be oxygen deficient due to the appearance of oxygen vacancies,4–7 and tin-doped In2O3 (indium tin oxide, ITO). The n-type conductivity has intuitively been attributed to the presence of these vacancies, but other sources have also been proposed8–11 and the matter remains a topic of debate. Accurate modelling of intrinsic and extrinsic defects is needed to understand the source of conductivity. This paper reports a comprehensive survey of the defect structure of these materials and of the relationship between their defect and electronic properties.ITO is a disordered system, which necessitates large length scale simulations of multiple atomic environments in the presence of charge carriers to understand its structural and electronic properties. Fully ab initio approaches to such problems are limited by both computational resources and methodological problems in the study of charged defects. Computational techniques based on interatomic potentials, in contrast, are particularly well suited to explore such systems, but require sufficiently accurate and transferable parameterisation. As shown below, previous work on the parameterisation of interatomic potentials suffered from a number of problems related to transferability and/or accuracy in the reproduction of essential physical properties of both parent SnO2 and In2O3 compounds. In this paper, we demonstrate the first transferable interatomic potential model that reproduces well the physical properties of SnO2 and In2O3 including their dielectric response and lattice energies. We then apply our methodology to develop a consistent and reliable set of models for the defect structure of the materials.
At low temperature and ambient pressure, In2O3 adopts the body-centred cubic bixbyite crystal structure (space group No. 206, Ia3, a = 10.117 Å), which contains 80 atoms i.e. 16 formula units in its conventional cubic unit cell. The structure can be viewed as a 2 × 2 × 2 supercell of the fluorite (CaF2) lattice with one fourth of the anionic sites vacant, which results in two types of cationic sites, 8b and 24d in Wyckoff's notation, as illustrated in Fig. 1. These structural vacant sites (Wyckoff 16c) provide interstitial sites and, as discussed below, interstitial oxygen can play a key role in the properties of ITO as the formation of such defects can compensate n-type carriers, which will detrimentally affect the conductivity.
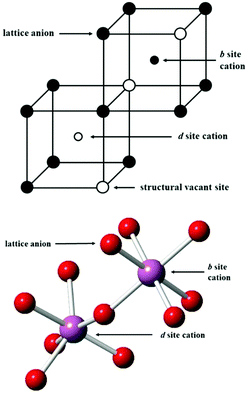 | ||
| Fig. 1 Lattice sites in In2O3. In the bottom figure, the coordination of the cations is shown, with indium ions represented by larger purple spheres and oxygen ions by smaller red spheres. | ||
After Rupprecht12 first carried out the study on the optical and electrical properties of In2O3 in 1950s, In2O3 and ITO have attracted considerable experimental and theoretical interest. Regarding the latter, there have been several studies on their electronic structure using quantum mechanical techniques.13–17 Using the local density approximation (LDA) and a LDA+U approach in Density Functional Theory (DFT), Reunchan et al.16 proposed that the oxygen vacancy is a double donor, while the indium vacancy is a triple acceptor in indium oxide; while Ágoston et al.17 investigated electron compensation in SnO2 and In2O3 using hybrid DFT and reported both SnO2 and In2O3 to be highly n-type dopable against the formation of intrinsic acceptors.
Methods based on interatomic potentials, while not allowing details of the electronic structure to be probed, do allow the exploration of much larger systems.18–21 Walsh et al.22 have investigated the formation of intrinsic point defects including all possible vacancies and interstitials in indium oxide using an accurate interatomic potential. The anion Frenkel pair is reported to be the predominant form of ionic disorder due to the presence, as noted above, of intrinsic interstitial sites in the lattice. Warschkow et al.23 explored clustering of oxygen interstitials with tin dopants in ITO using both atomistic (interatomic potential based) and DFT calculations. Strong preference was found for the formation of neutral defect clusters consisting of two substitutional Sn ions bound to an interstitial oxygen. Experimental studies have suggested that defect clusters of substitutional tin and interstitial oxygen should form in ITO.24 The 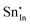 defect is positively charged (here we use the standard Kröger–Vink notation when describing defects, where ˙ signifies a positive charge, ′ a negative charge and × a neutral charge), which can compensate negatively charged
defect is positively charged (here we use the standard Kröger–Vink notation when describing defects, where ˙ signifies a positive charge, ′ a negative charge and × a neutral charge), which can compensate negatively charged 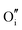 . Moreover, it is argued that the formation of oxygen interstitials will lead to lattice stress, while the
. Moreover, it is argued that the formation of oxygen interstitials will lead to lattice stress, while the 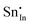 ion can relieve some of this stress due to its smaller size.
ion can relieve some of this stress due to its smaller size.
For TCO materials, native defects may act as donors resulting in intrinsic n-type conductivity as has been recently demonstrated by Buckeridge et al.25 Further extrinsic doping such as Sn in In2O3 is, however, required to achieve technologically desired concentrations of charge carriers. Hence, the main aim of this work is to explore defect properties of both SnO2 and In2O3 and the effects of defects on the electronic properties and structure of these materials. A new set of interatomic potentials is derived and applied which accurately reproduce the elastic and structural properties of the two binary oxides. In particular, atomistic simulations are used to investigate the energetics of point defects and intrinsic disorder in In2O3 and SnO2. The interatomic potential model, including a suitable approach to reproduce the fundamental band gaps, is shown to give reasonable intrinsic defect formation energies (in comparison with more accurate but computationally expensive electronic structure methods), indicating that the defect properties are modelled well. Furthermore, the formation energies of clusters of an oxygen interstitial surrounded by one or more tin substitutional defects in indium oxide are calculated and analysed. The results help explain experimental observations regarding the configurations of tin clusters in ITO.
2. Methodology
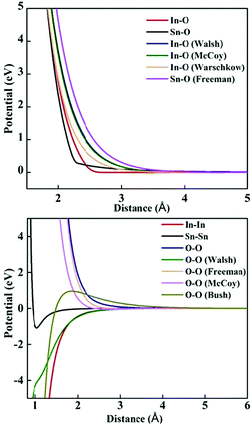
The lattice and defect energies in this paper are based on the Born model of the ionic solid.26 The pairwise interactions between the ions are modelled by a combination of the Buckingham,27 Lennard-Jones, constant offset and polynomial harmonic potentials to describe smooth monotonically decaying functions as shown in Fig. 2. Previously derived potential functions are also shown for comparison. In the range of bonding distances, our potentials typically have a similar gradient to the previous models, but are shifted down in energy, which, allowed us to reproduce the experimentally observed lattice energies – a key feature of our new models. Importantly, we have common oxygen parameters for SnO2 and In2O3.One significant new feature in our model is the addition of a repulsive 1/r4 potential, which helps to reproduce the rutile structure as the ground state for SnO2, and penalise a hypothetical anatase phase of this material. One possible rationalisation is that the unusual trigonal coordination of oxygen in a rutile environment results in its higher-order polarisability (deformation), which is not accounted for by the standard shell model. This potential could help to maintain the balance of the induced multipolar interactions in SnO2.
The Buckingham potential has the form:
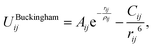 | (2.1) |
 | (2.2) |
| EPolynomial = C0 + C1(r − r0) + C2(r − r0)2 + ⋯ + Cn(r − r0)n, | (2.3a) |
| EHarmonic-Polynomial = (r − r0)2(C0 + C1r + C2r2 + ⋯ + Cnrn). | (2.3b) |
To model polarisable ions, we employ the shell model,28 where the shell (charge Y) is connected to the core by an harmonic spring (spring constant k) with the total charge equal to the charge assigned to the ion, which in the present case is the formal charge. The ionic polarisability in vacuo is given as:
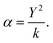 | (2.4) |
A careful choice of the potential parameters is crucial for the accurate modelling of both the structural and physical properties, which we will address in Section 3.1 below. The parameters of our model are given in Table 1.
| a The interaction between one atom's core and another atom's shell. | ||||||
|---|---|---|---|---|---|---|
| (a) Buckingham potential | ||||||
| Interaction | A (eV) | ρ (Å) | C (eV Å6) | |||
| Sn shell–O shell | 1805.11 | 0.32 | 0.00 | |||
| In shell–O shell | 1937.36 | 0.32 | 30.00 | |||
| O shell–O shell | 24.66 | 0.50 | 32.61 | |||
| O core–O shell | 41944.48 | 0.20 | 0.00 | |||
| (b) Lennard-Jones potential | ||||||
| Interaction | A (eV Åm) | B (eV Ån) | m | n | ||
| Sn core–Sn shella | 0 | 2.00 | 12 | 6 | ||
| Sn shell–Sn shell | 1 | 0 | 18 | 1 | ||
| Sn shell–O shell | 7.89 | 0 | 4 | 0 | ||
| Sn shell–O shell | 1 | 0 | 18 | 1 | ||
| In shell–In shell | 0 | 28 | 12 | 6 | ||
| In shell–In shell | 1 | 0 | 18 | 1 | ||
| In shell–O shell | 1 | 0 | 18 | 1 | ||
| O core–O shell | 10 | 0 | 12 | 6 | ||
| (c) Polynomial potential | ||||||
| Interaction | n | C 0 | r min | r max | ||
| Sn shell–O shell | 1 | −1.567 | 0.00 | 2.15 | ||
| In shell–O shell | 1 | −0.65 | 0.00 | 2.30 | ||
| (d) Polynomial harmonic potential | ||||||
| Interaction | n | C 0 | C 1 | C 2 | r min | r max |
| Sn shell–O shell | 2 | −280.31 | 236.42 | −43.67 | 2.15 | 2.30 |
| In shell–O shell | 2 | −44.17 | 47.29 | −11.41 | 2.30 | 2.70 |
| (e) Shell model | ||||||
| Species | Y (e) | k (eV Å−2) | ||||
| Sn | 4.34 | 94.05 | ||||
| In | 2.63 | 7.53 | ||||
| O | −3.16 | 70.51 | ||||
The resulting potentials were used to study point defects in both In2O3 and SnO2, using the Mott–Littleton method29,30 as implemented in the General Utility Lattice Package (GULP).31 Within the Mott–Littleton approach, the defective structure is divided into three regions with the point defect at the centre of the inner spherical region (region I). Interactions between atoms in region I are treated most accurately with explicit relaxation; beyond region I, the defect is treated in a linear-response approximation, where ionic displacements are calculated based on a harmonic representation of the true potential energy surface with an explicit account of all forces on ions in the nearest spherical shell region IIa and a more approximate treatment of the further region IIb extending to infinity, where only long-range Coulomb interactions with the defect are considered. In this work, the radius of region I is chosen as 15 Å (so that there are 1093 atoms for In2O3 and 1189 for SnO2 in the region) with a 30 Å radius for region IIa, which corresponds to the 15 Å cut-off used in the force field parameterisation. Our tests show that this choice provides an acceptable convergence of defect energies to ca. 0.1 eV or better with relatively low computational costs. The defect energy is defined as the energy required to form a point defect in the system by adding or removing constituent ions in their formal charge states from the gas phase (or vacuum) where the energy of such gas phase ions is set to zero. Defect energies resulting from Mott–Littleton calculations can in turn be used to calculate defect formation energies that refer to atoms removed from or added to their standard states to obtain energies of solution or of redox processes and can be combined to calculate e.g. Schottky and Frenkel formation energies.
3. Results
3.1. Interatomic potentials
The first interatomic potentials for SnO2 reported by Freeman and Catlow32 were fitted to static and high frequency dielectric and elastic constants of SnO2; the lattice energy and lattice parameter though were less well described, as shown in Table 2. A parameterisation of the Buckingham potential for In2O3 based on the oxide parameters of Freeman and Catlow32 and Bush et al.,27 with In–O parameters of McCoy et al.,33 was reported by Warschkow et al.,23 in which the dielectric properties were not, however, fitted. Walsh et al.22 reported an alternative parameterisation, which in contrast reproduced well the static and high-frequency dielectric constants (see Table 3), but the lattice energy again deviated from experiment and the oxide parameters were incompatible with Freeman's SnO2 potentials.| Parameter | Experimental | Present work | Freeman and Catlow32 |
|---|---|---|---|
| Lattice parameter, a (Å) | 4.737,35 4.73836 | 4.742 | 4.706 |
| Static dielectric constant | 14.037 | 16.724 | 13.8 |
| High frequency dielectric constant | 3.78537 | 3.889 | 3.894 |
| Lattice energy (eV) | −122.125 | −122.32 | −110.68 |
| Elastic constants38 | |||
| C 11 (GPa) | 261.7 | 290.55 | 299 |
| C 12 (GPa) | 177.2 | 191.07 | 212 |
| C 13 (GPa) | 156.0 | 249.45 | 198 |
| C 33 (GPa) | 450.0 | 620.61 | 522 |
| C 44 (GPa) | 103.07 | 119.20 | 111 |
| C 66 (GPa) | 207 | 236.36 | 228 |
| Parameter | Experimental | Present work | Walsh et al.22 | Warschkow et al.23 | McCoy et al.33 |
|---|---|---|---|---|---|
| Lattice parameter, a (Å) | 10.11744 | 10.119 | 10.121 | 10.120 | 10.115 |
| Static dielectric constant | 8.9–9.545 | 9.191 | 9.052 | 6.872 | 9.455 |
| High frequency dielectric constant | 446 | 3.941 | 3.903 | 3.534 | 4.907 |
| Lattice energy (eV) | −149.98 | −150.01 | −140.60 | −141.91 | −141.14 |
| Elastic constants | |||||
| C 11 (GPa) | 337.14 | 297.75 | 368.10 | 324.4 | |
| C 12 (GPa) | 154.99 | 141.78 | 150.11 | 151.7 | |
| C 44 (GPa) | 93.19 | 76.42 | 111.24 | 120.7 | |
In order to describe the crystal properties of both binary oxides and ITO, it is necessary to construct a common interatomic force field for In2O3 and SnO2 (as summarised in Table 1), which reproduces well the structure and dielectric constants. The new model was obtained by empirical fitting, using the GULP code, to calculate lattice parameters, lattice energy, and static and high-frequency dielectric constants and gave a better agreement with the experimental data compared to earlier work, as shown in Tables 2 and 3.
In the following sections we use the new model to explore the defect and electronic properties of the materials.
3.2. Electron and hole formation
Although methods based on interatomic potentials are incapable of calculating the electronic structure or electron states directly, it is still possible to estimate crudely the band gap hypothesizing that the valence band maximum can be represented by a hole localised on an anion, the conduction band minimum can be represented by an electron on a cation, and the difference in energy between the two gives the energy gap. Such an assumption is broadly supported by ab initio calculations on ionic compounds of most metals, including both SnO2 and In2O3. In our model, the hole state is obtained by the instantaneous ionisation of an oxide ion including high-frequency dielectric response (via shell relaxation) to form an O− ion on an oxide ion site (the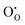 defect). As the on-site energy contributions – beyond dipolar polarisation – are not accounted for by the model, we also customarily subtract from the calculated ionisation potential the second O electron affinity (9.41 eV adopted from T. C. Waddington,34cf. 8.75 eV from Freeman and Catlow,32 8.89–9.58 eV from Ladd and Lee39). For the electron, the localised state would be the Sn3+ (for SnO2) or In2+ (for In2O3) ion on the appropriate cation site (
defect). As the on-site energy contributions – beyond dipolar polarisation – are not accounted for by the model, we also customarily subtract from the calculated ionisation potential the second O electron affinity (9.41 eV adopted from T. C. Waddington,34cf. 8.75 eV from Freeman and Catlow,32 8.89–9.58 eV from Ladd and Lee39). For the electron, the localised state would be the Sn3+ (for SnO2) or In2+ (for In2O3) ion on the appropriate cation site (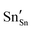 or
or 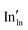 in the defect notation); the on-site fourth (third) ionisation potential of the gas phase Sn (In) is subtracted from the respective defect energy. All energy terms used to calculate the required quantities are collected in Table 4 for SnO2 and Table 5 for In2O3.
in the defect notation); the on-site fourth (third) ionisation potential of the gas phase Sn (In) is subtracted from the respective defect energy. All energy terms used to calculate the required quantities are collected in Table 4 for SnO2 and Table 5 for In2O3.
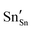 and
and 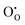 defect energies, fourth ionisation energy of Sn and second electron affinity of O are used to compute the ionisation potential I and electron affinity A of the material, the difference of which gives the band gap
defect energies, fourth ionisation energy of Sn and second electron affinity of O are used to compute the ionisation potential I and electron affinity A of the material, the difference of which gives the band gap
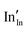 and
and 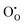 defect energies, third ionisation energy of In and second electron affinity of O are used to compute the ionisation potential I and electron affinity A of the material, the difference of which gives the band gap
defect energies, third ionisation energy of In and second electron affinity of O are used to compute the ionisation potential I and electron affinity A of the material, the difference of which gives the band gap
The calculated band gap of SnO2, by this crude procedure, is 5.21 eV, compared with the experimental value of 3.6 eV.40 For In2O3, we calculate the band gap of 6.71 eV, as compared to the experimental value of 2.7 eV4 (these experimental values are fundamental band gaps, so that excitonic effects, which we do not attempt to model in our procedure, are not included). Whereas the position of the valence band is determined by these calculations quite accurately (within ∼0.5 eV of available experimental data41–43), the conduction band is severely underbound, which can be clearly related to the one-site localisation model for an electron. While the latter approximation is reasonable for a hole, electrons in the conduction band are well known to be strongly delocalised. We will therefore use the difference between the calculated and experimental band gaps as a measure of electron localisation, which can subsequently be employed as a parameter of the electronic structure in calculations on more complex mixed materials including lightly doped ITO and solid solutions between tin and indium oxides. Therefore, the corresponding corrections for end member compounds are +1.65 eV and +4.01 eV of SnO2 and In2O3, respectively. The large difference can be provisionally attributed to the more stable environment for the localised electron used to model the CBM when situated on a Sn4+ site in SnO2 compared with an In3+ site in In2O3, due to the higher net positive charge and the shorter cation–anion bond length (circa 2.05 Å in SnO2vs. 2.18 Å in In2O3).
Next, we turn our attention to atomic defects.
3.3. Defect energies from Mott–Littleton calculations
The calculated intrinsic defect energies in SnO2 and In2O3 are presented in Tables 6 and 7.| Defect | Defect energy (eV) | Wyckoff's site | |
|---|---|---|---|
| Present work | Freeman and Catlow32 | ||
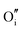
|
−11.35 | −8.31 | 4g |
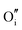
|
−11.62 | 4c | |

|
−77.08 | 4g | |
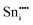
|
−79.52 | −68.23 | 4c |
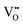
|
24.02 | 19.39 | 4f |
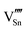
|
98.04 | 87.48 | 2a |
| Defect | Defect energy (eV) | Wyckoff's site | |
|---|---|---|---|
| Present work | Walsh et al.22 | ||
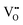
|
23.16 | 20.99 | 48e |
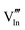
|
55.67 | 49.92 | 8b |
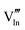
|
56.16 | 50.05 | 24d |
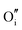
|
−15.33 | −13.29 | 8a |
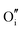
|
−15.82 | −14.61 | 16c |
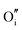
|
−12.86 | −12.08 | 24d |
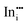
|
−40.52 | −35.57 | 8a |
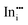
|
−41.68 | −36.21 | 16c |
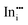
|
−39.78 | −34.89 | 24d |
The rutile structure of SnO2 (space group 136, or P42/mnm) has only one octahedrally coordinated lattice site for cations and one trigonal site for anions. We confirm the prediction by Hines et al.47 that the interstitial crystallographic site 4c, which is in the centre of an unoccupied oxygen octahedron, has a lower energy for an oxide ion compared to the 4g site explored by Freeman and Catlow,32 by about 0.27 eV. Of the two available cationic interstitial sites, the 4c site is more stable than 4g by 2.44 eV.
For In2O3, there are two symmetry-unique cation 6-coordinated lattice sites (the b site, which is slightly trigonally compressed octahedral coordinated, and the d site, which is highly distorted octahedrally coordinated; there are three times as many d sites as b sites in the crystal) and only one anion site showing a tetrahedral coordination. The possible anion interstitial sites are 8a, 16c, and 24d in Wyckoff's notation, which all feature 6-fold coordination by oxygen. Our calculations as presented in Table 7 show that both anion and cation interstitials have lower energies in the 16c site. On relaxation, the anionic interstitial changes its coordination from octahedral to tetrahedral with the nearest lattice oxygen ions moving substantially outwards (by 0.349 Å) and the nearest cations inwards (by 0.126 Å for site b and by 0.339 Å for site d). Compared to previous calculations, we predict a substantially lower energy of oxygen at interstitial sites in In2O3 by ∼5.0 eV compared to Warschkow and by ∼1.2 eV compared to Walsh et al. This big difference, in particular from the former report, can perhaps be attributed to an incomplete relaxation of the lattice around the interstitial site (possibly, due to an appearance of a small barrier for the movement of next nearest neighbours with some sets of interatomic potentials).
The oxygen vacancy energies are 26.64 eV and 22.59 eV for SnO2 and In2O3, respectively, based on a more accurate simulation using a hybrid quantum mechanical/molecular mechanical (QM/MM) approach.25 (Note that there is uncertainty in these values as they require a value for the second electron affinity of O, as discussed above if we are to make direct comparison with Mott–Littleton values.) Our calculated values of 24.02 eV and 23.16 eV for SnO2 and In2O3, respectively, are much closer to the DFT based estimates than those from previous atomistic simulations that predicted 19.39 eV for SnO232 and 20.99 eV for In2O3.22
3.4. Oxygen vacancy formation
The loss of oxygen from the lattice can be represented in the Kröger–Vink notation as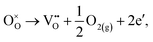 | (3.1) |
Here the reaction is assumed to occur in an environment containing an excess of O2(g), which is often referred to as “O-rich conditions” but corresponds approximately to the sample of interest being in air under ambient conditions. The neutral oxygen vacancy generated in the first step will provide two free electrons on ionisation. The energetics of this reduction process is
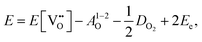 | (3.2) |
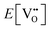 is the oxygen vacancy defect energy, DO2 is the oxygen molecule dissociation energy (5.136 eV48), A1–2O is the sum of the first and second electron affinities of oxygen, and Ee is the energy of introducing an electron into the conduction band from the vacuum (electron affinity of the material). This description is valid for any oxide material.
is the oxygen vacancy defect energy, DO2 is the oxygen molecule dissociation energy (5.136 eV48), A1–2O is the sum of the first and second electron affinities of oxygen, and Ee is the energy of introducing an electron into the conduction band from the vacuum (electron affinity of the material). This description is valid for any oxide material.
Alternatively, when the oxygen partial pressure is low, so that the sample of interest is under strongly reducing conditions (“O-poor conditions”), oxygen vacancy creation in SnO2 proceeds as:
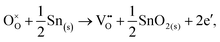 | (3.3) |
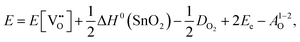 | (3.4) |
The calculated oxygen vacancy formation energies of SnO2 are 3.40 eV under O-rich/Sn-poor conditions and 0.36 eV under O-poor/Sn-rich conditions. Freeman and Catlow32 reported 3.65 eV for the O-rich conditions. If we include the correction discussed above their formation energy would shift down to 1.55 eV, significantly lower than our result. Using periodic ab initio models with the PBE0 exchange and correlation density functional, Scanlon et al.5 have reported the corresponding doubly charged oxygen vacancy formation energy to be ca. 6 eV under O-rich, and ca. 3.4 eV under O-poor conditions (extracted from Fig. 2 of ref. 5), which is somewhat different from the result of Ágoston et al.,7 who using the same density functional have reported the value of about 2.9 eV under O-poor conditions. More recently, Buckeridge et al.25 have used hybrid QM/MM embedded-cluster calculations, and have obtained with a meta-GGA hybrid BB1K exchange and correlation functional the values of 5.24 eV under O-rich and 2.20 eV under O-poor conditions. The energies of defect formation from the latter study are of course shifted from those in our study by the same amount as that reported above for the defect energies (the difference being due to the change in the reference point). Thus, our values are still underestimated by about 1.8 eV – again an improvement in the older work.
Direct comparisons of our results with experiment are difficult to make, which is why we judge the accuracy of our method by comparison with other theoretical studies. We cannot derive defect transition levels, which are the most common properties used for comparison with experiment. The measured heat of reduction of SnO2 under atmospheric conditions, which should be comparable to O-rich conditions, is 4.09 eV.49 This value should be compared with the formation energy of the oxygen vacancy in the neutral charge state, which unfortunately we cannot simulate accurately using the Born model and Mott–Littleton approach. We note that the density functional theory studies mentioned above do produce results that compare well with the experimental value.
For In2O3, the formation of the oxygen vacancy under In-rich/O-poor conditions can be described as:
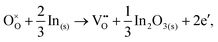 | (3.5) |
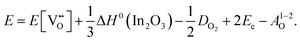 | (3.6) |
We obtain the energies of 2.76 eV under O-rich/In-poor conditions and −0.49 eV under O-poor/In-rich conditions for In2O3. Compared with SnO2, the results are in a similar correspondence with embedded-cluster based calculations by Buckeridge et al. (2.45 eV under O-rich and −0.75 eV under O-poor conditions using BB1k).25 Ágoston et al.7 have reported the oxygen vacancy formation energy of 1.2 eV under O-poor conditions using a hybrid HSE06 exchange and correlation functional.
We note that the calculations of defect formation energies, such as those presented in this section, are routinely determined using electronic structure techniques such as DFT. Moreover, such approaches should give results that are more accurate than those obtained using classical models. While possible for many cases involving point defects at the dilute limit, computing defect energetics using DFT (or beyond) for larger scale systems such as solid solutions, extended surfaces, interfaces or grain boundaries and materials containing line defects becomes intractable. We have demonstrated that our interatomic potential model can give defect formation energies comparable with those obtained using DFT. We can therefore conclude that the approach will be suitable to study defects in extended systems, as the lower computational load offers significant advantages over most electronic structure techniques. Such studies will be reported in future work. We now further validate our method by studying intrinsic disorder in more detail, and by analysing tin substitution and complex formation in ITO.
3.5. Frenkel and Schottky defects
Based on the calculated point defect formation energy (Tables 4 and 5) and the calculated lattice energy (E[SnO2] = −122.32 eV, E[In2O3] = −150.01 eV), we can predict the dominant mechanism of the intrinsic ionic disorder and defect formation. In Tables 8 and 9 we compare the relevant Frenkel and Schottky defects in SnO2 and In2O3.| Defect | Defect energy per defect (eV) | |
|---|---|---|
| Present work | Walsh et al.22 | |
| Anion Frenkel | 3.67 | 3.19 |
| Cation Frenkel | 7.00 | 6.85 |
| Schottky | 6.16 | 4.44 |
| Anti-Schottky | 3.83 | 4.87 |
An ion that leaves its lattice site and occupies a non-interacting interstitial site will form a Frenkel defect pair. The formation energies for anion and cation Frenkel defect pairs in SnO2 are calculated as:
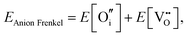 | (3.7) |
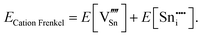 | (3.8) |
For Schottky defects, one formula unit of the compound is removed, while for the anti-Schottky defect, one formula unit of the compound is added as a stoichiometric interstitial:
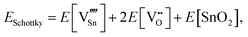 | (3.9) |
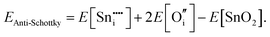 | (3.10) |
According to the calculations, we find that the primary type of the intrinsic disorder is the anion Frenkel pair in SnO2, which agrees with the prediction from two preceding atomistic studies of Freeman and Catlow32 and Hines et al.47 Based on the lowest-energy anion and cation interstitials and vacancies, a similar conclusion can be drawn on the dominance of the anion Frenkel pair in In2O3. We note that the energies of the intrinsic disorder reactions in SnO2 are high indicating that there will be very low levels of thermally generated defects. The Frenkel energies in In2O3 are somewhat lower.
3.6. Electron and hole reaction energies
ITO is a solid solution, in which Sn is doped into In2O3 at low concentrations, at which the electronic mechanism of charge compensation dominates,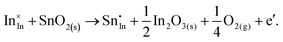 | (3.11) |
The chemical potential of gaseous oxygen could shift the balance to favour the formation of interstitial oxygen instead:
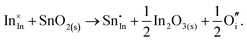 | (3.12) |
The calculated energies of reactions (3.11) and (3.12) of −2.24 eV and 0.05 eV, however, clearly show the dominance of the electronic disorder, which will be further discussed in the next section (see Table 11 below for the relevant defect energies). We have assumed O-rich conditions in the above reactions; the corresponding energies for O-poor conditions are obtained by shifting the energy downwards by 0.86 eV.
By combining the two reactions, the general reaction for the exchange of an electron in the conduction band for an oxygen interstitial is given by:
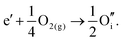 | (3.13) |
Similar defect reactions can be written for both electron and hole carriers, in which they are charge compensated by ionic defects either under O-rich (cation-poor) or O-poor (cation-rich) conditions, as has been proposed in earlier studies on equilibrium between electronic and ionic defects of wide band gap materials.50–52
The corresponding processes and their reaction energies are listed in Table 10. In both materials, holes are unstable and tend to form point defects, with energies −1.32 eV for In2O3 and −1.90 eV for SnO2 under O-rich conditions. In contrast, electrons are stable in both SnO2 and In2O3, which confirms and rationalises the n-type nature of these materials corroborating further the methodology we have established in our previous studies on wide band-gap semiconductors.25,53
3.7. Doping and defect cluster formation in In2O3
To understand the balance of point defects and charge carriers in ITO in more detail, we will first consider the limit of infinite dilution where a Sn ion can occupy two cationic lattice sites 8b and 24d, in Wyckoff's notation, and three interstitial sites including 8a, 16c (a lattice O site in the fluorite structure) and 24d. The corresponding reactions (3.11) and (3.12) for Sn substituting on the cationic sites are presented above. Alternatively, we can consider Sn stabilising on interstitial sites in In2O3. Our calculation shows that, as with intrinsic interstitial defects, interstitial tin also has a lower energy in the 16c site. These interstitial impurities can be compensated by oxygen interstitials according to (assuming O-rich conditions):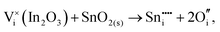 | (3.14) |
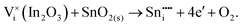 | (3.15) |
The energies of these reactions are, however, high (12.08 eV and 2.94 eV, respectively) (see Table 11 for the relevant defect energies), which should be compared with 0.05 and −2.24 eV for reactions (3.12) and (3.11). We, therefore, confirm that substitutional incorporation of Sn in In2O3 is much more favourable than interstitial incorporation, but in both cases compensation by electron carriers will dominate.
| Defect | Defect energy (eV) | Binding energy (eV) | Wyckoff's site | |
|---|---|---|---|---|
| Present work | Warschkow et al.23 | |||
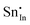
|
−39.35 | −35.47 | 8b | |
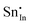
|
−39.34 | −35.52 | 24d | |
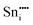
|
−76.94 | 8a | ||
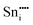
|
−78.58 | 16c | ||
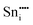
|
−76.30 | 24d | ||
| [OiSni]˙˙ | −98.21 | −3.80 | ||
| [2OiSni] | −116.82 | −6.59 | ||
| [3OiSni]′′ | −134.32 | −8.27 | ||
A preference for the substitutional site has also been seen experimentally, but, intriguingly a study using Mössbauer spectroscopy54 indicated that tin atoms tend to substitute for indium at the b-site rather than the d-site, despite there being three times more d than b sites. Our calculations show that the point defect energy of  is only 0.01 eV lower than that of
is only 0.01 eV lower than that of  . Although the energy ordering we obtain is compatible with experiment, the difference is so small that it cannot be the source of the observed higher b-site occupation.
. Although the energy ordering we obtain is compatible with experiment, the difference is so small that it cannot be the source of the observed higher b-site occupation.
Next, we consider the formation of defect clusters involving Sn impurities in In2O3, which, while possibly affecting the performance of ITO in technological applications, may also change the balance in the relative energies of substitutional vs. interstitial incorporation and, furthermore, the dominant compensation mechanism. Our results so far indicate that electron compensation is most likely, but of the possible ionic compensation species, the most probable for both substitutional and interstitial Sn under oxygen rich conditions would be an interstitial oxygen. We recall that the interstitial oxygen in In2O3 is tetrahedrally coordinated by four cations, with one b-site (¼, ¼, ¼) cation and three d-site (x, 0, ¼) cations, as shown in Fig. 3. The next-nearest-neighbour cationic sites around the interstitial oxygen are three b sites and nine d sites. We will consider defect clustering within the first and second coordination shells of the interstitial oxygen.
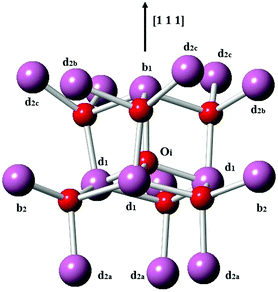 | ||
| Fig. 3 Interstitial oxygen in In2O3. In ions are represented by larger purple spheres while O ions are represented by smaller red spheres. | ||
The binding energy of a cluster is calculated as the energy of the cluster minus the energies of the isolated species comprising that cluster. The resulting defect binding energies of clusters involving Sn and O interstitial complexes, including up to three interstitial O, are given in Table 11, while those involving substitutional Sn, with a ratio of up to four Sn to one O are listed in Table 12. For each cluster type of different Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O stoichiometry, only the most stable combinations are given. Following the notation used by Warschkow et al.,23 we use the symbol “·” to represent the first cationic shell and “–” for the second cationic shell. From the results in Table 11, we see that forming clusters between interstitial Sn and O lowers the energy significantly. We note, however, that, combining the energies of reactions (3.15) and twice that of (3.13) and the binding energy of the complex involving one interstitial O, the formation energy of the double donor complex is 3.71 eV, a considerable reduction over that of reaction (3.14), which compensates the interstitial Sn by two interstitial O, but still much higher than the energies of the reactions involving substitutional Sn formation. Clusters involving more O interstitials result in even higher formation energies, indicating that, while cluster formation does lower the energy for the incorporation of interstitial Sn, substitutional Sn will remain in the lower energy solution mode.
O stoichiometry, only the most stable combinations are given. Following the notation used by Warschkow et al.,23 we use the symbol “·” to represent the first cationic shell and “–” for the second cationic shell. From the results in Table 11, we see that forming clusters between interstitial Sn and O lowers the energy significantly. We note, however, that, combining the energies of reactions (3.15) and twice that of (3.13) and the binding energy of the complex involving one interstitial O, the formation energy of the double donor complex is 3.71 eV, a considerable reduction over that of reaction (3.14), which compensates the interstitial Sn by two interstitial O, but still much higher than the energies of the reactions involving substitutional Sn formation. Clusters involving more O interstitials result in even higher formation energies, indicating that, while cluster formation does lower the energy for the incorporation of interstitial Sn, substitutional Sn will remain in the lower energy solution mode.
Sn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Oi ratio Oi ratio |
Defect cluster | Complex binding energy (eV) | |
|---|---|---|---|
| Present work | Warschkow et al.23 | ||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [SnIn·Oi]′ 1 [SnIn·Oi]′ |
(SnIn(d)·Oi)′ | −1.54 | −1.29 |
| (SnIn(b)·Oi)′ | −1.19 | −0.89 | |
| (SnIn(b)–Oi)′ | −0.93 | −1.16 | |
| (SnIn(d)–Oi)′ | −0.85 | −1.10 | |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [2SnIn·Oi]× 1 [2SnIn·Oi]× |
(2SnIn(d)·Oi)× | −2.64 | −1.91 |
| (SnIn(b)·SnIn(d)·Oi)× | −2.26 | −1.54 | |
| (SnIn(b)–SnIn(d)·Oi)× | −2.23 | −2.09 | |
| (SnIn(d)–SnIn(d)·Oi)× | −2.15 | −2.05 | |
| (SnIn(b)–SnIn(b)·Oi)× | −1.74 | −1.54 | |
| (SnIn(d)–SnIn(b)·Oi)× | −1.73 | −1.63 | |
| (2SnIn(b)–Oi)× | −1.66 | −2.08 | |
| (SnIn(b)·SnIn(d)–Oi)× | −1.58 | −2.00 | |
| (2SnIn(d)–Oi)× | −1.50 | −1.97 | |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [3SnIn·Oi]˙ 1 [3SnIn·Oi]˙ |
(3SnIn(d)·Oi)˙ | −3.31 | −1.86 |
| (SnIn(b)·2SnIn(d)·Oi)˙ | −2.90 | −1.49 | |
| (SnIn(d)–2SnIn(d)·Oi)˙ | −2.89 | −2.14 | |
| (2SnIn(b)–SnIn(d)·Oi)˙ | −2.55 | −2.35 | |
| (SnIn(b)·SnIn(d)–SnIn(d)·Oi)˙ | −2.44 | −2.31 | |
| (2SnIn(d)–SnIn(d)·Oi)˙ | −2.37 | −2.24 | |
| (3SnIn(b)–Oi)˙ | −2.18 | −2.55 | |
| (2SnIn(b)·SnIn(d)–Oi)˙ | −2.01 | −2.43 | |
| (2SnIn(d)–SnIn(b)·Oi)˙ | −1.96 | −1.88 | |
| (SnIn(b)·2SnIn(d)–Oi)˙ | −1.85 | −2.36 | |
| (3SnIn(d)–Oi)˙ | −1.83 | −2.33 | |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [4SnIn·Oi]˙˙ 1 [4SnIn·Oi]˙˙ |
(SnIn(b)·3SnIn(d)·Oi)˙˙ | −3.12 | −0.88 |
For clusters of nearest-neighbour 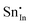 and
and 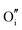 , the results show that substitutional tin has a lower energy in the d cation site over the b site. When substituting the same number of indium ions, the binding energies of clusters which contain
, the results show that substitutional tin has a lower energy in the d cation site over the b site. When substituting the same number of indium ions, the binding energies of clusters which contain  are at least 0.4 eV lower than the energies of clusters only including
are at least 0.4 eV lower than the energies of clusters only including  . Clustering of Sn proves to be stabilising from one to four substitutional Sn with binding energies of −1.54, −1.32, −1.10 and −0.78 eV per Sn ion.
. Clustering of Sn proves to be stabilising from one to four substitutional Sn with binding energies of −1.54, −1.32, −1.10 and −0.78 eV per Sn ion.
After taking into account the next-nearest-neighbour shell, we find a much lower energy for the tin substituting for indium at d sites within the first coordination shell of the O interstitial forming (SnIn(d)·Oi)′, (2SnIn(d)·Oi)× and (3SnIn(d)·Oi)˙. As the latter proves to be most energetically favoured, we conclude that single electron donor complexes will donate electron charge carriers under thermodynamic equilibrium with up to three impurities per one electron. Therefore, a strategy to make doping more effective would require preventing Sn ions from clustering under oxygen poor conditions. Our prediction of the Sn dominant occupation of d sites on the cationic sublattice corroborates the report of Warschkow et al.,23 who also found a strong d-site preference.
Considering defect formation energies of complexes between substitutional Sn and interstitial O, we should account for all involved reactants as shown in eqn (3.16)–(3.19):
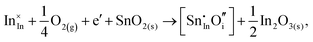 | (3.16) |
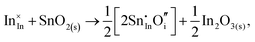 | (3.17) |
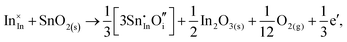 | (3.18) |
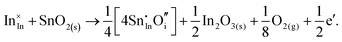 | (3.19) |
The calculated reaction energies allow us to compare the stability of Sn in different complexes with elementary substitutional sites. We obtain 1.14, −0.69, −1.80 and −1.87 eV for the respective reactions, which are, however, still above the SnIn energy of formation of −2.24 eV. From these observations we conclude that electronic rather than oxygen interstitial compensation will dominate in Sn doped In2O3, but that any available interstitial O will be complexed with Sn.
4. Conclusions
We have developed a new set of transferable pairwise interatomic potentials for SnO2 and In2O3. The new potentials offer an improvement over the previously available models, in particular for the lattice and defect properties, and give defect formation energies comparable with those obtained using DFT. Using the newly developed potentials, we have investigated isolated intrinsic defects along with electron and hole formation; Sn impurities in In2O3 and effects of impurity clustering, and their thermodynamic stability. Our calculations show a significant improvement – compared to older parameterisations that can be found in the literature – of lattice energies and oxygen vacancy formation energies of both SnO2 and In2O3 that are in acceptable agreement with experiment and available QM/MM results.25 The study of intrinsic defects reveals a lower energy for the formation of anion Frenkel pairs in both binary oxide materials, which, however, have higher energies than the formation energy of positively charged oxygen vacancies compensated by electrons and with oxygen loss. We show unambiguously the dominant electronic compensation mechanism stabilising Sn impurities at cation substitutional sites in In2O3. The study of impurity clustering with interstitial oxygen reveals a progressive stabilisation of Sn on cluster growth, which points to an increasing role of the ionic charge compensation with the level of doping in In2O3. Work is in progress on modelling ITO at finite levels of doping, results of which will be reported in the near future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Qing Hou acknowledges the support from the China Scholarship Council (CSC). We also acknowledge technical help from Alex Ganose and Mia Baise, and discussion with Julian Gale. John Buckeridge and Richard Catlow acknowledge funding from the EPSRC (grant EP/K016288/1).References
- B. G. Lewis and D. C. Paine, MRS Bull., 2000, 25, 22–27 CrossRef CAS.
- C. G. Granqvist and A. Hultåker, Thin Solid Films, 2002, 411, 1–5 CrossRef CAS.
- S. K. Park, J. I. Han, W. K. Kim and M. G. Kwak, Thin Solid Films, 2001, 397, 49–55 CrossRef CAS.
- O. Bierwagen, Semicond. Sci. Technol., 2015, 30, 024001 CrossRef.
- D. O. Scanlon and G. W. Watson, J. Mater. Chem., 2012, 22, 25236 RSC.
- S. Samson and C. G. Fonstad, J. Appl. Phys., 1973, 44, 4618–4621 CrossRef CAS.
- P. Ágoston, K. Albe, R. M. Nieminen and M. J. Puska, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef PubMed.
- Z. M. Jarzebski and J. P. Marton, J. Electrochem. Soc., 1976, 123, 333C–346C CrossRef CAS.
- Z. M. Jarzebski and J. P. Marton, J. Electrochem. Soc., 1976, 123, 299C–310C CrossRef CAS.
- Z. M. Jarzebski and J. P. Marton, J. Electrochem. Soc., 1976, 123, 199C–205C CrossRef CAS.
- A. K. Singh, A. Janotti, M. Scheffler and C. G. Van De Walle, Phys. Rev. Lett., 2008, 101, 1–4 Search PubMed.
- G. Rupprecht, Z. Phys., 1954, 139, 504–517 CrossRef CAS.
- S. H. Brewer and S. Franzen, Chem. Phys., 2004, 300, 285–293 CrossRef CAS.
- F. Fuchs and F. Bechstedt, Phys. Rev. B, 2008, 77, 155107 CrossRef.
- P. Erhart, A. Klein, R. G. Egdell and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–4 CrossRef.
- P. Reunchan, X. Zhou, S. Limpijumnong, A. Janotti and C. G. Van De Walle, Curr. Appl. Phys., 2011, 11, S296–S300 CrossRef.
- P. Ágoston, C. Körber, A. Klein, M. J. Puska, R. M. Nieminen and K. Albe, J. Appl. Phys., 2010, 108, 53511 CrossRef.
- D. Mora-Fonz, T. Lazauskas, M. R. Farrow, C. R. A. Catlow, S. M. Woodley and A. A. Sokol, Chem. Mater., 2017, 29, 5306–5320 CrossRef CAS.
- D. Mora-Fonz, T. Lazauskas, S. M. Woodley, S. T. Bromley, C. R. A. Catlow and A. A. Sokol, J. Phys. Chem. C, 2017, 121, 16831–16844 CrossRef CAS.
- A. J. Logsdail, D. O. Scanlon, C. R. A. Catlow and A. A. Sokol, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 1–8 CrossRef.
- A. J. Logsdail, D. Mora-Fonz, D. O. Scanlon, C. R. A. Catlow and A. A. Sokol, Surf. Sci., 2015, 642, 58–65 CrossRef CAS.
- A. Walsh, C. R. A. Catlow, A. A. Sokol and S. M. Woodley, Chem. Mater., 2009, 21, 4962–4969 CrossRef CAS.
- O. Warschkow, D. E. Ellis, G. B. Gonzalez and T. O. Mason, J. Am. Ceram. Soc., 2003, 86, 1700–1706 CrossRef CAS.
- G. Frank and H. Köstlin, Appl. Phys. A: Mater. Sci. Process., 1982, 27, 197–206 CrossRef.
- J. Buckeridge, C. R. A. Catlow, M. R. Farrow, A. J. Logsdail, D. O. Scanlon, T. W. Keal, P. Sherwood, S. M. Woodley, A. A. Sokol and A. Walsh, Phys. Rev. Mater., 2018, 2, 054604 CrossRef.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press, 1954 Search PubMed.
- T. S. Bush, J. D. Gale, C. R. A. Catlow and P. D. Battle, J. Mater. Chem., 1994, 4, 831 RSC.
- B. G. Dick Jr and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- C. R. A. Catlow, J. Chem. Soc., Faraday Trans. 2, 1989, 85(5), 335–340 RSC.
- J. D. Gale and A. L. Rohl, The General Utility Lattice Program (GULP), Mol. Simul., 2003, 29(5), 291–341 CrossRef CAS.
- C. M. Freeman and C. R. A. Catlow, J. Solid State Chem., 1990, 85, 65–75 CrossRef CAS.
- M. A. McCoy, R. W. Grimes and W. E. Lee, Philos. Mag. A, 1997, 76, 1187–1201 CAS.
- T. C. Waddington, Adv. Inorg. Chem. Radiochem., 1959, 1, 157–221 CrossRef CAS.
- J. Haines and J. M. Léger, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11144–11154 CrossRef CAS.
- W. H. Baur and A. A. Khan, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 2133–2139 CrossRef CAS.
- R. Summitt, J. Appl. Phys., 1968, 39, 3762–3767 CrossRef CAS.
- E. Chang and E. K. Graham, J. Geophys. Res., 1975, 80, 2595–2599 CrossRef CAS.
- M. F. C. Ladd and W. H. Lee, Acta Crystallogr., 1960, 13, 959 CrossRef CAS.
- K. Reimann and M. Steube, Solid State Commun., 1998, 105, 649–652 CrossRef CAS.
- A. J. Nozik and R. Memming, J. Phys. Chem., 1996, 100, 13061–13078 CrossRef CAS.
- A. Klein, C. Körber, A. Wachau, F. Säuberlich, Y. Gassenbauer, R. Schafranek, S. P. Harvey and T. O. Mason, Thin Solid Films, 2009, 518, 1197–1203 CrossRef CAS.
- M. V. Hohmann, P. Goston, A. Wachau, T. J. M. Bayer, J. Brötz, K. Albe and A. Klein, J. Phys.: Condens. Matter, 2011, 23, 334203 CrossRef PubMed.
- R. D. Shannon, J. L. Gillson and R. J. Bouchard, J. Phys. Chem. Solids, 1977, 38, 877–881 CrossRef CAS.
- I. Hamberg and C. G. Granqvist, J. Appl. Phys., 1986, 60, R123–R159 CrossRef CAS.
- Z. M. Jarzebski, Phys. Status Solidi, 1982, 71, 13–41 CrossRef CAS.
- R. I. Hines, N. L. Allan and W. R. Flavell, J. Chem. Soc., Faraday Trans., 1996, 92, 2057–2063 RSC.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2014 Search PubMed.
- P. Charvin, S. Abanades, F. Lemont and G. Flamant, AIChE J., 2008, 54, 2759–2767 CrossRef CAS.
- C. R. A. Catlow, A. A. Sokol and A. Walsh, Chem. Commun., 2011, 47, 3386–3388 RSC.
- A. Walsh, J. Buckeridge, C. R. A. Catlow, A. J. Jackson, T. W. Keal, M. Miskufova, P. Sherwood, S. A. Shevlin, M. B. Watkins, S. M. Woodley and A. A. Sokol, Chem. Mater., 2013, 25, 2924–2926 CrossRef CAS.
- A. Walsh, C. R. A. Catlow, M. Miskufova and A. A. Sokol, J. Phys.: Condens. Matter, 2011, 23, 334217 CrossRef PubMed.
- J. Buckeridge, C. R. A. Catlow, D. O. Scanlon, T. W. Keal, P. Sherwood, M. Miskufova, A. Walsh, S. M. Woodley and A. A. Sokol, Phys. Rev. Lett., 2015, 114, 016405 CrossRef CAS PubMed.
- K. Nomura, Y. Ujihira, S. Tanaka and K. Matsumoto, Hyperfine Interact., 1988, 42, 1207–1210 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |