Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anisotropy of CoII transferred to the Cr7Co polymetallic cluster via strong exchange interactions†
Elena
Garlatti‡
 a,
Tatiana
Guidi‡
a,
Tatiana
Guidi‡
 b,
Alessandro
Chiesa‡
ac,
Simon
Ansbro‡
de,
Michael L.
Baker‡
f,
Jacques
Ollivier‡
e,
Hannu
Mutka‡
e,
Grigore A.
Timco‡
b,
Alessandro
Chiesa‡
ac,
Simon
Ansbro‡
de,
Michael L.
Baker‡
f,
Jacques
Ollivier‡
e,
Hannu
Mutka‡
e,
Grigore A.
Timco‡
 d,
Inigo
Vitorica-Yrezabal‡
d,
Eva
Pavarini‡
cg,
Paolo
Santini‡
a,
Giuseppe
Amoretti‡
a,
Richard E. P.
Winpenny‡
d,
Inigo
Vitorica-Yrezabal‡
d,
Eva
Pavarini‡
cg,
Paolo
Santini‡
a,
Giuseppe
Amoretti‡
a,
Richard E. P.
Winpenny‡
 d and
Stefano
Carretta‡
d and
Stefano
Carretta‡
 *a
*a
aDipartimento di Scienze Matematiche, Fisiche e Informatiche, Università di Parma, I-43124 Parma, Italy. E-mail: stefano.carretta@unipr.it
bISIS Facility, Rutherford Appleton Laboratory, OX11 0QX Didcot, UK
cInstitute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany
dThe School of Chemistry, Photon Science Institute, The University of Manchester, M13 9PL Manchester, UK
eInstitut Laue-Langevin, 71 Avenue des Martyrs CS 20156, Grenoble Cedex 9 F-38042, France
fThe School of Chemistry, The University of Manchester at Harwell, Didcot, OX11 0FA, UK
gJARA High-Performance Computing, RWTH Aachen University, 52062 Aachen, Germany
First published on 7th March 2018
Abstract
The Cr7Co ring represents a model system to understand how the anisotropy of a CoII ion is transferred to the effective anisotropy of a polymetallic cluster by strong exchange interactions. Combining sizeable anisotropy with exchange interactions is an important point in the understanding and design of new anisotropic molecular nanomagnets addressing fundamental and applicative issues. By combining electron paramagnetic resonance and inelastic neutron scattering measurements with spin Hamiltonian and ab initio calculations, we have investigated in detail the anisotropy of the CoII ion embedded in the antiferromagnetic ring. Our results demonstrate a strong and anisotropic exchange interaction between the Co and the neighbouring Cr ions, which effectively transmits the anisotropy to the whole molecule.
1 Introduction
Single-Molecule Magnets (SMMs) are the first generation of molecular nanomagnets and have been considered as possible means to store information in single molecules since the early 1990s.1,2 Indeed, the combination of a large magnetic moment and a strong easy-axis magnetic anisotropy creates in these systems a double-well potential with an energy barrier for the reorientation of the magnetization, resulting in magnetic bistability for the single molecule below the so-called “blocking temperature”. Thus, increasing the temperature range where molecules display SMM behaviour, in order to build miniaturized memory units, is one of the main goals of the current research in molecular magnetism. Originally this was sought in exchange-coupled 3d-metal cage complexes, by exploiting high-spin ions like FeIII, MnII or CrIII to increase the total-spin of the molecular ground state.3–7 However, the quenching of the orbital momentum and the resulting small single-ion anisotropy have strongly limited the maximum achievable barriers. Recently it has been shown that monometallic complexes based on 3d transition metal ions can exhibit appreciably enhanced magnetic anisotropy with certain axial coordination environments that minimize Jahn–Teller distortions, leading to an almost unquenched orbital momentum.8 The second attempt has been to use the large anisotropy of rare-earth ions. Indeed, after the discovery of SMM behaviour in mononuclear TbIII and DyIII complexes,9,10 much focus has been on the design of highly-axial environments for single lanthanide ions, with the aim to reduce the efficiency of the tunnelling mechanism and to increase the blocking temperature of the molecule.11–15 This has led to a remarkable recent report of a DyIII sandwich complex that retains magnetization to 60 K.16 These advances with mononuclear lanthanide-based SMMs are important but distract from one crucial issue that has only been partially addressed, that is understanding magnetic exchange interactions in molecules containing highly anisotropic ions. This is important not only in dinuclear LnIII complexes, where the SMM behaviour results from the interplay between ligand fields and exchange interactions,17,18 but also in more diverse areas ranging from quantum information to biology. For example, highly anisotropic FeII centers are found in the active sites of proteins.19 Thus, we have focused our attention towards polymetallic complexes containing CoII, as test systems to investigate anisotropic exchange interactions. Indeed, CoII in the proper coordination environment can be highly anisotropic thanks to its non-quenched orbital moment.SMMs containing CoII ions have been largely investigated in the last years, thanks to their potential for the production of very large magnetic anisotropies and thus higher blocking temperatures.20–22 However, the interpretation of magnetic data for polynuclear complexes containing CoII centres is often difficult, due to their important orbital contribution. In particular, there is now a literature on CoII-based SMMs, but the precise nature of the magnetic exchange in these systems is still a crucial open question that need to be investigated.20 There have been several papers studying homometallic complexes including CoII23,24 and lanthanides,25 where exchange interactions have been investigated with different spectroscopic techniques, but studies where a highly anisotropic ion is included in a larger polymetallic complex remain rare. Anisotropic ions (such as CoII) coupled with other magnetic ions are important building blocks to implement efficient and scalable quantum information schemes.26 Moreover, this kind of compounds is expected to display rich physics associated with the unquenched orbital degrees of freedom. For instance, in antiferromagnetic highly anisotropic ring-like clusters the low-frequency dynamics should be characterized by Néel Vector Tunneling.27–32 Thus, it is important to understand in detail the anisotropic exchange interactions involving a CoII ion embedded in a large polymetallic cluster.
In this work we exploit the octagonal heterometallic ring [NH2Me2][Cr7CoF8(O2CCtBu)16] (hereafter Cr7Co ring) as a model system to understand how the insertion of an anisotropic Co ion strongly coupled to the Cr ones affects the anisotropy of the whole molecule. Cr–Cr exchange interactions and the Cr zero-field splittings have been already determined in the isostructural Cr8 and Cr7M (M = Ni, Mn, Zn) compounds.32–35 Thus, the combination of Electron Paramagnetic Resonance (EPR) and Inelastic Neutron Scattering (INS) techniques with ab initio and spin Hamiltonian calculations,36 allows us to investigate in detail the anisotropy of the CoII ion embedded in the antiferromagnetic ring and the Cr–Co anisotropic exchange interactions. By combining EPR measurement on the isotructural Ga7Co compound with ab initio calculations, we demonstrate that the CoII ion in this environment is highly anisotropic and we are able to determine the spectroscopic splitting tensor gCo. We have then performed INS measurements on both powder samples of Cr7Co at different temperatures and on single-crystal samples with different applied magnetic fields. Neutron scattering intensities on single-crystal samples have also been measured as a function of energy transfer and neutron momentum transfer (Qx, Qy, Qz) with the 4-dimensional INS (4D-INS) technique.32,37 Guided by ab initio calculations based on the density-functional theory + many-body approach (DFT + MB),36 and thanks to the thorough set of INS measurements described above, we determine the Cr–Co isotropic coupling J and anisotropic exchange tensor D. In agreement with ab initio calculations, we find that Cr7Co is characterised by a strong and highly anisotropic Cr–Co exchange interaction, which effectively transmits the anisotropy of CoII to the whole molecule. As discussed in the last part of the paper, these results suggest a promising way to reach the strong coupling regime between photons and individual molecules,38 a crucial step for building a scalable molecule-based quantum information architecture.
2 Results
2.1 Synthesis and structural considerations
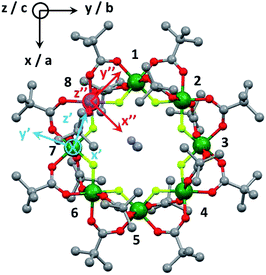
Cr7Co was made by the method described in ref. 39 with minor modifications detailed in the ESI.† Crystals large enough for INS studies were grown by evaporation of a solution of Cr7Co dissolved in Et2O/MeCN.The structure of Cr7Co is an octagon of metals bridged on each M⋯M edge by one fluoride and two pivalate ligands (Fig. 1). Therefore each metal is six-coordinate, with a F2O4 coordination sphere. At the centre of the ring is a dimethylammonium cation where the protonated N atom is involved in hydrogen-bonding to bridging fluorides. Using this cation and solvents the Cr7Co ring crystallises in a tetragonal crystal system with a four-fold rotation axis passing through the N-atom of the cation. This four-fold axis leads to the CoII ion being disordered about the eight metal sites of the ring, and to disorder of the cation.
2.2 Spin Hamiltonian model
The Cr7Co ring contains seven isotropic CrIII ions, behaving as pure spin si = 3/2, and one anisotropic CoII ion, that can be described at low temperatures as an effective spin sCo = 1/2, with highly anisotropic g tensor and exchange interactions40 (see the following Section). The magnetic properties of Cr7Co can therefore be described by the following spin Hamiltonian (with the Co ion on site 8):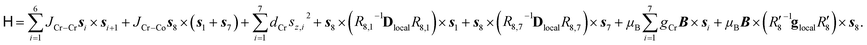 | (1) |
The first two terms in eqn (1) describe the dominant isotropic exchange interactions, while the third term corresponds to the axial single-ion zero-field-splitting term acting on Cr ions (with the z-axis perpendicular to the plane of the ring). The fourth and fifth terms take into account the anisotropic exchange interaction of the CoII ion with the two neighbouring Cr ions (labelled as s1 and s7 respectively), which is described by the traceless diagonal tensor Dlocal, referred to its local principal axis on each Cr–Co bond, with diagonal elements Dyy, Dzz and Dxx = −(Dyy + Dzz). The last terms in eqn (1) describe the Zeeman interaction with an applied magnetic field, where the spectroscopic splitting tensor is assumed isotropic for CrIII (gCr = 1.98) and anisotropic for the CoII ion (glocal). The local principal axis for both Dlocal and glocal tensors have been determined by the DFT + MB approach described below and are depicted in Fig. 1. The matrices R8,1−7 and R′8 in eqn (1) transform the Dlocal and glocal tensors from their local reference frames to the laboratory/unit cell reference system (see Fig. 1). At last, the delocalization of the CoII ion along the ring in the crystal (equal probability on each site) is taken into account in modeling the experimental results. Cr–Cr exchange interactions and Cr zero-field splittings have already been determined in the isostructural Cr8 and Cr7M (M = Ni, Mn, Zn) compounds, yielding JCr–Cr = 16.9 K and dCr = −0.44 K.33–35 Hence, here we can focus on CoII and Cr–Co interactions to extract JCr–Co, Dlocal and glocal by combining EPR and INS data with the spin Hamiltonian and ab initio calculations.
2.3 Ab initio DFT + MB results
Ab initio calculations based on the DFT + MB approach described in ref. 36 have been used as a guide for fitting the spin Hamiltonian parameters. In contrast with conventional DFT approaches, relying on approximations of the exchange-correlation functional (the most popular being LDA/GGA or their extensions, such as the hybrid B3LYP), here strong electron–electron correlations are explicitly included in the description of the low energy 3d electrons. This is achieved by constructing a system specific generalized Hubbard model (see details in the ESI†), explicitely including a Coulomb tensor, as well as inter-site electron hopping, crystal field splittings and spin orbit effects. The parameters of this model are deduced ab initio, by means of DFT based calculations either in the local-density (one-electron terms) or in the constrained-local-density approximations (Coulomb tensor). In a second step, the spin Hamiltonian is obtained by a canonical transformation of the Hubbard model, without any a priori assumption on its form.This method ensures an accurate description of strongly correlated systems (such as MNMs), as shown also by a recent study of a family of Cr7M compounds isostructural to Cr7Co.35 CoII (3d7 electronic configuration, S = 3/2) is embedded in a distorted octahedral cage of ligands (O and F). In perfect octahedral symmetry, spin–orbit coupling would split the twelve-fold degenerate (![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) = 1, S = 3/2) ground multiplet into a doublet, a quartet and a sextet.40 Here the distorted octahedral environment leads to a sequence of Kramers doublets, the lowest two being separated by about 180 K according to ab initio calculations (see details in the ESI†). Thus, at low temperatures we can restrict to the lowest-energy doublet and describe it as an effective spin 1/2. In this subspace, we obtain the spin Hamiltonian in eqn (1), with the principal axes of the Dlocal and glocal tensors sketched in Fig. 1. Our first-principles calculations predict an isotropic Cr–Co exchange constant of JCr–Co = 21 K and anisotropic exchange with Dzz = −11.2 K and Dyy = 10.4 K leading to (in K):
= 1, S = 3/2) ground multiplet into a doublet, a quartet and a sextet.40 Here the distorted octahedral environment leads to a sequence of Kramers doublets, the lowest two being separated by about 180 K according to ab initio calculations (see details in the ESI†). Thus, at low temperatures we can restrict to the lowest-energy doublet and describe it as an effective spin 1/2. In this subspace, we obtain the spin Hamiltonian in eqn (1), with the principal axes of the Dlocal and glocal tensors sketched in Fig. 1. Our first-principles calculations predict an isotropic Cr–Co exchange constant of JCr–Co = 21 K and anisotropic exchange with Dzz = −11.2 K and Dyy = 10.4 K leading to (in K):
 | (2) |
These results show two directions where the Cr–Co anisotropic exchange is strong but opposite in sign and a third direction where it is almost one order of magnitude weaker. Finally, we obtain glocal = (5.4, 3.3, 2.9). These parameters have been used as a guide for the final determination of the spin Hamiltonian based on EPR and INS data. DFT + MB calculations also indicate the presence of a significant Dzialoshinski–Moriya (D–M) interaction. However, here this interaction acts only at the second-order through the S-mixing41 and its effects are much weaker than those of anisotropic exchange. Thus, in the following we only consider the isotropic and anisotropic parts of the exchange interaction to keep the model with the minimum number of parameters.
2.4 EPR and INS spectroscopy
EPR measurements have been performed on powder samples of the isotructural compound Ga7Co (see the ESI†). Since GaIII is diamagnetic, these measurements have allowed us to selectively target the CoII ion embedded in the same environment as in the Cr7Co ring. In Fig. S2 of the ESI† we report Q- and W-band EPR spectra, whose main features can be reproduced by assuming a very anisotropic glocal for CoII, with principal values (6.8, 2.9, 2.7). The results obtained with the DFT + MB method are in good agreement with the EPR findings and are used to determine the principal axis of the spectroscopic splitting tensor for the CoII ion, reported in Fig. 1, yielding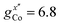 ,
, 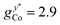 and
and 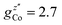 . These orientations are confirmed by the good agreement with single-crystal INS measurements in applied fields (see below). As a first step to investigate the Cr7Co ring, we have surveyed the full energy spectrum of a non-deuterated powder sample on the time-of-flight spectrometer IN5 at the Institute Laue Langevin in Grenoble.42 Measurements have been performed at three different temperatures, T = 1.5, 6, 15 K, with two different incident neutrons energies Ei, 1.9 and 8 meV (see Fig. S3 in the ESI†). The high-resolution/low-energy-transfer spectra show two cold transitions around 0.5 meV, whereas higher-energy data show magnetic excitations up to 5 meV, with three cold peaks at 1.8, 3.7 and 4.8 meV. The same measurements at T = 1.5 K have also been performed on a single-crystal sample of Cr7Co, where we have exploited the position-sensitive detectors of IN5 to implement the four-dimensional inelastic neutron scattering (4D-INS) technique.32 Thanks to this technique it is possible to measure the INS cross-section not only as a function of energy, but also as a function of the three component of the momentum transfer vector Q (see also the ESI†). The information accessible with this technique enables us to characterize the eigenstates of the system involved in the detected excitations.43 INS single-crystal spectra as a function of the energy-transfer, integrated over the full Q-space are reported in Fig. 2 and show the same magnetic transitions measured on the powder sample. In this configuration we have been able to obtain one crucial additional information on the Cr7Co energy spectrum, by detecting a low-energy transition below 0.1 meV (see the shoulder in Fig. 2). In order to check its magnetic origin, we have extracted the dependence of the INS intensity of this excitation on the two horizontal wavevector components Qx − Qy, integrated over the full experimental Qz range (−0.2 to 0.2 Å). The so-obtained experimental intensity map (Fig. 3-a) shows clear Q-dependent modulations whose pattern of maxima and minima clearly identify a magnetic transition. The intensity maps have been extracted also for the 0.5 meV peak (Fig. 3-c) and for the 1.8 meV excitation (Fig. S4 of the ESI†). These maps show the same pattern of intensity modulations in the explored Q range and all the maxima in each map have the same intensity, demonstrating the same occupation probability for CoII of all the ring sites. Indeed, the differences in the intensity pattern of each excitation are averaged-out by the delocalization of CoII along the ring (intensity maps calculated with the Co ion sitting on one single site are reported in Fig. S5 of the ESI†).
. These orientations are confirmed by the good agreement with single-crystal INS measurements in applied fields (see below). As a first step to investigate the Cr7Co ring, we have surveyed the full energy spectrum of a non-deuterated powder sample on the time-of-flight spectrometer IN5 at the Institute Laue Langevin in Grenoble.42 Measurements have been performed at three different temperatures, T = 1.5, 6, 15 K, with two different incident neutrons energies Ei, 1.9 and 8 meV (see Fig. S3 in the ESI†). The high-resolution/low-energy-transfer spectra show two cold transitions around 0.5 meV, whereas higher-energy data show magnetic excitations up to 5 meV, with three cold peaks at 1.8, 3.7 and 4.8 meV. The same measurements at T = 1.5 K have also been performed on a single-crystal sample of Cr7Co, where we have exploited the position-sensitive detectors of IN5 to implement the four-dimensional inelastic neutron scattering (4D-INS) technique.32 Thanks to this technique it is possible to measure the INS cross-section not only as a function of energy, but also as a function of the three component of the momentum transfer vector Q (see also the ESI†). The information accessible with this technique enables us to characterize the eigenstates of the system involved in the detected excitations.43 INS single-crystal spectra as a function of the energy-transfer, integrated over the full Q-space are reported in Fig. 2 and show the same magnetic transitions measured on the powder sample. In this configuration we have been able to obtain one crucial additional information on the Cr7Co energy spectrum, by detecting a low-energy transition below 0.1 meV (see the shoulder in Fig. 2). In order to check its magnetic origin, we have extracted the dependence of the INS intensity of this excitation on the two horizontal wavevector components Qx − Qy, integrated over the full experimental Qz range (−0.2 to 0.2 Å). The so-obtained experimental intensity map (Fig. 3-a) shows clear Q-dependent modulations whose pattern of maxima and minima clearly identify a magnetic transition. The intensity maps have been extracted also for the 0.5 meV peak (Fig. 3-c) and for the 1.8 meV excitation (Fig. S4 of the ESI†). These maps show the same pattern of intensity modulations in the explored Q range and all the maxima in each map have the same intensity, demonstrating the same occupation probability for CoII of all the ring sites. Indeed, the differences in the intensity pattern of each excitation are averaged-out by the delocalization of CoII along the ring (intensity maps calculated with the Co ion sitting on one single site are reported in Fig. S5 of the ESI†).
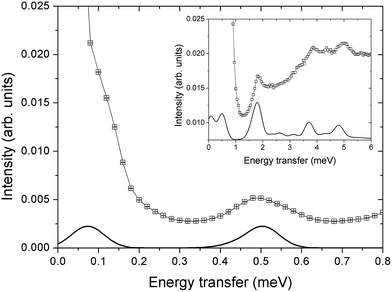 | ||
| Fig. 2 INS spectra for a Cr7Co single crystal collected on the IN5 spectrometer at T = 1.5 K with an incident neutron energy Ei = 1.9 meV (Ei = 8 meV in the inset) and integrated over the full measured Q range (black squares). The c axis of the single crystal is perpendicular to the horizontal scattering plane. Solid lines are simulations based on the spin Hamiltonian in eqn (1) with JCr–Co = 19 K and the local anisotropic exchange tensor obtained from the fitting of all the INS data. The delocalization of the Co ion along the ring is also taken into account in the simulations. | ||
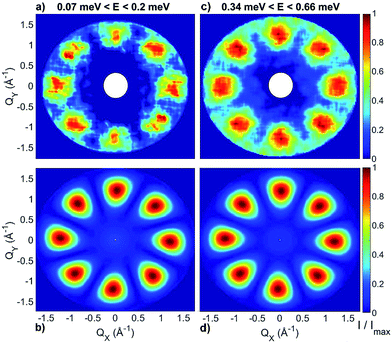 | ||
| Fig. 3 Constant-energy plots of the neutron scattering intensity measured on IN5 with an incident energy of 1.9 meV and with a sample temperature of 1.5 K. (a) and (c) Show the experimental dependency of the neutron scattering intensity of the inelastic excitations observed at 0.1 meV, 0.5 meV respectively on the two horizontal wavevector components Qx − Qy, integrated over the full experimental Qz data range (−0.2 to 0.2 Å). (b) and (d) Show the corresponding calculations based on the spin Hamiltonian in eqn (1) with JCr–Co = 19 K and the local anisotropic exchange tensor obtained from the fitting of all the INS data. The delocalization of the Co ion along the ring is also taken into account in the simulations. The cross-section has been integrated over energy ranges centred around the observed transition energies: 0.07 meV < E < 0.2 meV for (a, b) and 0.34 meV < E < 0.66 meV for (c, d). The colour bar reports the transition intensity normalized for the maximum in each panel. | ||
INS experiments on IN5 provide information on the low-lying energy levels of Cr7Co up to 6 meV and measurements in temperature allow us to distinguish between transitions involving or not the ground state. However, they are not sufficient to unambiguously identify the Cr–Co exchange parameters. Indeed, IN5 data can be reproduced with a high-anisotropy model (in agreement with DFT + MB results), but also with a weak-anisotropy one. In both cases the antiferromagnetic exchange interactions lead to a S = 1 ground multiplet. In the high-anisotropy case both the 0.1 meV and 0.5 meV INS peaks in Fig. 2 are due to intramultiplet transitions within the ground S = 1 manifold and therefore a strong and rhombic anisotropic Cr–Co exchange is responsible for the large 0.5 meV splitting of the ground multiplet. In this case the cold transition at 1.8 meV is the lowest-energy intermultiplet transition, yielding a large JCr–Co value, of the same order as JCr–Cr. Conversely, if we assume that the 0.5 meV peak is the lowest intermultiplet transition, we have to consider a weak Cr–Co anisotropic exchange leading to a small splitting of the S = 1 ground state multiplet of only 0.1 meV. In order to solve this puzzle, we have performed a targeted INS experiment in applied magnetic field. We have measured a single crystal sample of Cr7Co on the LET44 spectrometer at the ISIS facility, Rutherford Appleton Laboratory (Didcot, UK), at T = 1.8 K and with magnetic fields B = 0 T, 2.5 T, 5 T and 7 T (experimental details are given in the ESI†). The behaviour of the INS excitations as a function of the applied magnetic field enables us to distinguish the two situations and to evaluate the anisotropy of the molecule. Fig. 4-a shows the high-resolution spectra collected on the LET spectrometer with an incident neutron wavelength Ei = 1.5 meV and with different applied magnetic fields, while the higher energy-transfer spectra with Ei = 3 meV are reported in Fig. 4-b. The cold transitions at 0.5 meV and 1.8 meV are clearly visible in the zero-field spectra. A decisive information about the anisotropy of the Cr7Co has been provided by the magnetic-field dependence of the position of the lowest-energy cold peak, detected at 0.1 meV at zero-field (see Fig. 2). This transition is not visible in the B = 0 T and B = 2.5 T LET spectra, as it is underneath the elastic peak. Nevertheless, the peak moves to higher energies by increasing the magnetic field and becomes clearly visible at 0.3 meV with B = 7 T (see Fig. 4-a). This lowest-energy INS excitation corresponds to a transition within the S = 1 ground multiplet in both the high-anisotropy and weak-anisotropy model. The small observed energy shift (from 0.1 meV to only 0.3 meV) with the application of a strong a magnetic field of 7 T can be explained only by the high-anisotropy model. Indeed, a much larger field-induced shift is expected in the weak-anisotropy one, almost twice as large as the one detected by INS measurements (energy levels as a function of the applied magnetic field calculated with the weak-anisotropy model are reported in Fig. S7 of the ESI†).
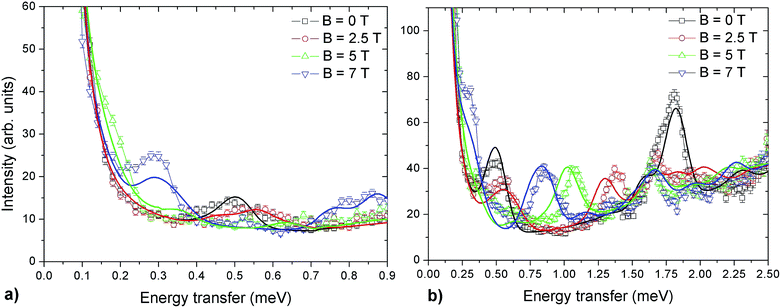 | ||
| Fig. 4 INS spectra for a Cr7Co single crystal, collected on the LET spectrometer with an incident neutron energy Ei = 1.5 meV (a) and Ei = 3 meV (b) at T = 1.8 K in different applied magnetic fields: B = 0 T (black squares), B = 2.5 T (red circles), B = 5 T (green triangles) and B = 7 T (blue triangles). Solid lines are simulations based on the spin Hamiltonian in eqn (1) with JCr–Co = 19 K and the local anisotropic exchange tensor obtained from the fitting of all the INS data. The magnetic field is applied in the plane of the ring (see Fig. S6 of the ESI†). | ||
The parameters of the spin Hamiltonian in eqn (1) have been determined by fitting all the INS data reported in Fig. 2 and 4, which are very well-reproduced with JCr–Co = 19 ± 2 K and a strong and rhombic Cr–Co anisotropic exchange term with Dzz = −10 ± 1 K and Dyy = 13.0 ± 1 K leading to (in K)
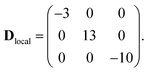 | (3) |
As in the DFT + MB results, there are two directions where the Cr–Co anisotropic exchange is strong but opposite in sign and a third one where it is almost one order of magnitude weaker. The spin Hamiltonian results also yield a strong Cr–Co isotropic exchange interaction and are therefore in good agreement with DFT + MB predictions. It is worth to note that this model also reproduces the IN5 intensity maps in Fig. 3 and S4 of the ESI.†32,37,43 The calculated low-lying energy levels and their magnetic field dependence are reported in Fig. 5.
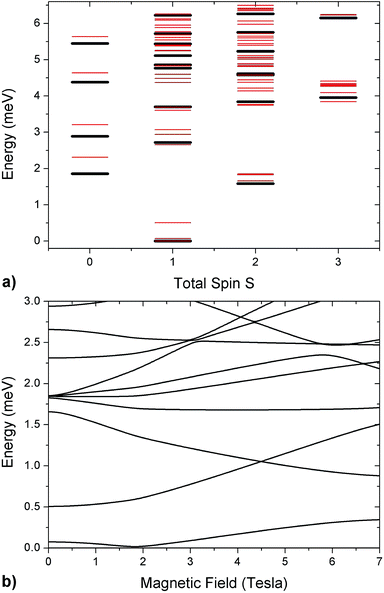 | ||
| Fig. 5 (a) Low-lying energy levels of the Cr7Co ring calculated taking into account the isotropic exchange terms of the spin Hamiltonian in eqn (1) with JCr–Co = 19 K (black lines). Red lines are obtained adding the ZFS term and the Cr–Co anisotropic exchange, given the local anisotropic exchange tensor in eqn (3). Since S is not a good quantum number for the full spin Hamiltonian, we have assigned to each level the total-spin value S with the major components in the corresponding eigenstate. (b) Magnetic field dependence of Cr7Co energy levels up to 7 T with the CoII ion on site 8. The magnetic field is applied in the plane of the ring (see experimental configuration in Fig. S6 of the ESI†). | ||
3 Discussion
The analysis of the EPR and INS experimental data supported by our DFT + MB calculations have allowed us to characterize the anisotropy of the Cr7Co ring, which has proven to be an ideal test system to study anisotropic exchange interactions. Our results demonstrate that the insertion of an anisotropic Co ion strongly coupled to the Cr ones determines the anisotropy of the whole molecule. Indeed, the strong and rhombic Cr–Co anisotropic exchange leads to a splitting of the S = 1 ground multiplet Δ = 0.5 meV, which is five times larger than the splitting of the S = 1 ground manifold of the parent compound Cr7Mn.33 Since MnII is essentially isotropic in Cr7Mn, the comparison between these two experimental splittings is practically a direct comparison between the effects of Cr–Co anisotropic exchange and of the seven Cr single-ion anisotropies. The ZFS due to the Cr ions is very similar in both Cr7Mn and Cr7Co and leads to a very small splitting of the S = 1 ground state. Indeed, if we neglect the Cr–Co anisotropic exchange, we obtain a splitting of about 0.1 meV in Cr7Co, practically identical to Cr7Mn. Thus, by inserting only one anisotropic ion we obtain a five times larger splitting of the ground state, confirming that the experimentally observed splitting is mostly due to the anisotropic exchange between CoII and the neighbouring Cr ions. The anisotropy of Cr7Co is also responsible for a strong S-mixing41 in the eigenstates of the molecule and therefore the total-spin S is not a really good quantum number for the full spin Hamiltonian in eqn (1). For instance, the strong Cr–Co anisotropic exchange leads to a mixing between the S = 1 ground multiplet and excited multiplets of about 10% (mainly with the lowest S = 2 manifold). This strong S-mixing significantly affects the physics of Cr7Co leading, for instance, to oscillations of the total spin45,46 for specific field values. Large anticrossings associated with these oscillations are induced by a magnetic field applied perpendicular to the plane of the ring (see Fig. S8 of the ESI†). In addition, S-mixing can play an important role in the dynamics of the Néel vector.28It is worth noting that the effective anisotropic exchange interaction in eqn (1) originates from the combined effect of the CoII ion zero-field splitting and of a real Cr–Co anisotropic exchange. In fact, our DFT + MB results show that the gCo tensor, which reflects the single-ion anisotropy of the CoII, and the Dlocal tensor, accounting for the effective Cr–Co anisotropic exchange, have different local principal axis (see Fig. 1). In order to better understand the effects of the Cr–Co anisotropic exchange on the magnetic behaviour of the molecule at low temperatures, we have applied second-order perturbation theory to project the Cr–Co anisotropic exchange interactions onto an effective S = 1 multiplet.41 With this procedure we have determined the principal axis of the effective anisotropy tensor acting on the S = 1. The easy-axis of the effective anisotropy lies within the plane of the ring and points in the radial direction from the centre of the ring towards the Co ion, whereas one of the two hard directions is perpendicular to the plane of the ring.
This study has allowed us to understand the nature of the Cr–Co anisotropic exchange interactions in the Cr7Co ring and their effects on the magnetic behaviour of the molecule. Moreover, it also represents an important starting point for the design of new systems where strong exchange interactions transmit the large anisotropy of CoII ions to the whole molecule. As a first attempt, more than one Co ion can be embedded in the antiferromagnetic ring to further increase the anisotropy of the cluster.47 Having fully characterized the Cr–Co anisotropic exchange, we are able to design the molecule in order to maximize the anisotropy-induced splitting of the ground states (which will be an S = 2 with two CoII ions within the ring). For instance, Co ions on opposite sites (e.g. sites 1 and 5 in Fig. 1) will produce a splitting about 40% larger than that obtained when the two Co ions have one CrIII in between (e.g. sites 6 and 8 in Fig. 1).§
The inclusion of anisotropic ions strongly coupled to high-spin ones (like MnII, FeIII or CrIII) in polymetallic clusters is important also in view of exploiting MNMs for quantum information processing (QIP). In particular, a crucial milestone would be to reach the so-called strong coupling between a single magnetic molecule and the quantized magnetic field (photons) of coplanar superconducting resonators.38 Indeed, this would allow the local control and read out of the molecule magnetic state38,52 and to implement QIP schemes similar to those used for superconducting qubits.53,54 The large spin-photon coupling needed to reach the strong coupling regime could be achieved with a molecule characterized by a large total spin and by a strong easy-plane anisotropy.38 These are often conflicting requirements, but the present results demonstrate that the inclusion of one or more anisotropic 3d ions in a high-spin polymetallic complex is a promising way of achieving this very important goal. At last, anisotropic ions coupled with molecular qubits can be used as a switch of the effective qubit–qubit interaction in the implementation of quantum gates.26
4 Conclusions
We have studied the Cr7Co ring as a model system to understand how the insertion of an anisotropic Co ion strongly coupled to the Cr ones affects the anisotropy of the whole molecule. Since the ring is isostructural with the other previously studied Cr7M AF rings, we have been able to focus on CoII single-ion anisotropy and on Cr–Co anisotropic exchange interactions. This characterization has been possible thanks to a combined use of EPR and INS techniques with spin Hamiltonian and DFT + MB calculations. EPR measurements on Ga7Co, where GaIII is diamagnetic, have allowed us to determine the strong single-ion anisotropy of CoII embedded in the ring. Then, the Cr7Co energy spectrum has been surveyed with a broad set of INS experiments. In-field INS measurements have been crucial to determine the Cr–Co anisotropic exchange parameters and therefore the anisotropy of the molecule. DFT + MB results have been used as a guide for fitting the spin Hamiltonian parameters and their agreement with experiments is good, especially considering the presence of an highly-anisotropic ion like Co and the many anisotropic terms in the spin Hamiltonian.We have found strong anisotropic exchange interactions between CoII and the neighbouring Cr ions. Thus, our results demonstrate that the anisotropy of CoII is efficiently transmitted to the anisotropy of the whole Cr7Co polymetallic cluster through strong effective anisotropic exchange interactions.
This study is also a starting point for the design of new systems, where strong exchange interactions transmit the large anisotropy of CoII ions to the whole molecule. On the one hand, a rich physics is expected in these systems, due to unquenched orbital degrees of freedom (e.g. Néel Vector Tunneling in the low-frequency dynamics). On the other hand, the combination of high-spin ions strongly coupled to a few very-anisotropic ions like CoII represents a promising route for building scalable quantum information architectures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Davide Albertini for his valuable help during the LET experiment at the ISIS facility and in the analysis of the data. E. G., A. C., S. C., P. S. and G. A. acknowledge financial support from PRIN Project 2015 No. HYFSRT of the MIUR (Italy). S. A., M. L. B., G. A. T., I. V.-Y. and R. E. P. acknowledge the support of the EPSRC(UK) for the purchase of an X-ray diffractometer (grant number EP/K039547/1) and for the support of the National EPR Facility. This work was supported within the CNR-STFC agreement 2014-2020 (No. 3420 2014-2020) concerning collaboration in scientific research at ISIS Spallation Neutron Source. The authors gratefully acknowledge the computing time granted via the JARA-HPC partition on the supercomputer JURECA at Forschungszentrum Jülich.Notes and references
- R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754–2755 CrossRef CAS PubMed.
- A. Caneschi, D. Gatteschi, J. Laugier, P. Rey, R. Sessoli and C. Zanchini, J. Am. Chem. Soc., 1991, 131, 5873 CrossRef.
- S. M. J. Aubin, M. W. Wemple, D. M. Adams, H.-L. Tsai, G. Christou and D. H. Hendrickson, J. Am. Chem. Soc., 1996, 118, 7746 CrossRef CAS.
- A.-L. Barra, P. Debrunner, D. Gatteschi, C. E. Schulz and R. Sessoli, J. Am. Chem. Soc., 1996, 35, 133 CAS.
- H. Andres, R. Basler, A. J. Blake, E. K. Brechin, C. Cadiou, G. Chaboussant, C. M. Grant, H.-U. Güdel, S. G. Harris, M. Murrie, S. Parsons, C. Paulsen, F. Semadini, V. Villar, W. Wernsdorfer and R. E. P. Winpenny, Chem.–Eur. J., 2002, 8, 4867–4876 CrossRef CAS.
- K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823 RSC.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8594 Search PubMed.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650 CrossRef CAS PubMed.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- F. Branzoli, P. Carretta, M. Filibian, G. Zoppellaro, M. J. Graf, J. R. Galan-Mascaros, O. Fuhr, S. Brink and M. Ruben, J. Am. Chem. Soc., 2009, 131, 4387–4396 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. Chilton and D. P. Mills, Nature, 2017, 584, 439 CrossRef PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed.
- J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS PubMed.
- M. Y. M. Pau, M. I. Davis, A. M. Orville, J. D. Lipscomb and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 1944–1958 CrossRef CAS PubMed.
- M. Murrie, Chem. Soc. Rev., 2010, 39, 1986–1995 RSC.
- E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130–9134 CrossRef CAS PubMed.
- V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795 CrossRef CAS PubMed.
- H. Andres, J. M. Clemente-Juan, M. Aebersold, H.-U. Güdel, E. Coronado, H. Büttner, G. Kearly, J. Melero and R. Burriel, J. Am. Chem. Soc., 1999, 121, 10028–10034 CrossRef CAS.
- A. B. Boeer, A.-L. Barra, D. C. L. F. Chibotaru, E. J. L. McInnes, R. A. Mole, G. G. Simeoni, G. A. Timco, L. Ungur, T. Unruh and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 4007–4011 CrossRef CAS PubMed.
- E. M. Pineda, N. F. Chilton, M. D. R. Marx, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef PubMed.
- J. Ferrando-Soria, E. M. Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- A. Chiolero and D. Loss, Phys. Rev. Lett., 1998, 80, 169 CrossRef CAS.
- P. Santini, S. Carretta, G. Amoretti, T. Guidi, R. Caciuffo, A. Caneschi, D. Rovai, Y. Qiu and J. R. D. Copley, Phys. Rev. B, 2005, 71, 184405 CrossRef.
- F. Meier and D. Loss, Phys. Rev. Lett., 2001, 86, 5373 CrossRef CAS PubMed.
- O. Waldmann, C. Dobe, H. U. Güdel and H. Mutka, Phys. Rev. B, 2006, 74, 054429 CrossRef.
- O. Waldmann, T. C. Stamatatos, G. Christou, H. U. Güdel, I. Sheikin and H. Mutka, Phys. Rev. Lett., 2009, 102, 157202 CrossRef CAS PubMed.
- M. L. Baker, T. Guidi, S. Carretta, J. Ollivier, H. Mutka, H. U. Güdel, G. A. Timco, E. J. L. McInnes and R. E. P. W. G. Amoretti, Nat. Phys., 2012, 8, 906 CrossRef CAS.
- R. Caciuffo, T. Guidi, G. Amoretti, S. Carretta, E. Liviotti, P. Santini, C. Mondelli, G. Timco, C. A. Muryn and R. E. P. Winpenny, Phys. Rev. B, 2005, 71, 174407 CrossRef.
- S. Carretta, P. Santini, G. Amoretti, T. Guidi, J. R. D. Copley, Y. Qiu, R. Caciuffo, G. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 167401 CrossRef CAS PubMed.
- A. Chiesa, S. Carretta, P. Santini, G. Amoretti and E. Pavarini, Phys. Rev. B, 2016, 94, 224422 CrossRef.
- A. Chiesa, S. Carretta, P. Santini, G. Amoretti and E. Pavarini, Phys. Rev. Lett., 2013, 110, 157204 CrossRef CAS PubMed.
- E. Garlatti, T. Guidi, S. Ansbro, P. Santini, G. Amoretti, J. Ollivier, H. Mutka, G. Timco, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, R. E. P. Winpenny and S. Carretta, Nat. Commun., 2017, 8, 14543 CrossRef CAS PubMed.
- M. Jenkins, T. Hümmer, M. J. Martínez-Pérez, J. García-Ripoll, D. Zueco and F. Luis, New J. Phys., 2013, 15, 095007 CrossRef.
- F. K. Larsen, E. J. L. McInnes, H. E. Mkami, J. Overgaard, S. Piligkos, G. Rajaraman, E. Rentschler, A. A. Smith, G. M. Smith, V. Boote, M. Jennings, G. A. Timco and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2003, 42, 101–105 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, Oxford, (UK), 1970 Search PubMed.
- E. Liviotti, S. Carretta and G. Amoretti, J. Chem. Phys., 2002, 117, 3361 CrossRef CAS.
- J. Ollivier and H. Mutka, J. Phys. Soc. Jpn., 2011, 80, SB003 CrossRef.
- A. Chiesa, T. Guidi, S. Carretta, S. Ansbro, G. A. Timco, I. Vitorica-Yrezabal, E. Garlatti, G. Amoretti, R. E. P. Winpenny and P. Santini, Phys. Rev. Lett., 2017, 119, 217202 CrossRef CAS PubMed.
- R. I. Bewley, J. W. Taylor and S. M. Bennington, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 637, 128–134 CrossRef CAS.
- S. Carretta, P. Santini, G. Amoretti, T. Guidi, J. R. D. Copley, Y. Qiu, R. Caciuffo, G. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 167401 CrossRef CAS PubMed.
- O. Waldmann, S. Carretta, P. Santini, R. Koch, A. G. M. Jansen, G. Amoretti, R. Caciuffo, L. Zhao and L. K. Thompson, Phys. Rev. Lett., 2004, 92, 096403 CrossRef CAS PubMed.
- G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem. Soc. Rev., 2013, 42, 1796 RSC.
- A. B. Boeer, D. Collison, C. A. Muryn, G. A. Timco, F. Tuna and R. E. P. Winpenny, Chem.–Eur. J., 2009, 15, 13150 CrossRef CAS PubMed.
- E. J. L. McInnes, G. A. Timco, G. F. S. Whitehead and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2015, 54, 14244 CrossRef CAS PubMed.
- M. Affronte, S. Carretta, G. A. Timco and R. E. P. Winpenny, Chem. Commun., 2007, 1789–1797 RSC.
- L. P. Engelhardt, C. A. Muryn, R. G. Pritchard, G. A. Timco, F. Tuna and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 924 CrossRef CAS PubMed.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682 RSC.
- A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R. S. Huang, J. Majer, S. Kumar, S. M. Girvin and R. J. Schoelkopf, Nature, 2004, 431, 162 CrossRef CAS PubMed.
- J. Majer, J. M. Chow, J. M. Gambetta, J. Koch, B. R. Johnson, J. A. Schreier, L. Frunzio, D. I. Schuster, A. A. Houck, A. Wallraff, A. Blais, M. H. Devoret, S. M. Girvin and R. J. Schoelkopf, Nature, 2007, 449, 443 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the experimental and theoretical procedures used and supplementary results. CCDC 1810773. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc00163d |
| ‡ E. G., A. C., P. S., G. A., and S. C. performed spin-Hamiltonian calculations, INS data simulations and fits, while A. C. and E. P. did DFT calculations. E. G., T. G., S. A., J. O., H. M. performed single crystal INS experiments and data analysis, while INS experiment on powders were performed by M. L. B., J. O. and H. M., M. L. B. did EPR experiments and simulations. All the samples were synthesized by G. T. and R. E. P. W., while the structure of the compound has been determined by I. J. V., E. G. and S. C. wrote the manuscript with inputs from all coauthors. |
| § Exchange of a protonated amine for an imidazolium cation enables the introduction of a second divalent ion in AF rings,48 although this does result in multiple isomers due to disorder of the divalent ion about the eight metal sites. However, this family of compounds exhibit considerable synthetic flexibility from which many derivatives are possible.49,50 Thus, opposing divalent sites can be obtained by changing the structure of the cycle.51 |
| This journal is © The Royal Society of Chemistry 2018 |