Effect of electrolyte concentration on uranium species adsorption: a molecular dynamics study

Abstract

Molecular dynamics (MD) simulations of uranyl species adsorption in montmorillonite pores in 0, 0.05 and 0.10 M NaCl were carried out to investigate the influence of internal electrolyte concentration on the uptake amount, species distribution and electrical double-layer (EDL) structures. Most cases revealed that the β- and d-planes of the adsorbates are located 4.3–4.6 Å and 5.5–5.8 Å from the clay planes, respectively. However, based on the split carbonate peaks, an exception, the left peaks near the clay surface for 0.10 M NaCl, formed more uranyl-(bi)carbonate complexes than the other peaks. Under this condition, each peak and minimum of cations shifted slightly farther away from the clay plane. For this outlying case, the charge density profile confirmed the charge inversion of carbonates near like-charged surfaces. Collectively, the simulations revealed the subtle influence of the internal NaCl concentration (0–0.05 M) on the EDL structure, uptake amount and species distribution. In particular, a threshold concentration (0.10 M NaCl in this study) for charge inversion within the β-plane may exist. Under this condition, a pronounced change in the EDL structure occurs, which in turn causes a dramatic alteration in the uranyl species adsorption relative to lower electrolyte concentrations.

---

Introduction

Uranium is a major radionuclide contaminant found at sites related to human activities, such as mill tailings, mining and nuclear tests, and potentially sites used for the geological disposal of waste. Therefore, the transportation of uranium in the environment has been studied by experimental and spectroscopic methods for decades.^1–27 No matter what conditions, such as pH, Eh, ionic strength and background ions, these studies used, the researchers assumed that the predominant species are linear uranyl ions (UO₂²⁺) and their complexes were based on thermodynamic calculations^{12–15,17–19} and/or spectroscopic studies.^{5,11,19–21,24–27}

As a major component of bentonite, which is the candidate backfill material for the deep geological repository of radioactive waste in many countries, montmorillonite is present throughout soil and aquatic systems. It has a high surface area and a notably high retention capacity for cations.^28,29 Therefore, a large number of batch experiments for the sorption of various cationic adsorbates onto montmorillonite have been carried out to investigate the retardation mechanism.^30–35 These studies were performed under a broad set of conditions, including pH, Eh, ionic strength and solid–liquid ratio. Recently, Miller and Wang reviewed the interaction of radionuclides with clays in dilute and heavily compacted systems³⁶ and concluded that for actinides, the uptake onto the clay minerals depended primarily on the ionic strength at lower pH, and was determined by pH at higher pH. The widely applied surface complexation models (SCMs) attribute this feature to two distinct adsorption mechanisms. At low pH, the interactions between the actinides and fixed structural charge sites are electrostatic, forming outer-sphere complexes. The electrostatic forces are not only specific for actinides but also attract other competitive cations. Consequently, the uptake amount at low pH depends on the ionic strength.³⁶ Another retardation mechanism dominates at higher pH: the fixed charge is still present, but the edge sites become more negative with increasing pH and dominate uptake due to stronger chemical interactions, leading to inner-sphere complexation.³⁶

Recently, computational methods have become popular in investigating uranyl adsorption.^37–40 Molecular dynamics (MD) simulations have provided atomic insight into the solute dynamics of aqueous solutions,⁴¹ structural and dynamic properties of bulk water^42,43 and behavior influenced by mineral–water interfaces.^44–56 A few studies incorporating these simulations have emphasized the fine electrical double-layer (EDL) structure near flat charged surfaces.^55,56 The MD results of Tournassat et al. have shown a good quantitative consistency with the modified Gouy–Chapman model for sodium ions.⁵⁵ However, the model also overestimated the anion exclusion for chloride ions by approximately 50%. Bourg et al. confirmed the existence of three distinct adsorption planes, which are often assumed in EDL models.⁵⁶ Several simulations have focused on uranyl ions and their complexes. Kerisit et al. followed the species-based diffusion concept and calculated the diffusion coefficients of various uranyl species in aqueous solution and near mineral surfaces.^41,51 Doudou et al. presented MD simulations to investigate the behavior of U(VI) in contact with different calcite surfaces.⁴⁷ Greathouse et al. investigated uranyl adsorption on the surfaces of quartz⁵² and several clay minerals, including montmorillonite, pyrophyllite and beidellite.^53,54 Stephanie et al. modeled systems including the competitive adsorption between potassium counterions and aqueous ions.⁵⁷ From their MD results, they calculated the coordination numbers of the uranyl species and the distance to ligands using the radial distribution function (RDF) and estimated the K_d values. They also investigated the influence of various initial uranyl–carbonate concentrations on the uranyl species distribution at equilibrium. They applied Lennard–Jones (L-J 93) walls at the bottom and top of their simulation cells. L-J 93 walls prevented atoms from entering the vacuum region and omitted the dipole interactions between adjacent MD cells.

As mentioned above, most researchers have employed SCMs to interpret the batch experimental data for actinide adsorption on clays.^{11–13,15,17–19} Fixed charge sites dominate uptake at low pH. Under this condition, the sorption amount decreases with increasing ionic strength because the interactions between the formed outer-sphere complex and the exchangeable sites on the clay surfaces are influenced by competition with the background electrolyte. The function between the uptake and the ionic strength is quantitatively described by various electrical double-layer models within the SCMs framework. However, our present understanding of this phenomenon cannot answer the following questions. (1) How do the cations distribute in the EDL near clay surfaces, especially surfaces that form complexes with ligands? (2) Do the background ions alter the EDL structure? (3) Does the ionic strength affect the uranyl species distribution in the confined clay pores? Therefore, the overarching purpose of this work is to study the influence of electrolyte concentration on the adsorption of uranyl onto montmorillonite internal surfaces using MD techniques at the atomic level.

Results and discussion

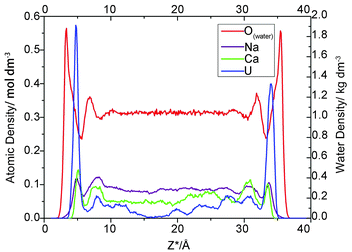
For each simulation, we calculated the atomic density profile of UO₂²⁺, Na⁺, Ca²⁺, CO₃²⁻ and Cl⁻ as a function of distance from the average height of the surface O atoms (Fig. 1). Because the Z dimension of each simulation cell varied slightly, Z* is introduced and defined as follows: Z* = Z − O_ave, where Z is the “actual” Z coordinate of the specific atom and O_ave is the average height of the left topmost O atoms of the corresponding cell. The use of the Z* coordinates allows us to investigate the influence of electrolyte concentration on adsorption in an explicit way.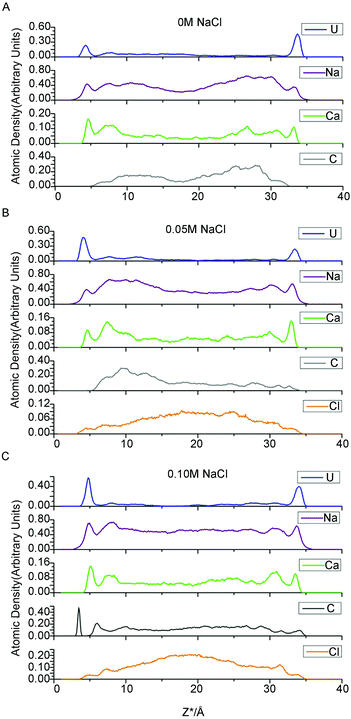

Fig. 1 Atomic density profiles for uranium, sodium, calcium, carbonate and chloride ion at NaCl concentrations of 0, 0.05 and 0.1 M.

Three types of adsorbate species are assumed to compose the EDL on charged solid surfaces in contact with an aqueous electrolyte solution: inner-sphere surface complexes (ISSC), outer-sphere surface complexes (OSSC), and diffuse swarm (DS) species. This view is adopted, for example, as the molecular basis for the widely applied triple-layer model (TLM), in which the distribution of ions near a charged planar solid surface is calculated under a set of simplifying assumptions that include assigning all ISSCs to a plane at the solid surface (0-plane), all OSSCs to a second plane deeper into the aqueous phase (β-plane), and all DS species to a region lying beyond a third plane even deeper into the aqueous phase than the β-plane (d-plane).⁵⁶

Ion adsorption

As indicated in Fig. 1, for all three electrolyte concentrations, the uranium adsorbed onto montmorillonite forms two prominent peaks at Z* = 4.3–4.8 Å and 33.5–33.9 Å, which correspond to an average distance from the most external oxygen atoms of ∼4.5 Å. Greathouse et al. reported a slightly smaller value of 4.0 Å based on simulations using an L-J 93 boundary, SPC water model and fewer solute species.^53,54

Furthermore, comparing the first peaks of water with the adsorbate peaks in atomic density profiles is a conventional method of identifying whether the formed surface complex is inner- or outer-sphere.^53,54 Take the 0.05 M case for example, there are intervening water molecules between the first cation peaks and the siloxane surface, implying the formation of an outer-sphere complex for uranium, sodium and calcium ions (Fig. 2).

Fig. 2 Atomic density profiles for adsorbed ions and water (NaCl concentration is 0.05 M).

As expected, in each simulation, the atomic density profiles of uranium are approximately symmetrical due to the solute contact with the identical clay planes. However, the shapes of all the first peaks for uranium in Fig. 1 are unique and vary slightly in either atomic density or peak width. For example, in Fig. 1C, the right first peak is more intense and broader than the left first peak. It should be noted that the carbonate atomic profile shows two clear split peaks near the left U peak in Fig. 1C, but no peak appears at the corresponding position in Fig. 1A and 1B. Obviously, the profile indicates the formation of different complexes near the identical clay surfaces. Our species analysis will verify this observation (see below).

The Ca²⁺ and Na⁺ ion density profiles show different features from that of uranium (Fig. 1). The first peaks for these two cations are lower, followed by higher, broader shoulder peaks, whereas the uranium yielded pronounced first adsorption peaks and much lower shoulder peaks. These profiles indicate that the majority of Na/Ca ions are located further from the clay surfaces, whereas most of the uranium ions are closer to the clay surfaces. In other words, the adsorption amount of Na/Ca is less than the diffusion amount, but for uranium, the adsorption is greater than the diffusion. Bourg et al. and Tournassat et al. carried out several fairly long simulations dedicated to the distribution of inorganic ions near clay surfaces.^55,56 Similar to the uranium atomic density profiles presented here, their results revealed sharp and easily identified first adsorption peaks of sodium/calcium ions on the montmorillonite basal planes followed by lower shoulder peaks. The most likely reason for this discrepancy is the complexity of the uranyl/carbonate/sodium ion/calcium ion system, which includes competition between the uranyl ions and other cations for adsorption onto clay surfaces. The “immobile” adsorbed uranium ions occupy closer interfacial areas and repel other cations from the clay planes.

Another notable feature is the absence of sodium ISSCs in the atomic density profiles in this study, despite being minor but discernible in the works of Bourg et al. and Tournassat et al.^55,56 Instead, Na⁺ only forms OSSCs at all three ionic strengths in this study. The difference in the potential parameters of sodium may lead to the absence of sodium ISSC. In addition, the Ca²⁺ profiles in this work indicate the formation of OSSCs, which is consistent with previous work.^55,56 Finally, our results indicating that Na⁺ and Ca²⁺ cannot access the 0-plane (formation ISSCs) are in agreement with the TLM hypothesis.

Density profiles of chloride ions, which are modeled as background electrolyte ions, are also mapped to investigate the exclusive effect of negatively charged clay surfaces on anions. Chloride ions (Fig. 1) form minor but discernible OSSC peaks followed by higher DS peaks and then increase continuously to a maximum at the center of the clay pore. Jardat et al.⁵⁸ presented a similar Cl⁻ profile in montmorillonite nanopores with a NaCl–montmorillonite system. Bourg et al.⁵⁶ studied a mixed NaCl–CaCl₂ solution in contact with smectite planes, reporting that chloride is positively adsorbed in a broad region beyond lower DS peaks.

In Fig. 1, the majority of carbonates present in the region of 8.0 Å < Z* < 31.0 Å, and the accompanying shoulders of the three cations present in this region as well. Carbonate is a well-known ligand for uranyl and calcium ions. Consequently, these cations formed complexes with the carbonato ligands, and these charged species tend to be repelled by the negative clay surfaces as well as some free carbonates. These free carbonates attract positively charged ions around them to maintain local electric neutrality.

EDL structure

Our results for the first peaks and minima of all ions (Fig. 1) are approximately identical. In addition, the first peaks for cations with intervening water molecules between them and clay planes are convincingly proven to form OSSCs in Fig. 2. Hence, following the suggestions of Bourg et al.,⁵⁶ the density maximum corresponding to OSSC coordination is associated with the TLM β-plane, whereas the minimum between OSSC and DS peaks is associated with the TLM d-plane. We define the region within the d-plane as the adsorption layer and ions beyond these planes as being diffuse. Consequently, the pore space was divided into three parts along the z-axis: two adsorbed layers and one diffuse layer.

Our results for the l locations of the β- and d-planes and DS peaks are tabulated in Table 1. The two values separated by slashes correspond to the two identical clay planes with which our aqueous solution is contact. We exclude carbonate in the table because it is a well-known ligand for uranyl and calcium ions, meaning that the complexes formed with these cations cannot be attributed to adsorption by the clay surfaces.

Table 1 Location (Å) of each peak and minima of cation density profiles in this work. Values shown here represent distance from most external oxygen plane of the vicinal clay surface. The OSSC peak and minima between OSSC and DS correspond to the β-plane and d-plane, respectively. There are two values separated by slashes due to the fact that our aqueous solution is in contact with two identical clay planes

	0 mol dm^−3	0.05 mol dm^−3	0.1 mol dm^−3
a Indiscernible peak/minima from the atomic density profile near corresponding clay plane.
Uranium
OSSC (β-plane)	4.4/4.4	4.4/4.3	4.8/4.3
OSSC/DS min (d-plane)	5.8/5.8	5.8/6.0	6.5/5.8
DS	7.7/7.6	7.6/7.6	7.9/7.6
Sodium
OSSC (β-plane)	4.5/4.5	4.4/4.5	4.9/4.4
OSSC/DS min (d-plane)	5.5/5.6	5.6/5.6	6.0/5.6
DS	7.7/7.8	7.7/7.7	8.2/7.6
Calcium
OSSC (β-plane)	4.6/4.5	4.6/4.6	5.1/4.6
OSSC/DS min (d-plane)	5.6/5.6	5.6/5.6	6.2/5.5
DS	7.6/7.8	7.6/7.7	7.9/7.6
Chloride
OSSC (β-plane)	—	4.5/^a	4.8/4.5
OSSC/DS min (d-plane)	—	5.4/^a	6.0/5.4
DS	—	7.1/^a	7.2/6.8

---

Except for the values obtained near the left clay plane in the 0.10 M NaCl background electrolyte, the adsorbate (uranium, sodium, calcium, chloride) coordinates in the β- and d-plane are almost identical (Z_β* = 4.50 ± 0.10 Å, Z_d* = 5.65 ± 0.15) at all three ionic strengths. Bourg et al.⁵⁶ reported similar values, i.e., Z_β* = 4.35 ± 0.10 Å and Z_d* = 5.65 ± 0.10 with a mixed electrolyte (NaCl–CaCl₂) solution despite using different potential parameters. Their results confirmed that the positions of the β- and d-plane are invariant with adsorbate type and suggested that the ionic strength does not effect the locations, which is consistent with the TLM hypothesis.

However, one set of our results, namely the locations near the left clay plane in 0.10 M NaCl background electrolyte, shift slightly (0.4 ± 0.10 Å) towards the aqueous region. The locations should be identical to the right one because the simulation cell is periodically duplicated. This result conflicts with the majority of results obtained here and in analogous works,⁵⁶ which suggest that the coordinates of the β- and d-planes are essentially independent of the type of ions and ionic strength. To the best of our knowledge, this result has never previously been reported in a MD simulation study. Because of the increasing electrolyte concentration and anion exclusion, more chloride ions are present in the middle region of the clay pore. These anions repel the like-charged carbonates towards the clay surfaces to form uranyl-(bi)carbonate(s) complexes, as indicated in the left side of Fig. 1C (the splitting carbonate density). These complexes may stabilize their negative ligands, carbonates, to overcome the repulsive force from the negatively charged surfaces. Hereafter, some of these ligands exist at the interfacial area within the β-plane. The presence of anions in the β-plane in the absence of a positively charged plane was previously presented by Bourg et al., who hypothesized that the Cl⁻ OSSCs in their study were stabilized by Ca²⁺ as CaCl⁺ ion pairs.⁵⁶ This fact can be verified by the charge density profile (Fig. 3), in which an apparent charge inversion phenomenon is observed due to the accumulation of negative ions near charged surfaces which means more uranyl-(bi)carbonate(s) are formed than other cases. These complexes with greater hydrated ion radius will occupy the finite interfacial areas and repel other cations from the clay planes. Hence, the corresponding planes shift farther from the clay plane. Collectively, our results suggest that the coordinates of the β- and d-planes are essentially independent of the type of ions and ionic strength provided that the charge inversion phenomenon does not occur within the d-plane.

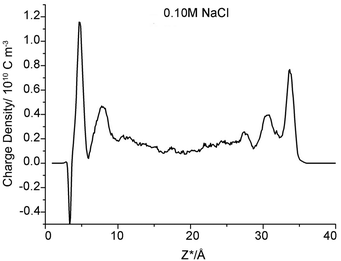Fig. 3 Charge density profile within clay pore spaces as a function of Z*-coordinates (NaCl concentration is 0.1 M).

Influence of NaCl concentration on uranium species adsorption

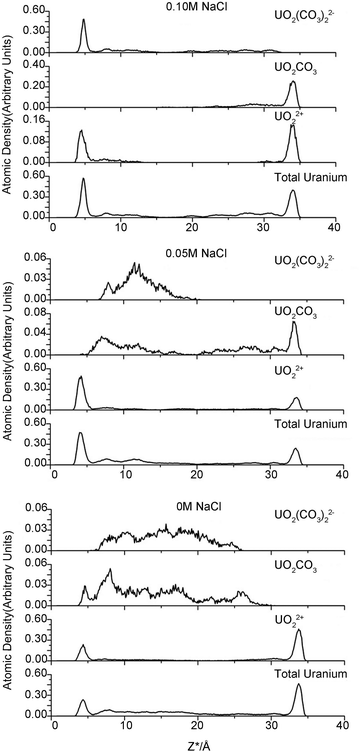
One purpose of this study is to investigate the influence of electrolyte concentration on uranium species adsorption. The various NaCl concentrations modeled in the clay pores represent different ionic strengths in the external solution. However, neither the accurate nor the analytical relationship between the internal and external electrolyte concentration is known. Therefore, we emphasize that the modeled NaCl concentration in clay pores is not the conventional ionic strength but can be considered as a proxy of the external ionic strength.

Various uranyl carbonate species (M_xUO₂(CO₃)^z_y with M = Na, Ca) are readily formed in natural microscopic intragrain domains.^20,21 To concisely investigate the uranium species adsorption, we determined which uranyl–carbonate complexes would form and then calculated their proportion during simulation. The distance between carbonate C and U atom in uranyl was set as 3.1 Å to evaluate the possible complexes. This protocol is similar to the conventional radial distribution function (RDF), which counts the numbers of atoms of interest that present in a sphere of a specific radius. The position of uranium atoms from each trajectory is considered as the sphere origin. For example, if two carbon atoms are located less than 3.1 Å from the central uranium atom, a bicarbonate uranyl complex is proposed. The calculations confirmed the presence of uranyl (UO₂²⁺) and three other uranyl–carbonate complexes (UO₂CO₃, UO₂(CO₃)₂²⁻ and UO₂(CO₃)₃⁴⁻). The results are shown in Fig. 4 and Table 2.

Fig. 4 Atomic density profiles for various uranium species.

Table 2 Percentage of adsorbates

	Adsorbed layer^a				Diffuse layer^b
	UO2^2+	UO2CO3	UO2(CO3)2^2−	UO2(CO3)3^4−	UO2^2+	UO2CO3	UO2(CO3)2^2−	UO2(CO3)3^4−
a Adsorbed layer is within the d-plane. b Diffuse region is greater the d-plane.
0 M	40.9%	1.4%	0.0%	0.0%	17.1%	20.6%	19.8%	0.2%
0.05 M	40.9%	4.3%	0.0%	0.0%	20.2%	16.3%	14.2%	0.1%
0.10 M	17.0%	17.4%	20.9%	0.0%	3.0%	10.6%	30.5%	0.5%
	Na^+	Ca^2+	Cl^−		Na^+	Ca^2+	Cl^−
0 M	13.0%	15.6%			87.0%	84.4%
0.05 M	12.1%	11.2%	1.8%		87.9%	88.8%	98.2%
0.10 M	13.9%	13.4%	3.8%		86.1%	86.6%	96.2%

---

The modeled NaCl concentrations in clay pores may correspond to a moderate external electrolyte concentration range, 0–0.5 M, which is roughly estimated using the MD results of Jardat et al.⁵⁸ Contrary to our expectation that the adsorbed uranium will decrease with increasing Na⁺ concentration, the changing internal concentration has only a minor influence on the amount of total uranium in the adsorbed layer. The moderate change in total sodium content may account for this result. As mentioned above, 0 M NaCl corresponds to 66 compensative sodium ions and zero NaCl pairs, whereas 0.05 and 0.10 M correspond to 66 compensative Na⁺ ions along with 10 and 20 Na⁺ ions in the clay pore, respectively. Therefore, the moderate change for sodium ions (66 to 86) definitely has a minor influence on the uptake of the total uranium. Interestingly, the third simulation, with respect to 0.10 M NaCl, has the highest adsorbed amount of U. The charge inversion mentioned above indicates that abundant carbonates are present within the d-plane. Consequently, there are more uranyl-(bi)carbonate(s) complexes in the adsorbed layer to maintain local electronic neutrality. UO₂²⁺ is the predominant species in the adsorbed layers in the first two simulations, whereas UO₂²⁺, UO₂CO₃ and UO₂(CO₃)₂²⁻ are essentially equal in the third simulation (0.10 M NaCl). The uranyl-(bi)carbonate(s) complexes were substantially more prevalent in the diffuse layer than in the adsorbed layers, and there are no remarkable distinctions in the uranyl species fractions between 0 M and 0.05 M NaCl. In addition, UO₂(CO₃)₃⁴⁻ species are only found in the diffuse layer, and it is scarce. Based on our MD results, we suggest that the moderate change in the concentrations of competitive ions in the clay pore has a small effect on either the uptake amount or the species distribution for internal NaCl concentrations of 0–0.05 M. Furthermore, our results suggest the existence of a threshold concentration beyond which the EDL structure changes significantly, which in turn influences the adsorption of uranyl species.

Molecular dynamics simulation methodology

Our simulation methodology is briefly reviewed as follows. According to clay mineralogy, the montmorillonite mineral structure was derived from the pyrophyllite structure through lattice substitutions for high-valence cations. The montmorillonite atomic coordinates used herein were fixed based on the pyrophyllite structure reported by Bickmore et al.⁵⁹ Low-charge montmorillonite (0.33 e per unit cell) with the average formula of Na_0.33[Si₈][Al_3.67Mg_0.33]O₂₀(OH)₄ was modeled. The negative structural charge arises from randomly scattered isomorphic substitutions of Al³⁺ by Mg²⁺ in the octahedral sheet. An exclusion rule was used to ensure that two substitutions could not occur on adjacent sites. Half of the total charge was compensated by 66 sodium cations in the pore aqueous region, whereas the other half was balanced in the interlayer. According to XRD results for water-saturated compacted Na-smectite at montmorillonite partial dry densities between 1.0 and 1.5 kg dm⁻³,^11,60,61 water molecules per unit cell were used to model a two-water-layer interlayer structure. Simulations were carried out for U/Ca/C compositions of 10/10/20 atoms, resulting in approximate bulk concentrations of 0.05, 0.05 and 0.1 mol dm⁻³, respectively. Additionally, 0/10/20 NaCl ion pairs, corresponding to 0/0.05/0.1 mol dm⁻³, were added to model various ionic strengths. Depending on the ionic strength, our periodically replicated simulation cell (Fig. 5) contained two montmorillonite layers (20 × 10 × 2 unit cells) with an interlayer region along with an aqueous pore space containing 11 120–11 150 water molecules, 20 carbonate ions, 10 uranyl ions, 10 calcium ions, 66–86 sodium ions and 0–20 chloride ions. It is worth noting that the NaCl electrolyte concentrations mentioned above are the “internal” concentrations in the clay pores, not the “external” ionic strength in the aqueous solution. Furthermore, these two concentrations are not equal due to the Donnan equilibrium at the interface between clay pores and external bulk solution at low ionic strength.⁵⁸ Understanding the uranyl adsorption behavior under these conditions is of great importance because most groundwater systems have relatively low electrolyte concentrations.

Fig. 5 A snapshot of the MD simulation cell. This figure shows a uranyl containing aqueous solution confined in a montmorillonite pore between parallel clay surfaces, with U (blue), C (gray), Na (purple), Ca (green), Cl (light green), O (red) and H (white) atoms in the pore region and Si (yellow), Al (violet) in the clay mineral structure.

The UO₂²⁺ potential parameters were mostly derived from Guilbaud and Wipff.^62,63 Based on these parameters and the modified carbonate parameters, Greathouse and co-workers obtained satisfying configurations for uranyl carbonate complexes and simulated the adsorption of uranyl onto clay basal planes with the SPC water model.^52–54,64 Recently, Kerisit and Liu successfully assembled a consistent set of potential parameters for modeling the diffusion of alkaline-earth uranyl carbonate species in solution.⁴¹ The assembled model used the uranyl potential parameters from Guilbaud and Wipff,^62,63 the carbonate parameters from Pavese et al.,⁶⁵ the calcium parameters taken from de Leeuw and Parker⁶⁶ and the SPC/E water model. MD studies relevant to aqueous diffusion problems preferred to use the SPC/E model, which could more accurately reproduce the water diffusivity than the SPC water model.^41,45,48,55 Therefore, we employed the same potential parameters taken from Greathouse and co-workers for the aqueous species (carbonate, uranyl), the extensively verified CLAYFF⁶⁷ for the montmorillonite and aqueous ions, and the SPC/E water model.

All simulations were carried out with the LAMMPS software package.⁶⁸ Constant NVT (number, volume, temperature of 298.15 K) or NPT (number, pressure of 0 atm, temperature of 298.15 K) ensembles were used with thermostat and barostat relaxation times of 0.1 ps and 0.5 ps, respectively. The electrostatic forces were calculated by the Ewald summation method. The Verlet leapfrog integration algorithm was used to integrate the equations of motion with a time step of 0.001 ps. Three simulations of 6000 ps with various ionic strengths were performed to investigate the influence of ionic strength on the adsorption of uranyl onto montmorillonite basal planes. First, 1000 ps NPT simulations were carried out to determine the cell dimensions at 298.15 K and constant gauge pressure P_z = 0. Thereafter, 5000 ps NVT simulations were performed at 298.15 K, and the trajectories dumped from the final 4000 ps were used to analyze the adsorption profiles.

Conclusions

Three internal NaCl concentrations (0 M, 0.05 M and 0.10 M) were modeled to investigate the influence of the electrolyte in clay pores on the uranium species adsorption using molecular dynamics simulations. General adsorption information has been obtained from atomic density profiles. Uranium, sodium and calcium were shown to form OSSCs and be positively adsorbed near clay surfaces. In most cases, the uranium adsorbed onto montmorillonite, forming two prominent peaks approximately 4.3–4.8 Å from the clay planes. The exception, namely, the left peaks near the clay surface for 0.10 M NaCl, formed uranyl-(bi)carbonate complexes unlike those formed in the other electrolyte concentrations. As expected, chloride, due to its exclusion from the like-charged surfaces, exhibited a slowly increasing parabolic adsorption profile. EDL structures were also studied. The locations of the β- and d-planes were identified, and the charge inversion of carbonate was verified by its charge density profile. Collectively, our results suggest that the coordinates of the β- and d-planes are essentially independent of the type of ions and completely independent of ionic strength provided that charge inversion does not occur within the d-plane. One purpose of this study was to investigate the influence of electrolyte concentration on uranium species adsorption. The simulations revealed a minor influence on either the uptake amount or the species distribution for internal NaCl concentrations ranging from 0–0.05 M. In particular, there may exist a threshold concentration (0.10 M NaCl in this study) beyond which the EDL structure changes significantly, which in turn strongly affects the uranyl species adsorption.

Acknowledgements

We would like to thank the National Natural Science Foundation of China (NSFC) (no. 11075006, 91026010), Special Foundation for High Level Waste Disposal, SASTIND (2007-840, 2012-851) and the Special Research Funds for Designated Doctoral Programs in HEIs (20120001110082) for financial support.

Notes and references

1. A. Tsunashima, G. W. Brindley and M. Bastovanov, Clays Clay Miner., 1981, 29, 10–16.
2. J. P. McKinley, J. M. Zachara, S. C. Smith and G. D. Turner, Clays Clay Miner., 1995, 43, 586–598.
3. M. C. Duff and C. Amrhein, Soil Sci. Soc. Am. J., 1996, 60, 1393–1400.
4. T. Yamaguchi, Y. Sakamoto, S. Nakayama and T. T. Vandergraaf, J. Contam. Hydrol., 1997, 26, 109–117.
5. R. A. Zielinski, D. T. Chafin, E. R. Banta and B. J. Szabo, Environ. Geol., 1997, 32, 124–136.
6. T. Yamaguchi and S. Nakayama, J. Contam. Hydrol., 1998, 35, 55–65.
7. J. R. Bargar, R. Reitmeyer and J. A. Davis, Environ. Sci. Technol., 1999, 33, 2481–2484.
8. M. H. Baik, S. P. Hyun and P. S. Hahn, J. Radioanal. Nucl. Chem., 2003, 256, 11–18.
9. M. Wazne, G. P. Korfiatis and X. G. Meng, Environ. Sci. Technol., 2003, 37, 3619–3624.
10. S. M. Aytas, S. Akyil and M. Eral, J. Radioanal. Nucl. Chem., 2004, 260, 119–125.
11. J. G. Catalano and G. E. Brown, Geochim. Cosmochim. Acta, 2005, 69, 2995–3005.
12. A. Krepelova, S. Sachs and G. Bernhard, Radiochim. Acta, 2006, 94, 825–833.
13. C. X. Liu, Z. Q. Shi and J. M. Zachara, Environ. Sci. Technol., 2009, 43, 6560–6566.
14. J. Bai, C. X. Liu and W. P. Ball, Environ. Sci. Technol., 2009, 43, 7706–7711.
15. S. Korichi and A. Bensmaili, J. Hazard. Mater., 2009, 169, 780–793.
16. L. M. Camacho, S. G. Deng and R. R. Parra, J. Hazard. Mater., 2010, 175, 393–398.
17. C. Joseph, K. Schmeide, S. Sachs, V. Brendler, G. Geipel and G. Bernhard, Chem. Geol., 2011, 284, 240–250.
18. S. Bachmaf and B. J. Merkel, Environ. Earth Sci., 2011, 63, 925–934.
19. M. M. Fernandes, B. Baeyens, R. Dahn, A. C. Scheinost and M. H. Bradbury, Geochim. Cosmochim. Acta, 2012, 93, 262–277.
20. J. P. McKinley, J. M. Zachara, C. X. Liu, S. C. Heald, B. I. Prenitzer and B. W. Kempshall, Geochim. Cosmochim. Acta, 2006, 70, 1873–1887.
21. C. X. Liu, J. M. Zachara, O. Qafoku, J. P. McKinley, S. M. Heald and Z. M. Wang, Geochim. Cosmochim. Acta, 2004, 68, 4519–4537.
22. Y. Shang, C. X. Liu, Z. M. Wang and J. M. Zachara, Environ. Sci. Technol., 2011, 45, 6025–6031.
23. W. M. Dong, T. K. Tokunaga, J. A. Davis and J. M. Wan, Environ. Sci. Technol., 2012, 46, 1565–1571.
24. D. S. Jordan, J. M. Troiano and F. M. Geiger, Environ. Sci. Technol., 2012, 46(20), 11154–11161.
25. T. Arnold, S. Utsunomiya, G. Geipel, R. C. Ewing, N. Baumann and V. Brendler, Environ. Sci. Technol., 2006, 40, 4646–4652.
26. J. N. Malin, J. G. Holland, S. A. Saslow and F. M. Geiger, J. Phys. Chem. C, 2011, 115(27), 13353–13360.
27. L. N. Moyes, R. H. Parkman, J. M. Charnock, D. J. Vaughan, F. R. Livens, C. R. Hughes and A. Braithwaite, Environ. Sci. Technol., 2000, 34, 1062–1068.
28. M. A. Glaus, B. Baeyens, M. H. Bradbury, A. Jakob, L. R. Van Loon and A. Yaroshchuk, Environ. Sci. Technol., 2007, 41, 478–485.
29. G. Montavon, E. Alhajji and B. Grambow, Environ. Sci. Technol., 2006, 40, 4672–4679.
30. B. Baeyens and M. H. Bradbury, J. Contam. Hydrol., 1997, 27, 199–222.
31. M. H. Bradbury and B. Baeyens, J. Contam. Hydrol., 1997, 27, 223–248.
32. M. H. Bradbury, B. Baeyens, H. Geckeis and T. Rabung, Geochim. Cosmochim. Acta, 2005, 69, 5403–5412.
33. T. Rabung, M. C. Pierret, A. Bauer, H. Geckeis, M. H. Bradbury and B. Baeyens, Geochim. Cosmochim. Acta, 2005, 69, 5393–5402.
34. X. Y. Gu, L. J. Evans and S. J. Barabash, Geochim. Cosmochim. Acta, 2010, 74, 5718–5728.
35. G. D. Turner, J. M. Zachara, J. P. McKinley and S. C. Smith, Geochim. Cosmochim. Acta, 1996, 60, 3399–3414.
36. A. W. Miller and Y. F. Wang, Environ. Sci. Technol., 2012, 46, 1981–1994.
37. M. Taoufik, K. C. Szeto, N. Merle, I. D. Rosal, L. Maron, J. Trebosc, G. Tricot, R. M. Gauvin and L. Delevoye, Chem. – Eur. J., 2014, 20, 4038–4046.
38. H. Geckeis, J. Lutzenkirchen, R. Polly, T. Rabung and M. Schmidt, Chem. Rev., 2013, 113, 1016–1062.
39. A. Kremleva, B. Martorell, S. Kruger and N. Rosch, Phys. Chem. Chem. Phys., 2012, 14, 5815–5823.
40. V. A. Glezakou and W. A. deJong, J. Phys. Chem. A, 2011, 115, 1257–1263.
41. S. Kerisit and C. X. Liu, Geochim. Cosmochim. Acta, 2010, 74, 4937–4952.
42. O. Teleman, B. Jonsson and S. Engstrom, Mol. Phys., 1987, 60, 193–203.
43. A. Wallqvist and O. Teleman, Mol. Phys., 1991, 74, 515–533.
44. V. Marry, B. Rotenberg and P. Turq, Phys. Chem. Chem. Phys., 2008, 10, 4802–4813.
45. V. Marry, E. Dubois, N. Malikova, S. Durand-Vidal, S. Longeville and J. Breu, Environ. Sci. Technol., 2011, 45, 2850–2855.
46. S. Kerisit, C. X. Liu and E. S. Ilton, Geochim. Cosmochim. Acta, 2008, 72, 1481–1497.
47. S. Doudou, D. J. Vaughan, F. R. Livens and N. A. Burton, Environ. Sci. Technol., 2012, 46, 7587–7594.
48. S. Kerisit and C. X. Liu, Environ. Sci. Technol., 2009, 43, 777–782.
49. B. Rotenberg, V. Marry, R. Vuilleumier, N. Malikova, C. Simon and P. Turq, Geochim. Cosmochim. Acta, 2007, 71, 5089–5101.
50. B. Rotenberg, V. Marry, J. F. Dufreche, N. Malikova, E. Giffaut and P. Turq, C. R. Chim., 2007, 10, 1108–1116.
51. S. Kerisit and C. X. Liu, Environ. Sci. Technol., 2012, 46, 1632–1640.
52. J. A. Greathouse, R. J. O'Brien, G. Bemis and R. T. Pabalan, J. Phys. Chem. B, 2002, 106, 1646–1655.
53. J. A. Greathouse and R. T. Cygan, Phys. Chem. Chem. Phys., 2005, 7, 3580–3586.
54. J. A. Greathouse and R. T. Cygan, Environ. Sci. Technol., 2006, 40, 3865–3871.
55. C. Tournassat, Y. Chapron, P. Leroy, M. Bizi and F. Boulahya, J. Colloid Interface Sci., 2009, 339, 533–541.
56. I. C. Bourg and G. Sposito, J. Colloid Interface Sci., 2011, 360, 701–715.
57. S. L. Teich-McGoldrick, J. A. Greathouse and R. T. Cygan, Mol. Simul., 2014, 40, 7–9.
58. M. Jardat, J. F. Dufreche, V. Marry, B. Rotenberg and P. Turq, Phys. Chem. Chem. Phys., 2009, 11, 2023–2033.
59. B. R. Bickmore, K. M. Rosso, K. L. Nagy, R. T. Cygan and C. J. Tadanier, Clays Clay Miner., 2003, 51, 359–371.
60. I. C. Bourg, G. Sposito and A. C. M. Bourg, Clays Clay Miner., 2006, 54, 363–374.
61. G. Kosakowski, S. V. Churakov and T. Thoenen, Clays Clay Miner., 2008, 56, 190–206.
62. P. Guilbaud and G. Wipff, J. Phys. Chem., 1993, 97, 5685–5692.
63. P. Guilbaud and G. Wipff, New J. Chem., 1996, 20, 631–642.
64. X. Y. Liu, C. Li, W. Y. Tian, T. Chen, L. H. Wang, Z. Zheng, J. B. Zhu, M. Sun and C. L. Liu, Acta Phys.-Chim. Sin., 2011, 27, 59–64.
65. A. Pavese, M. Catti, S. C. Parker and A. Wall, Phys. Chem. Miner., 1996, 23, 89–93.
66. N. H. deLeeuw and S. C. Parker, J. Chem. Soc., Faraday Trans., 1997, 93, 467–475.
67. R. T. Cygan, J. J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266.
68. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.

---

Footnote

† These authors contributed equally to this work.

---