Open Access Article
Open Access ArticleResolving local ordering and structure in MnxGe1−xTe alloys through thermodynamic ensembles of pair distribution functions†
Vanessa
Meschke
 a,
Andrew
Novick
a,
Andrew
Novick
 a,
Jen
Rogers
b,
Claire
Porter
a,
Jen
Rogers
b,
Claire
Porter
 a,
Remco
Chang
b,
Thomas
Proffen
a,
Remco
Chang
b,
Thomas
Proffen
 c and
Eric S.
Toberer
c and
Eric S.
Toberer
 *a
*a
aPhysics Department, Colorado School of Mines, Golden, CO 80401, USA. E-mail: etoberer@mines.edu
bDepartment of Computer Science, Tufts University, Medford, MA 02115, USA
cNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA
First published on 2nd August 2024
Abstract
Characterizing local bonding environments in complex materials is essential for understanding and optimizing their properties. Equally as important is the ability to predict local motifs as a function of synthesis conditions, enhancing chemists’ ability to design properties into materials. In this study, we present an approach to leverage statistical mechanics to generate temperature- and energy-informed ensemble averaged pair distribution functions (PDFs). This method, which we have named Thermodynamic Ensemble Averages of PDFs for Ordering and Transformations (TEAPOT), utilizes density functional theory (DFT) to relax supercells while incorporating energetic penalties for local order, enabling accurate and computationally efficient analysis of local structure. We apply this method to the neutron PDF measurements of the pseudobinary MnTe–GeTe (MGT) alloy, demonstrating its capability to resolve complex local distortions and chemical ordering. Our results reveal detailed insights into phase transformations and local distortions driven by Mn substitution. For compositions that globally present as rock salt, our analysis reveals that Ge coordination geometry is heavily impacted by synthesis temperature. We propose that high temperature synthesis conditions promote a lowered Ge polyhedra distortion, promoting high charge carrier mobility due to the alignment of local and global structure. Incorporating statistical mechanics and computation into experimental analysis thus guides synthesis of tailored local structure.
1 Introduction
The impact of local bonding environments on materials’ properties has been a persistent challenge to characterize for solid state chemistry.1–3 Whether the change is due to local distortions (strain) or order (chemical, magnetic, or other configurations), small lapses in periodicity can have a large impact on properties. For example, local distortions can be leveraged to improve optical properties of perovskites,4 enhance superconductivity,5 or tune the band gap in semiconductors.6,7 Additionally, local order (or disorder) can drive interesting magnetic properties1 or enhance performance for new cathode materials.8 To fully leverage the benefit that can come from changing local structure, solid state chemists would ideally be able to predict, synthetically control, and observe local order and distortions to influence materials properties.Experimentally, probing local structure has been challenging. Spectroscopic techniques such as X-ray absorption fine structure (XAFS) and X-ray absorption near-edge structure (XANES) can provide valuable qualitative information about the first and second nearest neighbor chemistries, but quantitative descriptions in complex alloys are generally lacking.9 Alternatively, electron diffraction can probe the overall structure of a hyperlocal section of a sample, but fail to pick up on the nuances of local coordination. To measure both local chemistry and bond distributions, though, one technique particularly shines, especially for complex materials: the pair distribution function (PDF).10,11 The PDF provides valuable insight into both the local bonding environment and mesoscale structure for bulk materials that isn’t accessible with other techniques.12 PDF is thus, in principle, an excellent technique for probing the impacts of local order and distortion in complex materials. However, analyzing the results of PDF measurements in materials with significant local order and distortions remains challenging. In this paper, we develop a thermodynamics-aware first-principles approach to analyzing disorder and distortion and apply it to the high-perfoming thermoelectric alloy MnxGe1−xTe (MGT).13–17 MGT is not only interesting due to its high thermoelectric performance; it also offers a temperature and composition driven phase change that significantly alters the local bonding environment.18–21
When analyzing a PDF using common small box approaches, a useful first fitting attempt is to approximate perfect chemical disorder by creating atoms that are fractionally occupied according to the overall stoichiometry.22 This average structure representation is computationally inexpensive and, for highly disordered but undistorted materials, fits reasonably well. Due to its simplicity, the average structure is unable to capture any degree of chemical ordering; however, it can capture a small amount of distortion when used in conjunction with the box-car refinement strategy. By refining the average structure's atomic positions and lattice constants over small r-intervals, a box-car refinement can provide insight into the change in average bond distributions at different length scales. However, this approach is more useful in extracting information about the length scales of order and distortion rather than truly capturing local distortions.3,23,24 As such, the averaged structure approach will ultimately fail to capture local order and distortions in more complex systems.
To more accurately capture local distortions, the special quasirandom structures (SQS) method is an attractive alternative to the average structure for materials with minimal local order.25,26 In SQS, a single supercell that mimics perfect chemical disorder is generated, and local distortions are accounted for by relaxing the supercell with molecular dynamics (MD) or density functional theory (DFT).27–29 However, for high-dimensional alloy spaces, these relaxations become prohibitively expensive, making this method ineffective for complex chemistries. Additionally, the SQS will still fail to model local order due to its overestimation of entropic contributions.
To incorporate local order as well as distortions, the Reverse Monte Carlo (RMC) technique is very popular in PDF analysis.30,31 RMC minimizes a goodness of fit parameter between calculated and experimental PDFs by swapping or hopping atoms from an initial structure, with local distortions again being realized from piping results to MD or DFT.32 RMC alone has already been used with fair results in disordered materials such as MGT at the end of its cubic phase transition,18 while RMC + MD method has been particularly effective for modeling dynamic disorder in superionic conductors.33 Similarly to SQS, RMC again becomes exceedingly expensive as more elements are incorporated, since complex spaces require the use of large supercells. Additionally, while RMC allows for geometric constraints, it has no concept of the energetic penalty of the various structural or chemical motifs motifs, only fit quality. As such, any order captured with RMC risks being nonphysical and simply one of many possible solutions that can describe the PDF pattern well.
To account for both local order and distortion while considering energetic penalties, building a cluster expansion (CE) to use with a Monte Carlo simulation (MC) and first principles relaxation is an elegant workflow. With this method, the energetic penalties of local order are calculated when fitting the model Hamiltonian for the CE. Entropy contributions are then accounted for by annealing a starting structure using MC at a given temperature. Finally, local distortions are incorporated by using MD or DFT to relax the annealed structure from the CE + MC simulation.
Szymanski, et. al. demonstrate an excellent example of the CE + MC workflow by analyzing the local order and distortions in two disordered oxyfluoride alloys.29 In their work, Szymanski, et. al. explicitly show the degree of complexity that can be added to a model by separately investigating the effects of ordering and distortion using the various methods outlined in this introduction. Ultimately, the energy-informed CE + MC approach they use captures the experimentally measured PDFs better than any energy-unaware approximations to structure for their complex alloy system. However, approaches that rely on CE + MC have constraints. First, developing a CE can be challenging for systems that exhibit strong local distortions, including materials undergoing phase transitions. Second, MC-based annealing is necessary at each temperature of interest. Finally, the chemical complexity of the alloy is constrained by the need to ultimately relax the supercell with first principles calculations.
In the work discussed above, the goal of PDF analysis is to use computation to resolve local structure, but not necessarily provide guidance on how to experimentally proceed in designing tailored local structure. Indeed, the overarching philosophy is to find a singular representation of a structure that is instead best viewed statistically. Here, we present an alternative approach to PDF analysis that takes inspiration from the success of modeling alloys’ structures and properties through the independent cell approximation.34–44 By leveraging statistical mechanics, we are able to create thermodynamic ensemble averages of PDFs for ordering and transformations (TEAPOT). By developing a statistical ensemble of supercells relaxed with DFT, we minimize the number of PDF fitting parameters while remaining energy-aware. Further, the ensemble approach of TEAPOT allows for intensive variables such as temperature to be swept gracefully without requiring additional calculations of local structure. As such, having determined the thermodynamic state of a given sample, we are able to hypothesize how alternative synthetic strategies could be employed to impact local structure.
We present a use case for TEAPOT through a comprehensive study of neutron PDF measurements of MGT alloys. To begin, we develop a benchmark by invoking perfect chemical disorder in the PDF refinements. Following this initial fitting, we delve into the results of TEAPOT, highlighting the impact of Mn on the local coordination through the phase transformation. Given the large amount of data generated by this technique, we also demonstrate complex dimension reduction techniques to increase understanding of the local bonding environments. Through this study, we pave the way for a more thorough comprehension of complex alloy structures and showcase the potential of our approach to accelerate PDF analysis.
2 Methods
2.1 Experimental procedure
Polycrystalline samples were prepared by weighing high purity Mn (99.999%, Alfa), Ge (99.999%, Indium Corp.), and Te (99.999%, 5N Plus) by ball milling using tungsten carbide vials (SPEX 8004) in a SPEX 8000D high energy milling machine. Following milling, the powders sealed under vacuum in cleaned fused silica ampules, annealed for 24 hours at 500 °C, and air quenched to room temperature. Following the anneal, samples were ground by hand with an agate mortar and pestle and passed through a 40 μm mesh sieve. Time-of-flight (TOF) neutron diffraction patterns and pair distribution functions (PDFs) were collected on the POWGEN instrument at the Spallation Neutron Source (SNS) at Oak Ridge National Lab. Data were collected at room temperature and reduced using Mantid Workbench.45 TOF patterns were refined using the Rietveld approach on TOPAS46 and PDFs were refined using the PDFFit2 Python package.222.2 Computational procedure
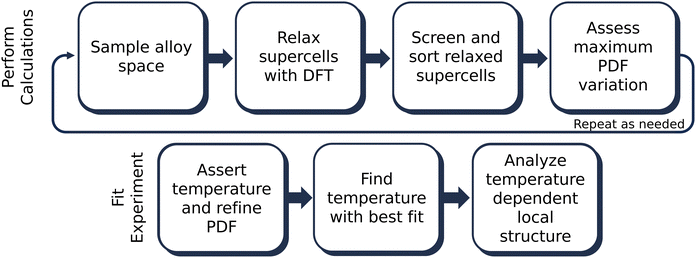
The overall methodology for this paper is shown in Fig. 1. Following the method outlined in Novick, et al., 100 supercells of various symmetry-inequivalent decorations and dimensions were sampled at each composition of interest using the Hart and Forcade method.40,47 Of the 100 supercells, 50 were initialized in space group 160 (R3mH) and 50 were initialized in space group 225 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to prevent bias towards either symmetry in the intermediate alloy space. Initial supercell volumes were scaled using Vegard's law between the cubic structures of GeTe and MnTe. To more closely match the experimentally studied compositions, supercell sizes ranged from 32 to 40 atoms, resulting in overall stoichiometries of 12.5, 20, 25, 30, and 35% Mn on the cation sublattice.
m) to prevent bias towards either symmetry in the intermediate alloy space. Initial supercell volumes were scaled using Vegard's law between the cubic structures of GeTe and MnTe. To more closely match the experimentally studied compositions, supercell sizes ranged from 32 to 40 atoms, resulting in overall stoichiometries of 12.5, 20, 25, 30, and 35% Mn on the cation sublattice.
The total energies of the supercells were calculated using density functional theory48,49 (DFT) as implemented in the Vienna Ab Initio Simulation Package (VASP).50 The exchange-correction energy functional was approximated with the Perdew–Burke–Ernzerhof (PBE) functional51 within the projector-augmented wave formalism.52 A planewave cutoff of 340 eV and a Γ-centered k-point mesh were used such that the energy converged to <3 meV per atom. Each Mn atom was initialized with a starting spin of ±5μB, and spin configurations were chosen such that each supercell had a net spin of zero. Spin polarized relaxations were conducted such that the volume, cell shape, atom positions, and magnetic moments were all optimized.
Following the calculation of the supercell energies, thermodynamic averages of the PDFs were fit to the experimental data. First, structures were sorted into ending in rhombohedral or rock salt structure by assessing the calculated PDFs. Fewer than 5 specimens per composition were unable to be sorted into either rhombohedral or rock salt and were left out of the ensemble. The ensemble averaged PDF (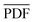 ) is calculated as:
) is calculated as:
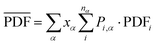 | (1) |
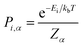 | (2) |
In calculating the probability of any PDF, Ei is the relaxed energy of supercell i, kb is the Boltzmann constant, and T is the temperature in K. The most significant portion of the probability is the normalization factor, Z, otherwise known as the partition function. The partition function for a given phase α is calculated as:
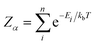 | (3) |
As shown in Fig. S10 (ESI†), the individual PDFs have significant variation. To assess the uncertainty in the high temperature PDF for a given ensemble size, the central limit theorem was employed. The resulting uncertainty across the PDF is shown in Fig. S7 (ESI†) and is sufficiently small. While not employed herein, the uncertainty for other temperatures can be determined following the methods outlined by Novick, et al.40
The resulting structures from the DFT relaxation were converted to the CIFs using Pymatgen, and PDFs were calculated from these CIFs using PDFFit2.22,53 PDF refinements were carried out from 2–15 Å for each composition in the alloy space at ensemble calculation temperatures ranging from 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Before temperature was considered, each supercell's lattice was isotropically dilated or compressed to match the experimental pattern's peak locations. This dilation constant was then used to scale the supercell's lattice across all refinements at all temperatures. Following individual lattice refinements, temperature dependent ensemble refinements commenced. For these refinements, a singular isotropic U was refined for all supercells at each temperature considered. Additionally, the relative fractions of each phase (rhombohedral and cubic) were refined for the ensemble at each temperature considered. SciPy was used to perform a non-linear least squares refinement using the curve fit method with the Levenberg–Marquardt algorithm.54
000 K. Before temperature was considered, each supercell's lattice was isotropically dilated or compressed to match the experimental pattern's peak locations. This dilation constant was then used to scale the supercell's lattice across all refinements at all temperatures. Following individual lattice refinements, temperature dependent ensemble refinements commenced. For these refinements, a singular isotropic U was refined for all supercells at each temperature considered. Additionally, the relative fractions of each phase (rhombohedral and cubic) were refined for the ensemble at each temperature considered. SciPy was used to perform a non-linear least squares refinement using the curve fit method with the Levenberg–Marquardt algorithm.54
In addition to calculating the ensemble PDFs, data were collected on the bond lengths and chemical coordination of individual atoms within the supercells. The coordination shells of all cations were collected using the Python library PyLaDa Light.55 All coordination shells were forced to have the same number of atoms as the corresponding coordination shells of a perfectly cubic structure (6, 12, 8, and 6 atoms for the first, second, third and fourth coordination shells, respectively).
3 Results
Given the complexity of the MGT pseudobinary alloy space, we will first analyze the global structure of the alloys by assessing the refined diffraction patterns using averaged structures. Finding good fit quality for the global structures, we will move on to fitting the PDFs. To benchmark the quality of the fits using TEAPOT against traditional methods, we will first assess the PDFs of all samples using averaged structures and box-car refinements. Following the benchmarking, we will introduce the DFT-relaxed structures for use in the TEAPOT method, focusing on discussions of local coordination and bond distributions. Then, we will assess the ability of the TEAPOT method to distinguish between the changes in PDF with temperature, ultimately leading to the TEAPOT-generated temperature dependent fits. We will end on a discussion of the TEAPOT results by using projection techniques to analyze the trends in Mn content with the alloy space.3.1 Long range structure
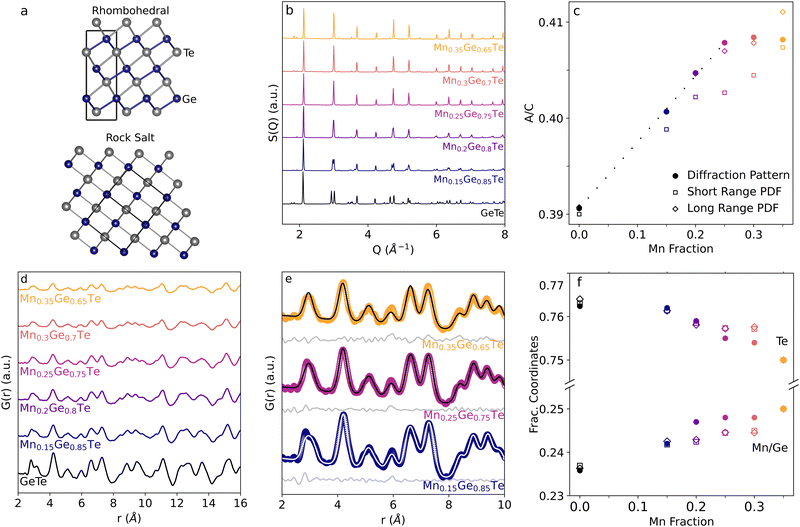
Before analyzing the short range structure via PDF in the MGT alloy space, we first fit out experimental neutron diffraction data with a simple, averaged structure approach as a benchmark and to ensure the experimental data follows the expected transition. Refinements were carried out using fractionally occupied cation sites with lattice parameters starting from the rhombohedral (space group 160, R3mH) GeTe structure using TOPAS Academic.46,56 Each structure was allowed to vary the a and c lattice parameters, the cation site positions, and the atomic displacement factors, resulting in structures that show good agreement with experimental data that will be discussed below. Individual refinements are shown in Fig. S1–S6 in the ESI.†Previous studies of the MGT phase diagram report a continuous rhombohedral to cubic phase transition as the Mn content is increased.57 This phase transition can be modeled as a growth of the ratios of the a and c lattice parameters, which vary from 4.165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å:
Å:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.663 Å = 0.391 (rhombohedral) to 4.164
10.663 Å = 0.391 (rhombohedral) to 4.164![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å:
Å:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.204 Å = 0.408 (rock salt). This transition is shown in Fig. 2(b). Previous studies have reported the alloy to be fully cubic for x ∼ 0.18 in MnxGe1−xTe from powder XRD, though x as high as 0.25 has been reported.19,20,57,58 Our experimental data shows agreement with the cubic phase transition being complete no earlier than x = 25%, and individual fits for each composition are shown in the ESI.† In Fig. 2(d), inspecting the peaks at ∼3 and 4.8 Å−1 show the merging of the doublet present for rhombohedral GeTe (bottom, black) to a single peak that is a hallmark of the rocksalt structure for cubic MGT. Additionally, by inspecting the a to c lattice parameter ratios, shown as filled circles in Fig. 2(c), a trend line can be approximated from the pure GeTe to x = 0.25 Mn content sample, showing the lattice parameters changing continuously throughout the phase transition until the rock salt a:c ratio (0.408) is reached.
10.204 Å = 0.408 (rock salt). This transition is shown in Fig. 2(b). Previous studies have reported the alloy to be fully cubic for x ∼ 0.18 in MnxGe1−xTe from powder XRD, though x as high as 0.25 has been reported.19,20,57,58 Our experimental data shows agreement with the cubic phase transition being complete no earlier than x = 25%, and individual fits for each composition are shown in the ESI.† In Fig. 2(d), inspecting the peaks at ∼3 and 4.8 Å−1 show the merging of the doublet present for rhombohedral GeTe (bottom, black) to a single peak that is a hallmark of the rocksalt structure for cubic MGT. Additionally, by inspecting the a to c lattice parameter ratios, shown as filled circles in Fig. 2(c), a trend line can be approximated from the pure GeTe to x = 0.25 Mn content sample, showing the lattice parameters changing continuously throughout the phase transition until the rock salt a:c ratio (0.408) is reached.
In addition to the lattice transition, the atomic site positions move from the distorted, non-symmetric rhombohedral positions (0.236 and 0.762 for (Mn,Ge) and Te, respectively) to high symmetry 0.25 and 0.75 positions, shown as the solid squares in Fig. 2(f). The shifting atomic sites fully completes the transition from rhombohedral to rock salt and merges all peaks to the expected space group 225 pattern by the end of the alloy series studied, with a similar slowing rate of change as x ∼ 25% is reached. In contrast to the lattice parameters, the atomic site positions show continued evolution after x = 25%. In summary, we see that the rhombohedral to cubic phase transition occurs slowly and continuously until 25% Mn, at which point atomic positions and lattice parameters largely converge to the expected cubic diffraction pattern.
3.2 Cation site averaged PDF analysis
Similarly to the diffraction patterns, the experimental PDF patterns (Fig. 2(d)) show a continuous transition from the rhombohedral to the cubic phase as the Mn content is increased in the alloy. Applying the same averaged structure fitting technique used to analyze the diffraction patterns, the PDFs of the alloy series can be fit using fractionally occupied cation sublattices. Refinements were initialized from the lattice parameters and atomic positions retrieved from the diffraction refinements of the global structure. Shown in Fig. 2(e), as the Mn content is increased in the alloy, the first nearest neighbors peak in the PDF transitions from an asymmetric doublet to the expected singlet peak near 3 Å. Averaged structure fits fail to capture the asymmetry of this peak for lower Mn content, but show overall good agreement with experiment beyond the first nearest neighbor peak.Despite the longer range structure being well fit across the sample space, the modeled nearest neighbors peak appears much less asymmetric than experiment suggests. The extracted a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c lattice parameters ratio and fractional atomic positions from the PDF refinements show interesting results. At a low-r box car range, increasing the Mn content results in increased disagreement for both parameters as compared to the diffraction pattern. However, good agreement between diffraction and PDF analysis is found for all boxcar ranges beyond 2–15 Å and is shown in ESI,† Fig. S9.
c lattice parameters ratio and fractional atomic positions from the PDF refinements show interesting results. At a low-r box car range, increasing the Mn content results in increased disagreement for both parameters as compared to the diffraction pattern. However, good agreement between diffraction and PDF analysis is found for all boxcar ranges beyond 2–15 Å and is shown in ESI,† Fig. S9.
Beyond the local coordination range, the averaged structures show varying fit quality from the local to the long range order. A summary of the fit quality over all selected box-car r ranges for all compositions is shown in the ESI.† Overall, the 25% Mn sample shows the best fit quality at all r ranges inspected, while the 35% Mn sample shows the worst. This is likely due to the degree of disorder present in the system at each of the compositions. The highest quality fits for all compositions lie in the 20–30 Å range, indicating the alloy shows local orderings that are not present at the intermediate range.
3.3 Boltzmann ensemble probability distributions
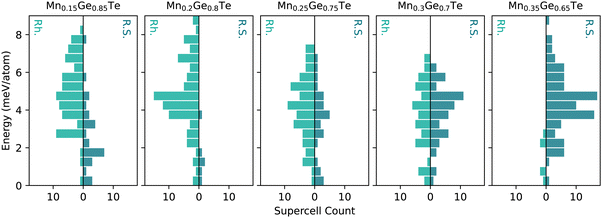
Given the limitations of the average structure approach, we move towards a more complex analysis of the MGT alloy space using the TEAPOT method. First, we will discuss the underlying energy distributions, or the thermodynamic density of states (TDOS), that are core to ensemble averages. Since the efficacy of the TEAPOT method hinges on the thorough sampling of structural motifs and their various energetic penalties, assessing the TDOS is an important step in ensuring reasonable results can be achieved. Additionally, the ending space groups of the parents in the alloy space should be accounted for when constructing the TDOS. For example, in the MGT system, the rhombohedral and cubic structures are known to exist for pure GeTe and the Mn0.5Ge0.5Te compounds, respectively. Treating the rhombohedral and cubic structures as separate energy distributions prevents us from presuming ergodicity in the intermediate alloy, removing some bias from our ensemble.As discussed in the Methods section, 50 supercells each were generated in the cubic and rhombohedral structures for each stoichiometry studied and relaxed using DFT. While this approach will not be able to discern information regarding the widths of the energetic wells of the possible structures in an alloy space, it is significantly less computationally intensive than fully sampling configuration space.59 No constraints were placed on the relaxations to prevent bias towards either end of the structural transition. Given the fraught nature of space group classification, relaxed structures were then sorted based on the shape of the first nearest neighbors peak of the calculated PDF. Supercells with a doublet as the first nearest neighbors peak were sorted into the rhombohedral category, while single peaks were considered cubic. Fewer than five structures at each stoichiometry were unable to be sorted into either category and were discarded. The sorted structures energies’ were then used to create two structure-based TDOS for each composition, shown in Fig. 3, that determine the probability of a structure.
For the MGT system, the TDOS for the rhombohedral (green) and cubic (teal) structures are shown for each composition in Fig. 3. All distributions were referenced to the lowest energy for that composition and structure to provide a consistent reference point for comparison in the plots. Within these distributions, the 15% and 25% Mn samples have particularly heavy samplings of the lowest energy states, particularly on the cubic side of the distribution. The remaining samples have relatively Gaussian samplings across the energy range. The spread of the energies within any TDOS is relatively tight, spanning less than 10 meV per atom from the most to least favorable configuration. While this energy spread is larger than the error of a DFT calculation, it is relatively small and may lead to issues with distinguishing between energetic configurations in this space.
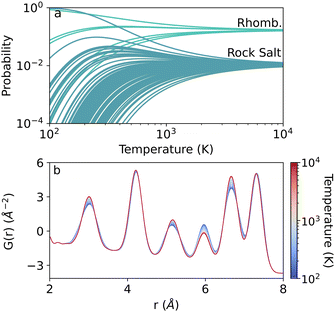
Incorporating the ensemble temperature viaeqn (1)–(3) turns the above energy distributions into probability distributions. With Boltzmann averaging, the prevalence of a single representation is dictated by the supercell energies and temperature, as discussed in the Methods. An example of the relationship between an individual representation's ensemble probability and temperature is shown in Fig. 4(a). At low temperatures, only the few lowest energy structures from the ensemble contribute to the average structure significantly. For the rhombohedral and cubic structures, this manifests as the singular green and teal curves with probabilities near unity at 100 K. At high temperatures, however, all structures contribute equally to the structure with 1/n weight, where n is the number of samples in the ensemble. Thus, the high temperature limit approximates perfect disorder similar to the average structure or SQS technique, indicating high degrees of disorder in the system. In Fig. 4(a), this limit is approached near 7000 K and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for the rhombohedral and cubic ensembles, respectively. The temperature dependent distributions for the remaining compositions are shown in the ESI,† in Fig. S8.
000 K for the rhombohedral and cubic ensembles, respectively. The temperature dependent distributions for the remaining compositions are shown in the ESI,† in Fig. S8.
The impact of temperature is realized as changes in the TEAPOT PDF, an example of which is shown in Fig. 4(b) for the 35% Mn ensemble. The averaged PDFs for Mn0.35Ge0.65Te were calculated from 100 K (blue) to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K (red) with all calculation parameters were kept constant. For this ensemble, the temperature mostly changes peak heights and broadness, but not peak location. This strong variation is imperative for the efficacy of the TEAPOT method. Without the temperature dependence, any nuances of local coordination are unable to be distinguished from the high temperature limit, providing little information for guiding synthetic conditions to change alloy structure.
000 K (red) with all calculation parameters were kept constant. For this ensemble, the temperature mostly changes peak heights and broadness, but not peak location. This strong variation is imperative for the efficacy of the TEAPOT method. Without the temperature dependence, any nuances of local coordination are unable to be distinguished from the high temperature limit, providing little information for guiding synthetic conditions to change alloy structure.
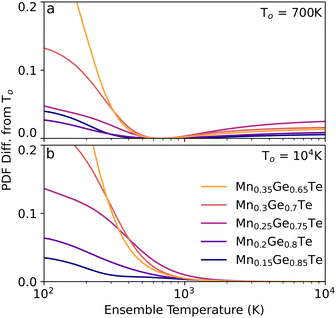
As such, considering the minimally achievable variation in TEAPOT PDFs is an important step in determining if the method can be successful in predicting structure changes. To quantify the potential impact of temperature on the ensemble structure, we consider two hypothetical situations. First, we construct a base dataset using the ensemble at 700 K. This pattern will be referred to as To. The degree of structural diversity compared to this base PDF can then be quantified by calculating the mean squared difference (MSD) between the PDF pattern at To and a PDF pattern at an arbitrary temperature T:
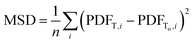 | (4) |
3.4 TEAPOT refinements
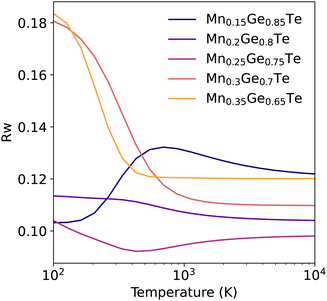
Given the theoretically achievable variation in local structure and associated TEAPOT PDFs, we move to considering the ensemble fits to the experimental neutron PDF patterns. The TEAPOT fits from 2–15 Å at the best fit temperatures are shown for each sample in Fig. 6, with the experimental patterns shown in color and the fits in black. To reach these optimal fits, we considered the impact of temperature (Fig. 7), atomic displacement parameter (Fig. S20, ESI†), and phase fractions (Fig. S19, ESI†). Overall, each TEAPOT PDF shows an excellent fit to the experimental dataset upon refinement. For the entire alloy space, the optimum fits acquired with TEAPOT provide similar quality to those achieved with the average structure approach (Rw ∼ 0.1) and the best fitting individual supercells (Rw ∼ 0.11–0.14, Fig. S11, ESI†).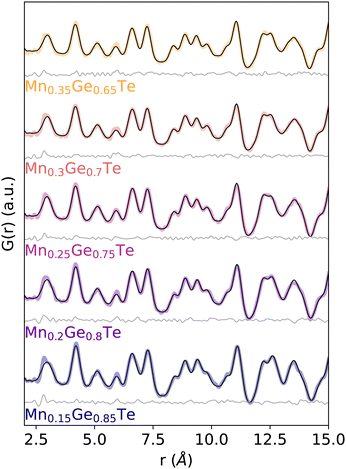 | ||
| Fig. 6 Experimental PDF patterns (color) and TEAPOT fits (black) with difference curves below (grey) at best temperature fit from 2–15 Å show quality fits with Rw ranging from 0.09–0.12 across the entire alloy series. The fit qualities are shown for all temperatures in Fig. 7. | ||
Considering this fitting space, the refined phase fraction transitioned from predominantly rhombohedral to rock salt with increasing Mn content. This evolution is consistent with prior understanding of the composition-driven phase transition in the MGT chemical space. The optimal atomic displacement value was consistent across the composition space (U ∼ 0.01 Å2); we’ll return to this in the context of the bond lengths from the DFT-relaxed supercells. The optimal temperature for each composition (Fig. 7) varied from the low to the high temperature limit. The highest Mn content samples showed the strongest temperature dependence, with the high temperature limit being a clear best fit. In contrast, the low Mn samples showed minima at finite temperature, though these minima were less well defined than the high Mn samples. In the following paragraphs, we will delve into the dependency of each composition across the entire fitting space.
For each of the best fits, the upper end of the 2–15 Å box-car fit exceptionally well, though the quality of the first nearest neighbors peak is again lacking. However, previous studies have shown that the left side of this doublet is associated with inelastic scattering associated with correlated motion between the sheets.60 We are delighted to see that with increasing Mn content, this correlated motion rapidly fades away, likely due to Mn's propensity for 6-fold coordination.
The two most Mn-rich samples show the Rw curve flattens out for temperatures above 1000 K. This result is unsurprising when considering the variation in the TEAPOT PDFs considered in Fig. 5(b), where differences in the PDF are nearly imperceptible from 1000 K to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. As such, none of these samples have a singular best fit temperature, though each of the PDFs is nearly equivalent to the high temperature limit. However, the change in fit and fit quality from the low to high energy PDFs is very evident and is consistent with our expectation from Fig. 5. In the high Mn compositions, the combination of a low enthalpy of mixing (Fig. 3) and high configurational entropy support a randomly disordered cation sublattice.
000 K. As such, none of these samples have a singular best fit temperature, though each of the PDFs is nearly equivalent to the high temperature limit. However, the change in fit and fit quality from the low to high energy PDFs is very evident and is consistent with our expectation from Fig. 5. In the high Mn compositions, the combination of a low enthalpy of mixing (Fig. 3) and high configurational entropy support a randomly disordered cation sublattice.
Next considering the 25% Mn sample, this composition has a high degeneracy of low energy states (Fig. 3), and as such significant structural averaging has already occurred even at low temperature. The low temperature ensemble structure proves an excellent fit. However, a further improvement in fit occurs with temperature, with a shallow minimum centered at 428 K. Inspecting the variation in the fits with temperature, shown in Fig. S12–S16 (ESI†), the quality of this fit is largely dictated by changes in fourth nearest neighbor peak (∼6 A) intensities. The impact of such longer-range ordering is typically outside the scope of SQS and related modelling techniques. Little variation is observed in peak locations, so we attribute most of the ensemble variation to differences in the cation bonding environments.
For the 20% and 15% Mn content refinements, the fit quality is again quite good at all temperatures, though little variation is observed in the PDF below 10 Å (Fig S12 and S13, ESI†). This is consistent with the dilute nature of these compositions. Given that ordering at this length scale is unlikely to be a primary driver in the system energetics, the variation in Rw with temperature is unlikely to be predictive of local structure for these two samples. These samples highlight the importance of inspecting the temperature-dependence of the PDF rather than simply focusing on the optimal Rw, especially in more dilute systems.
A common trend throughout the composition space is the critical role that peak intensity, rather than peak location, played in determining the optimal temperature. Since all TEAPOT PDFs were modeled with the same number and ratio of cations in all supercells, changes in peak intensity are caused by changes in the number of Mn–Mn, Ge–Ge, and Mn–Ge interactions in the second coordination shells. Given the signs of the scattering lengths for Ge, Mn, and Te (8.185 fm, −3.73 fm, and 5.80 fm, respectively),61 the cation pairwise interactions can either result in a net positive (Ge–Ge, Mn–Mn) or negative (Mn–Ge, Ge–Mn) intensity. For example, the second and fourth nearest neighbor peaks at ∼4.2 and 6 Å show the opposite trend in peak intensity with increasing temperature (Fig. S12–S16, ESI†). This trend is consistent with the evolution of the Ge–Mn fractional coordination counts with temperature (Fig. S17 and S18, ESI†). The tightening of the bond distributions can also contribute to the increased peak intensity; we primarily see this in the first peak at ∼3 Å.
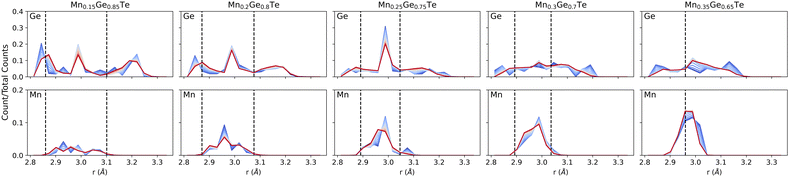
The energy-derived probabilities associated with each supercell provide direct insight into the statistics of bonding (Fig. 8). For comparison, we provide the bond lengths obtained using the average structure PDF fits from 2–15 Å as dashed lines. Beginning with low Mn content, Fig. 8 shows that the expected broad range (2.8–3.3 Å) of nearest neighbor bonds is present. However, the strong presence of ∼3 Å bonds in Ge-centered coordination shells indicates the presence of local octahedral motifs, even at this low Mn content. Compared the Ge-centered coordination shells, the distribution for Mn is significantly narrower. On the other compositional extreme, the Ge-centered bond length distribution continue to show a broad range of bond lengths, with peaks near 2.8 and 3.0 Å remaining through the structure transition. In contrast, the Mn distribution grows narrower as the Ge content decays. As such, we see the preference for Mn to retain its six-fold coordination driving the change in the overall structure from rhombohedral to cubic. While binary MnTe does not adopt the rock salt structure, the NiAs structure that it adopts is built from face sharing MnTe6 octahedra. The role of temperature is also considered in the bond length distributions of Fig. 8. Across all compositions, the largest impact of temperature is to smooth the bond length distributions and tighten the extrema inward. Little impact is seen on the average bond lengths, consistent with the temperature dependent PDFs shown in the ESI.†
Beyond the temperature dependent bond length distributions, the overall distortion of the coordination polyhedra can also be assessed. The degree of distortion of each polyhedron can be calculated using our bond distortion index, which is based off the quadratic elongation.62 We calculate the distortion as:
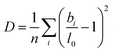 | (5) |
Histograms of the temperature dependent distortions for the first nearest neighbors coordination shell are shown for each composition at each studied temperature and composition in Fig. 9. Even at 15%, the Mn polyhedra are, on average, close to a regular octahedra and the Ge polyhedra do not resemble the parent distortion value (solid line) or the average structure distortion value (dashed line). With increased Mn content, the Ge polyhedra become less distorted.
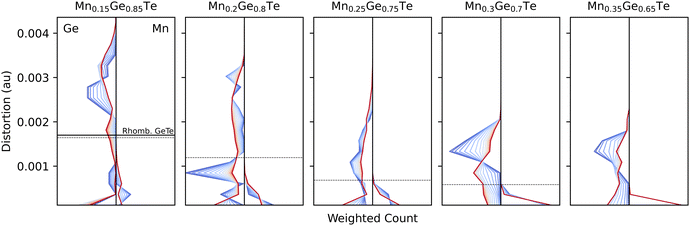 | ||
| Fig. 9 Distortion metric as defined in eqn (5) evolve across all compositions (panels) and temperatures (colors) for Ge-centered polyhedra (left) and Mn-centered (right). For comparison, the distortion values are also shown for pure rhombohedral GeTe (solid line, left panel) and the results from average structure refinements (dashed line). As Mn content increases, Ge-centered polyhedra distortions in the system unsurprisingly drop due to Mn's rigidity in its coordination preference, seen in each panel. | ||
Considering the temperature dependencies of the distortions shown in Fig. 9, Mn-centered polyhedra retain a regular octahedral coordination for all composition/temperature pairs. For Ge polyhedra in the Ge-rich samples, no clear trends emerge. However, at Ge-poor compositions, the Ge polyhedra show an inverse relationship between distortion and temperature. Chemically, this result is rather intuitive. Ge has previously been known to resist bonding in a perfect octahedron due to the presence of a lone pair that distorts its local bonding environment.63–65 Indeed, the distortion index distribution at low temperature is narrow and approximately the value of rhombohedral GeTe. At high temperatures, though, the entire configurational density of states (Fig. 3) is activated, thereby bringing in configurations that place the Ge into regular octahedral environments. We note that this is distinct from the impact of vibrations, as these calculations are relaxations, and thus the distortion index is strictly driven by next-nearest neighbor and beyond chemistry. In an effort to elucidate the driving force behind the temperature dependent trends, the UMAP projection method was used to find correlations in distortion metrics, partial PDFs, and coordination chemistry.66 However, selecting the appropriate featurization of the data proved rather challenging in the high dimensional alloy space, and no clear energy-dependent trends emerged from the projections.
In light of the TEAPOT results (Fig. 7), the Mn-rich samples considered here are best fit at the high temperature limit. As such, the fully random tiling of Ge and Mn lead to a preponderance of regular Ge octahedra. Using this result to intentionally design properties into this alloy space is slightly less intuitive. In one case, we might seek to maximize the electronic mobility to improve the thermoelectric efficiency. Here, annealing at high temperatures would more effectively align the local structure with the global rock salt structure; we hypothesize this will minimize charge carrier scattering and maximize the mobility. Alternatively, should a reduced lattice thermal conductivity be desired, we expect a lower annealing temperature would promote local site asymmetry and drive larger lattice anharmonicity. Thus, we expect that there is, unusually, anti-correlation between mobility and lattice thermal conductivity that can be tuned via synthetic temperature. In our Mn-rich samples, we expect they lie on one extreme based on the TEAPOT refinements shown in Fig. 7.
4 Conclusions
Modeling complex local structures is one important key to unlocking the relationship between structure, properties, and processing in materials. In this work, we demonstrate how local structure of materials can be effectively and efficiently modeled by incorporating statistical mechanics into PDF analysis for the high-performing MnxGe1−x Te thermoelectric alloy. We concurrently model distortion, disorder, and energetic impacts in alloys with a single round of DFT calculations, rapidly providing information about the local structure that can be difficult and expensive to attain through traditional analysis techniques such as RMC or CE + MC. Additionally, we note potential areas where the method could struggle, such as in chemically dilute limits of alloy or in systems with small energetic changes. However, systems are easily screened for candidacy through the generation of a TDOS.For the MGT system, we benchmark our thermodynamic average PDFs against the average structure method, showcasing our ability to accurately model local structures and to extract temperature-dependent knowledge about bonding environments. The knowledge extracted from these trends allows us to make informed extrapolations about synthetically controlled structures, highlighting the potential of this method for designing materials with tailored structures, and thus, properties. In conclusion, we show that thermodynamic averages offer an advancement in analyzing the PDFs of disordered, distorted materials, enabling accurate and efficient characterization of local structures.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The beam time was allocated to POWGEN on proposal number IPTS-29143. V. Meschke acknowledges support by the National Science Foundation (NSF) Graduate Research Fellowship Program under grant no. 1646713. A. Novick, V. Meschke, and E. S. Toberer acknowledge support by NSF EAGER program under grant no. 2334261. V. Meschke, A. Novick, E. S. Toberer, J. Rogers, and R. Chang acknowledge support by NSF Harnessing the Data Revolution program under grant no. 2118201.Notes and references
- A. Simonov and A. L. Goodwin, Nat. Rev. Chem., 2020, 4, 657–673 CrossRef CAS PubMed.
- S. J. L. Billinge, R. G. DiFrancesco, G. H. Kwei, J. J. Neumeier and J. D. Thompson, Phys. Rev. Lett., 1996, 77, 715–718 CrossRef CAS PubMed.
- J. Liu, A. Huq, Z. Moorhead-Rosenberg, A. Manthiram and K. Page, Chem. Mater., 2016, 28, 6817–6821 CrossRef CAS.
- N. J. Weadock, T. C. Sterling, J. A. Vigil, A. Gold-Parker, I. C. Smith, B. Ahammed, M. J. Krogstad, F. Ye, D. Voneshen, P. M. Gehring, A. M. Rappe, H.-G. Steinrück, E. Ertekin, H. I. Karunadasa, D. Reznik and M. F. Toney, Joule, 2023, 7, 1051–1066 CrossRef CAS.
- D. Louca, J. Yan, A. Llobet and R. Arita, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054522 CrossRef.
- P. F. Peterson, T. Proffen, I.-K. Jeong, S. J. L. Billinge, K.-S. Choi, M. G. Kanatzidis and P. G. Radaelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165211 CrossRef.
- Z. Q. Li and W. Pötz, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2109–2118 CrossRef CAS PubMed.
- Z. Moorhead-Rosenberg, A. Huq, J. B. Goodenough and A. Manthiram, Chem. Mater., 2015, 27, 6934–6945 CrossRef CAS.
- P. Fons, A. V. Kolobov, M. Krbal, J. Tominaga, K. S. Andrikopoulos, S. N. Yannopoulos, G. A. Voyiatzis and T. Uruga, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155209 CrossRef.
- T. Proffen, Z. Kristallogr. - Cryst. Mater., 2000, 215, 661–668 CrossRef CAS.
- T. Proffen, V. Petkov, S. J. L. Billinge and T. Vogt, Z. Kristallogr. - Cryst. Mater., 2002, 217, 47–50 CrossRef CAS.
- S. J. L. Billinge, Philos. Trans. R. Soc., A, 2019, 377, 20180413 CrossRef CAS PubMed.
- B. Zhou, W. Li, X. Wang, J. Li, L. Zheng, B. Gao, X. Zhang and Y. Pei, Sci. China Mater., 2019, 62, 379–388 CrossRef CAS.
- S. Duan, Y. Yin, G.-Q. Liu, N. Man, J. Cai, X. Tan, K. Guo, X. Yang and J. Jiang, Research, 2021, 2021, 1949070 CAS.
- Y. Zhong, S. Chen, J. Cai, Z. Zhang, F. Gao, S. Huo, J. Wu, C. Cui, X. Tan, G. Liu and J. Jiang, ACS Appl. Electron. Mater., 2024, 6, 2552–2559 CrossRef CAS.
- J. E. Lewis, H. Rodot and P. Haen, Phys. Status Solidi B, 1968, 29, 743–754 CrossRef CAS.
- J. Dong, J. Pei, H.-L. Zhuang, H. Hu, B. Cai and J.-F. Li, J. Mater. Chem. A, 2019, 7, 27361–27366 RSC.
- J. Dong, Y. Jiang, Y. Sun, J. Liu, J. Pei, W. Li, X. Y. Tan, L. Hu, N. Jia, B. Xu, Q. Li, J.-F. Li, Q. Yan and M. G. Kanatzidis, J. Am. Chem. Soc., 2023, 145, 1988–1996 CrossRef CAS PubMed.
- J. M. Adamczyk, F. A. Bipasha, G. A. Rome, K. Ciesielski, E. Ertekin and E. S. Toberer, J. Mater. Chem. A, 2022, 10, 16468–16477 RSC.
- Z. Zheng, X. Su, R. Deng, C. Stoumpos, H. Xie, W. Liu, Y. Yan, S. Hao, C. Uher, C. Wolverton, M. G. Kanatzidis and X. Tang, J. Am. Chem. Soc., 2018, 140, 2673–2686 CrossRef CAS PubMed.
- S. Chen, Y. Zhong, J. Cai, Z. Zhang, F. Gao, S. Huo, J. Wu, C. Cui, X. Tan, G. Liu, D. Fang and J. Jiang, Mater. Today Phys., 2024, 43, 101393 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- E. Aksel, J. S. Forrester, J. C. Nino, K. Page, D. P. Shoemaker and J. L. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104113 CrossRef.
- C. M. Culbertson, A. T. Flak, M. Yatskin, P. H.-Y. Cheong, D. P. Cann and M. R. Dolgos, Sci. Rep., 2020, 10, 3729 CrossRef CAS PubMed.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- A. van de Walle, P. Tiwary, M. de Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- B. K. Voas, T.-M. Usher, X. Liu, S. Li, J. L. Jones, X. Tan, V. R. Cooper and S. P. Beckman, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024105 CrossRef CAS.
- B. Jiang, D.-Y. Lin, X. Wang, S. M. Selbach and K. Page, J. Appl. Phys., 2022, 132, 224101 CrossRef CAS.
- N. J. Szymanski, Z. Lun, J. Liu, E. C. Self, C. J. Bartel, J. Nanda, B. Ouyang and G. Ceder, Chem. Mater., 2023, 35, 4922–4934 CrossRef CAS.
- R. L. McGreevy, J. Phys.: Condens. Matter, 2001, 13, R877 CrossRef CAS.
- R. L. McGreevy and L. Pusztai, Mol. Simul., 1988, 1, 359–367 CrossRef.
- Z. Bo, C. Li, H. Yang, K. Ostrikov, J. Yan and K. Cen, Nano-Micro Lett., 2018, 10, 33 CrossRef PubMed.
- S. Hull, S. T. Norberg, S. G. Eriksson and C. E. Mohn, J. Phys.: Condens. Matter, 2013, 25, 454205 CrossRef CAS PubMed.
- K. Yang, C. Oses and S. Curtarolo, Chem. Mater., 2016, 28, 6484–6492 CrossRef CAS.
- Y. Lederer, C. Toher, K. S. Vecchio and S. Curtarolo, Acta Mater., 2018, 159, 364–383 CrossRef CAS.
- P. Sarker, T. Harrington, C. Toher, C. Oses, M. Samiee, J.-P. Maria, D. W. Brenner, K. S. Vecchio and S. Curtarolo, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- C. Jiang and B. P. Uberuaga, Phys. Rev. Lett., 2016, 116, 105501 CrossRef PubMed.
- R. Woods-Robinson, V. Stevanović, S. Lany, K. N. Heinselman, M. K. Horton, K. A. Persson and A. Zakutayev, Phys. Rev. Mater., 2022, 6, 043804 CrossRef CAS.
- S. Divilov, H. Eckert, D. Hicks, C. Oses, C. Toher, R. Friedrich, M. Esters, M. J. Mehl, A. C. Zettel and Y. Lederer, et al. , Nature, 2024, 625, 66–73 CrossRef CAS PubMed.
- A. Novick, Q. Nguyen, R. Garnett, E. Toberer and V. Stevanović, Phys. Rev. Mater., 2023, 7, 063801 CrossRef CAS.
- V. Sorkin, T. L. Tan, Z. Yu and Y. Zhang, Phys. Rev. B, 2020, 102, 174209 CrossRef CAS.
- V. Sorkin, Z. Yu, S. Chen, T. L. Tan, Z. Aitken and Y. Zhang, Sci. Rep., 2022, 12, 11894 CrossRef CAS PubMed.
- V. Sorkin, Z. G. Yu, S. Chen, T. L. Tan, Z. Aitken and Y.-W. Zhang, Sci. Rep., 2023, 13, 22549 CrossRef CAS PubMed.
- C. Rom, A. Novick, M. McDermott, A. Yakovenko, J. Gallawa, G. Tran, D. Asebiah, E. Storck, B. McBride, R. Miller, A. Prieto, K. Persson, E. S. Toberer, V. Stevanović, A. Zakutayev and J. Neilson, J. Am. Chem. Soc., 2024, 146(6), 4001–4012 CrossRef CAS PubMed.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- G. L. W. Hart and R. W. Forcade, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224115 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- M. dAvezac, P. Graf, T. Paudal, H. Peng, L. Zhang, S. Stephen and V. Stevanovic, Pylada: a Comprehensive Python Framework for Preparing, Running, Monitoring, Analyzing, and Archiving High Throughput First Principles Calculations, 2010, https://github.com/pylada/pylada-light.
- M. Samanta, T. Ghosh, R. Arora, U. V. Waghmare and K. Biswas, J. Am. Chem. Soc., 2019, 141, 19505–19512 CrossRef CAS PubMed.
- W. Johnston and D. Sestrich, J. Inorg. Nucl. Chem., 1961, 19, 229–236 CrossRef CAS.
- Z. Liu, J. Sun, J. Mao, H. Zhu, W. Ren, J. Zhou, Z. Wang, D. J. Singh, J. Sui and C.-W. Chu, et al. , Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5332–5337 CrossRef CAS PubMed.
- V. Stevanović, Phys. Rev. Lett., 2016, 116, 075503 CrossRef PubMed.
- S. A. J. Kimber, J. Zhang, C. H. Liang, G. G. Guzmán-Verri, P. B. Littlewood, Y. Cheng, D. L. Abernathy, J. M. Hudspeth, Z.-Z. Luo, M. G. Kanatzidis, T. Chatterji, A. J. Ramirez-Cuesta and S. J. L. Billinge, Nat. Mater., 2023, 22, 311–315 CrossRef CAS PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- K. Robinson, G. V. Gibbs and P. H. Ribbe, Science, 1971, 172, 567–570 CrossRef CAS PubMed.
- M. Calderón-Cueva, E. Isotta, M. Rylko, B. Mukherjee, P. Scardi and A. Zevalkink, Chem. Mater., 2023, 35, 8984–8994 CrossRef.
- A. V. Kolobov, P. Fons and J. Tominaga, Phys. Status Solidi B, 2012, 249, 1902–1906 CrossRef CAS.
- A. Lou, Q.-B. Liu and H.-H. Fu, Phys. Rev. B, 2022, 105, 075431 CrossRef CAS.
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, 2020, https://arxiv.org/abs/1802.03426.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02896a |
| This journal is © The Royal Society of Chemistry 2024 |