Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spin-state dependent pressure responsiveness of Fe(II)-based triazolate metal–organic frameworks†
Silva M.
Kronawitter‡
 a,
Richard
Röβ-Ohlenroth‡
a,
Richard
Röβ-Ohlenroth‡
 b,
Sebastian A.
Hallweger
b,
Sebastian A.
Hallweger
 a,
Marcel
Hirrle
b,
Hans-Albrecht
Krug von Nidda
c,
Tobias
Luxenhofer
b,
Emily
Myatt
a,
Marcel
Hirrle
b,
Hans-Albrecht
Krug von Nidda
c,
Tobias
Luxenhofer
b,
Emily
Myatt
 d,
Jem
Pitcairn
d,
Jem
Pitcairn
 d,
Matthew J.
Cliffe
d,
Matthew J.
Cliffe
 d,
Dominik
Daisenberger
d,
Dominik
Daisenberger
 e,
Jakub
Wojciechowski
f,
Dirk
Volkmer
e,
Jakub
Wojciechowski
f,
Dirk
Volkmer
 *b and
Gregor
Kieslich
*b and
Gregor
Kieslich
 *a
*a
aTechnical University of Munich, TUM Natural School of Sciences, Lichtenbergstr. 4, Garching 85748, Germany. E-mail: gregor.kieslich@tum.de
bChair of Solid State and Materials Chemistry, Institute of Physics, University of Augsburg, Universitätsstr. 1, Augsburg 86159, Germany. E-mail: dirk.volkmer@physik.uni-augsburg.de
cExperimental Physics V, Center for Electronic Correlations and Magnetism, Institute of Physics, University of Augsburg, Universitätsstr. 1, Augsburg 86159, Germany
dSchool of Chemistry, University of Nottingham, Nottingham NG7 2RD, UK
eDiamond Light Source Ltd., Diamond House, Harwell Campus, Didcot OX11 ODE, UK
fRigaku Europe SE, Hugenottenallee 167, Neu-Isenburg, Germany
First published on 23rd February 2024
Abstract
Fe(II)-containing Metal–Organic Frameworks (MOFs) that exhibit temperature-induced spin-crossover (SCO) are candidate materials in the field of sensing, barocalorics, and data storage. Their responsiveness towards pressure is therefore of practical importance and is related to their longevity and processibility. The impact of Fe(II) spin-state on the pressure responsiveness of MOFs is yet unexplored. Here we report the synthesis of two new Fe(II)-based MOFs, i.e. Fe(cta)2 ((cta)− = 1,4,5,6-tetrahydrocyclopenta[d][1,2,3]triazolate) and Fe(mta)2 ((mta)− = methyl[1,2,3]triazolate), which are both in high-spin at room temperature. Together with the isostructural MOF Fe(ta)2 ((ta)− = [1,2,3]triazolate), which is in its low-spin state at room temperature, we apply these as model systems to show how spin-state controls their mechanical properties. As a proxy, we use their bulk modulus, which was obtained via high-pressure powder X-ray diffraction experiments. We find that an interplay of spin-state, steric effects, void fraction, and absence of available distortion modes dictates their pressure-induced structural distortions. Our results show for the first time the role of spin-state on the pressure-induced structural deformations in MOFs and bring us a step closer to estimating the effect of pressure as a stimulus on MOFs a priori.
Introduction
Metal–organic frameworks (MOFs) are built from inorganic metal nodes and multitopic organic linkers, providing a large chemical parameter space for synthesising materials with targeted functionalities. On the most fundamental level, designing material functionality means control over the materials’ responsiveness to stimuli such as pressure, temperature, electric and magnetic fields, and chemical triggers via composition and structure.1,2In this work, we focus on hydrostatic pressure as a stimulus. In 2008, it was proposed that “[The MOFs’] well documented structural complexities can be expected to yield unprecedented pressure-induced phenomena”.3 High-pressure research on MOFs over the past 15 years has fulfilled these expectations, revealing a variety of fascinating phenomena. Examples include pressure-induced structural flexibility with large volume changes as interesting for damping, shock absorbers, and mechanical energy storage;4–6 large negative linear compressibility as a potential starting point for new actuating technologies,7,8 pressure-induced postsynthetic modification reactions of the metal node,9 and defect-dependent material stabilities10 with implications for material processing parameters.
As MOFs move closer to practical use, their mechanical properties such as bulk modulus (B), or their compressibility as the inverse, hardness, Young's modulus, and stress stability are attracting increasing attention.11–14 Learning about the relationships between chemical composition, structure, and macroscopic mechanical properties, will allow these properties to be targeted synthetically. In this context, B, and its linear components, as a measure of the resistance of a MOF to hydrostatic pressure are important parameters. These parameters are tied to interatomic potentials and the inner energy of a crystal structure.15 Therefore, they are important measures of how the MOF's crystal chemistry as a whole, i.e. chemical bond strength, nature of chemical bonds, connectivity, available pore space, and defect chemistry together determine its pressure responsiveness.
Over the past years, a few important principles between a MOF's crystal chemistry and B have been discovered.12,16,17 For instance, in a comprehensive study by K. Chapman and O. Farha on isoreticular MOF series with fcu and scu topology, a relation between void fraction, linker length, and B has been established.18 It has been found that within an isoreticular MOF series, a larger void space (longer linkers) correlates to a reduction of B. Moreover, it has been pointed out that MOFs with rotated and out-of-plane bended linker molecules such as DUT-52 (B = 17(2) GPa) and PCN-57 (B = 4.6(1) GPa) show a significantly smaller B when compared to their isoreticular counterparts with linear linkers (B between 21.1(6) and 37.9(6) GPa). This finding suggests that pre-distorted linkers introduce preferred low-energy pathways for structural distortion as a response to hydrostatic pressure. Furthermore, it has been shown for NU-901 that post-synthetic incorporation of a linker between two open metal-sites, a process known as retrofitting,19 increases B.20 This result agrees with intuition and with recent results from computation where a positive correlation between metal-node connectivity and B has been found.21 Additionally, it has been discovered that the coordination bond strength between the linker and the metal-node22 and the concentration of point defects influences B.10 Importantly, both factors also influence the critical pressure where pressure-induced amorphisation occurs.23 There has been interest in the pressure-dependent spin-state of MOF-related Hoffman-type clathrates24–26 and the elastic properties of molecular Fe(II) SCO complexes,27,28 highlighting that changing the spin-state significantly impacts B. The impact of the spin-state of metal centres within the metal-node on the mechanical properties of MOFs has not been explored to our knowledge. Knowing about the role of coordinative bond strength in determining B, it can be anticipated that the metal-centre spin-state, which comes with a change in coordination bond length and strength, will significantly impact the material response to hydrostatic pressure.
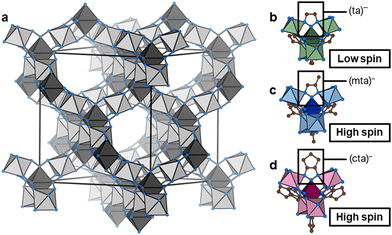
Fe(ta)2 is a MOF with thermal SCO, (ta)− = 1,2,3-triazolate.29 Fe(ta)2 belongs to a larger family of isostructural MOFs, M(ta)2 (with M2+ = Cu2+, Cd2+, Cr2+/3+, Mn2+, Co2+, Zn2+, and Mg2+),30–34 where the divalent metal centres are octahedrally coordinated by μ3-bridging 1,2,3-triazolate ligands to form a 3D network with two crystallographically independent Fe(II) sites, see Fig. 1. Notably, the underlying topology is of type dia, or when treating both Fe(II) sites independently, parallels to the structure of β-cristobalite can be drawn. Initially, Fe(ta)2 has high intrinsic electrical conductivity of 7.7 × 10−5 S cm−1,30 which is sensitive towards gas pressure35 and can be further increased upon partial oxidation of metal centres via I2 or thianthrenium tetrafluorborate.36 More recently, Fe(ta)2 has been shown to exhibit a large hysteresis SCO in a bistable region between 320 °C (heating) and 185 °C (cooling), associated with a change of unit cell volume of approximately 22%, while retaining its structural connectivity and cubic symmetry.37 Notably, the SCO comes with a significant change in Fe–N bond lengths (Δd = 0.18–0.21 Å), which accounts for the changes in unit cell volume. Long-range cooperativity was recently found to be responsible for the large hysteresis of the SCO in Fe(ta)2.38
Drawing inspiration from the extensive work on Fe(II)-containing SCO compounds such as Hofmann-type clathrates and molecular complexes,39 we expect that chemical modification of the (ta)− backbone impacts the critical temperature of the SCO transition. For our purpose, i.e. the study of Fe(II) spin-state on the pressure response, we seek to decrease the SCO temperature below room temperature while maintaining the overall connectivity and cubic symmetry of the material. Together with Fe(ta)2, such a compound would provide a model system for studying the impact of Fe(II) spin-state on the compressibility.
Here we report the synthesis of Fe(cta)2 ((cta)− = 1,4,5,6-tetrahydrocyclopenta[d][1,2,3]triazolate) and Fe(mta)2 ((mta)− = methyl[1,2,3]triazolate), two new Fe(II)-based MOFs that are in their high-spin state at room temperature. We apply Fe(cta)2 as model system for exploring the impact of spin-state on the pressure response of Fe(II) containing MOFs via high-pressure powder X-ray diffraction (HPPXRD). It is shown that Fe(ta)2 and Fe(cta)2 exhibit similar B which is ascribed to the difference in void fraction and Fe–N bond strengths as counteracting effects. The results advance our understanding of the crystal chemical factors that contribute to the mechanical properties of MOFs, knowledge that is of increasing importance when considering their potential as working media in barocalorics40 and mechanical energy storage.41
Results and discussion
Material synthesis and characterisation
Fe(ta)2 was synthesised by following a previously established route,29,35 and similar procedures were used for the synthesis of Fe(cta)2 and Fe(mta)2, see ESI† for synthetic details (S-2). We would like to mention that H-ta (1H-1,2,3-triazole) is commercially available, while H-cta (1,4,5,6-tetrahydrocyclopenta-1H-1,2,3-triazole) and H-mta (4-methyl-1H-1,2,3-triazole) were synthesised by following adapted synthetic procedures from the literature, see ESI† for details (S-2).42,43 After synthesis of the MOFs, IR spectroscopy was performed, where signals from stretch vibrations of cyclopentyl and methyl hydrogen atoms between 2800–3000 cm−1 confirm the presence of (chemically modified)-triazolate linkers in the obtained powders (Fig. S2, ESI†). To remove potential residual N,N-dimethylformamide (DMF), Fe(cta)2 and Fe(mta)2 were washed with methanol (MeOH) and dried in vacuo at room temperature (for Fe(cta)2) or at 280 °C (for Fe(mta)2). Thermogravimetrical analysis (TGA) and differential scanning calorimetry (DSC) of Fe(cta)2 and Fe(mta)2 show that both compounds exhibit a relatively high thermal stability with a decomposition onset at approximately 670 K (Fig. S4 and S5, ESI†). This is slightly higher than previously observed for Fe(ta)2, where decomposition processes start at approximately 613 K.29 Similarly to Fe(ta)2, no evidence for the release of solvent molecules from potential void space was observed for both compounds (Fig. S3–S5, ESI†).Since the applied synthetic route led to crystalline powders of Fe(ta)2, Fe(cta)2, and Fe(mta)2, powder X-ray diffraction (PXRD) was used for structure analysis, see ESI† for details (Fig. S13, S16, and Table S3). In an initial step, the synthesis of phase pure Fe(ta)2 was confirmed via a Pawley profile fit analysis, and subsequently, atomic positions were obtained by Rietveld refinements (Fig. 2(a) and Fig. S22, ESI†). Fe(ta)2 was refined in the previously reported cubic structure, space-group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (a = 16.5969 Å). The obtained Fe–N bond lengths (Fe1–N1 = 1.9736 Å and Fe2–N2 = 1.99082 Å) are indicative for Fe(II) centres in their low-spin state, which agree with the literature.29 Visual comparison of all PXRD pattern suggests that Fe(ta)2, Fe(cta)2, and Fe(mta)2 are isostructural MOFs, which was confirmed via Rietveld-based structure refinement, see ESI† for refinement details (Fig. 2 and Fig. S16, S-19–S-21).
m (a = 16.5969 Å). The obtained Fe–N bond lengths (Fe1–N1 = 1.9736 Å and Fe2–N2 = 1.99082 Å) are indicative for Fe(II) centres in their low-spin state, which agree with the literature.29 Visual comparison of all PXRD pattern suggests that Fe(ta)2, Fe(cta)2, and Fe(mta)2 are isostructural MOFs, which was confirmed via Rietveld-based structure refinement, see ESI† for refinement details (Fig. 2 and Fig. S16, S-19–S-21).
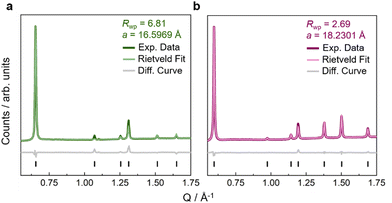 | ||
| Fig. 2 Rietveld refinements against high-resolution PXRD pattern at ambient pressure of Fe(ta)2 (a) in green and Fe(cta)2 (b) in purple. Experimental data is shown as dark line, the calculated data from Rietveld refinement as light line, and the difference curve (fit – data) as grey line. Reflection positions are shown as black vertical tick marks. Rietveld fit of Fe(mta)2 is given in the ESI† (Fig. S20). | ||
The structures of Fe(cta)2 and Fe(mta)2 were refined in the cubic space-group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with lattice parameters of a = 18.2301 Å (Fe(cta)2) and a = 17.3175 Å (Fe(mta)2) (Fig. 2). Compared to Fe(ta)2 (Fig. S20, ESI†), where Fe(II) centres are in their low-spin state at room temperature, the observed Fe–N bond lengths of Fe(cta)2 and Fe(mta)2 (i.e. Fe(II)–N > 2.0 Å) indicate that both compounds are in their high-spin state. This was confirmed by variable temperature magnetic susceptibility measurements in the temperature range between 2 and 700 K of all compounds, see ESI† for detailed data interpretation (Fig. S9 and S-12). To further verify structure refinement from PXRD data, 3D electron diffraction (3DED) at variable temperatures between 173 and 373 K was applied for structure solution from small crystallites, for experimental details and crystallographic outcomes see ESI† (Tables S8, S9 and Fig. S35–S38). The 3DED structures at room temperature, including bond distances and lattice parameters of the high-spin MOFs Fe(cta)2 (Fe1–N1 = 2.223(18) Å, Fe2–N2 = 2.231(15) Å, and a = 18.19(10) Å) and Fe(mta)2 (Fe1–N1 = 2.198(15) Å, Fe2–N2 = 2.117(14) Å, and a = 17.26(9) Å), are in close agreement to the results from the Rietveld analysis.
m with lattice parameters of a = 18.2301 Å (Fe(cta)2) and a = 17.3175 Å (Fe(mta)2) (Fig. 2). Compared to Fe(ta)2 (Fig. S20, ESI†), where Fe(II) centres are in their low-spin state at room temperature, the observed Fe–N bond lengths of Fe(cta)2 and Fe(mta)2 (i.e. Fe(II)–N > 2.0 Å) indicate that both compounds are in their high-spin state. This was confirmed by variable temperature magnetic susceptibility measurements in the temperature range between 2 and 700 K of all compounds, see ESI† for detailed data interpretation (Fig. S9 and S-12). To further verify structure refinement from PXRD data, 3D electron diffraction (3DED) at variable temperatures between 173 and 373 K was applied for structure solution from small crystallites, for experimental details and crystallographic outcomes see ESI† (Tables S8, S9 and Fig. S35–S38). The 3DED structures at room temperature, including bond distances and lattice parameters of the high-spin MOFs Fe(cta)2 (Fe1–N1 = 2.223(18) Å, Fe2–N2 = 2.231(15) Å, and a = 18.19(10) Å) and Fe(mta)2 (Fe1–N1 = 2.198(15) Å, Fe2–N2 = 2.117(14) Å, and a = 17.26(9) Å), are in close agreement to the results from the Rietveld analysis.
Therefore, the backbone modification of the triazolate linker impacts the critical temperature of the SCO effect and its nature. With increasing bulkiness of the chemical modification, i.e. (ta)− < (mta)− < (cta)−, the SCO temperature decreases and suppresses hysteretic behaviour. By drawing parallels to molecular SCO complexes,44 this is rationalised by steric effects which provide an energy penalty for compression of the frameworks into the low-spin state. Especially in the high-spin Fe(cta)2 framework, opposing hydrogen atoms of the (cta)− ligands are already in a repulsive range, with distances of H7A–H7A 2.1008(82) Å and H6A–H6A 2.1763(85) Å when looking at the 3DED data. In Fe(mta)2, the larger distances between the methyl groups allow for more flexibility, although their steric demand still results in a significant shift of the phase transition to lower temperatures, as well as a two-step transition behaviour. Moreover, residual DMF trapped in the voids of the as-synthesised Fe(mta)2-as seems to contribute to the steric crowding, causing a smeared-out transition at lower temperatures (Fig. S6, S7 and S9, ESI†). In addition, we calculated the void fraction of all three materials via Platon45 (SOLV option), see Table 1. As expected, chemical modification of the (ta)− backbone in Fe(cta)2 significantly decreases the existing void fraction compared to Fe(ta)2, which can be expected to significantly influence the materials’ pressure responsiveness.
| MOF | Fe(ta)2 | Fe(cta)2 |
|---|---|---|
| Spin-state | Low-spin | High-spin |
| Void fraction/%* | 25.8 | 5.9 |
| Fe(II)–N/Å | 1.9736(Fe1–N1) | 2.15631(Fe1–N1) |
| 1.99082(Fe2–N2) | 2.09172(Fe2–N2) | |
| B/GPa | 28.2 ± 0.2 | 29.5 ± 0.5 |
Overall, a series of isostructural triazole-based Fe(II) MOFs is obtained where Fe(II) centres are in different spin-states at ambient conditions. These represent a good model series to study the impact of spin-state on their pressure response. An overview of structural and magnetic data of Fe(ta)2 and Fe(cta)2 is given in Table 1 and full crystallographic data, including details of structure refinement is given in the ESI.†
High-pressure structural response
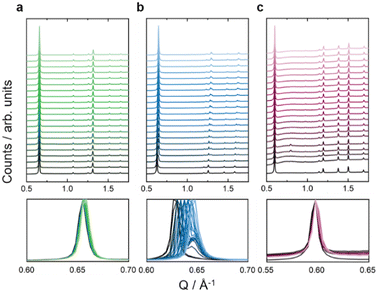
With the isostructural series of Fe(ta)2, Fe(cta)2, and Fe(mta)2 on hand, we used HPPXRD to investigate the impact of varying spin-state of Fe(II) on the MOF's response to hydrostatic pressure as a stimulus. HPPXRD was performed at beamline I15 at the Diamond Light Source (DLS, UK). For obtaining an excellent pressure resolution of our V(p) datasets, which is critical for obtaining accurate Bs, we have applied the “high-pressure jump cell”.46 This is a custom-made high-pressure cell that enables HPPXRD measurements up to pmax = 0.4 GPa with defined pressure increments of Δp = 0.02 GPa (Fig. 3), see ESI† for the measurement of a standard material (S-32). Silicone oil AP-100 was used as a pressure transmitting medium (PTM), which has previously been applied for HPPXRD experiments of Zr-based MOFs47 and molecular perovskites.48 To the best of our knowledge, silicone oil AP-100 acts as hydrostatic, non-penetrating PTM, enabling to study the mechanical response of the MOFs without any additional effects such as penetration of the PTM into the pores of the MOF.3,49From visual inspection of HPPXRD data (Fig. 3), none of the studied MOFs exhibits pressure-induced amorphisation up to 0.4 GPa.50 The analysis of the full-width at half maximum (fwhm) of the applied peak profile function of Fe(ta)2 and Fe(cta)2 confirms this observation (Fig. S26, ESI†). For Fe(mta)2, a pressure-induced phase transition complicates such an analysis, see below. This is expected since only a few MOFs, such as UiO-66 with a large concentration of point defects,10 and DMOF-1 with non-functionalized benzendicarboxylate linkers,51 have been reported to irreversibly amorphise at hydrostatic pressures below p < 0.4 GPa. Please note, that amorphisation under non-hydrostatic compression is known to occur significantly earlier, as reported for ZIF-8 and MOF-5.50,52 Upon increasing pressure, a peak shift is observed for Fe(ta)2, Fe(cta)2, and Fe(mta)2, showing structural compression (Fig. 3). For Fe(ta)2 and Fe(cta)2 no evidence for a phase transition is observed, while Fe(mta)2 undergoes a pressure-driven phase transition at approximately pcrit = 0.04 GPa. This can be expected due to the temperature dependent SCO just below room temperature. Therefore, Fe(ta)2 and Fe(cta)2 were selected as model systems to learn about the impact of spin-sate on the pressure responsiveness. Fe(mta)2 with its pressure-induced phase transition and open questions related to its ambient crystal structure, see S-43 (ESI†), displays a more complex case and will be addressed independently in a follow-up study. HPPXRD data of Fe(ta)2 and Fe(cta)2 have been analysed via Pawley profile fits and Rietveld-based structural refinements for extracting lattice parameters (a), volumes (V) and atomic positions as well as Fe–N bond length as a function of pressure, providing complete V(p) data sets up to pmax for both samples, see ESI† for a full list of Pawley profile fit results, i.e. lattice parameters, Rwp values, and fwhm (Tables S4, S5 and Fig. S21, S26).
For describing the mechanical resistance of Fe(ta)2 and Fe(cta)2 against pressure as a stimulus, we focus on B as the inverse of the material's compressibility. Bs were calculated by fitting a Birch–Murnaghan (B–M) equation of state to the V(p) data up to pmax = 0.4 GPa by using both second and third order B–M equation of state fits via EoSFit7-Gui (Table 1), see ESI† for details (Fig. S27 and S28).53 Similar results were obtained by using PASCal54 (Table S8, ESI†). We would like to note that for both methods, i.e. EOSFit and PASCal, only 2nd order B–M fits show standard errors (σB) in the range of the measured reference material (S-32, ESI†) and are used for further discussion.
For both MOFs, we obtain similar Bs, B(Fe(ta)2) = 28.2 ± 0.2 GPa and B(Fe(cta)2) = 29.5 ± 0.5GPa. Compared to other prototypical MOFs such as UiO-66(Zr) (B = 37.9(6) GPa),18 HKUST-1 (B = 30 GPa)3, ZIF-4(Zn) (B = 2–4.4 GPa),55 and ZIF-8 (B = 6.5 GPa),50 Fe(ta)2 and Fe(cta)2 can be considered relatively rigid or rather ‘hard MOFs’.56 To rationalise these values, we anticipate that the absence of a clear pressure-induced low-energy distortion pathway in the structures of Fe(ta)2 and Fe(cta)2 is key. Example for such pathways are pressure-induced wine-rack type network motions as observed in MOFs such as MIL-53(Al) (Al[O2C–C6H4–CO2]OH)57 and Cu2(DB-bdc)2dabco (DB-bdc = 2,5-dibutoxy-1,4-benzendicarboxylate, dabco = 1,4-diazabicyclo[2.2.2]octane)51 and MOFs with predistorted linkers such as DUT-52 and PCN-57.18 The structures of Fe(ta)2 and Fe(cta)2 are related to the structure of β-cristobalite, where temperature and pressure are known to activate tilts of polyhedra,58,59 however, the μ3-connectivity of 1,2,3-triazolate ligands makes similar distortions in Fe(ta)2 and Fe(cta)2 energetically unfavourable. Therefore, any pressure-induced structural deformation is coupled to bond-length compression and linker bending, where the latter becomes energetically favoured by void space, which reduces steric hindrance. The same argumentation applies to UiO-66(Zr) and HKUST-1, where presumably the metal-node coordination number is the dominating structural feature in defining B. This train of thought agrees with the observation that increasing the length of the linker leads to a reduction of B as previously shown for UiO-66(Zr) (B = 37.9(6) GPa) and UiO-67(Zr) (B = 21.1(6) GPa).18
Looking more specifically at the comparison of Fe(ta)2 and Fe(cta)2, the difference in the void fraction of Fe(ta)2 (0.26) and Fe(cta)2 (0.06) should first be emphasised. Therefore, based on previous HPPXRD studies,18 a significant smaller B for Fe(ta)2 is expected. In contrast, the similar B of Fe(ta)2 and Fe(cta)2 imply that other factors contribute to the structural response. Looking at the evolution of Fe–N bond length in both compounds between p = ambient − 0.4 GPa, very similar relative changes of approximately 0.008% for Fe(ta)2 and 0.009% for Fe(cta)2 are observed despite the difference in spin-state which makes bond-compression for Fe(ta)2 energetically more demanding, see ESI† for a full list of Rietveld refinement results, i.e. bond lengths and Rwp values (Tables S1 and S2). Therefore, we hypothesise that in Fe(ta)2, the larger bond strength is the dominating factor, which limits the effect of the relatively low packing density. In Fe(cta)2, the cyclopentyl backbone of the (cta)− linker is crowding the network, and instead of bond compression, the steric hindrance of the cyclopentyl molecules is sought to be the dominating structural feature. Notably, increased steric hindrance was recently found to lower B,60 which we do not observe for Fe(cta)2 in comparison to Fe(ta)2. Therefore, we identify the spin-state as determining factor over steric hindrance and void fraction for the mechanical properties of Fe(II) MOFs with different Fe(II) spin-states.
Conclusion
In conclusion, we report the synthesis of two new Fe(II)-containing MOFs based on modified triazolate linkers, i.e. (cta)− and (mta)−, which are in their high-spin states at ambient conditions. We thus show that design principles for Fe(II)-based MOFs rely on backbone modification of the linker, very much akin to what is known for SCO complexes; however, cooperative effects make property-by-design such as critical temperature of SCO and hysteresis effects very challenging. We then apply Fe(ta)2 and Fe(cta)2 as model systems to investigate their structural response to hydrostatic pressure, obtaining similar Bs despite a large difference in their void fraction which was previously identified as important factor in determining the high-pressure responsiveness of MOFs. Instead, we rationalise their similar behaviours based on the interplay of several counteracting factors such as spin-state and resulting differences in Fe–N bond-strength, steric effects due to linker-backbone modification and void fraction, overall demonstrating the complexity of comprehending MOFs’ response to pressure as a stimulus.In the bigger context, as MOFs move closer to application, the interest in learning about their responsiveness to pressure will further increase. High-pressure diffraction experiments return important application-oriented properties, such as mechanical stability related to processibility concerns and material longevity. Additionally, high-pressure diffraction experiments can reveal counterintuitive effects such as negative compressibility and pressure-induced phase transitions in flexible MOFs which might initiate new actuation, energy storage, and energy dissipation technologies in the future. In all these areas, material optimisation is coupled to an in-depth knowledge of factors that contribute to the pressure-responsive properties of MOFs, a gap that is in the process of being closed since a few years – with surely many exciting discoveries to follow.
Data availability
3D electron diffraction data have been deposited in the CCDC (2311804–2311811).†Author contributions
S. M. K.: methodology, validation, formal analysis, investigation, data curation, writing – original draft, review and editing, visualisation. R. R.: validation, formal analysis, investigation, data curation, writing – review and editing, visualisation. S. A. H., M. H., H. K., T. L., E. M., J. P., M. J. C., D. D., J. W.: investigation such as material synthesis, HPPXRD, magnetic measurements and 3DED. D. V.: conceptualisation, writing – review and editing, resources. G. K.: visualisation, conceptualisation, writing – review and editing, supervision, resources, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the DFG for financial support (project (450070835) and project SPP 1928 COORNETs Coordination Networks: Building Blocks for Functional Systems (107745057)) and the Diamond Light Source for granting HPPXRD beamtime (CY30815-2). G. K. acknowledges support from the Heisenberg program (524525093). The authors are grateful for help with DSC measurements from Dr Robert Horny. The authors would like to thank Dr Maciej Grzywa for assistance with 3DED measurements and Shinjoo Park for assistance with Rietveld analysis.Notes and references
- C. L. Hobday and G. Kieslich, Dalton Trans., 2021, 50, 3759–3768 RSC.
- A. P. Katsoulidis, D. Antypov, G. F. S. Whitehead, E. J. Carrington, D. J. Adams, N. G. Berry, G. R. Darling, M. S. Dyer and M. J. Rosseinsky, Nature, 2019, 565, 213–217 CrossRef CAS PubMed.
- K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2008, 130, 10524–10526 CrossRef CAS PubMed.
- P. Iacomi, J. S. Lee, L. Vanduyfhuys, K. H. Cho, P. Fertey, J. Wieme, D. Granier, G. Maurin, V. van Speybroeck, J.-S. Chang and P. G. Yot, Chem. Sci., 2021, 12, 5682–5687 RSC.
- X. Zhou, Y.-R. Miao, W. L. Shaw, K. S. Suslick and D. D. Dlott, J. Am. Chem. Soc., 2019, 141, 2220–2223 CrossRef CAS PubMed.
- G. F. Turner, S. C. McKellar, D. R. Allan, A. K. Cheetham, S. Henke and S. A. Moggach, Chem. Sci., 2021, 12, 13793–13801 RSC.
- A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216 CrossRef CAS PubMed.
- W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337 CrossRef CAS PubMed.
- A. J. R. Thom, G. F. Turner, Z. H. Davis, M. R. Ward, I. Pakamorė, C. L. Hobday, D. R. Allan, M. R. Warren, W. L. W. Leung, I. D. H. Oswald, R. E. Morris, S. A. Moggach, S. E. Ashbrook and R. S. Forgan, Chem. Sci., 2023, 14, 7716–7724 RSC.
- S. Dissegna, P. Vervoorts, C. L. Hobday, T. Düren, D. Daisenberger, A. J. Smith, R. A. Fischer and G. Kieslich, J. Am. Chem. Soc., 2018, 140, 11581–11584 CrossRef CAS PubMed.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- L. R. Redfern and O. K. Farha, Chem. Sci., 2019, 10, 10666–10679 RSC.
- S. A. Moggach and G. F. Turner, in Mechanical Behaviour of Metal – Organic Framework Materials, ed. J.-C. Tan, The Royal Society of Chemistry, 2023, pp. 205–266 Search PubMed.
- S. C. McKellar and S. A. Moggach, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 587–607 CrossRef CAS PubMed.
- R. Gross and A. Marx, Festkörperphysik, De Gruyter Oldenbourg, 2014 Search PubMed.
- P. Vervoorts, J. Stebani, A. S. J. Méndez and G. Kieslich, ACS Mater. Lett., 2021, 3, 1635–1651 CrossRef CAS.
- J.-C. Tan, Mechanical Behaviour of Metal – Organic Framework Materials, The Royal Society of Chemistry, 2023 Search PubMed.
- L. R. Redfern, L. Robison, M. C. Wasson, S. Goswami, J. Lyu, T. Islamoglu, K. W. Chapman and O. K. Farha, J. Am. Chem. Soc., 2019, 141, 4365–4371 CrossRef CAS PubMed.
- C. Schneider, D. Bodesheim, J. Keupp, R. Schmid and G. Kieslich, Nat. Commun., 2019, 10, 4921 CrossRef PubMed.
- L. Robison, R. J. Drout, L. R. Redfern, F. A. Son, M. C. Wasson, S. Goswami, Z. Chen, A. Olszewski, K. B. Idrees, T. Islamoglu and O. K. Farha, Chem. Mater., 2020, 32, 3545–3552 CrossRef CAS.
- P. Z. Moghadam, S. M. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron, V. van Speybroeck and D. Fairen-Jimenez, Matter, 2019, 1, 219–234 CrossRef.
- L. R. Redfern, M. Ducamp, M. C. Wasson, L. Robison, F. A. Son, F.-X. Coudert and O. K. Farha, Chem. Mater., 2020, 32, 5864–5871 CrossRef CAS.
- S. M. J. Rogge, P. G. Yot, J. Jacobsen, F. Muniz-Miranda, S. Vandenbrande, J. Gosch, V. Ortiz, I. E. Collings, S. Devautour-Vinot, G. Maurin, N. Stock and V. van Speybroeck, ACS Mater. Lett., 2020, 2, 438–445 CrossRef CAS PubMed.
- R. Li, G. Levchenko, F. J. Valverde-Muñoz, A. B. Gaspar, V. V. Ivashko, Q. Li, B. Liu, M. Yuan, H. Fylymonov and J. A. Real, Inorg. Chem., 2021, 60, 16016–16028 CrossRef CAS PubMed.
- I. R. Reddy, P. M. Oppeneer and K. Tarafder, J. Magn. Magn. Mater., 2021, 524, 167637 CrossRef CAS.
- R. Li, V. M. Kalita, H. Fylymonov, W. Xu, Q. Li, J. A. Real, B. Liu and G. Levchenko, Inorg. Chem., 2022, 61, 14752–14760 CrossRef CAS PubMed.
- D. Paliwoda, L. Vendier, L. Getzner, F. Alabarse, D. Comboni, B. Martin, S. E. Alavi, M. P. Bello, L. Salmon, W. Nicolazzi, G. Molnár and A. Bousseksou, Cryst. Growth Des., 2023, 23, 1903–1914 CrossRef CAS.
- M. Mikolasek, M. D. Manrique-Juarez, H. J. Shepherd, K. Ridier, S. Rat, V. Shalabaeva, A.-C. Bas, I. E. Collings, F. Mathieu, J. Cacheux, T. Leichle, L. Nicu, W. Nicolazzi, L. Salmon, G. Molnár and A. Bousseksou, J. Am. Chem. Soc., 2018, 140, 8970–8979 CrossRef CAS PubMed.
- M. Grzywa, R. Röβ-Ohlenroth, C. Muschielok, H. Oberhofer, A. Błachowski, J. Żukrowski, D. Vieweg, H.-A. K. von Nidda and D. Volkmer, Inorg. Chem., 2020, 59, 10501–10511 CrossRef CAS PubMed.
- F. Gándara, F. J. Uribe-Romo, D. K. Britt, H. Furukawa, L. Lei, R. Cheng, X. Duan, M. O'Keeffe and O. M. Yaghi, Chem. – Eur. J., 2012, 18, 10595–10601 CrossRef PubMed.
- X.-H. Zhou, Y.-H. Peng, X.-D. Du, J.-L. Zuo and X.-Z. You, CrystEngComm, 2009, 11, 1964 RSC.
- M. Grzywa, D. Denysenko, J. Hanss, E.-W. Scheidt, W. Scherer, M. Weil and D. Volkmer, Dalton Trans., 2012, 41, 4239–4248 RSC.
- J. G. Park, B. A. Collins, L. E. Darago, T. Runčevski, M. E. Ziebel, M. L. Aubrey, H. Z. H. Jiang, E. Velasquez, M. A. Green, J. D. Goodpaster and J. R. Long, Nat. Chem., 2021, 13, 594–598 CrossRef CAS PubMed.
- R. P. Nutakki, R. Röβ-Ohlenroth, D. Volkmer, A. Jesche, H.-A. K. von Nidda, A. A. Tsirlin, P. Gegenwart, L. Pollet and L. D. C. Jaubert, Phys. Rev. Res., 2023, 5, L022018 CrossRef CAS.
- C. Muschielok, A. Reiner, R. Röβ-Ohlenroth, A. Kalytta-Mewes, D. Volkmer, A. Wixforth and H. Oberhofer, ACS Appl. Mater. Interfaces, 2022, 14, 33662–33674 CrossRef CAS PubMed.
- J. G. Park, M. L. Aubrey, J. Oktawiec, K. Chakarawet, L. E. Darago, F. Grandjean, G. J. Long and J. R. Long, J. Am. Chem. Soc., 2018, 140, 8526–8534 CrossRef CAS PubMed.
- A. B. Andreeva, K. N. Le, K. Kadota, S. Horike, C. H. Hendon and C. K. Brozek, Chem. Mater., 2021, 33, 8534–8545 CrossRef CAS.
- M. C. Demuth, K. N. Le, M. Sciprint and C. H. Hendon, J. Phys. Chem. C, 2023, 127, 2735–2740 CrossRef CAS.
- Y. Garcia, V. Niel, M. C. Muñoz and J. A. Real, Spin crossover in transition metal compounds, Springer, Berlin, 2004, pp. 229–257 Search PubMed.
- D. Boldrin, Appl. Phys. Lett., 2021, 118, 170502 CrossRef CAS.
- J. Wieme, S. M. J. Rogge, P. G. Yot, L. Vanduyfhuys, S.-K. Lee, J.-S. Chang, M. Waroquier, G. Maurin and V. van Speybroeck, J. Mater. Chem. A, 2019, 7, 22663–22674 RSC.
- J. Thomas, S. Jana, S. Liekens and W. Dehaen, Chem. Commun., 2016, 52, 9236–9239 RSC.
- P. R. Clark, G. D. Williams, J. F. Hayes and N. C. O. Tomkinson, Angew. Chem., Int. Ed., 2020, 59, 6740–6744 CrossRef CAS PubMed.
- M. A. Hoselton, L. J. Wilson and R. S. Drago, J. Am. Chem. Soc., 1975, 97, 1722–1729 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- N. J. Brooks, B. L. L. E. Gauthe, N. J. Terrill, S. E. Rogers, R. H. Templer, O. Ces and J. M. Seddon, Rev. Sci. Instrum., 2010, 81, 64103 CrossRef PubMed.
- G. P. Robertson, S. Mosca, C. Castillo-Blas, F. A. Son, O. K. Farha, D. A. Keen, S. Anzellini and T. D. Bennett, Inorg. Chem., 2023, 62, 10092–10099 CrossRef CAS PubMed.
- S. Grover, S. Burger, K. T. Butler, K. Hemmer, P. Vervoorts, G. Kieslich and R. Grau-Crespo, CrystEngComm, 2023, 25, 3439–3444 RSC.
- A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., Int. Ed., 2011, 50, 11138–11141 CrossRef CAS PubMed.
- K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546–17547 CrossRef CAS PubMed.
- P. Vervoorts, J. Keupp, A. Schneemann, C. L. Hobday, D. Daisenberger, R. A. Fischer, R. Schmid and G. Kieslich, Angew. Chem., Int. Ed., 2021, 60, 787–793 CrossRef CAS PubMed.
- Y. H. Hu and L. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174103 CrossRef.
- J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377–1382 CrossRef CAS.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- P. Vervoorts, C. L. Hobday, M. G. Ehrenreich, D. Daisenberger and G. Kieslich, Z. Anorg. Allg. Chem., 2019, 645, 970–974 CrossRef CAS.
- M. T. Wharmby, F. Niekiel, J. Benecke, S. Waitschat, H. Reinsch, D. Daisenberger, N. Stock and P. G. Yot, Nanomaterials, 2020, 10, 1698 CrossRef CAS PubMed.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Chem. Phys., 2013, 138, 174703 CrossRef PubMed.
- W. W. Schmahl, I. P. Swainson, T. Dove and A. Graeme-Barber, Z. Kristallogr. – Cryst. Mater., 1992, 201, 125–146 CrossRef CAS.
- K. D. Hammonds, M. T. Dove, A. P. Giddy, V. Heine and B. Winkler, Am. Mineral., 1996, 81, 1057–1079 CAS.
- F. A. Son, K. M. Fahy, M. A. Gaidimas, C. S. Smoljan, M. C. Wasson and O. K. Farha, Commun. Chem., 2023, 6, 185 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2311804–2311811. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc00360h |
| ‡ Shared contribution. |
| This journal is © The Royal Society of Chemistry 2024 |