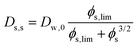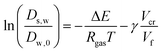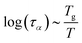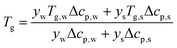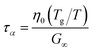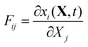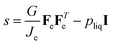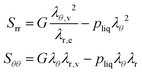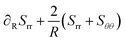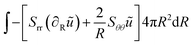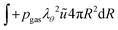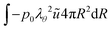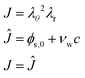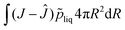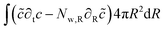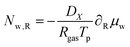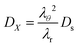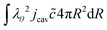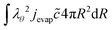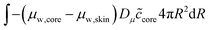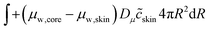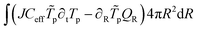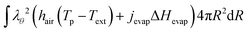DOI:
10.1039/D4SM00201F
(Paper)
Soft Matter, 2024,
20, 5183-5194
Pore development in viscoelastic foods during drying†
Received
11th February 2024
, Accepted 4th June 2024
First published on 14th June 2024
Abstract
In this paper, we present a numerical model that can describe the pore formation/cavitation in viscoelastic food materials during drying. The food material has been idealized as a spherical object, with a core/shell structure and a central gas-filled cavity. The shell represents a skin as present in fruits/vegetables, having a higher elastic modulus than the tissue, which we approximate as a hydrogel. The gas-filled pore is in equilibrium with the core hydrogel material, and it represents pores in food tissues as present in intercellular junctions. The presence of a rigid skin is a known prerequisite for cavitation (inflation of the pore) during drying. For modeling, we follow the framework of Suo and coworkers, describing the inhomogeneous large deformation of soft materials like hydrogels – where stresses couple back to moisture transport. In this paper, we have extended such models with energy transport and viscoelasticity, as foods are viscoelastic materials, which are commonly heated during their drying. To approach the realistic properties of food materials we have made viscoelastic relaxation times a function of Tg/T, the ratio of (moisture dependent) glass transition temperature and actual product temperature. We clearly show that pore inflation only occurs if the skin gets into a glassy state, as has been observed during the (spray) drying of droplets of soft materials like foods.
1 Introduction
During drying often pore development occurs, such as during drying of polymeric food materials1–4 or conventional air drying of vegetables.5–8 A requirement for this pore formation is the development of an elastic skin,4 which can happen either via gelling or via entering the glassy state.9 For vegetables, the skin formation is called case-hardening, where the biopolymer network of the cell wall material densifies with an increase in the elastic modulus. The case-hardened skin can even get into the glassy state.10
Further shrinkage of the food material leads to build up of elastic stresses in the skin. The gradients in the stress lead to the development of underpressure in the core of the material. If pre-existing pores exist they will expand, or otherwise, pores can nucleate if the underpressure reaches a critical value, which grows by an increase of the underpressure. This mechanism of pore formation during drying is valid using numerical models, representing vegetables as a hydrogel covered with an elastic skin and a central pore (cavity).11,12
In this model, we have assumed that the vegetable is a purely elastic hydrogel, with the stress and chemical potential of water following from a free energy functional, which can be viewed as a generalization of the Flory–Rehner theory. Vegetables as a hydrogel is a reasonable approximation, as the cell wall material can be regarded as a biopolymer network. Consequently, Flory–Rehner theory has been used to describe the hydration (water holding capacity) of vegetables.13 However, fruits and vegetables are also viscoelastic materials.14,15
Flory–Rehner theory is limited in modelling the drying, as it assumes isotropic and uniform deformation of the material. This limitation was overcome in the theory developed by Suo and coworkers, which is capable of handling anisotropic and inhomogeneous deformation16,17 – which has been applied in our earlier models.11,12 There we solved the mass balance for moisture, coupled to the steady state momentum equation (∇·σ = 0). Importantly, Suo and coworkers consider hydrogels as a single phase, governed by a single thermodynamic potential (i.e. a single stress tensor, chemical potential, and pressure), in line with Flory–Rehner theory.
We must note that in other fields similar systems have been treated as multiphase systems,18–21 where the polymer matrix and water are considered separate thermodynamic phases, each with its pressure – building on the work in poroelasticity. In our definition,22 one can speak of a multiphase system if the phases are immiscible and are bounded by interfaces. Porous media such as rock formations are an example of a multiphase system, where inert, non-hygroscopic particles are dispersed in a fluid, which can be a mixture of water and gas. Originally, the poroelastic theory was developed by Biot for porous media like soil and rock, and has probably contributed to the incorrect view of hydrogels as a multiphase system.
In this paper, we like to extend our previous model towards viscoelastic food materials. Pore formation occurs in several food applications: (a) spray drying of maltodextrin, where pore formation occurs via cavitation, if a gel-like skin is formed,4 (b) pore formation in pre-dried vegetable snacks via an instant pressure drop (DIC),23 and (c) pore formation during hot air drying of vegetables, as induced by case hardening,10 (d) pore formation during drying of seeds, and (e) puffing of bubbles in heated starchy snacks.10,24 The interplay between the pressure drop and time development of porosity also plays a role in the DIC treatment of non-predried mushrooms,25 but this system is different from the above, as the mushroom is a porous system with high interconnectivity, while the other systems have closed pores. It is shown in multiple publications14,15,26–29 that these food materials must be treated as viscoelastic materials, which dissipated elastic stresses at a time scale shorter or comparable to the time scales of drying.
These applications in food drying possess similarities to other problems in soft matter, such as cavitation in soft matter induced by drying.30–36 These studies are often inspired by the natural phenomenon like the spore dispersal by ferns, which use the conversion of the collapse of a cavity to kinetic energy for projecting spores37 or emboli formation in vascular tissues in trees.38
We intend to develop eventually a 3D finite element model in COMSOL, such that the model can also predict other mechanical instabilities like wrinkling and creasing. In previous models, we have assumed isothermal and pure elastic food materials.11,12 In this paper, we extend our earlier 1D model to viscoelastic food materials, which are also subject to heating. However, we retain the above simple spherical geometry. The extension of the model to 3D is for the future study.
The viscoelasticity model follows the concept of multiplicative decomposition, as is custom in the field of plasticity.39 This decomposition introduces an internal variable, which relaxes towards the current deformation. We will assume a single relaxation time, in the spirit of the classical Maxwell model. The relaxation time will be assumed to be a function of Tg/T, following our earlier observation of viscoelastic relaxation in carbohydrate polymers.28Tg/T is the ratio of the moisture-dependent glass transition temperature Tg and the actual temperature T. If T ≤ Tg, materials effectively behave as hard elastic solids (like dried pasta) and as viscoelastic rubber-like materials if T ≫ Tg. In this study, we are particularly interested in the evolution of the central pore as a function of drying temperature and relative humidity of drying air.
In the field of large deformation mechanics of hydrogels, there are few studies on similar problems as addressed in this paper. We are aware of the recent paper on cavitation in viscoplastic hydrogels.40 Here, inertial effects are taken into account, but we expect that these are negligible for slow food drying, which often contains pre-existing pores. Yet, interestingly this paper also links cavitation and fracturing.
2 Model description
2.1 Balance equations
The evolution of the pore inside the viscoelastic core–shell system during drying requires the simultaneous solution of the mass balance for the moisture, the momentum balance for calculating the stress, and the energy balance for the temperature. The mechanical energy created by deformation will be dissipated via viscoelastic relaxation. All equations hold for both the core and the shell material. They will differ only in material properties. The central pore is assumed to be filled with a mixture of air and water vapour. The air is assumed to be insoluble in the liquid water. The gas in the pore is treated as an ideal gas.
This problem of pore formation is a prime example of a multiphysics problem. In Fig. 1, we have indicated schematically the multiphysics coupling between the mass, momentum and energy balance equations, supplemented with the viscoelastic relaxation. With blue arrows we have indicated the coupling between the state variables, fluxes and potentials in various balance equations. In the caption of Fig. 1, all couplings are shortly described to give the reader a direct overview of the complexity. All equations and variables are further detailed below. In the Appendix section, one finds more details about solving the equations using the finite element method via the weak form.
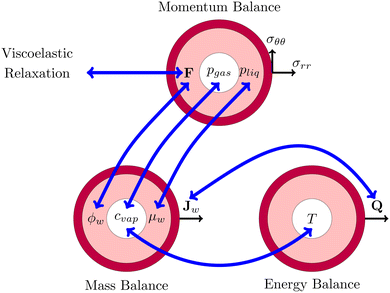 |
| | Fig. 1 Schematic representation of the multiphysics coupling in the model. During drying, there is heat and mass transfer via the fluxes Q and Jw, increasing temperature T and lowering water volume fraction ϕw. The fluxes are coupled via evaporative cooling. The vapour concentration cvap changes due to the temperature and the chemical potential (water activity) μw = RgasT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(aw) of the shell. The decrease of moisture leads to deformation F, leading to the development of stresses (σrr,σθθ) and pressures pliq and pgas. The pressure in the gel pliq couples back to the chemical potential μw, driving the mass fluxes Jw. The gas pressure is mainly determined by changes in the vapour pressure pvap = cvap/MwRgasT ≈ awpsat(T) and the stress in the core (pgas = −σrr(rin)). Stresses also decrease via viscoelastic relaxation, modelled using the multiplication decomposition of the deformation F. log(aw) of the shell. The decrease of moisture leads to deformation F, leading to the development of stresses (σrr,σθθ) and pressures pliq and pgas. The pressure in the gel pliq couples back to the chemical potential μw, driving the mass fluxes Jw. The gas pressure is mainly determined by changes in the vapour pressure pvap = cvap/MwRgasT ≈ awpsat(T) and the stress in the core (pgas = −σrr(rin)). Stresses also decrease via viscoelastic relaxation, modelled using the multiplication decomposition of the deformation F. | |
First, we describe the governing equations for the reference frame, co-moving with the deforming polymer network. The time derivative is in terms of the material derivative: Dt = ∂t + ∇·vs, where vs is the velocity of the solid phase. The mass balance for the water in the core and the shell is:
| | 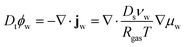 | (1) |
where
ϕw is the volume fraction of water,
jw is the diffusive water flux given by generalized Fick's law,
Ds is the self-diffusivity of water,
νw is the molar volume of water,
Rgas is the universal gas constant, and
μw is the chemical potential (in units of [J m
−3]).
The chemical potential will have two contributions: one due to the mixing energy of water and biopolymers and another due to the elastic energy due to the deformation:17
| | | μw = μw,mix + pliq = −Πmix + pliq | (2) |
The osmotic pressure
Πmix is the mixing contribution, and
pliq is the hydrostatic pressure in the solvent, resulting from the deformation. The mixing contribution follows the scaling law of Cloizeaux:
41| | Πmix = αG![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) β β | (3) |
with
β = 9/4 and
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif)
=
ϕs/
ϕref, which is the ratio of the (current) polymer volume fraction,
ϕs = 1 −
ϕw, and the polymer volume fraction in the reference state, as defined below.
α is a constant, defined in ref.
41, and
G is the elastic modulus.
During dehydration/swelling of soft matter, one assumes that it is in a steady state:17
where
σ is the stress tensor, which follows from the thermodynamic theory of Suo.
17 For spherical geometries, the stress has only non-zero diagonal components,
σrr, and
σθθ =
σϕϕ, which are formulated in terms of the stretches
λi of the polymer network in the principal directions. These stretches are the eigenvalues of the deformation gradient tensor
F. For our spherical symmetry problem,
F is a diagonal tensor. The stretch parameters are related under the incompressibility conditions:
| | ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) λrλθ2 = 1 λrλθ2 = 1 | (5) |
It is convenient to define the swelling factor
J =
λrλθ2 = det(
F). With
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif)
=
ϕs/
ϕref, which is the ratio of the (current) polymer volume fraction,
ϕs = 1 −
ϕw, and the polymer volume fraction in the reference state, as defined below.
We follow the Neo-Hookean model for the stress components.42 For pure elastic materials, the stress follows:
| | σii = ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Gλi2 − pliq Gλi2 − pliq | (6) |
Below, we will give the stress relationships for viscoelastic materials.
The energy balance reads:43
where
Ceff is the volumetric heat capacity, which changes due to moisture transfer.
43 Hence,
with
Ci as the volumetric heat capacity of each phase.
The heat flux Q follows:44
The first contribution accounts for heat conduction, and the second contribution accounts for the convection of heat by the water flow, which has the volumetric heat capacity
Cw. The latter contribution is often neglected in studies concerning thermosensitive hydrogels,
45–47 but it is correctly described in ref.
43 and
44.
We assume that the thermal conductivity k is a simple volume average:48
where
ki is the thermal conductivity of each phase.
For viscoelastic relaxation, we follow, ref. 49 where the deformation gradient is decomposed in an elastic and viscous contribution:
det(
Fe) =
Je =
J, det(
Fv) =
Jv = 1. Furthermore, we define the internal variable as:
which is related to the eigenvalues of
Fv,
i.e. the stretch parameter
λr,v. Also, we define the elastic stretch parameter as:
where
λθ,e is one of the eigenvalues of
Fe.
The internal variable evolves following a single relaxation time scheme:
| | 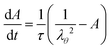 | (14) |
where
τ is the relaxation time.
The principal components of the stress can be rewritten as:
| | 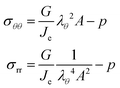 | (15) |
Thus,
via viscoelastic relaxation
λθ,e2 =
λθ2A will evolve towards unity,
i.e. a stress-free state.
2.2 Boundary conditions
For the mass balance, we use Robin-type boundary conditions. At the inner boundary, at r = rin, it holds:| | 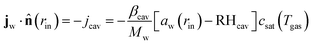 | (16) |
where aw(rin) is the water activity, related to the chemical potential of the hydrogel at the inner boundary via μw(rin) = RgasTp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(aw). RHcav is the relative humidity of the gas inside the pore, related to the vapour pressure via RHcav = pvap/psat(Tgas), where psat(T) is the saturated vapour pressure at temperature T. The gas temperature is assumed equal to the product temperature: Tgas = Tp(rin). csat(T) = Mwpsat(T)/RgasT is the saturated vapour concentration (in kg m−3). Mw is the molar mass of water. βcav = Dair/(rin/5) is the mass transfer coefficient for water transport inside the pore. rin/5 is the characteristic diffusion length.50
log(aw). RHcav is the relative humidity of the gas inside the pore, related to the vapour pressure via RHcav = pvap/psat(Tgas), where psat(T) is the saturated vapour pressure at temperature T. The gas temperature is assumed equal to the product temperature: Tgas = Tp(rin). csat(T) = Mwpsat(T)/RgasT is the saturated vapour concentration (in kg m−3). Mw is the molar mass of water. βcav = Dair/(rin/5) is the mass transfer coefficient for water transport inside the pore. rin/5 is the characteristic diffusion length.50
At the outer boundary, at r = rout, the mass flux reads:
| | 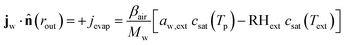 | (17) |
where
βair =
hair/
ρaircp,air is the mass transfer coefficient of the external boundary layer, and following the Lewis relationship, it is linear with the heat transfer coefficient of the boundary layer
hair.
ρaircp,air is the volumetric heat capacity of air. The water activity at the outer surface is defined by
μw(
rout) =
RgasTp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log(
aw,ext). RH
ext is the external relative humidity, and
Text is the temperature of the drying air, both of which are process settings of the drying process.
For the momentum balance, we impose pressures at the outer and inner boundaries:
| | σrr(rout) = p0;![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σrr(rin) = pgas σrr(rin) = pgas | (18) |
The gas pressure
pgas is the sum of the partial air and water pressures:
As the number of moles of air
Nair remains constant, we have:
| | 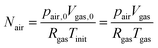 | (20) |
where
pair,0 =
p0 −
psat(
Tinit) is the initial air pressure,
Vgas,0 = 4/3π
Rin3 is the initial pore volume,
Tinit is the initial product temperature,
Vgas = 4/3π
rin3 is the actual pore volume.
Rin is the initial pore radius, and
p0 is the ambient pressure.
The partial water vapour pressure follows:
| | | pvapVgas = NvapRgasTgas | (21) |
with
| | 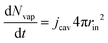 | (22) |
which will be integrated during simulations to obtain
Nvap.
The boundary condition for the heat flux at the outer boundary is:
| | Q·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) (rout) = +Qevap = hair(Tp − Text) + jevapΔHevap (rout) = +Qevap = hair(Tp − Text) + jevapΔHevap | (23) |
where Δ
Hevap is the heat of evaporation, expressed in J mol
−1.
At the inner boundary, we assume that the gas temperature is equal to the product temperature, and hence:
The model is implemented via the finite element method, using COMSOL. As common in models developed by Suo, we have formulated the model in the weak form. As this formalism is not commonplace in food science, we describe in the Appendix section the weak forms of the above equations and boundary conditions (if required).
2.3 Self-diffusion coefficient
Comparing the Darken relationship, the self-diffusion coefficient has a contribution for solutes Ds,s and water Ds,w:The latter will follow the free-volume theory,51 which we assume to hold universally for (hydrophilic) food materials. It has been validated for sugar solutions and maltodextrins.51–53 For aqueous solutions, Ds,s would follow the generalized Stokes–Einstein equation, but a biopolymer network cannot be represented as a solute. Hence, we follow the (modified) relationship by Tokita:11,54| | 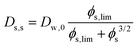 | (26) |
In this modified Tokita relationship, we have matched two asymptotics: (a) for ϕs → 0, it approaches the water self-diffusion (in water) Ds,s → Dw,0, and (b) for ϕs ≫ 0, it follows the original Tokita scaling Ds,s ∼ ϕs−3/2. ϕs,lim ≈ 0.03 is an arbitrary small number. Thus, the modified Tokita relationship avoids the singularity of the original theory at ϕs = 0.
The free-volume theory states:
| | 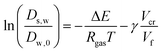 | (27) |
where Δ
E is an activation energy,
Vf is the free volume, and
Vcr is a kind of “activation volume”. In the maltodextrin sorption paper, we modified our original theory (in ref.
51), to account for the fact that the derivative of the free volume with
ϕs shows a discontinuity at the glass transition (which remains rather constant, leading to a plateau in
s,w, which is consistent with ref.
55). Although the parameters for the free volume theory are taken for sucrose,
cf.,
56 it is shown that this relationship holds for any polysaccharide – independent of its molecular weight.
51–53,57
2.4 Viscoelastic relaxation times
The viscoelastic relaxation times related to α-relaxation are assumed to depend on Tg/T, as we have found for starches and maltodextrins.28 For wet food materials, like fresh vegetables, Tg/T ≈ 0.5 and the viscoelastic relaxation times can be quite short, which can make the required time step quite short, and computation times quite long. To avoid this situation, we assume in series with the α-relaxation another Maxwellian relaxation process with a constant relaxation time τM:For nearly elastic skins, the viscoelastic relaxations are relatively slow, with τM ∼ 103⋯104 s. For viscoelastic hydrogels, the relaxation is assumed to be quite fast, with τM ∼ 10−1⋯10 s.14,15 For starch and maltodextrins, the logarithm of the relaxation time scales is linear with Tg/T:| | 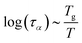 | (29) |
which can be viewed as a generalization of the Arrhenius relationship. In the glassy state, where Tg/T > 1 the food materials are assumed to be practically behaving as elastic solids.
T
g is a function of the moisture content, as captured by the Couchman–Karasz relationship:
| | 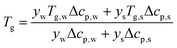 | (30) |
where
yi is the mass fraction of component
i,
Tg,i is its glass transition, and Δ
cp,i is its change in heat capacity at the glass transition.
3 Results
First, we have performed simulations for a nearly elastic system, such that the reader gets an impression of the system behaviour following our previous model. Results are shown in Fig. 2. Simulations are performed for Rin/Rout = 0.35, Gskin/Gcore = 20, τcore = 104 s, and τskin = 107 s. te = 10τskin. If the elastic skin has a sufficient high elastic modulus (Gskin/Gcore = 20), we observe that there is a significant amount of pore opening: rin(te) > Rin. The larger the external osmotic pressure Πext the larger the pore opening.
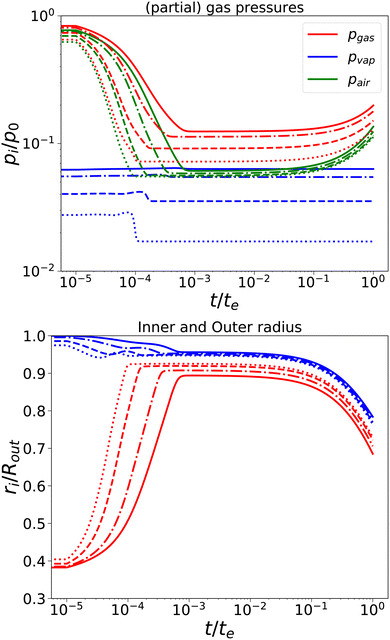 |
| | Fig. 2 Changes in (a) the (partial) gas pressures (top pane) and the inner and outer radii for a nearly elastic skinned hydrogel with the central pore and (b) the inner (red line) and outer radii (blue lines) of the system (bottom pane). The system was subject to external pressures Πext/Gcore = {100, 200, 500, 1000} (plotted with linstyles '-', '-.', '–', ':'). Rin/Rout = 0.35, and Gskin/Gcore = 20. | |
There are interesting dynamics in this problem. A quasi-steady state is obtained if the drying front has reached the inner pore, which is indicated by the moment that the vapour pressure reaches its final value. At this time, the outer radius is showing a minimal value. After this moment, the inner radius shows a further increase, due to the loss of moisture, but the external radius increases slowly. If most of the moisture is removed, the system enters a quasi-steady state, with stable pressures and inner/outer radii. However, due to the very long viscoelastic relaxation times, we observe a decrease in gas and air pressures and a concomitant decrease in the radii. As in the purely elastic case, the Finite element solver becomes unstable for Πext/Gcore ≥ 2000.
Subsequently, we have lowered the relaxation times to τcore = 102 s, and τskin = {103,105} s. We compare the response, as shown in Fig. 3, with the previous calculation. We observe that, for short times, the behaviour is comparable to the nearly elastic system, but with a lowered gas pressure and an increased pore size. However, at longer times, the mechanical stresses are relaxed, and the total gas and air pressures return to equilibrium values: i.e. the ambient pressure p0. Also, the pore radius decreases to an equilibrium value, which is independent of Πext, but is probably determined by the amount of air and the final temperature. Of course, the return to equilibrium is shorter if τskin = 103 s. Still, we observe numerical instability if Πext/Gcore ≥ 2000.
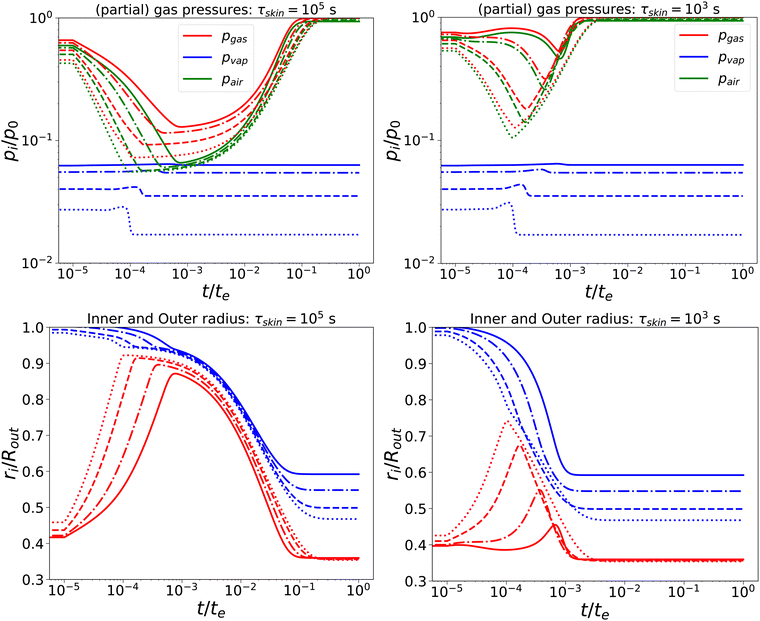 |
| | Fig. 3 Changes in (a) the (partial) gas pressures (top pane) and inner and outer radii (bottom pane) for a nearly elastic skinned hydrogel with the central pore, and (b) the inner (red line) and outer radii (blue lines) of the system for τskin{103,105} s (left and right) and τcore = 100 s, Πext/Gcore = {100, 200, 500, 1000} (plotted with linstyles '-', '-.', '–', ':'). Rin/Rout = 0.35, and Gskin/Gcore = 20. | |
For high-moisture food materials like fruits and vegetables, having lost turgor, the (main) viscoelastic relaxation times are in the order of 1 s.58–60 Food materials have a distribution of relaxation times, but we will take the simplifying assumption of only a single relaxation time, which is temperature and moisture-dependent. We assumed the following relationship for τα:
| | 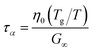 | (31) |
where
η0 is the zero shear viscosity of the biopolymeric matrix, and
G∞ is the value of elastic modulus biopolymers attained in the glassy state. For values of
η0, we follow the relationship we have found earlier for starch.
28 For biopolymers, we typically find
G∞ = 10
8⋯10
10 Pa.
28,29,61,62 For our simulations, we assumed the maximal value:
G∞ = 10 GPa, rendering
τα ≈ 1 at
Tg/
T = 1.
With a short relaxation time of 1 s, we expect that there is no initial pore growth, but only in the late stage of drying, if the skin enters into the glassy state, provided sufficient low external osmotic pressure Πext. Furthermore, we take an initial pore size more in line with actual pore sizes in fresh fruits and vegetables. Results are shown in Fig. 4, for simulations with τcore = τskin = 1 s, Rin/Rout = 0.01, Gskin/Gcore = 20, and Πext/Gcore = {100, 500, 1000, 1500}. We note that the upper bound of Πext/Gcore is limited by numerical stability, but calculations show that under these conditions aw ≈ 0.1,12 which is below the target of most food drying processes (aw ≈ 0.2). Hence, the upper bound is also a practical limit.
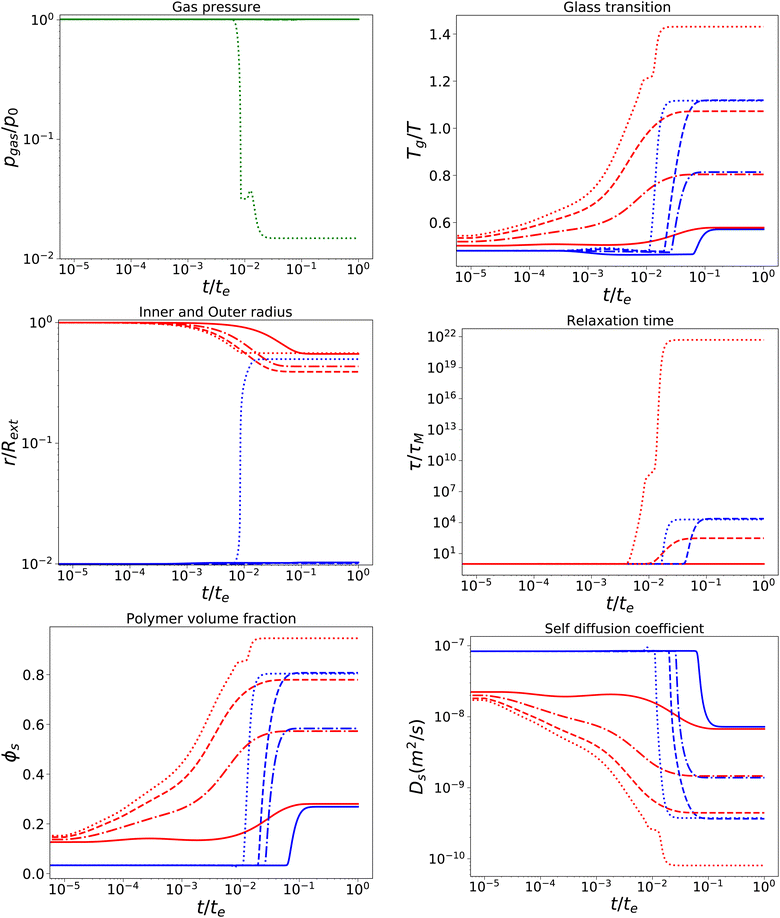 |
| | Fig. 4 Changes in various state parameters and material properties in the outer skin surface (solid lines) and inner cavity surface (dashed lines) as a function of time for a series of external osmotic pressures Πext/Gcore = {500, 1000, 1500, 1900} (plotted with linstyles '-', '-.', '–', ':'). The properties of the core are indicated in blue, while the skin properties are indicated in red. Simulations are performed for τcore = τskin = 1 s, Rin/Rout = 0.01, and Gskin/Gcore = 20. | |
We observe that the pore opening only occurs if it holds for the skin that Tg/T > 1.1. The pore opening occurs relatively suddenly, and it grows to a size about 50 times its original size. Such cavitation events have been observed for spray drying of food material droplets.1,4,63–66
In other cases, the relaxation times τ remain within the time scale of drying τ ≪ te, allowing stresses to relax away. If Tg/T > 1.1, the relaxation time of the skin becomes τ/te ≫ 103, meaning that it has become purely elastic. In the skin, the elastic stresses become frozen-in, leading to a difference in ϕs between the core and the skin. In the core, τ ∼ 104 s, meaning that viscoelastic stresses still can be relaxed away.
As an illustration of the sudden transition in pore opening, we have performed a more detailed parameter study where we have varied external osmotic pressures Πext around the transition Tg/T. In Fig. 5, we show how the final radii of the pore and the skin (rin,∞ and rout,∞) vary with the final value of Tg/T of the skin. We observe that at values Tg/T ≤ 1.1 the pore radius remains small, and the outer radius shrinks with increasing external osmotic pressure. However, if Tg/T > 1.1, we observe an increase in the final pore radius, approaching an asymptotic value at Tg/T > 1.5. Concomitantly, the pore inflation leads to an increase of the outer pore radius at increasing Tg/T values.
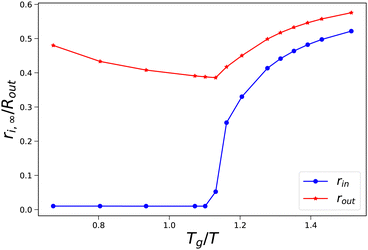 |
| | Fig. 5 Final pore radius rin and skin radius rout at the end of drying as a function of the (final) Tg/T value of the skin. Simulations are performed with Rin/Rout = 0.01, and 500 ≤ Πext/Gcore ≤ 1900. | |
The temporal evolution of stress profiles for the case Πext/Gcore = 1500 is shown in Fig. 6. At early times t/te < 10−2, there is little stress build-up due to fast viscoelastic relaxation times. At t/te = 10−2, the skin enters into a glassy state, with long relaxation times, leading to a strong build-up of stresses. At later times t/te > 10−2, the (nearly) glassy core also develops stresses, which are not relaxed away. Especially at the pore, the stress drops below −p0, causing the gas in the pore to expand. The changes in stress profiles and the pore opening develop indeed vary suddenly. After the pore opening, the stress profiles do not change anymore.
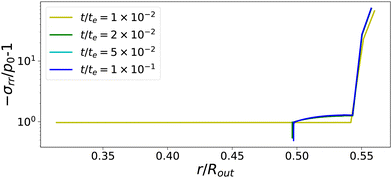 |
| | Fig. 6 Profiles of stress component σrr at various times for Πext/Gcore = 1500. If the skin enters into the glassy state, t/te > 10−2, the central the pore opens suddenly. First stresses develop in the glassy skin and later in the (nearly) glassy core, leading to −σrr(rin) ≪ p0, inflating the central pore. | |
4 Conclusions
In this paper, we have studied numerically the pore formation during the drying of a spherical viscoelastic core–shell system with a central gas-filled cavity, which approximates food materials like vegetables and fruits. For these materials, it is known that porosity increases during drying after the event of case hardening, i.e. the formation of a hard, elastic skin.10 Case hardening occurs if the dried material enters into the glassy state. A similar mechanism we have observed for the (idealized) viscoelastic core–shell system, with viscoelastic relaxation times depending on the ratio of Tg/T. When the material remains in the rubbery state, the viscoelastic relaxation times are short, and there is a little change in the pore size, or it can even be somewhat compressed. If the skin enters the glassy state, the relaxation times become so large that stresses cannot be relaxed away on the practical time scale of the food drying. The developed stresses prevent the skin from further shrinkage, and stresses develop also in the core upon further drying and shrinkage of the core material. Eventually, the stresses at the surface of the cavity lead to gas pressures significantly lower than the atmospheric pressure, leading to inflation of the pore.
Important for the modelling of the pore formation is the multiphysics coupling between the heat, momentum, mass transfer, and the material properties. Here we go beyond the current state-of-the-art food drying models, which are represented by the multiphysics models of Datta and coworkers.10,67 Similar to our model, Datta and coworkers have introduced large deformation mechanics, coupled to heat and mass transfer. Their models can model porosity development during intensive heating like baking, frying, or microwaving.67 Yet, their models lack the viscoelastic nature of food materials in the rubbery state, and there is no coupling of the stress to the driving force for mass transfer, i.e. the chemical potential. However, their framework is easily extended to incorporate the above features.
Our modelling results also have a strong resemblance with the cavity formation during (spray) the drying of droplets made of soft (food) materials.4,68 Also, here the formation of a rigid skin is said to be crucial for the cavity formation. The cavity can grow relatively large, leading to hollow particles with a thin shell. This morphology strongly resembles the morphology of our viscoelastic system, if subjected to drying conditions bringing the skin in the glassy state. Large pore formation is also observed during microwave puffing of food materials, where a large pore (blister) is surrounded by a thin (porous) crust.69 The cavity formation in drying droplets of soft matter solutions has been modelled.30 However, it was assumed that the material becomes elastic beyond a critical gelation concentration. Below that critical point drying is modelled via the common Fick model. While there is a coupling of elastic stress to the driving force of mass transfer, the model lacks viscoelasticity. Incorporating viscoelasticity avoids this discrete change of modelling and material properties at the critical concentration. Viscoelasticity is important if skin formation is via gelation. A transient large bubble can be formed, but at a later stage of drying, if the glassy state is not reached, the hollow particle can undergo either invagination70 or buckling and collapse.71 This collapse is also observed in our simulations if the materials are sufficiently elastic to stresses, but viscoelastic relaxation times are not long enough to maintain the expanded pore, as shown in Fig. 3, because we assume that the spherical geometry our model cannot show buckling. However, the modelling framework developed by Suo and coworkers, which we have followed here, has been used for the study of buckling of soft materials with a stiff skin.72–75 Of course, for describing buckling it requires 3D models.76
Hence, we think that the proposed modelling framework of Suo, extended with non-linear viscoelasticity, is the appropriate method for modelling the intricate three-dimensional deformation and structure formation during (spray) drying of food materials. However, realistic simulations of these phenomena require good knowledge of their rheological properties: how viscoelastic relaxation times and elastic loss moduli depend on the temperature and moisture content. We should note that many real food materials like vegetables and polysaccharides show a broad distribution of multiple relaxation times.14,15,26,28,77 This requires a generalization of the multimode Maxwell model. Recently, we have developed a first simple model along these lines,29 which explains the hysteresis during moisture sorption of maltodextrins. The model proposed in this paper can easily be expanded to a multimode approach by introducing multiple internal variables Ai for each viscoelastic relaxation mode. Each model will have its own relaxation time τi and elastic modulus Gi. Hence, in our future research, we will extend the presented model towards 3D, and include multiple relaxation modes.
Author contributions
Ruud van der Sman conceptualized and drafted the paper. Theory and model development was performed by all authors. Ruud van der Sman and Luciano Teresi reviewed and edited the paper.
Conflicts of interest
There are no conflicts to declare.
Appendix: weak forms in the material frame
In the mechanics of hydrogels, it is common to formulate the problem in a non-moving material frame.16 The stretch parameters are computed concerning this static material frame, which we denote below as the domain frame. Typically, the dry configuration is chosen as this domain frame. However, as we have a bilayer material (core–shell material), that is stress-free, fully relaxed, and uniformly swollen in the initial state, it can be proven that a dry configuration with zero stress and uniform deformation is physically not realizable. Hence, for our problem, it is more convenient to use the initial state as the domain frame, which we characterize with coordinates X.
In the general case, the deformation described in terms of the deformation gradient tensor F:16
| | 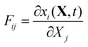 | (32) |
where x is the coordinate of a material point in the current deformed state, and
X is its position in the domain state. By our choice of the initial state as the domain frame, we have shown that in this case the deformation gradient tensor equals the identity matrix
F =
I. Yet, above we have stated that the hydrogel in the initial state is fully relaxed, thus
Fe =
I, and
Fv =
I.
The viscoelastic relaxations define an intermediate stress-free configuration, from which one computes the elastic deformation. It should be noted that the core and the shell will have intermedia configurations, as they differ in viscoelastic properties. This multiplicative decomposition and its connection to the three defined coordinate frames is nicely illustrated in Fig. 7.
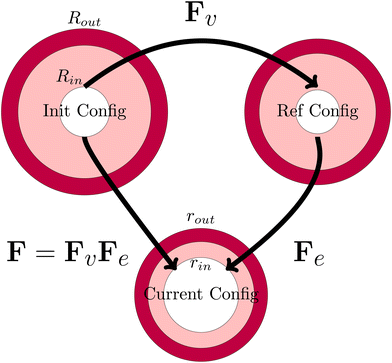 |
| | Fig. 7 Definition of the various configurations for defining the deformation. The initial configuration is used as the domain frame, defining the deformation F to the current (deformed) configuration. The elastic deformation Fe is defined as the intermediate reference configuration. It should be noted that, in all 3 configurations, the skin and the core have matching deformations at their interface. | |
We extend the incompressibility condition also towards the initial frame, where the control volume is characterized by radius r0, thickness dr0, and volume fraction ϕ0:
| | | ϕ0r02dr0 = ϕsr2dr = ϕrefR2dR | (34) |
We define
Λθ =
r/
r0,
λθ =
r/
rref,
Λr = d
r/d
r0,
λr = d
r/d
rref,
Je =
ϕref/
ϕs,
J0 =
λ03 =
ϕref/
ϕ0,
Jd =
ϕ0/
ϕs and hence:
| | | Jd−1Λθ2Λr = Je−1λθ2λr = J0−1λ03 = 1 | (35) |
The elastic stretch parameters λe,i are related to the eigenvalues of the (elastic) Cauchy tensor (which removes any contribution from the solid body rotation):
The eigenvalues of
Ce are
λe,i2.
The momentum balance in the material frame is formulated in terms of the first Piola stress tensor S:
where ∇
X is differentiation concerning the material frame. The Piola stress is related to true stress
via a pull-back:
with the conjugate:
J = det(
F) =
λθ2λr.
The following relationship holds for the true stress for viscoelastic materials:49
| | 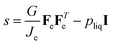 | (40) |
Using Je = λθ,e2λr,e, the Piola stress in components follows:
| | 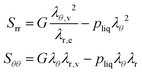 | (41) |
The momentum balance in spherical coordinates reads:
| | 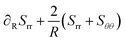 | (42) |
The weak form is:
| | 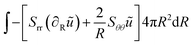 | (43) |
where
ũ is the test function, related to the stretch parameters:
λθ = 1 +
u/
R,
λr = 1 + ∂
u/∂
R. Below, we will indicate other test functions also with the tilde symbol.
The boundary conditions are also formulated in the weak form. For the inner boundary, it holds:
| | 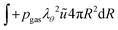 | (44) |
and for the outer boundary:
| | 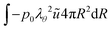 | (45) |
The liquid pressure pliq follows from the incompressibility condition:
| | 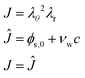 | (46) |
where
ϕs,0 is the polymer volume fraction in the initial state,
νw is the molar volume of water, and
c is the moles of water per unit of volume in the domain frame. The volume fraction of water in the initial state is:
ϕw,0 =
νwc0. Hence, in the initial state
J = 1. The pressure field is calculated as a Lagrangian multiplier to control the incompressibility condition
via the weak form:
| | 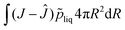 | (47) |
The mass balance is formulated in terms of the state variable c as the number of moles of water per unit of volume of the domain (initial) configuration. The strong form of the mass balance in the material frame is:
The corresponding weak form is:
| | 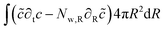 | (49) |
with the molar flux equal to:
| | 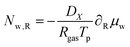 | (50) |
where
DX is the contravariant diffusion coefficient, which follows from the mapping from the current frame to the material frame.
12 It follows:
| | 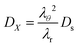 | (51) |
In short,
λθ2 accounts for changes in the surface area between the control volume, and
λr corrects for changes in the thickness of control volumes.
The boundary conditions are implemented via the weak form. The inner boundary holds:
| | 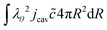 | (52) |
and the outer boundary holds:
| | 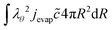 | (53) |
The skin and the core have different elastic properties, and they will be treated as two different domains, each with their state variables ccore and cskin. At their interface, the chemical potential should be continuous. We enforce this via the weak forms:
| | 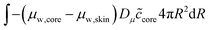 | (54) |
and
| | 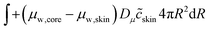 | (55) |
where
Dμ is a constant, determining the rate where this local equilibrium is enforced.
The weak form of the energy balance is:
| | 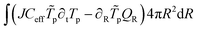 | (56) |
with the heat flux equal to:
| | | QR = −kX∂RTp + Nw,RCwTpνw | (57) |
where
kX =
kλθ2/
λr is the contravariant thermal conductivity.
The boundary conditions at the outer boundary in the weak form:
| | 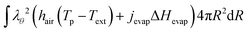 | (58) |
At the inner boundary, we have the natural boundary conditions ∂RTp = 0, which does not require a weak form.
Finally, we note that the COMSOL model is available as ESI,† saved as a Java script, which can be uploaded into any version of COMSOL.
Notes and references
- J. Bouman, P. Venema, R. J. de Vries, E. van der Linden and M. A. Schutyser, Food Res. Int., 2016, 84, 128–135 CrossRef CAS.
- T. K. Nguyen, S. Khalloufi, M. Mondor and C. Ratti, Food Res. Int., 2018, 103, 215–225 CrossRef.
- E. Both, R. Boom and M. Schutyser, Powder Technol., 2020, 363, 519–524 CrossRef CAS.
- I. Siemons, R. Politiek, R. Boom, R. van der Sman and M. Schutyser, Food Res. Int., 2020, 131, 108988 CrossRef CAS.
- N. Zogzas, Z. Maroulis and D. Marinos-Kouris, Drying Technol., 1994, 12, 1653–1666 CrossRef CAS.
- V. Karathanos, N. Kanellopoulos and V. Belessiotis, J. Food Eng., 1996, 29, 167–183 CrossRef.
- S. Khalloufi, A. Kharaghani, C. Almeida-Rivera, J. Nijsse, G. van Dalen and E. Tsotsas, Trends Food Sci. Technol., 2015, 45, 179–186 CrossRef CAS.
- M. U. Joardder, C. Kumar and M. Karim, Crit. Rev. Food Sci. Nutr., 2018, 58, 2896–2907 CrossRef.
- I. Siemons, J. Veser, R. Boom, M. Schutyser and R. van der Sman, Food Hydrocolloids, 2022, 126, 107442 CrossRef CAS.
- T. Gulati and A. K. Datta, J. Food Eng., 2015, 166, 119–138 CrossRef CAS.
- X. Jin and R. van der Sman, Food Struct., 2022, 32, 100269 CrossRef CAS.
- R. van der Sman, M. Curatolo and L. Teresi, Curr. Res. Food Sci., 2024, 100762 CrossRef CAS.
- R. Van der Sman, E. Paudel, A. Voda and S. Khalloufi, Food Res. Int., 2013, 54, 804–811 CrossRef CAS.
- O. K. Ozturk and P. Singh Takhar, Drying Technol., 2019, 37, 1833–1843 CrossRef CAS.
- O. K. Ozturk and P. S. Takhar, J. Texture Stud., 2020, 51, 532–541 CrossRef.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS.
- W. Hong, Z. Liu and Z. Suo, Int. J. Solids Struct., 2009, 46, 3282–3289 CrossRef CAS.
- W. M. Lai, J. Hou and V. C. Mow, J. Biomech. Eng., 1991, 113, 245–258 CrossRef CAS.
- J. M. Huyghe and J. D. Janssen, Int. J. Eng. Sci., 1997, 35, 793–802 CrossRef.
- S. Achanta, M. R. Okos, J. H. Cushman and D. P. Kessler, AIChE J., 1997, 43, 2112–2122 CrossRef CAS.
- P. P. Singh, J. H. Cushman and D. E. Maier, Chem. Eng. Sci., 2003, 58, 2409–2419 CrossRef CAS.
- R. Van der Sman and A. Van der Goot, Soft Matter, 2009, 5, 501–510 RSC.
- X. Li, J. Bi, X. Jin, J. Lyu, X. Wu, B. Li and X. Li, J. Food Eng., 2021, 293, 110379 CrossRef.
- R. Van der Sman and J. Broeze, J. Phys.: Condens. Matter, 2014, 26, 464103 CrossRef CAS.
- L. Hu, J. Bi, X. Jin, Y. Qiu and R. van der Sman, Foods, 2021, 10, 769 CrossRef CAS.
- I. Siemons, J. Veser, R. Boom, M. Schutyser and R. van der Sman, Food Hydrocolloids, 2022, 107442 CrossRef CAS.
- L. Hu, J. Bi, X. Jin and R. van der Sman, J. Food Eng., 2023, 351, 111506 CrossRef CAS.
- R. Van der Sman, J. Ubbink, M. Dupas-Langlet, M. Kristiawan and I. Siemons, Food Hydrocolloids, 2022, 124, 107306 CrossRef CAS.
- R. van der Sman, Food Hydrocolloids, 2023, 108481 CrossRef CAS.
- F. Meng, M. Doi and Z. Ouyang, Phys. Rev. Lett., 2014, 113, 098301 CrossRef.
- H. Wang and S. Cai, J. Appl. Phys., 2015, 117, 154901 CrossRef.
- H. Wang and S. Cai, Soft Matter, 2015, 11, 1058–1061 RSC.
- J. Zhou, X. Man, Y. Jiang and M. Doi, Adv. Mater., 2017, 29, 1703769 CrossRef.
- F. Giorgiutti-Dauphiné and L. Pauchard, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 1–15 CrossRef.
- P. T. A. Nguyen, M. Vandamme and A. Kovalenko, Soft Matter, 2020, 16, 9693–9704 RSC.
- M. Bruning, M. Costalonga, J. Snoeijer and A. Marin, Phys. Rev. Lett., 2019, 123, 214501 CrossRef CAS.
- J. Kang, K. Li, H. Tan, C. Wang and S. Cai, J. Appl. Phys., 2017, 122, 225105 CrossRef.
- T. D. Wheeler and A. D. Stroock, Nature, 2008, 455, 208–212 CrossRef CAS.
- J. C. Simo, Comput. Methods Appl. Mech. Eng., 1988, 66, 199–219 CrossRef.
- Y. Tang, J. Kang and Y. Q. Wang, Int. J. Non Linear Mech., 2022, 144, 104076 CrossRef.
- R. Van der Sman, Food Hydrocolloids, 2015, 48, 94–101 CrossRef CAS.
- R. Van der Sman, Soft Matter, 2015, 11, 7579–7591 RSC.
-
H. Li, Smart Hydrogel Modelling, Springer, 2009, pp. 219–293 Search PubMed.
- J. Moya, S. Lorente-Bailo, M. Salvador, A. Ferrer-Mairal, M. Martnez, B. Calvo and J. Grasa, J. Food Eng., 2021, 298, 110498 CrossRef CAS.
- A. Drozdov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 1–13 CrossRef CAS.
- Z. Ding, W. Toh, J. Hu, Z. Liu and T. Y. Ng, Mech. Mater., 2016, 97, 212–227 CrossRef.
- R. Brighenti and M. P. Cosma, J. Mech. Phys. Solids, 2022, 169, 105045 CrossRef CAS.
- R. Van der Sman, J. Food Eng., 2008, 84, 400–412 CrossRef.
- N. Bosnjak, S. Nadimpalli, D. Okumura and S. A. Chester, J. Mech. Phys. Solids, 2020, 137, 103829 CrossRef CAS.
- R. Van der Sman, J. Food Eng., 2003, 60, 383–390 CrossRef.
- R. Van der Sman and M. Meinders, Food Chem., 2013, 138, 1265–1274 CrossRef CAS.
- J. Perdana, R. G. van der Sman, M. B. Fox, R. M. Boom and M. A. Schutyser, J. Food Eng., 2014, 122, 38–47 CrossRef CAS.
- I. Siemons, R. Boom, R. Van der Sman and M. Schutyser, Food Hydrocolloids, 2019, 97, 105219 CrossRef CAS.
- M. Tokita and T. Tanaka, J. Chem. Phys., 1991, 95, 4613–4619 CrossRef CAS.
- B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC.
- X. He, A. Fowler and M. Toner, J. Appl. Phys., 2006, 100, 074702 CrossRef.
- H. Limbach and J. Ubbink, Soft Matter, 2008, 4, 1887–1898 RSC.
- V. Karathanos, A. Kostaropoulos and G. Saravacos, J. Food Eng., 1994, 23, 481–490 CrossRef.
- W. A. Aregawi, T. Defraeye, P. Verboven, E. Herremans, G. De Roeck and B. Nicolai, Food Bioprocess Technol., 2013, 6, 1963–1978 CrossRef.
- Z. Li, Z. Zhang and C. Thomas, Innovative Food Sci. Emerging Technol., 2016, 34, 44–50 CrossRef.
- P. S. Takhar, M. V. Kulkarni and K. Huber, J. Texture Stud., 2006, 37, 696–710 CrossRef.
- R. van der Sman, P. Chakraborty, N. Hua and N. Kollmann, Food Hydrocolloids, 2023, 135, 108195 CrossRef CAS.
- L. Malafronte, D. Ruoff, D. Z. Gunes, F. Lequeux, C. Schmitt and E. J. Windhab, Colloids Surf., A, 2019, 578, 123549 CrossRef CAS.
- E. Both, I. Siemons, R. Boom and M. Schutyser, Food Hydrocolloids, 2019, 94, 510–518 CrossRef CAS.
- H. Abdullahi, P. Neoptolemou, C. L. Burcham and T. Vetter, Chem. Eng. Sci., 2021, 245, 116879 CrossRef CAS.
- E. J. Sewalt, J. Kalkman, J. van Ommen, G. M. Meesters and V. van Steijn, Food Res. Int., 2022, 157, 111049 CrossRef CAS.
- T. Gulati, H. Zhu and A. K. Datta, Chem. Eng. Sci., 2016, 156, 206–228 CrossRef CAS.
- C. Sadek, L. Pauchard, P. Schuck, Y. Fallourd, N. Pradeau, C. Le Floch-Fouéré and R. Jeantet, Food Hydrocolloids, 2015, 48, 8–16 CrossRef CAS.
- R. Pompe, H. Briesen and A. K. Datta, J. Food Process Eng., 2020, 43, e13429 CrossRef.
- L. Pauchard and Y. Couder, Europhys. Lett., 2004, 66, 667 CrossRef CAS.
- C. Sadek, P. Schuck, Y. Fallourd, N. Pradeau, C. Le Floch-Fouere and R. Jeantet, Dairy Sci. Technol., 2015, 95, 771–794 CrossRef.
- Y.-P. Cao, B. Li and X.-Q. Feng, Soft Matter, 2012, 8, 556–562 RSC.
- B. Li, Y.-P. Cao, X.-Q. Feng and H. Gao, Soft Matter, 2012, 8, 5728–5745 RSC.
- Z. Liu, S. Swaddiwudhipong and W. Hong, Soft Matter, 2013, 9, 577–587 RSC.
- Y. Liu, X. Yang, Y. Cao, Z. Wang, B. Chen, J. Zhang and H. Zhang, Comput. Graph., 2015, 47, 68–77 CrossRef.
- M. Curatolo, G. Napoli, P. Nardinocchi and S. Turzi, Proc. R. Soc. A, 2021, 477, 20210243 CrossRef.
- M. Mahiuddin, M. I. H. Khan, N. D. Pham and M. Karim, Food Biosci., 2018, 23, 45–53 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
 Open Access Article
Open Access Article *ab,
Michele
Curatolo
c and
Luciano
Teresi
c
*ab,
Michele
Curatolo
c and
Luciano
Teresi
c
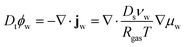
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) β
β![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = ϕs/ϕref, which is the ratio of the (current) polymer volume fraction, ϕs = 1 − ϕw, and the polymer volume fraction in the reference state, as defined below. α is a constant, defined in ref. 41, and G is the elastic modulus.
= ϕs/ϕref, which is the ratio of the (current) polymer volume fraction, ϕs = 1 − ϕw, and the polymer volume fraction in the reference state, as defined below. α is a constant, defined in ref. 41, and G is the elastic modulus.
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) λrλθ2 = 1
λrλθ2 = 1![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) = ϕs/ϕref, which is the ratio of the (current) polymer volume fraction, ϕs = 1 − ϕw, and the polymer volume fraction in the reference state, as defined below.
= ϕs/ϕref, which is the ratio of the (current) polymer volume fraction, ϕs = 1 − ϕw, and the polymer volume fraction in the reference state, as defined below.
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Gλi2 − pliq
Gλi2 − pliq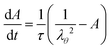
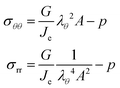
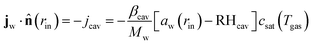
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(aw). RHcav is the relative humidity of the gas inside the pore, related to the vapour pressure via RHcav = pvap/psat(Tgas), where psat(T) is the saturated vapour pressure at temperature T. The gas temperature is assumed equal to the product temperature: Tgas = Tp(rin). csat(T) = Mwpsat(T)/RgasT is the saturated vapour concentration (in kg m−3). Mw is the molar mass of water. βcav = Dair/(rin/5) is the mass transfer coefficient for water transport inside the pore. rin/5 is the characteristic diffusion length.50
log(aw). RHcav is the relative humidity of the gas inside the pore, related to the vapour pressure via RHcav = pvap/psat(Tgas), where psat(T) is the saturated vapour pressure at temperature T. The gas temperature is assumed equal to the product temperature: Tgas = Tp(rin). csat(T) = Mwpsat(T)/RgasT is the saturated vapour concentration (in kg m−3). Mw is the molar mass of water. βcav = Dair/(rin/5) is the mass transfer coefficient for water transport inside the pore. rin/5 is the characteristic diffusion length.50
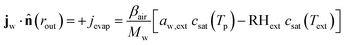
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(aw,ext). RHext is the external relative humidity, and Text is the temperature of the drying air, both of which are process settings of the drying process.
log(aw,ext). RHext is the external relative humidity, and Text is the temperature of the drying air, both of which are process settings of the drying process.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σrr(rin) = pgas
σrr(rin) = pgas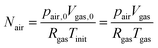
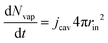
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) (rout) = +Qevap = hair(Tp − Text) + jevapΔHevap
(rout) = +Qevap = hair(Tp − Text) + jevapΔHevap