Open Access Article
Open Access ArticleComputational insights into aqueous speciation of metal-oxide nanoclusters: an in-depth study of the Keggin phosphomolybdate†
Jordi
Buils
 ab,
Diego
Garay-Ruiz
ab,
Diego
Garay-Ruiz
 *a,
Mireia
Segado-Centellas
*a,
Mireia
Segado-Centellas
 ab,
Enric
Petrus
ab,
Enric
Petrus
 ac and
Carles
Bo
ac and
Carles
Bo
 *ab
*ab
aInstitute of Chemical Research of Catalonia (ICIQ-CERCA), The Barcelona Institute of Science and Technology, Av. Països Catalans 16, 43007 Tarragona, Spain. E-mail: cbo@iciq.cat; dgaray@iciq.es
bDepartament de Química Física i Química Inorgànica, Universitat Rovira i Virgili (URV), Marcel·lí Domingo, 43007 Tarragona, Spain
cEawag: Swiss Federal Institute of Aquatic Science and Technology, Überlandstrasse 133, 8600 Dübendorf, Switzerland
First published on 27th July 2024
Abstract
Herein, we present a new computational methodology that unlocks the prediction of the complex multi-species multi-equilibria processes involved in the formation of complex metal-oxo nanoclusters. Relying on our recently introduced method named POMSimulator, we extended its capabilities and challenged its accuracy with the well-known phosphomolybdate [PMo12O40]3− Keggin anion system. We show how the use of statistical techniques enabled the processing of a vast number of speciation models and their associated systems of non-linear equations efficiently and in a scalable manner. Subsequently, this approach is applied to generate statistically averaged speciation diagrams and their associated error bars. Then, we unveil the previously unreported speciation phase diagram under varying [Mo]/[P] ratios vs. pH. Our findings align well with experimental data, indicating the prevalence of the Keggin {PMo12} as the primary species at low pH, but the lacunary {PMo11}and Strandberg {P2Mo5} anions also emerge as major species at other concentration ratios. Finally, from 7 × 104 speciation models we inferred a plausible reaction network across the diverse nuclearities present within the system, which underlines the role of trimers as key intermediate building blocks.
Introduction
Polyoxometalates (POMs) are molecular metal-oxide polyanions1 that form via self-assembly processes.2 Usually, POMs are formed by metal atoms of groups V (V, Nb, and Ta) and VI (Mo and W), and they can be classified between isopolyanions (IPAs) and heteropolyanions (HPAs) depending on the absence or presence of a heteroatom such as P, As, Si or even Al among others. The first-ever described polyoxometalate was the phosphomolybdate α-Keggin anion by Berzelius.3 It was not until a century after its first synthesis that J. F. Keggin established the crystal structure by powder X-ray diffraction4 of [PMo12O40]3−.Polyoxometalates form a wide range of well-defined structures of different sizes and shapes. The self-assembly formation processes of these structures depend on different factors such as pH, temperature, pressure, total metal concentration, ionic force, and the presence of reducing agents and counter-ions. Despite the complexity of controlling the synthesis, POMs are finding relevant applications in the fields of catalysis,5–9 electrochemistry,10 medicine,11–14 and information technologies.15–19 Mass spectrometry,20 X-ray diffraction,21,22 and NMR23 are the most important techniques used experimentally to determine POMs structures. On the other hand, quantum mechanics methods and molecular simulations have provided essential insight for understanding POMs chemistry, their electronic structure and reactivity, and their properties in solution.24 Yet, none of these techniques have described in detail the complex multi-species multi-equilibria processes that form polyoxometalates.
We recently presented a new computational method25–28 named POMSimulator that automatically generates and solves the multi-equilibria non-linear system of equations (NLE) for a given set of molecular oxo-clusters. POMSimulator computes the concentrations of all species at equilibrium, so it allows plotting speciation diagrams (conc. vs. pH) and speciation phase diagrams (total metal conc. vs. pH) from first principles calculations. This methodology was successfully employed to describe the speciation of Mo and W,25,26 and of V, Nb, and Ta27 isopolyanions (IPAs). In all these cases, our method resulted in an excellent agreement with experimental data. POMSimulator steadily evolved since its creation aimed at dealing with increasingly complex chemical systems. Several algorithmic improvements in the deduction of the nucleation mechanisms, generation of formation constants, and parallelization of code led to a 20× speed-up in the NLE resolution step. Recently, we have released a public open-source version of the code.29,30
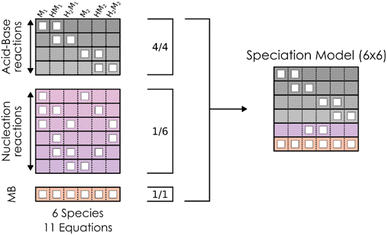
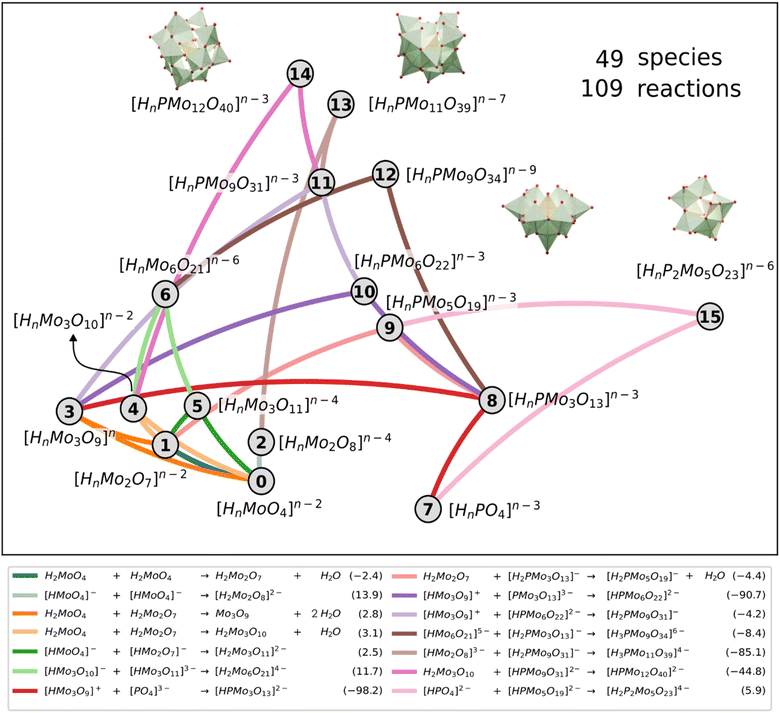
However, the main issue that limits the general application of our method is that, in such kinds of systems, there are indeed many more reactions than chemical compounds, and thus the resulting system of NLE is overdetermined. To tackle this problem, we introduce the concept of speciation model (SM): a unique subset of chemical reactions and a mass balance equation matching the number of compounds to produce a determined NLE system, as schematically shown in Fig. 1. Consequently, a SM describes the composition of the system at equilibrium. To define SMs, we assume that all protonation reactions in the set must be included (due to the importance of the acid–base behaviour of POMs), with only nucleation reactions varying across models. In this way, we can strongly reduce the total number of produced SMs: for the example in Fig. 1, we go from a total of 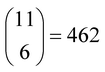 models, to only 6 (combining the 4 acid–base reactions and the mass balance with one nucleation reaction at a time). Then, all possible SMs were sorted according to their root mean squared error to the experimental data available, and finally, the single best speciation model was selected. This SM was then used to represent the system, employing its regression parameters to scale all computed equilibrium constants.
models, to only 6 (combining the 4 acid–base reactions and the mass balance with one nucleation reaction at a time). Then, all possible SMs were sorted according to their root mean squared error to the experimental data available, and finally, the single best speciation model was selected. This SM was then used to represent the system, employing its regression parameters to scale all computed equilibrium constants.
Although that procedure worked well for the simplest metal-oxo IPA clusters, the inherent dependence on experimental formation constants supposes an important drawback in the predictive power of the method. In most cases, neither full speciation diagrams nor datasets of formation constants are available. Instead, there is only qualitative data about the species which are formed, or the pH at which these appear.31,32 Moreover, the problem becomes untreatable as complexity increases, since the number of speciation models grows factorially with the number of species and reactions.
Aimed at broadening the applicability of the method and reducing its close dependence on experimental data, we herein present new developments that establish a basis for exploring huge chemical speciation spaces, guided by stochastic sampling and statistical analysis. First, we introduce the concept of SM ensembles with comparable behaviour and how to select representative models. This new approach allows simulating average speciation diagrams and their associated error bars without relying on experimental data. Then, we show how the new methodology can handle the overwhelming complexity arising from the presence of heteroatoms in the POM structure. Pursuing a better understanding of the mechanisms involved in the formation of the Keggin anion, we chose this well-known phosphomolybdate system to challenge our method. For the first time, computed speciation diagrams have enabled the identification of certain species detected in experiments but not yet fully characterized. Considering the presence of species containing both phosphorus and molybdenum, we offer two perspectives of the speciation phase diagram: one emphasizing the phosphorus percentages within the species and the other focusing on the molybdenum percentages. Moreover, the analysis of the reaction networks embedded into tens of thousands of speciation models permitted the identification of the most relevant reaction mechanisms in play.
Theoretical background and new developments
Originally, POMSimulator was developed to generate and solve the speciation equations of the simplest POMs having only one metal atom type, plus oxygen and hydrogen atoms. In more complex systems, the presence of additional atom types demands important adjustments in the systems of equations. For instance, a new mass balance equation must be included to account for any additional atom type. Moreover, the initial target system (Keggin phospho-molybdate) also implies a massive increase in the total number of speciation models. For a system of 49 species and 109 chemical reactions, the total number of SM would be 2.85 × 1031, thus showcasing the need for an alternative approach. Considering the paradigm stated in Fig. 1, the number of SMs is reduced to 3 × 108, which is still more than two orders of magnitude larger than the 1 × 106 SMs that were solved for vanadium IPAs.27 Therefore, we hypothesized that to properly treat heteropolyanions and even more complicated systems in an attainable computation timescale, the sheer complexity had to be reduced by selecting a subset of speciation models. Thus, we decided to sample the SM population, eventually calculating 1% of this number only. This still involved approximately 3 × 106 SMs, which is the largest system calculated by POMSimulator so far. As we are not solving the totality of the SMs, we need to ensure that the calculated sample is homogeneous, capturing the variability of the population. To this end, it is important to note that adjacent SMs as generated internally in POMSimulator include very similar reactions. For this reason, random sampling must be used to avoid biasing the results with consecutive models. In this way, we can use the sample to compute speciation diagrams, predict new formation constants unreported before, and give light to the complex speciation of POMs.The notion of SM ensembles has been introduced to consider the variability of the NLE systems that are under treatment: as the nucleation reactions selected among different SMs vary, the speciation predicted by every model can be dramatically distinct. It is noteworthy that small numerical changes in the equilibrium constants can lead to completely different speciation scenarios. Since assessing descriptors to categorize and compare SMs is not trivial, herein we decided on an approach based on identifying the most relevant features of the speciation diagram computed for every SM. The advantage of such an approach is that the speciation can be immediately referenced to experimental information, even when only qualitative data is available.
Because of the high variance in the speciation results, a naïve average of a complete collection of speciation diagrams would be unlikely to reflect well the actual behaviour of the system. In contrast, we pursue to apply a clustering approach over the collection of models to encounter the groups with the most distinct speciation behaviours. Then, we average only inside these groups, unravelling the key typologies that can be extracted from the data. Moreover, we also have access to the standard deviation of each group, which we can use to estimate the uncertainty associated with each of our speciation predictions.
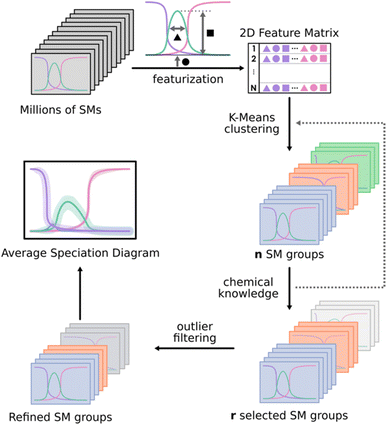
As shown in Fig. 2, the first step of the workflow is the featurization of the speciation diagrams, thus reducing the dimensionality. The collection of all the speciation diagrams is stored as a 3D array of size Nspecies·NpH·Nmodels. In general, the number of pH points (NpH) shall be relatively large, as the resolution of the NLE systems encoded in each model does not behave well for sparse pH grids. The goal of the featurization is to reduce the dimensionality along the pH axis, characterizing the speciation diagrams through a set of parameters related to the shape and location of each peak for each species: maximum height, width, area, and position of the maximum. After testing several feature subsets (see Fig. S8–S11 in the ESI†), we encountered that considering the height, width, and position of the peaks was enough to reproduce the behaviour of the whole diagram across the pipeline, reducing the input to a 2D matrix of shape (3Nspecies·Nmodels).
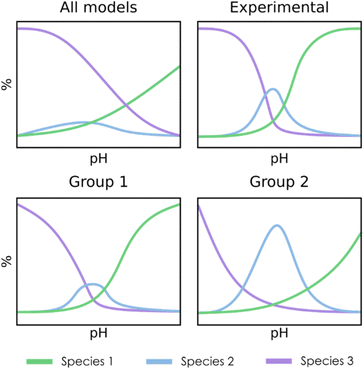
For the clustering stage, we selected an unsupervised K-means algorithm to group the SMs, applying also Principal Component Analysis (PCA) to visualize the spread of the detected clusters. While alternative approaches could be proposed (e.g. t-SNE, DBSCAN, autoencoders…), K-means was the most size-scalable method, which was essential to tackle large systems having more than 1 × 106 SMs. From these clusters, a chemistry-driven selection is performed, discarding the groups having predictions that are off from experimental results or chemical knowledge. The criterion for discarding a group could be, for example, related to the presence of large molar fractions for species that are not reported, or just by the appearance of peaks away from the expected pH. For instance, if we compare the second group with the experimental reference from Fig. 3, we find that the central peak is overestimated, and the shapes of the extreme peaks are not well-reproduced. Therefore, in this situation, we will select the first group to describe the speciation of the system. Although the number of desired clusters in K-Means must be specified beforehand, the proposed selection scheme which regroups all the clusters that have not been discarded makes the tuning of this parameter less critical.
Further refinement inside a given group of models can be achieved either through applying the clustering protocol a second time, if the number of models it contains is large enough, or else by filtering out its most extreme observations (outlier filtering). To achieve this (bottom part of Fig. 2), we select a given species in the diagram to be adjusted and then build the corresponding box and whisker plots for its molar fraction values at every pH point or a selected subrange of pH points. From there, the points that are further than 1.5 times the interquartile range of the sample (beyond the limits of the whiskers) can be discarded, consequently refining the description of the target species in the speciation. Then, the average speciation diagram is computed for each of these clusters, including error bands from the standard deviation (considering a ± σ interval from the average value).
In the original POMSimulator workflow, we generated speciation diagrams, speciation phase diagrams, and reaction mechanisms for the best SM, selected from the RMSE values obtained through linear regression against experimental data. In contrast, the novel approach uses a selected group of SMs rather than one single best model. In this way, we are now considering the diversity of different groups of SMs and the similarities among the models of a given group or groups.
Another important point to discuss is that the raw DFT computed formation constants are overestimated,25–27 so they need to be scaled, mainly due to limitations associated with the modelling of acid–base reactions and the corresponding solvation effects. As we did previously, and since experimental formation constants for this system were available,31,33,34 they can be employed to scale the overestimated DFT formation constants computed by our methodology. However, herein we rely on a randomly chosen SMs set, so looking for the best SM would not make sense. Instead, we propose to use the average slope and intercept values from the whole SMs approximately 3 × 106, avoiding the choice of a unique representative model. In this way, the treatment becomes more general and applicable to cases where random sampling is applied, leveraging the large set of models that the POMSimulator generates. This resonates well with previous findings hinting at a possible universal scaling for formation constants.28 As detailed in the ESI (Fig. S1),† the employed regression equation for all reported results was log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kexp = 0.28
Kexp = 0.28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KDFT − 2.02. This equation showcases the overestimation of the theoretical formation constants, which have to be scaled by a factor of 0.28, and then subtracted 2.02 logarithmic units.
KDFT − 2.02. This equation showcases the overestimation of the theoretical formation constants, which have to be scaled by a factor of 0.28, and then subtracted 2.02 logarithmic units.
To validate this approach, we selected three of the systems that we had already successfully explored: W, Nb, and V IPAs. As shown in Table 1, these selected systems enable us to check the adequacy of our clustering approach for widely different numbers of SMs, to test how well the process scales, and for increasingly complex speciation diagrams. Details on the protocol followed for each of these systems, as well as the comparison between the predicted speciation diagrams and experimental results, are available in the Fig. S2–S7 in the ESI.† Nonetheless, as a general note, all three examples resulted in reasonable agreements between the clustering-based and the best-model-based methods, confirming the consistency of these two modes of operation. As we have proven from the W, Nb, and V systems, using sub-samples is enough to simulate the complex speciation of POMs. At this point, we were confident that the results obtained from the chosen sample (1%) were representative from a statistical point of view.
| Metal | Nspecies | Nreactions | Number of SMs | Number selected SMs | Acid/base behaviour |
|---|---|---|---|---|---|
| W | 51 | 67 | 50k | 1051 | Acidic |
| Nb | 39 | 66 | 500k | 6642 | Alkaline |
| V | 42 | 75 | 1M | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971 971 |
Amphoteric |
| PMo | 49 | 109 | 300M | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 761 |
Acidic |
Novel application: the self-assembly of phosphomolybdates
In 1986, Pettersson et al.34 reported speciation data for the phosphomolybdate system at [Mo]/[P] ratios 9 and 12, targeting the Wells–Dawson [P2Mo18O62]6− and the Keggin anion, respectively. More recently, in 2022, Cadot and co-workers33 revisited the speciation diagram for the Keggin phosphomolybdate system and identified the Keggin anion {PMo12}, the Strandberg anion {P2Mo5}, {PMo11} lacunary species. Yet, as well as Pettersson, they detected two {PMo9} species A-{PMo9} and B-{PMo9}, which appeared at distinct pH intervals and that has not been yet fully characterized. In Fig. 4a, A-{PMo9} is the orange peak at pH = 1.5 and B-{PMo9} the yellowish peak around pH = 5.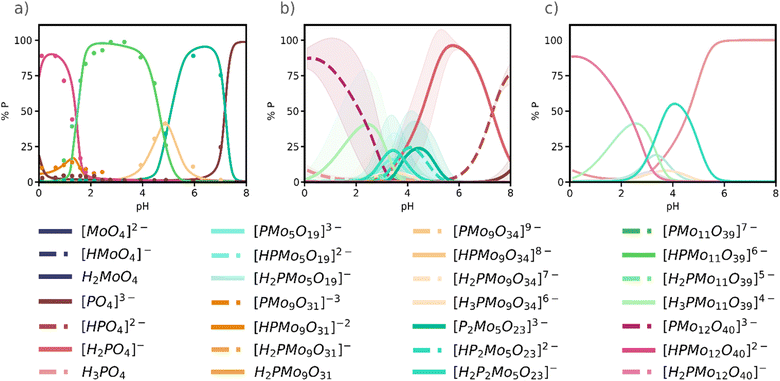 | ||
Fig. 4 (a) Experimental speciation diagram for phosphomolybdate system (adapted from Cadot et al.33); (b) Simulated speciation diagram from 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 761 selected SMs. Lines represent the average value of concentration, and the shading represents the deviation from that value; (c) simulated speciation diagram grouped by nuclearities. For a same nuclearity all protonation states were added into a single line. 761 selected SMs. Lines represent the average value of concentration, and the shading represents the deviation from that value; (c) simulated speciation diagram grouped by nuclearities. For a same nuclearity all protonation states were added into a single line. | ||
Our workflow starts indeed by defining a set of building blocks that, in the present case, comprises 49 chemical species ranging from phosphate [PO4]3− and molybdate [MoO4]2− monomers, to dimers, trimers, etc. until the {PMo12} species itself, at several protonation states (see Computational Details). For the Keggin anion, three species [PMo12O40]3-, [HPMo12O40]2− and [H2PMo12O40]− were included while larger species such as the Wells–Dawson {P2Mo18} were excluded to reduce complexity and enable comparison with recent experimental data.33 From there, we solved the NLE systems of the 3 × 106 randomly sampled SMs (1% of 3 × 108) for an array of pH values, and constructed the corresponding speciation diagram of every SM. After applying the statistical treatment described above, we ended up with a total of 2.5 × 104 SMs that were in reasonable agreement with experimental evidences.31–34 Finally, we simulated an average speciation diagram (Fig. 4b), representing the amount of each species at equilibrium expressed as their phosphate fraction, with their corresponding error bars (shaded areas), versus pH.
At first glance, comparing the experimental speciation diagram (Fig. 4a) with the simulated one (Fig. 4b) is not entirely satisfactory, as the protonation state of the various species suggested by the experiments does not always align precisely with the species predicted by the simulation. Note that for some species, the shadow areas in Fig. 4b, indicating the standard deviation of each curve, is very narrow thus the curve predicted is quite accurate. We can present the same results with much better agreement with the experimental results if we group species of the same nuclearity in the speciation diagram, as shown in Fig. 4c. As expected, the assembly of phosphomolybdates happens only at acidic pH: in alkaline conditions (pH > 7), only the acid–base processes of monomers are observed, in our case phosphate in Fig. 4. We predict the same main species as in the experiments: the Keggin anion {PMo12}, non-protonated or mono-protonated, appears as the major species at pH < 2. The lacunary {PMo11} is major species in the experimental diagram in the range 2<pH < 4, and it also appears in Fig. 4c although with lower intensity. Remarkably, the Strandberg anion {P2Mo5} also emerges in the simulated diagram but slightly displaced towards more acidic conditions. Additionally, we also found the two {PMo9} lacunary structures reported by Pettersson and by Cadot, although at lower concentrations. B-{PMo9} is the pink-yellowish peak centred at pH = 4 so it corresponds to [PMo9O34]9− species. Then, B-{PMo9} is [PMo9O31]3−, which appears at very low pH and as a minor species.
In general, we can see how as pH increases there is an important degree of disassembly, going from the most metal-rich species {PMo12} to smaller clusters. This evidence is explained because the self-assembly of phosphomolybdates is promoted by the presence of protons. We were also able to identify {PMo5}, the precursor of {P2Mo5}, which was previously unreported. The robustness of this approach is indeed confirmed by the presence of the key {P2Mo5} cluster, which was absent when applying the previous methodology that only considered the lowest-RMSE best model in the dataset (Fig. S11 in the ESI†). Even though the maximum concentrations do not fully match the experimental values, we predict the same dominant species in the same relative positions. This mismatch is a consequence of considering an average value across multiple speciation models, as explained above. Therefore, if we consider the standard deviation for each species, we obtain an error band that is closer to the expected values. Moreover, the Keggin anion is in any case predominant in the 0 < pH < 2 range, as expected. It is worth noting that all the speciation diagrams presented in Fig. 4 correspond to experimental conditions ([Mo]/[P] = 12) that favour the formation of the Keggin anion.
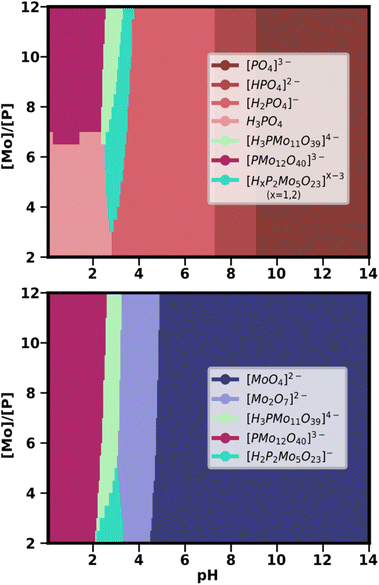
Given the success of the simulation of the PMo speciation diagram, the next step was the computation of the corresponding speciation phase diagram (see Fig. 5). Note that for generating speciation phase diagrams for IPAs, it was necessary to calculate the speciation for the single best SM for all pH points at different values of total metal concentration. When applying the same methodology to HPAs, however, there is a fundamental change. As HPAs contain both metal and heteroatom, the speciation is strongly dependent on the ratio between them. For this reason, the key parameter for the Y-axis of the speciation phase diagram was the [Mo]/[P] ratio, instead of the total metal concentration in the system. Also, under the current paradigm, the treatment of speciation ensembles required us to consider more than one SM to build the phase diagram.
We selected from the statistical treatment the SMs which were known to provide a good prediction of the speciation at a metal/heteroatom ratio of 12 (Fig. 4). From there, we took the same group of SMs to compute the average speciation phase diagram through a grid of 20 points for the [Mo]/[P] ratio (ranging from 2 to 12), and 280 points for the pH. As both metal and heteroatom percentages can be considered, we plotted two complementary speciation phase diagrams, employing the phosphate fraction (Fig. 5 above) and the molybdate fraction (Fig. 5 below). In this way, it is possible to analyse the preferred phases for phosphorus and molybdenum at any pH-ratio point and separately.
Up to pH = 2 and at a large [Mo]/[P] ratio (>7), the Keggin anion is the major phase for both P and Mo-containing species. However, if the relative amount of Mo decreases, free phosphoric acid becomes the dominant form of phosphorus. As pH increases, the Keggin-lacunary anion {PMo11} becomes dominant, appearing at large ratios for Mo and P. However, {PMo11} is competing with the Strandberg anion {P2Mo5}, which becomes the main phase, both at lower [Mo]/[P] ratios and at 2 < pH < 3. As aforementioned, this species was not predicted by the single best SM with the lowest RMSE. Therefore, its central role in the predicted phase diagrams is another confirmation of the adequacy of our approach. Above pH > 3.5, all dominant phosphorus species are phosphates in decreasing states of protonation. Molybdenum, in contrast, is present as the Mo2O7 dimer as another main species until pH = 5, where the molybdate [MoO4]2− becomes the only major species.
Originally, the reaction mechanism for the self-assembly of IPAs was acquired from the selection of a single best SM, which consists of a single set of reactions. Following the previous discussion, we took the same selected SMs group as in the speciation and phase diagrams to analyse the chemical reactions. For each nuclearity in the molecular set, we looked for all the reactions that formed it and calculated the frequency of each reaction appearing in the selected SMs group. From there we chose the reactions with the highest frequency to represent the formation of each nuclearity, as depicted in Fig. 6. Interestingly, the reactions for {Mo2} 1, {PMo9} 11, and {P2Mo5} 15 presented particularly high frequencies, hinting at their importance in the mechanism. In general terms, the preferred reaction was not the thermodynamically most favourable. Condensation reactions that allow growing larger clusters are driven forward by the complexity of the reaction network and the coupling of nucleation and acid–base equilibria, as already discussed in a previous work.27 This highlights the need for our approach, which includes acid–base equilibrium and condensation and addition reactions, to describe the reaction mechanism for the formation of such nanoclusters. A standard linear description of potential energy curves with only the most stable species would not adequately depict the pathway of cluster formation.
Regarding the formation of the Keggin anion 14, common chemical intuition assumed that trimers should play a key role.35,36 Simple visual analysis of Fig. 6 reveals that the trimeric species 3, 4 and 5 are highly interconnected. Particularly, the {Mo3} 3 that governs most of the cascade of reactions leading to Keggin through three consecutive additions: with phosphate 7 to lead {PMo3} 8, then with 8 towards {PMo6} 10, and with 10 to give {PMo9} 11. Finally, the resulting {PMo9} 11 reacts with the linear trimeric species {Mo3O10} 4 and forms the Keggin anion. Alternatively, the formation of the Keggin-lacunary 13 is achieved by the reaction of the {PMo9} 11 with a dimeric species 2. Finally, the other main compound {P2Mo5} 15 is formed after one {PMo3} 8 reacts with a dimeric species 1 to give the {PMo5} 9, which can react with another phosphate 7 to reach the Strandberg anion.
Noteworthily, the reaction network also shows the distinct nature and role of the two {PMo9} species. A-{PMo9} 11 is a highly connected node, with degree equal to 4, and is the intermediary step in the pathway towards lacunary 13 and Keggin 14. However, the other B-{PMo9} species, designated as 12 in the reaction network, exhibits degree two akin to species 13, 14, and 15. This indicates that all these species serve as endpoints in the network, representing potential reaction products achievable under favourable conditions.
The topological properties of the reaction network arising from our massive numerical analysis places a reactant at the same level as products. Actually, phosphate anion 7 is the only other node with degree 2 in the network because it relates to very few species, contrarily to the other reactants molybdate 0 or other Mo species having a larger degree. The network shows that the heteroatom P is indeed incorporated into the forming POM skeleton through an addition reaction with trimer 3, this step being computed as the most exergonic reaction in the network. Some other steps also show large negative ΔG values, particularly those reactions involving positive and negatively charged ions, as expected. However, other addition reactions between two negatively charged ions showed to be largely exergonic, which shows the importance of accounting for entropy effects. Fig. 6 depiction of the reaction network thus summarizes the most occurring connections between the different species independently of its protonation state, which depends on pH.
Computational details
The molecular set was subjected to geometry optimizations with DFT, using ADF2019.1 (ref. 37) package from SCM. PBE38,39 was used as functional and TZP as basis set. All calculations included relativistic effects using ZORA.40,41 Solvent effects were considered, and continuous solvent model COSMO was employed with water as solvent and using the Klamt radii.42 Analytical frequency calculations were also performed to characterize stationary points. Ground state Gibbs free energies were computed at 1 atm and 298.15 K. The molecular set is available in the ioChem-BD repository43 and can be accessed at https://doi.org/10.19061/iochem-bd-1-323.Conclusions
Speciation of molecular metal oxides challenges both experimental and computational methods because of the high complexity of the chemical reaction networks governing the self-assembly processes. Our recently introduced method, named POMSimulator, has accurately computed the pH-dependent equilibria for Mo, W, V, Nb, and Ta isopolyoxoanions, based on experimental data aided selection of the best speciation model. In this report, we transcend this dependence by carrying out a stochastic and statistical treatment of the whole space of speciation models, and their associated non-linear equations systems.By sampling randomly a vast number of speciation models, our workflow could process the data of more than 3 × 106 speciation diagrams: featurization and dimension reduction, K-means clustering, chemical-basis selection, and outliers filtering. This resulted in 2 × 104 finally selected speciation models, which were used to generate what we called a statistically average speciation diagram, accompanied by error bars. The final average diagram is in full agreement with experiment and allowed identifying two {Mo9} species previously reported in literature.
Furthermore, our work has uncovered the speciation phase diagram, i.e., total concentration vs. pH for an heteropolyoxometalate system. Indeed, for the first time, we introduced a speciation phase diagram in the form of [Metal]/[Heteroatom] ratio vs. pH. Moreover, we provide two views of the diagram, either focussed on the P-based or on the Mo-based species.
Moreover, our findings corroborate well with experimental data, revealing the dominance of the Keggin {PMo12} species at low pH levels. Interestingly, our analysis also highlights the significant presence of lacunary {PMo11} and Strandberg {P2Mo5} anions under varying concentration ratios, shedding light on the diverse molecular compositions that arise within the system. Additionally, our comprehensive examination of many speciation models has led to the inference of a plausible reaction mechanism, emphasizing the pivotal role of trimers as key intermediate building blocks in the speciation process.
The current understanding of the self-assembly processes that lead to the formation of large molecular metal-oxo clusters is based on an empirical trial-and-error basis. The novel understanding that this new simulation methodology can provide is of particular importance for improving the rational synthesis of polyoxometalates. To conclude, this work demonstrates a way to deal with the intricate reaction network governing the reactivity of phosphomolybdates and derives new and valuable insights into the distribution of species under different chemical conditions, thereby enriching our knowledge of complex systems speciation.
Data availability
The molecular set employed to run the simulations is available in the ioChem-BD repository and can be accessed through the following link: https://doi.org/10.19061/iochem-bd-1-323. A first release of the POMSimulator code is available on GitHub (https://github.com/petrusen/pomsimulator), and also on Zenodo repository (https://zenodo.org/records/10689769). The version used in this publication is available upon request.Author contributions
All authors contributed to the conceptualization of the project, which originated from an initial idea by CB. DG designed the statistical methodology used in this work and, along with JB and EP, developed the software. JB and DG performed curation and formal analysis of the data, under the supervision of MS, EP and CB, who was also responsible for funding acquisition. DG and JB created the original draft, which was subsequently edited and reviewed by all authors.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge the Spanish Ministry of Science and Innovation MCIN/AEI/10.13039/501100011033 for project PID2020-112806RB-I00 and CEX2019-000925-S, the European Union NextGenerationEU/PRTR (TED2021-132850B-I00), the ICIQ Foundation and the CERCA program of the Generalitat de Catalunya for funding.References
- M. T. Pope, Heteropoly and Isopoly Oxometalates, 1983, DOI:10.1007/978-3-662-12004-0.
- M. T. Pope and A. Müller, Polyoxometalate Chemistry : From Topology via Self-Assembly to Applications, 2002, DOI:10.1007/0-306-47625-8.
- J. J. Berzelius, Beitrag Zur Näheren Kenntniss Des Molybdäns, Ann. Phys., 1826, 82(4), 369–392, DOI:10.1002/andp.18260820402.
- J. F. Keggin, The Structure and Formula of 12-Phosphotungstic Acid, Proc. R. Soc. London, Ser. A, 1934, 144(851), 75–100, DOI:10.1098/rspa.1934.0035.
- S. Y. Wang and G. Yu, Recent Advances in Polyoxometalate-Catalyzed Reactions, Chem. Rev., 2015, 115(11), 4893–4962, DOI:10.1021/cr500390v.
- I. V. Kozhevnikov, Catalysis by Heteropoly Acids and Multicomponent Polyoxometalates in Liquid-Phase Reactions, Chem. Rev., 1998, 98(1), 171–198, DOI:10.1021/cr960400y.
- M. Blasco-Ahicart, J. Soriano-López, J. J. Carbó, J. M. Poblet and J. R. Galan-Mascaros, Polyoxometalate Electrocatalysts Based on Earth-Abundant Metals for Efficient Water Oxidation in Acidic Media, Nat. Chem., 2018, 10(1), 24–30, DOI:10.1038/nchem.2874.
- T. Gobbato, G. A. Volpato, A. Sartorel and M. Bonchio, A Breath of Sunshine: Oxygenic Photosynthesis by Functional Molecular Architectures, Chem. Sci., 2023, 14(44), 12402–12429, 10.1039/D3SC03780K.
- M. Yamaguchi, K. Shioya, C. Li, K. Yonesato, K. Murata, K. Ishii, K. Yamaguchi and K. Suzuki, Porphyrin–Polyoxotungstate Molecular Hybrid as a Highly Efficient, Durable, Visible-Light-Responsive Photocatalyst for Aerobic Oxidation Reactions, J. Am. Chem. Soc., 2024, 146(7), 4549–4556, DOI:10.1021/jacs.3c11394.
- N. I. Gumerova and A. Rompel, Synthesis, Structures and Applications of Electron-Rich Polyoxometalates, Nat. Rev. Chem, 2018, 2(2), 0112, DOI:10.1038/s41570-018-0112.
- A. Bijelic, M. Aureliano and A. Rompel, Polyoxometalates as Potential Next-Generation Metallodrugs in the Combat Against Cancer, Angew. Chem., Int. Ed., 2019, 58(10), 2980–2999, DOI:10.1002/anie.201803868.
- A. Bijelic, M. Aureliano and A. Rompel, The Antibacterial Activity of Polyoxometalates: Structures, Antibiotic Effects and Future Perspectives, Chem. Commun., 2018, 54(10), 1153–1169, 10.1039/C7CC07549A.
- M. Aureliano, N. I. Gumerova, G. Sciortino, E. Garribba, A. Rompel and D. C. Crans, Polyoxovanadates with Emerging Biomedical Activities, Coord. Chem. Rev., 2021, 447, 214143, DOI:10.1016/j.ccr.2021.214143.
- N. Song, M. Lu, J. Liu, M. Lin, P. Shangguan, J. Wang, B. Shi and J. Zhao, A Giant Heterometallic Polyoxometalate Nanocluster for Enhanced Brain-Targeted Glioma Therapy, Angew. Chem., Int. Ed., 2024, 63(10), e202319700, DOI:10.1002/anie.202319700.
- N. I. Gumerova, A. Roller, G. Giester, J. Krzystek, J. Cano and A. Rompel, Incorporation of Cr III into a Keggin Polyoxometalate as a Chemical Strategy to Stabilize a Labile {Cr III O 4 } Tetrahedral Conformation and Promote Unattended Single-Ion Magnet Properties, J. Am. Chem. Soc., 2020, 142(7), 3336–3339, DOI:10.1021/jacs.9b12797.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing Coherence in Molecular Spin Qubits via Atomic Clock Transitions, Nature, 2016, 531(7594), 348–351, DOI:10.1038/nature16984.
- M. Moors and K. Y. Monakhov, Capacitor or Memristor: Janus Behavior of Polyoxometalates, ACS Appl. Electron. Mater., 2024 DOI:10.1021/acsaelm.3c01751.
- Z. Qi, L. Mi, H. Qian, W. Zheng, Y. Guo and Y. Chai, Physical Reservoir Computing Based on Nanoscale Materials and Devices, Adv. Funct. Mater., 2023, 33(43), 2306149, DOI:10.1002/adfm.202306149.
- M. J. W. Budych, K. Staszak, A. Bajek, F. Pniewski, R. Jastrząb, M. Staszak, B. Tylkowski and K. Wieszczycka, The Future of Polyoxymetalates for Biological and Chemical Apllications, Coord. Chem. Rev., 2023, 493, 215306, DOI:10.1016/j.ccr.2023.215306.
- E. F. Wilson, N. M. Haralampos, M. H. Rosnes and L. Cronin, Real-Time Observation of the Self-Assembly of Hybrid Polyoxometalates Using Mass Spectrometry, Angew Chem. Int. Ed. Engl., 2011, 50(16), 3720–3724, DOI:10.1002/anie.201006938.
- J. Yin, L. Amidani, J. Chen, M. Li, B. Xue, Y. Lai, K. Kvashnina, M. Nyman and P. Yin, Spatiotemporal Studies of Soluble Inorganic Nanostructures with X-rays and Neutrons, Angew. Chem., Int. Ed., 2023, e202310953, DOI:10.1002/anie.202310953.
- I. Colliard, J. R. I. Lee, C. A. Colla, H. E. Mason, A. M. Sawvel, M. Zavarin, M. Nyman and G. J.-P. Deblonde, Polyoxometalates as Ligands to Synthesize, Isolate and Characterize Compounds of Rare Isotopes on the Microgram Scale, Nat. Chem., 2022, 14(12), 1357–1366, DOI:10.1038/s41557-022-01018-8.
- M. Pascual-Borràs, X. López, A. Rodríguez-Fortea, R. J. Errington and J. M. Poblet, 17O NMR Chemical Shifts in Oxometalates: From the Simplest Monometallic Species to Mixed-Metal Polyoxometalates, Chem. Sci., 2014, 5(5), 2031–2042, 10.1039/c4sc00083h.
- X. López, J. J. Carbó, C. Bo and J. M. Poblet, Structure, Properties and Reactivity of Polyoxometalates: A Theoretical Perspective, Chem. Soc. Rev., 2012, 41(22), 7537–7571, 10.1039/C2CS35168D.
- E. Petrus, M. Segado and C. Bo, Nucleation Mechanisms and Speciation of Metal Oxide Clusters, Chem. Sci., 2020, 11(32), 8448–8456, 10.1039/d0sc03530k.
- E. Petrus and C. Bo, Unlocking Phase Diagrams for Molybdenum and Tungsten Nanoclusters and Prediction of Their Formation Constants, J. Phys. Chem. A, 2021, 125(23), 5212–5219, DOI:10.1021/acs.jpca.1c03292.
- E. Petrus, M. Segado-Centellas and C. Bo, Computational Prediction of Speciation Diagrams and Nucleation Mechanisms: Molecular Vanadium, Niobium, and Tantalum Oxide Nanoclusters in Solution, Inorg. Chem., 2022, 61(35), 13708–13718, DOI:10.1021/acs.inorgchem.2c00925.
- E. Petrus, D. Garay-Ruiz, M. Reiher and C. Bo, Multi-Time-Scale Simulation of Complex Reactive Mixtures: How Do Polyoxometalates Form?, J. Am. Chem. Soc., 2023, 145(34), 18920–18930, DOI:10.1021/jacs.3c05514.
- E. Petrus, J. Buils, D. Garay-Ruiz, M. Segado-Centellas and C. Bo, POMSimulator: An Open-Source Tool for Predicting the Aqueous Speciation and Self-Assembly Mechanisms of Polyoxometalates, J. Comput. Chem., 2024 DOI:10.1002/jcc.27389.
- E. Petrus, J. Buils, D. Garay-Ruiz, POMSimulator, 2024, https://github.com/petrusen/pomsimulator Search PubMed.
- N. I. Gumerova and A. Rompel, Polyoxometalates in Solution: Speciation under Spotlight, Chem. Soc. Rev., 2020, 49(21), 7568–7601, 10.1039/d0cs00392a.
- N. I. Gumerova and A. Rompel, Speciation Atlas of Polyoxometalates in Aqueous Solutions, Sci. Adv., 2023, 9(25), eadi0814, DOI:10.1126/sciadv.adi0814.
- S. Yao, C. Falaise, N. Leclerc, C. Roch-Marchal, M. Haouas and E. Cadot, Improvement of the Hydrolytic Stability of the Keggin Molybdo- and Tungsto-Phosphate Anions by Cyclodextrins, Inorg. Chem., 2022, 61(9), 4193–4203, DOI:10.1021/acs.inorgchem.2c00095.
- L. Pettersson, I. Andersson and L.-O. Óhman, Contribution from the Speciation in the Aqueous H+-Mo042-HP042 System As Deduced from a Combined Emf-31P NMR Study, Inorg. Chem., 1986, 25, 4726–4733, DOI:10.1021/ic00246a028.
- S.-H. Wang and S. A. Jansen, Catalytic Implications for Keggin and Dawson Ions: A Theoretical Study of Stability Factors of Heteropolyoxoanions, MRS Online Proc. Libr., 1994, 368, 229, DOI:10.1557/PROC-368-229.
- L. J. Michot, E. Montargès-Pelletier, B. S. Lartiges, J.-B. d'Espinose de la Caillerie and V. Briois, Formation Mechanism of the Ga13 Keggin Ion: A Combined EXAFS and NMR Study, J. Am. Chem. Soc., 2000, 122(25), 6048–6056, DOI:10.1021/ja9941429.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967, DOI:10.1002/jcc.1056.
- J. P. Perdew, Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B, 1986, 33(12), 8822–8824, DOI:10.1103/PhysRevB.33.8822.
- J. P. Perdew, Erratum: Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B, 1986, 34(10), 7406, DOI:10.1103/PhysRevB.34.7406.
- E. V. Lenthe, E. J. Baerends and J. G. Snijders, Relativistic Regular Two-Component Hamiltonians, J. Chem. Phys., 1993, 99(6), 4597–4610, DOI:10.1063/1.466059.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-type Basis Sets for the Elements 1–118, J. Comput. Chem., 2003, 24(9), 1142–1156, DOI:10.1002/jcc.10255.
- A. Klamt, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena, J. Phys. Chem., 1995, 99(7), 2224–2235, DOI:10.1021/j100007a062.
- M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform, J. Chem. Inf. Model., 2014, 55(1), 95–103, DOI:10.1021/ci500593j.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03282a |
| This journal is © The Royal Society of Chemistry 2024 |