Towards an information-based theory of structure
Glenn D.
Hibbard
 and
John
Çamkıran
and
John
Çamkıran

Department of Materials Science and Engineering, University of Toronto, 184 College St, Toronto, ON M5S 3E4, Canada. E-mail: john.camkiran@utoronto.ca
First published on 11th September 2024
Abstract
We call for a theory of the particle-scale structure of materials that is based on the general notion of information rather than its special case of symmetry. An inherent limitation to the symmetry-based understanding of structure is described. The rapid decay in interaction strength with interparticle distance is used to argue for the representability of a system locally through the neighbourhoods of its constituent particles. The extracopularity coefficient E is presented as a local quantifier of information and compared to point group order |G|, a local quantifier of symmetry. The former is found to have nearly double the resolution of the latter for a set of commonly encountered coordination geometries. A proof is given for the generality of extracopularity over point symmetry. Some practical challenges and future perspectives are discussed.
Symmetry versus information
Much of the prevailing theory of the structure of materials at the particle scale hinges upon the notion of symmetry.1 Indeed, the discrete spatial symmetries characteristic of crystalline matter give rise to an elegant structural theory that has seen great success in predicting a long list of physical phenomena.2,3 A widely acknowledged shortcoming of this symmetry-based understanding, however, is that it offers limited insight into the structure of non-crystalline media4,5 – an area of growing scientific interest6 and technological importance.7 The origin of this shortcoming lies in the fact that symmetry merely constitutes a special case of a more general mathematical notion that encompasses all forms of regularity inherent to a data source, often called information.8 In this article, we consider the possibility of a general theory of materials structure in which the notion of information plays the role that has traditionally been played by symmetry.From positions to distances
Density functional theory reveals that the macroscopic properties of a solid are uniquely determined by its electronic density in ground state and that this density is obtainable from the external potential due to positively charged atomic nuclei.9 Supposing the charges of the nuclei are known, the potential is in turn recoverable from nuclear positions via Coulomb's law. Thus, the ground-state properties of a solid are fully determined by the positions of its nuclei. This provides a physical rationale for the mathematical representation of a material as a set of point-like particles per crystallography and the classical formulations of statistical mechanics and molecular dynamics.But while particle positions are what formally specify the state of a system, it is the distances between those particles that constitute the fundamental quantity underlying structure. This follows from the fact that particle positions can be recovered from interparticle distances up to translation, rotation, and reflection,10 which have no effect on the total energy of a system. Indeed, the information content of particle positions is simply the information content of interparticle distances plus some extraneous information regarding the system's overall position, orientation, and handedness. It is possible to express this relationship symbolically using Shannon's information entropy functional H as follows:8
| H(P) = H(D) + H(T), | (1) |
From distances to bond angles
A property common to all interactions among particles of atomic size of greater is that their strength decays rapidly with interparticle distance. As a direct result of this property, the structure of a particle system manifests most strongly in the neighbourhoods of its constituent particles.Particle neighbourhoods tend to be approximately spherical (i.e. characterised by neighbours nearly equidistant from the central particle) as a consequence of the isotropy of space. By virtue of this approximate sphericality, the distance between any two neighbours of a given particle depends almost entirely on the angle between the vectors that indicate their position relative to the central particle; such vectors are commonly called bonds,11 and the angles between them, bond angles.12Fig. 1 illustrates this dependence geometrically.
Just as with the position–distance relationship, the distance–angle relationship can be captured using the functional H. Observe that the triple consisting of bond angles Θ, bond length differences Δ, and the nearest-neighbour distance ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) fully determines and is determined by interparticle distances D. These quantities are thereby equivalent in information,
fully determines and is determined by interparticle distances D. These quantities are thereby equivalent in information,
H(D) = H(Θ, Δ, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ). ). | (2) |
Twice applying the chain rule8 to the right-hand side, then invoking the independence between Θ and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , we get the following general relationship:
, we get the following general relationship:
H(D) = H(Θ) + H(Δ|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Θ) + H( ,Θ) + H(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ). ). | (3) |
At the spherical neighbourhood limit, vanishing bond length differences render H(Δ) = 0. By monotonicity, H(Δ|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Θ) ≤ H(Δ), and nonnegativity, H(Δ|
,Θ) ≤ H(Δ), and nonnegativity, H(Δ|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Θ) ≥ 0, we also have H(Δ|
,Θ) ≥ 0, we also have H(Δ|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Θ) = 0.8 Thus, interparticle distances D are informationally equivalent to bond angles Θ, up to a contribution from the nearest-neighbour distance
,Θ) = 0.8 Thus, interparticle distances D are informationally equivalent to bond angles Θ, up to a contribution from the nearest-neighbour distance ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,
,
H(D) = H(Θ) + H(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ). ). | (4) |
In systems with a simple crystalline ground state, H(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) tends to 0 with increasing density, leaving H(D) = H(Θ). This underscores the importance of bond angles to structure at the particle scale.
) tends to 0 with increasing density, leaving H(D) = H(Θ). This underscores the importance of bond angles to structure at the particle scale.
Extracopularity and E
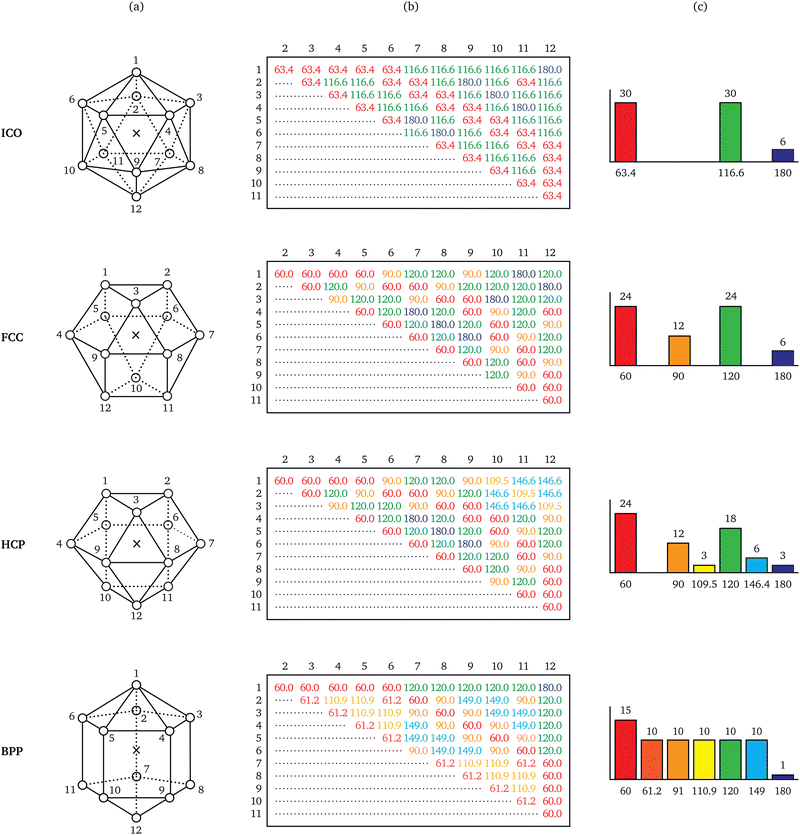
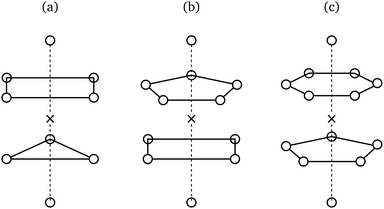
From elementary combinatorics, we know that a particle with k bonds has at most (k2 − k)/2 different bond angles. A key observation regarding energetically favourable neighbourhood geometries is that they exhibit a much lower diversity in bond angles than combinatorics would allow. Such geometries tend to resemble convex polyhedra with regular-polygonal faces,13 a few of which are illustrated in Fig. 2.Consider, for instance, the icosahedral geometry, which is of special importance to systems like supercooled liquids14 and metallic glasses.15 Observe that the 66 bond pairs implied by its 12 bonds make only three different angles, namely ∼63.4°, ∼116.6°, and 180°. These pairs are redundant in the sense that only three different angles suffice to describe all 66 of them; they are thus losslessly compressible.8 Repeating this exercise for the three other geometries in Fig. 2, the number of different bond angles is found to be a quantity able to distinguish between the various ways of arranging 12 neighbours around a particle.
In a previous work,16 the occurrence of fewer different bond angles than combinatorially possible was termed extracopularity. This phenomenon was quantified by a coefficient E, defined as the conditional Hartley entropy17 of bond pairs given bond angles,
| E = log2(n) − log2(m), n > 0, | (5) |
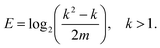 | (6) |
As a tool, E has found early application in the studies of convex polyhedra,18 cellular materials,19 and radiation damage.20
Local structure via symmetry and information
The phenomenon of extracopularity, as quantified by E, embodies the information-based approach to local structure in the same way that the phenomenon of point symmetry, as quantified by point group order |G|, embodies the symmetry-based approach. A basic performance criterion for local approaches to structural analysis is the extent to which distinct coordination geometries can be distinguished. Table 1 presents E and |G| for each of the four 12-coordinate geometries studied in Fig. 2. Observe that the ranking of these geometries by E resembles their ranking by |G|. This suggests that the symmetry- and information-based approaches to local structural analysis are comparable in analytical power for 12-coordinate geometries.| Geometry | Point symmetry | Extracopularity | |||
|---|---|---|---|---|---|
| G | |G| | k | m | E | |
| ICO | I h | 120 | 12 | 3 | 4.46 |
| FCC | O h | 48 | 12 | 4 | 4.04 |
| HCP | D 3h | 12 | 12 | 6 | 3.46 |
| BPP | D 5h | 20 | 12 | 7 | 3.24 |
Where the advantage of the information-based approach shows is in the analysis of coordination geometries that are symmetrically identical. Table 2 presents E and |G| for cubic geometries, which are characterised by the point group Oh. Here, |G| fails at the most basic level, being unable to make any distinction between those coordination geometries much less rank them on an ordinal scale.21 By contrast, E succeeds in both respects. The ranking implied by E is further observed to agree with that of the familiar atomic packing fraction (ηFCC = 0.74, ηBCC = 0.68, ηSC = 0.52). In this way, E appears to be able to capture the insights of point symmetry and packing fraction in a single quantity.
| Geometry | Point symmetry | Extracopularity | |||
|---|---|---|---|---|---|
| G | |G| | k | m | E | |
| FCC | O h | 48 | 12 | 4 | 4.04 |
| BCC | O h | 48 | 14 | 5 | 3.92 |
| SC | O h | 48 | 6 | 2 | 2.91 |
Table 3 expands the comparison to 22 of the most commonly encountered coordination geometries in the physical sciences. Both E and |G| are maximal for the icosahedral geometry but vary in their minima. For these 22 geometries, E is found to take 17 distinct values while |G| is found to take 9. With nearly double the resolution, E appears to be the more capable classifier. Moreover, in those 5 geometries with non-distinct E, differences in the bond angle distribution open up the possibility for an adjusted coefficient that can distinguish all 22 geometries. By contrast, the presence of only 13 distinct groups imposes a suboptimal upper bound on the resolution of symmetry-based approaches.
| Abbreviation | Coordination geometry | Polyhedral classification | k | m | E | G | |G| |
|---|---|---|---|---|---|---|---|
| TBP | Trigonal bipyramidal | Deltahedral, bipyramidal | 5 | 3 | 1.737 | D 3h | 12 |
| SDS | Snub disphenoidal | Deltahedral | 8 | 6 | 2.222 | D 2d | 8 |
| CTP | Capped trigonal prismatic | Prismatic | 7 | 4 | 2.392 | C 2v | 4 |
| PBP | Pentagonal bipyramidal | Deltahedral, bipyramidal | 7 | 4 | 2.392 | D 5h | 20 |
| BTP | Bicapped trigonal prismatic | Prismatic | 8 | 5 | 2.485 | C 2v | 4 |
| TET | Regular tetrahedral | Platonic, deltahedral | 4 | 1 | 2.585 | T d | 24 |
| HBP | Hexagonal bipyramidal | Bipyramidal | 8 | 4 | 2.807 | D 6h | 24 |
| CSA | Capped square antiprismatic | Antiprismatic | 9 | 5 | 2.848 | C 4v | 8 |
| CSP | Capped square prismatic | Prismatic | 9 | 5 | 2.848 | C 4v | 8 |
| TTP | Tricapped trigonal prismatic | Prismatic, deltahedral | 9 | 5 | 2.848 | D 3h | 12 |
| SC | Regular octahedral | Platonic, deltahedral, bipyramidal | 6 | 2 | 2.907 | O h | 48 |
| BSA | Bicapped square antiprismatic | Deltahedral, antiprismatic | 10 | 6 | 2.907 | D 4d | 16 |
| BSP | Bicapped square prismatic | Prismatic | 10 | 5 | 3.170 | D 4 | 8 |
| CPP | Capped pentagonal prismatic | Prismatic | 11 | 6 | 3.196 | C 5v | 10 |
| SA | Square antiprismatic | Antiprismatic | 8 | 3 | 3.222 | D 4d | 16 |
| HDR | Regular hexahedral | Platonic, prismatic | 8 | 3 | 3.222 | O h | 48 |
| BPP | Bicapped pentagonal prismatic | Prismatic | 12 | 7 | 3.237 | D 5 | 20 |
| HCP | Anticuboctahedral | Bicupolar | 12 | 6 | 3.459 | D 3h | 12 |
| BCC | Rhombic dodecahedral | Catalan | 14 | 6 | 3.923 | O h | 48 |
| FCC | Cuboctahedral | Bicupolar | 12 | 4 | 4.044 | O h | 48 |
| CPA | Capped pentagonal antiprismatic | Antiprismatic | 11 | 3 | 4.196 | C 5v | 10 |
| ICO | Regular icosahedral | Platonic, deltahedral, antiprismatic | 12 | 3 | 4.459 | I h | 120 |
A problem inherent to symmetry
Upon first glance, degeneracies of the kind exampled in Table 2 might appear resolvable through the use of space groups, as these more comprehensive groups readily distinguish between the lattices implied by cubic coordination geometries. There are, however, two issues with this approach: Firstly, it assumes that all geometries with identical point symmetry can tessellate to form a lattice, which, as illustrated in Fig. 3, is not the case. Secondly, and perhaps more fundamentally, the global structure of a crystal, as described by a space group, and its local structure around a single site, as described by a point group, fully determine each other and are thus informationally equivalent8 – the presence of a difference in their symmetric descriptions is at odds with this equivalence, pointing to a problem inherent to our current, symmetry-based conception of structure at the particle scale.Extracopularity generalises point symmetry
All of what has so far been discussed seems to suggest that extracopularity generalises point symmetry – that every geometry with point symmetry has extracopularity, while not every geometry with extracopularity has point symmetry. Under the idealisation of spherical neighbourhoods, this can in fact be proven.Theorem. Consider a geometry of k > 2 bonds, equal in length. Then, nontrivial point symmetry (|G| > 1) implies nontrivial extracopularity (E > 0), but not conversely.
Proof. We first prove the implication, then disprove its converse.
Part 1. The implication is proven directly.
Let |G| > 1. Then, there exists a map μ ∈ G such that {b,b′} and {β,β′} := {μ(b),μ(b′)} are two distinct bond pairs satisfying
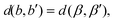 | (7) |
Since all four bonds are equal in length, the two pairs also make the same angle,
 | (8) |
But if two distinct bond pairs have the same angle, then the number of different bond angles is less than the total number of bond pairs, m < n. Recalling that E = log2(n) − log2(m), we have
| E > 0. | (9) |
Part 2. The converse is disproven by counterexample.
Consider a geometry of k > 3 bonds for which there exists a unique pair of distinct bond pairs {b,b′} ≠ {b,b′′} such that
| d(b,b′) = d(b,b′′). | (10) |
This has the following two consequences:
• There exists an angular equality. This implies that there are fewer bond angles than bond pairs, m < n. As a result,
| E > 0. | (11) |
• There does not exist a nontrivial isometry μ ∈ G. Since point groups consist only of isometries, G must be trivial. Thus,
| |G| = 1. | (12) |
This counterexample is illustrated in Fig. 4
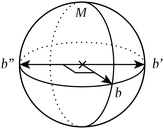 | ||
| Fig. 4 Introducing a fourth bond pointing anywhere off the meridional circle M on this sphere trivialises point symmetry but not extracopularity. | ||
Discussion
It is encouraging that a quantity based simply on the occurrence of fewer bond angles than combinatorially possible should lend itself to the characterisation of as complex a matter as structure. Through E, we observe the consistency of extracopularity with some of what is already known and understand that it generalises symmetry in a basic sense. This coefficient is, nevertheless, just one possible information-based quantifier of extracopularity, and indeed, structure.There are two noteworthy challenges to the informational study of structure through E in particular. Firstly, the number of different bond angles, m, can be difficult to ascertain in practice, with a variety of factors like thermal fluctuations ensuring that this is not as simple as counting the number of distinct angles.22 Secondly, the extracopularity coefficient does not in its current form account for variation in bond lengths; such variation could constitute an important feature of structure, especially in higher entropy systems like liquids and polydisperse packings.
In addition to addressing the above limitations, it will be necessary to link structure as it is observed locally by E to structure as it prevails globally to determine properties. Here, various statistical techniques present a promising avenue forward, in particular, simple descriptive statistics like the mean and variance, the joint distribution of neighbouring particle coefficients, and a coefficient correlation function similar in spirit to the radial distribution function.22
Concluding remarks
Notwithstanding the challenges that yet lie ahead, it seems that a general, information-based theory of the particle-scale structure of materials is conceivable, if only in principle. This is in contrast to the prevailing, symmetry-based understanding, which for its many strengths, is fundamentally specialised to crystals; indeed, it is beset by crucial issues even in this comparatively simple setting. Ultimately, the study of structure through information constitutes a new bridge between the physical and statistical sciences. And if prior such links are to give any indication, it is that there is much to be gained by further work in this direction.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge the contributions of Fabian Parsch to the development of the ideas discussed in this work.Notes and references
- M. De Graef and M. E. McHenry, The Structure of Materials, Cambridge University Press, Cambridge, UK, 2nd edn, 2012 Search PubMed.
- J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford University Press, 1985 Search PubMed.
- K. Bowman, Mechanical Behavior of Materials, John Wiley & Sons, Hoboken, NJ, 1st edn, 2004 Search PubMed.
- J. D. Bernal, Nature, 1959, 183, 141–147 CrossRef CAS.
- H. Tanaka, H. Tong, R. Shi and J. Russo, Nat. Rev. Phys., 2019, 1, 333–348 CrossRef.
- L. Berthier and D. R. Reichman, Nat. Rev. Phys., 2023, 5, 102–116 CrossRef.
- K. Gao, X. Zhu, L. Chen, W. Li, X. Xu, B. Pan, W. Li, W. Zhou, L. Li, W. Huang and Y. Li, J. Mater. Sci. Technol., 2022, 131, 115–121 CrossRef CAS.
- T. M. Cover and J. A. Thomas, Elements of Information Theory, Wiley, 2nd edn, 2012 Search PubMed.
- M. L. Cohen and S. G. Louie, Fundamentals of Condensed Matter Physics, Cambridge University Press, 2016 Search PubMed.
- T. F. Cox and M. A. A. Cox, Multidimensional scaling, Chapman & Hall, 1994 Search PubMed.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784–805 CrossRef CAS.
- G. J. Ackland and A. P. Jones, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 054104 CrossRef.
- A. Malins, S. R. Williams, J. Eggers and C. P. Royall, J. Chem. Phys., 2013, 139, 234506 CrossRef PubMed.
- T.-Y. Chang, Z. Wang and D. Xu, J. Mater. Res., 2023, 38, 179–186 CrossRef CAS.
- M. Kumar, E. Nicholson, D. W. Kirk, S. J. Thorpe and C. V. Singh, J. Alloys Compd., 2019, 787, 840–850 CrossRef CAS.
- J. Çamkran, F. Parsch and G. D. Hibbard, J. Chem. Phys., 2022, 156, 091101 CrossRef PubMed.
- R. V. L. Hartley, Bell Syst. Tech. J., 1928, 7, 535–563 CrossRef.
- J. Çamkran, F. Parsch and G. D. Hibbard, Eur. Phys. J. B, 2023, 96, 72 CrossRef.
- S. Choukir, D. A. van Egmond, B. D. Hatton, G. D. Hibbard and C. V. Singh, Int. J. Eng. Sci., 2023, 188, 103863 CrossRef.
- J. Stimac, C. Serrao and J. Mason, J. Nucl. Mater., 2023, 585, 154633 CrossRef CAS.
- S. S. Stevens, Science, 1946, 103, 677–680 CrossRef PubMed.
- J. Çamkran, F. Parsch and G. D. Hibbard, Local-order fluctuations in Kob-Andersen-type glass formers, 2022 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(
sin(