A p-type semi-conducting copper(I)-1,3-benzenedithiolate 2D coordination polymer with high Seebeck coefficient

Abstract

A new p-type semi-conducting and 2D coordination polymer (CP) based on a thiolate ligand and Cu(+I) exhibits a record Seebeck coefficient among CPs, equivalent to that obtained for inorganic compounds. Such a high value originates from the 1D {Cu–S}_n tubular inorganic network, which is connected through the bridging 1,3-benzenedithiolate ligand.

---

Considering the actual global warming and our over-reliance on fossil fuels, there is a tremendous need for new energy technologies with low environmental and societal impacts. Thermoelectricity, which is the ability of a material to convert heat into electricity and vice versa, is an ideal technology that would allow transforming waste heat from industries, engines, power plants, household appliances and even human bodies into power, providing sustainable energetic cycles. To reach this goal, a thermoelectric material should have a good performance and its efficiency is evaluated by a dimensionless figure of merit, ZT = S²σT/κ, where S, σ, T and κ are the Seebeck coefficient, the electrical conductivity, the absolute temperature and the thermal conductivity, respectively. Bearing in mind the Carnot cycle, the ZT value of a material should be greater than 3 for device efficiency.¹

Since the discovery of the thermoelectricity phenomenon, extensive studies have been carried out on inorganic materials, mostly the chalcogenides such as Bi₂Te₃, Sb₂Te₃, PbTe and SnSe. Those thermoelectric (TE) materials have high Seebeck coefficient, up to around 500 μV K⁻¹, but they have high thermal conductivity, which results in a modest ZT, still below 1.² The record ZT value has been reported in 2019 for an alloy, Fe₂V_0.8W_0.2Al, with a ZT value of 5 to 6.³ In addition, these thermoelectric inorganic materials have the drawbacks of poor processability, high cost and toxicity, preventing their further sustainable applications. In the meantime, π-delocalized organic polymers, such as poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS) or polyaniline (PANI), have appeared as good alternatives as TE materials with good shaping opportunities, light weight, non-toxicity, low cost and more importantly low thermal conductivity (∼0.2 W m⁻¹ K⁻¹).⁴ Nevertheless, the organic materials have low Seebeck coefficient (∼30 μV K⁻¹) resulting in still modest ZT. Thus, there is a huge need to further improve the ZT value of materials to achieve Carnot efficiency, and significant efforts have to be devoted to the development of TE materials exhibiting high Seebeck coefficient, high electrical conductivity, and low thermal conductivity. An alternative is to use hybrid materials to take advantage of the inorganic and organic networks. Thus, TE composite materials which are a mixture of two compounds, are a good strategy, but the synergy between the two entities is difficult to control and requires multistep syntheses.⁵

Metal organic frameworks (MOFs) and coordination polymers (CPs), constructed from metal ions bonded to organic moieties, offer a diversity of structural topologies ranging from one-dimensional (1D) to three-dimensional (3D) arrangements, with possible porosity coupled with other different functionalities, which allows fine tuning of their electronic structures, resulting in intrinsic physical properties.⁶ Those MOFs and CPs have recently appeared as potential TE materials (Table S1, ESI†).⁷ Indeed, the 2D copper-benzenehexathiolate, Cu_xBHT, exhibits a record electrical conductivity up to 2000 S cm⁻¹, due to the delocalized charge through the π–d conjugated system.⁸ The TE properties have been evaluated for different formula of Cu_xBHT with x = 3, 4 and 5.5 and the best ZT of 0.08 at RT has been obtained with a Seebeck coefficient of 80 μV K⁻¹ and a thermal conductivity of 0.59 W m⁻¹ K⁻¹.⁹ The lowest thermal conductivity of 0.2 W m⁻¹ K⁻¹ has been measured in the two Ni₃(2,3,6,7,10,11-hexaiminotriphenylene)₂ and [Ni₃(perthiolated coronene)]_n CPs; nevertheless, their low Seebeck coefficients of −12 and 47 μV K⁻¹ imply low ZT of 1.19 × 10⁻³ and 0.003, respectively.¹⁰ Zn-HAB (HAB: hexaaminobenzene), a 3D porous network, shows the best intrinsic Seebeck coefficient of 200 μV K⁻¹ at RT and under vacuum, but this MOF presents a low conductivity and suffers from instability under O₂, due to the weak interactions between Zn(II) and the amino groups.¹¹ Consequently, there is still a tremendous need to explore more MOF/CP systems as new TE materials to understand the impacts of the metal ions, their oxidation state, the coordinating functions, the topology of the ligands and the dimensionality of the network on the electric and thermal properties. Based on the record properties of Cu_xBHT and the high stability of copper-thiolate compounds, due to the strong interactions between the thiolate ligands (soft base) and the Cu(+I) (soft acid), copper-thiolate CPs are very promising systems as TE materials.¹² Apart from Cu_xBHT, a few more conducting copper-monothiolate CPs have been reported, such as [Cu(6-mna)]_n (5.4 × 10⁻⁵ S cm⁻¹ at RT),¹³ {[Cu₂(6-Hmna)(6-mna)]·NH₄}_n (11 S cm⁻¹ at RT on single crystal)¹⁴ (6-Hmna = 6-mercaptonicotinic acid, 6-mna = 6-mercaptonicotinate), [Cu(p-SPhOH)]_n (120 S cm⁻¹),¹⁵ and Cu[Cu(pdt)₂], (pdt = 2,3-pyrazinedithiolate) (6.10⁻⁴ S cm⁻¹ at RT), pointing out their ability as semiconducting CPs.¹⁶ Here we report, copper(I)-1,3-benzenedithiolate, [Cu₂(1,3-BDT)]_n, a new 2D CP that is made of aligned 1D Cu–S tubes connected together through the bridging ligands. This CP exhibits intrinsic and bulk electrical conductivity of 1.5 mS cm⁻¹ under air at RT and a Seebeck coefficient of 420 μV K⁻¹, a record value among CPs and MOFs, and equivalent to inorganic materials.

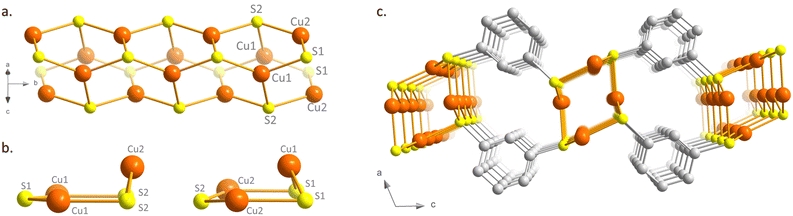
[Cu₂(1,3-BDT)]_n is obtained by mixture of two equivalents of copper(I) chloride with one equivalent of 1,3-benzenedithiol in an acidic aqueous solution, heated in a sealed vial at 120 °C. As shown by the scanning electron microscopy image (Fig. S1, ESI†), thin needles of a few micrometer length are formed. Elemental and thermo-gravimetric analyses lead to the chemical formula of [Cu₂(1,3-BDT)]_n, which confirms the S/Cu(I) = 1 ratio and the charge balance (see ESI,† and Fig. S2). The infrared spectrum also confirms the coordination of the thiolate functions with the absence of a thiol function, usually observed at 2500 cm⁻¹ (Fig. S3, ESI†). The powder X-ray diffraction (PXRD) data, collected at the CRISTAL beamline of the SOLEIL synchrotron facility (Gif-Sur-Yvette, France), show good crystallinity of the compound and allow its ab initio structural determination. The final Rietveld refinement (Fig. S4, ESI†) leads to a satisfactory model indicator and profile factors (Table S2, ESI†). [Cu₂(1,3-BDT)]_n crystallizes in the monoclinic P2₁/c space group. Its structure is made of inorganic Cu–S chains, where copper and sulphur atoms are three coordinated, forming distorted Cu₃S₃ hexagons packed together along the b axis (Fig. 1a and b and Fig. S5, ESI†). These Cu–S tubular chains are then connected together through the bridging 1,3-BDT ligands to form a 2D network (Fig. 1c), totally different to that observed for the 3D [Ag₂(1,3-BDT)]_n analogue.¹⁷ Such Cu(I)–S tubular chains made of distorted Cu₃S₃ hexagons have been already observed in a few [Cu(SR)]_n CPs with monotopic thiolate ligands, with R = Me,¹⁸ Ph, p-PhMe, p-PhOMe¹⁹ and o-PhCO₂H.²⁰ In this 2D CP, the Cu–S distances range from 2.20(2) Å to 2.26(3) Å, the Cu–S–Cu angles from 75.0(7)° to 125(1)° and the S–Cu–S angles from 109.1(7)° to 127.2(8)° (Table S3, ESI†). However, [Cu₂(1,3-BDT)]_n is the first 2D copper-thiolate CP bearing these 1D Cu–S tubular chains, thus making it possible to combine in one compound a 1D inorganic chain and a 2D metal-π-conjugated path. The Cu–Cu distances of 2.947(4) Å and 3.797(3) Å point out the absence of cuprophilic interactions, which can sometimes be observed in d¹⁰ coinage metal compounds.²¹ The X-ray photoelectron spectroscopy (XPS) of [Cu₂(1,3-BDT)]_n also confirms the oxidation state of Cu(I). Indeed, the 2p-copper core levels exhibit dominant peaks at 932.8 eV and 952.6 eV, corresponding to Cu(I) 2p3/2 and Cu(I) 2p1/2, respectively (Fig. S6, ESI†).

Fig. 1 Structure of [Cu₂(1,3-BDT)]_n: (a) the Cu–S chain along the b axis; (b) the two deformed Cu₃S₃ hexagons and (c) the central projection along the b axis. Orange, yellow and gray spheres correspond to copper, sulfur and carbon atoms. Hydrogen atoms were omitted for clarity.

The direct band gap obtained from the Tauc plot of the UV-visible absorption spectroscopy curve is 2.26 eV (Fig. S7, ESI†), which is of the same order of magnitude as that of the other reported 1D copper(I)-thiolate CPs (2.23–2.68 eV).^19,20

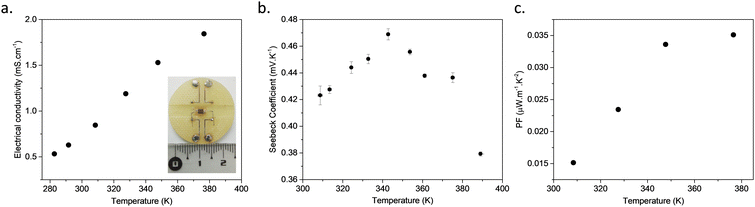
The thermoelectric properties of [Cu₂(1,3-BDT)]_n were evaluated from dense pellets with a diameter of 4 mm and a thickness of 1 mm (Fig. S8, ESI†), prepared at room temperature under pressure, with typically around 40 mg of crushed sample pressed at 0.6 MPa for 15 minutes. PXRD data of these pellets show that the sample remains crystalline and stable under this mechanical pressure, and that no decomposition is observed when it is stored under air for a few months (Fig. S8, ESI†).

The electrical transport properties were investigated first by the four-probe method at the surface of the pellet from RT to 390 K. At RT, the current–voltage measurements on the pellets in the four-probe configuration show a linear behaviour following Ohm's law (Fig. S9, ESI†), which reveals an electrical conductivity of 8.3 × 10⁻⁴ S cm⁻¹. This modest value is close to that of the 1D [Cu(SPh)]_n analogue, which has an electrical conductivity of 3.7 × 10⁻⁴ S cm⁻¹, pointing out the implication of the Cu–S chains in the electron transport rather than the aromatic benzene ring.²²

The variable-temperature measurements with a four-probe configuration using metallic tips applied on the surface of a pressed pellet show that the electrical conductivity increases with the rise in temperature, which is consistent with bulk transport dominated by a thermally activated process (Fig. 2a and Fig. S10, ESI†). Fitting the data with the Arrhenius equation yields an activation energy (E_a) of 0.13 eV (Fig. S11, ESI†).²³ In order to ensure that the electrical conductivity is not a surface effect on the pressed pellet, bulk conductivity was also measured. For that, a corded saw was used to cut the sintered pellet into a rectangular cuboid of 1.4 × 2 × 2.5 × 4 mm (Fig. S12, ESI†) and two electrodes were welded on the metallised sides of this cuboid to apply a uniform current. The voltage is then measured between differently spaced electrodes, alloying the measurements of the voltage drop as a function of distance, in order to extract the resistance and the contact resistance (see inset of Fig. 2a and Fig. S13, ESI†). A low contact resistance of 0.017 kΩ was determined (two orders of magnitude lower than that of the sample). The bulk electrical conductivity of the CP measured in this configuration is 15 × 10⁻⁴ S cm⁻¹, close to the value obtained with the previous surface four-probe experiment, proving that the electrons can move through the bulk pressed pellet prepared without any care of orientation.

Fig. 2 (a) Temperature dependence of the electrical conductivity measured on a [Cu₂(1,3-BDT)]_n pressed pellet by surface four-probe configuration and photo of the device to apply the bulk measurement of the electrical conductivity; (b) Seebeck coefficient with temperature (errors come from the linear fits of the raw data) and (c) the power factor with temperature.

The Seebeck coefficient (S) was measured on bulk samples of [Cu₂(1,3-BDT)]_n, inserted in a primary vacuum chamber, at different temperatures ranging from RT to 400 K, below the decomposition temperature of 520 K (Fig. S2, ESI†). The S value at RT is positive and high: +420 ± 10 μV K⁻¹ (Fig. S14, ESI†). The positive sign indicates that the dominant charge carriers are holes with a Fermi level close to the valence band. This S is the highest reported among conducting MOFs, CPs, composite materials and organic polymers (Table S1, ESI†).⁷ Interestingly, the S increases upon heating up to a certain temperature, around 350 K, from which it decreases reversibly up to 380 K (see Fig. 2b). This unusual existence of temperature maximum will be correlated below to the particularities of the electronic band structure.²⁴ The power factor (PF), expressed as PF = S²σ, is 0.026 μW m⁻¹ K⁻² at RT and reaches 0.034 μW m⁻¹ K⁻² at 349 K. Due to the modest electrical conductivity of [Cu₂(1,3-BDT)]_n, this PF is below the best values reported for MOFs and CPs with a record of 88.2 μW m⁻¹ K⁻² for the nanosheets of Cu_xBHT (Table S1, ESI†).^9b Nevertheless, as mentioned earlier, the electrical conductivity of [Cu₂(1,3-BDT)]_n is an average over all the directions of the needle-like crystallites constituting the powder, which has been simply pressed to form pellets. Further studies on aligned crystallites or on a single crystal would allow extraction of the intrinsic conductivity of the 1D-CuS chains that might be much higher.

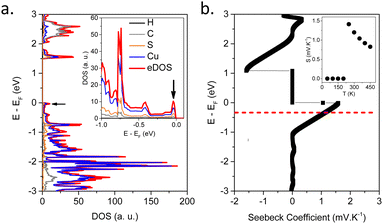
In order to understand the origin of the high Seebeck values and its anomalous temperature dependence in [Cu₂(1,3-BDT)]_n, the electronic band structure has been calculated and the Seebeck coefficient using ab initio DFT calculations determined. In the optimized [Cu₂(1,3-BDT)]_n unit cell, the sulfur atoms are negatively charged, while the copper is in the Cu(I) oxidation state. The electronic band structure along the main symmetry directions is reported in the ESI,† (Fig. S15a). A direct band gap of 1.5 eV is extracted from the band structure. This value is underestimated at the current theoretical level, but is sufficient to analyse the nature of the electronic states, which mainly contribute to the electrical conductivity and the Seebeck coefficient. Interestingly, the band structure exhibits very flat bands along the directions in momentum space perpendicular to the Cu–S chains, confirming the 1D-like character of the electrical conduction. These flattened bands result in peaks when integrated in momentum as shown in the total, eDOS, and projected electron density of states, p-eDOS (see black arrows on Fig. 3a and Fig. S15b, ESI†). Moreover, at the Fermi level, near the top of the valence band, the p-eDOS shows that the dominant character of the propagating electronic states is provided by sulfur and copper orbitals, indicating that there is no conduction between the Cu–S chains, which also confirms that the conduction takes place in the 1D-like Cu–S channels.²⁴ On the other hand, at the bottom of the conduction band, a more significant contribution of the C-backbone appears, which indicates an inter-chain conduction.

Fig. 3 (a) Calculated density of states (DOS) of [Cu₂(1,3-BDT)]_n: projected electronic DOS (p-eDOS) with a grey line for C, black for H, orange for S and blue for Cu electrons and the total electronic DOS (eDOS) in red. The inset is a zoomed-in view close to the Fermi level and with switched axes. The black arrows show the shard peaks associated with high Seebeck coefficient. (b) Calculated Seebeck coefficient at 300 K. The inset shows its temperature dependence at constant energy represented by the dotted red line in (b).

It is well-known in the eDOS that sharp features close to the Fermi level result in large values of the Seebeck coefficient.²⁵ From the transport integrals, the Seebeck is enhanced by sharp and thermally activated electronic singularities in the eDOS. As a direct consequence of the 1D-like character of the valence bands close to the Fermi level, the eDOS of [Cu₂(1,3-BDT)]_n exhibits such sharp peaks (see black arrow on Fig. 3a). This explains the large and abrupt changes of the Seebeck coefficient according to energy close to the Fermi level as seen in Fig. 3b, which can also be observed by varying the temperature as shown in the inset of Fig. 3b (and Fig. S16, ESI†). This qualitatively explains the high positive Seebeck values observed experimentally and also the maximum observed in the temperature dependence of the Seebeck (inset in Fig. 3b). Thus, the reasons for both the high Seebeck values and a maximum value around 350 K are due to the strong quasi-1D character of the electronic transport. This can be seen from the ab initio simulated electronic band structures (Fig. S16, ESI†); the flatness of the bands along the Cu–S chains is responsible for peaks (Van Hove singularities) in the eDOS and the temperature dependence of S(T).

Conclusions

A neutral 2D copper-thiolate CP, [Cu₂(1,3-BDT)]_n, has been synthesized under hydrothermal conditions. This CP shows good air stability, due to the strong soft base–soft acid interactions between the thiolate functions and the copper(I) ions, and it remains crystalline upon pressure for pellet formation. This Cu(I)-thiolate network exhibits at RT a mild conductivity of 1.5 mS cm⁻¹ and a record Seebeck coefficient of 420 μV K⁻¹ among CPs, equivalent to inorganic solids. The resulting PF is 0.03 μW m⁻¹ K⁻². Theoretical studies showed that the conductivity originates from the 1D inorganic Cu–S chains and explained the high Seebeck coefficient by the presence of a significant peak in the total electronic DOS at the Fermi level, near the top of the valence band. This study highlights that CPs, and more especially copper-thiolates, hold great promise as emerging TE materials. In addition, compared to the highly conducting 2D copper-benzenehexathiolate, which required multistep synthesis of the ligand, 1,3-benzenedithiol is commercially available, reducing considerably the time and cost of the final material production, and allowing the formation of large pressed pellets under air. Finally, systematic syntheses of different copper-thiolate CPs and in-depth electronic and theoretical studies have to be done in order to increase the electrical conductivity while keeping a good Seebeck coefficient. Changing ligand functionalities,^12b mixing sulfur, using selenium or tellurium-based linkers,²⁶ carrying out metal doping or synthesising heterometallic composition CPs are some paths to improve the electrical conductivity.²⁷

Author contributions

C. A., S. H., A. A. and J. L. R. performed the synthetic experiments and routine characterizations; A. M. and N. G. solved the structure; F. P. was involved in the purification; S. W. hosted A. D.; T. N. performed the DFT, R. D. and C. A. carried out the conductivity; O. B. executed the XPS; S. P. and A. D. conceived the ideas, designed the experiments and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge SOLEIL synchrotron (Gif-sur-Yvette, France) for provision of radiation facilities (BAG for X-ray diffraction 20201440) and Erik Elkaïm for assistance in using the CRISTAL beamline. This work was supported by the French National Agency (MOTIC ANR-21-CE08-0045). S. H. acknowledges the CNRS for her PhD grant and A. A. the Fondation de la Maison de la Chimie for his postdoctoral position. The European Commission is acknowledged by A. D. for her Marie Skłodowska-Curie Individual Fellowship (101031503 – AniMOC – H2020-MSCA-IF-2020). S. P. acknowledges V. Giordano and S. Le Floch for their support in using the Seebeck apparatus and the pellet press, respectively. The pellets, and the thermoelectric and XPS measurements were performed using the facilities at the platforms “PLECE, Transport and PLYRA@ILMTech”, respectively.

Notes and references

1. Z.-G. Chen, G. Han, L. Yang, L. Cheng and J. Zou, Prog. Nat. Sci.: Mater. Int., 2012, 22, 535.
2. R. Freer, et al. , J. Phys. Energy, 2022, 4, 022002.
3. B. Hinterleitner, I. Knapp, M. Poneder, Y. Shi, H. Müller, G. Eguchi, C. Eisenmenger-Sittner, M. Stöger-Pollach, Y. Kakefuda, N. Kawamoto, Q. Guo, T. Baba, T. Mori, S. Ullah, X.-Q. Chen and E. Bauer, Nature, 2019, 576, 85.
4. B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc and R. A. Segalman, Nat. Rev. Mater, 2016, 1, 16050.
5. M. Massetti, F. Jiao, A. J. Ferguson, D. Zhao, K. Wijeratne, A. Würger, J. L. Blackburn, X. Crispin and S. Fabiano, Chem. Rev., 2021, 121, 12465.
6. (a) H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444; (b) R. Freund, O. Zaremba, G. Arnauts, R. Ameloot, G. Skorupskii, M. Dincă, A. Bavykina, J. Gascon, A. Ejsmont, J. Goscianska, M. Kalmutzki, U. Lächelt, E. Ploetz, C. S. Diercks and S. Wuttke, Angew. Chem., Int. Ed., 2021, 60, 23975.
7. Y. Fan, Z. Liu and G. Chen, Small, 2021, 17, 2100505.
8. (a) X. Huang, P. Sheng, Z. Tu, F. Zhang, J. Wang, H. Geng, Y. Zou, C.-A. Di, Y. Yi, Y. Sun, W. Xu and D. Zhu, Nat. Commun., 2015, 6, 7408; (b) X. Huang, S. Zhang, L. Liu, L. Yu, G. Chen, W. Xu and D. Zhu, Angew. Chem., Int. Ed., 2018, 57, 146.
9. (a) X. Huang, Y. Qiu, Y. Wang, L. Liu, X. Wu, Y. Liang, Y. Cui, Y. Sun, Y. Zou, J. Zhu, W. Fang, J. Sun, W. Xu and D. Zhu, Angew. Chem., Int. Ed., 2020, 59, 22602; (b) R. Tsuchikawa, N. Lotfizadeh, N. Lahiri, S. Liu, M. Lach, C. Slam, J. Louie and V. V. Deshpande, Phys. Status Solidi A, 2020, 217, 2000437.
10. (a) L. Sun, B. Liao, D. Sheberla, D. Kraemer, J. Zhou, E. A. Stach, D. Zakharov, V. Stavila, A. A. Talin, Y. Ge, M. D. Allendorf, G. Chen, F. Léonard and M. Dincă, Joule, 2017, 1, 168; (b) Z. Chen, Y. Cui, Y. Jin, L. Liu, J. Yan, Y. Sun, Y. Zou, Y. Sun, W. Xu and D. Zhu, J. Mater. Chem. C, 2020, 8, 8199.
11. J. Park, A. C. Hinckley, Z. Huang, G. Chen, A. A. Yakovenko, X. Zou and Z. Bao, J. Am. Chem. Soc., 2020, 142, 20531.
12. (a) O. Veselska and A. Demessence, Coord. Chem. Rev., 2018, 355, 240; (b) X. Deng, S.-L. Zheng, Y.-H. Zhong, J. Hu, L.-H. Chung and J. He, Coord. Chem. Rev., 2022, 450, 214235.
13. K. Hassanein, C. Cappuccino, P. Amo-Ochoa, J. López-Molina, L. Maini, E. Bandini and B. Ventura, Dalton Trans., 2020, 49, 10545.
14. A. Pathak, J.-W. Shen, M. Usman, L.-F. Wei, S. Mendiratta, Y.-S. Chang, B. Sainbileg, C.-M. Ngue, R.-S. Chen, M. Hayashi, T.-T. Luo, F.-R. Chen, K.-H. Chen, T.-W. Tseng, L.-C. Chen and K.-L. Lu, Nat. Commun., 2019, 10, 1721.
15. K.-H. Low, V. A. L. Roy, S. S.-Y. Chui, S. L.-F. Chan and C.-M. Che, Chem. Commun., 2010, 46, 7328.
16. S. Takaishi, M. Hosoda, T. Kajiwara, H. Miyasaka, M. Yamashita, Y. Nakanishi, Y. Kitagawa, K. Yamaguchi, A. Kobayashi and H. Kitagawa, Inorg. Chem., 2009, 48, 9048.
17. S. Hawila, A. Abdallah, J.-L. Rukemampunzi, A. Fateeva, G. Ledoux, R. Debord, S. Paihlès, N. Guillou, F. Massuyeau, R. Gautier, A. Mesbah and A. Demessence, Chem. Commun., 2022, 58, 8081.
18. M. Baumgartner, H. Schmalle and C. Baerlocher, J. Solid State Chem., 1993, 107, 63.
19. C.-M. Che, C.-H. Li, S. S.-Y. Chui, V. A. L. Roy and K.-H. Low, Chem. – Eur. J., 2008, 14, 2965.
20. O. Veselska, N. Guillou, M. Diaz-Lopez, P. Bordet, G. Ledoux, S. Lebègue, A. Mesbah, A. Fateeva and A. Demessence, ChemPhotoChem, 2022, 6, e202200030.
21. N. V. S. Harisomayajula, S. Makovetskyi and Y.-C. Tsai, Chem. – Eur. J., 2019, 25, 8936.
22. J. Troyano, Ó. Castillo, P. Amo-Ochoa, J. I. Martínez, F. Zamora and S. Delgado, CrystEngComm, 2019, 21, 3232.
23. L. Sun, M. G. Campbell and M. Dincă, Angew. Chem., Int. Ed., 2016, 55, 3566.
24. S. Moshfeghyeganeh, A. N. Cote, J. J. Neumeier and J. L. Cohn, J. Appl. Phys., 2016, 119, 095105.
25. M. S. Dresselhaus, G. Chen, M. Y. Tang, R. G. Yang, H. Lee, D. Z. Wang, Z. F. Ren, J.-P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043.
26. G. Xing, Y. Li, Z. Feng, D. J. Singh and F. Pauly, ACS Appl. Mater. Interfaces, 2020, 12, 53841.
27. (a) Y. Jin, Y. Fang, Z. Li, X. Hao, F. He, B. Guan, D. Wang, S. Wu, Y. Li, C. Liu, X. Dai, Y. Zou, Y. Sun and W. Xu, Nat. Commun., 2022, 13, 6294; (b) R. Toyoda, N. Fukui, D. H. L. Tjhe, E. Selezneva, H. Maeda, C. Bourgès, C. M. Tan, K. Takada, Y. Sun, I. Jacobs, K. Kamiya, H. Masunaga, T. Mori, S. Sasaki, H. Sirringhaus and H. Nishihara, Adv. Mater., 2022, 34, 2106204.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and instrumental descriptions, SEM, TGA, FT-IR, PXRD, XPS, UV-vis and conductivity data. CCDC 2232011. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3tc02379f

---