Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Novel melamine – salicylic salt solvates and co-crystals; an analysis of the energetic parameters of the intermolecular hydrogen bonds stabilizing the crystal structure†
Kinga
Wzgarda-Raj
 *a,
Agnieszka J.
Rybarczyk-Pirek
*a,
Agnieszka J.
Rybarczyk-Pirek
 a,
Sławomir
Wojtulewski
b and
Marcin
Palusiak
a
a,
Sławomir
Wojtulewski
b and
Marcin
Palusiak
a
aDepartment of Physical Chemistry, Faculty of Chemistry, University of Lodz, Pomorska 163/165, Lodz, 90-236, Poland. E-mail: kinga.raj@chemia.uni.lodz.pl
bInstitute of Chemistry, University of Bialystok, Ciolkowskiego 1K, Bialystok, 15-245, Poland
First published on 27th June 2022
Abstract
Two novel crystal structures based on melamine and salicylic acid, with either water (I) (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 molecular ratio) or ethanol (II) (2
8 molecular ratio) or ethanol (II) (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molecular ratio), can be treated as salt solvates. In these structures, all molecular components are bound by expanded hydrogen bonding networks consisting of N–H⋯N, N–H⋯O, O–H⋯O, and O–H⋯N interactions among the solvent molecules and acid–base complexes; these stabilize the crystal architecture. Special attention is paid to the N+–H⋯O− hydrogen bonds formed between cationic melamine molecules and the ionized carboxyl group (COO−) of anions of salicylic acid. These salt bridges exist as single contact or bifurcated double donor/acceptor hydrogen bonds which are additionally accompanied by N–H⋯O interactions. This present study uses quantum chemistry methods (DFT, QTAIM) to understand their nature and their energetic parameters.
1 molecular ratio), can be treated as salt solvates. In these structures, all molecular components are bound by expanded hydrogen bonding networks consisting of N–H⋯N, N–H⋯O, O–H⋯O, and O–H⋯N interactions among the solvent molecules and acid–base complexes; these stabilize the crystal architecture. Special attention is paid to the N+–H⋯O− hydrogen bonds formed between cationic melamine molecules and the ionized carboxyl group (COO−) of anions of salicylic acid. These salt bridges exist as single contact or bifurcated double donor/acceptor hydrogen bonds which are additionally accompanied by N–H⋯O interactions. This present study uses quantum chemistry methods (DFT, QTAIM) to understand their nature and their energetic parameters.
Introduction
Melamine (2,4,6-triamine−1,3,5-triazine), classified to heterocyclic aromatic compounds, has some interesting properties from the perspective of supramolecular chemistry. Its molecule possesses several hydrogen bonding donor/acceptor groups which can be used to construct various supramolecular motifs. The most widely-recognized is the R22(8) graph-set ring motif,1 which is usually formed between azine nitrogen and amine atoms of adjacent molecules.2 Its co-crystallization with other chemical compounds results in the formation of several types of crystal architecture. Complex structures, such as rings, rosettes, ribbons, sheets, and two or three dimensional nets are often constructed from hydrogen-bonded molecules of melamine.3–7 Moreover, melamine molecule characterized by multiple hydrogen bonding sites, also possesses trigonal D3h symmetry and an almost flat structure. The latter property enables the formation of a layered arrangement stabilized by π-stacking interactions.8,9Melamine has a wide range of applications, being used for the production of synthetic resins, decorative laminates, flame-retardants, paints and varnishes and wood-based panels, as well as adhesives and household items. It is also used in the paper industry, the textile industry for producing auxiliaries and in the electrical industry as plastics.10–13 Therefore, on ongoing interest there are novel materials including this compound. An interesting problem of crystal architecture is also posed by the influence of various solvents on the creation of polymorphic structures, particularly porous materials.14
The presented work focuses on the synthesis of two novel multicomponent structures of melamine and salicylic acid using different solution conditions.
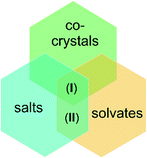
Intensive researches on new crystalline systems as well as discoveries in the field production of multicomponent materials required the definition or redefinition of many chemical concepts. Among them is a term “co-crystal”, especially in reference to such definitions as “salt” or “solvate”.
A cocrystal is a solid with specified properties, composed of two or more components in one crystal lattice. A crystal salt differs from a co-crystal in the occurrence of proton transfer. It is formed by the transfer of a proton from an acid to a base. If this effect is absent, then a molecular cocrystal is formed. On the other hand, the solvate is formed by combining an ion or a solute molecule with solvent molecules.15,16
Taking this into account, the presented in this paper structures (I) and (II), we can be firstly treated as salts and then as solvates. In particular, structure (I) because of presence of neutral melamine molecules in crystal lattice apart anions and cations, may be also defined as co-crystal (see Scheme 1).
The title multicomponent crystal structures were obtained by co-crystallization with water (I) or ethanol (II). The two structures significantly differ from each other (stoichiometric ratio, melamine molecule, protonation, space group, and crystal system) but demonstrate similar melamine-acid ionic synthons. The obtained hydrogen bonding motifs were subjected to detailed investigation by means of structural analysis involving both our original XRD experiments and the CSD data (Cambridge Structural Database),17 as well as computational analysis, including electron-density analysis based on the Quantum Theory of Atoms in Molecules (QTAIM).18
Results and discussion
Intermolecular synthons of melamine: CSD analysis
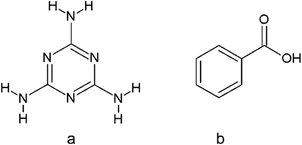
The search of the Cambridge Structural Database17 was performed to find crystal structures containing molecules of melamine (a) and benzoic acid derivatives (b) (Scheme 2).The CSD analysis identified 10 crystal structures without evidence of disorder, including cocrystals, salts, solvates of water, and dimethylformamide. This group of crystals shared one common feature, a pair of two hydrogen bonds linking melamine nitrogen with carboxylic oxygen atoms, which appears to be responsible for maintaining the stability of the melamine – benzoic acid complex. The set of these two hydrogen bonds allows the formation of a cyclic R22(8) intermolecular graph-set motif 1.1 Due to the possible transfer of a proton from the carboxyl to the imine group, the motif can present a neutral or an ionic scheme (see Fig. 1). The neutral motif 1 is characterized by two hydrogen bonds of the type N–H⋯O and O–H⋯N, with both molecules (melamine and carboxylic acid) simultaneously acting as proton donors and acceptors (ETAZEF, HOWQUG, JIWQIQ, MAQBEM, VAXHIN, XOJPOD).19–25 In contrast, ionic motif 1 demonstrated an ionic hydrogen bridge N+–H⋯O−, as a result of proton transfer via the O–H⋯N hydrogen bond (JIWQIQ, MAQBEM, MAQBIQ, OMIJEZ, ZUSPIP).20–23,26
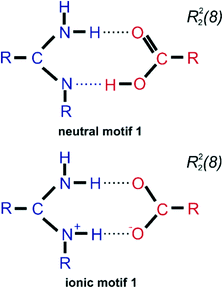 | ||
| Fig. 1 Scheme of two cyclic synthons of N–H⋯O and O–H⋯N/N+–H⋯O− interactions forming motif 1 (neutral and ionic ones) that occur between melamine (blue) and benzoic acid derivatives (red). | ||
In the latter case, in the crystalline state, a melamine molecule becomes a cation and a double proton donor in hydrogen bonding interactions, while the carboxylate anion acts as a double hydrogen bond acceptor. In such cases, between the adjacent ionic molecules of melamine and salicylic acid, there is a neutral hydrogen bond N–H⋯O and a charge-assisted N+–H⋯O− CAHB(±)bond, also known as a salt bridge.27,28
Crystallographic results
In the course of our research, two novel crystal structures based on melamine and salicylic acid were created: one with water (I) (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 molecular ratio) and the other with ethanol (II) (2
8 molecular ratio) and the other with ethanol (II) (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molecular ratio). Fig. 2 presents the general molecular structures of the obtained crystal components.
1 molecular ratio). Fig. 2 presents the general molecular structures of the obtained crystal components.
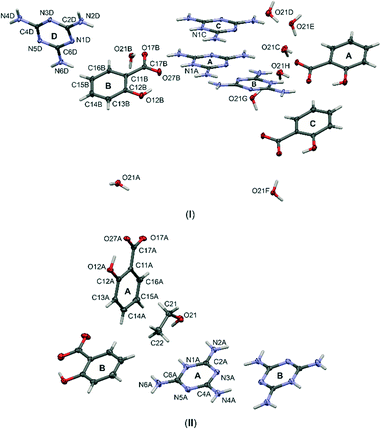 | ||
| Fig. 2 Labelling schemes of all molecular components of cocrystals (I) and (II). Anisotropic displacement parameters of non-hydrogen atoms are drawn as ellipsoids with a 50% probability level. | ||
Note, that the two structures can be treated as separate solvates of the salts formed by melamine mixed with salicylic acid. In structure (I), water is the crystallizing solvent, while in structure (II), it is ethanol. The influence of the solvent on the crystallization process is visible when comparing structures. The crystal structure (I) crystallize in the triclinic crystal system with the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and (II) in the monoclinic crystal system with the P21/n space group. Stoichiometry of melamine and acid amounts to 4
space group and (II) in the monoclinic crystal system with the P21/n space group. Stoichiometry of melamine and acid amounts to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for (I) and 1
3 for (I) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for (II). Moreover, compound (I) demonstrates eight molecules of water in the asymmetric unit while (II) only includes one ethanol molecule.
2 for (II). Moreover, compound (I) demonstrates eight molecules of water in the asymmetric unit while (II) only includes one ethanol molecule.
The analysis of structures (I) and (II) showed that during the crystallization process, there was an intermolecular transfer of the hydrogen atom (proton) from the carboxylate group of acid (O17A, O27B, O27C in structure (I) and O27A, O27B in structure (II)) to the nitrogen atoms of the aromatic melamine rings (N1A, N1B, N1C). Following this proton transfer reaction, it can be seen that both structures present a salt-like type of crystal, which results from the difference in the dissociation constant of melamine and salicylic acid (melamine pKα = 5.0 and salicylic acid pKα = 2.98).
It is also worth noting that, in structure (I), only three of the four melamine molecules are protonated, which is consistent with the stoichiometric ratio of acid–base pairs: only three acid molecules are in the asymmetric unit, despite there being four melamine molecules. Thus, the N1D atom of molecule D is not protonated, it exists as a neutral form (see Fig. 2). Interestingly, in the asymmetric unit of (I), there is one neutral melamine molecule (D): this structure can therefore be regarded as a co-crystal of salt. In turn, in structure (II) there are two molecules of melamine and two molecules of acid (molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The observed structure was formed by proton transfer from acid to base molecules. Therefore, in both crystal structures (I) and (II), the pairs of melamine (cation) and salicylic acid (anion) are joined by hydrogen bonding interactions; both present the same ionic motif (1) (Fig. 1 – ionic motif 1).
1). The observed structure was formed by proton transfer from acid to base molecules. Therefore, in both crystal structures (I) and (II), the pairs of melamine (cation) and salicylic acid (anion) are joined by hydrogen bonding interactions; both present the same ionic motif (1) (Fig. 1 – ionic motif 1).
Crystal architecture as an interplay of hydrogen bonds
In crystal structures (I) and (II), all molecular components are bound into more expanded complexes linked by various types of hydrogen bonds. Strongly electronegative elements, such as nitrogen and oxygen play the role of hydrogen bonding donors and acceptors in intra- and intermolecular interactions. These exist as N–H⋯N, N–H⋯O, O–H⋯O and O–H⋯N, which occur in both structures. Fig. 3a and b present the general scheme of hydrogen bonds between molecules in the asymmetric unit, Table 1 summarizes the geometric parameters of these interactions. The corresponded interatomic distances are within typical ranges.29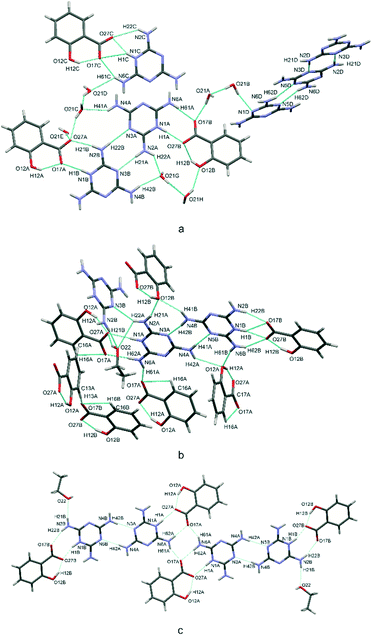 | ||
| Fig. 3 Scheme of hydrogen bonds, presented as blue dotted lines, in the crystal structures (I) – a and (II) – b and c. | ||
| D–H⋯A | d(D–H) | d(H⋯A) | d(D⋯A) | <(D–H⋯A) | Symmetry | |
|---|---|---|---|---|---|---|
| N–H⋯N (melamine – melamine) | ||||||
| I | N(6C)–H(62C)⋯N(5C) | 0.83(3) | 2.34(2) | 3.157(2) | 172(3) | 2 − x, 1 − y, 1 − z |
| N(2A)–H(21A)⋯N(3B) | 0.86(2) | 2.04(2) | 2.895(2) | 176(2) | x, y, z | |
| N(6B)–H(62B)⋯N(5A) | 0.87(2) | 2.03(2) | 2.899(2) | 175(3) | −1 + x, −1 + y, z | |
| N(2B)–H(22B)⋯N(3A) | 0.91(2) | 2.11(2) | 3.023(2) | 176(2) | x, y, z | |
| N(6D)–H(62D)⋯N(5D) | 0.89(2) | 2.04(2) | 2.930(2) | 178(3) | 2 − x, 2 − y, −z | |
| N(2D)–H(21D)⋯N(3D) | 0.90(3) | 2.09(3) | 2.977(2) | 175(3) | 2 − x, 1 − y, −z | |
| N(6A)–H(62A)⋯N(5B) | 0.88(3) | 2.17(2) | 3.040(2) | 171(3) | 1 + x, 1 + y, z | |
| N(2C)–H(21C)⋯N(3C) | 0.89(2) | 2.11(2) | 2.996(2) | 174(2) | 1 − x, −y, 1 − z | |
| II | N(4B)–H(42B)⋯N(3A) | 0.91(2) | 2.01(2) | 2.908(2) | 172(2) | 1/2 + x, 3/2 − y, −1/2 + z |
| N(4A)–H(42A)⋯N(5B) | 0.87(2) | 2.185(2) | 3.054(2) | 178(2) | −1/2 + x, 3/2 − y, 1/2 + z | |
| N(2A)–H(22A)⋯N(3B) | 0.85(2) | 2.224(2) | 2.965(2) | 145(2) | 1 − x, 1 − y, 1 – z | |
| N–H⋯O (melamine – salicylic acid) | ||||||
| I | N(1B)–H(1B)+⋯O(17A)− | 0.91(3) | 1.88(3) | 2.786(2) | 175(3) | 1 − x, 1 − y, 1 – z |
| N(1C)–H(1C) +⋯O(17C)− | 0.96(3) | 2.50(3) | 3.260(2) | 136(3) | x, y, z | |
| N(6A)–H(61)⋯O(17B) | 0.93(3) | 1.97(3) | 2.886(2) | 172(2) | x, y, z | |
| N(6C)–H(61C)⋯O(17C) | 0.89(2) | 2.23(2) | 3.072(2) | 159(2) | x, y, z | |
| N(6D)–H(61D)⋯O(12A) | 0.88(3) | 2.48(3) | 3.203(2) | 141(2) | x, y, z | |
| N(4D)–H(42D)⋯O(12C) | 0.91(3) | 2.22(3) | 3.088(2) | 159(2) | 2 − x, 1 − y, −z | |
| N(4D)–H(41D)⋯O(12A) | 0.90(2) | 2.43(2) | 3.253(2) | 152(3) | 2 − x, 2 − y, −z | |
| N(2D)–H(22D)⋯O(12C) | 0.86(3) | 2.56(2) | 3.240(2) | 137(2) | x, y, z | |
| II | N(4B)–H(41B)⋯O(12B) | 0.93(2) | 2.15(2) | 2.911(2) | 139(2) | x, 1 + y, z |
| N(4A)–H(41A)⋯O(12A) | 0.88(2) | 2.37(2) | 3.009(2) | 131(2) | 1/2 − x, 1/2 + y, 1/2 − z | |
| N(2A)–H(21A)⋯O(12B) | 0.93(2) | 2.02(2) | 2.919(2) | 162(2) | −1/2 + x, 1/2 − y, 1/2 + z | |
| N(6B)–H(61B)⋯O(12A) | 0.90(2) | 2.12(2) | 3.011(2) | 167(2) | 1 − x, 1 − y, −z | |
| N(2B)–H(22B)⋯O(17B) | 0.90(2) | 1.96(2) | 2.824(2) | 162(2) | −1/2 + x, 1/2 − y, −1/2 + z | |
| N(6A)–H(61A)⋯O(17A) | 0.89(2) | 1.92(2) | 2.808(2) | 175(2) | 1 − x, −y, 1 − z | |
| N(6A)–H(62A)⋯O(17A) | 0.88(2) | 1.97(2) | 2.782(2) | 153(2) | x, y, z | |
| N(1B)–H(1B)+⋯O(17B)− | 0.96(2) | 2.40(2) | 3.167(2) | 137(2) | −1/2 + x, 1/2 − y, −1/2 + z | |
| C/O–H⋯O (salicylic acid – salicylic acid) | ||||||
| I | O(12C)–H(12C)⋯O(17C) | 0.95(3) | 1.64(3) | 2.539(2) | 157(3) | x, y, z |
| O(12A)–H(12A)⋯O(17A) | 0.96(3) | 1.73(3) | 2.591(2) | 147(3) | x, y, z | |
| II | C(13A)–H(13A)⋯O(17B) | 0.93 | 2.50 | 3.213(2) | 133.2 | x, y, z |
| O–H⋯O (melamine – water) | ||||||
| I | N(1C)–H(1C)⋯O(27C) | 0.96(3) | 1.76(3) | 2.687(2) | 163(3) | x, y, z |
| N(4B)–H(42B)⋯O(21G) | 0.88(2) | 2.08(2) | 2.940(2) | 168(2) | x, y, z | |
| N(4B)–H(41B)⋯O(21B) | 0.89(2) | 2.14(3) | 2.940(2) | 150(2) | −1 + x, y, z | |
| N(4C)–H(42C)⋯O(21D) | 0.88(3) | 2.01(2) | 2.806(2) | 151(2) | 2 − x, 1 − y, 1 − z | |
| N(4C)–H(41C)⋯O(21E) | 0.88(2) | 2.08(2) | 2.920(2) | 159(2) | 1 − x, 1 − y, 1 − z | |
| N(1A)–H(1A)⋯O(27B) | 0.97(3) | 1.74(3) | 2.707(2) | 176(3) | x, y, z | |
| N(4A)–H(42A)⋯O(21F) | 0.91(3) | 2.08(2) | 2.968(2) | 165(2) | 2 − x, 1 − y, 1 − z | |
| N(4A)–H(41A)⋯O(21C) | 0.87(2) | 2.20(2) | 2.969(2) | 147(2) | 1 − x, 1 − y, 1 − z | |
| N(6C)–H(61C)⋯O(21D) | 0.89(2) | 2.43(2) | 3.004(2) | 122(2) | x, y, z | |
| N(6B)–H(61B)⋯O(21F) | 0.91(2) | 2.04(2) | 2.811(2) | 142(2) | 1 − x, −y, 1 − z | |
| N(2C)–H(22C)⋯O(21E) | 0.86(2) | 2.28(2) | 2.921(2) | 132(2) | x, − 1 + y, z | |
| N(2C)–H(22C)⋯O(27C) | 0.86(2) | 2.38(2) | 3.070(2) | 138(2) | x, y, z | |
| N(2B)–H(21B)⋯O(27A) | 0.90(2) | 1.90(2) | 2.784(2) | 168(2) | 1 − x, 1 − y, 1 − z | |
| N(2A)–H(22A)⋯O(21G) | 0.87(3) | 2.06(3) | 2.764(2) | 138(2) | x, y, z | |
| O–H⋯O (melamine – ethanol) | ||||||
| II | N(6B)–H(62B)⋯O(27B) | 0.84(2) | 2.36(2) | 3.088(2) | 145(2) | −1/2 + x, 1/2 − y, −1/2 + z |
| N(1A)–H(1A)⋯O(27A) | 0.92(2) | 1.90(2) | 2.819(2) | 177(2) | 1 − x, −y, 1 − z | |
| N(1B)–H(1B)⋯O(27B) | 0.96(2) | 1.82(2) | 2.744(2) | 160(2) | −1/2 + x, 1/2 − y, −1/2 + z | |
| O–H⋯O (salicylic acid – water) | ||||||
| I | O(12B)–H(12B)⋯O(27B) | 0.91(4) | 1.70(4) | 2.526(2) | 149(3) | x, y, z |
| O(12C)–H(12C)⋯O(21D) | 0.82 | 2.64 | 3.224(2) | 129.8 | x + 1, y, z | |
| O–H⋯O (salicylic acid – ethanol) | ||||||
| II | O(12A)–H(12A)⋯O(27A) | 0.96(2) | 1.65(2) | 2.542(2) | 154(2) | x, y, z |
| O(12B)–H(12B)⋯O(27B) | 0.97(3) | 1.58(3) | 2.501(2) | 157(3) | x, y, z | |
| O–H⋯N (water – melamine) | ||||||
| I | O(21A)–H(21 L)⋯N(1D) | 0.95(3) | 2.03(3) | 2.955(2) | 166(3) | −1 + x, y, z |
| O–H⋯O (ethanol – ethanol) | ||||||
| II | O(22)–H(22)⋯O(27A) | 0.93(3) | 2.06(2) | 2.928(2) | 155(2) | 1/2 − x, 1/2 + y, 1/2 − z |
As seen in Fig. 3, typical intramolecular hydrogen bonds are formed between hydroxyl and carboxylate groups within salicylic acid molecules. This results in the formation of cyclic S(6) motifs1 assisted by a negative charge CAHB(−) O–H⋯O−.
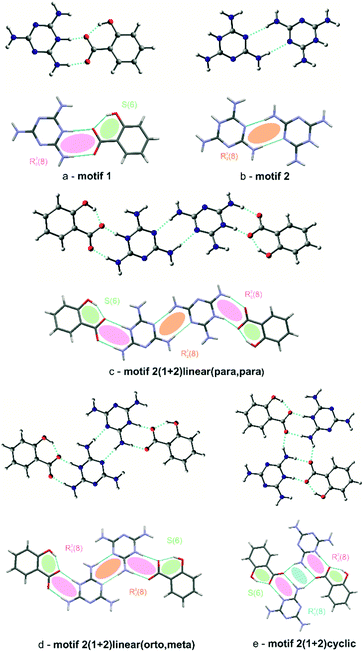
Special attention should be paid to the intermolecular hydrogen bonds upon proton transfer, i.e. N+–H⋯O− interactions in salt bridges.27 In both (I) and (II), these interactions are formed between the hydrogenated nitrogen atoms (NH+) of cationic melamine molecules and the ionized carboxylate groups (COO−) of the salicylic acid anions. The intermolecular bonds can exist in a form of a single N+–H⋯O−contact or bifurcated double donor/acceptor hydrogen bonds, which are additionally accompanied by N–H⋯O interactions (see Fig. 3a). This type of interaction, next to the neutral N–H⋯O hydrogen bond, is responsible for the formation of melamine (cation) – salicylic acid (anion) dimers. These two types of hydrogen bonds: mixed salt bridges (N+–H⋯O−) and charge-assisted hydrogen bonds (N–H⋯O) result in the creation of a R22(8) intermolecular cyclic graph-set motif (1). This synthon also includes a system of double donor (NH+) and double acceptor (O−) bifurcated interactions, i.e. a dimer built from three condensate hydrogen bonding rings; these are assisted by intramolecular O–H⋯O− hydrogen bonds (motif 1, synthons presented with pink and green ellipses in Fig. 4a).
In turn, another synthon formed by homonuclear N–H⋯N hydrogen bonds can be seen between melamine molecules. Also a typical synthon found in melamine-containing crystal structures is a dimeric centrosymmetric system of melamine molecules linked by two hydrogen bonds (motif 2, presented with orange ellipses in Fig. 4b). In (I), there are three types of melamine complexes: a centrosymmetric dimer built of C molecules, an infinite chain of dimers formed by two crystallographically-independent molecules A and B, and an infinite chain formed by neutral D molecules. Compound (II) also includes dimers of molecules A and B.
The coexistence of motifs 1 and 2 (Fig. 4a and b) in the same crystal structure allows them to be combined into more complex structures. Various combinations can arise depending on the addition of crystallization solvent. For example, (I) demonstrates a linear arrangement of melamine/salicylic acid molecules which can be assigned as a (1+2)linear(orto,meta) (c) motif, built of melamine molecules A and B, or a (1+2)linear(meta,meta) motif, built of a centrosymmetric pair of melamine C molecules, (compare Fig. 4c). In turn, in (II) the same molecules are arranged slightly differently in complex structures, forming (1+2)linear(para,para) (d) motifs (see Fig. 4d). In contrast to the non-symmetric structure of (c) in (I), this motif in (II) may be regarded as symmetrical.
Compound (II) also includes four simultaneously interacting molecules in the (1+2)cyclic (e) motif (presented in blue in Fig. 4e). The –NH2 group of the melamine molecule is a double hydrogen bond donor and the oxygen atom of carboxylate group of the salicylic acid is a double acceptor. Taking into account that these two finite motifs of complex ions, viz. (d) and (e), are joined to each other, one final large centrosymmetric octamer may also be indicated (compare Fig. 3c).
The unit cell also includes several types of hydrogen bonding between glue solvent molecules and acid–base complexes in (I) and (II), which stabilize the crystal architecture. The presented structures can be treated as an example of salt solvates: polymorphs varying due to the co-crystalizing solvent (water, ethanol). In the case of (I), water molecules are mainly responsible for the stabilization of the ionic melamine-acid complexes (compare Fig. 3a).
To get a better insight into the nature of hydrogen bond synthons found in (I) and (II), a computational analysis of their energy parameters was performed. At this point, we should note one important issue in regard to the super molecular method used in our work for the estimation of the interaction energy. Our approach estimated the interaction energy in the complex as the difference between the total energy of the complex and the sum of total energies of its components (fragments, mostly of closed-shell nature). In this context, it is crucial to have a clear definition of the molecular fragments forming the complex. Usually, this is not a problem. For instance, when one considers a water dimer, each of the water molecules is treated as (closed-shell) a separate fragment. However, in the present case, where there is evidence of proton transfer along with hydrogen bonds, the situation is not so clear. Firstly, the exact location of the hydrogen atoms indicated by experimental X-ray diffraction data is disputable due to the well-known experimental problem of the difference between the position of its nuclei and the maximum electron density.30
In addition, the interatomic distances in the hydrogen bridges may in part indicate the molecule to which a certain hydrogen atom should belong after complex fragmentation (parent atom, parent molecular fragment). However, a simple comparison of donor/acceptor⋯hydrogen (D/A⋯H) distances with hydrogen atom lying close to the intermediate distance between the donor (D) and the acceptor (A) centers, seems to be insufficient.
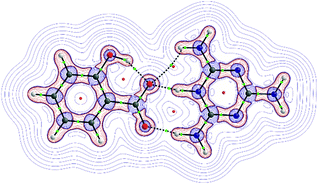
To resolve this, we chose to analyze the electron density and its Laplacian for the most representative two-molecule complex observed in both the tested crystal structures; namely, the melamine – salicylic acid complex, in which the proton transfer occurs spontaneously both in the crystal state and in the corresponding computational model. Fig. 5 shows the molecular graph in which the bonds are represented as bond paths, according to QTAIM theory. The graph shows also the topology of the Laplacian of electron density (∇2ρ). In general, negative ∇2ρ values indicate a concentration of electronic charge while positive values indicate its depletion. Naturally, a region between two closed-shell fragments (e.g. two molecules in the hydrogen bonded complex) will be characterized by positive ∇2ρ values. As seen in Fig. 5, the border of this region runs between the fragments of melamine–salicylic acid complex in such a way that the hydrogen bridging proton belongs to the valence region of the melamine moiety: the separation line runs through the critical points of the green bonds. This suggests that when estimating interaction energy by means of the super molecular approach, the complex should be divided into two ionic fragments, that is, a melamine cation and a salicylate anion. This solution is adopted in the further part of our analysis reported in this paper.
As mentioned in the experimental section, all geometries of the discussed molecular systems were fully optimized (crystal state geometries were used as starting points); therefore, only the stationary points on the potential energy hypersurface were analyzed. The arrangement of molecules in all cases corresponds to the experimental observations, even if some geometry parameters were changed during the geometry optimization procedure, as expected.
The first characteristic motif is the anion–cation pair shown in Fig. 4a. The total interaction energy stabilizing such complexes is −112.5 kcal mol−1. Although this is a relatively large value, it is nevertheless comparable with other ± charge assisted hydrogen bonds (salt bridges).31 Obviously such interaction must have a very important role in stabilizing the crystal state. Another characteristic motif is the dimer of two melamine cations (Fig. 4b). In this case, the total interaction energy is positive, being 36.5 kcal mol−1. The positive sign indicates that there is a loss of energy due to formation of the dimer. Note that even if the formation of the hydrogen bond leads to loss of energy, the dimer is still energetically stable and it fulfills all optimization procedure criteria. Note also that this loss of energy due to complexation may be compensated by other stabilizing effects when passing from isolated dimer into infinite crystal net. Both these synthons can be found in the more complex interaction patterns observed in the crystal structures of (I) and (II).
Moving to the analysis of the four-molecule patterns present in the crystal structures of (I) and (II), which combine dimers (a) and (b), shown in Fig. 4, we will first compare two tetramers which combine the same dimeric bricks in different structural modes, i.e. systems (c) and (d) in Fig. 4. Tetramer (c) has a linear structure while the tetramer (d) is the kinked analogue of (c); however, both structures possess more total interaction energy than the sum of the interaction energies of pairs (a) and (b), being −231.9 kcal mol−1 for (c) and 233.7 kcal mol−1 for (d). Therefore, the non-specific interaction through the space between anions and cations in tetramers provides extra stabilization of tetrameric patterns. Additionally, this spatial stabilizing arrangement appears slightly more effective in the case of the kinked structure (d). In addition to (c) and (d), another tetrameric interaction pattern (e) can be found in (II) (compare Fig. 3c), i.e. the tetramer given in Fig. 4. In this case, like in (c) and (d), the structure includes two ionic dimers (a); however, the spatial arrangement excludes the presence of diatonic dimer (b). As a result, the interaction energy is larger than in the case of tetramers (c) and (d), being 236.4 kcal mol−1. Undoubtedly, the interaction energies in the hydrogen-bonded systems shown in Fig. 4 are large and have an important role in stabilizing crystals of (I) and (II).
As structure (I) crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, the crystal architecture is governed by inversion symmetry. Firstly, N–H⋯N hydrogen bonded parallel chains of melamine cations (molecules A and B) can be seen, which extend along the [110] direction (see Fig. 6a) and centrosymmetric pairs arranged in parallel (molecules C). Each pair of melamine cations within a chain or dimer are linked with two salicylic carboxylate anions, forming the N–H⋯O/N+–H⋯O− tetrameric (1,2)linear(orto,meta) and (1,2)linear(meta,meta) motifs discussed above (compare the central part of the unit cell in Fig. 6b). In this way, alternating chains and tetramers of cation–anion complexes are formed, surrounded by co-crystallizing water molecules; these are stabilized by several types of hydrogen bonding interactions. In turn, in the crystal structure, these layers are separated by chains of neutral melamine molecules (again linked by N–H⋯N hydrogen bonds) extending along the [010] crystallographic direction. Non-protonated melamine molecules are embedded by a hydrogen bond to water O1B molecules (compare Fig. 3a). It is worth noting that due to the presence of anion–cation layers, as well as neutral water and melamine molecules, structure (I) may be classified as a solvated (hydrated) co-crystal of a salt.
space group, the crystal architecture is governed by inversion symmetry. Firstly, N–H⋯N hydrogen bonded parallel chains of melamine cations (molecules A and B) can be seen, which extend along the [110] direction (see Fig. 6a) and centrosymmetric pairs arranged in parallel (molecules C). Each pair of melamine cations within a chain or dimer are linked with two salicylic carboxylate anions, forming the N–H⋯O/N+–H⋯O− tetrameric (1,2)linear(orto,meta) and (1,2)linear(meta,meta) motifs discussed above (compare the central part of the unit cell in Fig. 6b). In this way, alternating chains and tetramers of cation–anion complexes are formed, surrounded by co-crystallizing water molecules; these are stabilized by several types of hydrogen bonding interactions. In turn, in the crystal structure, these layers are separated by chains of neutral melamine molecules (again linked by N–H⋯N hydrogen bonds) extending along the [010] crystallographic direction. Non-protonated melamine molecules are embedded by a hydrogen bond to water O1B molecules (compare Fig. 3a). It is worth noting that due to the presence of anion–cation layers, as well as neutral water and melamine molecules, structure (I) may be classified as a solvated (hydrated) co-crystal of a salt.
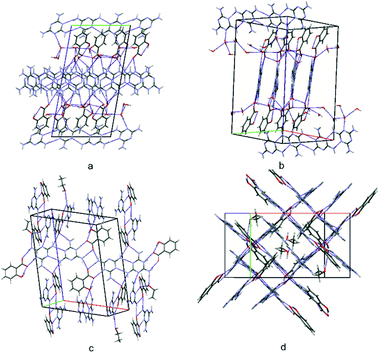 | ||
| Fig. 6 A view of the packing of the unit cells for structure (I) (a and b) and for structure (II) (c and d). | ||
No similar molecular arrangement can be seen in (II) (P21/n); however, this structure can be described as built of acid–base octamers, i.e. condensed (1,2)linear(para,para) and (1+2)cyclic motifs, intertwined with neutral ethanol molecules. These octamers are arranged roughly perpendicular to each other in the crystal state (Fig. 6c and d).
Experimental
Preparation of crystals
Cocrystals were obtained from commercially available reagents (Aldrich Chemical Co.) and used without further purification.Preparation of Cocrystal (I)
Salicylic acid (0.5 mmol) was mixed with melamine (0.5 mmol) in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. It was then dissolved in 4 ml of propan-1-on and 6 ml of water. The crystals were obtained within 2 weeks by slowly evaporating the solvent at room temperature.
2. It was then dissolved in 4 ml of propan-1-on and 6 ml of water. The crystals were obtained within 2 weeks by slowly evaporating the solvent at room temperature.
Preparation of Cocrystal (II)
Salicylic acid (0.5 mmol) was mixed with melamine (0.5 mmol) in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It was then dissolved in 4 ml of ethanol and 6 ml of water. The crystals were obtained within 2 weeks by slowly evaporating the solvent at room temperature.
1. It was then dissolved in 4 ml of ethanol and 6 ml of water. The crystals were obtained within 2 weeks by slowly evaporating the solvent at room temperature.
X-ray structure determination
All X-ray Diffraction Data were collected on a four-circle Oxford Diffraction Supernova Dual diffractometer using a two-dimensional area CCD detector and a low-temperature device (Oxford Cryosystem cooler). Integration of intensities and corrections for Lorentz effects, polarization effects, and analytical absorption were performed with CrysAlis PRO.32 Crystal structures were solved by direct methods and refined in F2 using a full-matrix least-squares procedure (SHELXL-2014).33 The positions of the hydrogen atoms of the NH and OH groups were found on a Fourier difference map and refined isotropically without any restraints. The hydrogen atoms of the aromatic rings were introduced in the calculated positions with an idealized geometry; these were restricted using a rigid body model, with isotropic displacement parameters equal to 1.2 of the equivalent displacement parameters of their parent atoms. Positions of water hydrogen atoms were generated automatically on base of electron density with tetrahedral H–O–H angles and refined using AFIX 147 instruction in SHELX program. The molecular geometries were calculated using the Platon34 and WinGX programs.35 A summary of the relevant crystallographic data is given in Table 2. The atomic coordinates, displacement parameters, and structure factors of the analyzed crystal structures were deposited with the Cambridge Crystallographic Data Centre (CCDC).36| (I) | (II) | |
|---|---|---|
| Empirical formula | 3(C7O3H5) × 3(C3N6H7) × C3N6H6 × 8(H2O) | 2(C7O3H5) × 2(C3N6H7) × C2OH6 |
| Formula weight/g mol−1 | 1063.03 | 574.58 |
| Temperature/K | 100 | 100 |
| Crystal system | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n |
| a/Å | 10.6489(3) | 14.8757(2) |
| b/Å | 12.0796(3) | 9.5734(1) |
| c/Å | 21.1891(5) | 18.7224(2) |
| α/° | 95.540(2) | 90 |
| β/° | 98.304(2) | 101.680(1) |
| γ/° | 115.065(3) | 90 |
| Volume/Å3 | 2405.0(2) | 2611.1(1) |
| Z | 2 | 4 |
| ρcalc g cm−3 | 1.468 | 1.462 |
| μ/mm1 | 1.025 | 0.950 |
| F(000) | 1120.0 | 1208.0 |
| Crystal size/mm3 | 0.029 × 0.152 × 0.466 | 0.048 × 0.155 × 0.288 |
| Radiation | CuKα (λ = 1.54184) | CuKα (λ = 1.54184) |
| 2θ range for data collection/° | 8.208 to 136.992 | 6.944 to 136.978 |
| Index ranges | −12 ≤ h ≤ 12 | −17 ≤ h ≤ 17 |
| −14 ≤ k ≤ 14 | −11 ≤ k ≤ 11 | |
| −25 ≤ l ≤ 25 | −22 ≤ l ≤ 22 | |
| Reflections collected | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414 414 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
| Independent reflections | 8852 | 4806 |
| R int = 0.0644 | R int = 0.0357 | |
| R sigma = 0.0335 | R sigma = 0.0176 | |
| Data/restraints/parameters | 8852/0/681 | 4806/0/391 |
| Goodness-of-fit on F2 | 1.041 | 1.065 |
| Final R indexes [I > = 2σ (I)] | R 1 = 0.0549 | R 1 = 0.0398 |
| wR2 = 0.1306 | wR2 = 0.1056 | |
| Final R indexes [all data] | R 1 = 0.0635 | R 1 = 0.0440 |
| wR2 = 0.1376 | wR2 = 0.1099 | |
| Largest diff. peak/hole/e Å−3 | 0.42/−0.33 | 0.23/−0.32 |
| CCDC number | 2166109 | 2166110 |
Cambridge structural database (CSD) analysis
The search for CSD (Cambridge Structural Database, release 2021)17 was carried out to find crystal structures containing molecules of melamine (a) and benzoic acid (b) (Scheme 1). In particular, multicomponent crystal structures were investigated. To obtain data for analysis, the search results were additionally restricted to crystal structures of organic compounds without evidence of disorder.Quantum-theoretical computations
All the theoretically studied molecular systems were fully optimized without any symmetry restraints. When applicable, structural data from the X-ray experiment was used as a starting point in the optimization procedure. Interaction energies were estimated by means of super molecular approach.37,38 Calculations were performed using B3LYP functional39 in conjunction with 6-311++G(d,p) Pople's basis set.40,41 The Gaussian 09 set of codes was implemented for calculations.42 For one selected fully-optimized molecular complex, the analysis of electron density and its Laplacian was performed in the framework of QTAIM theory.18 The AIMAll software was used for that purpose.43Conclusions
Two novel salt crystals were created based on salicylic acid and melamine, a very common, water-soluble, hydrogen-bonding donor molecule. The two molecules differ from each other by the presence of water as a solvent in (I) and ethanol in (II). These structures may be treated as an example of salt solvates (two other solvatomorphic systems).Interestingly, in both structures, similarly to other melamine-acid crystals, the acid–base complex is stabilized by a system of double N–H⋯O/O–H⋯N or N–H⋯O/N+–H⋯O− hydrogen bonds (R22(8) graph-set ring motif). According to theoretical DFT (B3LYP/6-311++G[d,p]) and QTAIM computations, these interactions stabilize the anion–cation complex with an energy of −112.5 kcal mol−1. However, in the crystal state, anion–cation pairs co-exist in more complex tetrameric structures (linear symmetric, non-symmetric, or cyclic motifs), with the stabilization energy varying from 231.9 kcal mol−1 to 236.4 kcal mol−1. These tetramers are also linked to infinite chains by hydrogen bonding, either by N–H⋯N hydrogen bonds (I) or finite centrosymmetric octamers (II).
Noteworthy, structure (I) represents a very interesting crystalline material: a multicomponent crystal classified as a solvated co-crystal of salt.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
KWR acknowledges financial support from grant number IDUB B2111101000008.07. The theoretical computations using the Gaussian 09 set of codes were carried out in the Wrocław Center for Networking and Supercomputing (https://www.wcss.wroc.pl). Access to HPC machines and licensed software is gratefully acknowledged.Notes and references
- M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256 CrossRef PubMed.
- A. Santoro, G. Bella, G. Bruno, G. Neri, Z. Akbari and F. Nicolo, J. Mol. Struct., 2021, 1229, 12801 CrossRef.
- J. A. Zerkowski, J. C. MacDonald, C. T. Seto, D. A. Wierda and G. M. Whitesides, J. Am. Chem. Soc., 1994, 116, 2382 CrossRef CAS.
- X. L. Zhang and X. M. Chen, Cryst. Growth Des., 2005, 5, 617 CrossRef CAS.
- X. L. Zhang, B. H. Ye and X. M. Chen, Cryst. Growth Des., 2005, 5, 1609 CrossRef CAS.
- J. Janczak, J. Mol. Struct., 2020, 1207, 127833 CrossRef CAS.
- J. A. Zerkowski, J. C. MacDonald, C. T. Seto, D. A. Wierda and G. M. Whitesides, J. Am. Chem. Soc., 1994, 116, 2382 CrossRef CAS.
- R. F. M. Lange, F. H. Beijer, R. P. Sijbesma, R. W. Hooft, H. Kooijman, A. L. Spek, J. Kroon and E. W. Meijer, Angew. Chem., 1997, 36, 969 CrossRef CAS.
- L. Vella-Zerb, D. Braga, A. G. Orpen and U. Baisch, CrystEngComm, 2014, 16, 8147 RSC.
- W. H. Binder and M. Dunky, Encyclopedia of Polymer Science and Technology, John Wiley & Sons, Inc., New York, 2002 Search PubMed.
- J. Zhang, M. Lewin, E. Pearce, M. Zammarano and J. W. Gilman, Polym. Adv. Technol., 2008, 19, 928 CrossRef CAS.
- L. Ricciotti, G. Roviello, O. Tarallo, F. Barbone, C. Ferone, F. Colangelo, M. Catauro and R. Cioffi, Int. J. Mol. Sci., 2013, 14, 18200 CrossRef PubMed.
- S. Ullah, M. A. Bustam, F. Ahmad, M. Nadeem, M. Y. Naz, M. Sagire and A. M. Shariff, J. Chin. Chem. Soc., 2015, 62, 182 CrossRef CAS.
- P. Li, H. D. Arman, H. Wang, L. Weng, K. Alfooty, R. F. Angawi and B. Chen, Cryst. Growth Des., 2015, 15, 1871 CrossRef CAS.
- E. Grothe, H. Meekes, E. Vlieg, J. H. ter Horst and R. de Gelder, Cryst. Growth Des., 2016, 16, 3237 CrossRef CAS.
- Ch. B. Aakeroy, M. E. Fasulo and J. Desper, Mol. Pharmaceutics, 2007, 4(3), 317 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Clarendon Press, Oxford, 1994 Search PubMed.
- S. SeethaLekshmi and T. N. G. Row, CrystEngComm, 2011, 13, 4886 RSC.
- L. Bian, H. Shi, X. Wang, K. Ling, H. Ma, M. Li, Z. Cheng, Ch. Ma, S. Cai, Q. Wu, N. Gan, X. Xu, Z. An and W. Huang, J. Am. Chem. Soc., 2018, 140, 10734 CrossRef CAS PubMed.
- S. Eppel and J. Bernstein, Cryst. Growth Des., 2009, 9, 1683 CrossRef CAS.
- Z. Xiu-Lian and Ch. Xiao-Ming, Cryst. Growth Des., 2005, 5, 617 CrossRef.
- S. Hisamatsu, H. Masu, M. Takahashi, K. Kishikawa and S. Kohmoto, Tetrahedron Lett., 2012, 53, 3903 CrossRef CAS.
- S. Kohmoto, S. Sekizawa, S. Hisamatsu, H. Masu, M. Takahashi and K. Kishikawa, Cryst. Growth Des., 2014, 14, 2209 CrossRef CAS.
- B. Zhou, Q. Zhao, L. Tang and D. Yan, Chem. Commun., 2020, 56, 7698 RSC.
- I. Karle, R. D. Gilardi, C. C. Rao, K. M. Muraleedharan and S. Ranganathan, J. Chem. Crystallogr., 2003, 33, 727 CrossRef CAS.
- G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1 CrossRef CAS.
- B. Bankiewicz and M. Palusiak, Comput. Theor. Chem., 2011, 966, 113 CrossRef CAS.
- R. Taylor, O. Kennard and W. Versichel, J. Am. Chem. Soc., 1984, 106, 244 CrossRef CAS.
- A. J. Rybarczyk-Pirek, M. Małecka and M. Palusiak, Cryst. Growth Des., 2016, 16(12), 6841 CrossRef CAS.
- B. Bankiewicz, P. Matczak and M. Palusiak, J. Phys. Chem. A, 2012, 116(1), 452 CrossRef CAS.
- CrysAlisPRO software system, Oxford Diffraction/Agilent Technologies UK Ltd, Yarnton, England, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849 CrossRef CAS.
- The Cambridge Crystallographic Data Centre, 12, Union Road, Cambridge CB2 1EZ, UK, https://www.ccdc.cam.ac.uk/conts/retrieving.html.
- M. Domagała, S. Simon and M. Palusiak, Int. J. Mater. Sci., 2022, 23(1), 233 Search PubMed.
- J. Dominikowska, A. J. Rybarczyk-Pirek and F. Guerra, Cryst. Growth Des., 2021, 21(1), 597 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- W. J. Radom, L. von R. Schleyer and P. Pople, J. AB INITIO Molecular Orbital Theory, John Wiley & Sons, Inc., Hoboken, NJ, USA, 1986 Search PubMed.
- K. B. Wiberg, J. Comput. Chem., 2004, 25, 1342 CrossRef CAS PubMed.
- M. J. Frisch, et al., GAUSSIAN09, Gaussian Inc., Wallingford, CT, USA, 2009 Search PubMed.
- T. A. Keith, AIMAll (Version 17.01.25), TK Gristmill Software, Overland Park, KS, USA, 2017, (https://aim.tkgristmill.com) Search PubMed.
Footnote |
| † CCDC 2166109 and 2166110. For crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00684g |
| This journal is © The Royal Society of Chemistry 2022 |