Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-pressure polymorphism in L-threonine between ambient pressure and 22 GPa†
Nico
Giordano
 ab,
Christine M.
Beavers‡
ab,
Christine M.
Beavers‡
 *bc,
Konstantin V.
Kamenev
*bc,
Konstantin V.
Kamenev
 d,
William G.
Marshall
e,
Stephen A.
Moggach§
d,
William G.
Marshall
e,
Stephen A.
Moggach§
 a,
Simon D.
Patterson
a,
Simon J.
Teat
a,
Simon D.
Patterson
a,
Simon J.
Teat
 *b,
John E.
Warren¶
*b,
John E.
Warren¶
 f,
Peter A.
Wood
f,
Peter A.
Wood
 g and
Simon
Parsons
g and
Simon
Parsons
 *a
*a
aCentre for Science at Extreme Conditions and EaStCHEM School of Chemistry, The University of Edinburgh, King's Buildings, West Mains Road, Edinburgh, Scotland EH9 3FD, UK. E-mail: S.Parsons@ed.ac.uk; Tel: +44 (0) 131 650 5804
bAdvanced Light Source, 1 Cyclotron Road, Lawrence Berkeley National Laboratory, Berkeley, CA 94720-8229, USA
cDepartment of Earth & Planetary Sciences, University of California, 1156 High Street Santa Cruz, Santa Cruz, CA 95064, USA
dCentre for Science at Extreme Conditions and School of Engineering, The University of Edinburgh, King's Buildings, West Mains Road, Edinburgh, Scotland EH9 3FD, UK
eISIS Pulsed Neutron and Muon Facility, STFC Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Harwell Oxford, Didcot OX11 0QX, UK
fSynchrotron Radiation Source, CCLRC Daresbury Laboratory, Warrington, Cheshire WA4 4AD, UK
gCambridge Crystallographic Data Centre, 12 Union Road, Cambridge, England CB2 1EZ, UK
First published on 9th May 2019
Abstract
The crystal structure of L-threonine has been studied to a maximum pressure of 22.3 GPa using single-crystal X-ray and neutron powder diffraction. The data have been interpreted in the light of previous Raman spectroscopic data by Holanda et al. (J. Mol. Struct. (2015), 1092, 160–165) in which it is suggested that three phase transitions occur at ca. 2 GPa, between 8.2 and 9.2 GPa and between 14.0 and 15.5 GPa. In the first two of these transitions the crystal retains its P212121 symmetry, in the third, although the unit cell dimensions are similar either side of the transition, the space group symmetry drops to P21. The ambient pressure form is labelled phase I, with the successive high-pressure forms designated I′, II and III, respectively. Phases I and I′ are very similar, the transition being manifested by a slight rotation of the carboxylate group. Phase II, which was found to form between 8.5 and 9.2 GPa, follows the gradual transformation of a long-range electrostatic contact becoming a hydrogen bond between 2.0 and 8.5 GPa, so that the transformation reflects a change in the way the structure accommodates compression rather than a gross change of structure. Phase III, which was found to form above 18.2 GPa in this work, is characterised by the bifurcation of a hydroxyl group in half of the molecules in the unit cell. Density functional theory (DFT) geometry optimisations were used to validate high-pressure structural models and PIXEL crystal lattice and intermolecular interaction energies are used to explain phase stabilities in terms of the intermolecular interactions.
1 Introduction
The amino acids have been studied extensively in the context of high-pressure polymorphism because they serve as model systems for the behaviour of H-bonding in other, potentially more complex molecules, but also in part because of their biological significance.1,2 Glycine, the simplest amino acid, has three ambient pressure polymorphs which show differing stabilities under compression. α-Glycine has been shown to be stable to 23 GPa by Raman spectroscopy.3 The crystal structure has been determined by X-ray single-crystal and neutron powder diffraction at 6.2 (ref. 4) and 6.4 GPa,5 respectively. Very recent angle-dispersive X-ray diffraction measurements show that the phase persists to 50 GPa.6 By contrast, β-glycine transforms to δ-glycine at 0.8 GPa, while the γ-form gradually yields the ε-polymorph between 2.0 and 4.3 GPa.4,7 ε-Glycine transforms back to the γ-form via a, sixth, short-lived ζ-polymorph.8L-Serine has four high-pressure polymorphs.9–14 The ambient pressure form, L-serine I, transforms to L-serine II and III on rapid compression at ca. 5 and 8 GPa and to L-serine IV above 5.6 GPa on slow compression.15L-Cysteine I transforms on compression above 1.8 GPa to give L-cysteine III and then again on decompression from 4.2 to 1.7 GPa to form L-cysteine IV.16 Structural changes in L-α-glutamine were studied to 4.9 GPa but it does not undergo any phase transitions.17L-Alanine also remains in the same ambient pressure phase on compression to 13.6 GPa but it undergoes reversible amorphisation at 15 GPa.18,19The role of H-bonding and other non-bonding interactions are important in understanding phase stability as a structure evolves under compression to fill space more efficiently and avoid short repulsive contacts.20 Crystallographic studies of complex molecular materials, however, rarely achieve pressures beyond 10 GPa. The Cambridge Structural Database (CSD) (v.4.0, November 2018) contains almost 3000 entries which specify the pressure of the structure determination, and a list of these is included in Microsoft Excel format in the ESI.† There are 2561 entries determined at above 10 atm, and 2457 above 1000 atm (0.1 GPa). Only 14 molecular compounds have been studied above 10 GPa (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm), only one of which is an amino acid, L-alanine (LALNIN51), whose structure was determined by powder methods at 13.6 GPa (see Table S1, ESI†).18 The highest pressure entry is that of CO2 at 28 GPa (SACBAA) which was also obtained by powder diffraction;21 the next highest pressure entry is that of benzene (BENZEN09) at 24 GPa but the entry lacks 3D coordinates.22 The highest pressure entry in the CSD of a complex molecular compound, determined by single-crystal diffraction and with refined 3D coordinates is that of palladium(II) oxathioether (NONWES30) at ca. 14 GPa.23
000 atm), only one of which is an amino acid, L-alanine (LALNIN51), whose structure was determined by powder methods at 13.6 GPa (see Table S1, ESI†).18 The highest pressure entry is that of CO2 at 28 GPa (SACBAA) which was also obtained by powder diffraction;21 the next highest pressure entry is that of benzene (BENZEN09) at 24 GPa but the entry lacks 3D coordinates.22 The highest pressure entry in the CSD of a complex molecular compound, determined by single-crystal diffraction and with refined 3D coordinates is that of palladium(II) oxathioether (NONWES30) at ca. 14 GPa.23
A search of the Inorganic Crystal Structure Database (ICSD) for non-metal compounds at pressures greater than or equal to 10 GPa results in 187 hits. Amongst the molecular elements,24–26 oxygen becomes metallic at 96 GPa.27 The structure of a high-pressure phase of molecular nitrogen has been determined by single-crystal X-ray diffraction at 56 GPa,25 and the structure of polymeric nitrogen, which forms at 110 GPa and 2000 K, has been determined using X-ray diffraction and Raman scattering at 115 GPa.28
Beyond the elements, there are 84 crystal structures of molecular solids at pressures greater than 10 GPa deposited in the ICSD, comprising 15 different compounds. Some notable examples include the single-crystal structure determinations of arsenolite and its helium clathrate to 30 GPa (ref. 29) and the van der Waals compound Kr(H2)4 whose structure was determined at 11.24 GPa.30 Xenon difluoride has been studied by powder X-ray diffraction and computational methods and is shown to undergo two phase transitions at 28 and 59 GPa, with metallisation predicted to occur at 152 GPa.31
Although crystal structures of complex molecular solids above 10 GPa are quite rare, spectroscopic methods, particularly Raman spectroscopy, have been very useful in detecting phase transitions. This approach has been used extensively to study amino acids.32 We now describe the crystal structure of L-threonine (Fig. 1) to 22.3 GPa with the aim of identifying the structural features associated with the three phase transitions which have been characterised by a series of Raman studies, most recently by Holanda et al.33
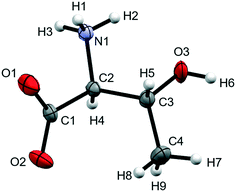 | ||
| Fig. 1 Molecular structure of L-threonine at ambient conditions showing the numbering scheme used. Ellipsoids are shown at the 50% probability level. | ||
2 Experimental
2.1 X-ray crystallography
L-Threonine (99% Sigma-Aldrich) was recrystallised from a 656 mM ethanol solution by slow evaporation; forming colourless, blade-shaped crystals. Single-crystal diffraction data were collected at ambient pressure and room temperature using a cut crystal measuring 0.2 × 0.2 × 0.1 mm3 on a Bruker 3-circle goniometer APEX-II diffractometer using Mo-Kα radiation (λ = 0.71073 Å).Below 7 GPa diffraction data were measured at room temperature using silicon (111) monochromated synchrotron radiation (λ = 0.4780 Å) on Station 9.8 at the Synchrotron Radiation Source, Daresbury, UK. A single crystal of L-threonine measuring ca. 0.1 mm3 was loaded in a Merrill-Bassett type diamond anvil cell (DAC) along with a ruby chip in 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–ethanol as a pressure-transmitting medium.34,35 A total of six diffraction measurements were carried out between 1.26 to 6.67 GPa using a Bruker-Nonius APEX II diffractometer following the collection strategy of Dawson et al.36
1 methanol–ethanol as a pressure-transmitting medium.34,35 A total of six diffraction measurements were carried out between 1.26 to 6.67 GPa using a Bruker-Nonius APEX II diffractometer following the collection strategy of Dawson et al.36
Single-crystal diffraction data between 4.0 and 22.3 GPa were measured at room temperature on Beamline 12.2.2 at the Advanced Light Source in Berkeley, California, USA, which has been described in detail elsewhere.37,38 Crystals measuring ca. 50 μm3 were cut from larger single crystals and mounted with a ruby sphere in a BX-90 type DAC39 consisting of 500 μm Boehler-Almax cut diamonds mounted in tungsten-carbide backing seats.40 The rhenium gasket hole had an initial diameter 320 μm and thickness of ca. 70 μm. The cell was gas-loaded in neon using a GSECARS/COMPRES gas-loader41 at the Advanced Light Source. Data were collected in steps of approximately 1.4 GPa; and on decompression at 13.0 GPa on a custom-built Huber diffractometer with silicon (111) monochromated synchrotron radiation (λ = 0.4959 Å) and a Perkin-Elmer amorphous silicon detector, using a combination of shutterless ϕ-scans at 0.25° and 1° step-widths across the half-opening angle (±40°) of the sample chamber and cell body. Additional low-pressure measurements were performed in the same manner from 2.6 to 5.9 GPa on a separate sample.
In all cases, pressure was measured using the ruby fluorescence method.42
2.2 Structure analysis
Diffraction data were processed using the APEX3 suite of programs.43 Data reduction was carried out using SAINT,44 employing dynamic masks generated by ECLIPSE45 to mask shaded detector areas. Absorption and shading corrections were applied using the multi-scan procedure SADABS.45 Data-sets were initially analysed using XPREP,46 the structures at ambient pressure and following a phase transition at 18.2 GPa were solved using direct methods (SHELXT)47 and then refined by full-matrix least-squares on |F|2 (SHELXL)48 using the ShelXLe graphical user interface.49 Otherwise refinements started from the atomic coordinates of the preceding pressure point.There is a single-crystal to single-crystal phase transition at 18.2 GPa which reduces the space group symmetry from P212121, to P21, though the unit cell metrics are similar either side of the transition. The structure was modelled with a two-fold axis about a as a twin law, but the twin fraction refined to 0.05(5). The orthorhombic cells of the structure below 18.2 GPa were placed in a non-standard setting to match that of the monoclinic phase in order to facilitate comparisons between phases.
Intramolecular bond distances in all high-pressure refinements were restrained to those of the ambient pressure structure. Data sets were modelled with isotropic displacement parameters in order to reduce the number of refined parameters. H-Atoms were placed in calculated positions and allowed to ride on their parent atoms. The hydroxyl hydrogen atom was placed on the site forming the most favourable H-bond geometry while also being staggered with respect to O3–C3. The refinement and H-atom placement strategies are discussed below. Selected crystal and refinement data of structures in the different phases are collected in Table 1. A full set of parameters for all structures collected over the course of this study are available in the ESI† (Table S2). CCDC 1903563–1903583 contains the supplementary crystallographic data for this paper.
| Pressure (GPa) | 0.00 | 2.05 | 3.23 | 8.50 |
|---|---|---|---|---|
| Phase | I | I | I′ | I′ |
| Crystal data | ||||
| Crystal system, space group | Orthorhombic, P212121 | Orthorhombic, P212121 | Orthorhombic, P212121 | Orthorhombic, P212121 |
| Temperature (K) | 298 | 296 | 296 | 298 |
| a, b, c (Å) | 5.1481(1), 13.6138(2), 7.7426(1) | 5.0359(6), 13.462(3), 7.2375(16) | 5.0055(2), 13.4104(9), 7.1162(4) | 4.879(3), 13.135(8), 6.658(6) |
| α, β, γ (°) | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 |
| V (Å3) | 542.64(2) | 490.67(16) | 477.68(5) | 426.7(5) |
| Radiation type | Mo Kα | Synchrotron, λ = 0.4780 Å | Synchrotron, λ = 0.4780 Å | Synchrotron, λ = 0.4959 Å |
| μ (mm−1) | 0.12 | 0.07 | 0.07 | 0.08 |
| Crystal size (mm) | 0.20 × 0.10 × 0.10 | 0.10 × 0.10 × 0.10 | 0.10 × 0.10 × 0.10 | 0.06 × 0.05 × 0.04 |
| Data collection | ||||
| Diffractometer | Bruker APEX-II CCD | Bruker-Nonius APEX II | Bruker-Nonius APEX II | Perkin-Elmer a-Si detector |
| Absorption correction | Multi-scan | Multi-scan | Multi-scan | Multi-scan |
| T min, Tmax | 0.676, 0.745 | 0.604, 0.744 | 0.629, 0.744 | 0.453, 0.744 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 5775, 1123, 1065 | 2455, 627, 542 | 2848, 738, 684 | 766, 227, 192 |
| R int | 0.025 | 0.055 | 0.041 | 0.089 |
| θ max (°) | 26.4 | 17.5 | 17.4 | 14.4 |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max (Å−1) θ/λ)max (Å−1) |
0.625 | 0.628 | 0.625 | 0.500 |
| Refinement | ||||
| R[F2 > 2σ(F2)], wR(F2), S | 0.026, 0.070, 0.82 | 0.064, 0.151, 1.09 | 0.062, 0.152, 1.05 | 0.062, 0.142, 1.08 |
| No. of parameters | 76 | 33 | 33 | 34 |
| No. of restraints | 0 | 17 | 17 | 17 |
| Δρmax, Δρmin (e Å−3) | 0.18, −0.13 | 0.33, −0.27 | 0.42, −0.31 | 0.26, −0.23 |
| Pressure (GPa) | 9.28 | 17.05 | 18.20 | 22.31 |
|---|---|---|---|---|
| Phase | II | II | III | III |
| Crystal data | ||||
| Crystal system, space group | Orthorhombic, P212121 | Orthorhombic, P212121 | Monoclinic, P21 | Monoclinic, P21 |
| Temperature (K) | 298 | 298 | 298 | 298 |
| a, b, c (Å) | 4.842 (6), 13.025 (17), 6.589 (12) | 4.768 (4), 12.883 (10), 6.353 (7) | 4.735 (5), 12.823 (13), 6.275 (8) | 4.620 (9), 12.52 (2), 6.037 (14) |
| α, β, γ (°) | 90, 90, 90 | 90, 90, 90 | 90, 91.14 (3), 90 | 90, 92.54 (4), 90 |
| V (Å3) | 415.5 (11) | 390.2 (6) | 380.9 (8) | 348.9 (12) |
| Radiation type | Synchrotron, λ = 0.4959 Å | Synchrotron, λ = 0.4959 Å | Synchrotron, λ = 0.4959 Å | Synchrotron, λ = 0.4959 Å |
| μ (mm−1) | 0.08 | 0.09 | 0.09 | 0.10 |
| Crystal size (mm) | 0.06 × 0.05 × 0.04 | 0.06 × 0.05 × 0.04 | 0.06 × 0.05 × 0.04 | 0.06 × 0.05 × 0.04 |
| Data collection | ||||
| Diffractometer | Perkin-Elmer a-Si detector | Perkin-Elmer a-Si detector | Perkin-Elmer a-Si detector | Perkin-Elmer a-Si detector |
| Absorption correction | Multi-scan | Multi-scan | Multi-scan | Multi-scan |
| T min, Tmax | 0.555, 0.744 | 0.408, 0.744 | 0.463, 0.744 | 0.610, 0.744 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 711, 329, 194 | 1101, 331, 208 | 901, 378, 305 | 334, 183, 156 |
| R int | 0.100 | 0.070 | 0.055 | 0.061 |
| θ max (°) | 18.1 | 18.1 | 16.1 | 14.3 |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max (Å−1) θ/λ)max (Å−1) |
0.625 | 0.627 | 0.558 | 0.499 |
| Refinement | ||||
| R[F2 > 2σ (F2)], wR(F2), S | 0.091, 0.245, 1.05 | 0.086, 0.228, 1.11 | 0.078, 0.192, 1.05 | 0.079, 0.196, 1.15 |
| No. of parameters | 34 | 33 | 67 | 66 |
| No. of restraints | 17 | 17 | 51 | 51 |
| Δρmax, Δρmin (e Å−3) | 0.36, −0.36 | 0.31, −0.34 | 0.30, −0.27 | 0.24, −0.30 |
2.3 Neutron powder diffraction at high pressure
In order to improve the precision of the equation of state (EOS) of L-threonine and to corroborate the X-ray measurements, a series of neutron powder diffraction measurements was collected on compression from 0.00 to 8.77 GPa in steps of ca. 0.55 GPa using the PEARL instrument at the ISIS facility, Rutherford Appleton Labs, Didcot, UK. Deuterated L-threonine (CDN Isotopes, used as received) was loaded into a TiZr capsule gasket with a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of deuterated methanol and ethanol, and a pellet of lead as a pressure marker. The sample was compressed using a type V3 Paris–Edinburgh cell with WC type anvils. Pressure measurements were obtained from the equation of state of lead.50 Unit cell parameters were extracted by the Pawley method using TOPAS.51
1 mixture of deuterated methanol and ethanol, and a pellet of lead as a pressure marker. The sample was compressed using a type V3 Paris–Edinburgh cell with WC type anvils. Pressure measurements were obtained from the equation of state of lead.50 Unit cell parameters were extracted by the Pawley method using TOPAS.51
2.4 PIXEL energy calculations
The PIXEL method is a semi-empirical computational technique for the calculation of lattice and intermolecular interaction energies in molecular crystal structures. The calculations are based on a pixelated model of the molecular electron densities within a cluster generated about a central reference molecule using the space group symmetry of the crystal structure. The interaction energies between the reference molecule and the other molecules in the cluster are obtained by summing the coulombic, polarisation, dispersion and repulsion terms between individual electron density pixels. The sum of energies within the cluster gives the lattice energy, and this is broken down into individual molecule–molecule contributions. The energies are also broken down into constituent coulombic, polarisation, dispersion and repulsion contributions. Full details of the method and its application are available in ref. 10 and 52–56.In this study the cluster radius was 15 Å, and the molecular electron densities were obtained from GAUSSIAN-09 (ref. 57) with the 6-31G** basis set at the MP2 level of theory. The PIXEL calculations themselves were accomplished with the CLP-PIXEL suite.54 The electron densities were calculated on a grid of dimensions 0.08 × 0.08 × 0.08 Å3, but in order to speed up subsequent energy calculations, blocks of 4 × 4 × 4 pixels were combined into superpixels (i.e. the condensation level was 4).
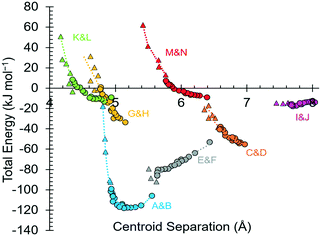
Individual intermolecular interaction energies obtained using PIXEL (and symmetry-adapted perturbation theory at the SAPT2+3 level, see below) are shown in Table 2 at ambient pressure and 17.1 GPa. A breakdown of the lattice energy at each pressure and a comparison of relative energies with those calculated by DFT (see below) are given in Tables S3 and S4 of the ESI.† Also available in the ESI† are listings of contact energies at 18.2 GPa (Tables S5 and S6†) and plots showing dimers formed within the first coordination spheres at 0, 17.1 and 18.2 GPa in Fig. S1–S4.†
| Label | Symmetry | Pressure (GPa) | Centroid | Coulombic | PIXEL | Repulsion | Total | SAPT 2+3 | Contacts | |
|---|---|---|---|---|---|---|---|---|---|---|
| Distance (Å) | Polarization | Dispersion | Total | |||||||
| A/B | 1/2 − x, 1 − y, 1/2 + z | 0.00 | 5.555 | −93.9 | −30.3 | −20.3 | 38.7 | −105.8 | −119.3 | N1H3⋯O2 = 1.94 Å |
| 1/2 − x, 1 − y, −1/2 + z | 17.05 | 4.960 | −150.7 | −58.4 | −41.9 | 144.8 | −106.2 | −118.4 | N1H3⋯O2 = 1.98 Å | |
| C/D | 1 − x, −1/2 + y, 3/2 − z | 0.00 | 6.965 | −82.6 | −32.6 | −11.7 | 71.8 | −55.1 | −59.9 | O3H6⋯O1 = 1.87 Å |
| 1 − x, 1/2 + y, 3/2 − z | 17.05 | 6.583 | −109.4 | −51.5 | −17.4 | 137.7 | −40.6 | −43.8 | O3H6⋯O1 = 1.73 Å | |
| E/F | 3/2 − x, 1 − y, 1/2 + z | 0.00 | 6.432 | −41.7 | −8.7 | −7.3 | 4.7 | −53.0 | −55.6 | N1H3⋯O1 = 2.65 Å |
| 3/2 − x, 1 − y, −1/2 + z | 17.05 | 5.633 | −101.3 | −35.7 | −22.9 | 73.9 | −86.0 | −85.5 | O1⋯H3(N1)/H2(N1) = 1.92/2.50 Å | |
| G/H | 1 + x, y, z | 0.00 | 5.148 | −23.5 | −27.0 | −20.9 | 37.7 | −33.6 | −26.8 | N1H1⋯O2 = 2.04 Å |
| −1 + x, y, z | 17.05 | 4.768 | −51.0 | −58.7 | −44.5 | 153.1 | −1.0 | 17.9 | N1H1⋯O2 = 1.83 Å | |
| I/J | −x, 1/2 + y, 3/2 − y | 0.00 | 8.031 | −9.4 | −2.5 | −1.9 | 0.1 | −13.7 | −13.4 | C4H7⋯O2 = 3.59 Å |
| −x, −1/2 + y, 3/2 − y | 17.05 | 7.677 | −10.4 | −4.4 | −3.5 | 1.7 | −16.6 | −18.1 | C4H7⋯O2 = 2.97 Å | |
| K/L | 1/2 + x, 1/2 − y, 1 − z | 0.00 | 4.934 | −3.6 | −12.9 | −21.9 | 29.4 | −9.0 | −5.6 | N1H2⋯O3 = 2.31 Å |
| −1/2 + x, 1/2 − y, 1 − z | 17.05 | 4.344 | −49.8 | −47.3 | −47.7 | 153.5 | 8.5 | 19.3 | N1H2⋯O3 = 2.04 Å | |
| M/N | −1/2 + x, 1/2 − y, 2 − z | 0.00 | 6.391 | −5.0 | −2.7 | −9.9 | 8.5 | −9.0 | −8.3 | C4H7⋯H5(C3) = 2.42 Å |
| 1/2 + x, 1/2 − y, 2 − z | 17.05 | 5.767 | −16.5 | −17.3 | −22.8 | 64.0 | 7.3 | 2.5 | C4H7⋯H5(C3) = 1.88 Å | |
2.5 Periodic density functional theory (DFT) calculations
Geometry optimisations were carried-out on the ambient pressure crystal structure as well as those at 3.97, 5.91, 6.12, 8.50, 9.82, 11.19, 13.94, 15.20, 15.78, 17.05, 18.20, 20.62 and 22.31 GPa, using the plane-wave pseudopotential method in the CASTEP58 code as incorporated in Materials Studio.59 The PBE exchange-correlation functional was used with the ‘on the fly’ pseudopotentials embedded in the program and the Tkatchenko–Scheffler correction for dispersion.60 The basis set cut-off energy was 780 eV and Brillouin zone integrations were performed with a Monkhorst–Pack61k-point grid spacing of 0.07 Å−1. These conditions gave a convergence in total energy of better than 1 meV per atom.The starting coordinates for the optimisations were taken from the single-crystal X-ray diffraction structures with distances to hydrogen normalised to typical neutron values. The cell dimensions were fixed to the experimental values, and the space group symmetry was retained. In geometry optimisations the energy convergence criterion was 5 × 10−6 eV per atom, with a maximum force tolerance of 0.01 eV Å−1 and a maximum displacement of 5 × 10−4 Å; the SCF convergence criterion was 1 × 10−8 eV per atom.
2.6 Symmetry-adapted perturbation theory (SAPT) calculations
SAPT calculations were performed at the SAPT2+3 level of theory on dimers taken from the ambient pressure and 17.1 GPa structures using the PSI4 code (version 1.0.54) with the aug-cc-pvdz basis set.62,632.7 Other programs used
Geometric parameters were calculated using PLATON.64 EoSFit7-GUI65 was used for EOS calculations. OLEX2–1.2,66 DIAMOND 3.0 (ref. 67) and MERCURY (CCDC)68 were used for structure visualisation. CONQUEST69 was used to survey the CSD and MR_PIXEL70 was used to facilitate setting-up of PIXEL calculations. Topology calculations were accomplished with TOPOSPRO.712.8 Validation of computational methods
In the following analysis, the results of PIXEL calculations are used to interpret the structural changes occurring on compression. The use of this method has been validated by comparison of lattice energy of L-threonine with the experimental value, by comparing the total energies of the compressed structures with those obtained by DFT calculations, and finally by comparing individual molecule–molecule energies at ambient pressure and 17.1 GPa with values obtained with symmetry adapted perturbation theory.The experimental enthalpy of sublimation of L-threonine is 161 kJ mol−1 at 298.15 K,72 but once proton transfer between the ammonium and carboxylate groups during sublimation is taken into account,73 the energy of sublimation of zwitterionic L-threonine is 270.7 ± 7 kJ mol−1, which compares with the PIXEL value of 252.0 kJ mol−1.
The pressure-dependence of the lattice energy of L-threonine was calculated using the PIXEL method and periodic DFT (see section 3.4.1 and Table S4 in the ESI†). The goodness-of-fit of the PIXEL calculated energies from ambient pressure to 22.3 GPa is 0.85, which improves to 0.93 if the highest-pressure structure is discounted.
Individual intermolecular interaction energies obtained using PIXEL and symmetry-adapted perturbation theory at the SAPT2+3 level are shown in Table 2 at ambient pressure and 17.1 GPa. At ambient pressure the mean (and median) differences are 1.4(−6.8) kJ mol−1; the corresponding figures at 17.1 GPa are −1.2 (1.3) kJ mol−1. The largest difference at 17.1 GPa is in interaction G/H, for which the PIXEL and SAPT energies are −1.0 and +17.9 kJ mol−1, respectively.
3 Results & discussion
3.1 Phase behaviour
The X-ray crystal structure of L-threonine was first determined by Shoemaker in 1950.74 It exists as a zwitterion in the solid–state with charged carboxylate and ammonium groups situated on the α-carbon (C2) and a hydroxyl and methyl group on the β-carbon (C3) with the chemical formula C4H9NO3. L-Threonine crystallises in the space group P212121 with four molecules in the unit cell (Z′ = 1) at ambient pressure and temperature, with the unit cell parameters: a = 5.14810(10) Å, b = 13.6138(2) Å, c = 7.74260(10) Å and V = 542.642(15) Å3. The atom labelling, which follows Shoemaker's work, is given in Fig. 1.The phase behaviour of L-threonine has been most recently studied using Raman spectroscopy by Holanda et al., who inferred three structural phase transitions at ca.2 GPa, between 8.2 and 9.2 GPa and between 14.0 and 15.5 GPa based on changes in the slopes of frequency-pressure plots and the splitting, appearance or disappearance of bands.33 We shall label the phases formed in these transitions I′, II and III, respectively. Over the course of this and two earlier Raman studies the transition to phase I′ had been observed between 1.1 and 1.6 GPa,33 at 1.9 GPa (in D-threonine)75 and at 2.2 GPa,76 the authors ascribing these differences to the influence of the different pressure-transmitting media used in the three studies (methanol–ethanol, Nujol and argon).
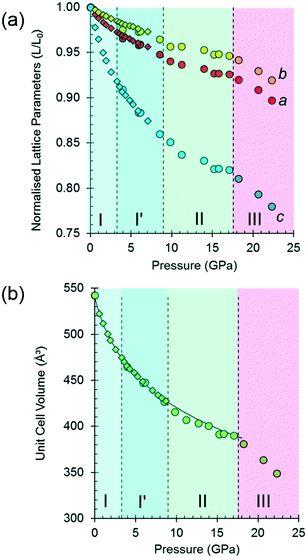
The variation of the unit cell volume and dimensions with pressure is shown in Fig. 2. The structure remains orthorhombic, space group P212121, from ambient pressure to 17.1 GPa, i.e. throughout the range for phases I, I′ and II,33 and it is clear that the structures of these phases are very closely related.
The discontinuity between 17.1 and 18.2 GPa, seen in all four curves, corresponds to the transition from phase II to III, which occurred between 14.0 and 15.5 GPa in Holanda's study. The difference in the transition pressure may, as these authors suggest, be the result of the influence of the pressure-transmitting medium (Ne in our case). Alternatively, it may reflect the sensitivity of spectroscopic methods to local structural changes, as was the case in [Cu(pyrazine)(H2O)2F2], where premonitory disordering of Jahn–Teller directions, observed by high pressure electron paramagnetic resonance, was not evident in the average structure obtained by analysis of Bragg scattering in single-crystal diffraction measurements.77
At 17.1 GPa the unit cell dimensions of phase II are a = 4.768(4), b = 12.883(10), c = 6.353(7) Å, V = 390.2(6) Å3, representing a volume reduction of 28% compared to the ambient-pressure structure. The cell dimensions after the transition to phase III at 18.2 GPa are a = 4.735(5), b = 12.823 (13), c = 6.275(8) Å, β = 91.14(3)°, V = 380.9 (8) Å3, so that after the phase transition, though the 21 operations along the a and c directions are lost, the translational symmetry of the lattice is preserved and Z is still equal to four, but Z′ = 2. The structure remains in phase III up to 22.3 GPa, the highest pressure reached in this study. At 22.3 GPa the unit cell volume is 348.9(12) Å3, representing a 36% reduction compared to ambient pressure. Pressure release from 22.3 GPa to 13.0 GPa re-forms phase II. Further X-ray decompression measurements were not performed, but Holanda's Raman measurements indicate full reversibility from 27 GPa to ambient pressure.
Fitting the pressure–volume data of L-threonine-d9 I and I′ obtained in the neutron powder diffraction experiment to a Vinet equation of state78 gives values of the bulk modulus (K0) and its first derivative (K′) of 15.23(8) GPa and 7.97(6), respectively. The zero-pressure volume in this fit was fixed to 540.236 Å3 and χ2 was 1.94. The bulk modulus of L-threonine is comparable to other hydrogen bonded amino acids, e.g.L-serine I is 23.4 GPa and those of polymorphs II and III are 14.7 and 13.9 GPa;79 and that of L-alanine is 13.1(6) GPa.18
Superposition of the equation of state curve on all the pressure–volume points collected in this study between ambient pressure and 17.1 GPa shows the points between 9.8 and 17.1 GPa lie to systematically lower volume, pointing to the formation of phase II between 8.7 and 9.8 GPa. This is consistent with the phase I′ to II transition observed between 8.2 and 9.2 GPa by Holanda et al.,33 albeit with a more subtle signature than the transition to phase III. The transition is also marked by a small discontinuity in the b-axis length [Fig. 2(a)].
It will be seen from Fig. 2(b) that all the points between ambient pressure and 8.7 GPa are consistent with the same equation of state, and there appears to be little indication in the plots for the I to I′ transition proposed by Holanda et al. near 2 GPa (see also below).
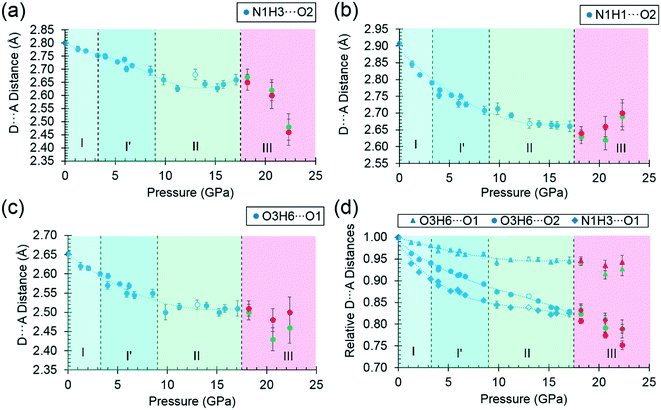
3.2 The effects of pressure on the intramolecular structure
High pressure data sets almost always suffer from low completeness as a result of the limited scattering geometry of the diamond anvil cell. Accordingly, the data-sets of threonine-I, I′ and II collected here had completenesses of between 43 and 73%, the corresponding figures for the lower symmetry phase III were 32–45%. As a result, it is usually necessary to place restraints on the structure refinements, and bond distances and angles were restrained to values observed at ambient pressure.In order to assess the suitability of the restraints applied, the structures of phase I at ambient pressure and phase III at 22.3 GPa were optimised by periodic DFT. The calculations indicated that bond distances change by as much as 0.071 Å, and bond angles by 5.43° (see Table S7 in the ESI†), while the root-mean-square deviations between the optimised and experimental molecular structures were 0.0284 and 0.131 Å, respectively (see Tables S9 and S10 in the ESI,† which also contains further comparison data). Use of the optimised model as a freely rotating rigid body in the refinement against the 22.3 GPa data set lowered the R-factor, but only slightly (0.17% for 183 reflections), so that it is not possible to state definitively whether the intramolecular bond distances and angles are significantly affected by pressure, as the differences are beyond the resolution of the data obtained in this study.
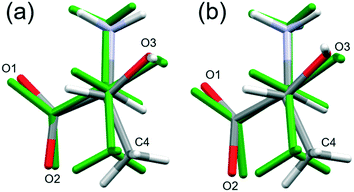
By contrast, the torsion angles do vary significantly with pressure. Fig. 3 shows differences in conformation between the ambient pressure and highest-pressure molecular structures, with differences apparent about the carboxylate, hydroxyl and methyl groups. Holanda et al. noted that the most prominent changes in the Raman spectra of threonine with pressure were associated with vibrations of the carboxylate moiety. The variation of the orientation of the carboxylate group with pressure, represented by the O2–C1–C2–C3 torsion angle (τ), is shown in Fig. 4. The features in these plots correlate with the phase transitions suggested by Holanda et al. and described in section 3.1.
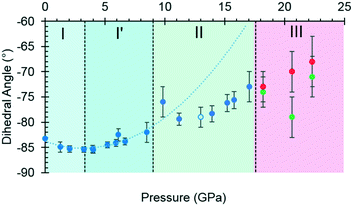 | ||
| Fig. 4 The O2–C1–C2–C3 torsion angle (τ) as a function of pressure. The green and red circles in phase III represent molecules A and B, and the open circle represents the decompression measurement. A second order polynomial was fitted to phase I and I′ data, the minimum of the parabolic function was determined to be −85.0° at 3.3 GPa. Extrapolating the curve to 17.1 GPa serves to highlight the slower rate of change exhibited in phase II. Plots of other torsion angles against pressure are available in the ESI.† | ||
Between 0.0 and 2.1 GPa τ decreases from −83.2(2)° to −85.3(6)°, but this trend appears to reverse between 2.1 and 3 GPa. These changes are small, but the pressure at which they occur is the same as the I to I′ transition inferred from the Raman data. The small magnitude of the change is consistent with lack of any obvious signature in the cell dimensions or volume at this pressure.
Beyond 3 GPa the value of τ continues to become more positive, but between 8.5 and 9.8 GPa it changes dramatically from −82(1)° to −76(2)°, the trend flattening-off again between 9.8 and 17.1 GPa. These changes coincide with the transition from phase I′ to II. The standard uncertainties of τ become large above the phase II to III transition at 17.1 GPa. However, with the change in Z′ from 1 to 2, it appears that the value continues to become gradually more positive in one molecule (molecule B) but more negative in the other.
Although H-atoms could not be located in difference maps, the changes in the positions of acceptor atoms imply that there is also a change in the orientation of the hydroxyl moiety over the course of the II to III transition. Hydrogen atoms were placed in calculated positions (see section 2), and based on this approach the torsion C4–C3–O3–H6 changes from −50° in phase II to −60° in molecule A, and to −78° in molecule B in phase III. The change in the position of H6 is also seen in DFT optimisations, but is less pronounced (Table S11 and Fig. S8 in ESI†); the corresponding torsional changes over the course of the II to III transition are: −45 to −41° and −47° in molecules A and B, respectively. The implications of the change in position of H6 are discussed in section 3.4.3.
3.3 Intermolecular interactions at ambient pressure
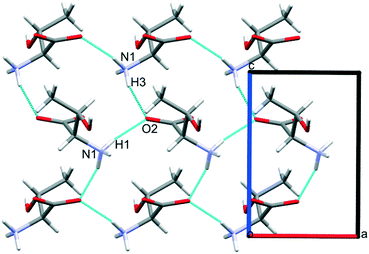
Intermolecular interaction energies in phase I at ambient pressure are listed in Table 2, where contacts are ordered by interaction energy and grouped in symmetry-equivalent pairs. Table 2 also lists the breakdown of the molecule–molecule energies into component coulombic, polarization, dispersion and repulsion terms obtained from the PIXEL calculations. Validation of the PIXEL results against those of other methods is described in section 2.8. Given that the PIXEL method is semi-empirical and developed using ambient-pressure structural and thermodynamic data, the level of agreement with other methods is remarkable.The strongest contacts comprising four pairs of crystallographically unique interactions labelled A/B–G/H. The strongest (A/B; −105.8 kJ mol−1) involves molecules connected by N1H3⋯O2 hydrogen bonds, with a hydrogen-acceptor separation of 1.94 Å forming a primary-level C(5) chain which runs along c. Interactions G and H involving N1H1⋯O2 hydrogen bonds (2.04 Å, −33.6 kJ mol−1) form a second primary-level C(5) chain which runs along a. The combination of these two C(5) chains generates a layer in the ac plane (Fig. 5).
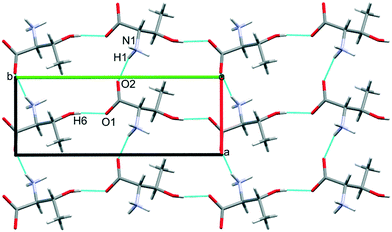
The third dimension of the H-bond network is completed by C(6) chains formed by O3H6⋯O1 hydrogen bonds between the carboxylate and hydroxyl groups along b, see Fig. 6 [interaction C/D in Table 2, the hydrogen-acceptor distance is 1.87 Å and the energy is −55.1 kJ mol−1]. This is the second most stabilising interaction in the ambient pressure structure. The coulombic interaction is almost as strong as in the A/B contacts (−82.6 versus −93.9 kJ mol−1), but the repulsion term is also much more positive (+71.8 versus 38.7 kJ mol−1), so that, paradoxically, the interaction with the shorter H-bond is also the less stabilising.
Interactions E and F are strongly stabilising, with an energy of −53.0 kJ mol−1 but featuring a rather long N1H3⋯O1 contact of 2.65 Å with a <N1H3⋯O1 angle of only 110.4°. This angle is too tight for a H-bond,80 and the component energies show that the interaction is predominantly coulombic with a much smaller dispersion contribution than the hydrogen bonds described above. The contact is therefore better regarded as a long-range intra-layer electrostatic contact than a hydrogen bond. This interaction has an important influence on the compression of L-threonine, as described in the following section.
The hydrogen bonding scheme described above appears to leave the potentially strong donor N1H2 unbound. There is an additional C(5) chain connected by N1H2⋯O3 interactions (labelled K and L in Table 2) though the DH⋯X separation is quite long at 2.31 Å. The contact has a modest coulombic component and is dominated by the dispersion term. It has an interaction energy of only −9.0 kJ mol−1. The low value of the coulombic contribution can be ascribed to the juxtaposition of both positive and negative regions of the electrostatic potentials of the contacting molecules.
In addition to the contacts listed above there are two pairs of longer-range interactions (I/J and M/N) with energies of −13.7 and −9.0 kJ mol−1 and H⋯O distances of between 3.59 and 2.42 Å. Topological analysis based on Voronoi–Dirichlet partitioning indicates that interactions I/J lie outside the first coordination sphere, a finding consistent with the low contributions of dispersion and repulsion to the energy of this interaction. The molecular centroids define a coordination sequence of 12–42–92, which is characteristic of an underlying face centred cubic topology. This arrangement persists at high pressure. Plots of the first coordination spheres at 0, 17.1 and 18.2 GPa are given in Fig. S5 in the ESI.†
3.4 The effects of pressure on intermolecular interactions
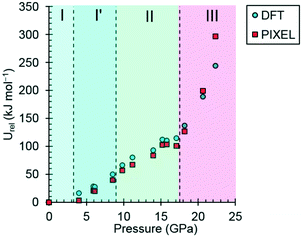 | ||
| Fig. 7 The variation of the lattice energy of threonine with pressure. The points are relative to ambient pressure (Urel). | ||
In phases I, I′ and II the lattice energies increase steadily with increasing pressure, which is expected as repulsion contributions increase as molecules are forced into close proximity. There is a discontinuity in the gradient at the II to III phase transition at 18.2 GPa leading to a sharp destabilisation of the lattice energy. Examination of the contributions of the interactions in the first coordination sphere to the lattice energy (Fig. 8) shows that all except the symmetry-related pair E and F are driven into destabilising regions of their potentials, that of the strongest H-bonding interaction A/B being particularly steep.
Based on the trends seen in Fig. 7, the lattice energy of phase II at 18.2 GPa would be expected to be approximately −126 kJ mol−1, compared to −124.9 kJ mol−1 for the observed phase III. Although phase III is less stable than phase II in terms of internal energy, at 18.2 GPa, the difference in molecular volume is 2.3 Å3. This figure, though apparently modest, contributes a pΔV term of −25 kJ mol−1 to the free energy change of the transition, which more than compensates for the change in lattice energy. Like most high-pressure phase transitions, therefore, the II to III transition in threonine is driven by the need to fill space efficiently at high pressure.
By far the biggest change within the ac layers occurs in interaction E/F. Between 0 and 9.82 GPa the N1H3⋯O1 distance in this interaction changes from 2.65 Å to 2.03 Å. The N1H3⋯O2 distance of interaction A/B barely varies over the same pressure range. The angles subtended at H3 in the two interactions are respectively 110.4 and 162.7° at ambient pressure and 120.9° and 136.2° at 9.8 GPa. Interactions E/F thus change from being long-range coulombic contacts at ambient pressure to ones mediated by a bifurcated H-bond at 9.8 GPa.
The change can be viewed as the positively-charged H3 adjusting its position within the large and strongly negative region of the combined electrostatic potentials of the molecules involved in interactions A/B and E/F. The interaction energy becomes simultaneously more negative, the only stabilising change to occur on compression, providing a lower energy pathway for the structure to accommodate compression. Since interactions E and F are generated by a screw axis along c, the c-axis compresses substantially more than either the a or b-axes (Fig. 2(a)). The gradual bifurcation of H3 reflects Holanda and co-workers' comment that the I′ to II transition is the final result of a long process which affects the carboxylate rocking motion from about ca. 4.8 GPa.33 Crystallographically, we can see that by this stage the H3⋯O1 distance is already around 2.3 Å.
While the principal structural effect of the I′ to II transition is seen in interactions E/F, effects are also seen in the other interactions formed in the ac plane. The H-bonded dimers A/B are also slightly stabilised by the bifurcation of H3 while in phase I′, but the energy begins to increase rapidly after the I′ to II phase transition. Similar comments apply to interactions G/H, which actually becomes repulsive in phase III.
The lengths of the a and c axes undergo more rapid compression after the II to III transition. The animation of the pressure series shows that the loss of the 21 axes along a and c, which occurs during the transition, enables neighbouring rows of molecules linked by N1H3⋯O2 to shift in alternate directions enabling them to approach more closely, and the molecules to pack more efficiently. The lowering of symmetry illustrates Dove's comment that high-pressure phase transitions generally favour distorted phases in order to maximise density.81
The C/D interaction energy does not show any initial stabilisation with pressure, in contrast to interactions A/B and E/F, a consequence, perhaps, of the repulsion term, which is appreciable even at ambient pressure. The energy becomes more positive as the pressure increases and does not exhibit any major discontinuities at the phase transitions.
The O3H6⋯O1 H-bond shortens steadily from 1.87 Å at ambient pressure to 1.77 Å at 8.50 GPa. The distance between H6 and the O2 atom of the same carboxylate group falls below 3 Å at 8.50 GPa, but is still very unsymmetrical at this stage, the angles subtended at H6 to O1 and O2 being 158.4 and 129.5°, respectively. The transition from phase I′ to II is marked by greater translational movement of the neighbouring rows generated by lattice repeats along a relative to each other. The compression of the O3H6⋯O2 H-bond begins to level-off at this point, to be replaced by an increasing bifurcation of H6. At 9.82 GPa the H6⋯O1 and O2 distances are 1.73 and 2.91 Å, and the corresponding angles at H6 are 156.9 and 128.5°. By 17.1 GPa the H6⋯O2 distance has shortened to 2.73 Å, though without much change in the other parameters (H6⋯O1 = 1.73 Å, angles at H6 are 128.3 and 159.6°). Thus, the phase I′ to II transition is marked along the b axis by a change in the way that the structure accommodates the applied pressure.
The symmetry reduction that occurs in the phase II to III transition is marked by a change in the orientation of the hydroxyl group in half of the molecules. The molecules labelled A retain the conformation of phase II, while H6B become more clearly bifurcated, so that at 18.2 GPa the O3BH6B⋯O1B increases to 1.97 Å, O3BH6B⋯O2B decreases to 2.62 Å, and respective angles at H6B are 122.1 and 129.8°. The corresponding parameters for the ‘A’ molecules are like those in phase II: 1.77 Å, 2.70 Å, 146.8° and 129.5°. The structural signature of the II to III transition is thus similar to the I′ to II transition in that it involves the bifurcation of a hydrogen bond. The difference between the transitions is that the change occurs in one pressure step, rather than being gradual, and involves a change in molecular conformation.
4 Conclusions
The crystal structure of L-threonine has been determined up to 22.3 GPa, one of the highest pressures ever achieved for a complex molecular material, providing amongst the most detailed information beyond 10 GPa ever published for this type of system.The structure undergoes two isosymmetric phase transitions on compression between 0.0 and 17.1 GPa. The ambient pressure phase I transforms to phase I′ between 2.1 and 3.0 GPa, the result of a subtle reorientation of the carboxylate group. The transformation of phase I′ to phase II between 8.5 and 9.8 GPa follows a gradual transformation of a long-range coulombic interaction into one mediated by a bifurcated hydrogen bond. The transition therefore reflects a change in the way the structure absorbs pressure rather than a distinct structural change, and in this regard it is somewhat akin to a second order thermal event such as a glass transition.
Further compression results in the transformation to phase III between 17.1 and 18.2 GPa. The II to III transition is driven by a discontinuous reduction in volume and is characterised by the rotation and bifurcation of the hydroxyl groups in half of the molecules in the unit cell.
The crystallographic results are consistent to those seen in the earlier Raman studies. Indeed, the interpretation of the crystallographic data has been substantially guided by the Raman results of Holanda et al.33 While the phase II to III transition involves a discontinuous change in volume and symmetry, phases I, I′ and II are all very similar, and the designation of these forms as separate phases is based on discontinuities of the trends seen in Holanda et al.'s Raman spectra with increasing pressure. In particular, the I and I′ transition is not at all obvious from examination of the crystallographic data alone, and it would probably have been missed without the Raman data. This said, while Raman spectra have proved to be an extremely sensitive tool for detecting the phase transitions, they are a less definitive guide to the magnitude of the structural changes.
Above 17.1 GPa the crystal structure of L-threonine destabilises rapidly. Holanda's Raman spectra suggest that the material remains crystalline to at least 27 GPa, but the ultimate response of a relatively complex crystal structure such as threonine to very rapid onset of destabilisation is largely unexplored territory. One possibility is amorphisation, as seen for L-alanine at 15 GPa.18 Cleavage of primary covalent bonds forms another potential route, exemplified by proton transfer in oxalic acid at 5.3 GPa,82 or even wholescale decomposition into amorphous networks such as is seen for benzene83,84 and pyridine.85,86
Although the hydrogen bonds in L-threonine are substantially compressed up to 22.3 GPa, it is remarkable that their distances all find precedents at ambient pressure, and none of them can be described as ‘abnormally short’ (Fig. 10). In the 5064 structures of amino acids, peptides and complexes in the CSD (v5.40 November 2018) there are 2105 individual hydrogen bond lengths (ca. 5%) which are equal to or shorter than the shortest hydrogen bond length in L-threonine at 22.3 GPa. This is in spite of a reduction in unit cell volume by over one-third. Hydrogen bonds are the strongest and most consistently-formed intermolecular interactions in organic crystal structures, and this study reveals that their robustness persists well above 10 GPa, even in relatively complex molecular crystals.
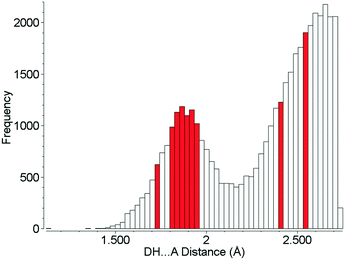 | ||
| Fig. 10 Hydrogen bond distances formed in the crystal structures of amino acids. Red bars show H-bond distances observed in L-threonine at 22.3 GPa. | ||
It has been shown that the strongest intermolecular interactions generally persist across phase transitions.87,88 However, the drive to reduce volume becomes ever more pressing as pressure is increased, leading to a perturbation in the hierarchy of intermolecular interactions. It will be fascinating to discover the point at which this effect finally wins out and hydrogen bonds give up the ghost.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. CMB and beamline 12.2.2 are supported by the Consortium for Materials Properties Research in Earth Sciences (COMPRES) under NSF Cooperative Agreement EAR 1606856. We also gratefully acknowledge The STFC (UK) for provision of beamtime at SRS Daresbury Laboratory and the ISIS Facility. NG is supported by an EPSRC Doctoral Training Account studentship (No. 1637415) and an ALS Doctoral Fellowship. SDP was supported by an EPSRC Doctoral Training Account studentship and the Cambridge Crystallographic Data Centre. We also thank Mr Matthew Reeves (University of Edinburgh) for his assistance with his program MR_PIXEL which facilitates preparation of data for PIXEL calculations. Computational work made use of high performance computing facilities at The University of Edinburgh.References
- C.-H. Görbitz, Crystallogr. Rev., 2015, 21, 160–212 CrossRef.
- S. A. Moggach, S. Parsons and P. A. Wood, Crystallogr. Rev., 2008, 14, 143–184 CrossRef CAS.
- C. Murli, S. M. Sharma, S. Karmakar and S. K. Sikka, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 339, 23–30 CrossRef CAS.
- A. Dawson, D. R. Allan, S. A. Belmonte, S. J. Clark, W. I. F. David, P. A. McGregor, S. Parsons, C. R. Pulham and L. Sawyer, Cryst. Growth Des., 2005, 5, 1415–1427 CrossRef CAS.
- A. Shinozaki, K. Komatsu, H. Kagi, C. Fujimoto, S. Machida, A. Sano-Furukawa and T. Hattori, J. Chem. Phys., 2018, 148, 044507 CrossRef PubMed.
- J. K. Hinton, S. M. Clarke, B. A. Steele, I. F. W. Kuo, E. Greenberg, V. B. Prakapenka, M. Kunz, M. P. Kroonblawd and E. Stavrou, CrystEngComm, 2019 10.1039/c8ce02123f , Ahead of Print.
- S. A. Moggach, W. G. Marshall, D. M. Rogers and S. Parsons, CrystEngComm, 2015, 17, 5315–5328 RSC.
- C. L. Bull, G. Flowitt-Hill, S. de Gironcoli, E. Küçükbenli, S. Parsons, C. H. Pham, H. Y. Playford and M. G. Tucker, IUCrJ, 2017, 4, 569–574 CrossRef CAS PubMed.
- S. A. Moggach, D. R. Allan, C. A. Morrison, S. Parsons and L. Sawyer, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 58–68 CrossRef PubMed.
- P. A. Wood, D. Francis, W. G. Marshall, S. A. Moggach, S. Parsons, E. Pidcock and A. L. Rohl, CrystEngComm, 2008, 10, 1154–1166 RSC.
- E. V. Boldyreva, E. N. Kolesnik, T. N. Drebushchak, H. Sowa, H. Ahsbahs and Y. V. Seryotkin, Z. Kristallogr., 2006, 221, 150 CAS.
- T. N. Drebushchak, H. Sowa, Y. V. Seryotkin, E. V. Boldyreva and H. Ahsbahs, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o4052–o4054 CrossRef CAS.
- S. A. Moggach, W. G. Marshall and S. Parsons, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 815–825 CrossRef PubMed.
- E. V. Boldyreva, H. Sowa, Y. V. Seryotkin, T. N. Drebushchak, H. Ahsbahs, V. Chernyshev and V. Dmitriev, Chem. Phys. Lett., 2006, 429, 474–478 CrossRef CAS.
- M. Fisch, A. Lanza, E. Boldyreva, P. Macchi and N. Casati, J. Phys. Chem. C, 2015, 119, 18611–18617 CrossRef CAS.
- S. A. Moggach, D. R. Allan, S. J. Clark, M. J. Gutmann, S. Parsons, C. R. Pulham and L. Sawyer, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 296–309 CrossRef PubMed.
- P. Lozano-Casal, D. R. Allan and S. Parsons, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 466–475 CrossRef CAS PubMed.
- N. P. Funnell, W. G. Marshall and S. Parsons, CrystEngComm, 2011, 13, 5841–5848 RSC.
- N. A. Tumanov, E. V. Boldyreva, B. A. Kolesov, A. V. Kurnosov and R. Quesada Cabrera, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 458–471 CrossRef CAS PubMed.
- R. D. L. Johnstone, D. Francis, A. R. Lennie, W. G. Marshall, S. A. Moggach, S. Parsons, E. Pidcock and J. E. Warren, CrystEngComm, 2008, 10, 1758–1769 RSC.
- C. S. Yoo, H. Kohlmann, H. Cynn, M. F. Nicol, V. Iota and T. LeBihan, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104103 CrossRef.
- M. M. Thiéry and J. M. Léger, J. Chem. Phys., 1988, 89, 4255–4271 CrossRef.
- J. P. Tidey, H. L. S. Wong, J. McMaster, M. Schroder and A. J. Blake, Acta Crystallogr., Sect. B: Struct. Sci., 2016, 72, 357–371 CrossRef CAS PubMed.
- F. Datchi and G. Weck, Z. Kristallogr. - Cryst. Mater., 2014, 229, 135 CAS.
- R. Turnbull, M. Hanfland, J. Binns, M. Martinez-Canales, M. Frost, M. Marqués, R. T. Howie and E. Gregoryanz, Nat. Commun., 2018, 9, 4717–4717 CrossRef PubMed.
- Y. Akahama, M. Nishimura, H. Kawamura, N. Hirao, Y. Ohishi and K. Takemura, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 060101 CrossRef.
- G. Weck, S. Desgreniers, P. Loubeyre and M. Mezouar, Phys. Rev. Lett., 2009, 102, 255503 CrossRef CAS PubMed.
- M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558 CrossRef CAS PubMed.
- P. A. Guńka, K. F. Dziubek, A. Gładysiak, M. Dranka, J. Piechota, M. Hanfland, A. Katrusiak and J. Zachara, Cryst. Growth Des., 2015, 15, 3740–3745 CrossRef.
- A. K. Kleppe, M. Amboage and A. P. Jephcoat, Sci. Rep., 2014, 4, 4989 CrossRef CAS.
- G. Wu, X. Huang, Y. Huang, L. Pan, F. Li, X. Li, M. Liu, B. Liu and T. Cui, J. Phys. Chem. C, 2017, 121, 6264–6271 CrossRef CAS.
- P. T. C. Freire, F. M. Barboza, J. A. Lima, F. E. A. Melo and J. M. Filho, in Raman Spectroscopy and Applications, ed. K. Maaz, IntechOpen, 2017, DOI:10.5772/65480, pp. 201–223.
- R. O. Holanda, J. A. Lima, P. T. C. Freire, F. E. A. Melo, J. Mendes Filho and A. Polian, J. Mol. Struct., 2015, 1092, 160–165 CrossRef CAS.
- L. Merrill and W. A. Bassett, Rev. Sci. Instrum., 1974, 45, 290–294 CrossRef.
- S. A. Moggach, D. R. Allan, S. Parsons and J. E. Warren, J. Appl. Crystallogr., 2008, 41, 249–251 CrossRef CAS.
- A. Dawson, D. R. Allan, S. Parsons and M. Ruf, J. Appl. Crystallogr., 2004, 37, 410–416 CrossRef CAS.
- L. J. McCormick, N. Giordano, S. J. Teat and C. M. Beavers, Crystals, 2017, 7, 382 CrossRef.
- C. V. Stan, C. M. Beavers, M. Kunz and N. Tamura, Quantum Beam Sci., 2018, 2, 4 CrossRef.
- I. Kantor, V. Prakapenka, A. Kantor, P. Dera, A. Kurnosov, S. Sinogeikin, N. Dubrovinskaia and L. Dubrovinsky, Rev. Sci. Instrum., 2012, 83, 125102 CrossRef CAS PubMed.
- R. Boehler and K. De Hantsetters, High Pressure Res., 2004, 24, 391–396 CrossRef.
- M. Rivers, V. B. Prakapenka, A. Kubo, C. Pullins, C. M. Holl and S. D. Jacobsen, High Pressure Res., 2008, 28, 273–292 CrossRef CAS.
- H. K. Mao, P. M. Bell, J. W. Shaner and D. J. Steinberg, J. Appl. Phys., 1978, 49, 3276–3283 CrossRef CAS.
- Bruker AXS Inc., APEX 3, Madison, Wisconsin, USA, 2017 Search PubMed.
- Bruker AXS Inc., SAINT, Madison, Wisconsin, USA, 2014/15 Search PubMed.
- S. Parsons, ECLIPSE- Program for masking high-pressure diffraction images and conversion between CCD image formats, The University of Edinburgh, 2014 Search PubMed.
- G. M. Sheldrick, XPREP Version 2008/2, Bruker AXS Inc., Madison, USA, 2008 Search PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- C. B. Hubschle, G. M. Sheldrick and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 1281–1284 CrossRef PubMed.
- A. Kuznetsov, V. Dmitriev, L. Dubrovinsky, V. Prakapenka and H. P. Weber, Solid State Commun., 2002, 122, 125–127 CrossRef CAS.
- A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218 CrossRef CAS.
- A. Gavezzotti, Z. Kristallogr., 2005, 220, 499–510 CAS.
- A. Gavezzotti, Molecular Aggregation: Structure Analysis and Molecular Simulation of Crystals and Liquids, Oxford University Press, Oxford, UK, 2007 Search PubMed.
- A. Gavezzotti, New J. Chem., 2011, 35, 1360–1368 RSC.
- L. Maschio, B. Civalleri, P. Ugliengo and A. Gavezzotti, J. Phys. Chem. A, 2011, 115, 11179–11186 CrossRef CAS PubMed.
- P. A. Wood, R. S. Forgan, D. Henderson, S. Parsons, E. Pidcock, P. A. Tasker and J. E. Warren, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 1099–1111 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford, USA, 2009 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567 CAS.
- Dassault Systèmes, BIOVIA, Materials Studio, San Diego, CA, USA, 2017 Search PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 104107 CrossRef PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- A. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- J. Angel Ross, M. Alvaro and J. Gonzalez-Platas, Z. Kristallogr. - Cryst. Mater., 2014, 229, 405 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- K. Bradenburg, DIAMOND Version 3.2, Crystal Impact GbR, Bonn, Germany, 1999 Search PubMed.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389–397 CrossRef.
- M. Reeves, S. Parsons and P. A. Wood, MR_PIXEL, The University of Edinburgh, Edinburgh, U.K., 2019, Manuscript in preparation Search PubMed.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586 CrossRef CAS.
- V. V. Tyunina, A. V. Krasnov, V. G. Badelin and G. V. Girichev, J. Chem. Thermodyn., 2016, 98, 62–70 CrossRef CAS.
- K. T. No, K. H. Cho, O. Y. Kwon, M. S. Jhon and H. A. Scheraga, J. Phys. Chem., 1994, 98, 10742–10749 CrossRef CAS.
- D. P. Shoemaker, J. Donohue, V. Schomaker and R. B. Corey, J. Am. Chem. Soc., 1950, 72, 2328–2349 CrossRef CAS.
- R. O. Holanda, P. T. C. Freire, J. A. F. Silva, F. E. A. Melo, J. M. Filho and J. A. Lima, Vib. Spectrosc., 2013, 67, 1–5 CrossRef CAS.
- B. L. Silva, P. T. C. Freire, F. E. A. Melo, J. M. Filho, M. A. Pimenta and M. S. S. Dantas, J. Raman Spectrosc., 2000, 31, 519–522 CrossRef CAS.
- A. Prescimone, C. Morien, D. Allan, J. A. Schlueter, S. W. Tozer, J. L. Manson, S. Parsons, E. K. Brechin and S. Hill, Angew. Chem., Int. Ed., 2012, 51, 7490–7494 CrossRef CAS PubMed.
- P. Vinet, J. Ferrante, J. H. Rose and J. R. Smith, J. Geophys. Res., [Solid Earth Planets], 1987, 92, 9319–9325 CrossRef CAS.
- D. A. Rychkov, J. Stare and E. V. Boldyreva, Phys. Chem. Chem. Phys., 2017, 19, 6671–6676 RSC.
- P. A. Wood, F. H. Allen and E. Pidcock, CrystEngComm, 2009, 11, 1563–1571 RSC.
- M. T. Dove, Structure and dynamics : an atomic view of materials, Oxford; New York, N.Y., Oxford University Press, Oxford; New York, N.Y., 2003 Search PubMed.
- N. Casati, P. Macchi and A. Sironi, Chem. Commun., 2009, 2679–2681, 10.1039/B823458B.
- S. Block, C. E. Weir and G. J. Piermarini, Science, 1970, 169, 586–587 CrossRef CAS PubMed.
- B. R. Jackson, C. C. Trout and J. V. Badding, Chem. Mater., 2003, 15, 1820–1824 CrossRef CAS.
- K. K. Zhuravlev, K. Traikov, Z. Dong, S. Xie, Y. Song and Z. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064116 CrossRef.
- S. Fanetti, M. Citroni and R. Bini, J. Chem. Phys., 2011, 134, 204504 CrossRef PubMed.
- M. Kazmierczak and A. Katrusiak, Cryst. Growth Des., 2014, 14, 2223–2229 CrossRef CAS.
- M. Kazmierczak and A. Katrusiak, CrystEngComm, 2015, 17, 9423–9430 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1903563–1903583. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce00388f |
| ‡ Present address: Diamond Light Source, STFC Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Harwell Oxford, Didcot, OX11 0QX, UK. |
| § Present address: The Centre for Microscopy, Characterisation and Analysis and School of Molecular Sciences, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia. |
| ¶ Present address: School of Materials, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. |
| This journal is © The Royal Society of Chemistry 2019 |