Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the predictability of supramolecular interactions in molecular cocrystals – the view from the bench†
Mérina K.
Corpinot
a,
Samuel A.
Stratford‡
b,
Mihails
Arhangelskis‡
b,
Jodie
Anka-Lufford‡
a,
Ivan
Halasz
c,
Nenad
Judaš
d,
William
Jones
b and
Dejan-Krešimir
Bučar
*ab
aDepartment of Chemistry, University College London, London, WC1H 0AJ, UK. E-mail: d.bucar@ucl.ac.uk
bDepartment of Chemistry, University of Cambridge, Cambridge, CB2 1EW, UK
cDivision of Physical Chemistry, Ruđer Bošković Institute, 10000 Zagreb, Croatia
dDepartment of Chemistry, Faculty of Science, University of Zagreb, 10000 Zagreb, Croatia
First published on 27th May 2016
Abstract
A series of theophylline cocrystals involving fluorobenzoic acids was prepared and structurally characterised. The cocrystals display compositions and hydrogen-bond patterns that could not be predicted based on extensive literature/database surveys and the use of other tools. The study demonstrates that – without the use of first-principles crystal structure prediction methods – it is still remarkably difficult to predict and understand the outcomes of cocrystallisation attempts involving small and rigid molecules.
Crystal engineering concerns the understanding, design, assembly and use of crystalline materials.1 Although great strides have been made in all four spheres in the last few decades,2,3 understanding and designing molecular crystals remains a substantial challenge for solid-state chemists.4 The design of organic crystals relies on the concept of supramolecular synthons,5i.e. persistent structural motifs within molecular assemblies that are formed through robust and directional non-covalent interactions, such as hydrogen or halogen bonds. The use of this concept has enabled the straightforward design and assembly of targeted discrete, one-, two- and three-dimensional structures using a single molecular building block.6 However, the assembly of more complex targeted structures, based on several molecules, is much more demanding7 and associated with more modest success rates.8–10
Early successful instances of the synthon approach to molecular assembly were informed by crystallographic studies of molecular crystals.11 It is widely believed that the design and construction of cocrystals involving complex molecules will be similarly enabled by further crystallographic studies focusing on synthon hierarchies in multicomponent crystals.12–16 At present, cocrystal design is also aided by the use of statistical tools (e.g. knowledge-based hydrogen-bond propensity calculations or HBPC17,18) and computational methods (e.g. predictions of molecular complementarity,19 ΔpKa calculations20 and calculations of molecular electrostatic potential surfaces21–23 or MEPS). Despite the availability of such tools, and despite our evolving understanding of how molecules interact in the solid state, it still remains impossible to empirically and statistically predict (i.e. without first principles calculations) the arrangement of individual or multiple molecules in a crystal lattice.9,24–26 Likewise, it is extremely difficult to empirically predict the formation of supramolecular synthons in cocrystals composed of molecules containing a broad range of functional groups.4,8,27
In order to facilitate the design of cocrystals containing such complex entities, it will be necessary to considerably deepen our understanding of self-assembly processes in the solid state.
The current contribution suggests that such understanding can only be reached through well-planned crystallographic studies, and by embracing modern computational solid-state methods (such as crystal structure prediction28,29 or CSP) as standard tools in crystal engineering. We present here a case study involving cocrystals of theophylline (thp) and fluorobenzoic acids (FBAs) (Scheme 1), i.e. cocrystals based on small and rigid molecules with multiple functional groups capable of hydrogen bonding. The study demonstrates the difficulty of empirically predicting compositions and synthon hierarchies in such cocrystals, and is complemented by information from crystallographic database surveys, as well as HBPC and MEPS calculations.
Thp is commonly used as a model compound in studies of pharmaceutical cocrystals,8,30–33 and as such has been primarily cocrystallised with carboxylic acids.34 It is well known that thp engages in cocrystallisation with carboxylic acids through the formation of either an O–H(carboxyl)⋯N(imidazole) hydrogen bond (marked as synthon A in Scheme 1) or a cyclic array of N–H(imidazole)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(carboxyl) and O–H(carboxyl)⋯O
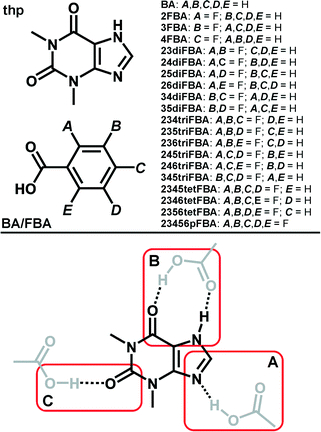
C(carboxyl) and O–H(carboxyl)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(amide) hydrogen bonds (marked as synthon B in Scheme 1). Our interest in (thp)·(FBA) cocrystals was sparked by our recent investigation of the (thp)·(BA) cocrystal (where BA = benzoic acid, Scheme 1). The latter is a solid reported in numerous prior studies,35,36 but one for which no crystal structure had been reported in the literature at the time we commenced our studies. Initial Cambridge Structural Database37 (CSD) surveys and HBPC suggested that interactions of type A and B are almost equally likely to occur in (thp)·(BA) (see ESI), while a subsequent single crystal X-ray diffraction study revealed that thp and BA interact through a type B synthon (Fig. 1a).38
C(amide) hydrogen bonds (marked as synthon B in Scheme 1). Our interest in (thp)·(FBA) cocrystals was sparked by our recent investigation of the (thp)·(BA) cocrystal (where BA = benzoic acid, Scheme 1). The latter is a solid reported in numerous prior studies,35,36 but one for which no crystal structure had been reported in the literature at the time we commenced our studies. Initial Cambridge Structural Database37 (CSD) surveys and HBPC suggested that interactions of type A and B are almost equally likely to occur in (thp)·(BA) (see ESI), while a subsequent single crystal X-ray diffraction study revealed that thp and BA interact through a type B synthon (Fig. 1a).38
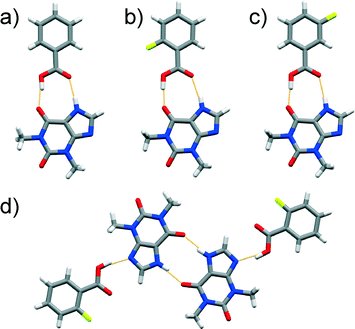 | ||
Fig. 1 Perspective views of thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BA and thp BA and thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FBA assemblies in the crystal structures of: a) (thp)·(BA), b) (thp)·(2FBA), c) (thp)·(3FBA) and d) (thp)·(2FBA)·(CH3NO2). FBA assemblies in the crystal structures of: a) (thp)·(BA), b) (thp)·(2FBA), c) (thp)·(3FBA) and d) (thp)·(2FBA)·(CH3NO2). | ||
Another study of FBA cocrystals performed in our laboratories39 then inspired us to investigate whether minimal structural changes in BA could potentially reorganise the self-assembly process to yield thp cocrystals based on type A synthons. The choice of FBAs as cocrystal formers appeared appropriate, as all mono, di-, tri-, tetra- and penta-substituted FBAs are similar in size and shape to BA due to the relatively small size difference between hydrogen and fluorine atoms (van der Waals radii: 120 pm vs. 147 pm, respectively).40 Moreover, organic fluorine is not likely to act as a hydrogen-bond acceptor,41,42 while short intermolecular C–H⋯F contacts in molecular crystals only make a minor contribution to the cohesive energy of a molecular crystal.43 It was therefore postulated that the presence of fluorine atoms in the (thp)·(FBA) cocrystals would only minimally interfere with the formation of O–H⋯N, N–H⋯O and O–H⋯O hydrogen bonds between the cocrystal components. This hypothesis was also in agreement with results of a recently published cocrystal study involving FBAs.44
The cocrystallisation of thp with all nineteen FBAs was attempted by liquid-assisted grinding45 (LAG) using equimolar amounts of thp and the relevant FBA (see ESI†). The formation of the cocrystals was recognised via powder X-ray diffraction (PXRD) in fifteen out of nineteen cases – only cocrystal screens involving 4FBA, 23diFBA, 24diFBA and 26diFBA did not result in cocrystal formation under the investigated crystallisation conditions.46 The crystal structures of all produced solids were determined either directly from the LAG samples using laboratory PXRD data (by simulated annealing,47 Rietveld refinement48 and CASTEP49 DFT geometry optimisation), or by single crystal X-ray diffraction (SCXRD) using crystals that were obtained through solution-mediated phase transformation50 (SMPT) or by slow solvent evaporation (see ESI†).
Cocrystallisation of thp with 2FBA and 3FBA yielded 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystals, (thp)·(2FBA) and (thp)·(3FBA). Both cocrystals are isostructural with the (thp)·(BA) cocrystal and feature discrete thp
1 cocrystals, (thp)·(2FBA) and (thp)·(3FBA). Both cocrystals are isostructural with the (thp)·(BA) cocrystal and feature discrete thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FBA assemblies being held together by type B synthons (Fig. 1b and c). Intriguingly, the mechanochemical synthesis of the (thp)·(2FBA) cocrystal could initially only be achieved in the Cambridge laboratory. Mechanochemical cocrystal screens performed under identical conditions in the London laboratory persistently yielded a cocrystal nitromethane solvate, namely (thp)·(2FBA)·(CH3NO2). The thp and 2FBA components in this solvate were unexpectedly sustained by type A synthon (Fig. 1d). The non-solvated (thp)·(2FBA) cocrystal was finally also obtained in London under SMPT conditions (using acetonitrile as a solvent).
FBA assemblies being held together by type B synthons (Fig. 1b and c). Intriguingly, the mechanochemical synthesis of the (thp)·(2FBA) cocrystal could initially only be achieved in the Cambridge laboratory. Mechanochemical cocrystal screens performed under identical conditions in the London laboratory persistently yielded a cocrystal nitromethane solvate, namely (thp)·(2FBA)·(CH3NO2). The thp and 2FBA components in this solvate were unexpectedly sustained by type A synthon (Fig. 1d). The non-solvated (thp)·(2FBA) cocrystal was finally also obtained in London under SMPT conditions (using acetonitrile as a solvent).
A cocrystal of an unexpected composition was formed in a LAG experiment involving equimolar amounts of thp and 25diFBA where PXRD and SCXRD revealed the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cocrystal, (thp)·(25diFBA)2. The structural study also showed that thp and 25diFBA formed discrete three-component assemblies, which were sustained by synthons of both type A and B (Fig. 2a). Several attempts to produce a 1
2 cocrystal, (thp)·(25diFBA)2. The structural study also showed that thp and 25diFBA formed discrete three-component assemblies, which were sustained by synthons of both type A and B (Fig. 2a). Several attempts to produce a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 thp
1 thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25diFBA cocrystal either mechanochemically or through solution-based crystallisation methods have, so far, failed.
25diFBA cocrystal either mechanochemically or through solution-based crystallisation methods have, so far, failed.
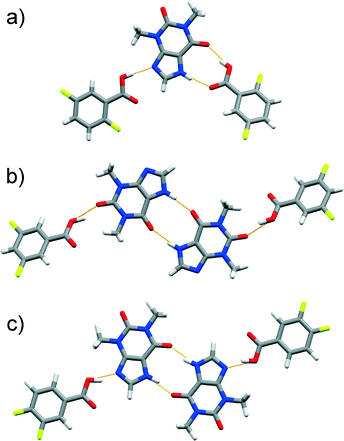 | ||
Fig. 2 Perspective views of thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FBA assemblies in the crystal structures of: a) (thp)·(25diFBA)2, b) (thp)·(35diFBA) and c) (thp)·(34diFBA) featuring distinct supramolecular synthons. FBA assemblies in the crystal structures of: a) (thp)·(25diFBA)2, b) (thp)·(35diFBA) and c) (thp)·(34diFBA) featuring distinct supramolecular synthons. | ||
Our investigations also led to the discovery of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal comprised of thp and 35diFBA, (thp)·(35diFBA). This material surprisingly exhibits discrete four-component assemblies featuring a O–H(carboxyl)⋯O
1 cocrystal comprised of thp and 35diFBA, (thp)·(35diFBA). This material surprisingly exhibits discrete four-component assemblies featuring a O–H(carboxyl)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(urea) synthon (marked as type C in Scheme 1 and shown in Fig. 2b) that are statistically less likely to occur than synthons A and B, as determined by HBPC (see ESI†). More predictable synthons were, however, found in the 1
C(urea) synthon (marked as type C in Scheme 1 and shown in Fig. 2b) that are statistically less likely to occur than synthons A and B, as determined by HBPC (see ESI†). More predictable synthons were, however, found in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (thp)·(34diFBA) cocrystal wherein thp and the FBA interact via type A synthon (Fig. 2c).
1 (thp)·(34diFBA) cocrystal wherein thp and the FBA interact via type A synthon (Fig. 2c).
Attempts to produce cocrystals using LAG and equivalent amounts of thp and tri-, tetra- and penta-FBAs yielded 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystals, namely (thp)·(234triFBA), (thp)·(235triFBA), (thp)·(236triFBA), (thp)·(245triFBA), (thp)·(246triFBA), (thp)·(345triFBA), (thp)·(2345tetFBA), (thp)·(2346tetFBA), (thp)·(2356tetFBA) and (thp)·(23456pFBA). Their crystal structures (except the one involving thp and 245triFBA) featured discrete four-component assemblies composed of two thp and two FBA molecules. In these assemblies, the thp molecules interact with each other via cyclic arrays of N–H(imidazole)⋯O
1 cocrystals, namely (thp)·(234triFBA), (thp)·(235triFBA), (thp)·(236triFBA), (thp)·(245triFBA), (thp)·(246triFBA), (thp)·(345triFBA), (thp)·(2345tetFBA), (thp)·(2346tetFBA), (thp)·(2356tetFBA) and (thp)·(23456pFBA). Their crystal structures (except the one involving thp and 245triFBA) featured discrete four-component assemblies composed of two thp and two FBA molecules. In these assemblies, the thp molecules interact with each other via cyclic arrays of N–H(imidazole)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(amide) hydrogen bonds, while the FBAs bind to the thp dimer through synthons of type A (some examples are featured in Fig. 3, others are illustrated in the ESI† file). Surprisingly, the crystal structure of (thp)·(245triFBA) exhibited assemblies that were held together by synthons of type B (Fig. 4a).
C(amide) hydrogen bonds, while the FBAs bind to the thp dimer through synthons of type A (some examples are featured in Fig. 3, others are illustrated in the ESI† file). Surprisingly, the crystal structure of (thp)·(245triFBA) exhibited assemblies that were held together by synthons of type B (Fig. 4a).
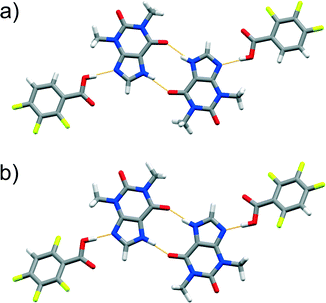 | ||
Fig. 3 Perspective views of thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FBA assemblies in the crystal structures of: a) (thp)·(234triFBA) and b) (thp)·(2346triFBA). FBA assemblies in the crystal structures of: a) (thp)·(234triFBA) and b) (thp)·(2346triFBA). | ||
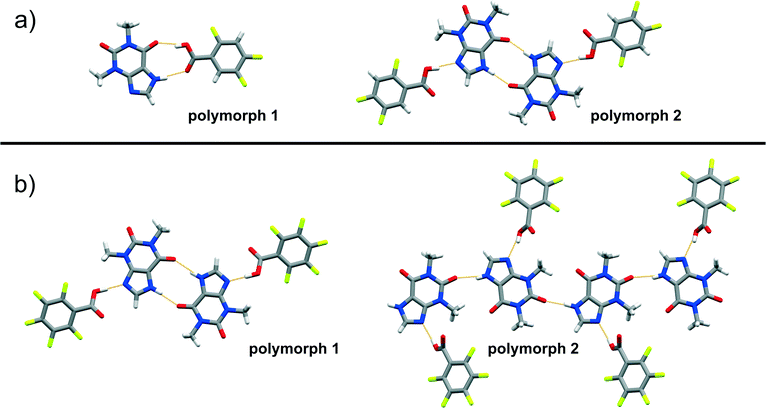 | ||
Fig. 4 Perspective views of thp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FBA assemblies in the crystal structures of cocrystal polymorphs: a) (thp)·(245triFBA) and b) (thp)·(23456pFBA). FBA assemblies in the crystal structures of cocrystal polymorphs: a) (thp)·(245triFBA) and b) (thp)·(23456pFBA). | ||
The (thp)·(FBA) cocrystals described above clearly demonstrate the unpredictability of synthon hierarchies in two-component cocrystals with several hydrogen-bonding functional groups. The observed supramolecular interactions could neither be predicted empirically nor with the use of HBPC and MEPS calculations. In particular, HBPC has been performed on all structurally characterised solids using Mercury 3.7 and the CSD 5.37 (see ESI†). Although the calculations encouragingly predicted the formation of the observed hydrogen bonds between thp and the FBA in each case, the synthon hierarchies could not be foreseen (see ESI†). In addition, DFT calculations of MEPS were also performed to predict optimal hydrogen-bond donor–acceptor pairs (see ESI†). The values of the electrostatic potentials on the hydrogen-bond donors and acceptors could, unfortunately, not be correlated to the formation of the observed synthons in the cocrystal series (see ESI†). We observed, however, that under the initially studied LAG conditions, almost all tri-, tetra- and penta-FBAs form cocrystals based on type A synthons, while the mono- and di-FBAs participated in hydrogen bonding through type A, B and C interactions (see ESI†).
The difficulty of predicting supramolecular synthons in cocrystals composed of thp and FBA is further highlighted by the discovery of polymorphs of four (thp)·(FBA) cocrystals, namely (thp)·(34diFBA), (thp)·(245triFBA), (thp)·(246triFBA) and (thp)·(23456pFBA). These polymorphs were observed during attempts to grow single crystals of the mechanochemically obtained crystal forms by crystallisation through slow solvent evaporation (see ESI†). Structural analyses revealed that the four solids exhibited both packing and synthon polymorphism.51 Packing polymorphism was observed in the case of (thp)·(34diFBA), whereas (thp)·(245triFBA), (thp)·(246triFBA) and (thp)·(23456pFBA) displayed synthon polymorphism. In particular, the synthon polymorphism of (thp)·(245triFBA) was realised through the formation of the type A synthon (Fig. 4a). On the other hand, synthon polymorphism in the cases of (thp)·(246triFBA) and (thp)·(23456pFBA) was realised through the occurrence of N–H(imidazole)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(urea) hydrogen bonds between two thp molecules, rather than the generally observed cyclic arrays of N–H(imidazole)⋯O
C(urea) hydrogen bonds between two thp molecules, rather than the generally observed cyclic arrays of N–H(imidazole)⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(amide) hydrogen bonds (Fig. 4b). The serendipitous discovery of the four polymorphs is not particularly surprising, considering the rapidly increasing number of studies reporting cocrystal polymorphs,51 while a recent study recognised that cocrystals exhibit polymorphism as readily as single-component organic crystals.52 In light of these findings, it appears that a better understanding of synthon hierarchies in cocrystals could be achieved by surveys of their structural landscapes29,53 through polymorph screens, which are not regularly performed at the present time.54
C(amide) hydrogen bonds (Fig. 4b). The serendipitous discovery of the four polymorphs is not particularly surprising, considering the rapidly increasing number of studies reporting cocrystal polymorphs,51 while a recent study recognised that cocrystals exhibit polymorphism as readily as single-component organic crystals.52 In light of these findings, it appears that a better understanding of synthon hierarchies in cocrystals could be achieved by surveys of their structural landscapes29,53 through polymorph screens, which are not regularly performed at the present time.54
So, what is the significance of the intriguing synthon diversity in the presented (thp)·(FBA) cocrystal series? The unpredictability of supramolecular interactions in the (thp)·(FBA) cocrystals, and lack of knowledge about the structural and electronic effects (on synthon hierarchies and cocrystal compositions) of fluorine substitutions in the cocrystal former, suggest that cocrystals are not as readily designed and predictably constructed as is so often portrayed in the literature. Supramolecular synthons are an incredibly useful synthetic tool that has greatly contributed to the development of advanced functional materials,55 and to the preparation of strikingly complex solid-state structures.56 The current state of the art in cocrystal design, however, does not support high-yielding supramolecular syntheses57 of cocrystals for cases entailing molecules with more than two functional groups. To improve our ability to better design and more accurately construct cocrystals comprised of complex multifunctional molecules (such as pharmaceuticals), more targeted and systematic crystallographic studies need to be pursued and published.11 But to fully understand cocrystals – their structural landscapes, synthon hierarchies and thermodynamic properties – computational methods (such as CSP29,58 or lattice energy calculations59 alone) need to be regularly used in crystal engineering. Comprehensive computational solid-state studies are very intensive (requiring a great deal of CPU time and time to process the generated data) and it can be argued that their use is, nowadays, only justified when dealing with specialty chemicals of particular interest (e.g. drug candidates in development for marketing).60 Recent reports, however, have shown that even less exhaustive predictions can contribute substantially to experimental cocrystal research.61 The maturity of contemporary first principles computational solid-state methods62–65 and their relevance to crystal engineering is now widely recognised,66,67 and it is time that they are equally widely embraced by the experimental community.
MKC and DKB gratefully acknowledge financial support from the UCL Faculty of Mathematical and Physical Sciences. DKB and WJ thank the Royal Society for a Newton International Fellowship and the Isaac Newton Trust (Trinity College, University of Cambridge) for funding. MA thanks the EPSRC for a studentship, while SAS acknowledges funding through the EPSRC CASE scheme with Pfizer. We are grateful for computational support from the UK national high performance computing service, ARCHER, for which access was obtained via the UKCP consortium and funded by EPSRC grant (EP/K013564/1). Lastly, we thank Prof. Sarah L. Price, Dr. Edward O. Pyzer-Knapp, Dr. Rui Guo and Mr Luca Iuzzolino for helpful discussions.
Notes and references
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- C. B. Aakeröy, N. R. Champness and C. Janiak, CrystEngComm, 2010, 12, 22–43 RSC.
- T. Friščić, Chem. Soc. Rev., 2012, 41, 3493–3510 RSC.
- M. J. Zaworotko, Cryst. Growth Des., 2007, 7, 4–9 CAS.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- J. D. Wuest, Chem. Commun., 2005, 5830–5837 RSC.
- B. R. Bhogala, S. Basavoju and A. Nangia, Cryst. Growth Des., 2005, 5, 1683–1686 CAS.
- D.-K. Bučar, R. F. Henry, G. G. Z. Zhang and L. R. MacGillivray, Cryst. Growth Des., 2014, 14, 5318–5328 Search PubMed.
- J. R. G. Sander, D.-K. Bučar, R. F. Henry, B. N. Giangiorgi, G. G. Z. Zhang and L. R. MacGillivray, CrystEngComm, 2013, 15, 4816–4822 RSC.
- P. M. Bhatt, Y. Azim, T. S. Thakur and G. R. Desiraju, Cryst. Growth Des., 2009, 9, 951–957 CAS.
- C. Aakeröy, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 387–391 CrossRef PubMed.
- J. A. Bis, P. Vishweshwar, D. Weyna and M. J. Zaworotko, Mol. Pharmaceutics, 2007, 4, 401–416 CrossRef CAS PubMed.
- T. R. Shattock, K. K. Arora, P. Vishweshwar and M. J. Zaworotko, Cryst. Growth Des., 2008, 8, 4533–4545 CAS.
- C. B. Aakeröy, M. Baldrighi, J. Desper, P. Metrangolo and G. Resnati, Chem. – Eur. J., 2013, 19, 16240–16247 CrossRef PubMed.
- N. K. Duggirala, G. P. F. Wood, A. Fischer, Ł. Wojtas, M. L. Perry and M. J. Zaworotko, Cryst. Growth Des., 2015, 15, 4341–4354 CAS.
- P. Kavuru, D. Aboarayes, K. K. Arora, H. D. Clarke, A. Kennedy, L. Marshall, T. T. Ong, J. Perman, T. Pujari, Ł. Wojtas and M. J. Zaworotko, Cryst. Growth Des., 2010, 10, 3568–3584 CAS.
- A. Delori, P. T. A. Galek, E. Pidcock and W. Jones, Chem. – Eur. J., 2012, 18, 6835–6846 CrossRef CAS PubMed.
- A. Delori, P. T. A. Galek, E. Pidcock, M. Patni and W. Jones, CrystEngComm, 2013, 15, 2916–2928 RSC.
- L. Fábián, Cryst. Growth Des., 2009, 9, 1436–1443 Search PubMed.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362–6365 RSC.
- C. B. Aakeröy, T. K. Wijethunga and J. Desper, New J. Chem., 2015, 39, 822–828 RSC.
- C. B. Aakeröy, K. Epa, S. Forbes, N. Schultheiss and J. Desper, Chem. – Eur. J., 2013, 19, 14998–15003 CrossRef PubMed.
- D. Musumeci, C. A. Hunter, R. Prohens, S. Scuderi and J. F. McCabe, Chem. Sci., 2011, 2, 883–890 RSC.
- G. M. Day and W. D. S. Motherwell, Cryst. Growth Des., 2006, 6, 1985–1990 CAS.
- K. B. Ghiassi, X. B. Powers, J. Wescott, A. L. Balch and M. M. Olmstead, Cryst. Growth Des., 2016, 16, 447–455 CAS.
- D.-K. Bučar, R. W. Lancaster and J. Bernstein, Angew. Chem., Int. Ed., 2015, 54, 6972–6993 CrossRef PubMed.
- D.-K. Bučar, R. F. Henry, X. Lou, R. W. Duerst, T. B. Borchardt, L. R. MacGillivray and G. G. Z. Zhang, Mol. Pharmaceutics, 2007, 4, 339–346 CrossRef PubMed.
- G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef.
- S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Int. J. Pharm., 2006, 320, 114–123 CrossRef CAS PubMed.
- L. Wang, M. Luo, J. Li, J. Wang, H. Zhang and Z. Deng, Cryst. Growth Des., 2015, 15, 2574–2578 CAS.
- A. Alhalaweh, W. Kaialy, G. Buckton, H. Gill, A. Nokhodchi and S. P. Velaga, AAPS PharmSciTech, 2013, 14, 265–276 CrossRef CAS PubMed.
- M. D. Eddleston, M. Arhangelskis, L. Fábián, G. J. Tizzard, S. J. Coles and W. Jones, Cryst. Growth Des., 2016, 16, 51–58 CAS.
- According to the CSD, more than 50% of the 63 unique crystal structures of thp salts and cocrystals feature a carboxylic acid or a carboxylate anion..
- K. Sekiguchi, Yakugaku Zasshi, 1961, 81, 675–680 CAS.
- S. L. Childs, G. P. Stahly and A. Park, Mol. Pharmaceutics, 2007, 4, 323–338 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr. B, 2016, 72, 171–179 CrossRef CAS PubMed.
- The mechanochemical synhesis and PXRD structural characterisation of the (thp)·(BA) cocrystal were recently reported: S. Heiden, L. Tröbs, K.-J. Wenzela and F. Emmerling, CrystEngComm, 2012, 14, 5128–5129 RSC.
- D.-K. Bučar, G. M. Day, I. Halasz, G. G. Z. Zhang, J. R. G. Sander, D. G. Reid, L. R. MacGillivray, M. J. Duer and W. Jones, Chem. Sci., 2013, 4, 4417–4425 RSC.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- V. R. Thalladi, H.-C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710 CrossRef CAS.
- J. D. Dunitz and R. Taylor, Chem. – Eur. J., 1997, 3, 89–98 CrossRef CAS.
- J. D. Dunitz and W. B. Schweizer, Chem. – Eur. J., 2006, 12, 6804–6815 CrossRef CAS PubMed.
- R. Dubey and G. R. Desiraju, Cryst. Growth Des., 2015, 15, 489–496 CAS.
- T. Friščić and W. Jones, Cryst. Growth Des., 2009, 9, 1621–1637 Search PubMed.
- The cocrystallisation of thp with 23diFBA and 26diFBA was successful under conditions different to those reported herein, while thp cocrystals involving 4FBA and 24diFBA remained elusive. These results may be discussed elsewhere..
- J. M. Newsam, M. W. Deem and C. M. Freeman, Direct Space Methods of Structure Solution From Powder Diffraction Data, Accuracy in Powder Diffraction II, NIST Special Publication 846, 1992 Search PubMed.
- H. Rietveld, Acta Crystallogr., 1967, 22, 151–152 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- G. G. Z. Zhang, R. F. Henry, T. B. Borchardt and X. Lou, J. Pharm. Sci., 2007, 96, 990–995 CrossRef CAS PubMed.
- S. Aitipamula, P. S. Chow and R. B. H. Tan, CrystEngComm, 2014, 16, 3451–3465 RSC.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- A. Mukherjee, Cryst. Growth Des., 2015, 15, 3076–3085 CAS.
- S. Aitipamula, P. S. Chow and R. B. H. Tan, Cryst. Growth Des., 2010, 10, 2229–2238 CAS.
- N. K. Duggirala, M. L. Perry, Ö. Almarsson and M. J. Zaworotko, Chem. Commun., 2016, 52, 640–655 RSC.
- N. A. Mir, R. Dubey and G. R. Desiraju, IUCrJ, 2016, 3, 96–101 CAS.
- C. B. Aakeröy, A. M. Beatty and B. A. Helfrich, J. Am. Chem. Soc., 2002, 124, 14425–14432 CrossRef.
- P. G. Karamertzanis, A. V. Kazantsev, N. Issa, G. W. A. Welch, C. S. Adjiman, C. C. Pantelides and S. L. Price, J. Chem. Theory Comput., 2009, 5, 1432–1448 CrossRef CAS PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr. B, 2011, 67, 535–551 CAS.
- K. Hoxha, D. H. Case, G. M. Day and T. J. Prior, CrystEngComm, 2015, 17, 7130–7141 RSC.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640–643 CrossRef CAS PubMed.
- A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman, C. C. Pantelides, S. L. Price, P. T. A. Galek, G. M. Day and A. J. Cruz-Cabeza, Int. J. Pharm., 2011, 418, 168–178 CrossRef CAS PubMed.
- The Cambridge Crystallographic Data Centre (CCDC), https://www.ccdc.cam.ac.uk/News/List/post-43/, 2015..
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077 RSC.
- E. Gibney, Nature, 2015, 527, 20–21 CrossRef CAS PubMed.
- S. L. Price, Science, 2014, 345, 619–620 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Crystallisation procedures, computational methods, statistical analyses and crystallographic data. CCDC 1451259–1451274 and 1476648–1476652. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce00293e |
| ‡ The authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |