Interface-controlled calcium phosphate mineralization: effect of oligo(aspartic acid)-rich interfaces

Abstract

The phase behavior of an amphiphilic block copolymer based on a poly(aspartic acid) hydrophilic block and a poly(n-butyl acrylate) hydrophobic block was investigated at the air–water and air–buffer interface. The polymer forms stable monomolecular films on both subphases. At low pH, the isotherms exhibit a plateau. Compression–expansion experiments and infrared reflection absorption spectroscopy suggest that the plateau is likely due to the formation of polymer bi- or multilayers. At high pH the films remain intact upon compression and no multilayer formation is observed. Furthermore, the mineralization of calcium phosphate beneath the monolayer was studied at different pH. The pH of the subphase and thus the polymer charge strongly affects the phase behavior of the film and the mineral formation. After 4 h of mineralization at low pH, atomic force microscopy shows smooth mineral films with a low roughness. With increasing pH the mineral films become inhomogeneous and the roughness increases. Transmission electron microscopy confirms this: at low pH a few small but uniform particles form whereas particles grown at higher pH are larger and highly agglomerated. Energy-dispersive X-ray spectroscopy and X-ray photoelectron spectroscopy confirm the formation of calcium phosphate. The levels of mineralization are higher in samples grown at high pH.

---

1. Introduction

Biomineralization is the formation of mostly inorganic deposits such as calcium carbonate and calcium phosphate (CP) with the aid of organic surfaces or matrices (templates) in living organisms under mild conditions.^1–9 Templates are proteins, lipids, carbohydrates, or combinations thereof. CP, a prominent biomineral in mammals, is the most important inorganic component of human bones and teeth and thus of importance to human health.^10–14 Dental calculus and arteriosclerosis are also associated with the precipitation of CP and other calcium minerals. Arteriosclerosis can cause heart attacks or strokes and is one of the most common causes of death in industrialized countries.¹ It is caused by the deposition of plaques from fat and calcium in the arteries and results in narrowing blood vessels and increasing blood pressure or limited nutrient supply to the brain and other organs. The controlled deposition (bones, teeth, tendons) and inhibition (calculus, arteriosclerosis) of CP and related minerals are therefore key issues for an aging society. In spite of this, the controlled growth of CP mimicking biological structures and the controlled inhibition or dissolution of CP remain a challenge.^15–17

A key question in this context is the role of surfaces and interfaces: bone formation, dental de- and remineralization, calculus deposition, and arteriosclerosis are all surface- or interface driven or at least associated with the formation of a mineral deposit on a surface. In spite of this, the vast majority of experiments on biomimetic CP formation are on mineralization from bulk aqueous solution.^17–19 Only few studies address the effects of surfaces and interfaces on CP precipitation.^17,19–26 There are also studies focusing on interface-controlled formation of other important (bio)minerals.^19,27–31

The air–water interface is a useful model system to observe and quantify interface effects on CP formation.³² In contrast to micelles in bulk aqueous solution (which have also been used as model systems) monolayers are much closer to a surface of a bulk biomaterial. Especially the radius of curvature of a micelle is often far from that of a real biomaterial. Consequently, Zhang et al. used surfactant monolayers for mineralization and observed a multi-stage growth process. First an amorphous, unstable precursor precipitated. This precursor transformed via an unstable calcium phosphate dihydrate crystal phase into stable, crystalline hydroxyapatite (HAP).²⁵ This model has been confirmed and refined by Dey et al., who identified five reaction steps until the formation of HAP.²⁴

Besides these studies on mineralization at films of low molecular weight compounds, there are complementary studies on the effects of block copolymer films on mineralization. The structure and architecture as well as the chemistry of the polymer monolayer have a tremendous influence on the nucleation and growth process, yielding a wide variety of CP particle shapes, sizes, crystal phases, and supramolecular organization.

Casse et al. showed that the subphase pH, calcium and phosphate concentrations, and stirring influences the mineralization at poly(n-butyl acrylate)-block-poly(acrylic acid) (PnBuA–PAA) monolayers. The resulting CP films are homogeneous when mineralized from solutions with low calcium and phosphate concentrations and a pH higher than 8. Stirring is also important for mineralization control; without stirring heterogeneous films were obtained.²⁰

Junginger et al. investigated CP mineralization beneath a monolayer of the amphiphilic block copolymer poly(n-butyl methacrylate)-block-poly[2-(dimethylamino)ethyl methacrylate] (PnBMA–PDMAEMA). At pH 5, very thin CP fibers, which aggregate to “cotton ball” features with diameters between 20 and 50 nm, were observed. In contrast at pH 8 dense aggregates with sizes between 200 and 700 nm form.²² Further studies on similar polymers show that also the dynamics of the polymer film affects the mineralization process.²¹ Casse et al.²⁰ and Junginger et al.^21–23 suggest that the most homogeneous CP films form when the polymer monolayer is highly charged. In the case of the polyacid used by Casse et al. this occurs at high pH values (pH 8–11, formation of negatively charged carboxylates). In the case of the polybase monolayers studied by Junginger et al. the highest charge density is realized at low pH values (pH 5, formation of positively charged ammonium groups). Moreover, similar observations of strong charge effects on calcium carbonate formation have been reported by Volkmer and coworkers.^33–38 This suggests that polyanions and polycations are good model systems to rationalize and quantify the mineralization of CP under biomimetic conditions.

Up to now all studies have focused on low molecular surfactants or polymers with molecular weights of about 30 000 g mol⁻¹ and higher, but there are no studies on the effects of oligomers at the air–water interface and their role on (bio)mineralization. From a basic scientific point of view and from an application point of view, it would, however, be interesting to (1) determine if there is a lower limit of efficient mineralization control and (2) to establish the methodology to analyze the resulting materials. The current study therefore evaluates the effect of an oligomeric molecule (M_w = 3060 g mol⁻¹) at the air–water interface on CP mineralization as a first model case serving as an initial starting point to address these questions.

2. Results and discussion

2.1. Phase behavior of the polymer at the air–water interface

Fig. 1 shows the structure of the amphiphilic block copolymer used in the current study. It consists of 10 aspartic acid units, 13 n-butyl acrylate units, and a bridging moiety of two glycine and one p-nitrophenylalanine units. The full monomer sequence of the polymer is Gly-(Asp)₁₀-(pNO₂Phe)-Gly-(nBuA)₁₃ (M_w = 3060 g mol⁻¹, PDI = 1.23). The advantage of using such a molecule over a molecule made by radical polymerization, for example, poly(acrylic acid) instead of poly(aspartic acid), is that in the current case it is possible to obtain near-perfect monodisperse water-soluble blocks, which should enable an accurate quantification of the effect on mineralization.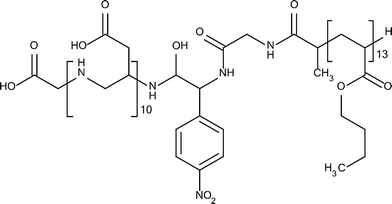

Fig. 1 Structure of the polymer used in the current study.³⁹

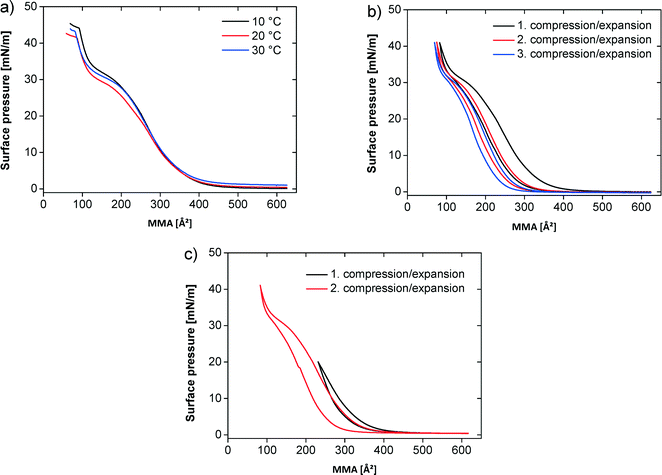
Fig. 2a shows the pressure–area (π–A) isotherms of the polymer at different temperatures on pure water. At all temperatures the monolayer exhibits a transition from the 2D gas to the liquid phase, which is completed around a mean molecular area (MMA) of ~450 Ų. The surface pressure increases only slightly in the plateau region, characterizing the coexistence between gas and liquid phase, to a value around 1 mN m⁻¹. On further compression the surface pressure steeply rises until an MMA of 200 Ų, where a quasi-plateau at 25–28 mN m⁻¹ appears. The quasi-plateau persists until ca. 120 Ų and ca. 33 mN m⁻¹. Finally the surface pressure rapidly rises until the film collapse. At 10 °C the collapse pressure is 44 mN m⁻¹ at a MMA of 90 Ų. At 20 and 30 °C the films collapse at a MMA of 90 Ų with a collapse pressure of 42 mN m⁻¹ (20 °C) and 43 mN m⁻¹ (30 °C), respectively.

Fig. 2 π–A isotherms of the polymer at the air–water interface. (a) On water at different temperatures. (b) Compression/expansion on water at 20 °C. (c) Incomplete (1. compression/expansion) and complete (2. compression/expansion) compression/expansion on water at 20 °C.

Fig. 2b shows three successive compression–expansion curves of a film at 20 °C to evaluate film stability. The curves are similar, but successively shift to lower MMAs with increasing compression–expansion cycle number indicating either some polymer dissolution into the subphase or a partially irreversible multilayer formation.

Fig. 2c shows two compression–expansion curves on water at 20 °C. The first compression–expansion curve on water was done until a surface pressure of 20 mN m⁻¹, that is, below the plateau region. The subsequent compression–expansion on water was performed along the entire isotherm until a surface pressure of 42 mN m⁻¹. All compression–expansion curves show a hysteresis, but it is more significant when the film is fully compressed and less pronounced when the films are re-expanded from lower surface pressures. The difference between the compression and expansion curves is 6.5% upon incomplete compression and 18.5% on complete compression.

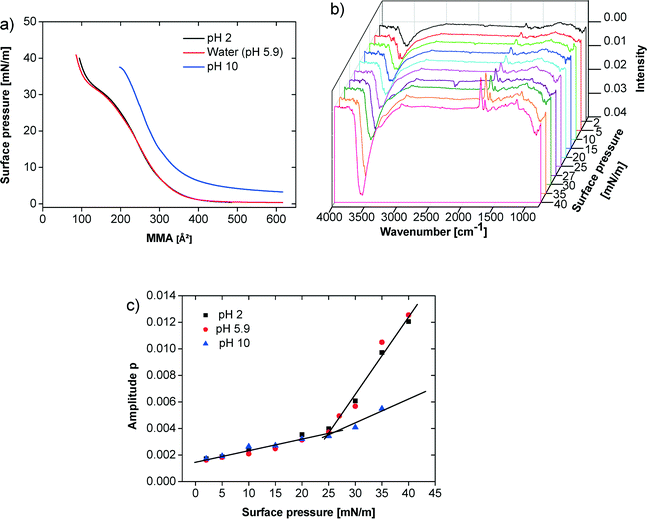
Fig. 3a shows isotherms at pH 2, 5.9, and 10. Here, the subphase pH was adjusted with NaOH and HCl, respectively. The isotherms at pH 2 and 5.9 essentially show the same phase behavior. The isotherm at pH 10 starts at much higher surface pressure.

Fig. 3 (a) π–A isotherms of the polymer at different pH values (pH 2 adjusted with HCl, pH 10 adjusted with NaOH). (b) IRRAS spectra on water at 20 °C, data for p-polarized light are shown. (c) Amplitude for C=O band at 1730 cm⁻¹ for pH 2, 5.9 and 10. Lines in (c) are only guides for the eye.

For these three pH values infrared reflection absorption spectroscopy (IRRAS) experiments were performed for specific surface pressures along the isotherms. Fig. 3b shows representative spectra obtained for one series at pH 5.9. In Fig. 3c the amplitude of the C=O band at 1730 cm⁻¹ is plotted against the surface pressure. At pH 2 and 5.9 the C=O band intensity continuously but slowly increases until the film reaches the plateau region between 25–27 mN m⁻¹. Thereafter, the C=O band intensity further increases more sharply. In contrast, the film at pH 10 shows a much less pronounced increase in the C=O band intensity above 25 mN m⁻¹. The same behavior can be observed using the OH-band around 3500 cm⁻¹.

Fig. 4a shows the π–A isotherms of the polymer at 20 °C at different pH values demonstrating an influence of the pH on the film behavior (note that from here on, glycocoll buffer was used, because this buffer was found efficient for the mineralization experiments described below. This does however not affect the general findings on film behavior). Up to an MMA of 400 Ų all isotherms are very similar and the surface pressure just slightly increases. The observed plateau characterizes the 2D gas–liquid transition. The transition pressure is higher on subphases with higher pH values. The compression of the liquid phase film at pH values between 7 and 10 leads to a continuous pressure increase until the collapse above 40 mN m⁻¹. At pH 5 and 6, an additional quasi-plateau is observed starting at ca. 200 Ų. The plateau at pH 6 is less pronounced than at pH 5.

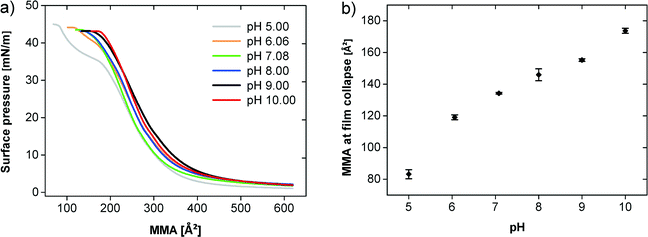Fig. 4 (a) π–A isotherms of the polymer at different pH values on a glycocoll subphase. (b) MMA and surface pressure during the film collapse at different pH values.

Fig. 4b illustrates that the film collapse occurs at a higher MMA with increasing pH. At pH 5 the film collapses at 81 Ų and a surface pressure of 45 mN m⁻¹ whereas at pH 10 the film collapse already takes place at 174 Ų and 43 mN m⁻¹.

2.2. Calcium phosphate mineralization beneath the monolayer

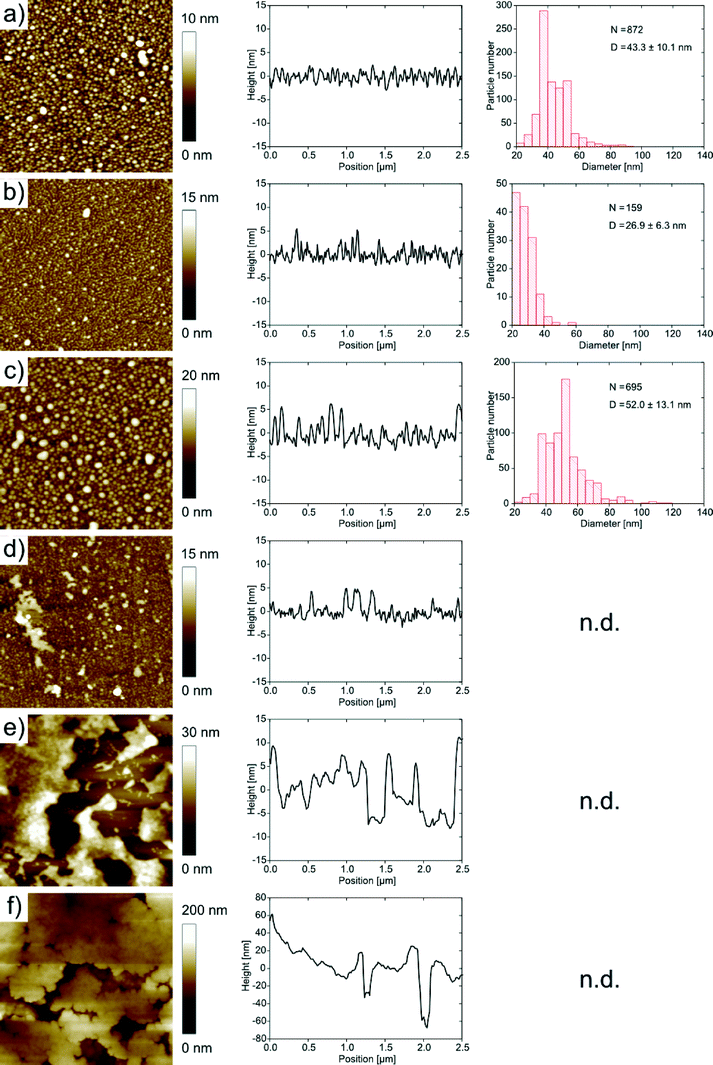
As stated in the introduction, we were interested in determining whether an oligomer with an only ten-amino-acid-long hydrophilic block (which is one order of magnitude shorter than the hydrophilic blocks studied so far for calcium phosphate mineralization^20–23) is able to control CP mineralization at the air–water interface. CP was therefore grown beneath monolayers of the oligomer shown in Fig. 1 at pH 5 to 10. To reduce the effects of the buffer chemistry on the mineralization process, the same buffer system was used in all experiments (glycocoll, see experimental part for details). Indeed, this is one of the first cases where buffer effects on mineralization can largely be eliminated because one and the same buffer has been used throughout the entire study.

Fig. 5 shows TEM images of samples obtained between pH 5 and 10 at a surface pressure of 30 mN m⁻¹. At pH 5 and 6 aggregated flakes dominate but smaller particles are also visible in the background. The aggregates appear more open in samples prepared at pH 5 than in the samples grown at pH 6–8. Samples obtained at pH 9 and pH 10 look different; they contain networks of spherical particles. The diameters of the particles obtained at pH 10 are roughly ten times smaller than those obtained at pH 9.

Fig. 5 Top: TEM images of mineral deposits formed at the polymer monolayers at pH 5 to 10. Bottom: qualitative graphical representation of the particle sizes and morphologies.

For further analysis the films were transferred to hydrophobic silicon wafers using the Langmuir–Blodgett technique. Fig. 6 shows AFM images and height profiles along with size distributions of the features observed in the AFM images of the mineralized monolayers. Films grown at pH 5, 6 and 7 exhibit spherical features on the order of 40 to 50 nm in diameter. The features have a relatively broad size distribution with a standard deviation of around 20%, but the films are nevertheless uniform in the sense that we do not observe any other morphologies besides the spherical objects.

Fig. 6 AFM images (2 μm × 2 μm) and corresponding height profiles and size distribution of samples synthesized at different pH values. Synthesis at (a) pH 5, (b) pH 6, (c) pH 7, (d) pH 8, (e) pH 9, (f) pH 10. n.d. = not determined due to too high roughness of these samples; N = number of particles measured; D = average particle diameter.

At pH 8, the samples exhibit spherical objects similar to those just described, but also larger features which appear to stem from the aggregation of individual smaller spheres. This observation is more pronounced for samples grown at higher pH. At pH 9 and 10 the features are larger and the spherical features observed at lower pH are not visible anymore. Instead, the films appear denser and the features are larger than in the films obtained at lower pH.

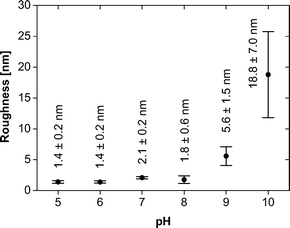
It is, however, difficult to quantify the feature sizes in quite some of the samples: in the samples obtained at pH 6, the individual features are hard to resolve, mostly because of strong interactions between the tip and the sample, and in the samples obtained from pH 8 onwards, the surface is too rough for an accurate size determination of the features. Fig. 7 summarizes the roughness vs. pH of film preparation.

Fig. 7 Roughness of the mineralized films vs. pH.

In summary, AFM and TEM show a diverse population of mineral shapes and sizes vs. the mineralization pH. Generally, we observe two particle shapes (flakes and spheres) at lower pH and one (spheres) at higher pH. As the flakes are highly aggregated, bent and intertwined, their sizes are difficult to quantify from either TEM or AFM images. We have thus only measured the diameters of the spherical objects vs. pH. At pH 5, they have a mean diameter of 43.3 ± 10.1 nm. At pH 6, they have a diameter of 26.9 ± 6.3 nm. At pH 7, the diameter is 52.0 ± 13.1 nm. These values were determined from AFM; the sizes of the samples with larger features obtained at pH 9 were determined from TEM and gave a diameter of 189.6 ± 41.8 nm. The samples grown at pH 8 and 10 gave inconclusive data due to poor sample-to-background contrast. AFM and TEM thus show a strong and fairly systematic (but hard to quantify) variation of particle sizes and shapes vs. pH.

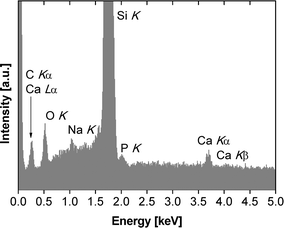
Unfortunately, it is impossible to use electron diffraction or high resolution TEM to assign the crystal phases of the mineral particles because the high electron beam intensity immediately destroys the samples, similar to an earlier study.²³ Moreover, powder X-ray diffraction (XRD),³¹P solid state NMR spectroscopy, Raman and infrared (IR) spectroscopies (both transmission and attenuated total reflection modes) fail due to too low signal intensities. We have therefore used X-ray photoelectron spectroscopy (XPS) and energy-dispersive X-ray spectroscopy (EDXS) to obtain further chemical information on the mineralized films. Even with EDXS and XPS, the data are noisy due to the low amounts of material recovered from the experiments, but they provide qualitative information, mostly on the chemical composition of the films obtained at higher pH. EDXS data (Fig. 8, Table 1) obtained from samples grown at pH 10 confirm the presence of calcium and phosphorus and thus suggest that CP has formed beneath the polymer monolayers. The Ca/P ratio of these particular samples is 1.56 ± 0.49, which is consistent with other CPs precipitated from aqueous solution, but lower than the theoretical value of 1.67 for stoichiometric hydroxyapatite.⁴⁰

Fig. 8 EDX spectrum of monolayer mineralized at pH 10.

Table 1 Results of EDX measurements on films obtained at pH 10. Data are the average and standard deviation of three separate measurements

Element	Mass%	Atom%
Ca	0.30 ± 0.10	0.14 ± 0.05
P	0.15 ± 0.04	0.09 ± 0.03
O	55.62 ± 1.25	66.64 ± 0.02
Si	40.50 ± 2.92	27.68 ± 2.62

---

Moreover the EDX spectra show signals that can be assigned to O, Si, and Na. The oxygen signal is caused by the polymer, the CP and SiO_x or silanol surface groups of the silicon wafer. The silicon signal stems from the silicon wafer. The mineralized monolayers obtained at pH values lower than 10 were either too thin or to weakly mineralized to yield a good signal-to-noise in EDXS. These spectra are dominated by Si signals (from the wafer) and occasionally by Na and Cl signals, likely from sodium chloride (which is present in the buffer, see experimental part) formed on the wafer during film transfer and drying.

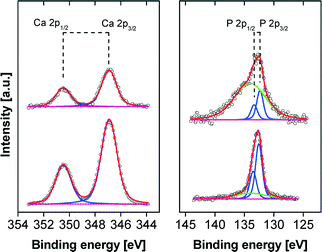
Fig. 9 shows the XP spectra for the Ca 2p and P 2p regions exemplarily for pH 9 and pH 10. The binding energies for Ca 2p_3/2 at 346.8 eV and the corresponding P 2p_3/2 at 132.4 eV are attributed to CP and are in a good agreement with literature.⁴¹ However, in the case of films formed at lower pH the weak P 2p peaks are dominated by the strong Si plasmon of the substrate and, therefore, a reliable quantification is hampered. Nevertheless, down to pH 6 the CP mineralization can be proved unambiguously by the appearance of the non-disturbed Ca 2p peak. In the C 1s region three components are observed at 285.0 eV (C–H), 286.6 eV (C–O, C–N), and 288.5 eV (O–C=O, HN–C=O) originating from the polymer. This is further corroborated by the N 1s peak at 399.8 eV which is attributed to the HN–C=O groups of the polymer.⁴²

Fig. 9 Ca 2p and P 2p XP spectra of films on silicon substrates obtained at pH 9 (top) and pH 10 (bottom). The green line in the P 2p spectra represents the cross-talking broad Si plasmon of the substrate.

2.3. General discussion

Monolayer properties and phase behavior. The goal of the current study is the investigation of a new oligomer with a monodisperse hydrophilic block as a template for CP mineralization. The study complements and expands our previous work^{20–23,43,44} on the effects of interfaces on CP (bio)mineralization.

The polymer forms a stable monomolecular film at the air–water and air–buffer interface (Fig. 2a, b). The films show a slight hysteresis upon compression and expansion (Fig. 2b). This can possibly be assigned to some polymer dissolution into the subphase or partially irreversible multilayer formation. Polymer dissolution into the subphase would be in line with previous observations by Junginger et al., who observed an, although smaller, loss of poly(butadiene)-block-poly[2-(dimethylamino)ethyl methacrylate] (PB–PDMAEMA, M_W = 38 000 g mol⁻¹), to the subphase.²¹ The somewhat more pronounced loss in the current case is likely due to the smaller molecular weight (M_W = 3060 g mol⁻¹) of the oligomer studied here.

Alternatively, the plateau and the hysteresis observed at low to neutral pH could also be due to polymer multilayer formation upon compression. This interpretation is supported by IRRAS data. At low compressions until 25–27 mN m⁻¹ the intensity of the C=O band at 1730 cm⁻¹ increases monotonously. At 25–27 mN m⁻¹, the intensity rises sharply in the case of subphases with pH 2 and 5.9 (Fig. 3). In contrast, at pH 10, the intensity of the same IRRAS band shows a much less distinct kink in the intensities of the C=O bands. This suggests that upon compression at pH 2 and 5.9, the packing density increases with increasing film compression, resulting in an increased number of C=O bonds per volume unit probed by the IRRAS laser. The distinct additional increase at 25–27 mN m⁻¹ could then be caused by the formation of bi- or multilayers, which leads to a further increase in the number of C=O bonds per volume because of increasing film thickness. This model is also supported by the observed increase of the OH-band intensity, which is directly proportional to the film thickness. This phenomenon is much less significant at pH 10. We therefore conclude that here, the monolayer is essentially simply compressed until the collapse pressure is reached. Likely, this is due to the high charge of these films, which prevents multilayer formation due to the higher hydrophilicity of the poly(aspartic acid) block and the stronger charge–charge repulsion.

Moreover, in contrast to the current study (Fig. 2b), Junginger et al. also observed a recovery of the initial surface pressure after ca. 10 minutes, indicating that the PB–PDMAEMA films studied by these authors are able to return to their initial state after compression.²¹ These data indicate that full film recovery needs relatively large molecular weights of the polymers. In contrast, a fraction of the lower molecular weight oligomers used here irreversibly dissolves into the subphase or/and forms multilayers at low pH. As a result, films made from oligomeric additives do not recover easily once they are compressed and re-expanded. In spite of this, the current monolayers are stable enough for mineralization, see the discussion below.

Temperature only has a negligible effect on the film behavior (Fig. 2a). In contrast, the subphase pH has a strong effect on the polymer film (Fig. 4a, b). The MMA significantly increases from pH 5 to 10. We assign this to charge–charge repulsion between neighboring polymer chains which become more highly charged with increasing pH. This is consistent with an earlier study on a PDMAEMA-based block copolymer on subphases with a pH between 5.9 and 8.5, which also finds a dependence of the degree of ionization vs. pH.⁴⁵ Furthermore the transition pressure between 2D gas and liquid phase rises with increasing pH. At high pH, the value for this phase transition is clearly higher than for low pH, likely again due to the stronger electrostatic repulsion.

Moreover, the isotherms of the polymer studied here show an additional plateau at pH 5. The same plateau is also present at pH 6, but much less pronounced, and is also visible on pure water (pH = 5.9) at all subphase temperatures investigated (Fig. 2a). This is similar to previous work by Junginger et al. and Rehfeldt et al. who observed a plateau with monolayers of amphiphilic block copolymers with different hydrophobic but an identical hydrophilic block, poly[2-(dimethylamino) ethyl methacrylate] (PDMAEMA).^21,22,45 The difference between these studies and the current work is the fact that the plateau here is observed at low pH, while the other studies report the plateau at high pH. The reason for this seemingly different observation is the fact that here a polyacid, which is deprotonated (charged) at high pH, has been used whereas other studies used a polybase, which is also deprotonated at high pH, but uncharged.

Interface-controlled mineralization. The molecular weight of the polymer used here is much smaller than those of the polymers used in previous mineralization studies at the air–water interface.^20–23 As a result, different effects on the mineralization can be expected.

Both AFM and TEM (Fig. 5 and 6) show that the mineral deposits are relatively uniform in the sense that only two morphologies (flakes and spheres) are observed at low pH and only one morphology (spheres) is observed at high pH. However, a more detailed analysis shows that the average particle sizes, the size distributions, the organization in the particle agglomerates, and the film homogeneity (as illustrated by the surface roughness, Table 1) are less well defined than in previous examples where polymers with higher molecular weights were used for monolayer formation.

For example, Casse et al.²⁰ showed that CP grown beneath a PnBA–PAA monolayer at high pH yields brittle, highly mineralized films with nanoparticles of uniform spherical shape, high monodispersity, and high order in the mineralized film. This possibly suggests that the longer polycarboxylate block used by Casse et al. is able to attract more calcium ions, to stabilize smaller nanoparticles more uniformly, and to provide a more well-defined local environment for crystal growth than the short hydrophilic block we have studied here. This higher degree of control would then not only be responsible for the uniform particle shapes and the narrow size distributions, but also for the fact that the work of Casse et al. did not find any evidence of particle morphologies other than spheres. Presumably, longer polyelectrolyte blocks more efficiently trap CP particles before they start growing into different shapes, especially at low pH.

Interestingly, Casse et al. found uniform spherical particles of roughly the same size as those observed here. The one notable exception is the samples precipitated at pH 9 (Fig. 5 and 6), which contain much larger spheres (possibly agglomerated nanospheres) than any of the mineral films described by Casse et al. This therefore suggests that the length of the polyelectrolyte block is important in controlling the homogeneity of nucleation and growth, but that under certain circumstances (suitable pH, presumably at least 8 in the current study) also small polyelectrolyte blocks are able to efficiently trap a spherical particle morphology. Possibly, this requires a minimum charge density on the polymer chains. Alternatively, the formation of spheres at higher pH is a synergistic effect, because hydroxyapatite precipitated from basic solutions has a spherical shape as well.^17,18,40,46

One significant difference to the work by Casse et al.²⁰ is the much higher homogeneity of the film and the much higher level of mineralization than in the films discussed here. The films in this previous study are, when grown at high pH, bright white and brittle materials, while the films grown here (at the same pH and with the same calcium and phosphate concentrations) are still nearly invisible even after extended times of mineralization. This suggests that the overall mineralization level of the current films is much lower than of the previous films. AFM, TEM, EDXS, and XPS (Fig. 5, 7–9; Table 1) indeed confirm a rather low level of mineralization.

Low mineralization levels are also consistent with work by Junginger et al.,^21–23 who observed rather poor mineralization beneath monolayers based on PDMAEMA, a basic polymer. We therefore conclude that either short poly(carboxylate) blocks or basic blocks such as those based on PDMAEMA are less efficient for mineralization than longer, negatively charged blocks. Moreover, the current data also show that shorter blocks tend to favor much rougher surfaces than longer chains. We presume that this is again due to the fact that the shorter blocks are not able to trap the growing calcium phosphate crystals as efficiently as the much longer blocks used in the previous studies.

An open question in this respect is the effect of hydrophilic blocks with a molecular weights between those that have already been studied; it is currently unknown if there is a gradual or abrupt transition in the efficiency of mineralization control in this regime. This question will need further work. A further question is related to the effect of betaine-type or ampholytic polymers, which could be able to enrich both calcium and phosphate at the polymer monolayer, but exhibit a significantly different behavior in aqueous phases.

While the current study clearly shows a correlation between the subphase pH and the mineral morphology, size, size distribution, and homogeneity of the mineralized film, the assignment of a crystal phase is challenging. This is, similar to previous studies,²³ mostly related to (1) the low mineralization levels and (2) the electron beam sensitivity of the mineralized samples. In spite of this, EDXS and XPS show that at all pH values studied here, calcium phosphate deposits form. Consistent with literature,^17,18,47 EDXS measurements reveal a Ca/P ratio of 1.56 ± 0.49, which is lower than the stoichiometric ratio of 1.67. Indeed, Bertoni et al.⁴⁸ reported that increasing amounts of poly(acrylic acid) reduce the Ca/P ratio in HAP from 1.67 to 1.56. It is conceivable that the oligomer used here has a similar effect, but this will need confirmation in the future. Alternatively, the lower Ca/P ratio could also originate from a mixture of two phases, but again, this will need more stable materials amenable to a higher resolution phase analysis.

3. Experimental section

Chemicals

Benzyl alcohol (Sigma Aldrich, ReagentPlus®, ≥99%), pyridine (Acros, +99%, extra pure), sodium hydrogen carbonate (Sigma Aldrich, puriss. p.a., ACS reagent, reag. Ph. Eur., ≥99.7%, powder), magnesium sulfate (VWR, ≥99.7%), copper(II) bromide (Sigma Aldrich, ≥99%), ammonium formate (Sigma Aldrich BioUltra, ≥99%), Pd/C (Sigma Aldrich, 10 wt.% loading), celite (Sigma Aldrich), hydrochloric acid (Roth-ROTIPURAN®, p.a., ACS, 37%), acetic acid (Alfa Aesar, glacial, ≥99%), benzotriazol-1-yl-oxytripyrrolidinophosphonium hexafluorophosphate (Applied Biosystems, Nova Biochem), 1-hydroxybenzotriazole (Sigma Aldrich, ≥97.0%), N,N-diisopropylethylamine (Acros Organics), triethylsilane (Sigma Aldrich, 97%), glycocoll (glycine; Pufferan®, Roth), calcium nitrate tetrahydrate (ABCR), diammonium hydrogen phosphate (Merck), calcium hydride (Acros, ca. 93%, extra pure, 0–20 mm grain size, up to 15% powder), potassium hydroxide (Sigma-Aldrich, ACS reagent, ≥85%, pellets), tetrahydrofuran (Sigma Aldrich, 99.5%), absolute ethanol (Sigma Aldrich, absolute, reag. ISO, reag. Ph. Eur., ≥99.8% (GC)), chloroform (spectroscopic grade, Roth), diethyl ether (VWR, 99.9%), dioxane (Sigma Aldrich, 99.5%), methanol (Merck, LiChrosolv®), silica gel (Sigma Aldrich, high purity grade) were used as received.

TentaGelSTRT-GlyFmoc resin (Rapp Polymere), Fmoc-4 (nitro)phenylalanine (Nova Biochem), Fmoc-Gly-H (Iris Biotech), Fmoc-ASP-H (Iris Biotech), were stored at −18 °C. 2-Bromopropionyl bromide (Sigma Aldrich, 97%), N,N,N′,N′,N′′-pentamethyldiethylenetriamine (Sigma Aldrich, 99%), were distilled and stored at 4 °C. Dichloromethane (Iris biotech, peptide grade) and acetonitrile (Sigma Aldrich, ACS reagent, ≥99.5%) were distilled over calcium hydride. Dimethylformamide (Sigma Aldrich, 99.8%) and trifluoroacetic acid (Acros Organics, 99.5%) were distilled. N,N-diisopropylethylamine (Acros Organics, Peptide Synthesis grade) was distilled over potassium hydroxide platelets and stored in the dark at 4 °C. n-Butyl acrylate (Sigma Aldrich, 99%) was distilled and stored in the dark at 4 °C. Copper(I) bromide (Sigma Aldrich, 98%) was stirred in pure acetic acid overnight, washed with dry methanol and diethyl ether and dried under reduced pressure.

Polymer synthesis

(1) The peptide with the sequence HO-(Gly)-(Asp)₁₀-(pNO₂Phe)-Gly-H was synthesized using a peptide synthesizer (ABI 433A, Applied Biosystems Darmstadt) using a TentaGelSTRT-GlyFmoc resin (0.435 g, 0.23 mmol g⁻¹) and standard Fmoc chemistry.

(2) Poly(n-butyl acrylate) was synthesized via atom transfer radical polymerization. Firstly the initiator benzyl-2-bromopropanoate was synthesized. In a bake-out flask filled with nitrogen 3.31 mL of benzyl alcohol (32 mmol) and 3.67 mL of pyridine (35 mmol) were dissolved in 20 mL of dichloromethane under nitrogen. The solution was cooled to 0 °C and 3.67 mL of 2-bromopropionyl bromide (35 mmol) were added drop by drop and the solution changed the color to light yellow and a white precipitate formed. The mixture was stirred for 3 h and terminated trough the addition of 20 mL of an ice/water mixture. Then 20 mL of dichloromethane were added and the organic phase was washed with aqueous sodium hydrogen carbonate and water and dried over magnesium sulfate. The solvent was removed by rotary evaporation and dried under reduced pressure. The product was purified via condensation in high vacuum (1 × 10⁻³ mbar) at 70 °C to yield 4.79 g of benzyl 2-bromopropanoate (19.7 mmol). ¹H-NMR (400 MHz, CDCl₃, δ [ppm]): 7.35 (s, 5H); 5.19 (s, 2H); 4.39 (q, 1H); 1.82 (d, 3H). Elemental analysis: calculated: C, 49.41%; H, 4.56%. Experimental: C, 48.23%; H, 4.25%.

In a Schlenk flask 0.3586 g (2.5 mmol) of CuBr and 0.0223 g (0.01 mmol) of CuBr₂ were provided and the flask was filled with nitrogen. Subsequently the nitrogen was exchanged by argon by reducing the pressure and filling the flask with argon (3 times). In a second flask 0.875 mL (5 mmol) of the initiator benzyl 2-bromopropanoate was dissolved in 2 mL of acetonitrile; the mixture was degassed with argon for 5 minutes. In a third flask 0.55 mL (2.63 mmol) of the ligand N,N,N′,N′,N′′-pentamethyldiethylenetriamine (PMDETA) were dissolved in 9.5 mL of acetonitrile and 21.5 mL (150 mmol) of n-butyl acrylate and degassed with argon. The contents of the third flask were transferred under argon to the flask with the copper salts and the copper salts were dissolved by stirring and ultrasound. Afterwards the flask was heated to 50 °C. The reaction was started by adding the initiator (content of flask 2). After 260 minutes the reaction was stopped by adding air. For removal of the catalyst, the sample was diluted in THF and filtered through a column filled with silica gel. The solvent was removed to yield 18.5 g (8.56 mmol) of the polymer. To remove the benzoyl ester protecting group, 18.5 g (8.56 mmol) of the polymer were dissolved in 233 mL of absolute ethanol and 3.13 g (49.67 mmol) of ammonium formate were added under a dry argon atmosphere. To the solution a tip of a spatula of Pd/C (10%) was added and the reaction mixture was stirred at 35 °C for 2 h and then for 48 h at room temperature. Then the solution was filtered over Celite and the solvent was removed under reduced pressure. The residue was dissolved in dichloromethane (DCM) and extracted once with 0.3 M hydrochloric acid and once with Millipore water. The organic phase was dried over MgSO₄ and the DCM was removed by rotary evaporation. NMR showed that the removal of the protecting group was not complete, so the last procedure was repeated. The viscous oil was dissolved in 20 mL acetone and precipitated in methanol/ice (80% MeOH + 20% ice). The precipitate was dissolved in DCM and dried with MgSO₄. The solvent was removed to yield 7.5 g (mmol) of poly(n-butyl acrylate). GPC (THF): M_w = 3288 g mol⁻¹; PDI = 1.42. ¹H-NMR (400 MHz, CDCl₃, δ [ppm]): 0.94 (3H, –CH₃); 1.19; 1.37 (2H, –CH₂–CH₂–CH₂–O); 1.60 (2H, –CH₂–CH₂–O); 1.85; 2.28 (1H, –CH₂–C(C=O)H–); 3.75; 4.04 (2H, –CH₂–O).

(3) The coupling of the PnBuA to the peptide was done as follows: the resin bearing the peptide (1) was washed with dimethylformamide (DMF). 208.12 mg (0.4 mmol) of benzotriazol-1-yl-oxytripyrrolidinophosphonium hexafluorophosphat (PyBOP) and 61.24 mg (0.4 mmol) of 1-hydroxybenzotriazole (HOBt) were dissolved in 5 mL of DMF. Then 103.44 mg (0.8 mmol) of N,N-diisopropylethylamine (DIPEA) were added. After a few minutes this solution was added to 948 mg (0.4 mmol) of the poly(n-butyl acrylate) (2). This PnBuA-containing solution was then added to the mixture containing the peptide-resin and this mixture was shaken overnight. The resin was washed with DMF and the coupling was repeated overnight. Thereafter, the resin was washed with DMF and DCM and dried. The cleavage of the polymer-peptide conjugate (Fig. 1) from the resin was carried out with a 100 mL solution of 50% trifluoroacetic acid (TFA), 49% DCM and 1% triethylsilane (TES) for 1 h. DCM was removed and the residual mixture was precipitated from hexane, centrifuged and freeze dried two times from dioxane to remove the TFA to yield 242 mg of the polymer with the sequence Gly(Asp)₁₀(pNO₂Phe)Gly(nBuA)₁₃. GPC (THF): M_w = 3060 g mol⁻¹; PDI = 1.23. ¹H-NMR (300 MHz, DMSO, δ [ppm]): 0.88 (t); 1.31 (q); 1.52 (m); 3.40 (m); 3.97 (m); 4.51 (m); 7.50 (m); 8.05 (m). ATR-IR ([small nu, Greek, tilde] [cm⁻¹]): 1725 (C=O stretching vibration of saturated esters); 1660 (C=O stretching vibration for secondary amines); 1523 (N–H deformation vibration; C–N stretching vibration for secondary amines); 1169 (symmetric C–O–C stretching vibration); 839 (“out-of-plane” deformation vibration of R–Ph–R). Elemental analysis: calculated: C, 55.22%; N, 6.13%; O, 31.53%; H, 7.12%. Experimental: C, 53.8%; N, 6.9%; H, 6.9%.

Langmuir monolayer experiments

Langmuir monolayer experiments were done on a homemade Langmuir trough with one moveable barrier placed on an anti-vibration table. The experiments were performed at 10, 20, and 30 °C on Millipore water. The isotherms were also recorded at 20 °C and pH values of 5, 6, 7, 8, 9 and 10 on a glycocoll buffer subphase.⁴⁹ For the glycocoll buffer 7.505 g (0.1 mol) of glycine and 5.844 g (0.1 mol) of sodium chloride were dissolved in 1 L of Millipore water yielding a 0.1 M buffer solution. The polymer (1.001 mg mL⁻¹) was dissolved in a choroform–methanol solution (90 : 10 v/v) and 25 μL were spread at the buffer–air interface. After 10 minutes the solvents were evaporated and the surface pressure was recorded with a Wilhelmy plate. The compression/expansion experiments were done at 20 °C. For all experiments the barriers were compressed and expanded with a speed of 14 Å/(molecule min).

Mineralization

All mineralization experiments were done at 23–24 °C and a surface pressure of 30 mN m⁻¹ on a Nima 611 trough (Nima Technology, UK) with two moveable barriers, a total area of 250 cm² and a subphase volume of 165 mL. Compression speed was 25 cm² min⁻¹. The glycocoll buffer was used as subphase at pH values 5, 6, 7, 8, 9 and 10. The subphase also contained 2 mM Ca(NO₃)₂·4H₂O.

The polymer (1.001 mg mL⁻¹) was spread from a chloroform/methanol solution (90 : 10 v/v). After evaporation of the organic solvents from spreading, 0.33 mL of a 1 M (NH₄)₂HPO₄ solution was injected behind the barriers using a Hamilton syringe, yielding a total (NH₄)₂HPO₄ concentration of 2 mM in the subphase. The subphase was constantly, but slowly, stirred during the mineralization using a magnetic stirrer in the dipping well of the trough. After 4 h, the mineralized films were transferred to silicon wafers using the Langmuir–Blodgett technique. After removing from the trough samples were blotted with filter paper to remove excess liquid. Samples for TEM were picked up directly from the surface with carbon-coated TEM copper grids and blotted with filter paper.

Atomic force microscopy (AFM)

AFM images were acquired in air with a Veeco Dimension 3100 in non-contact mode on films transferred to silicon. The resonance frequency of the cantilever was 285 kHz and the spring constant was 42 N m⁻¹.

Electron microscopy

Transmission electron microscopy (TEM) was done on a CM100 electron microscope (Philips, Eindhoven, The Netherlands) at 80 kV with a tungsten filament. Energy dispersive X-ray spectroscopy (EDXS) was done on an Oxford INCAx-act SN detector from 135 eV to 5.9 keV mounted on a JEOL JSM 6510 with a tungsten hairpin filament operated at 15 kV.

Infrared reflection absorption spectroscopy (IRRAS)

IRRAS data was recorded on an IFS 66 FT-IR spectrometer (Bruker) equipped with a liquid nitrogen cooled MCT (mercury cadmium telluride) detector attached to an external air/water reflection unit (XA-511, Bruker). The IR beam was focused onto the water surface of the thermostated Langmuir trough. The incident IR beam was polarized with a KRS-5 wire grid polarizer. Measurements were performed using a trough with two compartments. One compartment contains the monolayer system under investigation (sample), whereas the other is filled with the pure subphase (reference). The trough was shuttled so that the IR beam illuminated either the sample or the reference. The single-beam reflectance spectrum from the reference trough was taken as background for the single-beam reflectance spectrum of the monolayer in the sample trough to calculate the reflection–absorption spectrum as −log(R/R₀) to eliminate the water vapor signal.^50–55 To maintain a constant water vapor content, the whole system was placed into a hermetically sealed box. The resolution and scanner speed in all experiments were 8 cm⁻¹ and 20 kHz. For s-polarized light, spectra were co-added over 200 scans, and spectra with p-polarized light were co-added over 400 scans. The two different light polarizations provided information on molecular orientation. A change in the intensity ratio of p-polarized to s-polarized light (dichroic ratio) for a vibrational band indicates a change in the average orientation of the transition dipole moment and thus of the molecule. The intensity and shape of a reflection–absorption band depends on many variables: absorption coefficient, full-width at half-height, orientation of the transition dipole moment within the molecule, molecular tilt angle, polarization and angle of incidence of the incoming light, as well as on the layer thickness and its refractive index. In a first step, the layer thickness can be estimated from the OH stretching vibrational band in the range of 3800–3000 cm⁻¹.

X-ray photoelectron spectroscopy

XPS measurements were performed using a K-Alpha XPS instrument (Thermo Fisher Scientific, East Grinstead, UK). Data acquisition and processing using the Thermo Avantage software is described elsewhere.⁵⁶ All samples were analyzed using a microfocused monochromated Al Kα X-ray source (30–400 μm spot size). The K-Alpha charge compensation system was employed during analysis, using electrons of 8 eV energy and low-energy argon ions to prevent any localized charge build-up. The spectra were fitted with one or more Voigt profiles (binding energy uncertainty: ±0.2eV). The analyzer transmission function, Scofield sensitivity factors,⁵⁷ and effective attenuation lengths (EALs) for photoelectrons were applied for quantification. EALs were calculated using the standard TPP-2M formalism.⁵⁸ All spectra were referenced to the C1s peak of hydrocarbon at 285.0 eV binding energy controlled by means of the well-known photoelectron peaks of metallic Cu, Ag, and Au.

4. Conclusions

Calcium phosphate is one of the most important biominerals, but particularly the mechanisms of CP nucleation and growth at surfaces and interfaces are not fully understood so far. The current study focuses on the effects of a model oligomeric additive at the air–water interface on CP formation. The study bridges the knowledge gap between existing studies on the effects of (1) higher molecular weight polymers and (2) low molecular weight surfactants. The most important finding of the study is that even monolayers made from oligomers are able to control the formation of CP. However, the control (in terms of particle size, size distribution, particle morphology, particle arrangement) over CP mineralization is not as tight as in other examples with monolayers made from higher molecular weight polymers.^20–23 Rather the effects are similar to those observed for low molecular weight compounds.⁵⁹ Moreover, comparison with a study by Casse et al.²⁰ shows that the degree of mineralization is much lower in the current case. We postulate that these effects are due to the shorter hydrophilic block, which is not able to interact as efficiently with the incoming calcium and phosphate ions and with growing (nanoparticulate) calcium phosphate. The current results thus suggest that not only the charge and the subphase pH but also the length of the hydrophilic block provides a means to control the mineralization of CP at the air–water interface. As there is only very limited data available on this topic, further research into the subject will be necessary to elucidate the entire process in detail.

Acknowledgements

The authors thank I. Berndt for technical support and IRRAS measurements, A. Heilig for help with AFM, M. Gräwert for GPC measurements, R. Löbbicke for help with EDXS, Dr. J. Reiche for access to the Langmuir trough, and Dr. C. Günter for access to the EDXS. We thank ChemAxon LLC for a free license to MarvinSketch v5.12 and the Karlsruhe Nano Micro Facility (KNMF project 451) for XPS instrument time. Funding by the University of Potsdam and the Max Planck Institute of Colloids and Interfaces is gratefully acknowledged.

Notes and references

1. M. Epple, Biomaterialien Und Biomineralisation, Teubner, Wiesbaden, 2003.
2. K. Naka, C. K. Carney and H. Cölfen, Biomineralization I: Crystallization and Self-Organization Process, Springer, 2007.
3. K. Naka, C. K. Carney and H. Cölfen, Biomineralization II: Mineralization Using Synthetic Polymers and Templates, Springer, 2007.
4. E. Bäuerlein, Biomineralization: From Biology to Biotechnology and Medical Application, Wiley-VCH, 2000.
5. E. Bäuerlein and P. Behrens, Handbook of Biomineralization, in Biomimetic and Bioinspired Chemistry, Wiley-VCH, Weinheim, 2007.
6. E. Bäuerlein, P. Behrens and M. Epple, Handbook of Biomineralization: Biological Aspects and Structure Formation, Wiley-VCH, 2007.
7. E. Bäuerlein and P. Behrens, Biological Aspects and Structure Formation, in Handbook of Biomineralization, Wiley-VCH, Weinheim, 2007, vol. 2.
8. A. Sigel, H. Sigel and R. K. O. Sigel, Biomineralization: From Nature to Application, Wiley, 2008.
9. K. Simkiss and K. M. Wilbur, Biomineralization: Cell Biology and Mineral Deposition, Academic Press, 1989.
10. S. V. Dorozhkin and M. Epple, Biological and Medical Significance of Calcium Phosphates, Angew. Chem., Int. Ed., 2002, 41, 3130–3146.
11. W. Suchanek and M. Yoshimura, Processing and Properties of Hydroxyapatite-Based Biomaterials for Use as Hard Tissue Replacement Implants, J. Mater. Res., 1998, 13, 94–117.
12. L. L. Hench, Bioceramics: From Concept to Clinic, J. Am. Ceram. Soc., 1991, 74, 1487–1510.
13. D. J. White, Dental Calculus: Recent Insights into Occurrence, Formation, Prevention, Removal and Oral Health Effects of Supragingival and Subgingival Deposits, Eur. J. Oral Sci., 1997, 105, 508–522.
14. R. Vattikuti and D. A. Towler, Osteogenic Regulation of Vascular Calcification: An Early Perspective, Am. J. Physiol., 2004, 286, E686–E696.
15. S. Mann, Biomineralization - Principles and Concepts in Bioinorganic Materials Chemistry, Oxford Chemistry Masters, Oxford, 2001.
16. G. K. Hunter, P. V. Hauschka, A. R. Poole, L. C. Rosenberg and H. A. Goldberg, Nucleation and Inhibition of Hydroxyapatite Formation by Mineralized Tissue Proteins, Biochem. J., 1996, 317, 59–64.
17. K. Bleek and A. Taubert, New Developments in Polymer-Controlled, Bioinspired Calcium Phosphate Mineralization from Aqueous Solution, Acta Biomater., 2013, 9, 6283–6321.
18. S. Schweizer and A. Taubert, Polymer-Controlled, Bio-Inspired Calcium Phosphate Mineralization from Aqueous Solution, Macromol. Biosci., 2007, 7, 1085–1099.
19. T. Mai, K. Bleek and A. Taubert, Organic/Inorganic Hybrid Surfaces, in Biomaterials Surface Science, Wiley-VCH Verlag GmbH & Co. KGaA, 2013, pp. 311–336.
20. O. Casse, O. Colombani, K. Kita-Tokarczyk, A. H. E. Muller, W. Meier, A. Taubert and A. H. E. Müller, Calcium Phosphate Mineralization beneath Monolayers of Poly(n-Butylacrylate)-Block-Poly(acrylic Acid) Block Copolymers, Faraday Discuss., 2008, 139, 179–197.
21. M. Junginger, K. Bleek, K. Kita-Tokarczyk, J. Reiche, A. Shkilnyy, F. Schacher, A. H. E. Müller and A. Taubert, Calcium Phosphate Growth beneath a Polycationic Monolayer at the Air-Water Interface: Effects of Oscillating Surface Pressure on Mineralization, Nanoscale, 2010, 2, 2440–2446.
22. M. Junginger, K. Kita-Tokarczyk, T. Schuster, J. Reiche, F. Schacher, A. H. E. Müller, H. Cölfen and A. Taubert, Calcium Phosphate Mineralization beneath a Polycationic Monolayer at the Air–Water Interface, Macromol. Biosci., 2010, 10, 1084–1092.
23. M. Junginger, C. Kübel, F. H. Schacher, A. H. E. Müller and A. Taubert, Crystal Structure and Chemical Composition of Biomimetic Calcium Phosphate Nanofibers, RSC Adv., 2013, 3, 11301.
24. A. Dey, P. H. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. de With, N. A. J. M. Sommerdijk and G. D. With, The Role of Prenucleation Clusters in Surface-Induced Calcium Phosphate Crystallization, Nat. Mater., 2010, 9, 1010–1014.
25. L.-J. Zhang, H.-G. Liu, X.-S. Feng, R.-J. Zhang, Y.-D. Mu, J.-C. Hao, D.-J. Qian and Y.-F. Lou, Mineralization Mechanism of Calcium Phosphates under Three Kinds of Langmuir Monolayers, Langmuir, 2004, 20, 2243–2249.
26. K. Kita-Tokarczyk, M. Junginger, S. Belegrinou and A. Taubert, Amphiphilic Polymers at Interfaces, in Self Organized Nanostructures of Amphiphilic Block Copolymers II, ed. A. H. E. Müller and O. Borisov, Springer, Berlin Heidelberg, 2011, vol. 242, pp. 151–201.
27. A. L. Litvin, S. Valiyaveettil, D. L. Kaplan and S. Mann, Template-Directed Synthesis of Aragonite under Supramolecular Hydrogen-Bonded Langmuir Monolayers, Adv. Mater., 1997, 9, 124–127.
28. Y. Chen, J. Xiao, Z. Wang and S. Yang, Observation of an Amorphous Calcium Carbonate Precursor on a Stearic Acid Monolayer Formed during the Biomimetic Mineralization of CaCO(3), Langmuir, 2009, 25, 1054–1059.
29. K. Sato, Y. Kumagai, K. Watari and J. Tanaka, Hierarchical Texture of Calcium Carbonate Crystals Grown on a Polymerized Langmuir−Blodgett Film, Langmuir, 2004, 20, 2979–2981.
30. M. Maas, H. Rehage, H. Nebel and M. Epple, On the Formation of Calcium Carbonate Thin Films under Langmuir Monolayers of Stearic Acid, Colloid Polym. Sci., 2007, 285, 1301–1311.
31. E. DiMasi, V. M. Patel, M. Sivakumar, M. J. Olszta, Y. P. Yang and L. B. Gower, Polymer-Controlled Growth Rate of an Amorphous Mineral Film Nucleated at a Fatty Acid Monolayer, Langmuir, 2002, 18, 8902–8909.
32. A. Taubert, J. F. Mano and J. C. Rodríguez-Cabello, Biomaterials Surface Science, ed. A. Taubert, J. F. Mano and J. C. Rodríguez-Cabello, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2013.
33. M. Fricke and D. Volkmer, Crystallization of Calcium Carbonate Beneath Insoluble Monolayers: Suitable Models of Mineral–Matrix Interactions in Biomineralization?, in Biomineralization I SE - 63, ed. K. Naka, Springer, Berlin Heidelberg, 2007, vol. 270, pp. 1–41.
34. D. Volkmer, M. Fricke, M. Gleiche and L. Chi, Elucidating the Role of Charge Density on the Growth of CaCO3 Crystals underneath Calix[4]arene Monolayers, Mater. Sci. Eng., C, 2005, 25, 161–167.
35. M. Fricke and D. Volkmer, Crystallization of Calcium Carbonate Beneath Insoluble Monolayers: Suitable Models of Mineral–Matrix Interactions in Biomineralization?, in Biomineralization I SE - 63, ed. K. Naka, Springer, Berlin Heidelberg, 2007, vol. 270, pp. 1–41.
36. D. Volkmer, M. Fricke, D. Vollhardt and S. Siegel, Crystallization of (012) Oriented Calcite Single Crystals underneath Monolayers of tetra(carboxymethoxy)calix[4]arenes, J. Chem. Soc., Dalton Trans., 2002, 4547.
37. D. Volkmer, M. Fricke, C. Agena and J. Mattay, Interfacial Electrostatics Guiding the Crystallization of CaCO3 underneath Monolayers of Calixarenes and resorcarenes Electronic Supplementary Information (ESI) Available: Representative Optical and Scanning Electron Micrographs of CaCO3 Crystals Grown Und, J. Mater. Chem., 2004, 14, 2249.
38. D. Volkmer and M. Fricke, Growth of Calcite Single Crystals Underneath Monolayers of 5, 11, 17, 23-Tetra-T-Butyl-25, 26, 27, 28-tetrakis(carboxymethoxy)calix[4]arene, Z. Anorg. Allg. Chem., 2003, 629, 2381–2390.
39. Marvin Was Used for Drawing, Displaying and Characterizing Chemical Structures, Substructures and Reactions, Marvin 6.1.4, 2013, ChemAxon http://www.chemaxon.com.
40. S. V. Dorozhkin, Calcium Orthophosphates in Nature, Biology and Medicine, Materials, 2009, 2, 399–498.
41. A. Boyd, M. Akay and B. J. Meenan, Influence of Target Surface Degradation on the Properties of R.f. Magnetron-Sputtered Calcium Phosphate Coatings, Surf. Interface Anal., 2003, 35, 188–198.
42. T. Tischer, T. K. Claus, M. Bruns, V. Trouillet, K. Linkert, C. Rodriguez-Emmenegger, A. S. Goldmann, S. Perrier, H. G. Börner and C. Barner-Kowollik, Spatially Controlled Photochemical Peptide and Polymer Conjugation on Biosurfaces, Biomacromolecules, 2013, 14, 4340–4350.
43. S. Schweizer, T. Schuster, M. Junginger, G. Siekmeyer and A. Taubert, Surface Modification of Nickel/Titanium Alloy and Titanium Surfaces via a Polyelectrolyte Multilayer/Calcium Phosphate Hybrid Coating, Macromol. Mater. Eng., 2010, 295, 535–543.
44. R. Löbbicke, M. Chanana, H. Schlaad, C. Pilz-Allen, C. Günter, H. Möhwald and A. Taubert, Polymer Brush Controlled Bioinspired Calcium Phosphate Mineralization and Bone Cell Growth, Biomacromolecules, 2011, 12, 3753–3760.
45. F. Rehfeldt, R. Steitz, S. P. Armes, R. von Klitzing, A. P. Gast and M. Tanaka, Reversible Activation of Diblock Copolymer Monolayers at the Interface by pH Modulation, 1: Lateral Chain Density and Conformation, J. Phys. Chem. B, 2006, 110, 9171–9176.
46. S. V. Dorozhkin, Calcium Orthophosphates, J. Mater. Sci., 2007, 42, 1061–1095.
47. Calcium Phosphates in Biological and Industrial Systems, ed. Z. Amjad, Springer, US: Boston, MA, 1998.
48. E. Bertoni, A. Bigi, G. Falini, S. Panzavolta and N. Roveri, Hydroxyapatite/polyacrylic Acid Nanocrystals, J. Mater. Chem., 1999, 9, 779–782.
49. W. Rauscher and V. Friebe, Chemische Tabellen Und Rechentapfeln Für Die Analytische Praxis, Verlag Harri Deutsch, Frankfurt am Main, 2000.
50. R. Mendelsohn, J. W. Brauner and A. Gericke, External Infrared Reflection Absorption Spectrometry of Monolayer Films at the Air-Water Interface, Annu. Rev. Phys. Chem., 1995, 46, 305–334.
51. C. R. Flach, A. Gericke and R. Mendelsohn, Quantitative Determination of Molecular Chain Tilt Angles in Monolayer Films at the Air/Water Interface: Infrared Reflection/Absorption Spectroscopy of Behenic Acid Methyl Ester, J. Phys. Chem. B, 1997, 101, 58–65.
52. A. H. Muenter, J. Hentschel, H. G. Börner and G. Brezesinski, Characterization of Peptide-Guided Polymer Assembly at the Air/water Interface, Langmuir, 2008, 24, 3306–3316.
53. T. D. Andreeva, J. G. Petrov, G. Brezesinski and H. Möhwald, Structure of the Langmuir Monolayers with Fluorinated Ethyl Amide and Ethyl Ester Polar Heads Creating Dipole Potentials of Opposite Sign, Langmuir, 2008, 24, 8001–8007.
54. R. Mendelsohn, G. Mao and C. R. Flach, Infrared Reflection-Absorption Spectroscopy: Principles and Applications to Lipid-Protein Interaction in Langmuir Films, Biochim. Biophys. Acta, 2010, 1798, 788–800.
55. C. Stefaniu, G. Brezesinski and H. Möhwald, Langmuir Monolayers as Models to Study Processes at Membrane Surfaces, Adv. Colloid Interface Sci., 2014, 208C, 197–213.
56. K. L. Parry, A. G. Shard, R. D. Short, R. G. White, J. D. Whittle and A. Wright, ARXPS Characterisation of Plasma Polymerised Surface Chemical Gradients, 2006, pp. 1497–1504.
57. J. H. Scofield, Hartree-Slater Subshell Photoionization Cross-Sections at 1254 and 1487 eV, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 129–137.
58. S. Tanuma, C. J. Powell and D. R. Penn, Calculations of Electron Inelastic Mean Free Paths. V. Data for 14 Organic Compounds over the 50–2000 eV Range, Surf. Interface Anal., 1994, 21, 165–176.
59. L.-J. Zhang, H.-G. Liu, X.-S. Feng, R.-J. Zhang, Y.-D. Mu, J.-C. Hao, D.-J. Qian and Y.-F. Lou, Mineralization Mechanism of Calcium Phosphates under Three Kinds of Langmuir Monolayers, Langmuir, 2004, 20, 2243–2249.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ce02274b

---