Mechanical properties of zeolitic metal–organic frameworks: mechanically flexible topologies and stabilization against structural collapse

Abstract

We report on the elastic moduli of two large pore zeolitic metal–organic frameworks (rho- and sod-ZMOF). Their extremely low (1.93 GPa), and intermediate (5.57 GPa) moduli are compared with those of zeolites of identical topologies, finding similarities relative to frameworks in the same family. Whilst collapse upon ball-milling occurs quickly, common solvents can be used to stabilise the structure, a facile method which may be applicable to other porous hybrid frameworks.

---

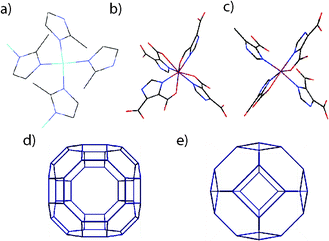
Zeolitic imidazolate frameworks (ZIFs) are a family of porous metal–organic frameworks (MOFs) which have been researched extensively over the past decade due to their potential in gas sorption and separation, catalysis and harmful substance storage applications.¹ Related materials called zeolitic metal–organic frameworks (ZMOFs) are comparatively unknown – despite the same enormous potential.^2,3 Structural similarities with zeolites are clear; the Zn(imidazolate dicarboxylate)₄ unit of ZMOFs and the Zn(imidazolate)₄ motif of ZIFs (Fig. 1) replace the primary SiO₄ building unit of zeolites, though the ≈145° angle subtended between metal nodes is unchanged and results in identical network architectures across the three families.⁴

Fig. 1 (a) Zn coordination environment in ZIF-8, (b) in 8-coordinate and (c) 6-coordinate environments in rho- and sod-ZMOF respectively. C – black, N – dark blue, O – red, In – pink, Zn – light blue, H atoms omitted. d) The ‘rho’ and (e) the ‘sod’ topologies/network architectures shared by ZIFs, ZMOFs and zeolites.

The mechanical properties of porous frameworks are of great importance when considering chemical sensing or filtering, where precise mechanical response, or intransient structural rigidity is required.⁵ Recent work has suggested that basic structural motifs may play a much larger role than chemical functionality in determining physical properties such as compressibility, elastic moduli and structural rigidity under processing conditions (e.g. ball-milling).^6–8 An investigation of topologically different systems of similar chemical functionalities is therefore required in order to further investigate the role of network architecture in determining physical response.

Rho- and sod-ZMOF, [DMA·In(HImDC)₂] and [H₂Im·In(HImDC)₂] (H₂Im: imidazole cation, C₃H₅N₂⁺, HImDC: imidazolate-dicarboxylate, C₅H₂N₂O₄³⁻, DMA: dimethylammonium, C₂H₈N₁⁺), hereby referred to as 1 and 2, are two large-pore ZMOFs which respectively contain eight- and six-coordinate In³⁺ ions, linked in a three dimensional array by HImDC ligands.⁹ Each In³⁺ ion is connected to four ligands through donor nitrogen atoms, in addition to one carboxylate group from each imidazolate in 1, and one from two of the four ligands in 2. The sodalite topology (sod) of the latter is shared by ZIF-8 [Zn(mIm)₂] (mIm: 2-methylimidazolate, C₄H₅N₂⁻) and a zeolite of the same name, whilst 1 can be compared with the inorganic zeolite of ‘rho’ topology. Both three-letter codes refer to the underlying network seen by only displaying metal ions (Fig. 1d and e).

Single crystal samples of 1 and 2 were synthesized solvothermally and evacuated according to previous literature (Fig. S1, S2‡),^2,9 being obtained as polyhedral single crystals of dimensions 0.1 × 0.15 × 0.15 mm and 0.3 × 0.3 × 0.15 mm. 1 crystallises in the cubic Im3̄m space group (a = 30.0622(7) Å, V = 29970.7(12) ų) and contains one pore of diameter 18 Å per unit cell, linked by apertures measuring 8 Å in diameter, whilst 2 crystallises in the cubic Fd3̄c space group (a = 36.0435(11) Å, V = 46825(2) ų) and contains one 12 Å central nanopore linked by 8 smaller channels. Both 1 and 2 are neutral, courtesy of charge balancing DMA and H₂Im cations (which could not be accurately located). Single crystal X-ray diffraction was used to perform face indexing, thereby enabling correlation of crystal facet and crystallographic direction (Fig. S3, S4‡).

Nanoindentation on 1 and 2 was performed in order to probe the elastic modulus, E, and hardness, H, at depths of up to 1000 nm. Load – displacement data (Fig. 2a, S5‡) were used to calculate E (Fig. 2B) and H (Fig. S6‡) for 1 and 2 along the (0,−1,−1) and (−1,−1,2) oriented facets respectively (Fig. 3) as a function of depth.

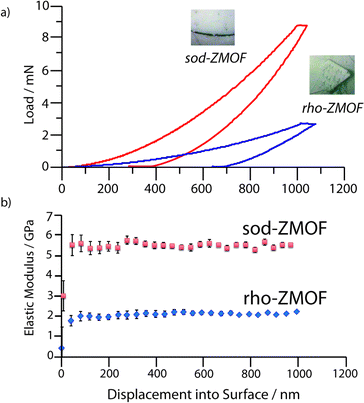Fig. 2 Representative (a) load vs. displacement curves and (b) elastic moduli values as a function of depth for 1 and 2. Error bars are taken from the standard deviation of more than 15 indents.

Fig. 3 View along (a) the (0,−1−1) crystallographic direction of 1 and (b) the (−1,−1,2) direction of 2.

Single crystal facets of 1 were observed to develop lower loads upon indenting, resulting in an extremely low elastic modulus (E_{(0,−1,−1)} = 1.93 ± 0.12 GPa), along with H = 0.19 ± 0.01 GPa. The results contrast strongly with the higher stiffness and hardness of 2 (E_{(−1,−1,2)} = 5.57 ± 0.16 GPa, H = 0.54 ± 0.03 GPa). Whilst both H values lie in the broad range expected for porous metal–organic framework materials (0.1–1.2 GPa), the resistance to plastic deformation of 1 was found to be lower than that of 2. The higher H and E of 2 are in agreement with the lower solvent accessible volume (SAV) (40% cf. 54%, Fig. S7‡), which causes large variations in the mechanical behaviour of metal–organic frameworks.¹⁰

Interestingly, the modulus determined for 1 is amongst the lowest E experimentally reported for a MOF thus far, though slightly lower values have been predicted for those which possess a flexible ‘wine-rack’ motif (e.g. MIL-53).¹¹

The sodalite topology of 2 is shared with ZIF-8, a framework of larger SAV (50%), which possesses the lowest reported experimental elastic modulus of the ZIF family (E₁₁₁ = 2.78 GPa). To provide accurate comparison of the mechanical properties of the two frameworks, we extracted an E_−1–12 value of 2.98 GPa for ZIF-8 using the experimental elastic tensors reported in the literature (ESI‡).¹² The significantly higher stiffness of 2 is agreement with its lower SAV, though surprisingly, is very similar to predictions that can be made for the elastic modulus of a ZIF of equal SAV.¹⁰ Whilst prior studies have shown that the flexibility of the metal polyhedral environments plays a large role in determining elastic moduli,¹³ similarities in M–N bond length (2 and 2.2 Å) and Zn²⁺–In³⁺ radii provide further evidence of the strong role of porosity in determining mechanical properties.

However, the elastic modulus of 1 remains anomalously low (a value of E = 3.5 GPa being predicted for a ZIF of 55% SAV), the experimental value (E = 1.93 GPa) suggesting the ‘rho’ topology might be particularly compliant. No experimental reports on the elastic modulus of any other system with the ‘rho’ topology could be found, though curiously a calculated E_min value of 26 GPa for the pure siliceous zeolite-rho was amongst the lowest for different zeolite topologies, suggesting a link between the two. The predicted value for sodalite is intermediate with respect to other zeolites, as is the case with the value for 2 reported here.¹⁴

The fundamentals of the mechanical properties of porous frameworks are currently of great interest, with the role of non-chemical effects being debated. Specifically, framework anisotropy,^11,14 geometry,¹⁵ connectivity,⁶ and topology¹⁶ have been proposed to heavily influence the mechanical behaviour of both zeolites and MOFs.

Whilst the absolute differences in elastic moduli between MOFs and zeolites (ca. 2–10 GPa and 40–100 GPa respectively⁵) of the same topology can be ascribed to the difference in strength between metal–ligand bonding, the similar relative positions in their respective families of (i) zeolite-rho and 1 and (ii) sodalite and 2, appear to be consistent with arguments based on topology.

Recent theoretical work performed on the ZIF family has suggested that the presence of four membered rings within certain topologies makes them prone to shear-induced mechanical instabilities, and the lower E for 1 may be related to the greater number of four membered rings in its unit cell.¹⁷ Although complimentary high-pressure or Brillouin-scattering experiments, along with DFT calculations are warranted to state precisely why 1 has such a low elastic modulus, it is clear that we may expect systems with identical topologies to behave in broadly similar manners.

The effect of pore occupancy on the elastic modulus of 1 was investigated by soaking a sample in ethanol for 24 hours. Retention of structural integrity was confirmed by powder X-ray diffraction (Fig. S8‡). Values of 2.19 ± 0.1 GPa and 0.19 ± 0.02 GPa (E and H respectively) subsequently extracted from load–displacement data (Fig. S10‡) are consistent with reports of small increases in E of in other MOFs upon solvation.¹⁰

Guest occupancy was shown to have a larger increase on MOF stability against ball-milling, a post-processing technique which has been shown to cause structural collapse and associated destruction of porosity and long range ordering. This propensity for collapse has previously been ascribed to their low minimal shear moduli,¹² and has proven problematic during (i) attempts to prepare devices incorporating MOF frameworks and (ii) the post-processing of MOF-powders into useful forms.^18,19 Thus far, the only information that exists on the kinetics of MOF structural collapse is centered on the ZIF family.^20–22

Evacuated, ethanol- and butanol- (prepared by the same method of soaking, ESI‡) containing bulk samples of 1 were ball-milled for successive 5 minute intervals, with characterization by powder X-ray diffraction at each stage (Fig. S11, S12‡). Whilst irreversible amorphization of 1 was completed in under 10 minutes (indicated by a loss of Bragg diffraction from the X-ray patterns, Fig. S13, S14‡), the solvent-containing samples retained crystallinity for a further 15 minutes.

Motivated by a desire to provide a quantitative analysis of the speed of collapse, the integral breadth of the last remaining diffraction peak was monitored over the course of the milling process, in accordance with previous literature on the crystallinity of UiO frameworks under pressure.²³ Whilst complete disappearance of Bragg diffraction occurred at the same point with both ethanol and butanol containing samples, the latter displayed a slightly greater resistance to collapse (Fig. 4, ESI‡). Infrared spectroscopy performed on the amorphous sample of 1 (Fig. S17‡) suggests that the material retains some of the structural features of its crystalline precursor.

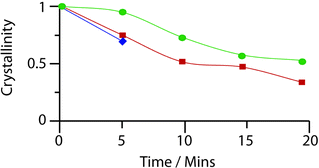Fig. 4 Evolution of the crystallinity of rho-ZMOF after milling for increasing amounts of time. Blue – evacuated, red – ethanol containing, green – butanol containing.

The presence of solvent has previously been shown to prevent pressure-induced structural collapse in silicalite SiO₂, through modification of low energy lattice vibrations which destabilize the crystalline structures.²⁴ Similarly, pressure-induced over-hydration (initial pore-filling by the hydrostatic media used) by solvent has been shown to decrease the compressibility of zeolites, depending on pore-occupancy and guest molecule size.^25,26 Compression of the Si–O bond length was found to be negligible in the latter case, though Si–O–Si angular distortions were evident.

Numerous MOF structures (termed 1st generation²⁷) collapse upon removal of templating, or guest ions, whilst others survive the removal of occluded species. Some enthalpic calculations have demonstrated that such molecules energetically stabilize these frameworks.²⁸ Guest occupation has also been observed to significantly alter the conditions of structural collapse of MOF-5 (modest ‘grinding’ pressure when evacuated²⁹ and 3.24 GPa when occupied with DMF³⁰), though the point of collapse under hydrostatic pressure is also dependent on molecular size of the pressure-transmitting fluid. Compression of the Zn–O bonding in the latter case was observed, which is consistent with its lower stability compared to the Si–O motifs in zeolites and silicates.

Ball-milling, or mechano-chemistry has been reported to induce structural collapse of zeolites, through breaking of ‘external’ M–O–M linkages.³¹ ZSM-5 was shown to be more resistant to collapse when ‘templating’ ions were present within the microporous structure. In this case, the framework Si/Al and O atoms were observed to approach those of the template molecule with the application of exterior mechanical forces, causing an increase in repulsion which countered, to some extent, the exterior pressure.³² However, no investigation of the necessity of the templating effect of the guest was made, and a study of non-templating guest-induced stabilization against ball-milling collapse of MOFs has not yet been attempted.

Prolongation of structural integrity here by any guest is particularly surprising given the presence of solvent is only slightly beneficial in raising the elastic modulus of 1. The stabilization of 1 by the introduction of solvent (either ethanol or butanol) is consistent with the above arguments in zeolites and MOFs. The identical mass lost for ethanol, and butanol containing samples of 1 at 300 °C (ca. 20%, Fig. S9‡), before framework decomposition, implies similar levels of guest present within the framework. The greater beneficial effect of butanol compared to ethanol may well then be attributed to its greater molecular size rather than amount present.

We therefore present evidence of the relationship between E and SAV across several topologically identical systems of different chemical functionality. Furthermore, we show that the ‘rho’ topology exhibits particularly low mechanical rigidity, (which is not fully explained by the trend), which leads to rho-ZMOF having an extremely low elastic modulus relative to other MOFs. In total, we assert that the topology of porous frameworks may play a bigger role in elastic response than previously thought. We also show that solvent addition plays a large role in preventing structural collapse against ball-milling. Further exploration of the network similarities between existing inorganic systems and MOFs will be of use in identifying mechanically interesting hybrid frameworks, and developing a targeted approach to frameworks with desirable physical properties, independent of chemical functionality.

Notes and references

1. R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Science, 2008, 319, 939–943.
2. F. Nouar, J. Eckert, J. F. Eubank, P. Forster and M. Eddaoudi, J. Am. Chem. Soc., 2009, 131, 2864–2870.
3. R. Ananthoji, J. F. Eubank, F. Nouar, H. Mouttaki, M. Eddaoudi and J. P. Harmon, J. Mater. Chem., 2011, 21, 9587–9594.
4. K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. D. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191.
5. J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080.
6. L. Sarkisov, R. L. Martin, M. Haranczyk and B. Smit, J. Am. Chem. Soc., 2014, 136, 2228–2231.
7. J. M. Ogborn, I. E. Collings, S. A. Moggach, A. L. Thompson and A. L. Goodwin, Chem. Sci., 2012, 3, 3011–3017.
8. T. D. Bennett and A. K. Cheetham, Acc. Chem. Res., 2014, 47, 1555–1562.
9. Y. L. Liu, V. C. Kravtsov, R. Larsen and M. Eddaoudi, Chem. Commun., 2006, 1488–1490.
10. J. C. Tan, T. D. Bennett and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9938–9943.
11. A. U. Ortiz, A. Boutin, A. H. Fuchs and F. X. Coudert, J. Chem. Phys., 2013, 138, 174703.
12. J. C. Tan, B. Civalleri, C. C. Lin, L. Valenzano, R. Galvelis, P. F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502.
13. T. D. Bennett, J. C. Tan, S. A. Moggach, R. Galvelis, C. Mellot-Draznieks, B. A. Reisner, A. Thirumurugan, D. R. Allan and A. K. Cheetham, Chem. – Eur. J., 2010, 16, 10684–10690.
14. F. X. Coudert, Phys. Chem. Chem. Phys., 2013, 15, 16012–16018.
15. I. E. Collings, M. G. Tucker, D. A. Keen and A. L. Goodwin, CrystEngComm, 2014, 16, 3498–3506.
16. C. Sanchez-Valle, S. V. Sinogeikin, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, K. E. Evans and J. D. Bass, J. Appl. Phys., 2005, 98, 053508.
17. J. C. Tan, B. Civalleri, A. Erba and E. Albanese, CrystEngComm, 2014 10.1039/C4CE01564A.
18. E. Proietti, F. Jaouen, M. Lefevre, N. Larouche, J. Tian, J. Herranz and J. P. Dodelet, Nat. Commun., 2011, 2, 416.
19. D. Bazer-Bachi, L. Assié, V. Lecocq, B. Harbuzaru and V. Falk, Powder Technol., 2014, 255, 52–59.
20. M. J. Cliffe, C. Mottillo, R. S. Stein, D. K. Bucar and T. Friscic, Chem. Sci., 2012, 3, 2495–2500.
21. C. Mottillo, Y. N. Lu, M. H. Pham, M. J. Cliffe, T. O. Do and T. Friscic, Green Chem., 2013, 15, 2121–2131.
22. T. Friscic, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimaki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66–73.
23. V. Guillerm, F. Ragon, M. Dan-Hardi, T. Devic, M. Vishnuvarthan, B. Campo, A. Vimont, G. Clet, Q. Yang, G. Maurin, G. Férey, A. Vittadini, S. Gross and C. Serre, Angew. Chem., Int. Ed., 2012, 51, 9267–9271.
24. J. Haines, O. Cambon, C. Levelut, M. Santoro, F. Gorelli and G. Garbarino, J. Am. Chem. Soc., 2010, 132, 8860–8861.
25. R. M. Hazen, Science, 1983, 219, 1065–1067.
26. J. A. Hriljac, Crystallogr. Rev., 2006, 12(2), 181–193.
27. S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
28. J. T. Hughes, T. D. Bennett, A. K. Cheetham and A. Nayrotsky, J. Am. Chem. Soc., 2013, 135, 598–601.
29. Y. H. Hu and L. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174103.
30. A. J. Graham, D. R. Allan, A. Muszkiewicz, C. A. Morrison and S. A. Moggach, Angew. Chem., Int. Ed., 2011, 50, 11138–11141.
31. C. Kosanovic, J. Bronic, B. Subotic, S. I. M. Stubicar, A. Tonejc and T. Yamamoto, Zeolites, 1993, 13, 261–268.
32. C. Kosanovic, A. Cizmek, B. Subotic, I. Smit, M. Stubicar and A. Tonejc, Zeolites, 1995, 15, 51–57.

---

Footnotes

† The authors thank Trinity Hall for funding (TDB) and Professor Anthony K. Cheetham (TDB) for use of lab facilities.

‡ Electronic supplementary information (ESI) available: Materials and methods, characterization, further nanoindentation data and profile fitting of rho-ZMOF with ball-milling. See DOI: 10.1039/c4ce02145b

---